Coupling-Independent Capacitive Wireless Power Transfer Using Frequency Bifurcation
Abstract
:1. Introduction
- optimize the efficiency of the system, e.g., for the wireless charging of high power applications as electric vehicles.
- optimize the power transfer to the load, e.g., charging transcutaneous biomedical implants.
- In a fixed frequency design, an impedance compensation network is added to realize optimum efficiency or power transfer at the operating frequency. The value of its components are independent of the coupling between transmitter and receiver, but for each different value of the coupling, another optimal load value applies. This approach has the advantage of realizing optimum efficiency or power transfer at a fixed operating frequency. However, at fluctuating coupling, the load value has to change to retain the optimal conditions.
- In a frequency agile design, optimum efficiency or power transfer can be achieved for a fixed load value, even at fluctuating coupling. With the same impedance compensation network as in the fixed frequency design, a constant efficiency or power transfer can be realized by changing the operating frequency, depending on the coupling between transmitter and receiver.
- determination of the power and transducer gain for a general CPT system;
- analytical calculation of the bifurcation conditions and frequencies, necessary to determine the optimal operating frequency;
- analytical computation of the optimal solution for achieving a practically coupling-independent CPT link;
- illustration of the similarities to IPT.
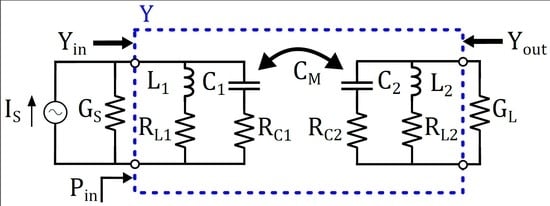
2. Methodology
- The power gain , defined as the ratio between the power dissipated by the load and the input power of the network. This definition corresponds with the efficiency definition often applied in the context of WPT [32]. Maximizing corresponds with maximizing the efficiency of the system.
- The transducer gain is defined as the ratio between the power dissipated by the load and the maximum available power of the generator. For a fixed , maximizing corresponds to maximizing the amount of power transferred to the load.
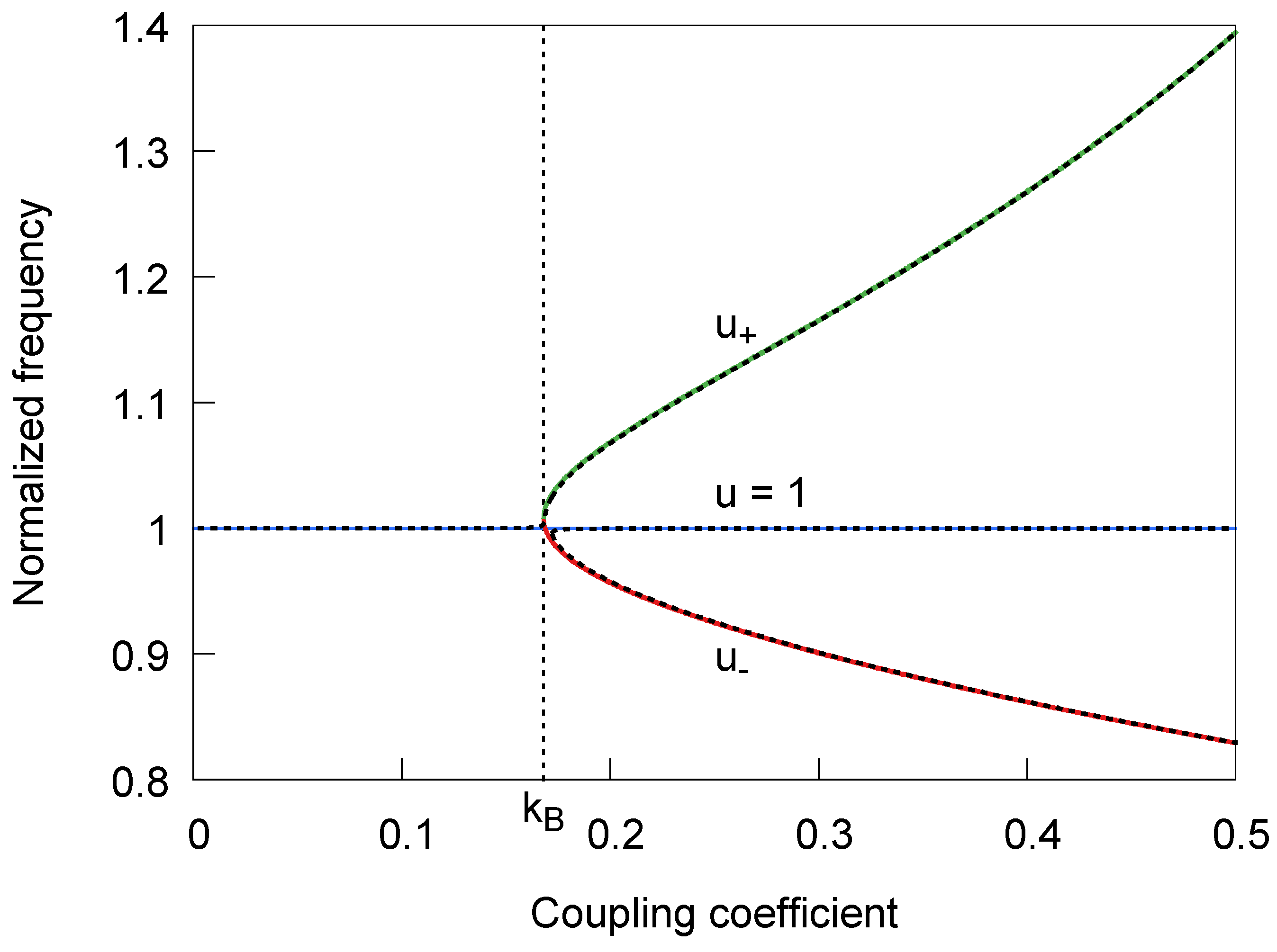
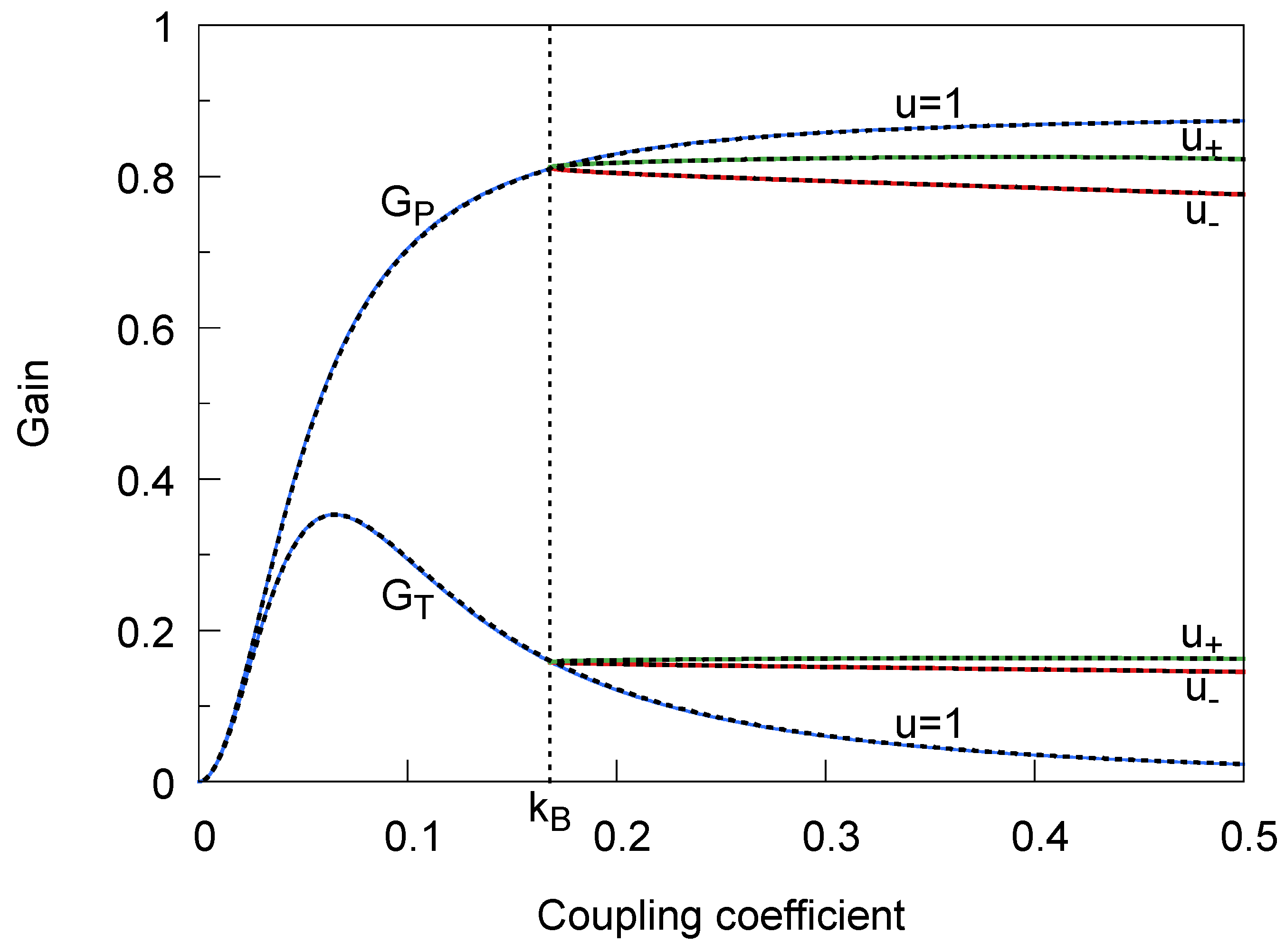
3. Discussion
4. Comparison to IPT
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Power Gain Expressions for a Two-Port as Function of the Admittance Parameters
Appendix A.1. Equivalent Circuit
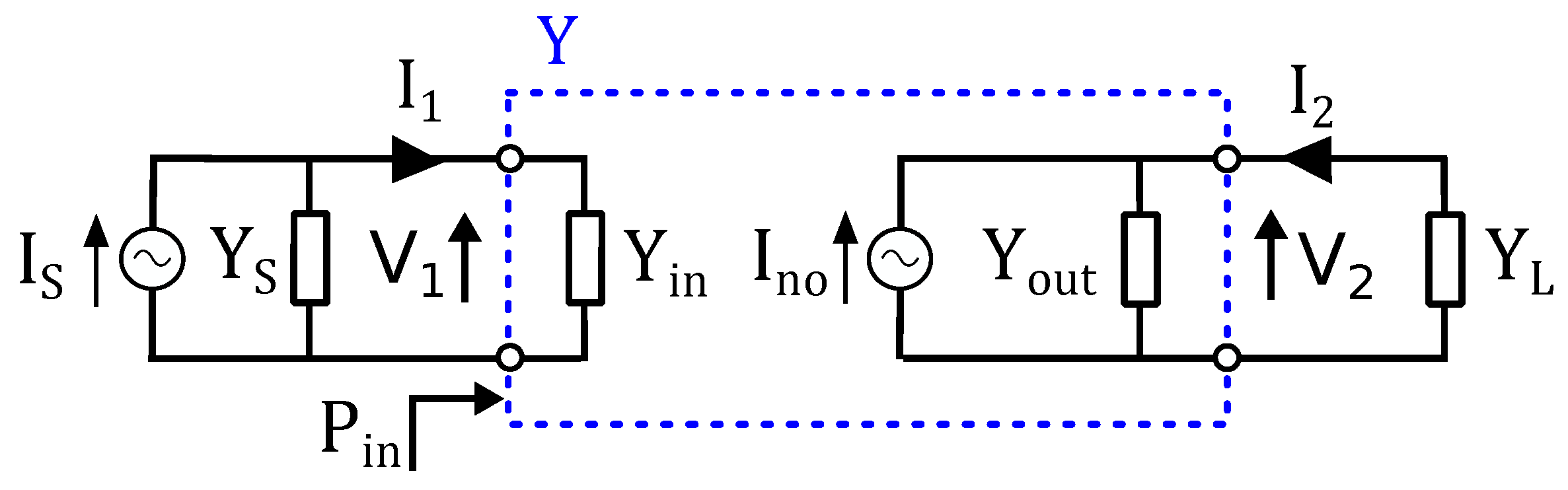
Appendix A.2. Power Gain
Appendix A.3. Transducer Gain
References
- Jawad, A.M.; Nordin, R.; Gharghan, S.K.; Jawad, H.M.; Ismail, M. Opportunities and challenges for near-field wireless power transfer: A review. Energies 2017, 10, 1022. [Google Scholar] [CrossRef]
- Barman, S.D.; Reza, A.W.; Kumar, N.; Karim, M.E.; Munir, A.B. Wireless powering by magnetic resonant coupling: Recent trends in wireless power transfer system and its applications. Renew. Sustain. Energy Rev. 2015, 51, 1525–1552. [Google Scholar] [CrossRef]
- Lu, X.; Wang, P.; Niyato, D.; Kim, D.I.; Han, Z. Wireless charging technologies: Fundamentals, standards, and network applications. IEEE Commun. Surv. Tutor. 2016, 18, 1413–1452. [Google Scholar] [CrossRef]
- Mou, X.; Sun, H. Wireless power transfer: Survey and roadmap. In Proceedings of the 2015 IEEE 81st Vehicular Technology Conference (VTC Spring), Glasgow, UK, 11–14 May 2015; pp. 1–5. [Google Scholar]
- Das, R.; Yoo, H. Wireless power transfer to a pacemaker by using metamaterials and yagi-uda antenna concept. In Proceedings of the 2015 International Workshop on Antenna Technology (iWAT), Seoul, Korea, 4–6 March 2015; pp. 353–354. [Google Scholar]
- Kim, S. Wireless powering of miniaturized neurostimulator. In Proceedings of the 2017 IEEE International Symposium on Radio-Frequency Integration Technology (RFIT), Seoul, Korea, 30 August–1 September 2017; pp. 96–98. [Google Scholar]
- Xu, Q.; Hu, D.; Duan, B.; He, J. A fully implantable stimulator with wireless power and data transmission for experimental investigation of epidural spinal cord stimulation. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 683–692. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhu, C.; Chan, C. A wireless power charging method for automated guided vehicle. In Proceedings of the 2014 IEEE International Electric Vehicle Conference (IEVC), Florence, Italy, 17–19 December 2014; pp. 1–5. [Google Scholar]
- Kawamura, A.; Ishioka, K.; Hirai, J. Wireless transmission of power and information through one high-frequency resonant AC link inverter for robot manipulator applications. IEEE Trans. Ind. Appl. 1996, 32, 503–508. [Google Scholar] [CrossRef]
- Cheng, Z.; Lei, Y.; Song, K.; Zhu, C. Design and loss analysis of loosely coupled transformer for an underwater high-power inductive power transfer system. IEEE Trans. Magn. 2015, 51, 1–10. [Google Scholar]
- Covic, G.A.; Boys, J.T. Modern trends in inductive power transfer for transportation applications. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 28–41. [Google Scholar] [CrossRef]
- Wu, H.H.; Gilchrist, A.; Sealy, K.; Bronson, D. A 90 percent efficient 5kW inductive charger for EVs. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 275–282. [Google Scholar]
- Shin, J.; Shin, S.; Kim, Y.; Ahn, S.; Lee, S.; Jung, G.; Jeon, S.J.; Cho, D.H. Design and implementation of shaped magnetic-resonance-based wireless power transfer system for roadway-powered moving electric vehicles. IEEE Trans. Ind. Electron. 2014, 61, 1179–1192. [Google Scholar] [CrossRef]
- Choi, S.Y.; Gu, B.W.; Jeong, S.Y.; Rim, C.T. Advances in wireless power transfer systems for roadway-powered electric vehicles. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 18–36. [Google Scholar] [CrossRef]
- Vamvakas, P.; Tsiropoulou, E.E.; Vomvas, M.; Papavassiliou, S. Adaptive power management in wireless powered communication networks: A user-centric approach. In Proceedings of the 2017 IEEE 38th Sarnoff Symposium, Newark, NJ, USA, 18–20 September 2017; pp. 1–6. [Google Scholar]
- Xie, L.; Shi, Y.; Hou, Y.T.; Sherali, H.D. Making sensor networks immortal: An energy-renewal approach with wireless power transfer. IEEE/ACM Trans. Netw. 2012, 20, 1748–1761. [Google Scholar] [CrossRef]
- Tsiropoulou, E.E.; Mitsis, G.; Papavassiliou, S. Interest-aware energy collection & resource management in machine to machine communications. Ad Hoc Netw. 2018, 68, 48–57. [Google Scholar]
- Ng, D.W.K.; Schober, R. Energy-efficient power allocation for M2M communications with energy harvesting transmitter. In Proceedings of the 2012 IEEE Globecom Workshops (GC Wkshps), Anaheim, CA, USA, 3–7 December 2012; pp. 1644–1649. [Google Scholar]
- Kim, J.; Yang, S.Y.; Song, K.D.; Jones, S.; Elliott, J.R.; Choi, S.H. Microwave power transmission using a flexible rectenna for microwave-powered aerial vehicles. Smart Mater. Struct. 2006, 15, 1243. [Google Scholar] [CrossRef]
- Minnaert, B.; Thoen, B.; Plets, D.; Joseph, W.; Stevens, N. Wireless energy transfer by means of inductive coupling for dairy cow health monitoring. Comput. Electron. Agric. 2018, 152, 101–108. [Google Scholar] [CrossRef]
- Kim, T.H.; Yun, G.H.; Lee, W.Y.; Yook, J.G. Asymmetric Coil Structures for Highly Efficient Wireless Power Transfer Systems. IEEE Trans. Microw. Theory Tech. 2018, 66. [Google Scholar] [CrossRef]
- Lu, F.; Zhang, H.; Mi, C. A Review on the Recent Development of Capacitive Wireless Power Transfer Technology. Energies 2017, 10, 1752. [Google Scholar] [CrossRef]
- Kim, T.H.; Yoon, S.; Yook, J.G.; Yun, G.H.; Lee, W.Y. Evaluation of power transfer efficiency with ferrite sheets in WPT system. In Proceedings of the 2017 IEEE Wireless Power Transfer Conference (WPTC), Taipei, Taiwan, 10–12 May 2017; pp. 1–4. [Google Scholar]
- Minnaert, B.; Stevens, N. Conjugate Image Theory Applied on Capacitive Wireless Power Transfer. Energies 2017, 10, 46. [Google Scholar] [CrossRef]
- Minnaert, B.; Stevens, N. Single variable expressions for the efficiency of a reciprocal power transfer system. Int. J. Circ. Theory Appl. 2017, 45, 1418–1430. [Google Scholar] [CrossRef]
- Halpern, M.E.; Ng, D.C. Optimal tuning of inductive wireless power links: Limits of performance. IEEE Trans. Circ. Syst. 2015, 62, 725–732. [Google Scholar] [CrossRef]
- Costanzo, A.; Dionigi, M.; Mastri, F.; Mongiardo, M.; Monti, G.; Russer, J.A.; Russer, P. The basic cell operating regimes for wireless power transfer of electric vehicles. In Proceedings of the 2016 IEEE Wireless Power Transfer Conference, Aveiro, Portugal, 5–6 May 2016; pp. 1–4. [Google Scholar]
- Mastri, F.; Costanzo, A.; Mongiardo, M. Coupling-independent wireless power transfer. IEEE Microw. Wirel. Compon. Lett. 2016, 26, 222–224. [Google Scholar] [CrossRef]
- Zhang, W.; Wong, S.C.; Chi, K.T.; Chen, Q. Analysis and comparison of secondary series- and parallel-compensated inductive power transfer systems operating for optimal efficiency and load-independent voltage-transfer ratio. IEEE Trans. Power Electron. 2014, 29, 2979–2990. [Google Scholar] [CrossRef]
- Huang, L.; Hu, A.P. Defining the mutual coupling of capacitive power transfer for wireless power transfer. Electron. Lett. 2015, 51, 1806–1807. [Google Scholar] [CrossRef]
- Mastri, F.; Mongiardo, M.; Monti, G.; Dionigi, M.; Tarricone, L. Gain expressions for resonant inductive wireless power transfer links with one relay element. In Wireless Power Transfer; River Publishers: PW Delft, The Netherlands, 2017; pp. 1–15. [Google Scholar]
- Kiani, M.; Jow, U.M.; Ghovanloo, M. Design and optimization of a 3-coil inductive link for efficient wireless power transmission. IEEE Trans. Biomed. Circ. Syst. 2011, 5, 579–591. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, C.G.; Dicke, R.H.; Purcell, E.M. Principles of Microwave Circuits; Short Run Press Ltd.: British Exeter, UK, 1948. [Google Scholar]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minnaert, B.; Mastri, F.; Stevens, N.; Costanzo, A.; Mongiardo, M. Coupling-Independent Capacitive Wireless Power Transfer Using Frequency Bifurcation. Energies 2018, 11, 1912. https://doi.org/10.3390/en11071912
Minnaert B, Mastri F, Stevens N, Costanzo A, Mongiardo M. Coupling-Independent Capacitive Wireless Power Transfer Using Frequency Bifurcation. Energies. 2018; 11(7):1912. https://doi.org/10.3390/en11071912
Chicago/Turabian StyleMinnaert, Ben, Franco Mastri, Nobby Stevens, Alessandra Costanzo, and Mauro Mongiardo. 2018. "Coupling-Independent Capacitive Wireless Power Transfer Using Frequency Bifurcation" Energies 11, no. 7: 1912. https://doi.org/10.3390/en11071912
APA StyleMinnaert, B., Mastri, F., Stevens, N., Costanzo, A., & Mongiardo, M. (2018). Coupling-Independent Capacitive Wireless Power Transfer Using Frequency Bifurcation. Energies, 11(7), 1912. https://doi.org/10.3390/en11071912