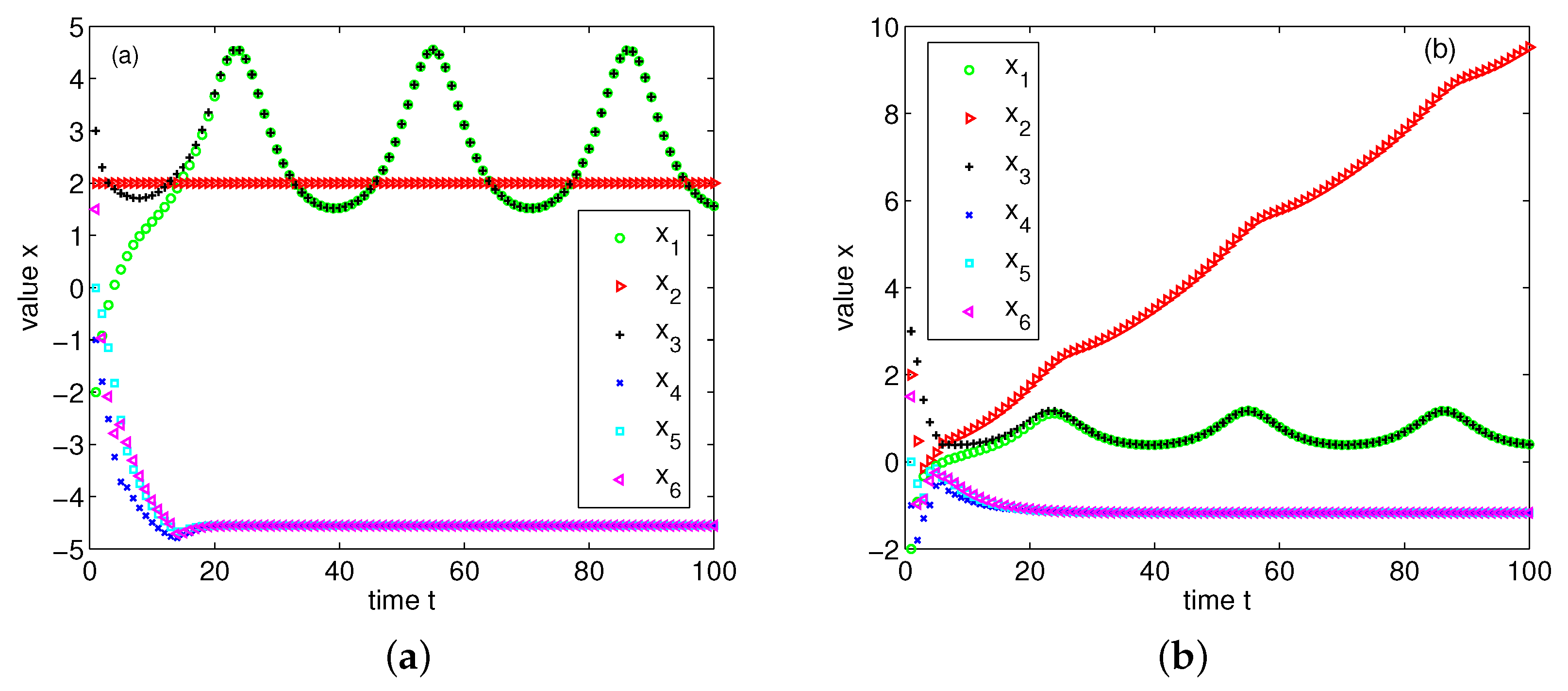
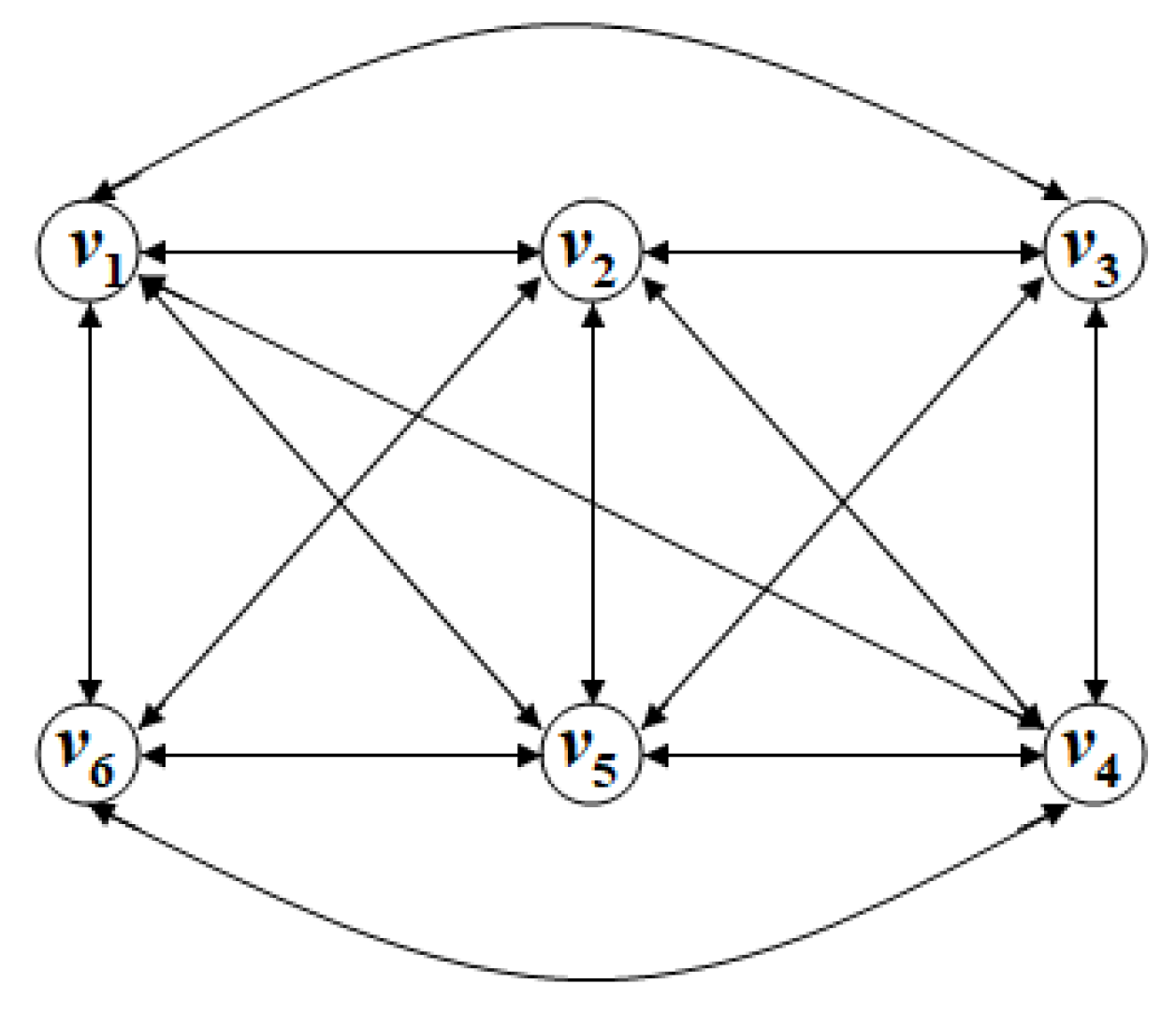
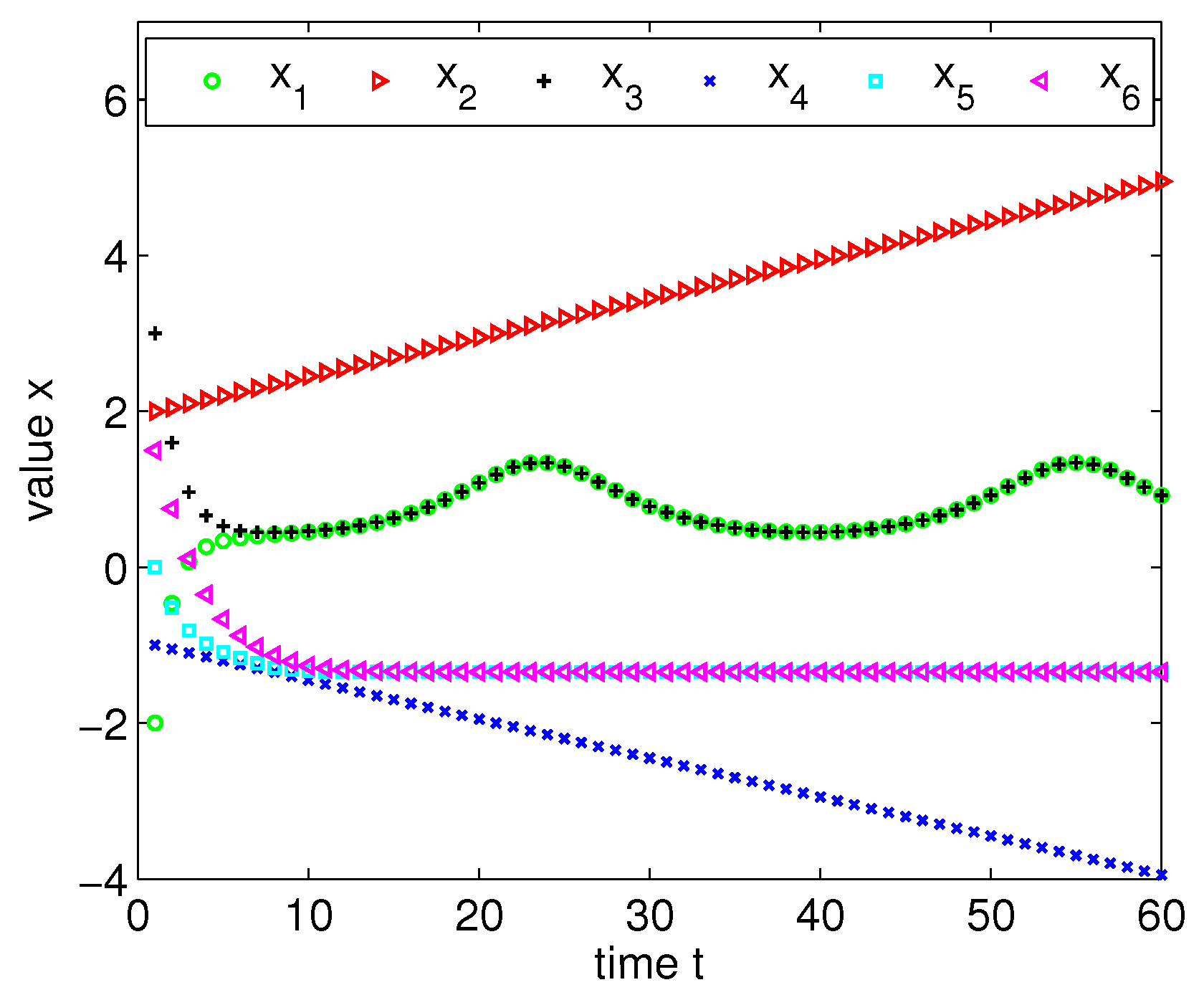
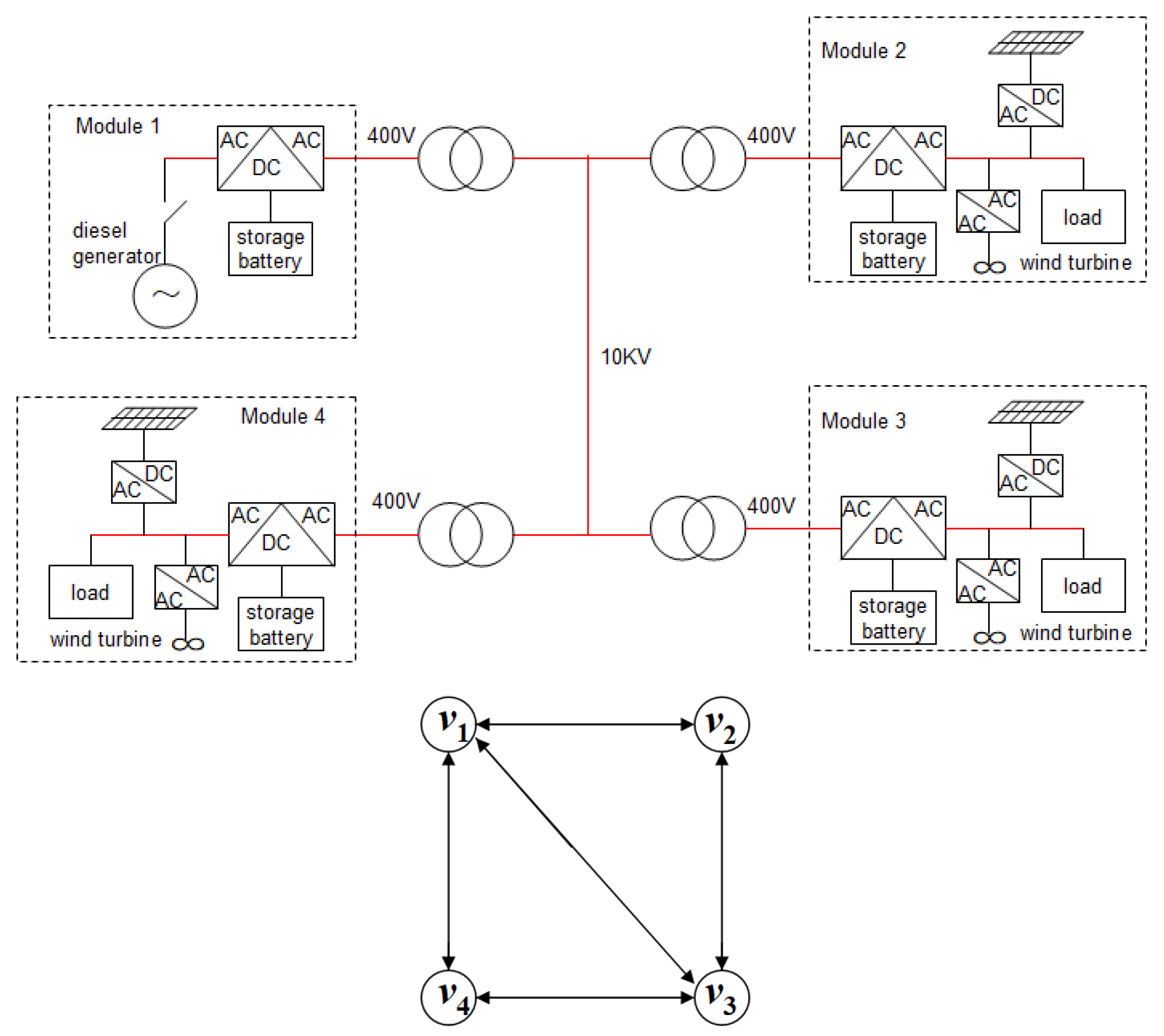
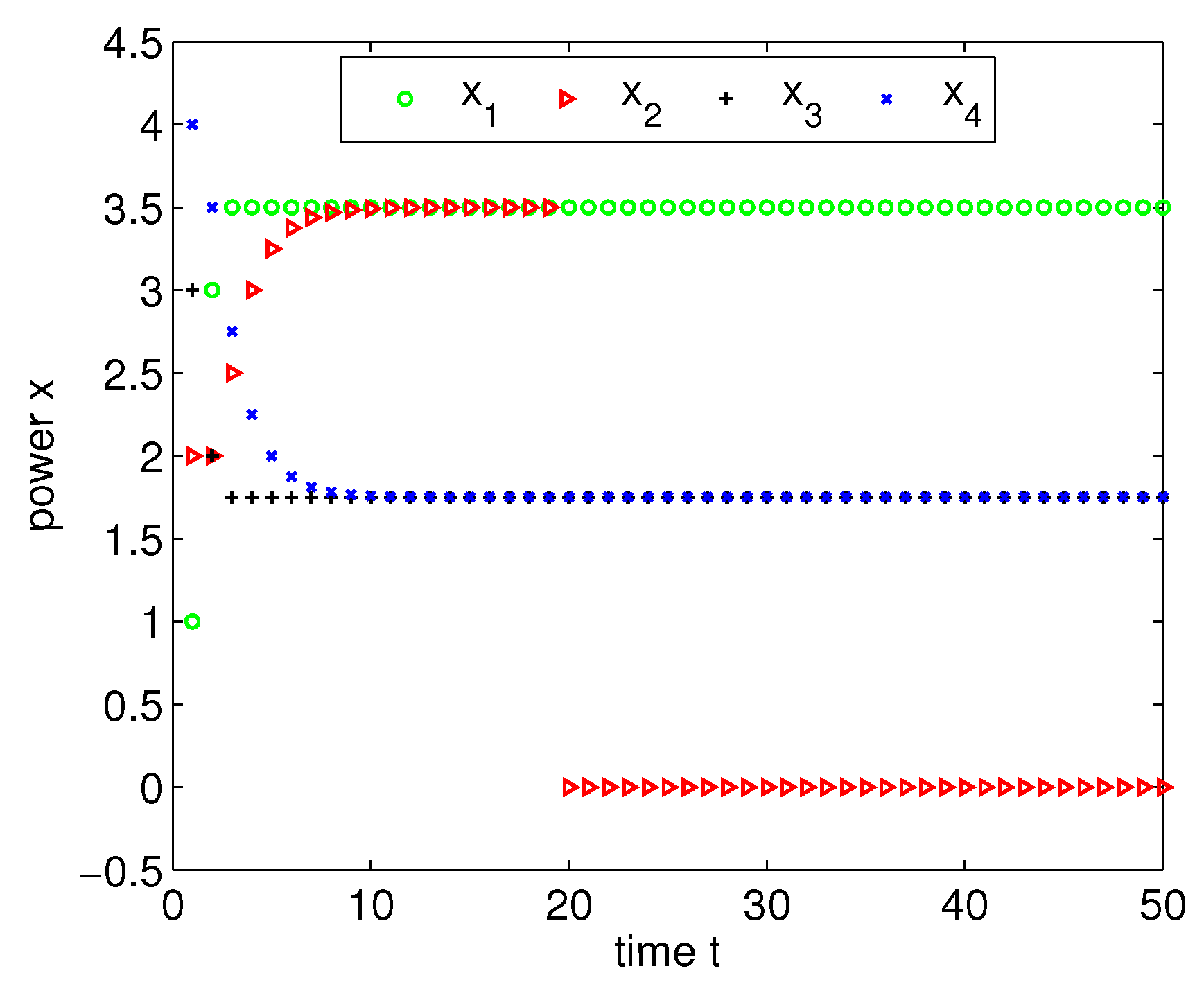
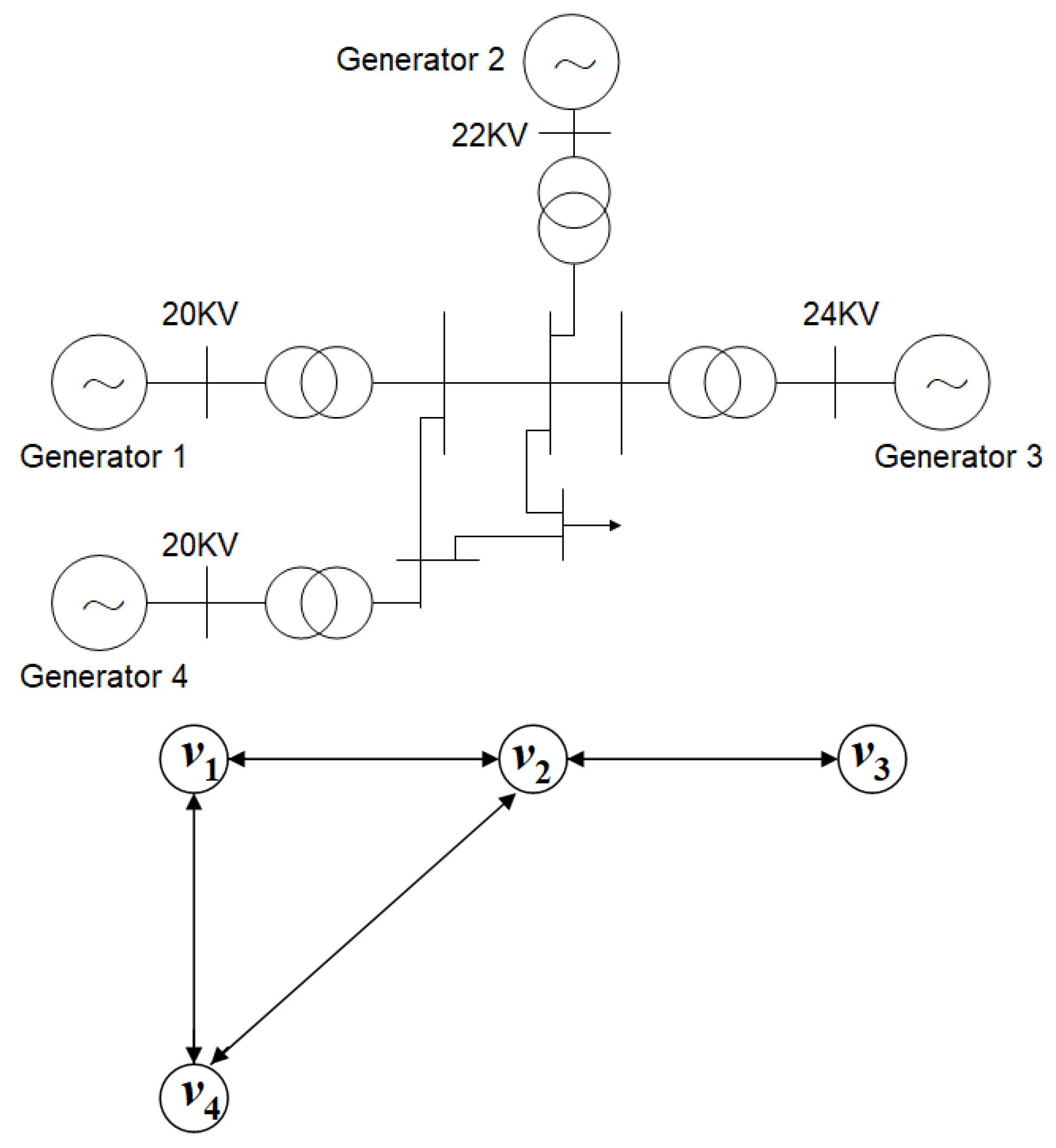
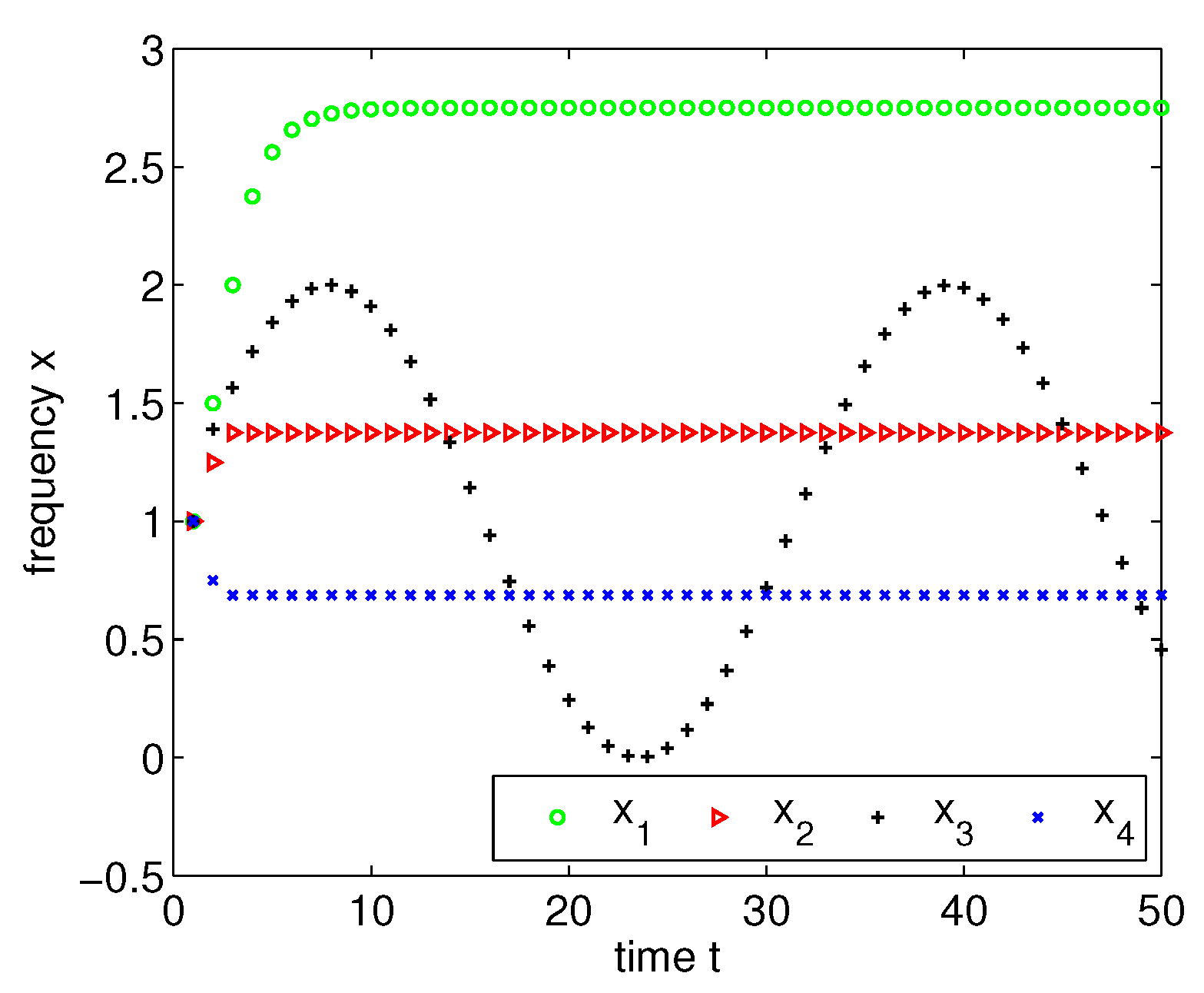
3.1. Multiscale Coordination in the Presence of Faulty Nodes
In the following, we establish some necessary and sufficient conditions for multiscale coordination in the globally/locally bounded model with faulty nodes. We consider time-invariant networks first, and then extend the results to time-dependent networks. The proofs are based on the techniques in [
19].
Theorem 1 (consensus in globally bounded model with faulty nodes). Consider a time-invariant network characterized by a digraph , where every cooperative node updates its value according to the multiscale filtering strategy with parameter . Therefore, in the -globally bound model having faulty nodes, multiscale consensus is reached if and only if is -robust.
Proof. (Necessity) Assume that is not an -robust graph. Thus, there are disjoint nonempty sets such that none of the statements (i)–(iii) in Definition 2 hold. Fix . Let for any node , and for any node . For , set for some fixed . Since , suppose that all nodes in and are faulty nodes and that they keep their values unchanged. Since there is at least one cooperative node in both and (because and ), the scaled values of such cooperative nodes cannot reach consensus by using the multiscale filtering strategy with parameter . Therefore, multiscale consensus can not be achieved.
(Sufficiency) From the comments in the beginning of this section, we may assume that . If , multiscale consensus is then reached. In what follows, we assume that and will show that it does not hold by using contradiction.
Choose satisfying . For and , we define two sets and . By the definition of , and are disjoint. Fix and . Let be the time step satisfying and for all .
Recall that
and
are nonempty disjoint sets. Noting that
is
-robust with at most
faulty nodes, there must be a cooperative node in their union which contains more than or a number equal to
neighbors outside of its set. We suppose, without loss of generality, that
has more than or equal to
neighbors outside of
. Since these neighbors’ values are at most equal to
and at least one of these values will be used by
, we obtain
where we have used the inequality
, and the fact that each cooperative node’s value is a convex combination of its own value and the values of its neighbors with coefficients larger than or equal to
and that the largest value
will use at time
no more than
according to the multiscale filtering strategy with parameter
. The expression (
4) also applies to the updated value of any cooperative node outside
since such a node will adopt its own value (which is also less than or equal to
) in the update process. Likewise, if
, which has more than or a number equal to
neighbors outside of
, we derive a similar inequality
which also applies to the cooperative nodes outside
.
Now, define and let . Notice that the sets and are disjoint. The discussion in the above paragraph implies that or holds. We can recursively define for each and note that . The above comments can be applied to every time step provided there still exist cooperative nodes in and . Since there are cooperative nodes in the entire graph, there is some such that either or is empty. However, as per the choice of . This means that every cooperative node at time has a value of no more than or has a value of at least . This contradicts the definition of or . The result then follows. ☐
For time-dependent networks, we show the following corollary.
Corollary 1. Consider a time-varying network characterized by a digraph , where every cooperative node updates its value according to the multiscale filtering strategy with parameter . Denote by the time steps in which is -robust. Therefore, in the -globally bound model with faulty nodes, multiscale consensus is reached if and there is a constant c such that for all k.
Proof. We proceed similarly as in Theorem 1. We now set and . Define to be the time step satisfying and for all . By assumption, there is such that is -robust. Let and . Reasoning as in the proof of Theorem 1, we see that or holds.
We can recursively define for . Similarly as in Theorem 1, we can prove that every cooperative node satisfying will satisfy for each . In the same manner, every cooperative node satisfying will satisfy for each . Therefore, we have or for every irrespective of the graph structure. By assumption, there exists an infinite sequence of where is -robust, both and are non-empty, and either or , or both, holds for . As there exist cooperative nodes in the entire graph and , there is some such that either or is empty. Recalling the definition of , we obtain . This gives rise to a contradiction similarly as in the proof of Theorem 1. ☐
Next, we extend the above results to solve resilient formation generation problems for multi-agent systems in the presence of adversarial nodes. In standard formation generation problems, the aim is to design distributed protocols to guarantee that each pair of neighboring agents reach a desired relative position with respect to each other [
3,
4,
28]. A certain pattern is thus formed by the agents as a whole. In the context of resilient multiscale coordination, we introduce the multiscale formation generation as follows.
Definition 5 (multiscale formation generation). Let . The agents in are said to achieve the multiscale formation g with respect to if for all and all initial conditions .
It is easy to see that the agents reach the multiscale formation
g if there exists a vector
such that for
,
tends to
as time goes to infinity. To this end, we design the following formation generation rule for each
:
where the weights
satisfy the same conditions in
Section 2.3. In the formation control problem, we will modify the three-step multiscale filtering strategy with parameter
introduced in
Section 2.3 in three places: first, the sorted list is created for
instead of
. Second, the largest
values that are strictly greater than
instead of
in the list are deleted. The same modification applies to the smaller values. Third, the update rule (
2) is replaced by (
6). We shall refer to this modified algorithm as the multiscale filtering-formation strategy with parameter
R.
Corollary 2 (formation generation in globally bounded model with faulty nodes). Consider a time-invariant graph characterized by a digraph , where every cooperative node updates its value according to the multiscale filtering-formation strategy with parameter . Therefore, in the -globally bounded model having faulty nodes, multiscale formation g is reached if and only if is -robust.
For a time-dependent network , let be the time steps where is -robust. Therefore, in the -globally bounded model having faulty nodes, multiscale formation g is reached if and there is a constant c satisfying for every k.
Proof. Let
and
for
. Then, the update rule (
6) becomes
for
.
For time-invariant network topology, it follows from Theorem 1 that is -robust if and only if multiscale consensus is achieved for , which in turn is equivalent to having a vector such that . The result then follows. In the case of time-varying topology, a similar argument applies by virtue of Corollary 1. ☐
For locally bounded models, where adversarial nodes are much more popular but the number of them are still bounded in every cooperative node’s neighborhood, we propose to characterize the network structure that is ideal for coping with fault nodes as follows.
Theorem 2 (consensus in locally bounded model with faulty nodes). Consider a time-invariant network characterized by a digraph , in which every cooperative node updates its value following the multiscale filtering strategy with parameter . Therefore, in the -locally bound model having faulty nodes, multiscale consensus is achieved if is -robust. Moreover, is -robust if multiscale consensus in the -locally bound model with faulty nodes is achieved.
Proof. (Necessity) Assume that is not -robust. Therefore, there exist disjoint nonempty sets such that every node in these two sets will have at most neighbors outside the set. Suppose that there exist cooperative nodes in both and . Fix . Let for any node , and for any node . For , set for some fixed . Clearly, the scaled values of nodes in and will not achieve consensus under the multiscale filtering strategy with parameter because they will not adopt any values from outside their own sets. Thus, multiscale consensus can not be reached.
(Sufficiency) We proceed similarly as in Theorem 1. Suppose that and . In what follows, we will prove by contradiction. For this purpose, assume that . Choose so that . For and , we consider two sets given by and . By the definition of , and are disjoint. Set and . Define to be the time step satisfying and for any .
Recall that the two sets and are nonempty and disjoint. Since is -robust, one of these two sets must be -reachable if not both. We suppose, without loss of generality, that is -reachable, and hence there exists a node which has no less than neighboring nodes outside its set. Because there exist no more than faulty nodes in , will adopt no less than one of its cooperative neighbors’ values outside under the multiscale filtering strategy with parameter . Consequently, proceeding as in the proof of Theorem 1, we derive . This also holds true for the renewed value of every cooperative node outside as such a node will adopt its own value in the renewal procedure. Analogously, if has more than or equal to neighbors outside its set, we have a similar bound , which also applies to the cooperative nodes outside . Now by defining which satisfies , we can use the same proof in Theorem 1, by setting recursively , for to produce the contradiction. We then proved the sufficiency part. ☐
Note that there is a gap between the sufficient condition and the necessary condition in Theorem 2. In fact, the example mentioned in ([
19], Figure 4) can also be used to show that the sufficient condition here is sharp. In the case of time-dependent networks, we show the following result, which more or less can be shown in the same way as Corollary 1.
Corollary 3. Given a time-dependent network characterized by a digraph , where every cooperative node updates its value following the multiscale filtering strategy with parameter . Let be the time steps where is -robust. Therefore, in the -locally bounded model having faulty nodes, multiscale consensus is reached if and there is a constant c satisfying for every k.
In parallel with Corollary 2, we have the following result for resilient multiscale formation generation under the locally bounded model.
Corollary 4 (formation generation in locally bounded model with faulty nodes). Consider a time-invariant network characterized by a digraph , where every cooperative node updates its value following the multiscale filtering-formation strategy with parameter . Therefore, in the -locally bounded model containing faulty nodes, multiscale formation g is achieved if is -robust. Moreover, is -robust if multiscale formation g in the -locally bounded model with faulty nodes is achieved.
For time-dependent network , let be the time steps where is -robust. Therefore, in the -locally bounded model having faulty nodes, multiscale formation g is reached if and there is a constant c satisfying for any k.
3.2. Multiscale Coordination in the Presence of Byzantine Nodes
In this subsection, we establish necessary and sufficient conditions for multiscale coordination in the globally and locally bounded model in the presence of Byzantine nodes. Recall that Byzantine nodes are able to forward different information to different neighbors at any time step, and thus they are harder to deal with. Define to be the subnetwork of induced by , where is made up of all directed edges among the cooperative nodes at time step t. Time-invariant network structure will be investigated first.
Theorem 3 (consensus in globally bounded model with Byzantine nodes). Consider a time-invariant network characterized by a digraph , in which every cooperative node updates its value following the multiscale filtering strategy with parameter . Therefore, in the -globally bounded model having Byzantine nodes, multiscale consensus is reached if and only if is -robust.
Proof. (Necessity) Suppose that is not -robust. Therefore, there exist two nonempty and disjoint sets which are not reachable. Thereby, every node in these two sets has no more than cooperative neighbors outside the set. Fix . Let for any node , and for any node . For , set for some fixed . Suppose that all Byzantine nodes always send the value to every node in , and the value to every node in at every time step t. Therefore, utilizing the multiscale filtering strategy having parameter , nodes in and will not adopt values from outside their own sets. Thus, multiscale consensus can not be reached.
(Sufficiency) Similarly, we suppose that and . Assume that . Choose satisfying . For and , we define two sets and . As per the definition of , and are disjoint. Fix which satisfies . Define as the time step satisfying and for every time step .
Recall that and are nonempty and disjoint. As is -robust with at most Byzantine nodes, there exists a node in or that has more than or equal to cooperative neighboring nodes outside of its set. Without loss of generality, we assume that has more than or equal to cooperative neighboring nodes outside of . With the same argument as in Theorem 1, we derive the inequality . This expression also holds true for the renewed value of every cooperative node outside . Likewise, if which has more than or equal to cooperative neighbors outside of , we have similarly , which also applies to the cooperative nodes outside .
Define , satisfying . Notice that the sets and are disjoint. The discussion in the above paragraph implies that or holds. We can recursively define for every and note that . The aforementioned discussion is applicable to every time step provided and are non-empty. Since contains cooperative nodes, there is some satisfying either or is in fact empty. On the other hand, according to the choice of . This implies that every cooperative node at time has a value of no more than or have values no less than . This contradicts the definition of or . We proved the sufficiency part. ☐
In the case of time-dependent networks, the following result can be established.
Corollary 5. Consider a time-dependent network characterized by a digraph , where every cooperative node updates its value following the multiscale filtering strategy with parameter . Let be the time steps where is -robust. Therefore, in the -globally bounded model having Byzantine nodes, multiscale consensus is reached if and there is a constant c satisfying for any k.
Proof. If becomes -robust, must be robust. It is due to the fact that there exist no more than Byzantine nodes in the whole network. In view of Theorem 3, we may conclude the proof by resorting to a similar argument as that in Corollary 1. ☐
The following result is given for resilient multiscale formation generation under the globally bounded model.
Corollary 6 (formation generation in globally bounded model with Byzantine nodes). Consider a time-invariant network characterized by a digraph , in which every cooperative node updates its value following the multiscale filtering-formation strategy with parameter . Therefore, in the -globally bounded model containing Byzantine nodes, multiscale formation g is achieved if and only if is -robust.
For a time-dependent network , let signify the time steps where is -robust. Therefore, in the -globally bounded model having Byzantine nodes, multiscale formation g is reached if and there exists a constant c satisfying for all k.
Now we move to locally bounded models having Byzantine nodes distributed over a time-invariant graph structure.
Theorem 4 (consensus in locally bounded model with Byzantine nodes). Consider a time-invariant network characterized by a digraph , where every cooperative node updates its value following the multiscale filtering strategy with parameter . Therefore, in the -locally bounded model containing Byzantine nodes, multiscale consensus is reached if and only if is -robust.
Proof. (Necessity) The same proof in Theorem 3 gives the necessity.
(Sufficiency) Proceeding similarly as in Theorem 3, we suppose that and . Assume that . Choose satisfying . For and , we signify two sets and . By the definition of , and turn out to be disjoint. Fix satisfying . Let be the time step satisfying and for any time step .
Recall that the sets and are both nonempty and disjoint. As is -robust, there must be a node in or that has more than or an equal number of cooperative neighboring nodes outside of its set. We suppose, without loss of generality, that has more than or equal to cooperative neighbors outside of . Since there are no more than Byzantine nodes in , will adopt at least one of its cooperative neighbors’ values outside under the multiscale filtering strategy with parameter . Based upon the same argument as in Theorem 1, we derive the estimation . This also holds true for the renewed value of every cooperative node outside . Analogously, if which has more than or an equal number of cooperative neighbors outside of , we have , which also applies to the cooperative nodes outside .
Define , satisfying . The same reasoning in the proof of Theorem 3 (by recursively defining for ) gives rise to the desired contradiction. We then proved the sufficiency part. ☐
For time-dependent networks, the following result can be established. The proof is similar to that of Corollary 5.
Corollary 7. Consider a time-dependent network characterized by a digraph , in which every cooperative node updates its value following the multiscale filtering strategy with parameter . Let be the time steps where is -robust. Therefore, in the -locally bounded model containing Byzantine nodes, multiscale consensus is reached if and there is a constant c satisfying for any k.
As an immediate consequence of Theorem 4 and Corollary 7, resilient multiscale formation generation in the locally bounded model containing Byzantine nodes is characterized in the following.
Corollary 8 (formation generation in locally bounded model with Byzantine nodes). Consider a time-invariant network characterized by a digraph , in which every cooperative node updates its value following the multiscale filtering-formation strategy with parameter . Therefore, in the -locally bounded model with Byzantine nodes, multiscale formation g is reached if and only if is -robust.
For a time-dependent network , let be the time steps where is -robust. Therefore, in the -locally bounded model having Byzantine nodes, multiscale formation g is reached if and there exists a constant c satisfying for each k.