Design and Line Fault Protection Scheme of a DC Microgrid Based on Battery Energy Storage System
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Contribution
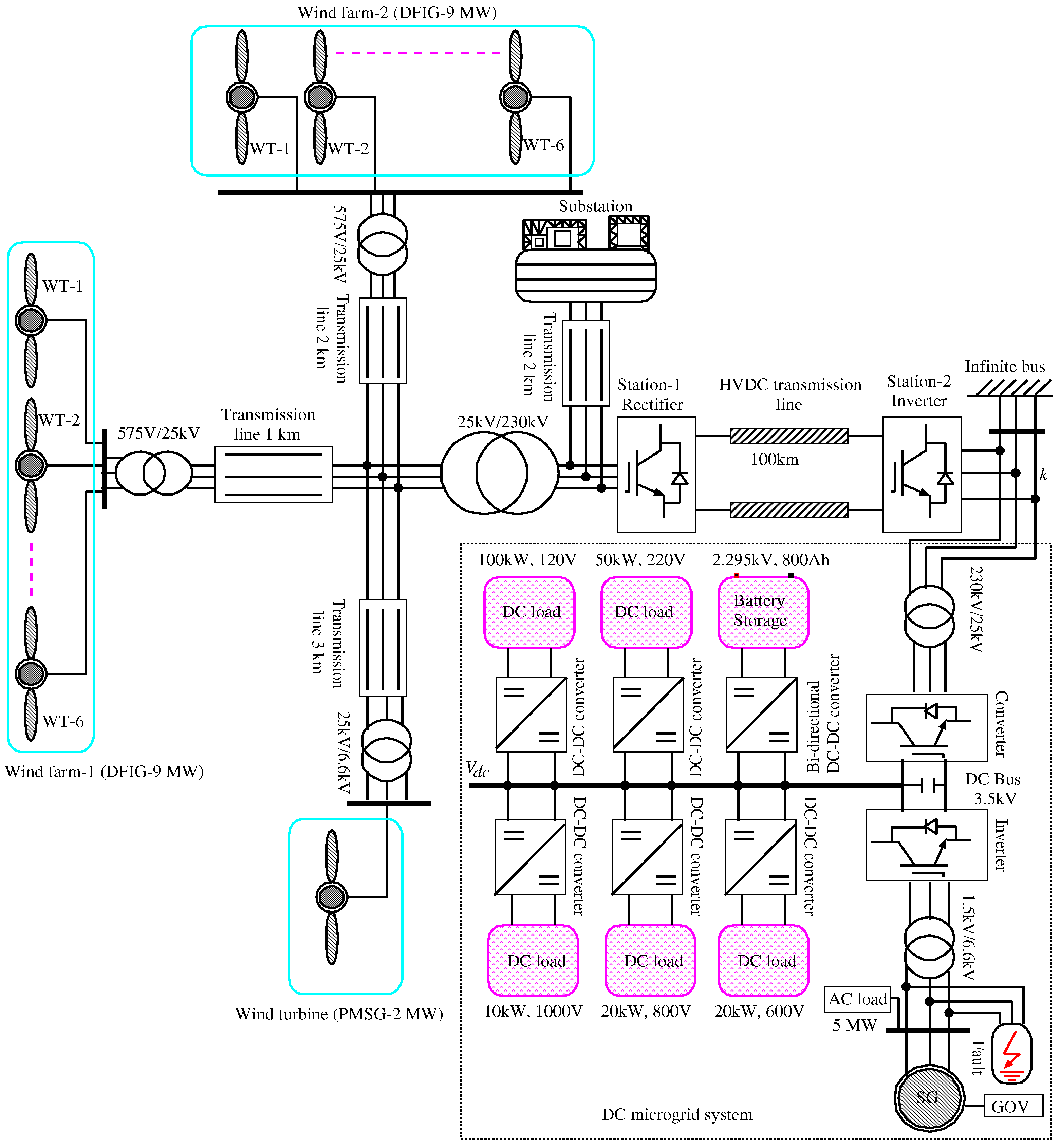
2. System Configuration
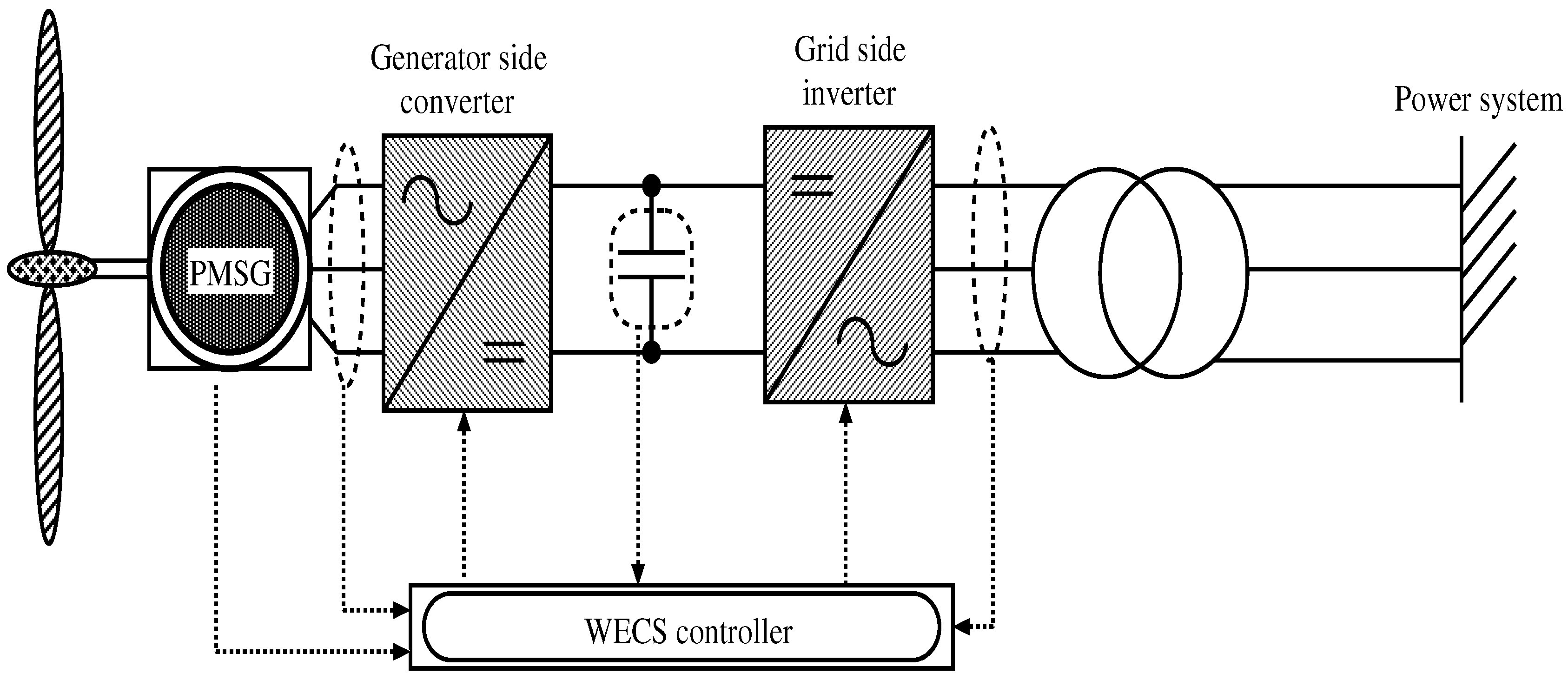
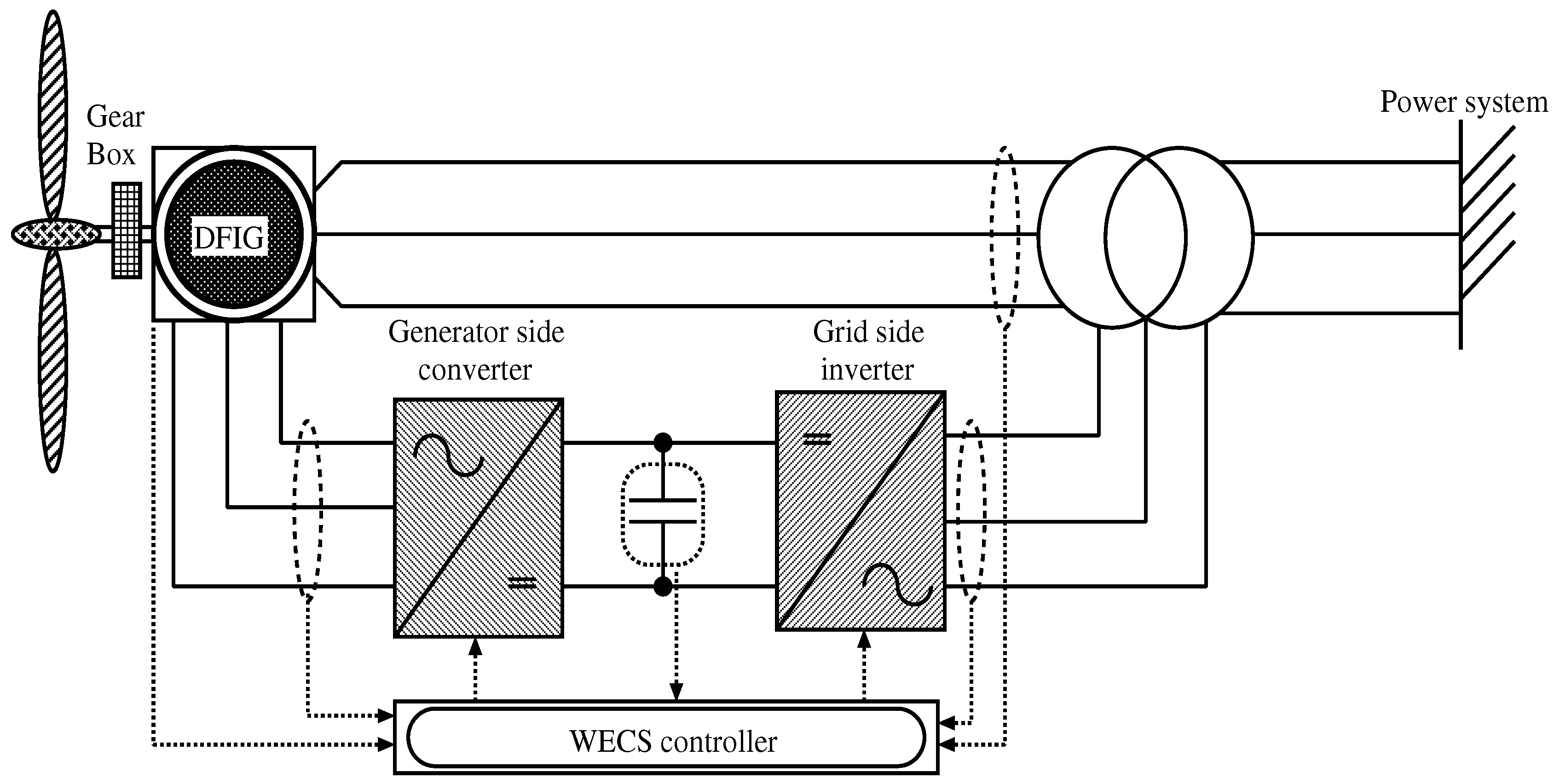
2.1. Wind Energy Conversion System
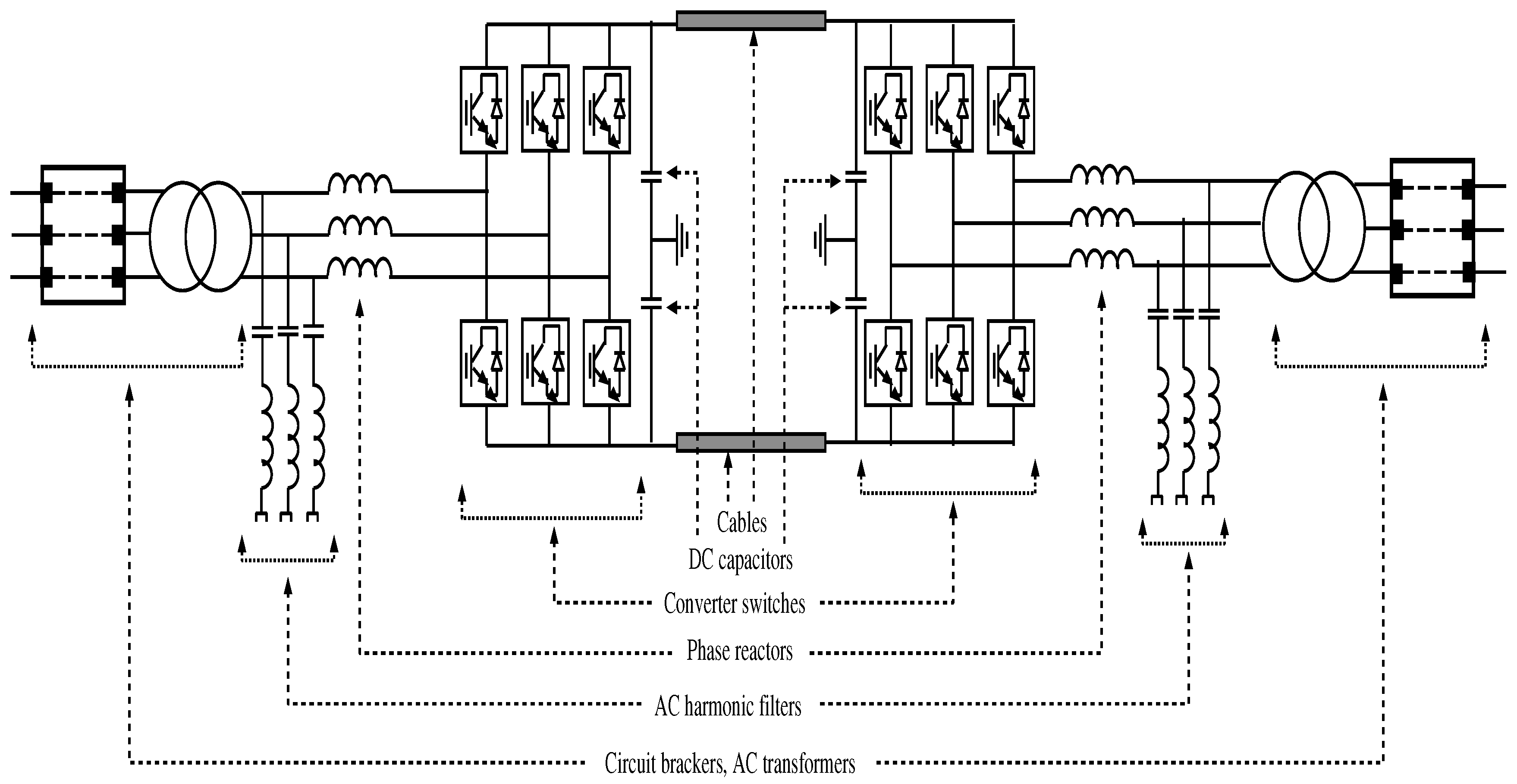
2.2. HVDC Link, Battery and Diesel Generator Systems
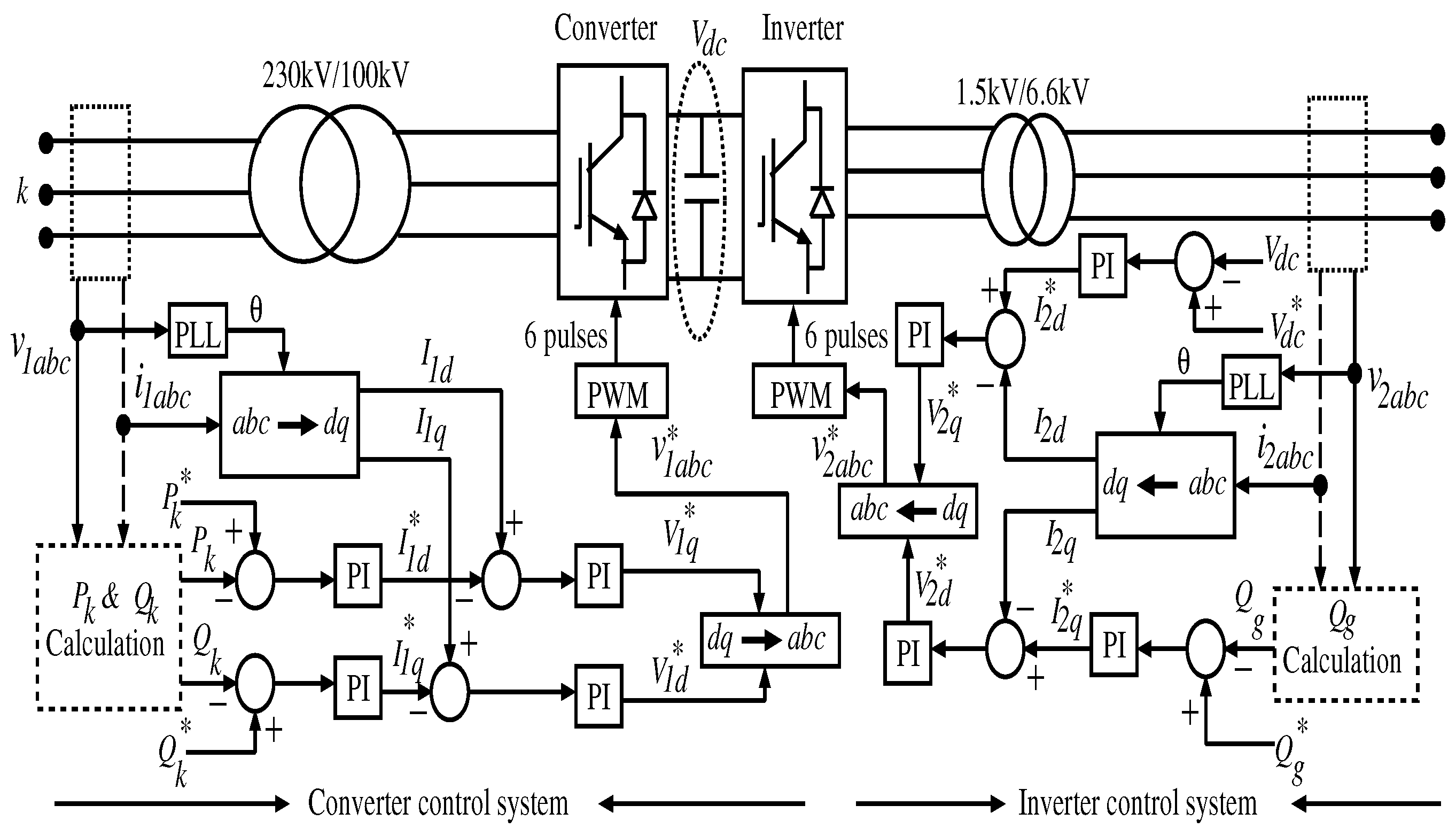
3. DC Microgrid Control System
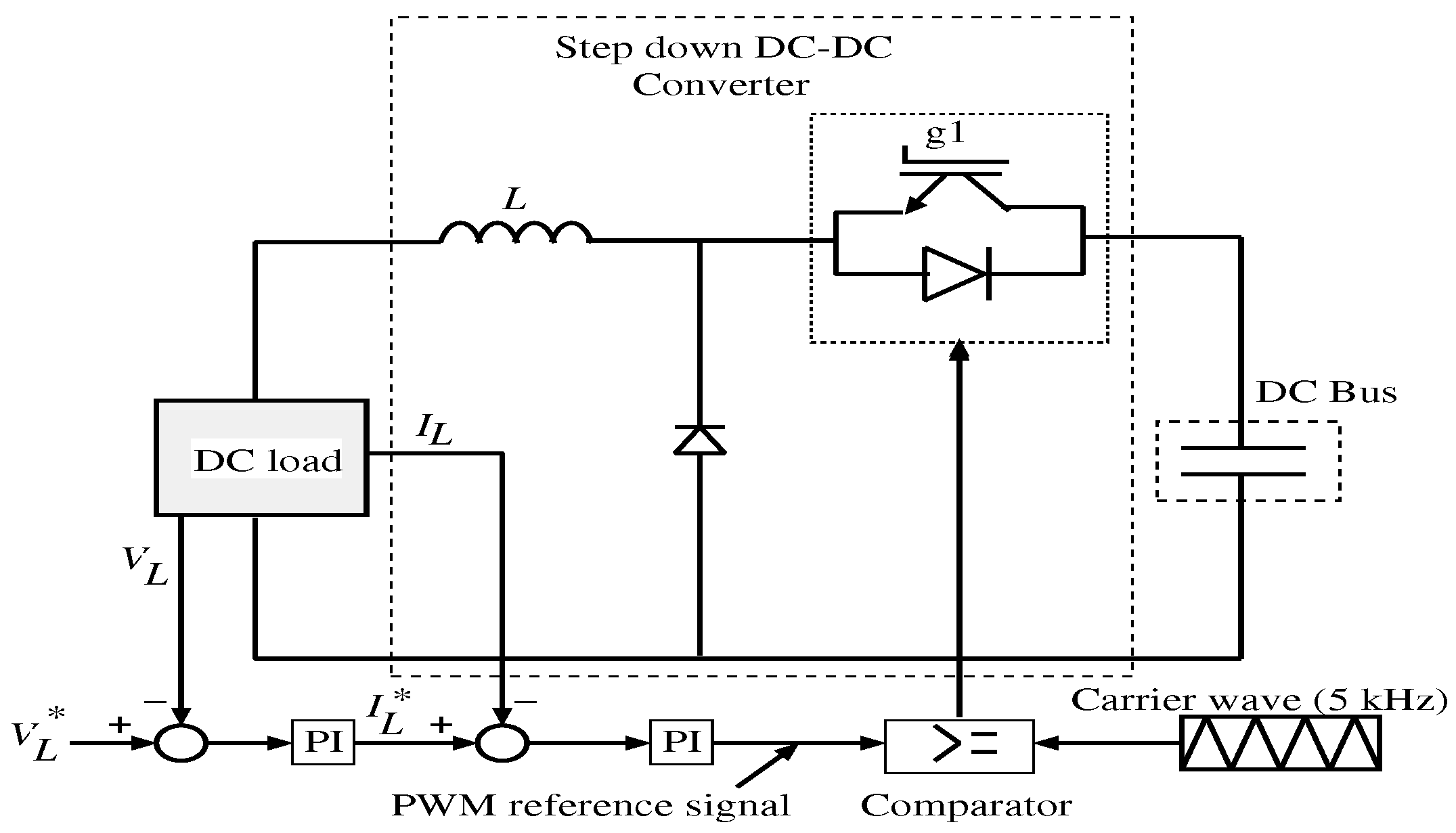
3.1. Converter Control System
3.2. Inverter Control System
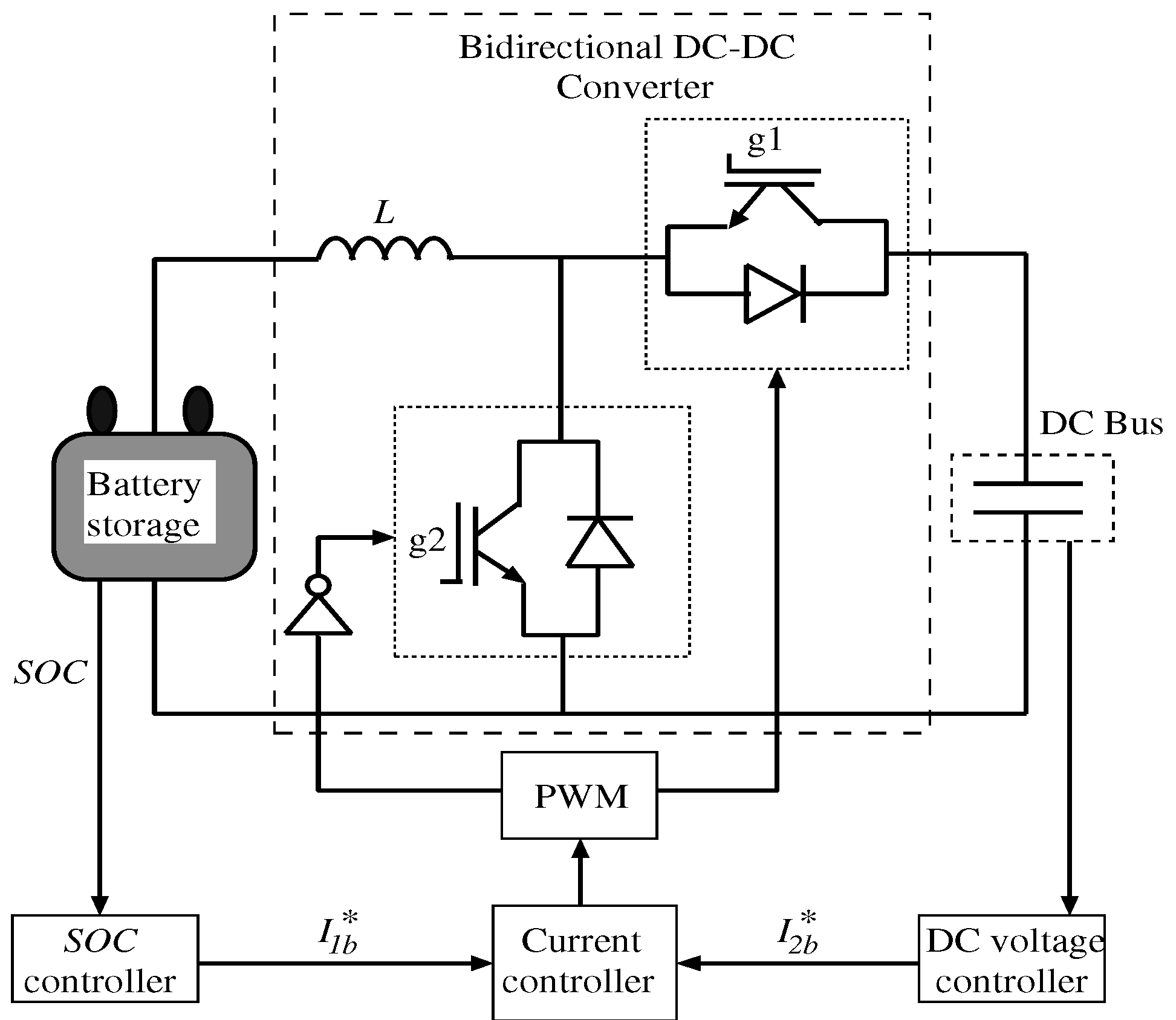
3.3. Battery Control System
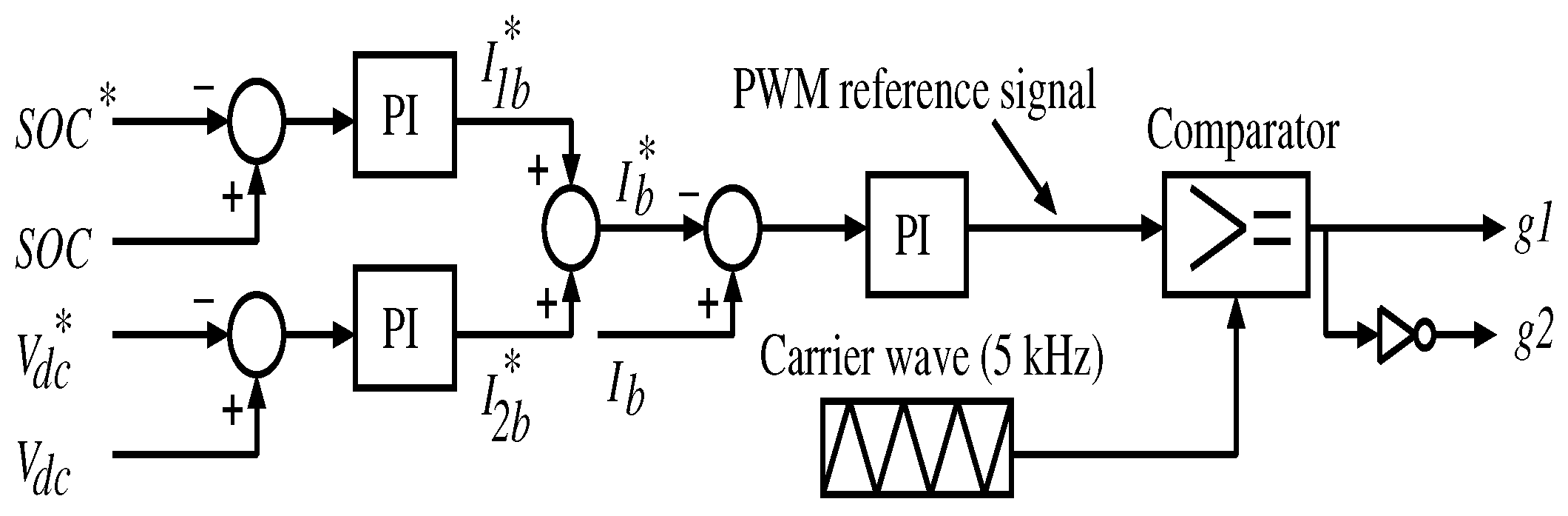
3.3.1. Control System for the Normal Operation
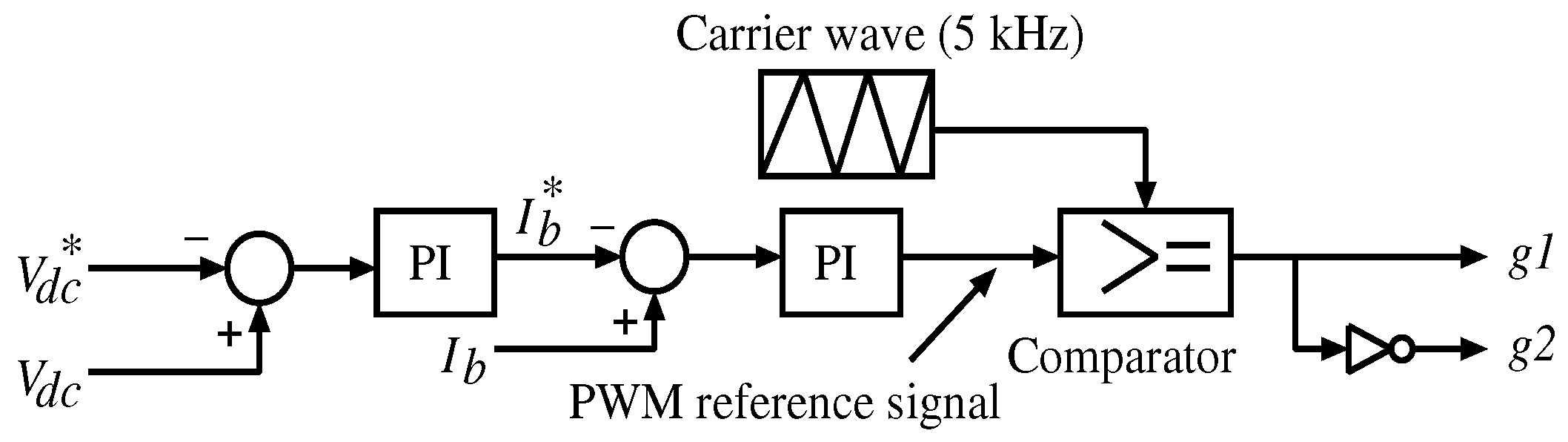
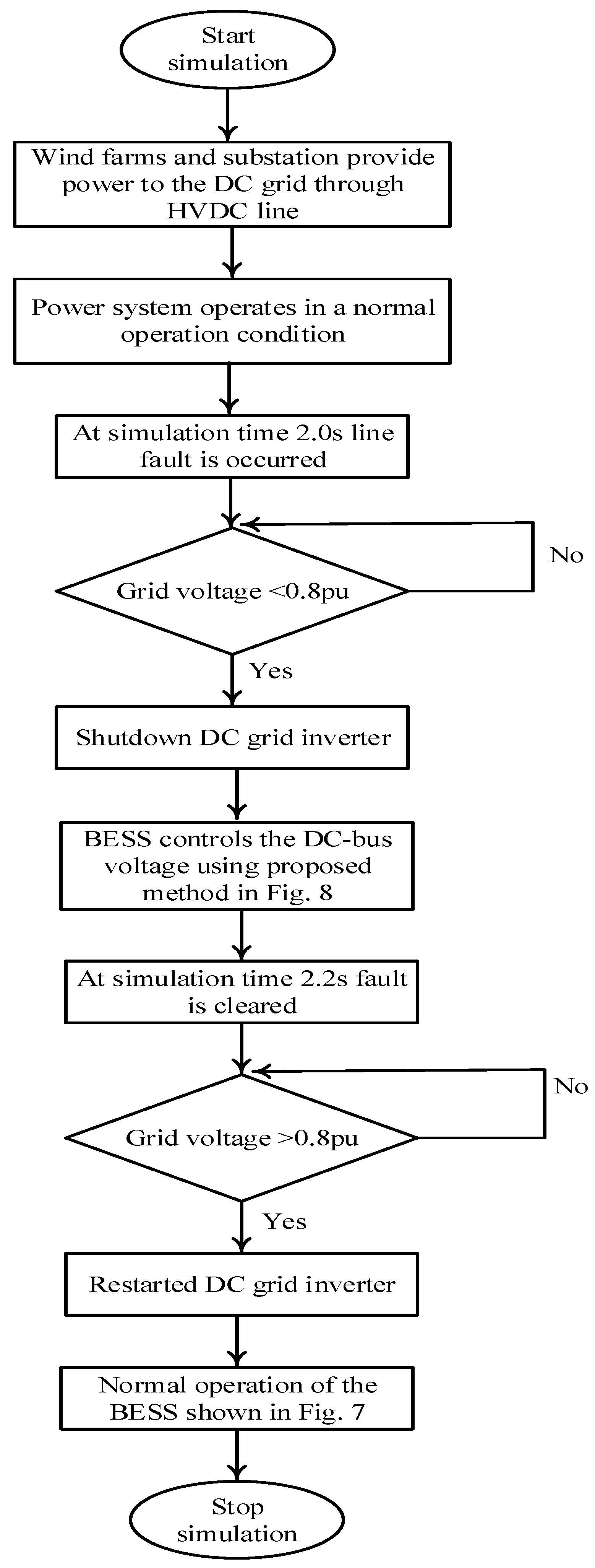
3.3.2. Control System of Fault Operation
3.4. Control System of Load
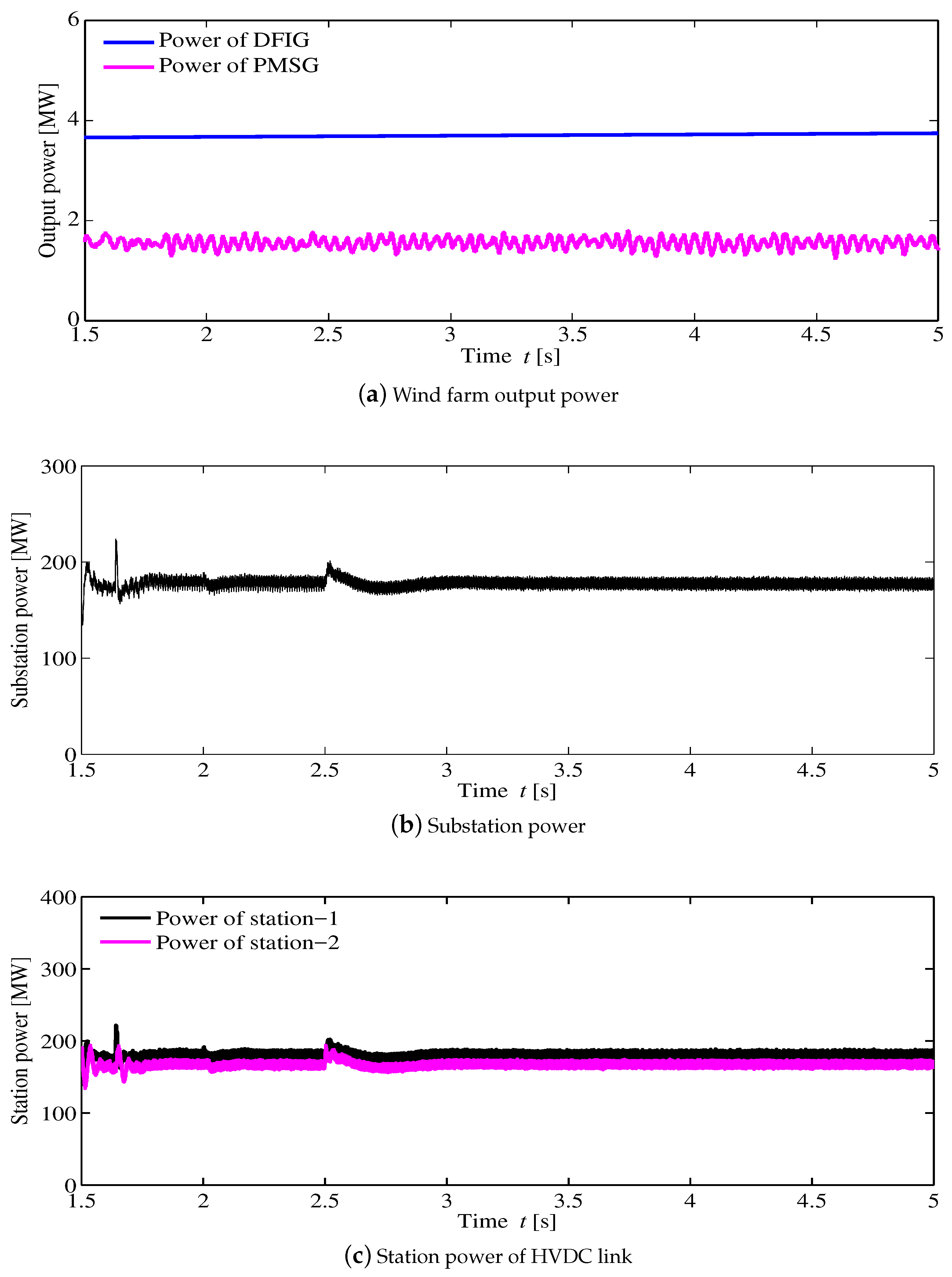
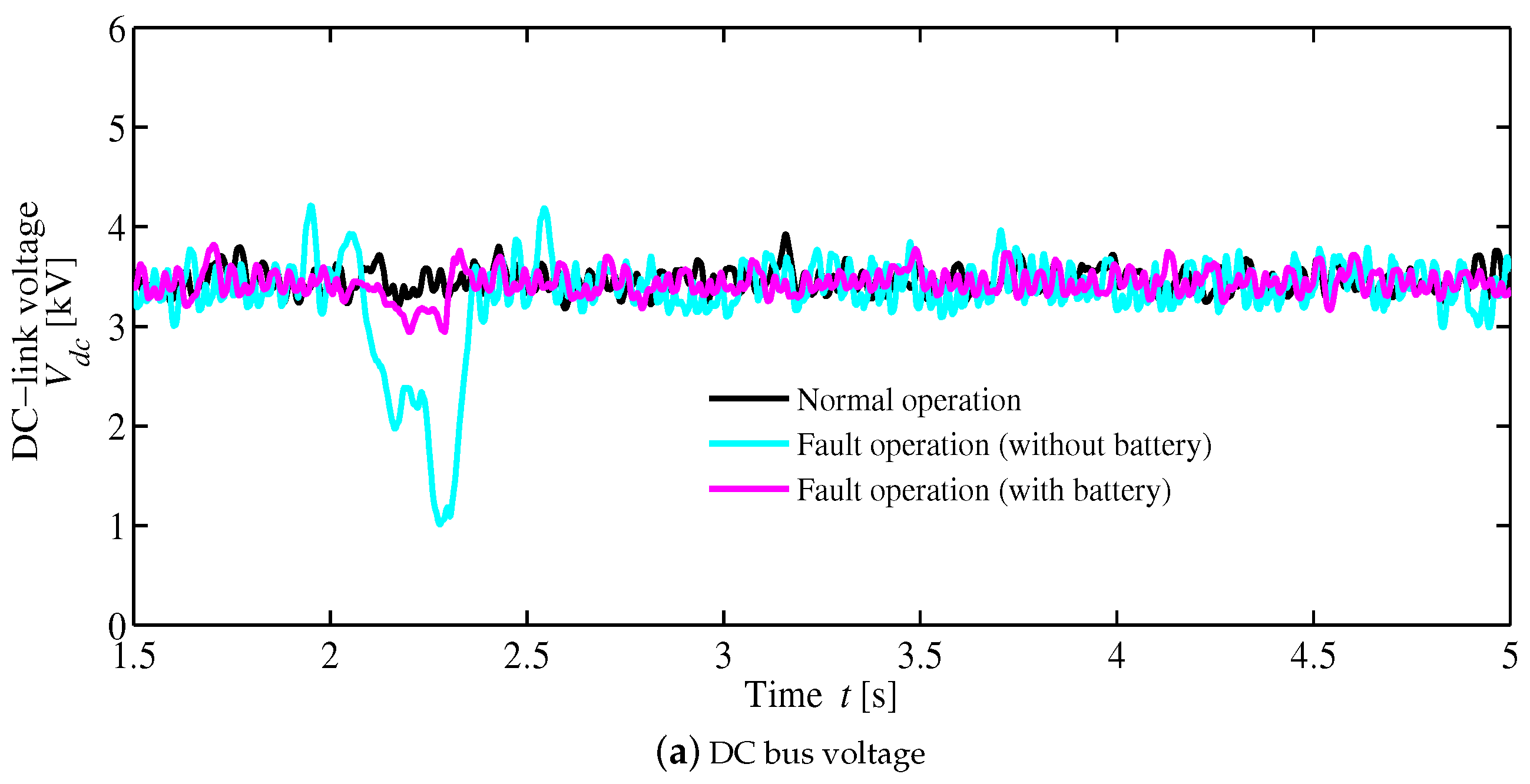
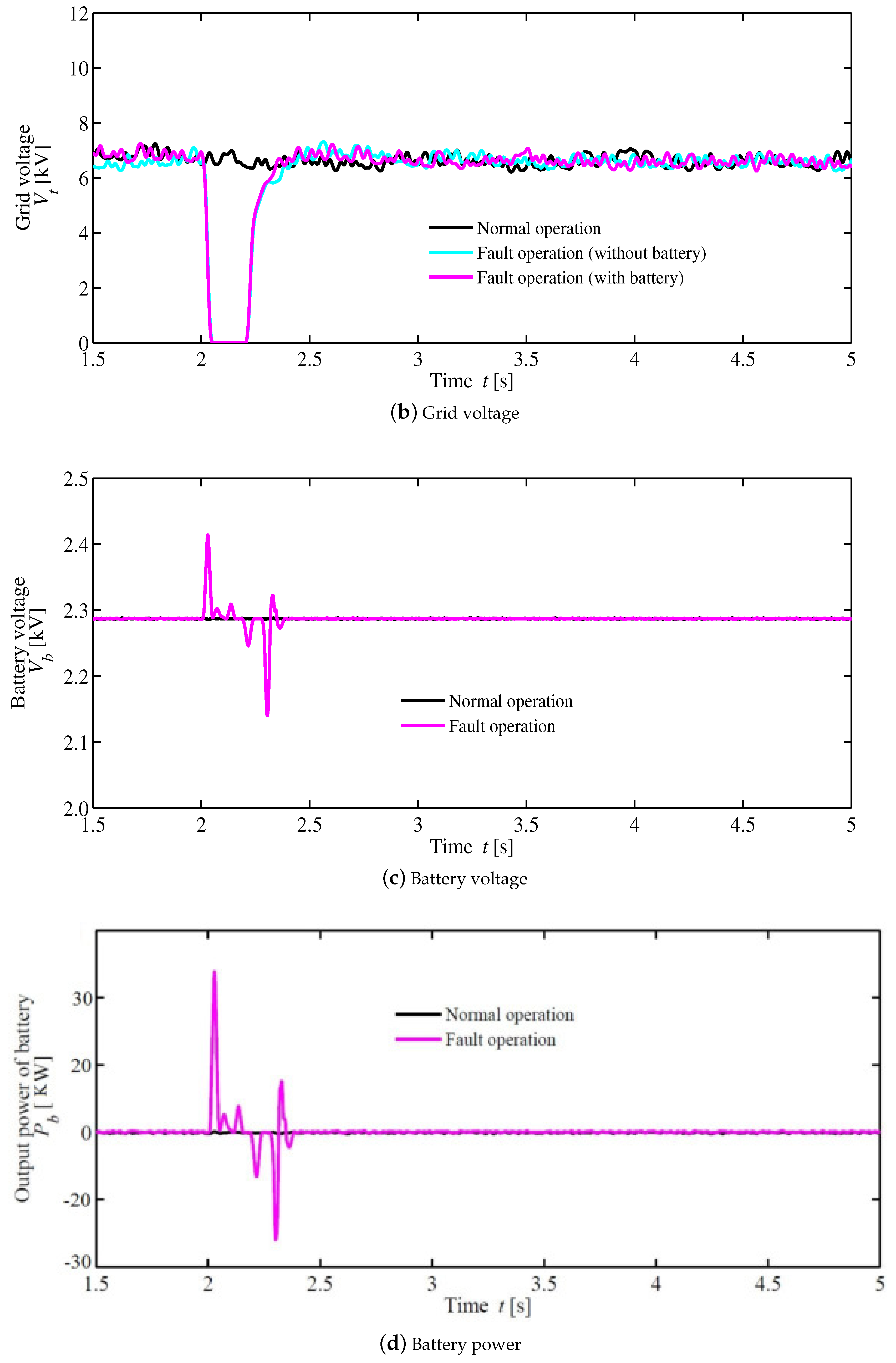
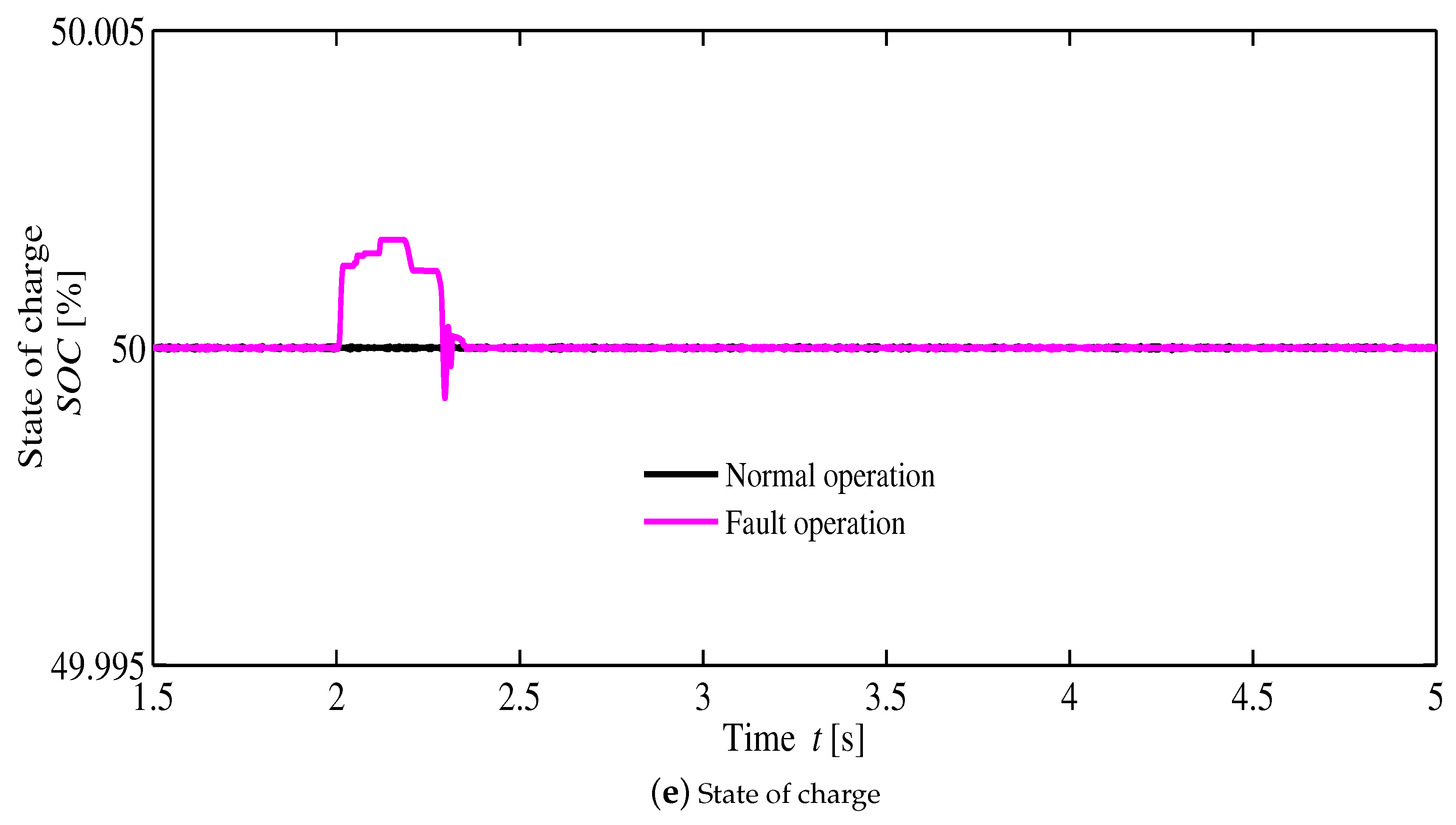
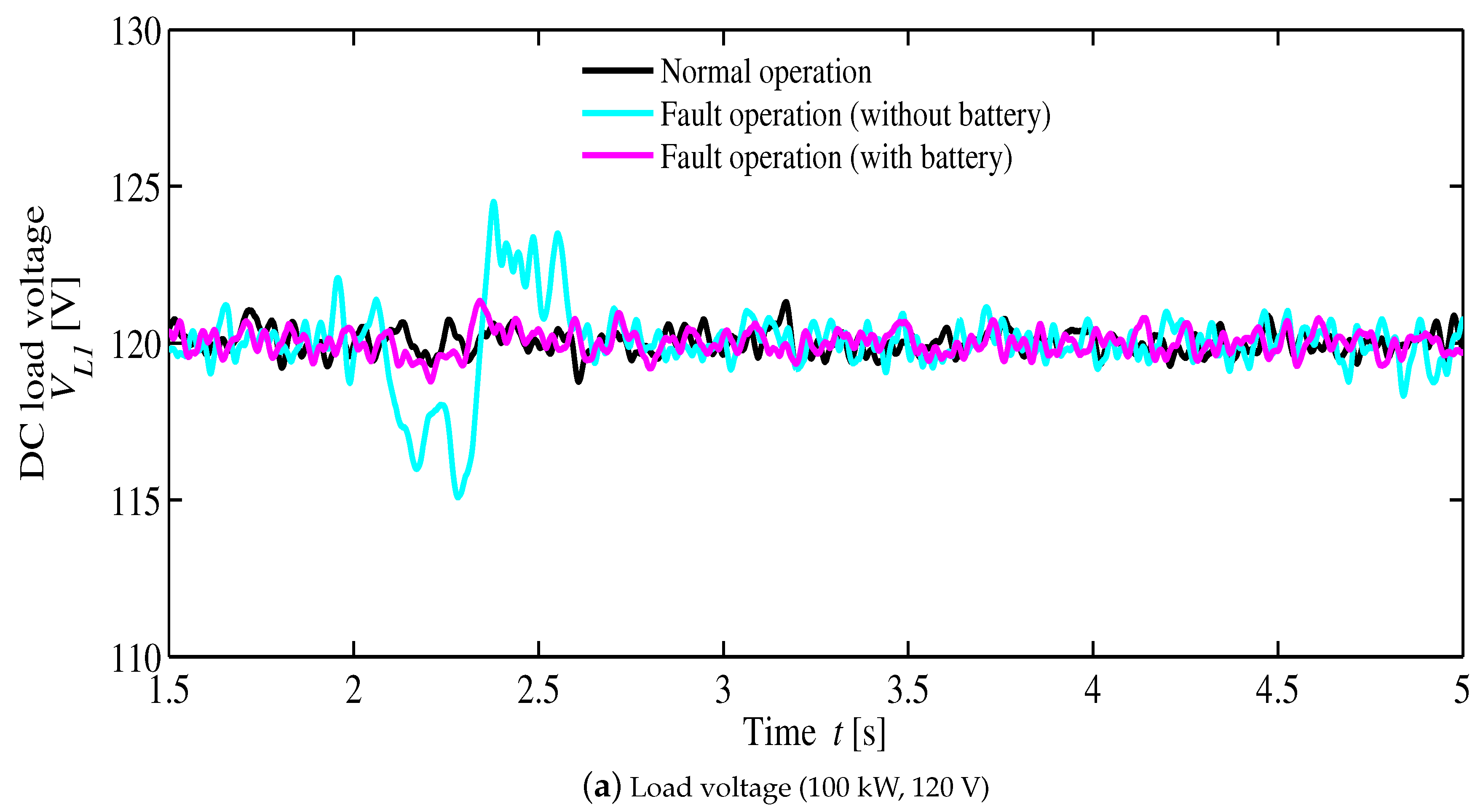
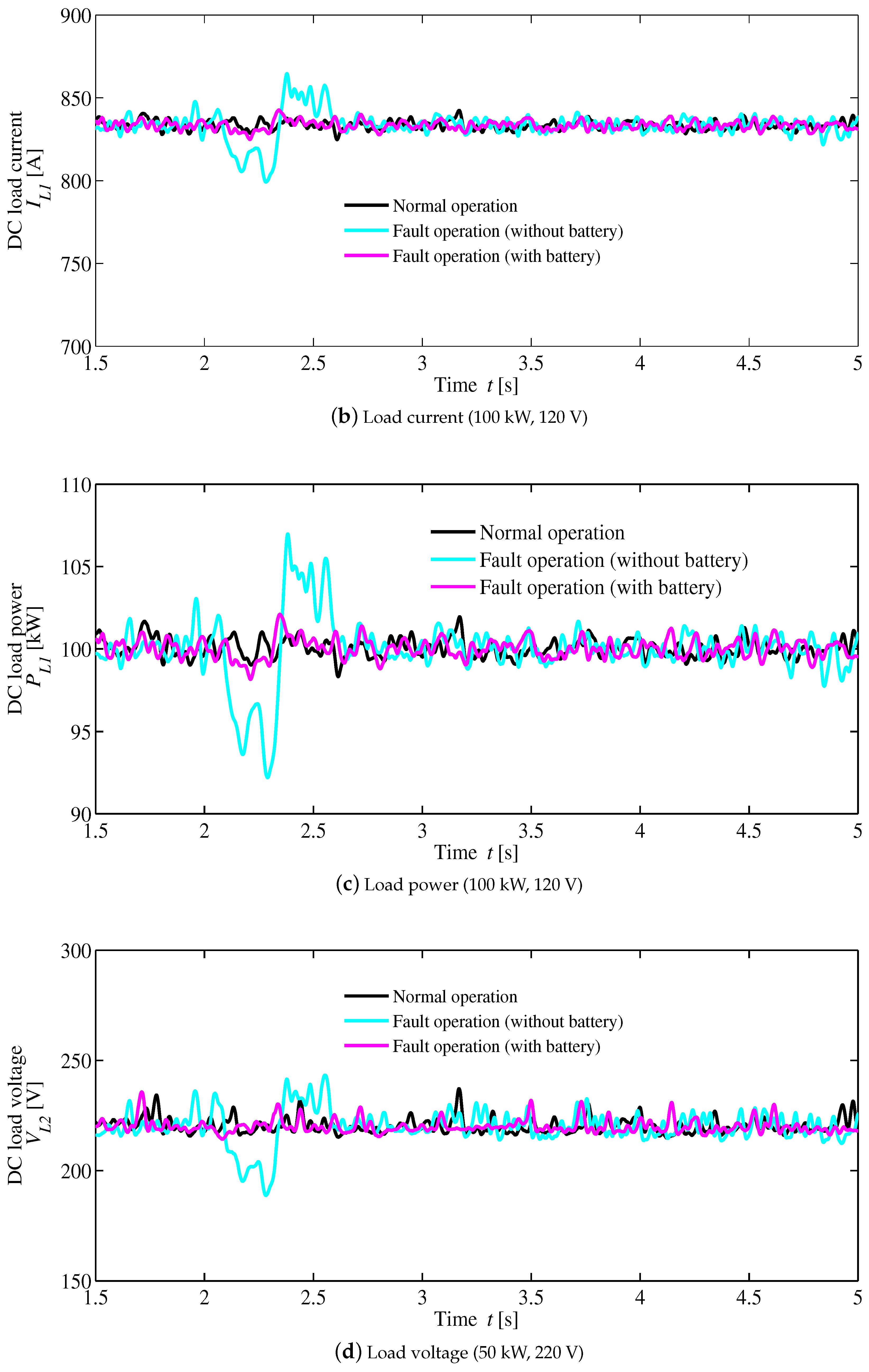
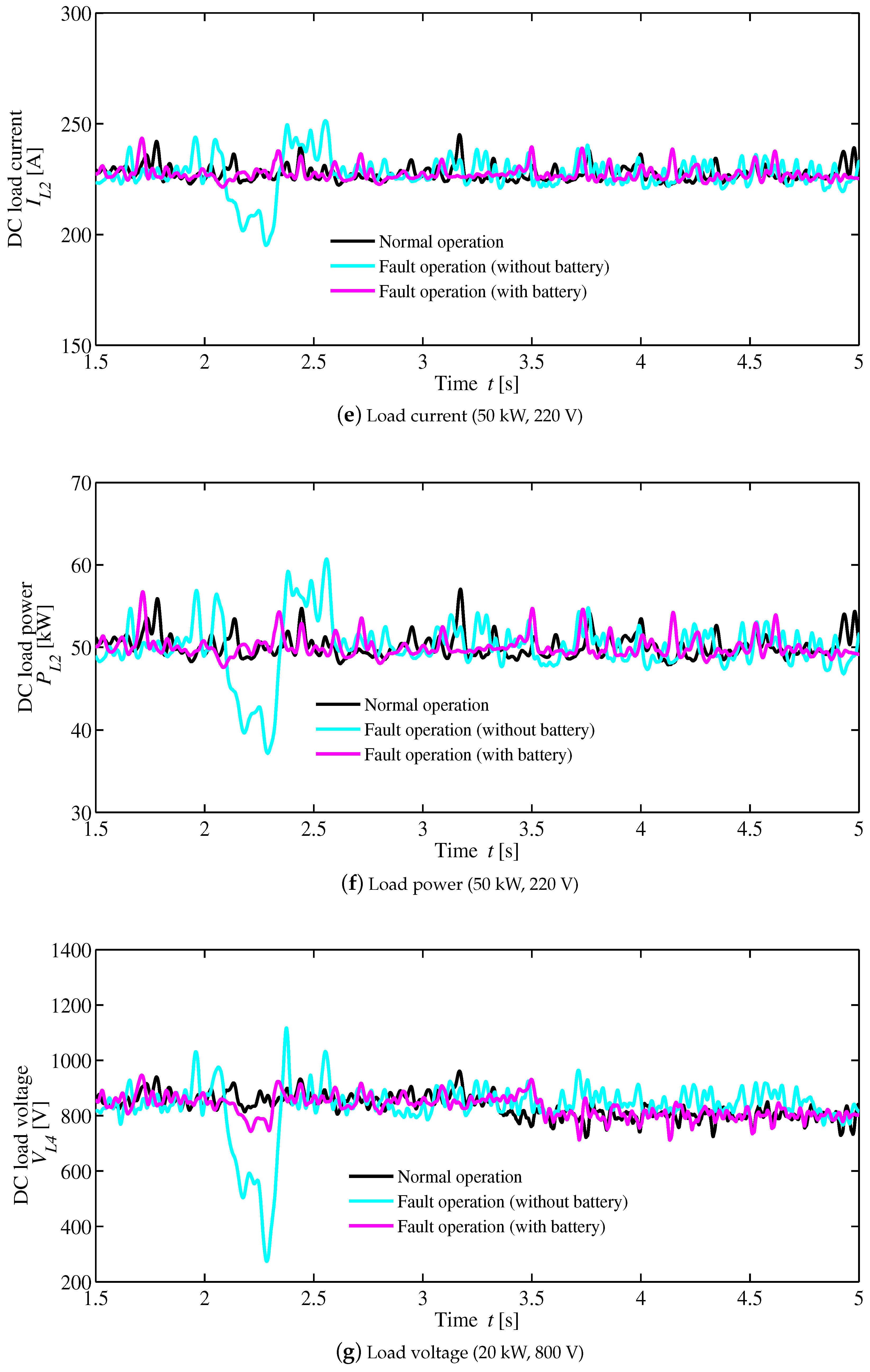
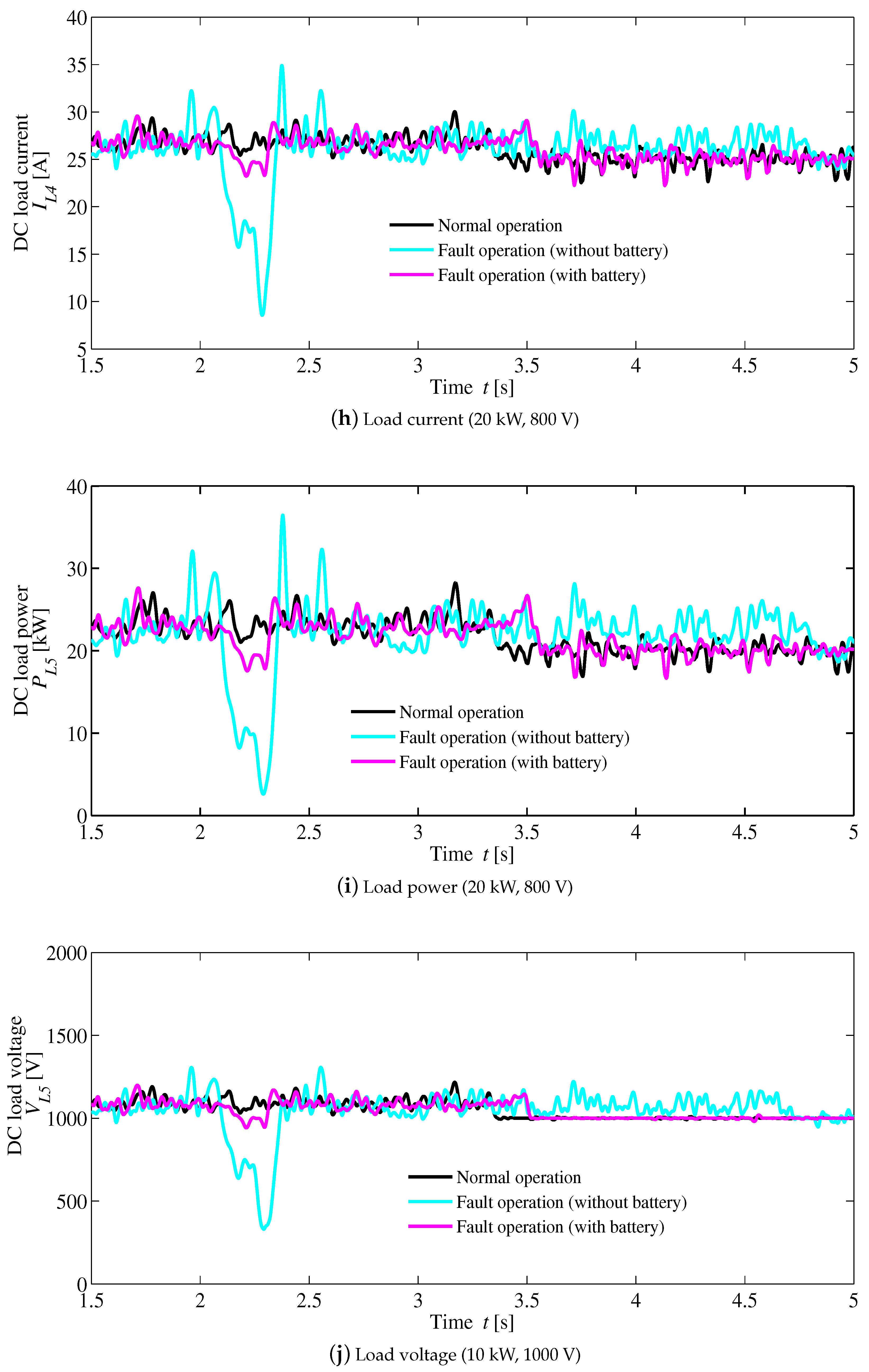
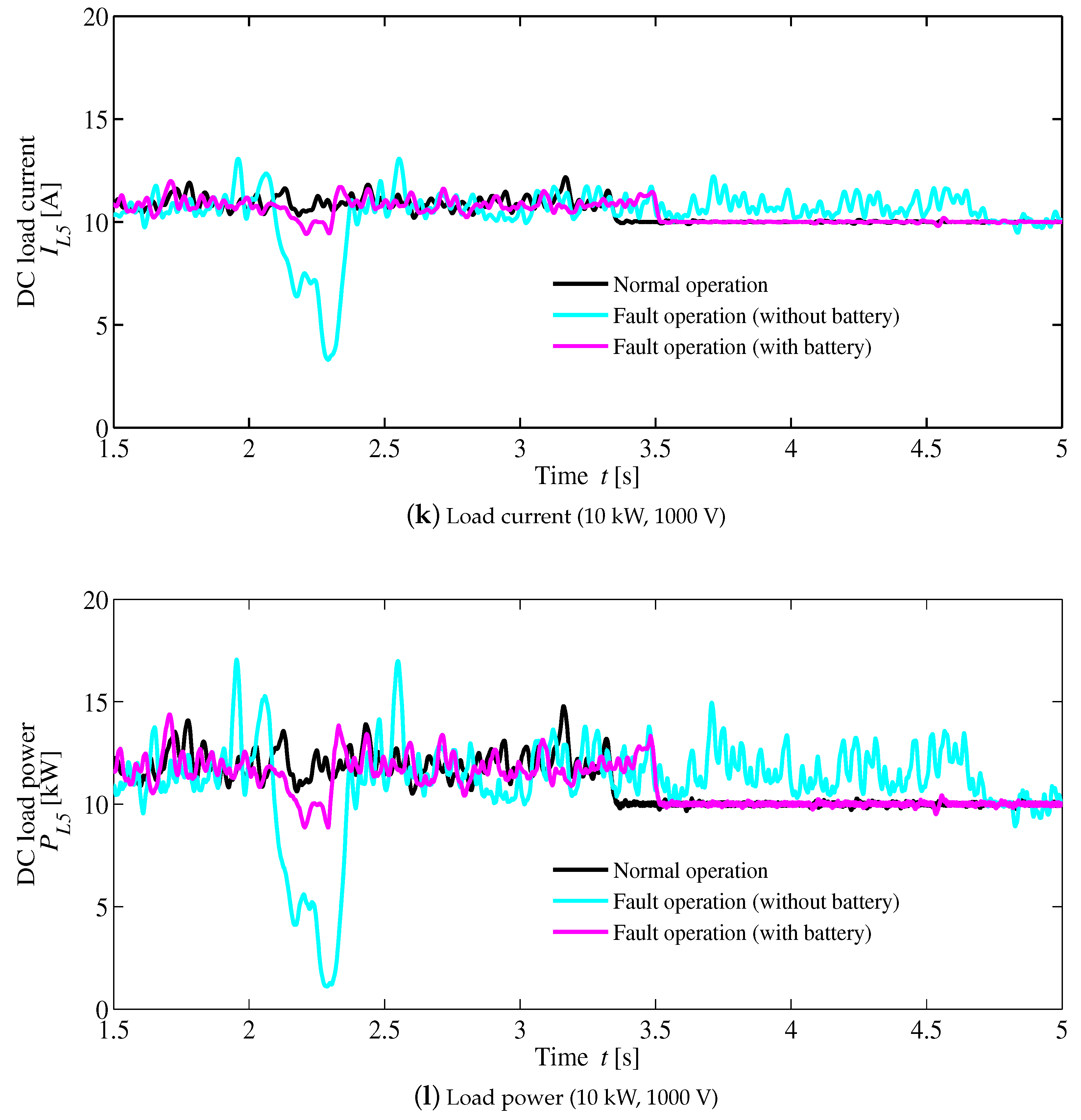
4. Simulation Results
- t = 2.0 s is the three-phase line to ground-fault starting time.
- The gate signals of the DC grid inverter are shutdown when the grid voltage is less than 0.8 pu.
- The line fault is cleared at t = 2.2 s.
- The gate signals of the inverter are re-started, when the AC-grid voltage is above 0.8 pu.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Direct current | |
| Distributed renewable energy sources | |
| Alternating current | |
| Distributed generator | |
| multi-modular converter | |
| High voltage DC | |
| Low voltage DC | |
| Voltage source converter | |
| Doubly-fed induction generator | |
| Permanent magnet synchronous generator | |
| Battery energy storage system | |
| Voltage source inverter | |
| synchronous generator | |
| Wind turbine blade radius | |
| Wind speed | |
| Air density | |
| Turbine input torque | |
| Rotational speed of the wind turbine | |
| Tip speed ratio | |
| Power coefficient | |
| Pitch angle | |
| d-axis voltage | |
| q-axis voltage | |
| d-axis current | |
| q-axis current | |
| Stator resistance | |
| d-axis inductance | |
| q-axis inductance | |
| Electrical rotational speed | |
| K | Permanent magnet flux |
| p | Number of pole pairs |
| Electromagnetic torque | |
| Magnetic flux | |
| v | Voltage |
| i | Current |
| s | Stator quantity |
| r | Rotor quantity |
| Stator self-inductance | |
| Rotor self-inductance | |
| Mutual inductance | |
| Rotor slip frequency | |
| Base angular frequency | |
| Stator resistance | |
| Rotor resistance | |
| D | Rotational damping |
| Equivalent inertia | |
| Load torque | |
| Mechanical rotational speed | |
| MPPT | Maximum power point tracking |
| PCC | Point of common coupling |
| SOC | State of charge |
| IGBT | Insulated gate bipolar transistor |
| AVR | Automatic voltage regulation |
| Active power reference | |
| DC bus voltage | |
| Reactive power of wind turbine | |
| Phase angle | |
| Reference load voltage | |
| Actual load voltage |
Appendix A
References
- Shi, R.; Semsar, S.; Lehn, P.W. Constant current fast charging of electric vehicles via DC grid using dual inverter drive. IEEE Trans. Ind. Electron. 2017, 64, 6940–6949. [Google Scholar] [CrossRef]
- Pascal, T.P.; Badel, A.; Auran, G. Superconducting fault current limiter for ship grid simulation and demonstration. IEEE Trans. Appl. Supercond. 2017, 27, 1–5. [Google Scholar] [CrossRef]
- Miyazato, Y.; Tobaru, S.; Uchida, K.; Muarapaz, C.C.; Howlader, A.M.; Senjyu, T. Multi-objective optimization for equipment capacity in Off-grid smart house. Sustainability 2017, 9, 117. [Google Scholar] [CrossRef]
- Savage, P.; Nordhaus, R.R.; Jamieson, S.P. DC Microgrids: Benefits and Barriers from Silos to Systems: Issues in Clean Energy and Climate Change; Yale Publications: New Haven, CT, USA, 2010; p. 51. [Google Scholar]
- Gharavi, H.; Ghafurian, R. Smart grid: The electric energy system of the future. Proc. IEEE 2011, 99, 917–921. [Google Scholar] [CrossRef]
- Dongxiao, N.; Di, P.; Shuyu, D. Ultra-short-term wind-power forecasting based on the weighted random forest optimized by the niche immune lion algorithm. Energies 2018, 11, 1098. [Google Scholar]
- Sheng, L.; Zhinong, W.; Yanan, M. Fuzzy load-shedding strategy considering photovoltaic output fluctuation characteristics and static voltage stability. Energies 2018, 11, 779. [Google Scholar]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; Vicuna, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids A general approach toward standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Kollimalla, S.K.; Mishra, M.K.; Ukil, A. DC grid voltage regulation using new HESS control strategy. IEEE Trans. Sustain. Energy 2017, 8, 772–781. [Google Scholar] [CrossRef]
- Davari, M.; Mohamed, Y.A.I. Robust DC-link voltage control of a full-scale PMSG wind turbine for effective integration in DC Grids. IEEE Trans. Power Electron. 2017, 32, 4021–4035. [Google Scholar] [CrossRef]
- Hao, Y.; Zhao, H.; Wu, Q. Coordinated control of multi-terminal DC grid for wind power integration. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; pp. 702–706. [Google Scholar]
- Sanz, I.M.; Chaudhuri, B.; Strbac, G. Inertial response from offshore wind farms connected through DC grids. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; p. 1. [Google Scholar]
- Jovcic, D.; Zhang, H. Dual channel control with DC fault ride through for MMC-based, Isolated DC/DC Converter. IEEE Trans. Power Deliv. 2017, 32, 1574–1582. [Google Scholar] [CrossRef]
- Kontos, E.; Bauer, P. Reactor design for DC fault ride-through in MMC-based multi-terminal HVDC grids. In Proceedings of the 2016 IEEE 2nd Annual Southern Power Electronics Conference (SPEC), Auckland, New Zealand, 5–8 December 2016; pp. 1–6. [Google Scholar]
- Mokhberdoran, A.; Carvalho, A.; Silva, N.; Leite, H.; Carrapatoso, A. Application study of superconducting fault current limiters in meshed HVDC grids protected by fast protection relays. Electr. Power Syst. Res. 2017, 143, 292–302. [Google Scholar] [CrossRef]
- Tzelepis, D.; Rousis, A.O.; Dysko, A.; Booth, C. Enhanced DC voltage control strategy for fault management of a VSC-HVDC connected offshore wind farm. In Proceedings of the 5th IET International Conference on Renewable Power Generation (RPG), London, UK, 21–23 September 2016; pp. 1–6. [Google Scholar]
- Daoud, M.I.; Massoud, A.M.; Abdel–Khalik, A.S.; Elserougi, A.; Ahmed, S. A flywheel energy storage system for fault ride through support of grid-connected VSC HVDC-based offshore wind farms. IEEE Trans. Power Syst. 2016, 31, 1671–1680. [Google Scholar] [CrossRef]
- Howlader, A.M.; Senjyu, T.; Saber, A.Y. An integrated power smoothing control for a grid-interactive wind farm considering wake effects. IEEE Syst. J. 2015, 9, 954–965. [Google Scholar] [CrossRef]
- Howlader, A.M.; Urasaki, N.; Saber, A.Y. Control strategies for wind-farm-based smart grid system. IEEE Trans. Ind. Appl. 2014, 50, 3591–3601. [Google Scholar] [CrossRef]
- Guo, W. Overview and development progress of a 1-MVA/1-MJ superconducting fault current limiter-magnetic energy storage system. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar] [CrossRef]
- Taj, T.A.; Hasanien, H.M.; Alolah, A.I.; Muyeen, S.M. Transient stability enhancement of a grid-connected wind farm using an adaptive neuro-fuzzy controlled-flywheel energy storage system. IET Renew. Power Gener. 2015, 9, 792–800. [Google Scholar] [CrossRef]
- Shi, M.X.; Chong, L. Line-to-Line Fault Analysis and Location in a VSC-Based Low-Voltage DC Distribution Network. Energies 2018, 11, 536. [Google Scholar]
- Yu, M.; Wang, Y.; Zhang, L.; Zhang, Z. DC short circuit fault analysis and protection of ring type DC microgrid. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 1694–1700. [Google Scholar]
- Park, J.D.; Candelaria, J.; Ma, L.; Dunn, K. DC ring-bus microgrid fault protection and identification of fault Location. IEEE Trans. Power Deliv. 2013, 28, 2574–2584. [Google Scholar] [CrossRef]
- Santos, R.C.; Blond, S.L.; Coury, D.B.; Aggarwal, R.K. A novel and comprehensive single terminal ANN based decision support for relaying of VSC based HVDC links. Electr. Power Syst. Res. 2016, 141, 333–343. [Google Scholar] [CrossRef]
- Ikema, H.; Matayoshi, H.; Howlader, A.M.; Senjyu, T.; Funabashi, T. MTDC transmission systems including dc resonant semiconductor breaker. In Proceedings of the 2015 International Symposium on Smart Electric Distribution Systems and Technologies (EDST), Vienna, Austria, 8–11 September 2015; pp. 442–446. [Google Scholar]
- Howlader, A.M.; Urasaki, N.; Senjyu, T.; Uehara, A.; Yona, A.; Saber, A.Y. Output power smoothing of wind turbine generation system for the 2-MW permanent magnet synchronous generators. In Proceedings of the 2010 International Conference on Electrical Machines and Systems, Incheon, Korea, 10–13 October 2010; pp. 452–457. [Google Scholar]
- Zheng, D.I.; Ouyang, J.; Xiong, X.; Xiao, C.; Mengyang, L. A System Transient Stability Enhancement Control Method Using Doubly Fed Induction Generator Wind Turbine with Considering Its Power Constraints. Energies 2018, 11, 945. [Google Scholar] [CrossRef]
- Schettler, F.; Huang, H.; Christl, N. HVDC transmission systems using voltage source converters-design and applications. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Seattle, WA, USA, 16–20 July 2000. [Google Scholar]
- Renaudin, F. Integration and Stability of a Large Offshore Wind Farm with HVDC Transmission in the Norwegian Power System; Institutt for Elkraftteknikk: Ålesund, Norway, 2009. [Google Scholar]
- Muyeen, S.M.; Ali, M.H.; Takahashi, R.; Murata, T.; Tamura, J. Damping of blade-shaft torsional oscillations of wind turbine generator system. Electr. Power Compon. Syst. 2018, 36, 195–211. [Google Scholar] [CrossRef]
- Monadi, M.; Zamani, M.A.; Candela, J.I.; Luna, A.; Rodriguez, P. Protection of AC and DC distribution systems Embedding distributed energy resources: A comparative review and analysis. Renew. Sustain. Energy Rev. 2015, 51, 1578–1593. [Google Scholar] [CrossRef]
- Zhang, L.; Tai, N.; Huang, W. A review on protection of DC microgrids. J. Mod. Power Syst. Clean Energy 2018, 6, 1–15. [Google Scholar] [CrossRef]
| Protection Method | Detection Scheme | Threshold | Comments |
|---|---|---|---|
| Voltage based method | The fault is detected by the voltage, dv/dt. | Depends on the voltage setting values when a fault occurs at the transmission line. | Stable performances against change in the direction of current. Appropriate threshold is required. Cannot provide adequate selectivity. |
| Current based method | The fault is detected by the current, di/dt. | Depends on the current setting values when a fault occurs at the transmission line. | Doesn’t require protection audit. Appropriate threshold is required. No systematic method to find the exact values of fault current limiting. |
| Hybrid method | The fault is detected by hybrid electrical quantities. | Depends on the hybrid electric quantities when a fault occurs at the transmission line. | Providing accurate setting for various operating conditions. Need to complex methods for threshold setting calculations. Sensitive to fault resistance. |
| Differential method | Differentiate the internal and external faults with current differential. | Depends on the over current of power electronics devices when a fault occurs at the transmission line. | Better sensitivity. Requirement to communication link which increase the cost of the implementation. Dependency on communication. |
| Event based method | Detect the fault locally and interconnect with other units to determine the fault. | Threshold setting similar to voltage based, current based, and hybrid methods. | Fault can be identified accurately. Isolating fault within 30 ms. |
| Loads | (100 kW) | (50 kW) | (20 kW) | (10 kW) |
|---|---|---|---|---|
| Voltage (Conventional method) | ±4% | ±10% | +25%, −62.5% | +20%, −52% |
| Voltage (Proposed method) | 0% | 0% | −1.2%, | 0% |
| Current (Conventional method) | ±4.7% | ±10% | +40%, −60% | +20%, −52% |
| Current (Proposed method) | 0% | 0% | −1.3% | 0% |
| Power (Conventional method) | ±5% | ±20% | ±90% | +70%, −80% |
| Power (Proposed method) | 0% | 0% | 1.5% | 0% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Howlader, A.M.; Matayoshi, H.; Sepasi, S.; Senjyu, T. Design and Line Fault Protection Scheme of a DC Microgrid Based on Battery Energy Storage System. Energies 2018, 11, 1823. https://doi.org/10.3390/en11071823
Howlader AM, Matayoshi H, Sepasi S, Senjyu T. Design and Line Fault Protection Scheme of a DC Microgrid Based on Battery Energy Storage System. Energies. 2018; 11(7):1823. https://doi.org/10.3390/en11071823
Chicago/Turabian StyleHowlader, Abdul Motin, Hidehito Matayoshi, Saeed Sepasi, and Tomonobu Senjyu. 2018. "Design and Line Fault Protection Scheme of a DC Microgrid Based on Battery Energy Storage System" Energies 11, no. 7: 1823. https://doi.org/10.3390/en11071823
APA StyleHowlader, A. M., Matayoshi, H., Sepasi, S., & Senjyu, T. (2018). Design and Line Fault Protection Scheme of a DC Microgrid Based on Battery Energy Storage System. Energies, 11(7), 1823. https://doi.org/10.3390/en11071823






