Preparation and Evaluation of a Coconut Shell-Based Activated Carbon for CO2/CH4 Separation
Abstract
1. Introduction
2. Material and Methods
2.1. Precursor Material
2.2. Activated Carbon Production
2.3. Adsorption Isotherms
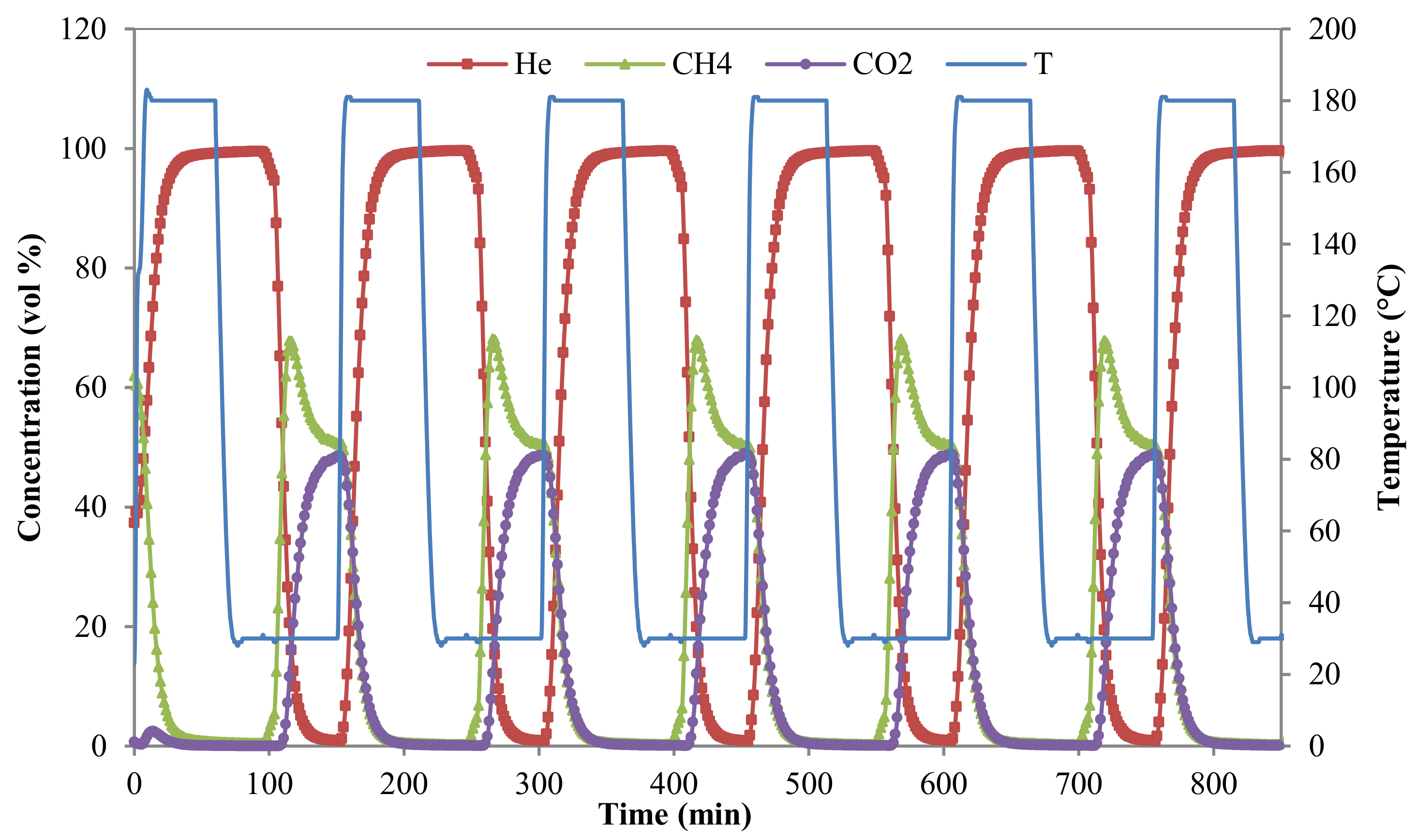
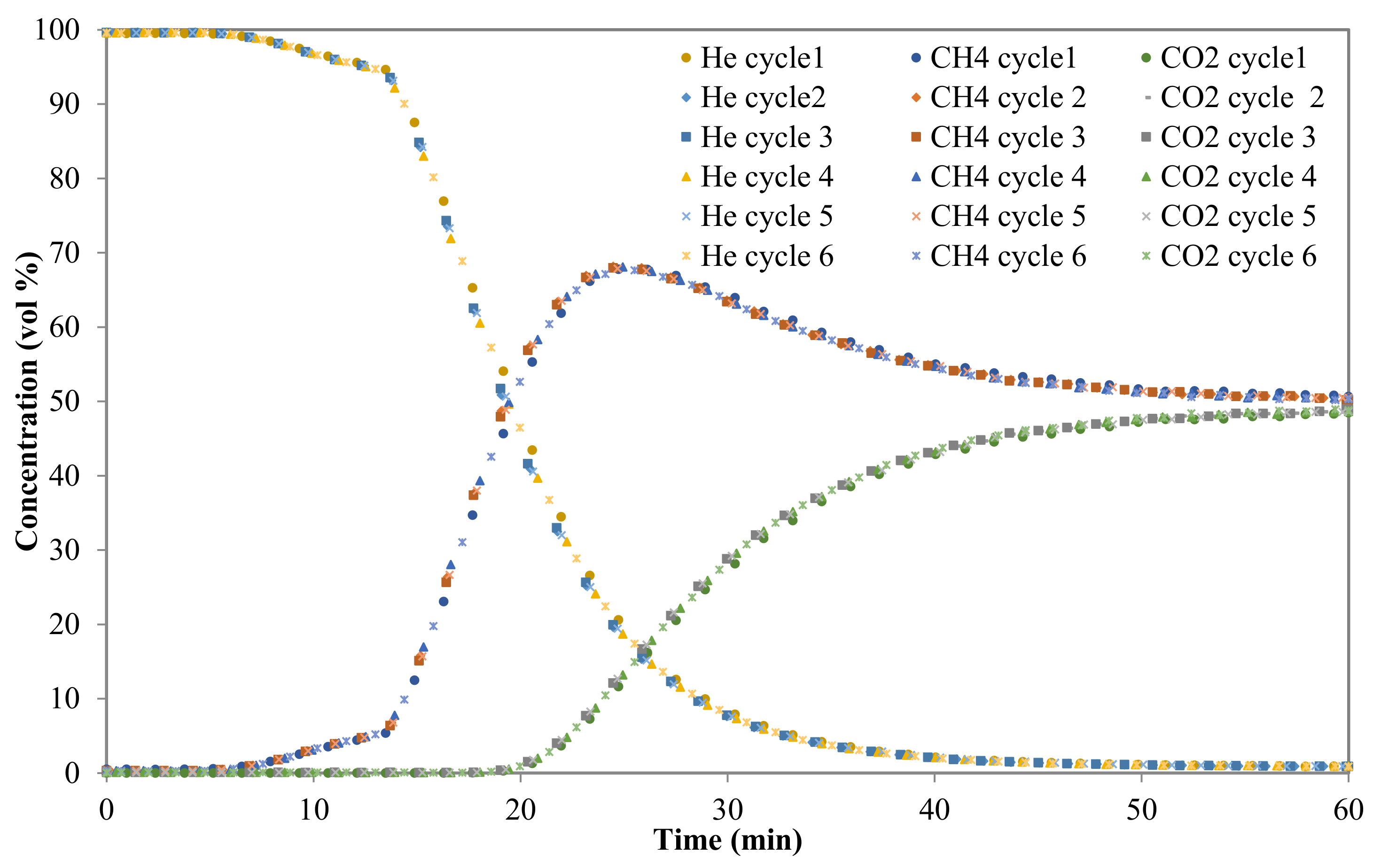
2.4. Breakthrough Measurements
3. Results and Discussion
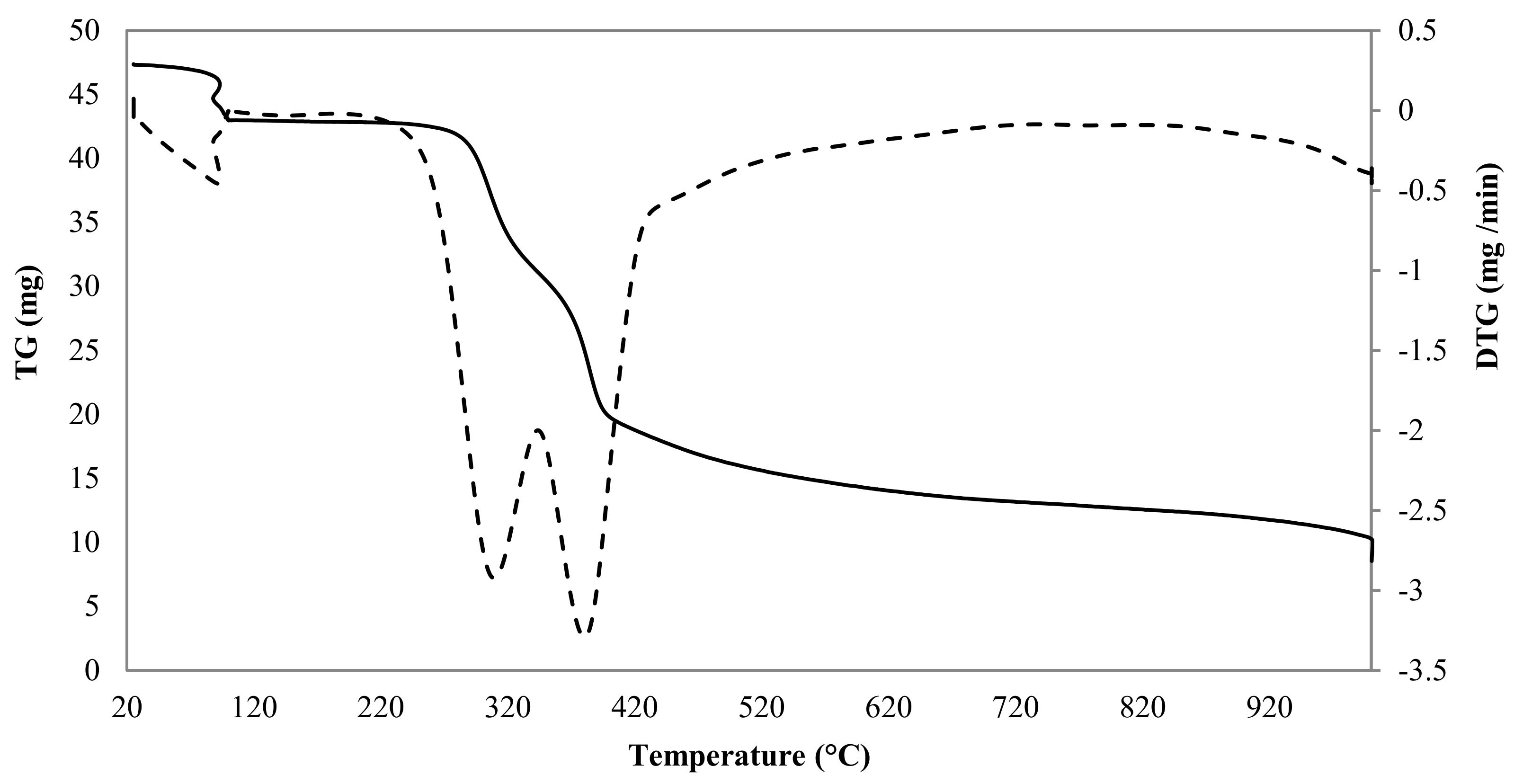
3.1. Precursor Material
3.2. (CNS )Activated Carbon Characterization and Evaluation
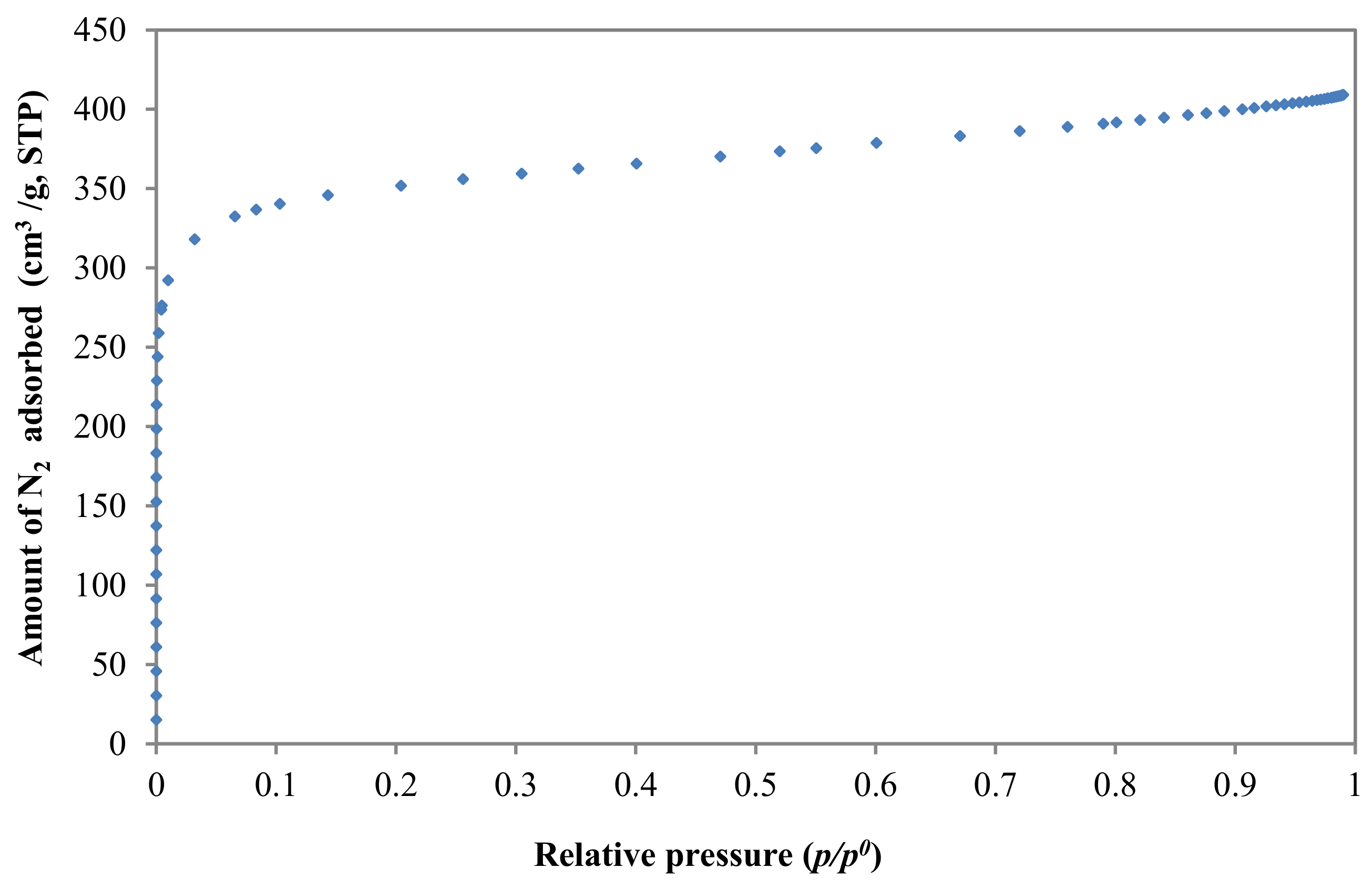
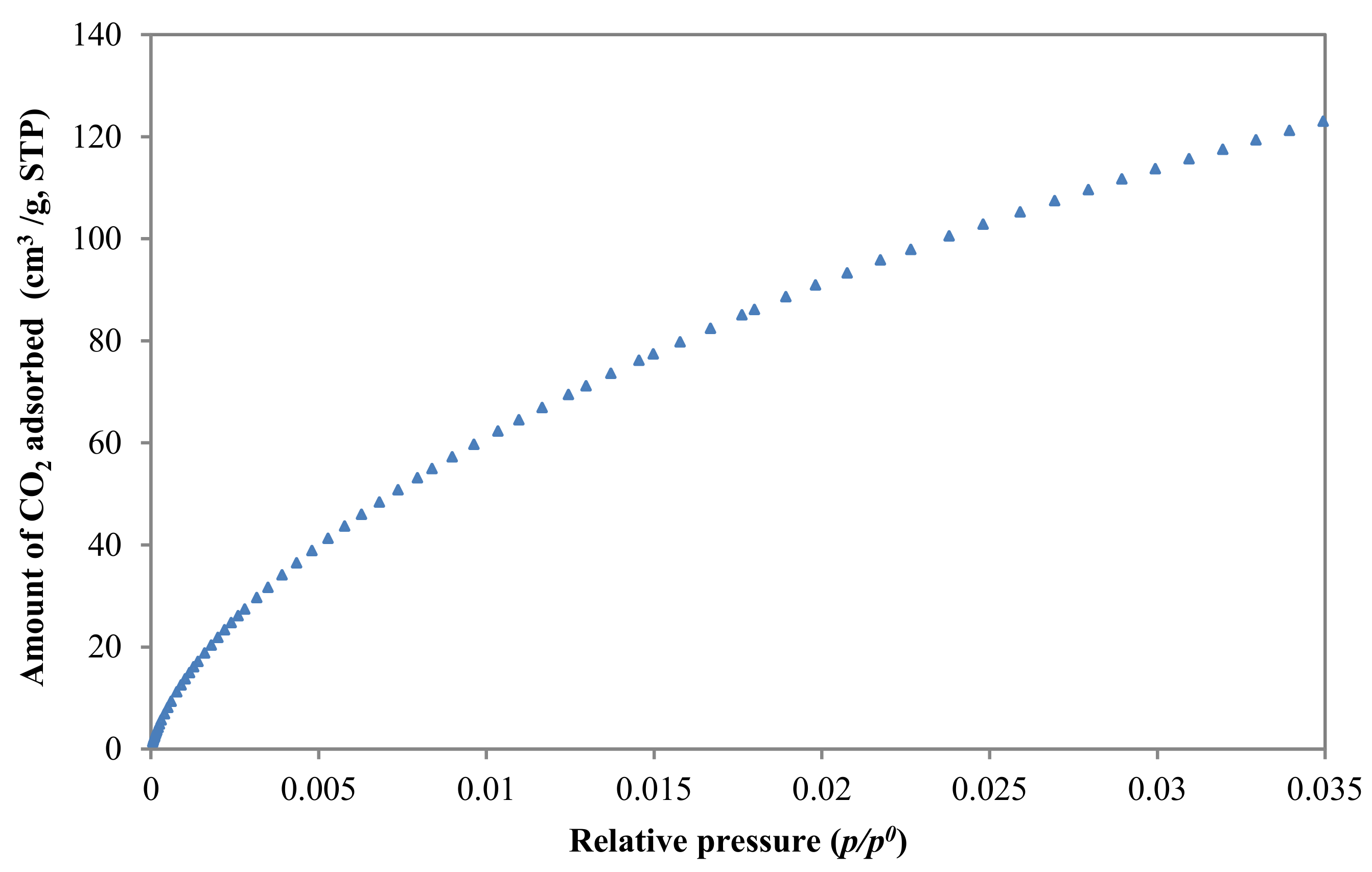
3.2.1. Textural Characterization
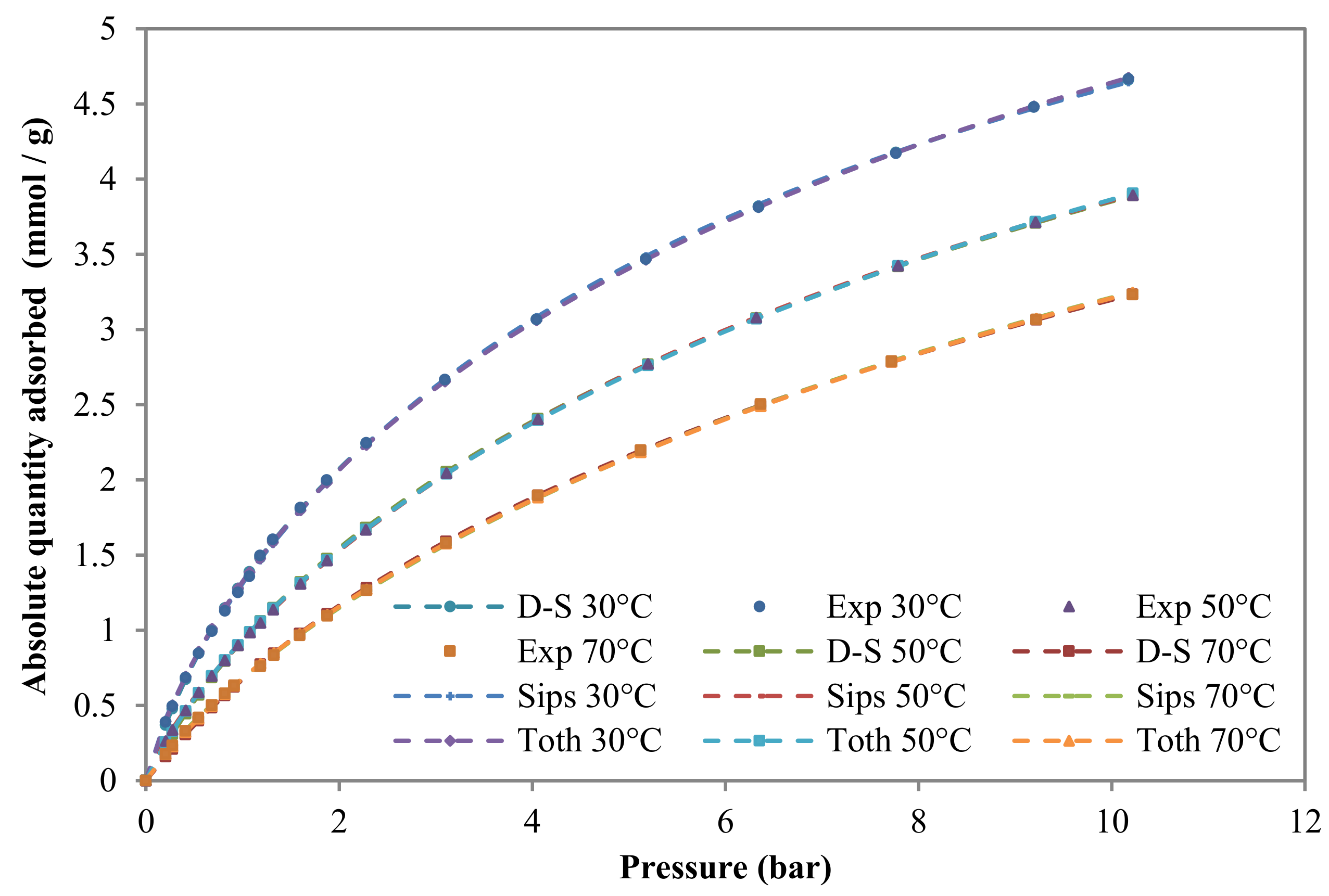
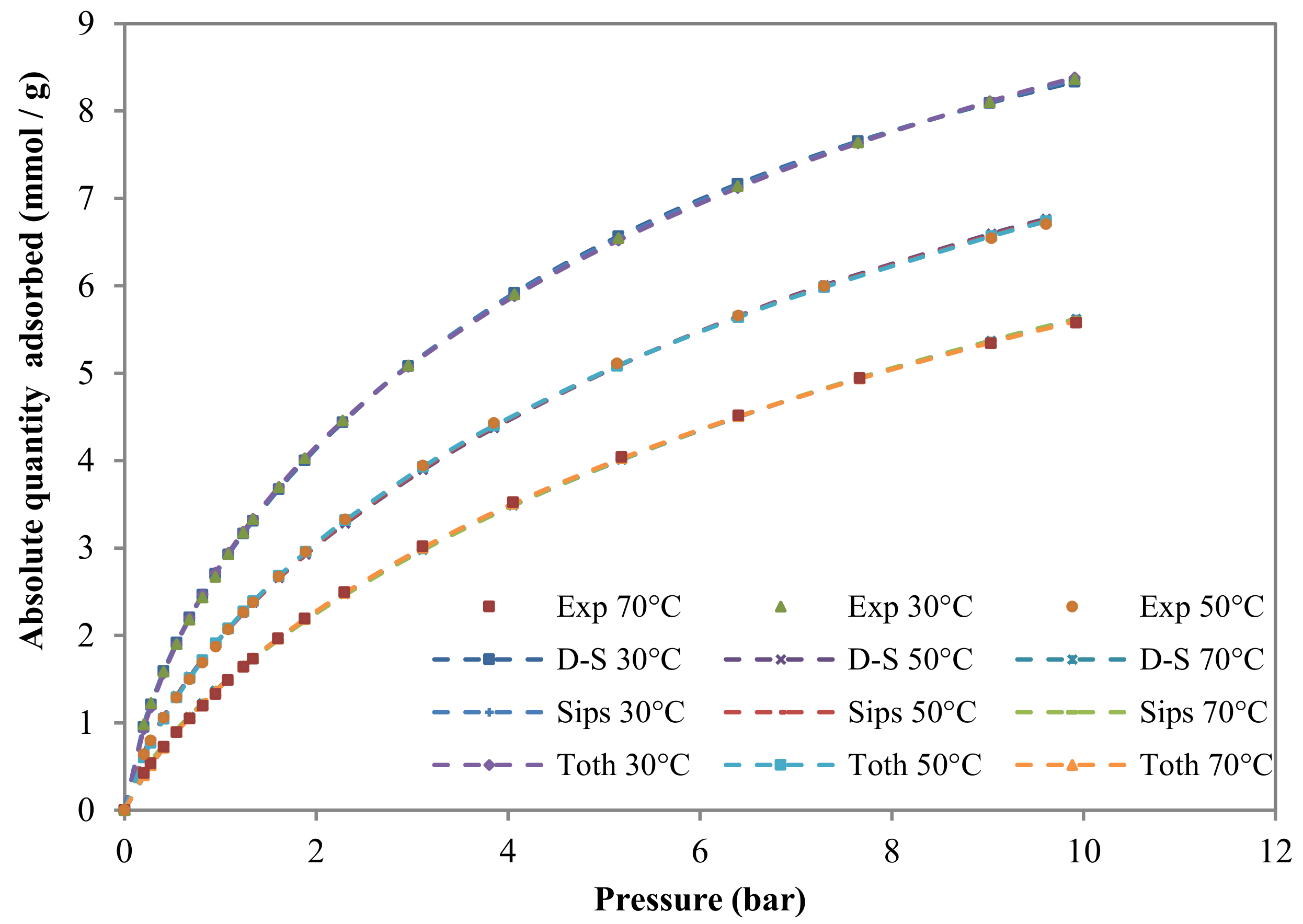
3.2.2. Adsorption Isotherms
3.2.3. Breakthrough Curves
3.2.4. Adsorption Selectivity
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zheng, B.; Xu, J. Carbon Capture and Storage Development Trends from a Techno-Paradigm Perspective. Energies 2014, 7, 5221–5250. [Google Scholar] [CrossRef]
- Rodrigues, C.F.A.; Dinis, M.A.P.; Lemos de Sousa, M.J. Review of European energy policies regarding the recent “carbon capture, utilization and storage” technologies scenario and the role of coal seams. Environ. Earth Sci. 2015, 74–2553. [Google Scholar] [CrossRef]
- Yoro, K.O.; Sekoai, P.T. The Potential of CO2 Capture and Storage Technology in South Africa’s Coal-Fired Thermal Power Plants. Environments 2016, 3, 24. [Google Scholar] [CrossRef]
- Lackner, K.S.; Park, A.H.A.; Miller, B.G. Eliminating CO2 emissions from coal-fired power plants. In Generating Electricity in a Carbon-Constrained World; Academic Press: Cambridge, MA, USA, 2010; pp. 127–173. [Google Scholar]
- Pires, J.C.M.; Martins, F.G.; Alvim-Ferraz, M.C.M.; Simões, M. Recent developments on carbon capture and storage: An overview. Chem. Eng. Res. Des. 2011, 89, 1446–1460. [Google Scholar] [CrossRef]
- Zhou, K.; Chaemchuen, S.; Verpoort, F. Alternative materials in technologies for Biogas upgrading via CO2 capture. Renew. Sustain. Energy Rev. 2017, 79, 1414–1441. [Google Scholar] [CrossRef]
- Sarkar, S.C.; Bose, A. Role of activated carbon pellets in carbon dioxide removal. Energy Convers. Manag. 1997, 38, S105–S110. [Google Scholar] [CrossRef]
- Horikawa, M.S.; Rossi, F.; Gimenes, M.L.; Costa, C.M.M.; Da Silva, M.G.C. Chemical absorption of H2S for biogas purification. Braz. J. Chem. Eng. 2004, 21, 415–422. [Google Scholar] [CrossRef]
- Yeo, Z.Y.; Chew, T.L.; Zhu, P.W.; Mohamed, A.R.; Chai, S.P. Conventional processes and membrane technology for carbon dioxide removal from natural gas: A review. J. Natl. Gas Chem. 2012, 21, 282–298. [Google Scholar] [CrossRef]
- Tuinier, M.J.; van Sint Annaland, M. Biogas Purification Using Cryogenic Packed-Bed Technology. Ind. Eng. Chem. Res. 2012, 51, 5552–5558. [Google Scholar] [CrossRef]
- Shigaki, N.; Mogi, Y.; Haraoka, T.; Sumi, I. Reduction of Electric Power Consumption in CO2-PSA with Zeolite 13X Adsorbent. Energies 2018, 11, 900. [Google Scholar] [CrossRef]
- Xu, G.; Liang, F.; Yang, Y.; Hu, Y.; Zhang, K.; Liu, W. An Improved CO2 Separation and Purification System Based on Cryogenic Separation and Distillation Theory. Energies 2014, 7, 3484–3502. [Google Scholar] [CrossRef]
- Abdeljaoued, A.; Relvas, F.; Mendes, A.; Chahbani, M.H. Simulation and experimental results of a PSA process for production of hydrogen used in fuel cells. J. Environ. Chem. Eng. 2018, 6, 338–355. [Google Scholar] [CrossRef]
- Maring, B.J.; Webley, P.A. A new simplified pressure/vacuum swing adsorption model for rapid adsorbent screening for CO2 capture applications. Int. J. Greenh. Gas Control 2013, 15, 16–31. [Google Scholar] [CrossRef]
- Ghouma, I.; Jeguirim, M.; Sager, U.; Limousy, L.; Bennici, S.; Däuber, E.; Asbach, C.; Ligotski, R.; Schmidt, F.; Ouederni, A. The Potential of Activated Carbon Made of Agro-Industrial Residues in NOx Immissions Abatement. Energies 2017, 10, 1508. [Google Scholar] [CrossRef]
- Ferella, F.; Puca, A.; Taglieri, G.; Rossi, L.; Gallucci, K. Separation of carbon dioxide for biogas upgrading to biomethane. J. Clean. Prod. 2017, 164, 1205–1218. [Google Scholar] [CrossRef]
- Siriwardane, R.V.; Shen, M.-S.; Fisher, E.P.; Poston, J.A. Adsorption of CO2 on Molecular Sieves and Activated Carbon. Energy Fuels 2001, 15, 279–284. [Google Scholar] [CrossRef]
- Li, G.; Xiao, P.; Webley, P.; Zhang, J.; Singh, R.; Marshall, M. Capture of CO2 from high humidity flue gas by vacuum swing adsorption with zeolite-13X. Adsorption 2008, 14, 415–422. [Google Scholar] [CrossRef]
- Millward, A.R.; Yaghi, O.M. Metal-Organic Frameworks with Exceptionally High Capacity for Storage of Carbon Dioxide at Room Temperature. J. Am. Chem. Soc. 2005, 127, 17998–17999. [Google Scholar] [CrossRef] [PubMed]
- Furukawa, H.; Ko, N.; Go, Y.B.; Aratani, N.; Choi, S.B.; Choi, E.; Yazaydin, A.O.; Snurr, R.Q.; O’Keeffe, M.; Kim, J.; et al. Ultrahigh Porosity in Metal-Organic Frameworks. Science 2010, 329, 424–428. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.; Drese, J.H.; Jones, C.W. Adsorbent materials for carbon dioxide capture from large anthropogenic point sources. ChemSusChem 2009, 2, 796–854. [Google Scholar] [CrossRef] [PubMed]
- Wei, H.; Deng, S.; Hu, B.; Chen, Z.; Wang, B.; Huang, J.; Yu, G. Granular Bamboo-Derived Activated Carbon for High CO2 Adsorption:The Dominant Role of Narrow Micropores. ChemSusChem 2012, 5, 2354–2360. [Google Scholar] [CrossRef] [PubMed]
- Samanta, A.; Zhao, A.; Shimizu, G.K.H.; Sarkar, P.; Gupta, R. Post-Combustion CO2 Capture Using Solid Sorbents: A Review. Ind. Eng. Chem. Res. 2012, 51, 1438–1463. [Google Scholar] [CrossRef]
- Jeguirim, M.; Limousy, L. Biomass Chars: Elaboration, Characterization and Applications. Energies 2017, 10, 2040. [Google Scholar] [CrossRef]
- Álvarez-Gutiérrez, N.; Gil, M.V.; Martínez, M.; Rubiera, F.; Pevida, C. Phenol-Formaldehyde Resin-Based Carbons for CO2 Separation at sub-atmospheric pressures. Energies 2016, 9, 189. [Google Scholar] [CrossRef]
- Guizani, C.; Jeguirim, M.; Valin, S.; Limousy, L.; Salvador, S. Biomass Chars: The Effects of Pyrolysis Conditions on Their Morphology, Structure, Chemical Properties and Reactivity. Energies 2017, 10, 796. [Google Scholar] [CrossRef]
- Heschel, W.; Klose, E. On the suitability of agricultural by-products for the manufacture of granular activated carbon. Fuel 1995, 1786–1791. [Google Scholar] [CrossRef]
- Kirubakaran, C.J.; Krishnaiah, K.; Seshadri, S.K. Experimental Study of the Production of Activated Carbon from Coconut Shells in a Fluidized Bed Reactor. Ind. Eng. Chem. Res. 1991, 30, 2411–2416. [Google Scholar] [CrossRef]
- Prauchner, M.J.; Rodríguez-Reinoso, F. Chemical versus physical activation of coconut shell: A comparative study. Microporous Mesoporous Mater. 2012, 152, 163–171. [Google Scholar] [CrossRef]
- Juárez-Galán, J.M.; Silvestre-Albero, A.; Silvestre-Albero, J.; Rodríguez-Reinoso, F. Synthesis of activated carbon with highly developed “mesoporosity”. Microporous Mesoporous Mater. 2009, 117, 519–521. [Google Scholar] [CrossRef]
- Bartocci, P.; Bidini, G.; Saputo, P.; Fantozzi, F. Biochar pellet carbon footprint. Chem. Eng. Trans. 2016, 50, 217–222. [Google Scholar] [CrossRef]
- Orrego-Romero, A.F.; Arbeláez-Pérez, O.F.; Bustamante-Londoño, F.; Villa-Holguín, A.L. Pelletization of catalysts supported on activated carbon. A Case Study: Clean synthesis of dimethyl carbonate from methanol and CO2. Revista Facultad de Ingeniería Universidad de Antioquia 2016, 38–47. [Google Scholar] [CrossRef]
- Chen, T.; Gu, W.; Li, G.; Wang, Q.; Liang, P.; Zhang, X.; Huang, X. Significant enhancement in catalytic ozonation efficacy: From granular to super-fine powdered activated carbon. Front. Environ. Sci. Eng. 2018, 12, 6. [Google Scholar] [CrossRef]
- Gil, M.V.; Álvarez-Gutiérrez, N.; Martínez, M.; Rubiera, F.; Pevida, C.; Morán, A. Carbon adsorbents for CO2 capture from bio-hydrogen and biogas streams: Breakthrough adsorption study. Chem. Eng. J. 2015, 269, 148–158. [Google Scholar] [CrossRef]
- Plaza, M.G.; González, A.S.; Pis, J.J.; Rubiera, F.; Pevida, C. Production of microporous biochars by single-step oxidation:Effect of activation conditions on CO2 capture. Appl. Energy 2014, 114, 551–562. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of gases in multimolecular layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Dubinin, M.M. Porous structure and adsorption properties of active carbons. In Chemistry and Physics of Carbon; Walker, P.L., Ed.; Marcel Dekker Inc.: New York, NY, USA, 1966; pp. 51–119. [Google Scholar]
- Stoeckli, F.; Ballerini, L. Evolution of microporosity during activation of carbon. Fuel 1991, 70, 557–559. [Google Scholar] [CrossRef]
- García, S.; Pis, J.J.; Rubiera, F.; Pevida, C. Predicting mixed-gas adsorption equilibria on activated carbon for precombustion CO2 capture. Langmuir 2013, 29, 6042–6052. [Google Scholar] [CrossRef] [PubMed]
- García, S.; Gil, M.V.; Martín, C.F.; Pis, J.J.; Rubiera, F.; Pevida, C. Breakthrough adsorption study of a commercial activated carbon for pre-combustion CO2 capture. Chem. Eng. J. 2011, 171, 549–556. [Google Scholar] [CrossRef]
- Rodríguez-Reinoso, F.; Molina-Sabio, M.; González, M.T. The use of steam and CO2 as activating agents in the preparation of activated carbons. Carbon 1995, 33, 15–23. [Google Scholar] [CrossRef]
- Do, D.D. Adsorption Analysis: Equilibria and Kinetics; Imperial College Press: London, UK, 1998. [Google Scholar]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Ritter, J.A.; Bhadra, S.J.; Ebner, A.D. On the use of the dual process Langmuir model for correlating unary equilibria and predicting mixed-gas adsorption equilibria. Langmuir 2011, 27, 4700–4712. [Google Scholar] [CrossRef] [PubMed]
- Bhadra, S.J.; Ebner, A.D.; Ritter, J.A. On the use of the dual process Langmuir model for predicting unary and binary isosteric heats of adsorption. Langmuir 2012, 28, 6935–6941. [Google Scholar] [CrossRef] [PubMed]
- Esteves, I.A.; Lopes, M.S.; Nunes, P.M.; Mota, J.P. Adsorption of natural gas and biogas components on activated carbon. Sep. Purif. Technol. 2008, 62, 281–296. [Google Scholar] [CrossRef]
- Álvarez-Gutiérrez, N.; García, S.; Gil, M.V.; Rubiera, F.; Pevida, C. Dynamic performance of biomass-based carbons for CO2/CH4 separation. Approximation to a pressure swing adsorption process for biogas upgrading. Energy Fuels 2016, 30, 5005–5015. [Google Scholar] [CrossRef]
- Ruthven, D.M.; Farooq, S.; Knaebel, K.S. Pressure Swing Adsorption; VCH Publishers: New York, NY, USA, 1994. [Google Scholar]
- Álvarez-Gutiérrez, N.; Gil, M.V.; Rubiera, F.; Pevida, C. Adsorption performance indicators for the CO2/CH4 separation: Application to biomass-based activated carbons. Fuel Proc. Technol. 2016, 142, 361–369. [Google Scholar] [CrossRef]
- Ben-Mansour, R.; Habib, M.; Bamidele, O.; Basha, M.; Qasem, N.; Peedikakkal, A.; Laoui, T.; Ali, M. Carbon Capture by Physical Adsorption: Materials, Experimental Investigations and Numerical Modeling and Simulations—A Review. Appl. Energy 2016, 161, 225–255. [Google Scholar] [CrossRef]
- Xu, X.; Zhao, X.; Sun, L.; Liu, X. Adsorption separation of carbon dioxide, methane, and nitrogen on Hβ and Na-exchanged β-zeolite. J. Natl. Gas Chem. 2008, 17, 391–396. [Google Scholar] [CrossRef]
- Altintas, C.; Avci, G.; Daglar, H.; Azar, A.N.V.; Velioglu, S.; Erucar, I.; Keskin, S. A database for CO2 Separation Performances of MOFs based on Computational Materials Screening. ACS Appl. Mater. Interfaces 2018. [Google Scholar] [CrossRef] [PubMed]
| Proximate Analysis (wt.%) | Ultimate Analysis (wt.%, daf) | ||||||
|---|---|---|---|---|---|---|---|
| Sample | Moisture | Ash (db) | C | H | N | S | O |
| CNS | 12.55 | 0.42 | 51.6 | 5.6 | 0.1 | 0 | 42.7 |
| Adsorbate | Vp (cm3/g) | SBET (m2/g) | Dubinin | ||||
|---|---|---|---|---|---|---|---|
| n | Smic (m2/g) | L0 (nm) | E0 (kJ/mol) | W0 (cm3/g) | |||
| N2 | 0.63 | 1378 | 2 | 1043 | 1.04 | 21.76 | 0.54 |
| CO2 | - | - | 1.77 | 1126 | 0.84 | 24.22 | 0.47 |
| Model | Component | T (°C) | qs1, qs2, qs and qs*(mol/kg) | b1, b2, b and b*(kPa) | n (Sips) t(Toth) | * | SSR (%) | |
|---|---|---|---|---|---|---|---|---|
| Dual-site | CH4 | 30 | 1.00 | 6.63 | 0.0137 | - | - | 0.04 |
| 0.0012 | ||||||||
| 50 | 0.0078 | - | - | |||||
| 0.0008 | ||||||||
| 70 | 0.0049 | - | - | |||||
| 0.0006 | ||||||||
| CO2 | 30 | 1.86 | 10.50 | 0.0235 | - | - | 0.20 | |
| 0.0017 | ||||||||
| 50 | 0.0133 | - | - | |||||
| 0.0010 | ||||||||
| 70 | 0.0078 | - | - | |||||
| 0.0006 | ||||||||
| Sips | CH4 | 30 | 8.32 | 0.0013 | 1.21 | 0.25 | 0.03 | |
| 50 | 0.0008 | 1.20 | ||||||
| 70 | 0.0006 | 1.18 | ||||||
| CO2 | 30 | 14.25 | 0.0016 | 1.30 | 0.22 | 0.12 | ||
| 50 | 0.0009 | 1.31 | ||||||
| 70 | 0.0006 | 1.29 | ||||||
| Toth | CH4 | 30 | 11.64 | 0.0022 | 0.54 | 0.21 | 0.03 | |
| 50 | 0.0013 | 0.56 | ||||||
| 70 | 0.0008 | 0.57 | ||||||
| CO2 | 30 | 20.73 | 0.0039 | 0.47 | 0.12 | 0.13 | ||
| 50 | 0.0022 | 0.47 | ||||||
| 70 | 0.0013 | 0.48 | ||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdeljaoued, A.; Querejeta, N.; Durán, I.; Álvarez-Gutiérrez, N.; Pevida, C.; Chahbani, M.H. Preparation and Evaluation of a Coconut Shell-Based Activated Carbon for CO2/CH4 Separation. Energies 2018, 11, 1748. https://doi.org/10.3390/en11071748
Abdeljaoued A, Querejeta N, Durán I, Álvarez-Gutiérrez N, Pevida C, Chahbani MH. Preparation and Evaluation of a Coconut Shell-Based Activated Carbon for CO2/CH4 Separation. Energies. 2018; 11(7):1748. https://doi.org/10.3390/en11071748
Chicago/Turabian StyleAbdeljaoued, Amna, Nausika Querejeta, Inés Durán, Noelia Álvarez-Gutiérrez, Covadonga Pevida, and Mohamed Hachemi Chahbani. 2018. "Preparation and Evaluation of a Coconut Shell-Based Activated Carbon for CO2/CH4 Separation" Energies 11, no. 7: 1748. https://doi.org/10.3390/en11071748
APA StyleAbdeljaoued, A., Querejeta, N., Durán, I., Álvarez-Gutiérrez, N., Pevida, C., & Chahbani, M. H. (2018). Preparation and Evaluation of a Coconut Shell-Based Activated Carbon for CO2/CH4 Separation. Energies, 11(7), 1748. https://doi.org/10.3390/en11071748






