Large-Signal Stabilization of Three-Phase VSR with Constant Power Load
Abstract
:1. Introduction
- (1)
- Obtaining a large-signal model of three-phase VSR with CPL based on mixed potential theory, whose stable boundary is derived when load power jumps.
- (2)
- Proposing a voltage control scheme to improve the large-signal stability based on ADRC, and whose control stability is proven.
- (3)
- Deriving the stable boundary of VSR with CPL based on ADRC, which proves that the proposed control scheme expands the load power jump range effectively.
2. Large-Signal Stability Analysis Based on Mixed Potential Theory under PI Control
2.1. Introduction to the Mixed Potential Theory
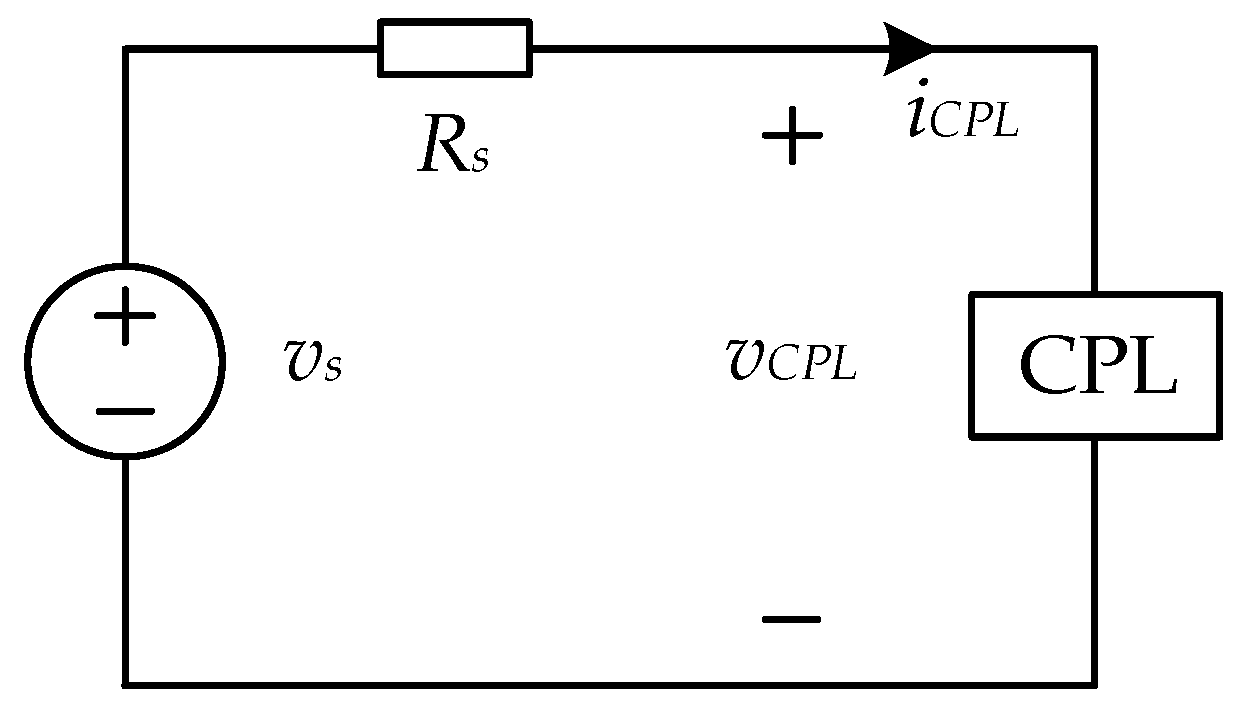
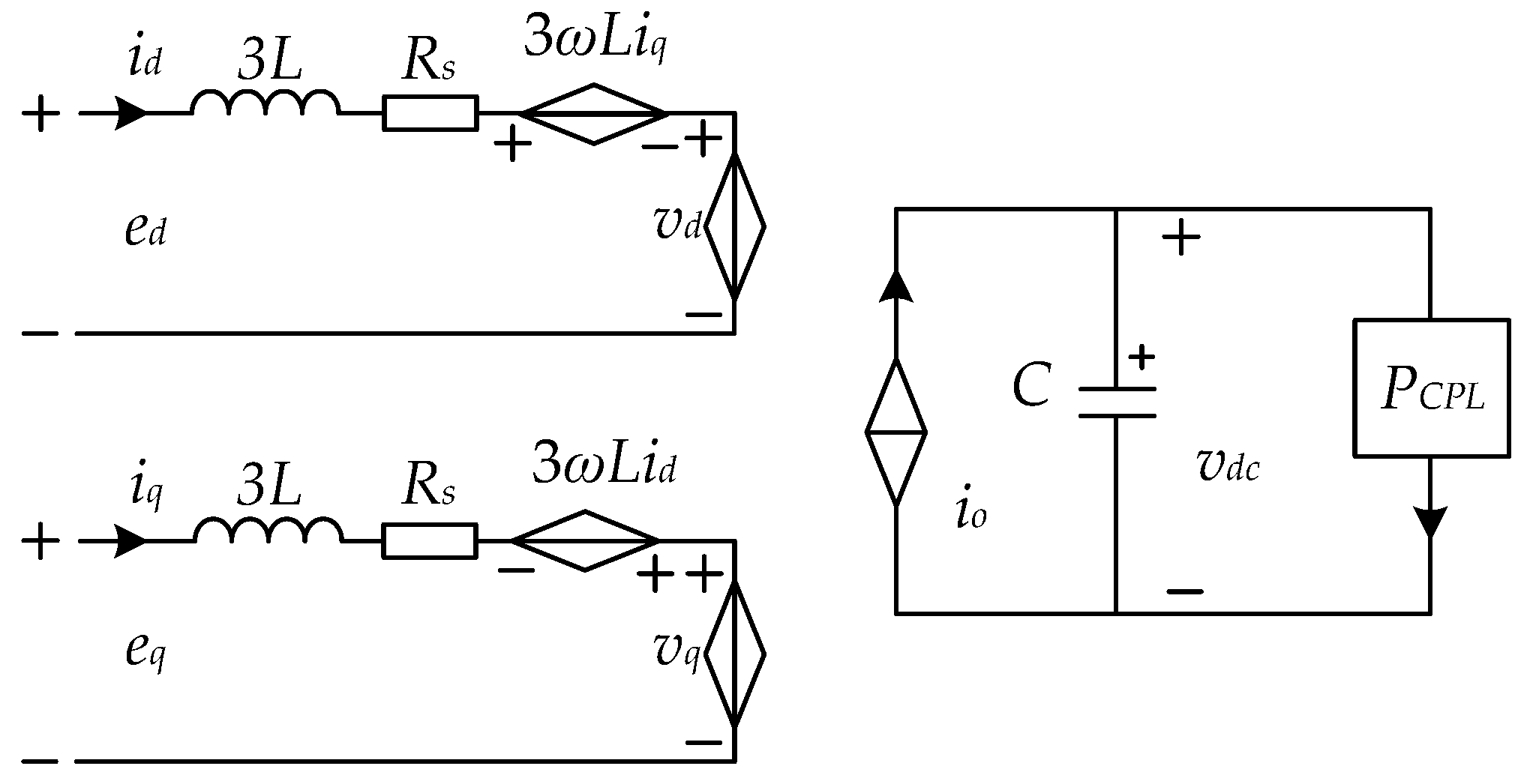
2.2. Stability Problems of the Three-Phase VSR with CPL
2.3. Analysis of Power Jump Range of Three-Phase VSR with CPL
3. Control Scheme and Stability Analysis Based on ADRC
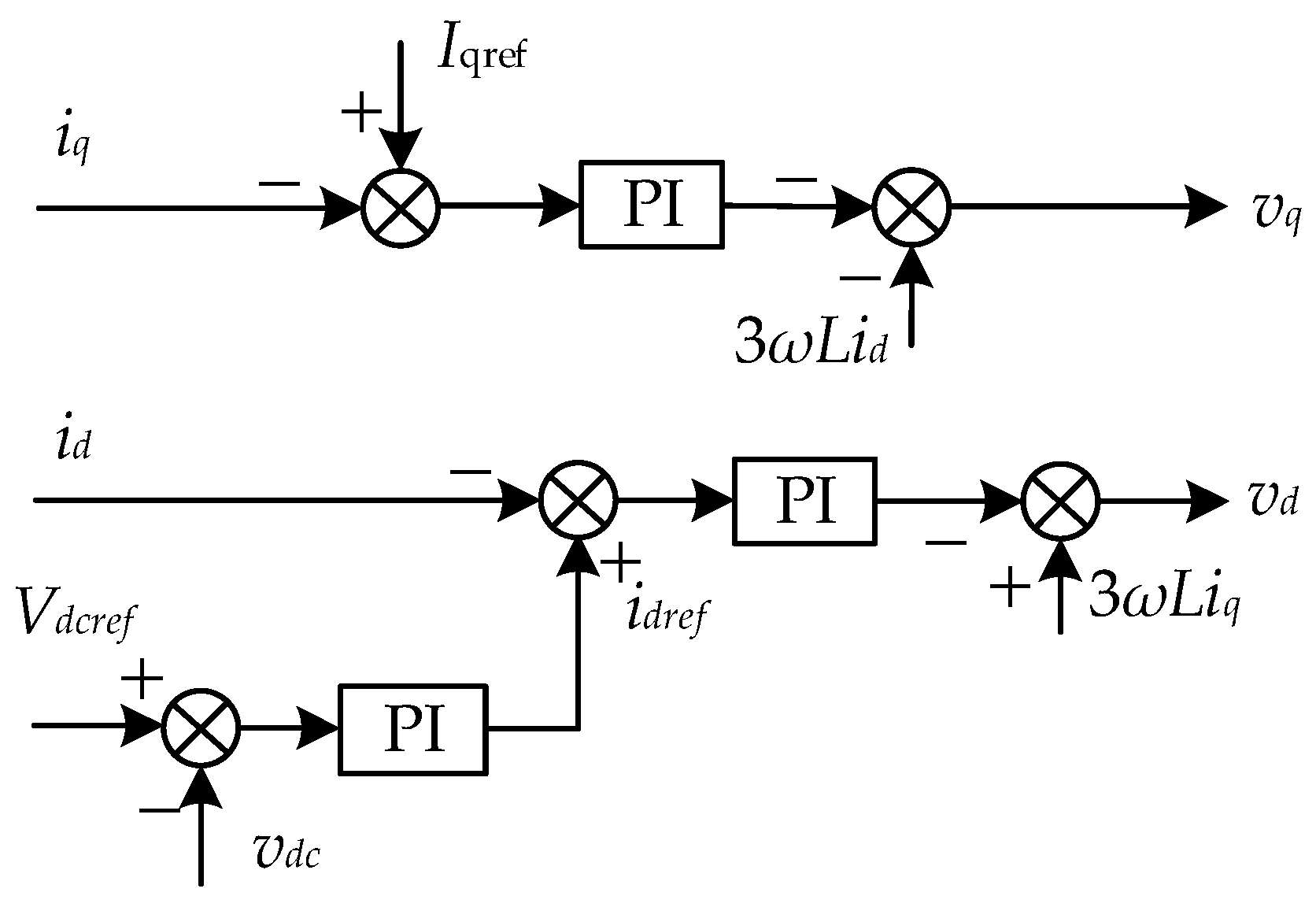
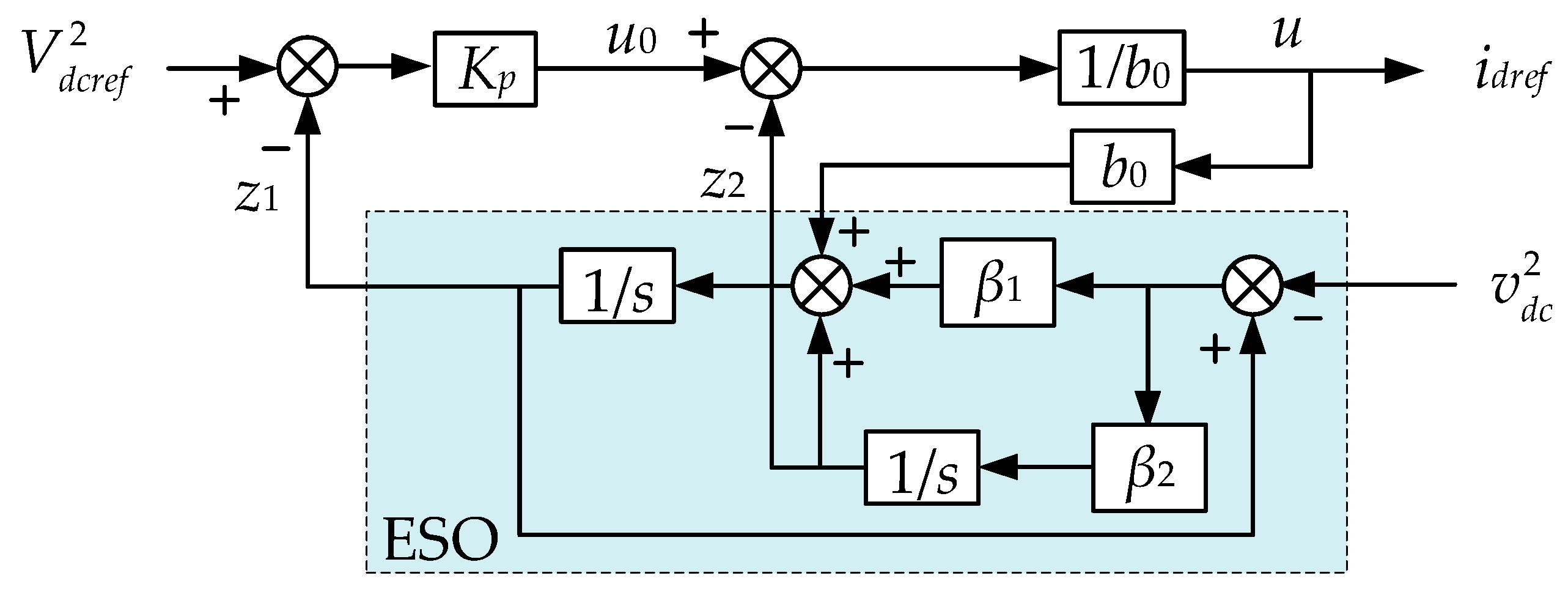
3.1. Voltage Loop Control Scheme Based on the First Order ADRC
3.2. Parameters Simplification and Stability Proof
3.3. Large Sigal Stability Analysis of Three-Phase VSR with CPL Based on ADRC
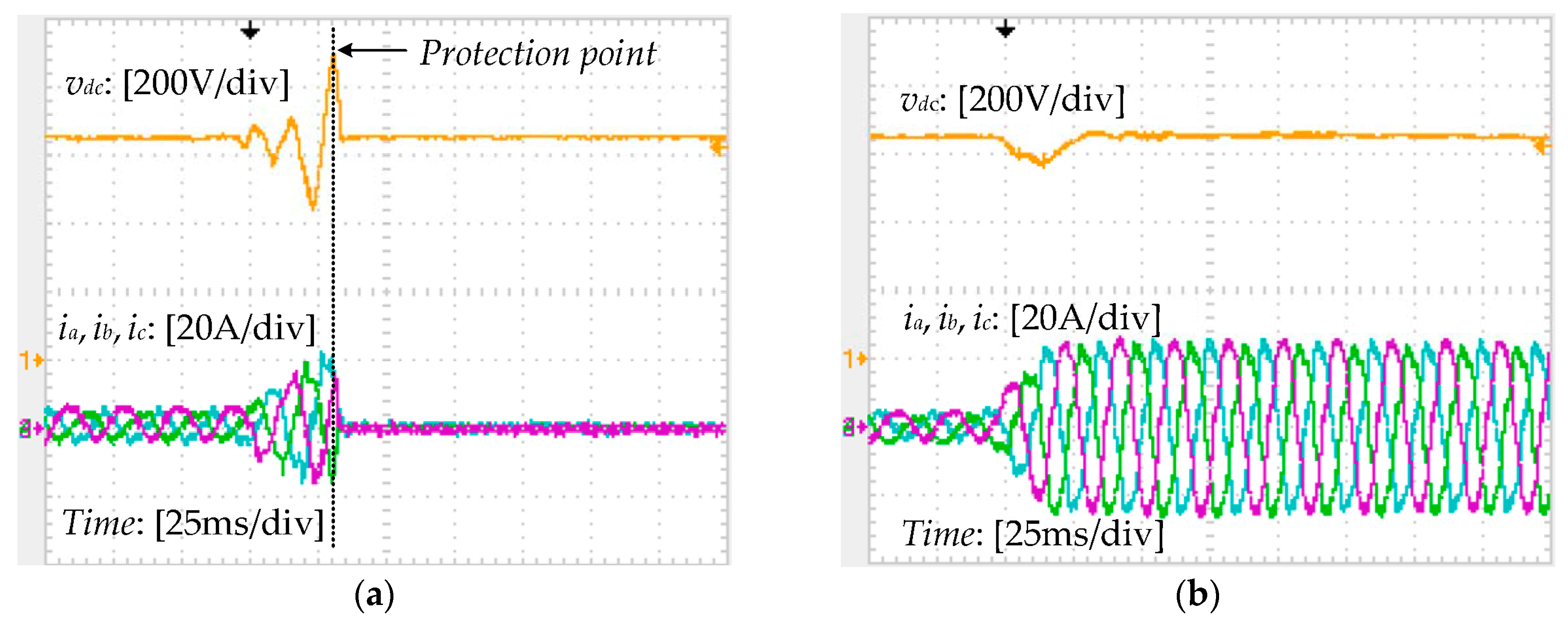
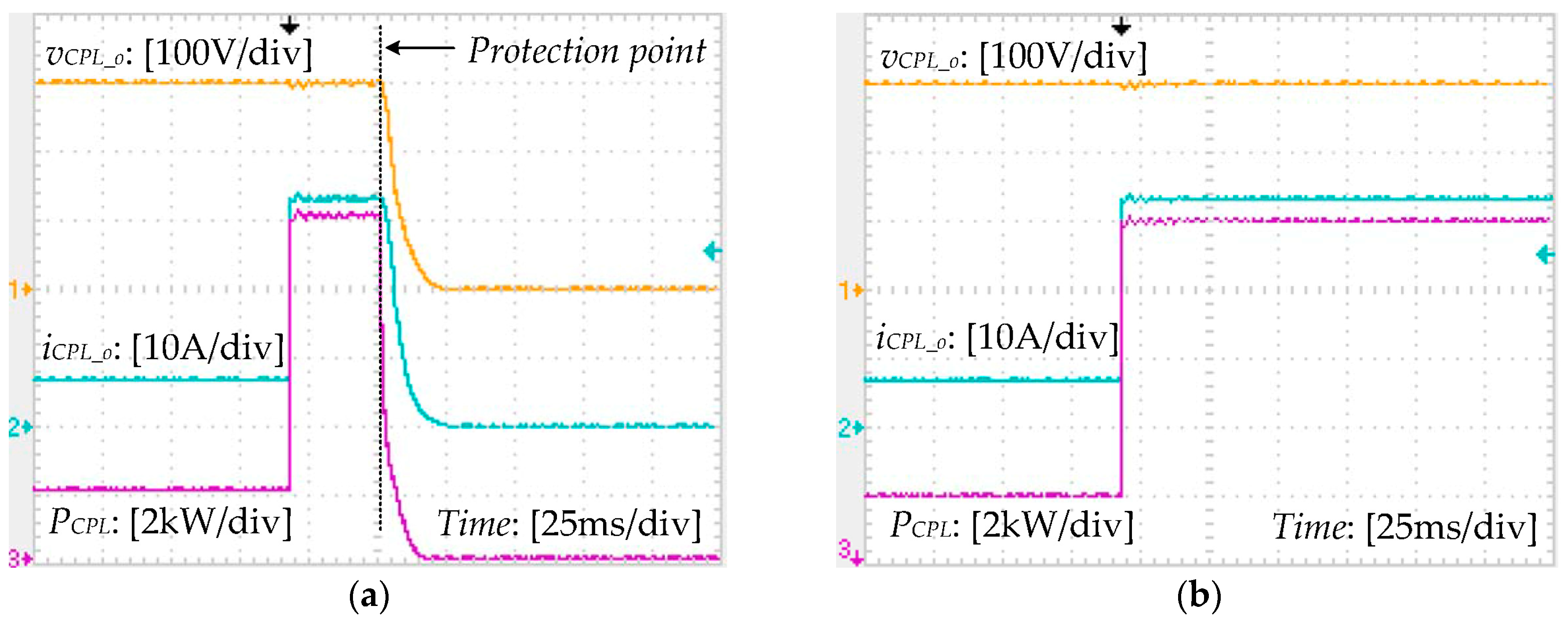
4. Experiments
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Mixed Potential Theory Stability Theorem 3
References
- Ramirez-Hernandez, J.; Araujo-Vargas, I.; Rivera, M.; Ramirez-Hernandez, J.; Araujo-Vargas, I.; Rivera, M. A Modular AC-DC Power Converter with Zero Voltage Transition for Electric Vehicles. Energies 2017, 10, 1386. [Google Scholar] [CrossRef]
- Nami, A.; Liang, J.; Dijkhuizen, F.; Demetriades, G.D. Modular Multilevel Converters for HVDC Applications: Review on Converter Cells and Functionalities. IEEE Trans. Power Electron. 2015, 30, 18–36. [Google Scholar] [CrossRef]
- Mehrasa, M.; Pouresmaeil, E.; Zabihi, S.; Vechiu, I.; Catalao, J.P.S. A multi-loop control technique for the stable operation of modular multilevel converters in HVDC transmission systems. Int. J. Electr. Power Energy Syst. 2018, 96, 194–207. [Google Scholar] [CrossRef]
- Zhang, X.; Zhong, Q.C.; Ming, W.L. Stabilization of a Cascaded DC Converter System via Adding a Virtual Adaptive Parallel Impedance to the Input of the Load Converter. IEEE Trans. Power Electron. 2015, 31, 1826–1832. [Google Scholar] [CrossRef]
- Du, W.; Zhang, J.; Zhang, Y.; Qian, Z. Stability Criterion for Cascaded System with Constant Power Load. IEEE Trans. Power Electr. 2013, 28, 1843–1851. [Google Scholar] [CrossRef]
- Mishima, T.; Akamatsu, K.; Nakaoka, M. A High Frequency-Link Secondary-Side Phase-Shifted Full-Range Soft-Switching PWM DC–DC Converter with ZCS Active Rectifier for EV Battery Chargers. IEEE Trans. Power Electr. 2013, 28, 5758–5773. [Google Scholar] [CrossRef]
- Shin, S.C.; Lee, H.J.; Kim, Y.H.; Lee, J.H.; Won, C.Y. Transient Response Improvement at Startup of a Three-Phase AC/DC Converter for a DC Distribution System in Commercial Facilities. IEEE Trans. Power Electron. 2014, 29, 6742–6753. [Google Scholar] [CrossRef]
- Cao, W.; Mecrow, B.C.; Atkinson, G.J.; Bennett, J.W.; Atkinson, D.J. Overview of Electric Motor Technologies Used for More Electric Aircraft (MEA). IEEE Trans. Ind. Electron. 2012, 59, 3523–3531. [Google Scholar] [CrossRef]
- Verma, A.K.; Jain, C.; Singh, B.; Shahani, D.T. Adaptive noise cancellation based harmonic elimination in grid integrated photovoltaic system. IET Renew. Power Gener. 2016, 10, 1096–1104. [Google Scholar] [CrossRef]
- Huang, M.; Peng, Y.; Chi, K.T.; Liu, Y.; Sun, J.; Zha, X. Bifurcation and large-signal stability analysis of three-phase voltage source converter under grid voltage dips. IEEE Trans. Power Electron. 2017, 32, 8868–8879. [Google Scholar] [CrossRef]
- Mehrasa, M.; Pouresmaeil, E.; Zabihi, S.; Catalao, J.P.S. Dynamic model, control and stability analysis of MMC in HVDC transmission systems. IEEE Trans. Power Deliv. 2016, 32, 1471–1482. [Google Scholar] [CrossRef]
- Mehrasa, M.; Pouresmaeil, E.; Zabihi, S.; Rodrigues, E.M.G.; Catalão, J.P.S. A control strategy for the stable operation of shunt active power filters in power grids. Energy 2016, 96, 325–334. [Google Scholar] [CrossRef]
- Pouresmaeil, E.; Shaker, H.R.; Mehrasa, M.; Shokridehaki, M.A.; Rodrigues, E.M.G. Stability analysis for operation of DG units in smart grids. In Proceedings of the IEEE International Conference on Power Engineering, Energy and Electrical Drives, Riga, Latvia, 11–13 May 2015; pp. 447–452. [Google Scholar]
- Pouresmaeil, E.; Bo, N.; Mehrasa, M.; Erdinc, O.; Catalao, J.P.S. A control algorithm for the stable operation of interfaced converters in microgrid systems. In Proceedings of the Innovative Smart Grid Technologies Conference Europe, Istanbul, Turkey, 12–15 October 2014; pp. 1–6. [Google Scholar]
- Rahimi, A.M.; Emadi, A. Active Damping in DC/DC Power Electronic Converters: A Novel Method to Overcome the Problems of Constant Power Loads. IEEE Trans. Ind. Electron. 2009, 56, 1428–1439. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, Y.; Zhang, W.; Ma, S. Stability Criteria for Constant Power Loads with Multistage LC Filters. IEEE Trans. Veh. Technol. 2011, 60, 2042–2049. [Google Scholar] [CrossRef]
- Zhang, M.; Li, Y.; Liu, F.; Luo, L.; Cao, Y.; Shahidehpour, M. Voltage Stability Analysis and Sliding Mode Control Method for Rectifier in DC Systems with Constant Power Loads. IEEE J. Emerg. Sel. Top. Power Electr. 2017, 5, 1621–1630. [Google Scholar] [CrossRef]
- Mitchell, D.M. Damped EMI Filters for Switching Regulators. IEEE Trans. Electromagn. Compat. 1978, EMC-20, 457–463. [Google Scholar] [CrossRef]
- Cespedes, M.; Xing, L.; Sun, J. Constant-Power Load System Stabilization by Passive Damping. IEEE Trans. Power Electr. 2011, 26, 1832–1836. [Google Scholar] [CrossRef]
- Liu, B.; Ben, H.; Zhang, X.; Meng, T.; Wang, X. Stabilization of a cascaded AC/DC system based on small signal analysis, in Book Stabilization of a cascaded AC/DC system based on small signal analysis. In Proceedings of the International Conference on Electrical Machines and Systems, Sydney, Australia, 11–14 August 2017; pp. 1–6. [Google Scholar]
- Hatua, K.; Jain, A.K.; Banerjee, D.; Ranganathan, V.T. Active Damping of Output LC Filter Resonance for Vector-Controlled VSI-Fed AC Motor Drives. IEEE Trans. Ind. Electron. 2012, 59, 334–342. [Google Scholar] [CrossRef]
- Dannehl, J.; Liserre, M.; Fuchs, F.W. Filter-Based Active Damping of Voltage Source Converters with LCL Filter. IEEE Trans. Ind. Electron. 2011, 58, 3623–3633. [Google Scholar] [CrossRef]
- Liu, S.; Zhou, L.; Lu, W. Simple analytical approach to predict large-signal stability region of a closed-loop boost DC–DC converter. IET Power Electron. 2013, 6, 488–494. [Google Scholar] [CrossRef]
- Weaver, W.W.; Iii, R.D.R.; Wilson, D.G.; Matthews, R.C. Metastability of Pulse Power Loads Using the Hamiltonian Surface Shaping Method. IEEE Trans. Energy Convers. 2017, 32, 820–828. [Google Scholar] [CrossRef]
- Zhang, X.N.; Vilathgamuwa, D.M.; Foo, G.; Tseng, K.J.; Kandasamy, K.; Gupta, A.K.; Chandana, G. Cascaded sliding mode control for global stability of three phase AC/DC PWM rectifier with rapidly varying power electronic loads. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–14 November 2013; pp. 4580–4587. [Google Scholar]
- Magne, P.; Nahid-Mobarakeh, B.; Pierfederici, S. Dynamic Consideration of DC Microgrids with Constant Power Loads and Active Damping System—A Design Method for Fault-Tolerant Stabilizing System. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 562–570. [Google Scholar] [CrossRef]
- Zhang, W.; Hou, Y.; Liu, X.; Zhou, Y. Switched Control of Three-Phase Voltage Source PWM Rectifier Under a Wide-Range Rapidly Varying Active Load. IEEE Trans. Power Electr. 2012, 27, 881–890. [Google Scholar] [CrossRef]
- Zhang, P.H.; Yang, G.J.; Tie-Cai, L.I. Direct Voltage Control of Three-phase PWM Rectifier Based on Feedback Linearization. Proc. CSEE 2010, 30, 39–46. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Tian, J.; Zhang, S.; Zhang, Y.; Li, T. Active disturbance rejection control based robust output feedback autopilot design for airbreathing hypersonic vehicles. ISA Trans. 2018, 74, 45–59. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Hong, Y.; Chen, X.; Huo, W. Switching control of wind turbine sub-controllers based on an active disturbance rejection technique. Energies 2016, 9, 793. [Google Scholar] [CrossRef]
- Brayton, R.K.; Moser, J.K. A theory of nonlinear networks. I. Q. Appl. Math. 1964, 2, 1–33. [Google Scholar] [CrossRef]
- Jeltsema, D.; Scherpen, J.M.A. On Brayton and Moser’s missing stability theorem. IEEE Trans. Circuits Syst. II Express Briefs 2005, 52, 550–552. [Google Scholar] [CrossRef]




| Symbol | Quantity | Value |
|---|---|---|
| Eabc | Grid phase voltage | 220 V |
| fg | Grid frequency | 50 Hz |
| fs | PWM frequency | 16 kHz |
| L | Input inductance | 3.2 mH |
| Vdcref | Bus voltage | 650 V |
| R | Equivalent resistance | 0.2 Ω |
| C | Bus capacitance | 100 μF |
| Kip | Proportional gain of the current PI regulator | 5 |
| Kii | Integral gain of the current PI regulator | 100 |
| Kvp | Proportional gain of the voltage PI regulator | 0.2 |
| Kvi | Integral gain of the voltage PI regulator | 80 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Ben, H.; Zhang, X. Large-Signal Stabilization of Three-Phase VSR with Constant Power Load. Energies 2018, 11, 1706. https://doi.org/10.3390/en11071706
Liu B, Ben H, Zhang X. Large-Signal Stabilization of Three-Phase VSR with Constant Power Load. Energies. 2018; 11(7):1706. https://doi.org/10.3390/en11071706
Chicago/Turabian StyleLiu, Bo, Hongqi Ben, and Xiaobing Zhang. 2018. "Large-Signal Stabilization of Three-Phase VSR with Constant Power Load" Energies 11, no. 7: 1706. https://doi.org/10.3390/en11071706
APA StyleLiu, B., Ben, H., & Zhang, X. (2018). Large-Signal Stabilization of Three-Phase VSR with Constant Power Load. Energies, 11(7), 1706. https://doi.org/10.3390/en11071706





