An Efficient Regional Sensitivity Analysis Method Based on Failure Probability with Hybrid Uncertainty
Abstract
:1. Introduction
2. Review of Random-Evidence Hybrid Reliability Analysis and CFP Plot
2.1. Fundamental Theory of Random-Evidence Hybrid Reliability Analysis
2.2. Brief Introduction to Random-Evidence Hybrid CPF Plot
- (1)
- For each JFE , generate samples of aleatory uncertainty variables according to their joint probability density function (PDF). Based on Equation (9), the corresponding output values are obtained.
- (2)
- Calculate the values by Equation (11).
- (3)
- Sort the samples of the random variables in ascending order and rename them as , the corresponding values of the indicator function Equation (11) are represented as .
- (4)
- The at q quantile for the random variable is estimated as follows according to Equation (12):
- (5)
- Taking the former k FEs of the aleatory uncertain variable , the corresponding can be given as follows according to Equation (16).
3. RS-MCS Procedure and KKTO Method
3.1. RS-MCS Procedure
- (1)
- Generate samples of random variables according to their joint PDF and denote as .
- (2)
- Generate samples of indicator variables and denoted as . Then obtain their corresponding JFEs according to Equation (21) and denote them as .
- (3)
- According to Equation (24), can be estimated by the following equation
- (4)
- Sort the samples of the random variables in ascending order and remark them as , where . Then, the at q quantile for the aleatory uncertain variable can be estimated as follows
- (5)
- Sort the sth column of in ascending order and denote it as and the corresponding JFEs are remarked as . The number of JFEs containing the former kth FEs of is denoted as . Then, the containing the former kth FEs of can be estimated as follows
3.2. KKTO Optimization Method
- (1)
- For the ith simulation sample , the lower bound and upper bound of are denoted as and , respectively. Then, the minimal vertex point is obtained by the following formulawhere , , and are the jth element of the vectors , , and , respectively.
- (2)
- Check whether meets the following condition
4. Random-Evidence Hybrid Based Active Learning Kriging Model
4.1. Basic Idea
4.2. ERF Based-Active Learning Kriging Surrogate Model
- (1)
- Generate a large quantity of candidate samples and denote as . For a random variable, the candidate samples can be sampled based on its PDF. For an evidence variable, it is first transformed to a random variable using the following uniformity approach [38,39],where and are upper bound and lower bound of ith FE of the jth evidence variable. can be considered as the PDF of epistemic uncertain variables, then the candidate sample of the evidence variables are generated.
- (2)
- Generate 12 initial training samples and denote them as . Then, obtain their corresponding response values of limit state function and construct an initial kriging model.
- (3)
- Select a sample with the largest ERF in candidate samples space based on Equation (32) and denote it as .
- (4)
- If the selected sample satisfies the following convergence criteria, go to step (6). Otherwise, go on.
- (5)
- Add into training samples and update the kriging model. Go to step (3)
- (6)
- Exit loop.
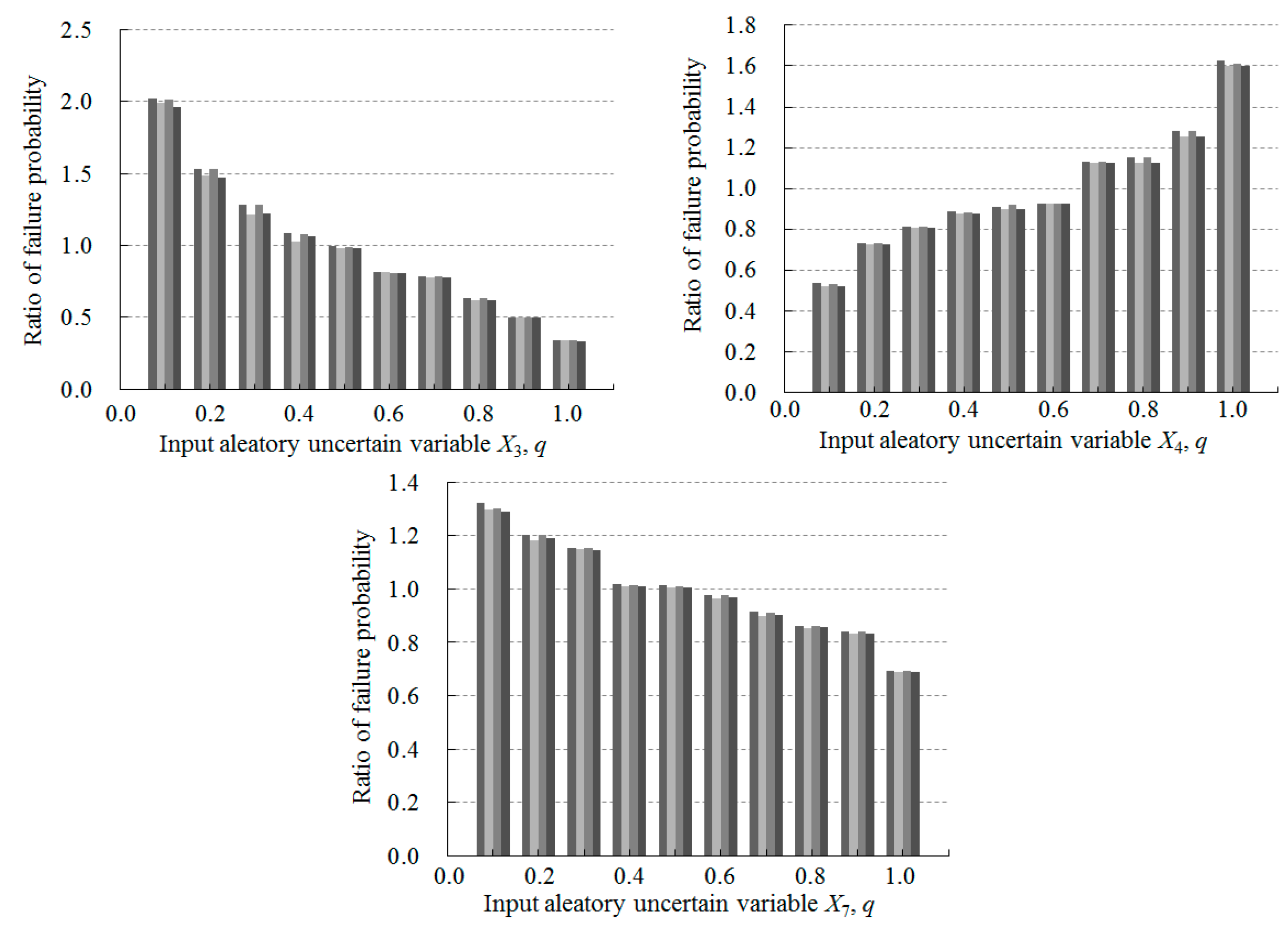
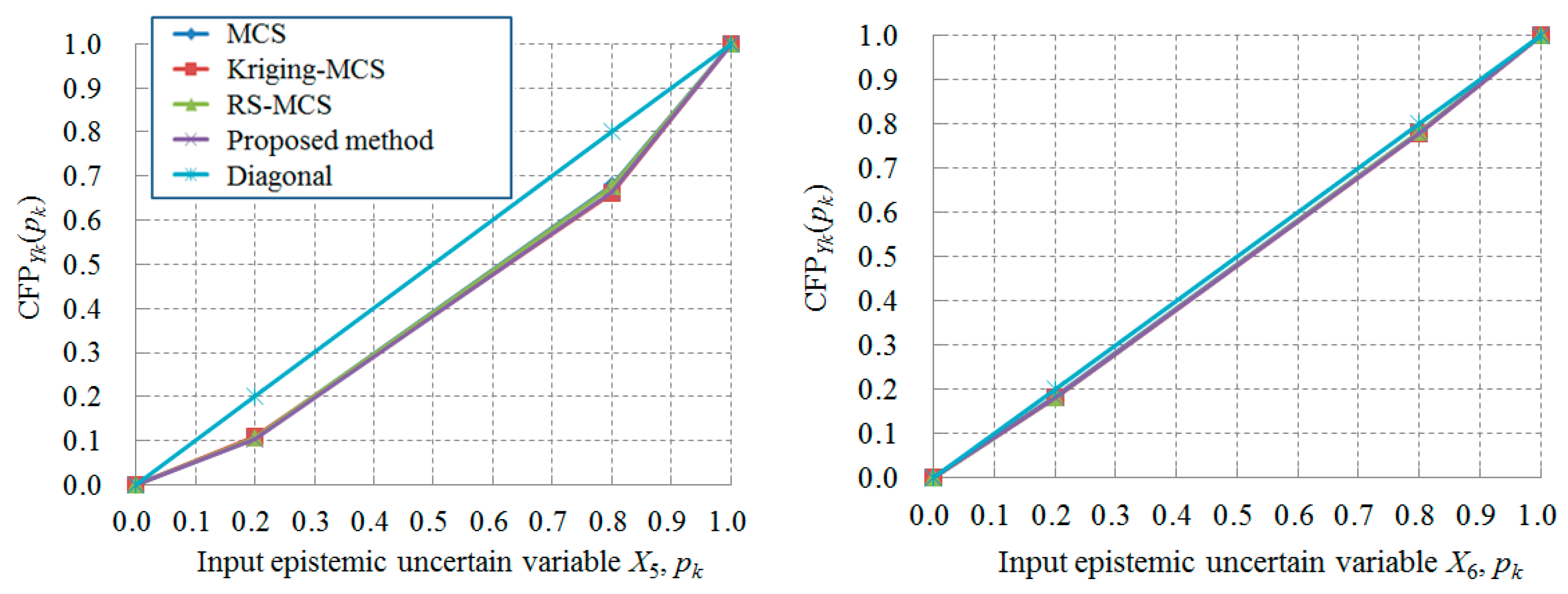
5. Examples and Discussion
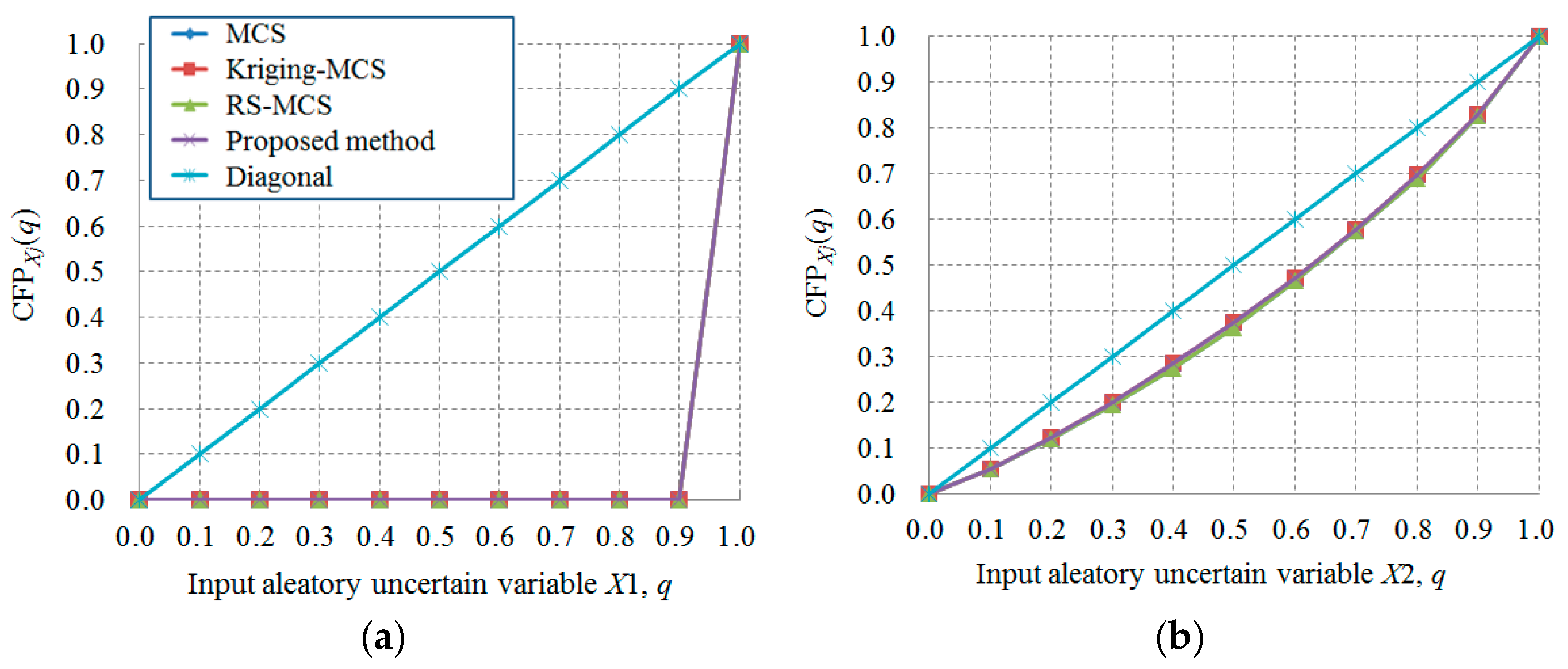
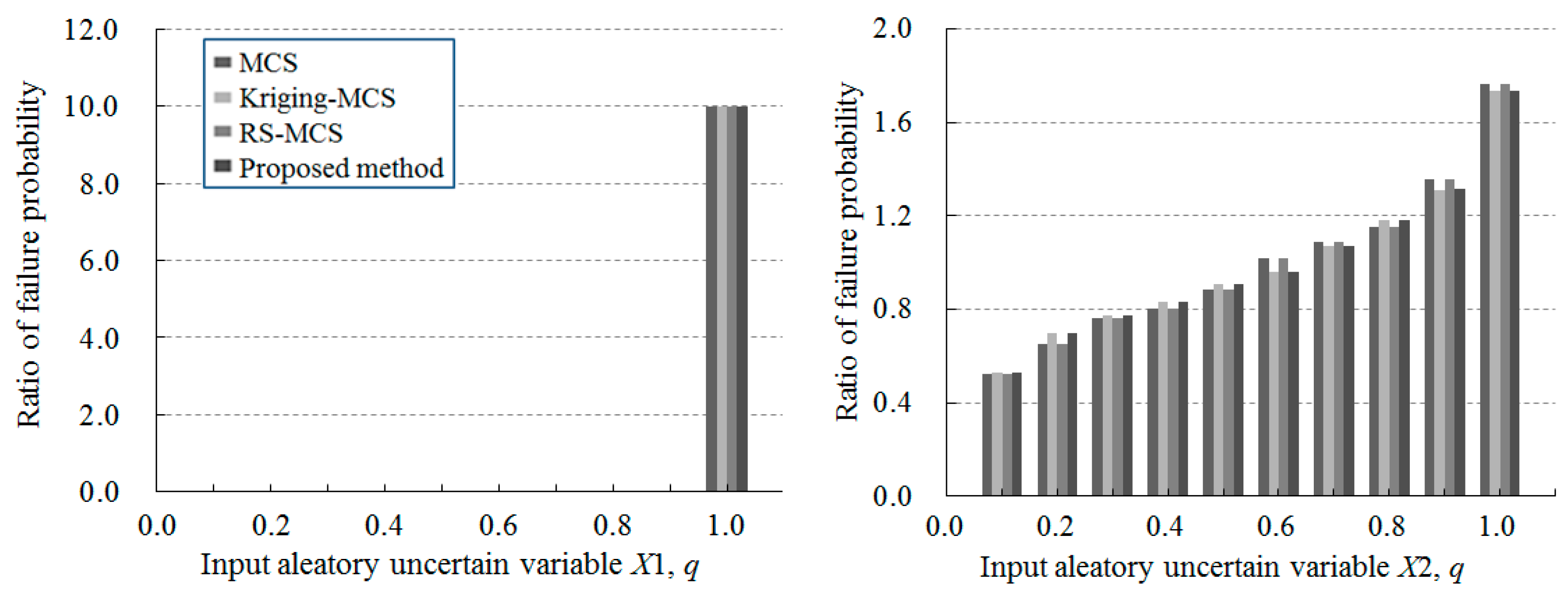
5.1. Example 1. Numerical Example
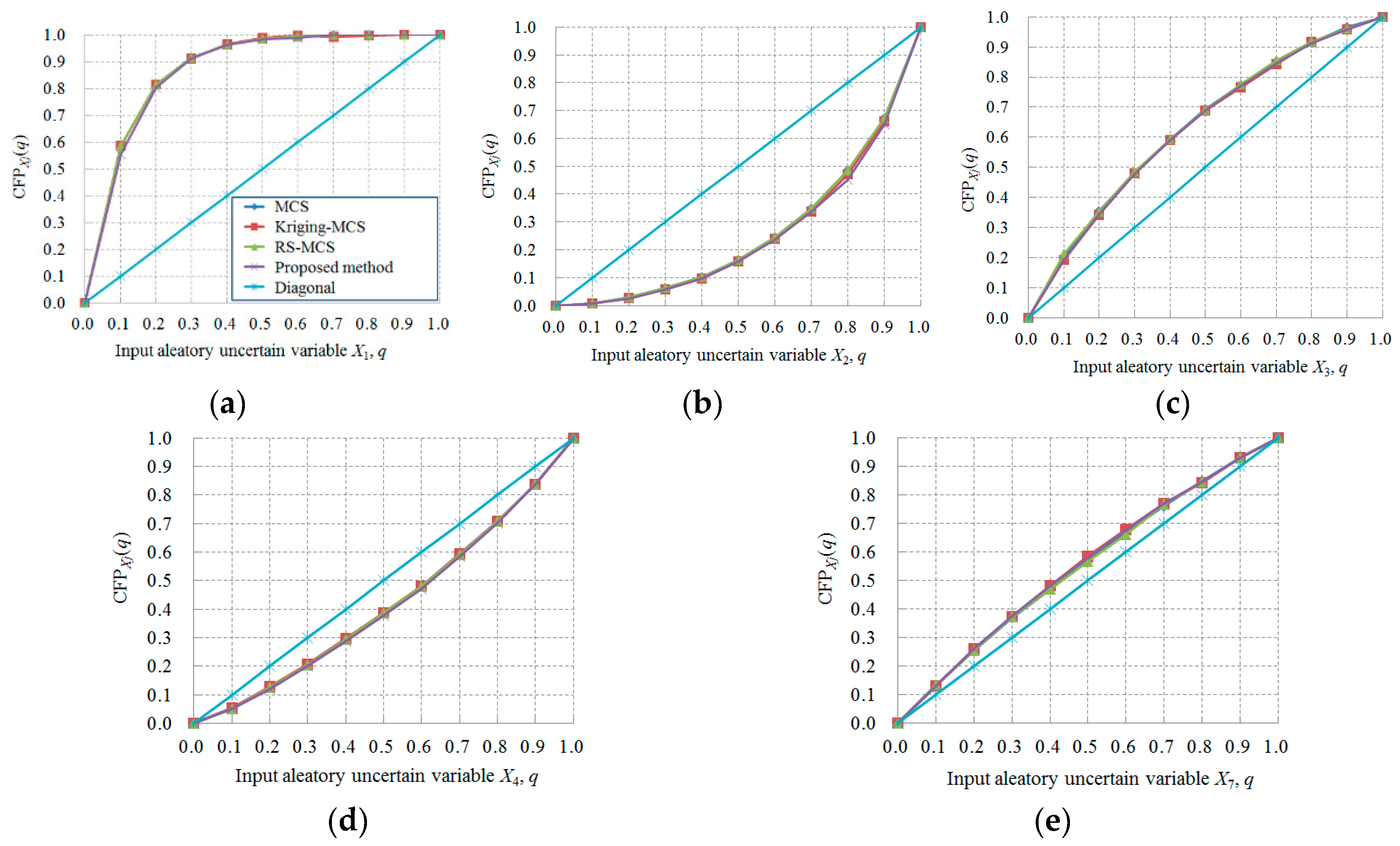
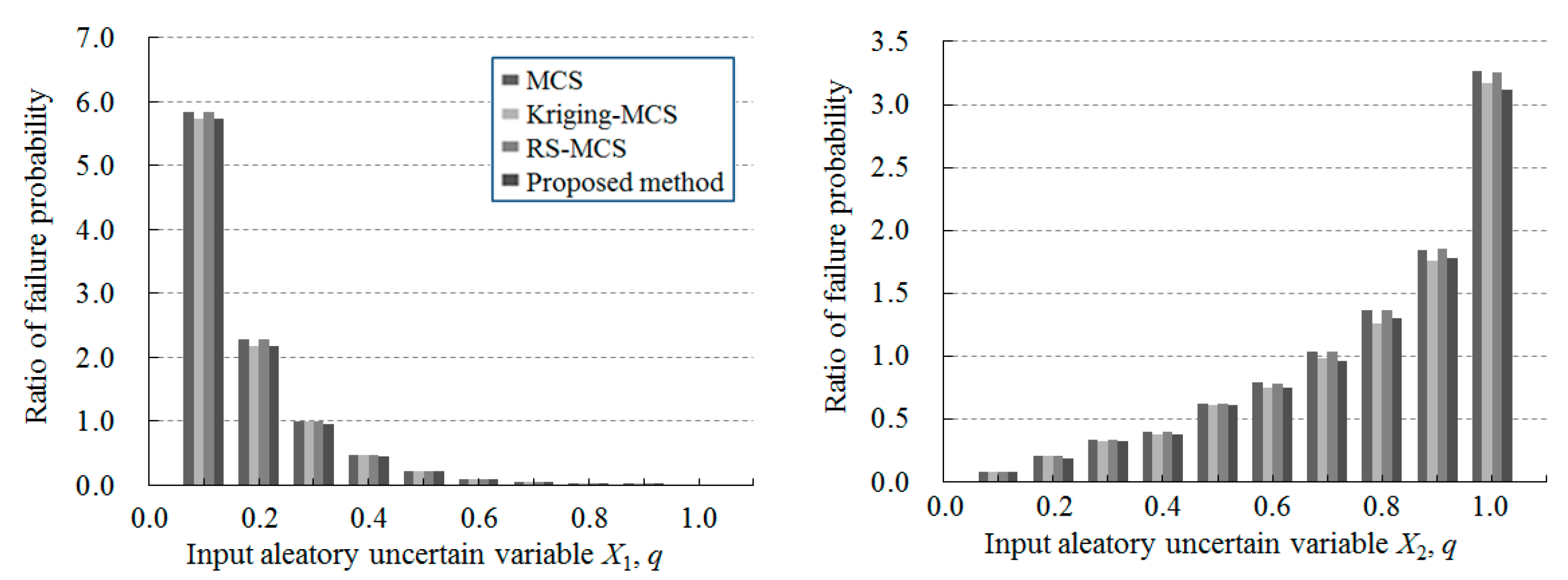
5.2. Example 2. A Certain System
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Lu, Z.; Song, S.; Yue, Z.; Wang, J. Reliability sensitivity method by line sampling. Struct. Saf. 2008, 30, 517–532. [Google Scholar] [CrossRef]
- Cui, L.; Lu, Z.; Wang, Q. Parametric sensitivity analysis of the importance measure. Mech. Syst. Signal Process. 2012, 28, 482–491. [Google Scholar] [CrossRef]
- Song, S.; Lu, Z.; Qiao, H. Subset simulation for structural reliability sensitivity analysis. Reliab. Eng. Syst. Saf. 2009, 94, 658–665. [Google Scholar] [CrossRef]
- Christen, J.L.; Ichchou, M.; Troclet, B.; Bareile, O.; Ouisse, M. Global sensitivity analysis and uncertainties in SEA models of vibroacoustic systems. Mech. Syst. Signal Process. 2017, 90, 365–377. [Google Scholar] [CrossRef]
- Helton, J.C.; Johnson, J.D.; Sallaberry, C.J.; Storlie, C.B. Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliab. Eng. Syst. Saf. 2006, 91, 1175–1209. [Google Scholar] [CrossRef] [Green Version]
- Rakovec, O.; Hill, M.C.; Clark, M.P.; Weerts, A.H.; Teuling, A.J. Distributed Evaluation of Local Sensitivity Analysis (DELSA), with application to hydrologic models. Water Resour. Res. 2014, 50, 409–426. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Lu, Z.; Cui, L.; Song, S. Reliability sensitivity algorithm based on stratified importance sampling method for multiple failure modes systems. Chin. J. Aeronaut. 2010, 23, 660–669. [Google Scholar]
- Sudret, B. Global sensitivity analysis using polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2008, 93, 964–979. [Google Scholar] [CrossRef]
- Wei, P.; Lu, Z.; Hao, W.; Wang, B. Efficient sampling methods for global reliability sensitivity analysis. Comput. Phys. Commun. 2012, 183, 1728–1743. [Google Scholar] [CrossRef]
- Zhou, C.; Lu, Z.; Li, L.; Feng, J.; Wang, B. A new algorithm for variance based importance analysis of models with correlated inputs. Appl. Math. Model. 2013, 37, 864–875. [Google Scholar] [CrossRef]
- Saltelli, A.; Marivoet, J. Non-parametric statistics in sensitivity analysis for model output: A comparison of selected techniques. Reliab. Eng. Syst. Saf. 1990, 28, 229–253. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Borgonovo, E.; Castaings, W.; Tarantola, S. Moment independent importance measures: New results and analytical test cases. Risk Anal. 2011, 31, 404–428. [Google Scholar] [CrossRef] [PubMed]
- Tang, Z.; Lu, Z.; Jiang, B.; Pan, W.; Zhang, F. Entropy-based importance measure for uncertain model inputs. AIAA J. 2013, 51, 2319–2334. [Google Scholar]
- Li, G.; Lu, Z.; Lu, Z.; Xu, J. Regional sensitivity analysis of aleatory and epistemic uncertainties on failure probability. Mech. Syst. Signal Process. 2014, 46, 209–226. [Google Scholar] [CrossRef]
- Bolado-Lavin, R.; Castaings, W.; Tarantola, S. Contribution to the sample mean plot for graphical and numerical sensitivity analysis. Reliab. Eng. Syst. Saf. 2009, 94, 1041–1049. [Google Scholar] [CrossRef]
- Tarantola, S.; Kopustinskas, V.; Bolado-Lavin, R.; Kaliatka, A.; Ušpuras, E.; Vaišnoras, M. Sensitivity analysis using contribution to sample variance plot: Application to a water hammer model. Int. J. Nonlinear Sci. Numer. Simul. 2015, 99, 62–73. [Google Scholar] [CrossRef]
- Ferson, S.; Kreinovick, V.; Ginzburg, L.; Sentz, F. Constructing Probability Boxes and Dempster-Shafer Structures; Technical Report; Sandia National Laboratories: Albuquerque, NM, USA, 2003. [Google Scholar]
- Sentz, K.; Ferson, S. Combination of Evidence in Dempster-Shafer Theory; Sandia National Laboratories: Albuquerque, NM, USA, 2002. [Google Scholar]
- Ferson, S.; Nelsen, R.B.; Hajagos, J.; Berleant, D.J.; Zhang, J.; Tucker, W.T.; Ginzburg, L.R.; Oberkampf, W.L. Dependence in Probabilistic Modeling, Dempster-Shafer Theory, and Probability Bounds Analysis; Report No. SAND2004-3072; Sandia National Laboratories: Albuquerque, NM, USA, 2004. [Google Scholar]
- Tonon, F. Using random set theory to propagate epistemic uncertainty through a mechanical system. Reliab. Eng. Syst. Saf. 2004, 85, 169–181. [Google Scholar] [CrossRef]
- Guo, S.; Zhen, L.U.; Feng, Y. A non-probabilistic model of structural reliability based on interval analysis. Chin. J. Comput. Mech. 2001, 18, 56–60. [Google Scholar]
- Li, L.; Lu, Z.; Hu, J.X. A new kind of regional importance measure of the input variable and its state dependent parameter solution. Reliab. Eng. Syst. Saf. 2014, 128, 1–16. [Google Scholar] [CrossRef]
- Wei, P.; Lu, Z.; Wu, D.; Zhou, C. Moment-independent regional sensitivity analysis: Application to an environmental model. Environ. Model. Softw. 2013, 47, 55–63. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, Z.; Cheng, L.; Hong, D. Moment-independent regional sensitivity analysis of complicated models with great efficiency. Int. J. Numer. Methods Eng. 2015, 103, 996–1014. [Google Scholar] [CrossRef]
- Oberguggenberger, M.; Fellin, W. Reliability bounds through random sets: Non-parametric methods and geotechnical applications. Comput. Struct. 2008, 86, 1093–1101. [Google Scholar] [CrossRef]
- Alvarez, D.A. On the calculation of the bounds of probability of events using infinite random sets. Int. J. Approx. Reason. 2006, 43, 241–267. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Gao, Y. Unified reliability analysis by active learning Kriging model combining with random-set based Monte Carlo simulation method. Int. J. Numer. Methods Eng. 2016, 108, 1343–1361. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Zhang, Y.; Yue, Z. Probability and convex set hybrid reliability analysis based on active learning Kriging model. Appl. Math. Model. 2015, 39, 3954–3971. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Gao, Y.; Zhang, Y.; Gao, Z. An active learning Kriging model for hybrid reliability analysis with both random and interval variables. Struct. Multidiscip. Optim. 2015, 51, 1003–1016. [Google Scholar] [CrossRef]
- Du, X. Uncertainty analysis with probability and evidence theories. In Proceedings of the ASME 2006 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Philadelphia, PA, USA, 10–13 September 2006; pp. 1025–1038. [Google Scholar]
- Du, X. Unified uncertainty analysis by the first order reliability method. J. Mech. Des. 2008, 130, 091401. [Google Scholar] [CrossRef]
- Li, G.; Lu, Z.; Tian, L.; Xu, J. The importance measure on the non-probabilistic reliability index of uncertain structures. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2013, 227, 651–661. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Ma, P. Structural reliability analysis under evidence theory using the active learning kriging model. Eng. Optim. 2017, 49, 1922–1938. [Google Scholar] [CrossRef]
- Kuhn, H.W.; Tucker, A.W. Nonlinear Programming. In Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1951; pp. 481–492. [Google Scholar]
- Gill, P.E.; Murray, W.; Saunders, M.A. SNOPT: An SQP algorithm for large-scale constrained optimization. SIAM Rev. 2005, 47, 99–131. [Google Scholar] [CrossRef]
- Sharma, G.; Martin, J. MATLAB®: A language for parallel computing. Int. J. Parallel Programm. 2009, 37, 3–36. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, C.; Wang, G.G.; Han, X. First and second order approximate reliability analysis methods using evidence theory. Reliab. Eng. Syst. Saf. 2015, 137, 40–49. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, Z.; Han, X.; Liu, J. A novel evidence-theory-based reliability analysis method for structures with epistemic uncertainty. Comput. Struct. 2013, 19, 1–12. [Google Scholar] [CrossRef]



| Y2 | = [0.8, 1.0] | = [1.0, 1.2] | = [1.2, 1.4] | |
| Y1 | mY2() = 0.3 | mY2() = 0.4 | mY2() = 0.3 | |
| = [4.0, 4.5] | CY1 = {,} | CY2 = {, } | CY3 = {, } | |
| mY1() = 0.6 | mY(CY1) = 0.18 | mY(CY2) = 0.24 | mY(CY3) = 0.18 | |
| = [4.5, 5.0] | CY4 = {, } | CY5 = {, } | CY6 = {, } | |
| mY1() = 0.4 | mY(CY4) = 0.12 | mY(CY5) = 0.16 | mY(CY6) = 0.12 | |
| Variable | Mean | Standard Deviation | Distribution |
|---|---|---|---|
| X1 | 4 | 0.8 | Normal |
| X2 | 6 | 0.6 | Normal |
| Variable | FEs | BPA |
|---|---|---|
| Y1 | [1, 1.1] | 0.2 |
| [1.1, 1.2] | 0.4 | |
| [1.2, 1.3] | 0.4 | |
| Y2 | [0.5, 0.6] | 0.1 |
| [0.6, 0.7] | 0.3 | |
| [0.7, 0.8] | 0.6 |
| Methods | NS | NC | NO | Pl(F) |
|---|---|---|---|---|
| MCS | ― | >9 × 106 | 9 × 106 | 0.0127 |
| Kriging-MCS | 9 | 9 × 103 | 9 × 106 | 0.0126 |
| RS-MCS | ― | >106 | 106 | 0.0127 |
| Proposed method | 1 | 53 | 300,034 | 0.0126 |
| Variables | X1 | X2 | X3 | X4 | X7 |
|---|---|---|---|---|---|
| Mean | 50 | 43 | 35 | 32 | 2 × 1011 |
| Standard deviation | 0.05 | 0.043 | 0.035 | 0.032 | 2 × 108 |
| Distribution | Normal | Normal | Normal | Normal | Normal |
| Variables | FEs | BPA |
|---|---|---|
| X5 | [980, 990] | 0.2 |
| [990, 1000] | 0.6 | |
| [1000, 1010] | 0.2 | |
| X6 | [990, 995] | 0.2 |
| [995, 1000] | 0.6 | |
| [1000, 1005] | 0.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Li, W.; Wu, X.; Liu, T. An Efficient Regional Sensitivity Analysis Method Based on Failure Probability with Hybrid Uncertainty. Energies 2018, 11, 1684. https://doi.org/10.3390/en11071684
Zhang D, Li W, Wu X, Liu T. An Efficient Regional Sensitivity Analysis Method Based on Failure Probability with Hybrid Uncertainty. Energies. 2018; 11(7):1684. https://doi.org/10.3390/en11071684
Chicago/Turabian StyleZhang, Dawei, Weilin Li, Xiaohua Wu, and Tie Liu. 2018. "An Efficient Regional Sensitivity Analysis Method Based on Failure Probability with Hybrid Uncertainty" Energies 11, no. 7: 1684. https://doi.org/10.3390/en11071684
APA StyleZhang, D., Li, W., Wu, X., & Liu, T. (2018). An Efficient Regional Sensitivity Analysis Method Based on Failure Probability with Hybrid Uncertainty. Energies, 11(7), 1684. https://doi.org/10.3390/en11071684






