1. Introduction
Load forecasting enables utility providers to model and forecast power loads to preserve a balance between production and demand, to reduce production cost, to estimate realistic energy prices and to manage scheduling and future capacity planning. The primary criterion used for the classification of forecasting models is the forecasting horizon. Mocanu et al. [
1] grouped electricity demand forecasting into three categories, short-term forecasts ranging between one hour and one week, medium term ranging between one week and one year and long-term spanning a time of more than one year. The literature reveals that short-term demand forecasting has attracted substantial attention. Such forecasting is important for power system control, unit commitment, economic dispatch, and electricity markets. Conversely, medium and long-term forecasting was not sufficiently studied despite their crucial inputs for the power system planning and budget allocation [
2].
In this paper, we focus on both short term and medium term monthly forecasting horizons. The rationale behind targeting simultaneously these two forecasting horizons is that deterministic models can be used successfully for both of them. However, in the case of long-term forecasting, stochastic models are needed to deal with uncertainties of forecasting parameters that always have a probability of occurrence [
3].
Two challenges are associated with the targeted forecasting horizons. In the short-term case, the accuracy is crucial for optimal day-to-day operational efficiency of electrical power delivery and the medium term case, the prediction stability is needed for the precise scheduling of fuel supplies and timely maintenance operations. For prediction stability, a low forecast error should be preserved for the medium term span. Thus, the forecasting model should keep performing accurately or at least should not be excessively sensitive to the elapsed time within the medium term frame.
Although several electric load forecasting approaches using traditional statistical techniques, time series analysis and recent machine learning were proposed, the need for more accurate and stable load forecasting models is still crucial [
4]. Recently, a particular attention is being paid to deep learning based approaches. These are based on artificial neural networks (ANNs) with deep architectures have gained attention of many research communities [
5,
6,
7] due to their ability of capturing data behavior when considering complex non-linear patterns and large amounts of data. As opposed to shallow learning, deep learning usually refers to having a larger number of hidden layers. These hidden layers in deep network makes the model able to learn accurately complex input-output relations.
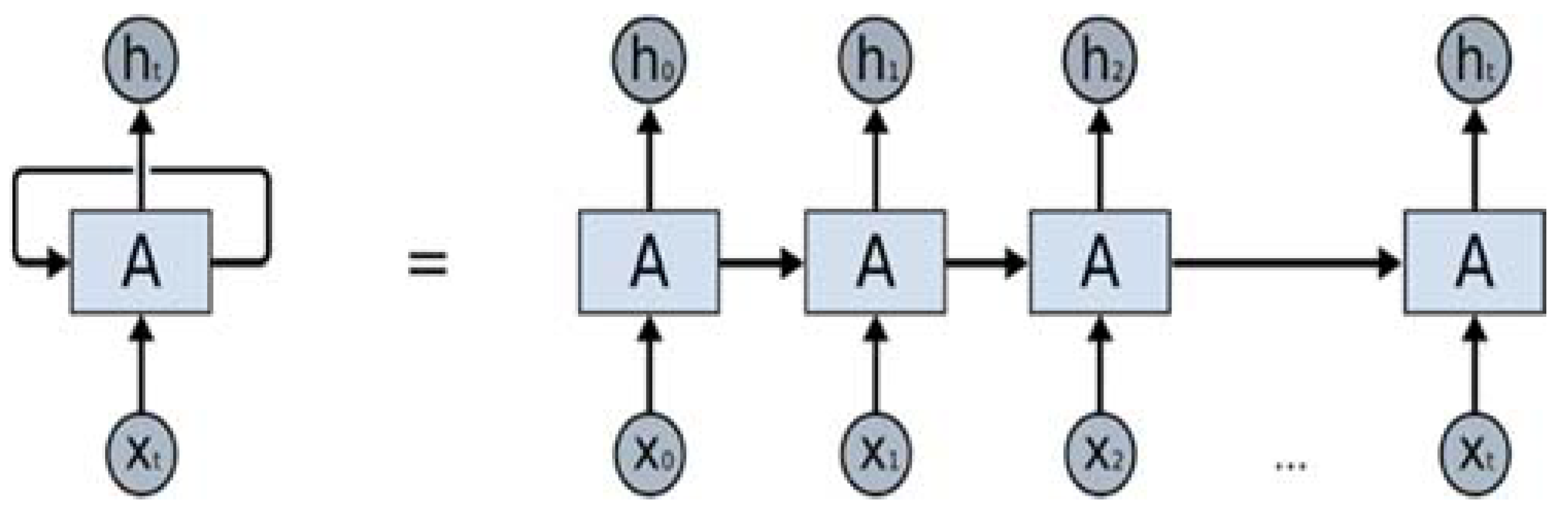
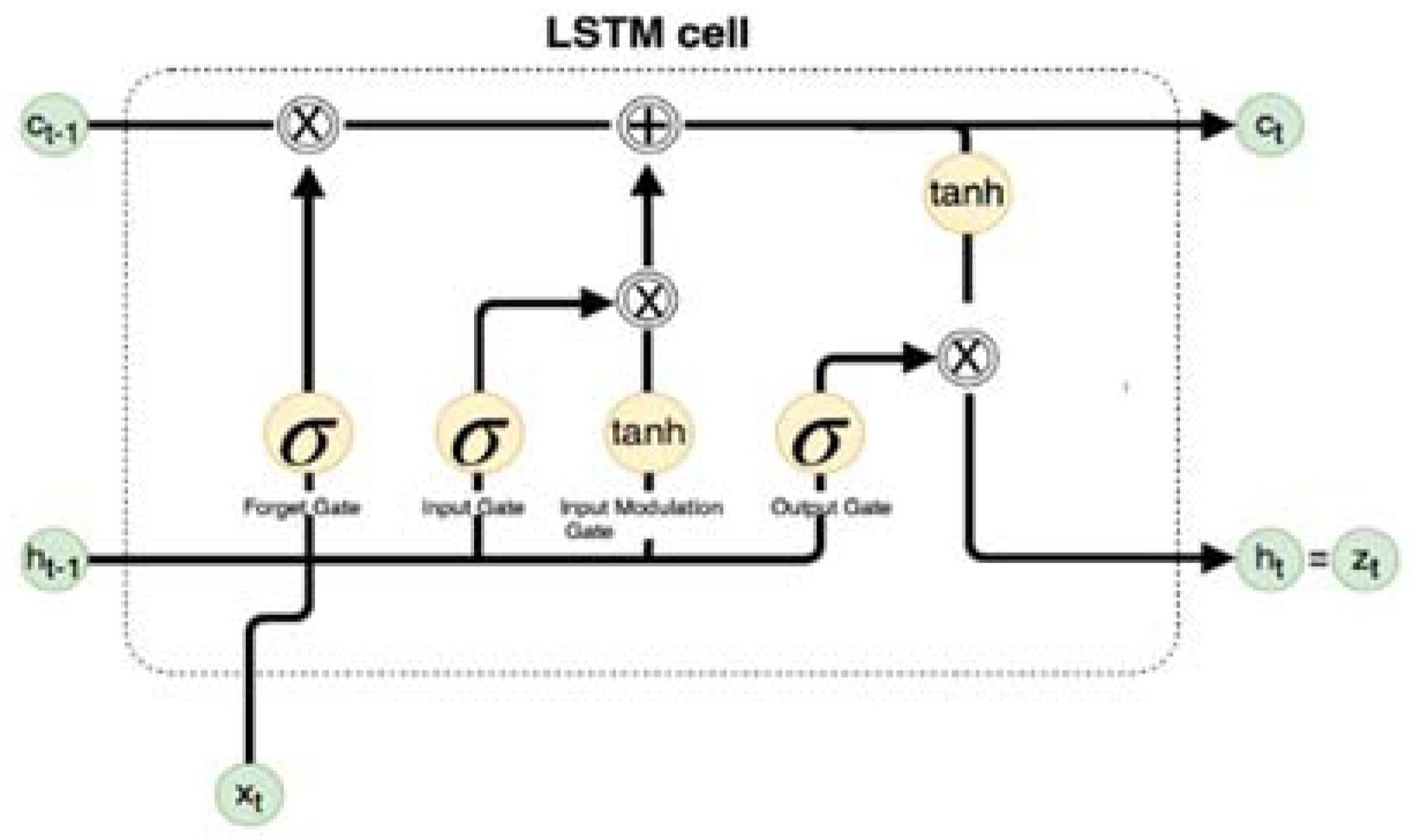
Long short-term memory (LSTM), a variation of deep Recurrent Neural Networks (RNN) originally developed Hochreiter et al. [
8] to allow the preservation of the weights that are forward and back-propagated through layers. LSTM-based RNNs are an attractive choice for modeling sequential data like time series as they incorporate contextual information from past inputs. Especially, LSTM technique for time series forecasting has gained popularity due to its end-to-end modeling, learning complex non-linear patterns and automatic feature extraction abilities.
Time series models commonly use lags to make their predictions based on past observations. Selection of appropriate time lags for the time series forecasting is an important step to eliminate redundant features [
9]. This helps to improve prediction model accuracy as well as gives a better understanding of the underlying process that generate the data. Genetic algorithm (GA), a heuristic search and optimization technique that mimics the process of evaluation with the objective to minimize or maximize some objective function [
10] can be used to find appropriate number of lags for time series model. GA works by creating a population of potential answers to the problem to be solved, and then submit it to the process of evolution.
In this paper, we propose a LSTM-RNN-based model for aggregated demand side load forecast over short- and medium-term monthly horizons. Commonly used machine learning approaches are implemented to be compared to our proposed model. Important predictor variables and optimal lag and number of layers selection are implemented using feature selection and GA approaches. The performances of forecasting techniques are measured by using several evaluation metrics such as coefficient of variation RMSE (CVRMSE), mean absolute Error (MAE) and root mean square error (RMSE). Using France Metropolitan’s electricity energy consumption data as a case study, our validation shows that LSTM-RNN based forecasting model outperforms the best of the studied alternative approaches with a high confidence.
The remainder of this paper is organized as follows:
Section 2 provides an overview of the literature on load forecasting.
Section 3 provides brief background on LSTM-RNN, benchmark machine learning models and on the forecasting evaluation metrics.
Section 4 describes the methodology of building our proposed forecast technique, its enhancement and validation.
Section 5 describes experimental results and alternative time series validation approach.
Section 6 provides discussion on threat to validity and
Section 7 draws the conclusions.
2. Literature Review
Different models for load forecasting can be broadly classified as engineering methods and data driven methods. Engineering methods, also known as, physics based models; use thermodynamic rules to estimate and analyze energy consumption. Commonly, these models rely on context characteristics such as building structure, weather information, heating, ventilation, and air conditioning (HVAC) system information to calculate energy consumption. Physics based models are used in energy simulator software for buildings such as
EnergyPlus and
eQuest. The limitation of these models resides in their dependence on the availability and the accuracy of input information [
11].
Data-driven methods, also known as artificial intelligence (AI) methods rely on historical data collected during previous energy consumption periods. These methods are very attractive for many groups of research, however little is known about their forecasting generalization. In other terms, their accuracy drops when they are applied on new energy data. The ability of generalization of data driven forecasting models remains an open problem. As reported for example in [
12], the accuracy of forecasting results varies considerably for micro-grids with different capacities and load characteristics. Similar to load forecasting, data driven models for electricity price prediction were also proposed to help decision making for energy providing companies. Commonly used price forecasting techniques include multi-agent, reduced-form, statistical and computational intelligence as reviewed in [
13].
Nowadays, the availability of relatively large amount of energy data makes it increasingly stimulating to use data-driven methods as an alternative to physics-based methods in load forecasting for different time horizons, namely, short, medium and long term [
11]. Short-term load forecasting (STLF) has attracted more attention in the smart grid, microgrids and buildings and because of its usefulness for demand side management, energy consumption, energy storage operation, peak load anticipation, energy shortage risk reduction, etc. [
14]. Many works were carried out for STLF. They ranged from classical time series analysis to recent machine learning approaches [
15,
16,
17,
18,
19,
20]. In particular, autoregressive and exponential smoothing models have remained the baseline models for time series prediction tasks for several years, however using these models necessitated careful selection of the lagged inputs parameter to identify the correct model configuration [
21]. An adaptive autoregressive moving-average (ARMA) model developed by Chen et al. [
22] to conduct day and week ahead load forecasts, reported superior performance compared to Box-Jenkins model. While these univariate time-series approaches directly model the temporal domain, they suffer from curse of dimensionality, accuracy dropping and require frequent retraining.
Various other approaches covering simple linear regression, multivariate linear regression, non-linear regression, ANN and support vector machines (SVMs) were applied for electricity demand forecasting primary for the short-medium term [
4,
23,
24] and lesser for the long term [
4]. Similarly, for price forecasting, Cincotti et al. used [
25] proposed three univariate models namely, ARMA-GARCH, multi-layer perceptron and support vector machines to particularly predict day ahead electricity spot prices. Results showed that SVMs performed much better than the benchmark model based on the random walk hypothesis but close to the ARMA-GARCH econometric technique. For a similar forecasting aim, a combination of wavelet transform neural network (WTNN) and evolutionary algorithms (EA) was implemented for day-ahead price forecasting. This combination resulted in more accurate and robust forecasting model [
26].
Noticeably, ANN was widely used for various energy-forecasting tasks because of its ability to model nonlinearity [
4]. Hippert, et al., in their review work [
20], have summarized most of the applications of ANN to STLF as well as its evolution. Furthermore, various structures of ANN have found their ways into load forecasting in order to improve models accuracy. Namely, the most common configuration of ANN, multilayer perceptron (MLP), was used to forecast a load profile using previous load data [
27], the fuzzy neural [
28], wavelet neural networks [
29], fuzzy wavelet neural network [
30] and self-originating map (SOM), neural network [
31], were used mainly for STLF.
Unlike the conventional ANN structures, a deep neural network (DNN) is an ANN with more than one hidden layer. The multiple computation layers structure increases the feature abstraction capability of the network, which makes them more efficient in learning complex non-linear patterns [
32]. To the best of our knowledge and according to Ryu et al. [
14] in 2017, only a few DNN-based load forecasting models are proposed. Recently, in 2016, Mocanu et al. [
1] employed, a deep learning approach based on a restricted Boltzmann machine, for single-meter residential load forecasting. Improved performance was reported compared to shallow ANN and support vector machine. The same year (2016), Marino et al. [
33] presented a novel energy load forecasting methodology using two different deep architectures namely, a standard LSTM and an LSTM with sequence to Sequence architecture that produced promising results. In 2017, Ryu et al. [
14] proposed a DNN based framework for day-ahead load forecast by training DNNs in two different ways, using a pre-training restricted Boltzmann machine and using the rectified linear unit without pre-training. This model exhibited accurate and robust predictions compared to shallow neural network and others alternatives (i.e., double seasonal Holt-Winters model and the autoregressive integrated moving average model). In 2018, Rahman et al. [
34] proposed two RNNs for medium to long-term electric forecast for residential and commercial buildings. A first model feeds a linear combination of vectors to the hidden MLP layer while a second model applies a shared MLP layer across each time step. The results were more accurate than using a 3-layer multi-layered perceptron model.
Seemingly closer to our current work, but technically distinct from it, Zheng et al. [
35] developed a hybrid algorithm for STLF that combined similar days selection, empirical mode decomposition and LSTM neural networks. In this work, Xgboost was used to determine features importance and k-means was employed to merge similar days into one cluster. The approach substantially improved LSTM predictive accuracy.
Despite the success of machine learning models, in particular the late deep learning, to perform better than traditional time series analysis and regression approaches, there is still a crucial need for improvement to better model non-linear energy consumption patterns while targeting high accuracy and prediction stability for the medium term monthly forecasting. Definitely, we share the opinion that optimally trained deep learning model derives more accurate forecasting outputs than those obtained with a shallow structure [
36]. Furthermore, we believe that the adoption of deep learning in solving load-forecasting problem needs more maturity though increasing the number of works with different forecasting configurations. These configurations include the aim and horizon of forecasting, the type or nature of inputs, the methods of determining their relevance, the selected variation of deep learning and the way of validating the derived forecasting model. For instance, using lagged features as inputs to enable deep models to see enough past values relevant for future prediction can cause overfitting if too many lags are selected. This is because deep models with lot of parameters can overfit due to increase in dimensionality. In this paper, we aim at proving that optimal LSTM-RNN will behave similarly in the context of electric load forecasting for both the short-and-medium horizon. Accordingly, our approach differs from the previous deep learning models in that:
- (i)
Implementing feature importance using wrapper and hybrid methods, optimal lag and number of layers selection for LSTM model using GA enabled us to prevent overfitting and resulted in more accurate and stable forecasting.
- (ii)
We train a robust LSTM-RNN model to forecast aggregate electric load for short- and medium term horizon using a large dataset for a complete metropolitan region covering a period of nine years at a 30 min resolution
- (iii)
We compare the LSTM-RNN model with the machine learning benchmark that is performing the best among several linear and non-linear models optimized with hyperparameter tuning.
4. Methodology
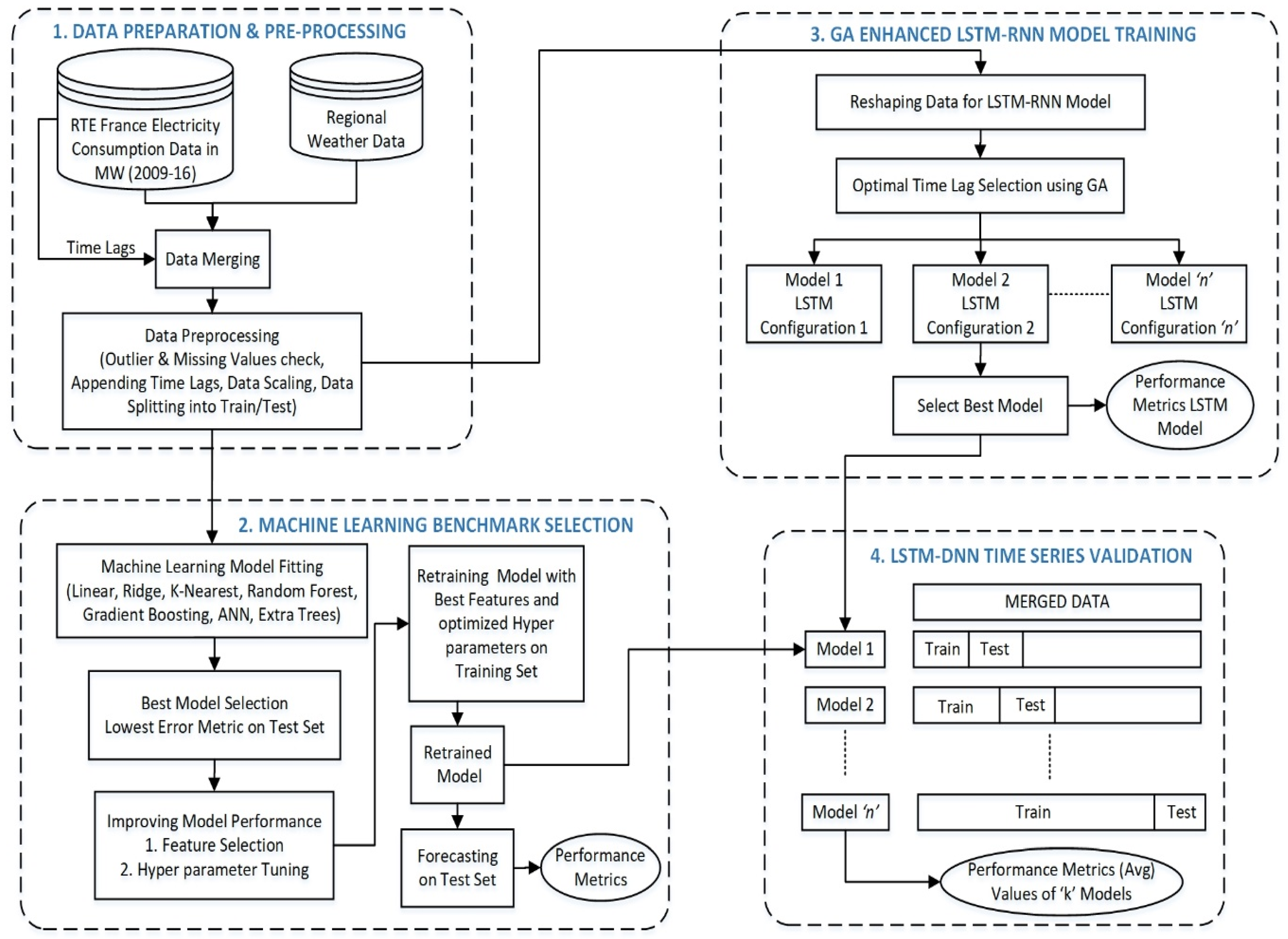
In this section, we describe the proposed methodology process for short and medium-term load forecasting LSTM-RNNs as depicted in
Figure 3. The proposed methodology process can be seen as a framework of four processing components, namely, data preparation and preprocessing component, the machine learning benchmark model construction component, LSTM-RNN training component and LSTM-RNN validation component. In the following, we present an overview of the methodology, and then we describe for each methodology components its detailed mission followed by an illustration on the
Réseau de Transport d'Électricité (RTE) power consumption data set, our case study.
4.1. Methodology Process Overview
The first processing step starts by merging the electric energy consumption data with weather data and time lags. The merging is performed because weather data and time lags are known to influence power demand. Then a preprocessing of data is carried out in order to check null values and outliers, scale the data to a given range and split the time series data into train and test subsets while retaining the temporal order. This step aims at preparing and cleaning data to be ready for the further analysis.
In the second processing step of our framework, benchmark model will be selected by fitting seven different linear and non-linear machine-learning algorithms to the data and choosing the model that performs the best. Further improvement in accuracies of selected model will be achieved by performing feature engineering and hyerparameter tuning. This benchmark would then be used for forecasting and its obtained performance would be compared with that of the LSTM-RNN model. In the third processing step of the process, a number of LSTM models with different model configurations like number of layers, number of neurons in each layer, training epochs, optimizer etc. will be tested. Optimal number of time lags and LSTM layers would be selected using GA. The best performing configuration will be determined empirically after several trails with different settings, and then it would be used for the final LSTM-RNN model.
4.2. Data Preparation and Pre-Processing
Time series forecasting is a special case of sequence modeling. The observed values correlate with their own past values, thus individual observations cannot be considered independent of each other. Exploratory analysis of electric load time-series can be useful to identifying trends, patterns and anomalies. We will plot electric load consumption box plot for various years, quarters and weekday indicator, which would give us a graphical display of data dispersion. Furthermore, correlation of electric consumption with time lags and weather variables will also be investigated to check for the strength of association between these variables.
4.2.1. Preliminary Data Analysis
Our research makes use of a RTE power consumption data set [
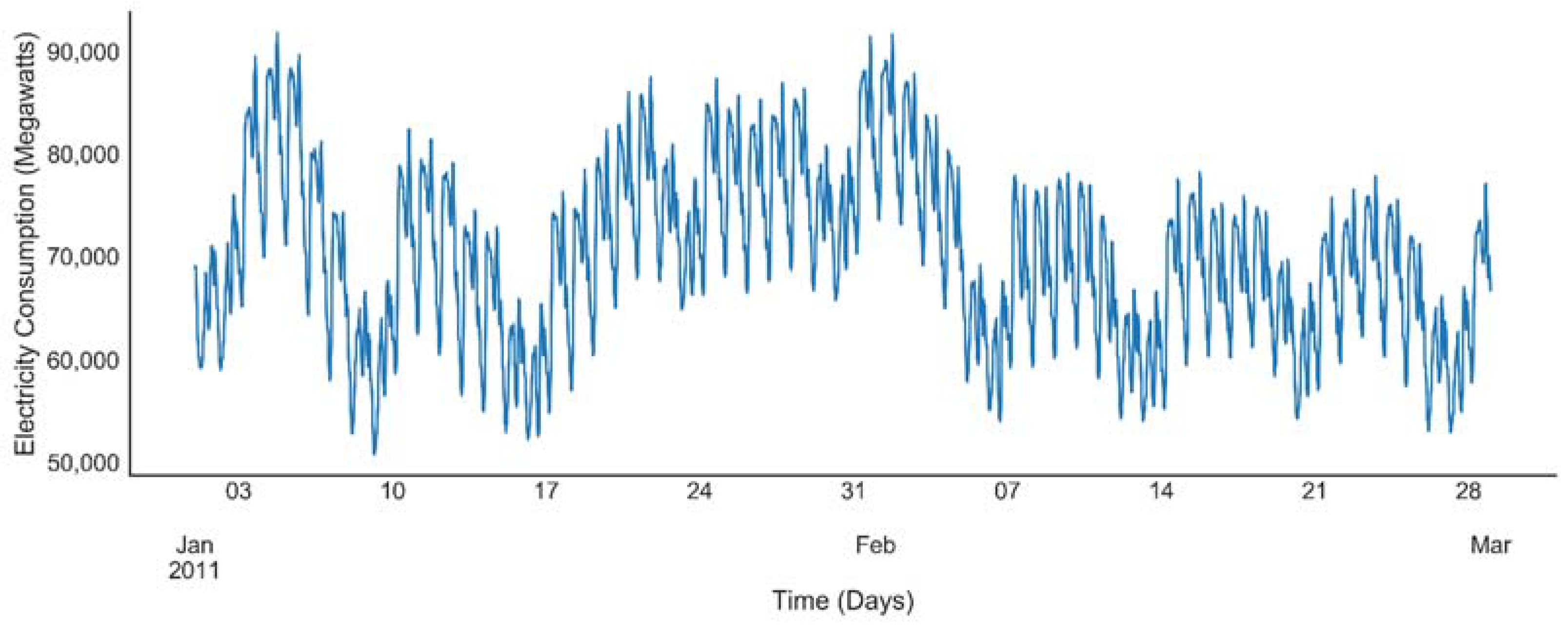
41], which gives us a unique opportunity to predict next half-hourly electrical consumption in MW containing nine years’ data in metropolitan France. The power consumption dataset ranges from January 2008 until December 2016. The load profile from January to February 2011 as depicted in the
Figure 4 follows cyclic and seasonal patterns, which can be related to human, industrial and commercial activities.
Box plots of load consumptions reveal that average load is almost constant across years (
Figure 5a) while quarterly plot shows low consumption in second and third quarter as compared to others (
Figure 5b). Power demand in France increases in first and fourth quarters due to heating load in winter months.
Holidays and weekends can affect the usage of electricity, as the usage patterns are generally quite different from usual. This can be used as a potential feature to our model.
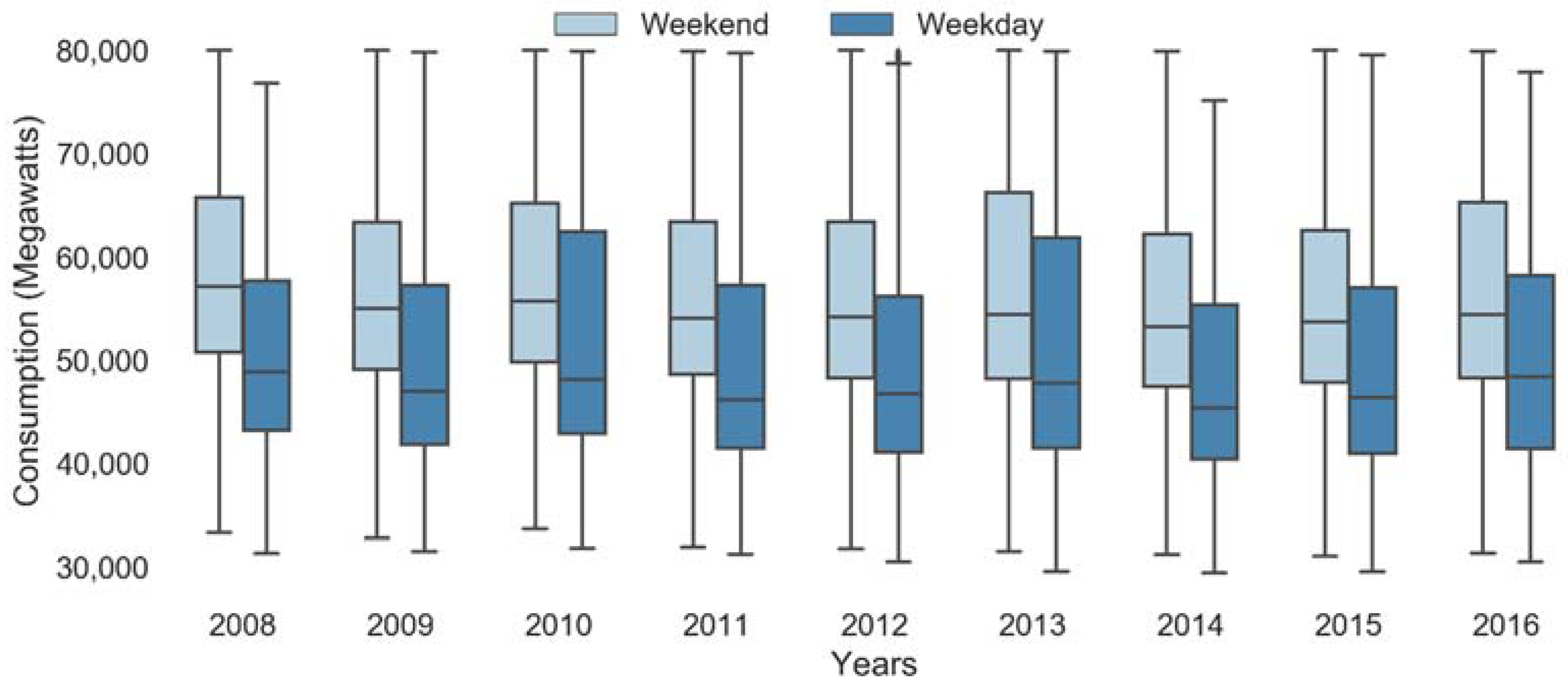
Figure 6 shows the box plot of consumption for weekdays and weekend. The weekend consumption is high compared to weekdays across all years.
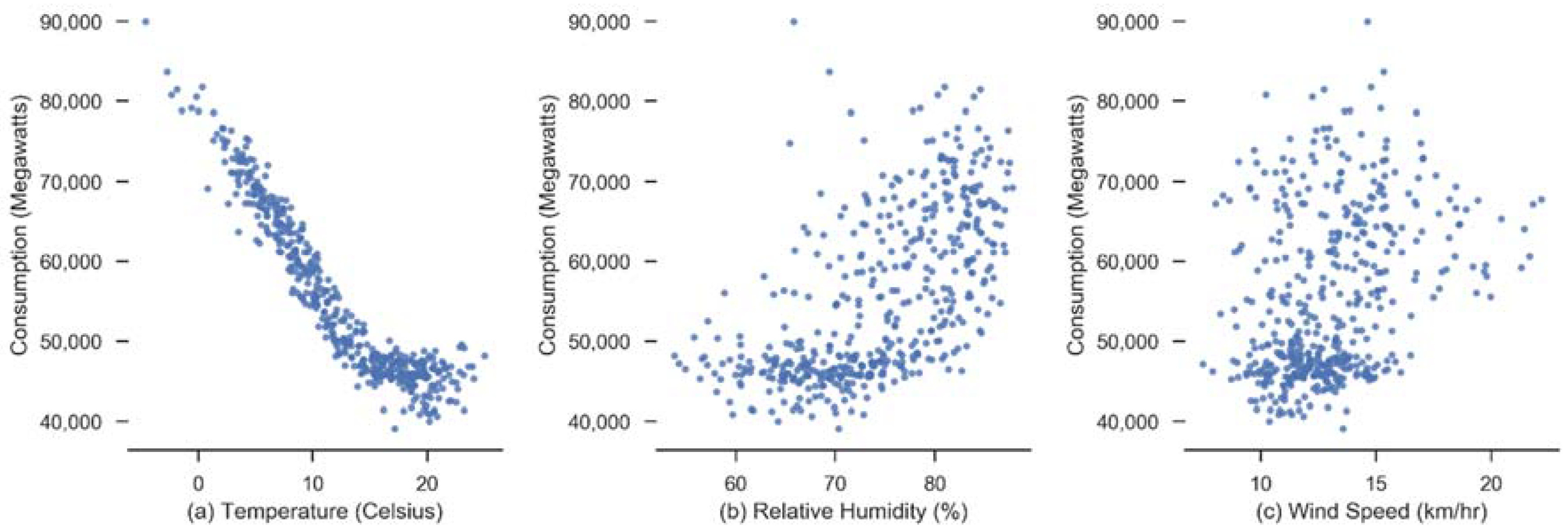
Correlation matrix of electric consumption showed a high correlation with previous several time lags (0.90–0.98). Amongst the weather variables, temperature had a high negative correlation with consumption since we are analyzing a cooling load. Humidity and wind speed have low correlation.
Figure 7 shows scatter plot of weather variables with consumption.
4.2.2. Data Pre-Processing
Data preprocessing is a vital step to obtain better performance and accuracies of machine learning as well as deep learning-based models. It is about dealing with inconsistent, missing and noisy data. Our dataset comes from RTE, which is the electricity transmission system operator of France. It has measurements of electric power consumption in metropolitan France with a thirty-minute sampling rate. There are two categories of power in the dataset, namely, definitive and intermediate. Here we will only use definitive data. Weather data comprising outdoor temperature, humidity and wind speed are merged as exogenous input with the consumption data. Further data preprocessing comprised data cleansing, normalization, and structure change. As machine learning and LSTM-RNN models are sensitive to the scale of the inputs, the data are normalized in the range [0, 1] by using feature scaling.
The data is split into train and test set while maintaining the temporal order of observations. Test data is used for evaluating accuracy of the proposed forecasting model and not used in training step. Standard practice for splitting data is performed using 80/20 or 70/30 ratios for machine learning models [
42]. The last 30 percent of the dataset is withheld for validation while the model is trained on the remaining 70 percent of the data. Since our data is large enough, both training and tests sets are highly representative of the original problem of load forecasting. Stationarity of time series is a desired characteristic to use Ordinary Least Square regression models for estimation of regression relationship. Regressing non-stationary time series can lead to spurious regressions [
43]. High R
2 and high residual autocorrelation can be signs of spurious regression. Dickey-Fuller test is conducted to check stationarity. The resulting
p-value is less 0.05, thus we reject the null hypothesis and conclude that the time series is stationary.
4.3. Selecting the Machine Learning Benchmark Model
Benchmarking is an approach that demonstrate new methodologies abilities to run as expected and thus comparing the result to existing methods [
44]. We will use linear regression, ridge, regression k-nearest neighbors, random forest, gradient boosting, ANN and extra trees Regressor as our selected machine learning models. The initial input to these models is the complete set of features comprising time lags, weather variables temperature, humidity, wind speed and schedule-related variables, month number (between 1 and 12), quarter and weekend or weekday. Use lagged versions of the variables in the regression model allows varying amounts of recent history to be brought into the forecasting model. Selected main parameters for various machine-learning techniques are shown in
Table 1.
All the implemented machine-learning models utilized in this study used the mean squared error as the loss function to be minimized. All trained models are evaluated on the same test set and performance is measured in terms of our evaluation metrics. For our baseline models comparison, we will leave parameters to their default values. Optimal parameters for the best model will be chosen later. The results are shown in
Table 2.
ANN models are known to overfit the data and show poor generalization when the dataset is large and training times are longer [
45]. From the above results, it is seen that ANN does not perform well. This is because in order to achieve good accuracies, ANN model needs to have optimal network structure and update weights, which may require several epochs and network configurations. During training of our models, it was also noticed that ANN took the longer time as compared to other approaches, which is an indication that the model overfits and as the result shows poor test set performance.
Since the ensemble approach of Extra Trees Regressor model is giving the best results, therefore we will use this as our benchmark model. The main difference of Extra Trees Regressor with other tree based ensemble methods is randomization of both attribute and cut-point choice while splitting a tree node. Since this model performs the best amongst all other models, it is selected as our benchmark.
4.3.1. Improving Benchmark Performance with Feature Selection & Hyper Parameter Tuning
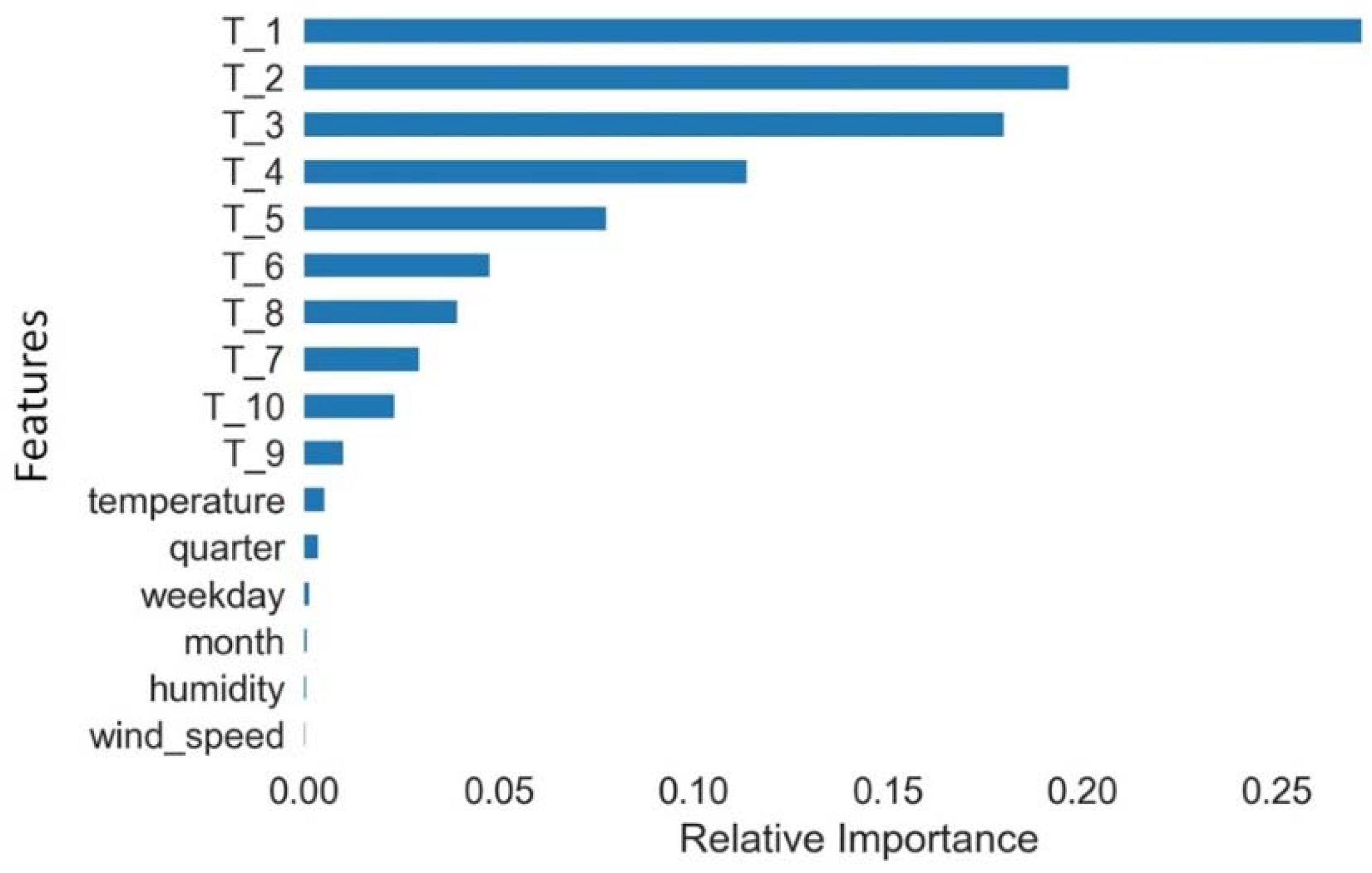
Wrapper and embedded are model based feature selection methods that can help remove redundant features and thus obtain better performing and less overfitting model. In wrapper method, feature importance is assessed using a learning algorithm while in embedded methods the learning algorithm performs feature selection as well in which feature selection and parameter selection space are searched simultaneously. We will use regression and ensembles based methods to identify both linear and non-linear relationships among features and thus ascertain both relevant and redundant features. In the regression case, recursive feature elimination works by creating predictive models, weighting features, and pruning those with the smallest weights. In the ensemble case, the Extra Trees Regressor decides feature importance based on the decrease in average impurity computed from all decision trees in the forest without making any assumption whether our data is linearly separable or not. Both the regression and ensemble-based models emphasized time lags as the most important features in comparison to weather and schedule related variables. With respect to our data set, among the weather and schedule related features, temperature and quarter number were found to be important after time lags.
Figure 8 shows the relative importance of each feature. Subsequently, the input vector to machine learning models should include time lags as features.
Various combinations of 5, 10, 20, 30 and 40 time lags were evaluated for Extra Trees Regressor model by training several models. Result showed using only 30 lagged variables as features or combination of lagged features with temperature and quarter produced similar performance for this model. This is an indication that temporal load brings information that is originally contained within the weather parameters.
Grid Search cross validation [
46] is a tuning method that uses cross validation to perform an exhaustive search over specified parameter values for an estimator. This validation method is used for hyperparameters tuning of our best Extra Trees Regressor model by using a fit and score methodology to find the best parameters. After tuning the best model, Extra Trees Regressor model is found to have 150 estimators with max depth of 200.
Table 3 shows the performance results of the best Extra Trees Regressor obtained after tuning.
4.3.2. Checking Overfitting for Machine Learning Model
With too many features, the model may fit the training set very well but fail to generalize to new examples. It is necessary to plot learning curve that shows the model performance on training and testing data over a varying number of training instances.
Mean squared errors for both the training and testing sets for our optimized Extra Tree model (i.e., after hyperparameter optimization) decrease with bigger sizes of training data and converge at similar values, which shows that our model is not overfitting, as reported in
Figure 9.
4.4. GA-Enhanced LSTM-RNN Model
As seen from the machine learning modeling results in the previous section, there was almost no change in the model performance when weather and schedule related variables were removed and only the time lags were used as inputs. Therefore, based on the results of feature importance and cyclical patterns identified in the consumption data, we will only use time lags for LSTM model to predict the future. These time lags are able to capture conditional dependencies between successive time periods in the model. A number of different time lags were used as features to machine learning model, thereby training model several times and selecting the best lag length window. However, experimenting the same with LSTM deep network which has large number of parameters to learn would be computationally very expensive and time consuming.
Finding optimal number of lags and number of hidden layers for LSTM model is a non-deterministic polynomial (NP) hard problem. Meta-heuristic algorithms like GA do not guarantee to find the global optimum solution, however, they do tend to produce suboptimal good solutions that are sometimes near global optimal. Selecting optimal among a large number of potential combinations is thus a search and optimization problem. Previous research has shown that GA algorithms can be effectively used to find a near-optimal set of time lags [
47,
48]. GA provides solution to this problem by an evolutionary process inspired by the mechanisms of natural selection and genetic science. The pseudo-code for the GA algorithm, crossover and mutation operations are shown in
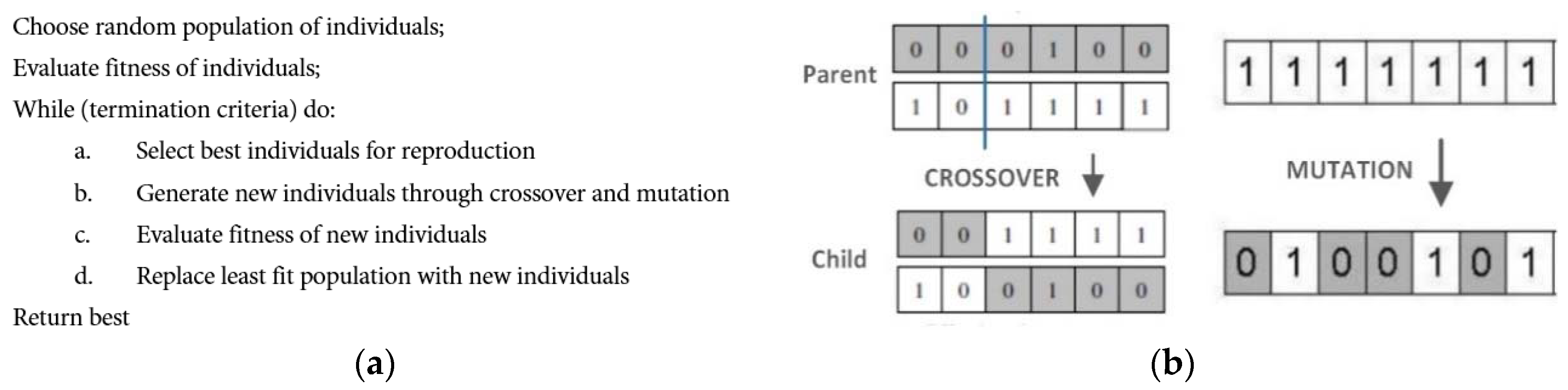
Figure 10.
4.4.1. GA Customization for Optimal Lag Selection
Choosing an optimal number of time lags and LSTM layers to include is domain specific and it could be different for each input feature and data characteristics. Using many lagged values increases the dimensionality of the problem, which can cause the deep model to overfit as well as difficult to train. GA inspired by the process of natural selection is used here for finding optimal number of time lags and layers for LSTM based deep network. Number of time lags will be tested from 1 to 99 and number of hidden layers from 3 to 10. A binary array randomly initialized using Bernoulli distribution is defined as a genetic representation of our solution. Thus, every chromosome represents an array of time lags. Population size and number of generations is set to 40. Various operators of GA are set as follows:
- (i)
Selection: roulette wheel selection was used to select parents according to their fitness. Better chromosomes have more chances to be selected
- (ii)
Crossover: crossover operator exchanges variables between two parents. We have used two-point crossover on the input sequence individuals with crossover probability of 0.7.
- (iii)
Mutation: This operation introduce diversity into the solution pool by means of randomly swapping bits. Mutation is a binary flip with a probability of 0.1
- (iv)
Fitness Function: RMSE on validation set will act as a fitness function.
GA solution would be decoded to get integer time lags size and number of layers, which would then be used to train LSTM model and calculate RMSE on validation set. The solution with highest fitness score is selected as the best solution. We reduced the training and test set size in order to speed up the GA search process on a single machine. The LSTM-RNN performed poorly on smaller number of time lags. Its most effective length found was 34 time lags with six hidden layers as shown in
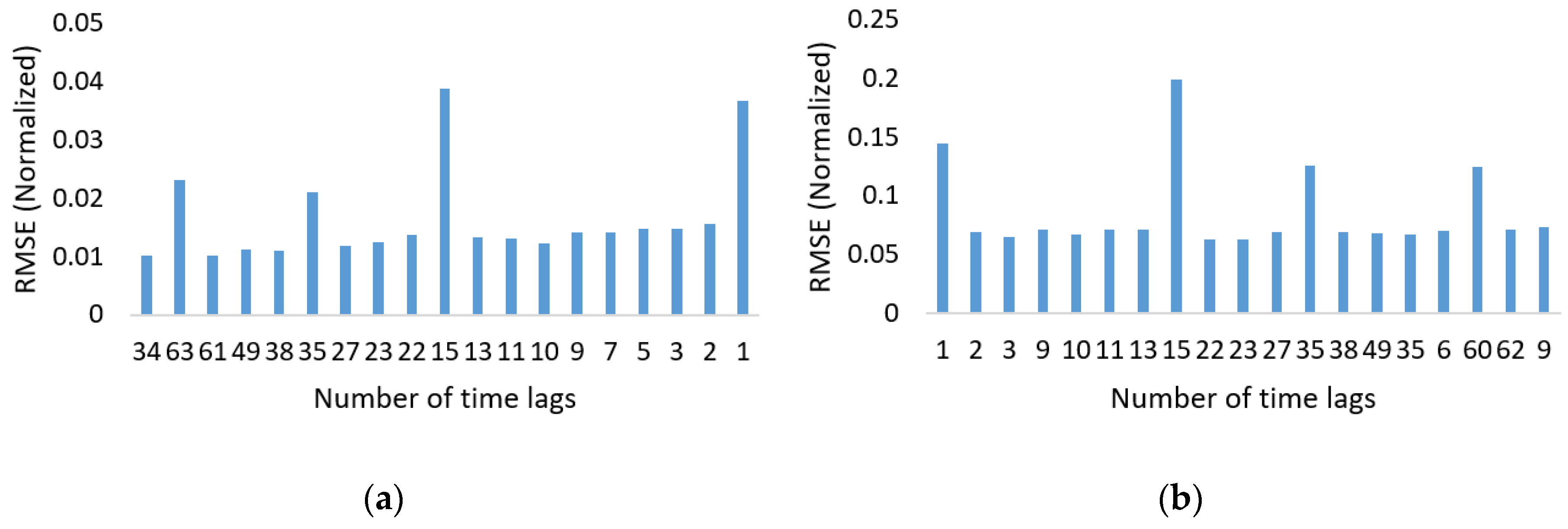
Figure 11.
4.4.2. GA-LSTM Training
To model our current forecasting problem as a regression one, we consider univariate electric load time series with N observations . The task of forecasting is to utilize these N data points to predict the next H data points in the future of the existing time series. LSTMs are specifically designed for sequential data that exhibits patterns over many time steps.
Generally the larger the dataset, more hidden layers and neurons can be used for modeling without overfitting. Since our dataset is large enough, we can achieve higher accuracy. If there are too less neuron per layer, our model will under fit during training. In order to achieve good performance for our model we aim to test various model parameters including number of hidden layers, number of neurons in each layer, number of epochs, batch sizes, activation and optimization function.
Neurons in the input layer of LSTM model matches the number of time lags in the input vector, hidden layers are dense fully connected and output layer has a single neuron for prediction with linear activation function. Means squared error is used as the loss function between the input and the corresponding neurons in the output layer.
5. Experimental Results: GA-LSTM Settings
This section is dedicated to empirically set the parameters of LSTM, to validate the obtained model and to discuss the summary results. After finding optimal lag length and number of layers, various other meta-parameters for the LSTM-RNN model were tested as follows:
The number of neurons in the hidden layers were tested from 20 to 100.
size was varied from 10 to 200 training examples and training epochs from 50 to 300.
Sigmoid, hyperbolic tangent (tanh) and rectified linear unit (ReLU) were tested as the activation functions in hidden layers.
gradient descent (SGD), Root Mean Square Propagation (RMSProp) and adaptive moment estimation (ADAM) were tested as optimizers.
We got significantly better results by having six hidden layers having 100, 60 and 50 neurons. The number of epochs used were 150 with batch size of 125 training examples. For our problem, nonlinear activation function ReLu performed the best and is thus used as activation function for each of the hidden layers. ReLU does not encounter vanishing gradient problem as with tanh and sigmoid activations. Amongst optimizers, ADAM performed the best and showed faster convergence than the conventional SGD. Furthermore, by using this optimizer, we do not need to specify and tune a learning rate as with SGD.
The final selected parameters were the best result available from within the tested solutions. Due to the space limitation, we cannot provide all the test results for different network parameters.
Table 4 shows the summary results of comparing LSTM-RNN with the Extra Trees Regressor model.
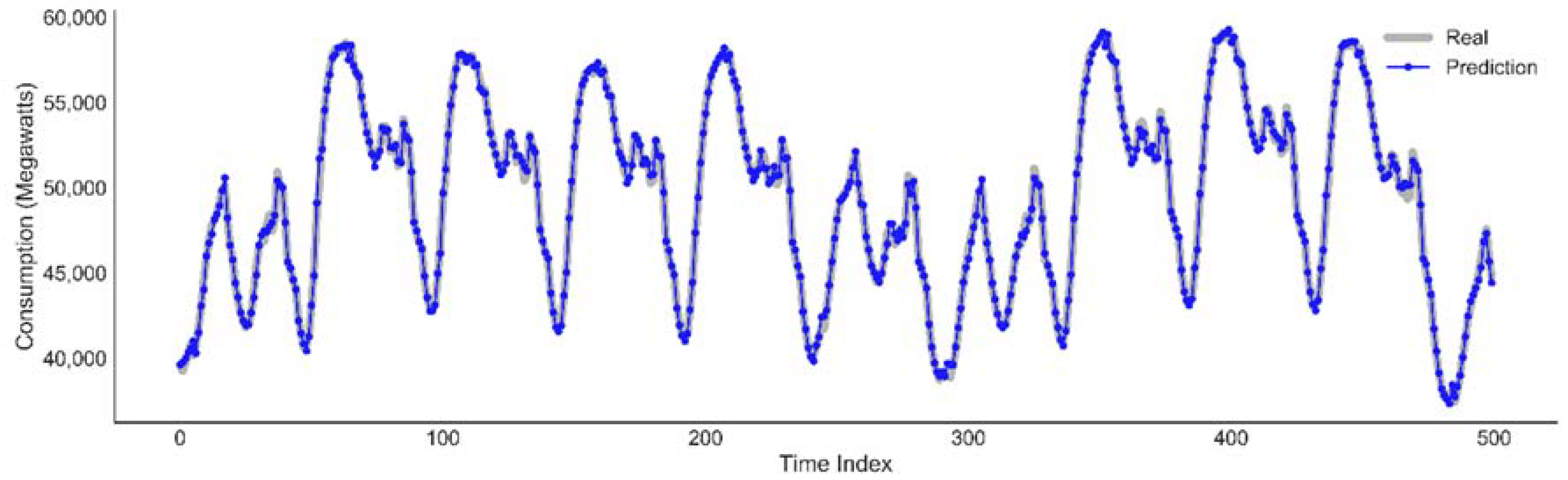
Plot of actual data against the predicted value by the LSTM model for the next two weeks, as medium term prediction.
Figure 12 shows a good fit and stable prediction for the medium term horizon.
5.1. Cross Validation of the LSTM Model
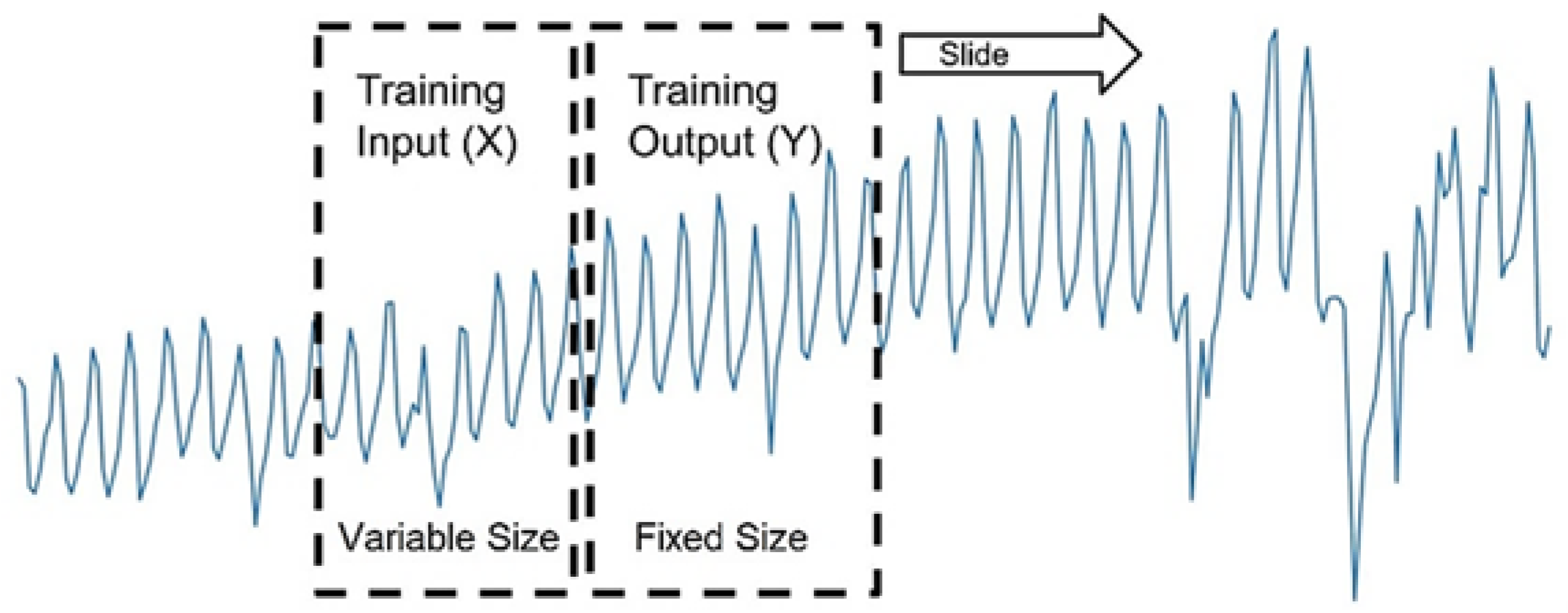
Time series split is a validation methods inspired by k-fold cross validation suitable for time series case [
49]. The method involves repeating the process of splitting the time series into train and test sets ‘k’ times. The test size remains fixed while training set size will increase for every fold as in
Figure 13. The sequential order of time series will be maintained. This additional computation will offer a more robust performance estimate of both our models on sliding test data.
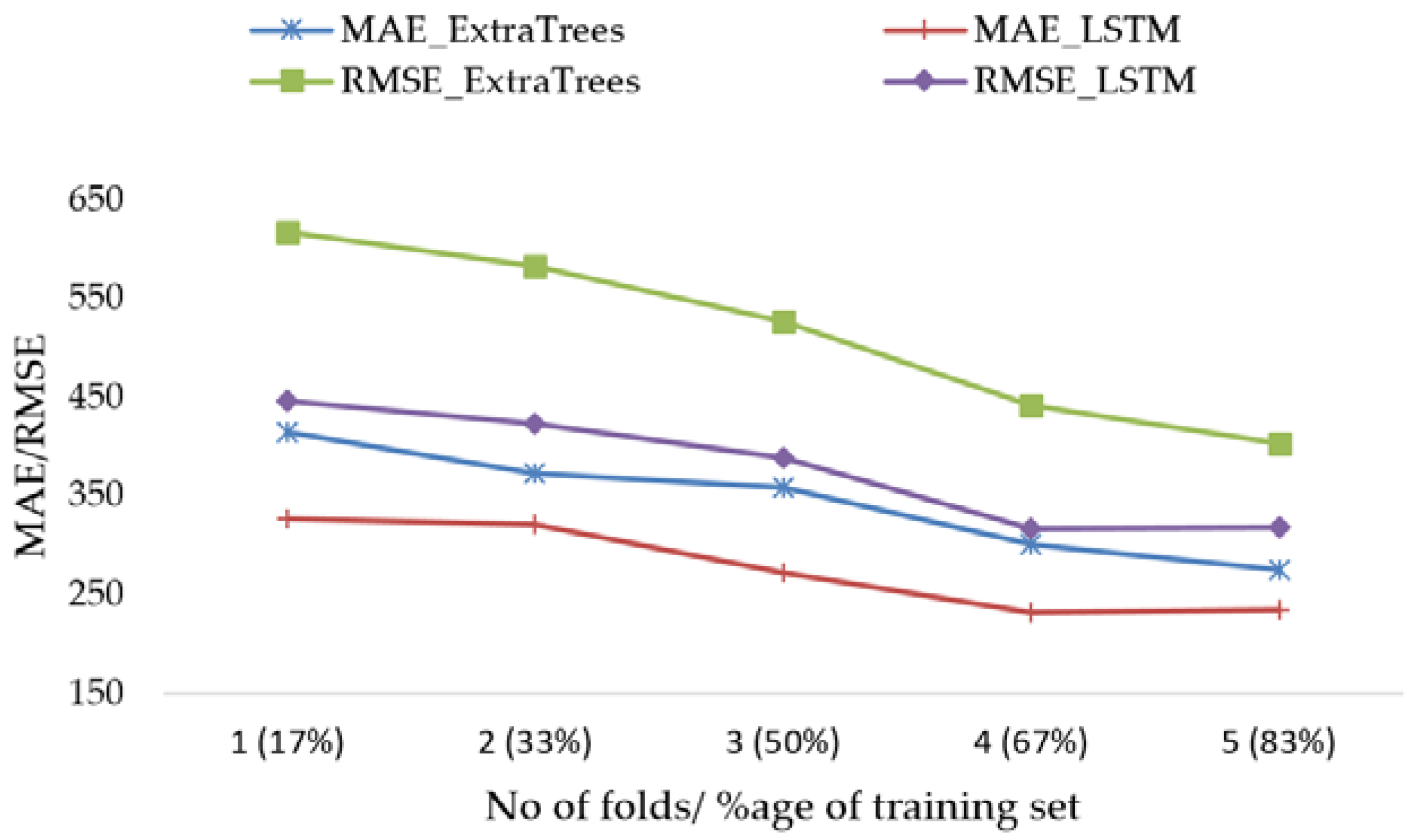
Indeed, we use 5-fold cross validation to train five Extra Trees and five LSTM-RNN models with fixed test size and increasing training set size in every fold, while maintaining the temporal order of data. Mean performance metrics of the results are plotted in
Figure 14.
Mean and standard deviation values are collected on RMSE, CV (RMSE) and MAE for LSTM-RNN model as well as for the best Extra Trees Regressor model. These results are shown in
Table 4. They confirm our previous results in
Table 5. Furthermore, LSTM showed lower forecast error compared to Extra Trees Model using this validation approach.
5.2. Short and Medium Term Forecasting Results
In order to check the model performance on short (i.e., accuracy) and medium term (i.e., stability) horizons, random sample of 100 data points were selected uniformly from various time ranges from one week to several months as in
Table 6. The means of the performance metrics values is computed of each range. Results show that error values are consistent with low standard deviation. The accuracy measured by CV (RMSE) is 0.61% for the short term and an average of 0.56% for the medium term for the medium term. With very comparable performances for both the short term and the medium term horizons, it is obvious that our LSTM-RNN is accurate and stable.
6. Discussion: Threat to Validity
In this section, we respond to some threats to construct validity, internal validity and external validity of our study. The construct validity in our study is concerned with two threats. The first one is related to sufficiency of time series data to well predict the energy load. This question was taken into account from the beginning of the methodology process and other source of data; in particular, weather information was added as the input rather than excluded by different feature selection techniques. The second threat is concerned with the algorithms used in the different steps and components of the methodology that could use some unrealistic assumptions inappropriate for our case study context. To avoid such a threat we have developed all the algorithms ourselves.
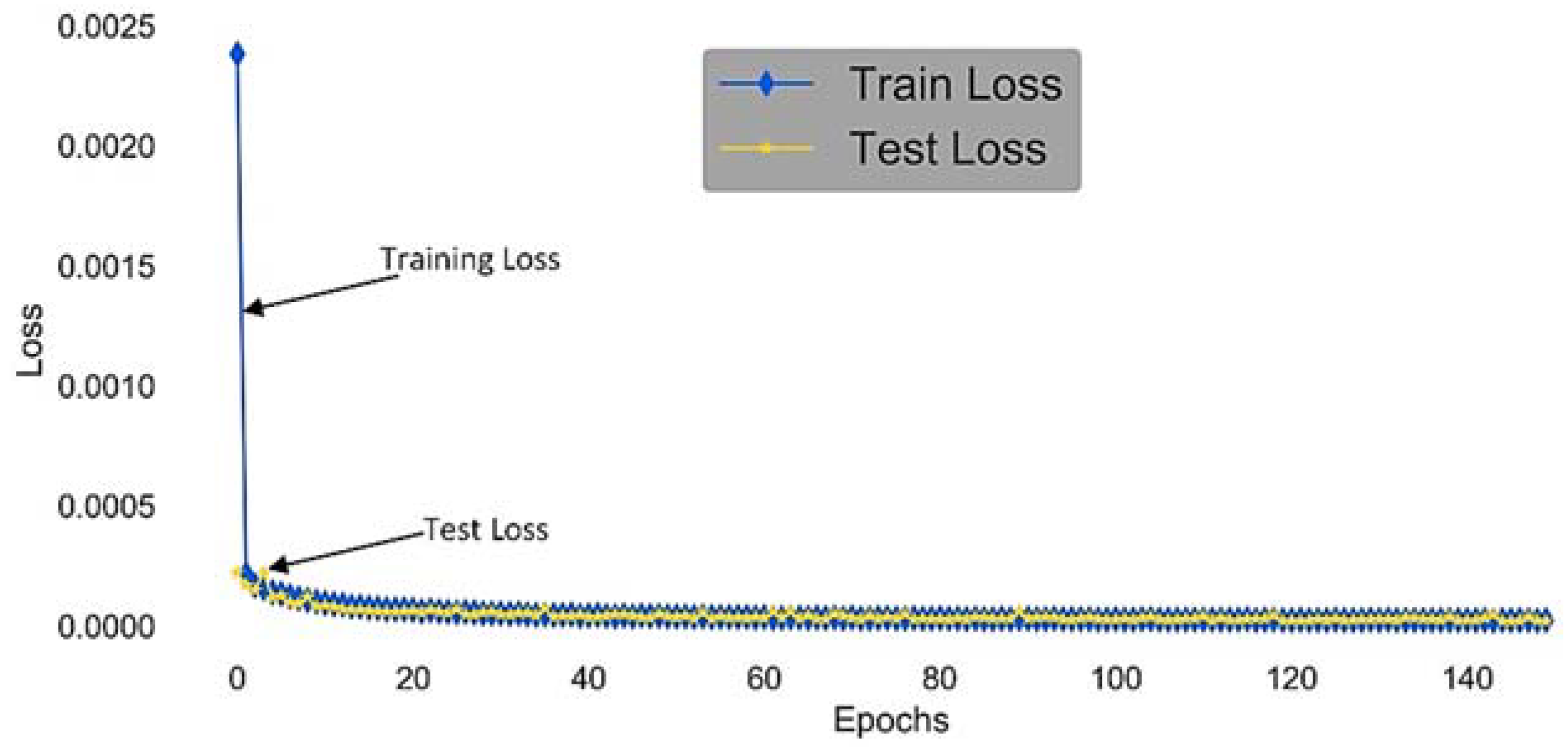
The internal validity in our case is concerned with three main threats. The first one is related to how much the data set is suitable to train a LSTM-RNN model that needs a large amount of data to mine historical patterns. The RTE power consumption data set ranges from January 2008 until December 2016. This data set is large enough to allow deep learning that is particularly targeted by LSTM-RNN. The second threat is LSTM-RNN overfitting. It can be observed by the learning curve that describes error rate according to the number of epochs. When overfitting occurs, after a certain point test error starts increasing while training error still decreases. Too much training with complex forecasting model leads to bad generalization. To prevent overfitting for our LSTM-RNN model, we have randomly shuffled the training examples at each epoch. This helps to improve generalization. Furthermore, early stopping is also used whereby training is stopped at the lowest error achieved on the test set. This approach is highly effective in reducing overfitting. The diagnostic plot of our LSTM-RNN model in
Figure 15 shows that the train and validation losses decrease as the number of epochs increases. The loss stabilizes around the same point showing a good fit. The third threat is related to the choice of the alternative machine learning for comparison. We may “miss-represent” the spectrum of techniques used for the energy prediction problem. For this concern, we have selected the most successful techniques according to our literature exploration. A stronger strategy to avoid this threat is to carry out a specific study to identify the top techniques for each class of prediction circumstances. This latter is one of the objectives of our future works.
The external validity in our case is concerned with the generalization of our results. In other terms, the LSTM-RNN may not perform well when it is used in very different circumstances of energy consumption. This threat is mitigated by two choices. The first is the fact that we are using a deep learning approach that is known to recognize good patterns and from a large amount of data and from the far history in the case of times series. Deep learning is a variation of ANN that produce a robust model. The second choice is the use of a large amount of training data (100 k out of more than 150 k examples) with a rigorous validation method that evaluates the robustness of the models against being trained on different training sets. Besides, one of our future works, will be applying our methodology and in particular LSTM-RNN modeling on many data sets from distant energy contexts and training more parameters of LSTM model via GA in a distributed manner. For instance, our approach could be applied for forecasting several decision variables such as the energy flow and the load in the context of urban vehicle networks [
50]. Many alternatives of validation methods for our approach can be inspired by the extended discussion on validation in [
51].