Combining Grey Model and Self-Adapting Intelligent Grey Model with Genetic Algorithm and Annual Share Changes in Natural Gas Demand Forecasting
Abstract
1. Introduction
1.1. Motivation
1.2. Relevant Literature Reviews
1.3. Contributions
- (1)
- A novel combined natural gas consumption forecasting model is proposed, which is based on the combination of GM(1,1), SIGM, and the changes of the annual share of natural gas consumption.
- (2)
- A GA is successfully used to determine the suitable combined weight coefficients between GM(1,1) and SIGM, and receives accurate forecasting performances; the change tendency of the annual share of natural gas consumption has been combined to excellently capture the regulation of the energy policy changing operational mechanism every four years.
- (3)
- The forecasting results demonstrate that the proposed GM-S-SIGM-GA model has received highest forecasting accuracy in terms of MAPE (4.48%), RMSE (11.59), and MAE (8.41), respectively; in the meanwhile, it also receives the significant test under 97.5% and 95% confident levels, respectively.
1.4. The Organization of This Paper
2. The Methods
2.1. The Grey Model (GM(1,1))
2.2. The Self-Adapting Intelligent Grey Model (SIGM)
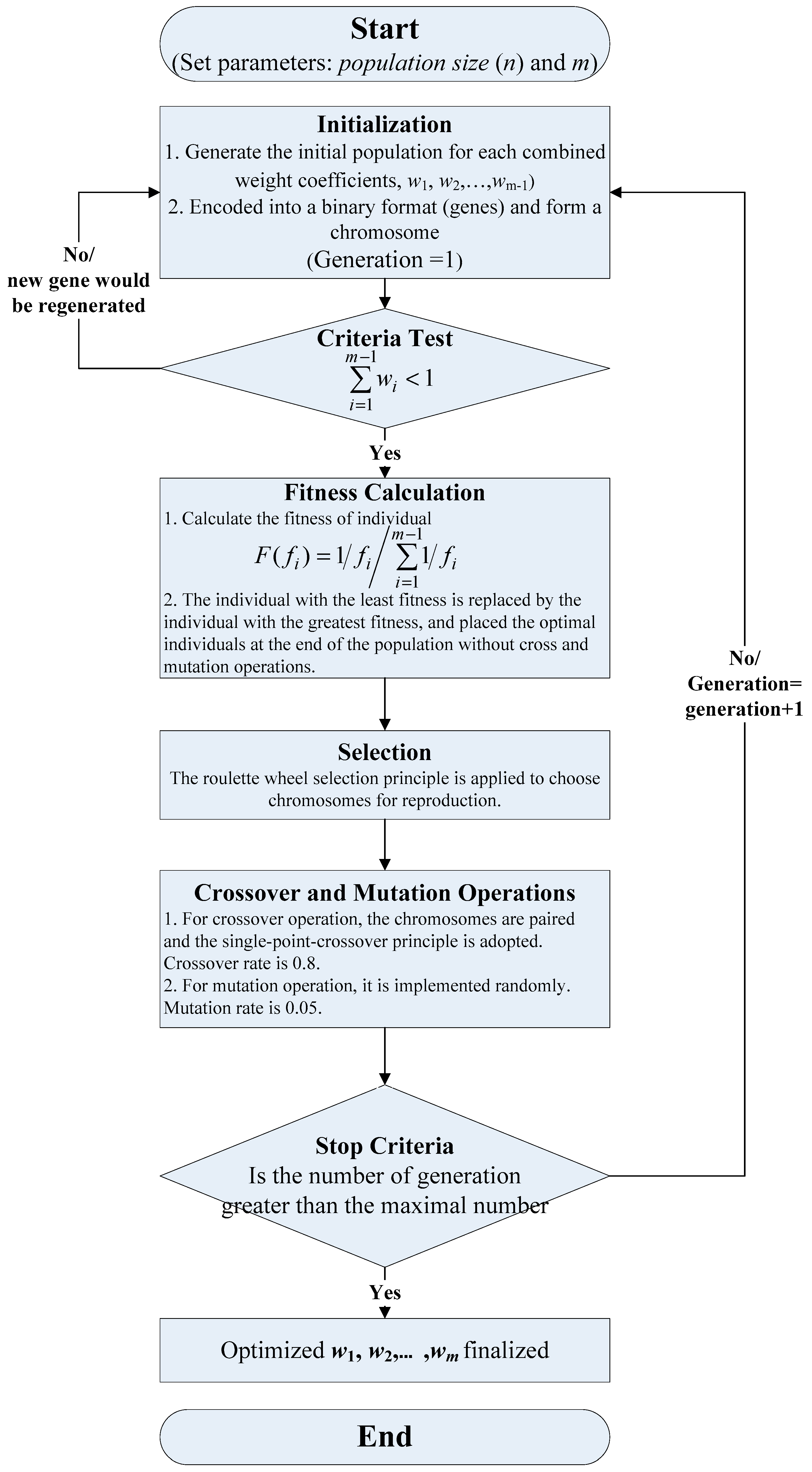
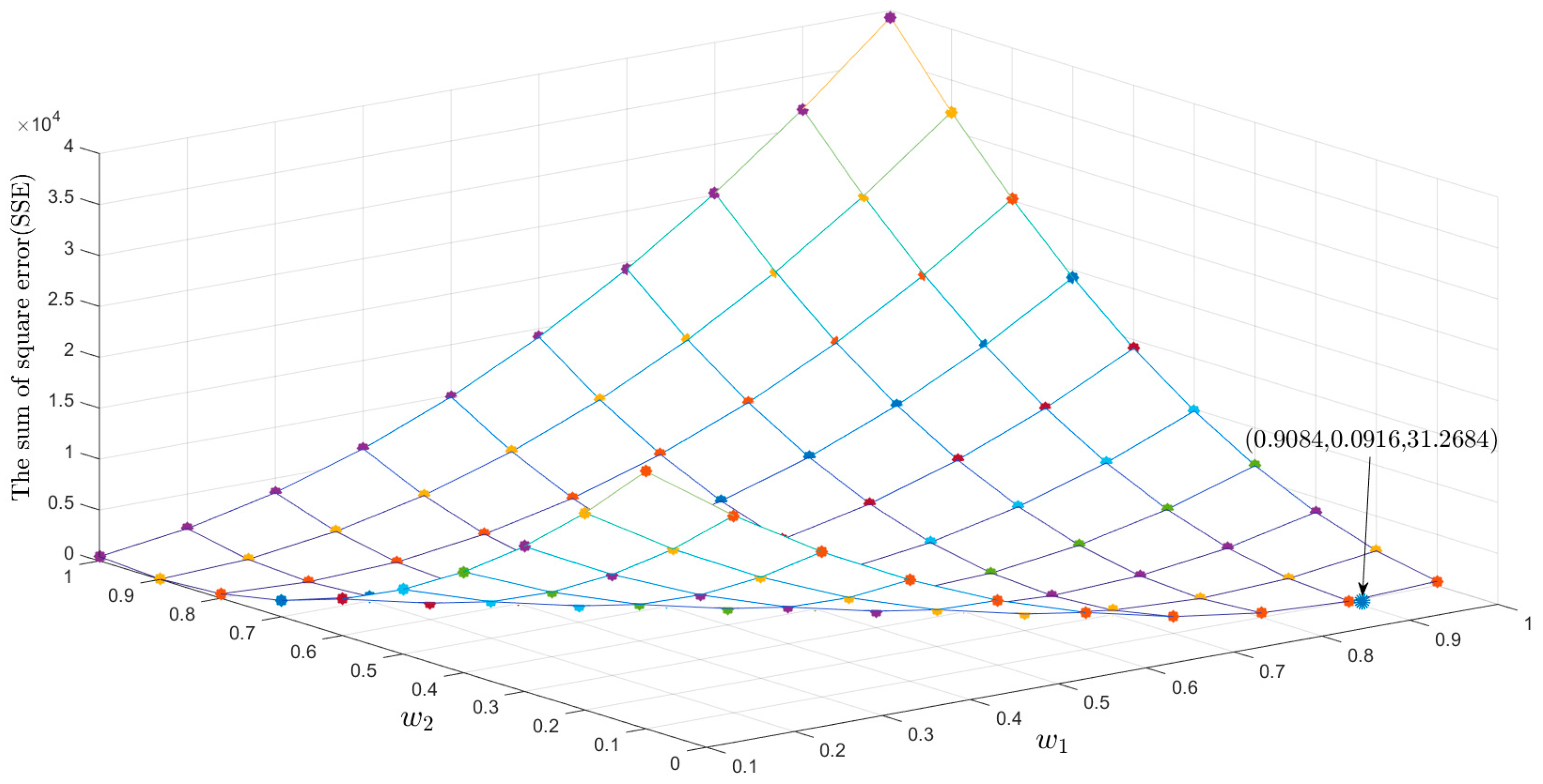
2.3. Calculating the Weight Coefficients of the Combined Model (GM(1,1) with SIGM) by a Genetic Algorithm
- Step 1
- Initialization. Generate the initial population for each combined weight coefficient, , with population size (n = 30). Then, these combined weight coefficients, , are encoded into a binary format, and are represented by a chromosome composed of “genes” of binary numbers. Each chromosome has (m − 1) genes, and each gene has 8 bits, i.e., the chromosome contains 8 × (m − 1) bits. would be calculated by .
- Step 2
- Criteria Test. Some of the population generated in Step 1 could not meet the constraint (based on Equation (23), right now, only (m − 1) combined weight coefficients are considered, thus, the constraint should be as ). To keep all individuals in the population to meet the constraints, all the chromosomes in the population are decoded into a decimal format to receive the associated real values. If the new constraint could not be met, the new gene would be regenerated for that chromosome until the constraint is met.
- Step 3
- Fitness Calculation. Due to looking for minimum forecasting residuals (the objective function), individuals with small values of the objective function always have greater fitness. Therefore, define the sum of accumulated countdown (SAC) of all individuals’ objective function values as Equation (25):where is the objective function value of the ith single forecasting model.Then, calculate the fitness of individual, , by Equation (26):At the same time, the individual with the least fitness is replaced by the individual with the greatest fitness, and placed the optimal individuals at the end of the population without cross and mutation operations.
- Step 4
- Selection. The roulette wheel selection principle is applied to choose chromosomes for reproduction, and individuals are selected for further operations.
- Step 5
- Crossover and Mutation Operations. For crossover operation, the chromosomes are paired randomly, and the proposed scheme adopts the single-point-crossover principle. Segments of paired chromosomes between two determined break-points are swapped. For mutation operation, it is implemented randomly. In this paper, the rates of crossover and mutation operations are set as 0.8 and 0.05 [36,37], respectively.
- Step 6
- Stop Criteria. If the number of generations is greater than a given scale, then, the best chromosome is determined, and the combined weight coefficients, , are also finalized; otherwise, go back to Step 1 and continue searching the next iteration.
2.4. The Total Procedure of the GM-S-SIGM-GA Model
- Step 1
- GM(1,1) and SIGM are modeled simultaneously. The training data of the collected annual natural gas dataset (from 2002 to 2010) are used to construct these two models and generate the simulation results. Please refer to Section 2.1 and Section 2.2 to learn more details about the modeling processes of these two models.
- Step 2
- GA is then employed to determine the combined weight coefficients, w. For these two modeled grey-based models, GM(1,1) and SIGM, construct the combined model, namely, the GM-SIGM-GA model, and apply the GA’s operations (selection, crossover, and mutation) to determine the most suitable combined weight coefficients. Please refer to Section 2.2 to learn more detail about the modeling process of the GM-SIGM-GA model.
- Step 3
- The annual share changing ratio is applied to adjust the effects of energy policy change every fixed period. The changes of annual shares of the natural gas consumption from the total energy consumption is taken into account to finish the final part of the proposed model, namely, the GM-S-SIGM-GA model. Please refer Section 3.3.2 to learn more details about the special adjustment mechanism.
3. Numerical Examples of the Proposed Model
3.1. Materials (Dataset of Numerical Examples)
3.2. Forecasting Accuracy Indexes and Forecasting Accuracy Significance Tests
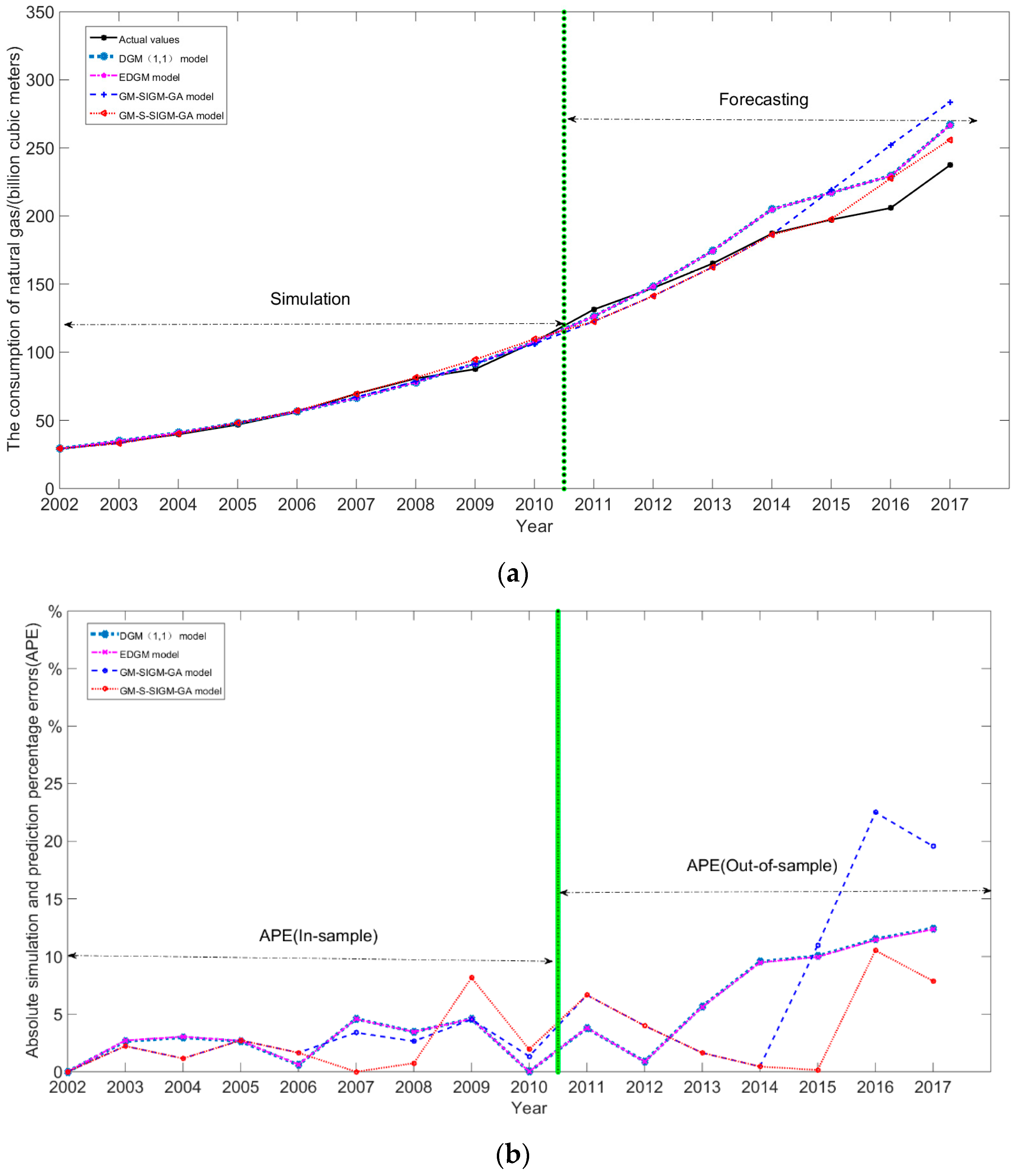
3.3. Forecasting Results and Improvement Analysis
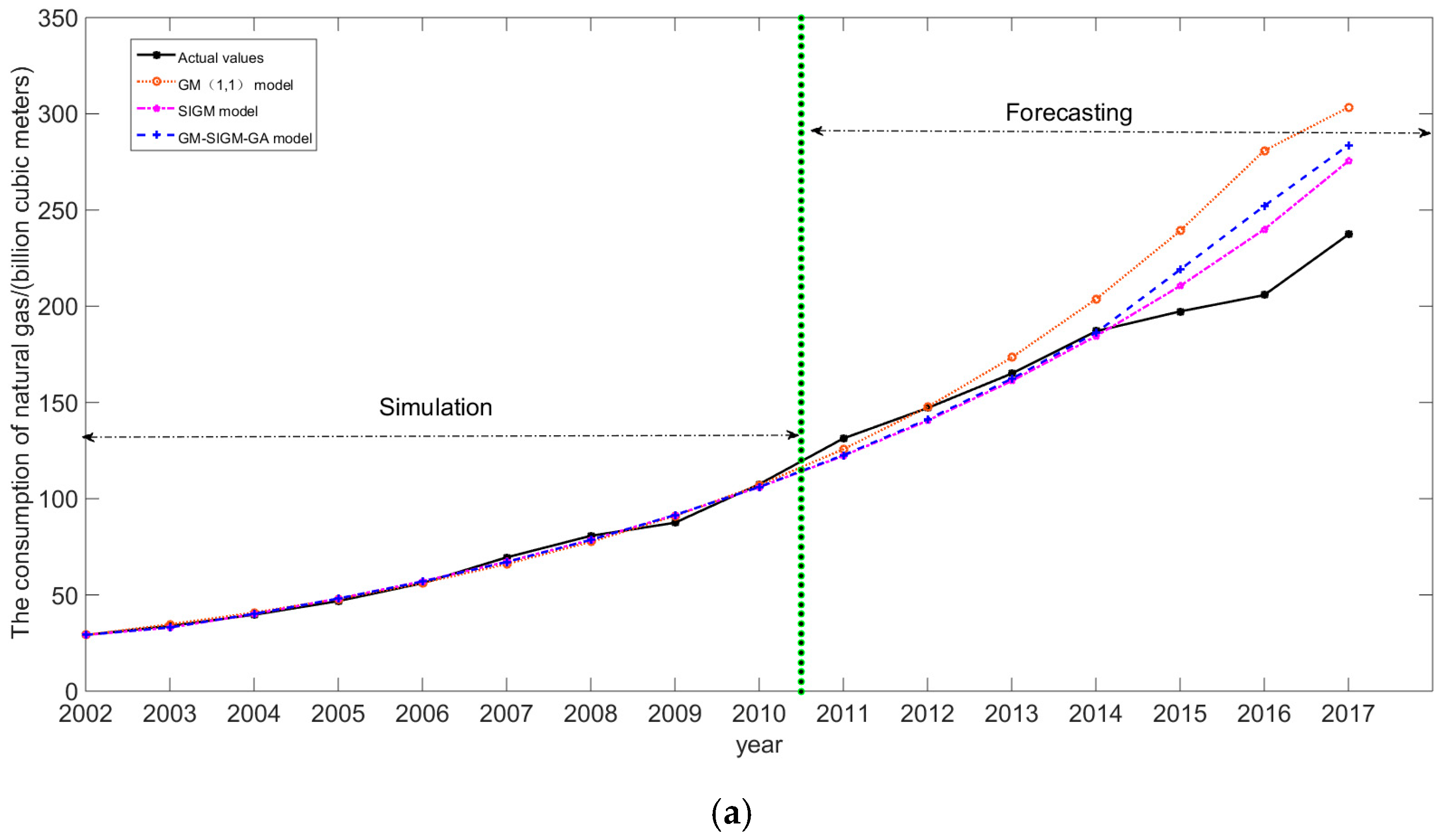
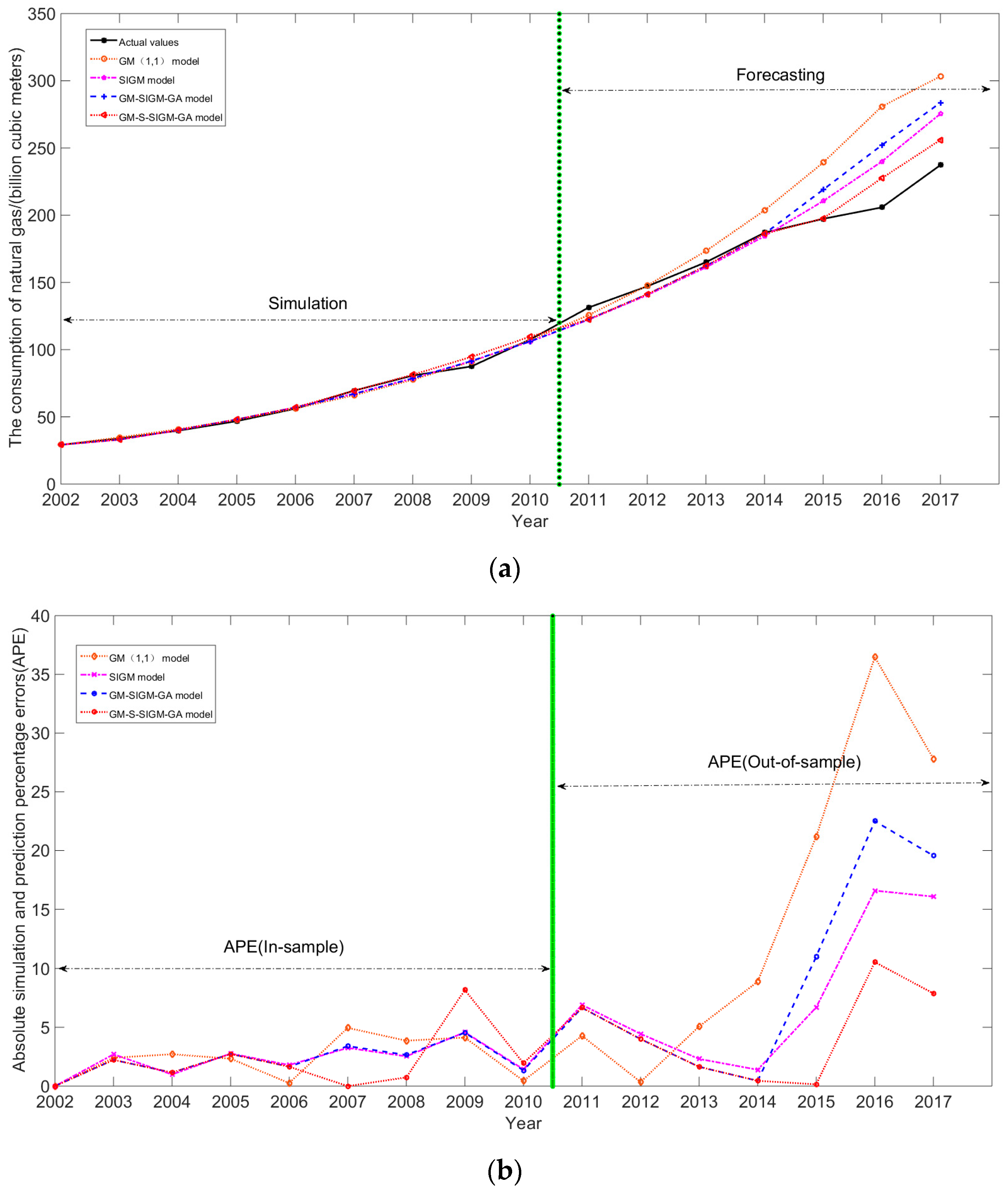
3.3.1. Forecasting Results
3.3.2. Improvement Analysis
3.4. Discussions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| the original time series | |
| the element of | |
| the first order accumulating generation operator of | |
| the element of | |
| the mean sequence of | |
| the element of | |
| a | the coefficient of development |
| b | the amount of grey action |
| u | the vector of a and b |
| c | the constant to expand from GM(1,1) to SIGM |
| the first parameter of the estimator of SIGM | |
| the second parameter of the estimator of SIGM | |
| the last parameter of the estimator of SIGM | |
| the combined weight coefficients | |
| the forecasting residual | |
| the objective function value of the ith single forecasting model | |
| the fitness of individual | |
| the changes of annual shares of the natural gas consumption from the total energy consumption | |
| S | the coefficient of adjustment (annual share changes) |
| the change ratio of two annual shares of the natural gas consumption from the total energy consumption | |
| the ith pair difference of the ith pair-forecasting error | |
| the value of is positive | |
| the value of is negative | |
| W | the statistic of the Wilcoxon signed-rank test |
References
- Zeng, B.; Li, C. Forecasting the natural gas demand in China using a self-adapting intelligent grey model. Energy 2016, 112, 810–825. [Google Scholar] [CrossRef]
- Ma, X.; Liu, Z. Application of a novel time-delayed polynomial grey model to predict the natural gas consumption in China. J. Comput. Appl. Math. 2017, 324, 17–24. [Google Scholar] [CrossRef]
- Bahrami, S.; Sheikhi, A. From demand response in smart grid toward integrated demand response in smart energy hub. IEEE Trans. Smart Grid 2016, 7, 650–658. [Google Scholar] [CrossRef]
- Sheikhi, A.; Rayati, M.; Bahrami, S.; Ranjbar, A.M.; Sattari, S. A cloud computing framework on demand side management game in smart energy hubs. Int. J. Electr. Power Energy Syst. 2015, 64, 1007–1016. [Google Scholar] [CrossRef]
- Amini, M.H.; Boroojeni, K.G.; Iyengar, S.S.; Blaabjerg, F.; Pardalos, P.M.; Madni, A.M. A panorama of future interdependent networks: From intelligent infrastructures to smart cities. In Sustainable Interdependent Networks; Amini, M., Boroojeni, K., Iyengar, S., Pardalos, P., Blaabjerg, F., Madni, A., Eds.; Springer: Cham, Switzerland; New York, NY, USA, 2018; Volume 145, pp. 1–10. ISBN 978-3-319-74411-7. [Google Scholar]
- Ding, S.; Hipel, K.W.; Dang, Y. Forecasting China’s electricity consumption using a new grey prediction model. Energy 2018, 149, 314–328. [Google Scholar] [CrossRef]
- Ervural, B.C.; Beyca, O.F.; Zaim, S. Model estimation of ARMA using genetic algorithms: A case study of forecasting natural gas consumption. Procedia Soc. Behav. Sci. 2016, 235, 537–545. [Google Scholar] [CrossRef]
- Yuan, C.Q.; Liu, S.F.; Fang, Z.G. Comparison of China’s primary energy consumption forecasting by using ARIMA (the autoregressive integrated moving average) model and GM (1, 1) model. Energy 2016, 100, 384–390. [Google Scholar] [CrossRef]
- Wadud, Z.; Himadri, S.; Dey, H.S.; Kabir, M.A.; Khan, S.I. Modeling and forecasting natural gas demand in Bangladesh. Energy Policy 2011, 39, 7372–7380. [Google Scholar] [CrossRef]
- Özmen, A.; Yılmaz, Y.; Weber, G.-W. Natural gas consumption forecast with MARS and CMARS models for residential users. Energy Econ. 2018, 70, 357–381. [Google Scholar] [CrossRef]
- Bianco, V.; Scarpa, F.; Tagliafico, L.A. Scenario analysis of nonresidential natural gas consumption in Italy. Appl. Energy 2014, 113, 392–403. [Google Scholar] [CrossRef]
- Forouzanfar, M.; Doustmohammadi, A.; Menhaj, M.B.; Hasanzadeh, S. Modeling and estimation of the natural gas consumption for residential and commercial sectors in Iran. Appl. Energy 2010, 87, 268–274. [Google Scholar] [CrossRef]
- Shaikh, F.; Ji, Q. Forecasting natural gas demand in China: Logistic modelling analysis. Int. J. Electr. Power Energy Syst. 2016, 77, 25–32. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, J. Forecasting natural gas consumption in China by Bayesian model averaging. Energy Rep. 2015, 1, 216–220. [Google Scholar] [CrossRef]
- Yuan, X.-C.; Sun, X.; Zhao, W.; Mi, Z.; Wang, B.; Wei, Y.-M. Forecasting China’s regional energy demand by 2030: A Bayesian approach. Resour. Conserv. Recycl. 2017, 127, 85–95. [Google Scholar] [CrossRef]
- Szoplik, J. Forecasting of natural gas consumption with artificial neural networks. Energy 2015, 85, 208–220. [Google Scholar] [CrossRef]
- Azadeh, A.; Asadzadeh, S.M.; Saberi, M.; Nadimi, V.; Tajvidi, A.; Sheikalishahi, M. A Neuro-fuzzy-stochastic frontier analysis approach for long-term natural gas consumption forecasting and behavior analysis: The cases of Bahrain, Saudi Arabia, Syria, and UAE. Appl. Energy 2011, 88, 3850–3859. [Google Scholar] [CrossRef]
- Kaynar, O.; Yilmaz, I.; Demirkoparan, F. Forecasting of natural gas consumption with neural network and neuro fuzzy system. Energy Educ. Sci. Technol. Part A Energy Sci. Res. 2011, 26, 221–238. [Google Scholar]
- Potočnik, P.; Soldo, B.; Šimunović, G.; Šarić, T.; Jeromen, A.; Govekar, E. Comparison of static and adaptive models for short-term residential natural gas forecasting in Croatia. Appl. Energy 2014, 129, 94–103. [Google Scholar] [CrossRef]
- Karadede, Y.; Ozdemir, G.; Aydemir, E. Breeder hybrid algorithm approach for natural gas demand forecasting model. Energy 2017, 141, 1269–1284. [Google Scholar] [CrossRef]
- Panapakidis, I.P.; Dagoumas, A.S. Day-ahead natural gas demand forecasting based on the combination of wavelet transform and ANFIS/genetic algorithm/neural network model. Energy 2017, 118, 231–245. [Google Scholar] [CrossRef]
- Rodger, J.A. A fuzzy nearest neighbor neural network statistical model for predicting demand for natural gas and energy cost savings in public buildings. Expert Syst. Appl. 2014, 41, 1813–1829. [Google Scholar] [CrossRef]
- Azadeh, A.; Asadzadeh, S.M.; Ghanbari, A. An adaptive network-based fuzzy inference system for short-term natural gas demand estimation: Uncertain and complex environments. Energy Policy 2010, 38, 1529–1536. [Google Scholar] [CrossRef]
- Bai, Y.; Li, C. Daily natural gas consumption forecasting based on a structure-calibrated support vector regression approach. Energy Build. 2016, 127, 571–579. [Google Scholar] [CrossRef]
- Zhu, L.; Li, M.S.; Wu, Q.H.; Jiang, L. Short-term natural gas demand prediction based on support vector regression with false neighbours filtered. Energy 2015, 80, 428–436. [Google Scholar] [CrossRef]
- Wu, Y.-H.; Shen, H. Grey-related least squares support vector machine optimization model and its application in predicting natural gas consumption demand. J. Comput. Appl. Math. 2018, 338, 212–220. [Google Scholar] [CrossRef]
- Fan, G.; Peng, L.-L.; Hong, W.-C.; Sun, F. Electric load forecasting by the SVR model with differential empirical mode decomposition and auto regression. Neurocomputing 2016, 173, 958–970. [Google Scholar] [CrossRef]
- Kaytez, F.; Taplamacioglu, M.C.; Cam, E.; Hardalac, F. Forecasting electricity consumption: A comparison of regression analysis, neural networks and least squares support vector machines. Int. J. Electr. Power Energy Syst. 2015, 67, 431–438. [Google Scholar] [CrossRef]
- Deng, J.L. Control problems of grey systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar]
- Wang, J.; Jiang, H.; Zhou, Q.; Wu, J.; Qin, S. China’s natural gas production and consumption analysis based on the multicycle Hubbert model and rolling Grey model. Renew. Sustain. Energy Rev. 2016, 53, 1149–1167. [Google Scholar] [CrossRef]
- Shaikh, F.; Ji, Q.; Shaikh, P.H.; Mirjat, N.H.; Uqaili, M.A. Forecasting China’s natural gas demand based on optimised nonlinear grey models. Energy 2017, 140, 941–951. [Google Scholar] [CrossRef]
- Liu, X.; Moreno, B.; García, A.S. A grey neural network and input-output combined forecasting model. Primary energy consumption forecasts in Spanish economic sectors. Energy 2016, 115, 1042–1054. [Google Scholar] [CrossRef]
- Hamzacebi, C.; Es, H.A. Forecasting the annual electricity consumption of Turkey using an optimized grey model. Energy 2014, 70, 165–171. [Google Scholar] [CrossRef]
- Ma, X.; Liu, Z. The kernel-based nonlinear multivariate grey model. Appl. Math. Model. 2018, 56, 217–238. [Google Scholar] [CrossRef]
- Mehrtash, M.; Kargarian, A.; Mohammadi, A. Partition-based bus renumbering effect on interior point-based OPF solution. In Proceedings of the 2018 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 8–9 February 2018; IEEE: College Station, TX, USA, 2018. [Google Scholar]
- Fan, G.-F.; Peng, L.-L.; Zhao, X.; Hong, W.-C. Applications of hybrid EMD with PSO and GA for an SVR-based load forecasting model. Energies 2017, 10, 1713. [Google Scholar] [CrossRef]
- Pai, P.-F.; Hong, W.-C. A recurrent support vector regression model in rainfall forecasting. Hydrol. Process. 2007, 21, 819–827. [Google Scholar] [CrossRef]
- The Annual Natural Gas Consumption in China. Available online: https://www.china5e.com/ (accessed on 10 May 2018).
- Lewis, C.D. Industrial and Business Forecasting Method; Butter-Worth-Heinemann: London, UK, 1982. [Google Scholar]
- Diebold, F.X.; Mariano, R.S. Comparing predictive accuracy. J. Bus. Econ. Stat. 1995, 13, 134–144. [Google Scholar]
- Wilcoxon, F. Individual comparisons by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Wu, L.F.; Liu, S.F.; Liu, D.L. Modeling and forecasting CO2 emissions in the BRICS (Brazil, Russia, India, China, and South Africa) countries using a novel multi-variable grey model. Energy 2015, 79, 489–495. [Google Scholar] [CrossRef]
- Xie, N.M.; Liu, S.F. Discrete grey forecasting model and its optimization. Appl. Math. Model. 2008, 33, 1173–1186. [Google Scholar] [CrossRef]
- Liu, S.F.; Yang, Y.J.; Wu, L.F. Grey Systems Theory and Applications, 7th ed.; Science Press: Beijing, China, 2014; ISBN 9787030409126. (In Chinese) [Google Scholar]



| Years | Natural Gas Consumption | Years | Natural Gas Consumption | Years | Natural Gas Consumption | Years | Natural Gas Consumption |
|---|---|---|---|---|---|---|---|
| 2002 | 29.2 | 2006 | 56.1 | 2010 | 107.5 | 2014 | 187.0 |
| 2003 | 33.9 | 2007 | 69.5 | 2011 | 131.3 | 2015 | 197.3 |
| 2004 | 39.7 | 2008 | 80.7 | 2012 | 147.1 | 2016 | 205.8 |
| 2005 | 46.8 | 2009 | 87.5 | 2013 | 165.0 | 2017 | 237.3 |
| MAPE | ≤10% | 10%~20% | 20%~50% | ≥50% |
|---|---|---|---|---|
| Evaluation | Highly accurate | Good | Reasonable | Inaccurate |
| Year | Total Annual Natural Gas Consumption (billion m3) | The GM(1,1) [42] | The SIGM [1] | The GM-SIGM-GA |
|---|---|---|---|---|
| 2002 | 29.2 | 29.2000 | 29.2000 | 29.2000 |
| 2003 | 33.9 | 32.9839 | 34.7180 | 33.1427 |
| 2004 | 39.7 | 40.0937 | 40.7752 | 40.1561 |
| 2005 | 46.8 | 48.0967 | 47.8891 | 48.0777 |
| 2006 | 56.1 | 57.1048 | 56.2442 | 57.0260 |
| 2007 | 69.5 | 67.2444 | 66.0570 | 67.1356 |
| 2008 | 80.7 | 78.6576 | 77.5818 | 78.5591 |
| 2009 | 87.5 | 91.5044 | 91.1173 | 91.4689 |
| 2010 | 107.5 | 105.9649 | 107.0143 | 106.0610 |
| MAPE | 2.23% | 2.35% | 2.19% | |
| RMSE | 1.87 | 2.05 | 1.86 | |
| MAE | 1.49 | 1.53 | 1.48 |
| Year | Total Annual Natural Gas Consumption (billion m3) | The GM(1,1) [42] | The SIGM [1] | The GM-SIGM-GA |
|---|---|---|---|---|
| 2011 | 131.3 | 122.2416 | 125.6849 | 122.5570 |
| 2012 | 147.1 | 140.5629 | 147.6128 | 141.2087 |
| 2013 | 165.0 | 161.1854 | 173.3664 | 162.3012 |
| 2014 | 187.0 | 184.3982 | 203.6133 | 186.1583 |
| 2015 | 197.3 | 210.5267 | 239.1372 | 219.0269 |
| 2016 | 205.8 | 239.9371 | 280.8589 | 252.095 |
| 2017 | 237.3 | 275.4491 | 303.2934 | 283.7216 |
| MAPE (2011–2017) | 7.77% | 14.87% | 9.40% | |
| RMSE (2011–2017) | 20.50 | 41.61 | 26.43 | |
| MAE (2011–2017) | 15.36 | 30.57 | 18.95 | |
| MAPE (2011–2014) | 3.76% | 4.64% | 3.19% | |
| RMSE (2011–2014) | 6.04 | 9.72 | 5.46 | |
| MAE (2011–2014) | 5.5 | 7.78 | 4.54 |
| Years | The Total Annual Consumption of Natural Gas (billion m3) | Simulation/Forecasting Values | The Parameters on the Share of Natural Gas Consumption from Total Energy Consumption | MAPE (per year) GM-S-SIGM-GA | ||||
|---|---|---|---|---|---|---|---|---|
| GM-SIGM-GA | GM-S-SIGM-GA | Ri | ΔRi | Δ2Ri | Ki | |||
| 2002 | 29.2 | 29.2 | 29.2 | 2.3 | −0.1 | -- | -- | 0.0000 |
| 2003 | 33.9 | 33.1 | 33.1 | 2.3 | 0.0 | 0.0 | 0.0 | 0.0223 |
| 2004 | 39.7 | 40.2 | 40.1 | 2.3 | 0.0 | 0 | 0.0 | 0.0115 |
| 2005 | 46.8 | 48.1 | 48.1 | 2.4 | 0.1 | 0.1 | 0.0 | 0.0273 |
| 2006 | 56.1 | 57.0 | 57.0 | 2.7 | 0.3 | 0.2 | 2.0 | 0.0165 |
| 2007 | 69.5 | 67.1 | 69.5 | 3.0 | 0.3 | 0.0 | 0.0 | 0.0000 |
| 2008 | 80.7 | 78.6 | 81.3 | 3.4 | 0.4 | 0.1 | 0.0 | 0.0074 |
| 2009 | 87.5 | 91.5 | 94.6 | 3.5 | 0.1 | −0.3 | −3.0 | 0.0817 |
| 2010 | 107.5 | 106.1 | 109.6 | 4.0 | 0.5 | 0.4 | −1.3 | 0.0195 |
| 2011 | 131.3 | 122.6 | 122.6 | 4.6 | 0.6 | 0.1 | 0.25 | 0.0666 |
| 2012 | 147.1 | 141.2 | 141.2 | 4.8 | 0.2 | −0.4 | −4.0 | 0.0400 |
| 2013 | 165.0 | 162.3 | 162.3 | 5.3 | 0.7 | 0.5 | −1.25 | 0.0164 |
| 2014 | 187.0 | 186.2 | 186.2 | 5.7 | 0.4 | −0.3 | −0.6 | 0.0045 |
| 2015 | 197.3 | 219.0 | 197.6 | 5.9 | 0.2 | −0.2 | 0.67 | 0.0015 |
| 2016 | 205.8 | 252.1 | 227.5 | 6.4 | 0.5 | 0.3 | −1.5 | 0.1054 |
| 2017 | 237.3 | 283.7 | 256.0 | -- | -- | -- | -- | 0.0788 |
| Years | The Total Annual Consumption of Natural Gas (billion m3) | The GM(1,1) [42] | The SIGM [1] | The GM-SIGM-GA | The GM-S-SIGM-GA | The DGM(1,1) [43] | The EDGM [44] |
|---|---|---|---|---|---|---|---|
| 2011 | 131.3 | 122.2 | 125.7 | 122.6 | 122.6 | 126. 3 | 126.3 |
| 2012 | 147.1 | 140.6 | 147.6 | 141.2 | 141.2 | 148.4 | 148.4 |
| 2013 | 165.0 | 161.2 | 173.4 | 162.3 | 162.3 | 174.3 | 174.4 |
| 2014 | 187.0 | 184.4 | 203.6 | 186.2 | 186.2 | 204.7 | 204.9 |
| 2015 | 197.3 | 210.5 | 239.1 | 219.0 | 197.6 | 217.0 | 217.1 |
| 2016 | 205.8 | 239.9 | 280.9 | 252.1 | 227.5 | 229.3 | 229.5 |
| 2017 | 237.3 | 275.4 | 303.3 | 283.7 | 256.0 | 266.6 | 266.9 |
| MAPE | 7.77% | 14.87% | 9.40% | 4.48% | 7.65% | 7.71% | |
| RMSE | 20.50 | 41.61 | 26.43 | 11.59 | 17.85 | 17.98 | |
| MAE | 15.36 | 30.57 | 18.95 | 8.41 | 15.12 | 15.23 |
| Compared Models | Wilcoxon Signed-Rank Test | |
|---|---|---|
| α = 0.025; W = 2 | α = 0.05; W = 3 | |
| GM-S-SIGM-GA vs. GM-SIGM-GA | 2 a | 2 a |
| GM-S-SIGM-GA vs. GM (1,1) [42] | 0 a | 0 a |
| GM-S-SIGM-GA vs. SIGM [1] | 2 a | 2 a |
| GM-S-SIGM-GA vs. DGM [43] | 0 a | 0 a |
| GM-S-SIGM-GA vs. EDGM [44] | 0 a | 0 a |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, G.-F.; Wang, A.; Hong, W.-C. Combining Grey Model and Self-Adapting Intelligent Grey Model with Genetic Algorithm and Annual Share Changes in Natural Gas Demand Forecasting. Energies 2018, 11, 1625. https://doi.org/10.3390/en11071625
Fan G-F, Wang A, Hong W-C. Combining Grey Model and Self-Adapting Intelligent Grey Model with Genetic Algorithm and Annual Share Changes in Natural Gas Demand Forecasting. Energies. 2018; 11(7):1625. https://doi.org/10.3390/en11071625
Chicago/Turabian StyleFan, Guo-Feng, An Wang, and Wei-Chiang Hong. 2018. "Combining Grey Model and Self-Adapting Intelligent Grey Model with Genetic Algorithm and Annual Share Changes in Natural Gas Demand Forecasting" Energies 11, no. 7: 1625. https://doi.org/10.3390/en11071625
APA StyleFan, G.-F., Wang, A., & Hong, W.-C. (2018). Combining Grey Model and Self-Adapting Intelligent Grey Model with Genetic Algorithm and Annual Share Changes in Natural Gas Demand Forecasting. Energies, 11(7), 1625. https://doi.org/10.3390/en11071625






