Network Features of the EU Carbon Trade System: An Evolutionary Perspective
Abstract
1. Introduction
2. Data
3. Methods
3.1. Construction of the Carbon Trade Network
3.2. Network Metric Indicators
3.3. Distribution of Network Degree
3.4. Time Windows for the Carbon Trading Networks
4. Results and Discussion
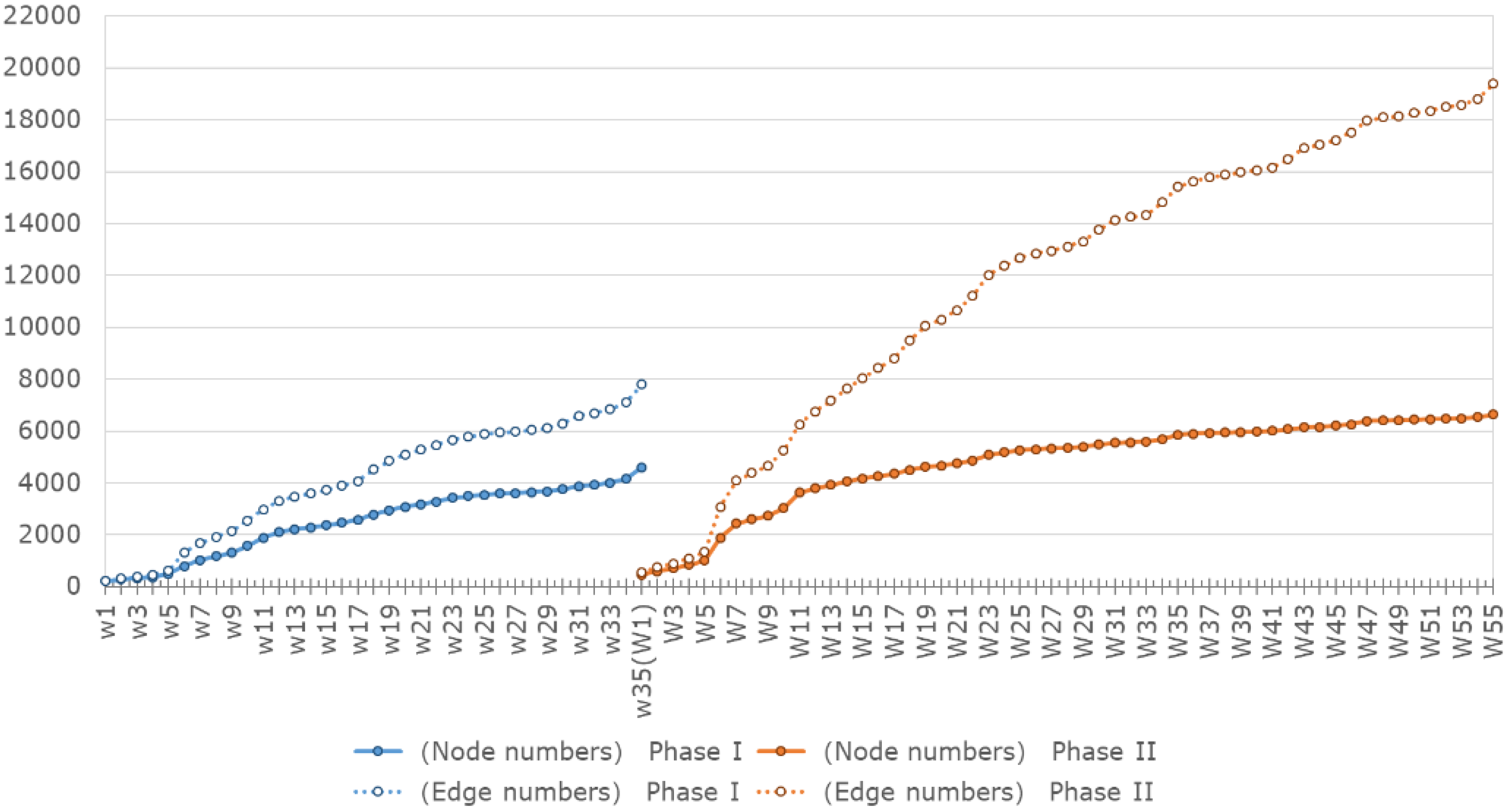
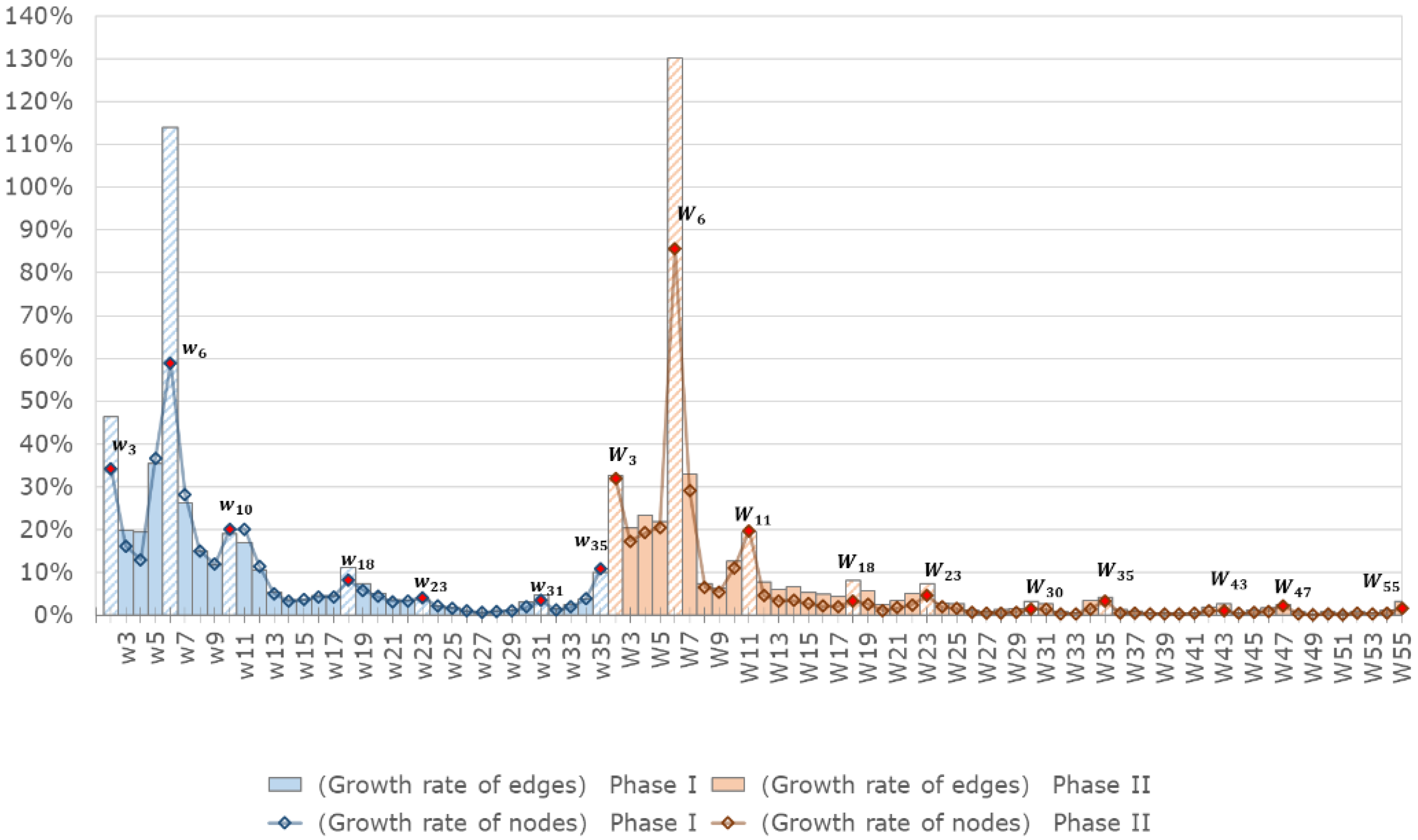
4.1. Growth Features of the Carbon Trading Network
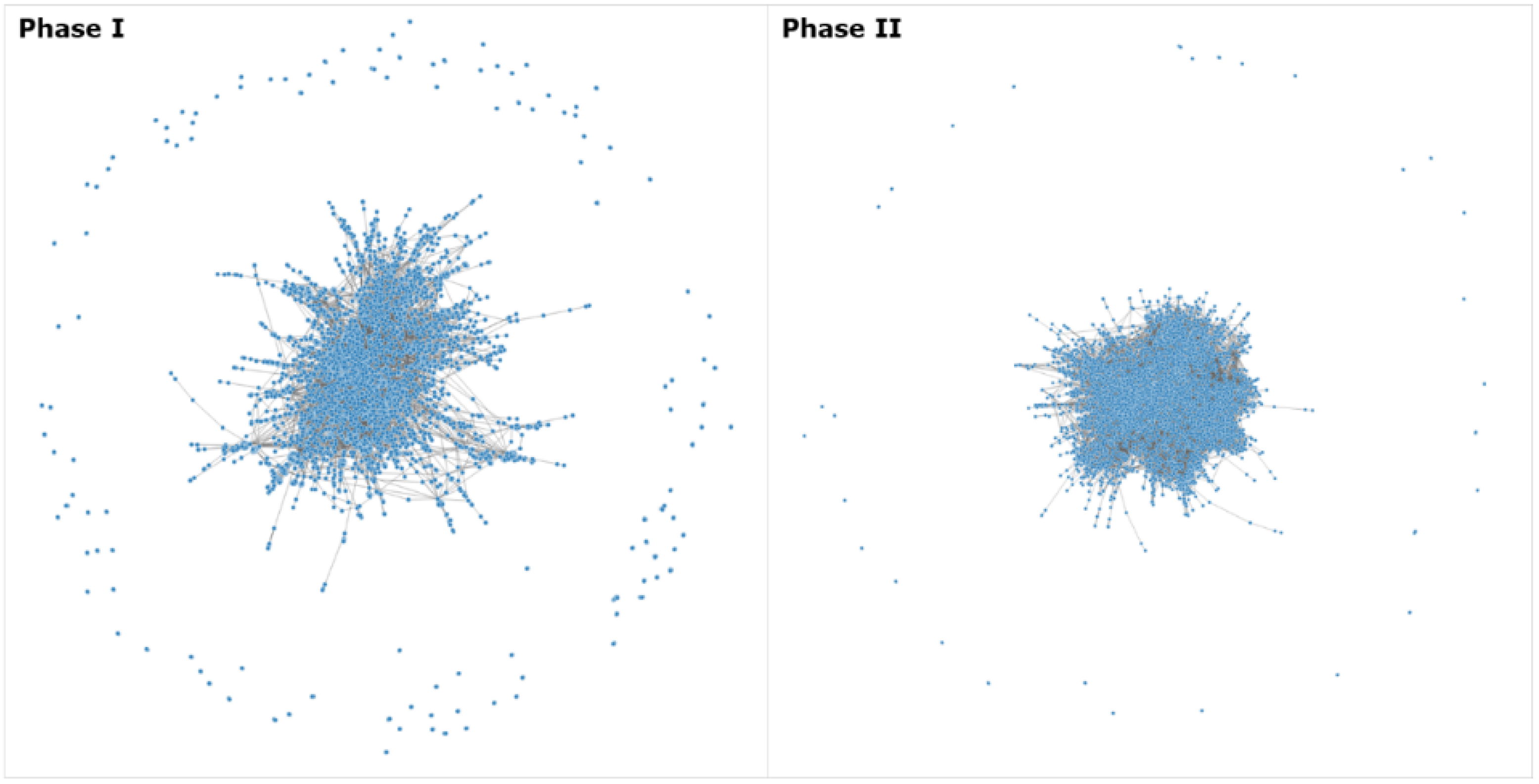
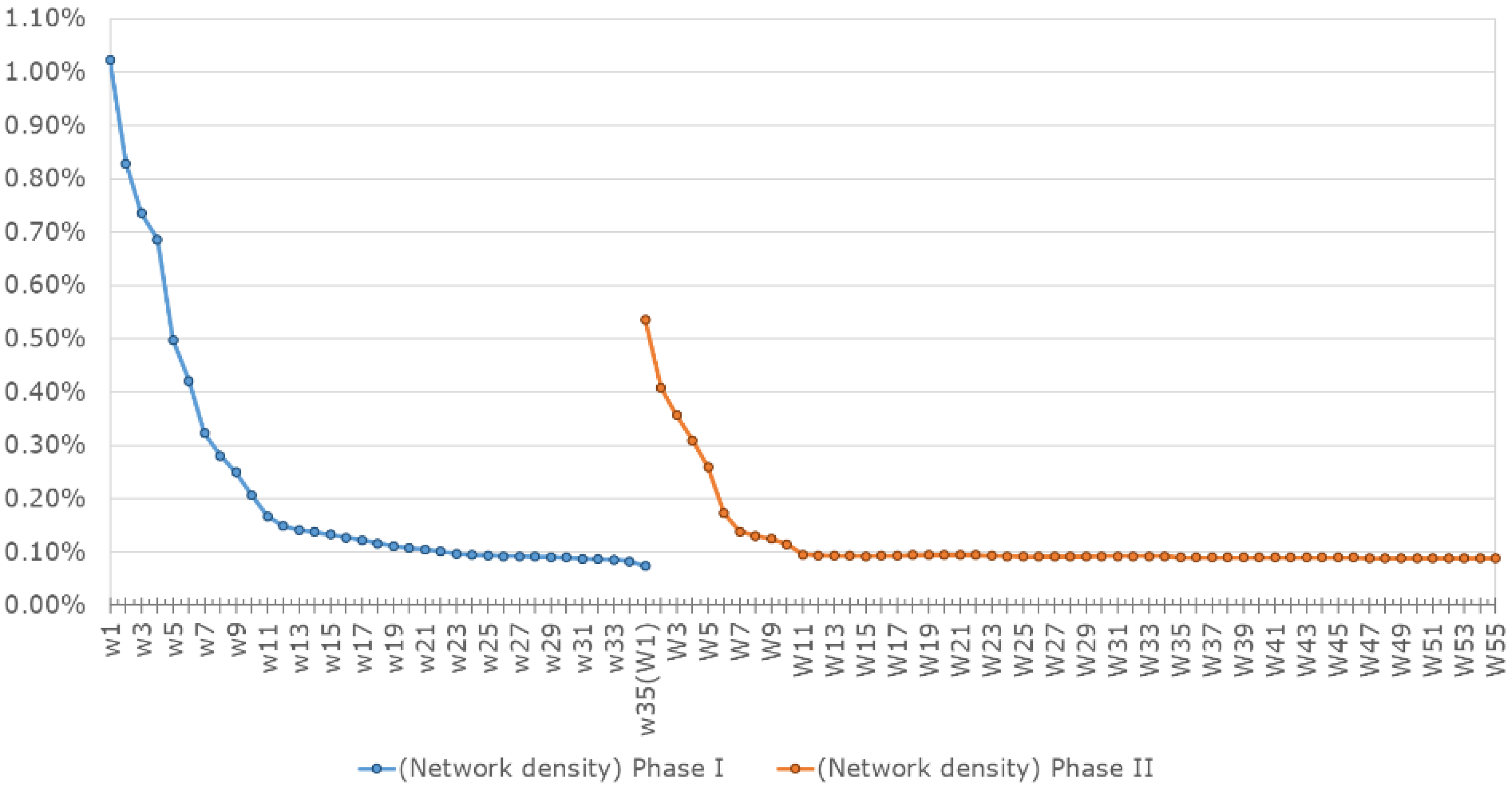
4.2. Structural Features of the Carbon Trading Network
4.3. Scale-Free Features of the Carbon Trading Network
5. Conclusions
- (1)
- We analyze the growth features of the carbon trading network for both Phase I and Phase II. Because the EU carbon market is an emerging market, the size of the market became increasingly larger with the development of the market. Over the long term, the growth rate decreased gradually over time, implying that there is a growth for the market. However, in the short run, the growth rate of the market is accelerated in May and December of each year. As the growth rate cooled down, the market structure become stable.
- (2)
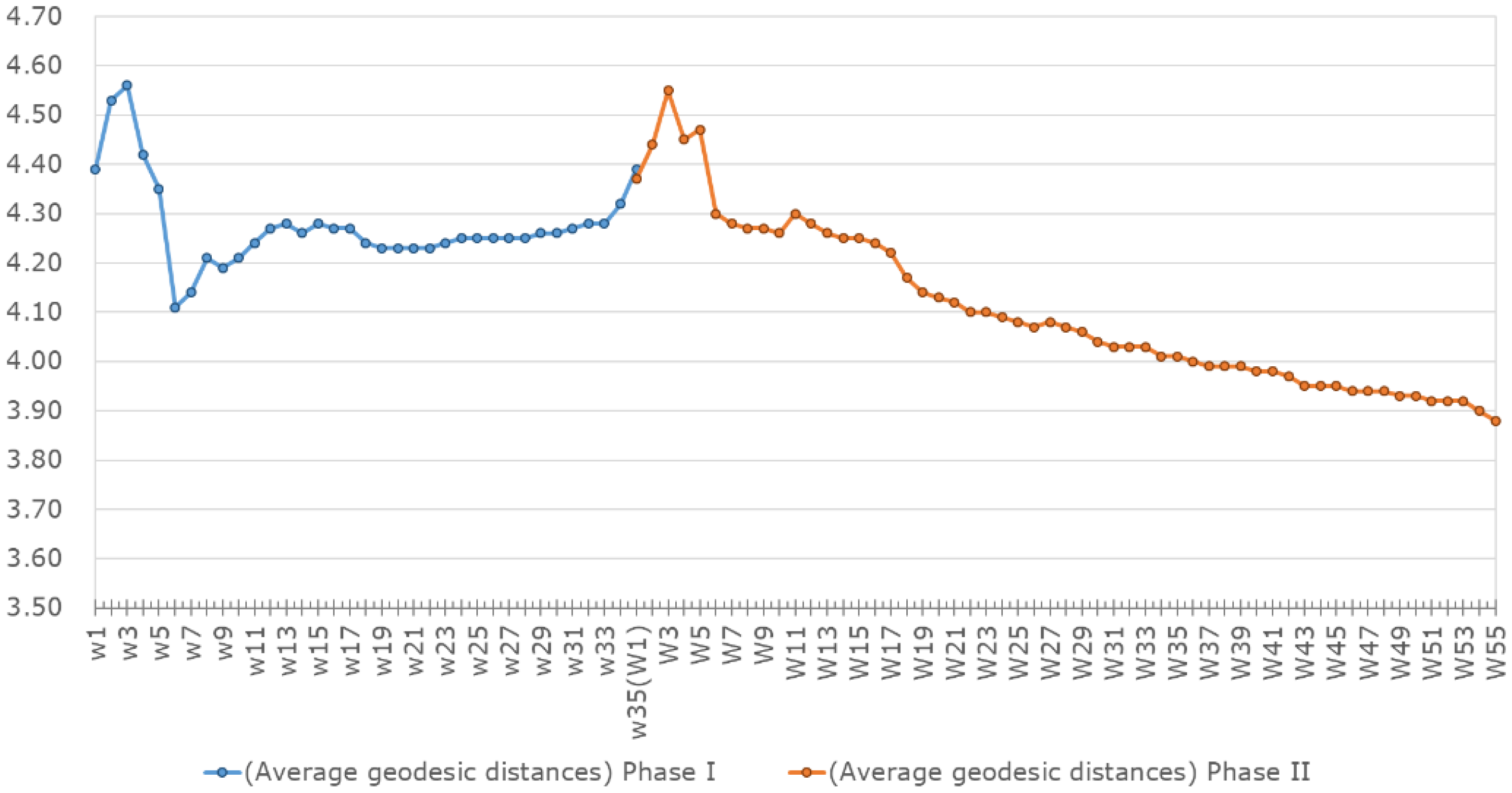
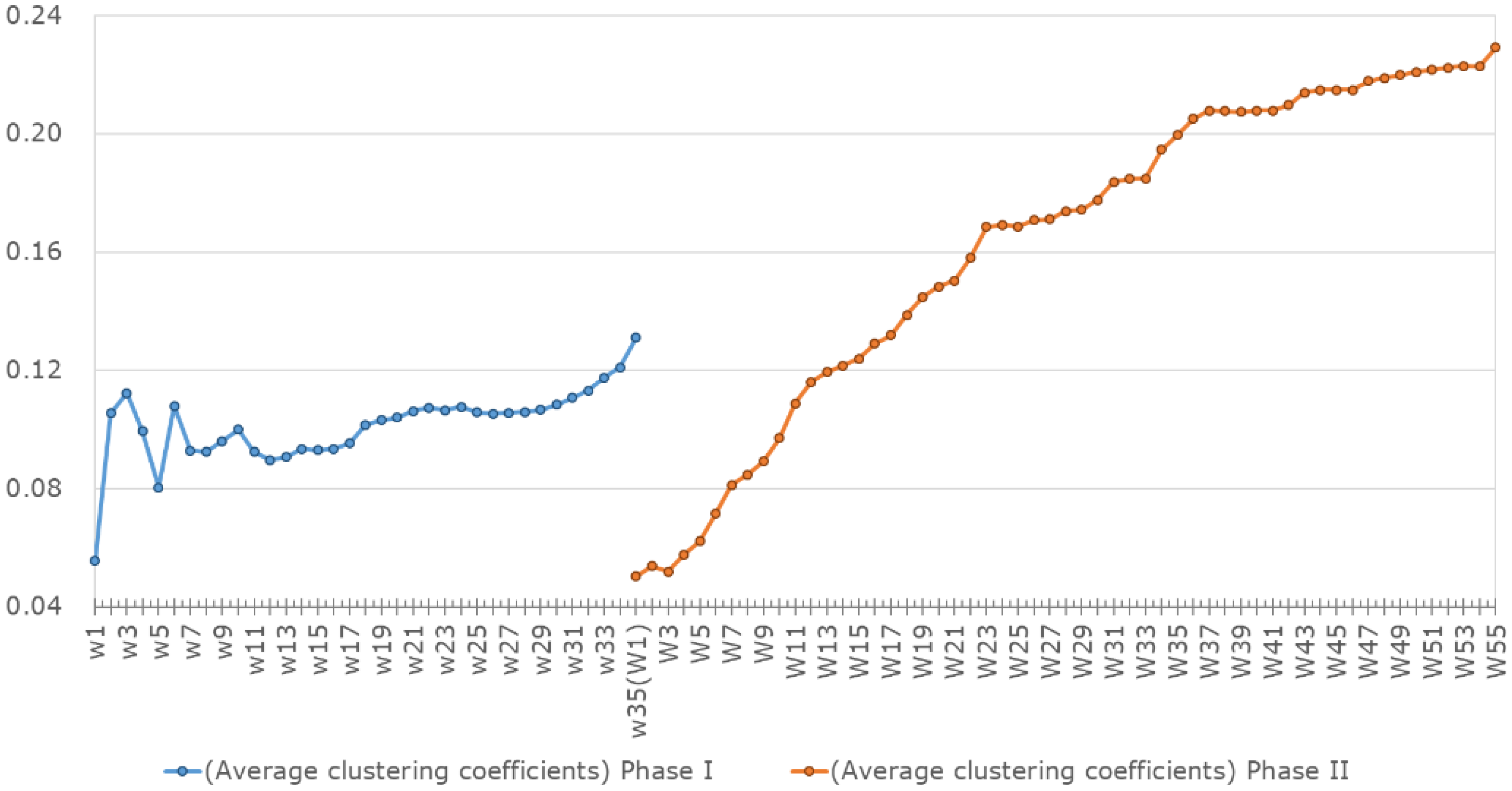
- We calculate the average geodesic distances and average clustering coefficients for the network model. Both metric indicators reveal that the market structures are evolving towards efficiency. First, the average geodesic distances are gradually decreasing, showing that over time the firms find it easier to find appropriate trading partners in the carbon trading network. Therefore, the market become more efficient in terms of transferring information and allowances. Second, the average clustering coefficients gradually increase over time, implying that firms are inclined to cluster together. Firms’ clustering behavior will potentially weaken the market power of firms with a dominant position in the trading networks, leading to a more structurally efficient market. Third, although the metric indicators’ trends are ideal, the actual changes were too small to significantly increase market efficiency.
- (3)
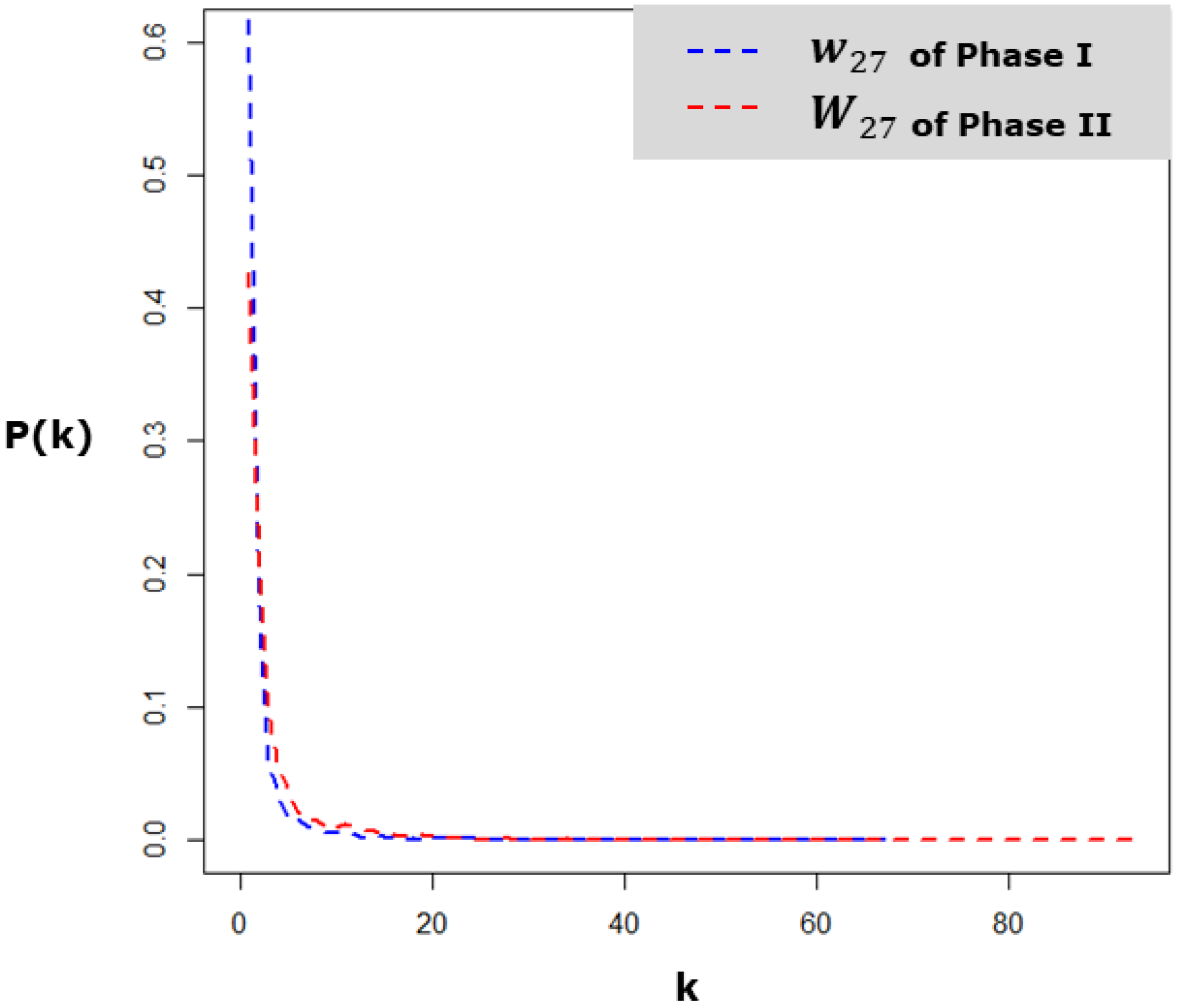
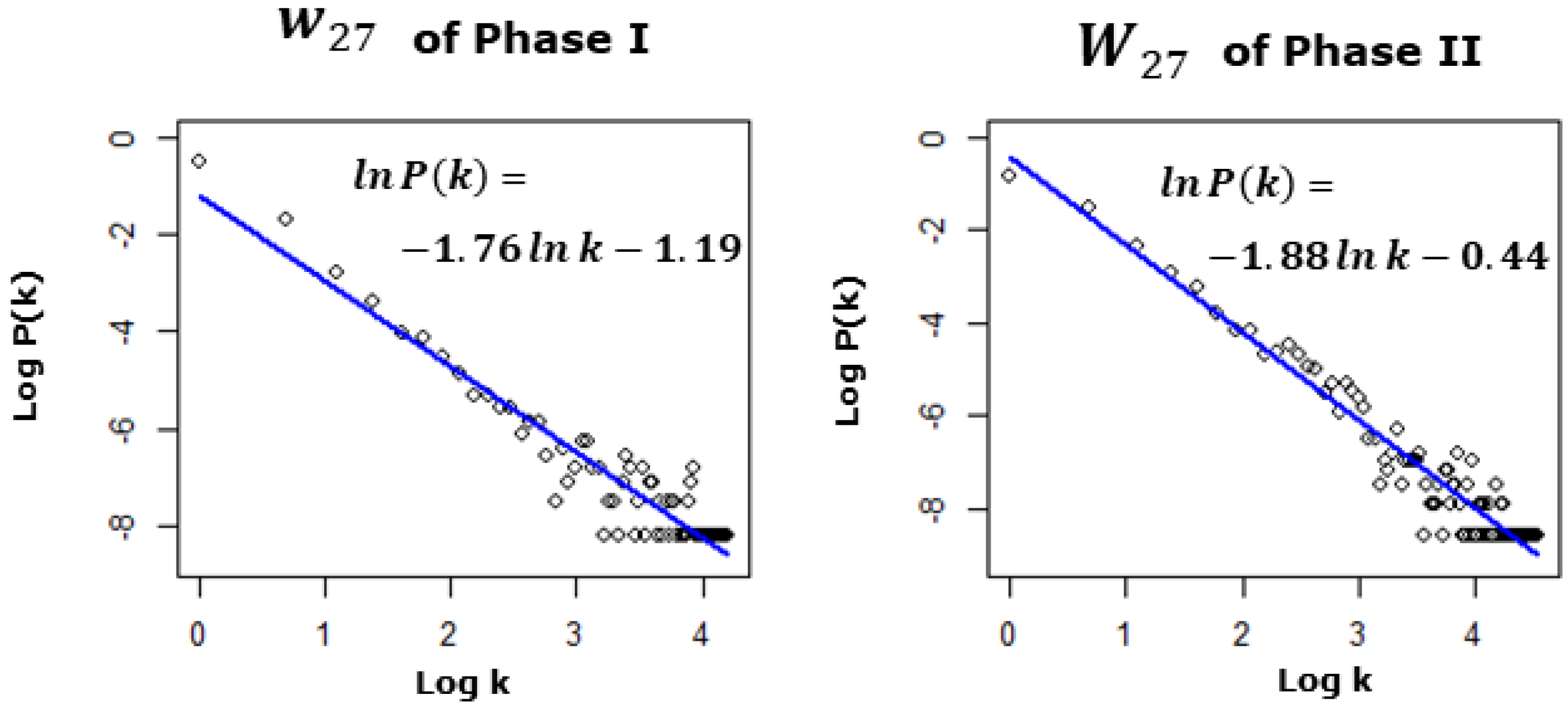
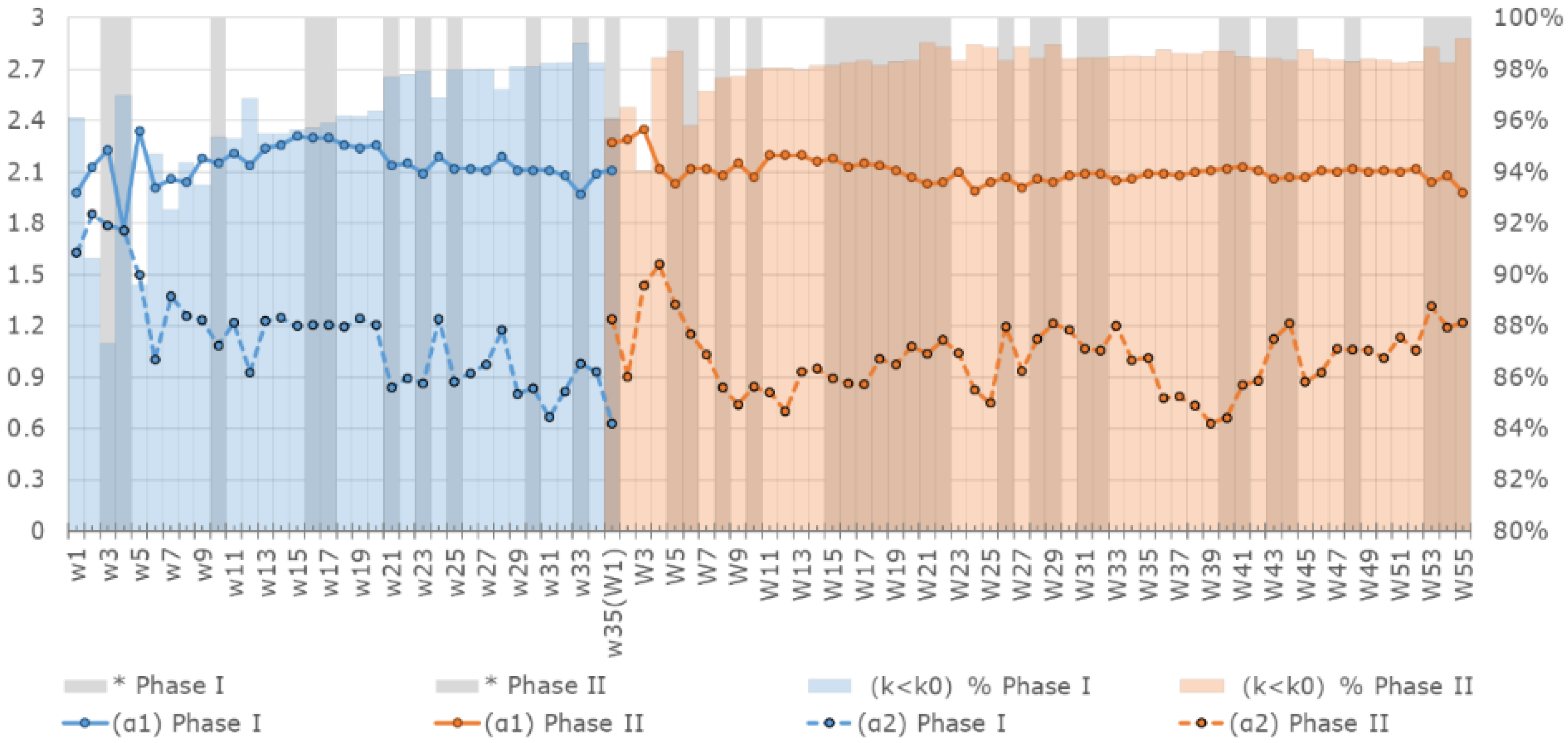
- Both a power law model and a broken power law model are built to test whether the carbon trading network is a scale-free network. Through a residuals analysis, the power law model is found to be invalid for the carbon trading network, although the estimation results are significant. By contrast, the significance and validity of the broken power law model prove that the degree distribution of the carbon trading network consisted of two power laws. The steeper degree distribution is suitable for modeling the heterogeneity of firms with fewer trading partners, which apply to more than 95% of all firms. Therefore, the broken power law can be approximately understood as a traditional power law, but the long tail effect should be noted when using the approximate power law model.
- (4)
- Finally, we test the network with the broken power law model in each time window. The results show that, for most of the time, the relationships between firms in the EU carbon market obey a similar broken power law as the one that apply to the overall market. The model only invalid when the market approaches a high growth rate.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Trotignon, R.; Delbosc, A. Allowance Trading Patterns During the EU ETS Trial Period: What Does the CITL Reveal? Eur. Environ. 2008, 13, 1–36. [Google Scholar]
- Zaklan, A. Why Do Emitters Trade Carbon Permits? DIW Discuss. Pap. 2013, 1275, 32. [Google Scholar]
- Ellerman, A.D.; Convery, F.J.; de Perthuis, C. Pricing Carbon: The European Union Emissions Trading Scheme; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Benz, E.; Trück, S. Modeling the Price Dynamics of CO2 Emission Allowances. Energy Econ. 2009, 31, 4–15. [Google Scholar] [CrossRef]
- Conrad, C.; Rittler, D.; Rotfuß, W. Modeling and Explaining the Dynamics of European Union Allowance Prices at High-Frequency. Energy Econ. 2012, 34, 316–326. [Google Scholar] [CrossRef]
- Koch, N.; Fuss, S.; Grosjean, G.; Edenhofer, O. Causes of the EU ETS price drop: Recession, CDM, renewable policies or a bit of everything? New evidence. Energy Policy 2014, 73, 676–685. [Google Scholar] [CrossRef]
- Chan, H.S.R.; Li, S.; Zhang, F. Firm competitiveness and the European Union emissions trading scheme. Energy Policy 2013, 63, 1056–1064. [Google Scholar] [CrossRef]
- Crossland, J.; Li, B.; Roca, E. Is the European Union Emissions Trading Scheme (EU ETS) informationally efficient? Evidence from momentum-based trading strategies. Appl. Energy 2013, 109, 10–23. [Google Scholar] [CrossRef]
- Martino, V.; Trotignon, R. Back to the Future: A Comprehensive Analysis of Carbon Transactions in Phase 1 of the EU ETS. Available online: https://www.chaireeconomieduclimat.org/en/publications-en/information-debates/id-27-a-comprehensive-analysis-of-carbon-transactions-in-phase-1-of-the-eu-ets/ (accessed on 8 June 2018).
- Balietti, A.C. Trader types and volatility of emission allowance prices. Evidence from EU ETS Phase I. Energy Policy 2016, 98, 607–620. [Google Scholar] [CrossRef]
- Bushnell, J.B.; Chong, H.; Mansur, E.T. Profiting from Regulation: Evidence from the European Carbon Market. Am. Econ. J. Econ. Policy 2013, 5, 78–106. [Google Scholar] [CrossRef]
- Oestreich, A.M.; Tsiakas, I. Carbon Emissions and Stock Returns: Evidence from the EU Emissions Trading Scheme. J. Bank. Financ. 2015, 58, 294–308. [Google Scholar] [CrossRef]
- Mizrach, B.; Otsubo, Y. The market microstructure of the European climate exchange. J. Bank. Financ. 2014, 39, 107–116. [Google Scholar] [CrossRef]
- Newman, M.E.J. The structure and function of complex networks. Siam Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- De Andrade, R.L.; Rêgo, L.C. The use of nodes attributes in social network analysis with an application to an international trade network. Phys. A Stat. Mech. Appl. 2018, 491, 249–270. [Google Scholar] [CrossRef]
- Sun, Q.; Gao, X.; Zhong, W.; Liu, N. The stability of the international oil trade network from short-term and long-term perspectives. Phys. A Stat. Mech. Appl. 2017, 482, 345–356. [Google Scholar] [CrossRef]
- Liang, S.; Feng, Y.; Xu, M. Structure of the Global Virtual Carbon Network: Revealing Important Sectors and Communities for Emission Reduction. J. Ind. Ecol. 2015, 19, 307–320. [Google Scholar] [CrossRef]
- Tian, X.; Geng, Y.; Sarkis, J.; Zhong, S. Trends and features of embodied flows associated with international trade based on bibliometric analysis. Resour. Conserv. Recyc. 2018, 131, 148–157. [Google Scholar] [CrossRef]
- Liu, Y.P.; Guo, J.F.; Fan, Y. A big data study on emitting companies’ performance in the first two phases of the European Union Emission Trading Scheme. J. Clean. Prod. 2017, 142, 1028–1043. [Google Scholar] [CrossRef]
- Fan, Y.; Liu, Y.P.; Guo, J.F. How to explain carbon price using market micro-behaviour? Appl. Econ. 2016, 48, 4992–5007. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, C.; Wang, X.; Huang, Q.; Zhang, X.; Yi, D. The degree-related clustering coefficient and its application to link prediction. Phys. A Stat. Mech. Appl. 2016, 454, 24–33. [Google Scholar] [CrossRef]
- Bauke, H. Parameter estimation for power-law distributions by maximum likelihood methods. Eur. Phys. J. B 2007, 58, 167–173. [Google Scholar] [CrossRef]
- Virkar, Y.; Clauset, A. Power-law distributions in binned empirical data. Ann. Appl. Stat. 2014, 8, 89–119. [Google Scholar] [CrossRef]
- Jóhannesson, G.; Björnsson, G.; Gudmundsson, E.H. Afterglow Light Curves and Broken Power Laws: A Statistical Study. Astrophys. J. 2006, 640, L5–L8. [Google Scholar] [CrossRef]
- Muggeo, V.M.R. Estimating regression models with unknown break-points. Stat. Med. 2003, 22, 3055–3071. [Google Scholar] [CrossRef] [PubMed]
- Muggeo, V.M.R. Segmented: An R package to fit regression models with broken-line relationships. R News 2008, 8, 20–25. [Google Scholar]
- Watts, D.J. Networks, dynamics, and the small-world phenomenon. Am. J. Sociol. 2016, 105, 493–527. [Google Scholar] [CrossRef]
- Choromański, K.; Matuszak, M.; MiȩKisz, J. Scale-Free Graph with Preferential Attachment and Evolving Internal Vertex Structure. J. Stat. Phys. 2013, 151, 1175–1183. [Google Scholar] [CrossRef]
- Barabási, A.-L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [PubMed]
- Pachon, A.; Sacerdote, L.; Yang, S. Scale-free behavior of networks with the copresence of preferential and uniform attachment rules. Phys. D Nonlinear Phenom. 2018, 371, 1–12. [Google Scholar] [CrossRef]

| Features | Phase I | Phase II |
|---|---|---|
| Account-level data | ||
| OHA | 8214 | 13,408 |
| PHA | 782 | 4285 |
| Total account | 8996 | 17,693 |
| Trades | 48,931 | 311,314 |
| Firm-level data | ||
| Emitter | 4711 | 6349 |
| Financial institution | 15 | 332 |
| Total firms | 4726 | 6681 |
| Trades | 41,490 | 298,177 |
| Phase I | Phase II | |
|---|---|---|
| Labels | ||
| 1 January 2005 | 1 January 2008 | |
| 1 May 2008 | 1 January 2013 | |
| 6 months | 6 months | |
| 1 month | 1 month | |
| From 1 to 35 | From 1 to 55 |
| Phase I | Phase II | |
|---|---|---|
| Number of nodes— | 4605 | 6644 |
| Number of edges— | 7803 | 19,393 |
| Network density— | 0.074% | 0.088% |
| Estimated Results | of Phase I | of Phase II |
|---|---|---|
| 1.76 *** | 1.88 *** | |
| Goodness of fit () | 0.91 | 0.94 |
| Shapiro-Wilk test of the residuals | 0.97 | 0.96 ** |
| p-value of Shapiro-Wilk test | 6.2% | 1.1% |
| Durbin-Watson test of the residuals | 1.35 ** | 1.16 |
| p-value of Durbin-Watson test | 0.2% | 7.0% |
| Estimation Results | of Phase I | of Phase II |
|---|---|---|
| 2.09 *** | 2.01 *** | |
| 0.96 ** | 0.94 ** | |
| 3.24 | 4.01 | |
| 25.53 | 55.14 | |
| Goodness of fit () | 93% | 95% |
| % of nodes of which degree is smaller than | 98.0% | 98.9% |
| Residuals Analysis | ||
| Shapiro-Wilk test of the residuals | 0.98 | 0.98 |
| p-value of Shapiro-Wilk test | 24.8% | 7.3% |
| Durbin-Watson test of the residuals | 1.83 | 1.94 |
| p-value of Durbin-Watson test | 14.0% | 26.5% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Gao, X.; Guo, J. Network Features of the EU Carbon Trade System: An Evolutionary Perspective. Energies 2018, 11, 1501. https://doi.org/10.3390/en11061501
Liu Y, Gao X, Guo J. Network Features of the EU Carbon Trade System: An Evolutionary Perspective. Energies. 2018; 11(6):1501. https://doi.org/10.3390/en11061501
Chicago/Turabian StyleLiu, Yinpeng, Xiangyun Gao, and Jianfeng Guo. 2018. "Network Features of the EU Carbon Trade System: An Evolutionary Perspective" Energies 11, no. 6: 1501. https://doi.org/10.3390/en11061501
APA StyleLiu, Y., Gao, X., & Guo, J. (2018). Network Features of the EU Carbon Trade System: An Evolutionary Perspective. Energies, 11(6), 1501. https://doi.org/10.3390/en11061501





