A Novel Battery State of Charge Estimation Method Based on a Super-Twisting Sliding Mode Observer
Abstract
:1. Introduction
2. Battery Modeling
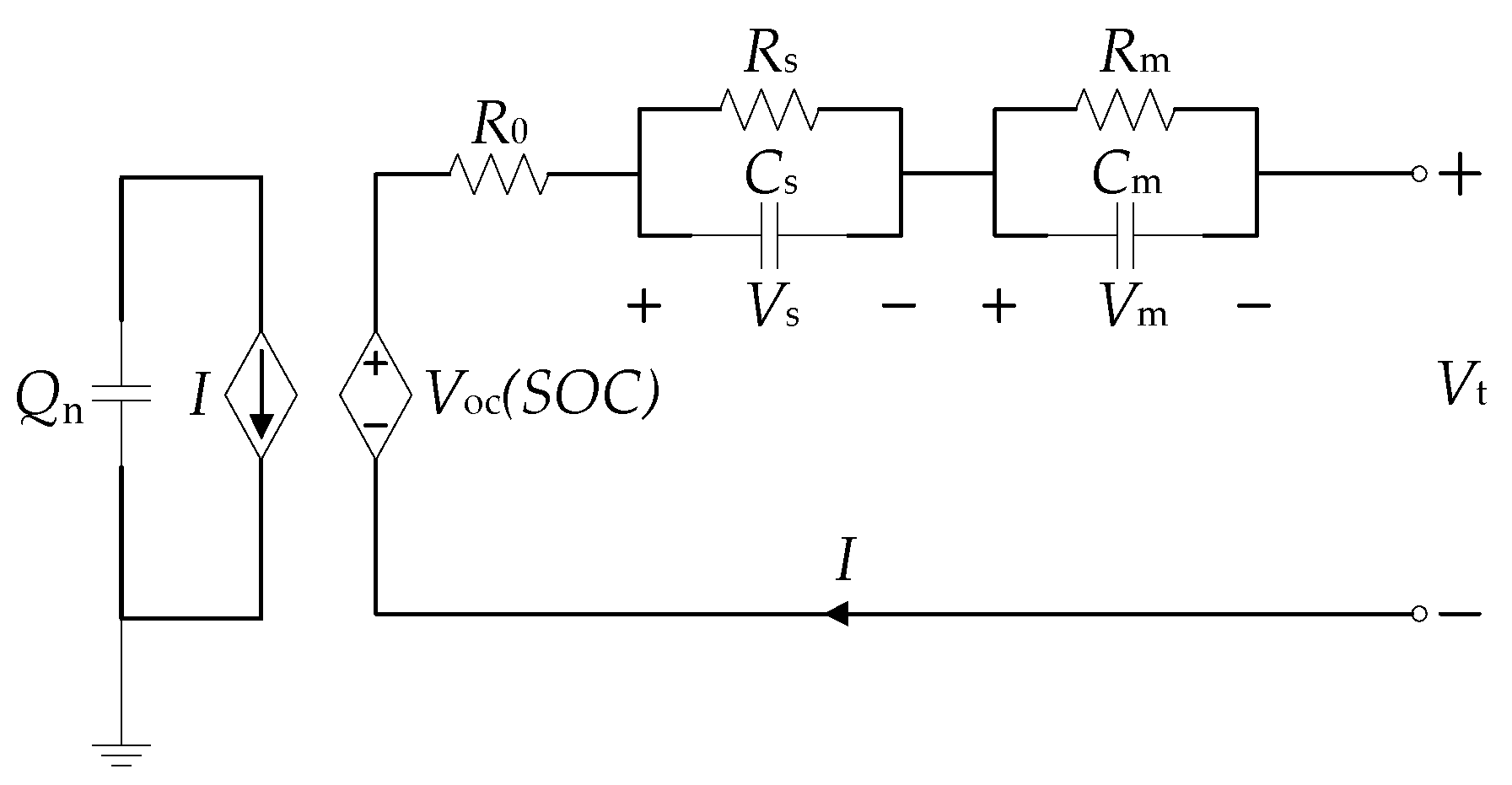
2.1. The Second-Order RC Equivalent Circuit Model
- (1)
- The capacitor Qn represents the total stored energy in the battery. The controlled voltage source Voc(SOC) is used to establish the nonlinear relationship between the SOC and the OCV, as shown in Figure 2.
- (2)
- R0 is the ohmic resistance, which indicates the internal energy loss of the battery during the charge/discharge process.
- (3)
- The parallel network RsCs represents the concentration polarization which reflects the effect of the diffusion of the reactant and product in the electrochemical reaction. RmCm represents the electrochemical polarization, which describes the structure of the double layer of the electrode/solution interface.
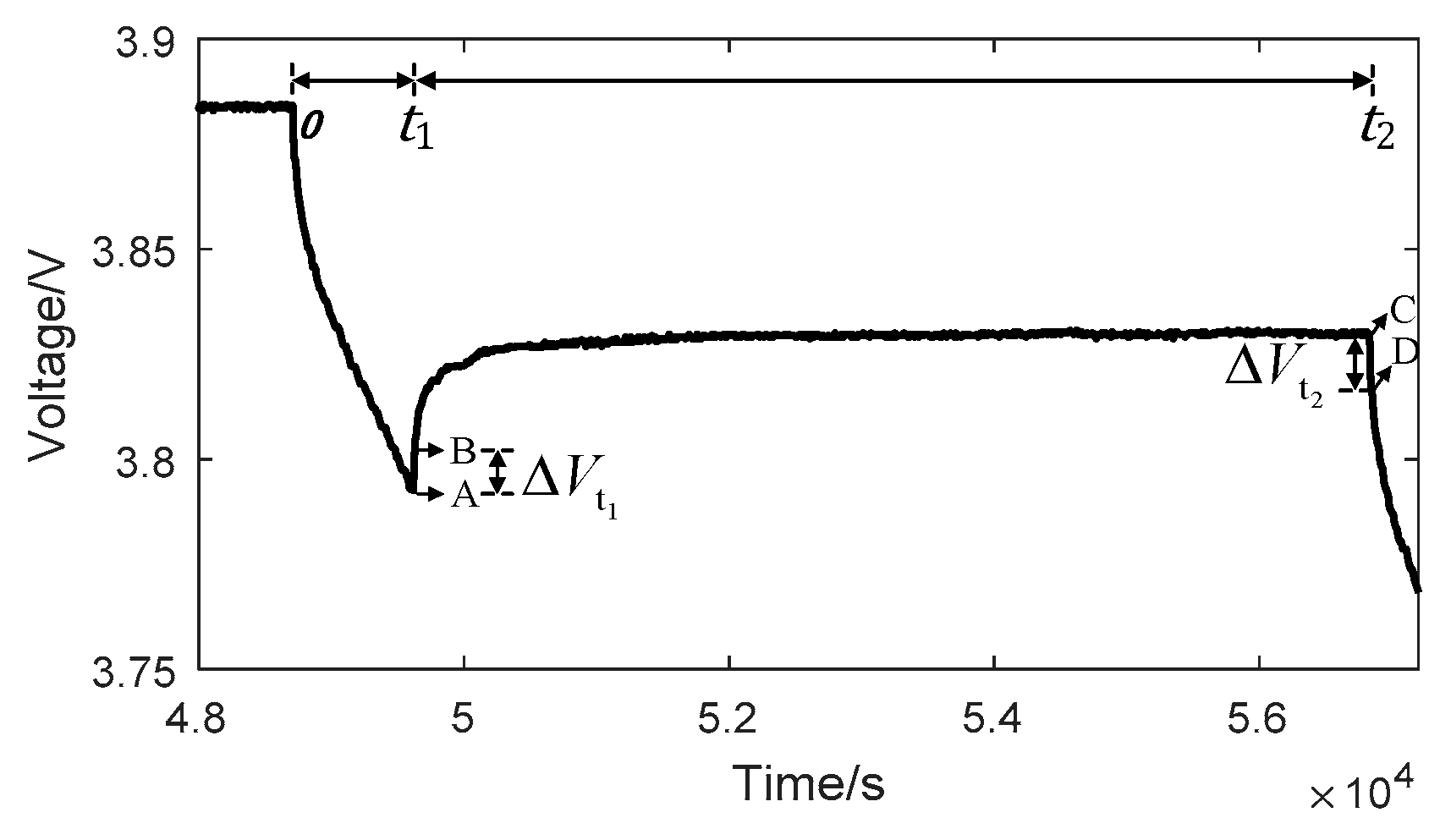
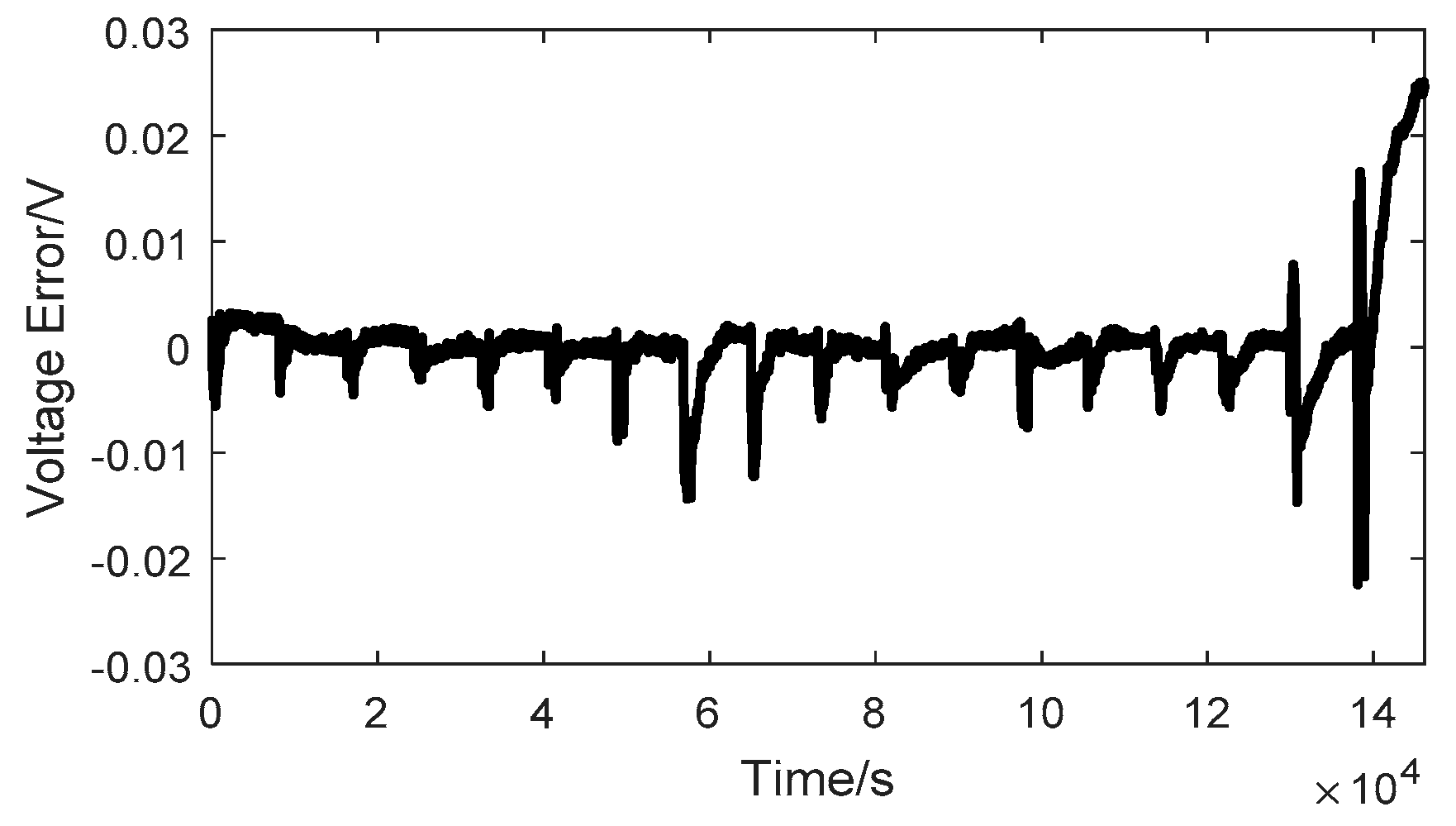
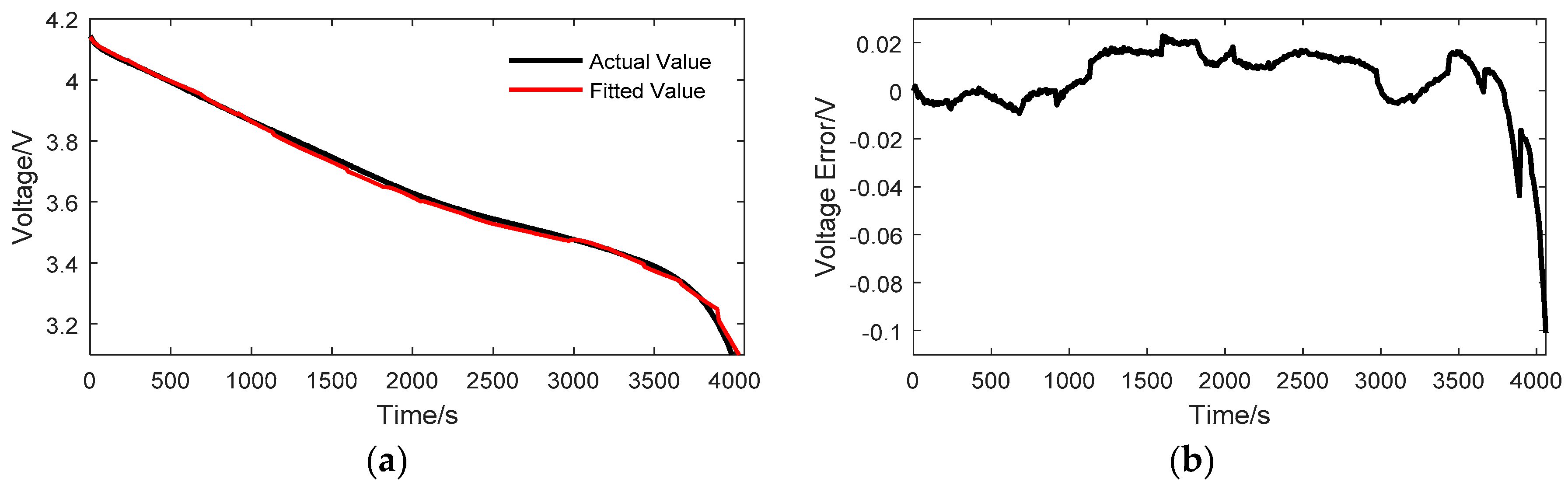
2.2. Model Parameter Identification
3. The Design of the Super-Twisting Sliding Mode Observer for SOC Estimation
3.1. Super-Twisting Sliding Mode Observer
3.2. Stability Proof
3.3. Coefficients of the STSMO
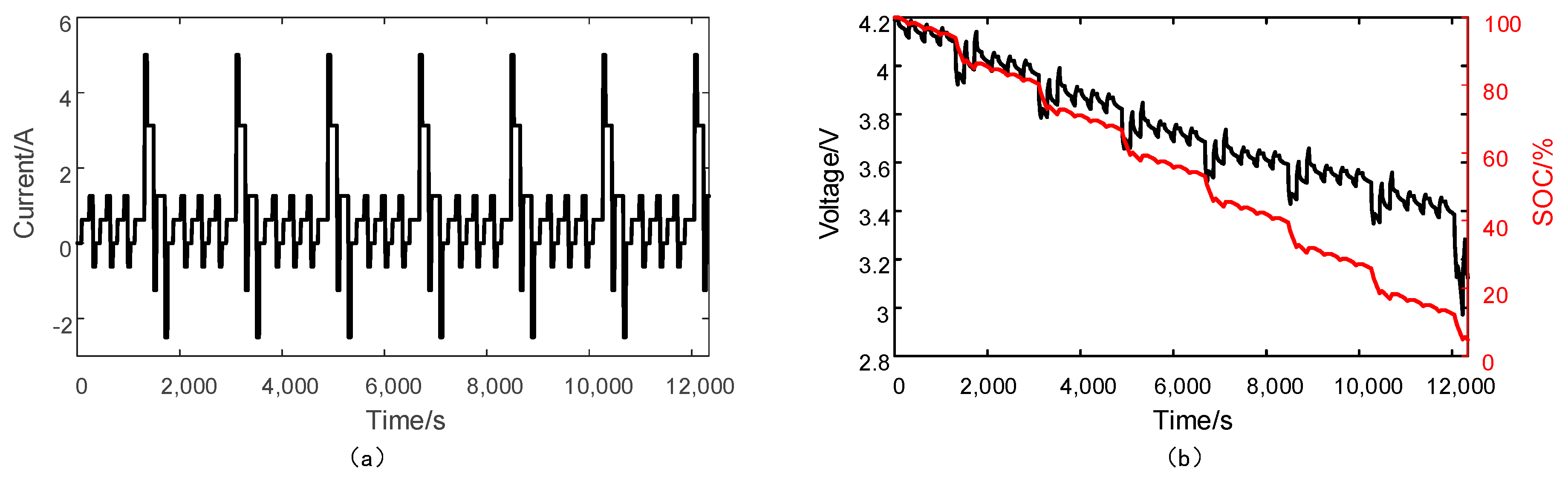
4. Experimental Results for SOC Estimation
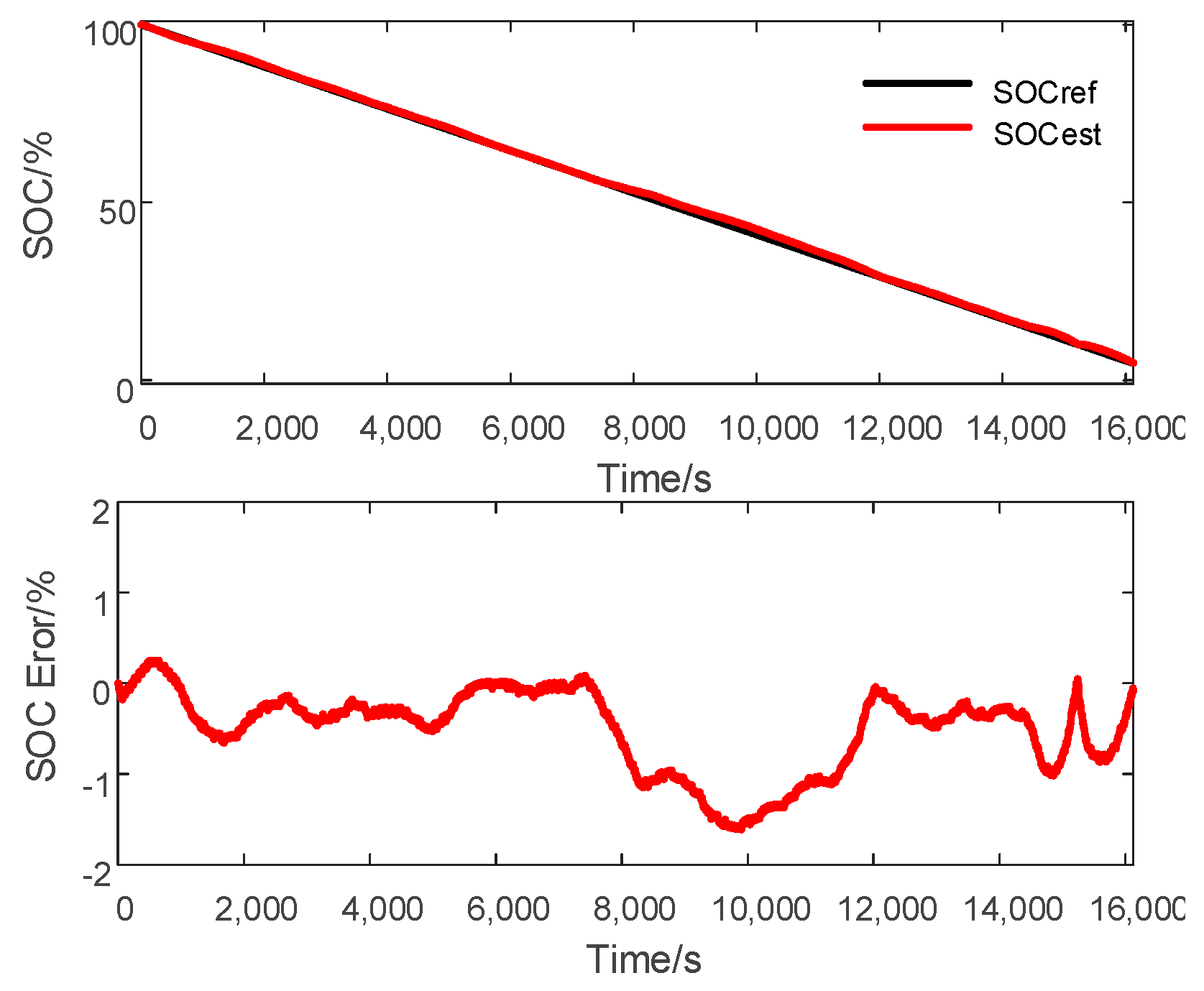
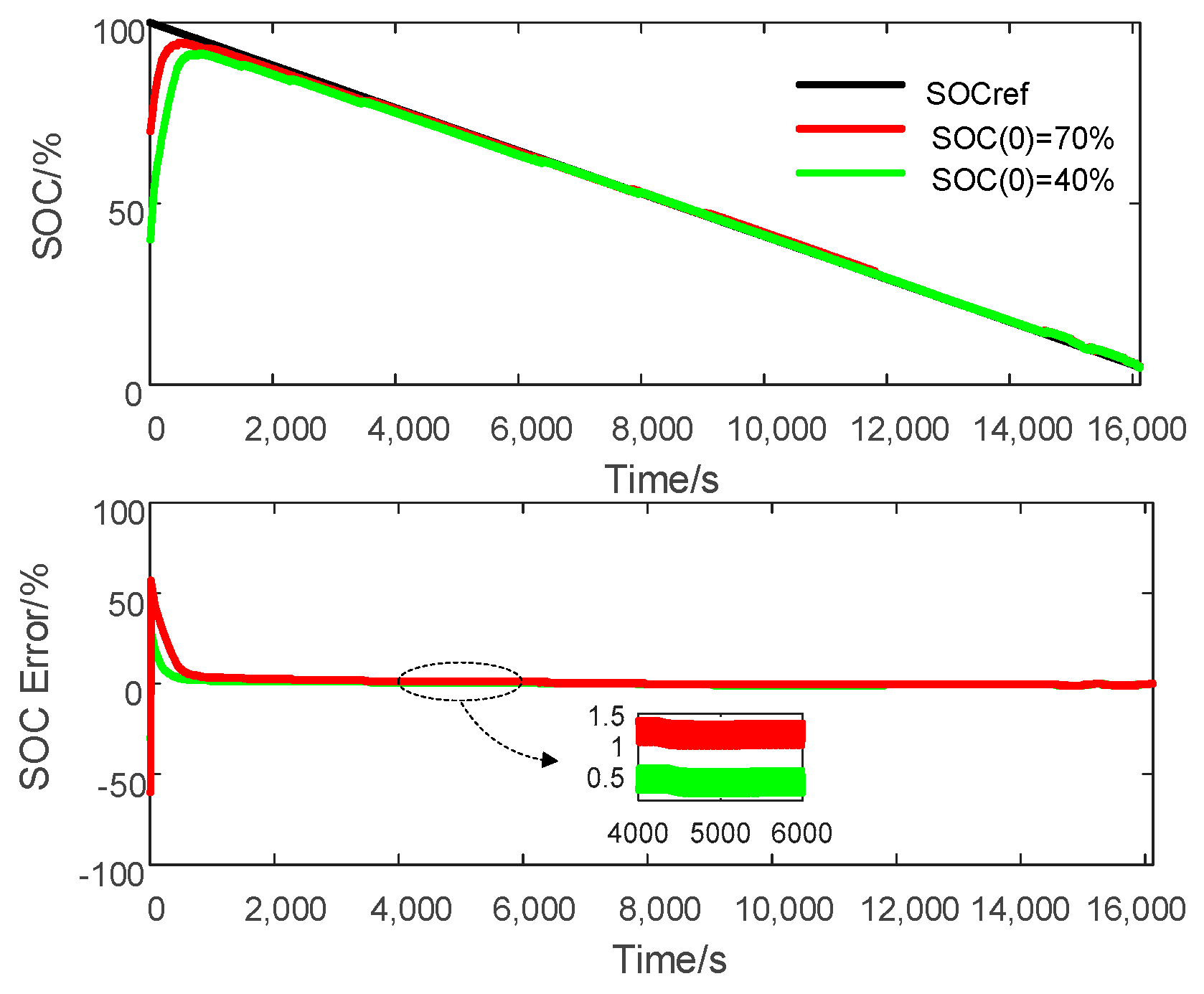
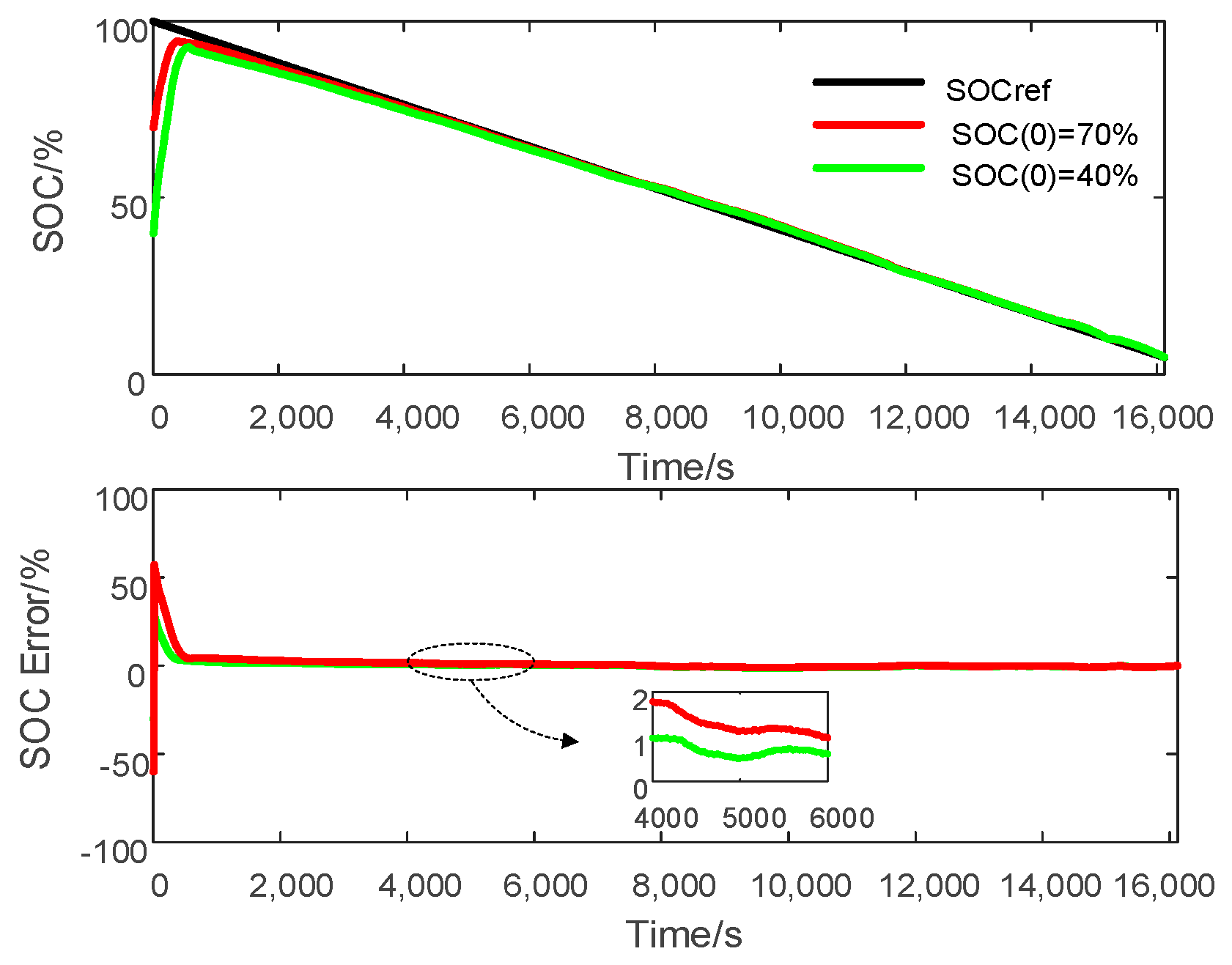
4.1. Comparison between STSMO and CSMO
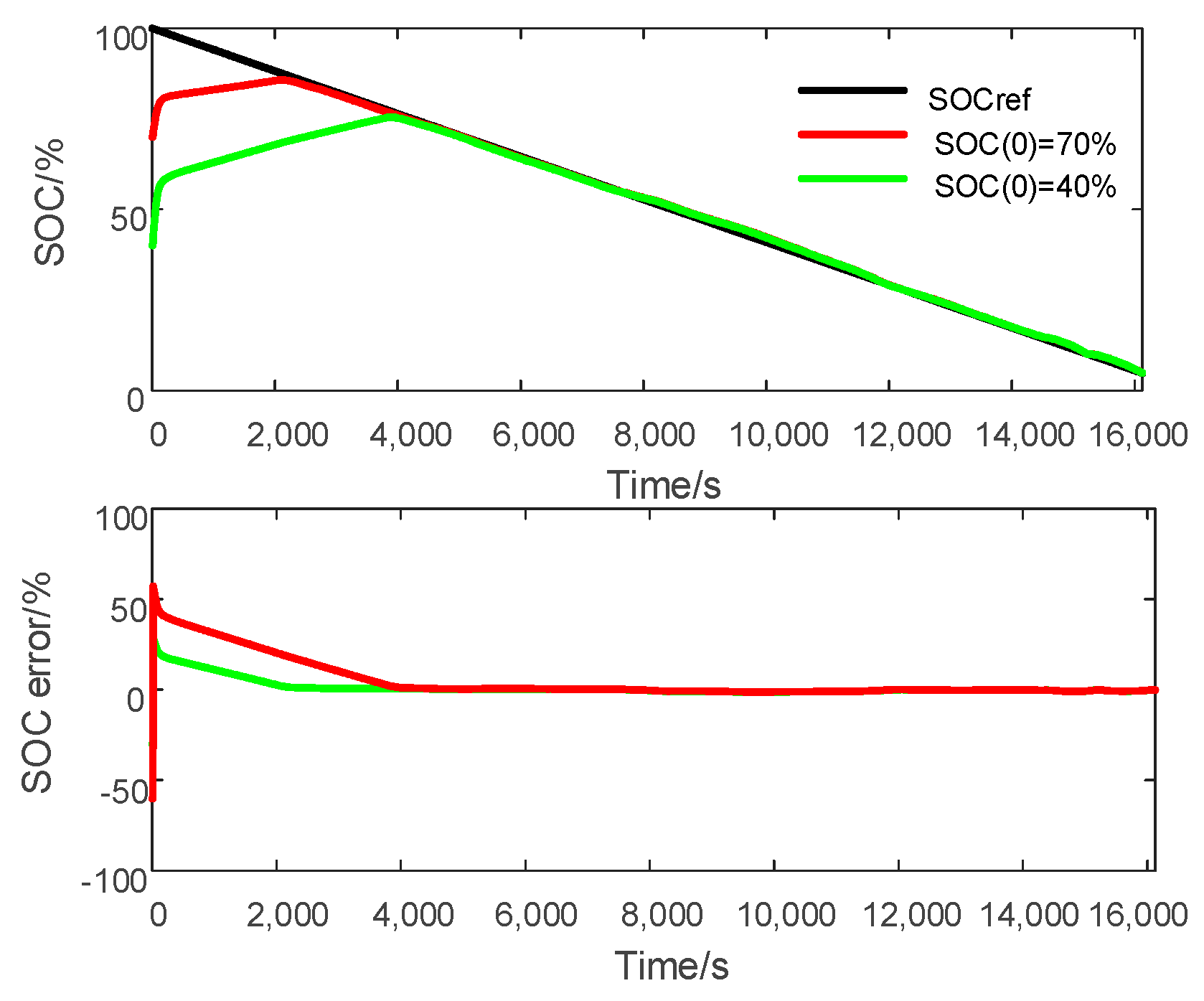
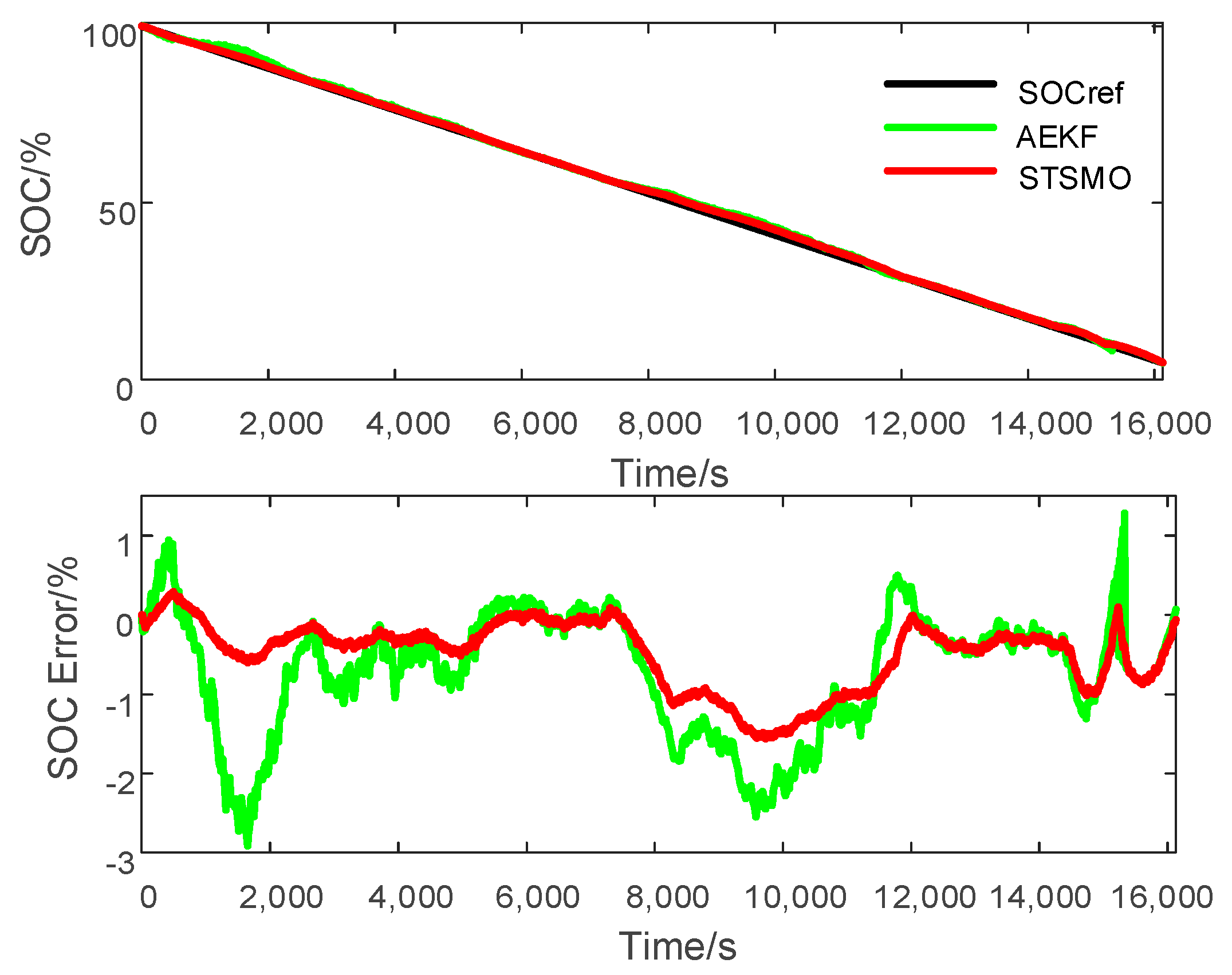
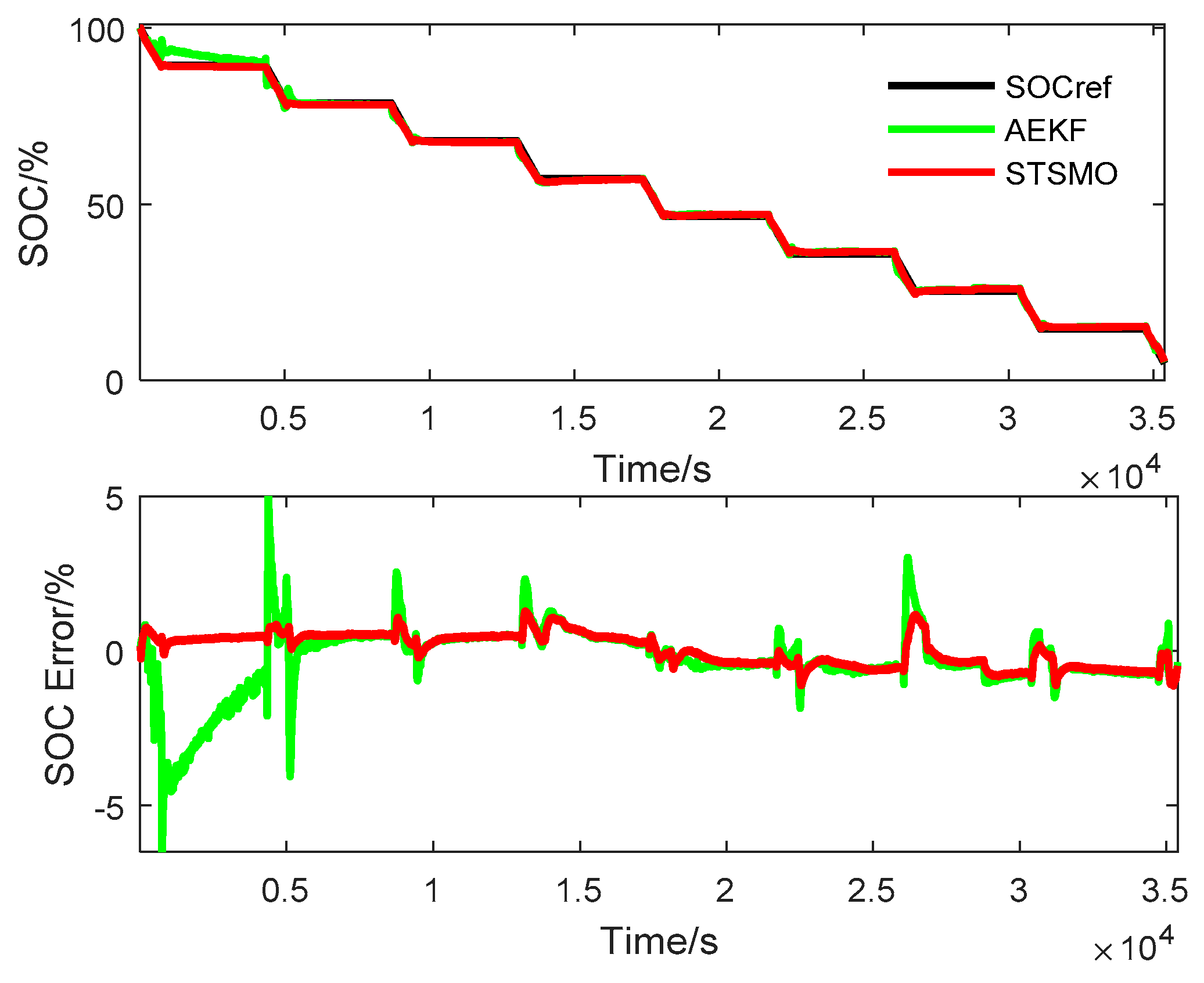
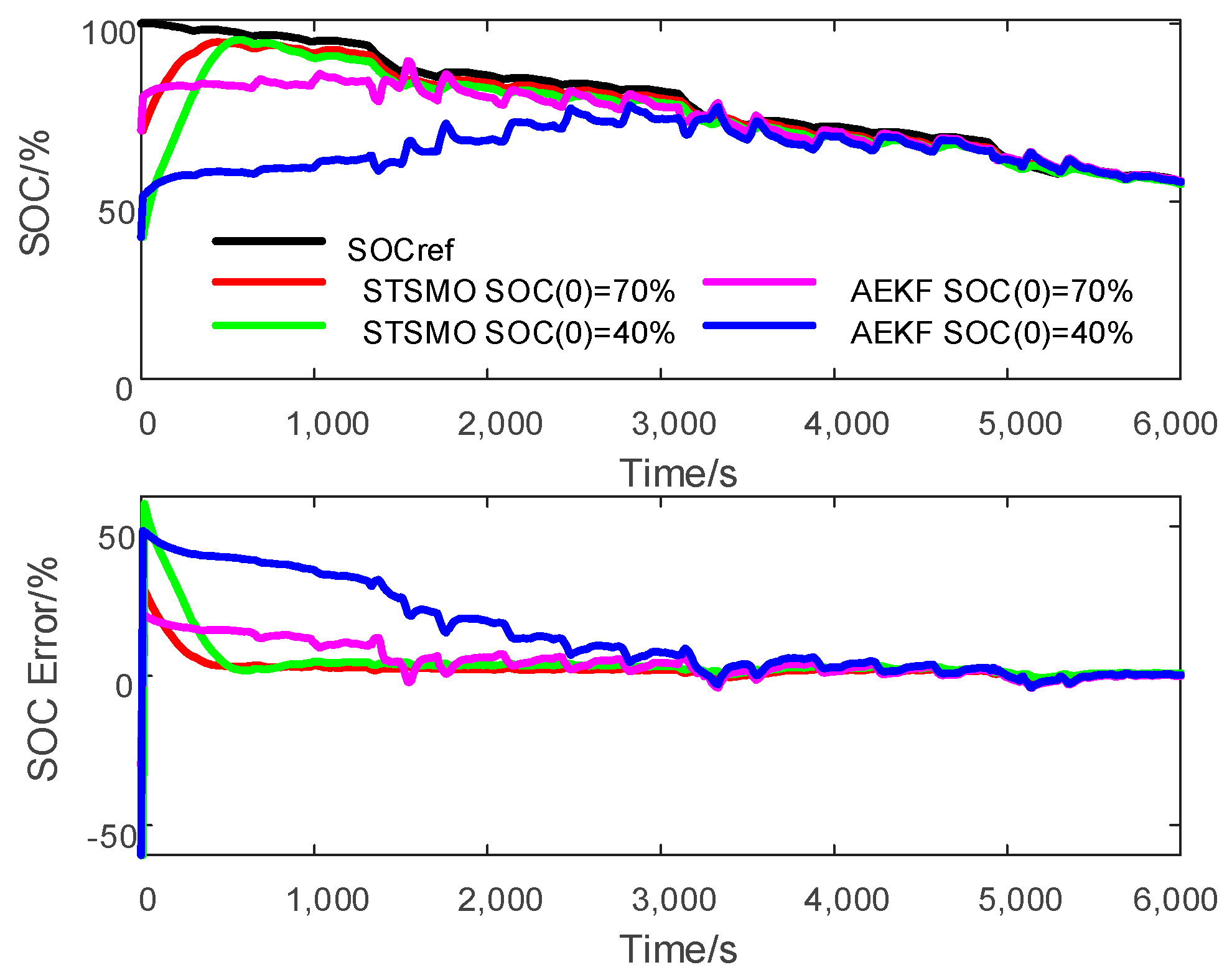
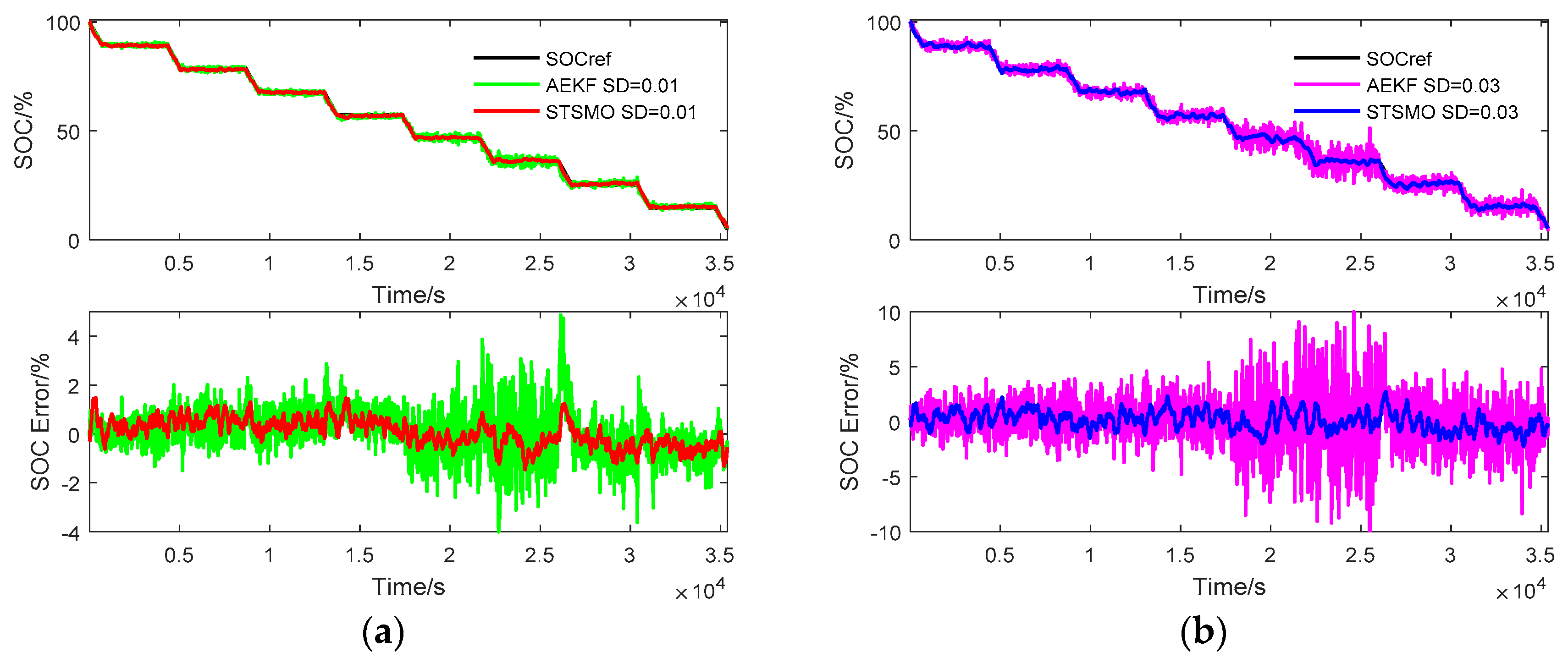
4.2. Comparison between STSMO and AEKF
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Hannan, M.; Lipu, M.; Hussain, A.; Mohamed, A. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Jaguemont, J.; Boulon, L.; Dubé, Y. A comprehensive review of lithium-ion batteries used in hybrid and electric vehicles at cold temperatures. Appl. Energy 2016, 164, 99–114. [Google Scholar] [CrossRef]
- Xing, Y.; He, W.; Pecht, M.; Tsui, K.L. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Duong, V.; Bastawrous, H.A.; Lim, K.; See, K.W.; Zhang, P.; Dou, S.X. Online state of charge and model parameters estimation of the LiFePO 4 battery in electric vehicles using multiple adaptive forgetting factors recursive least-squares. J. Power Sources 2015, 296, 215–224. [Google Scholar] [CrossRef]
- Chen, J.; Ouyang, Q.; Xu, C.; Su, H. Neural Network-Based State of Charge Observer Design for Lithium-Ion Batteries. IEEE Trans. Control Syst. Technol. 2018, 26, 313–320. [Google Scholar] [CrossRef]
- Chen, Z.; Mi, C.C.; Fu, Y.; Jun, X.; Gong, X. Online battery state of health estimation based on Genetic Algorithm for electric and hybrid vehicle applications. J. Power Sources 2013, 240, 184–192. [Google Scholar] [CrossRef]
- Antón, J.; Nieto, P.; Viejo, C.B.; Vilan, J.A.V. Support Vector Machines Used to Estimate the Battery State of Charge. IEEE Trans. Power Electron. 2013, 28, 5919–5926. [Google Scholar] [CrossRef]
- Waag, W.; Fleischer, C.; Sauer, D.U. Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles. J. Power Sources 2014, 258, 321–339. [Google Scholar] [CrossRef]
- Yuan, S.; Wu, H.; Yin, C. State of Charge Estimation Using the Extended Kalman Filter for Battery Management Systems Based on the ARX Battery Model. Energies 2013, 6, 444–470. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, C.; Pan, R.; Chen, Z. Modeling and state-of-charge prediction of lithium-ion battery and ultracapacitor hybrids with a co-estimator. Energy 2017, 121, 739–750. [Google Scholar] [CrossRef]
- Li, D.; Ouyang, J.; Li, H.; Wan, J. State of charge estimation for LiMn2O4, power battery based on strong tracking sigma point Kalman filter. J. Power Sources 2015, 279, 439–449. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.; Sun, F.; Zhao, K. Evaluation on State of Charge Estimation of Batteries with Adaptive Extended Kalman Filter by Experiment Approach. IEEE Trans. Veh. Technol. 2013, 62, 108–117. [Google Scholar] [CrossRef]
- Xiong, R.; Gong, X.; Mi, C.C.; Sun, F.C. A robust state-of-charge estimator for multiple types of lithium-ion batteries using adaptive extended Kalman filter. J. Power Sources 2013, 243, 805–816. [Google Scholar] [CrossRef]
- Yu, Q.; Xiong, R.; Lin, C.; Shen, W.; Deng, J. Lithium-Ion Battery Parameters and State-of-Charge Joint Estimation Based on H-Infinity and Unscented Kalman Filters. IEEE Trans. Veh. Technol. 2017, 66, 8693–8701. [Google Scholar] [CrossRef]
- He, Z.; Chen, D.; Pan, C.; Chen, L.; Wang, S. State of charge estimation of power Li-ion batteries using a hybrid estimation algorithm based on UKF. Electrochim. Acta 2016, 211, 101–109. [Google Scholar]
- Wang, Y.; Zhang, C.; Chen, Z. A method for joint estimation of state-of-charge and available energy of LiFePO4 batteries. Appl. Energy 2014, 135, 81–87. [Google Scholar] [CrossRef]
- Chen, C.; Xiong, R.; Shen, W. A lithium-ion battery-in-the-loop approach to test and validate multi-scale dual H infinity filters for state of charge and capacity estimation. IEEE Trans. Power Electron. 2018, 33, 332–342. [Google Scholar] [CrossRef]
- Hu, X.; Sun, F.; Zou, Y. Estimation of State of Charge of a Lithium-Ion Battery Pack for Electric Vehicles Using an Adaptive Luenberger Observer. Energies 2010, 3, 1586–1603. [Google Scholar] [CrossRef]
- Xu, J.; Mi, C.C.; Cao, B.; Deng, J.; Chen, Z.; Li, S. The State of Charge Estimation of Lithium-Ion Batteries Based on a Proportional-Integral Observer. IEEE Trans. Veh. Technol. 2014, 63, 1614–1621. [Google Scholar]
- Xia, B.; Chen, C.; Tian, Y.; Sun, W.; Xu, Z.; Zheng, W. A novel method for state of charge estimation of lithium-ion batteries using a nonlinear observer. J. Power Sources 2014, 270, 359–366. [Google Scholar] [CrossRef]
- Li, W.; Liang, L.; Liu, W.; Wu, X. State of Charge Estimation of Lithium-Ion Batteries Using a Discrete-Time Nonlinear Observer. IEEE Trans. Ind. Electron. 2017, 64, 8557–8565. [Google Scholar] [CrossRef]
- Kim, I. Nonlinear State of Charge Estimator for Hybrid Electric Vehicle Battery. IEEE Trans. Power Electron. 2008, 23, 2027–2034. [Google Scholar]
- Kim, I. A Technique for Estimating the State of Health of Lithium Batteries through a Dual-Sliding-Mode Observer. IEEE Trans. Power Electron. 2010, 25, 1013–1022. [Google Scholar]
- Huangfu, Y.; Zhuo, S.; Rathore, A.K.; Breaz, E.; Nahid-Mobarakeh, B.; Gao, F. Super-Twisting Differentiator-Based High Order Sliding Mode Voltage Control Design for DC-DC Buck Converters. Energies 2016, 9, 494. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. A Lyapunov approach to second-order sliding mode controllers and observers. In Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 2856–2861. [Google Scholar]
- Chen, X.; Shen, W.; Cao, Z.; Kapoor, A. A novel approach for state of charge estimation based on adaptive switching gain sliding mode observer in electric vehicles. J. Power Sources 2014, 246, 667–678. [Google Scholar] [CrossRef]
- Du, J.; Liu, Z.; Wang, Y.; Wen, C. An adaptive sliding mode observer for lithium-ion battery state of charge and state of health estimation in electric vehicles. Control Eng. Pract. 2016, 54, 81–90. [Google Scholar] [CrossRef]
- Liu, J.; Laghrouche, S.; Wack, M. Observer-based higher order sliding mode control of power factor in three-phase AC/DC converter for hybrid electric vehicle applications. Int. J. Control 2014, 87, 1117–1130. [Google Scholar] [CrossRef]
- Liu, J.; Laghrouche, S.; Harmouche, M.; Wack, M. Adaptive-gain second-order sliding mode observer design for switching power converters. Control Eng. Pract. 2014, 30, 124–131. [Google Scholar] [CrossRef]
- Wei, Z.; Lim, T.M.; Skyllas-Kazacos, M.; Wai, N.; Tseng, K.J. Online state of charge and model parameter co-estimation based on a novel multi-timescale estimator for vanadium redox flow battery. Appl. Energy 2016, 172, 169–179. [Google Scholar] [CrossRef]
- Dávila, A.; Moreno, J.A.; Fridman, L. Optimal Lyapunov function selection for reaching time estimation of Super Twisting algorithm. In Proceedings of the 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference, Shanghai, China, 16–18 December 2009; pp. 8405–8410. [Google Scholar]
- Davila, J.; Fridman, L.; Levant, A. Second-order sliding-mode observer for mechanical systems. IEEE Trans. Autom. Control 2005, 50, 1785–1789. [Google Scholar] [CrossRef]
- Levant, A. Robust Exact Differentiation via Sliding Mode Technique; Pergamon Press: Great Britain, UK, 1998; pp. 379–384. [Google Scholar]


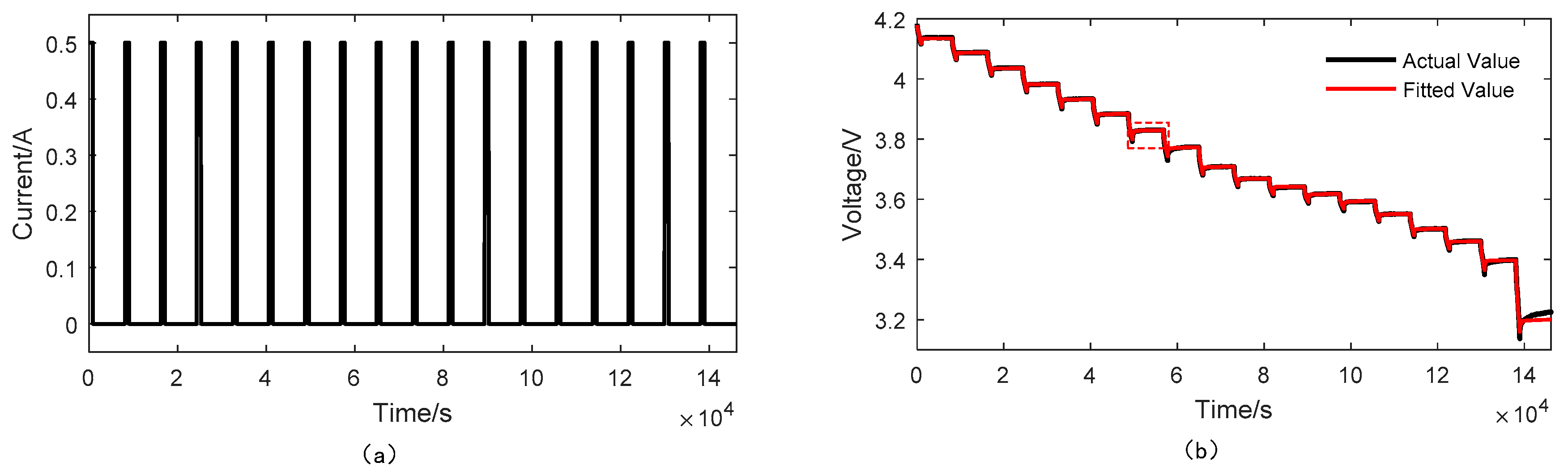


| SOC/% | R0/ | Rs/ | Cs/ | Rm/ | Cm/F | RMSE |
|---|---|---|---|---|---|---|
| 94.76 | 0.0264 | 0.008584 | 3732.644 | 0.009537 | 106,104.117 | 0.0003100 |
| 89.47 | 0.0244 | 0.018162 | 10,712.065 | 0.010226 | 316,767.837 | 0.0002974 |
| 84.18 | 0.0242 | 0.013808 | 6829.023 | 0.011565 | 233,693.832 | 0.0003114 |
| 78.88 | 0.0242 | 0.020700 | 4206.285 | 0.008464 | 594,984.058 | 0.0002933 |
| 73.59 | 0.0211 | 0.028880 | 3778.073 | 0.013616 | 213,823.684 | 0.0003333 |
| 68.30 | 0.0242 | 0.032760 | 4248.438 | 0.013616 | 200,075.697 | 0.0003505 |
| 63.00 | 0.0242 | 0.029560 | 6915.270 | 0.020227 | 94,861.243 | 0.0004321 |
| 57.71 | 0.0277 | 0.023700 | 9624.565 | 0.052784 | 82,412.212 | 0.0004613 |
| 52.41 | 0.0274 | 0.015984 | 4761.230 | 0.022965 | 158,123.287 | 0.0004096 |
| 47.12 | 0.0257 | 0.014854 | 6539.284 | 0.013976 | 113,536.039 | 0.0003467 |
| 41.83 | 0.0246 | 0.023920 | 5917.342 | 0.022495 | 543,751.792 | 0.0002856 |
| 36.53 | 0.0243 | 0.023320 | 5616.457 | 0.019622 | 162,009.005 | 0.0003895 |
| 31.24 | 0.0248 | 0.026183 | 9794.163 | 0.023851 | 1,327,933.778 | 0.0004613 |
| 25.95 | 0.0233 | 0.014850 | 4102.350 | 0.013964 | 141,097.755 | 0.0002885 |
| 20.65 | 0.0218 | 0.016850 | 5861.450 | 0.018432 | 164,482.341 | 0.0002609 |
| 15.36 | 0.0257 | 0.020440 | 5919.380 | 0.021389 | 258,695.694 | 0.0003332 |
| 10.06 | 0.0283 | 0.034840 | 5972.873 | 0.062329 | 152,623.871 | 0.0004734 |
| 4.77 | 0.0239 | 0.050860 | 4865.582 | 0.163047 | 56,329.285 | 0.0007226 |
| Method | DST | 0.5 C PCD | 0.2 C CCD |
|---|---|---|---|
| STSMO | 0.0082 | 0.0052 | 0.0065 |
| AEKF | 0.0182 | 0.0123 | 0.0105 |
| Method | DST | 0.5 C PCD | 0.2 C CCD |
|---|---|---|---|
| STSMO | 0.1266 | 0.1508 | 0.1261 |
| AEKF | 0.2257 | 0.5154 | 0.2718 |
| Method | SOC(0) = 70% | SOC(0) = 40% |
|---|---|---|
| STSMO | 360 s | 480 s |
| AEKF | 1450 s | 2830 s |
| Method | SD = 0.03 | SD = 0.01 | SD = 0 |
|---|---|---|---|
| STSMO | 2.0%/−2.1% | 1.4%/−1.2% | 1.1%/−1.1% |
| AEKF | 10.0%/−10.0% | 5.0%/−4.0% | 5.0%/−6.0% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huangfu, Y.; Xu, J.; Zhao, D.; Liu, Y.; Gao, F. A Novel Battery State of Charge Estimation Method Based on a Super-Twisting Sliding Mode Observer. Energies 2018, 11, 1211. https://doi.org/10.3390/en11051211
Huangfu Y, Xu J, Zhao D, Liu Y, Gao F. A Novel Battery State of Charge Estimation Method Based on a Super-Twisting Sliding Mode Observer. Energies. 2018; 11(5):1211. https://doi.org/10.3390/en11051211
Chicago/Turabian StyleHuangfu, Yigeng, Jiani Xu, Dongdong Zhao, Yuntian Liu, and Fei Gao. 2018. "A Novel Battery State of Charge Estimation Method Based on a Super-Twisting Sliding Mode Observer" Energies 11, no. 5: 1211. https://doi.org/10.3390/en11051211
APA StyleHuangfu, Y., Xu, J., Zhao, D., Liu, Y., & Gao, F. (2018). A Novel Battery State of Charge Estimation Method Based on a Super-Twisting Sliding Mode Observer. Energies, 11(5), 1211. https://doi.org/10.3390/en11051211






