Fundamental Material Properties of the 2LiBH4-MgH2 Reactive Hydride Composite for Hydrogen Storage: (I) Thermodynamic and Heat Transfer Properties
Abstract
1. Introduction
2. Experimental Details
2.1. Sample Preparation
2.2. Experimental Methods
2.2.1. Thermodynamic and Kinetic Studies
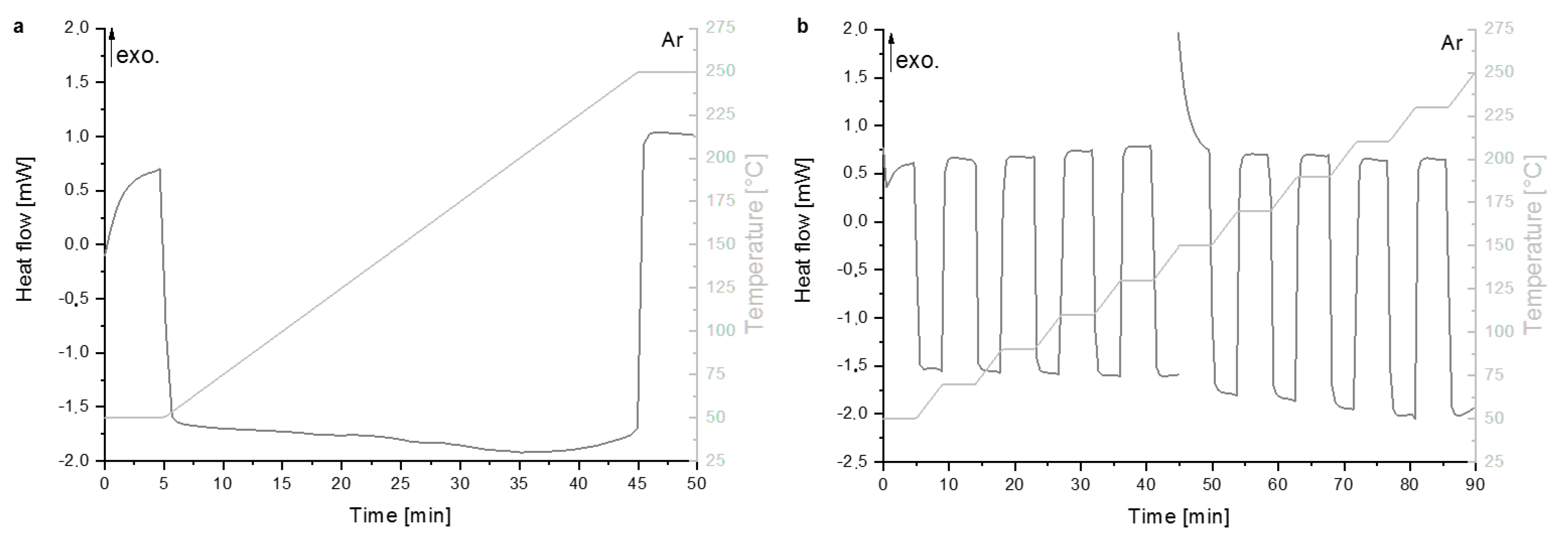
2.2.2. Heat Capacity Measurements
2.2.3. Thermal Conductivity Measurements
3. Results
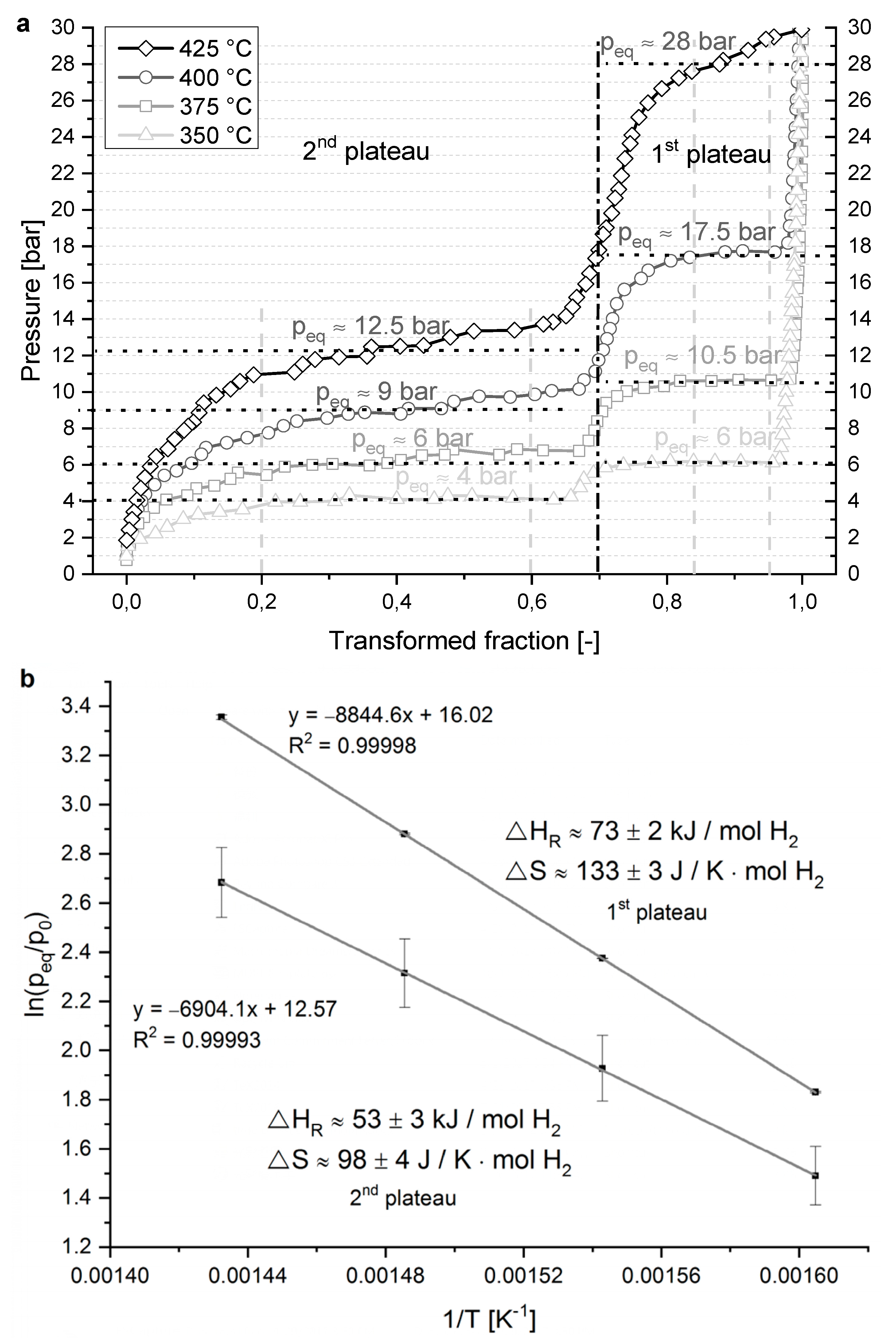
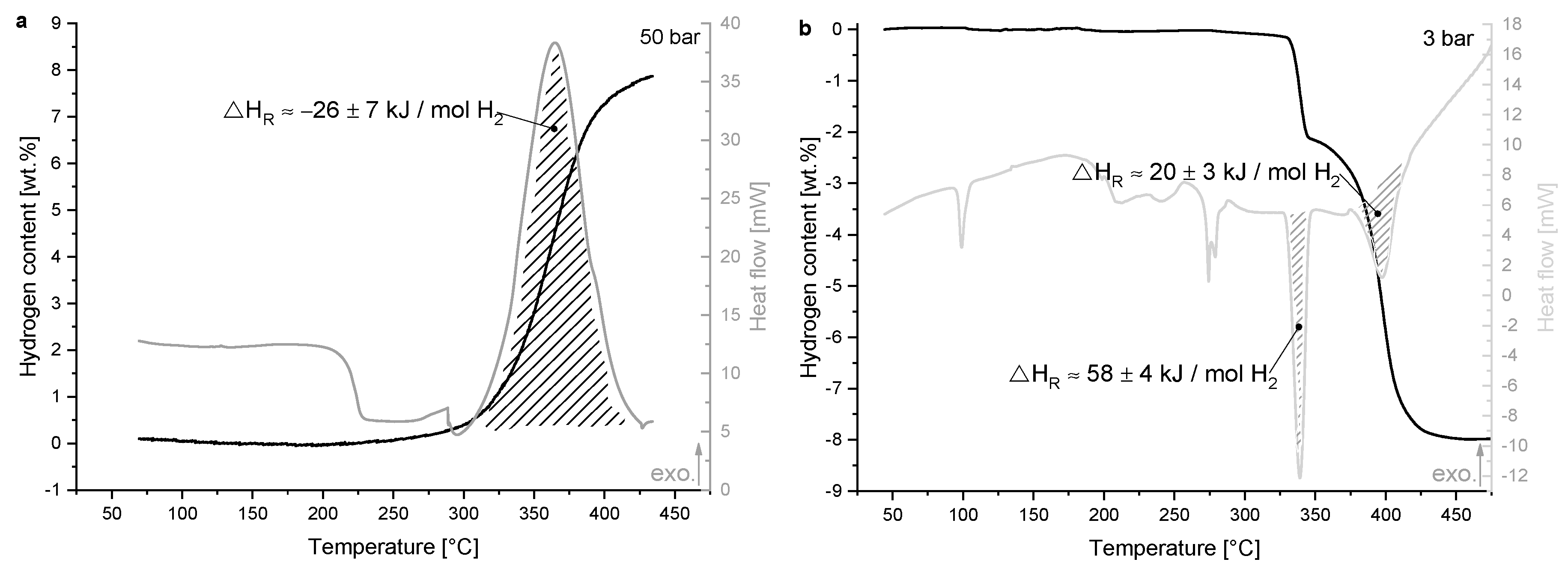
3.1. Thermodynamic Properties
3.2. Heat Transfer Properties
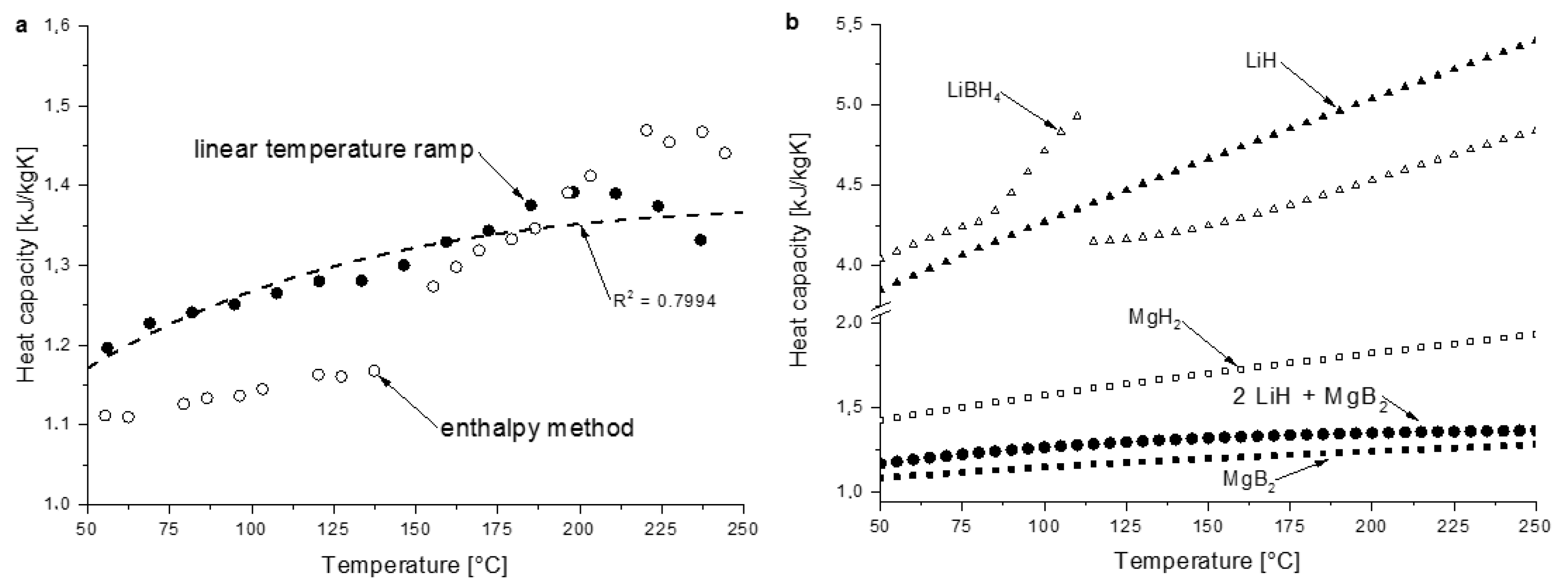
3.2.1. Heat Capacity
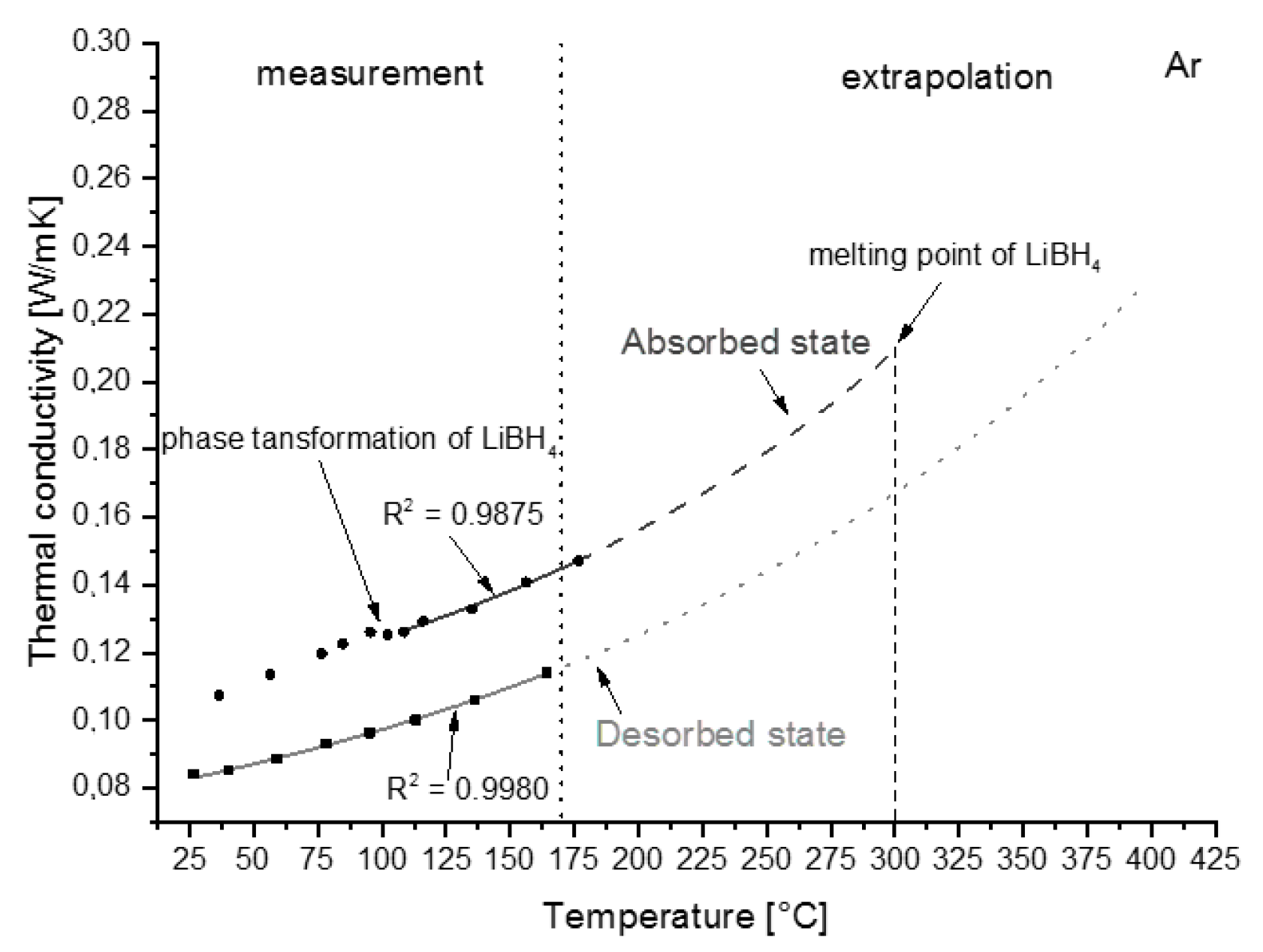
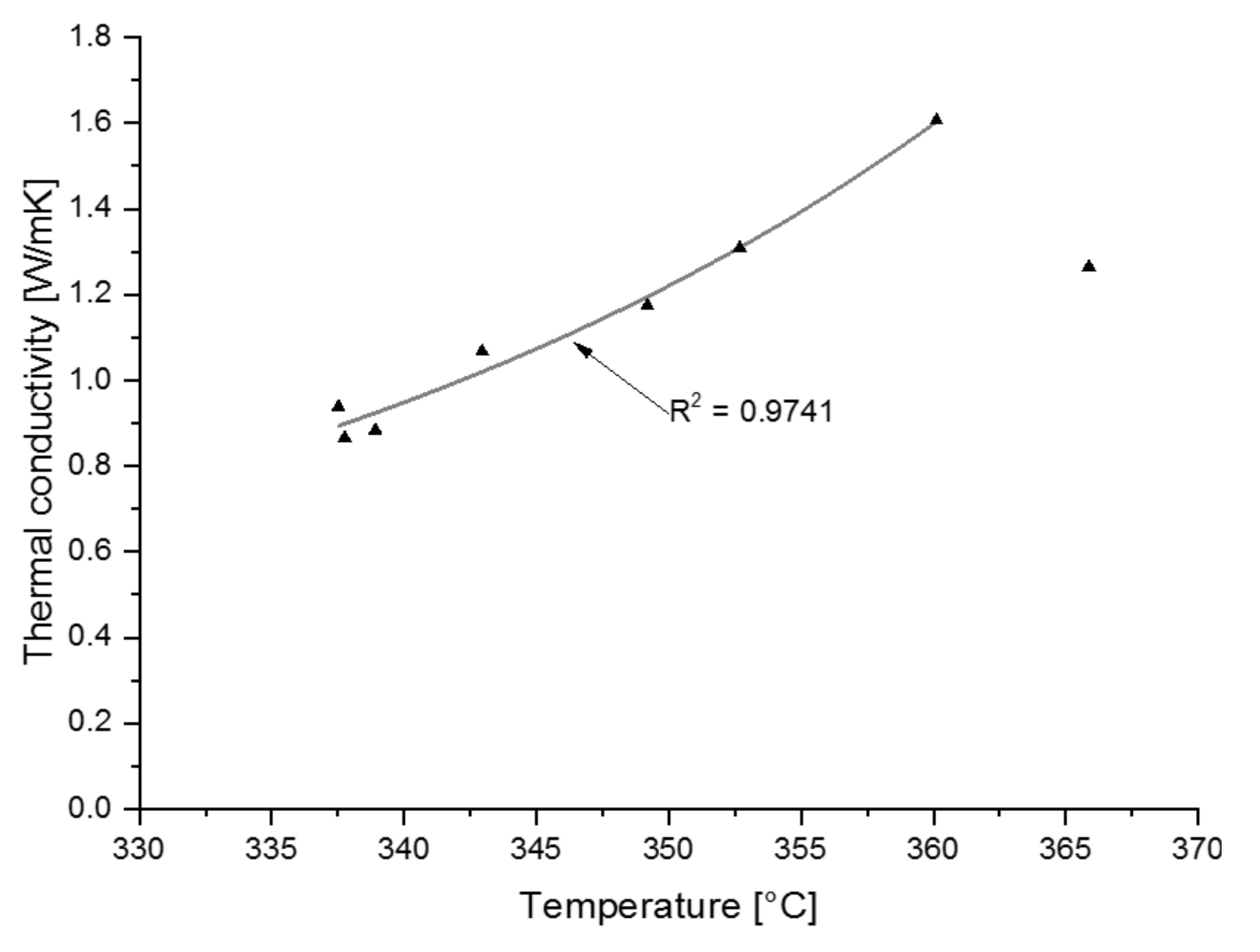
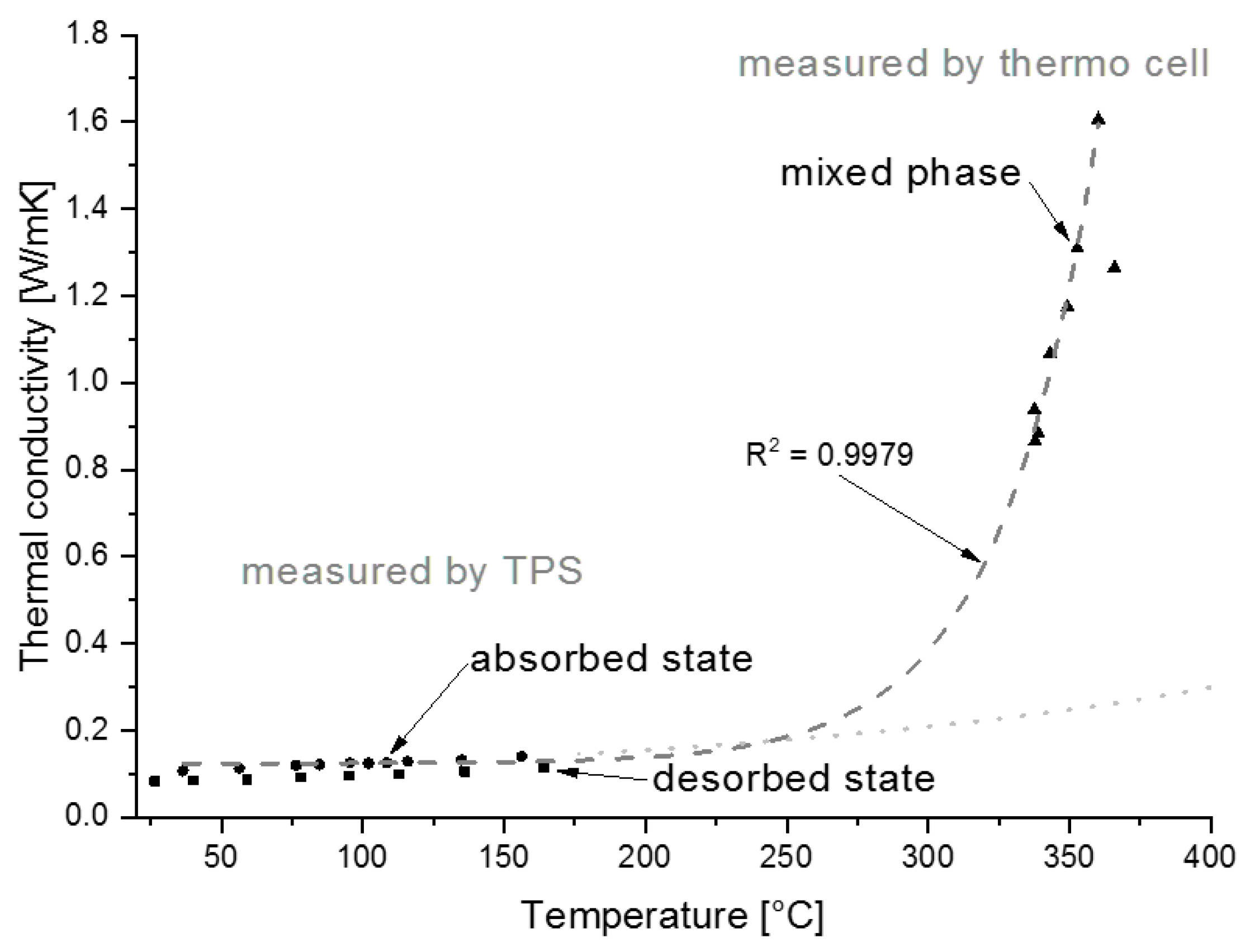
3.2.2. Thermal Conductivity
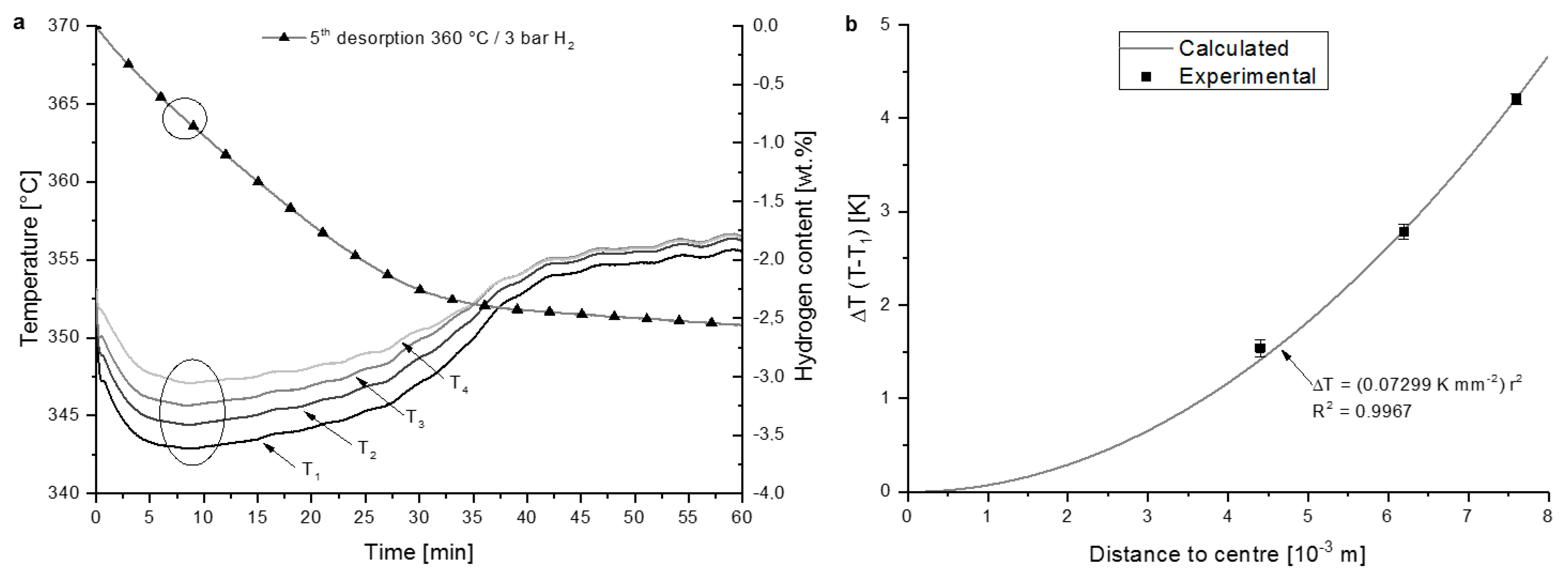
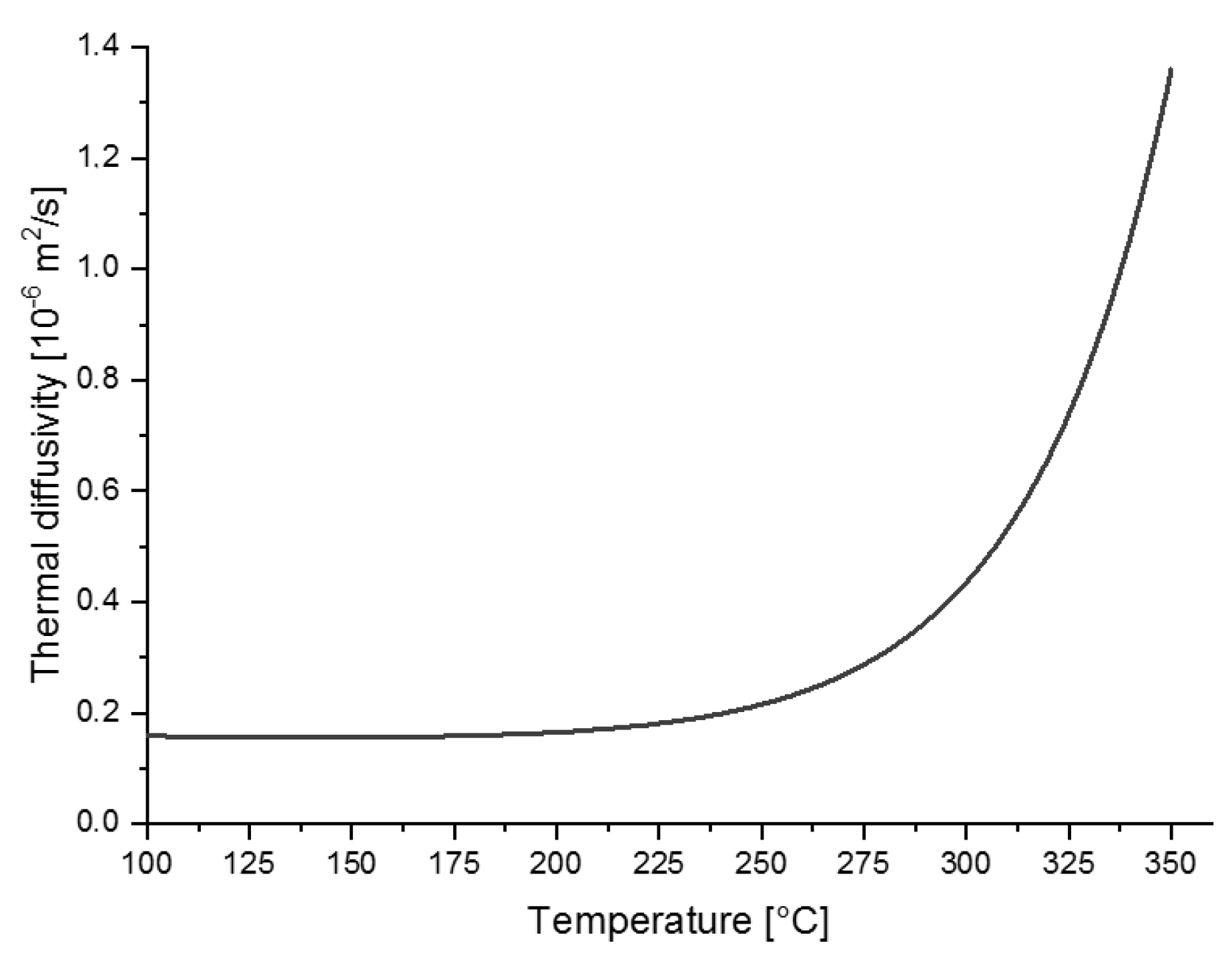
3.2.3. Thermal Diffusivity
4. Discussion
4.1. Reaction Mechanism
4.2. Thermodynamic Properties
4.3. Heat Transfer Properties
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Description |
| a | Thermal diffusivity |
| c0/c1 | Constant |
| cp | Specific heat capacity |
| Cp | Heat capacity |
| ∆H | Enthalpy |
| m | Mass |
| n | Constant |
| p | Pressure |
| Q | Heat energy |
| Heat flux (reaction) | |
| r | Distance |
| R | Gas constant |
| R2 | Coefficient of determination |
| ∆S | Entropy |
| t | Time |
| T | Temperature |
| α | Transformed fraction |
| β | Heating rate |
| λ | Thermal conductivity |
| Φ | Heat flux |
| ρ | Density |
| Indexes | |
| Index | Description |
| 0 | Normal/Initial |
| b | Blank |
| eff | Effective |
| end | Final |
| eq | Equilibrium |
| F | Formation |
| R | Reaction |
| S | Sample |
| start | Initial |
References
- Züttel, A.; Borgschulte, A.; Schlapbach, L. Hydrogen as a Future Energy Carrier; WILEY-VCH Verlag: Weinheim, Germany, 2008. [Google Scholar]
- BP Statistical Review of World Energy; BP: London, UK, June 2017.
- Dornheim, M.; Eigen, N.; Barkhordarian, G.; Klassen, T.; Bormann, R. Tailoring Hydrogen Storage Materials Towards Application. Adv. Eng. Mater. 2006, 8, 377–385. [Google Scholar] [CrossRef]
- Schlapbach, L.; Zuttel, A. Hydrogen-storage materials for mobile applications. Nature 2001, 414, 353–358. [Google Scholar] [CrossRef] [PubMed]
- Züttel, A. Materials for hydrogen storage. Mater. Today 2003, 6, 24–33. [Google Scholar] [CrossRef]
- Sakintunaa, B.; Weinbergera, B.; Lamari-Darkrim, F.; Hirscher, M.; Dogan, B. Comparative study of Hydrogen Storage Efficiency and Thermal Effects of Metal Hydrides vs. Carbon Materials. In Proceedings of the WHEC, Lyon, France, 13–16 June 2006. [Google Scholar]
- Dornheim, M.; Doppiu, S.; Barkhordarian, G.; Boesenberg, U.; Klassen, T.; Gutfleisch, O.; Bormann, R. Hydrogen storage in magnesium-based hydrides and hydride composites. Scr. Mater. 2007, 56, 841–846. [Google Scholar] [CrossRef]
- Westerwaal, R.J.; Haije, W.G. Evaluation Solid-State Hydrogen Storage Systems; Energy Council of the Northeast: Bedford, NH, USA, 2008. [Google Scholar]
- Barkhordarian, G.; Klassen, T.; Dornheim, M.; Bormann, R. Unexpected kinetic effect of MgB2 in reactive hydride composites containing complex borohydrides. J. Alloys Compd. 2007, 440, L18–L21. [Google Scholar] [CrossRef]
- Züttel, A.; Wenger, P.; Rentsch, S.; Sudan, P.; Mauron, P.; Emmenegger, C. LiBH4 a new hydrogen storage material. J. Power Sources 2003, 118, 1–7. [Google Scholar] [CrossRef]
- Lide, D.R. Handbook of Chemistry and Physics; CRC Press: London, UK, 1994. [Google Scholar]
- Siegel, D.J.; Wolverton, C.; Ozoliņš, V. Thermodynamic guidelines for the prediction of hydrogen storage reactions and their application to destabilized hydride mixtures. Phys. Rev. B 2007, 76, 134102. [Google Scholar] [CrossRef]
- Jepsen, J.; Bellosta von Colbe, J.M.; Klassen, T.; Dornheim, M. Economic potential of complex hydrides compared to conventional hydrogen storage systems. Int. J. Hydrogen Energy 2012, 37, 4204–4214. [Google Scholar] [CrossRef]
- Lozano, G.A.; Eigen, N.; Keller, C.; Dornheim, M.; Bormann, R. Effects of heat transfer on the sorption kinetics of complex hydride reacting systems. Int. J. Hydrogen Energy 2009, 34, 1896–1903. [Google Scholar] [CrossRef]
- Delhomme, B.; de Rango, P.; Marty, P.; Bacia, M.; Zawilski, B.; Raufast, C.; Miraglia, S.; Fruchart, D. Large scale magnesium hydride tank coupled with an external heat source. Int. J. Hydrogen Energy 2012, 37, 9103–9111. [Google Scholar] [CrossRef]
- Jepsen, J. Technical and Economic Evaluation of Hydrogen Storage Systems Based on Light Metal Hydrides; HZG Report 2014-2; Helmut-Schmidt-University: Hamburg, Germany, 2014. [Google Scholar]
- Varin, R.A.; Czujko, T.; Wronski, Z.S. Nanomaterials for Solid State Hydrogen Storage; Springer: New York, NY, USA, 2009. [Google Scholar]
- Mettler-Toledo. Measuring Specific Heat Capacity; Mettler-Toledo: Greifensee, Switzerland, June 1998. [Google Scholar]
- Gustafsson, S.E.; Karawacki, E.; Khan, M.N. Transient hot-strip method for simultaneously measuring thermal conductivity and thermal diffusivity of solids and fluids. J. Phys. D Appl. Phys. 1979, 12, 1411. [Google Scholar] [CrossRef]
- Gustafsson, S.E. Transient plane source techniques for thermal conductivity and thermal diffusivity measurements of solid materials. Rev. Sci. Instrum. 1991, 62, 797–804. [Google Scholar] [CrossRef]
- El Kharbachi, A.; Nuta, I.; Hodaj, F.; Baricco, M. Above room temperature heat capacity and phase transition of lithium tetrahydroborate. Thermochim. Acta 2011, 520, 75–79. [Google Scholar] [CrossRef]
- Kubaschewski, O.; Alcock, C.B.; Spencer, P.J. Materials Thermochemistry; Pergamon Press: Oxford, UK, 1993; Volume 6. [Google Scholar]
- Bösenberg, U.; Doppiu, S.; Mosegaard, L.; Barkhordarian, G.; Eigen, N.; Borgschulte, A.; Jensen, T.R.; Cerenius, Y.; Gutfleisch, O.; Klassen, T.; et al. Hydrogen sorption properties of MgH2-LiBH4 composites. Acta Mater. 2007, 55, 3951–3958. [Google Scholar] [CrossRef]
- Baehr, H.D.; Stephan, K. Heat and Mass Transfer; Springer: Berlin, Germany, 2006. [Google Scholar]
- Jepsen, J.; Milanese, C.; Girella, A.; Lozano, G.A.; Pistidda, C.; Bellosta von Colbe, J.M.; Marini, A.; Klassen, T.; Dornheim, M. Compaction pressure influence on material properties and sorption behaviour of LiBH4–MgH2 composite. Int. J. Hydrogen Energy 2013, 38, 8357–8366. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhu, H.; Shaw, L.L.; Ramprasad, R. Ab Initio Computational Studies of Mg Vacancy Diffusion in Doped MgB2 Aimed at Hydriding Kinetics Enhancement of the LiBH4 + MgH2 System. J. Phys. Chem. C 2010, 114, 21801–21807. [Google Scholar] [CrossRef]
- Hu, J.Z.; Kwak, J.H.; Yang, Z.; Wan, X.; Shaw, L.L. Direct observation of ion exchange in mechanically activated LiH + MgB2 system using ultrahigh field nuclear magnetic resonance spectroscopy. Appl. Phys. Lett. 2009, 94, 141905. [Google Scholar] [CrossRef]
- Hu, J.Z.; Kwak, J.H.; Yang, Z.; Wan, X.; Shaw, L.L. Detailed investigation of ion exchange in ball-milled LiH+MgB2 system using ultra-high field nuclear magnetic resonance spectroscopy. J. Power Sources 2010, 195, 3645–3648. [Google Scholar] [CrossRef]
- Shaw, L.L.; Wan, X.; Hu, J.Z.; Kwak, J.H.; Yang, Z. Solid-State Hydriding Mechanism in the LiBH4 + MgH2 System. J. Phys. Chem. C 2010, 114, 8089–8098. [Google Scholar] [CrossRef]
- Gosalawit-Utke, R.; Milanese, C.; Javadian, P.; Jepsen, J.; Laipple, D.; Karmi, F.; Puszkiel, J.; Jensen, T.R.; Marini, A.; Klassen, T.; et al. Nanoconfined 2LiBH4–MgH2–TiCl3 in carbon aerogel scaffold for reversible hydrogen storage. Int. J. Hydrogen Energy 2013, 38, 3275–3282. [Google Scholar] [CrossRef]
- Fichtner, M. Properties of nanoscale metal hydrides. Nanotechnology 2009, 20, 204009. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, T.K.; Besenbacher, F.; Jensen, T.R. Nanoconfined hydrides for energy storage. Nanoscale 2011, 3, 2086–2098. [Google Scholar] [CrossRef] [PubMed]
- Capurso, G.; Agresti, F.; Crociani, L.; Rossetto, G.; Schiavo, B.; Maddalena, A.; Lo Russo, S.; Principi, G. Nanoconfined mixed Li and Mg borohydrides as materials for solid state hydrogen storage. Int. J. Hydrogen Energy 2012, 37, 10768–10773. [Google Scholar] [CrossRef]
- Vajo, J.J.; Skeith, S.L.; Mertens, F. Reversible Storage of Hydrogen in Destabilized LiBH4. J. Phys. Chem. B 2005, 109, 3719–3722. [Google Scholar] [CrossRef] [PubMed]
- Vajo, J.J.; Mertens, F.; Ahn, C.C.; Bowman, R.C.; Fultz, B. Altering Hydrogen Storage Properties by Hydride Destabilization through Alloy Formation: LiH and MgH2 Destabilized with Si. J. Phys. Chem. B 2004, 108, 13977–13983. [Google Scholar] [CrossRef]
- Züttel, A.; Borgschulte, A.; Orimo, S.-I. Tetrahydroborates as new hydrogen storage materials. Scr. Mater. 2007, 56, 823–828. [Google Scholar] [CrossRef]
- Price, T.E.C.; Grant, D.M.; Telepeni, I.; Yu, X.B.; Walker, G.S. The decomposition pathways for LiBD4–MgD2 multicomponent systems investigated by in situ neutron diffraction. J. Alloys Compd. 2009, 472, 559–564. [Google Scholar] [CrossRef]
- Rongeat, C.; Llamas-Jansa, I.; Doppiu, S.; Deledda, S.; Borgschulte, A.; Schultz, L.; Gutfleisch, O. Determination of the heat of hydride formation/decomposition by High-Pressure Differential Scanning Calorimetry (HP-DSC). J. Phys. Chem. B 2007, 111, 13301–13306. [Google Scholar] [CrossRef] [PubMed]
- Bogdanović, B.; Bohmhammel, K.; Christ, B.; Reiser, A.; Schlichte, K.; Vehlen, R.; Wolf, U. Thermodynamic investigation of the magnesium–hydrogen system. J. Alloys Compd. 1999, 282, 84–92. [Google Scholar] [CrossRef]
- Oelerich, W. Sorptionseigenschaften von Nanokristallinen Metallhydriden für die Wasserstoffspeicherung; GKSS: Geesthacht, Germany, 2000. [Google Scholar]
- Bogdanovic, B.; Brand, R.A.; Marjanovic, A.; Schwickardi, M.; Tolle, J. Metal-doped sodium aluminium hydrides as potential new hydrogen storage materials. J. Alloys Compd. 2000, 302, 36–58. [Google Scholar] [CrossRef]
- Schwarz, R.B.; Khachaturyan, A.G. Thermodynamics of Open Two-Phase Systems with Coherent Interfaces. Phys. Rev. Lett. 1995, 74, 2523–2526. [Google Scholar] [CrossRef] [PubMed]
- Bogdanovic, B.; Reiser, A.; Schlichte, K.; Spliethoff, B.; Tesche, B. Thermodynamics and dynamics of the Mg-Fe-H system and its potential for thermochemical thermal energy storage. J. Alloys Compd. 2002, 345, 77–89. [Google Scholar] [CrossRef]
- Riktor, M.D.; Deledda, S.; Herrich, M.; Gutfleisch, O.; Fjellvåg, H.; Hauback, B.C. Hydride formation in ball-milled and cryomilled Mg–Fe powder mixtures. Mater. Sci. Eng. B 2009, 158, 19–25. [Google Scholar] [CrossRef]
- Mauron, P.; Buchter, F.; Friedrichs, O.; Remhof, A.; Bielmann, M.; Zwicky, C.N.; Zuttel, A. Stability and Reversibility of LiBH4. J. Phys. Chem. B 2007, 112, 906–910. [Google Scholar] [CrossRef] [PubMed]
- Cabo, M.; Garroni, S.; Pellicer, E.; Milanese, C.; Girella, A.; Marini, A.; Rossinyol, E.; Suriñach, S.; Baró, M.D. Hydrogen sorption performance of MgH2 doped with mesoporous nickel- and cobalt-based oxides. Int. J. Hydrogen Energy 2011, 36, 5400–5410. [Google Scholar] [CrossRef]
- Shao, H.; Felderhoff, M.; Weidenthaler, C. Kinetics Enhancement, Reaction Pathway Change, and Mechanism Clarification in LiBH4 with Ti-Catalyzed Nanocrystalline MgH2 Composite. J. Phys. Chem. C 2015, 119, 2341–2348. [Google Scholar]
- Puszkiel, J.A.; Castro Riglos, M.V.; Ramallo-Lopez, J.M.; Mizrahi, M.; Karimi, F.; Santoru, A.; Hoell, A.; Gennari, F.C.; Larochette, P.A.; Pistidda, C.; et al. A novel catalytic route for hydrogenation-dehydrogenation of 2LiH + MgB2 via in situ formed core-shell LixTiO2 nanoparticles. J. Mater. Chem. A 2017, 5, 12922–12933. [Google Scholar] [CrossRef]
- Ghaani, M.R.; Catti, M.; Nale, A. Thermodynamics of Dehydrogenation of the 2LiBH4–Mg2FeH6 Composite. J. Phys. Chem. C 2012, 116, 26694–26699. [Google Scholar] [CrossRef]
- Filippo, A.; Ashish, K.; Giovanni, C.; Sergio Lo, R.; Amedeo, M.; Giovanni, P. Improvement of dehydrogenation kinetics of LiBH4 dispersed on modified multi-walled carbon nanotubes. Nanotechnology 2010, 21, 065707. [Google Scholar]
- Dedrick, D.E.; Kanouff, M.P.; Replogle, B.C.; Gross, K.J. Thermal properties characterization of sodium alanates. J. Alloys Compd. 2005, 389, 299–305. [Google Scholar] [CrossRef]
- Kaplan, Y. Effect of design parameters on enhancement of hydrogen charging in metal hydride reactors. Int. J. Hydrogen Energy 2009, 34, 2288–2294. [Google Scholar] [CrossRef]
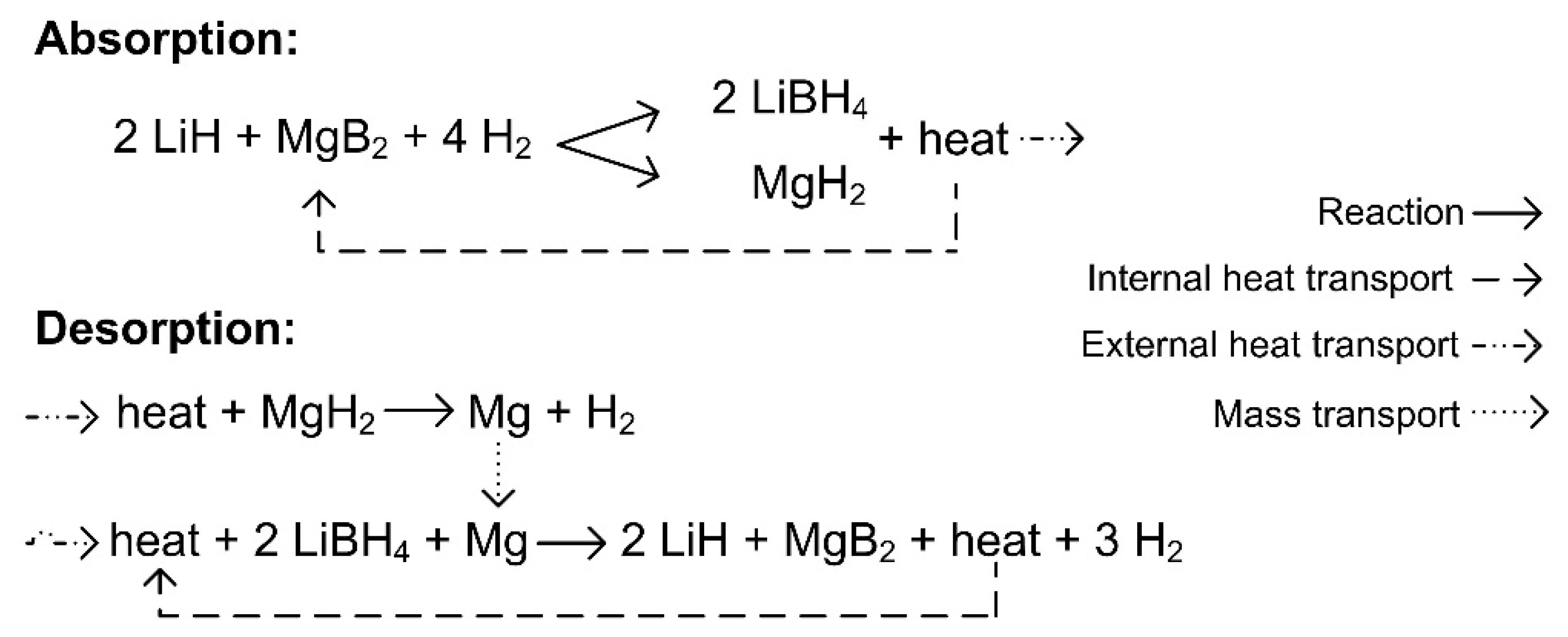


| Material/Composite | A × 100 | B × 103 | C × 103 | D × 10−5 | Temp. Range | Reference |
|---|---|---|---|---|---|---|
| LiH | 16.40 | 52.72 | 0 | −2.93 | - | [22] |
| LiBH4 | 23.479 | 543.9 | −0.7885 | −30.1 | 25–81 °C | [21] |
| LiBH4 | −29,738.586 | 107,620 | −108.78 | 6724.6 | 81–113 °C | [21] |
| LiBH4 | −494.068 | 1594 | −1.13 | 205 | 113–280 °C | [21] |
| MgB2 | 49.79 | 22.72 | 0 | −7.61 | - | [22] |
| MgH2 | 27.2 | 49.37 | 0 | −5.86 | - | [22] |
| 2 LiH + MgB2 | 114.63 | -35.19 | 0 | −32.2 | 50–250 °C | this study |
| ΔHR [kJ mol−1 H2] | Absorption | Desorption | ||
|---|---|---|---|---|
| - | 1st Step | 2nd Step | Overall Reaction | |
| PCI | - * | 73 ± 2 | 53 ± 3 | 58 ± 2 |
| HP-DSC | −26 ± 7 | 58 ± 4 | 20 ± 3 | 29 ± 3 |
| PCI literature (Vajo et al. [34]) | −40.5 | - * | - * | - * |
| Theoretic value [22] | −45.9 | 76.1 | 35.8 | 45.9 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jepsen, J.; Milanese, C.; Puszkiel, J.; Girella, A.; Schiavo, B.; Lozano, G.A.; Capurso, G.; Bellosta von Colbe, J.M.; Marini, A.; Kabelac, S.; et al. Fundamental Material Properties of the 2LiBH4-MgH2 Reactive Hydride Composite for Hydrogen Storage: (I) Thermodynamic and Heat Transfer Properties. Energies 2018, 11, 1081. https://doi.org/10.3390/en11051081
Jepsen J, Milanese C, Puszkiel J, Girella A, Schiavo B, Lozano GA, Capurso G, Bellosta von Colbe JM, Marini A, Kabelac S, et al. Fundamental Material Properties of the 2LiBH4-MgH2 Reactive Hydride Composite for Hydrogen Storage: (I) Thermodynamic and Heat Transfer Properties. Energies. 2018; 11(5):1081. https://doi.org/10.3390/en11051081
Chicago/Turabian StyleJepsen, Julian, Chiara Milanese, Julián Puszkiel, Alessandro Girella, Benedetto Schiavo, Gustavo A. Lozano, Giovanni Capurso, José M. Bellosta von Colbe, Amedeo Marini, Stephan Kabelac, and et al. 2018. "Fundamental Material Properties of the 2LiBH4-MgH2 Reactive Hydride Composite for Hydrogen Storage: (I) Thermodynamic and Heat Transfer Properties" Energies 11, no. 5: 1081. https://doi.org/10.3390/en11051081
APA StyleJepsen, J., Milanese, C., Puszkiel, J., Girella, A., Schiavo, B., Lozano, G. A., Capurso, G., Bellosta von Colbe, J. M., Marini, A., Kabelac, S., Dornheim, M., & Klassen, T. (2018). Fundamental Material Properties of the 2LiBH4-MgH2 Reactive Hydride Composite for Hydrogen Storage: (I) Thermodynamic and Heat Transfer Properties. Energies, 11(5), 1081. https://doi.org/10.3390/en11051081










