Theoretical and Computational Analysis on Double-End Submerged Hollow Fibre Membrane Modules
Abstract
1. Introduction
- (1).
- Analytically model hollow fibres in a double-end suction configuration;
- (2).
- Identify fibre design parameters affecting the permeate output of hollow fibres;
- (3).
- Analyse the changes to permeate pressure profile in relation to permeate output increase due to the change in configurations;
- (4).
- Correlate the relative output increase between single-end and double-end fibres, to geometrical parameters (i.e., fibre inner diameter, membrane thickness, and membrane permeability).
2. Methodology
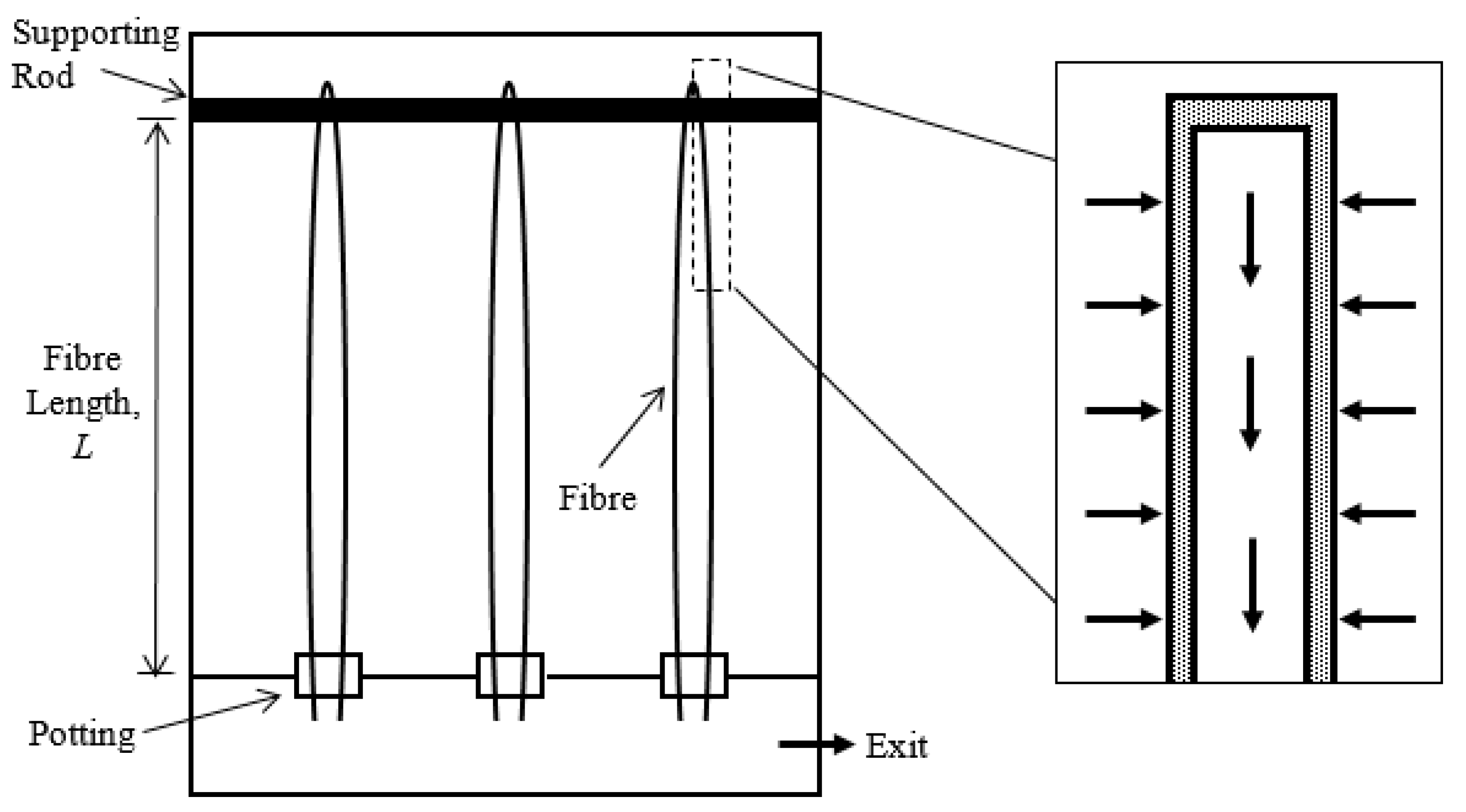
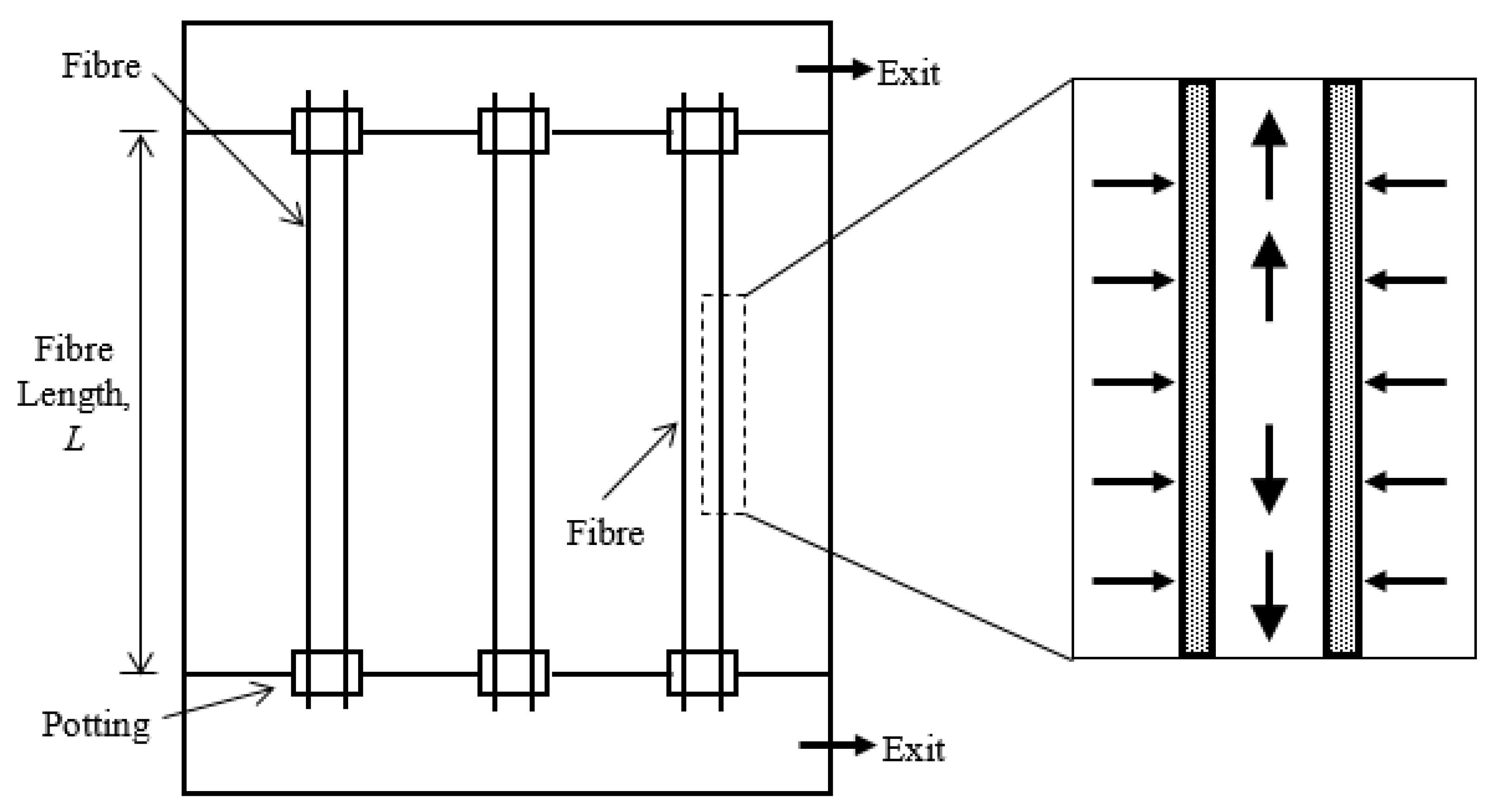
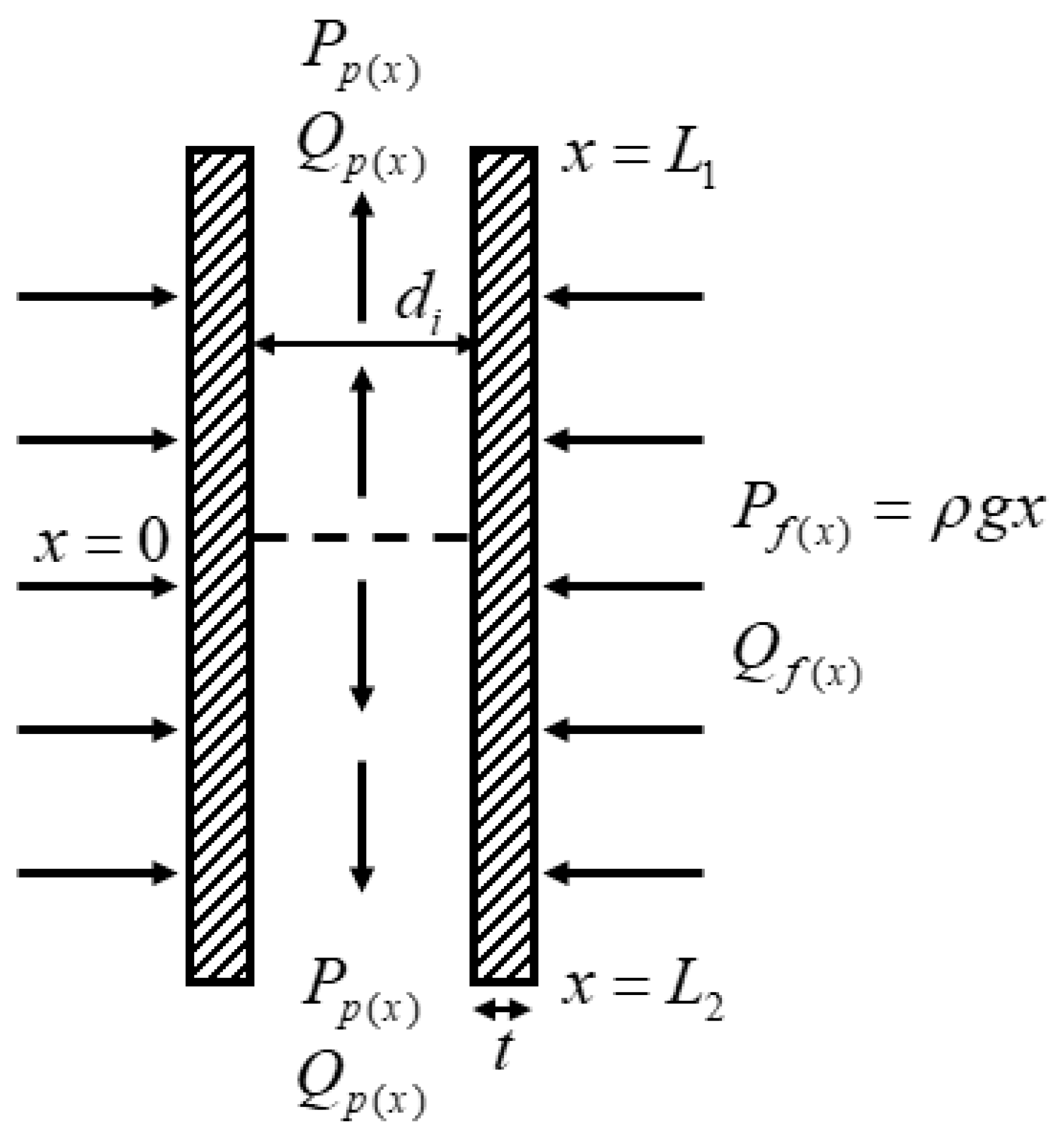
2.1. Theoretical Model and Assumptions
- Fibres with half the initial length will be used instead. These fibres will be ported on both ends, with the inner channel open for the permeate output from both the top and bottom end.
- Another permeate channel will be placed on the top of the housing, and the supporting rod removed.
- Pressure head required to operate per unit will be doubled due to the increase of permeate channel to 2.
2.2. CFD Methodology
2.2.1. Numerical model
- The above estimation neglects pressure loss within the fibre lumen. Hence, TMP along the entire fibre length of 1 m is consistent.
- Having these assumptions overestimates the amount of water flowing through the membrane. Hence, in all actual cases simulated, the cumulative outlet velocity and the Reynolds number are expected to be lower.
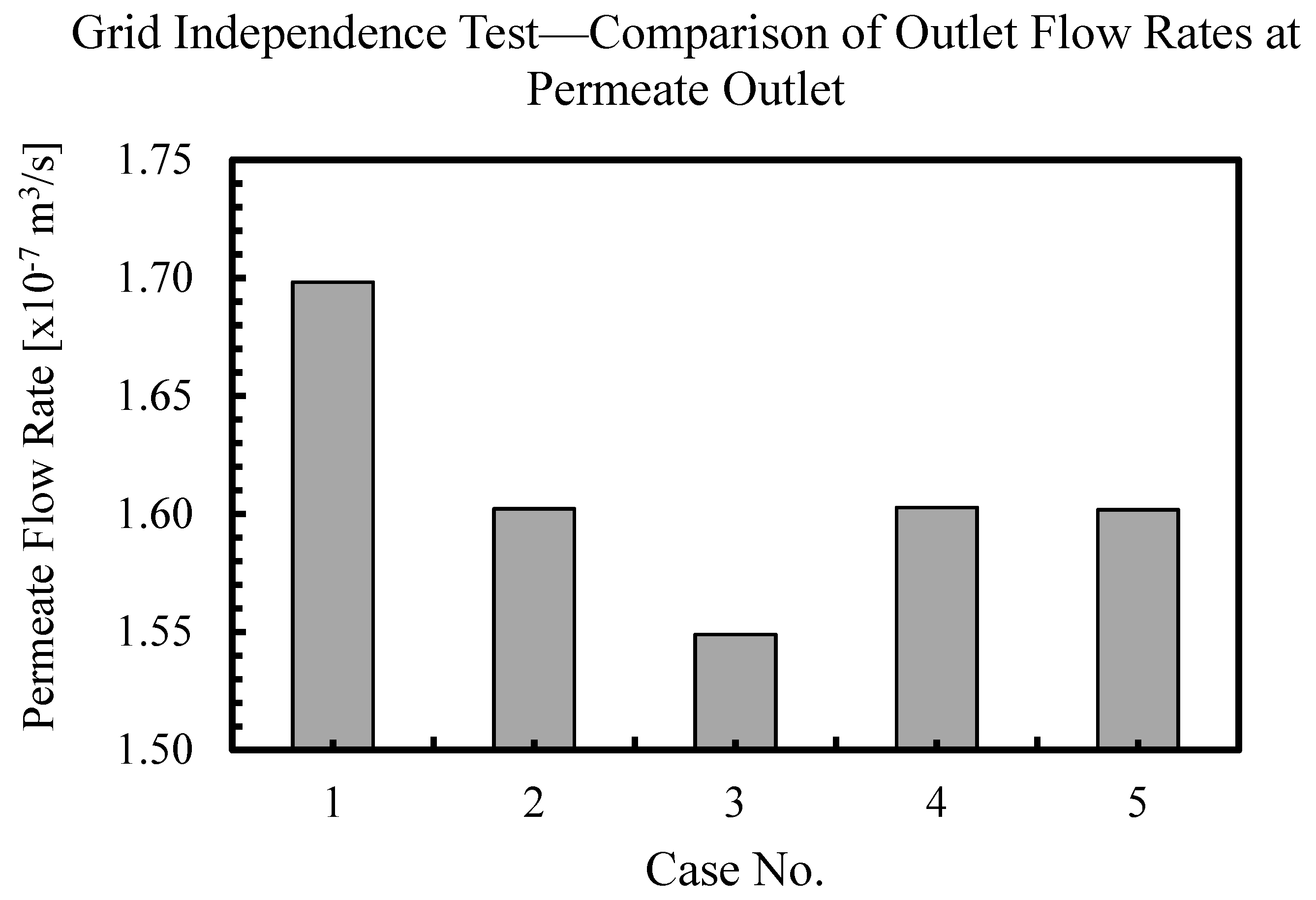
2.2.2. Meshing of CFD Model
2.2.3. Boundary Conditions and Solver Settings Used in CFD Simulations
- denotes the fluid velocity in m/s;
- P denotes the static pressure in Pa;
- ρ denotes the fluid density in kg/m3;
- μ denotes the fluid viscosity in Pa∙s; and
- k denotes membrane permeability in m2.
2.2.4. Parameters Studied and Case Setup
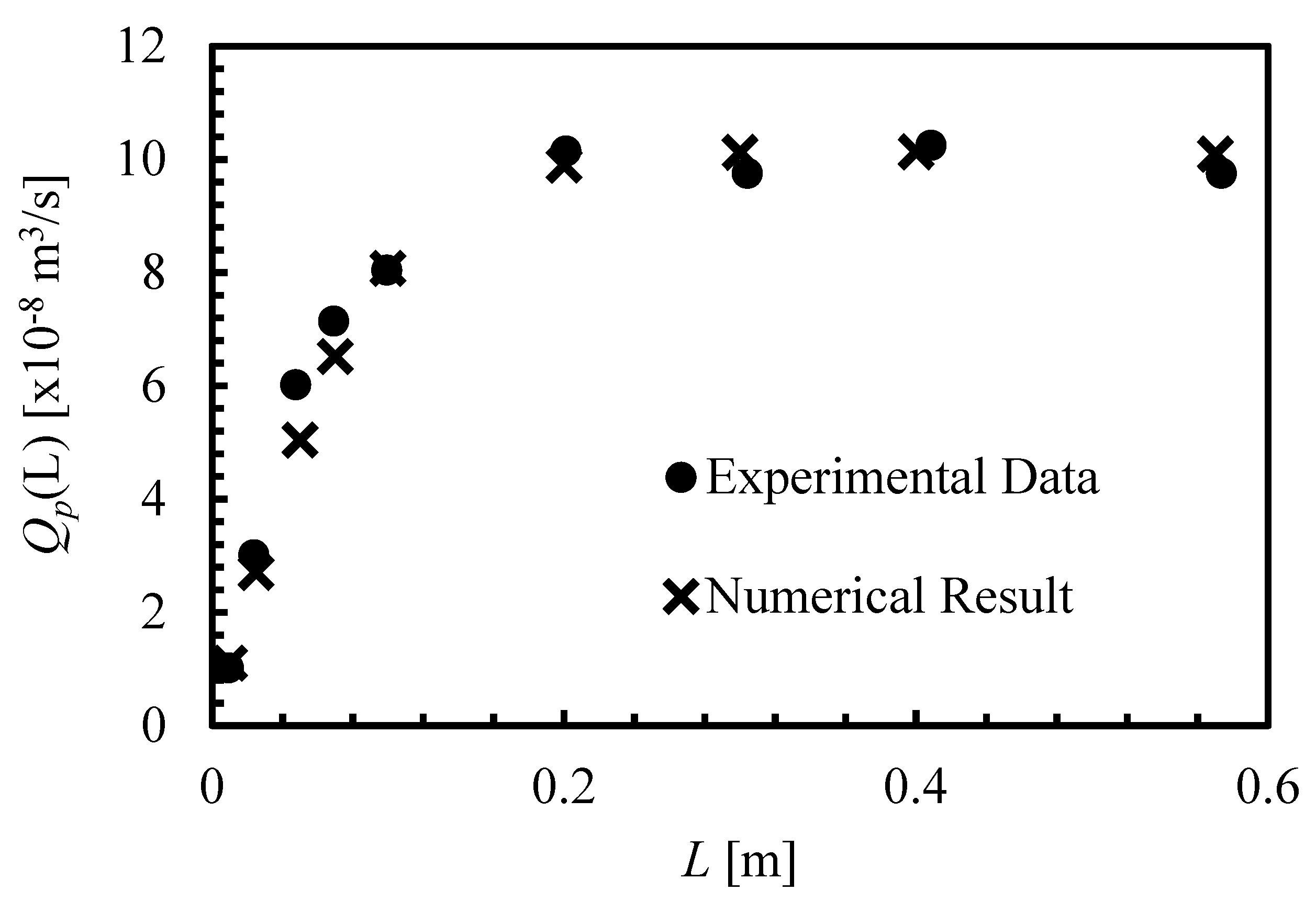
3. Validation of the Numerical Model
- Hollow Fibre Membrane
- Outer Diameter: 0.55 mm
- Inner Diameter: 0.25 mm
- Original Fibre Length: 0.6 m
- Water Properties
- Temperature: 20 °C
- Viscosity: 0.0012 Pa∙s
4. Results and Discussion
4.1. The Effects of Fibre Inner Diameter, Membrane Thickness, and Membrane Permeability on Permeate Pressure Profile and Output Permeate Flow Rate
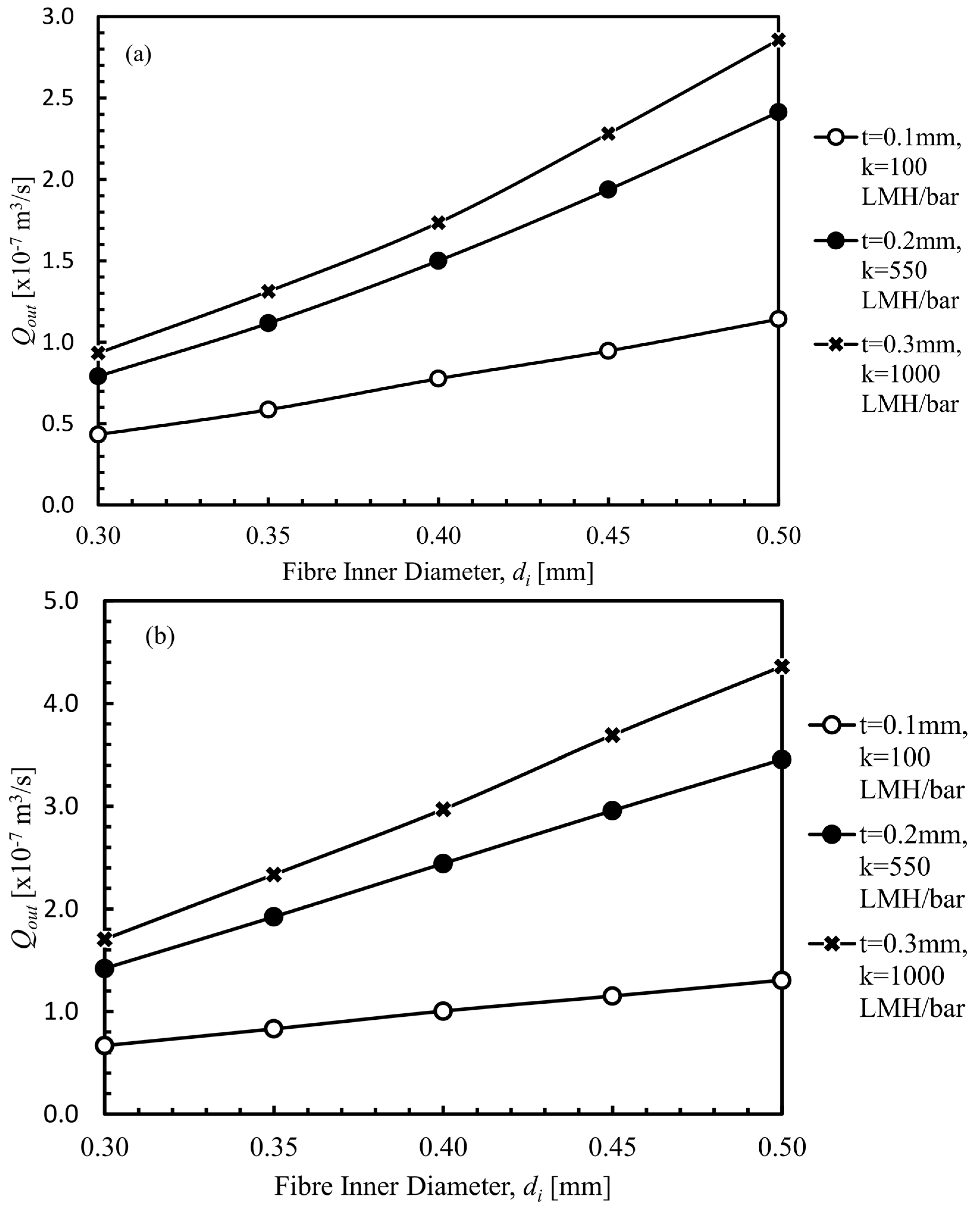
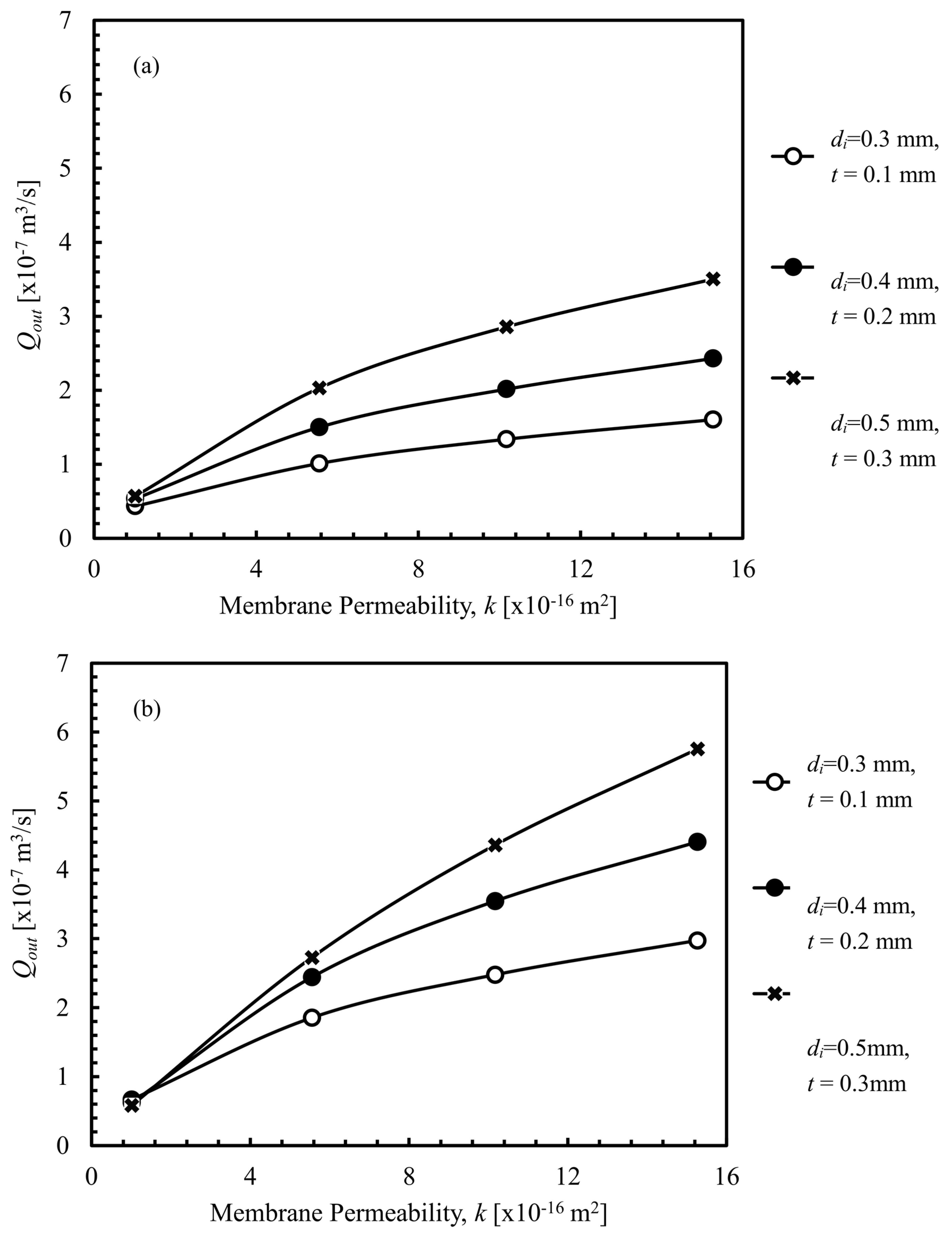
4.1.1. Fibre Inner Diameter
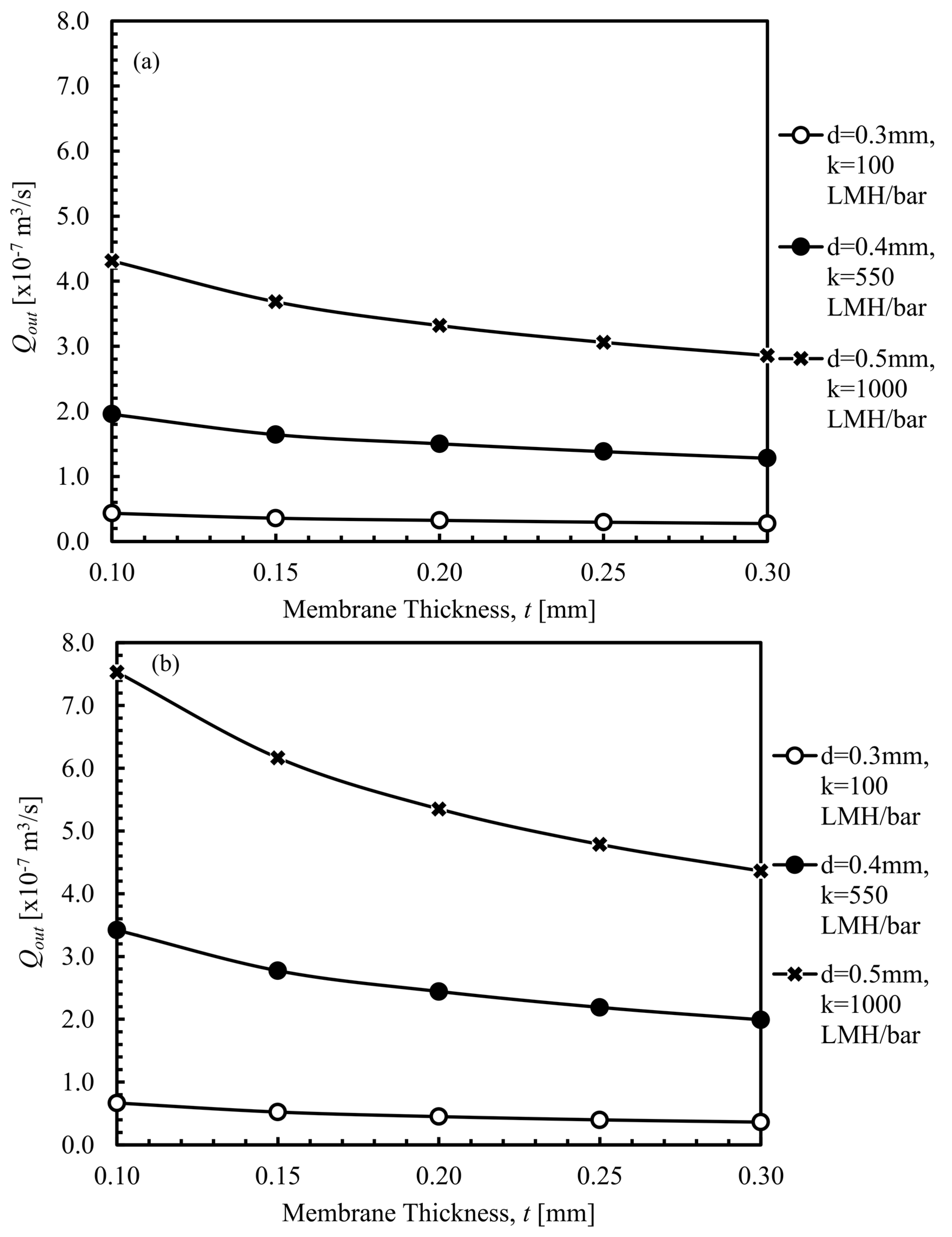
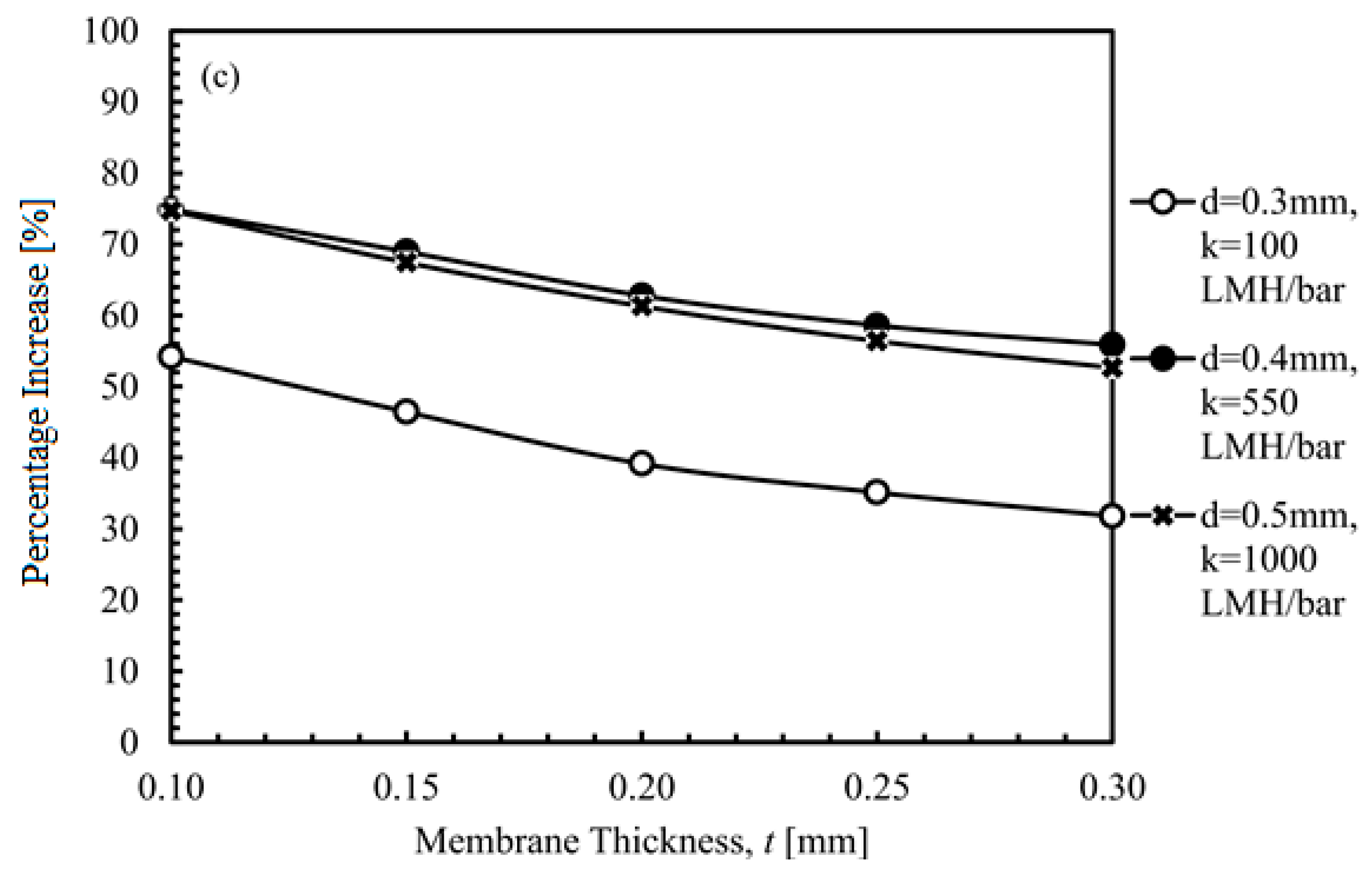
4.1.2. Membrane Thickness
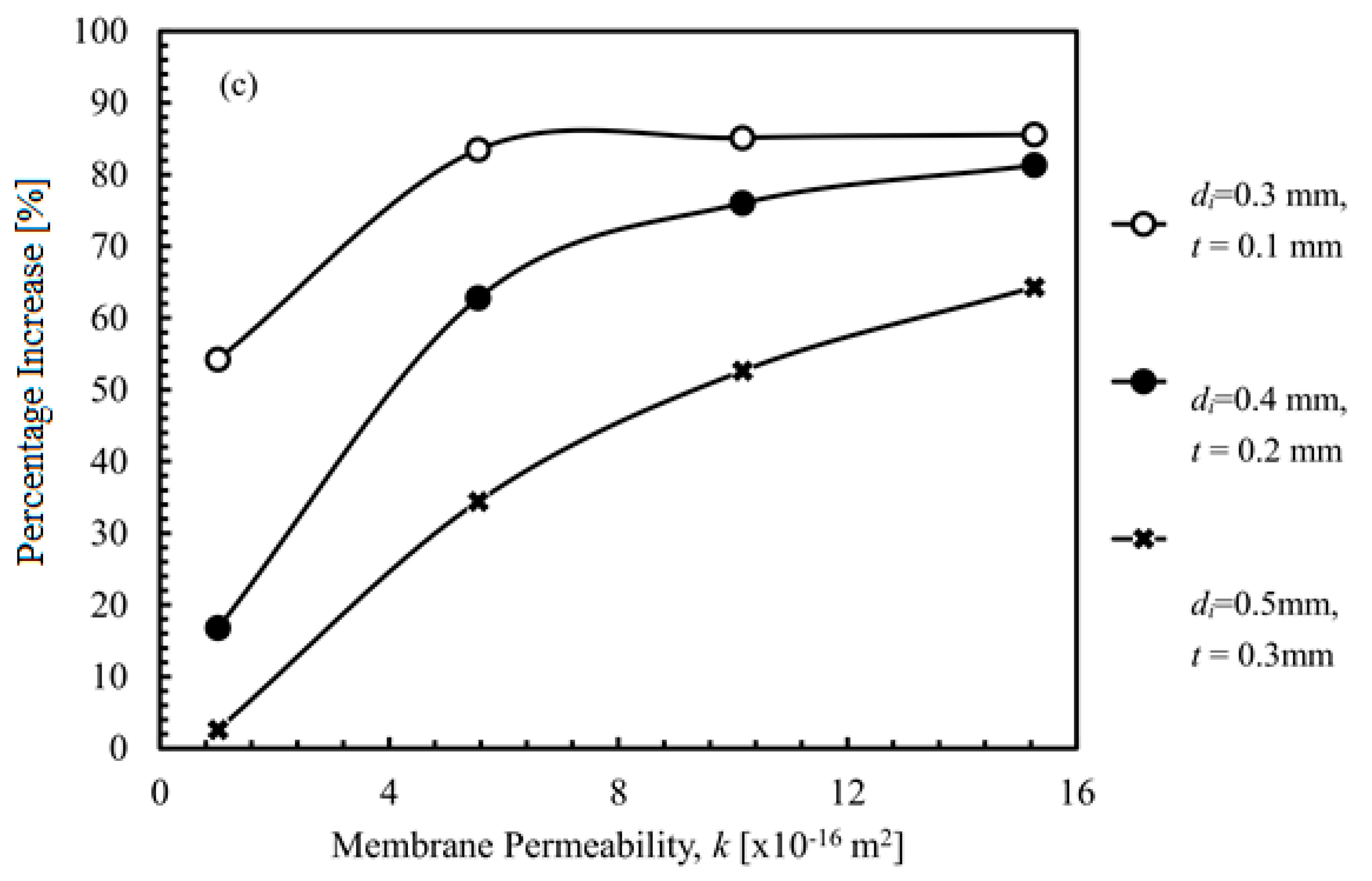
4.1.3. Membrane Permeability
4.2. Derivation of a Single Quantifiable Parameter to Identify Fibre Cross-Sectional Geometry
4.2.1. The Need for a Single Quantifiable Parameter
4.2.2. Permeate Output Flow Rate Calculation for Single-End Bottom Suction Configuration
- Pf(x) denotes feed pressure at point x along the fibre length;
- Pp(x) denotes permeate pressure at point x along the fibre length;
- denotes membrane flux at point x along the fibre length;
- k denotes membrane permeability in m2;
- de denotes fibre external diameter in m;
- µ denotes dynamic viscosity of water in Pa∙s; and
- t denotes membrane thickness in m.
4.2.3. Permeate Output Flow Rate Calculation for Double-End Suction Configuration
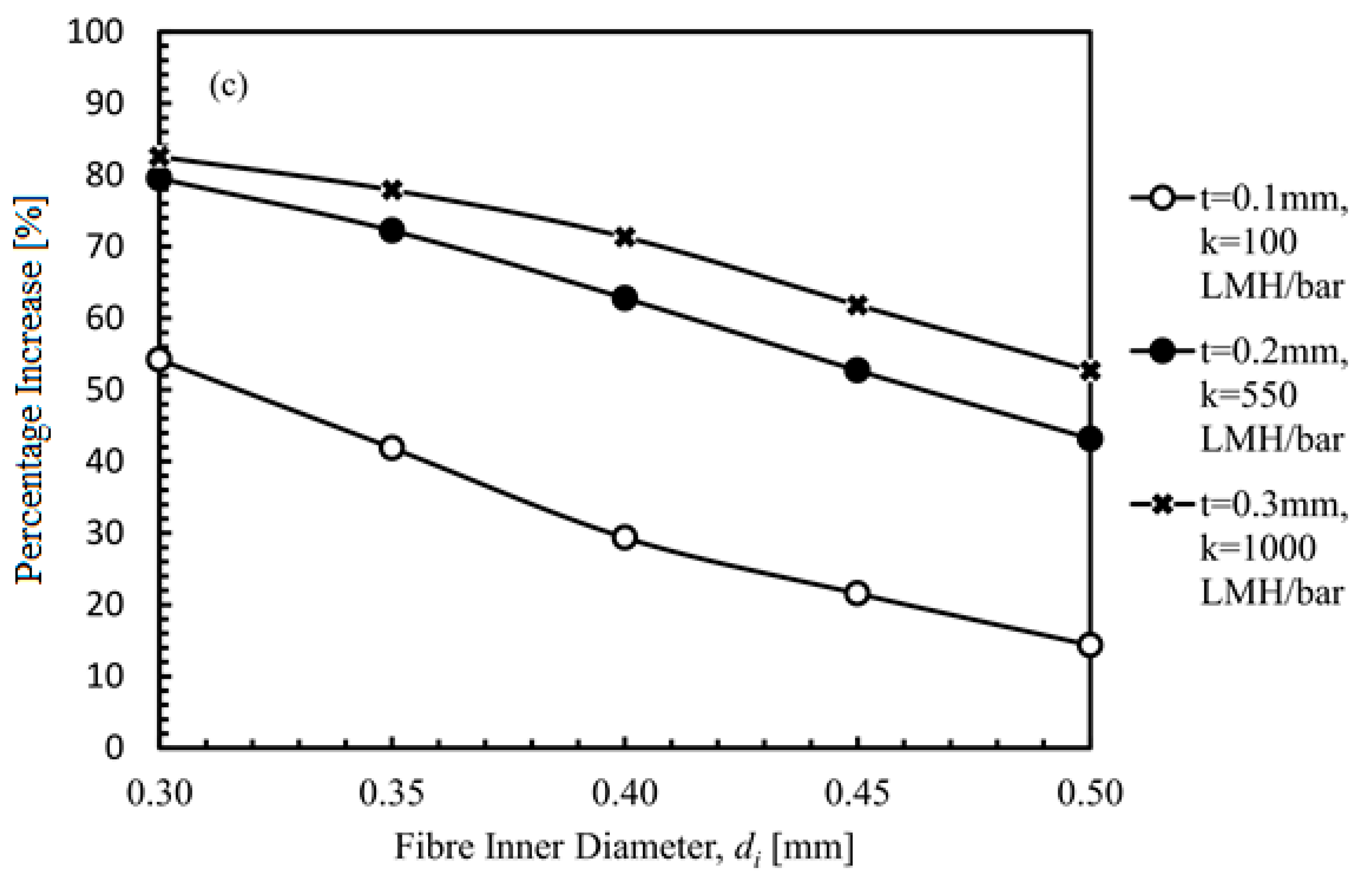
4.2.4. Increase in Permeate Flow Rate by Means of Configuration Change from Single-End to Double-End Suction.
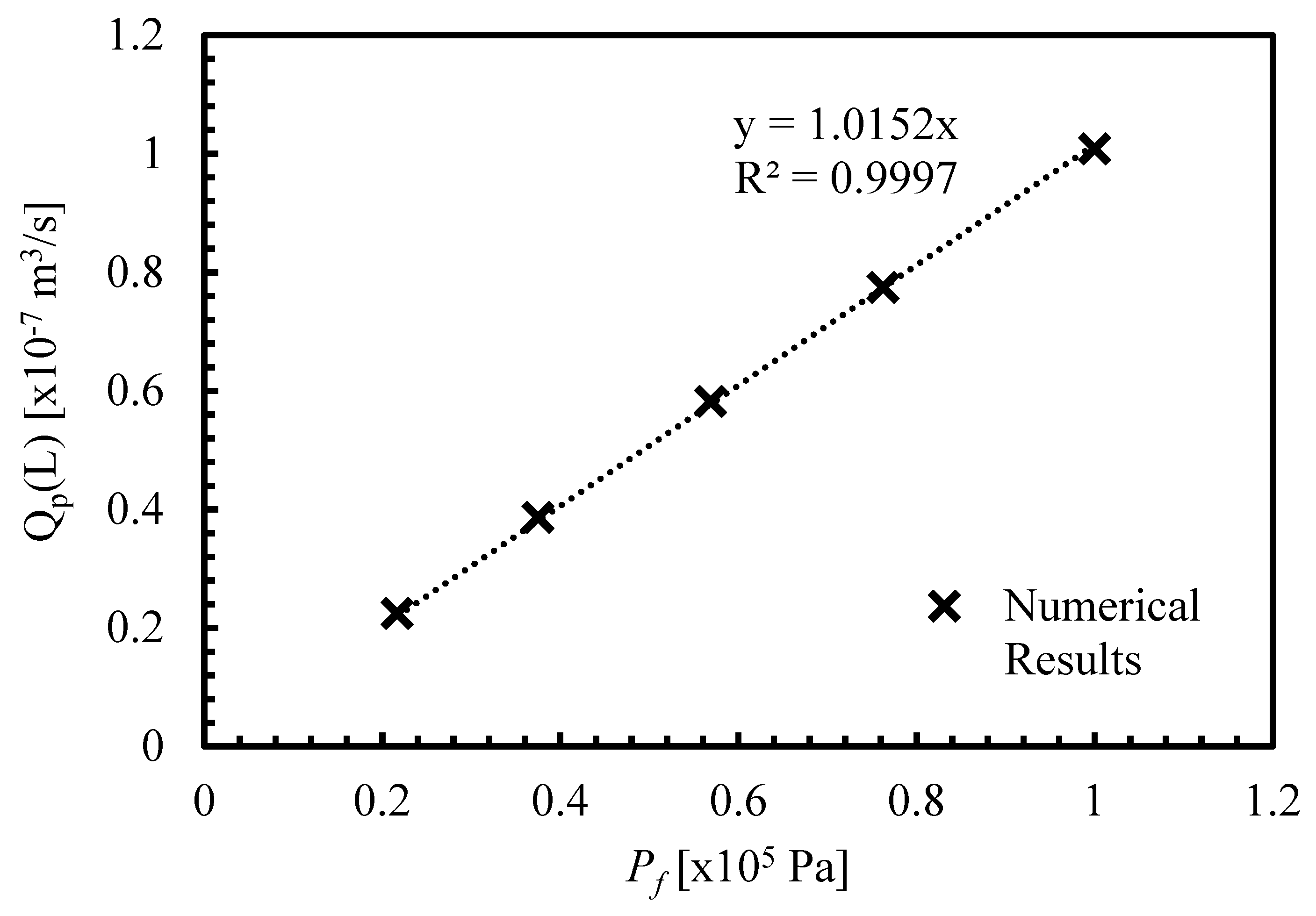
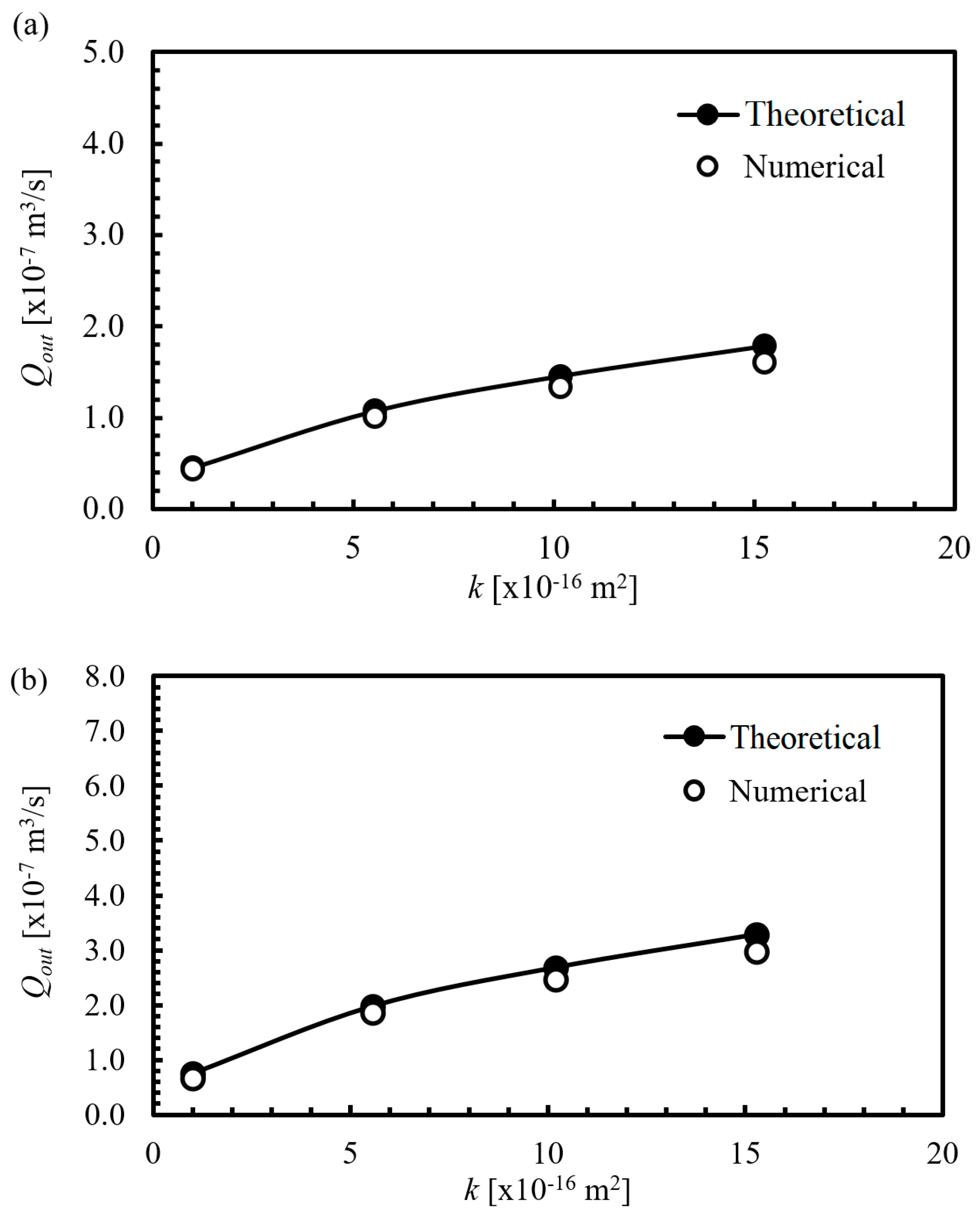
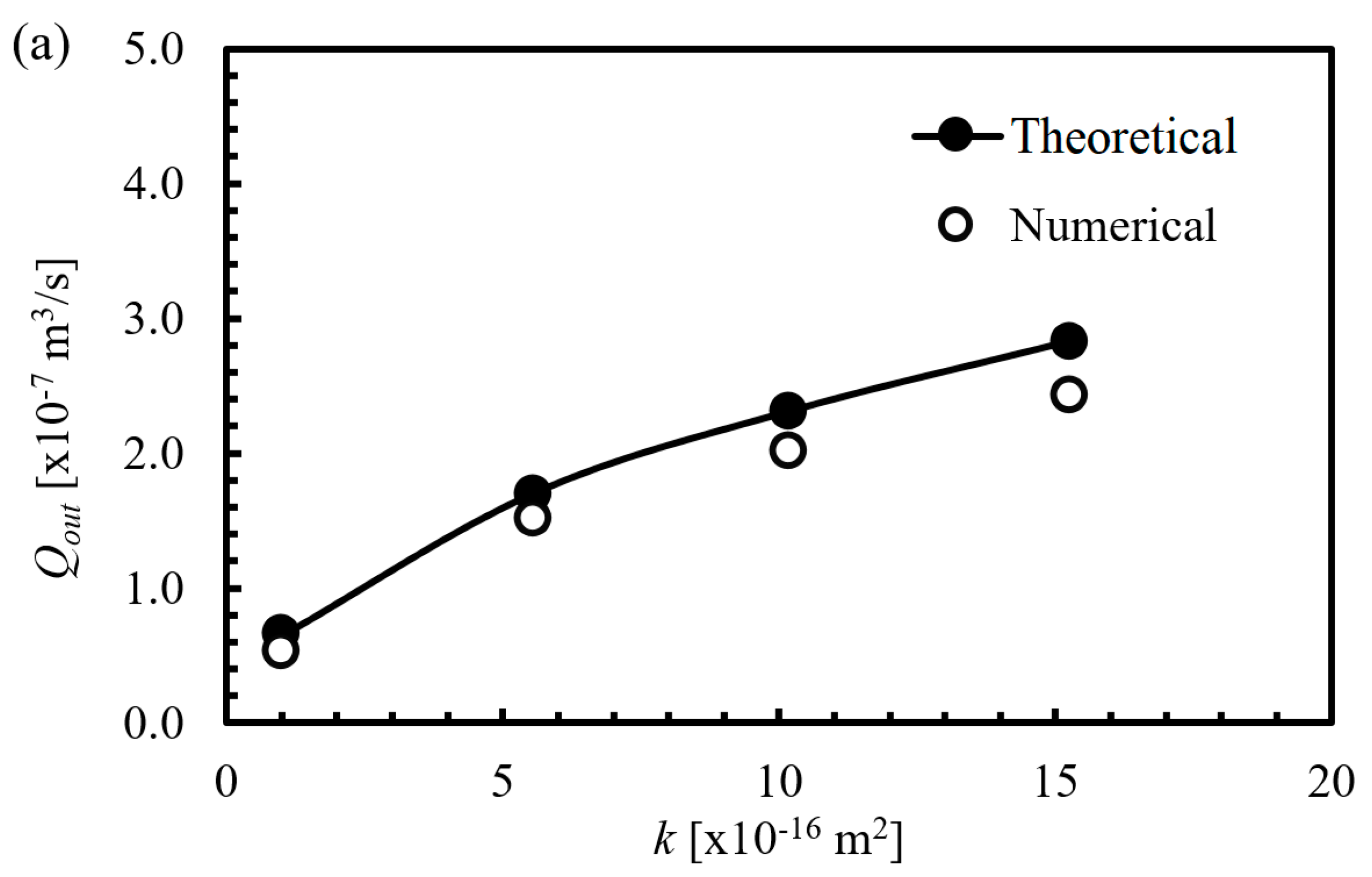
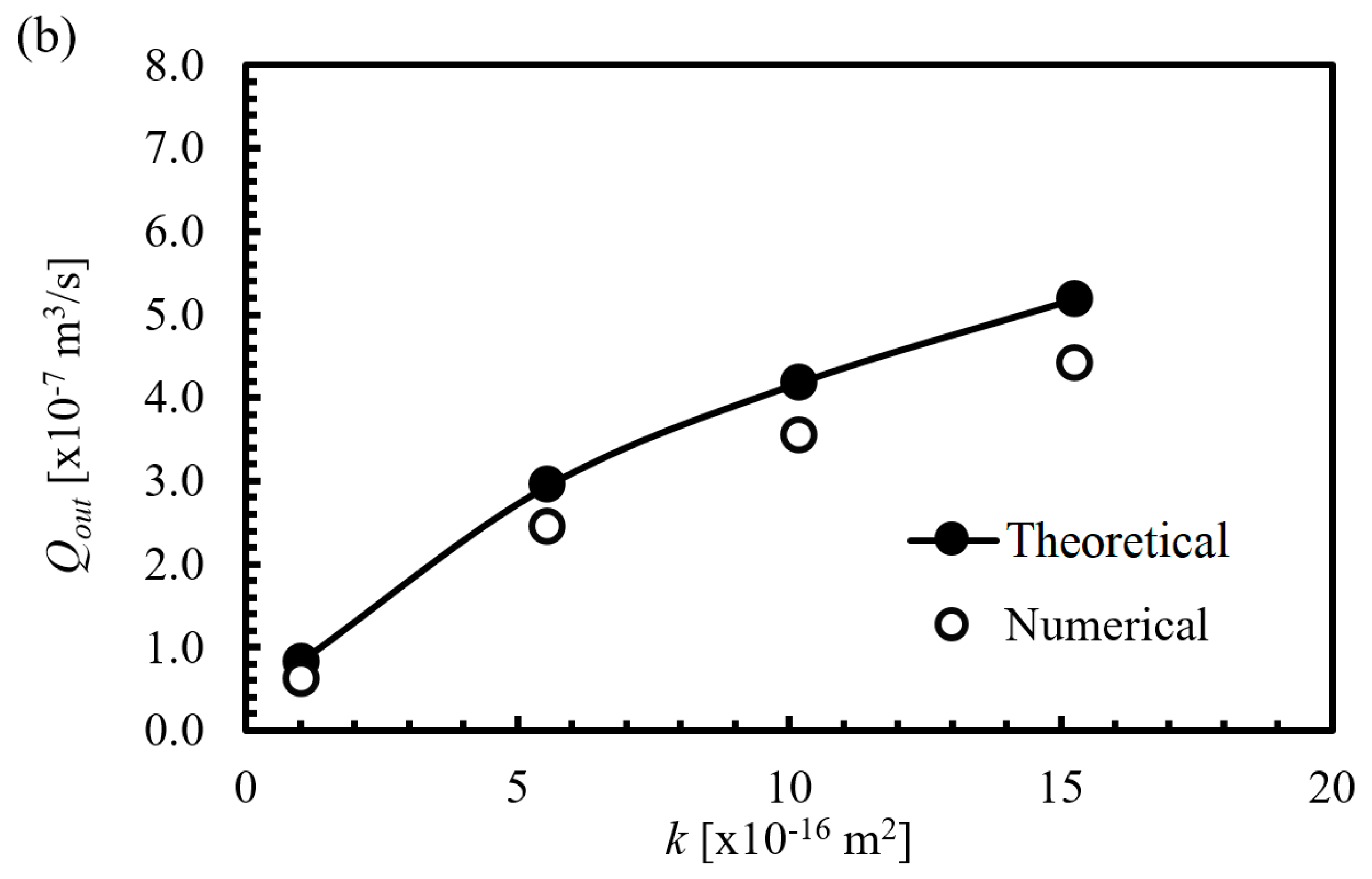
4.3. Comparison of Output Flowrate between Theoretical and Numerical Results
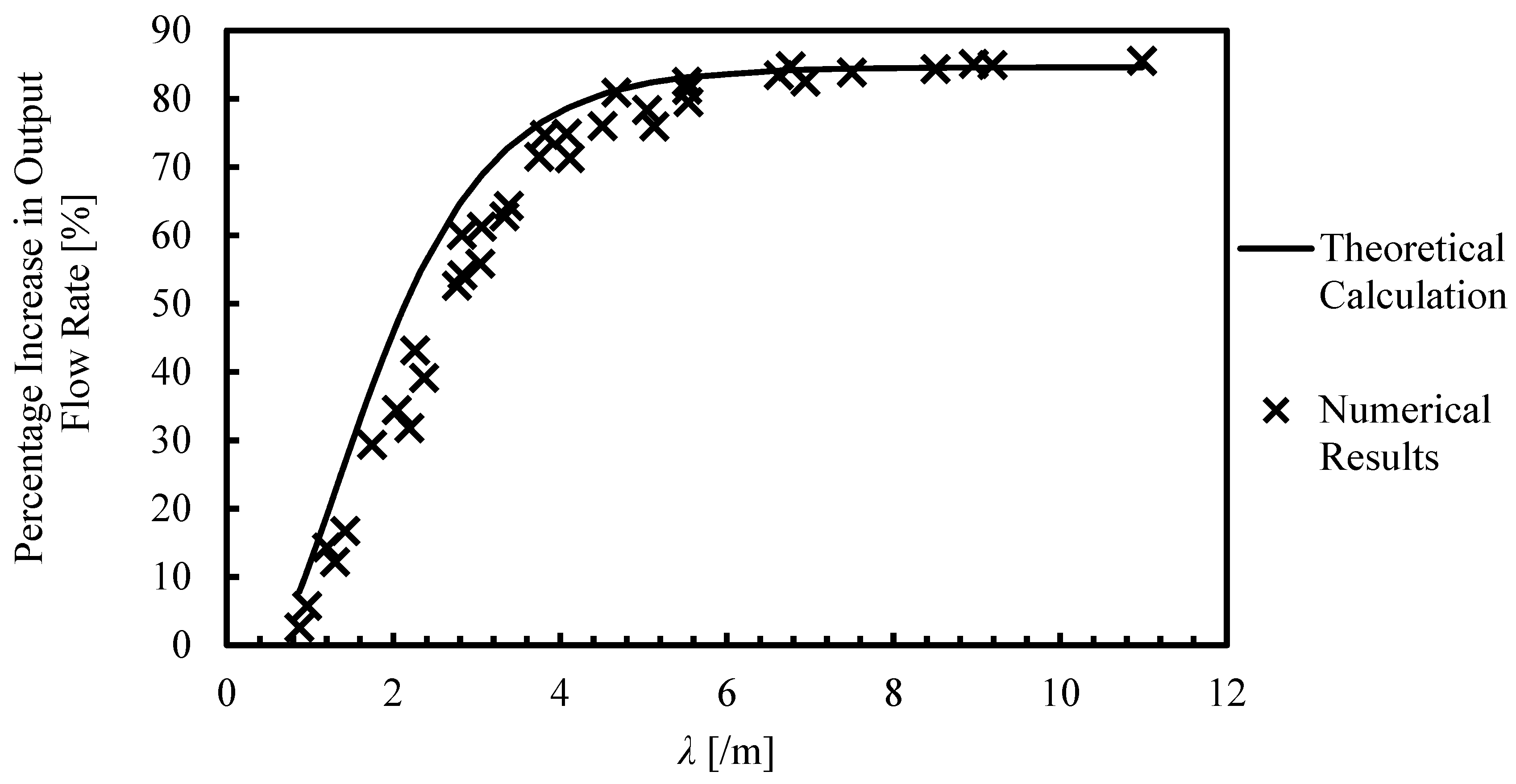
4.4. Correlation between λ and the Increase in Permeate Output Flow Rate Due to Change in Configurations
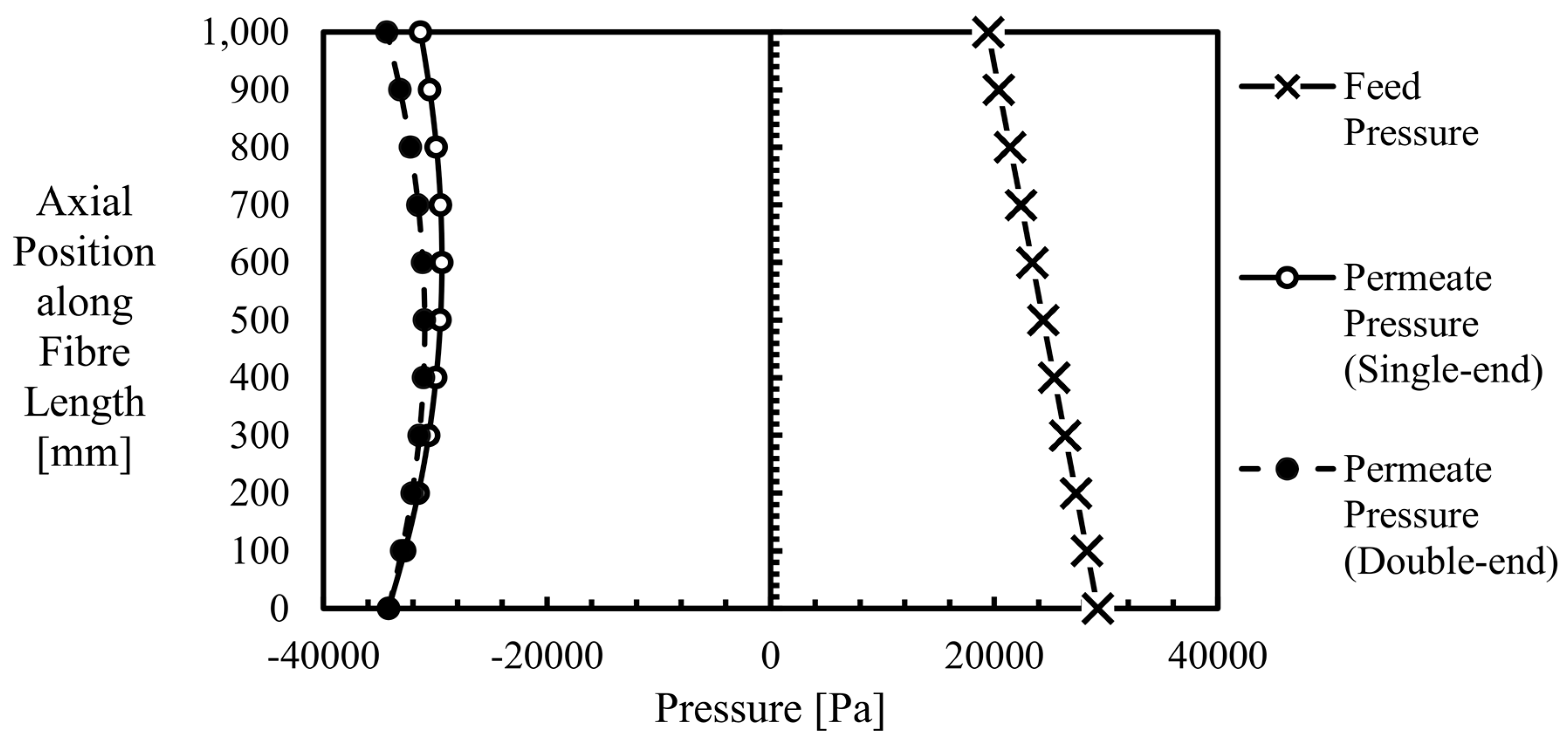
4.5. Correlation between λ and Permeate Pressure Profile
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| di | Internal diameter of fibre (m) |
| de | External diameter of fibre (m) |
| do | Outer boundary diameter of fluid envelope (m) |
| x | Axial position along membrane length (m) |
| L | Length of fibre (m) |
| L1 | Length of top portion of double-end fibre in which water flows towards the top exit (m) |
| L2 | Length of bottom portion of double-end fibre in which water flows towards the bottom exit (m) |
| Fluid velocity (m/s) | |
| P | Pressure (Pa) |
| Ps | Suction pressure (Pa) |
| μ | Dynamic viscosity of water (Pa∙s) |
| k | Membrane permeability (m2) |
| t | Membrane thickness (m) |
| λ | Value characterised by membrane geometry (/m) [6,9] |
| pf(x) | Pressure at feed region (Pa) |
| pp(x) | Pressure at permeate region (Pa) |
| Qf(x) | Flowrate of feed through membrane wall at axial position x (m3/s) |
| Qp(x) | Flowrate of permeate along inner channel at axial position x (m3/s) |
| Qout | Permeate flowrate at outlet (m3/s) |
References
- Fane, A.G.; Chang, S.; Chardon, E. Submerged Hollow Fibre Membrane Module—Design Options and Operational Considerations. Desalination 2002, 146, 231–236. [Google Scholar] [CrossRef]
- Doshi, M.R.; Gill, W.N.; Kabadi, V.N. Optimal Design of Hollow Fiber Modules. AlChE J. 1997, 23, 765–767. [Google Scholar] [CrossRef]
- Soltanieh, M.; Gill, W.N. A Note on the Effect of Fibre Length on the Productivity of Hollow Fibre Modules. Chem. Eng. Commun. 1983, 22, 109. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Wang, J.; Wang, H.; He, B.; Zhang, H.; Guo, W.; Ngo, H.H. Experimental Investigation of Local Flux Distribution and Fouling Behavior in Double-end and Dead-end Submerged Hollow Fiber Membrane Modules. J. Membr. Sci. 2014, 453, 18–26. [Google Scholar] [CrossRef]
- Carroll, T.; Booker, N.A. Axial Features in the Fouling of Hollow Fibre Membranes. J. Membr. Sci. 2000, 168, 203–212. [Google Scholar] [CrossRef]
- Chang, S.; Fane, A.G.; Waite, T.D. Analysis of Constant Permeate Flow Filtration Using Dead-end Hollow Fibre Membranes. J. Membr. Sci. 2006, 286, 132–141. [Google Scholar] [CrossRef]
- Carroll, T. The Effect of Cake and Fibre Properties on Flux Declines in Hollow-fibre Microfiltration Membranes. J. Membr. Sci. 2001, 189, 167–178. [Google Scholar] [CrossRef]
- Serra, C.; Clifton, M.J.; Moulin, P.; Rouch, J.-C.; Aptel, P. Dead-end Ultrafiltration in Hollow Fibre Modules: Module Design and Process Simulation. J. Membr. Sci. 1998, 145, 159–172. [Google Scholar] [CrossRef]
- Popovic´, S.; Dittrich, M.; Cakl, J. Modelling of Fouling of Outside-in Hollow-fiber Membranes by TiO2 Particles. Sep. Purif. Technol. 2015, 156, 28–35. [Google Scholar] [CrossRef]
- Chang, S. Application of Submerged Hollow Fibre Membrane in Membrane Bioreactors: Filtration Principles, Operation, and Membrane Fouling. Desalination 2011, 283, 31–39. [Google Scholar] [CrossRef]
- Chang, S.; Fane, A.G. The Effect of Fibre Diameter on Filtration and Flux Distribution—Relevance to Submerged Hollow Fibre Module. J. Membr. Sci. 2001, 184, 221–231. [Google Scholar] [CrossRef]
- Günther, J.; Schmitz, P.; Albasi, C.; Lafforgue, C. A Numerical Approach to Study the Impact of Packing Density on Fluid Flow Distribution in Hollow Fibre Module. J. Membr. Sci. 2010, 348, 277–286. [Google Scholar] [CrossRef]
- Zhuang, L.W.; Guo, H.F.; Wang, P.H.; Dai, G. Study on the Flux Distribution in a Dead-end Outside-in Hollow Fibre Membrane Module. J. Membr. Sci. 2015, 495, 372–383. [Google Scholar] [CrossRef]
- Wang, Y.; Brannock, M.; Cox, S.; Leslie, G. CFD Simulations of Membrane Filtration Zone in a Submerged Hollow Fibre Membrane Bioreactor Using a Porous Media Approach. J. Memb. Sci. 2010, 363, 57–66. [Google Scholar] [CrossRef]
- Vinther, F.; Pinelo, M.; Brøns, M.; Jonsson, G.; Meyer, A.S. Mathematical Modelling of Dextran Filtration through Hollow Fibre Membranes. Sep. Purif. Technol. 2014, 125, 21–36. [Google Scholar] [CrossRef]
- Happel, J. Viscous Flow Relative to Arrays of Cylinders. AlChE J. 1959, 5, 174–177. [Google Scholar] [CrossRef]
- Lim, K.B.; Wang, P.C.; An, H.; Yu, S.C.M. Computational Studies for the Design Parameters of Hollow Fibre Membrane Modules. J. Membr. Sci. 2017, 529, 263–273. [Google Scholar] [CrossRef]
- Filloux, E.; Teychene, B.; Tazi-Pain, A.; Croue, J.P. Ultrafiltration of Biologically Treated Domestic Wastewater: How Membrane Properties Influence Performance. Sep. Purif. Technol. 2014, 134, 178–186. [Google Scholar] [CrossRef][Green Version]




| Mesh | Node Distribution | Mesh Resolution | Element Count | |||
|---|---|---|---|---|---|---|
| Axial Fibre Length | Radial Permeate | Radial Membrane | Radial Feed | |||
| 1 | 2500 | 3 | 3 | 4 | 2500 × 10 | 25,000 |
| 2 | 5000 | 5 | 5 | 8 | 5000 × 18 | 90,000 |
| 3 | 7500 | 5 | 5 | 8 | 7500 × 18 | 135,000 |
| 4 | 10,000 | 7 | 5 | 8 | 10,000 × 20 | 200,000 |
| 5 | 20,000 | 14 | 10 | 16 | 20,000 × 40 | 800,000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, K.B.; An, H.; Wang, P.C.; Liu, G.; Yu, S.C.M. Theoretical and Computational Analysis on Double-End Submerged Hollow Fibre Membrane Modules. Energies 2018, 11, 1042. https://doi.org/10.3390/en11051042
Lim KB, An H, Wang PC, Liu G, Yu SCM. Theoretical and Computational Analysis on Double-End Submerged Hollow Fibre Membrane Modules. Energies. 2018; 11(5):1042. https://doi.org/10.3390/en11051042
Chicago/Turabian StyleLim, Keng Boon, Hui An, Peng Cheng Wang, Guiqin Liu, and Simon Ching Man Yu. 2018. "Theoretical and Computational Analysis on Double-End Submerged Hollow Fibre Membrane Modules" Energies 11, no. 5: 1042. https://doi.org/10.3390/en11051042
APA StyleLim, K. B., An, H., Wang, P. C., Liu, G., & Yu, S. C. M. (2018). Theoretical and Computational Analysis on Double-End Submerged Hollow Fibre Membrane Modules. Energies, 11(5), 1042. https://doi.org/10.3390/en11051042




