A Heuristic T-S Fuzzy Model for the Pumped-Storage Generator-Motor Using Variable-Length Tree-Seed Algorithm-Based Competitive Agglomeration
Abstract
:1. Introduction
2. VTSA–CA Algorithm
2.1. CA Algorithm
2.2. Variable-Length TSA
2.2.1. The Basic TSA
2.2.2. The Variable-Length TSA
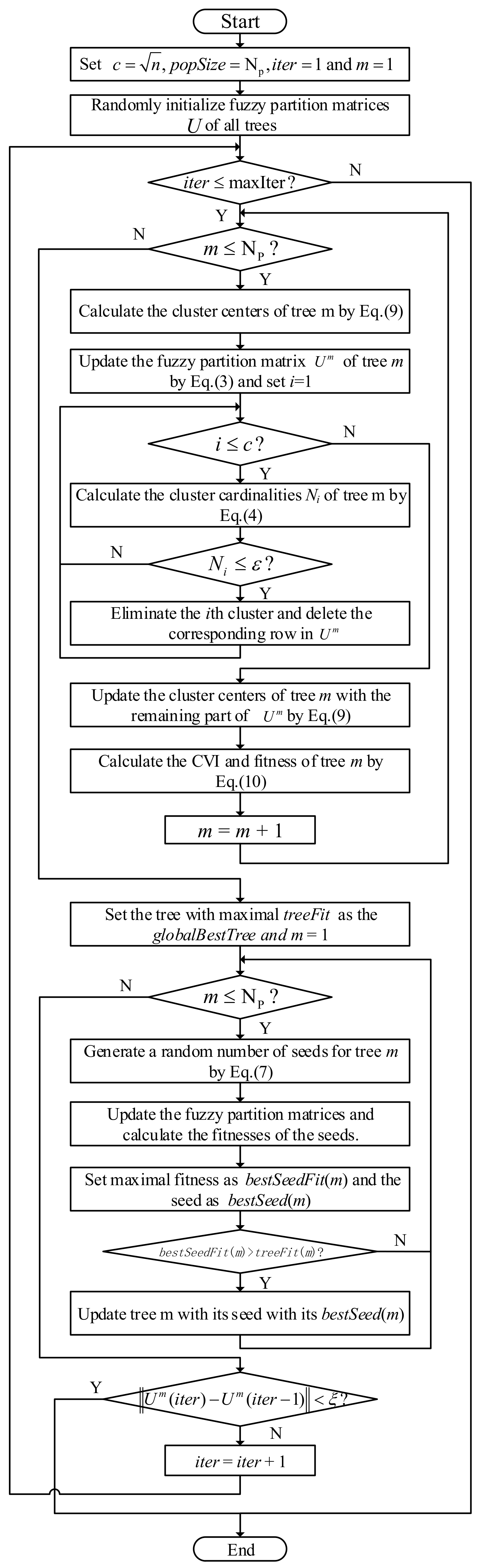
2.3. VTSA-CA Algorithm
- Step 1:
- Suppose a n×d dimensional dataset, where n and d represent the number of data samples and the dimension of each sample, respectively. As the rule of thumb, predefine the initial number of clusters as , set the size of trees to be and then randomly initialize the c×n dimensional fuzzy partition matrix for each tree in the population, where , denotes the fuzzy membership of the jth sample to the ith cluster center in tree m and subjects to and .
- Step 2:
- Calculate the initial cluster centers according to Equation (9) with the initial fuzzy partition and the data samples for each tree, respectively:where, and denotes the kth dimension of i-th cluster center in tree m.
- Step 3:
- Set the number of evolutionary iterations and start the evolutionary optimization iterations of VTSA-CA.
- Step 4:
- Update the fuzzy partition matrix of the data set using the update equation given in Equation (3) for each tree in the population.
- Step 5:
- Repeat the following cluster elimination operations for each tree: calculate the cardinalities of all the clusters by Equation (4). If there exists the clusters whose cardinalities are smaller than the predefined cluster cardinality threshold ε, then take these clusters as the redundant ones and discard them.
- Step 6:
- Delete the rows in the fuzzy partition matrix that correspond to the eliminated clusters for each tree.
- Step 7:
- Update the locations of cluster centers with the remaining part of the fuzzy memberships by Equation (9) repeatedly for all trees and take them as the current solution of VTSA-CA.
- Step 8:
- Define a cluster validity index (CVI) to evaluate the comprehensive compactness and concision performances of the fuzzy partition (see Equation (10A)). Calculate the CVI and the fitness of each tree in the population with the cluster centers, the data samples and the fuzzy partition matrix using the following Equation (10). Set the tree with minimal fitness as the global best tree in this iteration and record the cluster number of the global best tree as the current number of clusters c. Then, Set the number of evolutionary iterations :
- Step 9:
- If iter reaches the predefined maximum iteration, end the optimization algorithm, else, go to Step 10.
- Step 10:
- If the optimal number of clusters c in the current iteration is equivalent to that in the last iteration and the square root of sum of squares of errors of the fuzzy partition matrix between the last two iterations (see Equation (11)) is smaller than the predefined variation threshold , end the algorithm, else, continue to Step 11:
- Step 11:
- Generate a random number of seeds for every tree referring to the seed production equations in Equation (7). Then, obtain the fuzzy partition matrices of the seeds and calculate their fitnesses. If the best fitness of the seeds is larger than that of its mother tree, replace the location of the tree with that of the best seed, if not, remain the location of the tree. Then repeat this operation for all trees in the population.
- Step 12:
- Go back to Step 4.
3. VTSA-CA Based T-S Fuzzy Model
3.1. T-S Fuzzy Model
3.2. The Incorporation of VTSA-CA to T-S Fuzzy Model
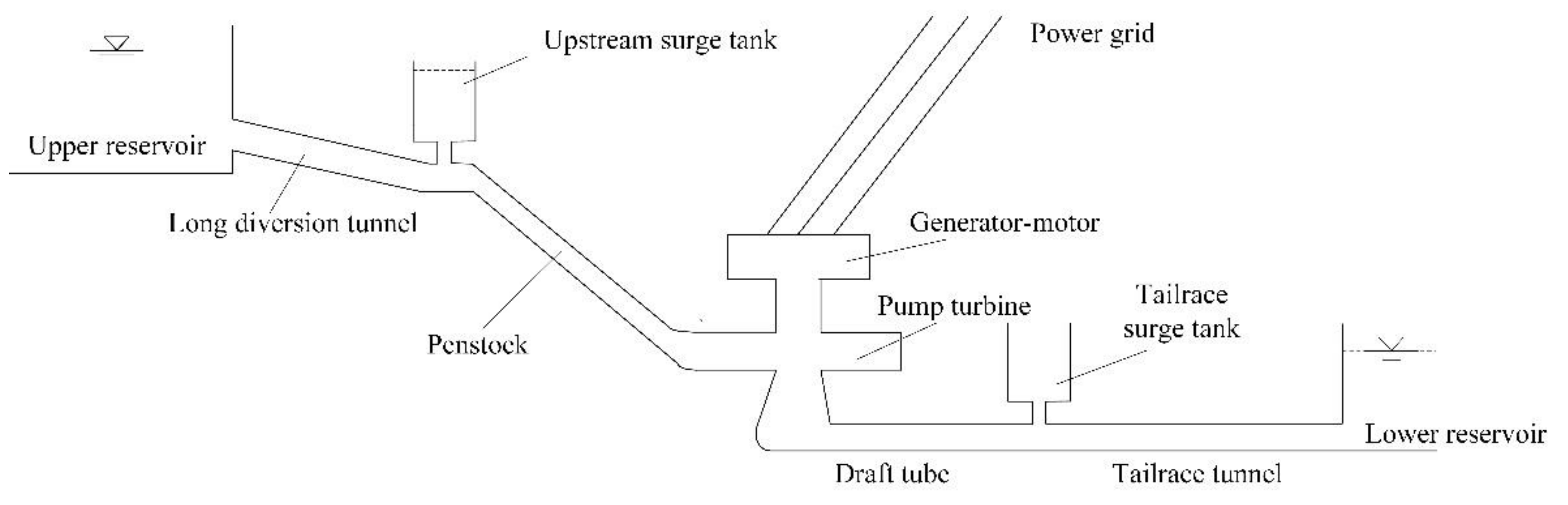
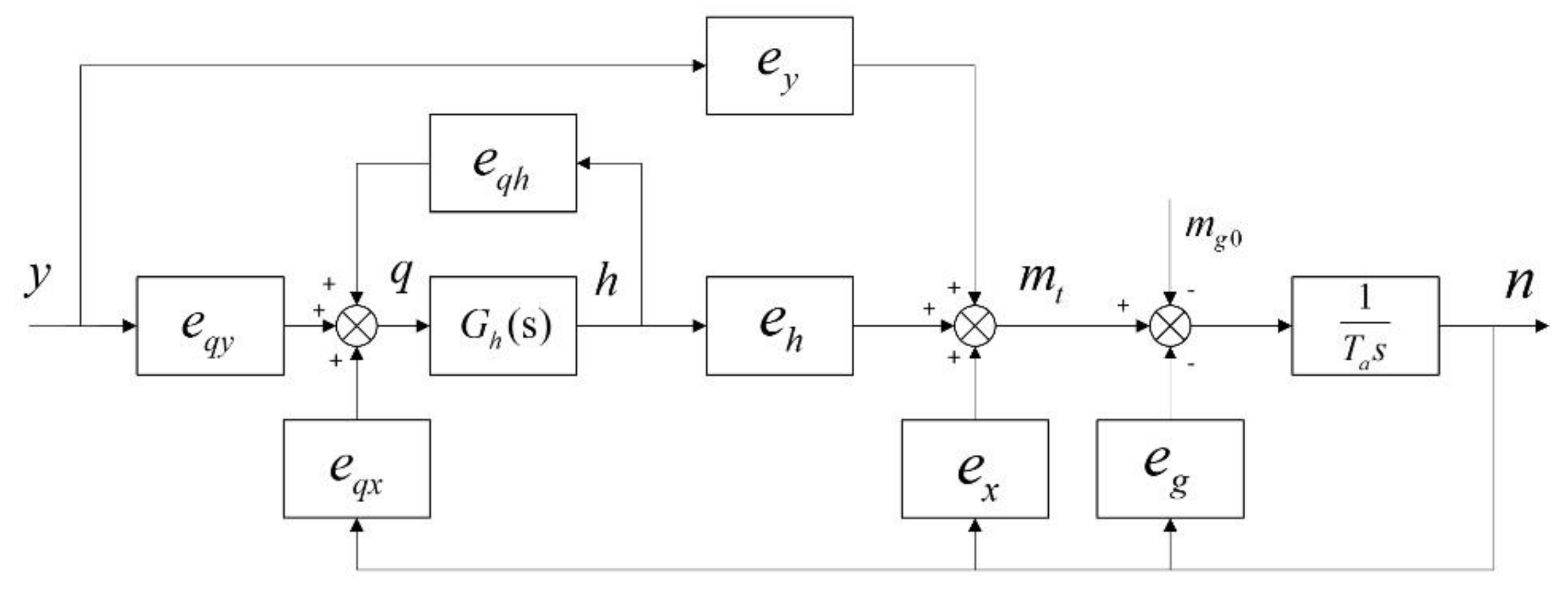
4. CAR Model of PSGM based on Precise Modeling of Water Diversion System
4.1. The Preliminary Transfer Function Based Order Determination of CAR Model
4.2. Parameter Reduction Using F-Test Strategy
- Step 1:
- Determine the time delay of the original CAR model : delete the parameters in the controlled term one by one successively from to by iterations. In the i-th iteration, whether the parameter should be deleted or not is judged by two F-tests. The economical parameter CAR model without is used to make comparison with the economical parameter CAR model with and original CAR model with no parameter discarded, respectively. Only if both of the two F-test results are acceptable, the parameter can be deleted from the controlled parameter sequence. And then the time delay is updated as . Once the is considered to be preserved in the CAR model (namely anyone of the two F-tests is not passed), the iterations of time delay are ended and the time delay is set as .
- Step 2:
- Record the economical parameter model as considering the time delay determined by Step 1.
- Step 3:
- Determine the redundant controlled parameters: delete the rest controlled parameters one by one in in the inverted order from to by iterations. In the j-th iteration, whether should be deleted from is judged by the F-test between the economical parameter model with the parameter and the economical parameter model without it. If , can be deleted from due to the parameter-saving principle, then replace with the economical model without the parameter and go to the next iteration. Else, the parameter should be preserved in and step to the next iteration.
- Step 4:
- Record the economical parameter model as considering both the time delay determined by Step 1 and the redundant controlled parameters reduction by Step 3.
- Step 5:
- Determine the redundant autoregressive parameters: delete the autoregressive parameters one by one in in the inverted order from to by iterations. In the p-th iteration, whether should be deleted from is judged by the F-test between the economical model with the parameter and the economical model without it. If , can be deleted from , then replace with the economical model without the parameter and go to the next iteration. Else, the parameter should be preserved in and step to the next iteration.
- Step 6:
- Record the economical parameter model as considering the time delay, the redundant parameters of both autoregressive and controlled parameters. is therefore considered as the final economical parameter CAR model of PSGM system.
4.3. The Issues for Model Application in PSGM
5. Model Validation and Result Analysis
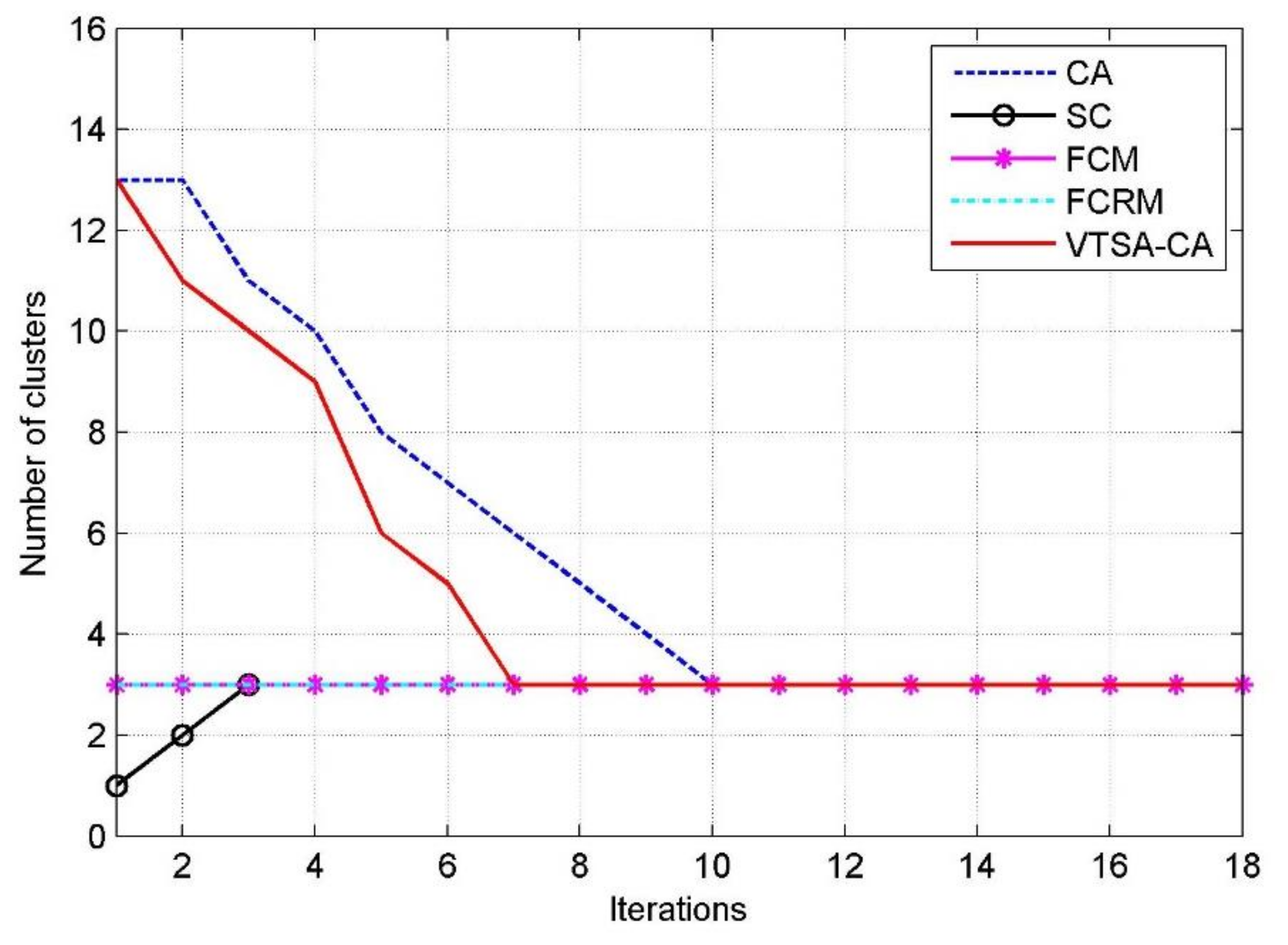
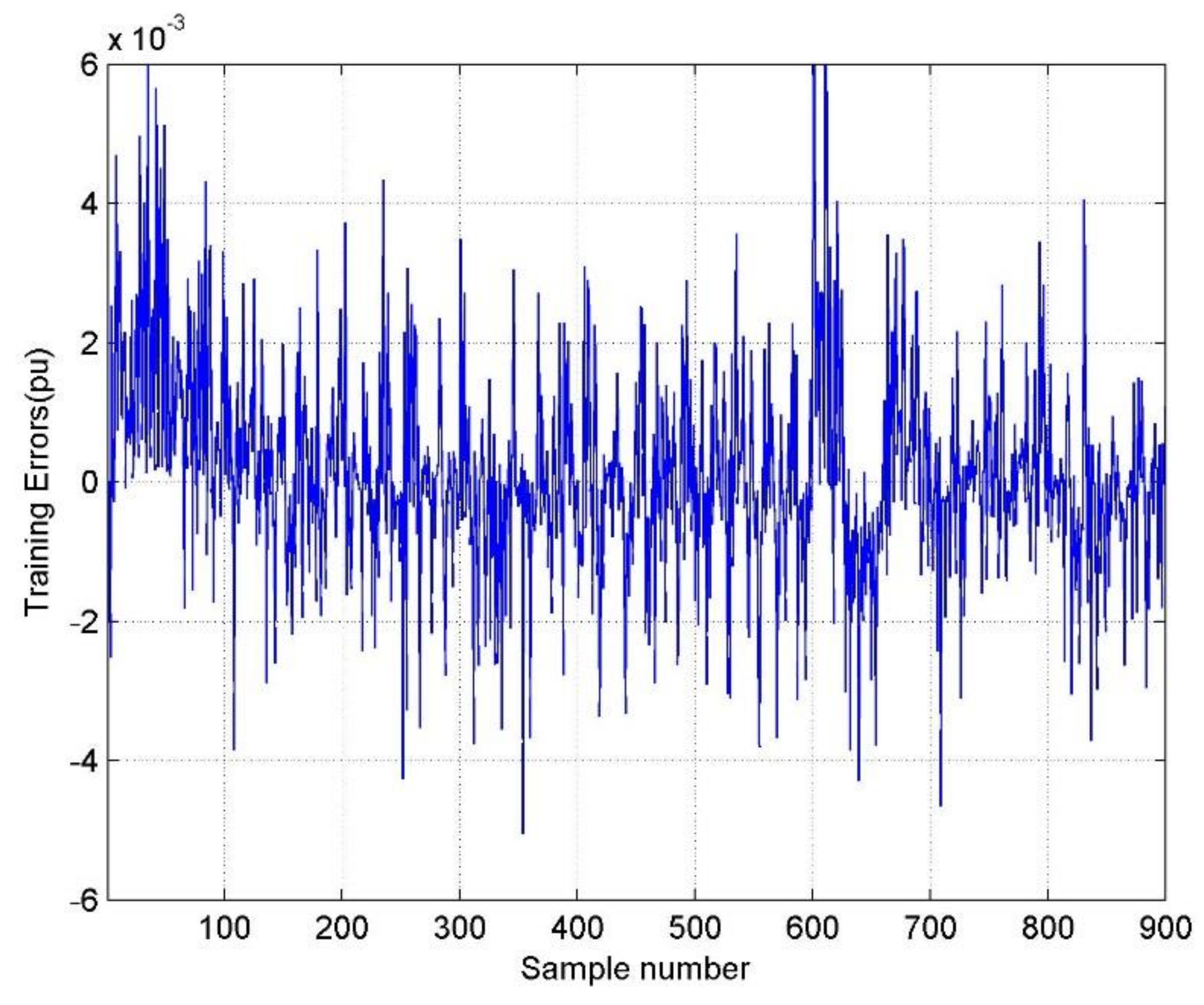
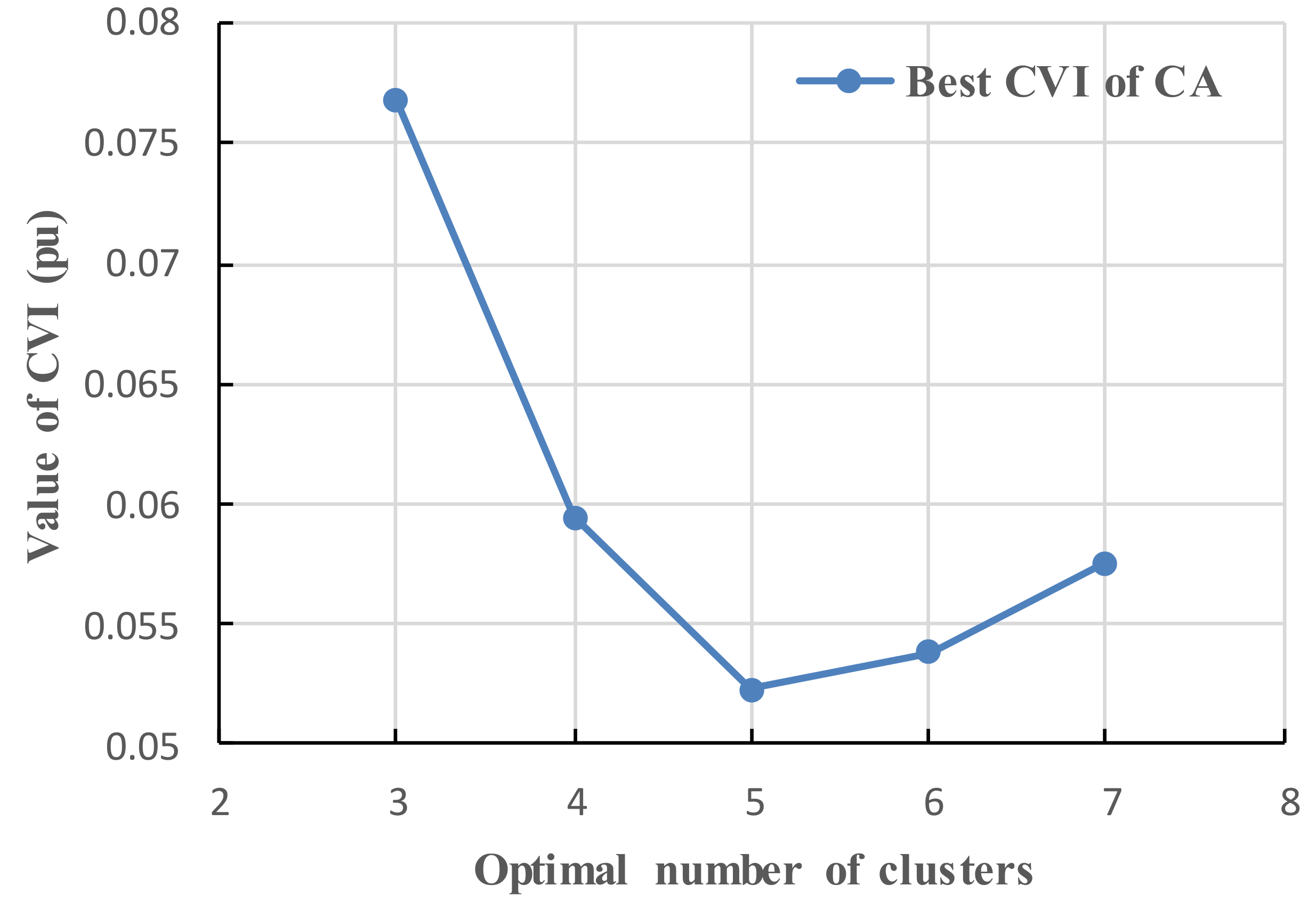
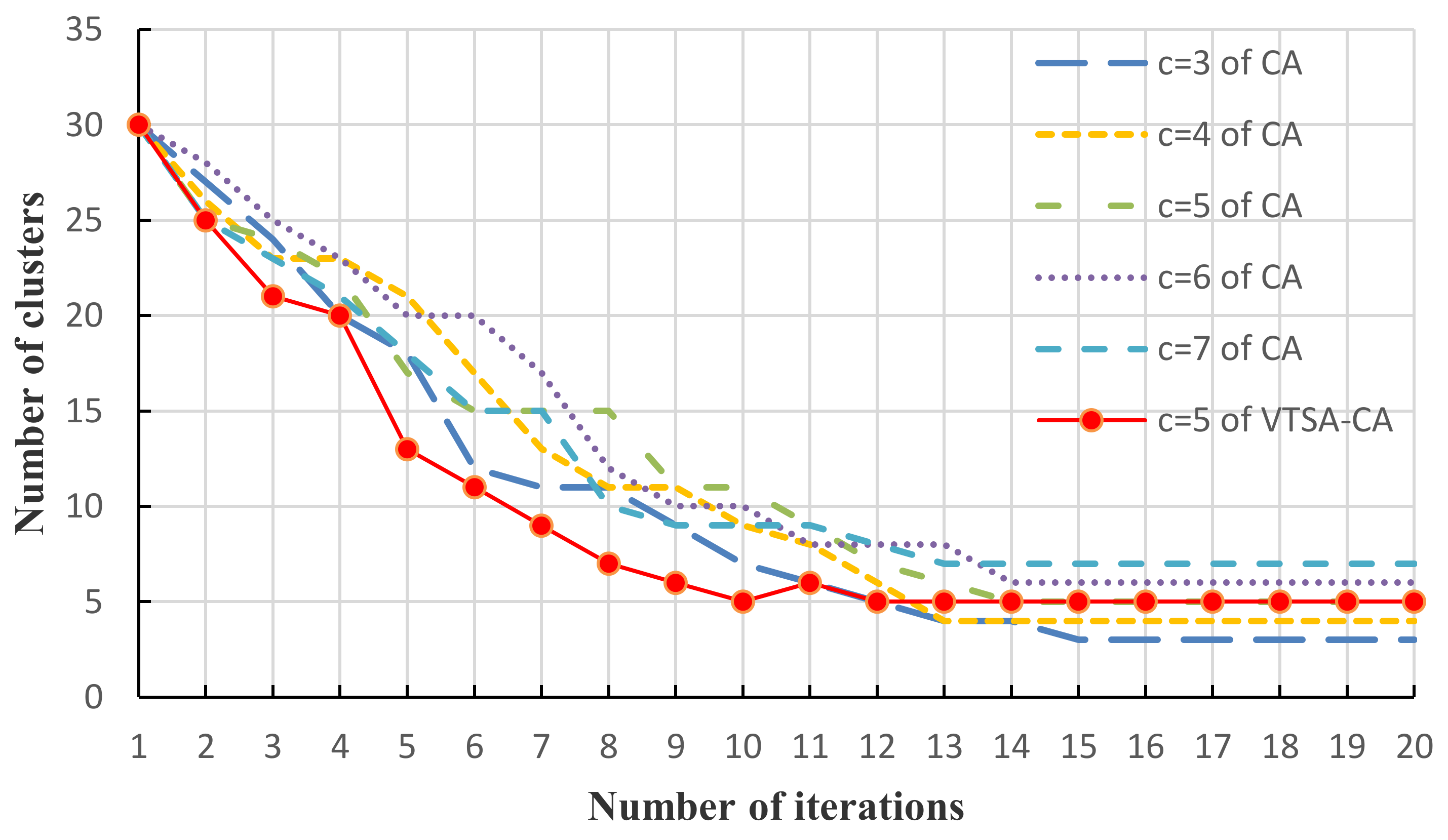
5.1. Results of the Premise Identification of T-S Fuzzy Model
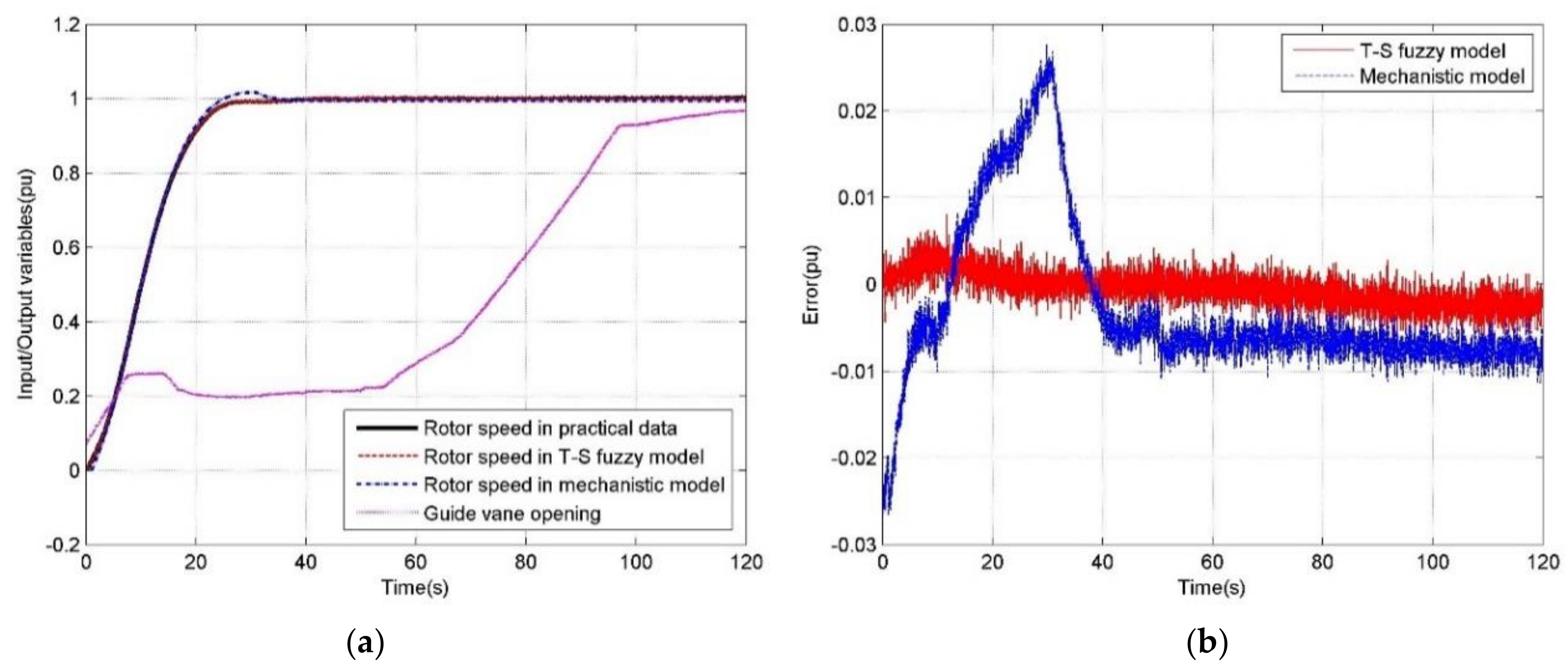
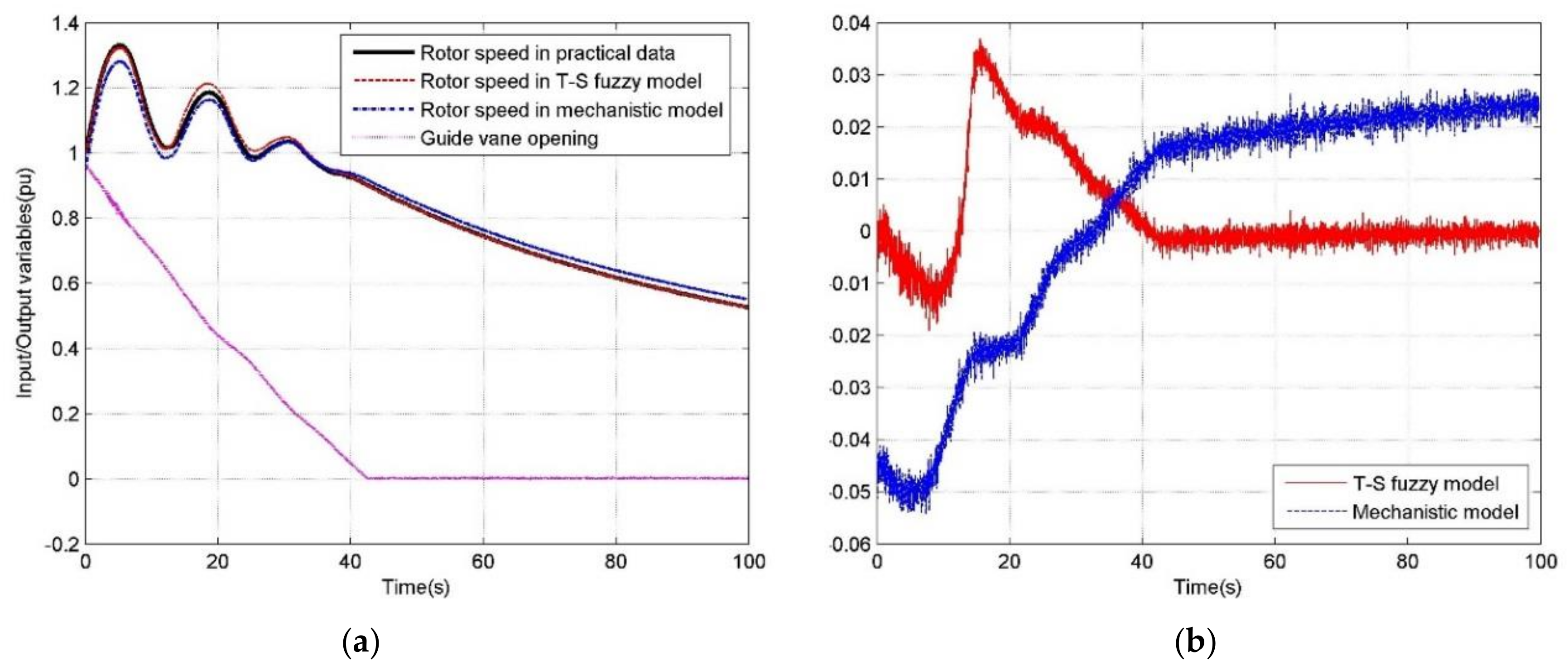
5.2. Simulations under Different Operating Conditions
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
References
- Yang, W.; Yang, J.; Guo, W.; Zeng, W.; Wang, C.; Saarinen, L.; Norrlund, P. A Mathematical Model and Its Application for Hydro Power Units under Different Operating Conditions. Energies 2015, 8, 10260–10275. [Google Scholar] [CrossRef]
- Chaudhry, M. Applied Hydraulic Transients; Van Nostrand Reinhold Co.: New York, NY, USA, 1979. [Google Scholar]
- Derakhshan, S.; Nourbakhsh, A. Experimental study of characteristic curves of centrifugal pumps working as turbines in different specific speeds. Exp. Therm. Fluid Sci. 2008, 32, 800–807. [Google Scholar] [CrossRef]
- Yoo, I.; Park, M.; Hwang, S.; Yoon, E. Complete Characteristic Curve for a Reactor Coolant Pump. J. Fluid Mach. 2012, 15, 5–10. [Google Scholar] [CrossRef]
- Zheng, X.; Guo, P.; Tong, H.; Luo, X. Improved Suter-transformation for complete characteristic curves of pump-turbine. In Proceedings of the 26th Iahr Symposium On Hydraulic Machinery And Systems, Beijing, China, 19–23 August 2012; Volume 15, p. 062015. [Google Scholar]
- Izquierdo, J.; Iglesias, P. Mathematical modelling of hydraulic transients in simple systems. Math. Comput. Model. 2002, 35, 801–812. [Google Scholar] [CrossRef]
- Nicolet, C.; Greiveldinger, B.; Herou, J.; Kawkabani, B.; Allenbach, P.; Simond, J.; Avellan, F. High-Order Modeling of Hydraulic Power Plant in Islanded Power Network. IEEE Trans. Power Syst. 2007, 22, 1870–1880. [Google Scholar] [CrossRef]
- Sim, W.G.; Park, J. Transient analysis for compressible fluid flow in transmission line by the method of characteristics. J. Mech. Sci. Technol. 1997, 11, 173–185. [Google Scholar] [CrossRef]
- Souza, O.H.; Barbieri, N.; Santos, A. Study of hydraulic transients in hydropower plants through simulation of nonlinear model of penstock and hydraulic turbine model. IEEE Trans. Power. Syst. 1999, 14, 1269–1272. [Google Scholar] [CrossRef]
- Fang, H.; Chen, L.; Dlakavu, N.; Shen, Z. Basic Modeling and Simulation Tool for Analysis of Hydraulic Transients in Hydroelectric Power Plants. IEEE Trans. Energy Convers. 2008, 23, 834–841. [Google Scholar] [CrossRef]
- Guo, W.; Yang, J.; Chen, J.; Wang, M. Nonlinear modeling and dynamic control of hydro-turbine governing system with upstream surge tank and sloping ceiling tailrace tunnel. Nonlinear Dyn. 2016, 84, 1383–1397. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J. Parameters identification of hydraulic turbine governing system using improved gravitational search algorithm. Energy Convers. Manag. 2011, 52, 374–381. [Google Scholar] [CrossRef]
- Strah, B.; Kuljaca, O.; Vukic, Z. Speed and active power control of hydro turbine unit. IEEE Trans. Energy Convers. 2005, 20, 424–434. [Google Scholar] [CrossRef]
- Zeng, W.; Yang, J.; Yang, W. Instability analysis of pumped-storage stations under no-load conditions using a parameter-varying model. Renew. Energy 2016, 90, 420–429. [Google Scholar] [CrossRef]
- Liu, Y.; Fang, Y. BGNN Neural Network Based on Improved E.Coli Foraging Optimization Algorithm Used in the Nonlinear Modeling of Hydraulic Turbine. Int. Symp. Neural Netw. Adv. Neural Netw. 2009, 5551, 624–634. [Google Scholar]
- Yi, J.; Yan, J.; Fang, X. Modeling of hydraulic turbine systems based on a Bayesian-Gaussian neural network driven by sliding window data. Front. Inf. Technol. Electron. Eng. 2010, 11, 56–62. [Google Scholar]
- Chen, R.; Zhen, J.; Liu, Y. Inverse Model Design of Hydraulic Turbine System Using Bayesian Inferring Method. Intell. Syst. 2011, 2, 87–91. [Google Scholar]
- Lin, L.; Zhong, S.; Xie, X. A Type Design Method of Large Hydraulic Turbine Based on the Gaussian Mixture Model. Prz. Elektrotechniczn. 2012, 88, 153–156. [Google Scholar]
- Zhong, S.; Wang, T.; Ding, G.; Bu, L. Multi-attribute grey fuzzy optimized decision-making model of large-scale hydraulic turbine design scheme. Comput. Integr. Manuf. Syst. 2008, 14, 1905–1912. [Google Scholar]
- Li, C.; Zhou, J.; Xiang, X.; Li, Q.; An, X. T–S fuzzy model identification based on a novel fuzzy c-regression model clustering algorithm. Eng. Appl. Artif. Intell. 2009, 22, 646–653. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J.; Xiao, J.; Xiao, H. Hydraulic turbine governing system identification using T–S fuzzy model optimized by chaotic gravitational search algorithm. Eng. Appl. Artif. Intell. 2013, 26, 2073–2082. [Google Scholar] [CrossRef]
- Sugeno, M.; Yasukawa, T. A fuzzy-logic-based approach to qualitative modeling. IEEE Trans. Fuzzy Syst. 1993, 1, 7. [Google Scholar] [CrossRef]
- Kim, E.; Park, M.; Ji, S.; Park, M. A new approach to fuzzy modeling. IEEE Trans. Fuzzy Syst. 1997, 5, 328–337. [Google Scholar]
- Kim, E.; Park, M.; Kim, S.; Park, M. A transformed input-domain approach to fuzzy modeling. IEEE Trans. Fuzzy Syst. 1998, 6, 596–604. [Google Scholar]
- Du, H.; Zhang, N. Application of evolving Takagi-Sugeno fuzzy model to nonlinear system identification. Appl. Soft Comput. 2008, 8, 676–686. [Google Scholar] [CrossRef]
- Du, Y.; Lu, X.; Chen, L.; Zeng, W. An interval type-2 T-S fuzzy classification system based on PSO and SVM for gender recognition. Multimedia Tools Appl. 2016, 75, 987–1007. [Google Scholar] [CrossRef]
- Su, Z.; Wang, P.; Shen, J.; Zhang, Y.; Chen, L. Convenient T–S fuzzy model with enhanced performance using a novel swarm intelligent fuzzy clustering technique. J. Process Control 2012, 22, 108–124. [Google Scholar] [CrossRef]
- Niu, B.; Li, L. Design of T-S Fuzzy Model Based on PSODE Algorithm. Int. Conf. Intell. Comput. 2008, 5227, 384–390. [Google Scholar]
- Su, H.; Yang, Y. Differential evolution and quantum-inquired differential evolution for evolving Takagi–Sugeno fuzzy models. Expert Syst. Appl. 2011, 38, 6447–6451. [Google Scholar] [CrossRef]
- Frigui, H.; Krishnapuram, R. Clustering by competitive agglomeration. Pattern Recogn. 1997, 30, 1109–1119. [Google Scholar] [CrossRef]
- Gandy, L.; Rahimi, S.; Gupta, B. A modified competitive agglomeration for relational data algorithm. In Proceedings of the Annual Meeting of the North-American-Fuzzy-Information-Processing-Society, Detroit, MI, USA, 26–28 June 2005; pp. 210–215. [Google Scholar]
- Jeng, J.; Chuang, C.; Tao, C. Interval competitive agglomeration clustering algorithm. Int. J. Fuzzy Syst. 2010, 37, 6567–6578. [Google Scholar] [CrossRef]
- Zhao, L.; Qian, F.; Yang, Y.; Zeng, Y.; Su, H. Automatically extracting T–S fuzzy models using cooperative random learning particle swarm optimization. Appl. Soft Comput. 2010, 10, 938–944. [Google Scholar] [CrossRef]
- Srikanth, R.; George, R.; Warsi, N.; Prabhu, D.; Petry, F.; Buckles, B. A variable-length genetic algorithm for clustering and classification. Pattern Recogn. Lett. 1995, 16, 789–800. [Google Scholar] [CrossRef]
- Sjahputera, O.; Scott, G.; Claywell, B.; Klaric, M.N.; Hudson, N.J.; Keller, J.M.; Davis, C.H. Clustering of Detected Changes in High-Resolution Satellite Imagery Using a Stabilized Competitive Agglomeration Algorithm. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4687–4703. [Google Scholar] [CrossRef]
- Kiran, M.S. TSA: Tree-seed algorithm for continuous optimization. Expert Syst. Appl. 2015, 42, 6686–6698. [Google Scholar] [CrossRef]
- Kiran, M.S. An Implementation of Tree-Seed Algorithm (TSA) for Constrained Optimization. In Proceedings of the 19th Asia Pacific Symposium on Intelligent and Evolutionary Systems, Bangkok, Thailand, 22–25 November 2016; Volume 5, pp. 189–197. [Google Scholar]
- Takagi, T.; Sugeno, M. Fuzzy Identification of Systems and Its Applications to Modeling and Control. IEEE Trans. Syst. Cybern. 1985, 15, 387–403. [Google Scholar] [CrossRef]
- Pang, Z.; Cui, H. System Identification and Adaptive Control: The MATLAB Simulation, 1st ed.; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 2009. [Google Scholar]
- Zeng, Y.; Guo, Y.; Zang, L.; Xu, T.; Dong, H. Nonlinear hydro turbine model having a surge tank. Math. Comput. Model. Dyn. Syst. 2012, 19, 1–17. [Google Scholar] [CrossRef]
- Rawlings, J.; Mayne, D. Model Predictive Control: Theory and Design; Nob Hill Publishing LLC: Madison, WI, USA, 2000; pp. 3430–3433. [Google Scholar]
- Deng, Z. Structure Identification Of Multivariable Carma Models. Acta Autom. Sin. 1986, 12, 18–24. [Google Scholar]
- Wang, S.; Cui, H. Generalized F test for high dimensional linear regression coefficients. J. Multivar. Anal. 2013, 117, 134–149. [Google Scholar] [CrossRef]
- Steinberger, L. The relative effects of dimensionality and multiplicity of hypotheses on the F-test in linear regression. Electron. J. Stat. 2016, 10, 2584–2640. [Google Scholar] [CrossRef]
- Li, C.; Mao, Y.; Yang, J.; Wang, Z.; Xu, Y. A nonlinear generalized predictive control for pumped storage unit. Renew. Energy 2017, 114, 945–959. [Google Scholar] [CrossRef]


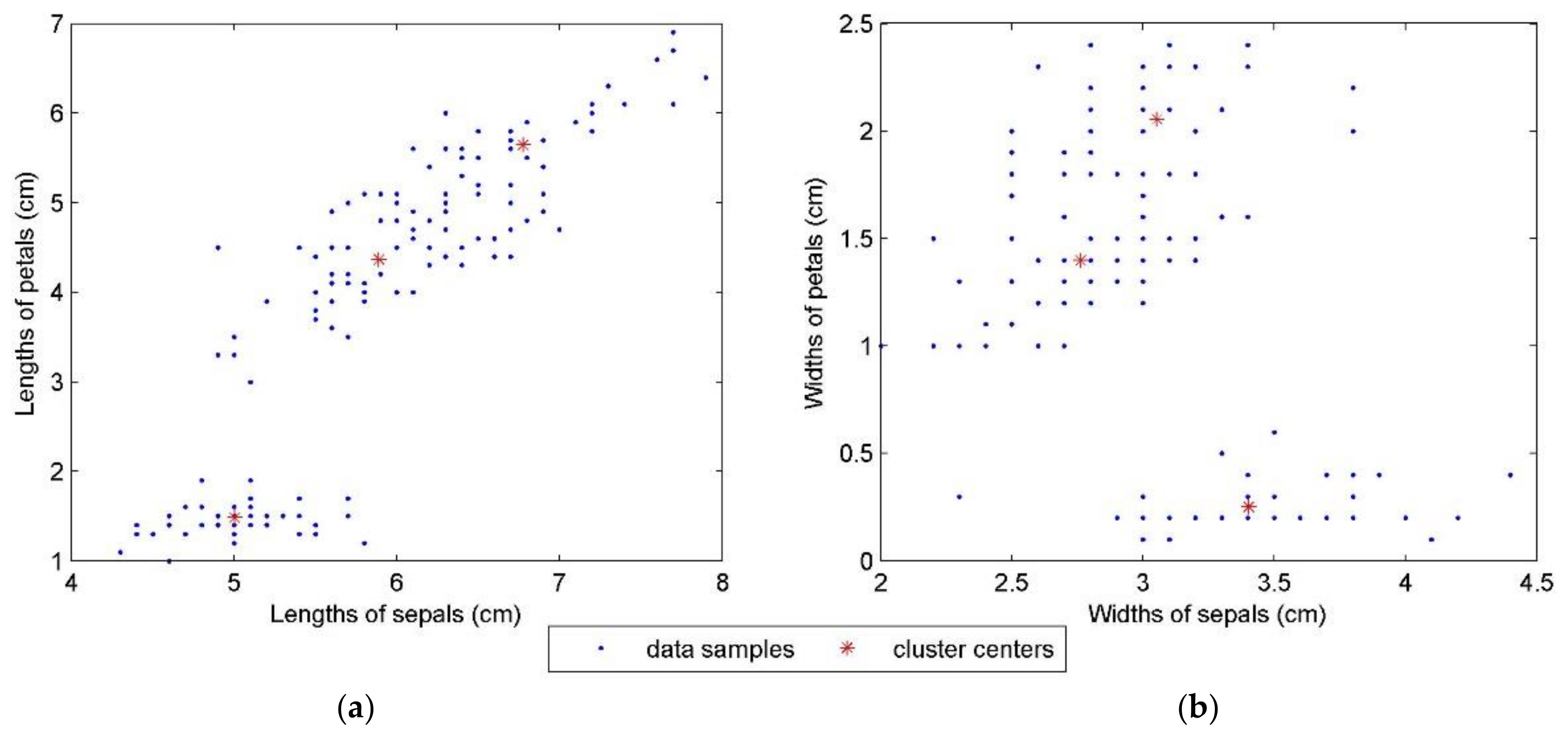
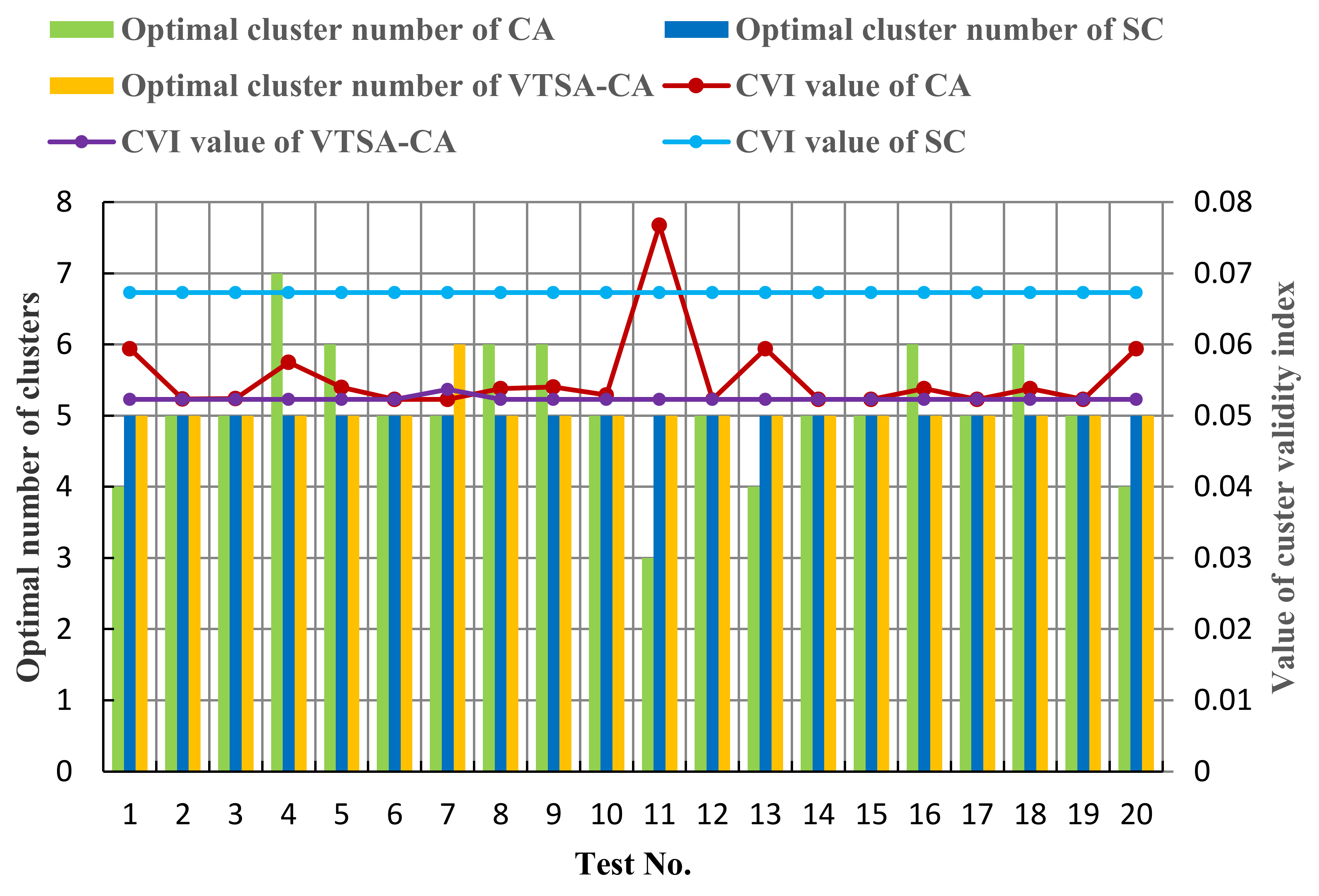
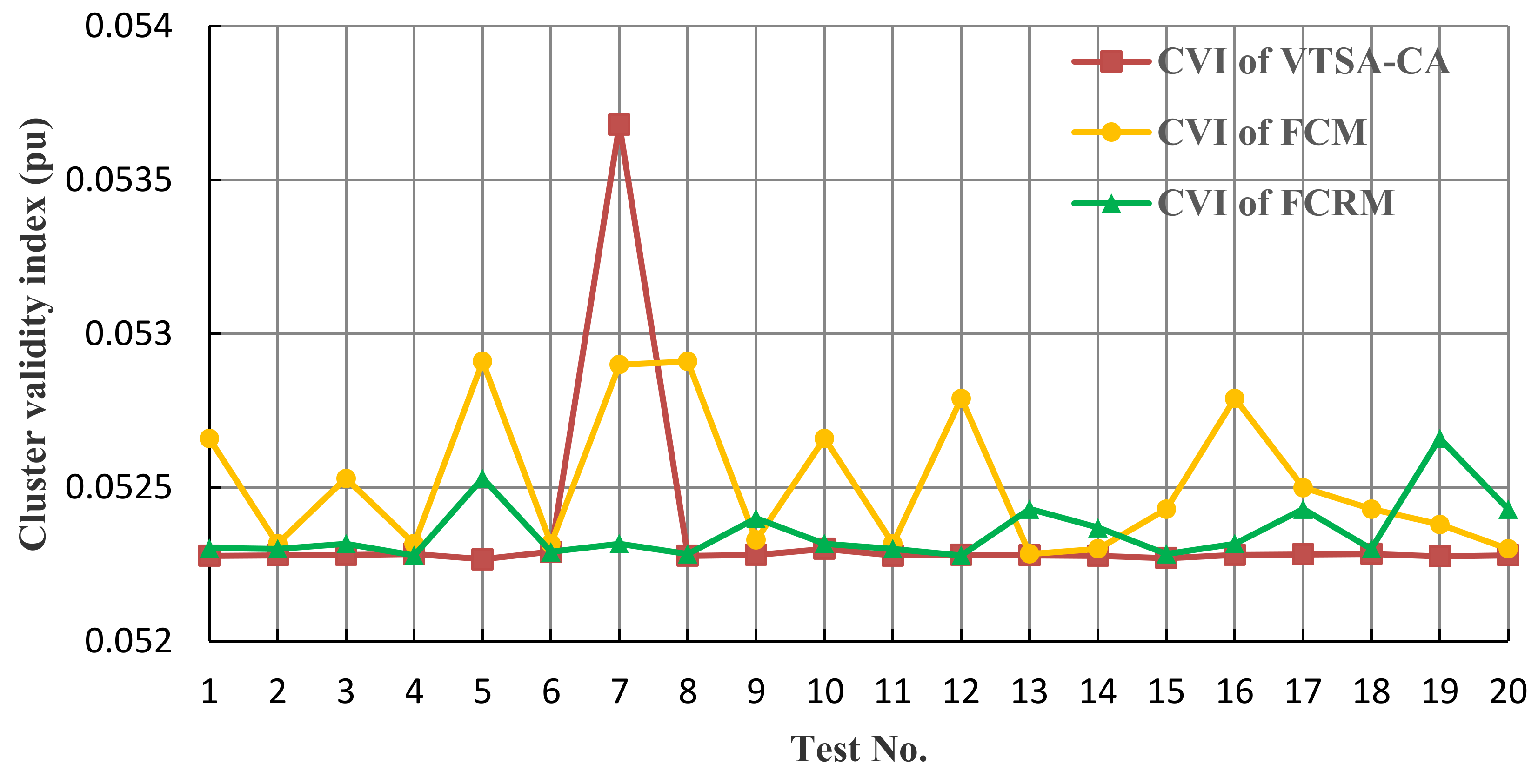

| Optimal c | Value of CVI | Locations of Cluster Centers |
|---|---|---|
| c = 2 | 0.066664 | v1 = (5.0209, 3.3732, 1.5653, 0.2851) |
| v2 = (5.0209, 3.3732, 1.5653, 0.2851) | ||
| c = 3 | 0.063019 | v1 = (5.0036, 3.4030, 1.4850, 0.2516) |
| v2 = (5.8897, 2.7614, 4.3650, 1.3978) | ||
| v3 = (6.7758, 3.0526, 5.6478, 2.0540) | ||
| c = 4 | 0.073146 | v1 = (6.2560, 2.8862, 4.9138, 1.6960) |
| v2 = (7.0072, 3.1043, 5.8971, 2.1183) | ||
| v3 = (5.0000, 3.4070, 1.4722, 0.2454) | ||
| v4 = (5.6387, 2.6562, 4.0253, 1.2421) | ||
| c = 5 | 0.086057 | v1 = (5.5853, 2.6169, 3.9494, 1.2122) |
| v2 = (6.5256, 3.0376, 5.4476, 2.0845) | ||
| v3 = (7.4382, 3.0797, 6.2781, 2.0529) | ||
| v4 = (6.1908, 2.8780, 4.7102, 1.5573) | ||
| v5 = (4.9981, 3.4060, 1.4701, 0.2440) | ||
| c = 6 | 0.100100 | v1 = (5.2554, 3.6803, 1.5062, 0.2794) |
| v2 = (7.4489, 3.0757, 6.2910, 2.0536) | ||
| v3 = (4.7574, 3.1440, 1.4423, 0.2037) | ||
| v4 = (5.6131, 2.6331, 3.9972, 1.2274) | ||
| v5 = (6.2006, 2.8751, 4.7358, 1.5719) | ||
| v6 = (6.5366, 3.0433, 5.4633, 2.0950) |
| Condition Name | Number of Samples |
|---|---|
| Start-up to no-load operating process | 150 |
| Synchronizing process to rated load operation | 200 |
| Shut down process in generation direction | 50 |
| Load rejection from rated load state | 250 |
| Pump start to rated power in pumping direction | 20 |
| Shut down process in pumping direction | 30 |
| Pumping convert to generation transients | 200 |
| Model | Max Error | Min Error | SSE | MSE | RMSE | MAPE (%) |
|---|---|---|---|---|---|---|
| Mechanistic | 0.0277 | 0 | 0.5661 | 9.450 × 10−5 | 0.0097 | 2.2879 |
| T-S fuzzy | 0.0081 | 1.021 × 10−6 | 0.0267 | 4.457 × 10−6 | 0.0021 | 0.5517 |
| Model | Max Error | Min Error | SSE | MSE | RMSE | MAPE (%) |
|---|---|---|---|---|---|---|
| Mechanistic | 0.0542 | 1.425 × 10−5 | 2.893 | 5.797 × 10−4 | 0.0241 | 2.6416 |
| T-S fuzzy | 0.0370 | 1.096 × 10−6 | 0.552 | 1.106 × 10−4 | 0.0105 | 0.6149 |
| Model | Max Error | Min Error | SSE | MSE | RMSE | MAPE (%) |
|---|---|---|---|---|---|---|
| Mechanistic | 0.0376 | 0 | 1.1276 | 1.599 × 10−4 | 0.0126 | 6.1434 |
| T-S fuzzy | 0.0234 | 3.14 × 10−6 | 0.2243 | 3.182 × 10−5 | 0.0056 | 1.2219 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Zheng, Y.; Xu, Y.; Liu, H.; Chen, D. A Heuristic T-S Fuzzy Model for the Pumped-Storage Generator-Motor Using Variable-Length Tree-Seed Algorithm-Based Competitive Agglomeration. Energies 2018, 11, 944. https://doi.org/10.3390/en11040944
Zhou J, Zheng Y, Xu Y, Liu H, Chen D. A Heuristic T-S Fuzzy Model for the Pumped-Storage Generator-Motor Using Variable-Length Tree-Seed Algorithm-Based Competitive Agglomeration. Energies. 2018; 11(4):944. https://doi.org/10.3390/en11040944
Chicago/Turabian StyleZhou, Jianzhong, Yang Zheng, Yanhe Xu, Han Liu, and Diyi Chen. 2018. "A Heuristic T-S Fuzzy Model for the Pumped-Storage Generator-Motor Using Variable-Length Tree-Seed Algorithm-Based Competitive Agglomeration" Energies 11, no. 4: 944. https://doi.org/10.3390/en11040944
APA StyleZhou, J., Zheng, Y., Xu, Y., Liu, H., & Chen, D. (2018). A Heuristic T-S Fuzzy Model for the Pumped-Storage Generator-Motor Using Variable-Length Tree-Seed Algorithm-Based Competitive Agglomeration. Energies, 11(4), 944. https://doi.org/10.3390/en11040944





