Impulsive Noise Characterization in Narrowband Power Line Communication
Abstract
:1. Introduction
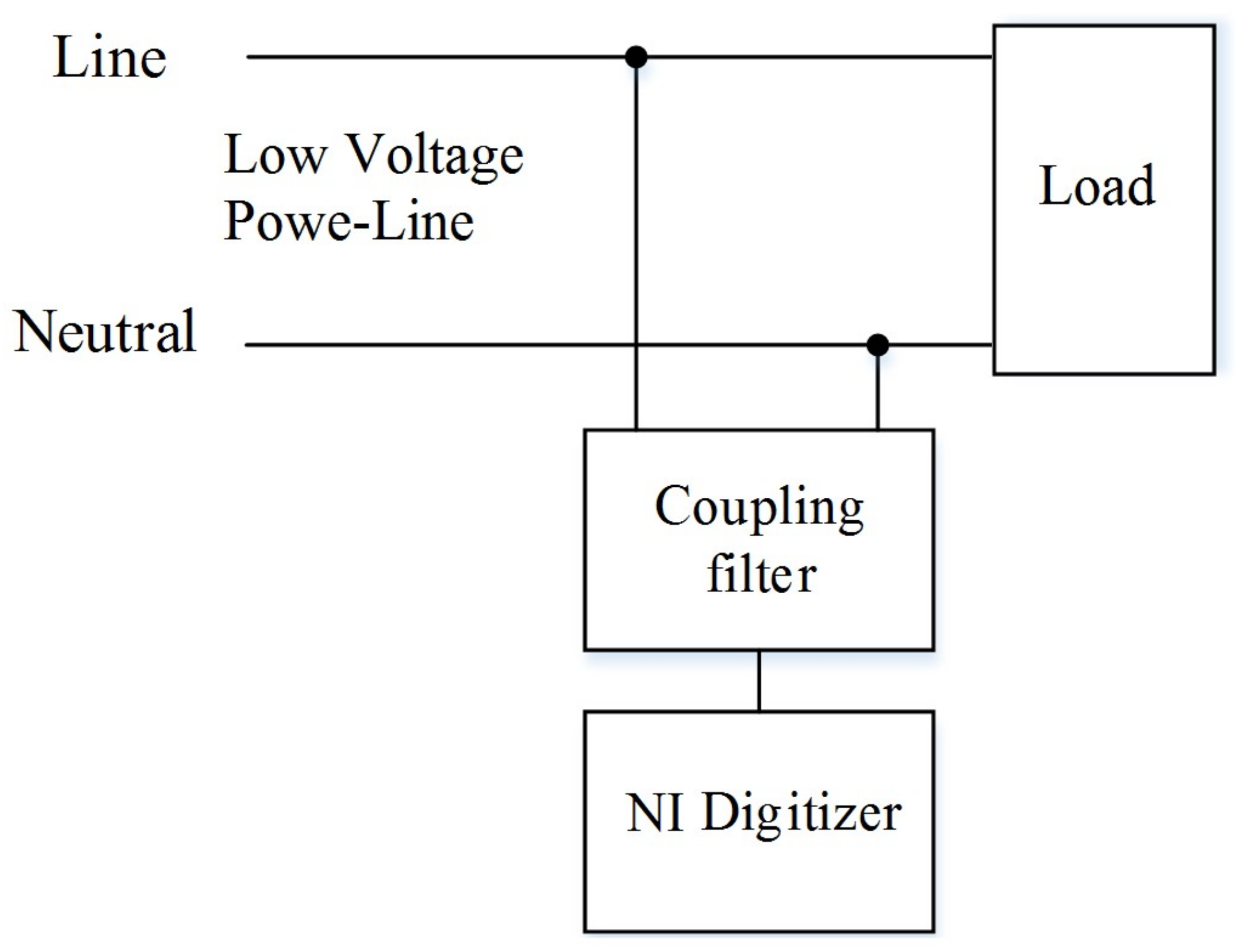
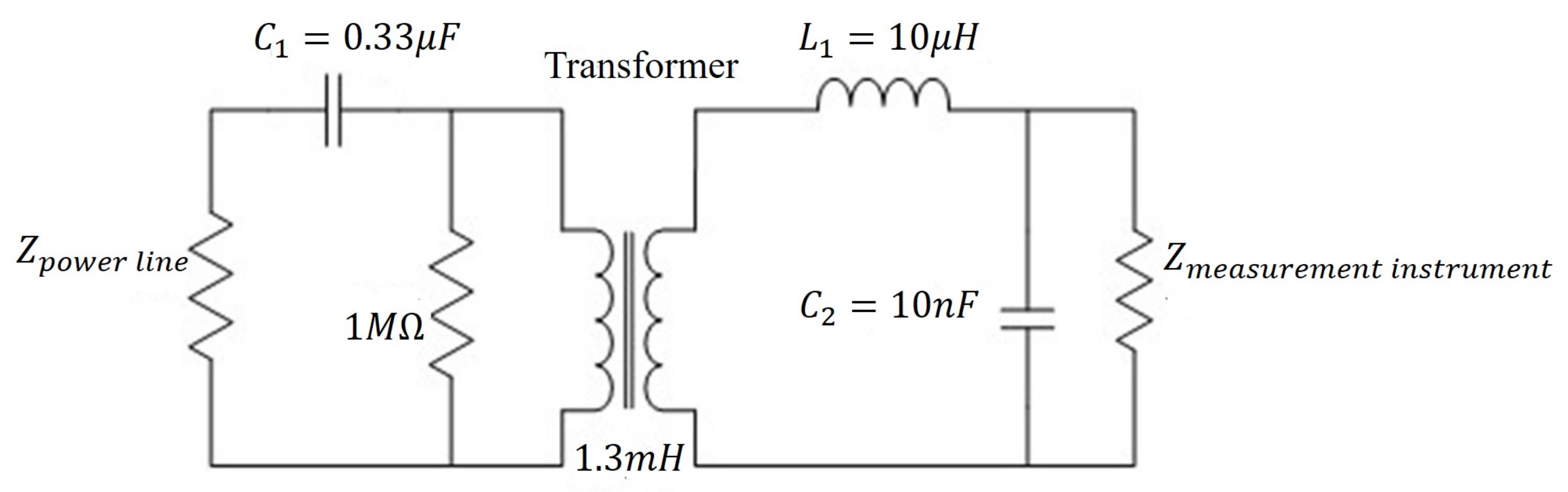
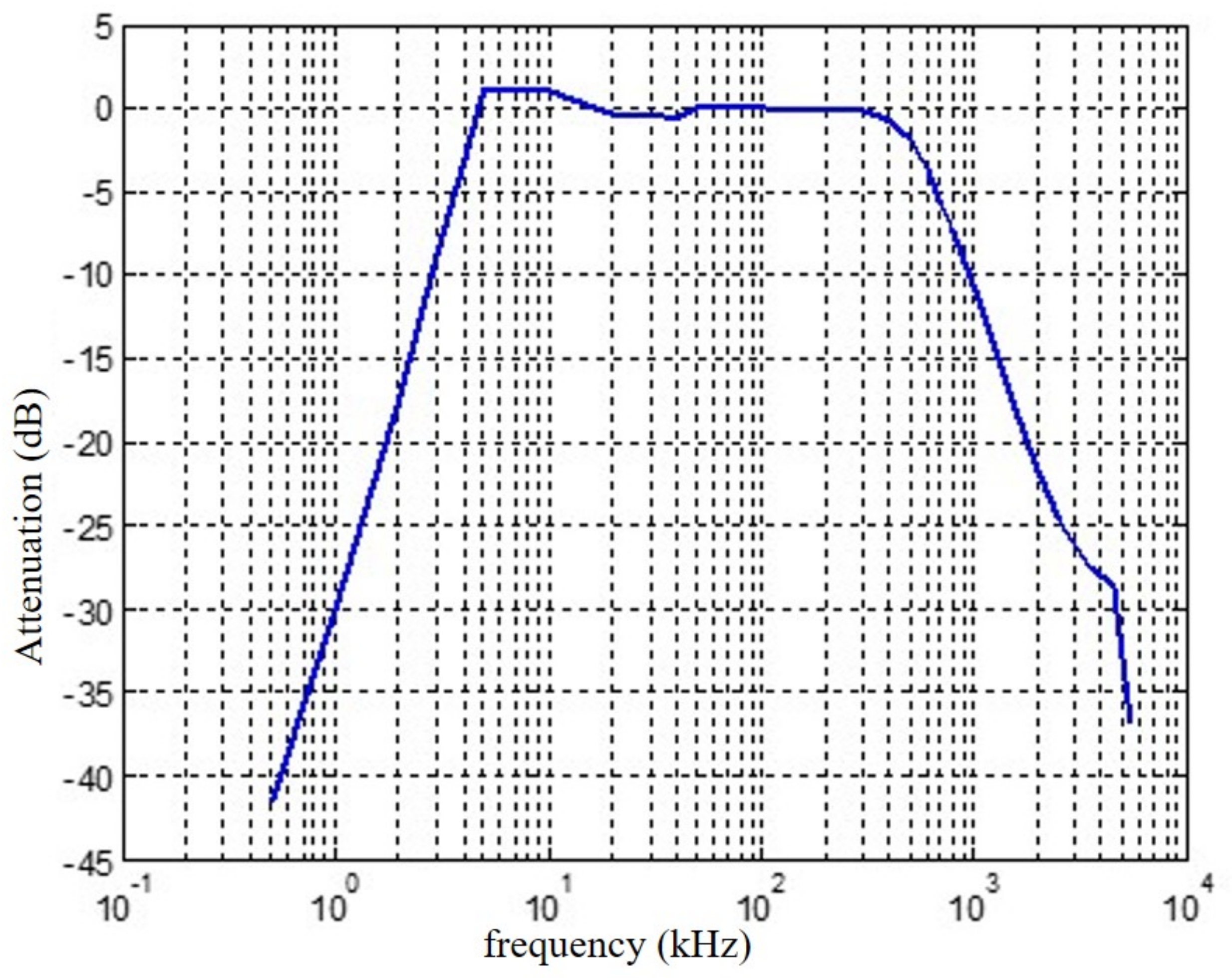
2. Measurement Setup in China and Itlay
3. Basic Time and Frequency Domain Analysis of Noise
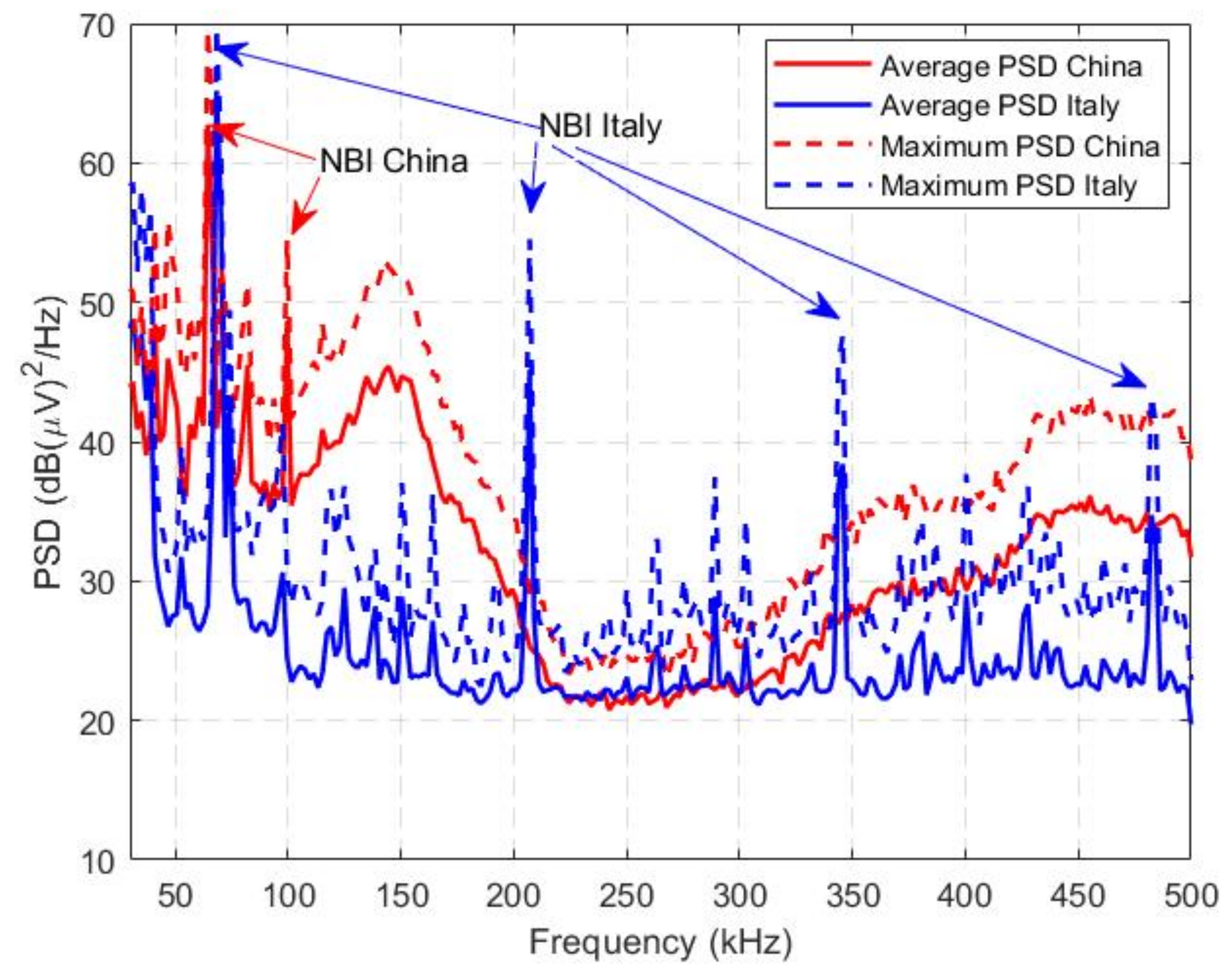
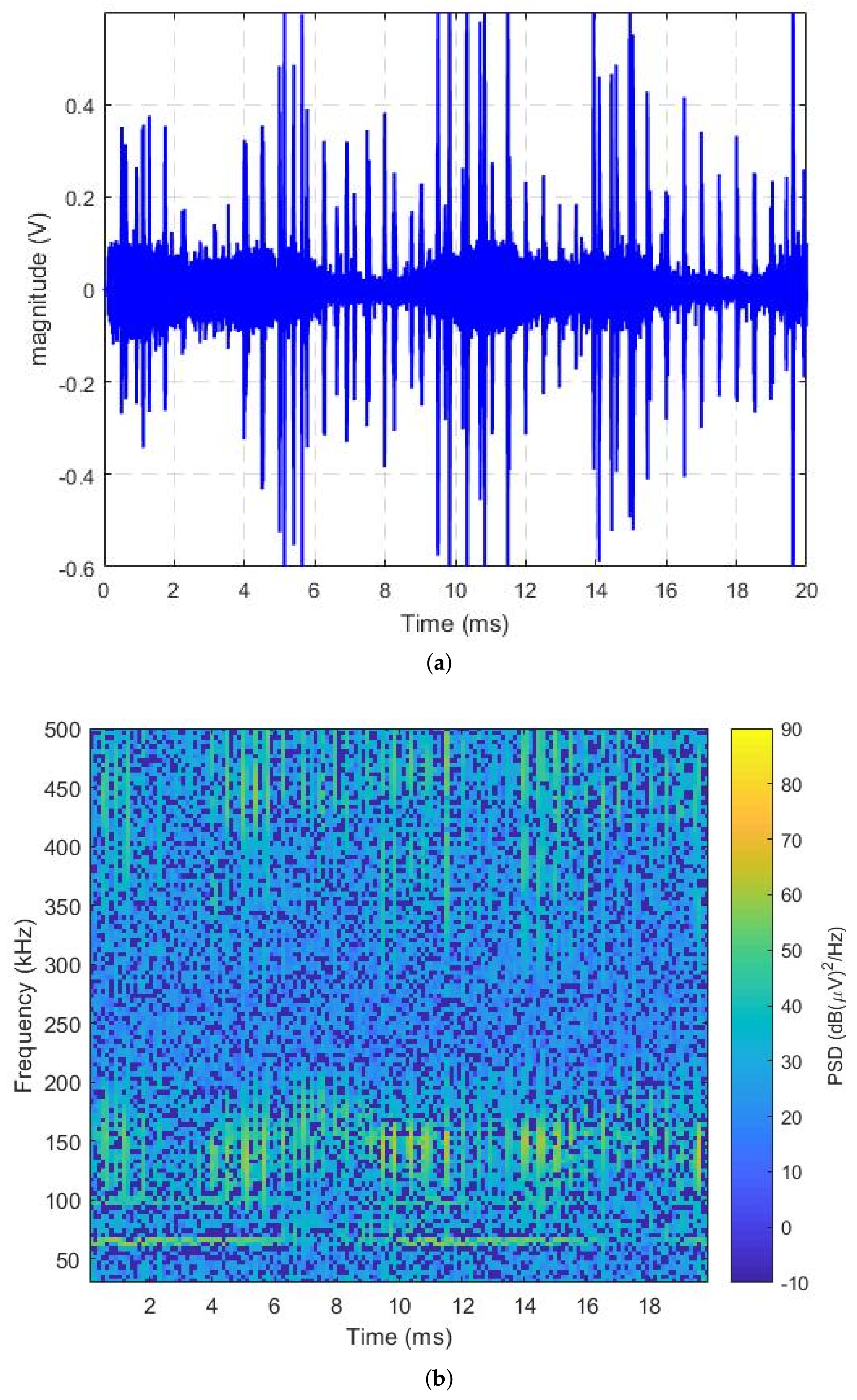
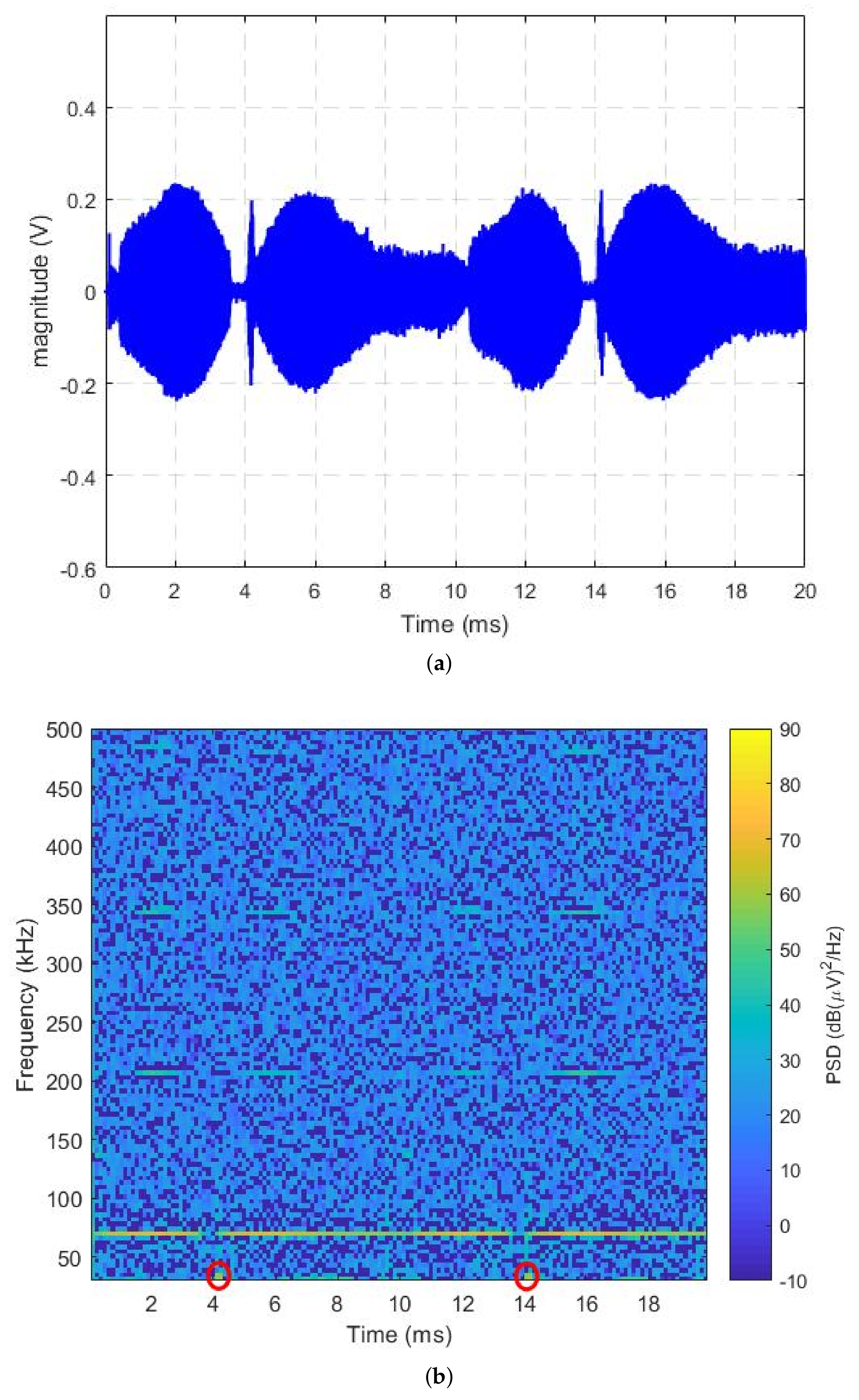
3.1. Power Spectrum Density Analysis
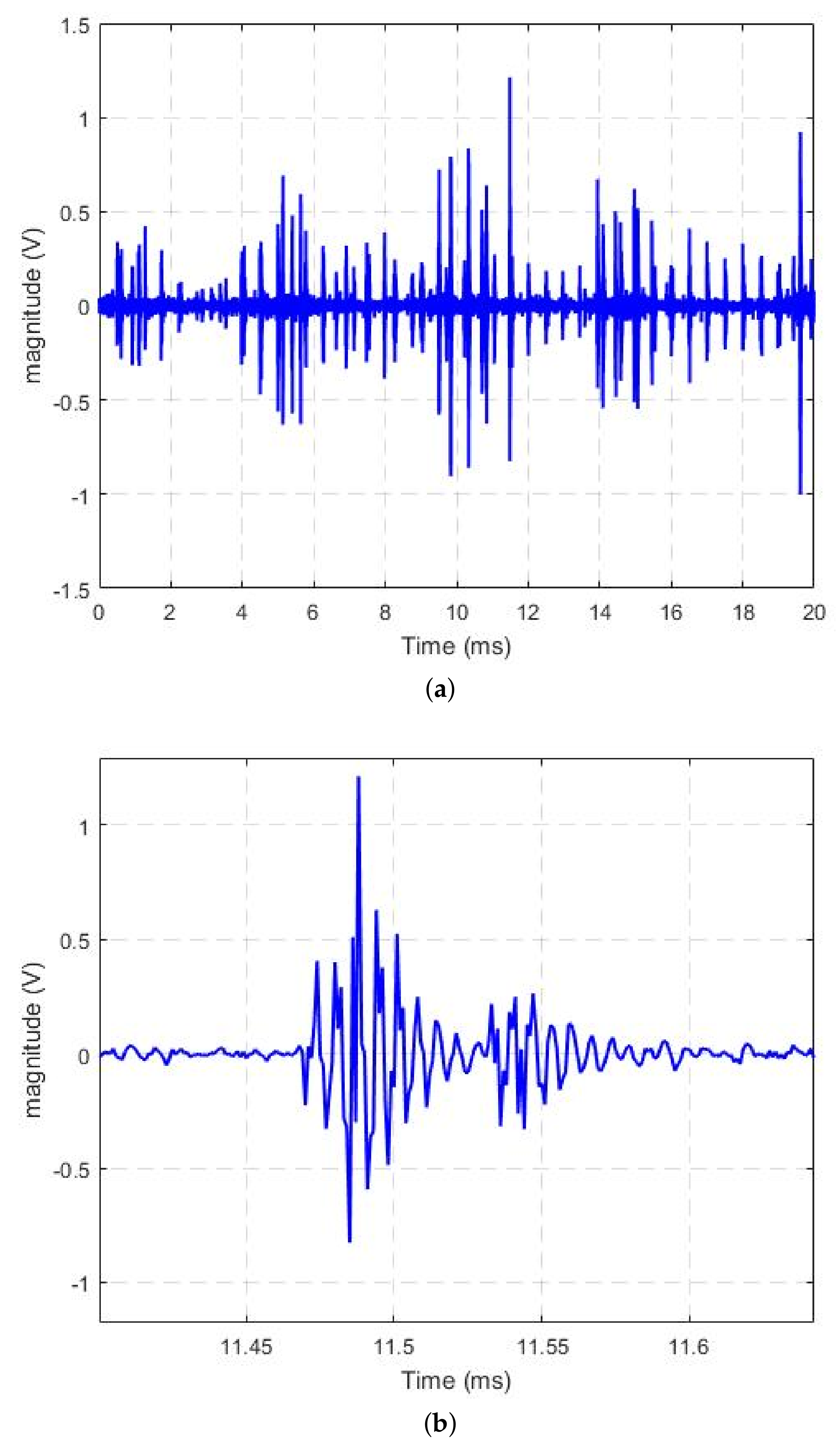
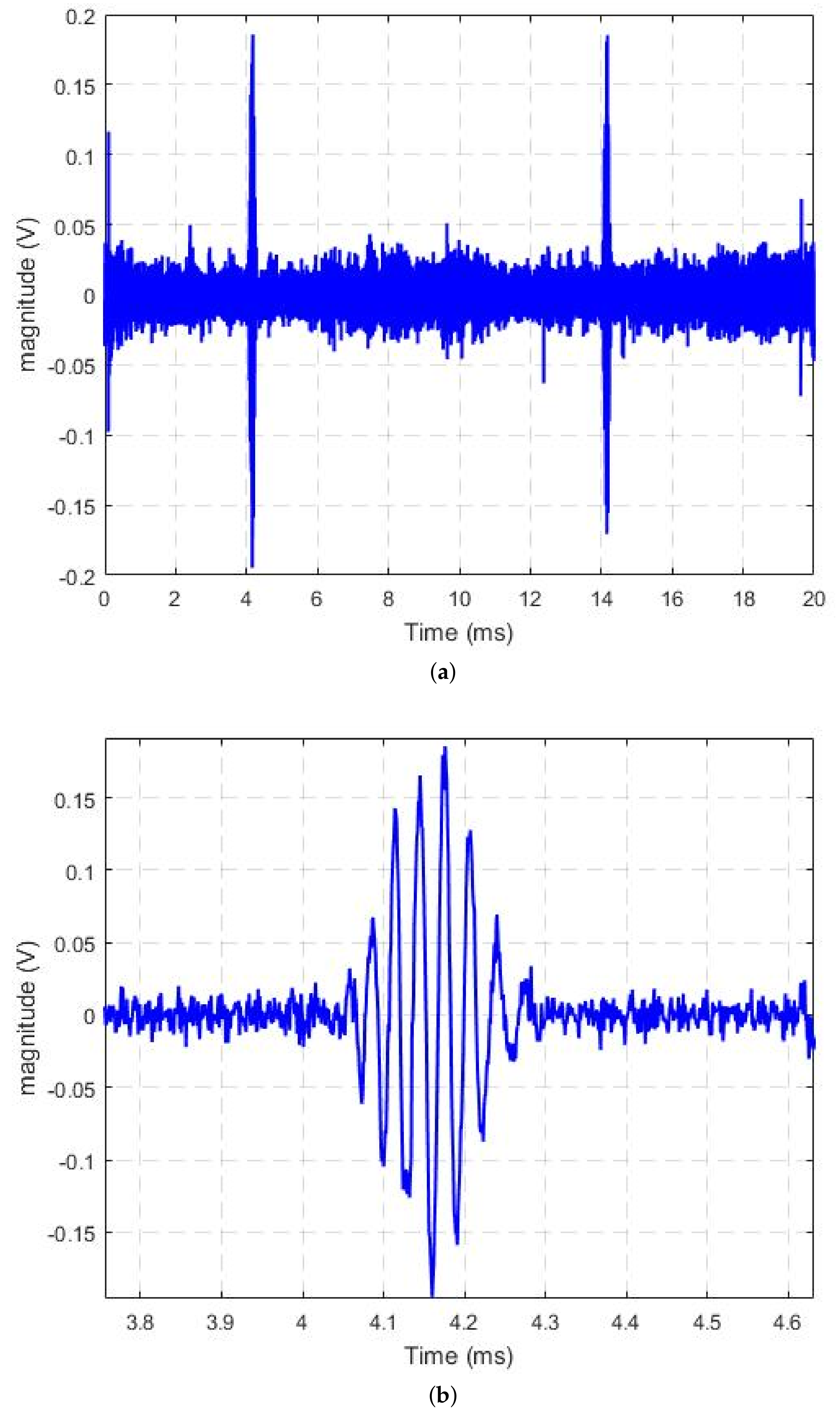
3.2. Time-Frequency Analysis
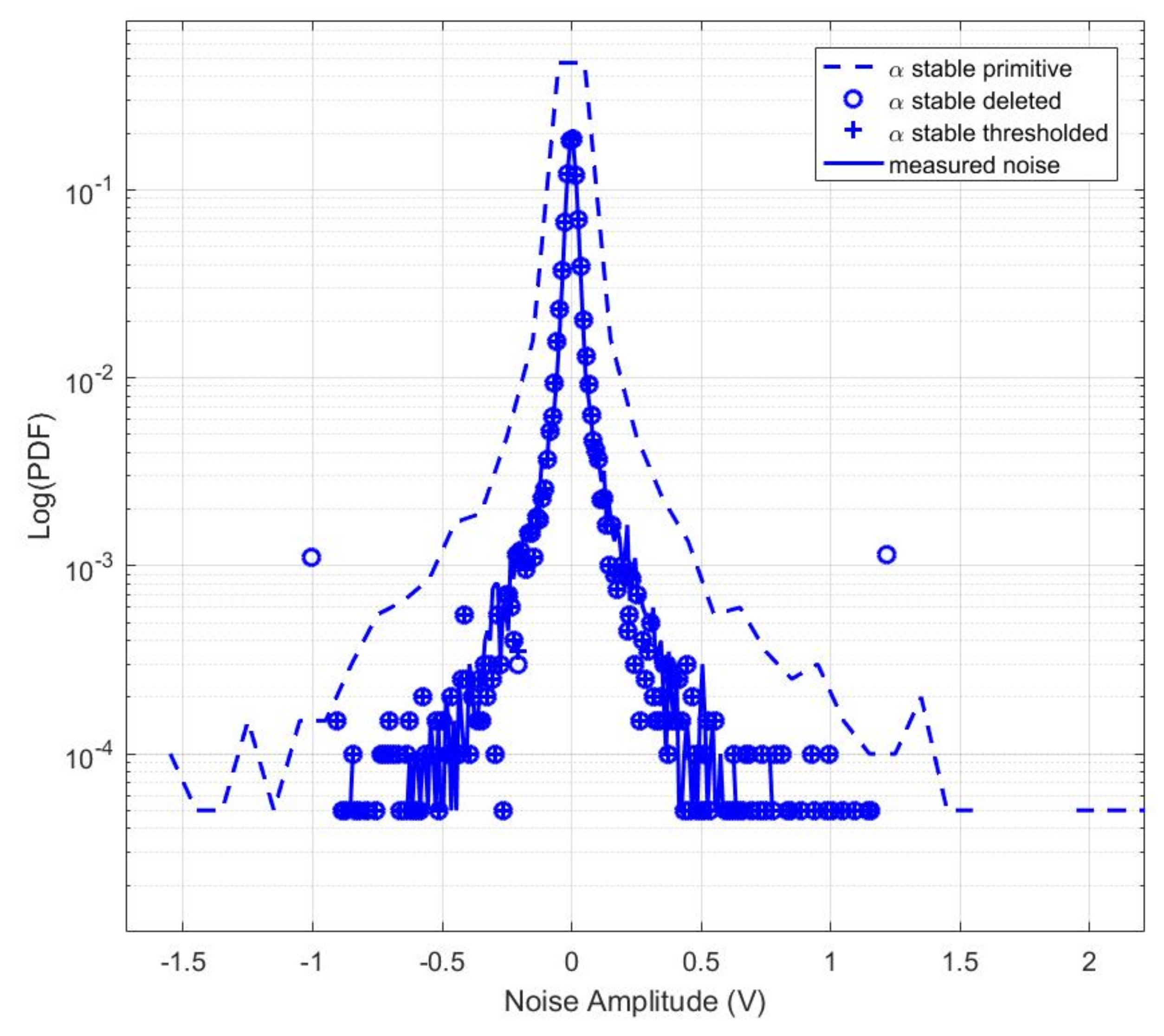
4. Impulsive Noise Modeling
4.1. Model Methods
4.1.1. Middleton Class-A Model
4.1.2. -Stable Model
4.2. Results of Impulsive Noise Modeling
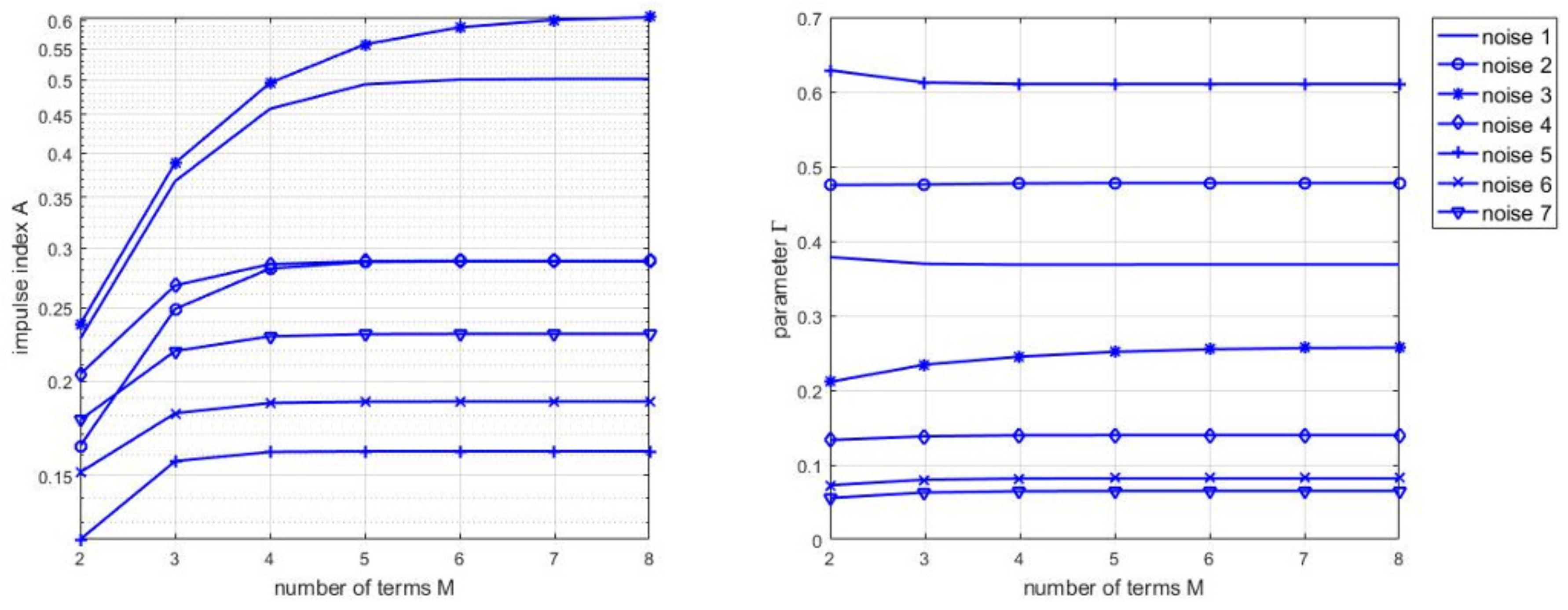
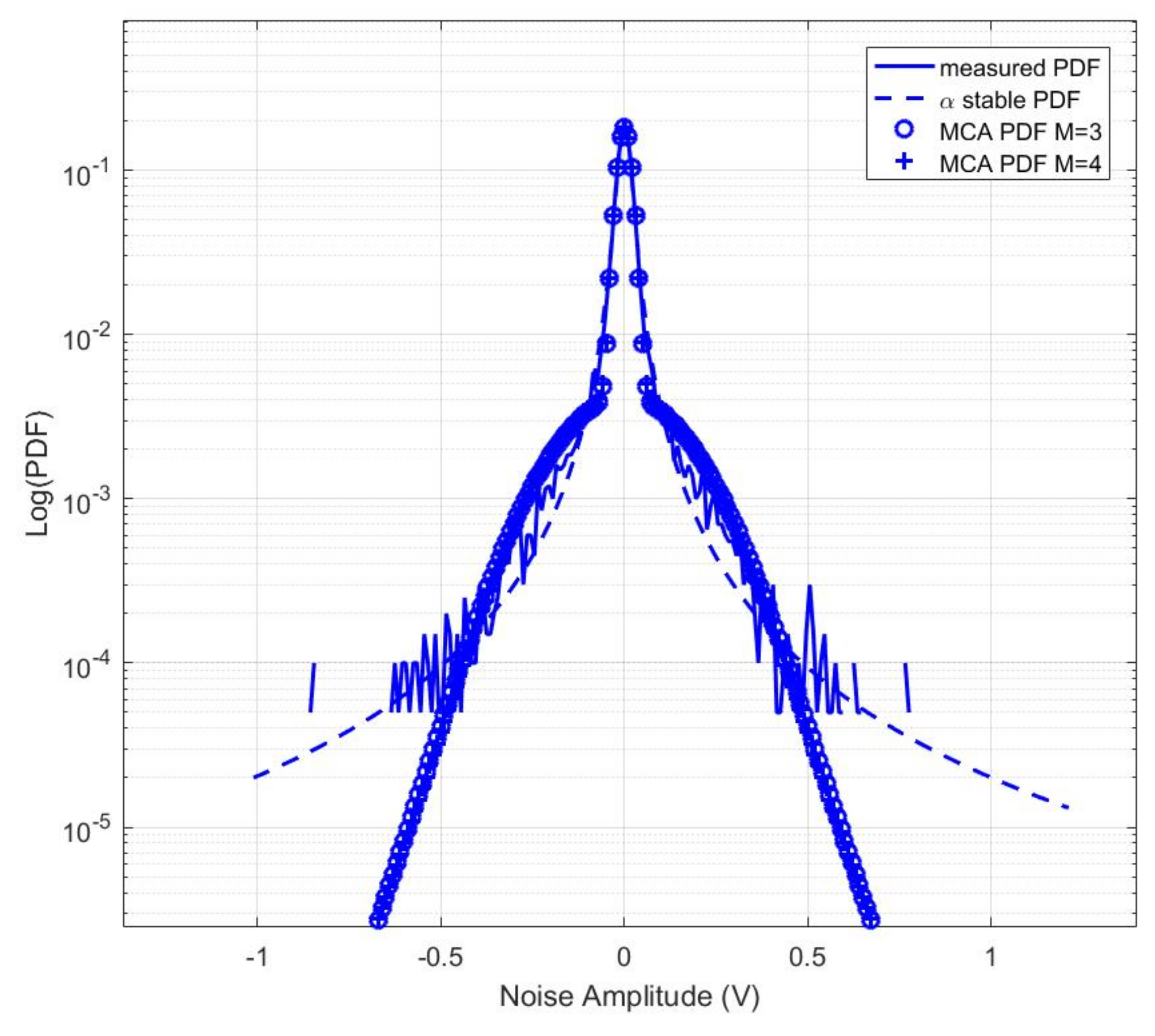
4.2.1. Middleton Class A model
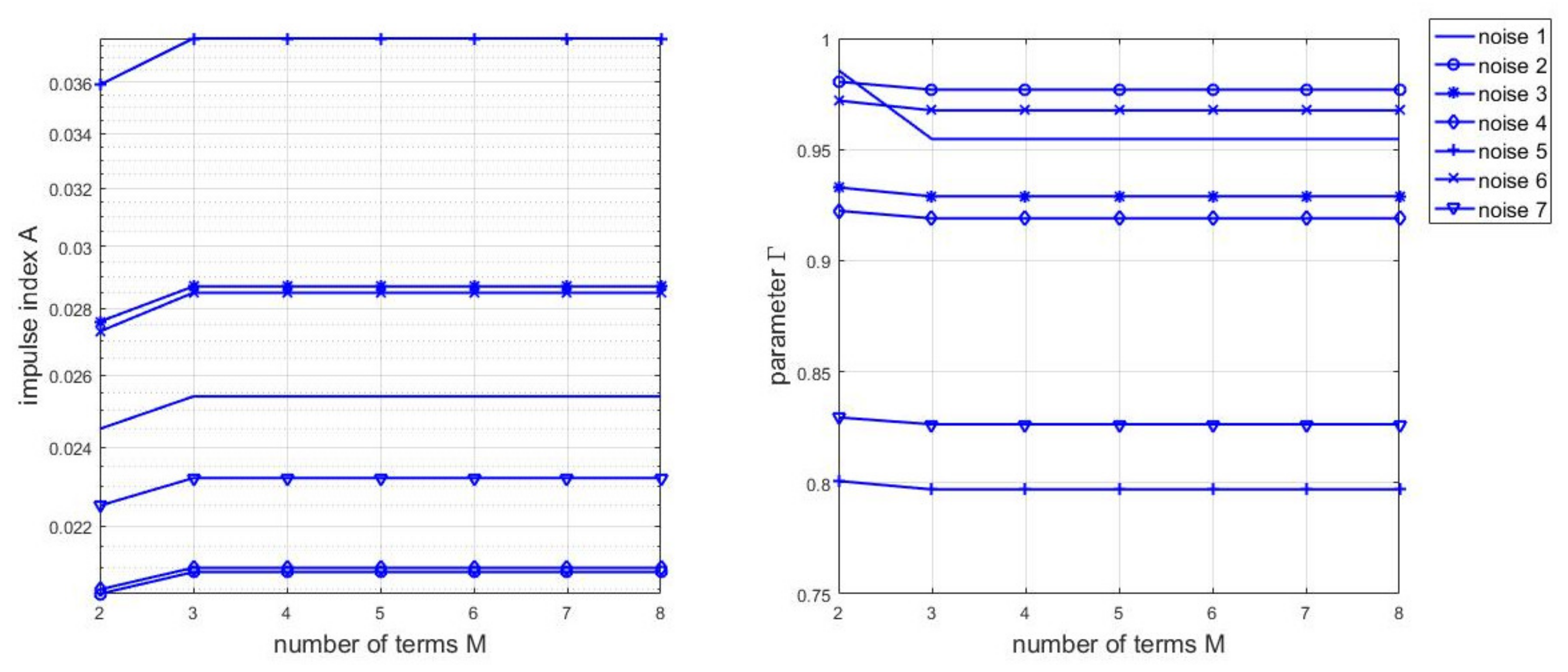
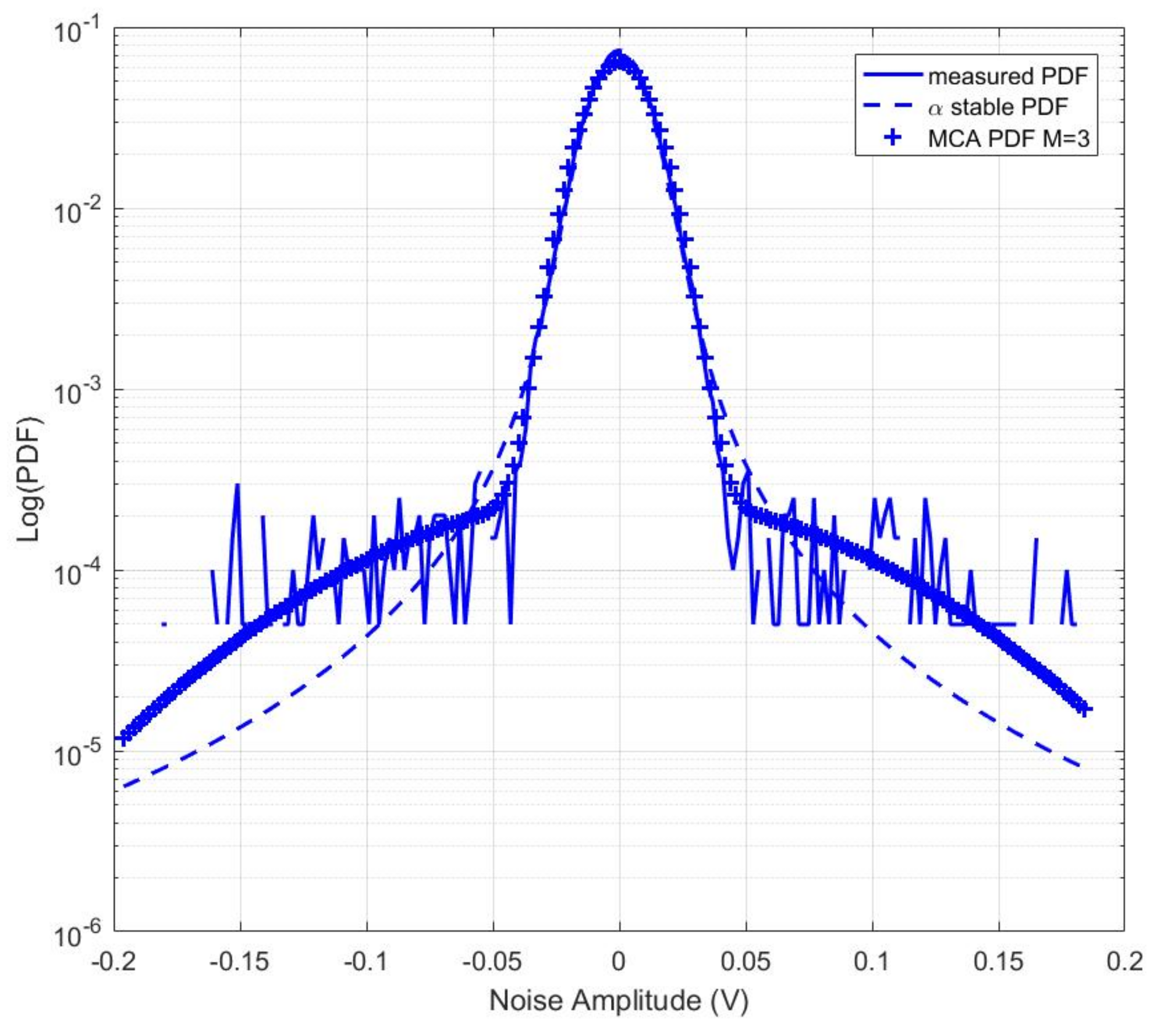
4.2.2. Stable Distribution Model
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ferreira, H.C.; Grove, H.M.; Hooijen, O.; Han Vinck, A.J. Power line communications: An overview. In Proceedings of the IEEE AFRICON 4th AFRICON, Stellenbosch, South Africa, 27 September 1996; Volume 9, pp. 142–149. [Google Scholar]
- Cano, C.; Pittolo, A.; Malone, D.; Lampe, L.; Tonello, A.M.; Dabak, A.G. State of the Art in Power Line Communications: From the Applications to the Medium. IEEE J. Sel. Areas Commun. 2016, 7, 1935–1952. [Google Scholar] [CrossRef]
- Gu, Z.; Liu, H.; Liu, D.; Man, K.L.; Liang, H. Modeling the Noise in NarrowBand Power Line Communication. Int. J. Control Autom. 2016, 2, 41–48. [Google Scholar] [CrossRef]
- Pereira, S.C.; Caporali, A.S.; Casella, I.R.S. Power line communication technology in industrial network. In Proceedings of the 2015 International Symposium on Power Line Communications and its Applications (ISPLC), Austin, TX, USA, 29 March–1 April 2015; Volume 7. [Google Scholar]
- O’Neal, J.B. The Residential Power Circuit as a Communication Medium. IEEE Trans. Consum. Electron. 1986, 8, 567–577. [Google Scholar] [CrossRef]
- Vines, R.M.; Joel Trissell, H.; Gale, L.J.; O’neal, J.B. Noise on Residential Power Distribution Circuits. IEEE Trans. Electromagn. Compat. 1984, 11, 161–168. [Google Scholar] [CrossRef]
- Cooper, D.; Jeans, T. Narrowband, low data rate communications on the low-voltage mains in the CENELEC frequencies. I. Noise and attenuation. IEEE Trans. Power Deliv. 2012, 7, 718–723. [Google Scholar] [CrossRef]
- IEEE Standard on Channel and Noise Measurements; P1901.2; IEEE: New York, NY, USA, 2011.
- Emleh, A.; de Beer, A.S.; Ferreira, H.C.; Han Vinck, A.J. Noise generated by modern lamps and the influence on the smart-grid communication network. In Proceedings of the 2015 IEEE International Conference on Smart Grid Communications (SmartGridComm), Miami, FL, USA, 2–5 November 2015; Volume 3. [Google Scholar]
- Dalichau, H.; Täger, W. Description of the technology and comparison of the performance of two different approaches for a powerline modem in the Cenelec-band. In Proceedings of the 4 th International Symposium on Powerline Communications, Limerick, Ireland, 5–7 April 2000; Volume 4. [Google Scholar]
- Gassara, H.; Rouissi, F.; Ghazel, A. Narrowband stationary noise characterization and modelling for power line communication. In Proceedings of the 13th International Symposium on Communications and Information Technologies (ISCIT), Surat Thani, Thailand, 4–6 September 2013; Volume 10. [Google Scholar]
- Gassara, H.; Rouissi, F.; Ghazel, A. A Novel Stochastic Model for the Impulsive Noise in the Narrowband Indoor PLC Environment. In Proceedings of the 2015 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Pisa, Italy, 11–14 May 2015; Volume 7. [Google Scholar]
- Hagmann, W. A spread spectrum communication system for load management and distribution automation. IEEE Trans. Power Deliv. 1989, 1, 75–81. [Google Scholar] [CrossRef]
- Tanaka, M. High frequency noise power spectrum, impedance and transmission loss of power line in Japan on intrabuilding power line communications. IEEE Trans. Consum. Electron. 1988, 5, 321–326. [Google Scholar] [CrossRef]
- Lasciandare, A.; Garotta, S.; Veroni, F.; Saccani, E.; Guerrieri, L.; Arrigo, D. Experimental field trials of a utility AMR power line communication system analyzing channel effects and error correction methods. In Proceedings of the IEEE International Symposium on Power Line Communications and Its Applications, Pisa, Italy, 26–28 March 2007; Volume 6. [Google Scholar]
- Zimmermann, M.; Dostert, K. Analysis and Modeling of Impulsive Noise in Broad-Band Powerline Communications. IEEE Trans. Electromagn. Compat. 2002, 7, 249–258. [Google Scholar] [CrossRef]
- Han, B.; Stoica, V.; Kaiser, C.; Otterbach, N.; Dostert, K. Noise characterization and emulation for low-voltage power line channels across narrowband and broadband. Digit. Signal Process. 2017, 69, 259–274. [Google Scholar] [CrossRef]
- Meng, H.; Guan, Y.L.; Chen, S. Modeling and analysis of noise effects on broadband power-line communications. IEEE Trans. Power Deliv. 2005, 4, 630–637. [Google Scholar] [CrossRef]
- Andreadou, N.; Pavlidou, F.N. Modeling the Noise on the OFDM Power-Line Communications System. IEEE Trans. Power Deliv. 2009, 12, 150–157. [Google Scholar] [CrossRef]
- Bauer, M.; Liu, W.Q.; Dostert, K. Channel emulation of low-speed PLC transmission channels. In Proceedings of the IEEE International Symposium on Power Line Communications and Its Applications (ISPLC), Dresden, Germany, 29 March–1 April 2009; Volume 5. [Google Scholar]
- Nieman, K.F.; Lin, J.; Nassar, M.; Waheed, K.; Evans, B.L. Cyclic spectral analysis of power line noise in the 3–200 kHz band. In Proceedings of the IEEE International Symposium on Power Line Communications and Its Applications (ISPLC), Johannesburg, South Africa, 24–27 March 2013; Volume 6. [Google Scholar]
- Kaiser, C.; Otterbach, N.; Dostert, K. Spectral correlation analysis of narrowband power line noise. In Proceedings of the IEEE International Symposium on Power Line Communications and its Applications (ISPLC), Madrid, Spain, 3–5 April 2017; Volume 4. [Google Scholar]
- Nassar, M.; Dabak, A.; Kim, H., II; Pande, T.; Evans, B.L. Cyclostationary noise modeling in narrowband powerline communication for Smart Grid applications. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; Volume 8. [Google Scholar]
- Middleton, D. Statistical-Physical Models of Electromagnetic Interference. IEEE Trans. Electromagn. Compat. 1977, 8, 106–127. [Google Scholar] [CrossRef]
- Ndo, G.; Labeau, F.; Kassouf, M. A Markov-Middleton Model for Bursty Impulsive Noise: Modeling and Receiver Design. IEEE Trans. Power Deliv. 2013, 8, 2317–2325. [Google Scholar] [CrossRef]
- Rouissi, F.; Han Vinck, A.J.; Gassara, H.; Ghazel, A. Statistical characterization and modelling of impulse noise on indoor narrowband PLC environment. In Proceedings of the 2017 IEEE International Symposium on Power Line Communications and its Applications (ISPLC), Madrid, Spain, 3–5 April 2017; Volume 4. [Google Scholar]
- Shao, M.; Nikias, C.L. Signal processing with fractional lower order moments: stable processes and their applications. Proc. IEEE 1993, 7, 986–1010. [Google Scholar] [CrossRef]
- Tran, T.H.; Do, D.D.; Huynh, T.H. PLC Impulsive Noise in Industrial Zone: Measurement and Characterization. Int. J. Comput. Electr. Eng. 2013, 2, 48–51. [Google Scholar] [CrossRef]
- Laguna-Sanchez, G.; Lopez-Guerrero, M. An experimental study of the effect of human activity on the alpha-stable characteristics of the power-line noise. In Proceedings of the IEEE International Symposium on Power Line Communications and its Applications (ISPLC), Glasgow, UK, 30 March–2 April 2014; Volume 5. [Google Scholar]
- Laguna-Sanchez, G.; Lopez-Guerrero, M. On the Use of Alpha-Stable Distributions in Noise Modeling for PLC. IEEE Trans. Power Deliv. 2015, 1, 1863–1870. [Google Scholar] [CrossRef]
- Gassara, H.; Chaker Bali, M.; Duval, F.; Rouissi, F.; Ghazel, A. Coupling interface circuit design for experimental characterization of the narrowband power line communication channel. In Proceedings of the IEEE International Symposium onElectromagnetic Compatibility (EMC), Pittsburgh, PA, USA, 6–10 August 2012; Volume 8. [Google Scholar]
- Welch, P. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 6, 70–73. [Google Scholar] [CrossRef]
- Standard CENELEC. EN 50065-1:2012. Signaling in Low-Voltage Electrical Installations in the Frequency Range 3 kHz– 148. 5 kHz- Part 1: General Requirements Frequency Bands and Electromagnetic Disturbances; European Committee for Electrotechnical Standardization: Brussels, Belgium, 2011; Volume 4. [Google Scholar]
- Artale, G.; Cataliotti, A.; Cosentino, V.; Di Cara, D.; and Fiorelli, R.; Guaiana, S.; Tine, G. A New Low Cost Coupling System for Power Line Communication on Medium Voltage Smart grids. IEEE Trans. Smart Grid 2016, PP, 1. [Google Scholar] [CrossRef]
- Mishra, A.; Tayal, H.; Khan, M.A.; Raza, M. Suitable PHY layer of narrow-band power line carrier communication in emerging advanced metering infrastructure scenario. In Proceedings of the 2015 IEEE Conference on Standards for Communications and Networking (CSCN), Tokyo, Japan, 28–30 October 2015; Volume 10. [Google Scholar]
- Cortés, J.A.; Sanz, A.; Estopiñán, P.; García, J.I. On the suitability of the Middleton class A noise model for narrowband PLC. In Proceedings of the International Symposium on Power Line Communications and its Applications (ISPLC), Bottrop, Germany, 20–23 March 2016; Volume 5. [Google Scholar]
| Frequency Range | PRIME | G3 | IEEE P1901.2 | G.HNEM |
|---|---|---|---|---|
| CEN A | 42–89 kHz | 39.9–90.6 kHz | 39.9–90.6 kHz | 39.9–90.6 kHz |
| FCC | / | 159.4–478.1 kHz | 35.9–487.5 kHz | 34.4–478.1 kH |
| Noise | ||||
|---|---|---|---|---|
| noise 1 | 1.59264 | −0.00636769 | 0.0189837 | 7.06 × 10 |
| noise 2 | 1.56769 | −0.0165415 | 0.016261 | 9.62 × 10 |
| noise 3 | 1.63601 | −0.0257861 | 0.0212625 | 2.10 × 10 |
| noise 4 | 1.25285 | −0.00828737 | 0.0165645 | 3.28 × 10 |
| noise 5 | 1.43699 | −0.00552512 | 0.012531 | 9.54 × 10 |
| noise 6 | 1.21431 | −0.0104543 | 0.0148703 | 7.41 × 10 |
| noise 7 | 1.18904 | −0.00616141 | 0.0165906 | 3.46 × 10 |
| Noise | ||||
|---|---|---|---|---|
| noise 1 | 1.75966 | 0.0282014 | 0.00760994 | −3.33 × 10 |
| noise 2 | 1.78562 | 0.00118321 | 0.0078767 | 1.21 × 10 |
| noise 3 | 1.75686 | 0.0565987 | 0.00792512 | −1.16 × 10 |
| noise 4 | 1.7938 | −0.0211009 | 0.00790263 | 3.57 × 10 |
| noise 5 | 1.74286 | 0.0265969 | 0.00835163 | −6.45 × 10 |
| noise 6 | 1.77606 | −0.0156829 | 0.00890917 | 2.53 × 10 |
| noise 7 | 1.85054 | −0.022285 | 0.0108844 | 4.48 × 10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, L.; Tucci, M.; Barmada, S.; Raugi, M.; Zheng, T. Impulsive Noise Characterization in Narrowband Power Line Communication. Energies 2018, 11, 863. https://doi.org/10.3390/en11040863
Bai L, Tucci M, Barmada S, Raugi M, Zheng T. Impulsive Noise Characterization in Narrowband Power Line Communication. Energies. 2018; 11(4):863. https://doi.org/10.3390/en11040863
Chicago/Turabian StyleBai, Li, Mauro Tucci, Sami Barmada, Marco Raugi, and Tao Zheng. 2018. "Impulsive Noise Characterization in Narrowband Power Line Communication" Energies 11, no. 4: 863. https://doi.org/10.3390/en11040863
APA StyleBai, L., Tucci, M., Barmada, S., Raugi, M., & Zheng, T. (2018). Impulsive Noise Characterization in Narrowband Power Line Communication. Energies, 11(4), 863. https://doi.org/10.3390/en11040863





