Hybrid GA-PSO Optimization of Artificial Neural Network for Forecasting Electricity Demand
Abstract
:1. Introduction
2. The Tamil Nadu Electricity Sector
Factors Affecting Electricity Demand
- (1)
- GSDP: Even though the linkage between GSDP growth and electricity demand growth are not as strong as it was in the past, it is worth considering the impact on the society of high GDP growth itself since they are linked to each other. A high GSDP growth rate year after year means higher manufacture of products and provision of services at an unprecedented pace leading to higher electricity demand. The electricity demand continues to grow in the state because of high level to continue in a business as usual scenario.
- (2)
- Electricity consumption per capita (E.Con) has increased from 510 kWh in year 2000–2001 to 1065 kWh in 2011–2012, that is more than 100% increase. Hence per capita consumption has been taken as an independent factor.
- (3)
- Income growth rate (per capita): The vision 2023 document of the state of Tamil Nadu aims at doubling the per capita income by 2023. It is also seen that any increase in family income leads to spurt in consumption.
- (4)
- Consumer Price Index (CPI): Prices have an indirect impact on the electricity demand by affecting the purchase of luxury goods such as air conditioners, washing machines etc.
3. Methodology
3.1. Artificial Neural Network
3.2. Particle Swarm Optimization (PSO)
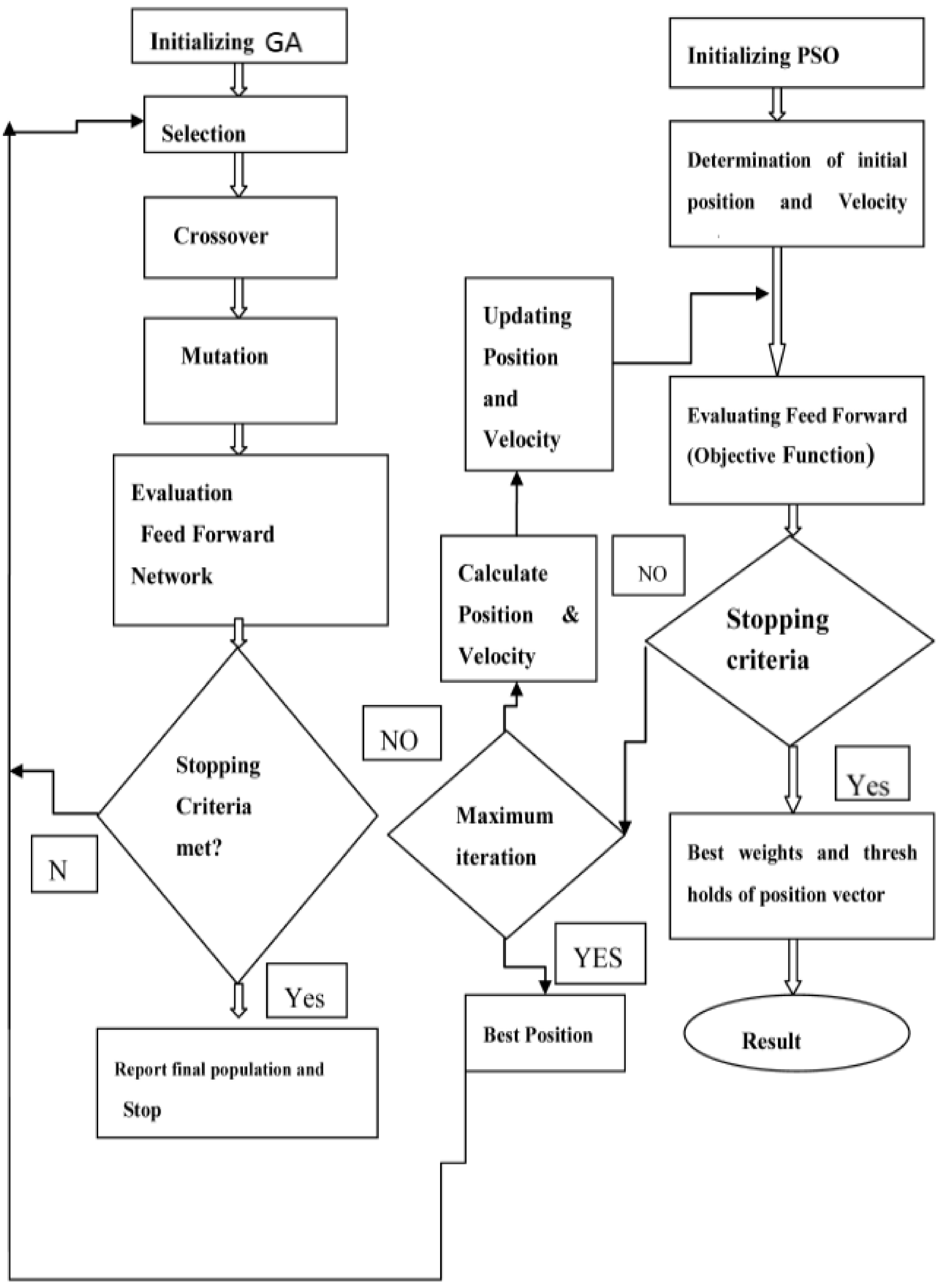
4. ANN-GA-PSO Models
4.1. Two Form Estimation Method
4.2. GA-PSO Hybrid Optimization Algorithm
- Step 1:
- First, we initialize a population size of 100 and assign positions and velocities of particles. The number of weights and biases are used to calculate the fitness function for all the particles.
- Step 2:
- The best position value achieved by particle p is set as pbest. The pbest with best value is set as gbest and this value is stored.
- Step 3:
- The desired optimization fitness function f(x) is evaluated for each particle.
- Step 4:
- The evaluated fitness value fp of each particle is compared with its pbest value. If fp < pbest then pbest = fp and bestxp = xp, where xp represents the current coordinates of particle p and bestxp represents the coordinates corresponding to particle p’s best fitness so far.
- Step 5:
- After objective function value is calculated for new positions of each particle the overall best fitness value of the swarm becomes the gbest value of the swarm.
- Step 6:
- Next, the velocity and location of the particle is updated according to Equations (1) and (2). The best position is fed into the General Algorithm as selection.
- Step 7:
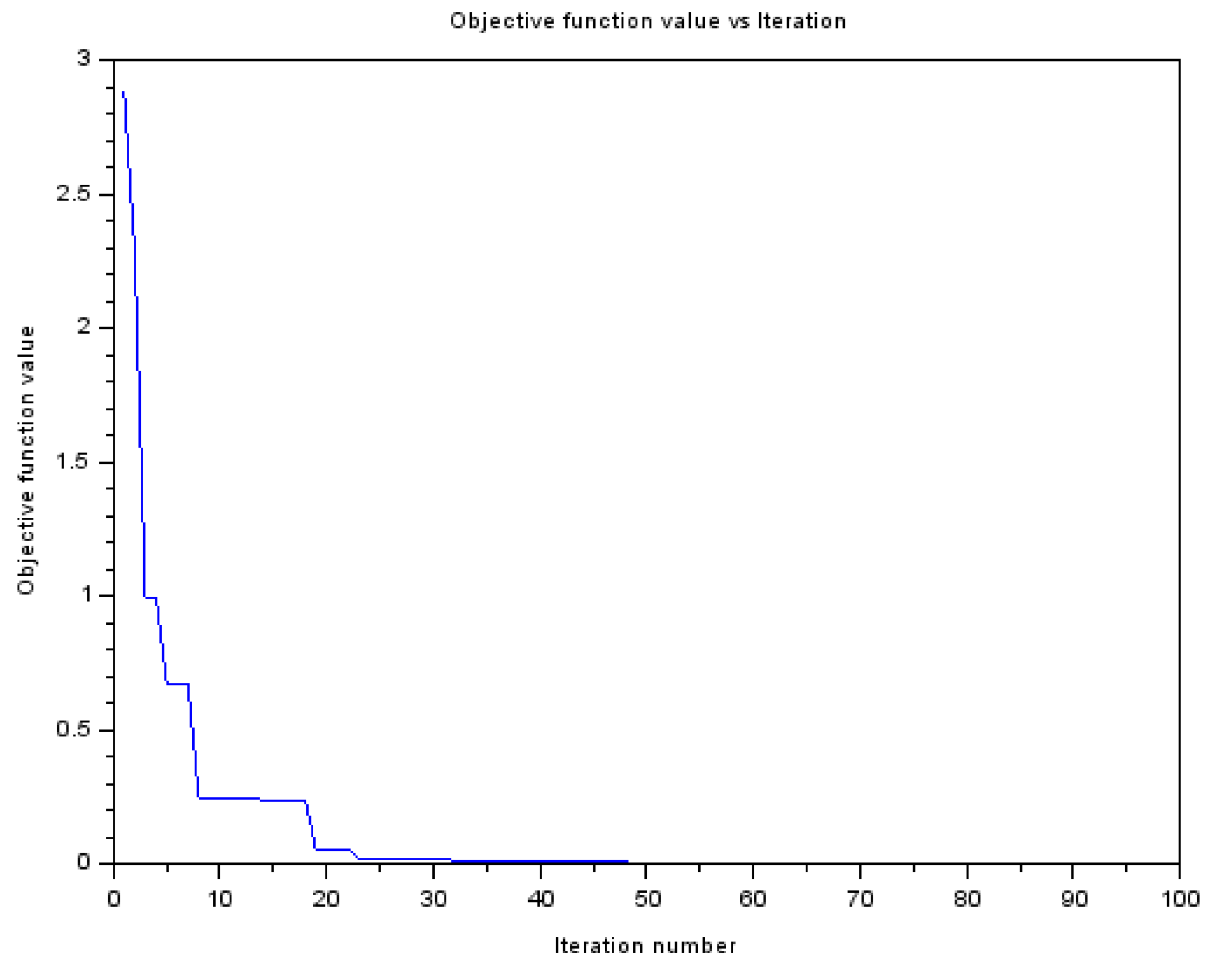
- The calculation is stopped when the maximum number of iteration reaches 200 or if the convergence occurs before it otherwise Loop to step 3 until convergence. In the present study, the convergence occurs around 50 iterations as shown in Figure 2.
- Step 8:
- The pop size of M particles obtained by GA and M particles are combined to form new pop size particles.
- Step 9:
- Let , then step 3 is carried out.
- Step 10:
- The best fitness values and solutions, namely, the position are outputted.
4.3. Computational Environment and Data Management
4.4. Evaluation of the Forecast Performance
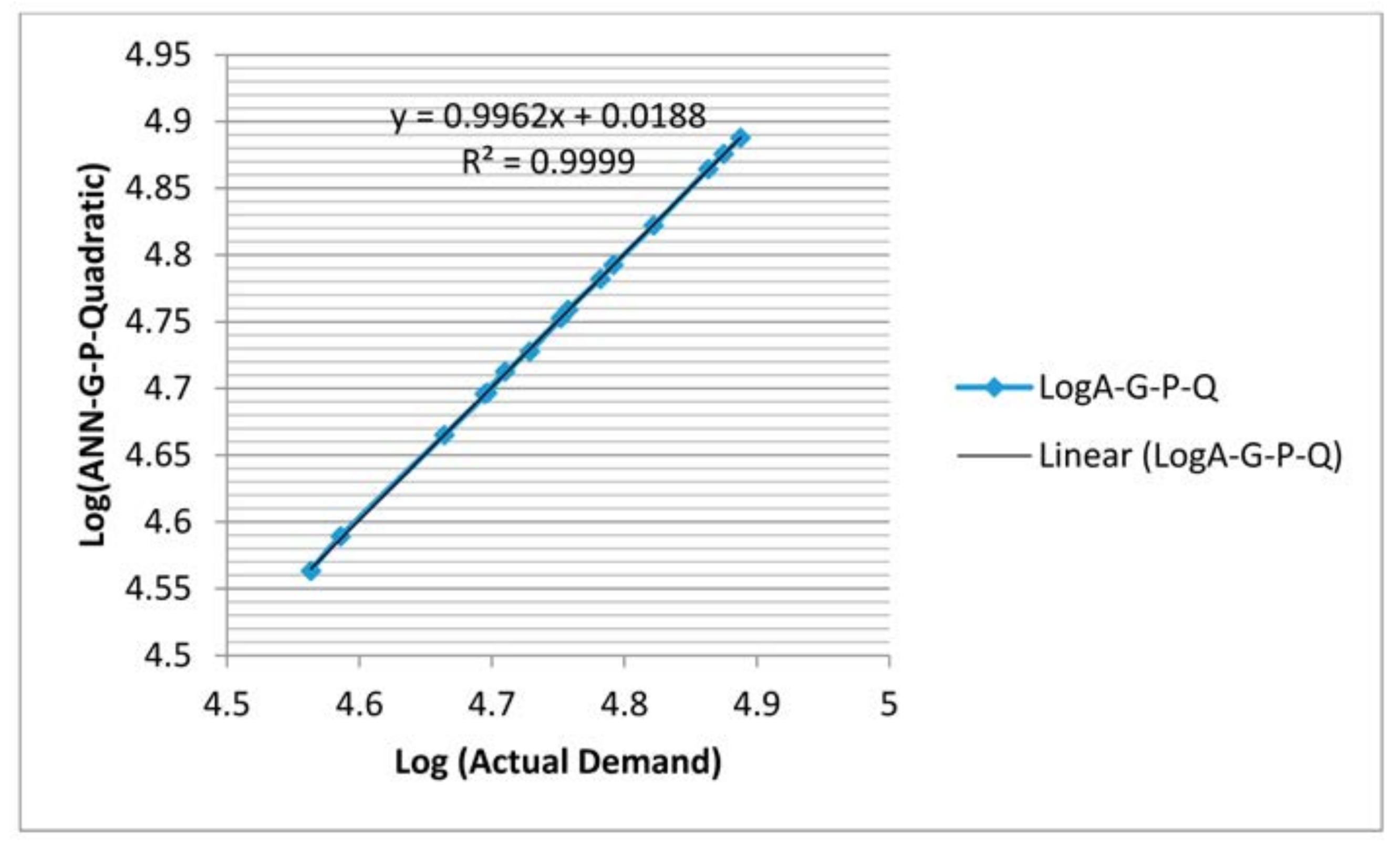
5. Results
5.1. Future Estimation
5.2. Relationship between GSDP and Electricity Demand
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Schweizer, V.J.; Morgan, M.G. Bounding US electricity demand in 2050. Technol. Forecast. Soc. Chang. 2016, 105, 215–223. [Google Scholar] [CrossRef]
- Perez-Garcia, J.; Moral-Carcedo, J. Analysis and Long term forecasting of electricity demand trough a decomposition model. A case study for Spain. Energy 2016, 97, 127–143. [Google Scholar] [CrossRef]
- Granger, C.W.J. Combining forecast-twenty years later. J. Forecast. 1989, 8, 167–173. [Google Scholar] [CrossRef]
- Parikh, J.; Purohit, P.; Maitra, P. Demand projections of petroleum products and natural gas in India. Energy 2007, 32, 1825–1837. [Google Scholar] [CrossRef]
- Zhang, M.; Mu, H.; Li, G.; Ning, Y. Forecasting the transport energy demand based on PLSR method in China. Energy 2009, 34, 1396–1400. [Google Scholar] [CrossRef]
- Limanond, T.; Jomnonkwao, S.; Srikaew, A. Projection of future transport energy demand of Thailand. Energy Policy 2011, 39, 2754–2763. [Google Scholar] [CrossRef]
- Jenkins, G.M.; Reinsel, G.C. Time Series Analysis: Forecasting and Control; Holden Day: San Francisco, CA, USA, 1976. [Google Scholar]
- Ediger, V.S.; Akbar, S. ARIMA forecasting of primary energy demand by fuel in Turkey. Energy Policy 2007, 35, 1701–1708. [Google Scholar] [CrossRef]
- Tepedino, C.; Guarnaccia, C.; Iliev, S.; Popova, S.; Quartieri, J. A Forecasting Model Based on Time Series Analysis Applied to Electrical Energy Consumption. Int. J. Math. Models Methods Appl. Sci. 2015, 9, 432–445. [Google Scholar]
- O’Connell, N.; Pinson, P.; Madsen, H. Benefits and Challenges of electrical demand response: A critical Review. Renew. Sustain. Rev. 2014, 39, 686–699. [Google Scholar] [CrossRef]
- Trotter, I.M.; Blkesjo, T.F.; Feres, J.G.; Hollanda, L. Climate Change and Electricity Demand in Brazil: A stochastic Approach. Energy 2016, 102, 596–604. [Google Scholar] [CrossRef]
- Fan, G. A method to estimating the parameters of logistic model and application. Math. Econ. 2010, 27, 105–110. [Google Scholar]
- Kandananond, K. Forecasting Electricity Demand in Thailand with an Artificial Neural Network Approach. Energies 2011, 4, 1246–1257. [Google Scholar] [CrossRef]
- Amjady, N.; Keynia, F. Day ahead forecasting of electricity markets by a mixed data model and hybrid forecast method. Int. J. Electr. Power Energy Syst. 2008, 30, 533–546. [Google Scholar] [CrossRef]
- Abdul Hamid, M.B.; Abdul Rahman, T.K. Short Term Load Forecasting Using an Artificial Neutral Network Trained by Artificial Immune System Learning Algorithm. In Proceedings of the 12th International Conference on Computer Modelling and Simulation, Cambridge, UK, 24–26 March 2010. [Google Scholar]
- Cincotti, S.; Gallo, G.; Ponta, L.; Raberto, M. Modeling and forecasting of electricity spot prices: Computational intelligence vs. Classical econometrics. AI Commun. 2014, 27, 301–314. [Google Scholar]
- Yin, F.; Wang, J.; Guo, C. Advances in Neural Networks ISNN 2004. In Proceedings of the International Symposium on Neural Networks, Dalian, China, 19–21 August 2004; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley Publishing Corporation, Inc.: Boston, MA, USA, 1989. [Google Scholar]
- Canyurt, O.E.; Ozturk, H.K. Application of genetic algorithm (GA) technique on demand estimation of fossil fuels in Turkey. Energy Policy 2008, 36, 2562–2569. [Google Scholar] [CrossRef]
- Ceylan, H.; Ozturk, H.K. Estimating energy demand of Turkey based on economic indicators using genetic algorithm approach. Energy Convers. Manag. 2004, 45, 2525–2537. [Google Scholar] [CrossRef]
- Haldenbilen, S.; Ceylan, H. Genetic Algorithm approach to estimate transport energy demand in Turkey. Energy Policy 2005, 33, 89–98. [Google Scholar] [CrossRef]
- Assareh, E.; Behrang, M.A.; Assari, M.R.; Ghanbarzadeh, A. Application of PSO and GA techniques on demand estimation of oil in Iran. Energy 2010, 35, 5223–5229. [Google Scholar] [CrossRef]
- Bi, T.; Yan, Z.; Wen, F.; Ni, Y.; Shen, C.M.; Wu, F.F.; Yang, Q. On-line fault section estimation in Power Systems with radial basis function neural network. Int. J. Electr. Power Energy Syst. 2002, 24, 321–328. [Google Scholar] [CrossRef]
- Lu, N.; Zhou, J. Particle Swarm Optimization-Based RBF Neural Network Load Forecasting Model. In Proceedings of the 2009 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 27–31 March 2009. [Google Scholar]
- Banda, E.; Folly, K.A. Short Term Load Forecasting Based on Hybrid ANN and PSO. In Advances in Swarm and Computational Intelligence, Proceedings of the International Conference in Swarm Intelligence, Beijing, China, 25–28 June 2015; Springer: Cham, Switzerland, 2015; pp. 98–106. [Google Scholar]
- Yang, S.D.; Li, X. A new ANN optimized by improved PSO algorithm combined with chaos and its application in short term load forecasting. In Proceedings of the 2006 International Conference on Computational Intelligence and Security, Guangzhou, China, 3–6 November 2006; Volume 2. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1947. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Parameter selection in Particle Swarm Optimization. In Evolutionary Programming; Springer: Berlin/Heidelberg, Germany, 1998; Volume 7, pp. 611–616. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Fuzzy adaptive particle swarm optimization. In Proceedings of the 2001 Congress on Evolutionary Computation, Seoul, Korea, 27–30 May 2001. [Google Scholar]
- Anand, A.; Suganthi, L. Forecasting of Electricity Demand by Hybrid ANN-PSO Models. Int. J. Energy Optim. Eng. 2017, 6, 66–83. [Google Scholar] [CrossRef]
- Bates, J.M.; Granger, C.W. The combination of forecasts. Oper. Res. Soc. 1969, 20, 451–468. [Google Scholar] [CrossRef]
- Nazari1, H.; Kazemi1, A.; Hashemi, M.-H. Selecting the appropriate scenario for forecasting energy demands of residential and commercial sectors in Iran using two metaheuristic algorithms. Iran. J. Manag. Stud. 2016, 9, 101–123. [Google Scholar]
- Unler, A. Improvement of energy demand forecasts using swarm intelligence: The case of Turkey with projections to 2015. Energy Policy 2008, 36, 1937–1944. [Google Scholar] [CrossRef]
- Younes, M.; Farid, B. Genetic Algorithm-Particle Swarm Optimisation (GA-PSO) for Economic Load Dispatch. Prz. Elektrotech. 2011, 87, 369–372. [Google Scholar]
- EL-Araby, E.E.; Yorino, N. A hybrid PSO technique for procuring VAR ancillary service in the deregulated electricity markets. Int. J. Electr. Power Energy Syst. 2010, 32, 664–670. [Google Scholar] [CrossRef]
- Jarndal, A.; Hamdan, S. Forecasting of peak electricity demand using ANN GA and ANN-PSO approaches. In Proceedings of the 7th International Conference on Modeling, Simulation, and Applied Optimization (ICMSAO), Sharjah, UAE, 4–6 April 2017. [Google Scholar]
- Ekonomou, L. Greek long-term energy consumption prediction using artificial neural networks. Energy 2010, 35, 512–517. [Google Scholar] [CrossRef]
- Bunn, D.W. Forecasting with more than one model. J. Forecast. 1989, 8, 161–166. [Google Scholar] [CrossRef]
- Donaldson, R.G.; Kamstra, M. Forecast combining with neural networks. J. Forecast. 1996, 15, 46–91. [Google Scholar] [CrossRef]
- Chen, H.Y. Research on combination forecasting model based on effective measure of forecasting methods. Forecasting 2001, 20, 72–73. [Google Scholar]
- Fatai, K.; Oxley, L.; Scrimgeour, F.G. Modeling and Forecasting the demand for electricity in New Zealand: A comparison of alternative approaches. Energy J. 2003, 24, 75–102. [Google Scholar] [CrossRef]
- Weron, R. Electricity price forecasting: A review of the state-of -art with a look in to the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef]
- Vision Tamil Nadu 2023. Available online: www.spc.tn.gov.in (accessed on 18 January 2018).
- Kostyannikova, D. Economic Growth and Energy Consumption in OECD Countries: A Causality Analysis. Master’s Thesis, City College of New York, New York, NY, USA, 2012. [Google Scholar]



| Year | Electricity (kWr) | Income Growth | GSDP | Price | Demand |
|---|---|---|---|---|---|
| Consumption | Rate per Capita (%) | (Billion Rs) | Index | (in mWh) | |
| 1991 | 295 | 10.97 | 4.81 | 48 | 17,173 |
| 1992 | 303 | 11.9 | 5.27 | 55 | 19,130 |
| 1993 | 334 | 12.9 | 5.74 | 65 | 20,289 |
| 1994 | 350 | 13.9 | 6.2 | 79 | 23,193 |
| 1995 | 421 | 14.8 | 6.6 | 82 | 24,610 |
| 1996 | 435 | 15.7 | 7.1 | 85 | 25,805 |
| 1997 | 449 | 16.8 | 7.5 | 89 | 26,943 |
| 1998 | 459 | 17.9 | 8 | 92 | 27,862 |
| 1999 | 496 | 18.8 | 8.5 | 94 | 30,434 |
| 2000 | 510 | 14.7 | 10.9 | 101 | 33,418 |
| 2001 | 539 | 15 | 10.88 | 103 | 36,578 |
| 2002 | 708 | 15.2 | 15.01 | 107 | 38,529 |
| 2003 | 740 | 15.3 | 17.56 | 109 | 46,130 |
| 2004 | 780 | 15.5 | 18.66 | 110 | 49,712 |
| 2005 | 860 | 17.23 | 17.73 | 115 | 51,282 |
| 2006 | 960 | 19.99 | 20.44 | 117 | 49,485 |
| 2007 | 1000 | 12.58 | 12.98 | 124 | 56,493 |
| 2008 | 1000 | 13.73 | 14.4 | 136 | 53,506 |
| 2009 | 1080 | 18.83 | 19.53 | 151 | 57,212 |
| 2010 | 1040 | 17.27 | 18.07 | 166 | 60,518 |
| 2011 | 1074 | 18.06 | 16.7 | 163.02 | 61,897 |
| 2012 | 1118 | 18.29 | 17.66 | 159.01 | 66,391 |
| 2013 | 1161 | 16.3 | 19.98 | 157.39 | 72,987 |
| 2014 | 2130 | 17.89 | 42.27 | 143.52 | 74,990 |
| 2015 | 2007 | 12.94 | 38.45 | 138.77 | 77,218 |
| Input Layer | Factors | 1 | E.Con (electricity consumption) |
| 2 | Income growth rate | ||
| 3 | GSDP | ||
| 4 | CPI | ||
| Number of Units | 59 | ||
| Hidden Layer(s) | Number of Hidden Layers | 1 | |
| Number of Units in Hidden Layer 1 | 6 | ||
| Activation Function | Hyperbolic tangent | ||
| Output Layer | Dependent Variables | 1 | Electricity Demand |
| Number of Units | 1 | ||
| Rescaling Method for Scale Dependents | Standardized | ||
| Activation Function | Identity | ||
| Error Function | Sum of Squares | ||
| Training | Sum of Squares Error | 0.004 |
| Relative Error | 0.001 | |
| Stopping Rule Used | Training error ratio criterion (0.001) achieved | |
| Training Time | 0:00:00.23 |
| Year | E.Con | Income | GSDP | CPI | Sq-E.Con | Sq-Income | Sq-GSDP | Sq-CPI |
| 2001 | 0 | 0.153846 | 0 | 0 | 0 | 0.023669 | 0 | 0 |
| 2002 | 0.313544 | 0.153846 | 0.363636 | 0.038835 | 0.09831 | 0.023669 | 0.132231 | 0.001508 |
| 2003 | 0.372913 | 0.153846 | 0.636364 | 0.058252 | 0.139064 | 0.023669 | 0.404959 | 0.003393 |
| 2004 | 0.447124 | 0.230769 | 0.727273 | 0.067961 | 0.19992 | 0.053254 | 0.528926 | 0.004619 |
| 2005 | 0.595547 | 0.307692 | 0.636364 | 0.116505 | 0.354677 | 0.094675 | 0.404959 | 0.013573 |
| 2006 | 0.781076 | 0.538462 | 0.818182 | 0.135922 | 0.61008 | 0.289941 | 0.669421 | 0.018475 |
| 2007 | 0.855288 | 0 | 0.181818 | 0.203883 | 0.731517 | 0 | 0.033058 | 0.041568 |
| 2008 | 0.855288 | 0.076923 | 0.272727 | 0.320388 | 0.731517 | 0.005917 | 0.07438 | 0.102649 |
| 2009 | 1.003711 | 0.461538 | 0.818182 | 0.466019 | 1.007435 | 0.213018 | 0.669421 | 0.217174 |
| 2010 | 0.929499 | 0.307692 | 0.636364 | 0.61165 | 0.863969 | 0.094675 | 0.404959 | 0.374116 |
| 2011 | 0.992579 | 0.384615 | 0.545455 | 0.582524 | 0.985213 | 0.147929 | 0.297521 | 0.339335 |
| 2012 | 1.074212 | 0.384615 | 0.636364 | 0.543689 | 1.15393 | 0.147929 | 0.404959 | 0.295598 |
| 2013 | 1.153989 | 0.230769 | 0.818182 | 0.524272 | 1.33169 | 0.053254 | 0.669421 | 0.274861 |
| 2014 | 2.953618 | 0.384615 | 2.818182 | 0.398058 | 8.723858 | 0.147929 | 7.942149 | 0.15845 |
| 2015 | 2.723562 | 0 | 2.454545 | 0.349515 | 7.417791 | 0 | 6.024793 | 0.12216 |
| 2016 | 3.022263 | 0.153846 | 2.909091 | 0.38835 | 9.134076 | 0.023669 | 8.46281 | 0.150815 |
| Year | X12 | X13 | X14 | X23 | X24 | X32 | X34 | Demand |
| 2001 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2002 | 0.048237 | 0.055944 | 0.012176 | 0.055944 | 0.005975 | 0.055944 | 0.014122 | 0.053338 |
| 2003 | 0.057371 | 0.097902 | 0.021723 | 0.097902 | 0.008962 | 0.097902 | 0.03707 | 0.261141 |
| 2004 | 0.103183 | 0.167832 | 0.030387 | 0.167832 | 0.015683 | 0.167832 | 0.049426 | 0.359068 |
| 2005 | 0.183245 | 0.195804 | 0.069384 | 0.195804 | 0.035848 | 0.195804 | 0.074139 | 0.40199 |
| 2006 | 0.420579 | 0.440559 | 0.106166 | 0.440559 | 0.073189 | 0.440559 | 0.111209 | 0.352862 |
| 2007 | 0 | 0 | 0.174379 | 0 | 0 | 0 | 0.03707 | 0.544453 |
| 2008 | 0.065791 | 0.020979 | 0.274024 | 0.020979 | 0.024645 | 0.020979 | 0.087379 | 0.462792 |
| 2009 | 0.463251 | 0.377622 | 0.467749 | 0.377622 | 0.215086 | 0.377622 | 0.381289 | 0.56411 |
| 2010 | 0.286 | 0.195804 | 0.568529 | 0.195804 | 0.1882 | 0.195804 | 0.389232 | 0.654492 |
| 2011 | 0.381761 | 0.20979 | 0.578201 | 0.20979 | 0.224048 | 0.20979 | 0.317741 | 0.692192 |
| 2012 | 0.413158 | 0.244755 | 0.584037 | 0.244755 | 0.209111 | 0.244755 | 0.345984 | 0.815053 |
| 2013 | 0.266305 | 0.188811 | 0.605004 | 0.188811 | 0.120986 | 0.188811 | 0.42895 | 0.99538 |
| 2014 | 1.136007 | 1.083916 | 1.175712 | 1.083916 | 0.153099 | 1.083916 | 1.121801 | 1.050139 |
| 2015 | 0 | 0 | 0.951925 | 0 | 0 | 0 | 0.857899 | 1.11105 |
| 2016 | 0.464964 | 0.447552 | 1.173695 | 0.447552 | 0.059746 | 0.447552 | 1.129744 | 1.211196 |
| Year | E.Con | Income | GSDP | CPI | x1 | x2 | x3 | x4 | x5 |
|---|---|---|---|---|---|---|---|---|---|
| 2016 | 2167 | 14.88 | 43.06 | 142.9 | −1.93 | 0.91 | −1.005 | −1.63 | −1.14 |
| 2017 | 2341 | 17.11 | 48.23 | 147.22 | −1.94 | 0.54 | −1.56 | −0.41 | −1.25 |
| 2018 | 22 | 19.68 | 54 | 151.64 | −1.98 | −0.1 | −0.179 | −1.64 | −1.12 |
| 2019 | 2730 | 22.63 | 60.5 | 156.19 | −2 | 0.39 | −1.05 | −0.86 | 0.77 |
| 2020 | 2949 | 26.03 | 67.76 | 160.87 | −2 | −1.4 | −0.68 | −0.76 | 0.99 |
| 2021 | 3185 | 29.93 | 75.89 | 165.7 | −1.99 | 0.19 | −1.58 | −1.23 | −0.63 |
| 2022 | 3439 | 34.4 | 85 | 170.7 | −2 | −1 | −1.95 | −1.2 | −0.31 |
| 2023 | 3715 | 39.58 | 95.2 | 175.8 | −1.99 | 0.28 | 0.28 | −1.71 | 0.62 |
| 2024 | 4012 | 45.52 | 106.6 | 181 | −2 | 0.41 | −0.9 | −0.21 | −0.49 |
| 2025 | 4333 | 52.35 | 119.42 | 186.5 | −2 | −1.26 | 0.127 | −0.76 | 0.03 |
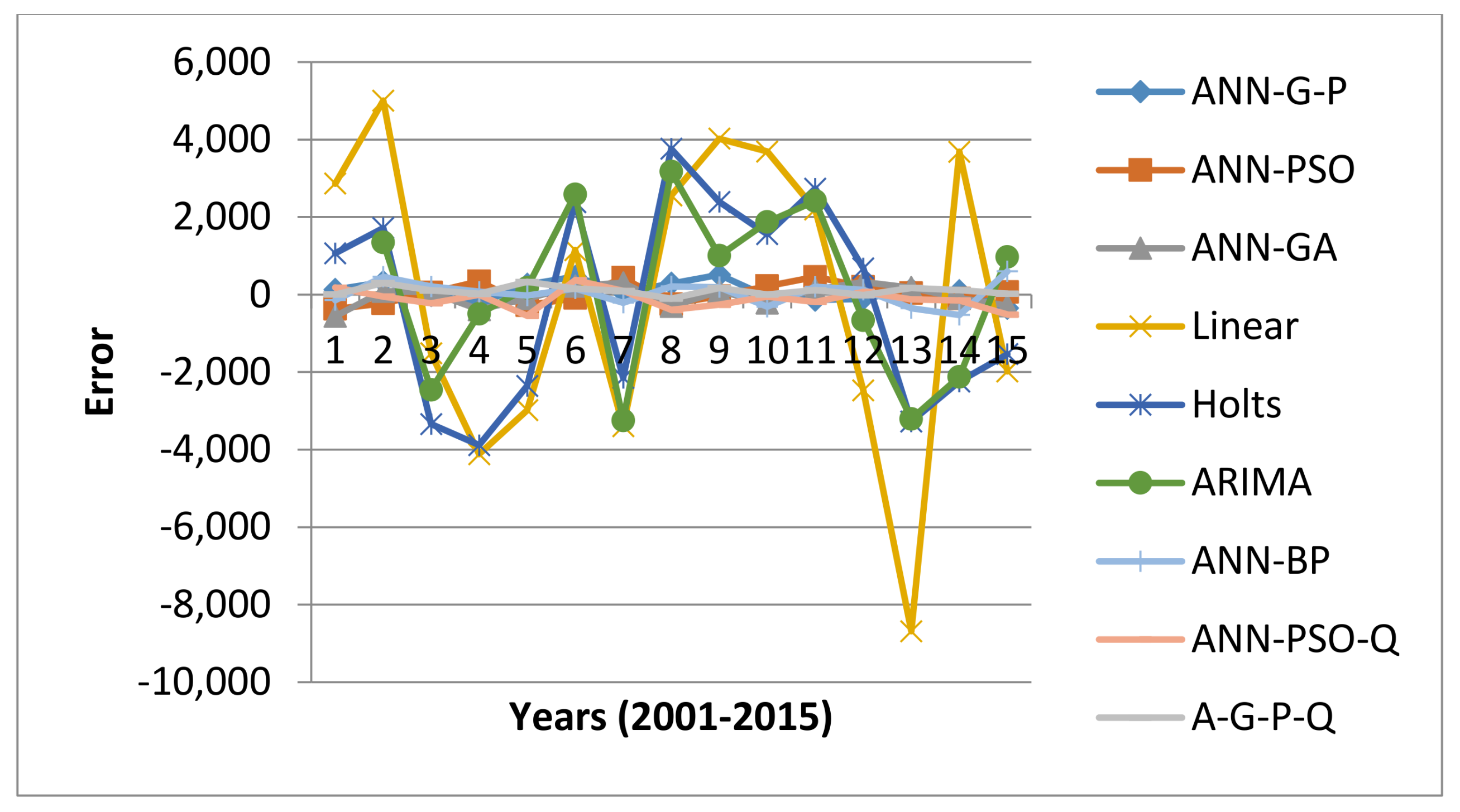
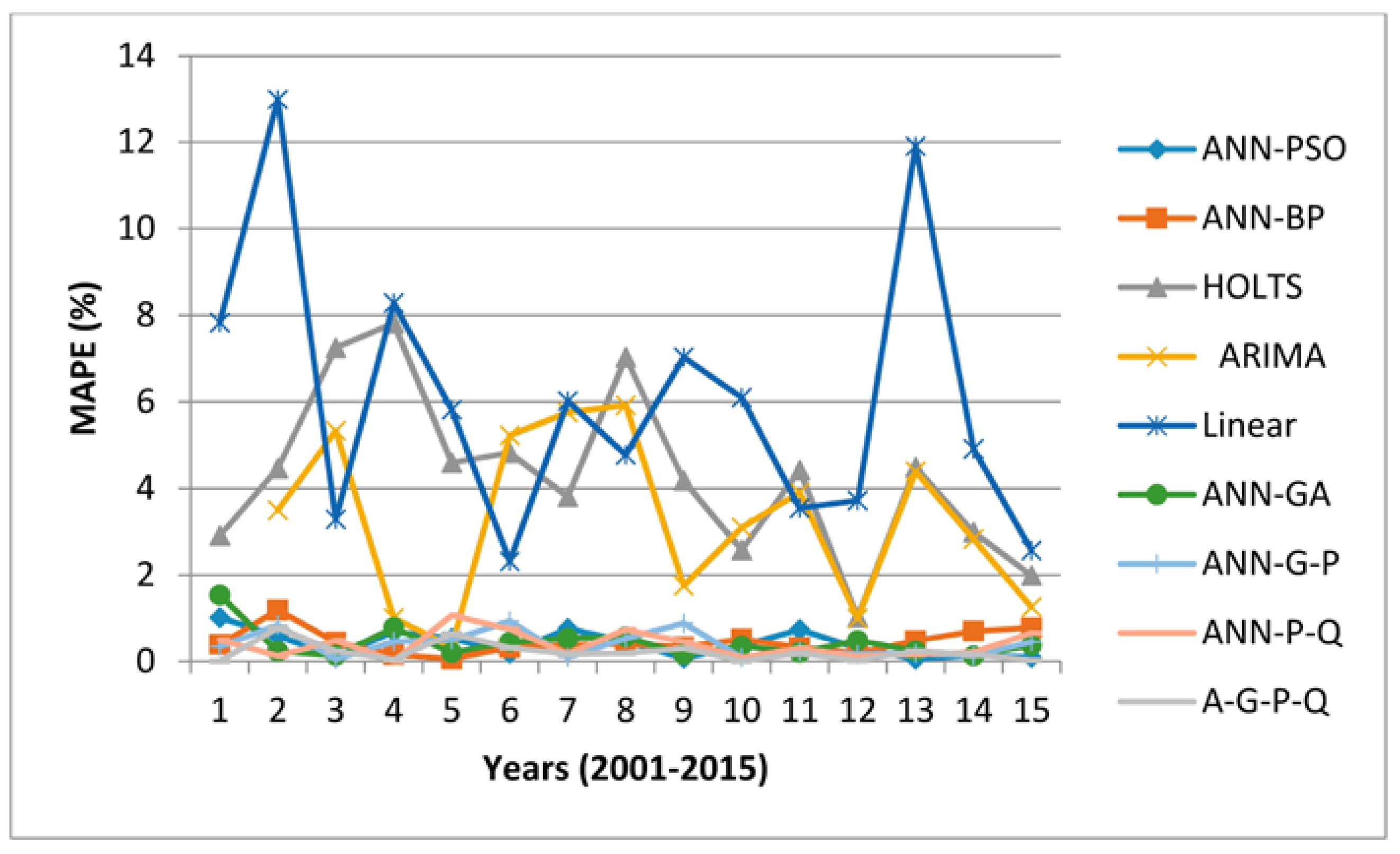
| Year | Act Total | ANN-Pso | Linear | Holts | ANN-BP | ANN-G-P | ARIMA | ANN-GA | A-G-P-Q |
|---|---|---|---|---|---|---|---|---|---|
| 2001 | 36,578 | 36,206 | 39,441 | 37,643 | 36,434 | 36,705 | 36,018 | 36,582 | |
| 2002 | 38,529 | 38,302 | 43,532 | 40,247 | 38,987 | 38,854 | 39,876 | 38,618 | 38,827 |
| 2003 | 46,130 | 46,180 | 44,614 | 42,787 | 46,337 | 46,109 | 43,671 | 46,192 | 46,238 |
| 2004 | 49,712 | 50,054 | 45,595 | 45,829 | 49,786 | 49,484 | 49,214 | 49,323 | 49,731 |
| 2005 | 51,282 | 51,007 | 48,299 | 48,925 | 51,254 | 51,540 | 51,458 | 51,179 | 51,611 |
| 2006 | 49,485 | 49,394 | 50,630 | 51,870 | 49,643 | 49,949 | 52,069 | 49,707 | 49,640 |
| 2007 | 56,493 | 56,927 | 53,094 | 54,343 | 56,282 | 56,546 | 53,244 | 56,795 | 56,586 |
| 2008 | 53,506 | 53,257 | 56,060 | 57,267 | 53,719 | 53,792 | 56,676 | 53,201 | 53,404 |
| 2009 | 57,212 | 57,172 | 61,235 | 59,603 | 57,404 | 57,720 | 58,214 | 57,303 | 57,383 |
| 2010 | 60,518 | 60,737 | 64,208 | 62,076 | 60,205 | 60,465 | 62,391 | 60,302 | 60,522 |
| 2011 | 61,897 | 62,353 | 64,090 | 64,631 | 62,098 | 61,757 | 64,313 | 62,024 | 62,011 |
| 2012 | 66,391 | 66,593 | 63,920 | 67,069 | 66,515 | 66,282 | 65,730 | 66,713 | 66,378 |
| 2013 | 72,987 | 73,023 | 64,302 | 69,712 | 72,635 | 73,126 | 69,779 | 73,164 | 73,160 |
| 2014 | 74,990 | 74,890 | 78,675 | 72,748 | 74,464 | 75,084 | 72,866 | 74,898 | 75,109 |
| 2015 | 77,218 | 77,285 | 75,235 | 75,681 | 77,818 | 76,870 | 78,189 | 76,930 | 77,242 |
| Linear | Holts | ARIMA | ANN-BP | ANN-GA | ANN-P | ANN-G-P | A-G-P-Q |
|---|---|---|---|---|---|---|---|
| 6.07 | 0.85 | 3.02 | 0.44 | 0.42 | 0.4 | 0.3 | 0.22 |
| Linear | Holts | ARIMA | ANN-BP | ANN-GA | ANN-P | ANN-G-P | A-G-P-Q |
|---|---|---|---|---|---|---|---|
| 0 | 0.15 | 0 | 0.56 | 0.58 | 0.6 | 0.7 | 0.78 |
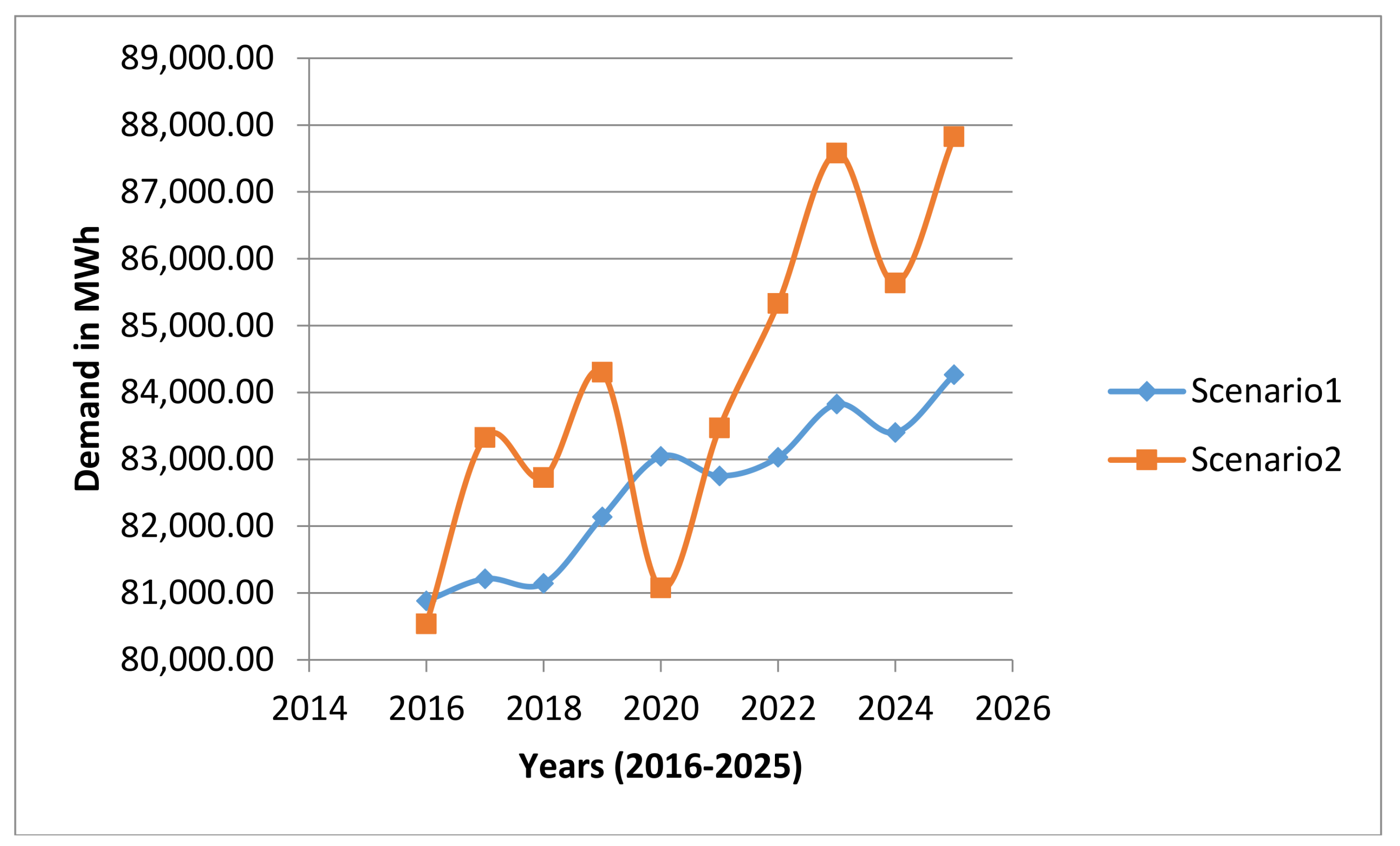
| Year | Scenario 1 | Scenario 2 |
|---|---|---|
| 2016 | 80,881 | 80,537 |
| 2017 | 81,213 | 83,324 |
| 2018 | 81,142 | 82,726 |
| 2019 | 82,137 | 84,301 |
| 2020 | 83,044 | 81,074 |
| 2021 | 82,752 | 83,469 |
| 2022 | 83,029 | 85,331 |
| 2023 | 83,826 | 87,581 |
| 2024 | 83,401 | 85,636 |
| 2025 | 84,263 | 87,825 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anand, A.; Suganthi, L. Hybrid GA-PSO Optimization of Artificial Neural Network for Forecasting Electricity Demand. Energies 2018, 11, 728. https://doi.org/10.3390/en11040728
Anand A, Suganthi L. Hybrid GA-PSO Optimization of Artificial Neural Network for Forecasting Electricity Demand. Energies. 2018; 11(4):728. https://doi.org/10.3390/en11040728
Chicago/Turabian StyleAnand, Atul, and L Suganthi. 2018. "Hybrid GA-PSO Optimization of Artificial Neural Network for Forecasting Electricity Demand" Energies 11, no. 4: 728. https://doi.org/10.3390/en11040728
APA StyleAnand, A., & Suganthi, L. (2018). Hybrid GA-PSO Optimization of Artificial Neural Network for Forecasting Electricity Demand. Energies, 11(4), 728. https://doi.org/10.3390/en11040728