A New Exact Mathematical Approach for Studying Bifurcation in DCM Operated dc-dc Switching Converters
Abstract
:1. Introduction
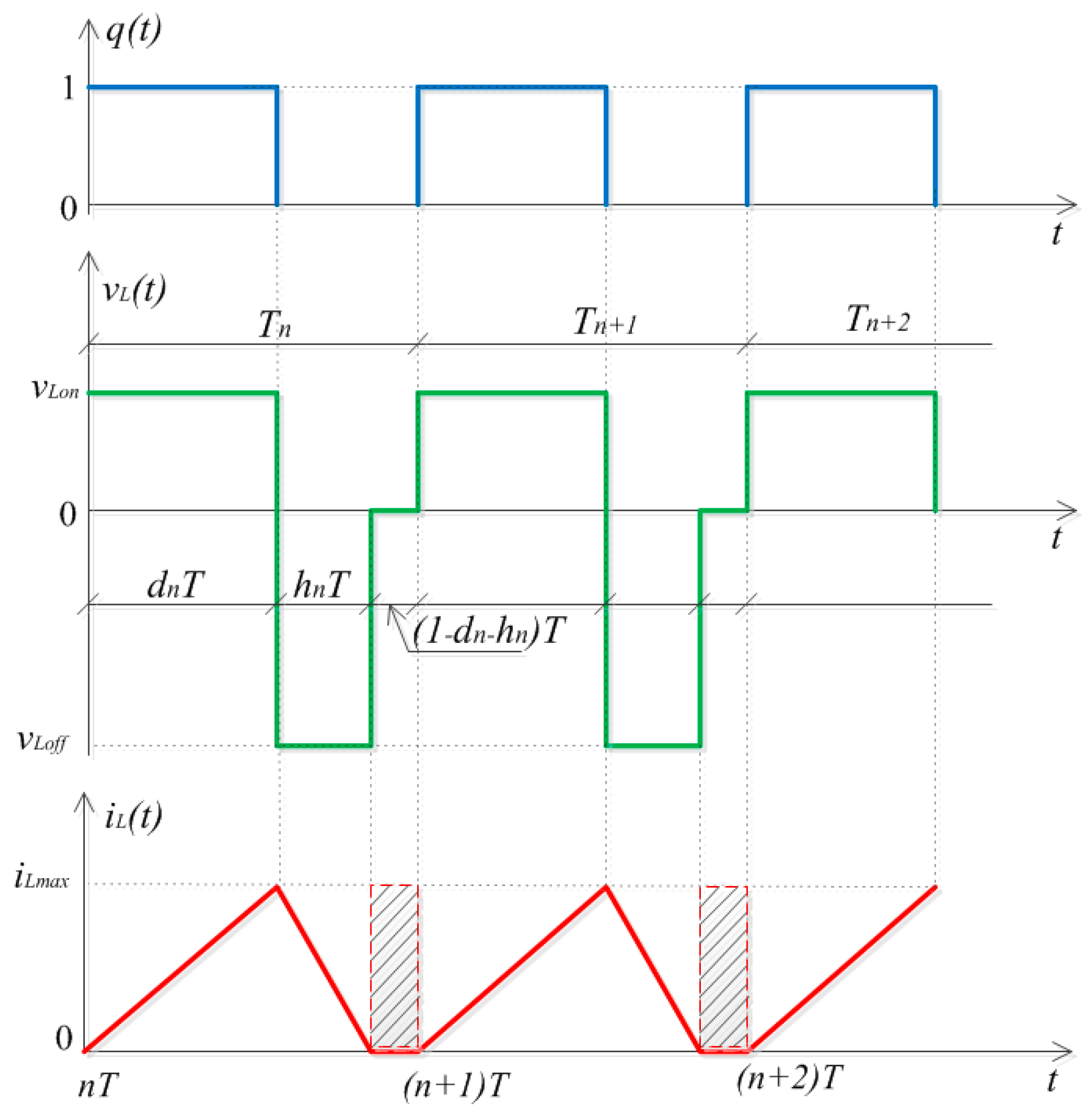
2. State-Space Description of the Discontinuous Conduction Mode
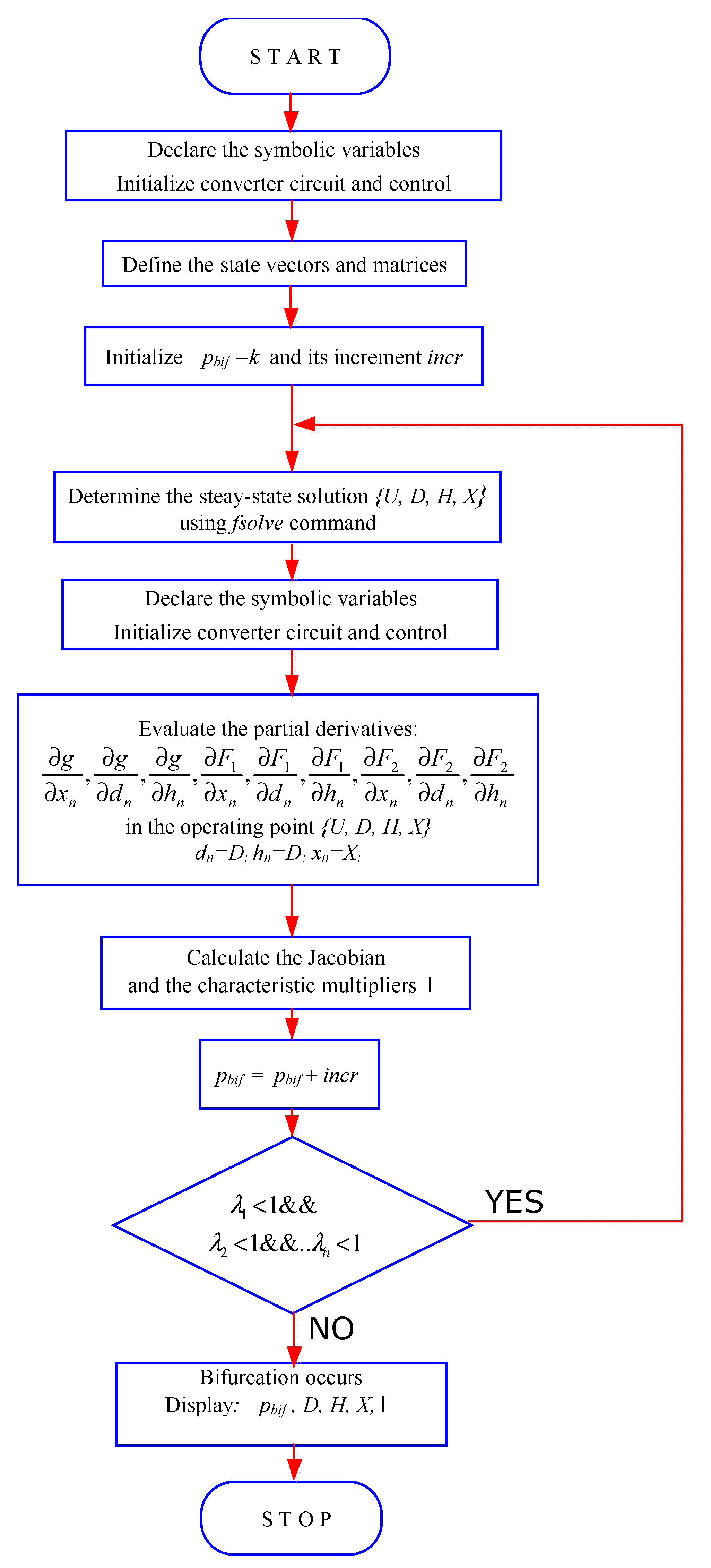
3. The New Method for Determining Bifurcation Parameter
4. Partial Derivatives of Functions g, F1, F2 and Exact Steady-State Operating Point Calculation
5. Bifurcation Analysis Using the Proposed Mathematical Model
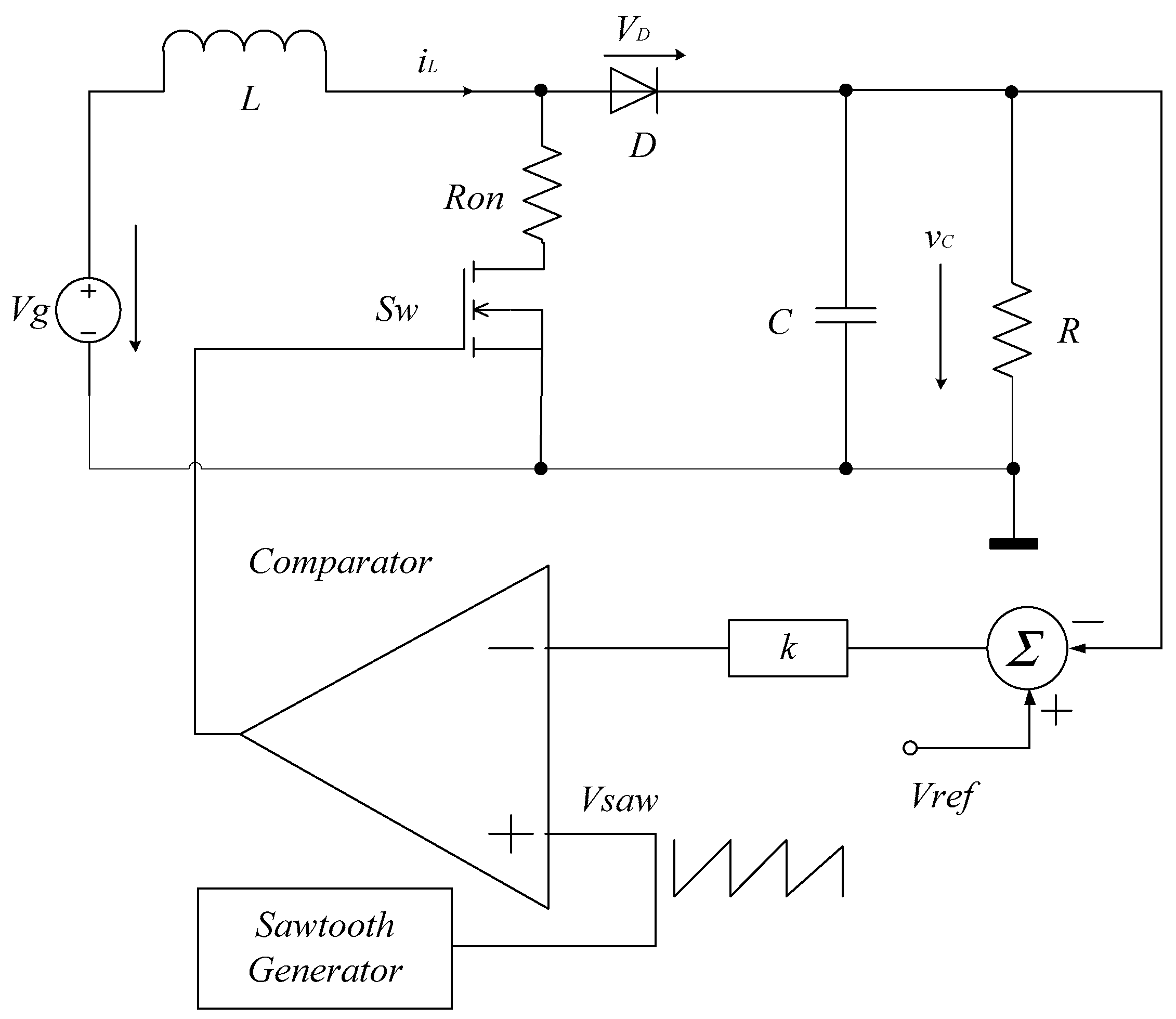
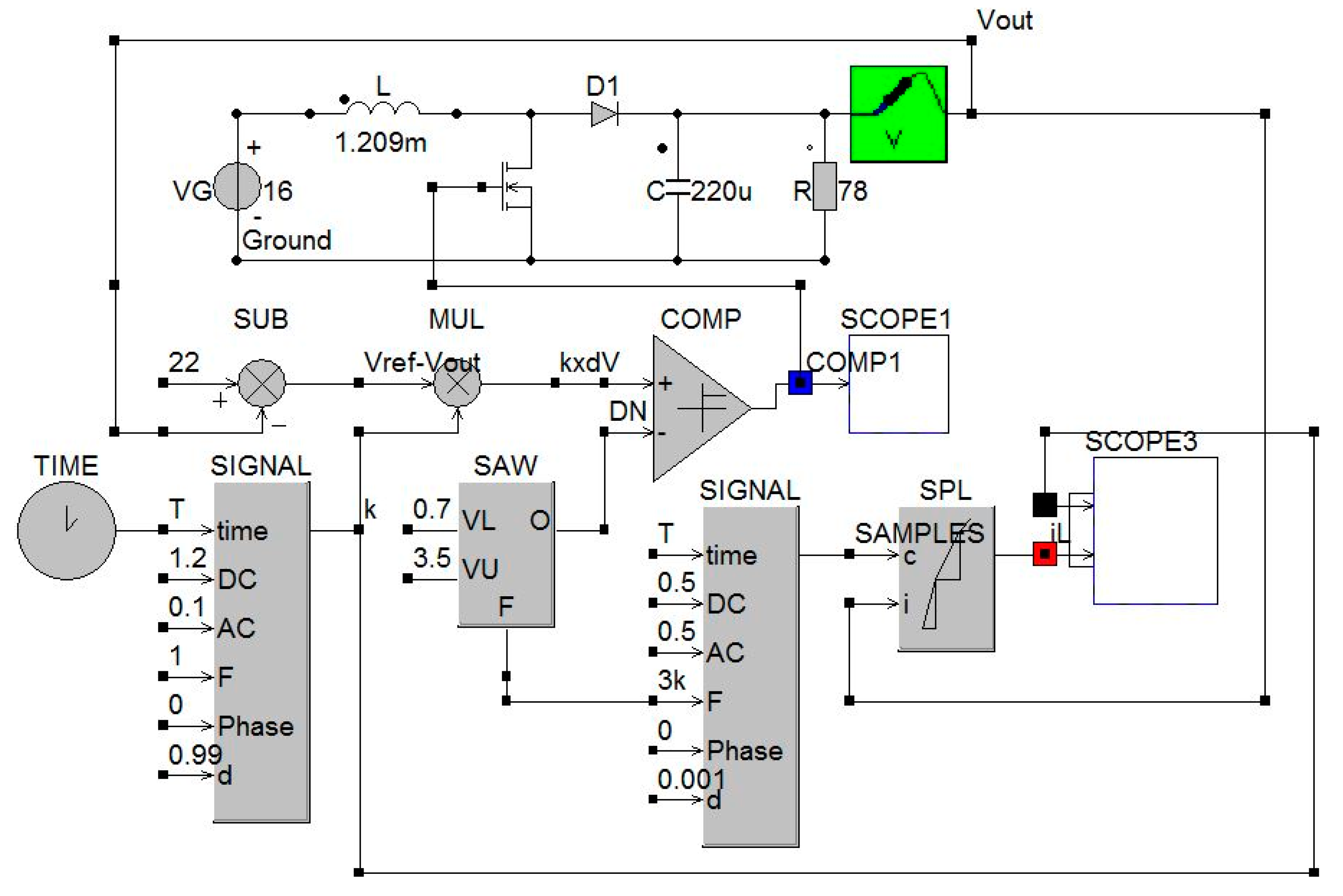
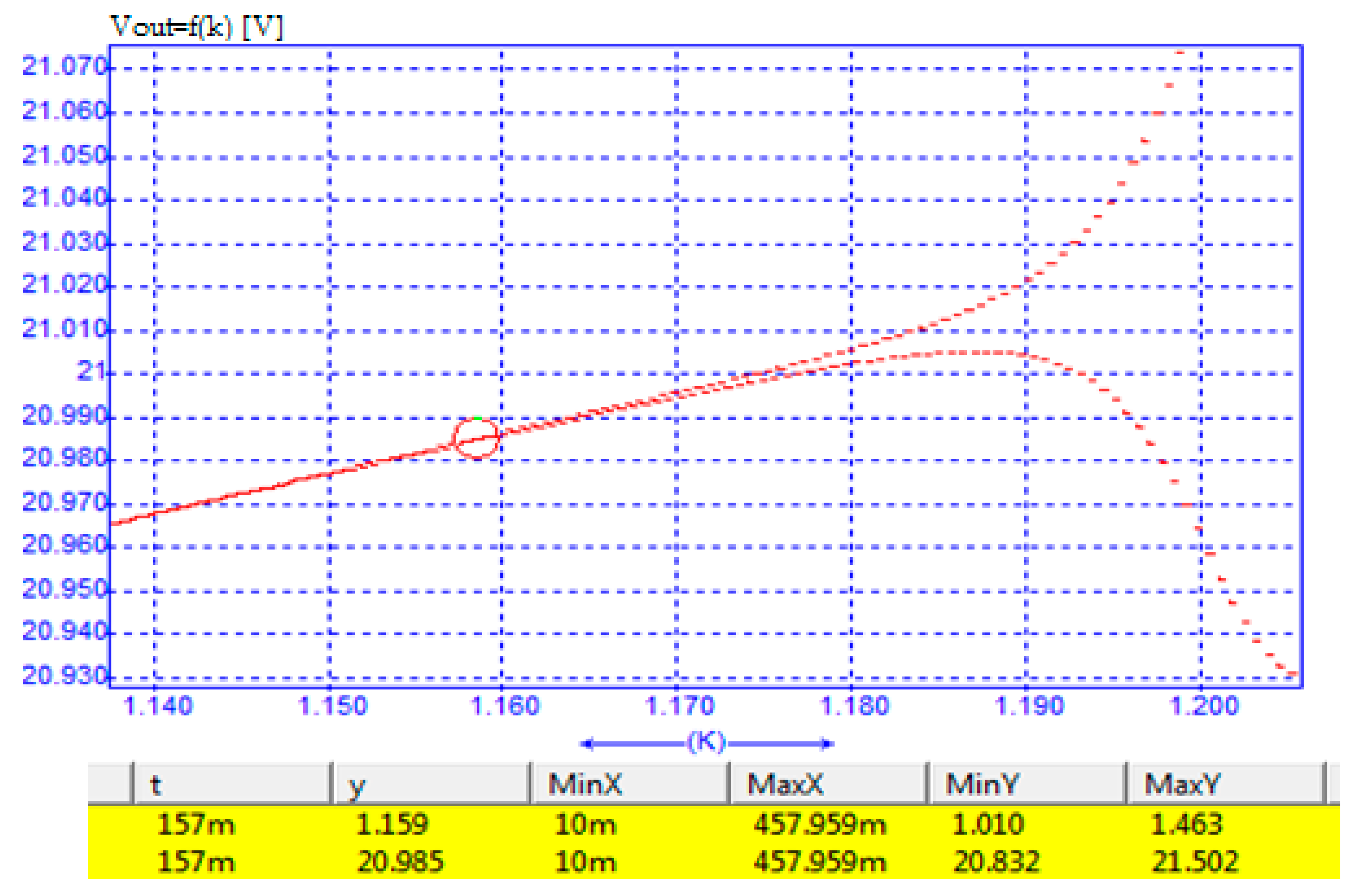
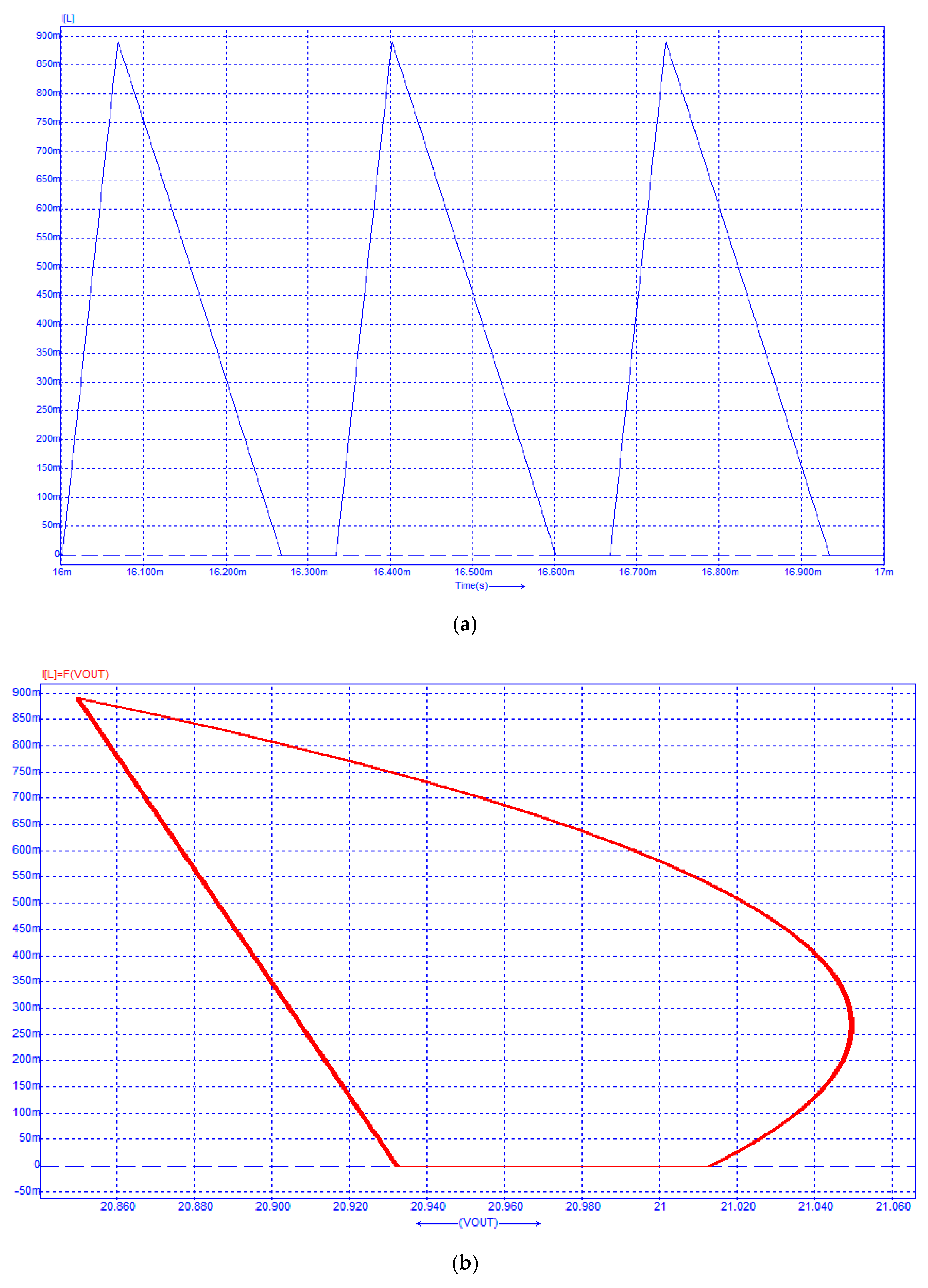
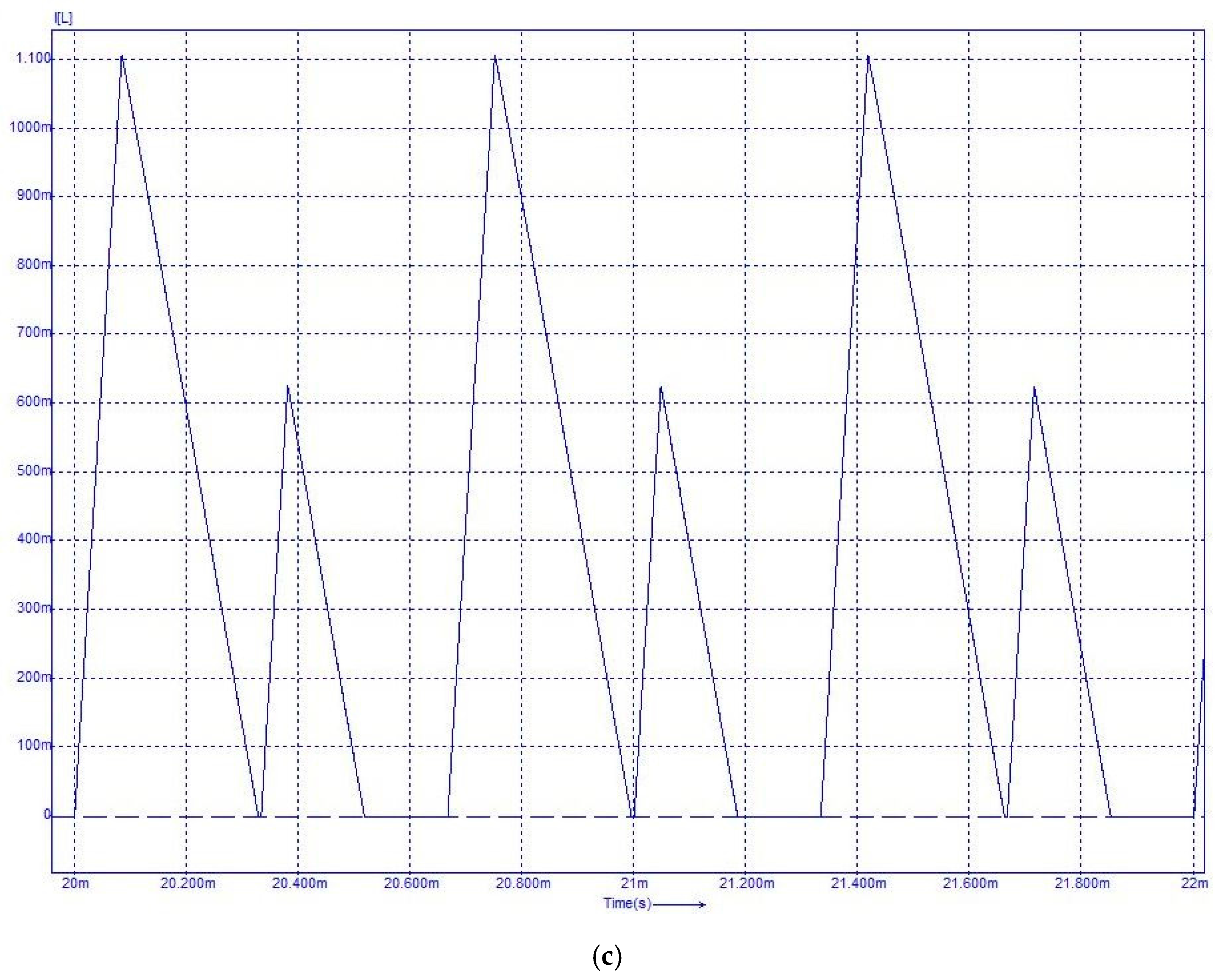
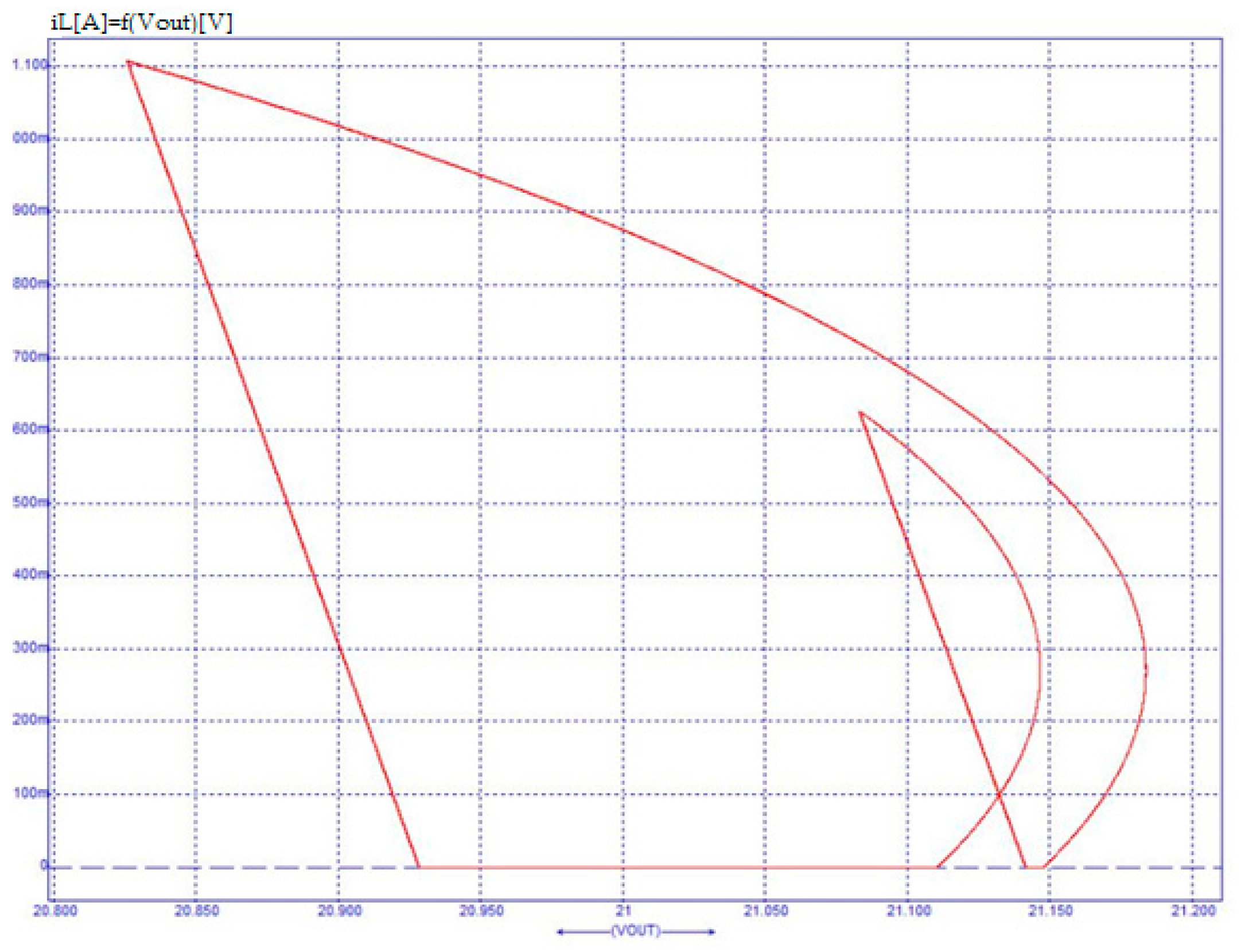
6. Validation through Circuit Simulation
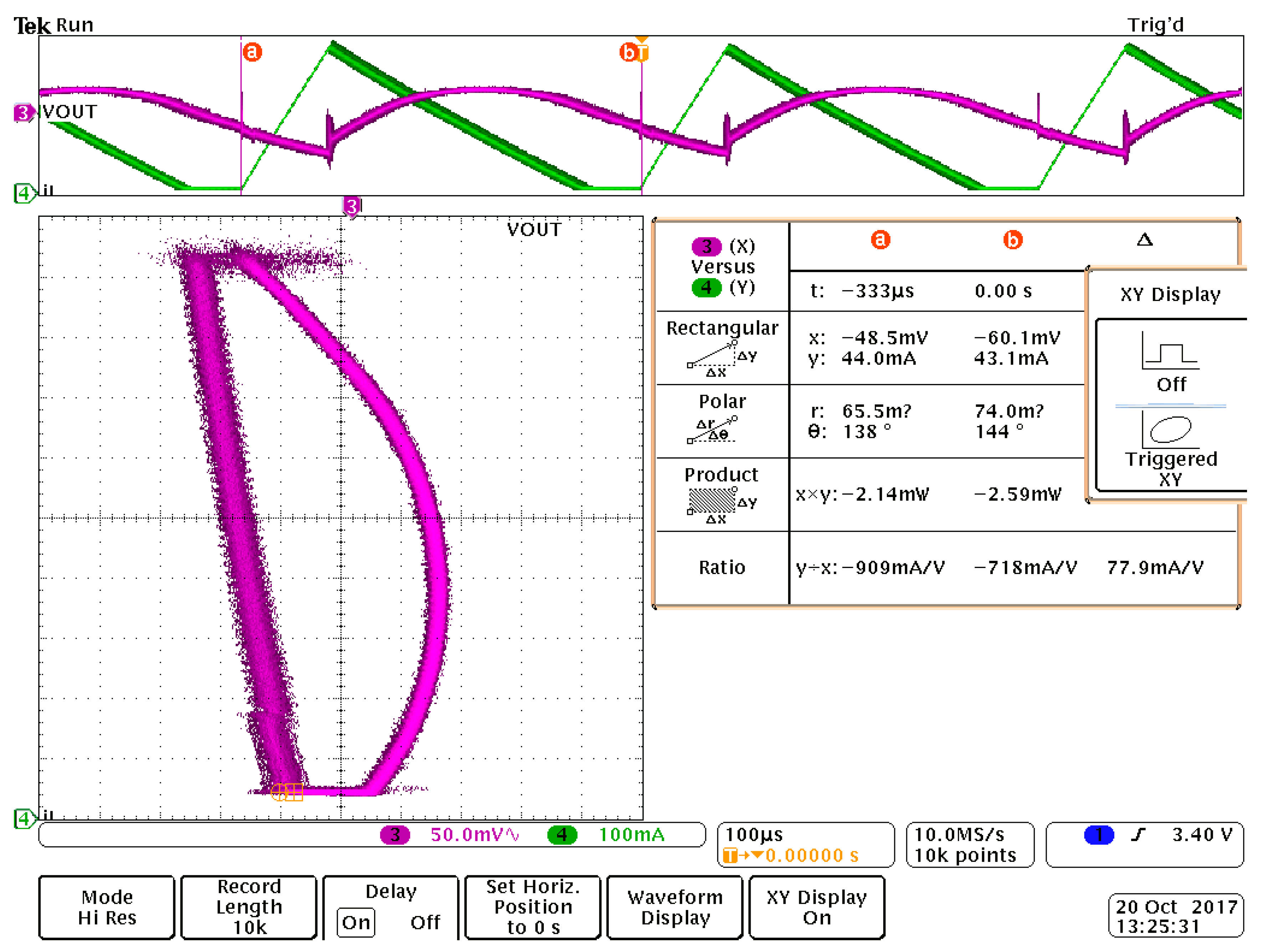
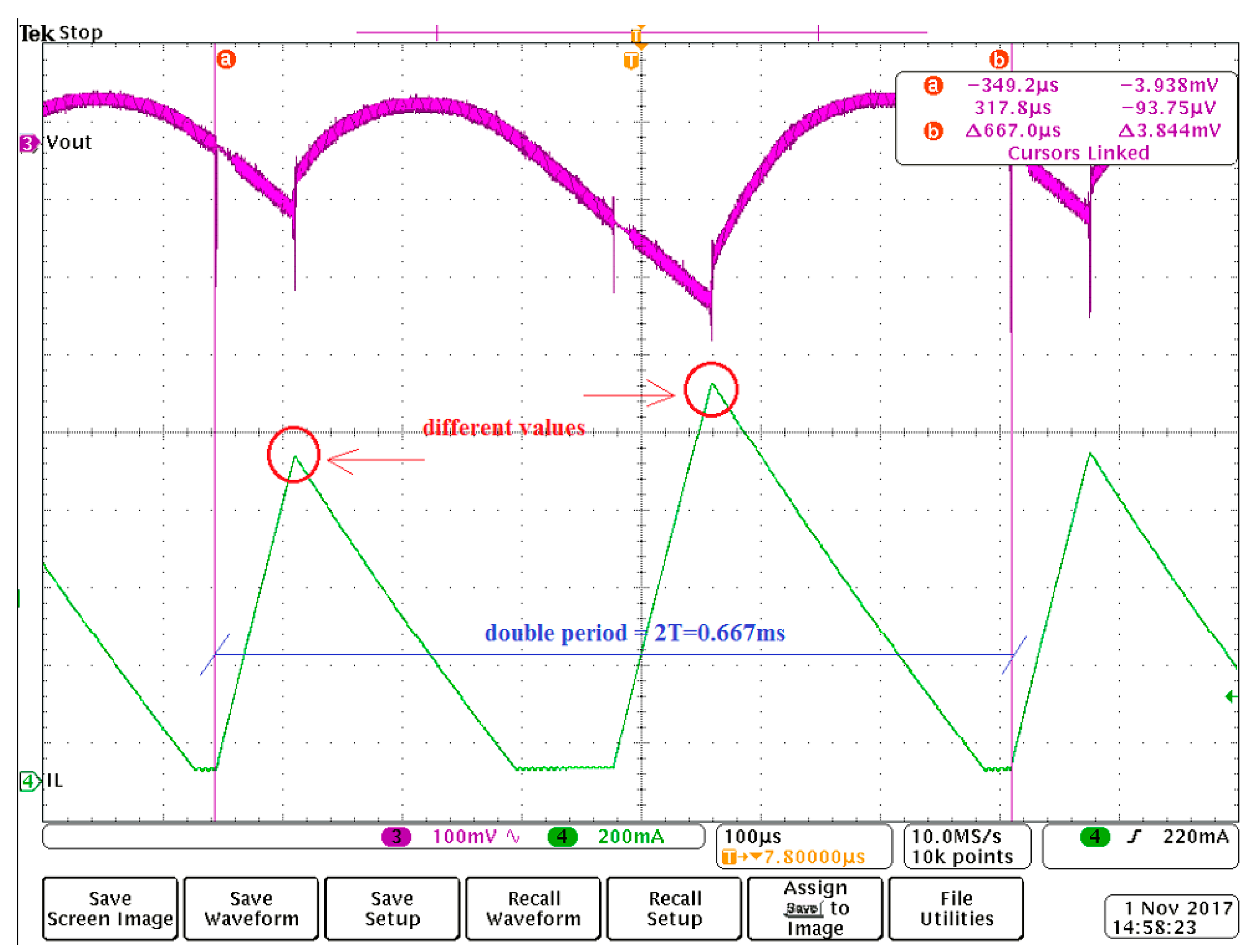
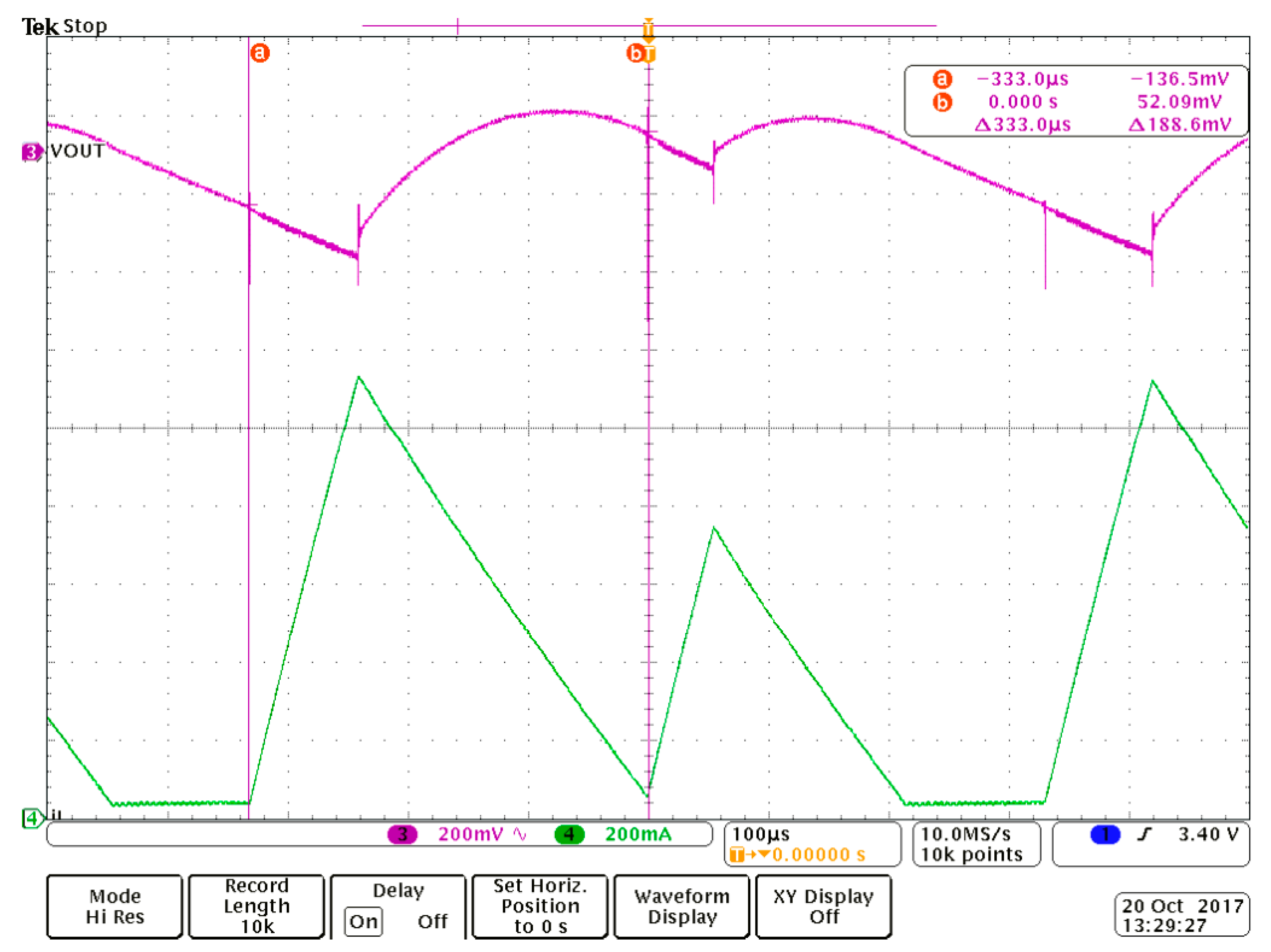
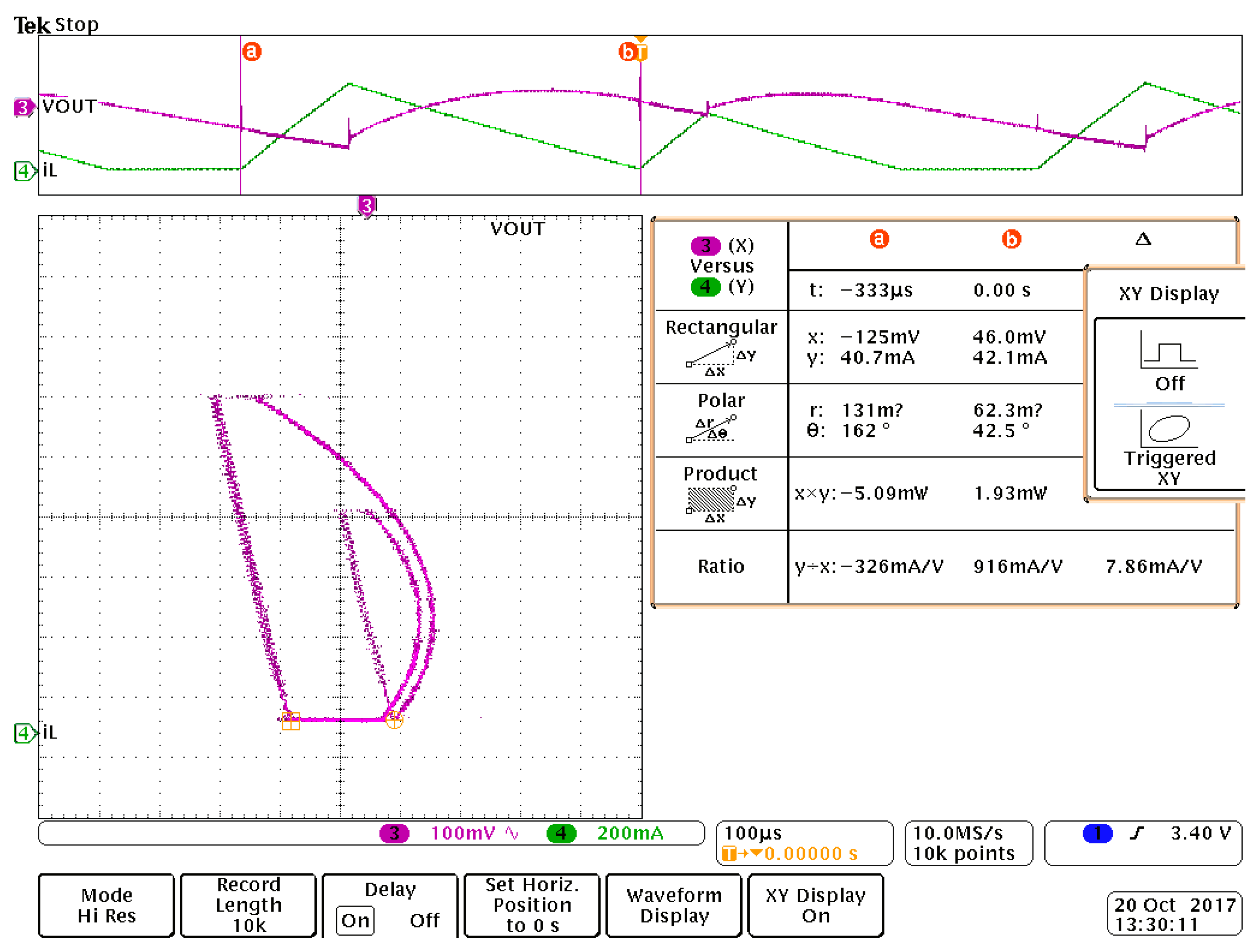
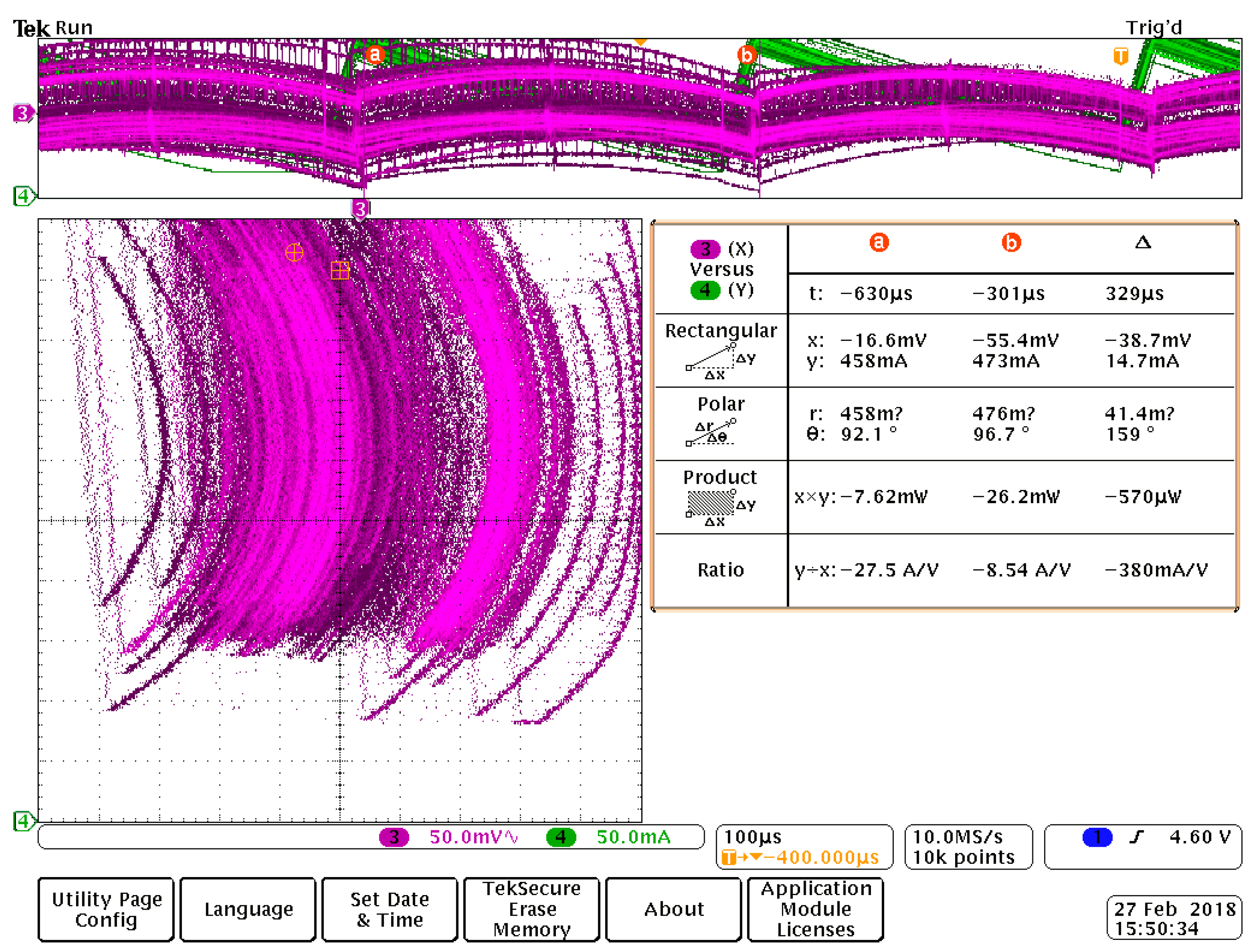
7. Experimental Results
8. Input Voltage as a Bifurcation Parameter
9. Conclusions
Author Contributions
Conflicts of Interest
Appendix A
Appendix B
Nomenclature
Main Symbols
| Ai, Bi | State matrices |
| VD | Diode voltage |
| vsaw | Sawtooth signal |
| Ri | Resistor |
| k | Gain |
| Vref | Reference voltage |
| VU, VL | The peak and the valley value of the sawtooth signal |
| q(t) | Transistor switching function |
| vL(t) | Inductor voltage |
| vc(t) | Output voltage |
| iL(t) | Inductor current |
| dn | Duty cycle |
| hnT | Second state |
| (1 − dn − hn)T | Third state |
| u(t) | Input vector |
| D | Dc duty cycle |
| H | Dc on state of diode |
| X | Steady state vector |
| U | Dc input vector |
| Vg | Input voltage |
| T, Tn, Tn + 1 | Switching period |
| Vexv | Extracts the capacitor voltage from state vector |
| C | Capacitor |
| L | Inductor |
| Ron | Transistor on resistance |
| Pi | Potentiometer |
| Vg | Second state and the third state respectively |
| x(t) | State vector |
| Vout | Output voltage |
Abbreviations
| PWM | Pulsed width modulated |
| ICi | Integrated circuits |
| OP | Operating point |
| SUB | Substract |
| MUL | Multiplicator |
| SIGNAL | Signal generator |
| TIME | Clock signal |
| SPL | Sample and Hold |
| DCM | Discontinuous conduction mode |
| CCM | Continuous conduction mode |
| CMPT | Current-mode pulse train |
| LTI | Linear time invariant |
Greek Symbols
| , | Transfer matrices |
| λ | Eigenvalue |
References
- Tse, C.-K. Complex Behavior of Switching Power Converters, 1st ed.; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA; Washington, DC, USA, 2003; pp. 91–106. [Google Scholar]
- Banerjee, S.; Verghese, G.C. Nonlinear Phenomena in Power Electronics, 1st ed.; IEEE Press: New York, NY, USA, 2001; pp. 25–52. [Google Scholar]
- Banerjee, S.; Chakrabarty, K. Nonlinear modeling and bifurcations in the boost converter. IEEE Trans. Power Electron. 1998, 13, 252–260. [Google Scholar] [CrossRef]
- Fang, C.-C.; Abed, E.-H. Sampled-Data Modeling and Analysis of PWM DC-DC Converters Part I. Closed-Loop Crcuits; Office of Naval Research: Arlington, TX, USA, 1998. [Google Scholar]
- Gurbina, M.; Draghici, D.; Ciresan, A.; Lascu, D. A New General Mathematical Technique for Stability and Bifurcation Analysis of DC-DC Converters Applied to One-Cycle Controlled Buck Converters with Non-Ideal Reset; Optimization of Electrical and Electronic Equipment (OPTIM): Bran, Romania, 2014; pp. 576–581. [Google Scholar]
- Gurbina, M.; Lica, S.; Lascu, D. Stability and bifurcation aspects in charge controlled DC-DC converters. In Proceedings of the 11th International Symposium on Electronics and Telecommunications (ISETC), Timisoara, Romania, 14–15 November 2014; pp. 1–4. [Google Scholar]
- Aroudi, A. A New Approach for Accurate Prediction of Subharmonic Oscillation in Switching Regulators—Part I: Mathematical Derivations. IEEE Trans. Power Electron. 2017, 32, 5651–5665. [Google Scholar] [CrossRef]
- Aroudi, A. A New Approach for Accurate Prediction of Subharmonic Oscillation in Switching Regulators—Part II: Case Studies. IEEE Trans. Power Electron. 2017, 32, 5835–5848. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, J.; Bao, B.; Zhou, G. Asynchronous-switching map-based stability effects of circuit parameters in fixed off-time controlled buck converter. IEEE Trans. Power Electron. 2016, 31, 6686–6697. [Google Scholar] [CrossRef]
- Parui, S.; Banerjee, S. Bifurcations due to transition from continuous conduction mode to discontinuous conduction mode in the boost converter. IEEE Trans. Circuits Syst. I 2003, 50, 1464–1469. [Google Scholar] [CrossRef]
- Tse, C.-K. Chaos from a buck switching regulator operating in discontinuous mode. Int. J. Circuit Theory Appl. 1994, 22, 263–278. [Google Scholar] [CrossRef]
- Vilamitjana, E.; Aroudi, A.; Alarcon, E. Chaos in Switching Converters for Power Management. Designing for Prediction and Control; Springer: Berlin, Germany, 2013; pp. 31–38. [Google Scholar]
- Xie, F.; Yang, R.; Zhang, B. Bifurcation and border collision analysis of voltage-mode-controlled flyback converter based on total ampere-turns. IEEE Trans. Circuits Syst. I 2011, 58, 2269–2280. [Google Scholar] [CrossRef]
- Xuesong, F.; Chuang, B.; Yong, X.; Qian, Z. Dynamical Analysis of the DCM Buck Converter; Communications, Circuits and Systems (ICCCAS): Chengdu, China, 2013; pp. 442–445. [Google Scholar]
- Jin, S.; Jianping, X.; Bocheng, B. Effects of circuit parameters on dynamics of current-mode-pulse-train-controlled buck converter. IEEE Trans. Ind. Electron. 2014, 61, 1562–1573. [Google Scholar]
- Parui, S.; Basak, B. Inherent oscillation in Cuk converter and its effect on bifurcation phenomena. In Proceedings of the TENCON 2014 IEEE Region 10 Conference, Bangkok, Thailand, 22–25 October 2014; pp. 1–6. [Google Scholar]
- CASPOC. User Manual. Available online: http://www.simulation-research.com (accessed on 11 January 2018).
- Ivan, C.; Lascu, D.; Popescu, V. Hopf Bifurcation in a Discontinuous Capacitor Voltage Mode Ćuk dc-dc Converter. In Proceedings of the 6th WSEAS International Conference on Instrumentation, Measurement, Circuits and Systems, Hangzhou, China, 15–17 April 2007; pp. 78–83. [Google Scholar]
- Suntiom, T. Unified average and small-signal modeling of direct-on-time control. IEEE Trans. Ind. Electron. 2006, 53, 287–295. [Google Scholar] [CrossRef]



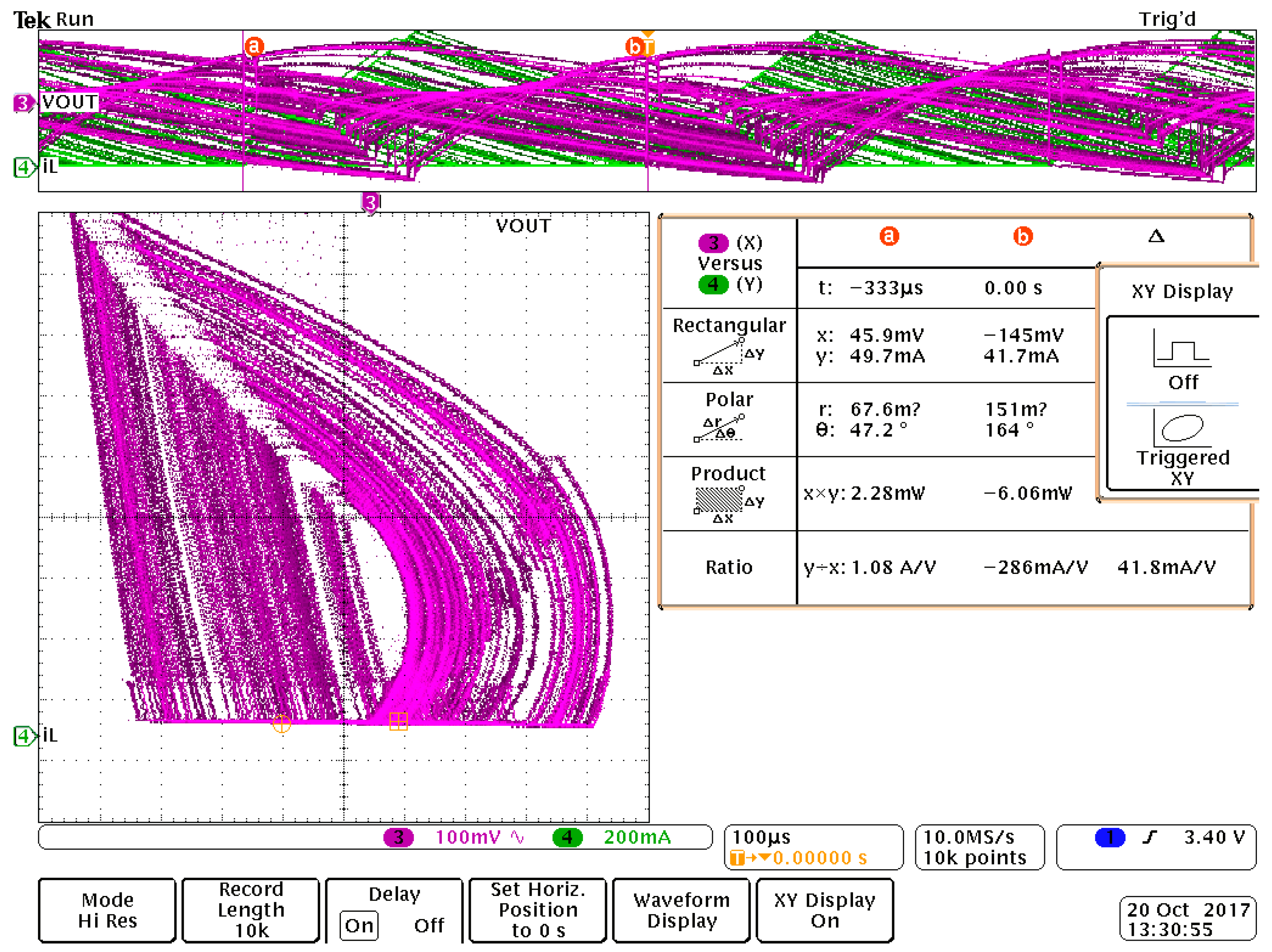
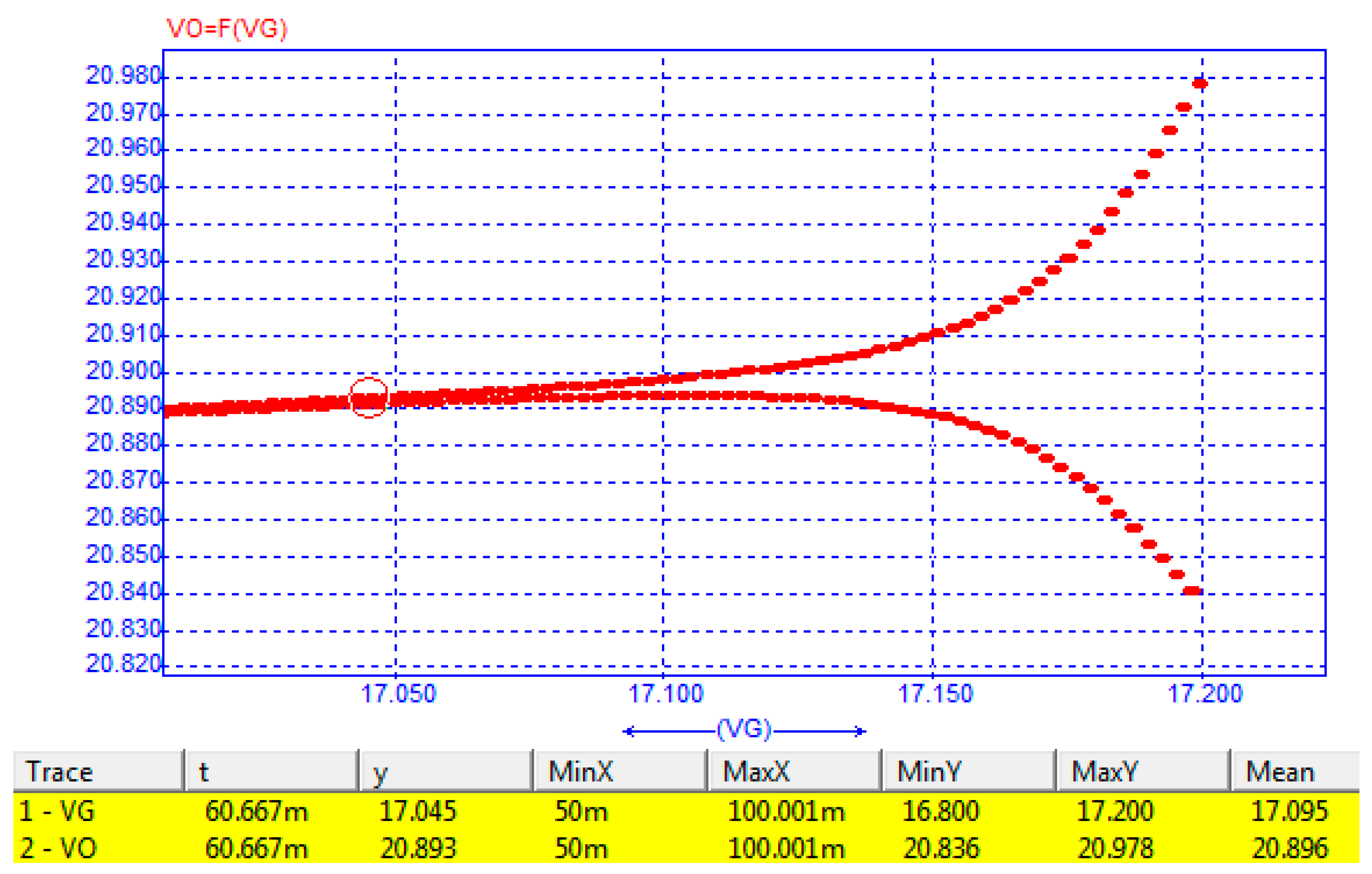
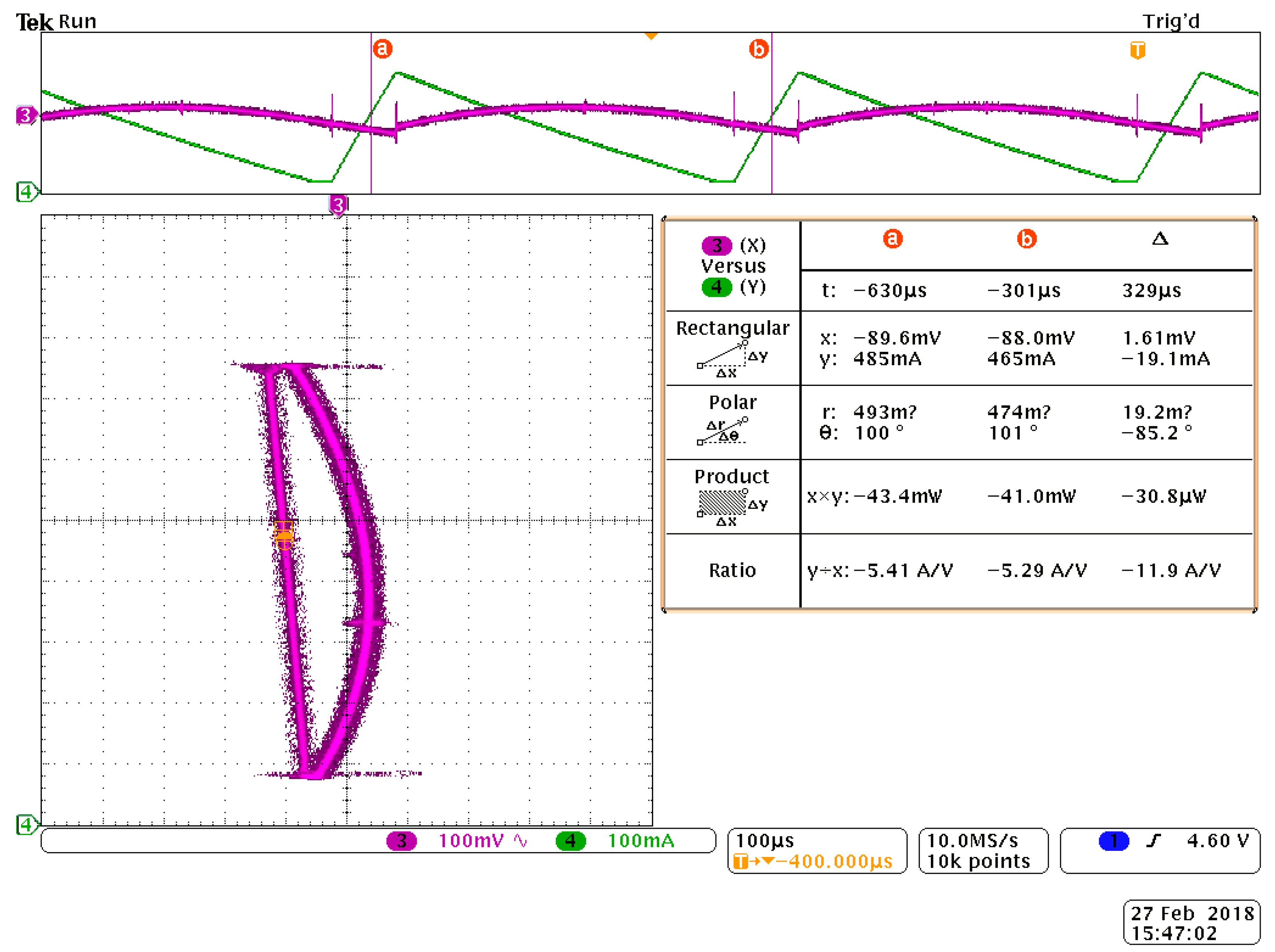
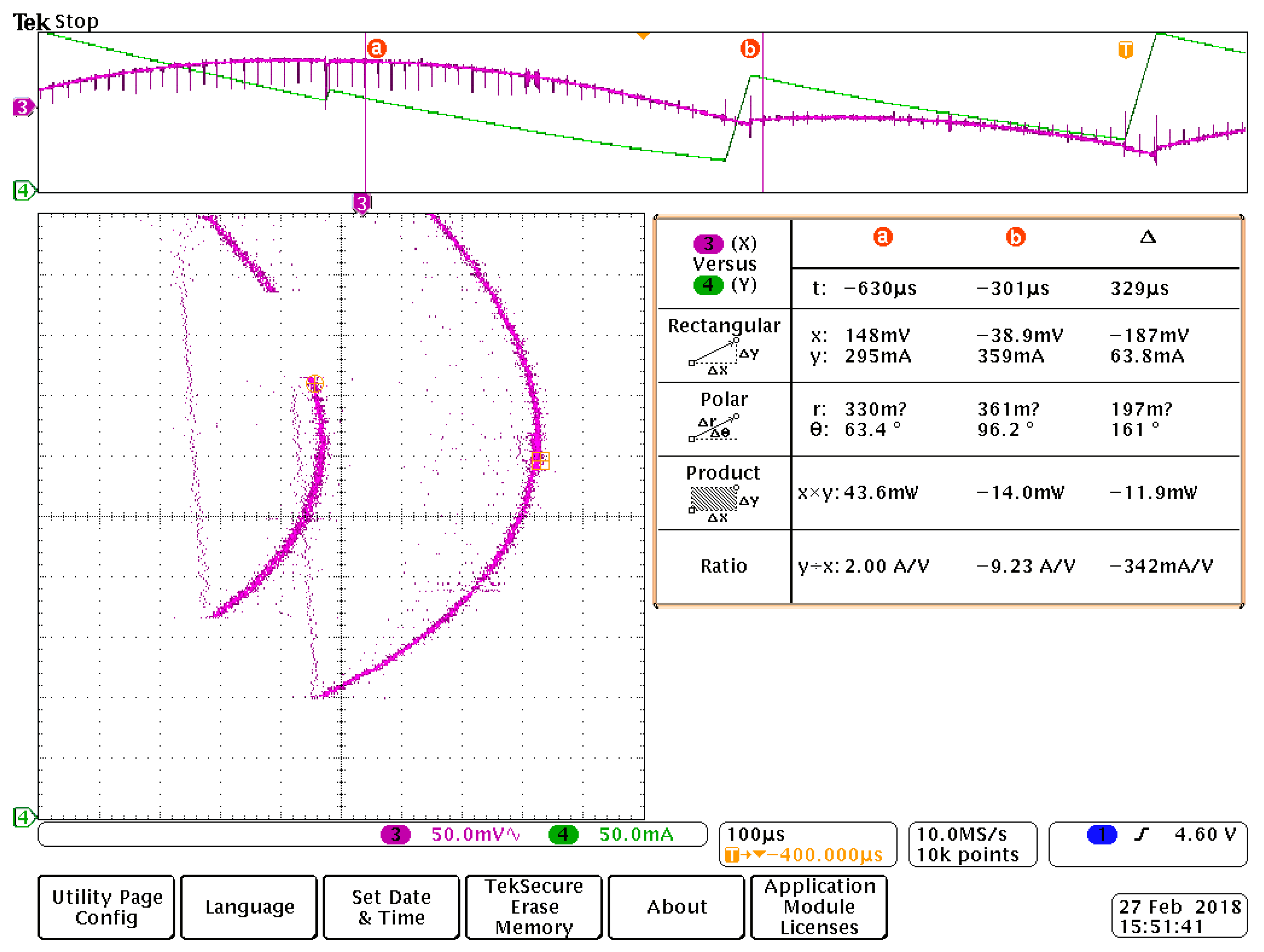
| Gain k | Eingenvalue l1 | Eingenvalue l2 | Remark |
|---|---|---|---|
| 1.1560 | −0.9945 | 0.0000 | stable |
| 1.1570 | −0.9964 | 0.0000 | stable |
| 1.1580 | −0.9983 | 0.0000 | stable |
| 1.1589 | −1.0000 | 0.0000 | Bifurcation |
| 1.1600 | −1.0020 | 0.0000 | Bifurcation |
| 1.2000 | −1.0775 | 0.0000 | Bifurcation |
| 1.3000 | −1.2715 | 0.0000 | Bifurcation |
| Voltage Vg | Eingenvalue l1 | Eingenvalue l2 | Remark |
|---|---|---|---|
| 16.6000 | −0.8623 | 0.0000 | stable |
| 16.8000 | −0.8983 | 0.0000 | stable |
| 17.0000 | −0.9751 | 0.0000 | stable |
| 17.1250 | −1.0000 | 0.0000 | Bifurcation |
| 17.2000 | −1.0138 | 0.0000 | Bifurcation |
| 17.4000 | −1.0572 | 0.0000 | Bifurcation |
| 17.6000 | −1.1040 | 0.0000 | Bifurcation |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gurbina, M.; Ciresan, A.; Lascu, D.; Lica, S.; Pop-Calimanu, I.-M. A New Exact Mathematical Approach for Studying Bifurcation in DCM Operated dc-dc Switching Converters. Energies 2018, 11, 663. https://doi.org/10.3390/en11030663
Gurbina M, Ciresan A, Lascu D, Lica S, Pop-Calimanu I-M. A New Exact Mathematical Approach for Studying Bifurcation in DCM Operated dc-dc Switching Converters. Energies. 2018; 11(3):663. https://doi.org/10.3390/en11030663
Chicago/Turabian StyleGurbina, Mircea, Aurel Ciresan, Dan Lascu, Septimiu Lica, and Ioana-Monica Pop-Calimanu. 2018. "A New Exact Mathematical Approach for Studying Bifurcation in DCM Operated dc-dc Switching Converters" Energies 11, no. 3: 663. https://doi.org/10.3390/en11030663
APA StyleGurbina, M., Ciresan, A., Lascu, D., Lica, S., & Pop-Calimanu, I.-M. (2018). A New Exact Mathematical Approach for Studying Bifurcation in DCM Operated dc-dc Switching Converters. Energies, 11(3), 663. https://doi.org/10.3390/en11030663






