A Multi-Parameter Optimization Model for the Evaluation of Shale Gas Recovery Enhancement
Abstract
:1. Introduction
2. Optimization Method and Objective Function Setting
2.1. Design of Experiments
2.2. Response Surface Methodology
2.3. Objective Function
- Maximize cumulative gas production
- Minimize treatment cost
3. Brief Description of Numerical Forward Model for Shale Gas Reservoir Simulations
3.1. Fully Coupled Hydro-Mechanical FEC-DPM
3.1.1. Reservoirs Deformation
3.1.2. Gas Flow in Matrix
3.1.3. Gas Flow in Natural Fracture Network
3.1.4. Gas Flow in Hydraulic Fractures
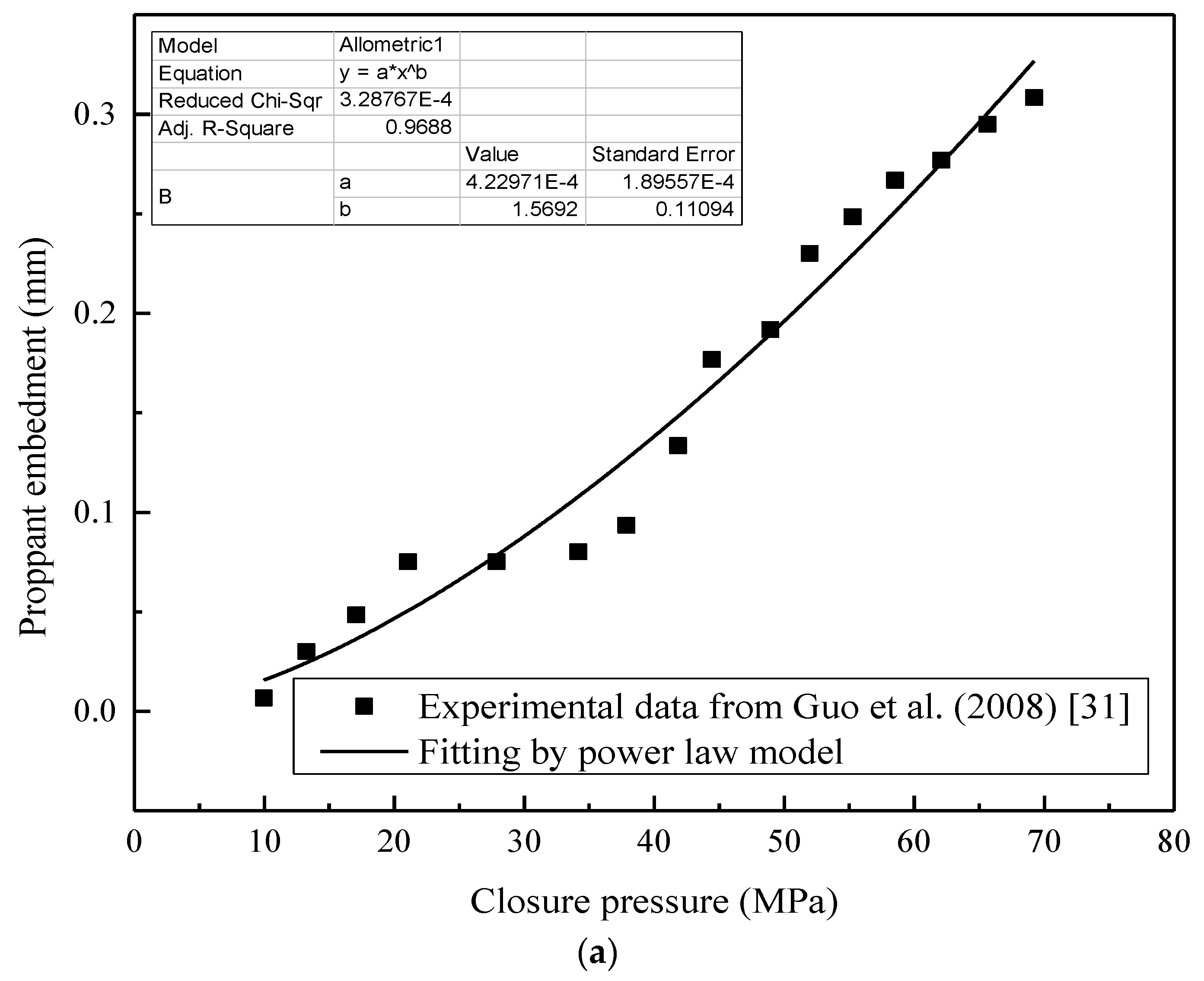
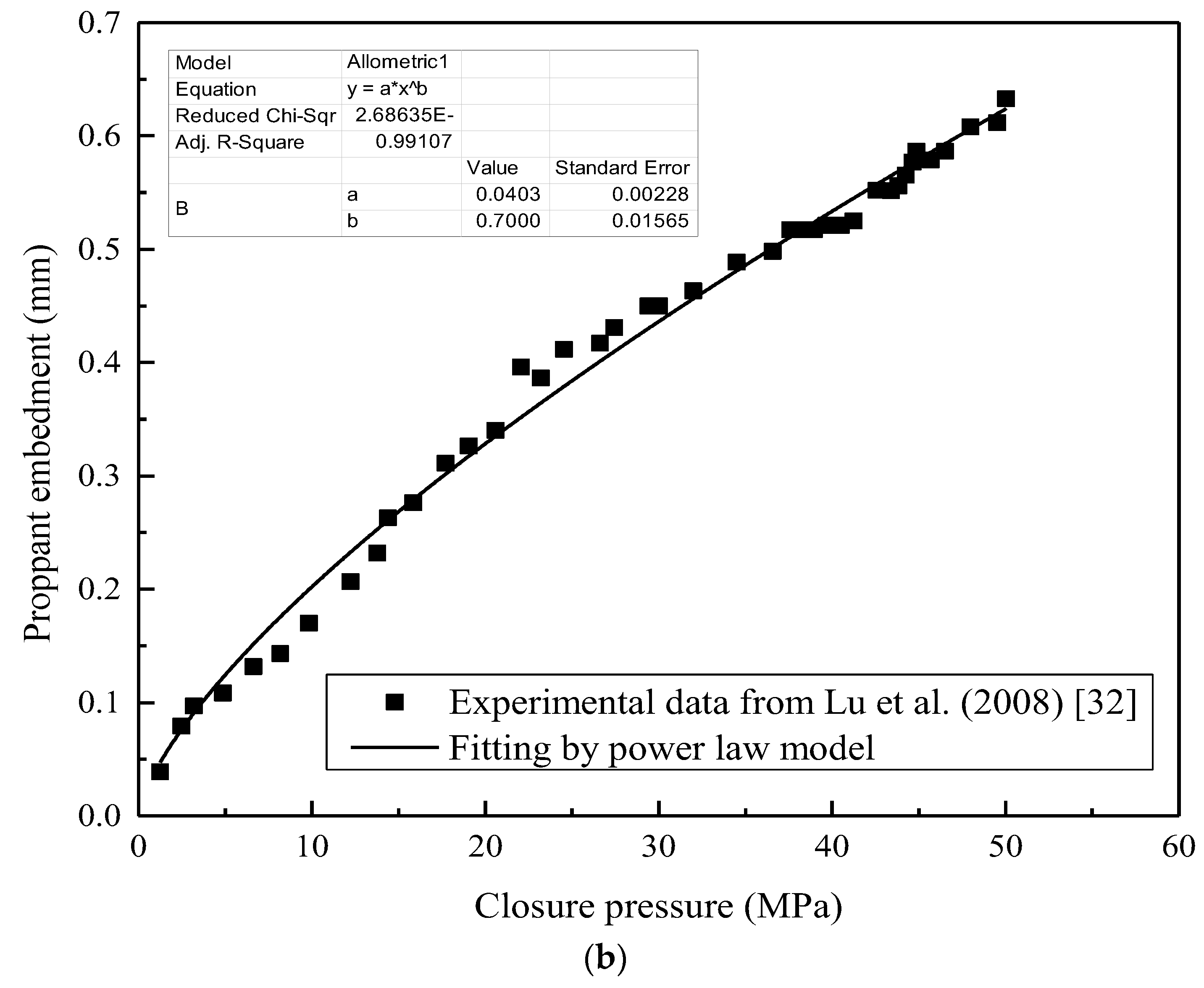
3.2. Proppant-Pack Hydraulic Fracture Conductivity
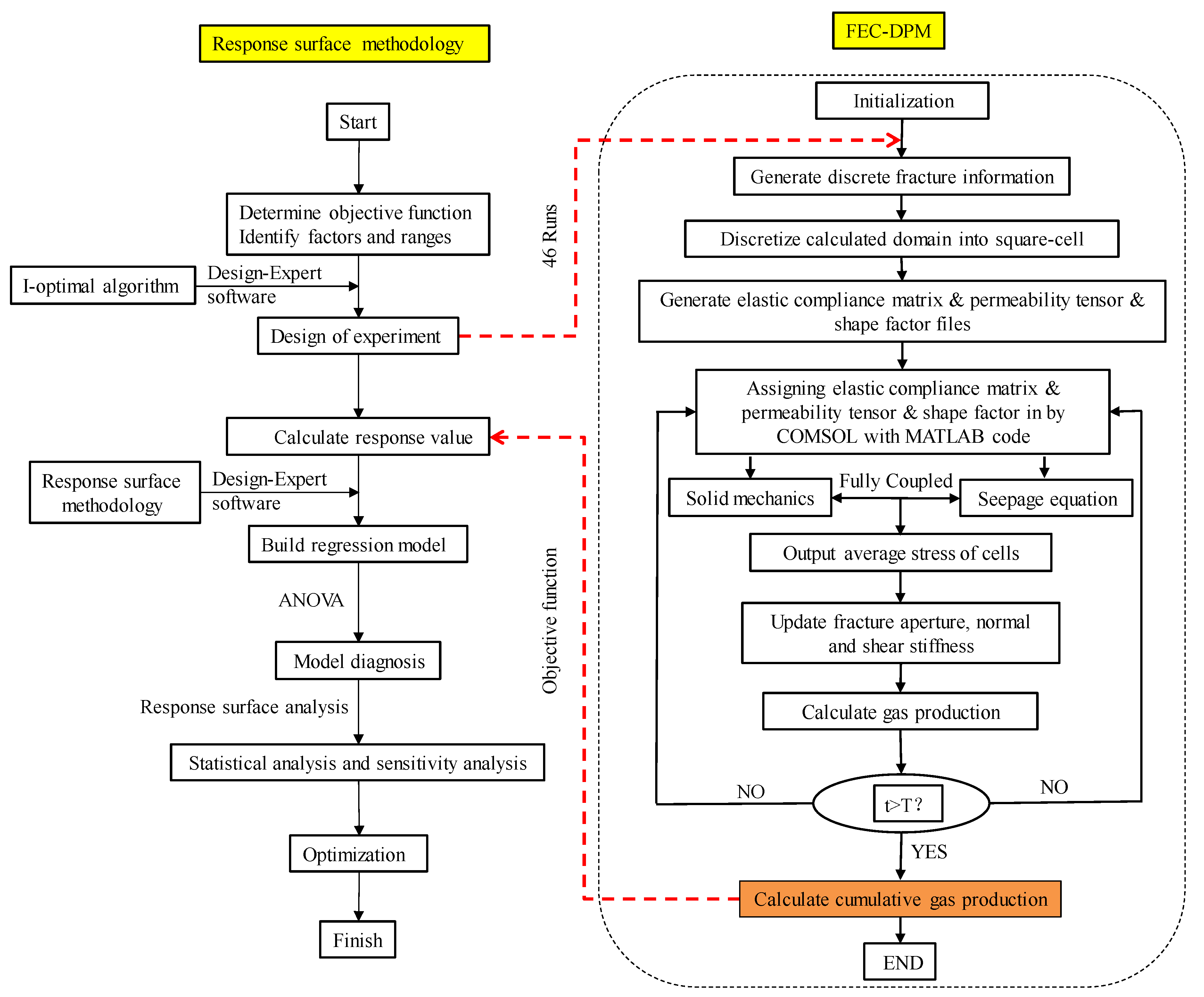
3.3. Model Setup and Numerical Implementation Procedure
3.4. FEC-DPM Model Validation
4. Results and Discussions
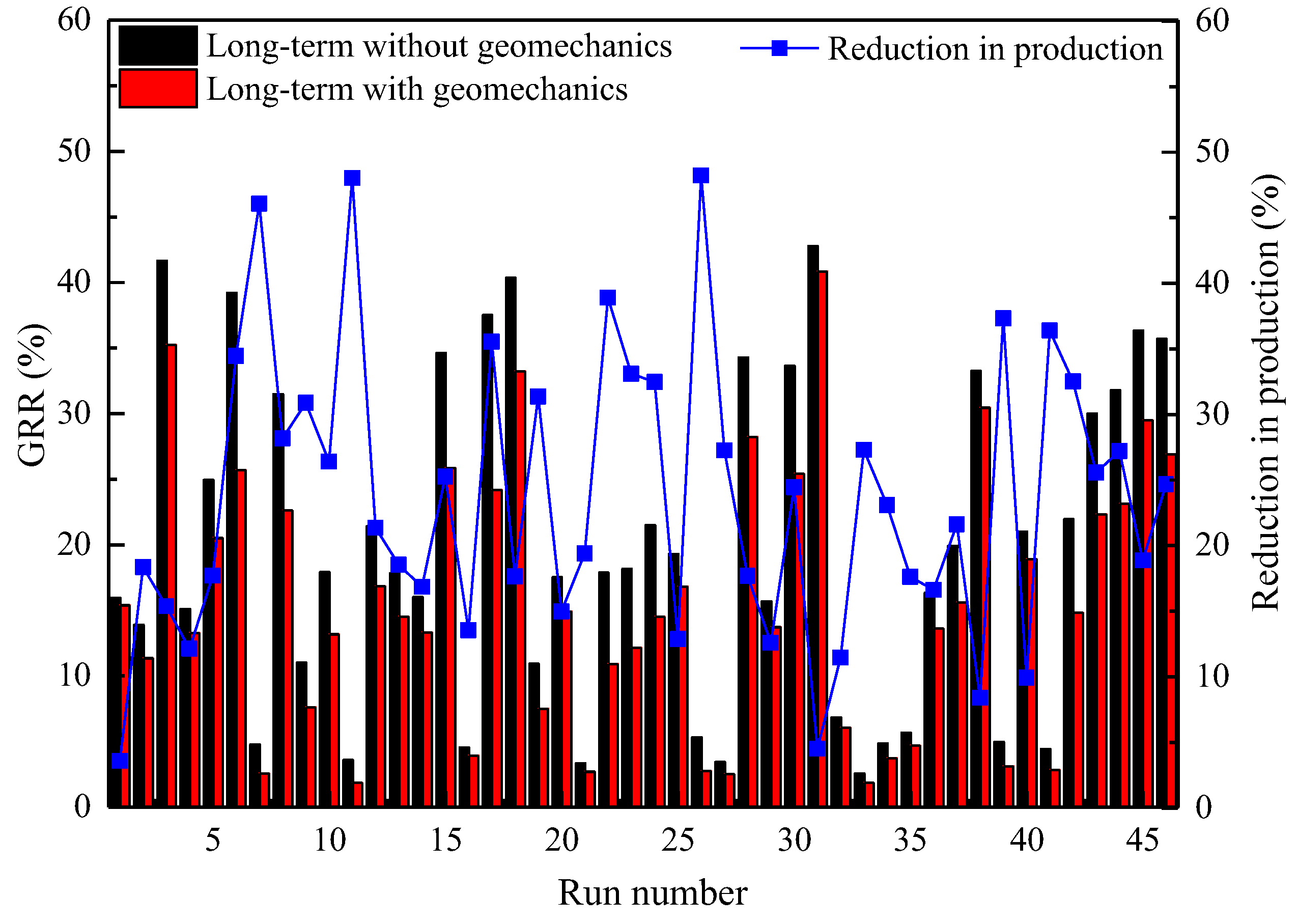
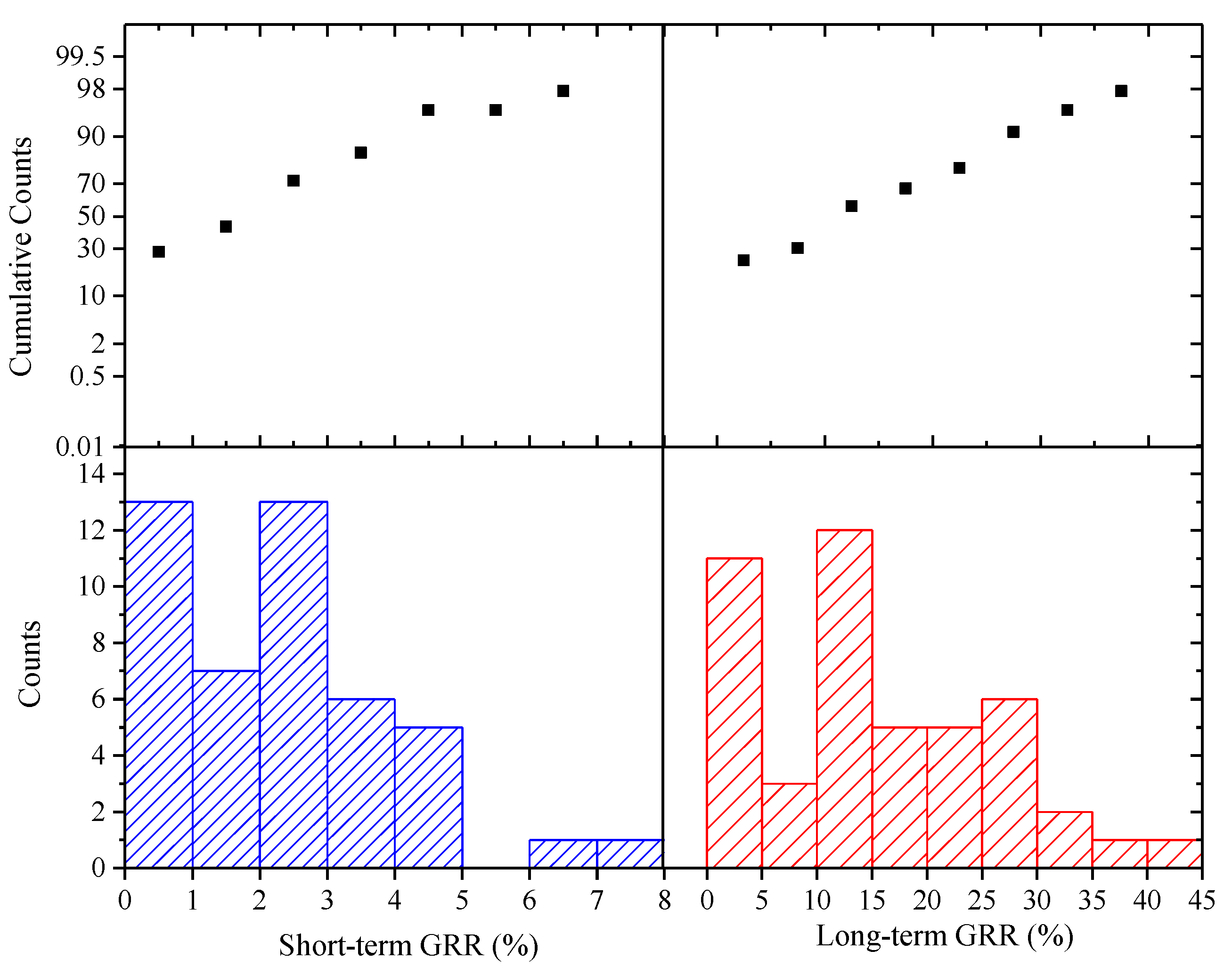
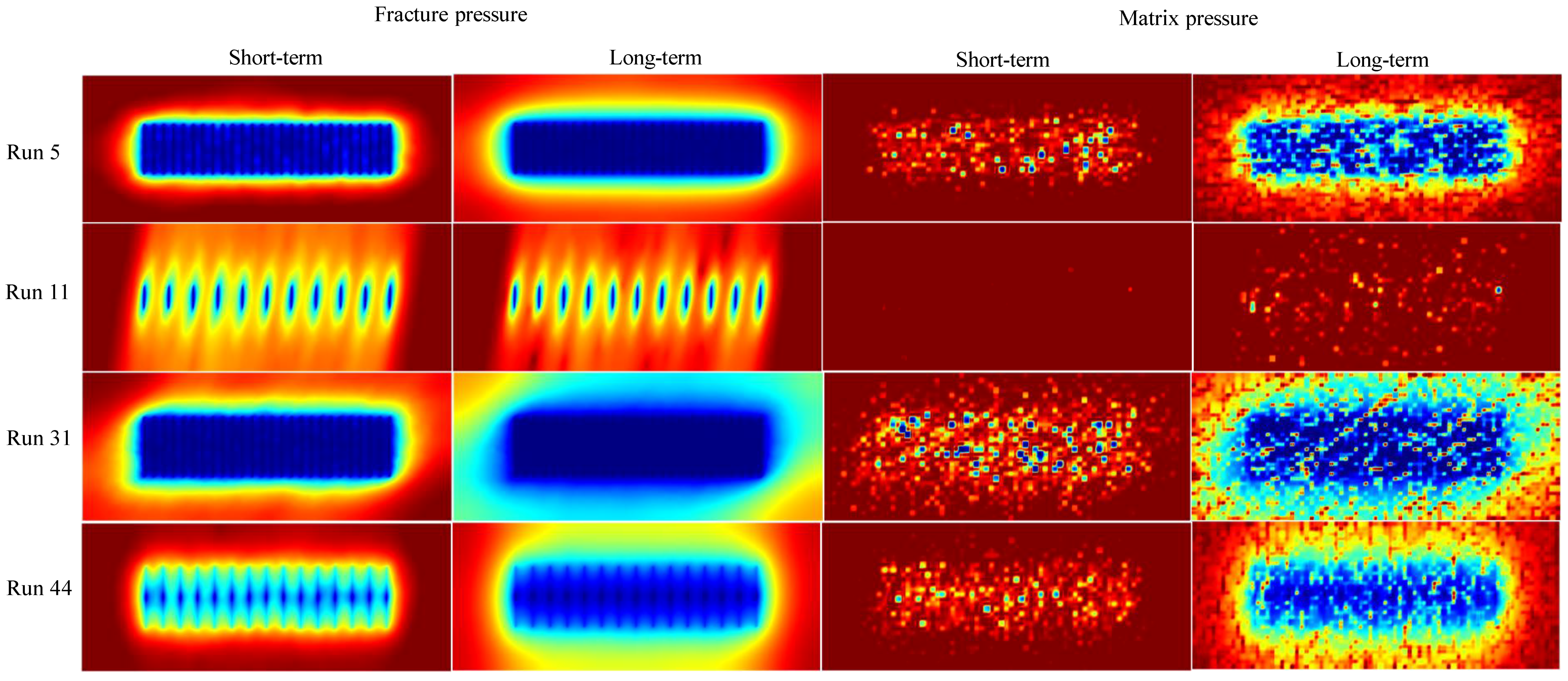
4.1. Simulation Results
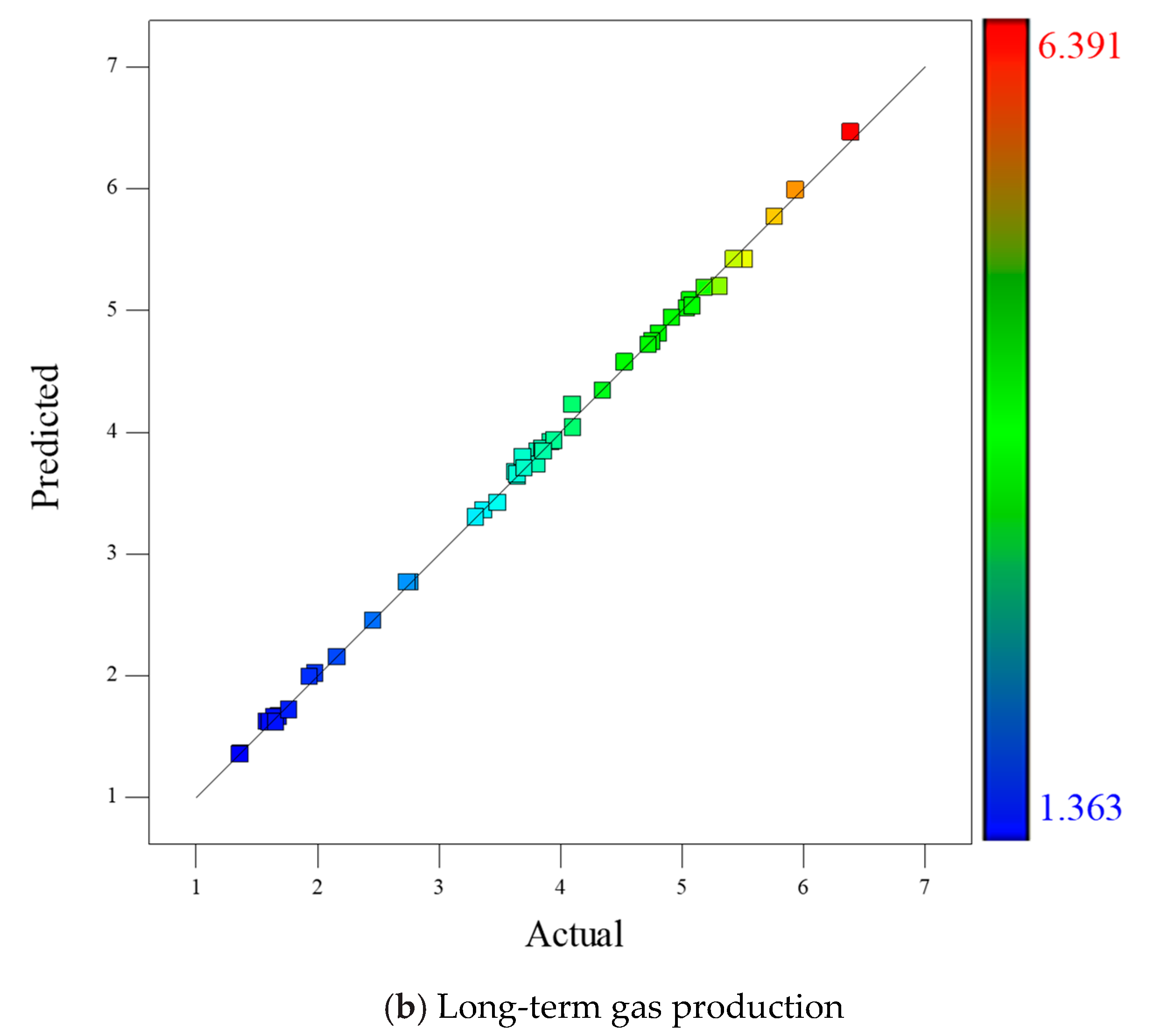
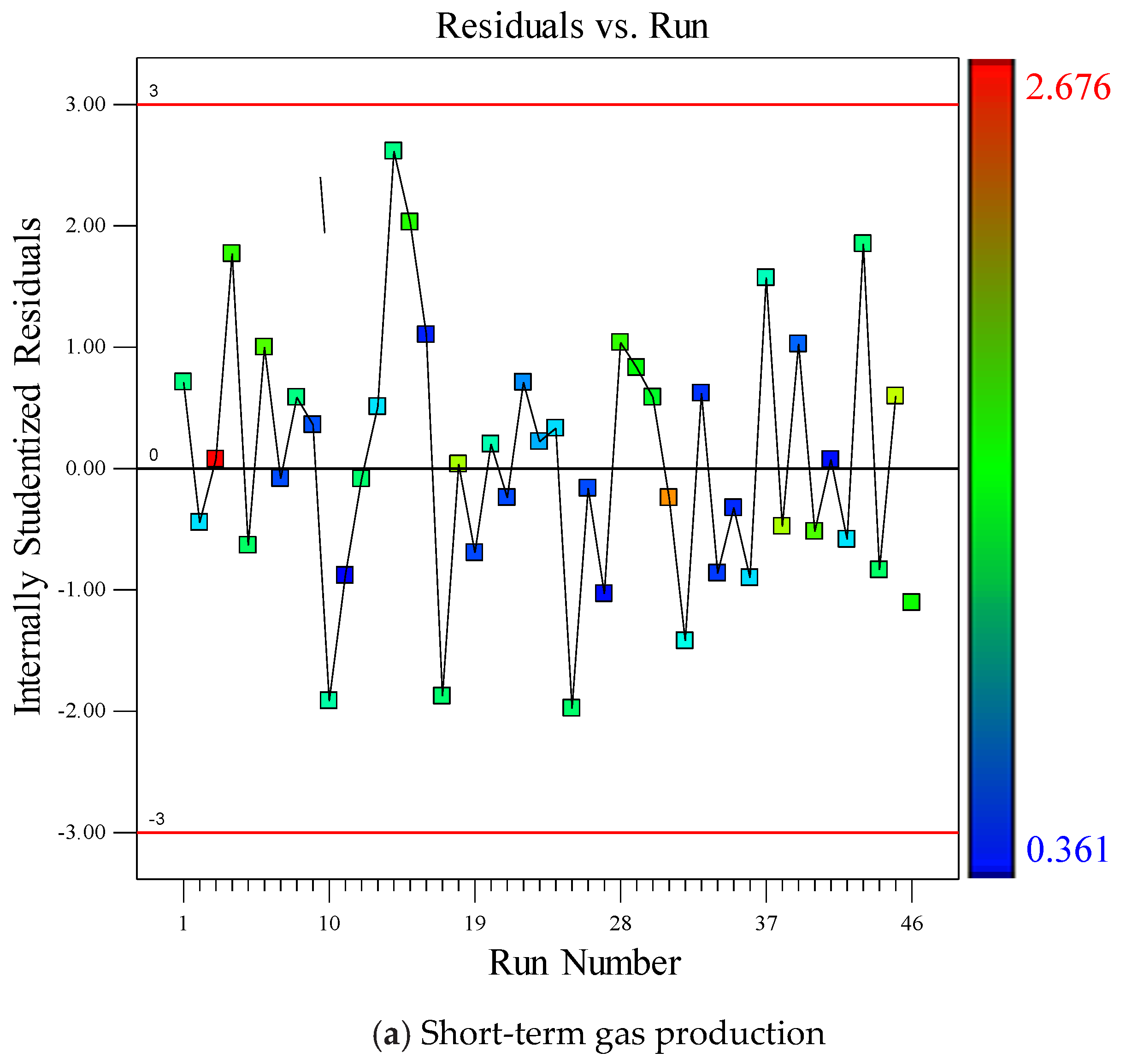
4.2. Regression Model and Statistical Analysis
4.2.1. Fitting Equations
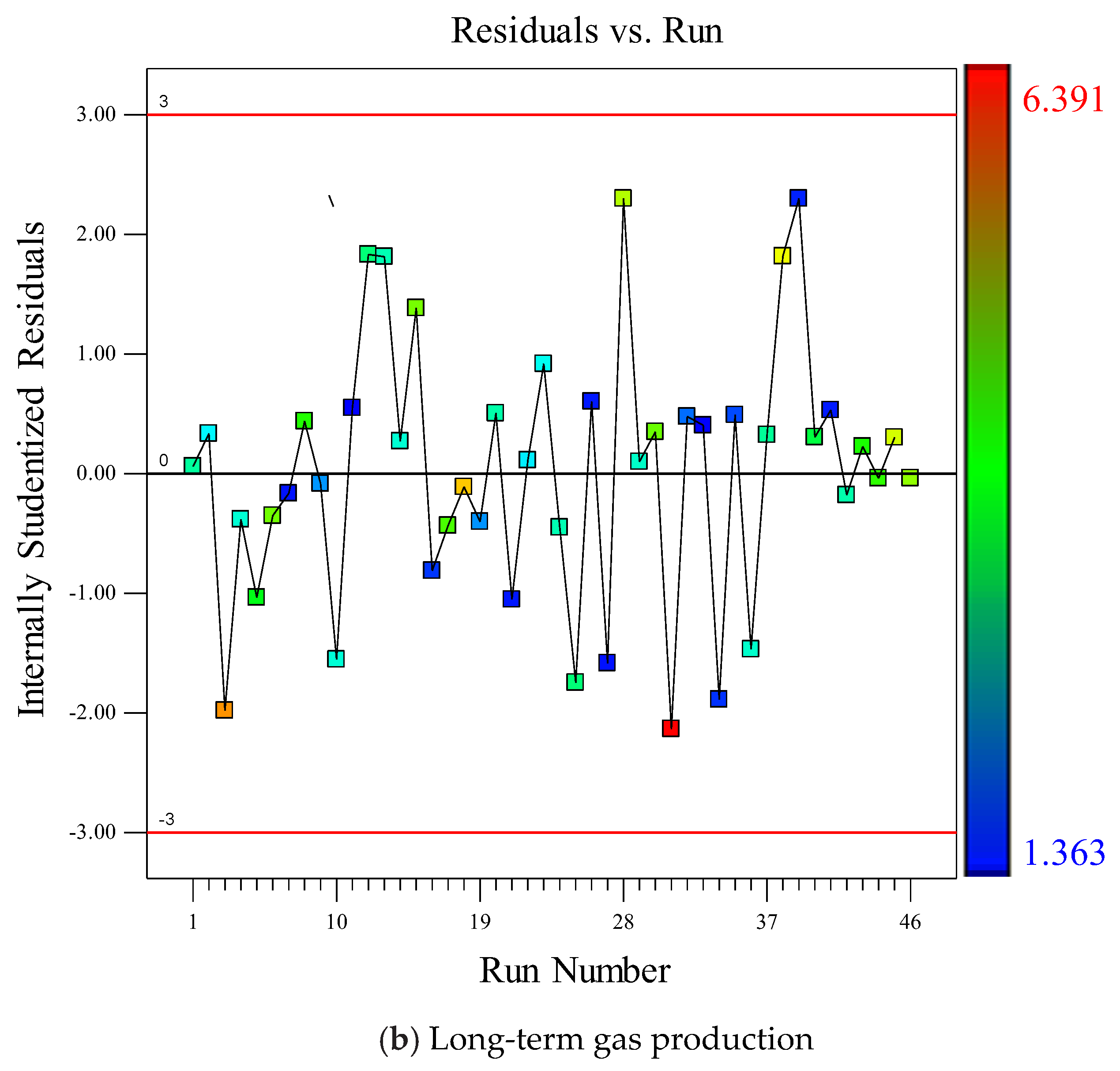
4.2.2. Analysis of Variance (ANOVA)
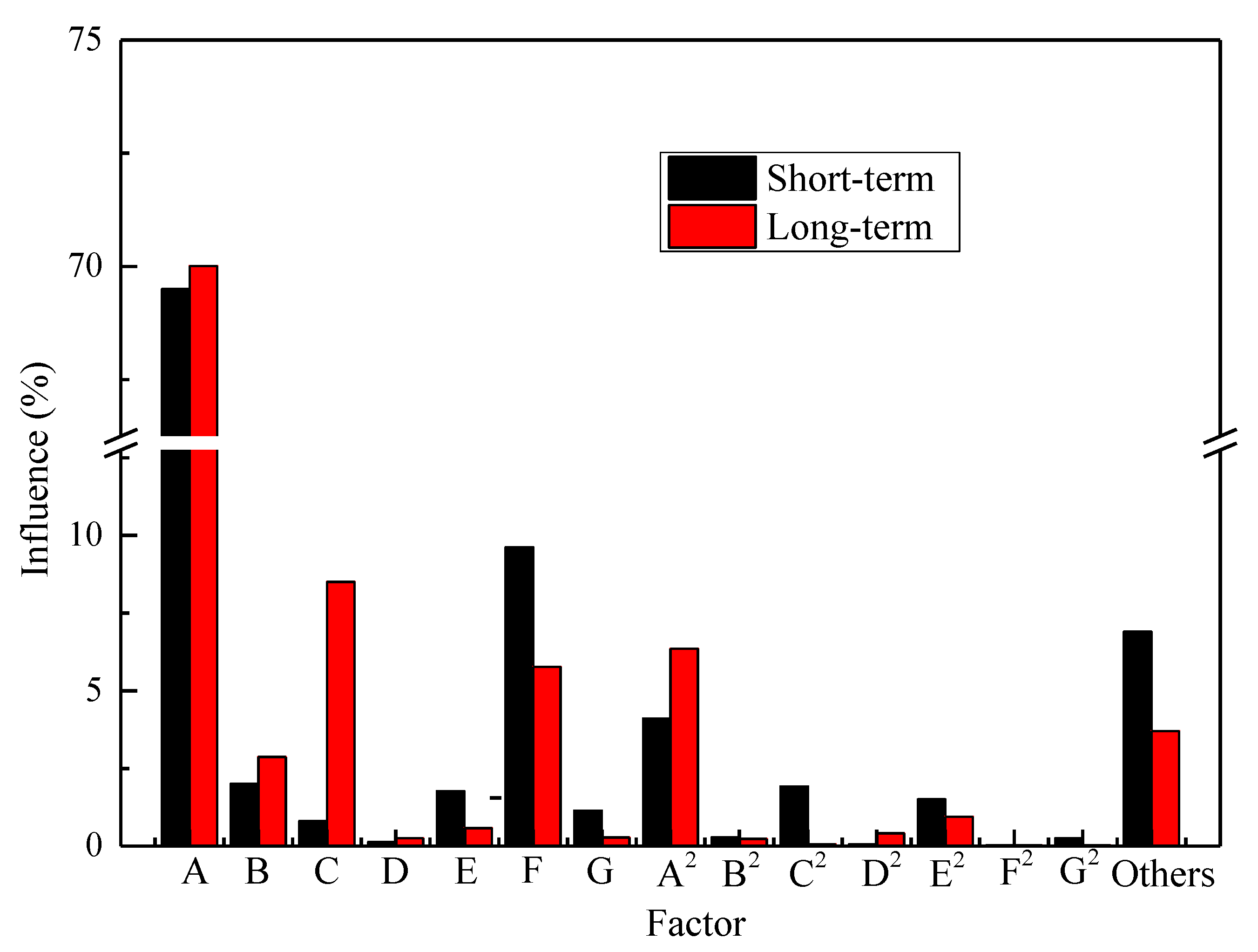
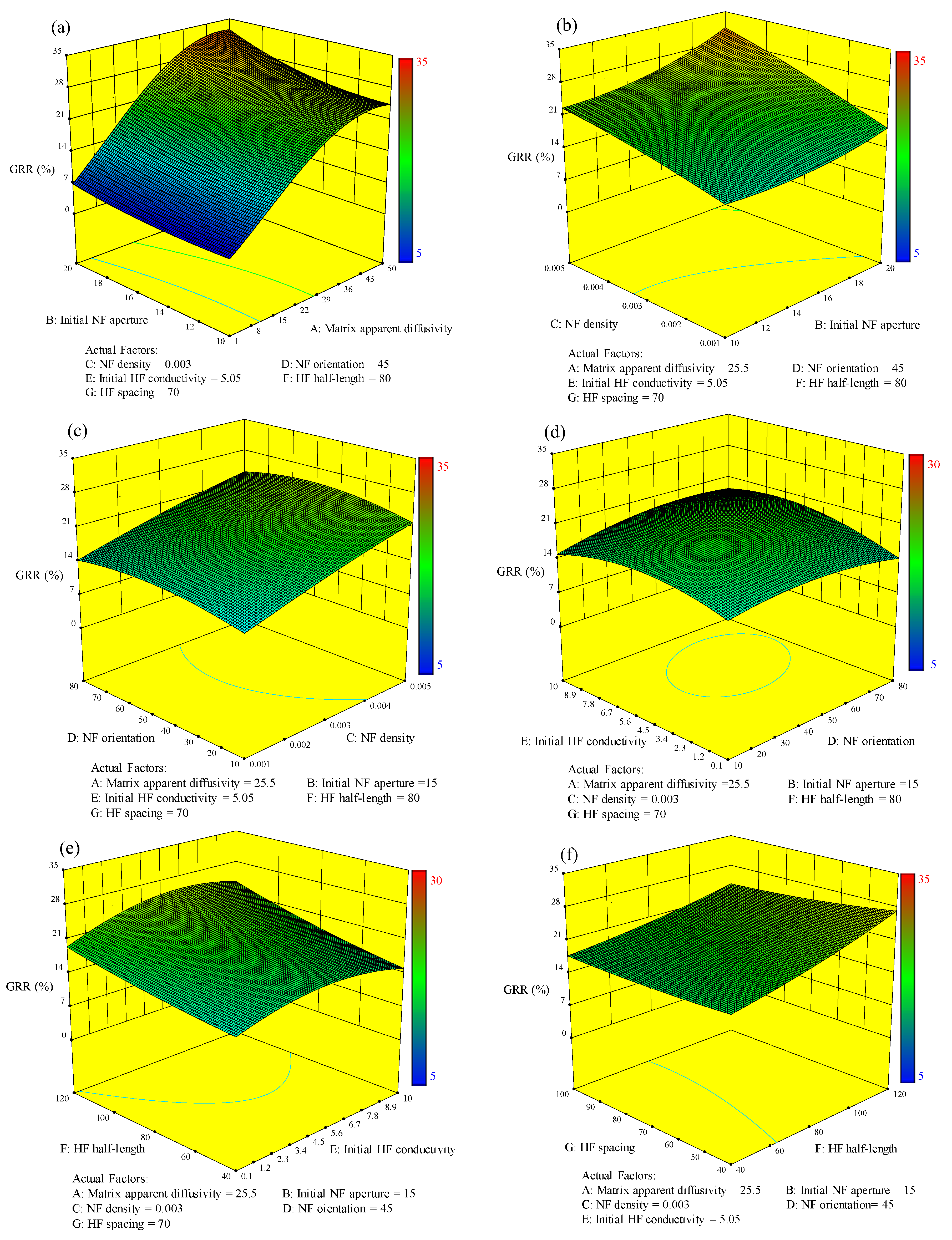
4.3. Sensitivity Analysis
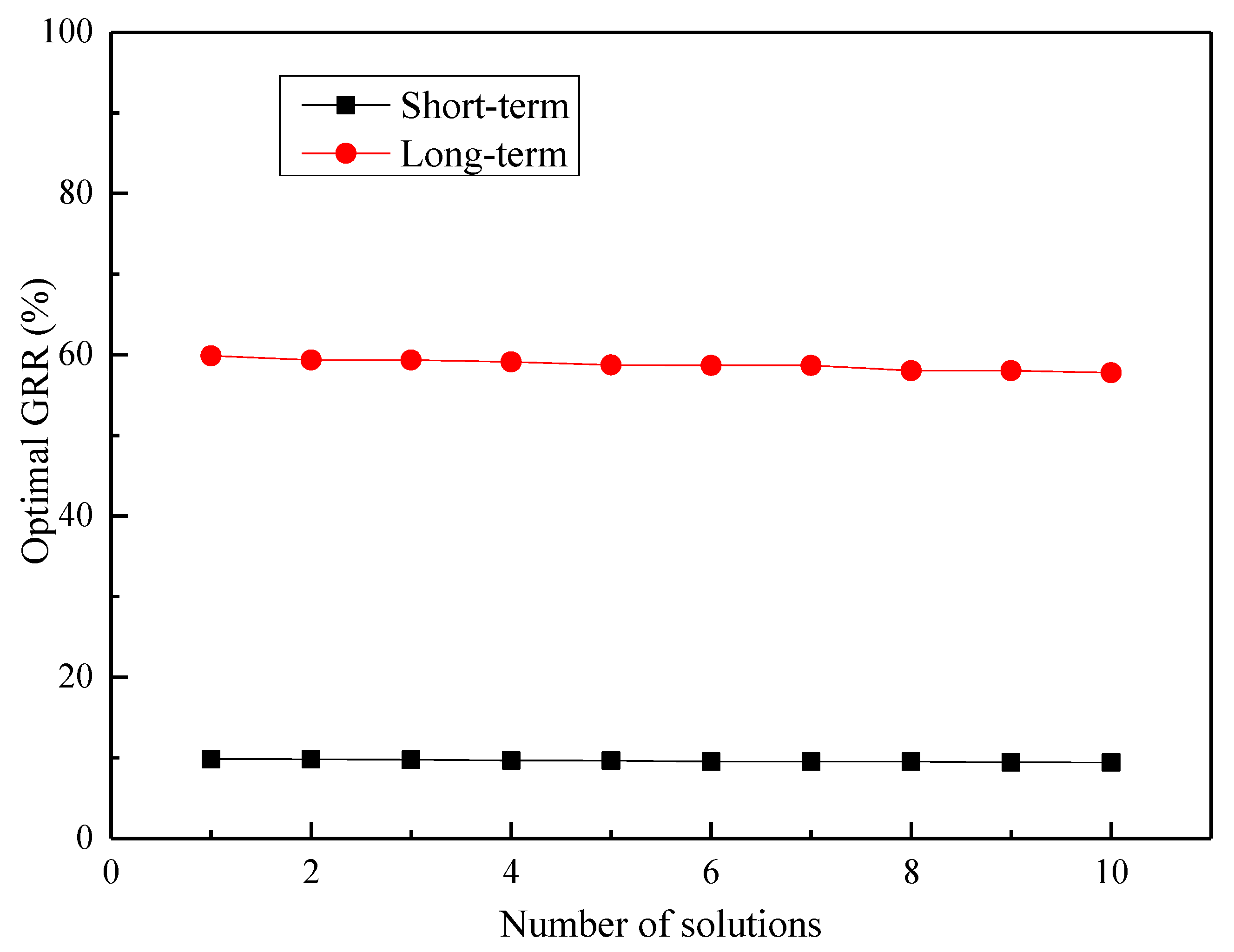
4.4. Optimization Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Proppant pack compressibility index, dimensionless | |
| 4th order elasticity tensor which is the inverse of the total elastic compliance tensor, GPa | |
| Gas apparent diffusivity in shale matrix, m2/s | |
| Body force, N/m3 | |
| Shape factor, m−2 | |
| Identity tensor | |
| GRR objective function with key parameters, % | |
| Solid bulk modulus of the grain, GPa | |
| Permeability of hydraulic fractures, m2 | |
| Fracture normal stiffness, GPa/m | |
| Total fracture shear stiffness, GPa/m | |
| , | Shear stiffness before and after shear, respectively, GPa/m |
| Permeability tensor of natural fracture, m2 | |
| Apparent molecular weight of shale gas, kg/mol | |
| Initial reservoir pressure, Pa | |
| Langmuir pressure constant, Pa | |
| Gas pressure at standard condition, Pa | |
| Bottom hole pressure, Pa | |
| Universal gas constant, J·mol−1·K−1 | |
| Reservoirs temperature, K | |
| Displacement vector, m | |
| Vector of the unknown parameters | |
| Optimal combination of the parameters | |
| Reservoir volume, m3 | |
| Langmuir volume (at standard condition), m3/m3 | |
| Fracture width, mm | |
| Z-factor of shale gas, dimensionless | |
| Greek symbols | |
| Porosity for shale matrix, fractures system and hydraulic fracture, fraction | |
| Effective shear dilation angle, rad | |
| Total stress, Pa | |
| Effective stress acting on fracture surface, Pa | |
| Volumetric strain, dimensionless | |
| Density of adsorbed gas | |
| Shale gas density, kg/m3 | |
| Shale gas density at standard condition, kg/m3 | |
| , | Fitting parameters, dimensionless |
| Maximum closure of natural fracture | |
| shear stress of fracture, Pa | |
| shear strength of fracture, Pa | |
| Gas viscosity, Pa·s | |
| Total gas content, kg/m3 | |
| Subscripts | |
| Matrix | |
| Natural fractures | |
| Hydraulic fractures | |
References
- Ambrose, R.J.; Hartman, R.C.; Campos, M.D.; Akkutlu, I.Y.; Sondergeid, C. Shale Gas-in-Place Calculations Part I: New Pore-Scale Considerations. SPE J. 2012, 17, 219–229. [Google Scholar] [CrossRef]
- Yu, W.; Sepehrnoori, K. An efficient reservoir-simulation approach to design and optimize unconventional gas production. J. Can. Pet. Technol. 2014, 53, 109–121. [Google Scholar] [CrossRef]
- Liu, J.; Wang, J.G.; Gao, F.; Ju, Y.; Zhang, X.; Zhang, L. Flow consistency between non-Darcy flow in fracture network and nonlinear diffusion in matrix to gas production rate in fractured shale gas reservoirs. Transp. Porous Media 2016, 111, 97–121. [Google Scholar] [CrossRef]
- Liu, J.; Wang, J.G.; Gao, F.; Ju, Y.; Tang, F. Impact of micro- and macro-consistent flows on well performance in fractured shale gas reservoirs. J. Nat. Gas Sci. Eng. 2016, 36, 1239–1252. [Google Scholar] [CrossRef]
- Zhang, C.; Gamage, R.P.; Perera, M.S.A.; Zhao, J. Characteristics of clay-abundant shale formations: use of CO2 for production enhancement. Energies 2017, 10, 1887. [Google Scholar] [CrossRef]
- Yu, W.; Luo, Z.; Javadpour, F.; Varavei, A.; Sepehrnoori, K. Sensitivity analysis of hydraulic fracture geometry in shale gas reservoirs. J. Pet. Sci. Eng. 2014, 113, 1–7. [Google Scholar] [CrossRef]
- Hyman, J.D.; Jiménezmartínez, J.; Viswanathan, H.S.; Carey, J.W.; Porter, M.L.; Rougier, E.; Karra, S.; Kang, Q.; Frash, L.; Chen, L.; et al. Understanding hydraulic fracturing: A multi-scale problem. Philos. Trans. 2016, 374, 20150426. [Google Scholar] [CrossRef] [PubMed]
- Salama, A.; Amin, M.F.E.; Kumar, K.; Sun, S. Flow and Transport in Tight and Shale Formations: A Review. Geofluids 2017, 2017, 4251209. [Google Scholar] [CrossRef]
- Kim, J.; Kang, J.M.; Park, C.; Park, Y.; Park, J.; Lim, S. Multi-objective history matching with a proxy model for the characterization of production performances at the shale gas reservoir. Energies 2017, 10, 579. [Google Scholar] [CrossRef]
- Zhang, D.; Dai, Y.; Ma, X.; Zhang, L.; Zhong, B.; Wu, J.; Tao, Z. An analysis for the influences of fracture network system on multi-stage fractured horizontal well productivity in shale gas reservoirs. Energies 2018, 11, 414. [Google Scholar] [CrossRef]
- Pan, Z.; Connell, L.D. Reservoir simulation of free and adsorbed gas production from shale. J. Nat. Gas Sci. Eng. 2015, 22, 359–370. [Google Scholar] [CrossRef]
- Gao, F.; Liu, J.; Wang, J.G.; Ju, Y.; Leung, C. Impact of micro-scale heterogeneity on gas diffusivity of organic-rich shale matrix. J. Nat. Gas Sci. Eng. 2017, 45, 75–87. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, J.; Pan, Z.; Connell, L.D. A sequential model of shale gas transport under the influence of fully coupled multiple processes. J. Nat. Gas Sci. Eng. 2015, 27, 808–821. [Google Scholar] [CrossRef]
- Liu, J.; Wang, J.G.; Gao, F.; Leung, C.F.; Ma, Z.G. A fully coupled fracture equivalent continuum-dual porosity model for hydro-mechanical process in fractured shale gas reservoirs. Comput. Geotech. 2017. in review. [Google Scholar]
- Liu, G.R.; Zhou, J.J.; Wang, J.G. Coefficient identification in electronic system cooling simulation through genetic algorithm. Comput. Struct. 2002, 80, 23–30. [Google Scholar] [CrossRef]
- Rahman, M.M.; Sarma, H.K.; Dhabi, A. Maximizing tight gas recovery through a new hydraulic fracture optimization model. In Proceedings of the SPE Reservoir Characterisation and Simulation Conference and Exhibition, Abu Dhabi, UAE, 9–11 October 2011. [Google Scholar]
- Holt, S. Numerical Optimization of Hydraulic Fracture Stage Placement in a Gas Shale Reservoir. Master’s Thesis, TU Deflt University, Deflt, The Netherlands, 2011. [Google Scholar]
- Ma, X.; Plaksina, T.; Gildin, E. Optimization of Placement of Hydraulic Fracture Stages in Horizontal Wells Drilled in Shale Gas Reservoirs. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 12–14 August 2013; pp. 1479–1489. [Google Scholar]
- Li, J.C.; Gong, B.; Wang, H.G. Mixed integer simulation optimization for optimal hydraulic fracturing and production of shale gas fields. Eng. Opt. 2016, 48, 1378–1400. [Google Scholar] [CrossRef]
- Rammay, M.H.; Awotunde, A.A. Stochastic optimization of hydraulic fracture and horizontal well parameters in shale gas reservoirs. J. Nat. Gas Sci. Eng. 2016, 36, 71–78. [Google Scholar] [CrossRef]
- Yu, W.; Sepehrnoori, K. Optimization of multiple hydraulically fractured horizontal wells in unconventional gas reservoirs. J. Pet. Eng. 2013, 2013, 151898. [Google Scholar]
- Wang, Y.; Li, X.; Zhang, B.; Zhao, Z. Optimization of multiple hydraulically fractured factors to maximize the stimulated reservoir volume in silty laminated shale formation, Southeastern Ordos Basin, China. J. Pet. Sci. Eng. 2016, 145, 370–381. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Hu, R.; Ma, C.; Zhao, Z.; Zhang, B. Numerical evaluation and optimization of multiple hydraulically fractured parameters using a flow-stress-damage coupled approach. Energies 2016, 9, 325. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; John Wiley and Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Kazemi, H.; Gilman, J.R.; Elsharkawy, A.M. Analytical and numerical solution of oil recovery from fractured reservoirs with empirical transfer functions. SPE Reserv. Eng. 1992, 7, 219–227. [Google Scholar] [CrossRef]
- Wen, Q.; Wang, S.; Duan, X.; Li, Y.; Wang, F.; Jin, X. Experimental investigation of proppant settling in complex hydraulic-natural fracture system in shale reservoirs. J. Nat. Gas Sci. Eng. 2016, 33, 70–80. [Google Scholar] [CrossRef]
- Tan, Y.; Pan, Z.; Liu, J.; Wu, Y.; Haque, A.; Connell, L.D. Experimental study of permeability and its anisotropy for shale fracture supported with proppant. J. Nat. Gas Sci. Eng. 2017, 44, 250–264. [Google Scholar] [CrossRef]
- Li, K.; Gao, Y.; Lyu, Y.; Wang, M. New mathematical models for calculating proppant embedment and fracture conductivity. SPE J. 2015, 20, 496–507. [Google Scholar] [CrossRef]
- Li, H.; Wang, K.; Xie, J.; Li, Y.; Zhu, S. A new mathematical model to calculate sand-packed fracture conductivity. J. Nat. Gas Sci. Eng. 2016, 35, 567–582. [Google Scholar] [CrossRef]
- Neto, L.B.; Khanna, A.; Kotousov, A. Conductivity and performance of hydraulic fractures partially filled with compressible proppant packs. Int. J. Rock Mech. Min. Sci. 2015, 74, 1–9. [Google Scholar]
- Guo, J.C.; Lu, C.; Zhao, J.Z. Experimental research on propant embedment. J. China Coal Soc. 2008, 33, 661–664. (In Chinese) [Google Scholar]
- Lu, C.; Guo, J.; Wang, W. Experimental research on proppant embedment and its damage to fractures conductivity. Nat. Gas Ind. 2008, 28, 99–101. [Google Scholar]
- Grieser, B.; Shelley, B.; Soliman, M. Predicting production outcome from multi-stage, horizontal Barnett completions. In Proceedings of the SPE Production and Operations Symposium, Oklahoma City, OK, USA, 4–8 April 2009. Paper SPE 120271. [Google Scholar]
- Garcia-Teijeiro, X.; Rodriguez-Herrera, A.; Fischer, K. The interplay between natural fractures and stress as controls to hydraulic fracture geometry in depleted reservoirs. J. Nat. Gas Sci. Eng. 2016, 34, 318–330. [Google Scholar] [CrossRef]
- Iranmanesh, S.; Mehrali, M.; Sadeghinezhad, E.; Ang, B.C.; Ong, H.C.; Esmaeilzadeh, A. Evaluation of viscosity and thermal conductivity of graphene nanoplatelets nanofluids through a combined experimental–statistical approach using respond surface methodology method. Int. Commun. Heat Mass Transf. 2016, 79, 74–80. [Google Scholar] [CrossRef]
- Kazemi-Beydokhti, A.; Namaghi, H.Z.; Heris, S.Z. Identification of the key variables on thermal conductivity of Cuo nanofluid by a fractional factorial design approach. Numer. Heat Transf. Part B Fundam. 2013, 64, 480–495. [Google Scholar] [CrossRef]
- Teng, T.; Wang, J.G.; Gao, F.; Ju, Y. Complex thermal coal-gas interactions in heat injection enhanced CBM recovery. J. Nat. Gas Sci. Eng. 2016, 34, 1174–1190. [Google Scholar] [CrossRef]
- Kang, Y.L.; Chen, M.J.; Chen, Z.X.; You, L.J.; Hao, Z.W. Investigation of formation heat treatment to enhance the multiscale gas transport ability of shale. J. Nat. Gas Sci. Eng. 2016, 35, 265–275. [Google Scholar] [CrossRef]
- Yu, W.; Sepehrnoori, K. Simulation of gas desorption and geomechanics effects for unconventional gas reservoirs. Fuel 2014, 116, 455–464. [Google Scholar] [CrossRef]
- Yu, W.; Zhang, T.; Du, S.; Sepehrnoori, K. Numerical study of the effect of uneven proppant distribution between multiple fractures on shale gas well performance. Fuel 2015, 142, 189–198. [Google Scholar] [CrossRef]









| Parameters | Coded Symbol | Minimum (−1) | Maximum (+1) | Unit |
|---|---|---|---|---|
| Matrix diffusivity | A | 1 | 50 | 10−8 m2/s |
| Initial NF aperture | B | 10 | 20 | µm |
| Density of NF | C | 0.001 | 0.005 | fraction |
| Orientation of NF | D | 10 | 80 | degree |
| Initial HF conductivity | E | 0.1 | 10 | µm2·cm |
| HF half-length | F | 40 | 120 | m |
| HF spacing | G | 40 | 100 | m |
| Run | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 1 | 50.00 | 10.00 | 0.001 | 10.00 | 2.38 | 40 | 40 |
| 2 | 42.65 | 10.00 | 0.001 | 80.00 | 0.10 | 40 | 100 |
| 3 | 50.00 | 10.00 | 0.005 | 80.00 | 10.00 | 120 | 40 |
| 4 | 19.87 | 10.00 | 0.001 | 80.00 | 5.20 | 120 | 40 |
| 5 | 17.42 | 10.00 | 0.005 | 10.00 | 3.86 | 100 | 40 |
| 6 | 50.00 | 17.00 | 0.005 | 42.20 | 0.10 | 40 | 40 |
| 7 | 1.00 | 15.08 | 0.001 | 50.60 | 6.04 | 40 | 70 |
| 8 | 16.93 | 20.00 | 0.004 | 56.20 | 10.00 | 80 | 100 |
| 9 | 2.23 | 12.65 | 0.004 | 47.80 | 8.52 | 120 | 70 |
| 10 | 28.56 | 20.00 | 0.001 | 80.00 | 0.10 | 40 | 40 |
| 11 | 1.00 | 10.00 | 0.005 | 80.00 | 10.00 | 40 | 100 |
| 12 | 50.00 | 16.90 | 0.001 | 56.55 | 0.10 | 100 | 70 |
| 13 | 28.20 | 20.00 | 0.002 | 10.00 | 0.64 | 60 | 70 |
| 14 | 27.71 | 14.75 | 0.001 | 33.80 | 10.00 | 80 | 40 |
| 15 | 50.00 | 10.00 | 0.004 | 49.55 | 5.10 | 80 | 100 |
| 16 | 1.00 | 20.00 | 0.005 | 80.00 | 0.10 | 40 | 70 |
| 17 | 44.12 | 20.00 | 0.005 | 55.15 | 0.10 | 40 | 100 |
| 18 | 50.00 | 20.00 | 0.005 | 80.00 | 0.25 | 120 | 100 |
| 19 | 2.23 | 12.65 | 0.004 | 47.80 | 8.52 | 120 | 70 |
| 20 | 50.00 | 20.00 | 0.001 | 10.00 | 10.00 | 40 | 100 |
| 21 | 1.00 | 16.35 | 0.002 | 13.50 | 0.10 | 120 | 40 |
| 22 | 15.70 | 13.40 | 0.004 | 17.00 | 2.08 | 40 | 100 |
| 23 | 15.70 | 13.40 | 0.004 | 17.00 | 2.08 | 40 | 40 |
| 24 | 30.79 | 10.00 | 0.003 | 43.95 | 10.00 | 40 | 70 |
| 25 | 48.53 | 14.02 | 0.001 | 24.35 | 5.57 | 80 | 100 |
| 26 | 1.00 | 15.08 | 0.001 | 50.6 | 6.04 | 40 | 70 |
| 27 | 1.00 | 19.70 | 0.004 | 10.00 | 10.00 | 40 | 40 |
| 28 | 17.17 | 18.10 | 0.005 | 74.05 | 5.20 | 100 | 40 |
| 29 | 20.36 | 18.90 | 0.001 | 10.00 | 6.49 | 120 | 100 |
| 30 | 48.78 | 16.75 | 0.003 | 80.00 | 6.83 | 60 | 70 |
| 31 | 50.00 | 20.00 | 0.003 | 29.25 | 5.99 | 120 | 40 |
| 32 | 1.00 | 20.00 | 0.001 | 80.00 | 10.00 | 120 | 40 |
| 33 | 1.00 | 10.00 | 0.002 | 10.00 | 10.00 | 80 | 100 |
| 34 | 2.23 | 16.70 | 0.002 | 80.00 | 1.83 | 100 | 100 |
| 35 | 1.00 | 20.00 | 0.005 | 10.00 | 0.10 | 120 | 100 |
| 36 | 25.34 | 11.00 | 0.002 | 10.00 | 0.30 | 80 | 70 |
| 37 | 50.00 | 20.00 | 0.001 | 80.00 | 0.84 | 40 | 100 |
| 38 | 50.00 | 10.00 | 0.003 | 10.00 | 9.26 | 120 | 40 |
| 39 | 1.00 | 10.00 | 0.001 | 25.40 | 0.10 | 120 | 100 |
| 40 | 44.12 | 12.53 | 0.001 | 80.00 | 10.00 | 120 | 100 |
| 41 | 1.00 | 10.00 | 0.004 | 73.00 | 0.10 | 60 | 40 |
| 42 | 30.79 | 10.00 | 0.003 | 43.95 | 10.00 | 40 | 40 |
| 43 | 50.00 | 13.50 | 0.003 | 10.00 | 0.10 | 120 | 100 |
| 44 | 32.85 | 10.50 | 0.005 | 80.00 | 0.10 | 120 | 70 |
| 45 | 46.08 | 16.80 | 0.005 | 10.00 | 10.00 | 80 | 70 |
| 46 | 48.78 | 16.75 | 0.003 | 80.00 | 6.83 | 60 | 40 |
| Parameters | Value |
|---|---|
| Model size, m | 1500 × 600 × 100 |
| Elastic modulus, E (GPa) | 20.68 |
| Solid bulk modulus, ks (GPa) | 37.82 |
| Poisson’s ratio, ν | 0.25 |
| Bulk density, ρ (kg/m3) | 2400 |
| Maximum horizontal stress, (MPa) | 43.34 |
| Minimum horizontal stress, (MPa) | 39.01 |
| Initial reservoir pressure, pi (MPa) | 28.27 |
| Bottom hole pressure, pw (MPa) | 15 |
| Biot coefficient, αB | 0.64 |
| Fracture shear stiffness, (GPa/M) | 434 |
| Initial normal stiffness, Kn0 (GPa/M) | 434 |
| Friction angle, (°) | 24.9 |
| Dilation angle, (°) | 5 |
| Methane dynamic viscosity, μ (Pa·s) | 2.01 × 10−5 |
| Reservoir temperature, T (K) | 350 |
| Langmuir pressure constant, PL (MPa) | 10 |
| Langmuir volume constant, VL (m3/m3) | 10 |
| Density of adsorbed gas in the organic pores, ρads (kg/m3) | 370 |
| Matrix porosity φm | 0.04 |
| Hydraulic fracture porosity φF | 0.3 |
| Source | Std. Dev. | R-Squared | Adjusted R-Squared | Predicted R-Squared | PRESS | Fit or Not | |
|---|---|---|---|---|---|---|---|
| (a) | |||||||
| Linear | 0.25 | 0.8495 | 0.8218 | 0.7799 | 3.38 | - | |
| 2FI | 0.26 | 0.9265 | 0.8054 | −0.0031 | 15.40 | - | |
| Quadratic | 0.065 | 0.9972 | 0.9874 | 0.8706 | 1.99 | Suggested | |
| Cubic | 0.025 | 0.9999 | 0.9982 | - | - | Aliased | |
| (b) | |||||||
| Linear | 0.51 | 0.8862 | 0.8653 | 0.8296 | 14.96 | - | |
| 2FI | 0.63 | 0.9235 | 0.7975 | −0.3208 | 115.93 | - | |
| Quadratic | 0.097 | 0.9989 | 0.9952 | 0.9485 | 4.52 | Suggested | |
| Cubic | 0.029 | 1.0000 | 0.9996 | - | - | Aliased | |
| Source | Sum of Squares | df | Mean Square | F Value | p-Value Prob > F | Significant or Not |
|---|---|---|---|---|---|---|
| (a) | ||||||
| Model | 15.31 | 35 | 0.44 | 101.97 | <0.0001 | significant |
| A | 8.85 | 1 | 8.85 | 2061.94 | <0.0001 | - |
| B | 0.26 | 1 | 0.26 | 59.46 | <0.0001 | - |
| C | 0.10 | 1 | 0.10 | 23.76 | 0.0006 | - |
| D | 0.016 | 1 | 0.016 | 3.73 | 0.0823 | - |
| E | 0.23 | 1 | 0.23 | 52.56 | <0.0001 | - |
| F | 1.22 | 1 | 1.22 | 285.53 | <0.0001 | - |
| G | 0.14 | 1 | 0.14 | 33.69 | 0.0002 | - |
| AB | 3.759 × 10−3 | 1 | 3.759 × 10−3 | 0.88 | 0.3713 | - |
| AC | 0.43 | 1 | 0.43 | 99.09 | <0.0001 | - |
| AD | 2.101 × 10−3 | 1 | 2.101 × 10−3 | 0.49 | 0.5000 | - |
| AE | 8.553 × 10−3 | 1 | 8.553 × 10−3 | 1.99 | 0.1883 | - |
| AF | 0.071 | 1 | 0.071 | 16.62 | 0.0022 | - |
| AG | 0.017 | 1 | 0.017 | 4.06 | 0.0714 | - |
| BC | 0.019 | 1 | 0.019 | 4.47 | 0.0607 | - |
| BD | 0.061 | 1 | 0.061 | 14.33 | 0.0036 | - |
| BE | 0.038 | 1 | 0.038 | 8.85 | 0.0139 | - |
| BF | 3.217 × 10−3 | 1 | 3.217 × 10−3 | 0.75 | 0.4068 | - |
| BG | 5.927 × 10−3 | 1 | 5.927 × 10−3 | 1.38 | 0.2670 | - |
| CD | 0.011 | 1 | 0.011 | 2.53 | 0.1430 | - |
| CE | 0.021 | 1 | 0.021 | 4.96 | 0.0500 | - |
| CF | 4.226 × 10−3 | 1 | 4.226 × 10−3 | 0.99 | 0.3443 | - |
| CG | 0.015 | 1 | 0.015 | 3.42 | 0.0943 | - |
| DE | 6.599 × 10−3 | 1 | 6.599 × 10−3 | 1.54 | 0.2432 | - |
| DF | 1.172 × 10−6 | 1 | 1.172 × 10−6 | 2.733×10−4 | 0.9871 | - |
| DG | 0.030 | 1 | 0.030 | 6.98 | 0.0247 | - |
| EF | 0.028 | 1 | 0.028 | 6.62 | 0.0278 | - |
| EG | 0.081 | 1 | 0.081 | 18.85 | 0.0015 | - |
| FG | 0.025 | 1 | 0.025 | 5.94 | 0.0350 | - |
| A2 | 0.52 | 1 | 0.52 | 121.85 | <0.0001 | - |
| B2 | 0.036 | 1 | 0.036 | 8.37 | 0.0160 | - |
| C2 | 0.24 | 1 | 0.24 | 56.93 | <0.0001 | - |
| D2 | 6.635 × 10−3 | 1 | 6.635 × 10−3 | 1.55 | 0.2420 | - |
| E2 | 0.19 | 1 | 0.19 | 44.65 | <0.0001 | - |
| F2 | 2.860 × 10−3 | 1 | 2.860 × 10−3 | 0.67 | 0.4333 | - |
| G2 | 0.032 | 1 | 0.032 | 7.46 | 0.0211 | - |
| Residual | 0.043 | 10 | 4.290 × 10−3 | - | ||
| Lack of Fit | 0.042 | 8 | 5.207 × 10−3 | 8.36 | 0.1112 | not significant |
| Pure Error | 1.246 × 10−3 | 2 | 6.230 × 10−4 | - | ||
| Cor Total | 15.35 | 45 | - | |||
| (b) | ||||||
| Model | 87.68 | 35 | 2.51 | 267.44 | <0.0001 | significant |
| A | 53.13 | 1 | 53.13 | 5672.42 | <0.0001 | - |
| B | 2.18 | 1 | 2.18 | 232.70 | <0.0001 | - |
| C | 6.45 | 1 | 6.45 | 689.12 | <0.0001 | - |
| D | 0.19 | 1 | 0.19 | 20.42 | 0.0011 | - |
| E | 0.44 | 1 | 0.44 | 46.94 | <0.0001 | - |
| F | 4.37 | 1 | 4.37 | 466.98 | <0.0001 | - |
| G | 0.21 | 1 | 0.21 | 22.32 | 0.0008 | - |
| AB | 0.048 | 1 | 0.048 | 5.08 | 0.0478 | - |
| AC | 0.36 | 1 | 0.36 | 38.06 | 0.0001 | - |
| AD | 0.035 | 1 | 0.035 | 3.76 | 0.0810 | - |
| AE | 0.035 | 1 | 0.035 | 3.75 | 0.0816 | - |
| AF | 0.21 | 1 | 0.21 | 22.53 | 0.0008 | - |
| AG | 0.099 | 1 | 0.099 | 10.55 | 0.0088 | - |
| BC | 0.14 | 1 | 0.14 | 15.11 | 0.0030 | - |
| BD | 0.57 | 1 | 0.57 | 61.09 | <0.0001 | - |
| BE | 0.44 | 1 | 0.44 | 46.61 | <0.0001 | - |
| BF | 5.167 × 10−5 | 1 | 5.167 × 10−5 | 5.516 × 10−3 | 0.9423 | - |
| BG | 1.154 × 10−4 | 1 | 1.154 × 10−4 | 0.012 | 0.9138 | - |
| CD | 9.434 × 10−3 | 1 | 9.434 × 10−3 | 1.01 | 0.3392 | - |
| CE | 0.028 | 1 | 0.028 | 3.03 | 0.1126 | - |
| CF | 0.25 | 1 | 0.25 | 26.87 | 0.0004 | - |
| CG | 0.13 | 1 | 0.13 | 13.88 | 0.0039 | - |
| DE | 0.22 | 1 | 0.22 | 23.34 | 0.0007 | - |
| DF | 2.136 × 10−3 | 1 | 2.136 × 10−3 | 0.23 | 0.6432 | - |
| DG | 1.290 × 10−3 | 1 | 1.290 × 10−3 | 0.14 | 0.7183 | - |
| EF | 0.092 | 1 | 0.092 | 9.78 | 0.0107 | - |
| EG | 0.049 | 1 | 0.049 | 5.27 | 0.0446 | - |
| FG | 0.095 | 1 | 0.095 | 10.14 | 0.0098 | - |
| A2 | 4.82 | 1 | 4.82 | 514.41 | <0.0001 | - |
| B2 | 0.17 | 1 | 0.17 | 18.27 | 0.0016 | - |
| C2 | 0.049 | 1 | 0.049 | 5.20 | 0.0457 | - |
| D2 | 0.31 | 1 | 0.31 | 32.94 | 0.0002 | - |
| E2 | 0.72 | 1 | 0.72 | 76.44 | <0.0001 | - |
| F2 | 0.015 | 1 | 0.015 | 1.64 | 0.2290 | - |
| G2 | 0.018 | 1 | 0.018 | 1.90 | 0.1984 | - |
| Residual | 0.094 | 10 | 9.367 × 10−3 | - | ||
| Lack of Fit | 0.092 | 8 | 0.012 | 13.86 | 0.0690 | not significant |
| Pure Error | 1.660 × 10−3 | 2 | 8.300 × 10−4 | - | ||
| Cor Total | 87.77 | 45 | - | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Wang, J.; Leung, C.; Gao, F. A Multi-Parameter Optimization Model for the Evaluation of Shale Gas Recovery Enhancement. Energies 2018, 11, 654. https://doi.org/10.3390/en11030654
Liu J, Wang J, Leung C, Gao F. A Multi-Parameter Optimization Model for the Evaluation of Shale Gas Recovery Enhancement. Energies. 2018; 11(3):654. https://doi.org/10.3390/en11030654
Chicago/Turabian StyleLiu, Jia, Jianguo Wang, Chunfai Leung, and Feng Gao. 2018. "A Multi-Parameter Optimization Model for the Evaluation of Shale Gas Recovery Enhancement" Energies 11, no. 3: 654. https://doi.org/10.3390/en11030654
APA StyleLiu, J., Wang, J., Leung, C., & Gao, F. (2018). A Multi-Parameter Optimization Model for the Evaluation of Shale Gas Recovery Enhancement. Energies, 11(3), 654. https://doi.org/10.3390/en11030654






