A Gas–Solid–Liquid Coupling Model of Coal Seams and the Optimization of Gas Drainage Boreholes
Abstract
:1. Introduction
2. Gas–Solid–Liquid Coupling Model
2.1. Stress Field Equation
2.2. Seepage Field Equation
2.2.1. The Permeability Model of the Matrix
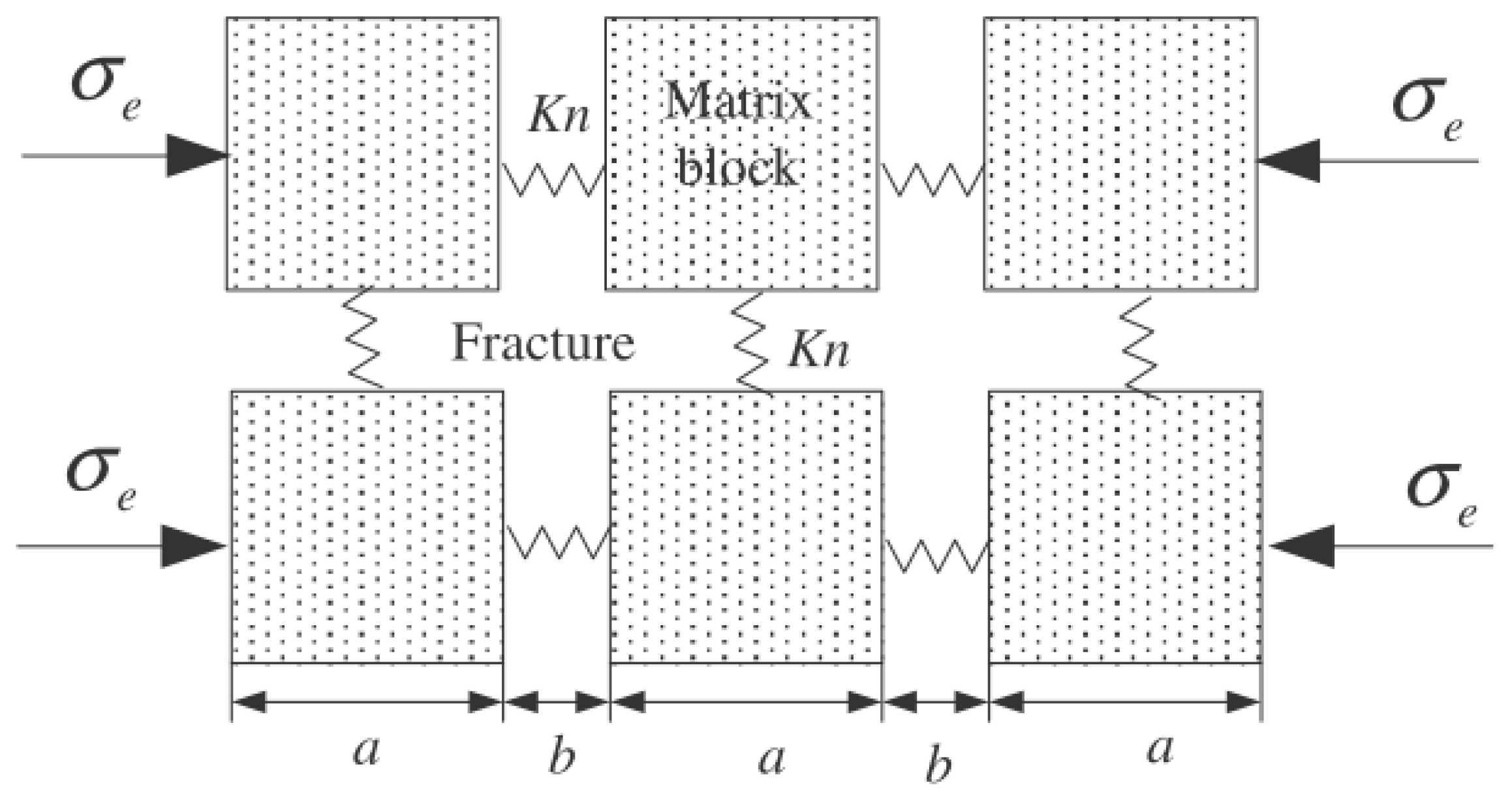
2.2.2. Fracture Permeability Model
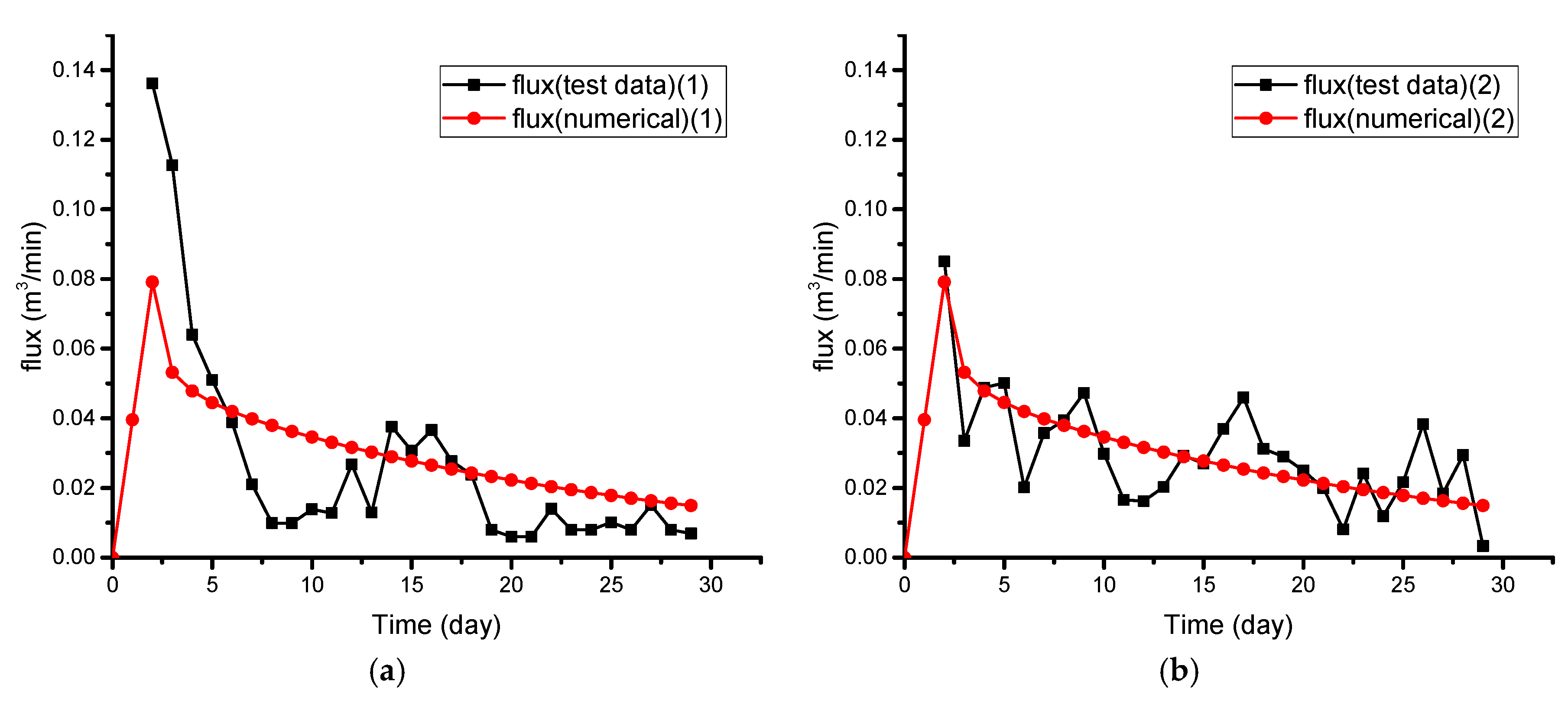
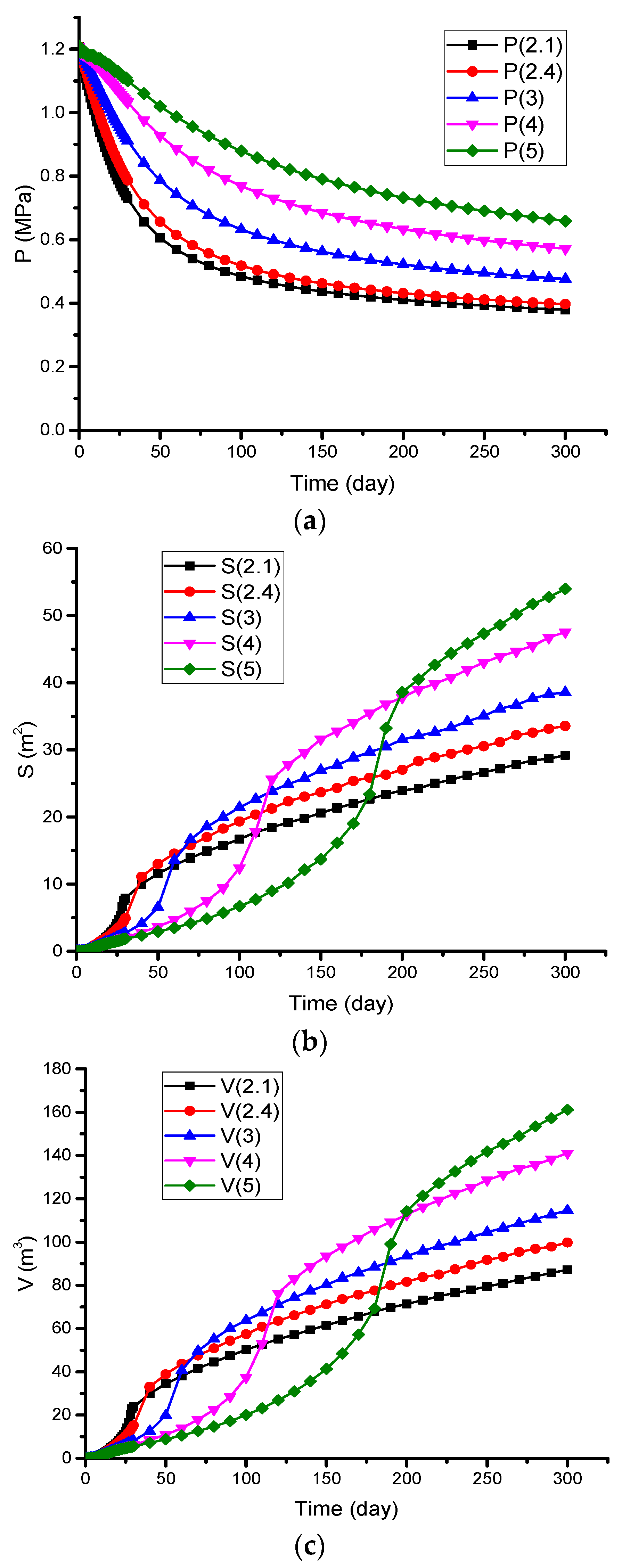
3. Model Verification
4. Numerical Simulation Analysis of the Optimization of Gas Drainage Boreholes
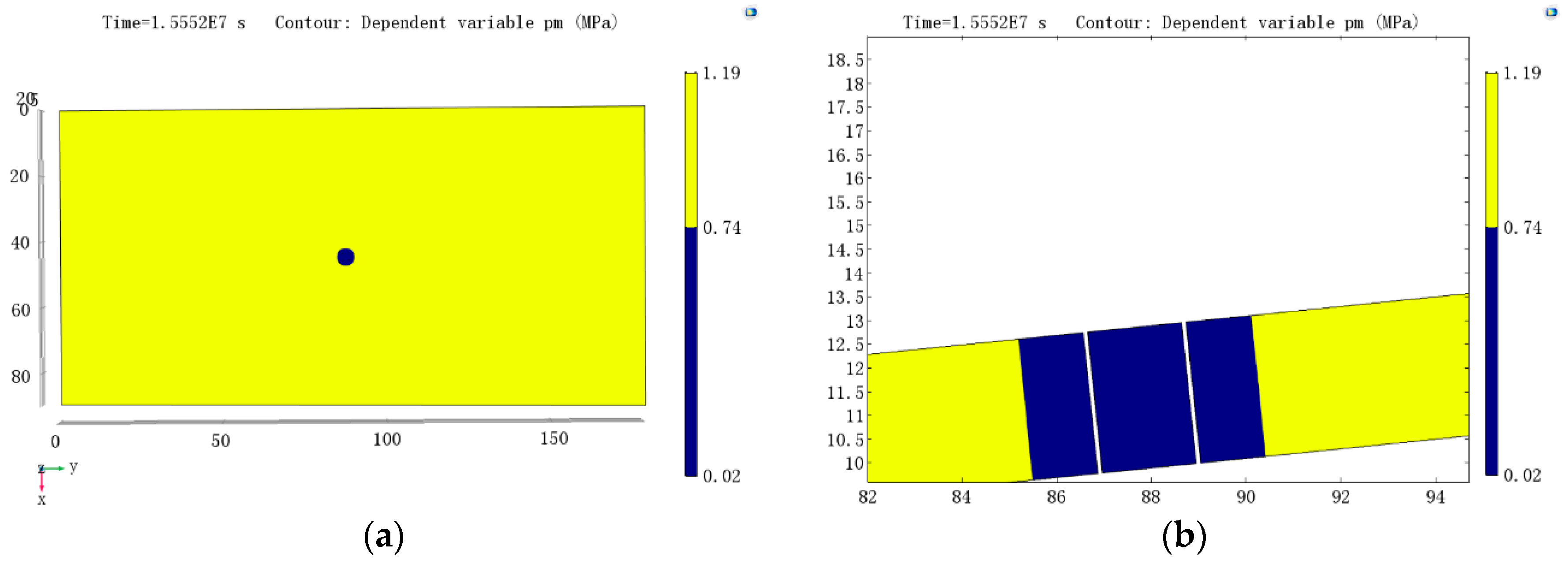
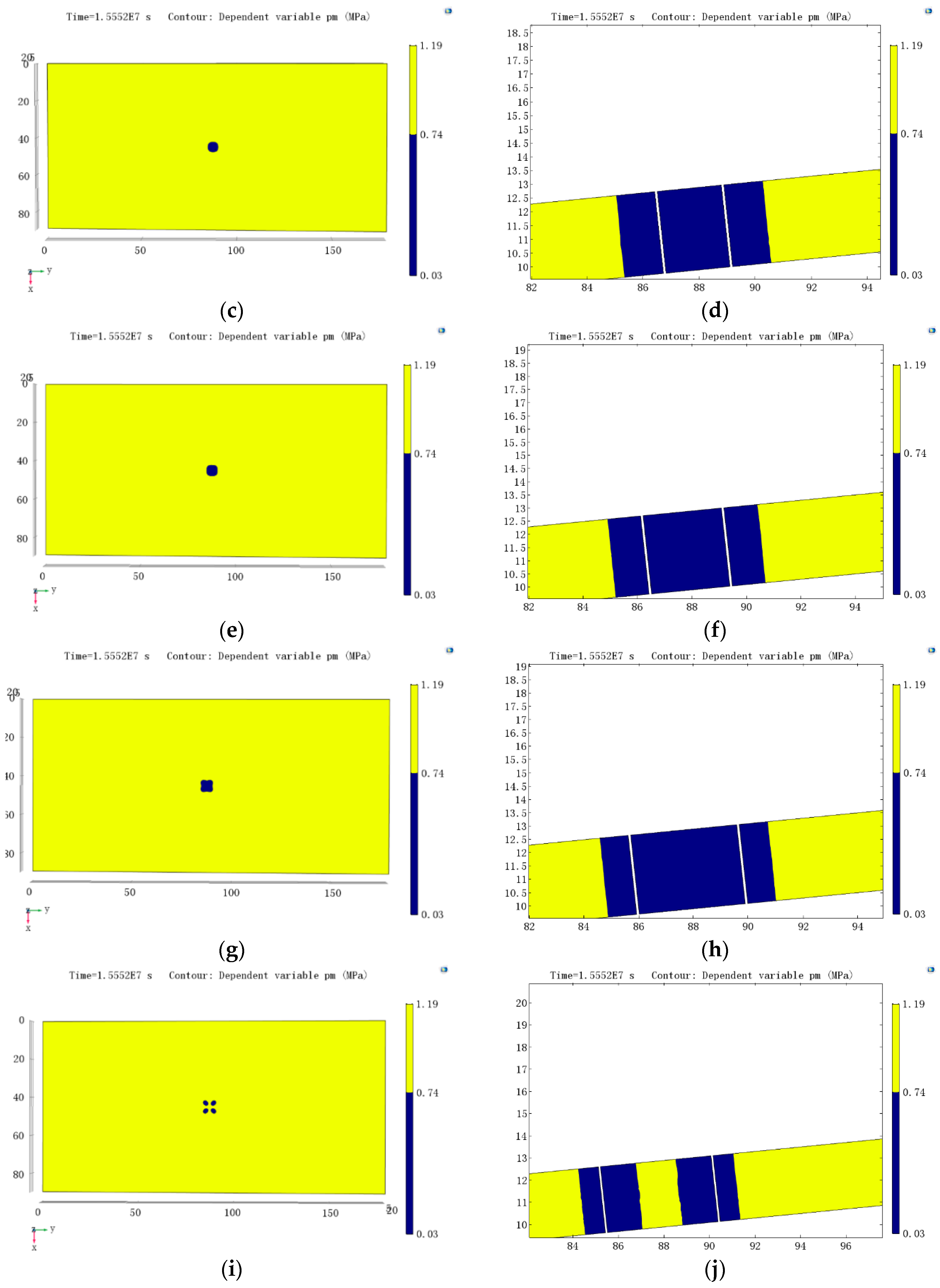
4.1. Optimization of Gas Drainage Boreholes When the Mutual Influences of Gas Drainage Boreholes Are Not Considered
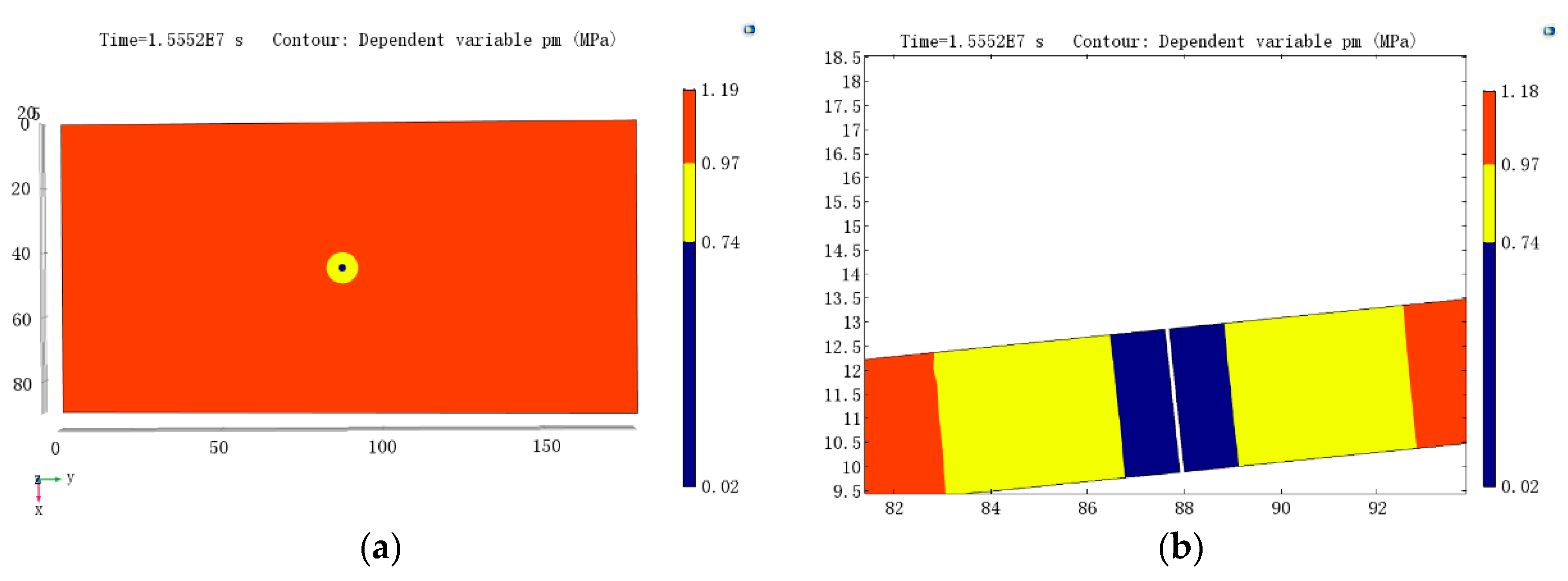
4.2. The Effective Drainage Radius and Influence Radius of a Single Borehole
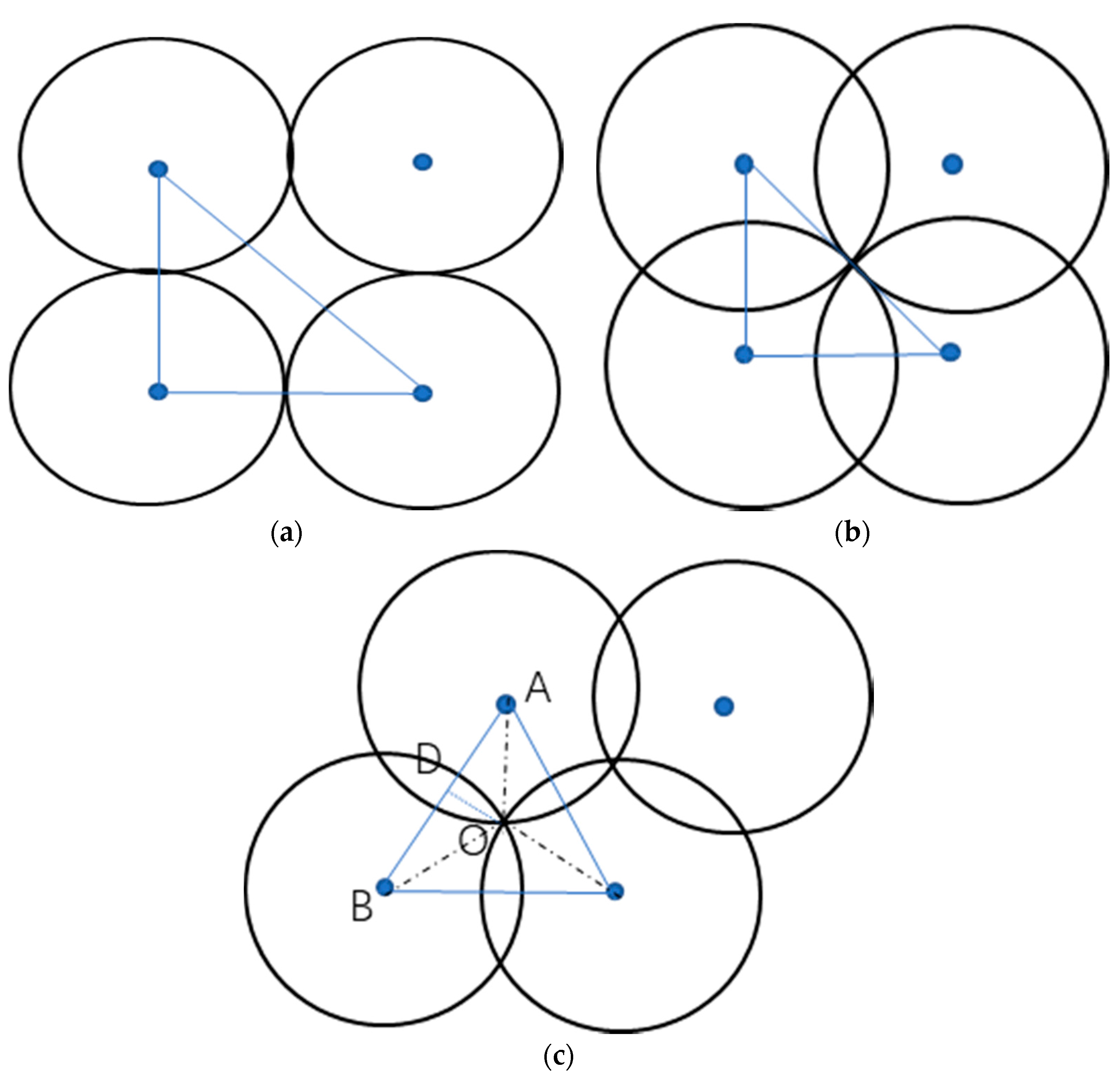
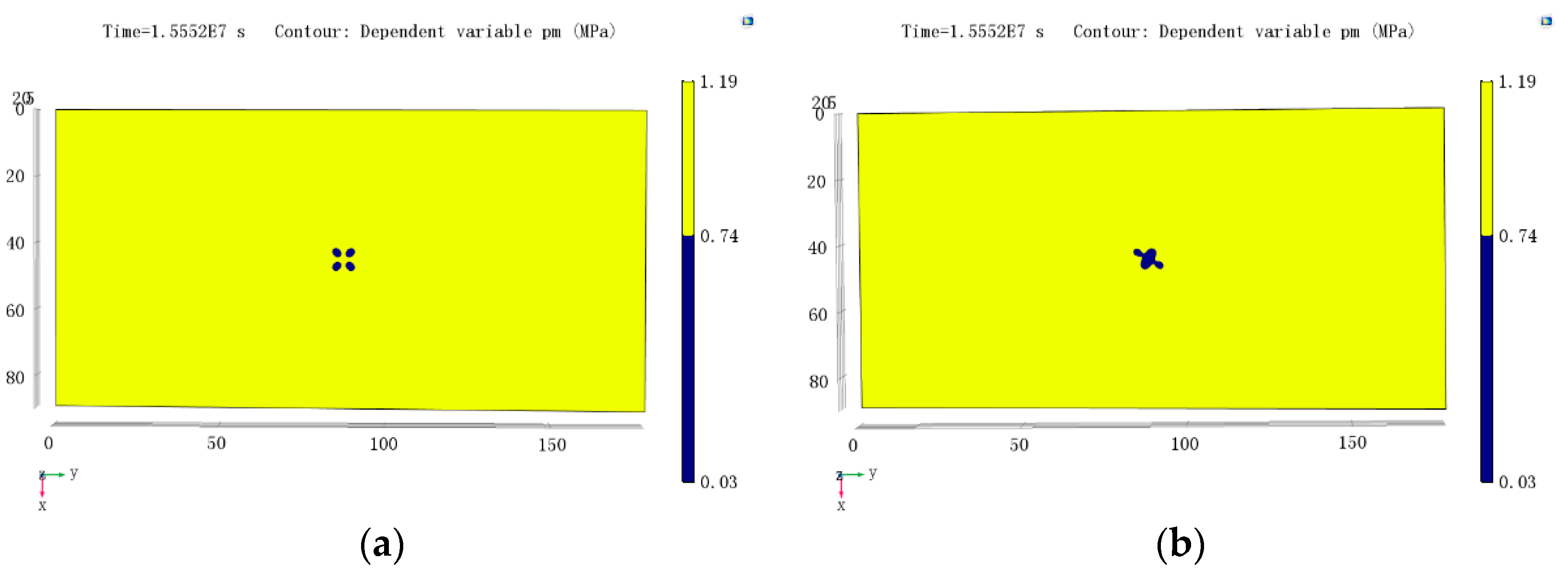
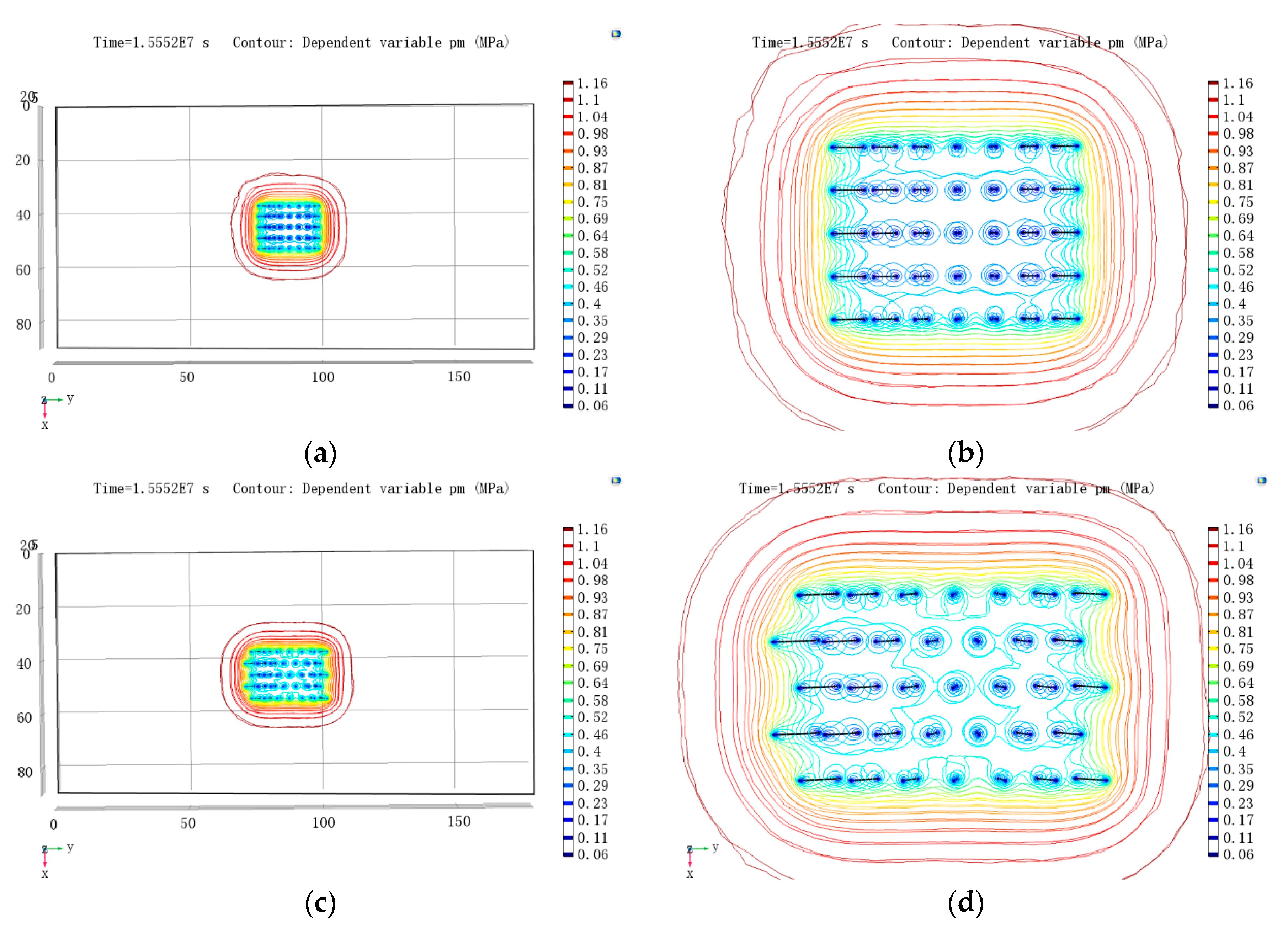
4.3. The Mutual Influence of Gas Drainage Boreholes
4.4. Optimization of Gas Drainage Boreholes When the Mutual Influence of Gas Drainage Boreholes is Considered
5. Conclusions
- A gas–solid–liquid coupling model was established for a coal seam based on elasticity and seepage mechanics, which considered the effective stress, sorption and desorption, and wet strain. In addition, the model was verified to be correct.
- The established model was incorporated in COMSOL to simulate the gas drainage process from boreholes in a coal mine. To achieve the aim of regional outburst risk elimination within 180 days of gas drainage and reduce the number of boreholes as much as possible to save cost, the spacing of boreholes was optimized. Considering the superimposed effect of boreholes, the borehole spacing could be set within r ≤ L ≤ R, where r and R represent the effective gas drainage radius and the influence radius of gas drainage, respectively.
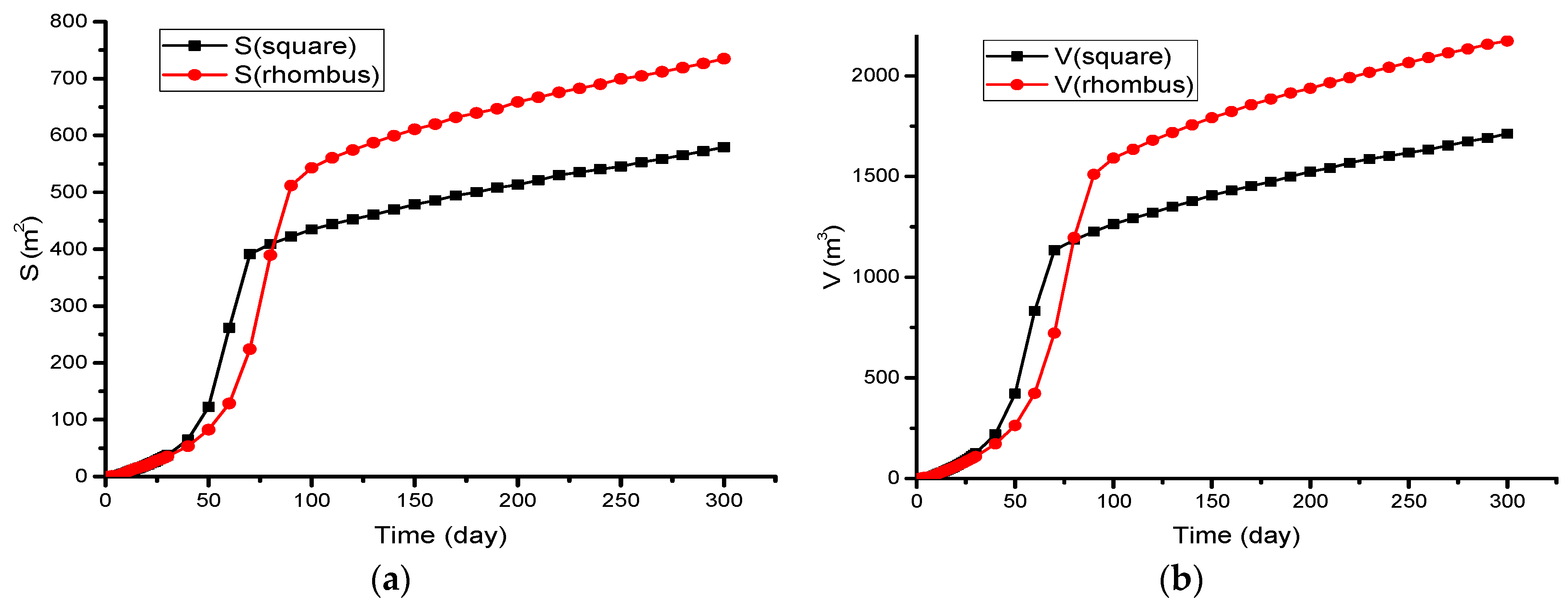
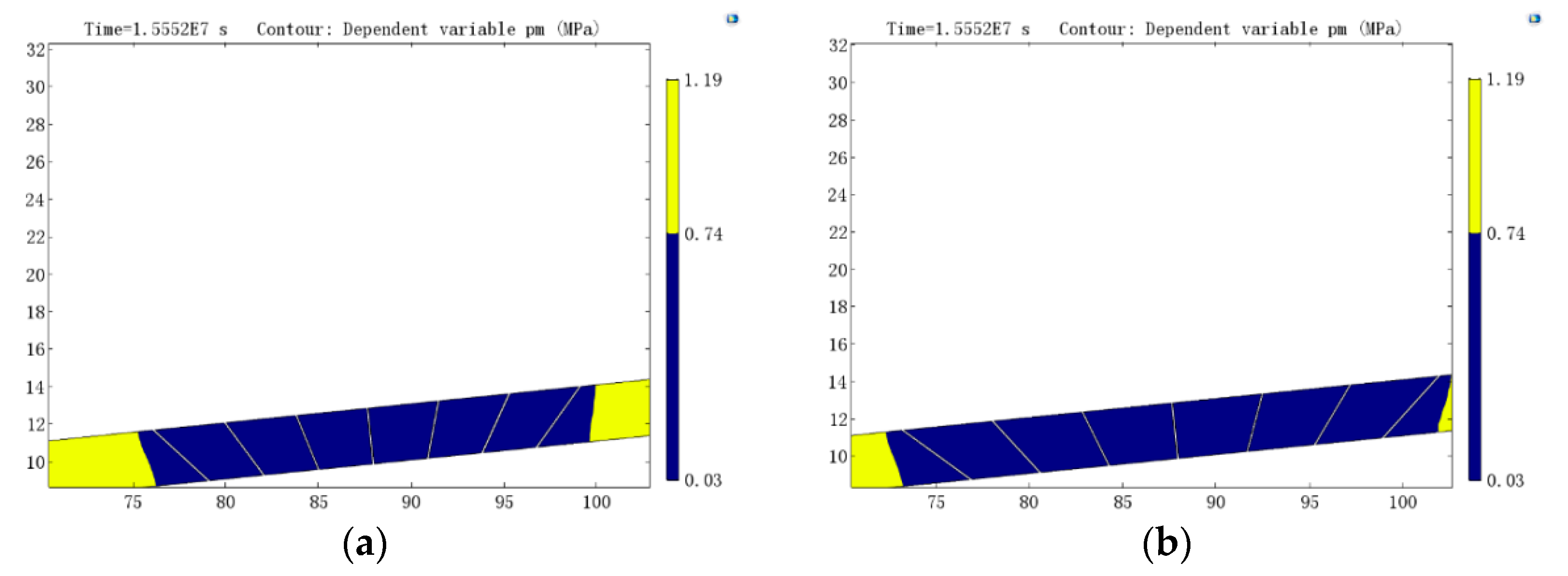
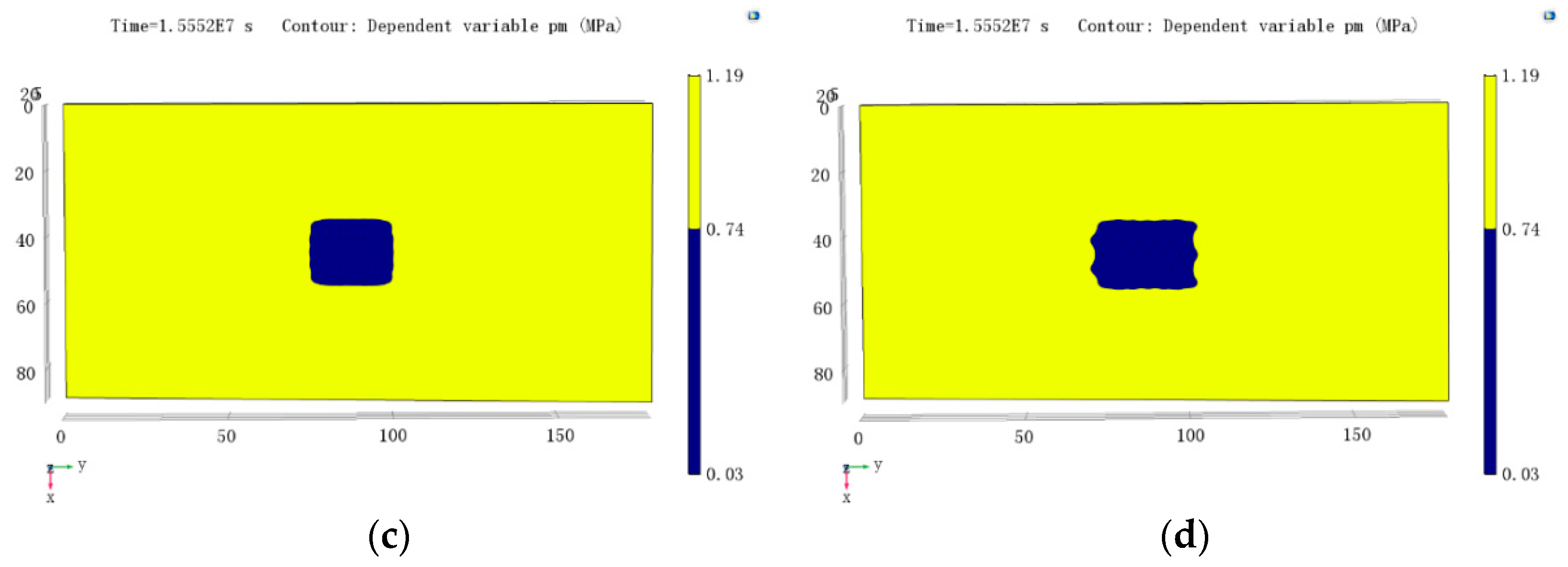
- For gas drainage from boreholes in a floor roadway running upwards and passing through coal seams, when the boreholes were arranged in a rectangular configuration, regional outburst risk elimination could not be realized within 180 days at a borehole spacing of 5 m; however, arranging the boreholes in a rhomboidal configuration under the same conditions resulted in regional outburst risk elimination. Furthermore, the 35 boreholes arranged on a rectangular grid at a spacing of 4 m and those set in a rhomboidal configuration at a spacing of 5 m were simulated and compared. The results indicated that after 180 days of gas drainage, both layouts could realize regional outburst risk elimination; however, using the rhomboidal configuration resulted in greater outburst risk elimination areas on the borehole bottom plane and larger outburst elimination volumes in the coal seam. To achieve the same outburst elimination area, the rhomboidal configuration required fewer boreholes and was thus cheaper. When the corresponding parameters are input into COMSOL Multiphysics software, the method can also be applied for other coal mines.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bao, Q.; Fang, Q.; Zhang, Y.; Chen, L.; Yang, S.; Li, Z. Effects of gas concentration and venting pressure on overpressure transients during vented explosion of methane air mixtures. Fuel 2016, 175, 40–48. [Google Scholar] [CrossRef]
- Skoczylas, N.; Dutka, B.; Sobczyk, J. Mechanical and gaseous properties of coal briquettes in terms of outburst risk. Fuel 2014, 134, 45–52. [Google Scholar] [CrossRef]
- Xie, Z.C.; Zhang, D.M.; Song, Z.L.; Li, M.H.; Liu, C.; Sun, D.L. Optimization of Drilling Layouts Based on Controlled Presplitting Blasting through Strata for Gas Drainage in Coal Roadway Strips. Energies 2017, 10, 1228. [Google Scholar] [CrossRef]
- Yan, F.Z.; Lin, B.Q.; Zhu, C.J.; Shen, C.M.; Zou, Q.L.; Guo, C.; Liu, T. A novel ECBM extraction technology based on the integration of hydraulic slotting and hydraulic fracturing. J. Nat. Gas Sci. Eng. 2015, 22, 571–579. [Google Scholar] [CrossRef]
- Yan, F.Z.; Lin, B.Q.; Zhu, C.J.; Zhou, Y.; Liu, X.; Guo, C.; Zou, Q.L. Experimental investigation on anthracite coal fragmentation by high-voltage electrical pulses in the air condition: Effect of breakdown voltage. Fuel 2016, 183, 583–592. [Google Scholar] [CrossRef]
- Yang, C.; Li, X.; Ren, Y.; Zhao, Y.; Zhu, F. Statistical analysis and countermeasures of gas explosion accident in coal mines. Procedia Eng. 2014, 84, 166–171. [Google Scholar]
- Karacan, C.Ö.; Ruiz, F.A.; Cote, M.; Phipps, S. Coal mine methane: a review of capture and utilization practices with benefits to mining safety and to greenhouse gas reduction. Int. J. Coal Geol. 2011, 86, 121–156. [Google Scholar] [CrossRef]
- Hou, Z.; Xie, H.; Zhou, H.; Were, P.; Kolditz, O. Unconventional gas resources in China. Environ. Earth Sci. 2015, 73, 5785–5789. [Google Scholar] [CrossRef]
- Gensterblum, Y.; Merkel, A.; Busck, A.; Krooss, B.M. High-pressure CH4 and CO2 sorption isotherms as a function of coal maturity and the influence of moisture. Int. J. Coal Geol. 2013, 118, 45–57. [Google Scholar] [CrossRef]
- Joubert, J.I.; Grein, C.T.; Bienstock, D. Sorpion of methane in moist coal. Fuel 1973, 52, 181–185. [Google Scholar] [CrossRef]
- Yee, D.; Seidle, J.P.; Hanson, W.B. Gas sorption on coal and measurement of gas content. AAPG Stud. Geol. 1993, 38, 203–218. [Google Scholar]
- Zhu, W.C.; Wei, C.H.; Liu, J.; Xu, T.; Elsworth, D. Impact of gas adsorption induced coal matrix damage on the evolution of coal permeability. Rock Mech. Rock Eng. 2013, 46, 1353–1366. [Google Scholar] [CrossRef]
- Pan, Z.; Connell, L.D. Modelling of anisotropic coal swelling and its impact on permeability behaviour for primary and enhanced coalbed methane recovery. Int. J. Coal Geol. 2011, 85, 257–267. [Google Scholar] [CrossRef]
- Lu, M.; Connell, L.D. A model for the flow of gas mixtures in adsorption dominated dual porosity reservoirs incorporating multi-component matrix diffusion: Part I. Theoretical development. J. Petrol. Sci. Eng. 2007, 59, 17–26. [Google Scholar] [CrossRef]
- Xue, D.J.; Zhou, H.W.; Chen, C.F.; Jiang, D.Y. A combined method for evaluation and prediction on permeability in coal seams during enhanced methane recovery by pressure-relieved method. Environ. Earth Sci. 2015, 73, 5963–5974. [Google Scholar] [CrossRef]
- Gilman, A.; Beckie, R. Flow of coal-bed methane to a gallery. Transp. Porous Media 2000, 41, 1–16. [Google Scholar] [CrossRef]
- Wang, S.; Elsworth, D.; Liu, J. Permeability evolution in fractured coal: The roles of fracture geometry and water-content. Int. J. Coal Geol. 2011, 87, 13–25. [Google Scholar] [CrossRef]
- Wang, S.; Elsworth, D.; Liu, J. Permeability evolution during progressive deformation of intact coal and implications for instability in underground coal seams. Int. J. Rock Mech. Min. 2013, 58, 34–45. [Google Scholar] [CrossRef]
- Zuber, M.D.; Williamson, J.R.; Hill, D.G.; Sawyer, W.K.; Frantz, J.H. A comprehensive reservoir evaluation of a shale reservoir—The new Albany shale. In Proceedings of the SPE 77469, SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 29 September–2 October 2002. [Google Scholar]
- McKee, C.R.; Bumb, A.C.; Koeing, R.A. Stress-dependent Permeability and Porosity of Coal. In Proceedings of the 1987 Coalbed Methane Symposium, University of Alabama, Tuscaloosa, AL, USA, 16–19 November 1987. [Google Scholar]
- Cui, X.; Bustin, R.M. Volumetric strain associated with methane desorption and its impact on coalbed gas production from deep coal seams. AAPG Bull. 2005, 89, 1181–1202. [Google Scholar] [CrossRef]
- Palmer, I.; Mansoori, J. How permeability depends on stress and pore pressure in coalbeds, a new model. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 6–9 October 1996. [Google Scholar]
- Palmer, I.; Mansoori, J. Permeability depends on stress and pore pressure in coalbeds, a new model. SPE Reserv. Eval. Eng. 1998, 1, 539–544. [Google Scholar] [CrossRef]
- Seidle, J.P.; Huitt, L.G. Experimental measurement of coal matrix shrinkage due to gas desorption and implications for cleat permeability increases. In Proceedings of the 1995 SPE International Meeting on Petroleum Engineering, Beijing, China, 14–17 November 1995. Paper SPE 30010. [Google Scholar]
- Wu, Y.; Liu, J.S.; Elsworth, D.; Chen, Z.W.; Connell, L.; Pan, Z.J. Dual poroelastic response of a coal seam to CO2 injection. Int. J. Greenh. Gas Control 2010, 4, 668–678. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, J.; Elsworth, D.; Miao, X.; Mao, X. Development of anisotropic permeability during coal bed methane production. J. Nat. Gas Sci. Eng. 2010, 2, 197–210. [Google Scholar] [CrossRef]
- Robertson, E.P.; Christiansen, R.L. A permeability model for coal and other fractured, sorptive-elastic media. In Proceedings of the 2006 SPE Eastern Regional Meeting, Canton, OH, USA, 11–13 October 2006. Paper SPE 104380. [Google Scholar]
- Wang, K.; Zang, J.; Wang, G.; Zhou, A. Anisotropic permeability evolution of coal with effective stress variation and gas sorption: Model development and analysis. Int. J. Coal Geol. 2014, 130, 53–65. [Google Scholar] [CrossRef]
- Liu, Q.Q.; Cheng, Y.P.; Wang, H.F.; Zhou, H.X.; Wang, L.; Li, W.; Liu, H.Y. Numerical assessment of the effect of equilibration time on coal permeability evolution characteristics. Fuel 2015, 140, 81–89. [Google Scholar] [CrossRef]
- Kong, X.G.; Wang, E.Y.; Liu, Q.L.; Li, Z.H.; Li, D.X.; Cao, Z.Y.; Niu, Y. Dynamic permeability and porosity evolution of coal seam rich in CBM based on the flow-solid coupling theory. J. Nat. Gas Sci. Eng. 2017, 40, 61–71. [Google Scholar] [CrossRef]
- Xia, T.Q.; Gao, F.; Kang, J.H.; Wang, X.X. A fully coupling coal–gas model associated with inertia and slip effects for CBM migration. Environ. Earth Sci. 2016, 75, 582. [Google Scholar] [CrossRef]
- Lu, S.Q.; Cheng, Y.P.; Li, W. Model development and analysis of the evolution of coal permeability under different boundary conditions. J. Nat. Gas Sci. Eng. 2016, 31, 129–138. [Google Scholar] [CrossRef]
- Li, S.; Fan, C.J.; Han, J.; Luo, M.K.; Yang, Z.H.; Bi, H.J. A fully coupled thermal-hydraulic-mechanical model with two-phase flow for coalbed methane extraction. J. Nat. Gas Sci. Eng. 2016, 33, 324–336. [Google Scholar] [CrossRef]
- Ren, J.; Zhang, L.; Ren, S.; Lin, J.D.; Meng, S.Z.; Ren, G.J.; Gentzis, T. Multi-branched horizontal wells for coalbed methane production: Field performance and well structure analysis. Int. J. Coal Geol. 2014, 131, 52–64. [Google Scholar] [CrossRef]
- Liu, Z.D.; Cheng, Y.P.; Jiang, J.Y.; Li, W.; Jin, K. Interactions between coal seam gas drainage boreholes and the impact of such on borehole patterns. J. Nat. Gas Sci. Eng. 2017, 38, 597–607. [Google Scholar] [CrossRef]
- Li, B.; Sun, D.H.; Zhang, L.L. Study on rational space between gas drainage boreholes passing through seam in coal mine. Coal Sci. Technol. 2016, 44, 121–126. [Google Scholar] [CrossRef]
- Xia, T.; Zhou, F.; Liu, J.; Hu, S.; Liu, Y. A fully coupled coal deformation and compositional flow model for the control of the pre-mining coal seam gas extraction. Int. J. Rock Mech. Min. Sci. 2014, 72, 138–148. [Google Scholar] [CrossRef]
- Alexeev, A.D.; Nedodayev, N.V.; Alexeev, A.D.; Nedodayev, N.V. Ultimate State of Rocks; Naukova Dumka: Kiev, Russian, 1982. [Google Scholar]
- Feng, X.T.; Zhang, X.W.; Kong, R.; Wang, G. A Novel Mogi Type True Triaxial Testing Apparatus and Its Use to Obtain Complete Stress–Strain Curves of Hard Rocks. Rock Mech. Rock Eng. 2016, 49, 1649–1662. [Google Scholar] [CrossRef]
- Alexeev, A.D.; Revva, V.N.; Alyshev, N.A.; Zhitlyonok, D.M. True triaxial loading apparatus and its application to coal outburst prediction. Int. J. Coal Geol. 2004, 58, 245–250. [Google Scholar] [CrossRef]
- Zhu, W.C.; Wei, C.H.; Liu, J.; Qu, H.Y.; Elsworth, D. A model of coalegas interaction under variable temperatures. Int. J. Coal Geol. 2011, 86, 213–221. [Google Scholar] [CrossRef]
- Tao, Y.Q.; Xu, J.; Cheng, M.J.; Li, S.C.; Peng, S.J. Theoretical analysis and experimental study on permeability of gas-bearing coal. Chin. J. Rock Mech. Eng. 2009, 28, 3364–3370. [Google Scholar]
- An, F.H.; Cheng, Y.P.; Wang, L.; Li, W. A numerical model for outburst including the effect of adsorbed gas on coal deformation and mechanical properties. Comput. Geotech. 2013, 54, 222–231. [Google Scholar] [CrossRef]
- Xia, T.; Zhou, F.; Gao, F.; Kang, J.; Liu, J.; Wang, J. Simulation of coal self-heating processes in underground methane-rich coal seams. Int. J. Coal Geol. 2015, 141, 1–12. [Google Scholar] [CrossRef]
- Xu, H.; Tang, D.Z.; Tang, S.H.; Zhao, J.L.; Meng, Y.J.; Tao, S. A dynamic prediction model for gasewater effective permeability based on coalbed methane production data. Int. J. Coal Geol. 2014, 121, 44–52. [Google Scholar] [CrossRef]
- Liu, S.J.; Ma, G.; Lu, J.; Lin, B.Q. Relative pressure determination technology for effective radius found on gas content. J. China Coal Soc. 2011, 36, 1715–1719. [Google Scholar]

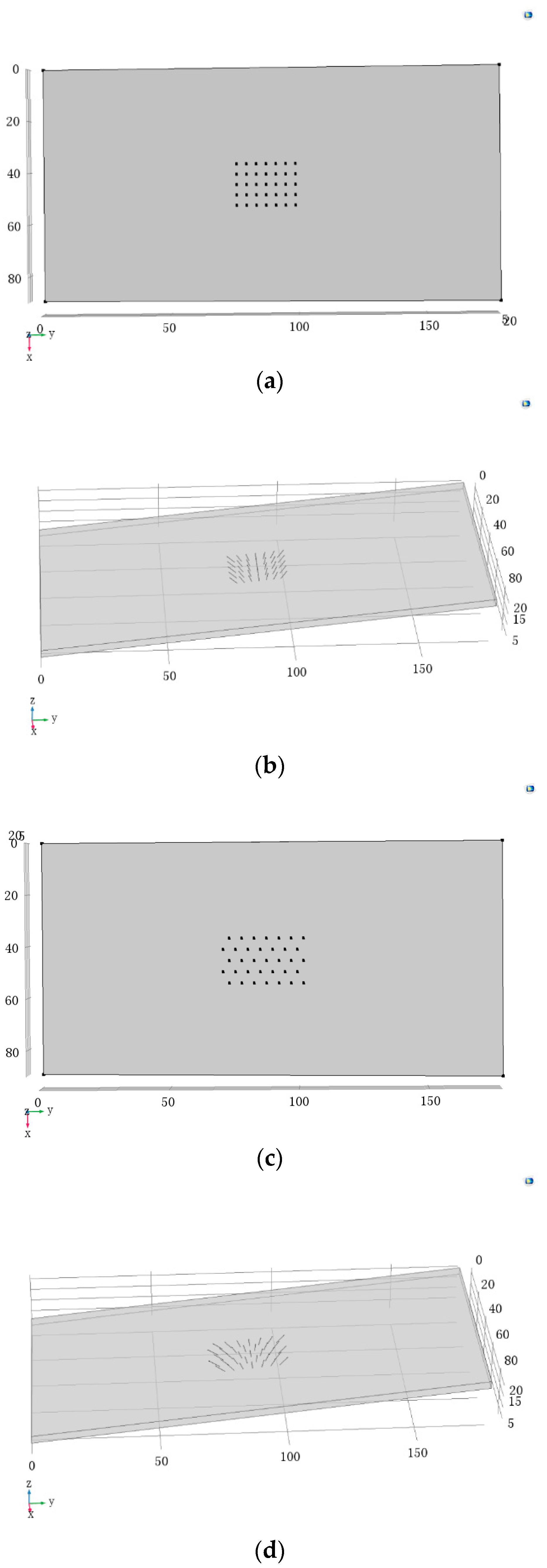
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Elastic modulus of coal | E | 2.8 × 109 | Pa |
| Elastic modulus of coal skeleton | ES | 8.4 × 109 | Pa |
| Fracture stiffness | Kn | 4.8 × 109 | Pa |
| Poisson’s ratio of coal | 0.33 | ||
| Density of coal skeleton | 1.35 × 103 | kg/m3 | |
| Density of water at standard condition | 1000 | kg/m3 | |
| Initial porosity for coal matrix | 0.07 | ||
| Initial porosity for fracture | 0.02 | ||
| Initial permeability for fracture | kf0 | 0.26 × 10−16 | m2 |
| Gas dynamic viscosity | 1.03 × 10−5 | Pa·s | |
| Water dynamic viscosity | 1.01 × 10−3 | Pa·s | |
| Initial gas pressure in fracture | pmg0 | 1.2 × 106 | Pa |
| Initial gas pressure in matrix | pfg0 | 1.2 × 10−6 | Pa |
| Coefficient for sorption-induced volumetric strain | 0.043 | kg/m3 | |
| Initial water saturation | sw0 | 0.4 | |
| Endpoint relative permeability of water | krw0 | 1 | |
| Endpoint relative permeability of gas | krg0 | 0.756 | |
| Irreducible water saturation | swr | 0.2 | |
| Residual gas saturation | sgr | 0.05 | |
| Adsorption time | 153,360 | s | |
| Langmuir pressure constant | PL | 2.45 | MPa |
| Langmuir volume constant | VL | 0.016 | m3/kg |
| Initial fracture aperture | b0 | 1 × 10−4 | m |
| Initial matrix size | a0 | 1 × 10−2 | m |
| Capillary pressure | pcgw | 0.05 | MPa |
| Wet swell coefficient | 0.1 × 10−4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Xu, J.; Peng, S.; Yan, F.; Fan, C. A Gas–Solid–Liquid Coupling Model of Coal Seams and the Optimization of Gas Drainage Boreholes. Energies 2018, 11, 560. https://doi.org/10.3390/en11030560
Chen Y, Xu J, Peng S, Yan F, Fan C. A Gas–Solid–Liquid Coupling Model of Coal Seams and the Optimization of Gas Drainage Boreholes. Energies. 2018; 11(3):560. https://doi.org/10.3390/en11030560
Chicago/Turabian StyleChen, Yuexia, Jiang Xu, Shoujian Peng, Fazhi Yan, and Chaojun Fan. 2018. "A Gas–Solid–Liquid Coupling Model of Coal Seams and the Optimization of Gas Drainage Boreholes" Energies 11, no. 3: 560. https://doi.org/10.3390/en11030560
APA StyleChen, Y., Xu, J., Peng, S., Yan, F., & Fan, C. (2018). A Gas–Solid–Liquid Coupling Model of Coal Seams and the Optimization of Gas Drainage Boreholes. Energies, 11(3), 560. https://doi.org/10.3390/en11030560





