1. Introduction
Climate change has become a major global issue, and reducing carbon emissions is considered to be necessary for human welfare. The Paris agreement which entered into force in November 2016 has strengthened the global response to the threat of climate change, and the participating countries across the world have outlined their Intended Nationally Determined Contributions (INDCs) (The Paris Agreement.
http://unfccc.int/paris_agreement/items/9485.php). Effectively achieving low carbon emissions, however, is much more complicated and often requires a combination of various kinds of efforts. Using a single policy instrument, even the most advanced system, such as the European Union (EU) Emissions Trading System (EU ETS), has clear disadvantages. The EU ETS covers only approximately 40% of the sources of emissions in the EU, and the design of the system has often been criticized. Additional abatement policies (i.e., energy efficiency standards, carbon taxes) can be adopted to form a policy mix to ensure effective emissions reductions.
China, the biggest user of fossil fuel-based energy in the world and the largest source of carbon dioxide (CO2) emissions, has been actively engaged in reducing CO2 emissions in recent years. Jointly with the second-largest source of carbon-based emissions, the United States, China has pledged that the peak of its CO2 emissions will occur no later than 2030. It is necessary and urgent for the Chinese government to design an effective policy mix to achieve such an ambitious goal. Noticeably, China has already established seven emissions-trading pilot programs and aims to introduce a nationwide emissions trading system (ETS) in 2017. Meanwhile, other supplementary policies, such as energy-savings subsidies and laws mandating the use of renewable energy, either have already been implemented or will be implemented.
It is perhaps easier to comment on the effectiveness of a single policy because a policy mix can be more complicated, as different policies can interact with one another. Take subsidies, for example; Fredriksson shows that subsidies for pollution abatement are inefficient when a Pigovian pollution tax is available [
1]. He also explains the use of pollution abatement subsidies in environmental policy as a primary tool for redistribution. The equilibrium level of a subsidy depends on the elasticity of the subsidy in terms of pollution abatement and lobby group membership. Its effectiveness does not involve a simple aggregation of the impacts from each individual policy.
Two interrelated policies may be mutually complementary to increase effectiveness, but they can also be substitutional, which leads to lower aggregate impacts. For example, previous studies, such as Böhringer and Keller, suggest that other abatement policies in the EU ETS may not bring further emissions reductions [
2]. Instead, they may reduce carbon prices and cause economic distortion. It is therefore important to study the interrelationship of policy instruments within a policy mix and evaluate their joint effectiveness. In addition, Dechezlepretre and Sato present an ex-post evaluation and discuss the impact of environmental regulations with a combination of different instruments (i.e., carbon price and compensations) on productivity, employment, trade, industry location and innovation [
3]. They note that a reasonable compensation level is important. In the EU ETS, overcompensation to secure profits of regulated firms in energy intensive industries can result in paradoxically high levels of subsidies. Policies such as these may have no direct environmental benefits but instead generate negative effects on the cost-effective measures.
Some recent studies address this question based on the ETS framework. Lecuyer and Quirion analyze overlapping policy instruments for the same emissions sources [
4]. It can be socially beneficial to implement an additional abatement policy instrument (i.e., renewable energy subsidy) when carbon prices drop to zero or when a carbon tax is politically difficult to implement. Fischer and Newell estimate the impact on carbon emissions reductions from different abatement policies, and they suggest that a policy mix combining abatement, learning, and R&D is more effective than a single policy instrument [
5].
Policies for encouraging emissions reductions have to be consistent with economic incentives in order to be effective. A general concern at the early stage of the EU ETS was how much negative impact would be created for the covered industries by increasing carbon abatement costs. Thus, a free allocation or payback mechanism was considered to offset the rising costs. Arlinghaus presents a review of the literature on the ex-post empirical evaluations of the impacts of carbon prices on indicators of competitiveness [
6]. She notes that although most of the studies found that carbon pricing could result in emissions abatement, the studies fail to measure any economically meaningful competitiveness effects as a consequence of these policies. Additionally, she suggests that to ensure that these results hold in the absence of this measure, future research could focus on comparing the effects of carbon prices on firms paying the full rate of the carbon price to firms that are exempt or pay a rebate. In addition, this future research could be important in estimating competitiveness effects among different sectors considering sectoral heterogeneity. Demailly and Quirion analyze the impacts of grandfathering and output-based allocation (OBA) on emissions reduction, firm competitiveness, and carbon leakage [
7]. They find that an optimal free allocation share exists, and it would be beneficial to firm competitiveness. In another study, Demailly and Quirion show that a reasonable free allocation in the EU ETS can increase firm competitiveness without hurting their profitability [
8]. The results show that both OBA and emissions-based allocation (EBA) are helpful. Meunier et al., on the contrary, find that OBA is not the best option when global carbon taxation and border adjustment policies are absent [
9]. They suggest that the best choice for the EU would be to combine these two allocation methods.
The situation may be even more complicated when multiple emissions reduction policies are applied to multiple sectors. In other words, the impacts of a policy mix can vary across industries. For example, the objective of energy-savings subsidies is to offset losses in profit, whereas the objective of ETS is to reduce emissions through a cap-and-trade system. As a result, their impacts on different industries can vary significantly. A series of studies have noted that the adoption of output-based rebating in an emissions trading scheme plays important roles in affecting sectoral competitiveness [
8,
9,
10,
11,
12,
13]. Quantitative assessments of the impact of unilateral emissions abatement policies on energy intensive industries, such as emissions trading, carbon taxes and border carbon adjustments, can also be found in some recent studies [
2,
8,
14,
15,
16,
17]. Evaluating multipolicy effects in multisector setups is, to a large extent, missing. Top-down approaches, such as the computable general equilibrium (CGE) models, are often used in multi-sector studies and are widely used when studying the economic effects of policies on given countries or specific areas. Goulder, for example, uses the dynamic CGE model to simulate the impact of carbon tax policy on the economy in the United States [
18]; Carbone and Rivers consider the measurement of competitiveness due to climate policies in computable general equilibrium (CGE) models and discuss the weaknesses of the existing approach [
19]. CGE models also have been shown to be useful in the assessment of the impact of the EU 20 energy and climate package (European Union (EU), 2020 Climate & Energy Package.
https://ec.europa.eu/clima/policies/strategies/2020_en). These models, however, have noticeable problems, for example, the underlying mechanism is less clear, and it is hard to adapt the models to a particular sector.
Models for multipolicy, multicountry analyses have been developed; for example, Branger and Quirion use a stochastic model to rank different policies according to their expected total social costs [
20]. They found that a tax is preferred to caps, and relative caps are preferred to fixed caps in the US and emerging countries, whereas a fixed cap is a better choice over a relative cap in Europe and Japan. In terms of the policy impacts in single sector studies, a partial equilibrium model is often used, such as in Lecuyer and Quirion [
4], and Demailly and Quirion [
7]. The only problem with these existing partial equilibrium models is that they are applied mostly to a single sector, and are thus unable to address sectoral differences.
This paper first builds a multisector model following the framework in Lecuyer and Quirion [
4]. Instead of focusing on the impact of overlapping instruments to cover the same emission sources in one sector, we are focusing on a heterogeneous multisector case. Specifically, we extend the single sector partial equilibrium framework to a multisector model to investigate the diverse responses of different sectors, as well as the inter-sectoral interaction, under the given abatement policy mix. The other unique features of our model are summarized as follows:
- (1)
This study aims to investigate the potential interaction of different policies from the perspective of the social optimum. The emission targets in accordance with equilibrium carbon price levels are derived by social welfare maximization, consisting of more than one sector, which are linked through the carbon market. Relaxing the constant emissions reduction target but holding the social optimum in our analysis can contribute to the literature in terms of understanding the interaction effects on policy mix design and evaluation.
- (2)
Energy-savings subsidies and output-based rebates have been introduced as additional policy options together with an emissions trading scheme in our model. In addition, the analytical solutions have been derived from a two-sector case. We explain how and why the sectoral responses to the same policy can vary substantially by comparing the analytical solutions. In addition, we also present some inconsistent conclusions on the effectiveness of policy mixes from previous studies under the social welfare maximization. For example, we show that emissions reductions in one sector can decrease with energy-savings subsidies. We believe that the findings on policy mix distortion among sectors can help improve the efficiency of the design of emissions trading schemes, as well as complementary policy options.
Based on the results of our extended multisector partial equilibrium model, we evaluate the following cases using empirical data from China: the effectiveness of multiple reduction policies on one sector, different responses from multiple sectors to a single policy, and the interactions and effects of multiple policies in a multisector environment. We further investigate the impact on social welfare and total emissions, which leads to relevant policy discussions. The rest of this paper proceeds as follows:
Section 2 builds the multisector partial equilibrium model;
Section 3 describes our case study and results for two energy intensive sectors in China; and
Section 4 concludes.
2. Analytical Framework
In this paper, we assume that three policy instruments are available, namely, ETS with a full auction for allowances, ETS together with energy-savings subsidies, and ETS with output-based rebating (OB). We examine three combinations of these policy instruments (
Table 1) in our multiple policy analysis. To simplify the analysis, we further assume that transactions occur among sectors rather than at the firm level (in other words, each of the sectors has one representative firm). All of the sectors are price takers (perfect competition) in the allowance market, and their trading behavior cannot affect carbon prices.
Two policy mixes have been considered in our analysis. For energy-savings subsidies, they have already been launched for the energy intensive sectors in China as a part of the 11th Five Year Plan [
21], which was developed by the government to incentivize sectors to reduce energy consumption and achieve energy savings targets. The subsidy level is set as a certain monetary refund per unit of energy savings (per ton of standard coal). This subsidy may still exist even after the implementation of ETS. For output-based rebates, they have been partially adopted as part of the allowance allocation in the power sector in China’s planned national Emission Trading Scheme. This rebating policy is also being considered for implementation in other sectors covered by the national ETS.
The unit and description of variables and parameters used in the model are listed in
Table 2.
2.1. Base Case
Assume that there are completely heterogeneous
J energy-intensive sectors, whose demand functions, production cost functions, and emissions reduction cost functions are all independent. The demand function for sector
j can be written as
where
is price,
is output, and
and
are the intercept and slope of the demand curve, respectively. In addition, the demand uncertainty proposed by Lecuyer and Quirion [
4] is not included as we are focusing on the diverse sectoral responses to the given abatement policy mix (We appreciate the comments given by an anonymous reviewer that note this issue and think this can be our next step to further improve the model) and for simplicity.
The cost function of sector
can be written as
. Following Lecuyer and Qurion [
4], it takes a linear form. Here,
is the marginal cost of production, and we further assume
.
The abatement cost curve is in a quadratic form (Meunier et al. [
9])
where
is the level of carbon abatement in sector
, and
and
are the coefficients.
The cost of the carbon permit in sector
is
, which can be written as
where
is the carbon price, which is unified for all sectors.
is the carbon intensity of sector
before carbon emissions reduction.
The profit function of sector
can be expressed as
The negative impacts of emissions on society (the negative externality) are included in the social welfare function through carbon prices. Total net CO
2 emissions can be represented as
The cost of purchasing emissions permits is supposed to be paid back to society. Therefore, the social welfare function can be expressed as
where
is the consumer surplus in sector
, represented as
;
is the loss function that resulted from the sectoral CO
2 emissions, which depicts the social damage from carbon emissions; and
is the unit damage coefficient. The environmental loss function is regularly used to depict the environmental damage from harmful emissions, such as sulfur dioxide (SO
2) and nitrogen oxides (NO
X), in classical environmental economic models (i.e., Nordhaus [
22]). Unlike other pollutants, carbon emissions have a cumulative effect. In other words, the damage from CO
2 is determined not by annual emissions but by the total amount accumulated in the atmosphere, and Nordhaus relates cumulative emissions to changes in CO
2 concentrations and in temperature for the damage function [
22]. The function form proposed by Nordhaus [
22] can not be used in our sectoral-level partial equilibrium analysis [
22].
We refer to Lecuyer and Quirion [
4] by using a linear damage function in the model, in which the model only accounts for the damage that results from the increment CO
2 emissions without considering the CO
2 stock in the atmosphere. There are two advantages in using this function; first, the emissions control target is generally set to the incremental level of emissions rather than stocks. Second, the linear function simplifies the environmental damage of emissions and thus allows us to address multisector issues analytically.
After substitution, the social welfare function can be written as
It should be noted that, in the welfare function (7), the costs of the carbon permit cancel each other out after substitution, for we assume that the cost of purchasing the CO2 permit will be paid back or come from society. That is, the CO2 permit purchasing/selling cost has no influence on the total welfare.
2.2. Extension 1: Multi_ES (Auction Plus Energy-Savings Subsidies)
In addition to the ETS with a full auction in the base case, policymakers can also give sector subsidies to achieve their energy savings , which results in , and the unit of the energy-savings subsidy is , which is exogenously given in our model.
In most energy-intensive sectors, energy savings
and carbon emissions reductions
are, to a large extent, equivalent (with an adjustment coefficient
) because saving fossil fuel-based energy (different forms of fossil fuel-based energy, such as coal, oil, and natural gas, can be converted to standard coal and thus are comparable) is the main option for these sectors to reduce emissions. Their relationship satisfies the following condition:
The energy-savings subsidy function can be rewritten as
where
is the unit of the energy-savings subsidy after adjustment. The demand function, abatement cost function, and production cost function are the same as in the base case. It is worth to note that the discussion here is essentially short-term oriented. In the long-term, fuel switching and moving to a low-carbon production process are possible solutions to emission. For example, Arens et al. study the low-carbon pathways in Germany and suggest that the German steel sector is highly unlikely to meet its climate target regardless of what production pathway they choose [
23]. An alternative way is to develop new carbon free production process, such as switching to hydrogen or using carbon free electricity.
The profit function of sector
is
Energy-savings subsidies are supposed to come from society. Therefore, the social welfare function under the “Multi_ES” case can be written as
2.3. Extension 2: Multi_OB (Auction Plus OB)
In this case, output-based allowance rebating (OB) is combined with the ETS and an auction. Output-based rebating has already been implemented in New Zealand and California [
9,
15]. Furthermore, Canada has put into practice an output-based pricing system for industrial facilities that emit above a certain threshold, with an opt-in capability for smaller facilities with emissions that are below the threshold. The pan-Canadian approach to pricing carbon pollution provides jurisdictions the flexibility to implement an explicit price-based system, for example, a hybrid approach composed of a carbon levy, or an output-based pricing system such as in Alberta [
24], Environment and Climate Change Canada [
25].
Output-based allowance rebating is a subsidy in the form of rebated allowances associated with output. Each sector receives a given number of allowances per unit of output. Assume that the per-unit rebating rate is
(the range of
can be set from 0 to 1), and the free allowances permit that sector
obtains is
. Because the permit can be sold in the ETS, it could be seen as a part of the income of these sectors (output incentive mechanism). The additional income in sector
due to permits returned is
. The profit in sector
can be revised to
Each sector maximizes its profit by choosing an optimal level of production and emissions reductions. Again, all of the permits returned to sectors are supposed to come from society, so the social welfare function can be expressed as
2.4. Solving the Model
It is worth noting that the model is essentially static in nature. We assume that the ETS auction system is set to optimize the total social welfare. Therefore, the first thing to do is to find an optimal carbon price level that maximizes the total social welfare (it varies in different cases). Given the optimal carbon price level, each sector set its production and abatement level to maximize profit.
The equilibrium level of carbon emissions can be written as
where
and
are functions of
and vary in different cases. The equilibrium solution of these factors is given in the
Appendix A.1,
Appendix A.2 and
Appendix A.3.
Table 3 summarizes the analytical solutions to the model among the three cases. For the equilibrium carbon price, the solution is based on the coverage of two sectors.
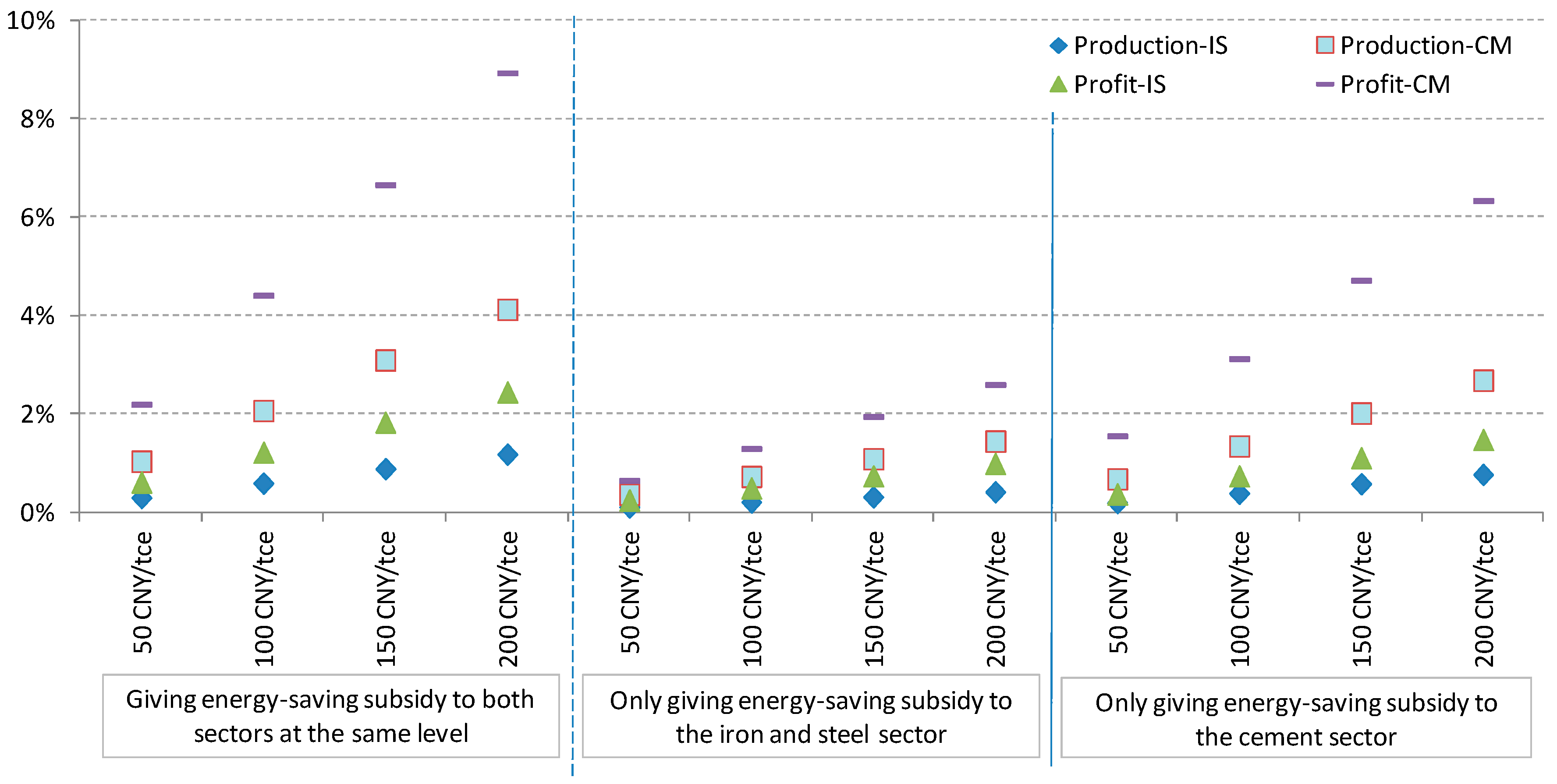
In the Multi_ES case, it can be seen that is inversely proportional to the subsidy level, , when compared to that in the base case. From the perspective of production, an incentive to the output can be observed after the introduction of the energy-savings subsidies. Furthermore, the output from the other sector will also increase, even if the subsidy is only given to one sector (given will also be decreased when the subsidies are introduced to only one sector).
From the perspective of emissions reductions, the emissions reductions in the sector with the energy-savings subsidy depend on the changes in the equilibrium carbon price level , as well as the energy subsidy level . Specifically, for the sector with the energy-savings subsidy, given , if , an increase in emissions reductions within the sector can be observed, otherwise its emissions reductions will decrease. However, the emissions reductions of the other sector will decrease due to the fall of the equilibrium carbon price level.
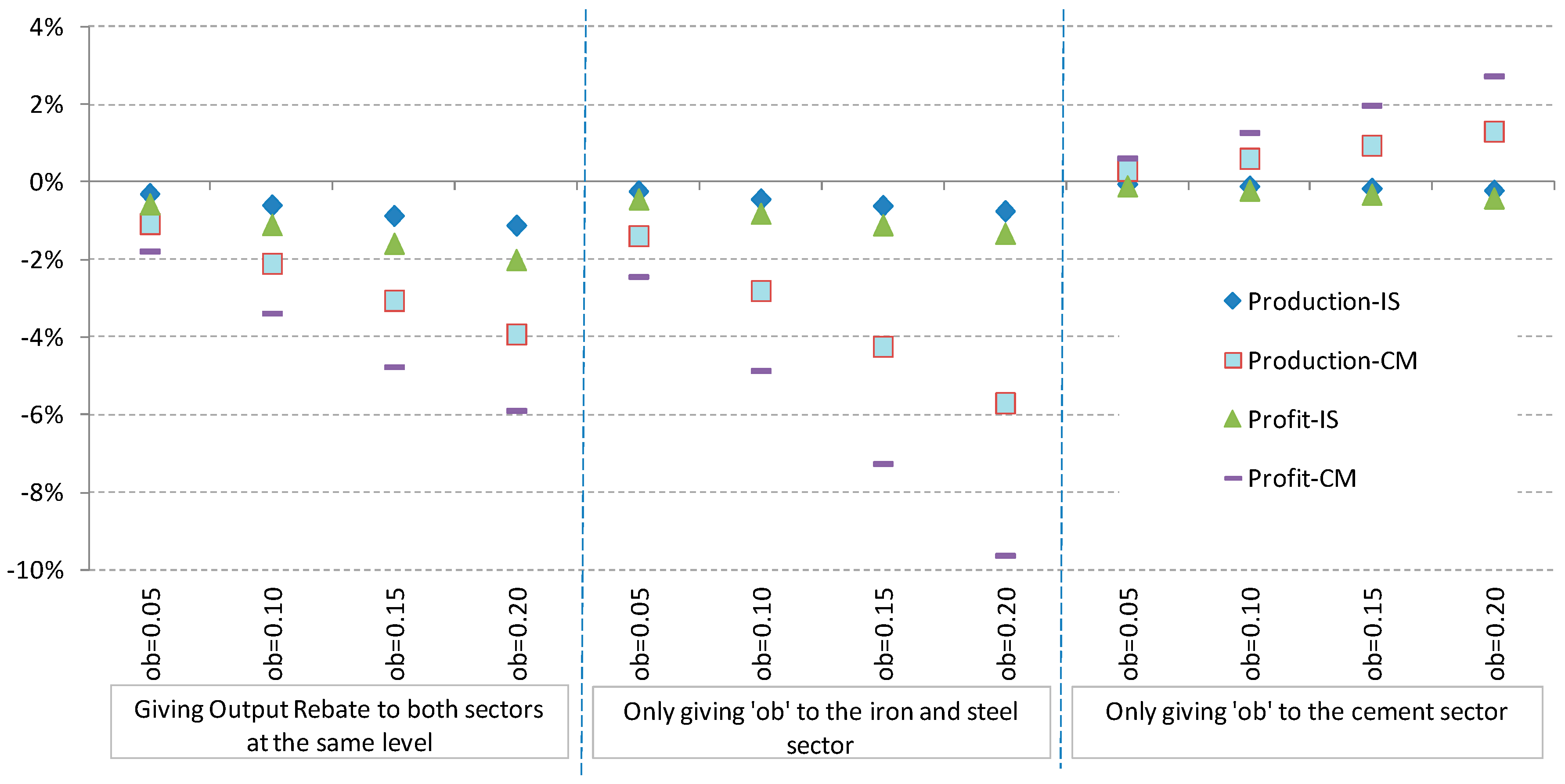
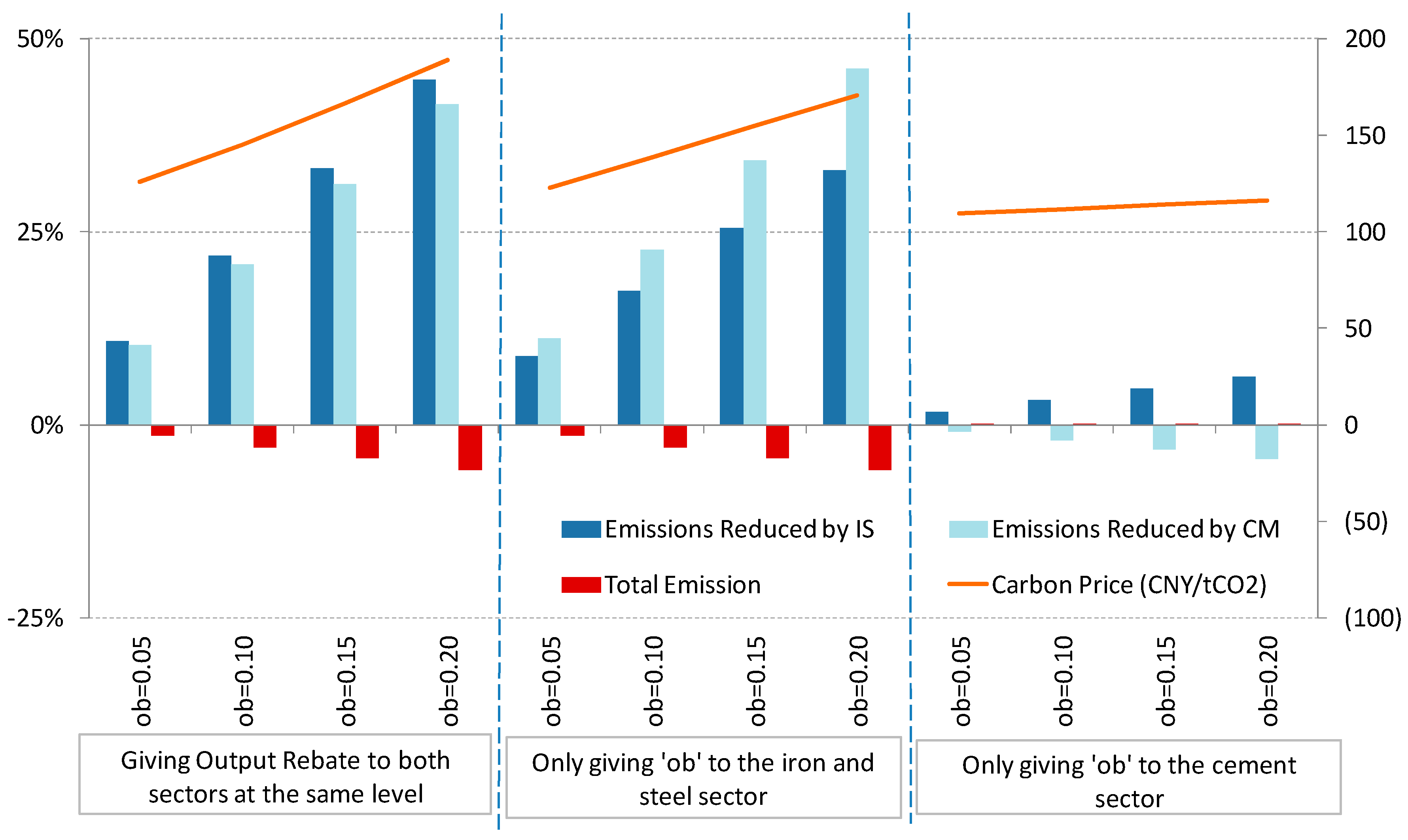
In the Multi_OB case, the solution form of the equilibrium carbon price level is more complicated with the introduction of output-based allowance rebating. The equilibrium carbon price will increase with the level of ob, which ranges from 0 to 1. From the perspective of production, it is obvious that the increase in the ob rate will raise output levels when the carbon price level remains unchanged, although the carbon price is also related to the ob rate. Specifically, given , this output of this sector increases if , otherwise its output will be decreased. Furthermore, the output of the other sector will decrease even if the ob is only given to one sector (given will be increased with the introduction of ob).
One could argue that this is contrary to the initial design of output-based rebating, which is applied to compensate for losses in sectoral competitiveness that result from implementing ETS and can provide incentives for sectoral output [
7,
8]. The output incentive effects of output-based rebating make sense if we look at the analytical solution of
under the Multi_OB case. In our model, each
ob rate corresponds to an equilibrium carbon price level, and the increase in the equilibrium carbon price level can offset the output incentive that resulted from the increasing
ob rate and even make sectoral performance worse after implementation of output-based rebating.
From the perspective of emissions reductions, the emissions reductions in the sector with an output-based rebate depends on the changes in the equilibrium carbon price level , as well as the ob rate. Specifically, for the sector with ob, given , if , an increase in emissions reductions within the sector can be observed. However, the emissions reductions of the other sector will increase due to the increase in the equilibrium carbon price level.
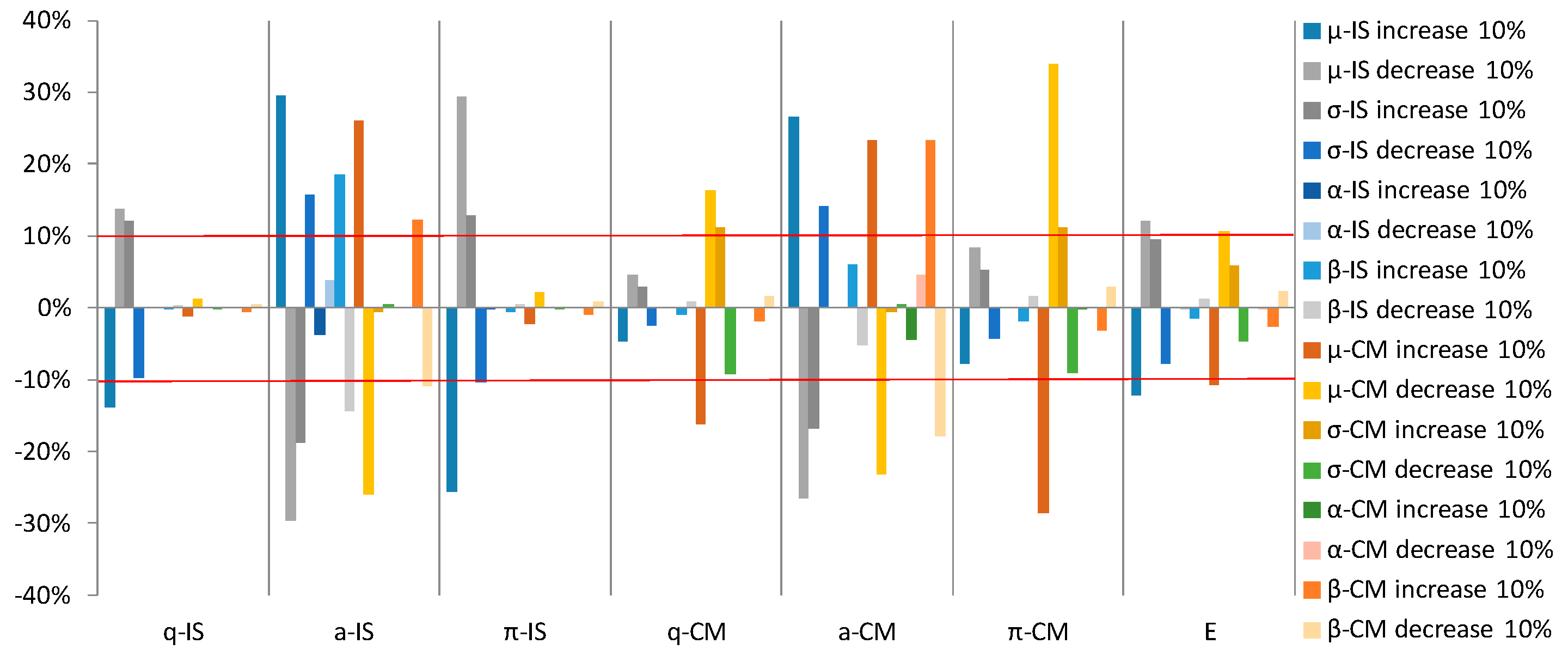
In addition, one concern about the analysis above is that the assumption of one representative firm, as well as the demand of sectoral outputs are set as independent, may generate unrealistic predictions. In
Appendix A.5–
Appendix A.6, we presented the theoretical analysis on the situations of: (1) relax the assumption of one representative firm and allow more than one firm in each sector; and (2) consider the correlation of demands across sectors. Under the condition of welfare maximization, although the form of analytical solutions to the alternative models vary from the basic model, for example,
is now a function of firms’ numbers across two sectors (
Appendix A.5). It is therefore including sector size into the model, though the general indication when comparing three cases within each model setup do not change.
4. Discussion and Conclusions
A multisector partial equilibrium model is established to analyze the impacts of multiple CO2 abatement policies (energy-savings subsidies and OBA) in two sectors on the basis of ETS (auction). Empirical data on China’s iron and steel sector and cement sector are used to illustrate the impacts of various policy mixes relative to the auction-based ETS (base case). Specifically, we are interested in the impacts on production decisions, carbon prices, emissions reductions, and social welfare.
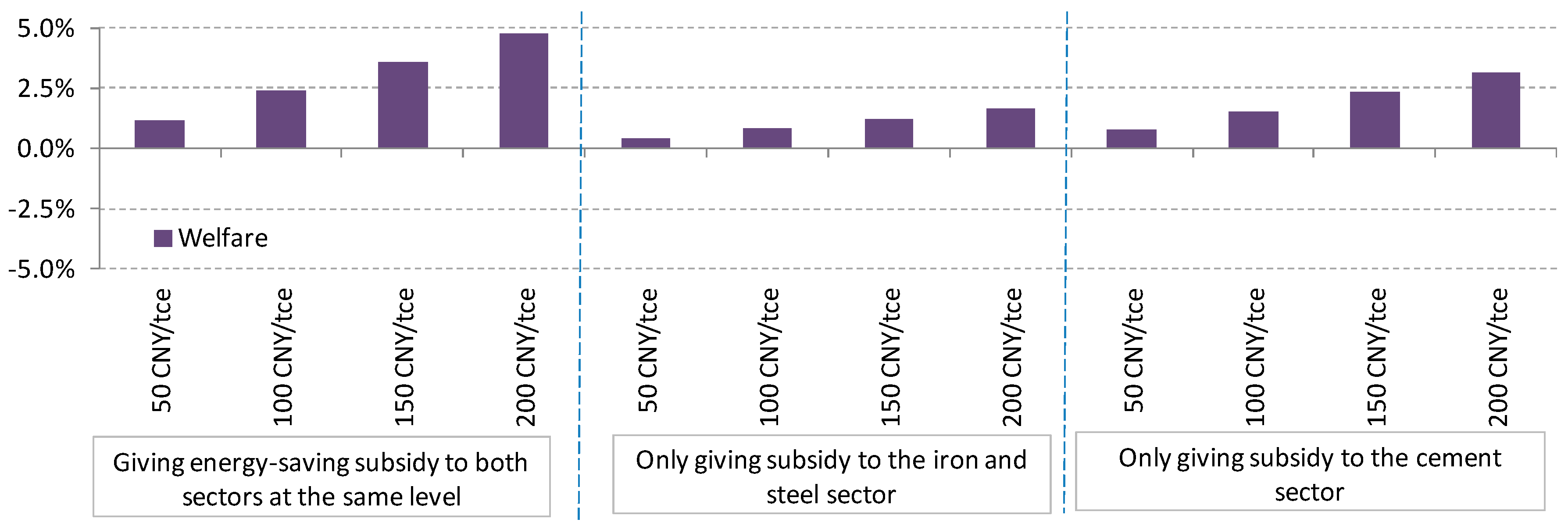
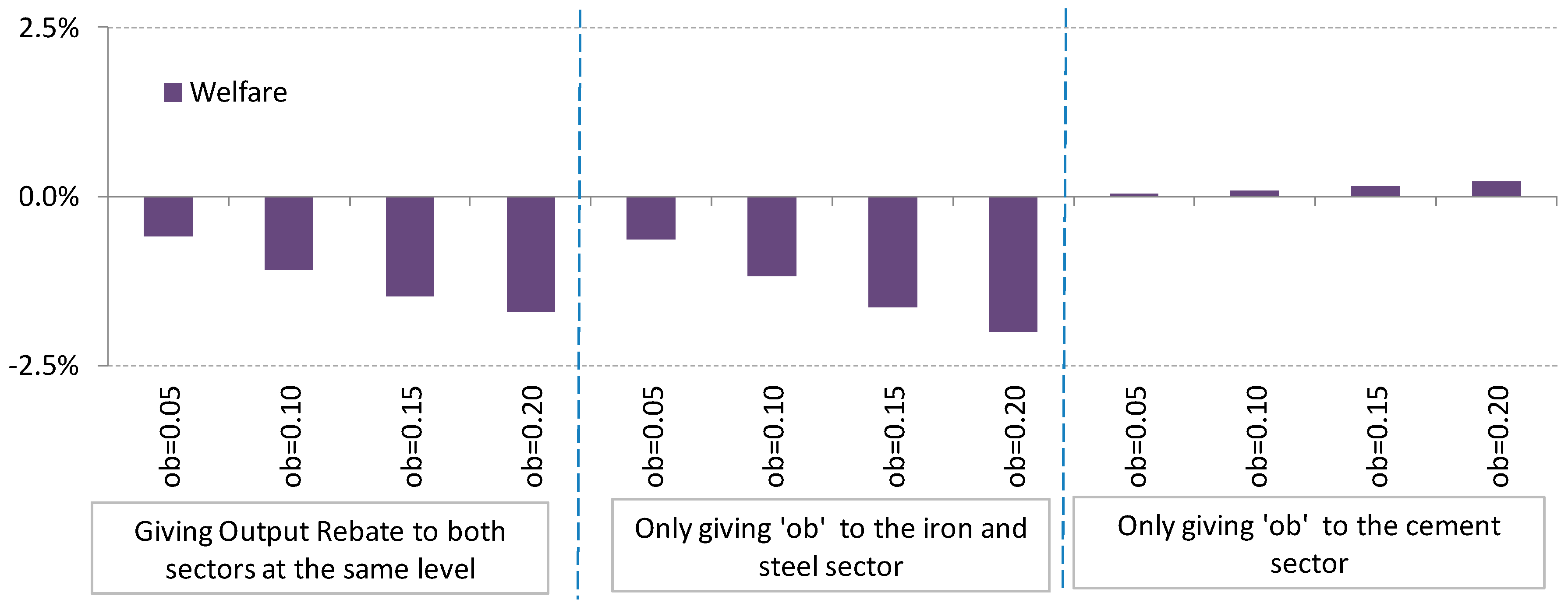
It is clear that these two policy mixes have distinctively different effects on the two sectors. Energy-savings subsidies play a substitution role for carbon prices because they encourage reductions in energy use and reduce equilibrium carbon prices. We find that even when a subsidy is given only to one sector, both sectors increase their production/profit. Total emissions levels increase because fewer efforts are made by these sectors to reduce emissions (except when subsidies are given only to the IS sector, which can increase abatement). Moreover, the equilibrium results show that the CM sector is more sensitive to the energy-savings subsidies. Carbon prices fall in response to incremental energy-savings subsidies. The results are based on the assumption that these two policies are set up independently, whereas they may be considered jointly by the policymakers in reality. In a scenario that the subsidy scheme is included in the cap of ETS, price may not necessarily fall. The policy independence assumption and its associated price impacts might be a bit too strong, it is nonetheless suggesting that energy saving subsidies are supplemental to ETS and failure to incorporate it to the ETS can weaken the pricing signal to carbon markets.
The policy mix with output-based rebating (in addition to auction-based ETS) of allowances, however, shows clearly different patterns. If identical policies are applied to both sectors, then the carbon prices increase significantly, both sectors lower production/profit, and consequently, the goal of lower emissions is achieved. Total social welfare, however, is reduced. In addition, the responses show a totally different trend with discriminatory output-based rebating: Almost identical patterns are seen when OBA is applied to only the IS sector, but when it is applied only to the CM sector, the production and profit increase, and total emissions, carbon prices, and social welfare are all slightly higher. Moreover, it should be noted that the findings in the IS and CM sectors may not applicable to other sectors, as each sector has its own special features in terms of demand and abatement.
Given that energy-savings subsidies are independent from the ETS and play a substitutive role, whereas output-based rebating is designed to compensate for the loss of competitiveness by the firms covered by the ETS, it is not surprising to see that the effect of subsidies is intuitively clearer. The role of output-based rebating is, on the contrary, more complicated. Policymakers should bear these effects in mind when additional policies are introduced along with the ETS. China has recently announced the National Emission Trading Scheme (Market Construction Plan of National Carbon Emission Trading (in Chinese).
http://www.ndrc.gov.cn/gzdt/201712/W020171220577386656660.pdf), which has been viewed as a significant policy movement to achieve the committed emission target in the Paris Agreement. The national platform means larger scale of participation in the system and the effectiveness of multiple policy mix is more important to the policymakers. Although it is hard to accommodate all policies (such as resource efficiency regulations) into our model, the results do confirm different roles of each policy instrument in the mix and provide important information to the policy makers.
It should be acknowledged that several limitations exist in our study. First, this paper shows that two policy combinations can have clearly different impacts on sectoral performance, emissions, carbon prices, and social welfare. Results may differ when more policy instruments are included, though the general implication should stand. Second, the model provides a simplified partial equilibrium solution with only two energy intensive sectors, which are assumed to be independence from each other. A more general framework that allows linkages across sectors may be more informative, though a simple extension in
Appendix A.5,
Appendix A.6,
Appendix A.7 and
Appendix A.8 shows that the general conclusion remains.
Third, it is worth noting that the presence of market power will potentially affect the results of our model. For example, Hahn’s model suggests that participants in the ETS with market power could manipulate the price to make the allocated permit price differ from that in the market equilibrium and then exercise their influence over the compliance costs in the ETS [
33]. A simple extension with more than one firms in each sector is discussed briefly in
Appendix A.5, which shows general consistency of our model, though a more advanced model that allows firms with market power maybe interesting for future research.
In addition, according to Wang et al., the eco-efficiency indicators of cement industry in China are still at a low level [
34]. And the resource cycle rates in the iron and steel and cement sectors are expected to rise in the future. How to link the factors of resource cycling to the emission trading scheme design, as well as taking the material flow of the products in energy intensive sectors into consideration, will be potential directions in our future study.