Abstract
Wind power generation has presented an important development around the world. However, its integration into electrical systems presents numerous challenges due to the variable nature of the wind. Therefore, to maintain an economical and reliable electricity supply, it is necessary to accurately predict wind generation. The Wind Power Prediction Tool (WPPT) has been proposed to solve this task using the power curve associated with a wind farm. Recurrent Neural Networks (RNNs) model complex non-linear relationships without requiring explicit mathematical expressions that relate the variables involved. In particular, two types of RNN, Long Short-Term Memory (LSTM) and Echo State Network (ESN), have shown good results in time series forecasting. In this work, we present an LSTM+ESN architecture that combines the characteristics of both networks. An architecture similar to an ESN is proposed, but using LSTM blocks as units in the hidden layer. The training process of this network has two key stages: (i) the hidden layer is trained with a descending gradient method online using one epoch; (ii) the output layer is adjusted with a regularized regression. In particular, the case is proposed where Step (i) is used as a target for the input signal, in order to extract characteristics automatically as the autoencoder approach; and in the second stage (ii), a quantile regression is used in order to obtain a robust estimate of the expected target. The experimental results show that LSTM+ESN using the autoencoder and quantile regression outperforms the WPPT model in all global metrics used.
1. Introduction
In many countries around the world, renewable energies are gradually replacing traditional energy sources, mainly because of the unprecedented and irreversible environmental damage caused by fossil and nuclear fuels and the continuing reduction of renewable technology costs [1,2]. Among the main sources of renewable energies, wind energy has presented an important development, being an attractive alternative in terms of its costs and low environmental impact [3]. However, the integration of wind power into electrical systems presents several challenges due to its uncertainty and variability, as its generation depends on a stochastically-behaved primary energy resource [4]. For example, the short-term generation scheduling of an electrical system must provide reliable estimates of how much wind power will be produced to obtain the optimal selection of dispatched units and the optimal generation levels of conventional units. Forecasting errors can increase generation costs of the system, due to the need for dispatching peak units to supply an unexpected resource shortage, which also decreases its reliability. This issue limits wind power penetration since it may put at risk the planning and economic operation of the electricity markets, as well as the safety and reliability of the power system. Therefore, forecasting tools that precisely describe and predict wind power generation behavior are critical in keeping the electricity supply economical and reliable.
Research proposals attempting to build an accurate prediction model for wind power can be divided mainly into physical methods (which use numerical weather prediction based on meteorological processes), traditional statistical methods (data-driven modeling as time series) and artificial intelligence or machine learning models [5,6]. From a statistical point of view, time series forecasting is a common problem in many fields of science and engineering, and different approaches can be applied in the context of wind power prediction. One of such approaches is the Autoregressive Fractionally-Integrated Moving Average (ARFIMA) methodology for fitting a class of linear time series models with long-term dependencies. However, most of those models assume linearity and stationary conditions over the time series, and these restrictions are not always met with real wind power data [7,8]. It is also common to find hybrid methods based on combinations of physical and statistical models, using different strategies [6], where basically the statistical model operates as a complement of the physical models using the data generated by some numerical weather prediction.
In recent years, more complex techniques from the area of Artificial Intelligence (AI) have gained popularity. Specifically, from the machine learning community (sub-area of AI), we can find proposals using different models such as support vector machines, random forests, clustering, fuzzy logic and artificial neural networks, among others. Particularly, Artificial Neural Networks (ANN) have shown good performance, surpassing various state of the art techniques [9]. Nevertheless, most of those approaches are based on univariate time series without considering exogenous variables. Thus, adding characteristics of the studied phenomenon could improve the models performance [10,11].
Recurrent Neural Networks (RNN) are a particular class of ANN that is gaining increased attention, since they can model the temporal dynamics of a series in a natural way [12]. The process of constructing the relationships between the input and output variables is addressed by certain general purpose learning algorithms. An RNN is a neural network that operates over time. At each time step, an input vector activates the network by updating its (possibly high-dimensional) hidden state via non-linear activation functions and uses it to make a prediction of its output. RNNs form a rich class of models because their hidden state information is stored as high-dimensional distributed representations (as opposed to a hidden Markov model, whose hidden state is essentially log n-dimensional). Their nonlinear dynamics allow modeling and forecasting tasks for sequences with highly complex structures. Some drawbacks of the practical use of RNN are the long time consumed in the modeling process and the large amount of data required in the training process. Furthermore, the process of learning the weights of the network, by means of a gradient descent-type optimization method, makes it difficult to find the optimal values of the model. To tackle some of these problems, two recurrent network models, named Long Short-Term Memory (LSTM) and Echo State Networks (ESN), have been proposed.
This paper addresses the problem of predicting wind power with a forecast horizon from 1–48 h ahead, by devising a neural network that uses LSTM memory blocks as units in the hidden layer, within an architecture of the ESN type. The proposal has two stages: (i) first, the hidden layer is trained by the gradient descent-based algorithm, using the input as the target, inspired by a classic autoencoder to extract characteristics automatically from the input signal; (ii) second, only the output layer weights are trained by a regularized quantile regression; this reduces the cardinality of the hypothesis space, where it might be easier to find a consistent hypothesis. The advantages of this proposal are three-fold: (i) the design of the memory blocks that store and control the information flowing through the hidden layer; (ii) the sparsely-connected recurrent hidden layer of the ESN that contains fewer features and, hence, is less prone to overfitting; (iii) adjusting the weights with quantile regression provides a more robust estimation of wind power.
The proposal is evaluated and contrasted with data provided by the wind power forecasting system developed at Technical University of Denmark (DTU): the Wind Power Prediction Tool (WPPT). This system predicts the wind power production in two steps. First, it transforms meteorological predictions of wind speed and wind direction into predictions of wind power for a specific area using a power curve-like model. Next, it calculates an optimal weight between the observed and the predicted production in the area, so that the final forecast can be generated. For more details, please refer to [13].
In summary, the proposed model uses historical wind power data and meteorological data provided by a Numerical Weather Prediction (NWP) system. This forecasting technique does not make a priori assumptions about the underlying distribution of the process generated by the series, and it incorporates meteorological variables that improve the predictions.
The paper is organized as follows: Section 2 describes general techniques for wind power forecasting; Section 3 provides a brief description of RNN, specifically focusing on LSTM and ESN; Section 4 presents the details of the proposed model; Section 5 provides a description and preprocessing of the dataset used, the metrics used to evaluate the forecasting accuracy and the experimental study used to validate the proposed model; finally, Section 6 presents the conclusions.
2. Wind Power Forecasting
Many different methods for predicting wind power or wind speed have been proposed in the literature [6]. They are usually categorized based on two main aspects: the time horizon of the forecast and the methodology used. In terms of the former aspect, Chang proposes the following categorization based on a literature review [1]:
- Ultra-short-term forecasting: from few minutes to 1 h ahead.
- Short-term forecasting: from 1 h to several hours ahead.
- Medium-term forecasting: from several hours to one week ahead.
- Long-term forecasting: from one week to one year or more ahead.
On the other hand, four categories can be distinguished according to the methodology used as follows.
2.1. Persistence Method
This simple technique is based on the assumption that future wind speed or wind power will be the same as in the present day. That is, if is wind power measured at time t, then the power at instant is given by [1]. Despite its simplicity, this approach is sometimes more accurate than other models and is commonly used as a benchmark, but its performance decreases rapidly as the forecast horizon increases.
2.2. Physical Methods
These models are based on detailed physical descriptions of the geographical locations of interest. When modeling the atmospheric conditions at a particular place (such as temperature, atmospheric pressure, etc.), as well as the topography of the land, historical data are not explicitly required to find the parameters of the model [5]. For instance, Al-Deen et al. [14] devised a technique to improve the spatial resolution of wind speed based on a Microclimatic Analysis System for Complex Lands (MASCOT) [15]. In [16], the authors used a physical approach, applying a Kalman filter to improve the forecast produced by a Numerical Weather Prediction (NWP) model. Later, Li et al. [17] proposed to predict wind power based on flow fields pre-calculated by means of computational fluid dynamics modeling. It is also possible to find slightly older prediction systems, resulting from large-scale institutional efforts. Among those, we can mention LocalPred, which is a forecast system built by the National Renewable Energy Centre (CENER), located in Spain, designed for complex terrains that integrates the results of several NWP models (provided by European meteorological institutes belonging to the High Resolution Limited Area Model, HIRLAM program). In order to make predictions from 1 h–7 days ahead, the results are processed by a set of statistical algorithms [18]. Prediktor is another system developed by Risoe National Laboratory in Denmark, which feeds on the HIRLAM forecasts and is integrated with the WAsP (Wind Atlas Analysis and Application Program) and MOS (Model Output Statistics) [19] models. Previento is another system developed by the University of Oldenburg in Germany, whose procedure is very similar to the approach developed by Prediktor [20].
2.3. Statistical Methods
These approaches take advantage of the dependency structure of data described by the autocovariance (for univariate series) and cross-covariances [6] (for multiple time series) functions. One example of these methods is [21], a hybrid method that uses a wavelet transform-based technique to decompose the original series. Then, for each resulting sub-series, the Improved Time Series Method (ITSM) is applied to optimize the modeling steps of the classical one. Later, Wang et al. [22] built an ARIMA model on wind speed series. Then, they model the residuals by means of a GARCH model. In [23], a Vector Autoregressive Model (VAR) is proposed to forecast temperature, solar radiation and wind speed of 61 locations around the United States. Recently, Cadenas et al. [24] compared the predictive capacity of a univariate ARIMA model for wind speed against a nonlinear autoregressive exogenous model (NARX) model using as input the wind direction, temperature, pressure, solar radiation, relative humidity and speed of the wind. The main assumption of the statistical methods is that these assume a family of underlying stochastic processes that are generally stationary, linear and homoscedastic, but most of the time series analyzed do not comply with these restrictions, since they have characteristics of heteroscedasticity and present long-term dependencies [7,8].
2.4. Machine Learning Methods
These techniques attempt to discover underlying relationships, without an a priori structural hypothesis that relates wind power with several historical meteorological variables [2,25]. In this category, we can mention the work of Olaofe and Folly [26], who present a recurrent neural network to estimate the wind power of a turbine from 1–288 h ahead. In [27], a set of feedforward neural networks is used to make predictions several steps ahead (from 30 min to 6 h 30 min with 30 min in between). The networks are fed with historical data of wind speed, direction and temperature. The final output is a linear combination of the outputs of the networks. In [28], a new method is proposed to train a two-layer feedforward neural network to predict wind speed in an online fashion, without using additional information. In [29], the authors study four optimization algorithms to train a NARX model (Levenberg–Marquardt, Polak–Ribiere conjugate gradient, scaled conjugate gradient algorithms and Bayesian regularization). Performance is evaluated by using wind speed as the input variable and either direction, temperature or relative humidity as the exogenous variable. Experiments conclude that adding direction obtains better results than considering the rest of the exogenous variables. Later, Aquino et al. studied the performance of three models: an echo state network, a feedforward neural network and a fuzzy inference system, for short-term forecasting of wind speed based on the wind speed, temperature, humidity and solar radiation series [30].
On the other hand, Sun et al. [31] decompose a wind speed time series by means of a technique called “Fast Ensemble Empirical Model Decomposition” (FEEMD), which generates Intrinsic Mode Functions (IMFs). These functions are then modeled by a Least Squares Support Vector Machine (LSSVM) that is fit by the Bat Algorithm (BA). Following the previous idea, Wu and Peng modify the decomposition of the series by using the EEMD technique and using PCA to reduce the number of attributes to train the LSSVM [32]. Ghorbani et al. [33] devised a neural network trained by means of a Genetic Expression Programming (GEP) algorithm.
In [34], a wavelet recurrent neural network is implemented. The original wind speed series is transformed using wavelet decomposition. The resulting series is pre-processed using a semi-parametric approach based on the Parzen window, which is then fed to a recurrent neural network in order to predict the generated power. The experimental results confirm the effectiveness of the proposal, tested over one entire year of data.
Then, Chang et al. [35] proposed an ARIMA model to transform non-stationary wind speed and temperature series into stationary ones. The transformed series are fed to a radial basis neural network for wind speed forecasting. This network can also be used for wind power forecasting if the target it learns is the generated wind power. Experimental results show that the proposal outperforms the ARIMA model, feed forward neural networks and radial basis neural networks in terms of accuracy.
Later on, a Spiking Neural Network (SNN) based model was proposed to predict wind farm energy production [36]. This work implemented an SNN by means of a NeuCube computational framework, using as input a six-dimensional vector made of the hourly wind speed and wind direction gathered from three anemometric towers and using the generated wind power after one hour as the target. Experimental results show low MAD, MAPE and RMSE values for the proposal.
In [37], a hybrid system composed of an ARIMA model and two feedforward neural networks is proposed. Wind speed, humidity, atmospheric pressure, temperature and wind direction time series are used as inputs to the system. Each series is first modeled using an ARIMA model, after which their individual outputs are used to train feed forward neural networks, whose outputs are then finally used as inputs to another feed forward neural network that forecasts wind speed. Once wind speed has been forecasted, wind power is estimated using the power curve.
In general terms, the different proposals from the machine learning community include broadly known methods such as multilayer perceptron, radial basis function neural networks, support vector machines, extended Kalman filter and Recurrent Neural Networks (RNN). This last class of models is receiving special interest nowadays, since it allows one to work with time series in a natural way, being an alternative to nonlinear models based on data. RNNs select a hypothesis using little a priori information about the underlying relationship between variables. These algorithms operate in the time domain, such that at every instant t, they receive an input vector, update their hidden state through non-linear activation functions and use the result of the latter to make a prediction of the expected output. This type of neural networks can store information as highly dimensional distributed representations, and their non-linear dynamics can implement powerful computations. Thus, RNNs perform modeling and sequence prediction tasks with highly complex structures. In spite of the practical advantages that these models present over the other categories when working with wind power time series, adjusting their parameters when using the gradient descent method is their drawback [38].
Recently, different variants have have tried to solve this problem, the Long Short-Term Memory networks (LSTM) [39] and Echo State Networks (ESN) [40] being the ones that stand out from the others. However, the complexity of LSTMs demands an excessive amount of computing time, making it difficult to achieve optimal performance. On the other hand, the simplicity of the ESNs can limit their generalization capabilities.
3. Recurrent Neural Networks
A recurrent neural network [41,42] is a type of artificial neural network where the connections of its units (called artificial neurons) present cycles. These recurrent connections allow one to describe targets as a function of inputs at previous time instants, this being the reason it is said that the network has “memory”. Hence, the network can capture the temporal dynamic of the series [12]. Formally, under a standard architecture [43], it can be defined as: given a sequence of inputs , each in , the network computes a sequence of hidden states , each in , and a sequence of predictions , each in , by iterating the equations:
where , and are the weight matrices of the input layer, hidden layer and output layer, respectively; and are the biases, and are pre-defined vector valued functions, which are typically non-linear with a well-defined Jacobian. A predefined value is set as the state of the network. The objective function associated with an RNN for a single pair is defined as , where is the model parameters vector and L is a distance function that measures the deviation of the prediction from the target output (e.g., the squared error). The overall objective function for the whole training set is simply given by the average of the individual objectives associated with each training example [44].
Despite its advantages, this type of network suffers from the problem of “vanishing/exploding gradient” [45], which produces the effect of making the training of the hidden layers more difficult the closer they are to the input layer, which in turn hinders learning the underlying patterns. Since data flow over time, an RNN is equivalent to a multi-layered feedforward neural network, as shown in Figure 1. That is, it is possible to unfold the recurrent network l times into the past, resulting in a deep network with l hidden layers.
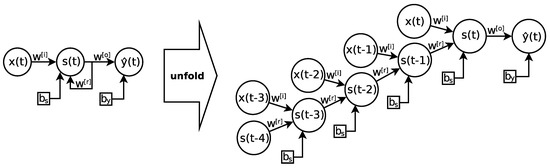
Figure 1.
Recurrent neural network architecture.
Recently, different RNN variants have tried to solve this problem, Long Short-Term Memory (LSTM) and Echo State Networks (ESN) becoming the most popular approaches.
3.1. Long Short-Term Memory
This model replaces the traditional neuron of the perceptron with a memory block (see Figure 2). This block generally contains a memory cell and some “gateways” (sigmoidal activation functions in the range [0,1]) that control the information flow passing through the cell. Each memory cell is a self-connected linear unit called the “Constant Error Carouse ” (CEC), whose activation is considered the state of the cell. This new network is known as Long Short-Term Memory [39].
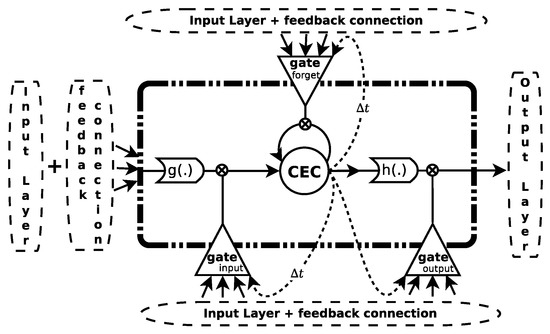
Figure 2.
LSTM memory block. CEC, Constant Error Carousel.
The CEC mitigates the vanishing (exploding) problem of the gradient, since the backward flow of the local error remains constant within the CEC, without increasing or decreasing as long as no new input or external error signal is present. The training of this model is based on a modification of both the backpropagation through time [46] and real-time recurrent learning [47] algorithms. Let , and be linear combinations of the inputs weighted with the weights for the different gates (input, forget and output, respectively) at time t for block j. Let , and be the outputs of the activation functions for each gate. Let be the weighted entry to the block j and the cell state at time t. Let be the output of the j-th block. Then, the information flow forward is expressed as:
where is the weight that connects unit m to unit j and the super index indicates to which component of the block it belongs. Additionally indicates recurrent weights, and indicates direct weights between the cell and a particular gate; is the input signal to the m-th neuron of the input layer; is the output of the m-th block in time ; , and are sigmoidal activation functions in the range [0,1], [−2,2] and [−1,1], respectively. For a more detailed study of this model, please refer to [48].
3.2. Echo State Networks
Another type of recurrent network comes from the paradigm Reservoir Computing (RC) [49], a field of research that has emerged as an alternative gradient descent-based method. The key idea behind reservoir computing is to use a hidden layer formed by a large number of sparsely-connected neurons. This idea resembles kernel methods [50], where input data are transformed to a high-dimensional space in order to perform a particular task.
One of the pioneering models within this field is known as the Echo State Network (ESN) [40]. The model, in a practical sense, is very simple and easy to implement: it consists of three layers (input, hidden and output), where the hidden layer (reservoir) is formed by a large number of neurons (∼1000) and randomly connected with a low connectivity rate between them (allowing self-connections) (see Figure 3).
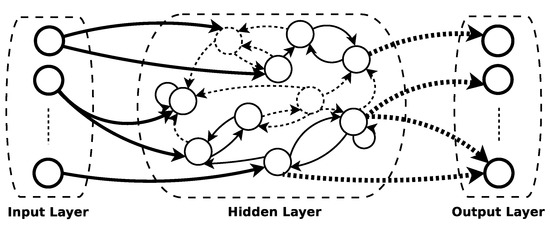
Figure 3.
The Echo State Network (ESN) scheme.
The novelty of this model is that during the training phase, the weights of the connections within the reservoir are not updated, and only the output layer is trained (the weights that connect the reservoir with the last layer), usually by means of ridge regression [51]. Then, the reservoir acts as a non-linear dynamic filter that temporarily maps the input to a high-dimensional space, without training the hidden layer weights.
Let r be the number of neurons in the reservoir; an matrix with the weights of the reservoir connections; an array , where k is the number of neurons in the output layer and n the number of neurons in the input layer. When designing an ESN, a spectral radius of close to one (the maximum proper value in absolute value) must be ensured. In order to do this, the weight matrix must be pre-processed using the following steps:
- The reservoir connection matrix is randomly initialized.
- The matrix is updated as .
Here, is the spectral radius of , and therefore, the spectral radius of is equal to . Since the spectral radius determines how fast the influence of an input vanishes through time in the reservoir, a larger value is required for tasks that need longer memory [52].
In addition, the neuron outputs of the reservoir (known as states) are obtained by the following expression:
where is the output of a hidden neuron at time t, is a “leaking rate” that regulates the update speed in the dynamics of the reservoir, is an activation function and is a linear combination of the input signals. Since the states are initialized to zero, , it is necessary to set an amount of points in the series to run the network and initialize the internal dynamics of the reservoir. If is a matrix with the states of all hidden layer neurons for , then the following matrix equation calculates the weights of the output layer:
where is the transpose of , is a regularization parameter, is an identity matrix and is a matrix with the actual outputs, that is .
Additionally, in order to obtain prediction intervals, in [53], an ESN ensemble is proposed using Quantile Regression (QR) [54] to calculate the output layer weights of each network. This technique is supported by the fact that quantiles associated with a random variable Y, of order , are position measures that indicate the value of Y to reach a desired cumulative probability , that is,
where corresponds to the order quantile . For example, the median is the best known quantile and is characterized as the value that meets
.
Then, quantile regression proposes that is written as a linear combination of some known regressors and unknown coefficients, analogous to modeling the conditional mean by using a multiple linear regression, that is,
where and K are called regressors (explanatory variables) and are the unknown coefficients based on , which is determined from a set of observations . The loss function to be minimized to find the coefficients is defined by:
where is the error between the variable y and the -th desired quantile q. Figure 4 shows the loss function for different values. Then, the -conditional quantile can be found by looking for the parameters that minimize:
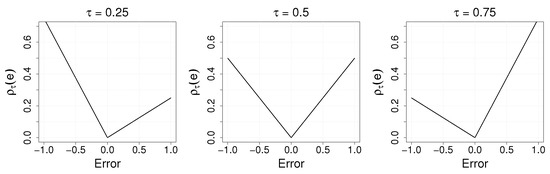
Figure 4.
Quantile regression loss function for different .
4. LSTM+ESN Proposed Model
Despite the fact that the LSTM has shown good performance in forecasting [55,56], its training process can be computationally expensive, due to the complexity of its architecture. As a consequence, the computational training cost increases as the number of blocks increases. In addition, it might overfit depending on the values of its hyperparameters such as the number of blocks, the learning rate or the maximum number of epochs.
On the other hand, good performance has also been reported for the ESN [57,58]; however, it is possible to improve its results by adjusting the hidden layer weights (sacrificing its simplicity). An example is the work of Palangi [59], where all the weights of the network are learned. The proposal exhibited improvement over the traditional ESN, tested in a phone classification problem on the TIMIT dataset.
Inspired by the advantages of both networks, we propose a novel neural network called LSTM+ESN, a recurrent neural network model based on the architecture of an ESN using as hidden neurons LSTM units (see Figure 5). Following the work of Gers [48], all the layers are allowed to be trained using truncated gradients, but with some restrictions imposed by the ESN architecture.
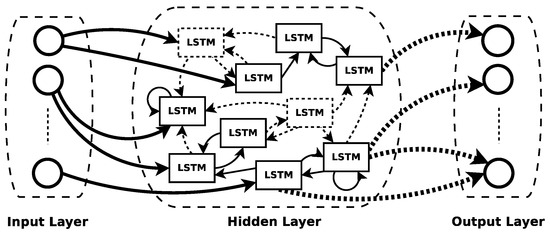
Figure 5.
Proposed network architecture: LSTM+ESN.
Let M be the number of input neurons, J the number of blocks in the hidden layer and K the number of neurons in the output layer. Let be an matrix with the weights connecting the input layer to the input of the blocks; , , are matrices with the weights of the connections from the input layer to the input, forget and output gates, respectively. Let be a matrix with the weights of the recurrent connections between the blocks of the hidden layer. , , are matrices with the weights of the connections from the recurring signals of the outputs of the blocks to the input, forget and output gates, respectively. Let , , be matrices with the weights that directly connect the CEC with their respective input, forget and output gates. Let , , , be row vectors of dimension J with the weights bias associated with the entry of each block, input gate, forget and output, respectively. Let be a vector with the CEC states for each block of the hidden layer at instant t.
Let be a matrix with the weights of the output layer, where if there is a direct connection from the layer input with the output, otherwise. Let be a vector with the entry for the output layer at time t.
To train this architecture, it is necessary to include all the steps described in Algorithm 1.
| Algorithm 1 LSTM+ESN training scheme |
| 1: Dataset is split in two: for training and for validating. |
| 2: Randomly initialize sparse hidden weights matrices , , and from a uniform distribution with range (−0.1, 0.1). |
| 3: Initialize hidden weight matrices , , , , , , , , , and from a uniform distribution with range (−0.1, 0.1). |
| 4: Set as or . |
| 5: Set the value for Regularization. |
| 6: TrainNet_by_LSTM() |
| 7: TrainNet_by_ESN(, Regularization) |
| 8: repeat |
| 9: TrainNet_by_LSTM() |
| 10: TrainNet_by_ESN(, Regularization) |
| 11: until Convergence using the validation set as the early stopping condition. |
In order to update the matrices initialized in Steps 2 and 3, Step 6 chooses the weight matrices that minimize the error of the LSTM output with respect to a vector with the expected target at instant t, , defined as and set in Step 4. Here, can be the real target (in order to learn the original output) or the input in order to learn a representation of the original input resembling the classic autoencoder approach. The loss function is defined to minimize the mean square error “online” (at each instant t) given by Equation (6):
Then, the gradient associated with is given by the following equation:
where ⊙ represents the element-to-element multiplication between matrices or vectors and represents the derivative of the activation function associated with the output neurons. If we consider that , we can write:
Then, the gradients for the other weight matrices are:
where are the different matrices associated with the forget gate, represents the vector with the inputs of each . is the transpose of the vector with all the inputs of the forget gate, represents the matrix with all the weights associated with the forget gate, is the derivative of the activation function of the gates and is the matrix with the weights that connects only the hidden layer with the output layer.
here, and is the element-wise product of a vector with each row of a matrix, i.e.,
Algorithm 2, called TrainNet_by_LSTM, systematically describes Step 3 of Algorithm 1, used to train the network. First, the network is trained online with the AdaDelta [60] optimization algorithm as in the LSTM training, using only one epoch (Step 6). We choose this optimization technique because it has been shown that it converges faster than other algorithms of the descending gradient type [61]. In addition, to preserve the imposed requirements of the ESN reservoir, after each weight update, the matrix of recurring connections is kept sparse by zeroing out those weights that were initially set as zero (Step 7). In order to avoid producing diverging output values when updating the output weights or the influence of the LSTM gates being biased by some very large weights, a filter is applied that resets to zero weights that exceed a threshold (Step 10 and Step 12). Since online training is performed, the matrix of recurring connections will be re-scaled to maintain a spectral radius at each instant t. The parameter MaxEpoch indicates the maximum number of epochs to use; means the maximum value that can take the weights; fixedWo indicates if the output weights are updated or not; keepSR indicates if the spectral ratio is kept or not; and cleanHW controls if the weights that exceed are reset to zero.
| Algorithm 2 TrainNet_by_LSTM() |
| Input: A set of instances |
| Input: MaxEpoch = 1, , fixedWo=False, keepSR=True, cleanHW=True |
| 1: Define |
| 2: while MaxEpoch do |
| 3: |
| 4: for T do |
| 5: ForwardPropagate(, network) |
| 6: UpdateWeights(, , network) |
| 7: Sparse connectivity is maintained by setting the inactive weights back to zero. |
| 8: if cleanHW == True then |
| 9: if fixedWo == False then |
| 10: ssi |
| 11: end if |
| 12: ssi , output layer |
| 13: end if |
| 14: end for |
| 15: if keepSR == True then |
| 16: |
| 17: end if |
| 18: end while |
| Output: Net’s Weights |
Later, in order to update the output layer weights , the weights that solve the multi-linear regression are chosen in Step 4 of Algorithm 1, called TrainNet_by_ESN(). This can be done, for example, using ridge regression as in Equation (2) or by means of quantile regression [54]. The latter approach gets a more robust estimation of . Recall that the model needs to use a regularized regression because is a singular matrix. Currently, there are different alternatives in the literature to do this, but for this proposal, we used a regularized quantile regression model based on an elastic network, implemented in the R-project package hqreg.
At last, a fine tuning stage is carried out in two steps: (i) TrainNet_by_LSTM is performed using as the target output; (ii) TrainNet_by_ESN is performed using the same regression as in Step 7 from Algorithm 1.
Both steps are repeated until early stopping conditions using are met.
Thus, the LSTM+ESN architecture can lead to different variants depending on the way that is chosen in Step 4, Algorithm 1, and the parameter regressionis set in Step 5, Algorithm 1. For instance, LSTM+ESN+Y+RR denotes the LSTM+ESN architecture trained with as a target in Step 4 and Ridge Regression in Step 5.
In this work, we use LSTM+ESN, training the hidden layer using as in the autoencoder and Ridge Regression (LSTM+ESN+X+QR) for wind power forecasting, since extracting a representation of the original input and taking advantage of the robustness of QR might improve prediction performance. However, in Section 5, we assess the proposal against other LSTM+ESN architecture variants.
Algorithm 3 corresponds to a detailed version of Algorithm 1 describing the particular setting LSTM+ESN+X+QR that we use in this work. The parameter validate indicates if the input dataset is split or not in dataset-valid and dataset-train; MaxEpochGlobal indicates the maximum number of epochs in the fine tuning stage; and Regularization refers to the regularization used by the TrainNet_by_ESN step; which in this case is always set to QR.
| Algorithm 3 LSTM+ESN+X+QR |
| Input: A set of instances . |
| 1: validate=True, MaxEpochGlobal = 1, Regularization = QR |
| 2: |
| 3: if validate == True then |
| 4: |
| 5: |
| 6: end if |
| 7: TrainNet_by_LSTM() |
| 8: TrainNet_by_ESN(,Regularization) |
| 9: if validate == True then |
| 10: CalculateForecastError() |
| 11: end if |
| 12: Save(network) |
| 13: Define , attempts=1, MaxAttemtps=10 |
| 14: whileMaxEpochGlobal do |
| 15: |
| 16: RestartOutputs(network) |
| 17: RestartGradients(network) |
| 18: TrainNet_by_LSTM(; fixedWo=True) |
| 19: if validate == True then |
| 20: TrainNet_by_ESN(,Regularization) |
| 21: CalculateForecastError() |
| 22: if then |
| 23: |
| 24: Save(network) |
| 25: else |
| 26: attempts←attempts + 1 |
| 27: end if |
| 28: else |
| 29: Save(network) |
| 30: end if |
| 31: if attempts>MaxAttemtps then |
| 32: break |
| 33: end if |
| 34: end while |
| 35: LoadSavedNet() |
| 36: TrainNet_by_ESN() |
| Output: Last network saved |
5. Experiments
5.1. Data Description and Preprocessing
In order to assess the proposed models, we used data from the Klim Fjordholme wind farm [62] that consists of generated power measurements and predictions of several meteorological variables such as wind speed, wind direction and ambient temperature, generated by the HIRLAM model: a NWP system that is used by the Danish Meteorological Institute. These predictions are made 48 h ahead every 6 h, and they might present missing values. To avoid overlapping of the predictions (as depicted in Figure 6), a resulting series (in red) is generated, only considering the first six points of each forecast.
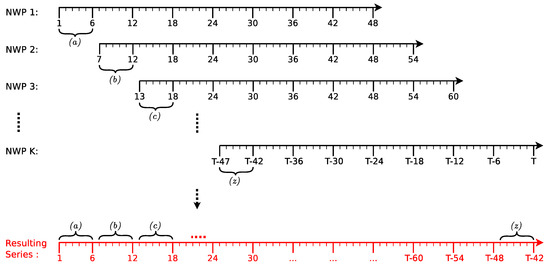
Figure 6.
Preprocessing data scheme. Original forecasts in black, merged series in red. NWP, Numerical Weather Prediction.
An RNN-based model is not capable of working with missing data. A missing value is imputed by means of a linear interpolation on and plus an additive Gaussian noise . In addition to the aforementioned characteristics, to increase the performance of our proposal, we add the date of each record using three variables: (month, day and hour). Given the above, the input vector at each time step t is a lag one vector composed of the following characteristics: wind speed, wind direction, temperature, month, day, hour and wind power. All features were normalized to the range using the min-max method. Finally, the resulting series is composed of 5376 observations from 00:00 on 14 January 2002 to 23:00 on 25 August 2002.
5.2. Forecasting Accuracy Evaluation Metrics
In order to assure generalization capabilities for the proposed model, the time series is divided into subseries, and the performance of the model is evaluated in each of them; analogous to what is done when performing cross-validation to test a model performance. Each subseries is generated using a sliding window of approximately 111.96 days (approximately 3.7 months), with a step size of approximately 10 days that slides over the original series, as shown in Figure 7.

Figure 7.
Time series split scheme.
The performance of the models is measured on the prediction of 48 h and then averaged over the subseries in order to get a global measure. These predictions are generated using the multi-stage approach [63]. For a single subseries r, different evaluation metrics are used based on the error at h steps ahead, defined as:
where is the desired output at instant , T is the index of the last point of the series used during training, h is the number of steps ahead, from 1–48, and is the estimated output at time generated by the model.
The metrics to be used are the Mean Squared Error (MSE), the Mean Absolute Error (MAE), the Mean Absolute Error Percentage (MAPE) and the Standard Deviation of Error (SDE) defined as follows:
where MSE(h) and MAE(h) are the MSE and MAE for each h step ahead, respectively, H indicates the maximum number of steps ahead and the subindex r indicates the used subseries.
The hyperparameters settings where selected using one of the following criteria:
- s1: the one that achieves the lowest MSE averaged over every subseries and every step ahead of the test set, as in Equation (22).
- s2: the one that achieves the lowest weighted average of:
where and . Hence, errors from predictions closer to the last value are used as the training weight more than those further ahead.
5.3. Case Study and Results
In this section, we compare our proposal against a persistence model, the forecast generated by the Wind Power Prediction Tool (WPPT) [62], and some variants of the LSTM+ESN framework: the first trains the hidden layer using as target and uses ridge regression instead of quantile regression (LSTM+ESN+Y+RR); the second one trains the hidden layer using as in the autoencoder and ridge regression (LSTM+ESN+X+RR); and the third one trains the hidden layer using as the target and quantile regression (LSTM+ESN+Y+QR). Each of the variants may use either s1 or s2 selection criterion, for example, LSTM+ESN+Y+QR+s1 would denote the third variant using s1 criterion. S. is used when choosing either criterion obtains the same hyperparameters values.
The configuration of the hyperparameters for the algorithms used in the LSTM+ESN models are shown in Table 1, Table 2 and Table 3.

Table 1.
Algorithm 2 setting.

Table 2.
Algorithm 3 setting.

Table 3.
AdaDelta Algorithm setting.
The other parameters are tuned according to the following scheme: First, we tune the number of blocks of the hidden layer , keeping fixed the spectral radius and the regularization parameter , using either s1 or s2 as the selection criterion. Next, and are tuned, selecting both parameters always by means of the s1 criterion.
Moreover, the identity function was used as the output layer activation function. Direct connections were also used from the input layer to the output layer, but these connections were omitted when using Algorithm 2 the first time (Step 7 of Algorithm 3). Matrices are generated sparsely, having the same positions for their zero values, since recurrent connection between unit i and unit j is represented by the values coming from the four recurrent matrices. Non-zero weights of each matrix are generated from a uniform distribution , independently of each other. Sparse arrays were also used when connecting the input layer with the hidden layer, that is and .
Table 4 shows the parameter tuning for different LSTM+ESN variants. The ID column shows a short name for the model, used hereinafter. Now, we assess the following models: persistence, WPPT, and LSTM+ESN variants

Table 4.
Configurations with the lowest test error. RR, Ridge Regression; QR, Quantile Regression; s1, Setting 1.
Is it important to mention that, since WPPT presents missing values in its forecasting, the error is calculated only for those points present in the WPPT forecast. Table 5 shows the global results averaging over all subseries. The symbol * indicates when the corresponding algorithm outperforms WPPT. Best results are marked in bold.

Table 5.
Average MSE, MAE, MAPE and Standard Deviation of Error (SDE). WPPT, Wind Power Prediction Tool.
Results show that M6 outperforms both M1 and WPPT, in all metrics. Besides, M1 exhibits worse performance than WPPT in terms of MAE, MAPE and SDE. Since M1 does not use either QR or the autoencoder inspired approach, we can note that both artifacts improve the performance of the LSTM+ESN network. A similar behavior is detected when comparing M7 with WPPT: M7 is better than WPPT in all metrics except in SDE.
On the other hand, our proposal is also better in all metrics than both M2 and M3, both of which include the autoencoder idea, but without using QR. This suggests that by using a robust Y estimation on automatically-extracted features, better performance is achieved. Our proposal also performs better when compared with both M4 and M5, both of which use QR, but without automatic extraction of features. This indicates that it is not enough to use a robust estimation method to achieve a lower error.
Comparing all algorithms, M7 achieves the best overall MSE; however, M6 reports the best performance in terms of MAE, MAPE and SDE. Given that the M6 model achieves the smallest error in three out of four global metrics, we choose this model to analyze and compare the MSE and MAPE for each step ahead individually using Equations (18) and (19) respectively against the WPPT forecast.
Just as before, the missing values in the WPPT forecast are not considered in the computed error for M6. In particular, is discarded because it is not present in the WPPT forecast. Figure 8 shows MSE(h) on the left and MAE(h) on the right, for each step ahead (from 1–47) averaged over the 10 subseries. It is observed that M6 obtains a lower MSE 51.06% of the time (24 out of 47 predictions) and 57.45% of the time (27 out of 47 predictions) when using MAE. In addition, it is observed that M6 underperforms compared to WPPT until . However, as h increases, we can identify time stretches (when and ) where the proposal outperforms WPPT.
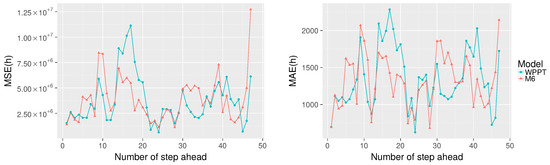
Figure 8.
Left: MSE for each step ahead. Right: MAE for each step ahead.
Finally, Figure 9, Figure 10 and Figure 11 show the WPPT and M6 forecasts for subseries r=1, 5 and 10, respectively. From Figure 9, we note that the proposal tends to follow the trend of the real curve, omitting the jumps that occur in and in . It is also possible to contrast and , where the proposal gets better global performance in terms of MSE and MAE. This confirms that the M6 Algorithm tends to mimic the real curve.
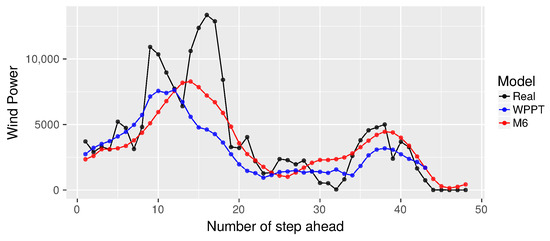
Figure 9.
Forecasting using subseries .
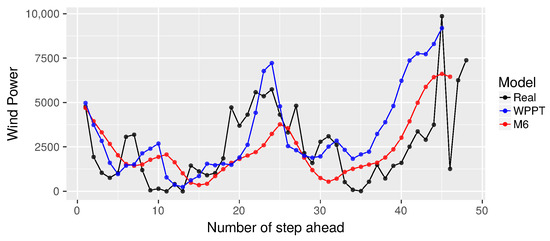
Figure 10.
Forecasting using subseries .
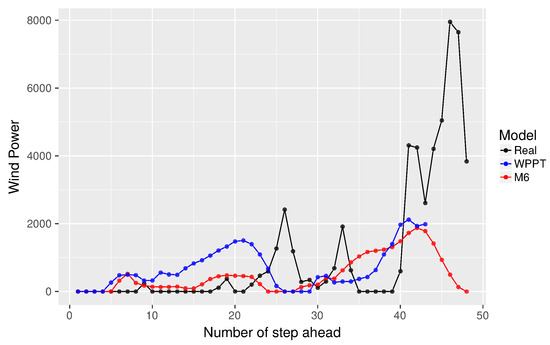
Figure 11.
Forecasting using subseries .
On the other hand, from Figure 10, it is again confirmed that when , the proposal exhibits a forecast closer to the real curve. However, when , there are some differences, where our proposal does not reach the curve’s highest points. This may be due to the cost function used to minimize, which is more restrictive for estimating the median. On the contrary, in Figure 11, the opposite behavior is observed, that is the proposal achieves a greater similarity in , but has difficulties in . In addition, M6 appears more like the real curve in contrast to WPPT from to , then tends to present a behavior similar to WPPT.
6. Conclusions
In this paper, a neural network model is presented combining the characteristics of two recurrent neural networks to predict wind power from 1–48 steps forward, modeling meteorological variables and historical wind power. The proposal uses an architecture type ESN of three layers (input-hidden-output), where the hidden units are LSTM blocks. The proposal is trained in a two-stage process: (i) the hidden layer is trained by means of a descending gradient method, using as a target the X input or the Y output, being the first option inspired by the autoencoder approach; (ii) the weights of the output layer are adjusted by means of a quantile regression or ridge regression, following the proposal of a traditional ESN.
The experimental results show that the best overall results in terms of MSE, MAE, MAPE and SDE are obtained when the hidden layer of an LSTM+ESN network is trained as an autoencoder and when adjusting the output layer weights using quantile regression. That is, it is not enough to only make a robust Y estimation (based on the cost function to be minimized) to improve performance; nor is it enough to only model the X input by extracting characteristics. It is necessary to combine these two approaches to achieve better performance.
In addition, when we compare the results with the forecast generated by WPPT, the proposal also achieves a better global performance in all proposed metrics. When analyzing the results of MSE (h) and MAE (h) for each step ahead, the proposal shows time stretches where it achieves the best performance. From the forecast curves, it is observed that the proposal often tries to follow the real trend, and there are time stretches where the proposal is closer to the real curve than the WTTP model.
It is important to remark that this proposal only models wind power from available data, without the need to use power plant information, such as the power curve. Moreover, the evaluated proposal is fed only with current data (lag = 1) and uses only two epochs in the training process: (i) one epoch to train the hidden layer and the output layer sequentially, Lines 6–7 of the Algorithm 3; (ii) and one epoch to perform the “fine tuning” stage, Lines 13–33 of Algorithm 3 using MaxEpochGlobal = 1; making it an efficient machine learning approach. Finally, our proposal trains all the layers of the model, taking advantage of the potential of its architecture in automatically modeling the underlying temporal dependencies of the data.
Acknowledgments
This work was supported in part by Fondecyt 1170123, in part by Basal Project FB0821, in part by Basal Project FB0008, in part by Research Project Dirección General de Investigación, Innovación y Postgrado de la Universidad Técnica Federico Santa María, Chile (DGIIP-UTFSM)116.24.2 and in part funded by the Centre for IT-Intelligent Energy Systems in Cities (CITIES) project (DSF 1305-00027B). The authors would like to thank Mr. Ignacio Araya for his valuable comments and suggestions to improve the quality of the paper.
Author Contributions
In this article, all the authors were involved in the data analysis and preprocessing phase, simulation, results analysis and discussion and manuscript preparation. All authors have approved the submitted manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chang, W.-Y. A Literature Review of Wind Forecasting Methods. J. Power Energy Eng. 2014, 2, 161–168. [Google Scholar] [CrossRef]
- Perera, K.S.; Aung, Z.; Woon, W. Machine learning techniques for supporting renewable energy generation and integration: A survey. In Data Analytics for Renewable Energy Integration; Woon, W.L., Aung, Z., Madnick, S., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 81–96. [Google Scholar]
- Schmidt, T.S.; Born, R.; Schneider, M. Assessing the costs of photovoltaic and wind power in six developing countries. Nat. Clim. Chang. 2012, 2, 548–553. [Google Scholar] [CrossRef]
- De Aguiar, B.C.G.; Valenca, M.J.S. Using reservoir computing for forecasting of wind power generated by a wind farm. In Proceedings of the Sixth International Conference on Advanced Cognitive Technologies and Applications, Venice, Italy, 25–29 May 2014. [Google Scholar]
- Lei, M.; Shiyan, L.; Chuanwen, J.; Hongling, L.; Yan, Z. A review on the forecasting of wind speed and generated power. Renew. Sustain. Energy Rev. 2009, 13, 915–920. [Google Scholar] [CrossRef]
- Jung, J.; Broadwater, R.P. Current status and future advances for wind speed and power forecasting. Renew. Sustain. Energy Rev. 2014, 31, 762–777. [Google Scholar] [CrossRef]
- Fortuna, L.; Nunnari, S.; Guariso, G. Fractal order evidences in wind speed time series. In Proceedings of the 2014 International Conference on Fractional Differentiation and Its Applications (ICFDA), Catania, Italy, 23–25 June 2014; pp. 1–6. [Google Scholar]
- Shen, Z.; Ritter, M. Forecasting Volatility of Wind Power Production; Humboldt University: Berlin, Germany, 2015. [Google Scholar]
- Fazelpour, F.; Tarashkar, N.; Rosen, M.A. Short-term wind speed forecasting using artificial neural networks for Tehran, Iran. Int. J. Energy Environ. Eng. 2016, 7, 377–390. [Google Scholar] [CrossRef]
- Kadhem, A.A.; Wahab, N.I.A.; Aris, I.; Jasni, J.; Abdalla, A.N. Advanced wind speed prediction model based on a combination of weibull distribution and an artificial neural network. Energies 2017, 10, 1744. [Google Scholar] [CrossRef]
- Zheng, D.; Shi, M.; Wang, Y.; Eseye, A.T.; Zhang, J. Day-ahead wind power forecasting using a two-stage hybrid modeling approach based on scada and meteorological information, and evaluating the impact of input-data dependency on forecasting accuracy. Energies 2017, 10, 1988. [Google Scholar] [CrossRef]
- Hallas, M.; Dorffner, G. A Comparative Study on Feedforward and Recurrent Neural Networks in Time Series Prediction Using Gradient Descent Learning. 1998. Available online: http://www.smartquant.com/references/NeuralNetworks/neural22.pdf (accessed on 1 February 2018).
- Madsen, H.; Nielsen, H.A.; Nielsen, T.S. A tool for predicting the wind power production of off-shore wind plants. In Proceedings of the Copenhagen Offshore Wind Conference & Exhibition, Copenhagen, Denmark, 25–28 October 2005. [Google Scholar]
- Al-Deen, S.; Yamaguchi, A.; Ishihara, T. A physical approach to wind speed prediction for wind energy forecasting. In Proceedings of the Fourth International Symposium on Computational Wind Engineering, Yokohama, Japan, 16–19 July 2006. [Google Scholar]
- Ishihara, T.; Yamaguchi, A.; Fujino, Y. A Nonlinear Model MASCOT: Development and Application. In Proceedings of the European Wind Energy Conference, Madrid, Spain, 16–19 June 2003. [Google Scholar]
- Cassola, F.; Burlando, M. Wind speed and wind energy forecast through Kalman filtering of Numerical Weather Prediction model output. Appl. Energy 2012, 99, 154–166. [Google Scholar] [CrossRef]
- Li, L.; Liu, Y.-Q.; Yang, Y.-P.; Han, S.; Wang, Y.-M. A physical approach of the short-term wind power prediction based on CFD pre-calculated flow fields. J. Hydrodyn. 2013, 25, 56–61. [Google Scholar] [CrossRef]
- Marti, I.; Cabezon, D.; Villanueva, J.; Sanisisdro, M.J.; Loureiro, Y.; Cantero, E. LocalPred and RegioPred, Advanced tolos for wind energy prediction in complex terrain. In Proceedings of the European Wind Energy Conference & Exhibition, Madrid, Spain, 16–19 June 2003. [Google Scholar]
- Landberg, L. Short-term prediction of local wind conditions. J. Wind Eng. Ind. Aerodyn. 2001, 89, 235–245. [Google Scholar] [CrossRef]
- Focken, U.; Lange, M.; Waldl, H.-P. Previento—A wind power prediction system with an innovative upscaling algorithm. In Proceedings of the European Wind Energy Conference & Exhibition, Copenhagen, Denmark, 2–6 July 2001. [Google Scholar]
- Liu, H.; Tian, H.-Q.; Chen, C.; Li, Y.-F. A hybrid statistical method to predict wind speed and wind power. Renew. Energy 2010, 35, 1857–1861. [Google Scholar] [CrossRef]
- Wang, M.-D.; Qiu, Q.-R.; Cui, B.-W. Short-Term wind speed forecasting combined time series method and ARCH model. In Proceedings of the 2012 International Conference on Machine Learning and Cybernetics, Xian, China, 15–17 July 2012. [Google Scholar]
- Liu, Y.; Roberts, M.C.; Sioshansi, R. A vector autoregressive weather model for electricity supply and demand modeling. J. Mod. Power Syst. Clean Energy 2014, 1–14. [Google Scholar] [CrossRef]
- Cadenas, E.; Rivera, W.; Campos-Amezcua, R.; Heard, C. Wind speed prediction using a univariate ARIMA model and a multivariate NARX model. Energies 2016, 9, 109. [Google Scholar] [CrossRef]
- Foley, A.M.; Leahy, P.G.; Marvuglia, A.; McKeogh, E.J. Current methods and advances in forecasting of wind power generation. Renew. Energy 2012, 37, 1–8. [Google Scholar] [CrossRef]
- Olaofe, Z.O.; Folly, K.A. Wind power estimation using recurrent neural network technique. In Proceedings of the IEEE Power and Energy Society Conference and Exposition in Africa: Intelligent Grid Integration of Renewable Energy Resources (PowerAfrica), Johannesburg, South Africa, 9–13 July 2012; pp. 1–7. [Google Scholar]
- Cadenas-Barrera, J.L.; Meng, J.; Castillo-Guerra, E.; Chang, L. A neural network approach to multi-step- ahead, short-term wind speed forecasting. In Proceedings of the 12th International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 4–7 December 2013. [Google Scholar]
- Cheggaga, N. Improvements in wind speed forecasting using an online learning. In Proceedings of the 2014 5th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 25–27 March 2014; pp. 1–6. [Google Scholar]
- Kishore, G.R.; Prema, V.; Rao, K.U. Multivariate wind power forecast using artificial neural network. In Proceedings of the IEEE Global Humanitarian Technology Conference, South Asia Satellite (GHTC-SAS), Trivandrum, India, 26–27 September 2014. [Google Scholar]
- De Aquino, R.R.B.; Souza, R.B.; Neto, O.N.; Lira, M.M.S.; Carvalho, M.A.; Ferreira, A.A. Echo state networks, artificial neural networks and fuzzy system models for improve short-term wind speed forecasting. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015. [Google Scholar]
- Sun, W.; Liu, M.; Liang, Y. Wind speed forecasting based on FEEMD and LSSVM optimized by the Bat algorithm. Energies 2015, 8, 6585–6607. [Google Scholar] [CrossRef]
- Wu, Q.; Peng, C. Wind power generation forecasting using least squares support vector machine combined with ensemble empirical mode decomposition, principal component analysis and a bat algorithm. Energies 2016, 9, 261. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Khatibi, R.; FazeliFard, M.H.; Naghipour, L.; Makarynskyy, O. Short-term wind speed predictions with machine learning techniques. Meteorol. Atmos. Phys. 2016, 128, 57–72. [Google Scholar] [CrossRef]
- Bonanno, F.; Capizzi, G.; Sciuto, G.L.; Napoli, C. Wavelet recurrent neural network with semi-parametric input data preprocessing for micro-wind power forecasting in integrated generation systems. In Proceedings of the 2015 International Conference on Clean Electrical Power (ICCEP), Taormina, Italy, 16–18 June 2015; pp. 602–609. [Google Scholar]
- Chang, G.W.; Lu, H.J.; Hsu, L.Y.; Chen, Y.Y. A hybrid model for forecasting wind speed and wind power generation. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Brusca, S.; Capizzi, G.; Sciuto, G.L.; Susi, G. A new design methodology to predict wind farm energy production by means of a spiking neural network-based system. Int. J. Numer. Model. Electron. Netw. Devices Fields 2017, 30. [Google Scholar] [CrossRef]
- De Alencar, D.B.; de Mattos Affonso, C.; de Oliveira, R.C.L.; Rodríguez, J.L.M.; Leite, J.C.; Filho, J.C.R. Different models for forecasting wind power generation: Case study. Energies 2017, 10, 1976. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Jaeger, H. The “Echo State” Approach to Analysing and Training Recurrent Neural Networks; GMD Report 148; GMD—German National Research Institute for Computer Science: Hanover, Germany, 2001. [Google Scholar]
- Del Brío, B.M.; Molina, A.S. Neural Networks and Fuzzy Systems, 3rd ed.; Springer: Berlin, Germany, 2006. (In Spanish) [Google Scholar]
- Giles, C.L.; Lawrence, S.; Tsoi, A.C. Noisy time series prediction using recurrent neural networks and grammatical inference. Mach. Learn. 2001, 44, 161–183. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Martens, J.; Sutskever, I. Learning recurrent neural networks with hessian-free optimization. In Proceedings of the 28th International Conference on Machine Learning (ICML 2011), Bellevue, WA, USA, 28 June–2 July 2011; pp. 1033–1040. [Google Scholar]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the 30th International Conference on International Machine Learning (ICML’13), Atlanta, GA, USA, 16–21 June 2013; Volume 28, pp. III-1310–III-1318. [Google Scholar]
- Werbos, P.J. Backpropagation through time: What it does and how to do it. Proc. IEEE 1990, 78, 1550–1560. [Google Scholar] [CrossRef]
- Williams, R.J.; Zipser, D. A learning algorithm for continually running fully recurrent neural networks. Neural Comput. 1989, 1, 270–280. [Google Scholar] [CrossRef]
- Gers, F. Long Short-Term Memory in Recurrent Neural Networks. Ph.D. Thesis, École Polytechnique Fédérale de Laussanne, Lausanne, Switzerland, 2001. [Google Scholar]
- Lukoševičius, M.; Jaeger, H. Reservoir computing approaches to recurrent neural network training. Comput. Sci. Rev. 2009, 3, 127–149. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Goga, C.; Shehzad, M.A. Overview of Ridge Regression Estimators in Survey Sampling; Université de Bourgogne: Dijon, France, 2010. [Google Scholar]
- Lukoševičius, M. Neural Networks: Tricks of the Trade, 2nd ed.; Chapter A Practical Guide to Applying Echo State Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 659–686. [Google Scholar]
- Lv, Z.; Zhao, J.; Liu, Y.; Wang, W. Use of a quantile regression based echo state network ensemble for construction of prediction intervals of gas flow in a blast furnace. Control Eng. Pract. 2016, 46, 94–104. [Google Scholar] [CrossRef]
- Nielsen, H.A.; Madsen, H.; Nielsen, T.S. Using quantile regression to extend an existing wind power forecasting system with probabilistic forecasts. Wind Energy 2006, 9, 95–108. [Google Scholar] [CrossRef]
- Schmidhuber, J.; Gagliolo, M.; Gomez, F. Training recurrent networks by evolino. Neural Comput. 2007, 19, 757–779. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Chen, W.; Wu, X.; Chen, P.C.Y.; Liu, J. LSTM network: A deep learning approach for short-term traffic forecast. IET Intell. Transp. Syst. 2017, 11, 68–75. [Google Scholar] [CrossRef]
- Liu, D.; Wang, J.; Wang, H. Short-term wind speed forecasting based on spectral clustering and optimised echo state networks. Renew. Energy 2015, 78, 599–608. [Google Scholar] [CrossRef]
- Sheng, C.; Zhao, J.; Liu, Y.; Wang, W. Prediction for noisy nonlinear time series by echo state network based on dual estimation. Neurocomputing 2012, 82, 186–195. [Google Scholar] [CrossRef]
- Palangi, H.; Deng, L.; Ward, R.K. Learning input and recurrent weight matrices in echo state networks. arXiv, 2013; arXiv:1311.2987. [Google Scholar]
- Zeiler, M.D. ADADELTA: An adaptive learning rate method. arXiv, 2012; arXiv:1212.5701. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv, 2016; arXiv:1609.04747. [Google Scholar]
- Iversen, E.B.; Morales, J.M.; Møller, J.K.; Trombe, P.-J.; Madsen, H. Leveraging stochastic differential equations for probabilistic forecasting of wind power using a dynamic power curve. Wind Energy 2017, 20, 33–44. [Google Scholar] [CrossRef]
- Cheng, H.; Tan, P.; Gao, J.; Scripps, J. Advances in Knowledge Discovery and Data Mining. In Proceedings of the 10th Pacific-Asia Conference (PAKDD 2006), Singapore, 9–12 April 2006; Chapter Multistep-Ahead Time Series Prediction. Springer: Berlin/Heidelberg, Germany, 2006; pp. 765–774. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).