Estimation of Effective Diffusion Coefficient of O2 in Ash Layer in Underground Coal Gasification by Thermogravimetric Apparatus
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theoretical Section
2.2. Experimental Section
3. Results and Discussion
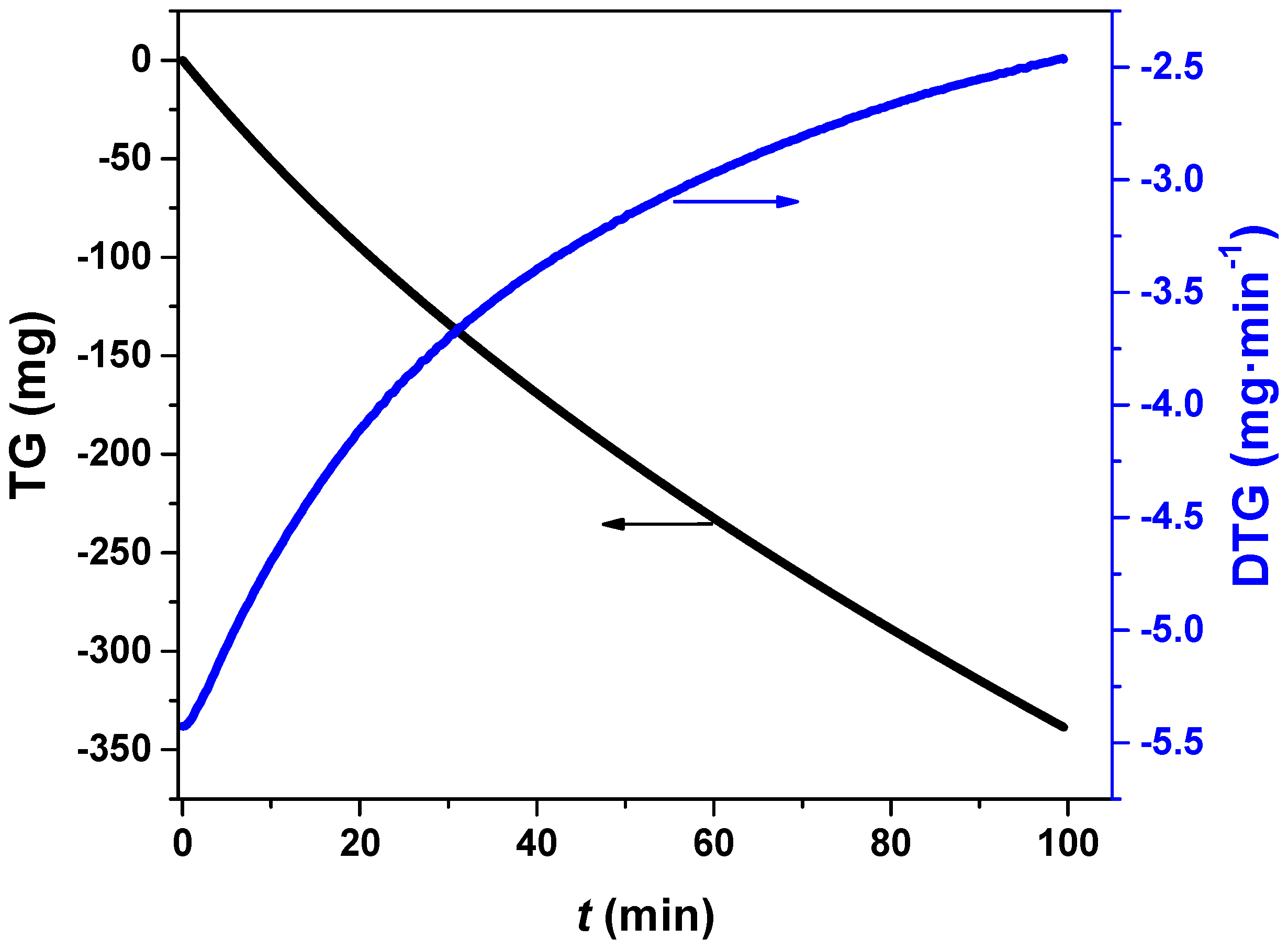
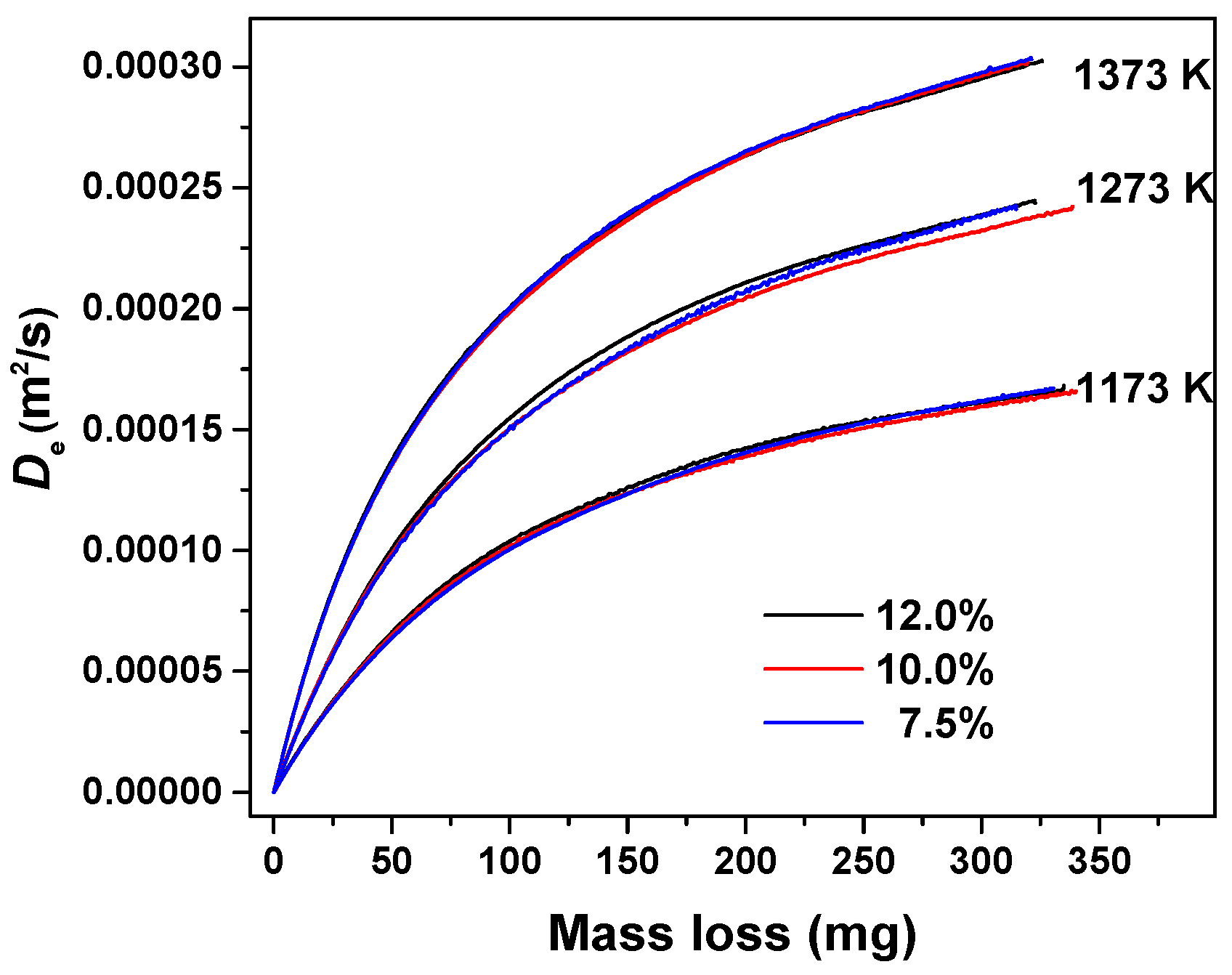
3.1. Estimation of Effective Diffusion Coefficient
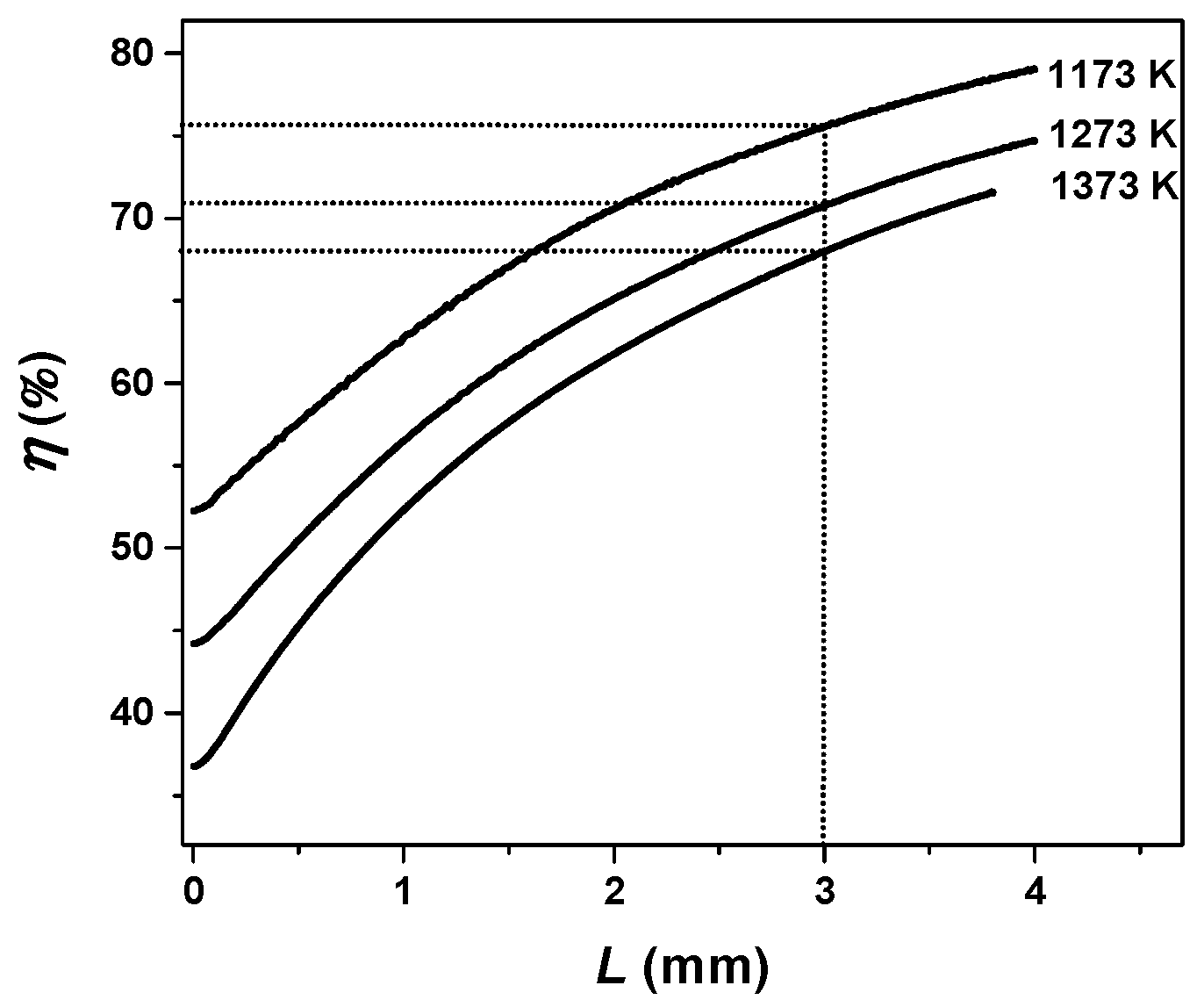
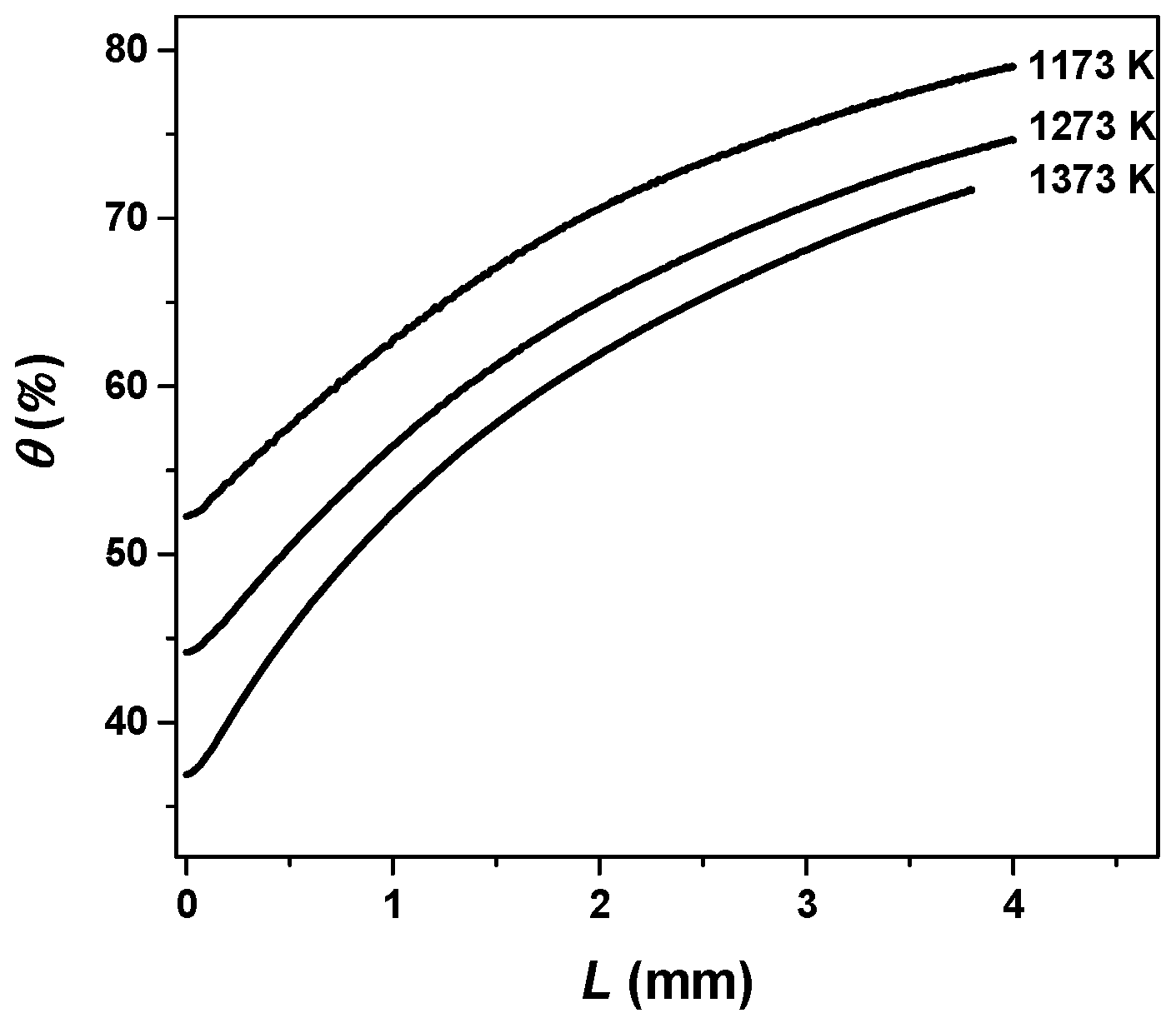
3.2. Internal Diffusion Resistance
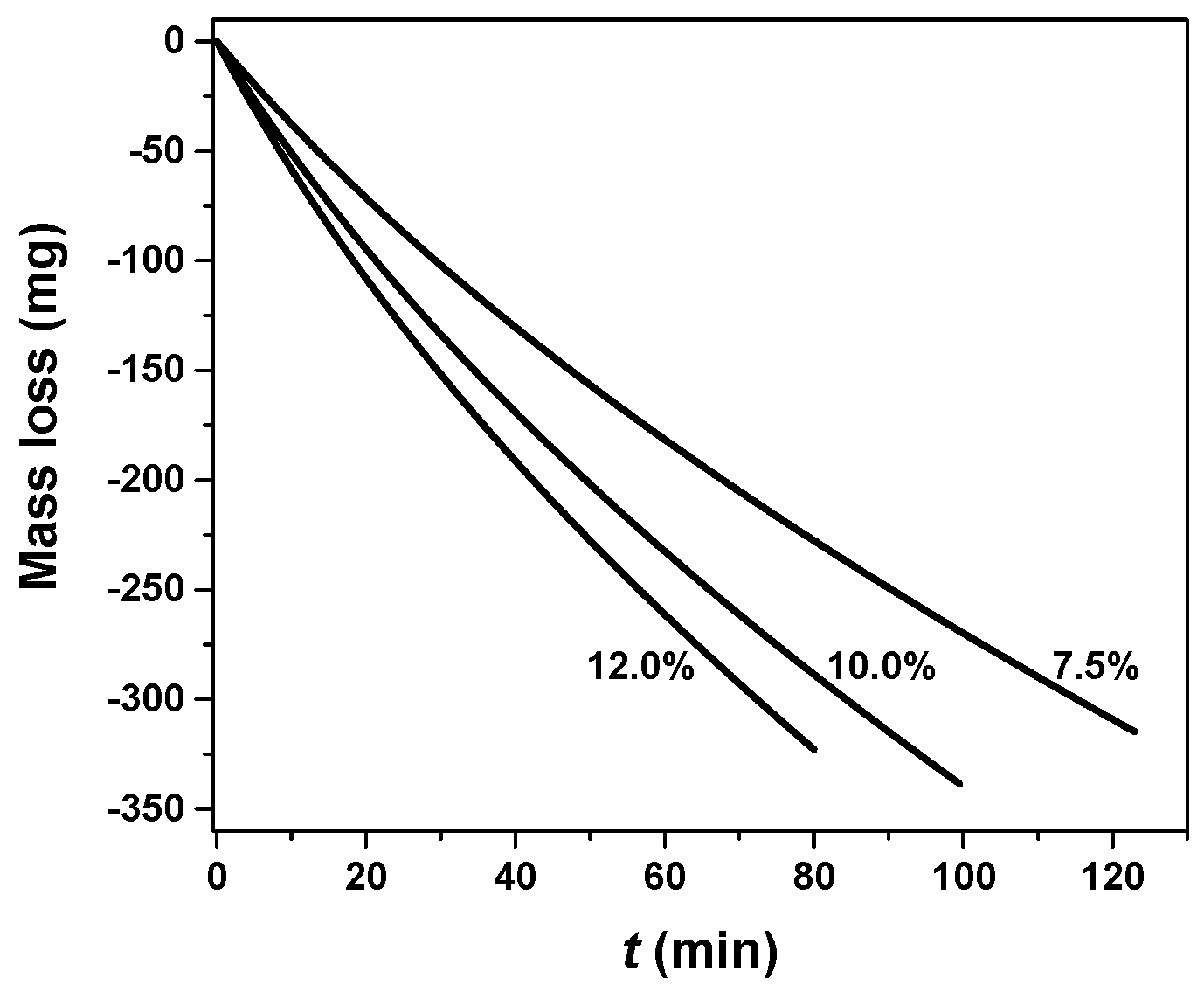
3.3. The Influence of Gas Concentration
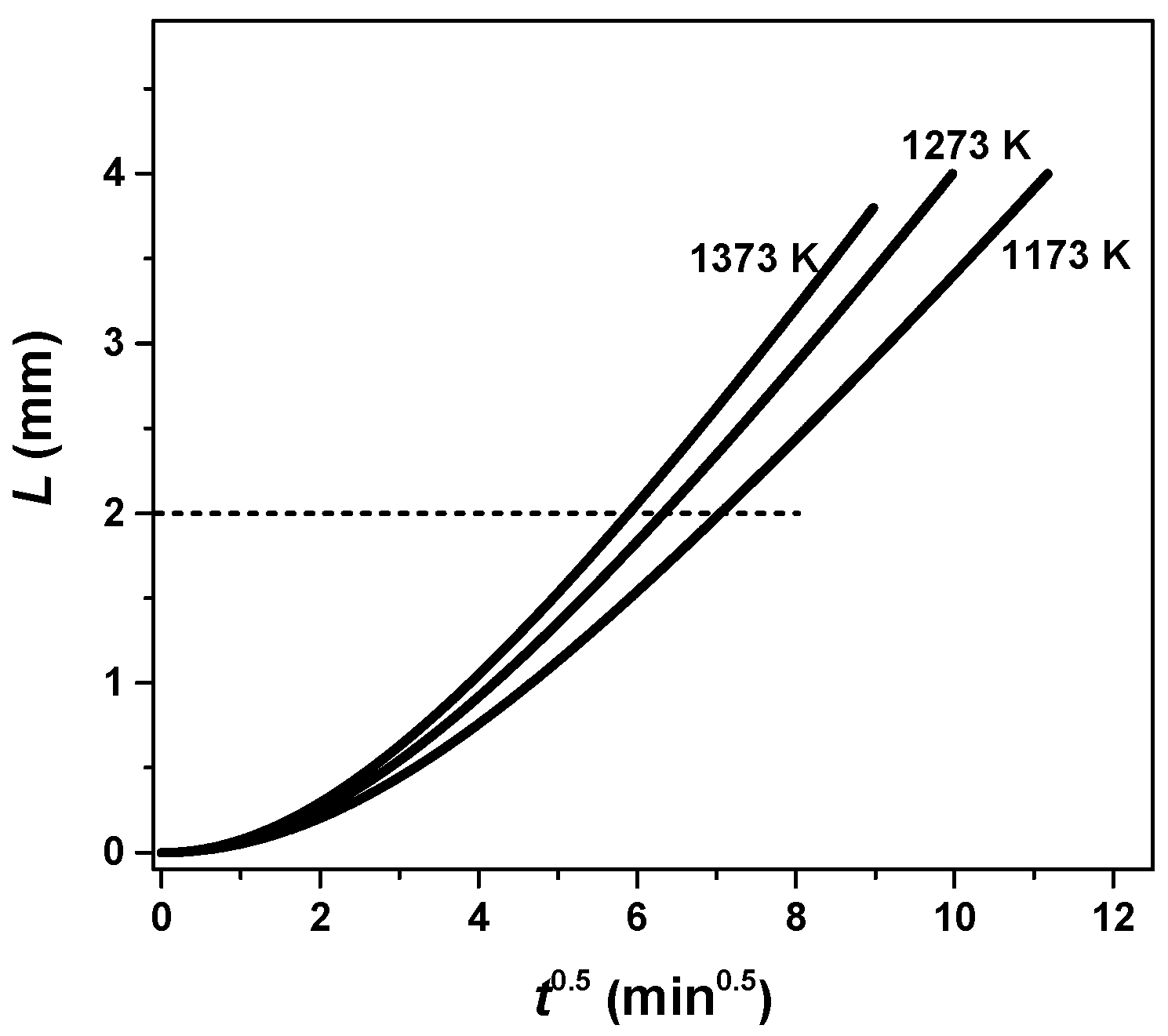
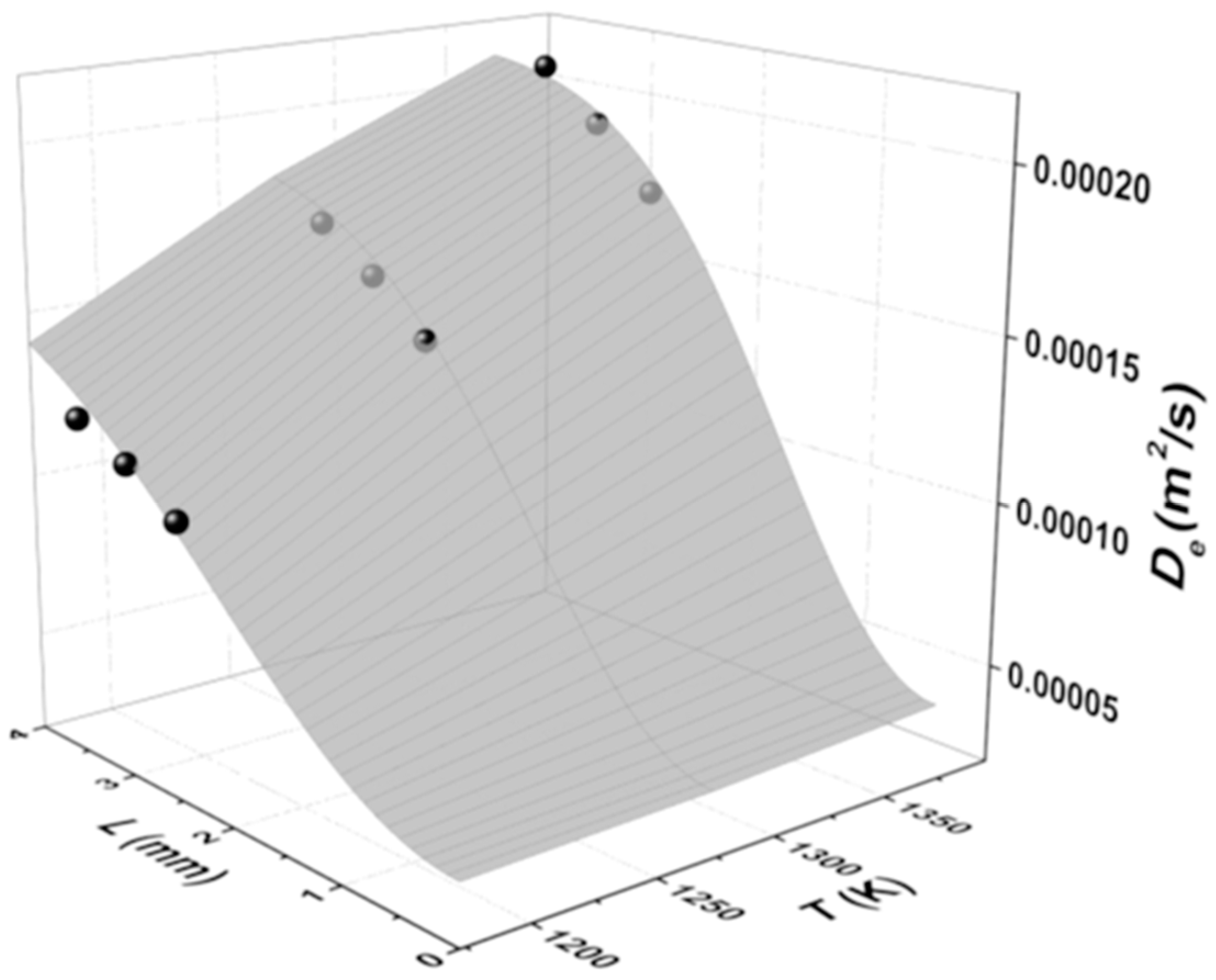
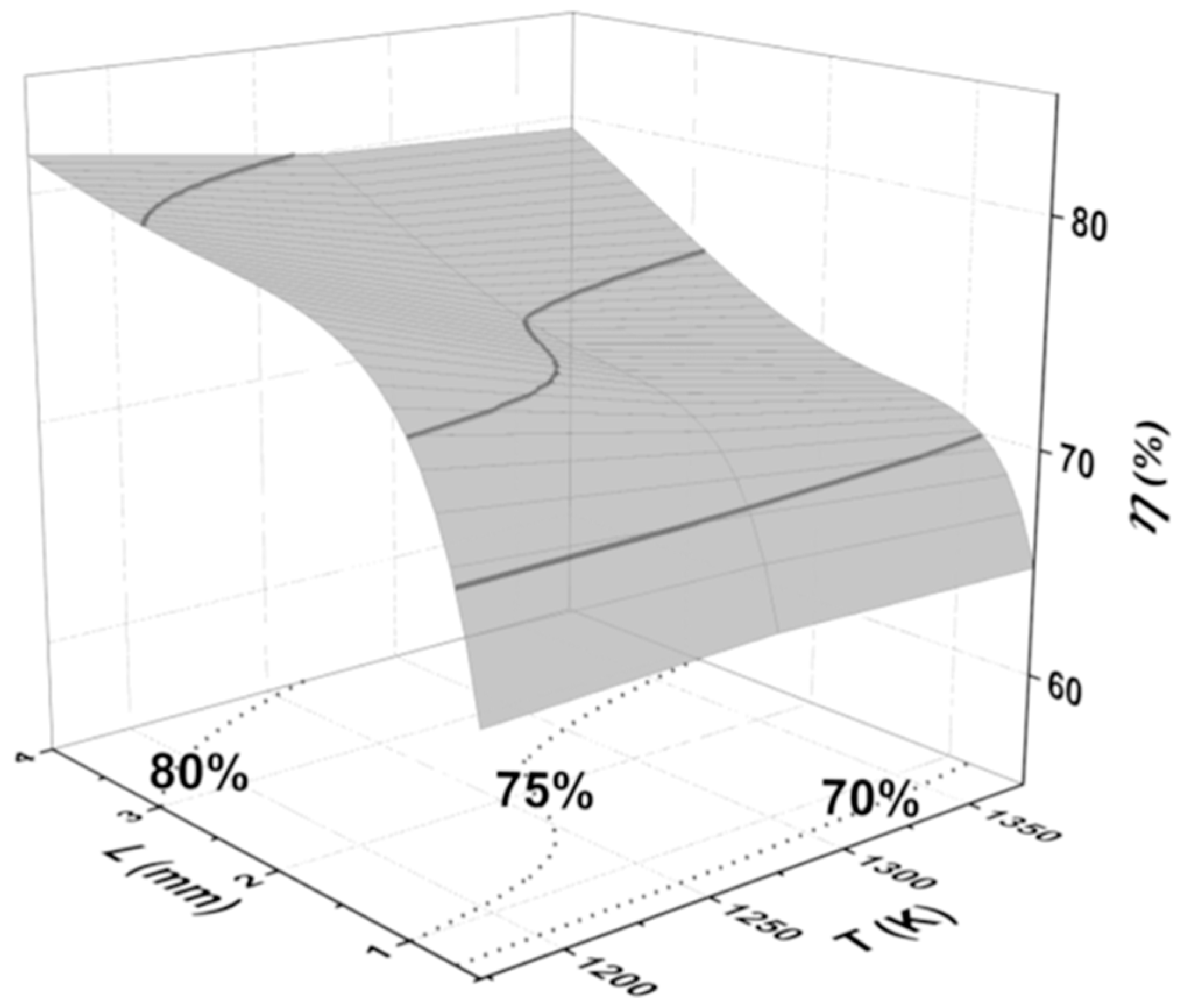
3.4. Effective Diffusion Coefficient with Temperature and Ash Layer Thickness
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Najafi, M.; Jalali, S.M.E.; KhaloKakaie, R. Thermal–mechanical–numerical analysis of stress distribution in the vicinity of underground coal gasification (UCG) panels. Int. J. Coal Geol. 2014, 134–135, 1–16. [Google Scholar] [CrossRef]
- Otto, C.; Kempka, T. Prediction of steam jacket dynamics and water balances in underground coal gasification. Energies 2017, 10, 739. [Google Scholar] [CrossRef]
- Shafirovich, E.; Varma, A. Underground coal gasification: a brief review of current status. Ind. Eng. Chem. Res. 2009, 48, 7865–7875. [Google Scholar] [CrossRef]
- Urych, B. Determination of kinetic parameters of coal pyrolysis to simulate the process of underground coal gasification (UCG). J. Sustain. Min. 2014, 13, 3–9. [Google Scholar] [CrossRef]
- Prabu, V.; Jayanti, S. Simulation of cavity formation in underground coal gasification using bore hole combustion experiments. Energy 2011, 36, 5854–5864. [Google Scholar] [CrossRef]
- Konstantinou, E.; Marsh, R. Experimental study on the impact of reactant gas pressure in the conversion of coal char to combustible gas products in the context of underground coal gasification. Fuel 2015, 159, 508–518. [Google Scholar] [CrossRef]
- Hamanaka, A.; Su, F.; Itakura, K.; Takahashi, K.; Kodama, J.; Deguchi, G. Effect of injection flow rate on product gas quality in underground coal gasification (UCG) based on laboratory scale experiment: development of Co-Axial UCG system. Energies 2017, 10, 238. [Google Scholar] [CrossRef]
- Ollero, P.; Serrera, A.; Arjona, R.; Alcantarilla, S. Diffusional effects in TGA gasification experiments for kinetic determination. Fuel 2002, 81, 1989–2000. [Google Scholar] [CrossRef]
- Sadhukhan, A.K.; Gupta, P.; Saha, R.K. Modelling of combustion characteristics of high ash coal char particles at high pressure: shrinking reactive core model. Fuel 2010, 89, 162–169. [Google Scholar] [CrossRef]
- Park, K.Y.; Edgar, T.F. Modeling of early cavity growth for underground coal gasification. Ind. Eng. Chem. Res. 1987, 26, 237–246. [Google Scholar] [CrossRef]
- Perkins, G.; Sahajwalla, V. Modelling of heat and mass transport phenomena and chemical reaction in underground coal gasification. Chem. Eng. Res. Des. 2007, 85, 329–343. [Google Scholar] [CrossRef]
- Su, F.; Nakanowataru, T.; Itakura, K.; Ohga, K.; Deguchi, G. Evaluation of structural changes in the coal specimen heating process and UCG model experiments for developing efficient UCG Systems. Energies 2013, 6, 2386–2406. [Google Scholar] [CrossRef]
- Prabu, V.; Jayanti, S. Heat-affected zone analysis of high ash coals during ex-situ experimental simulation of underground coal gasification. Fuel 2014, 123, 167–174. [Google Scholar] [CrossRef]
- Wang, Z.; Liang, J.; Shi, L.; Xi, J.; Li, S.; Cui, Y. Expansion of three reaction zones during underground coal gasification with free and percolation channels. Fuel 2017, 190, 435–443. [Google Scholar] [CrossRef]
- Daggupati, S.; Mandapati, R.N.; Mahajani, S.M.; Ganesh, A.; Mathur, D.K.; Sharma, R.K.; Aghalayam, P. Laboratory studies on combustion cavity growth in lignite coal blocks in the context of underground coal gasification. Energy 2010, 35, 2374–2386. [Google Scholar] [CrossRef]
- Cena, R.J.; Britten, J.A.; Thorsness, C.B. Excavation of the partial CRIP underground coal gasification test site. In Proceedings of the 13th Annual Underground Coal Gasification Symposium, Laramie, WY, USA, 24–30 August 1987. [Google Scholar]
- Yang, L.H. Three-Dimensional non-linear numerical analysis on the oxygen concentration field in underground coal gasification. Fuel Process. Technol. 2004, 85, 1605–1622. [Google Scholar] [CrossRef]
- Eftekhari, A.A.; Wolf, K.H.; Rogut, J.; Bruining, H. Mathematical modeling of alternating injection of oxygen and steam in underground coal gasification. Int. J. Coal Geol. 2015, 150, 154–165. [Google Scholar] [CrossRef]
- Kuyper, R.A.; Meer, T.H.V.D.; Hoogendoorn, C.J. Turbulent natural convection flow due to combined buoyancy forces during underground coal gasification of thin seams. Chem. Eng. Sci. 1994, 49, 851–861. [Google Scholar] [CrossRef]
- Elliott, M.A. Chemistry of Coal Utilization; John Wiley and Sons: New York, NY, USA, 1981; pp. 1835–1836. [Google Scholar]
- Huang, J.; Bruining, J.; Wolf, K.-H.A.A. Modeling of gas flow and temperature fields in underground coal fires. Fire Saf. J. 2001, 36, 477–489. [Google Scholar] [CrossRef]
- Barea, A.G.; Ollero, P.; Arjona, R. Reaction-diffusion model of TGA gasification experiments for estimating diffusional effects. Fuel 2005, 84, 1695–1704. [Google Scholar] [CrossRef]
- Yan, J.; Ni, M.; Zhao, H.; Cen, K. Gas diffusion through the ash layer of coal particle during the combustion process. Int. J. Thermophys. 1994, 15, 341–344. [Google Scholar] [CrossRef]
- Liu, J.G.; Yan, J.W.; Han, X.X.; Jiang, X.M. Study on the anisotropy of mass transfer for oxygen in the ash layer of shale char particles. Energy Fuels 2010, 24, 3488–3497. [Google Scholar] [CrossRef]
- Hwang, M.; Song, E.; Song, J. One-dimensional modeling of an entrained coal gasification process using kinetic parameters. Energies 2016, 9, 99. [Google Scholar] [CrossRef]
- Lin, X.; Liu, Q.; Liu, Z.; Guo, X.; Wang, R.; Shi, L. The role of ash layer in syngas combustion in underground coal gasification. Fuel Process. Technol. 2016, 143, 169–175. [Google Scholar] [CrossRef]
- Bews, I.M.; Hayhurst, A.N.; Richardson, S.M.; Taylor, S.G. The order, Arrhenius parameters, and mechanism of the reaction between gaseous oxygen and solid carbon. Combust. Flame 2001, 124, 231–245. [Google Scholar] [CrossRef]
- Khan, M.M.; Mmbaga, J.P.; Shirazi, A.S.; Trivedi, J.; Liu, Q.; Gupta, R. Modelling underground coal gasification—A review. Energies 2015, 8, 12603–12668. [Google Scholar] [CrossRef]
- Yang, L.H.; Zhang, X.; Liu, S.Q.; Yu, L.; Zhang, W.L. Field test of large-scale hydrogen manufacturing from underground coal gasification (UCG). Int. J. Hydrogen Energy 2008, 33, 1275–1285. [Google Scholar] [CrossRef]
- Su, J.L.; Perlmutter, D.D. Effect of Pore Structure on Char Oxidation Kinetics. AIChE J. 1985, 31, 973–981. [Google Scholar] [CrossRef]
- Chen, C.; Kojima, T. Single char particle combustion at moderate temperature: effects of ash. Fuel Process. Technol. 1996, 47, 215–232. [Google Scholar] [CrossRef]
- Sotirchos, S.V.; Amundson, N.R. Dynamic behavior of a porous char particle burning in an oxygen-containing environment. AlChE J. 1984, 30, 537–549. [Google Scholar] [CrossRef]
- Wen, C.Y. Non-Catalytic Heterogeneous Solid-Fluid Reaction Models. Ind. Eng. Chem. 1968, 60, 34–54. [Google Scholar] [CrossRef]
- Perkins, G. Mathematical Modelling of Underground Coal Gasification. Ph.D. Thesis, The University of New South Wales, Sydney, Australia, 2005. [Google Scholar]
- Perkins, G.; Sahajwalla, V. A numerical study of the effects of operating conditions and coal properties on cavity growth in underground coal gasification. Energy Fuels 2006, 20, 596–608. [Google Scholar] [CrossRef]
- Sadhukhan, A.K.; Gupta, P.; Saha, R.K. Analysis of the dynamics of coal char combustion with ignition and extinction phenomena: shrinking core model. Int. J. Chem. Kinet. 2008, 40, 569–582. [Google Scholar] [CrossRef]
- Kelebopile, L.; Sun, R.; Wang, H.; Zhang, X.; Wu, S.H. Pore development and combustion behavior of gasified semi-char in a drop tube furnace. Fuel Process. Technol. 2013, 111, 42–54. [Google Scholar] [CrossRef]
- Parlange, J.Y. Reviewed Work: Dynamics of Fluids in Porous Media by J. BEAR. Am. Sci. 1973, 6, 758–759. [Google Scholar]
- Kingery, W.D. Introduction to Ceramics, 1st ed.; Wiley: New York, NY, USA, 1960; p. 380. ISBN 0471478601. [Google Scholar]
- Hill, R.W.; Hill, C.B. Summary Report on Large Block Experiments in Underground Coal Gasification, Tono Basin, Washington: Volume 1. Experimental Description and Data Analysis; Report No. UCRL-53305; Lawrence Livermore National Laboratory, University of California: Berkeley, CA, USA, 9 July 1982.





| Parameter | Sample 1 | Sample 3 | Sample 2 | Sample 4 |
|---|---|---|---|---|
| t (min) | 20 | 30 | 65 | 175 |
| Porosity | 0.68 | 0.69 | 0.70 | 0.70 |
| diameter (nm) | 1397 | 1401 | 1601 | 1710 |
| Resistance | 1173 K | 1273 K | 1373 K |
|---|---|---|---|
| 1/K | 0.3 | 0.07 | 0.02 |
| 1/Kc | 6.4 | 5.6 | 5.0 |
| L/De (L = 1 mm) | 10.8 | 7.3 | 5.5 |
| L/De (L = 2 mm) | 15.4 | 10.5 | 8.1 |
| L/De (L = 3 mm) | 19.8 | 13.5 | 10.6 |
| Parameter | 1173 K | 1273 K | 1373 K |
|---|---|---|---|
| B | 0.530 | 0.548 | 0.556 |
| F | 114,914 | 210,240 | 279,638 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, X.; Liu, Q.; Liu, Z. Estimation of Effective Diffusion Coefficient of O2 in Ash Layer in Underground Coal Gasification by Thermogravimetric Apparatus. Energies 2018, 11, 460. https://doi.org/10.3390/en11020460
Lin X, Liu Q, Liu Z. Estimation of Effective Diffusion Coefficient of O2 in Ash Layer in Underground Coal Gasification by Thermogravimetric Apparatus. Energies. 2018; 11(2):460. https://doi.org/10.3390/en11020460
Chicago/Turabian StyleLin, Xi, Qingya Liu, and Zhenyu Liu. 2018. "Estimation of Effective Diffusion Coefficient of O2 in Ash Layer in Underground Coal Gasification by Thermogravimetric Apparatus" Energies 11, no. 2: 460. https://doi.org/10.3390/en11020460
APA StyleLin, X., Liu, Q., & Liu, Z. (2018). Estimation of Effective Diffusion Coefficient of O2 in Ash Layer in Underground Coal Gasification by Thermogravimetric Apparatus. Energies, 11(2), 460. https://doi.org/10.3390/en11020460




