Insights into Dynamic Tuning of Magnetic-Resonant Wireless Power Transfer Receivers Based on Switch-Mode Gyrators
Abstract
:1. Introduction
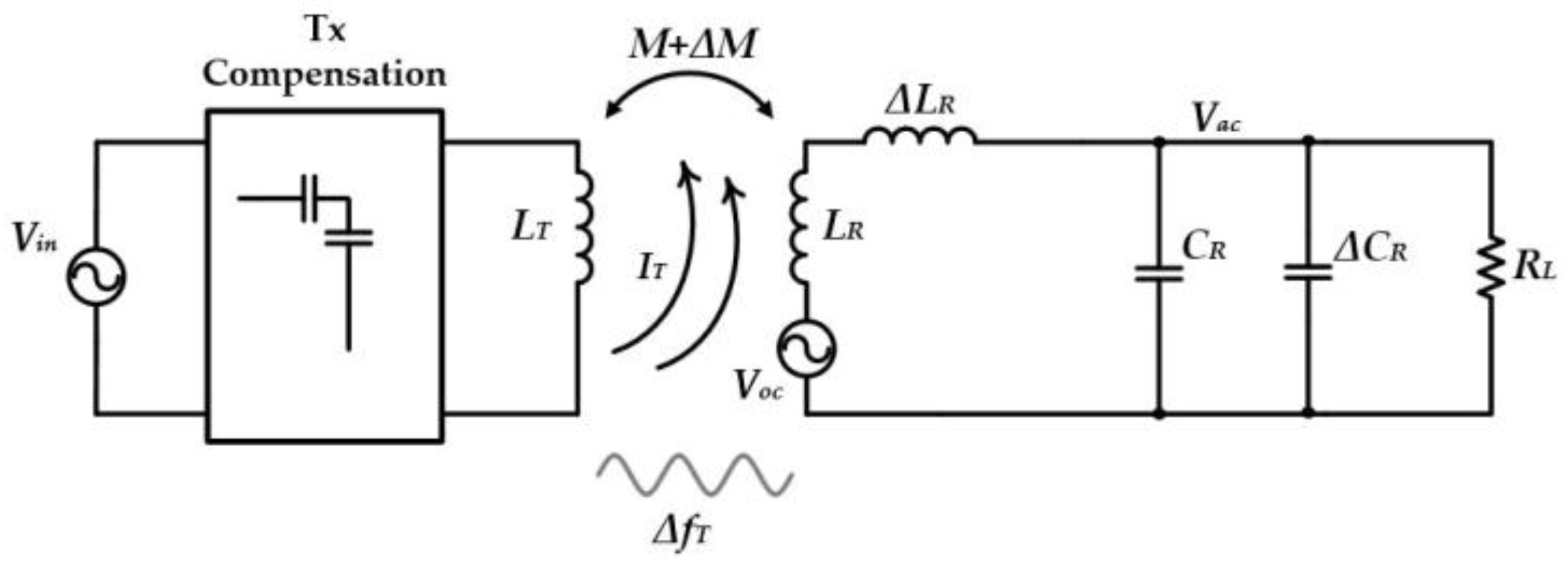
2. Parallel-Compensated WPT Receivers
2.1. Principles of Parallel-Compensated WPT Receivers
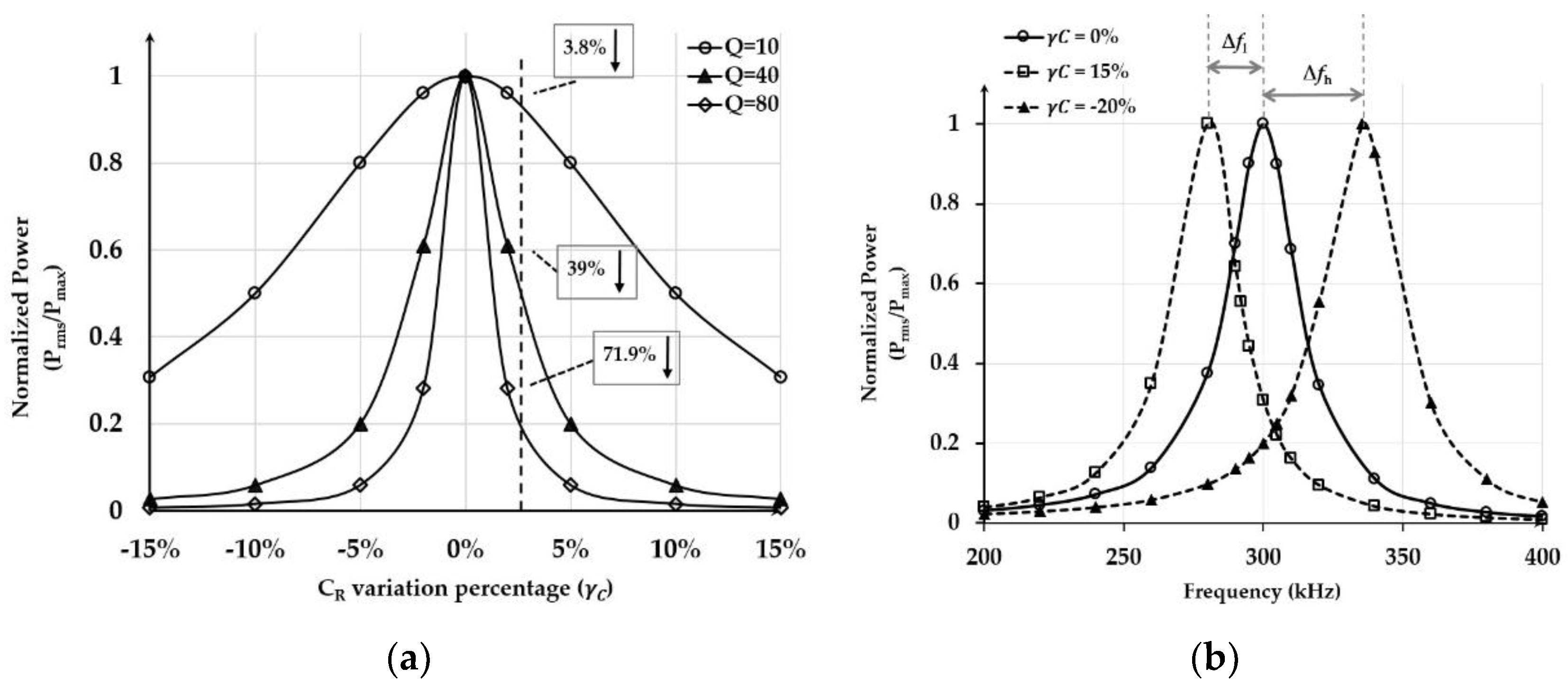
2.2. Mistuning Effect on Power Delivery
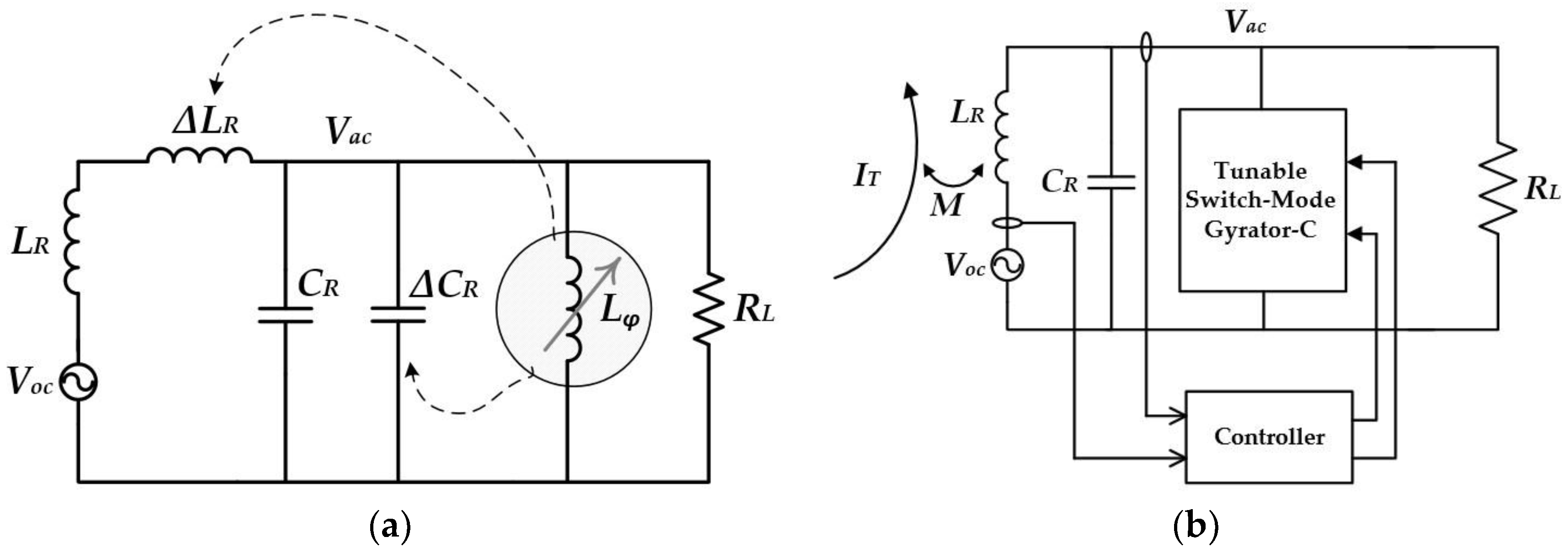
3. Dynamic Tuning by Means of Gyrator-Based Reactives
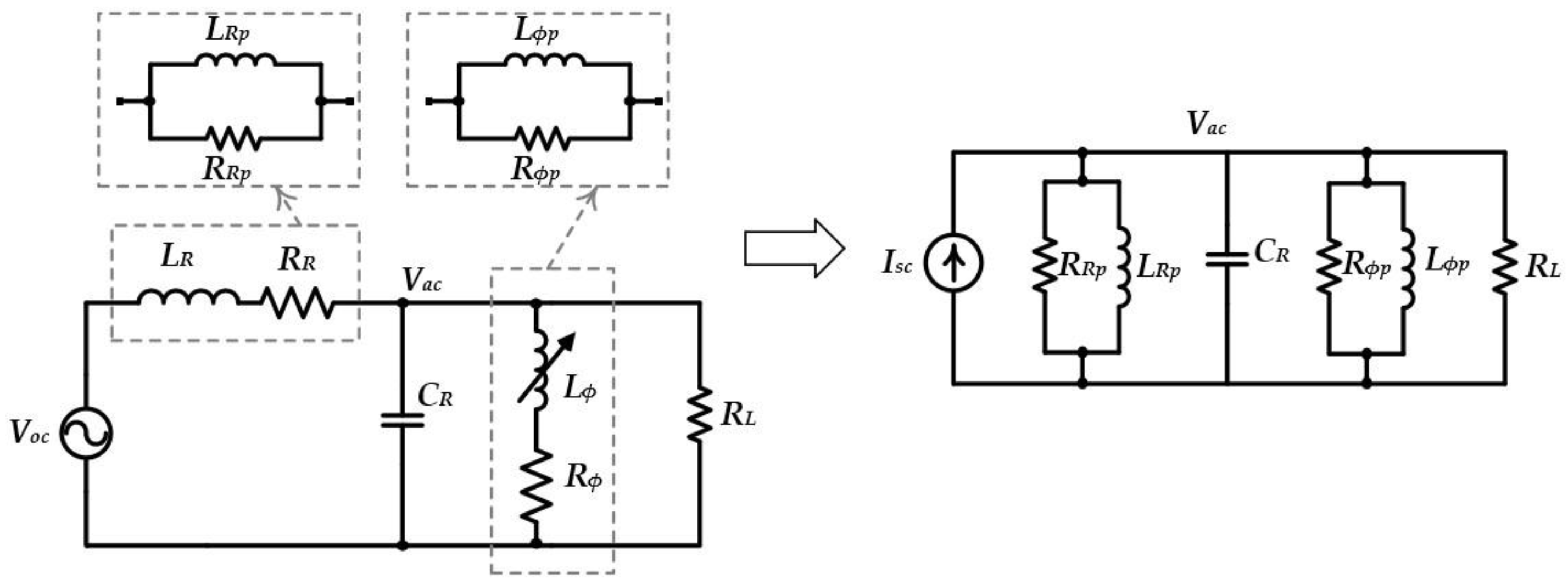
3.1. Generalized Model for The Proposed Dynamic Tuning Approach
3.2. Impedance Emulation By Means of Gyrators—A Spotlight
4. Switch-Mode Gyrator-Enabled Variable Inductance
4.1. Gyrators in Power Processing Applications
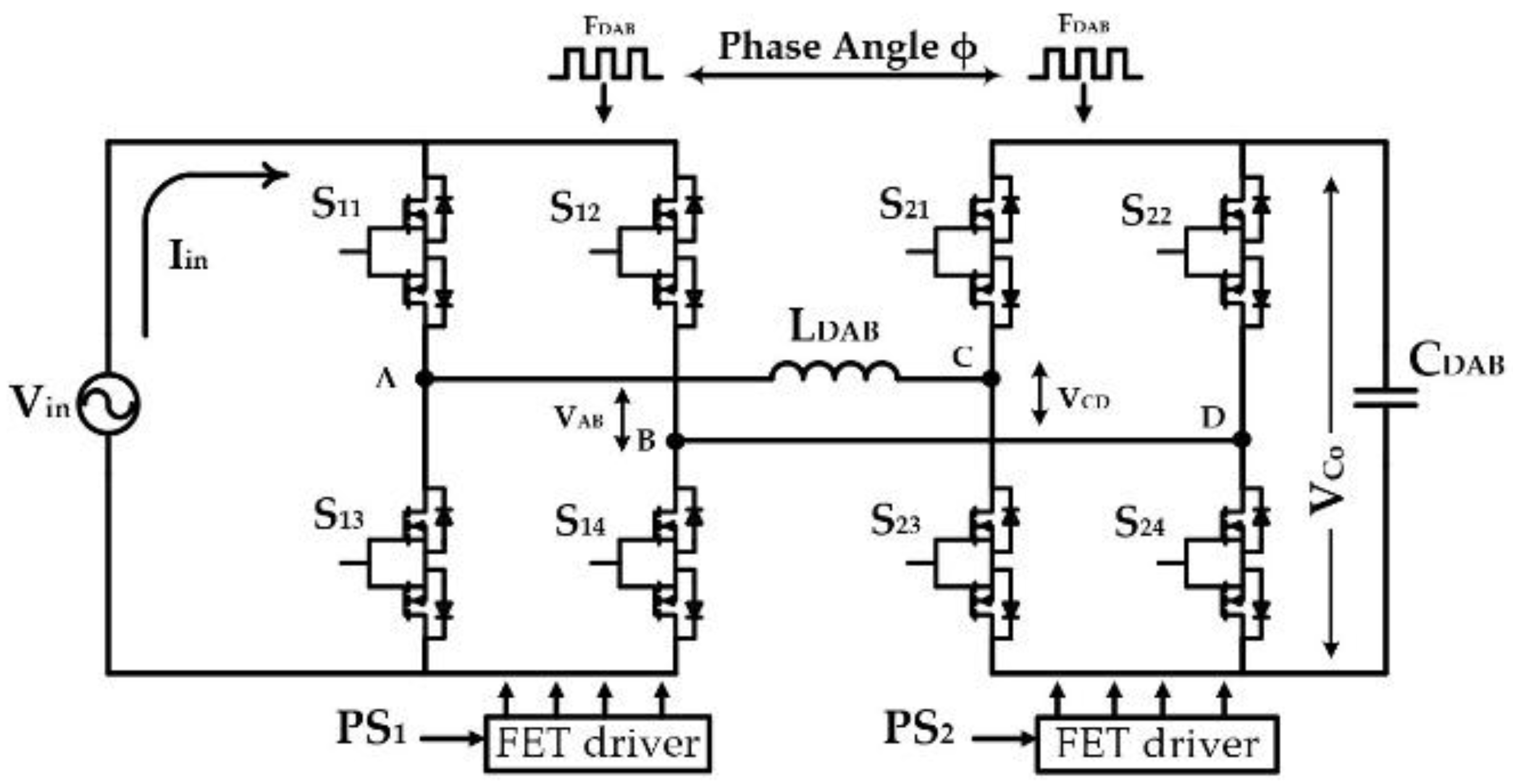
4.2. DAB as a Switch-Mode Natural Gyrator—Revisiting
4.3. DAB-Based Variable Inductance Design
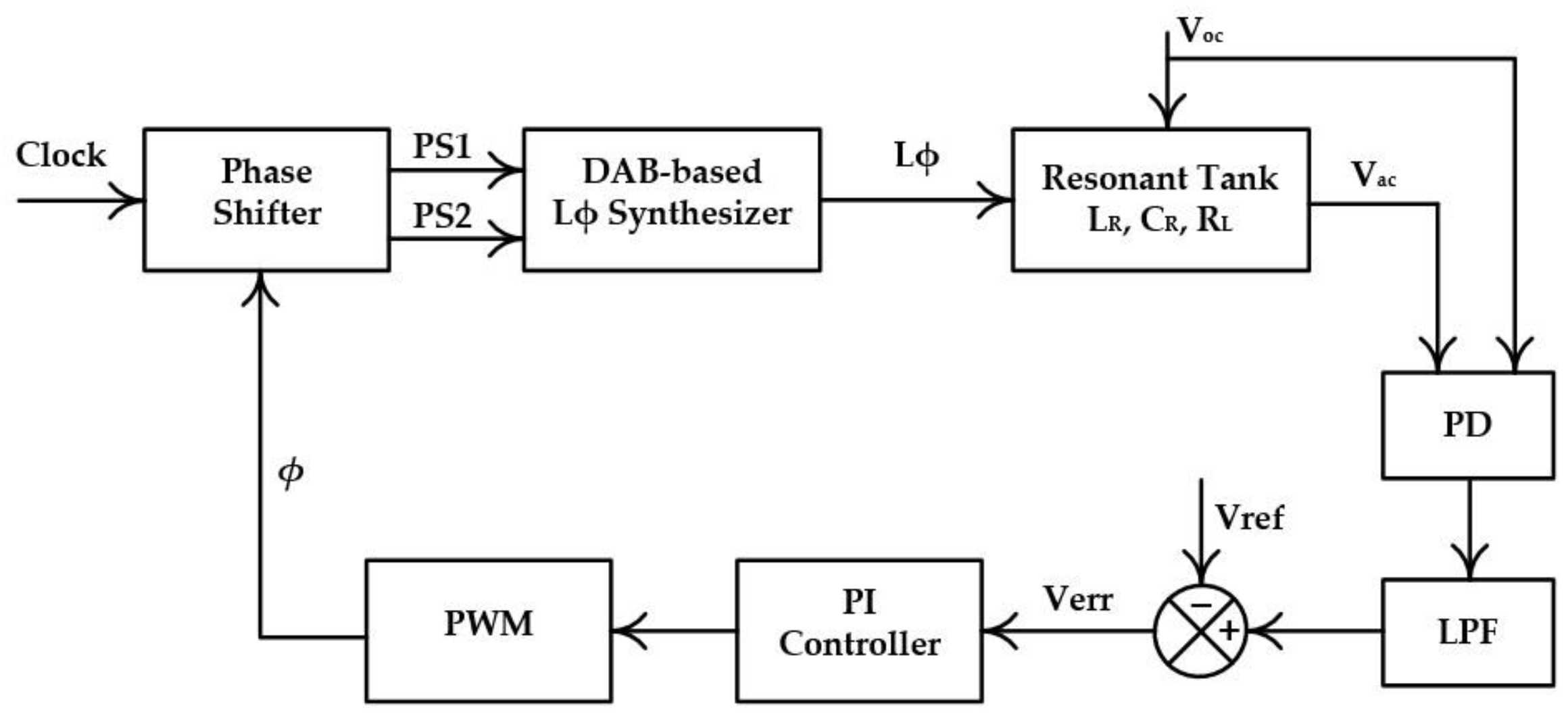
5. Implementation of Dynamic Frequency Tuning Control
5.1. PLL-Like Control—Theory and Operation
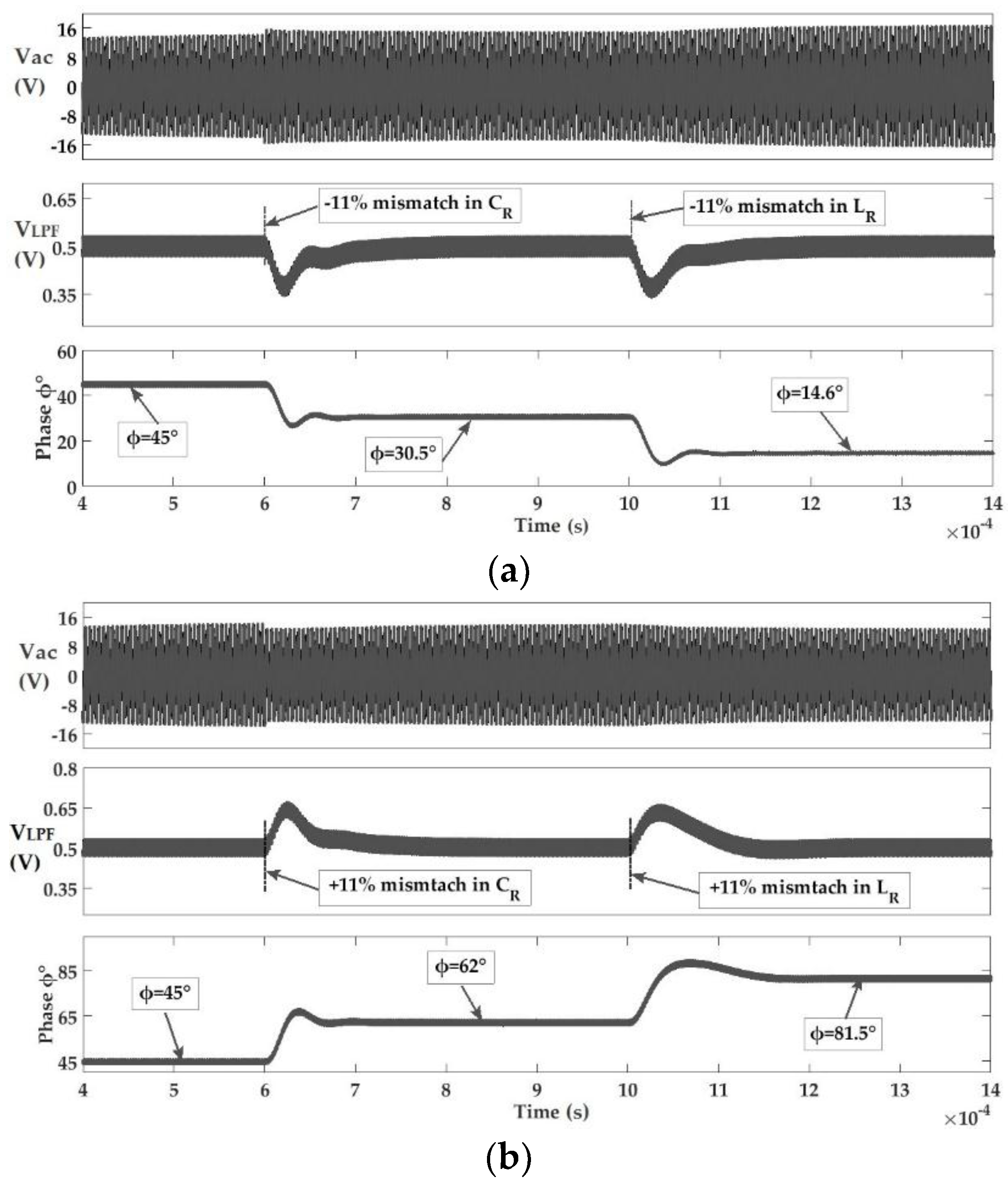
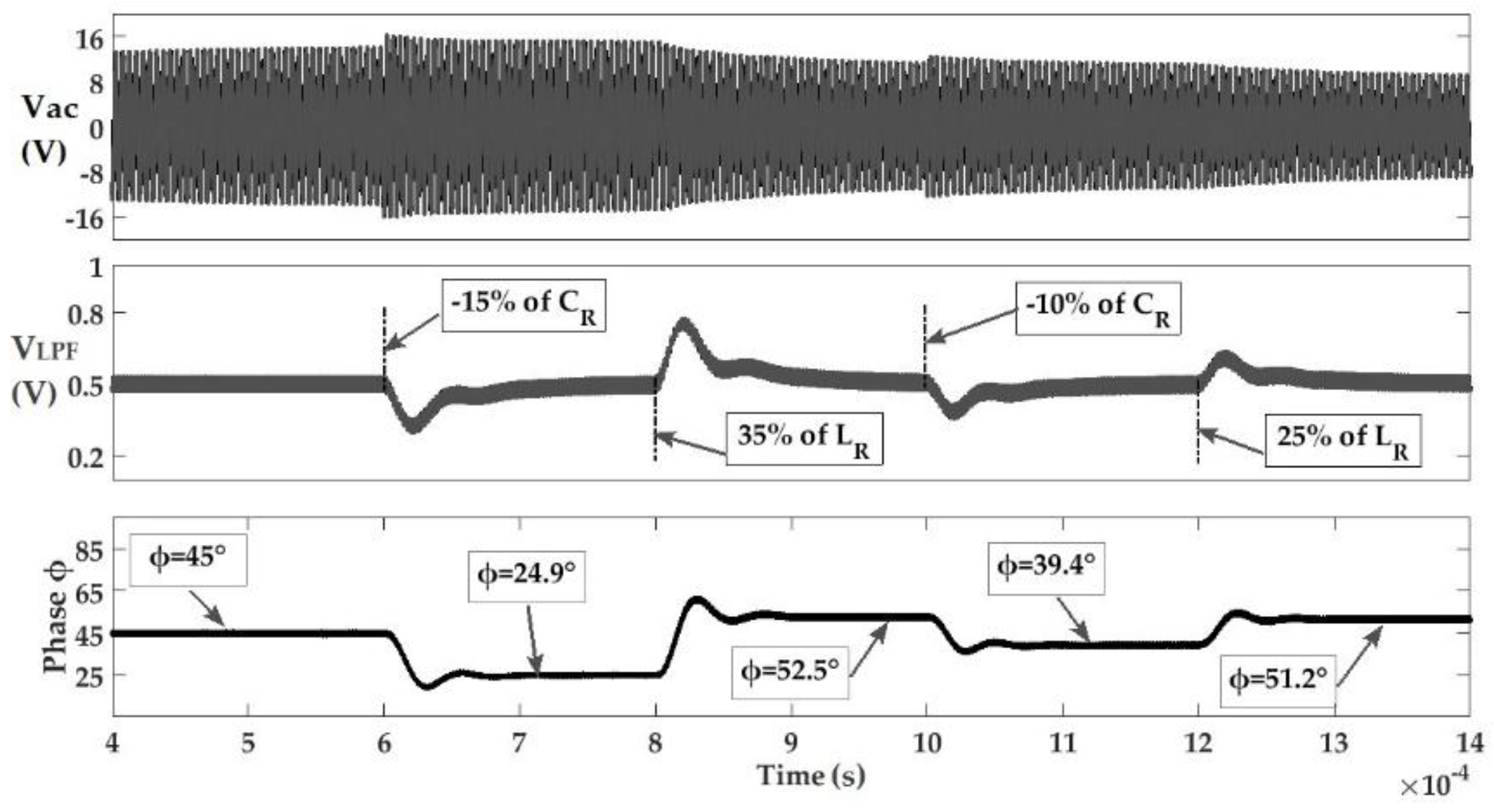
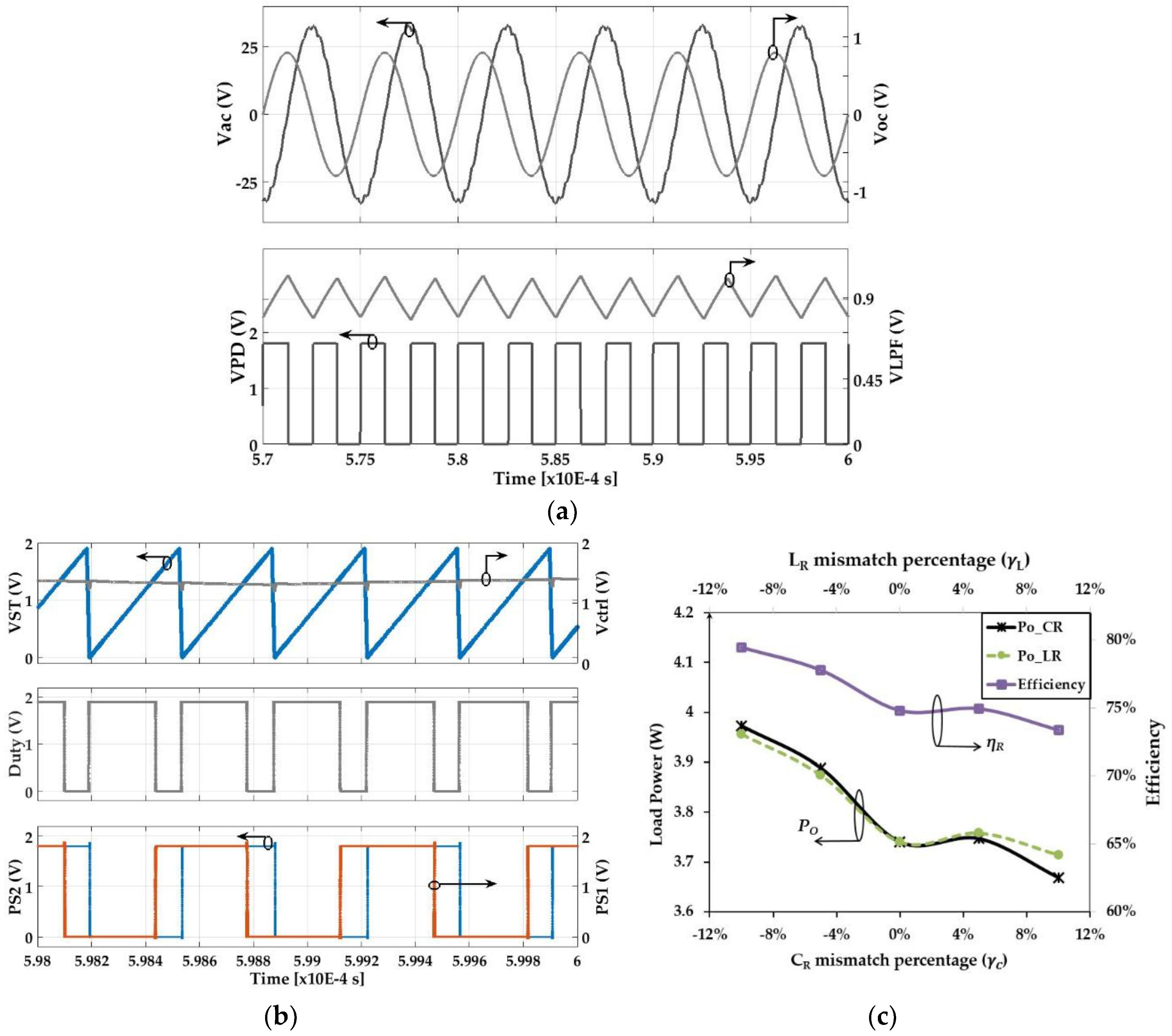
5.2. System Integration and Validation Results
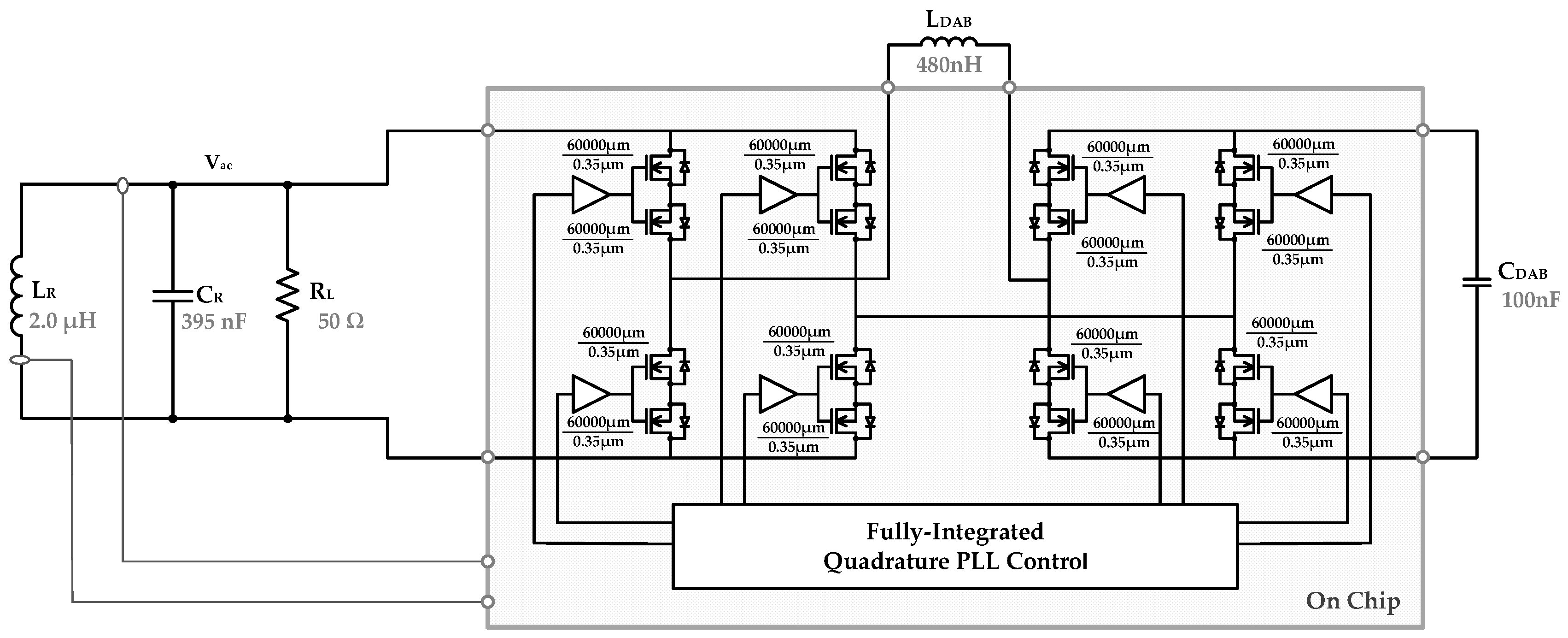
6. Chip Implementation for the Proposed DAB-based Inductance Synthesizer
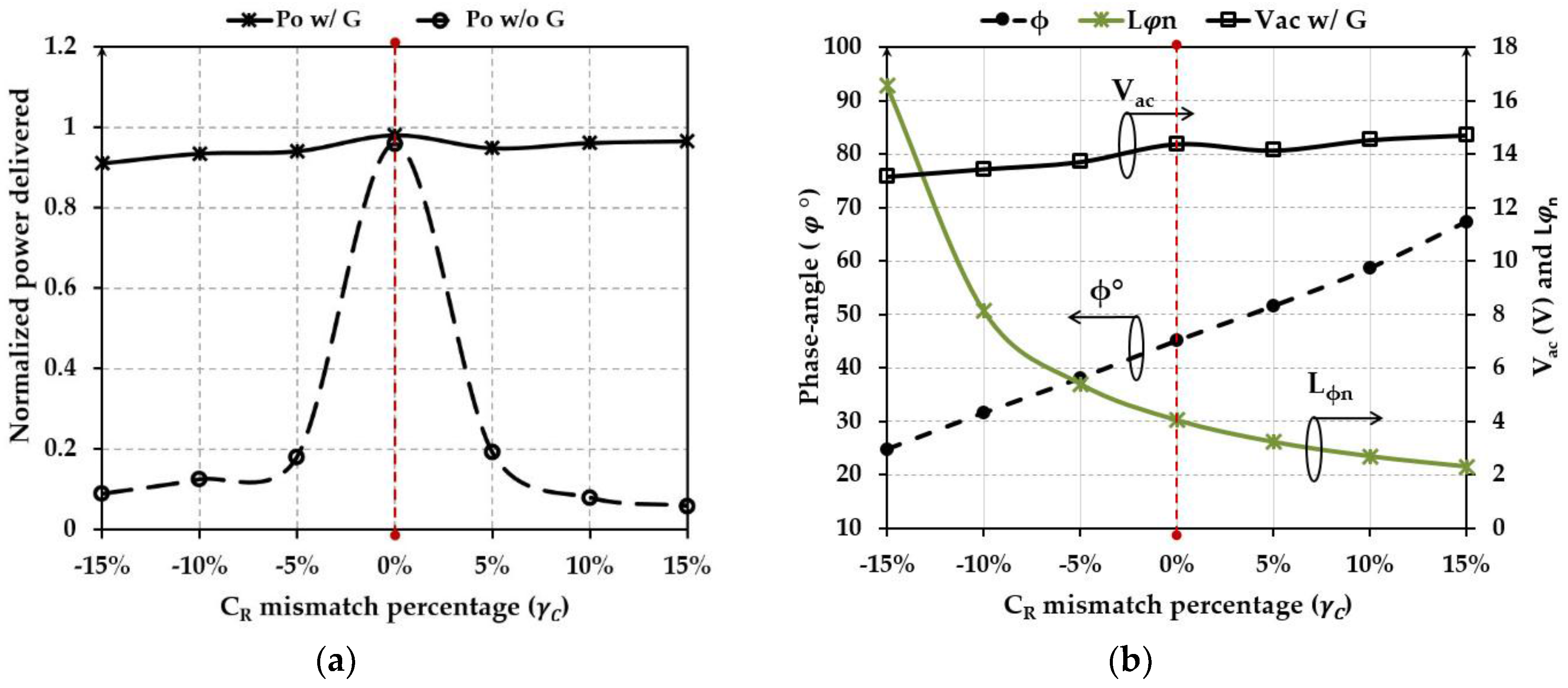
7. System Design Consideration—Performance Discussion
7.1. Efficiency and Quality Factor
7.2. Comparison with Other Solutions in the Literature
7.3. Design Oriented Characterization
7.4. Complexity and Cost
8. Conclusions
- The proposed dynamic tuning approach by means of a gyrator-based reactive components synthesis has shown a potential for proper performance in terms of autonomous tunability in WPT receivers.
- While DAB converter was studied as a natural gyrator, this study is meant to open the door for the concept of gyrator based control of power delivery in WPT systems. Despite the circuit complexity of the DAB, more simple and compact switch-mode gyrator would greatly support the adoption of tunable gyrators for power flow control in WPT systems.
- This paper has given a detailed insights into the feasibility of adopting switch-mode gyrators in adaptive tuning of WPT receivers. Despite that no experimental validation has been practiced, still the theory and analysis given here could be applicable by means of more compact switch-mode gyrator topologies without loss of generality.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, X.; Tsui, C.Y.; Ki, W.H. A 13.56 MHz Wireless Power Transfer System with Reconfigurable Resonant Regulating Rectifier and Wireless Power Control for Implantable Medical Devices. IEEE J. Solid-State Circ. 2015, 50, 978–989. [Google Scholar] [CrossRef]
- Wang, C.; Stielau, O.H.; Covic, G.A. Load models and their application in the design of loosely coupled inductive power transfer systems. In Proceedings of the PowerCon 2000 International Conference on Power System Technology, Perth, Australia, 4–7 December 2000; pp. 1053–1058. [Google Scholar]
- Boys, J.T.; Covic, G.A.; Green, A.W. Stability and control of inductively coupled power transfer systems. IEE Proc.-Electr. Power Appl. 2000, 147, 37. [Google Scholar] [CrossRef]
- Wang, C.; Covic, G.A.; Stielau, O.H. Power Transfer Capability and Bifurcation Phenomena of Loosely Coupled Inductive Power Transfer Systems. IEEE Trans. Ind. Electron. 2004, 51, 148–157. [Google Scholar] [CrossRef]
- Huang, C.Y.; Boys, J.T.; Covic, G.A. LCL pickup circulating current controller for inductive power transfer systems. IEEE Trans. Power Electron. 2013, 28, 2081–2093. [Google Scholar] [CrossRef]
- Pantic, Z.; Bai, S.; Lukic, S.M. ZCS LCC-compensated resonant inverter for inductive-power-transfer application. IEEE Trans. Ind. Electron. 2011, 58, 3500–3510. [Google Scholar] [CrossRef]
- Xue, R.F.; Cheng, K.W.; Je, M. High-efficiency wireless power transfer for biomedical implants by optimal resonant load transformation. IEEE Trans. Circ. Syst. I Regul. Pap. 2013, 60, 867–874. [Google Scholar] [CrossRef]
- Cannon, B.L.; Hoburg, J.F.; Stancil, D.D.; Goldstein, S.C. Magnetic Resonant Coupling As a Potential Means for Wireless Power Transfer to Multiple Small Receivers. IEEE Trans. Power Electron. 2009, 24, 1819–1825. [Google Scholar] [CrossRef]
- Pantic, Z.; Lukic, S.M. Framework and Topology for Active Tuning of Parallel Compensated Receivers in Power Transfer Systems. IEEE Trans. Power Electron. 2012, 27, 4503–4513. [Google Scholar] [CrossRef]
- Waffenschmidt, E. Dynamic Resonant Matching Method for a Wireless Power Transmission Receiver. IEEE Trans. Power Electron. 2015, 30, 6070–6077. [Google Scholar] [CrossRef]
- Lim, Y.; Tang, H.; Lim, S.; Park, J. An adaptive impedance-matching network based on a novel capacitor matrix for wireless power transfer. IEEE Trans. Power Electron. 2014, 29, 4403–4413. [Google Scholar] [CrossRef]
- Zaheer, M.; Patel, N.; Hu, A.P. Parallel tuned contactless power pickup using saturable core reactor. In Proceedings of the 2010 IEEE International Conference on Sustainable Energy Technologies (ICSET), Kandy, Sri Lanka, 6–9 December 2010; pp. 1–6. [Google Scholar]
- Si, P.; Hu, A.; Malpas, S.; Budgett, D. Switching Frequency Analysis of Dynamically Detuned ICPT Power Pick-ups. In Proceedings of the 2006 International Conference on Power System Technology, Chongqing, China, 22–26 October 2006; pp. 1–8. [Google Scholar]
- Saad, M.; Bou-Balust, E.; Alarcon, E. Switch-mode gyrator-based emulated inductor enabling self-tunability in WPT receivers. In Proceedings of the 2017 IEEE International Symposium on Circuits and Systems (ISCAS), Baltimore, MD, USA, 28–31 May 2017; pp. 1–4. [Google Scholar]
- Saad, M.; Martinéz-García, H.; Alou, P.; Alarcón, E. A PLL Control for Self-Tuning of Parallel Wireless Power Transfer Receivers Utilizing Switch-Mode Gyrator Emulated Inductors. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE 2017 ECCE Europe), Warsaw, Poland, 11–14 September 2017; pp. 1–10. [Google Scholar]
- Keeling, N.A.; Covic, G.A.; Boys, J.T. A unity-power-factor IPT pickup for high-power applications. IEEE Trans. Ind. Electron. 2010, 57, 744–751. [Google Scholar] [CrossRef]
- Hu, A.P.; Hussmann, S. Improved power flow control for contactless moving sensor applications. IEEE Power Electron. Lett. 2004, 2, 135–138. [Google Scholar] [CrossRef]
- Tellegen, D.H. The Gyrator, a New Electric Network Element. Philips Res. Rep. 1948, 3, 81–101. [Google Scholar]
- Hu, F.; Mouthaan, K. A high-selectivity active bandpass filter using gyrator based resonators in 0.13-μm CMOS. In Proceedings of the 2014 IEEE International Wireless Symposium, Xi’an, China, 24–26 March 2014; pp. 1–4. [Google Scholar]
- Andriesei, C.; Goras, L. On frequency and quality factor independent tuning possibilities for rf band-pass filters with simulated inductors. Rom. J. Inf. Sci. Technol. 2008, 11, 367–382. [Google Scholar]
- Casson, A.J.; Rodriguez-Villegas, E. A Review and Modern Approach to LC Ladder Synthesis. J. Low Power Electron. Appl. 2011, 1, 20–44. [Google Scholar] [CrossRef]
- Black, G.G.A.; Friedmann, R.T.; Sedra, A.S. Gyrator implementation with integrable current conveyors. IEEE J. Solid-State Circ. 1971, 6, 396–399. [Google Scholar] [CrossRef]
- Singer, S. Loss-free gyrator realization. IEEE Trans. Circ. Syst. 1988, 35, 26–34. [Google Scholar] [CrossRef]
- Singer, S. Gyrators Application in Power Processing Circuits. IEEE Trans. Ind. Electron. 1987, IE-34, 313–318. [Google Scholar] [CrossRef]
- Ehsani, M.; Husain, I.; Bilgic, M.O. Power converters as natural gyrators. IEEE Trans. Circ. Syst. I Fundam. Theory Appl. 1993, 40, 946–949. [Google Scholar] [CrossRef]
- Zeltser, I.; Ben-Yaakov, S. Modeling, analysis and simulation of ‘AC inductor’ based converters. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 2128–2134. [Google Scholar]
- Saad, M.; Egidos, N.; Bou-Balust, E.; Alarcon, E. On tunable switch-mode reactive networks: A gyrator-based resonator emulation. In Proceedings of the 2016 IEEE International Symposium on Circuits and Systems (ISCAS), Montréal, QC, Canada, 22–25 May 2016; pp. 642–645. [Google Scholar]
- Saad, M.; Alarcon, E. Tunable switch-mode emulated inductive elements for enhanced power converter miniaturization. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 1184–1189. [Google Scholar]
- Kheraluwala, M.H.; Gascoigne, R.W.; Divan, D.M.; Baumann, E.D. Performance Characterization of a High-Power Dual Active Bridge dc-to-dc Converter. IEEE Trans. Ind. Appl. 1992, 28, 1294–1301. [Google Scholar] [CrossRef]
- Shmilovitz, D. Loss-free complex impedance network elements. IEEE Trans. Circ. Syst. I Regul. Pap. 2006, 53, 704–711. [Google Scholar] [CrossRef]
- Sridhar, A.R.P.A.; Weise, N. DC ripple current rejection in a bidirectional SiC single-phase AC-DC converter for V2G application. In Proceedings of the 2015 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 14–17 June 2015. [Google Scholar]
- Qin, H.; Kimball, J.W. Ac-ac dual active bridge converter for solid state transformer. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 3039–3044. [Google Scholar]
- Di Capua, G.; Femia, N.; Lisi, G. Impact of losses and mismatches on power and efficiency of Wireless Power Transfer Systems with controlled secondary-side rectifier. Integr. VLSI J. 2016, 55, 384–392. [Google Scholar] [CrossRef]
- Qin, H.; Kimball, J.W. A comparative efficiency study of silicon-based solid state transformers. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 1458–1463. [Google Scholar]
- Lee, W.-S.; Lee, H.-L.; Oh, K.-S.; Yu, J.-W. Switchable Distance-Based Impedance Matching Networks for a Tunable HF System. Prog. Electromagn. Res. 2012, 128, 19–34. [Google Scholar] [CrossRef]
- Duong, T.; Lee, J.-W. A Dynamically Adaptable Impedance-Matching System for Midrange Wireless Power Transfer with Misalignment. Energies 2015, 8, 7593–7617. [Google Scholar] [CrossRef]
- Huang, C.-Y.; James, J.E.; Covic, G.A. Design Considerations for Variable Coupling Lumped Coil Systems. IEEE Trans. Power Electron. 2015, 30, 680–689. [Google Scholar] [CrossRef]
- Kissin, M.; Huang, C.-Y.; Covic, G.A.; Boys, J.T. Detection of the tuned point of a fixed-frequency LCL resonant power supply. IEEE Trans. Power Electron. 2009, 24, 1140–1143. [Google Scholar] [CrossRef]
- Hsu, J.-U.W.; Hu, A.P. Determining the variable inductance range for an LCL wireless power pick-up. In Proceedings of the 2007 IEEE Conference on Electron Devices and Solid-State Circuits, San Francisco, CA, USA, 11–15 February 2007; pp. 489–492. [Google Scholar]
- Hsu, J.-U.W.; Hu, A.P.; Swain, A. A Wireless Power Pickup Based on Directional Tuning Control of Magnetic Amplifier. IEEE Trans. Ind. Electron. 2009, 56, 2771–2781. [Google Scholar] [CrossRef]
- Li, S.; Li, W.; Deng, J.; Nguyen, T.D.; Mi, C.C. A Double-Sided LCC Compensation Network and Its Tuning Method for Wireless Power Transfer. IEEE Trans. Veh. Technol. 2015, 64, 2261–2273. [Google Scholar] [CrossRef]
- Vilamitjana, E.R. Chaos in Switching Converters for Power Management; Springer: New York, NY, USA, 2014. [Google Scholar]
- Abdolkhani, A. Fundamentals of Inductively Coupled Wireless Power Transfer Systems. In Wireless Power Transfer–Fundamentals and Technologies; InTech: London, UK, 2016; pp. 3–26. [Google Scholar]
- Li, S.; Mi, C.C. Wireless power transfer for electric vehicle applications. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 4–17. [Google Scholar]
- Covic, G.A.; Boys, J.T.; Tam, A.M.W.; Peng, J.C.H. Self tuning pick-ups for inductive power transfer. In Proceedings of the Power Electronics Specialists Conference, PESC 2008, Rhodes, Greece, 15–19 June 2008; pp. 3489–3494. [Google Scholar]
- Cervera, A.; Mordechai Peretz, M. Resonant switched-capacitor voltage regulator with ideal transient response. IEEE Trans. Power Electron. 2015, 30, 4943–4951. [Google Scholar] [CrossRef]

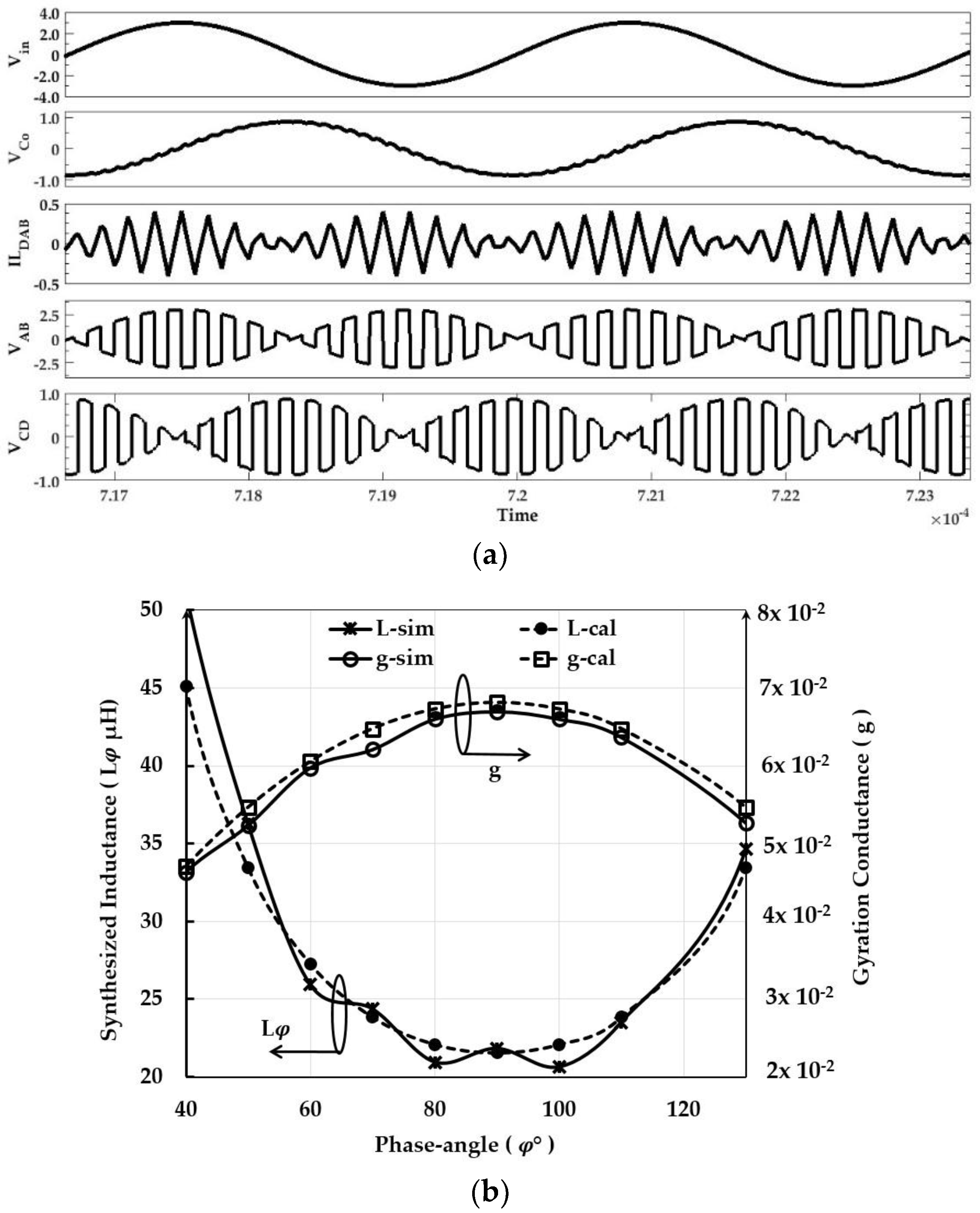
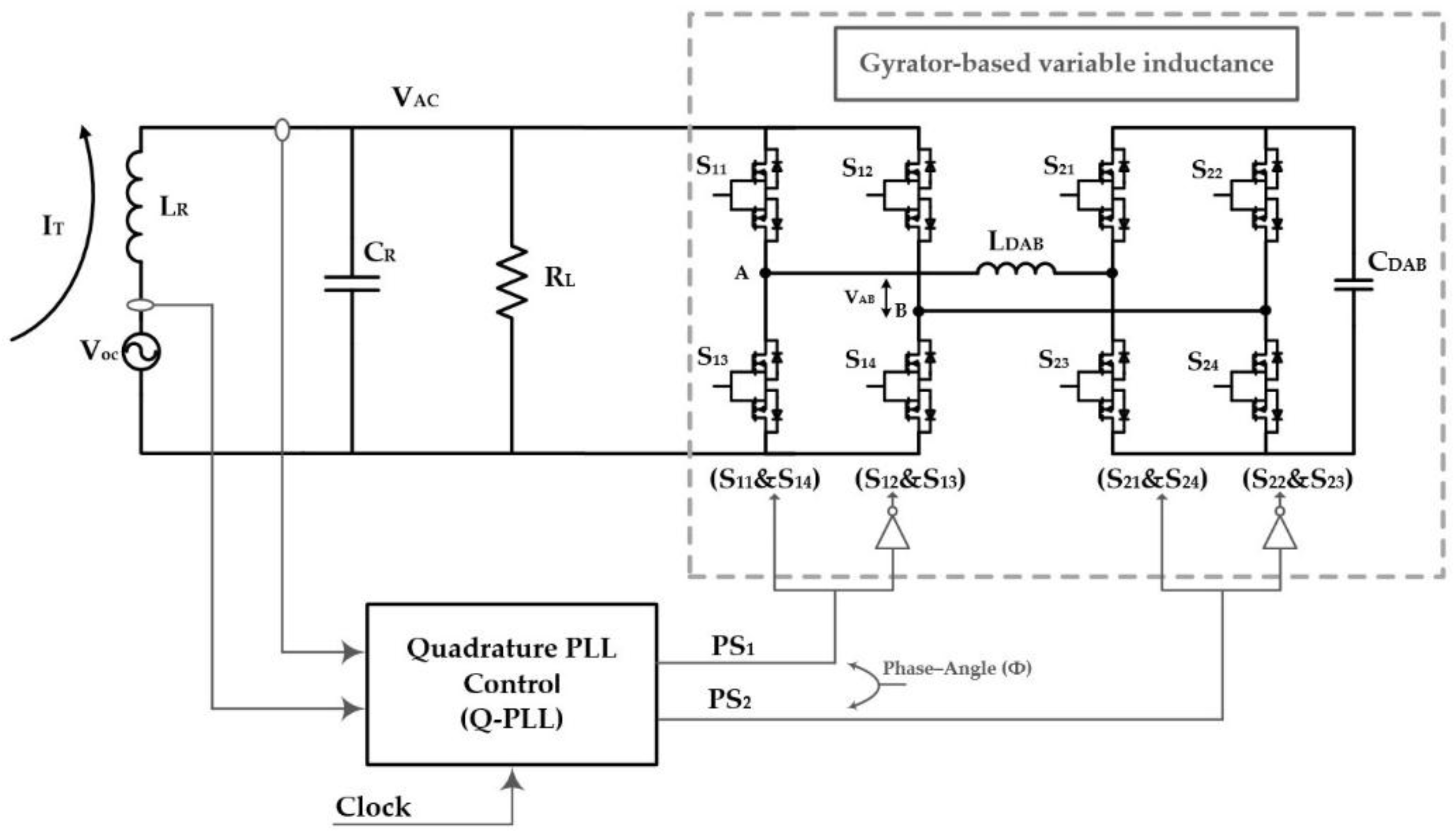
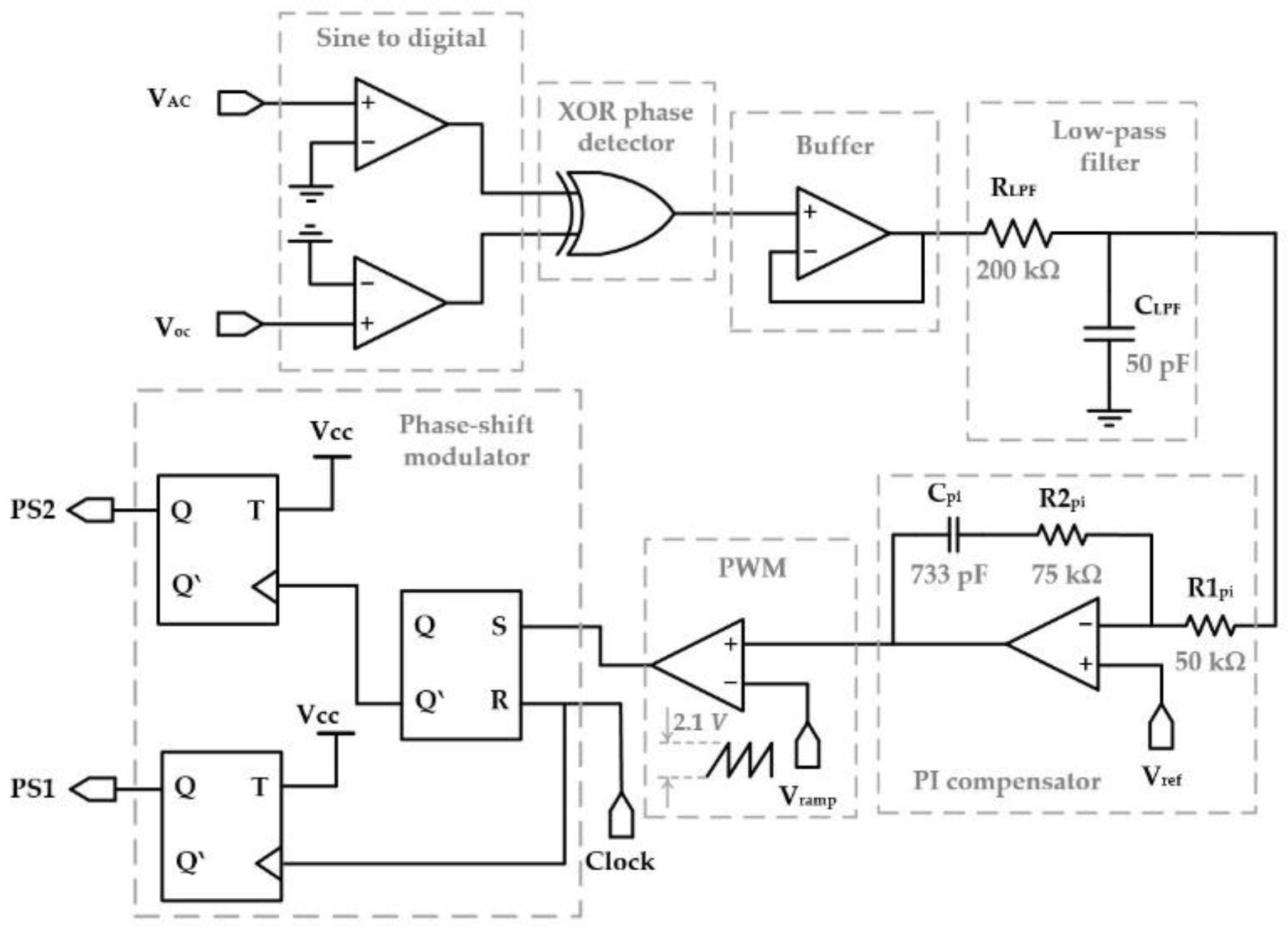
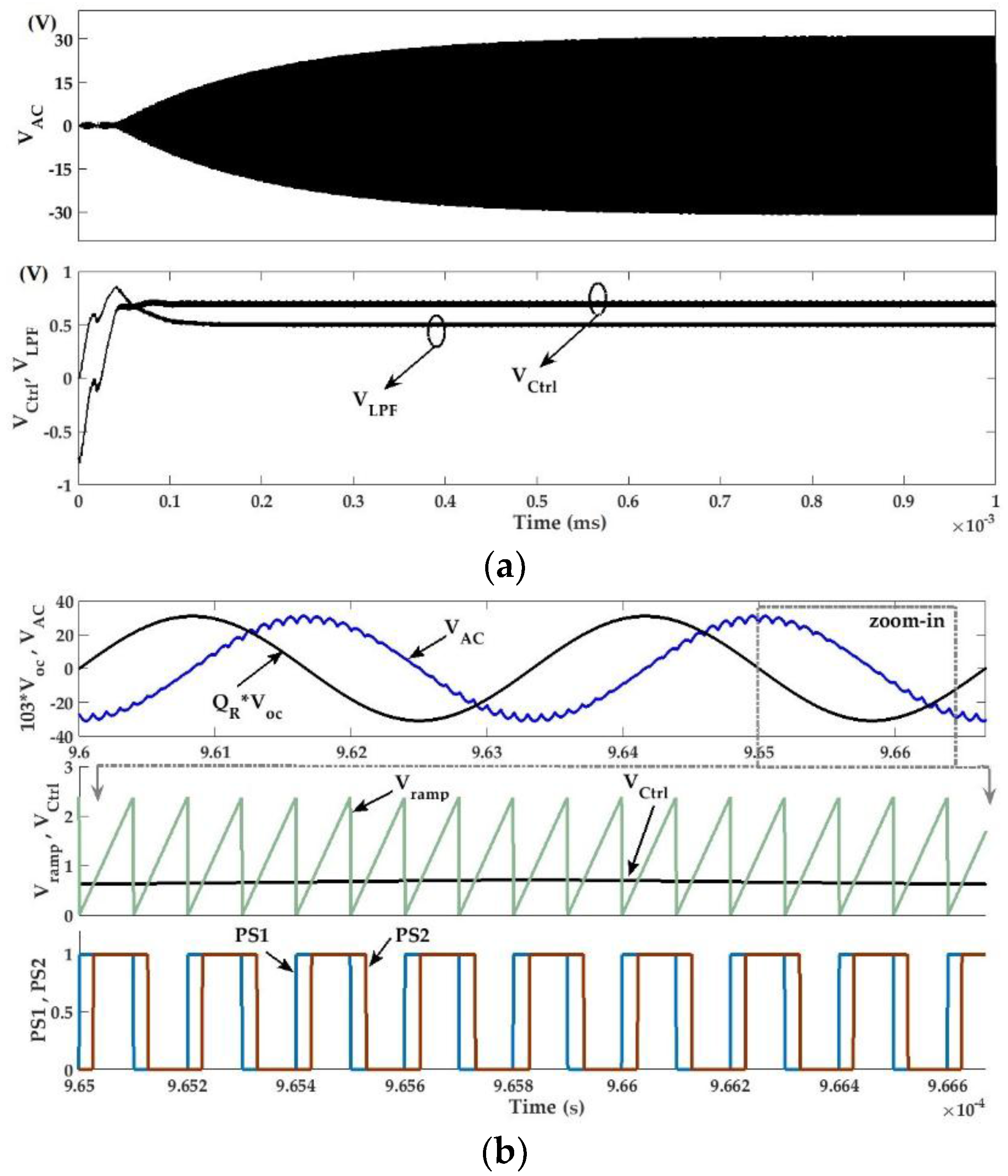
| Parameter | fT | fDAB | LDAB | CDAB |
|---|---|---|---|---|
| Value | 300 kHz | 5 MHz | 367 nH | 100 nF |
| Parameter | Value |
|---|---|
| WPT link parameters | |
| Vin | 2.12 Vrms |
| fT | 200 kHz |
| LT | 10 μH |
| CT | 63.97 nF |
| M | 447.2 nF (k ≈ 0.1) |
| LR | 2.0 μH |
| CR | 395 nF |
| RL | 200 Ω (nominal) |
| DAB gyrator parameters | |
| fDAB | 1.5 MHz |
| LDAB | 480 nF |
| CDAB | 100 nF |
| Bidirectional-switch RON | 4 mΩ |
| φ | 45° (nominal) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saad, M.; Alarcón, E. Insights into Dynamic Tuning of Magnetic-Resonant Wireless Power Transfer Receivers Based on Switch-Mode Gyrators. Energies 2018, 11, 453. https://doi.org/10.3390/en11020453
Saad M, Alarcón E. Insights into Dynamic Tuning of Magnetic-Resonant Wireless Power Transfer Receivers Based on Switch-Mode Gyrators. Energies. 2018; 11(2):453. https://doi.org/10.3390/en11020453
Chicago/Turabian StyleSaad, Mohamed, and Eduard Alarcón. 2018. "Insights into Dynamic Tuning of Magnetic-Resonant Wireless Power Transfer Receivers Based on Switch-Mode Gyrators" Energies 11, no. 2: 453. https://doi.org/10.3390/en11020453
APA StyleSaad, M., & Alarcón, E. (2018). Insights into Dynamic Tuning of Magnetic-Resonant Wireless Power Transfer Receivers Based on Switch-Mode Gyrators. Energies, 11(2), 453. https://doi.org/10.3390/en11020453




