Stationary-Frame Modeling of VSC Based on Current-Balancing Driven Internal Voltage Motion for Current Control Timescale Dynamic Analysis
Abstract
:1. Introduction
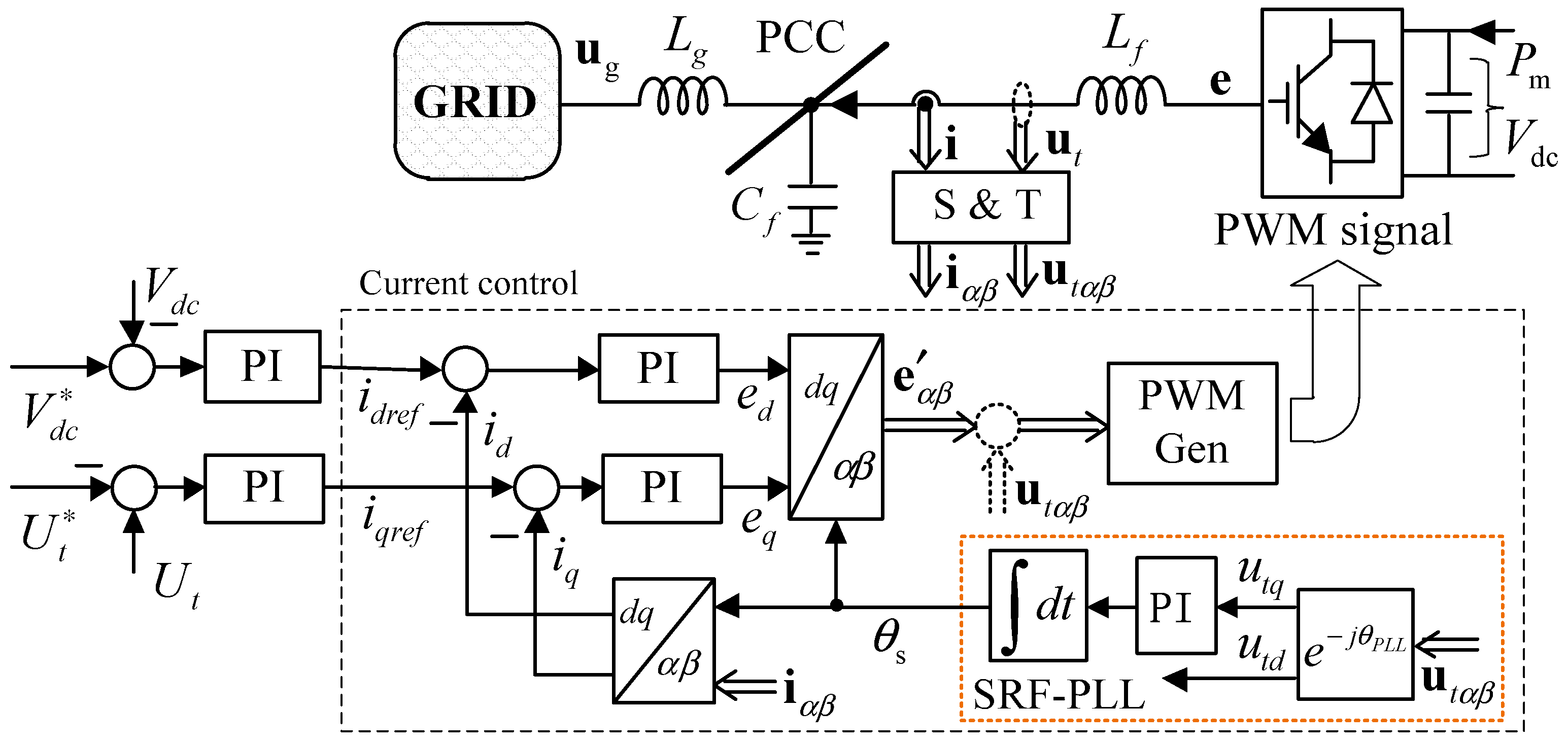
2. Description of VSC Current Control System and Fundamental Concept
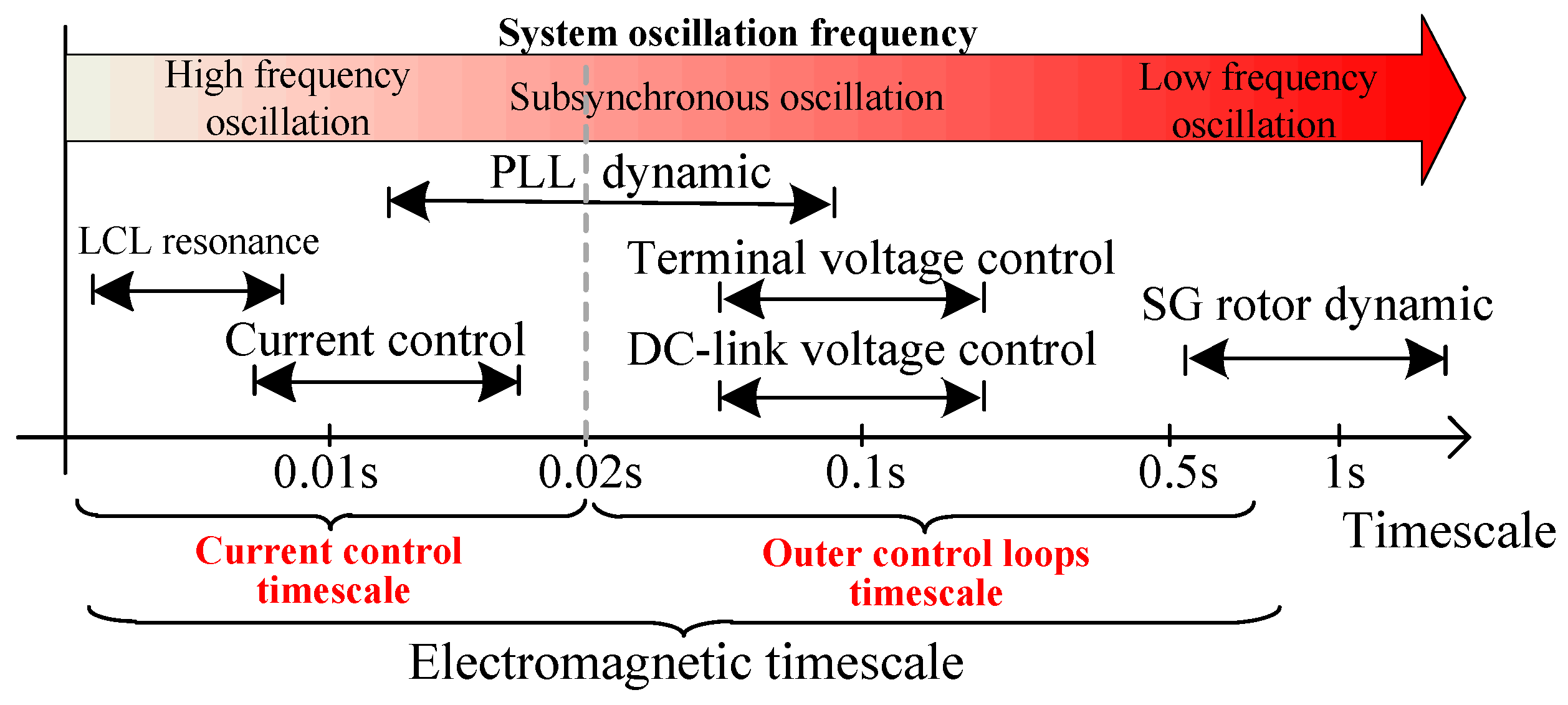
2.1. Definition of Current Control Timescale
2.2. The Internal Voltage of VSCs in Current Control Timescale
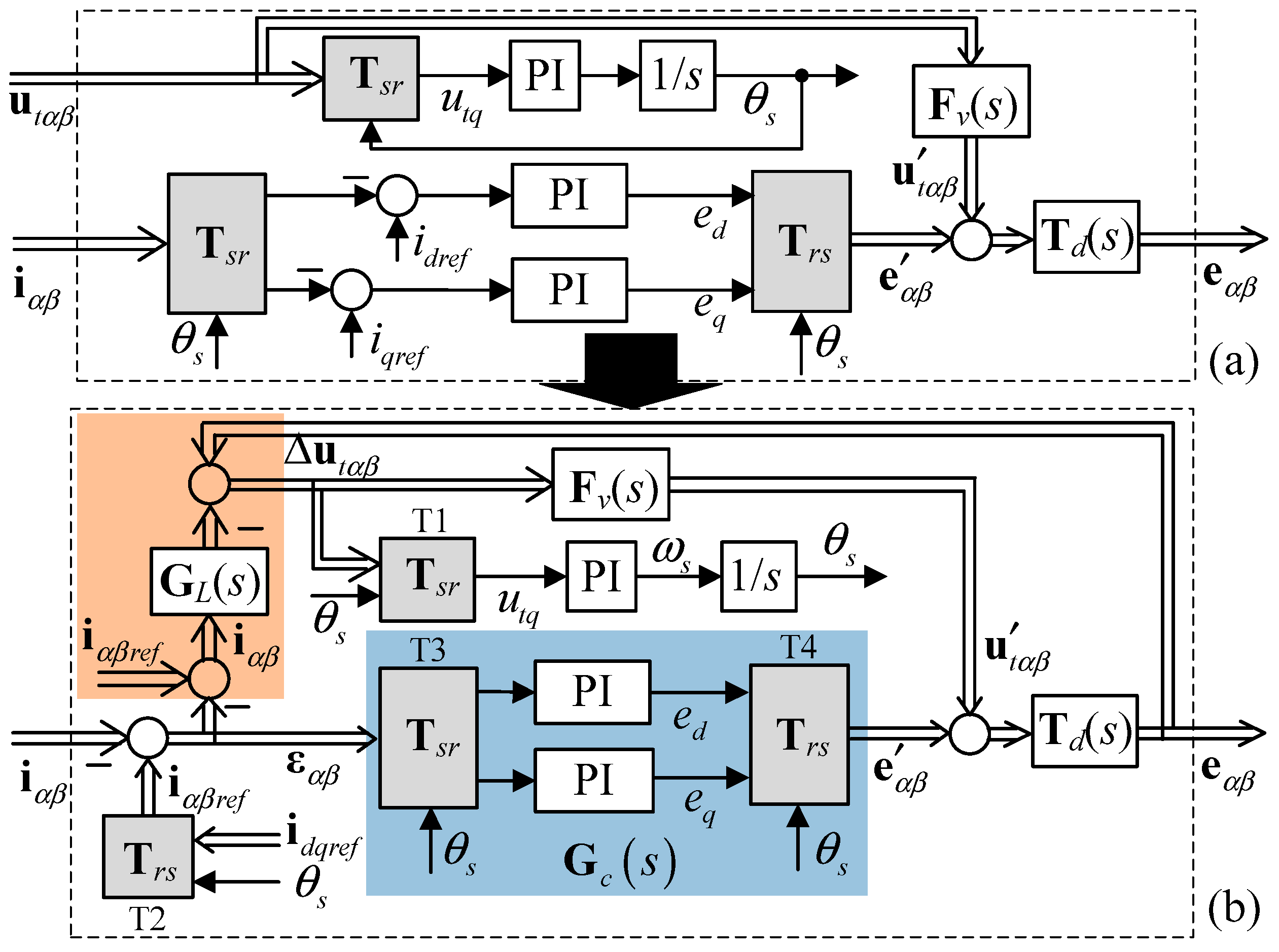
3. Current-Balancing Driven Internal Voltage Motion Model of VSCs in Stationary Frame
3.1. The Modeling of VSCs in Stationary Frame
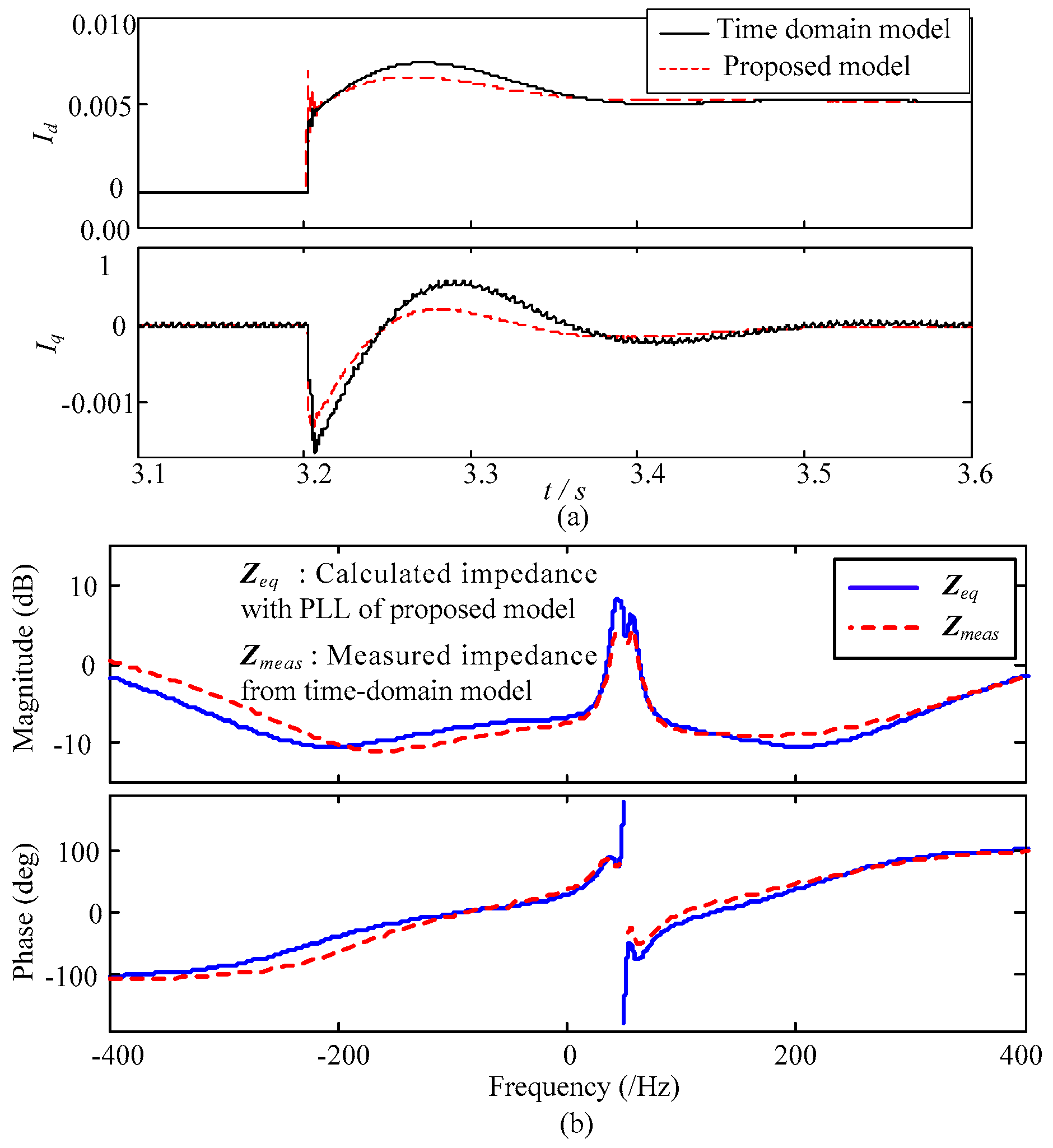
3.2. Verification of the Proposed Model
4. VSC Dynamic Characteristic Analysis in Current Control Timescale
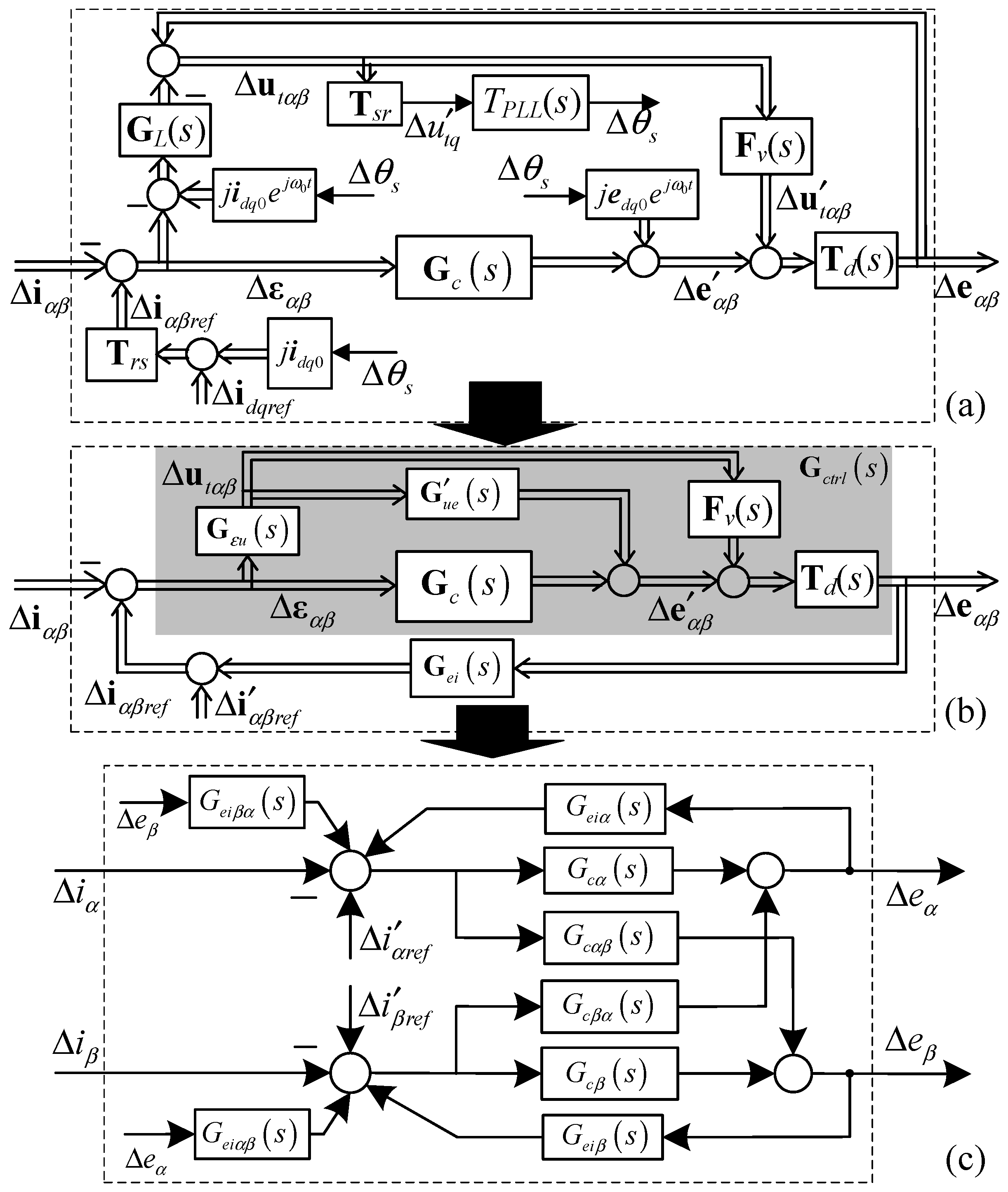
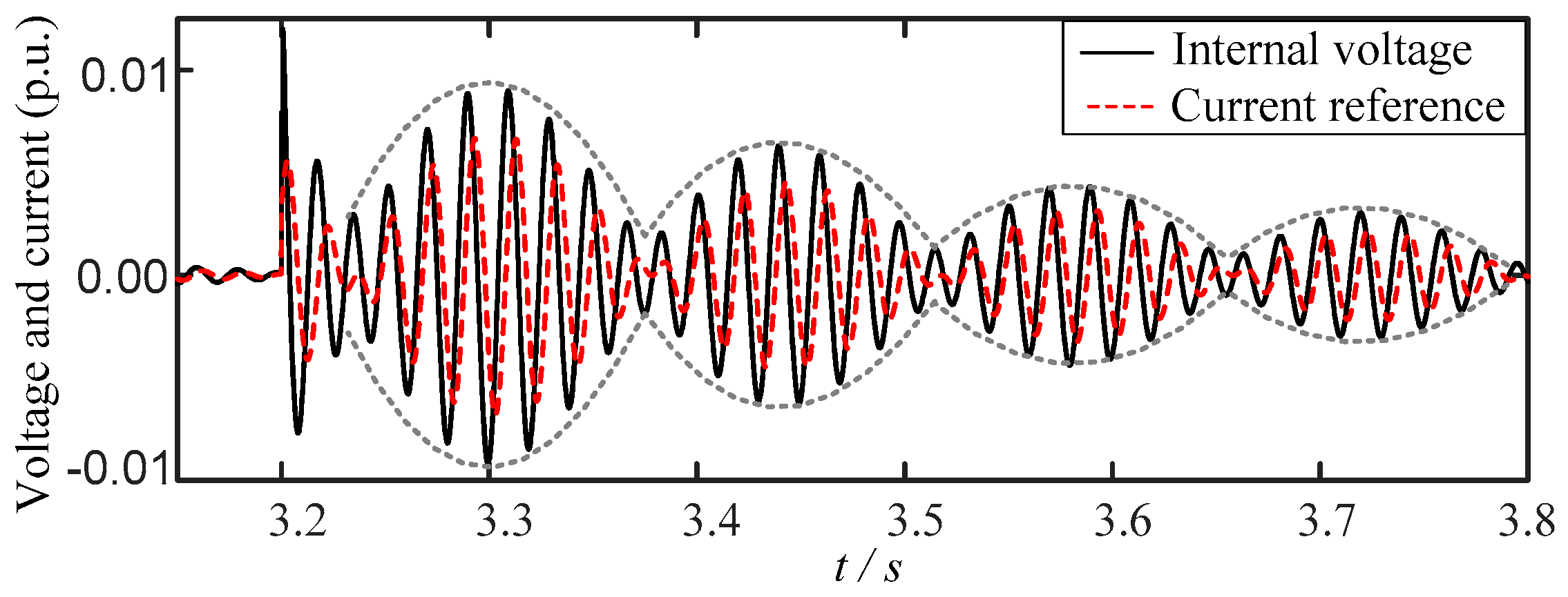
4.1. The VSC Characteristic of Variable Current References in Stationary Frame
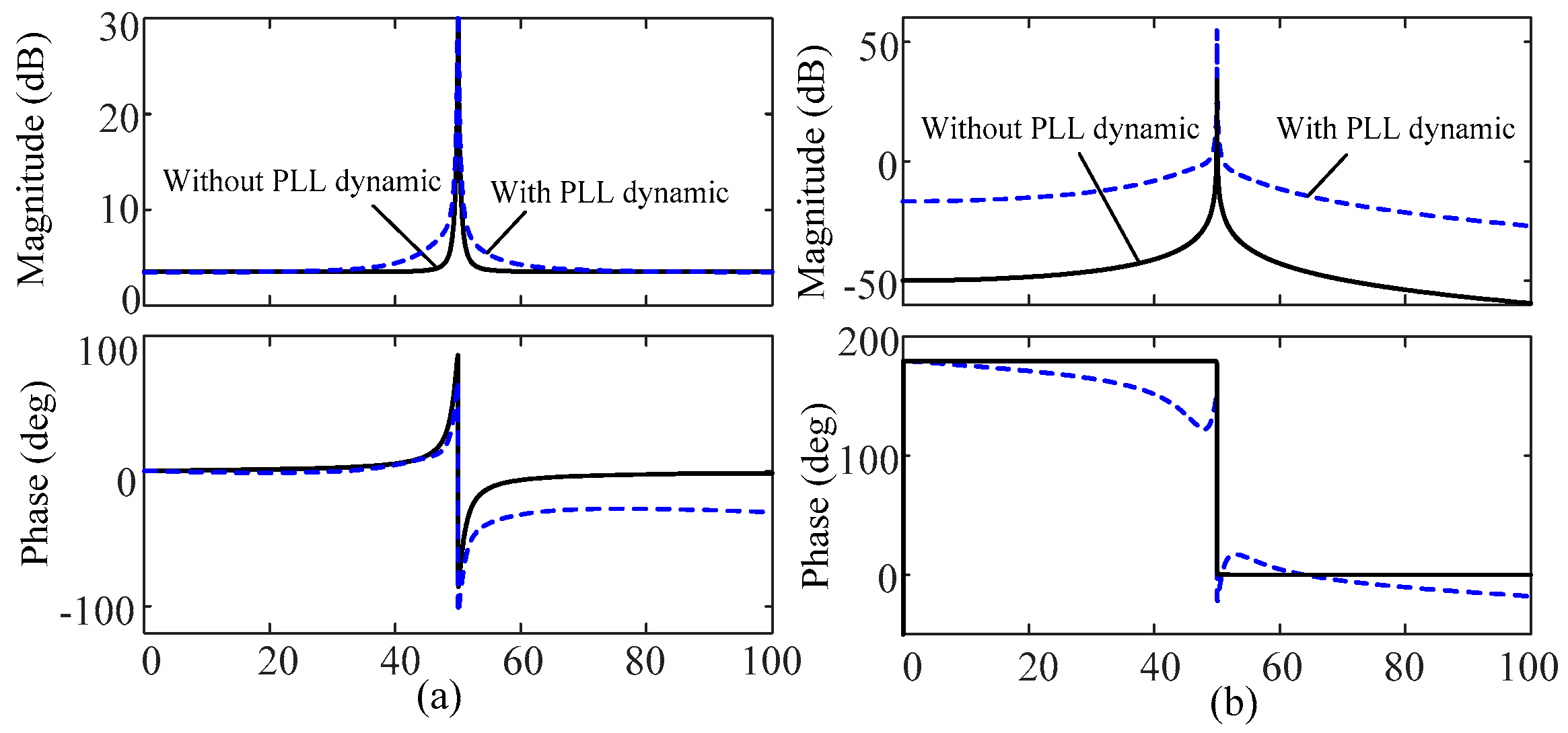
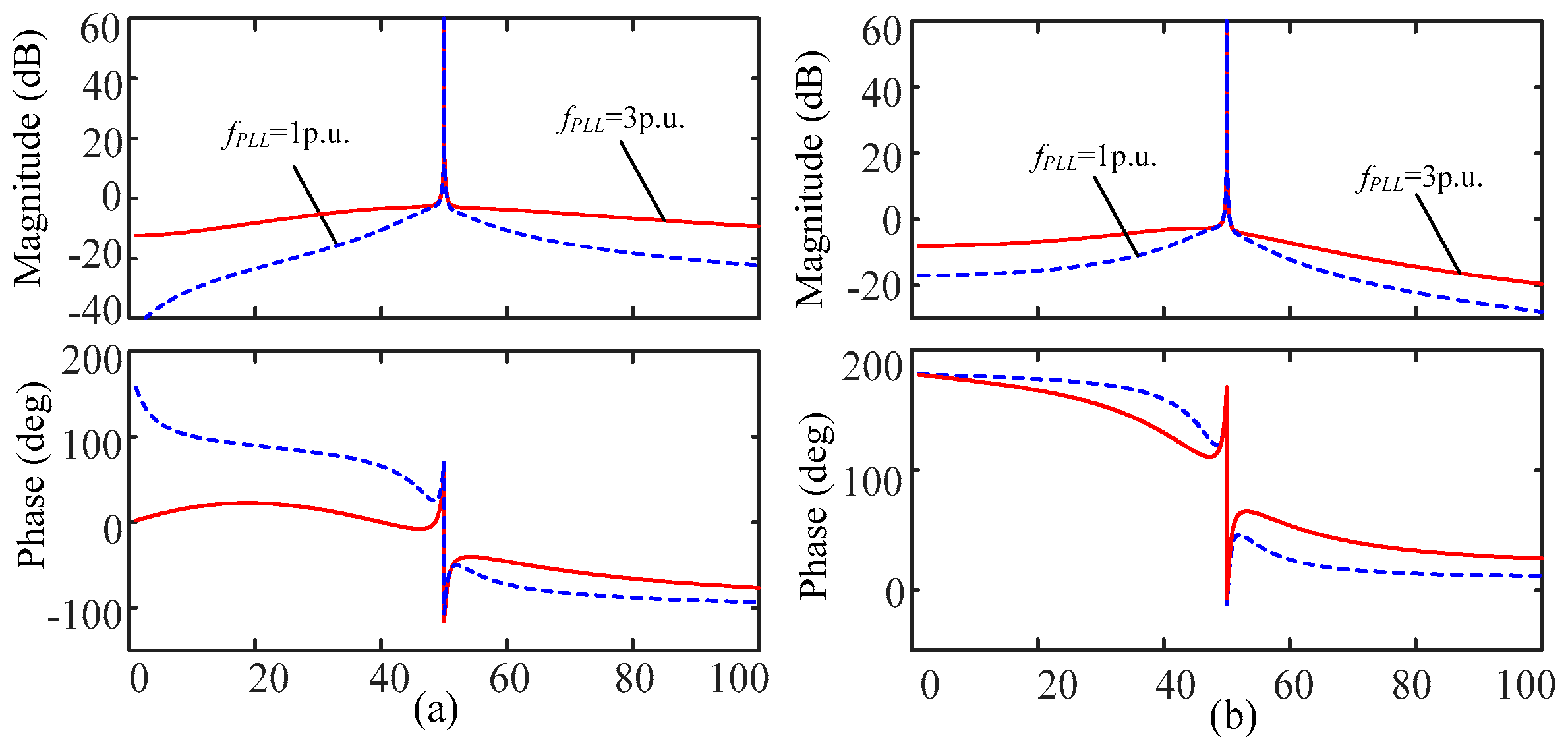
4.2. Control Characteristic of the VSC in Stationary Frame
5. Application of the Proposed Model in Stability Analyses of a Grid-Connected VSC
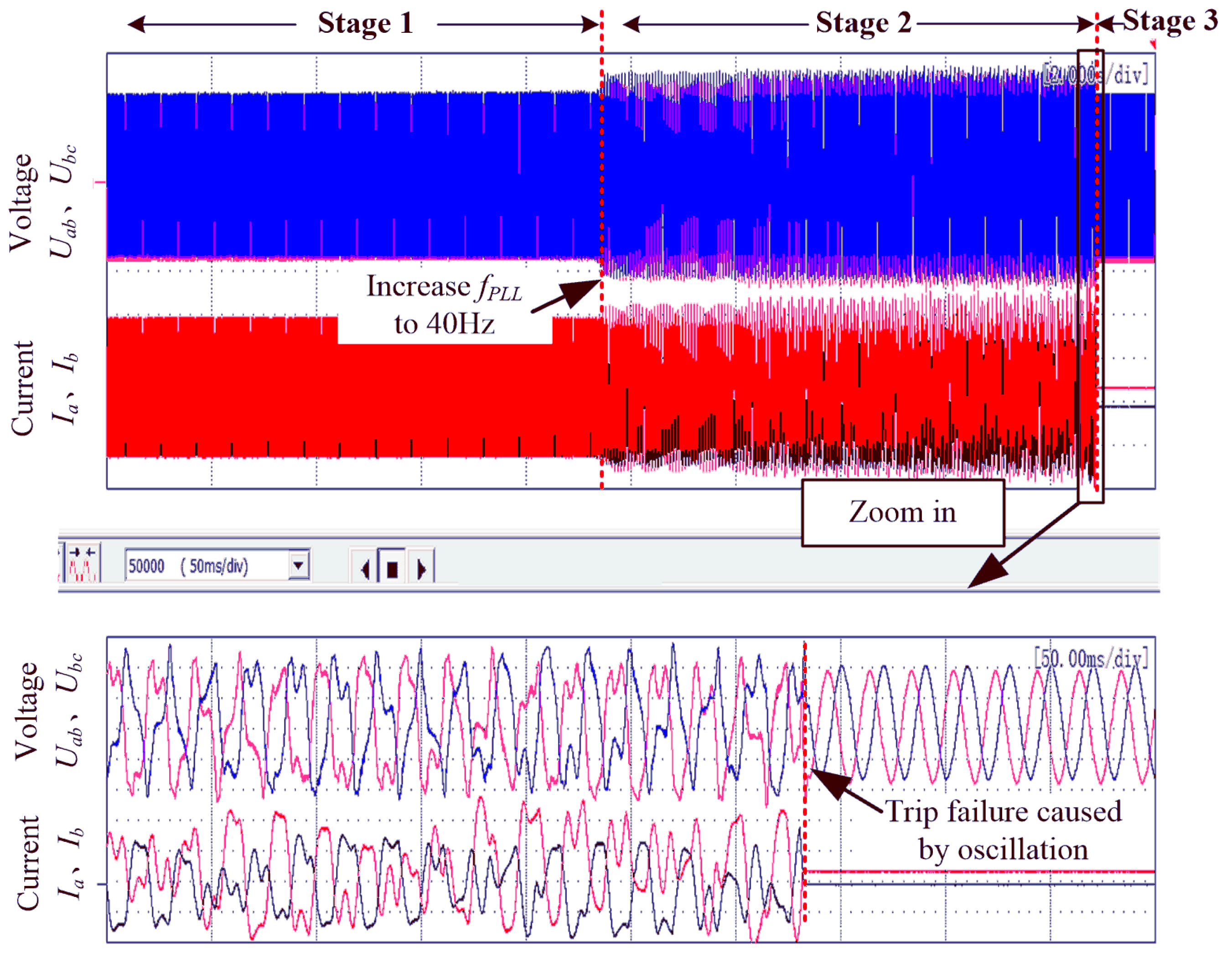
- Stage 1: the system is in a state of stable operation with 10 kW of active power output;
- Stage 2: the PLL bandwidth is changed to 40 Hz; and
- Stage 3: a trip failure caused by oscillations leads to disconnection of the VSC.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Linearization of the Coordinate Transformation

Appendix B. The Expression of Gui+(s), Gui−(s), Gue+(s), and Gue−(s)
References
- Adams, C.; Carter, C.; Huang, S.H. ERCOT experience with Sub-synchronous Control Interaction and proposed remediation. In Proceedings of the IEEE PES Transmission and Distribution Conference and Exposition, Orlando, FL, USA, 7–10 May 2012; pp. 1–5. [Google Scholar]
- Shun-Hsien, H.; Schmall, J.; Conto, J.; Adams, J.; Zhang, Y.; Carter, C. Voltage control challenges on weak grids with high penetration of wind generation: ERCOT experience. In Proceedings of the IEEE PES General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Zhao, M.; Yuan, X.; Hu, J.; Yan, Y. Voltage Dynamics of Current Control Time-Scale in a VSC-Connected Weak Grid. IEEE Trans. Power Syst. 2015, 31, 2925–2937. [Google Scholar] [CrossRef]
- Buchhagen, C.; Rauscher, C.; Menze, A.; Jung, J. BorWin1—First Experiences with harmonic interactions in converter dominated grids. In Proceedings of the International ETG Congress: Die Energiewende—Blueprints for the New Energy Age, Bonn, Germany, 17–18 November 2015; pp. 1–7. [Google Scholar]
- Kroutikova, N.; Hernandez-Aramburo, C.; Green, T. State-space model of grid-connected inverters under current control mode. IET Electr. Power Appl. 2007, 1, 329–338. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Blaabjerg, F.; Chen, Z. Harmonic Instability Assessment Using State-Space Modeling and Participation Analysis in Inverter-Fed Power Systems. IEEE Trans. Ind. Electron. 2017, 64, 806–816. [Google Scholar] [CrossRef]
- Blasko, V.; Kaura, V. A novel control to actively damp resonance in input LC filter of a three-phase voltage source converter. IEEE Trans. Ind. Appl. 1997, 33, 542–550. [Google Scholar] [CrossRef]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values. IEEE Trans. Power Electron. 2006, 21, 263–272. [Google Scholar] [CrossRef]
- Brogan, P. The stability of multiple, high power, active front end voltage sourced converters when connected to wind farm collector systems. In Proceedings of the EPE Wind Energy Chapter Seminar, Stafford, UK, 15–16 April 2010. [Google Scholar]
- Harnefors, L.; Bongiorno, M.; Lundberg, S. Input-Admittance Calculation and Shaping for Controlled Voltage-Source Converters. IEEE Trans. Ind. Electron. 2007, 54, 3323–3334. [Google Scholar] [CrossRef]
- Sun, J. Impedance-Based Stability Criterion for Grid-Connected Inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Wu, W. Modeling and Analysis of Harmonic Stability in an AC Power-Electronics-Based Power System. IEEE Trans. Power Electron. 2014, 29, 6421–6432. [Google Scholar] [CrossRef]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Analysis of D-Q Small-Signal Impedance of Grid-Tied Inverters. IEEE Trans. Power Electron. 2016, 31, 675–687. [Google Scholar] [CrossRef]
- Yuan, H.; Yuan, X.; Hu, J. Modeling of Grid-Connected VSCs for Power System Small-Signal Stability Analysis in DC-Link Voltage Control Timescale. IEEE Trans. Power Syst. 2017, 32, 3981–3991. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- He, W.; Yuan, X.; Hu, J. Inertia Provision and Estimation of PLL-Based DFIG Wind Turbines. IEEE Trans. Power Syst. 2017, 32, 510–521. [Google Scholar] [CrossRef]
- Sun, J. Small-Signal Methods for AC Distributed Power Systems—A Review. IEEE Trans. Power Electron. 2009, 24, 2545–2554. [Google Scholar]
- Dalton, P.M.; Gosbell, V.J. A study of induction motor current control using the complex number representation. In Proceedings of the Conference Record on IEEE Industry Applications Society Annual Meeting, San Diego, CA, USA, 1–5 October 1989; Volume 1, pp. 355–361. [Google Scholar]
- Harnefors, L. Modeling of Three-Phase Dynamic Systems Using Complex Transfer Functions and Transfer Matrices. IEEE Trans. Ind. Electron. 2007, 54, 2239–2248. [Google Scholar] [CrossRef]
- Sun, J.; Bing, Z.H.; Karimi, K.J. Input Impedance Modeling of Multipulse Rectifiers by Harmonic Linearization. IEEE Trans. Power Electron. 2009, 24, 2812–2820. [Google Scholar]
- Cespedes, M.; Sun, J. Impedance Modeling and Analysis of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Electron. 2014, 29, 1254–1261. [Google Scholar] [CrossRef]
- Martin, K.W. Complex signal processing is not complex. IEEE Trans. Circuits Syst. I Regul. Pap. 2004, 51, 1823–1836. [Google Scholar] [CrossRef]
- Yuan, X.; Merk, W.; Stemmler, H.; Allmeling, J. Stationary-frame generalized integrators for current control of active power filters with zero steady-state error for current harmonics of concern under unbalanced and distorted operating conditions. IEEE Trans. Ind. Appl. 2002, 38, 523–532. [Google Scholar] [CrossRef]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Zhou, J.Z.; Ding, H.; Fan, S.; Zhang, Y.; Gole, A.M. Impact of Short-Circuit Ratio and Phase-Locked-Loop Parameters on the Small-Signal Behavior of a VSC-HVDC Converter. IEEE Trans. Power Deliv. 2014, 29, 2287–2296. [Google Scholar] [CrossRef]
- Wen, B.; Dong, D.; Boroyevich, D.; Mattavelli, P.; Burgos, R.; Shen, Z. Impedance-Based Analysis of Grid-Synchronization Stability for Three-Phase Paralleled Converters. IEEE Trans. Power Electron. 2016, 31, 26–38. [Google Scholar] [CrossRef]
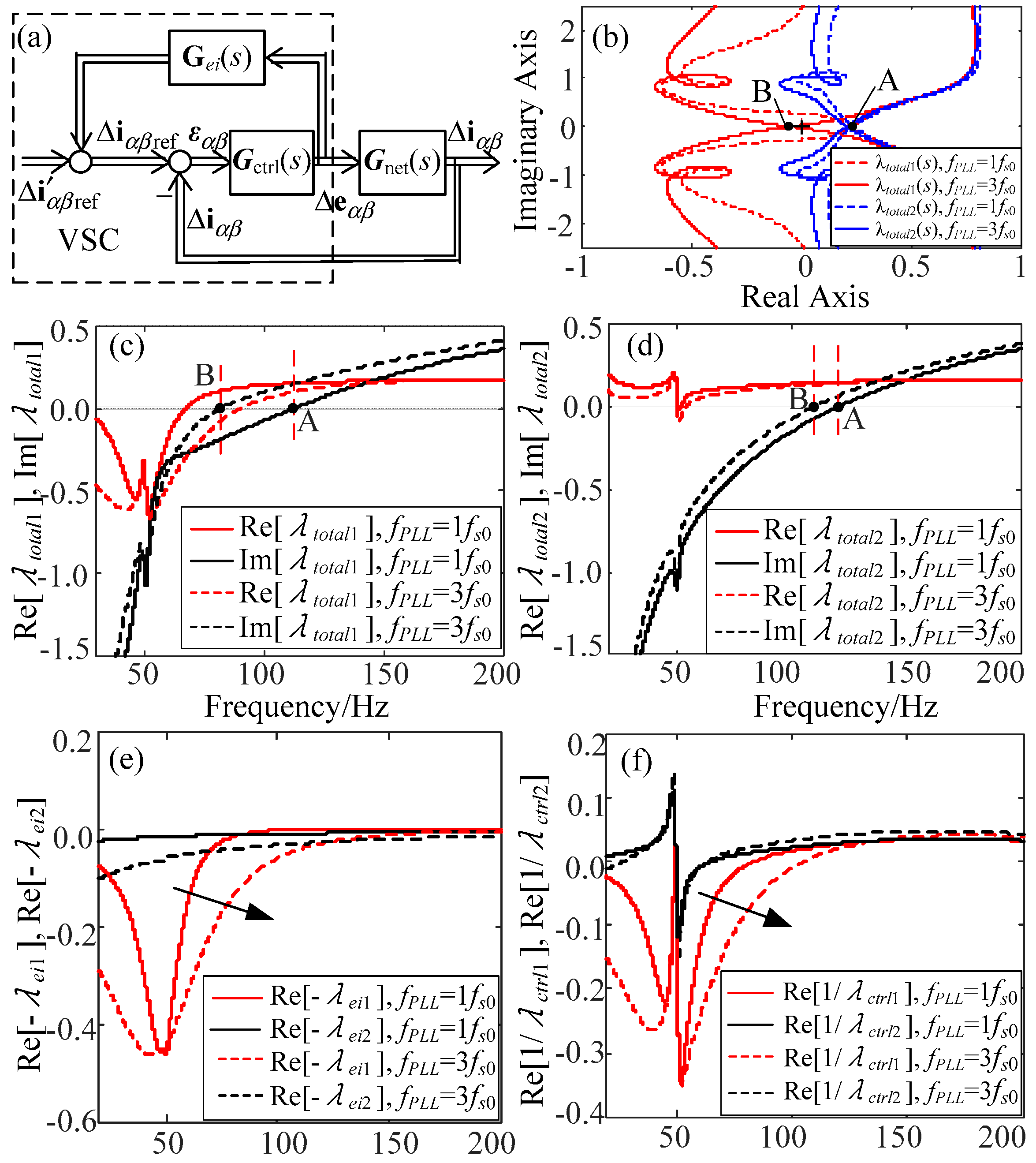
| Symbol | Quantity | Values (p.u. a) |
|---|---|---|
| Lg | grid equivalent inductor | 0.667 |
| Lf | filter inductor | 0.15 |
| Cf | filter capacitor | 0.17 |
| Rd | damping resistor | 1.00 |
| kpc | proportionality coefficient of current controller | 1 |
| kic | integral coefficient of current controller | 20.0 |
| kps | initial proportionality coefficient of SFR-PLL | 0.194 |
| kis | initial integral coefficient of SFR-PLL | 4.456 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Y.; Yuan, X.; Hu, J. Stationary-Frame Modeling of VSC Based on Current-Balancing Driven Internal Voltage Motion for Current Control Timescale Dynamic Analysis. Energies 2018, 11, 374. https://doi.org/10.3390/en11020374
Yan Y, Yuan X, Hu J. Stationary-Frame Modeling of VSC Based on Current-Balancing Driven Internal Voltage Motion for Current Control Timescale Dynamic Analysis. Energies. 2018; 11(2):374. https://doi.org/10.3390/en11020374
Chicago/Turabian StyleYan, Yabing, Xiaoming Yuan, and Jiabing Hu. 2018. "Stationary-Frame Modeling of VSC Based on Current-Balancing Driven Internal Voltage Motion for Current Control Timescale Dynamic Analysis" Energies 11, no. 2: 374. https://doi.org/10.3390/en11020374
APA StyleYan, Y., Yuan, X., & Hu, J. (2018). Stationary-Frame Modeling of VSC Based on Current-Balancing Driven Internal Voltage Motion for Current Control Timescale Dynamic Analysis. Energies, 11(2), 374. https://doi.org/10.3390/en11020374




