An Investigation of Parallel Post-Laminar Flow through Coarse Granular Porous Media with the Wilkins Equation
Abstract
:1. Introduction
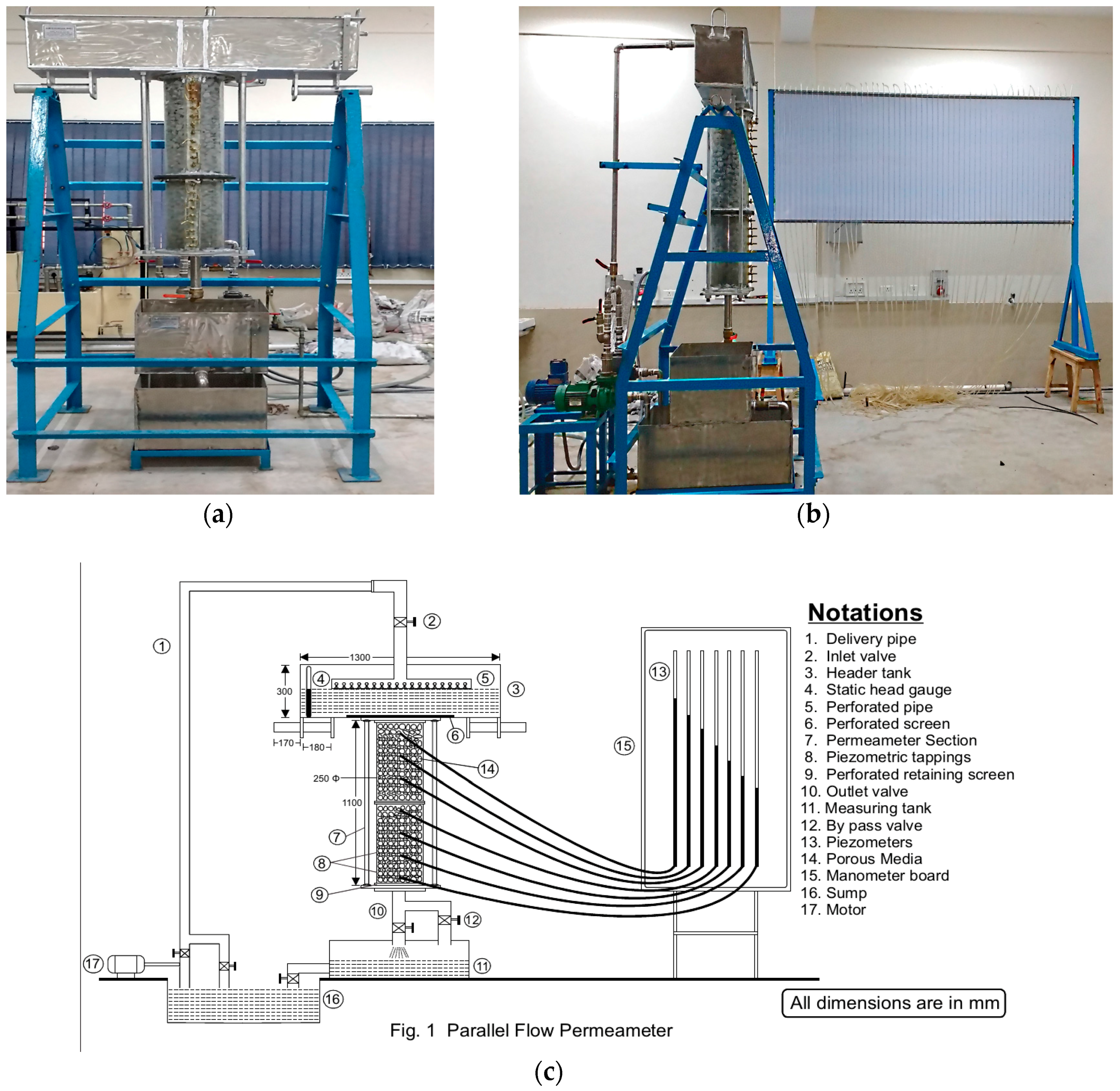
2. Experiments and Methodology
3. Correction Factors
3.1. Wall Correction
3.2. Tortuosity Correction
3.3. Porosity Correction
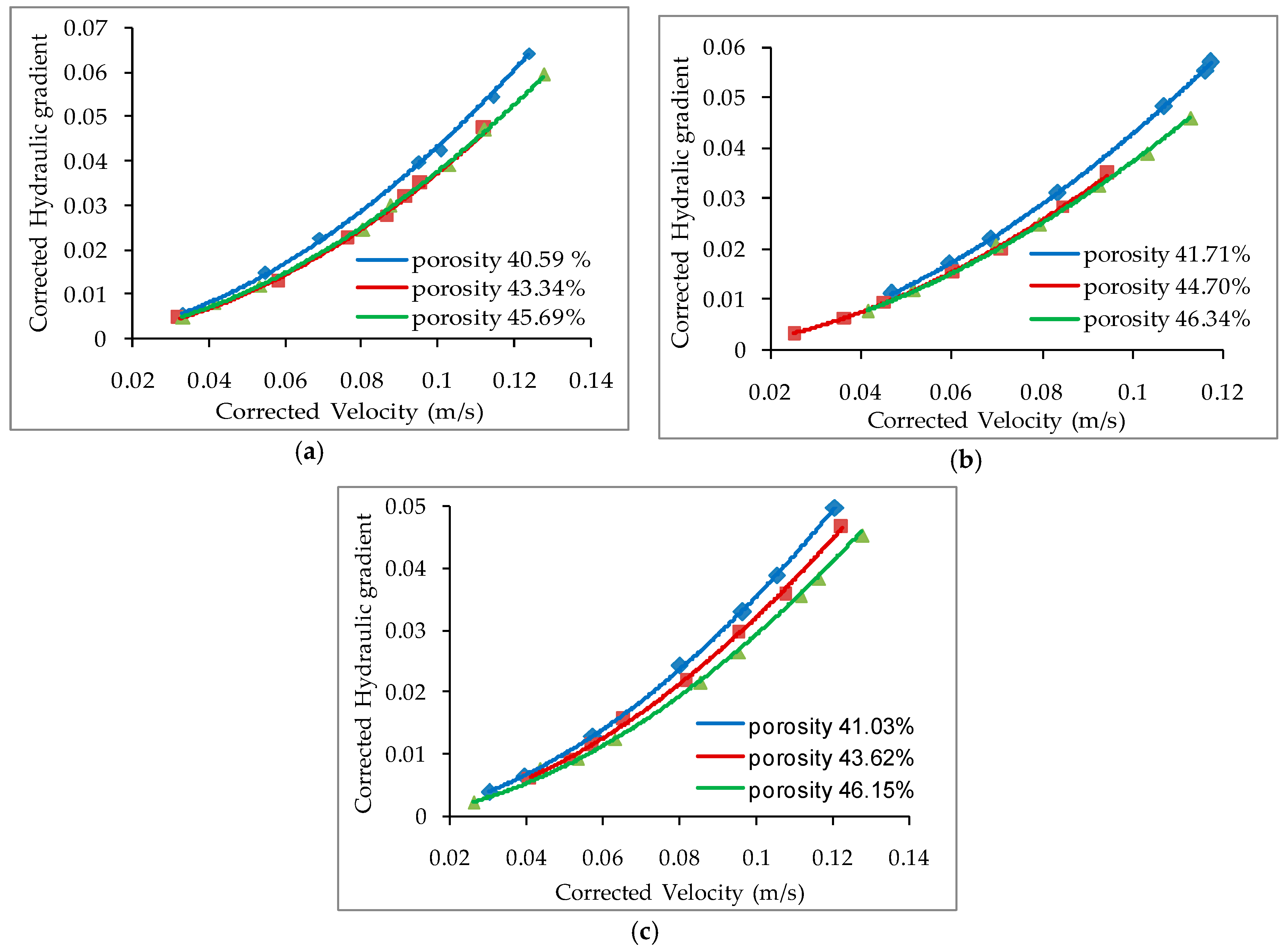
4. Data Analysis
5. The Behavior of the Wilkins Coefficients with Independently Varying Media Size and Porosity
6. Numerical Modelling
6.1. Turbulence Modelling
6.2. Model Description
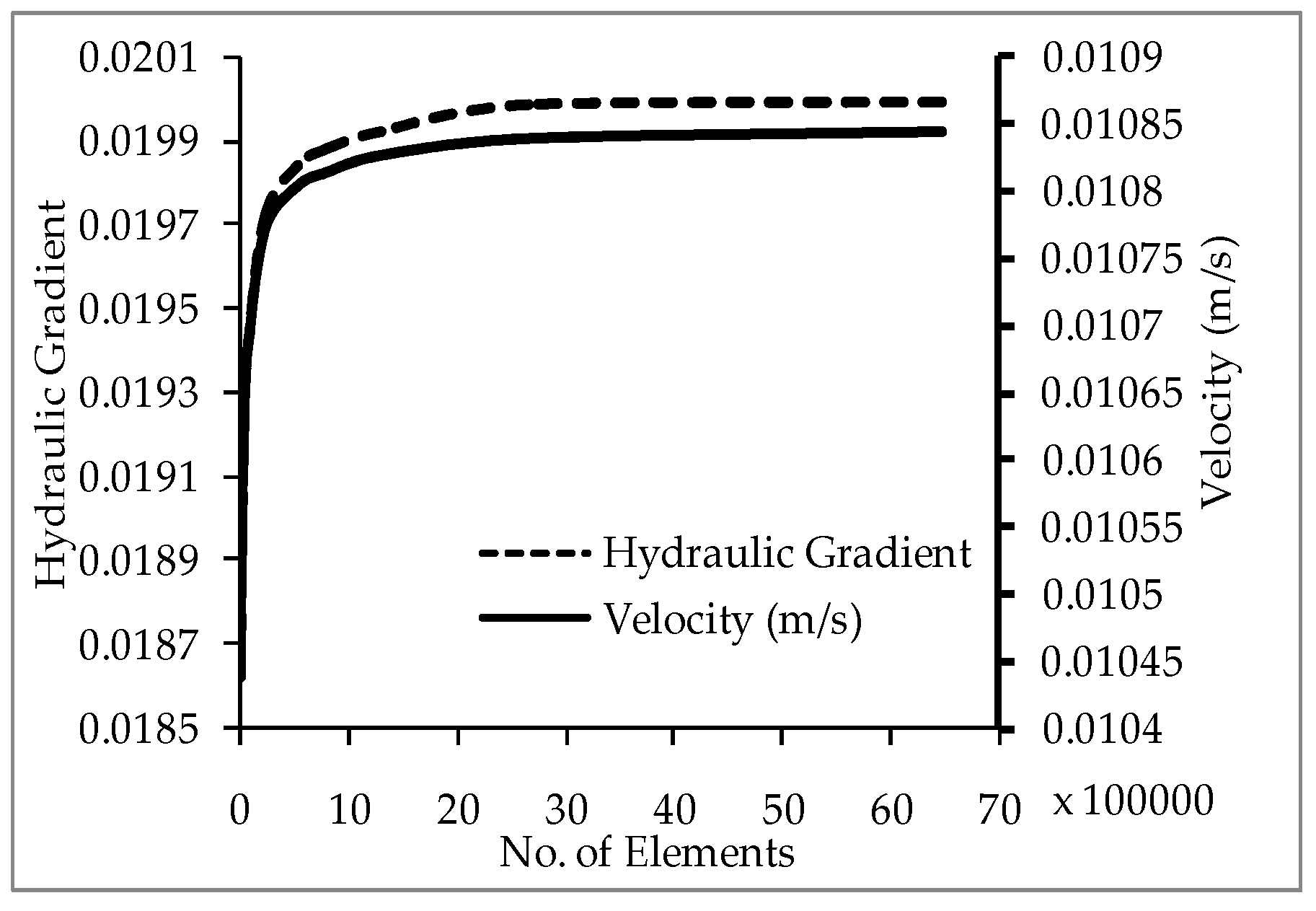
6.3. Meshing
6.4. Boundary Conditions
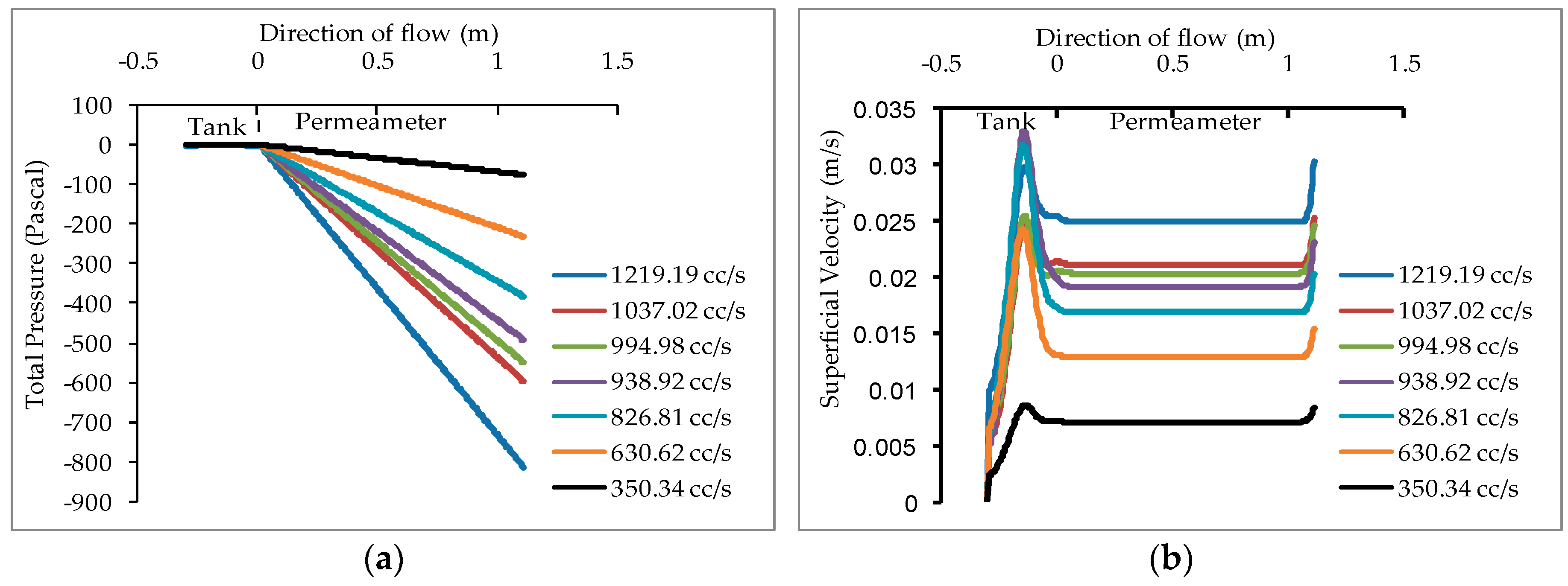
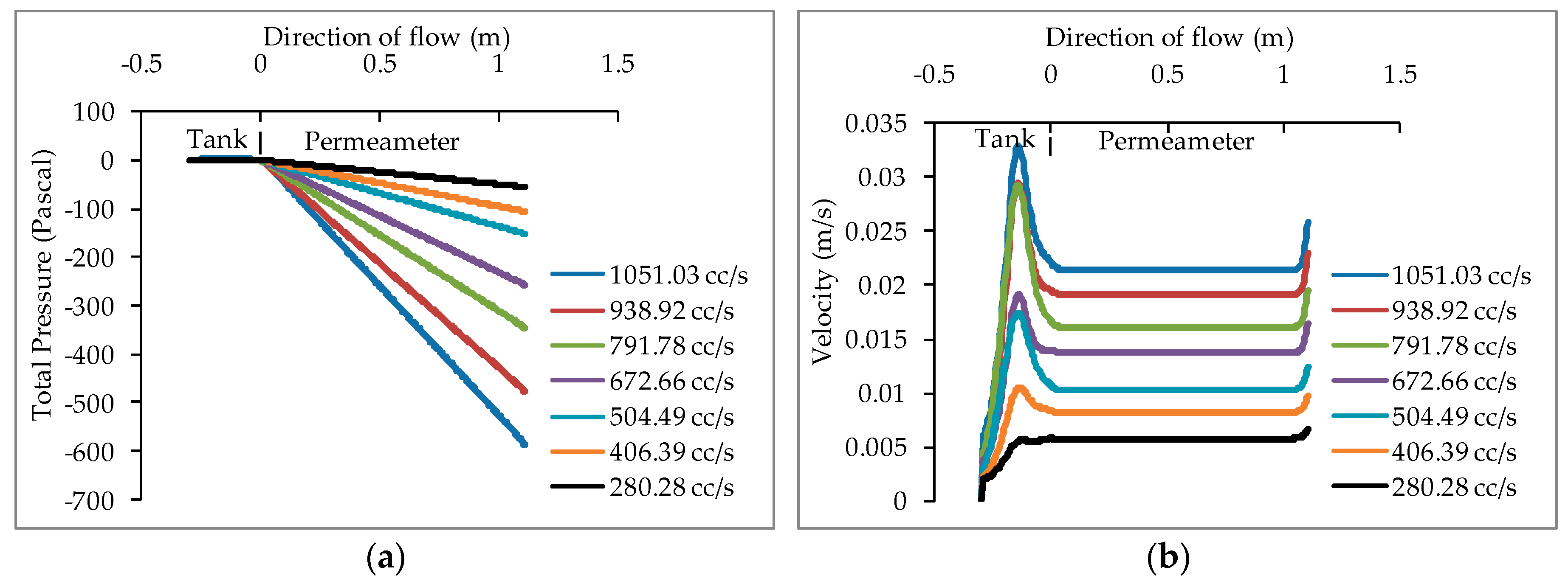
7. Results and Discussion
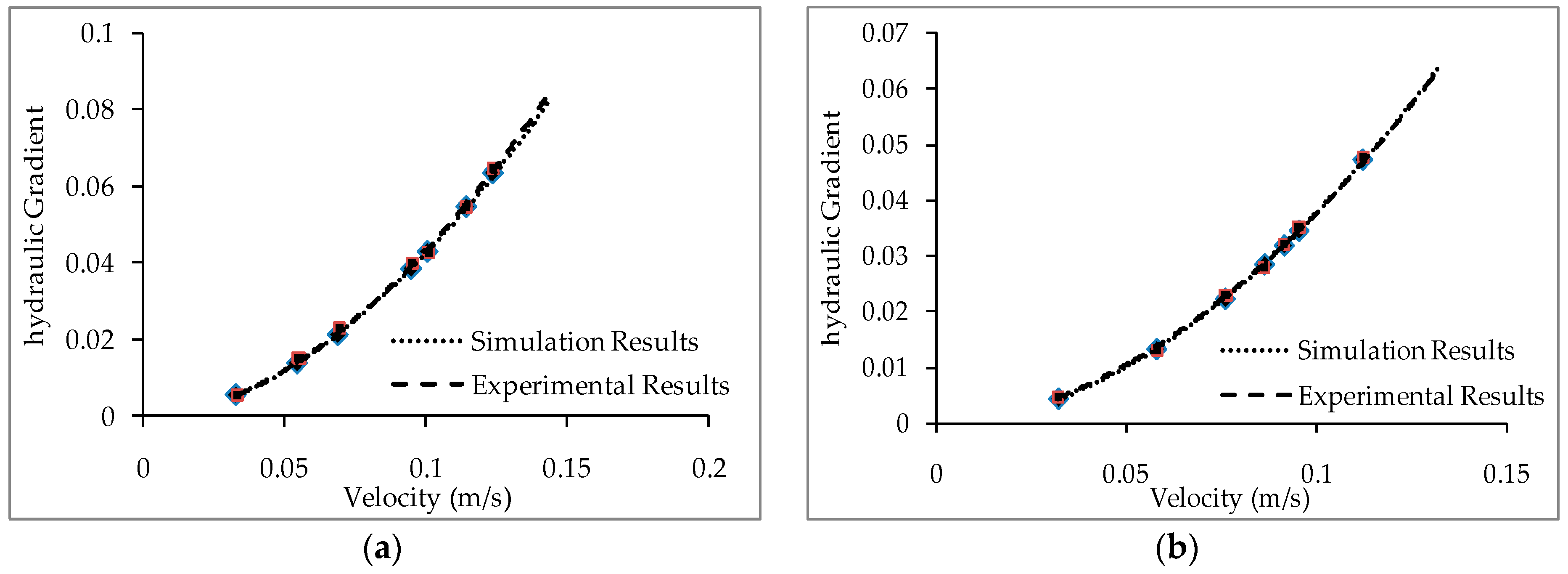
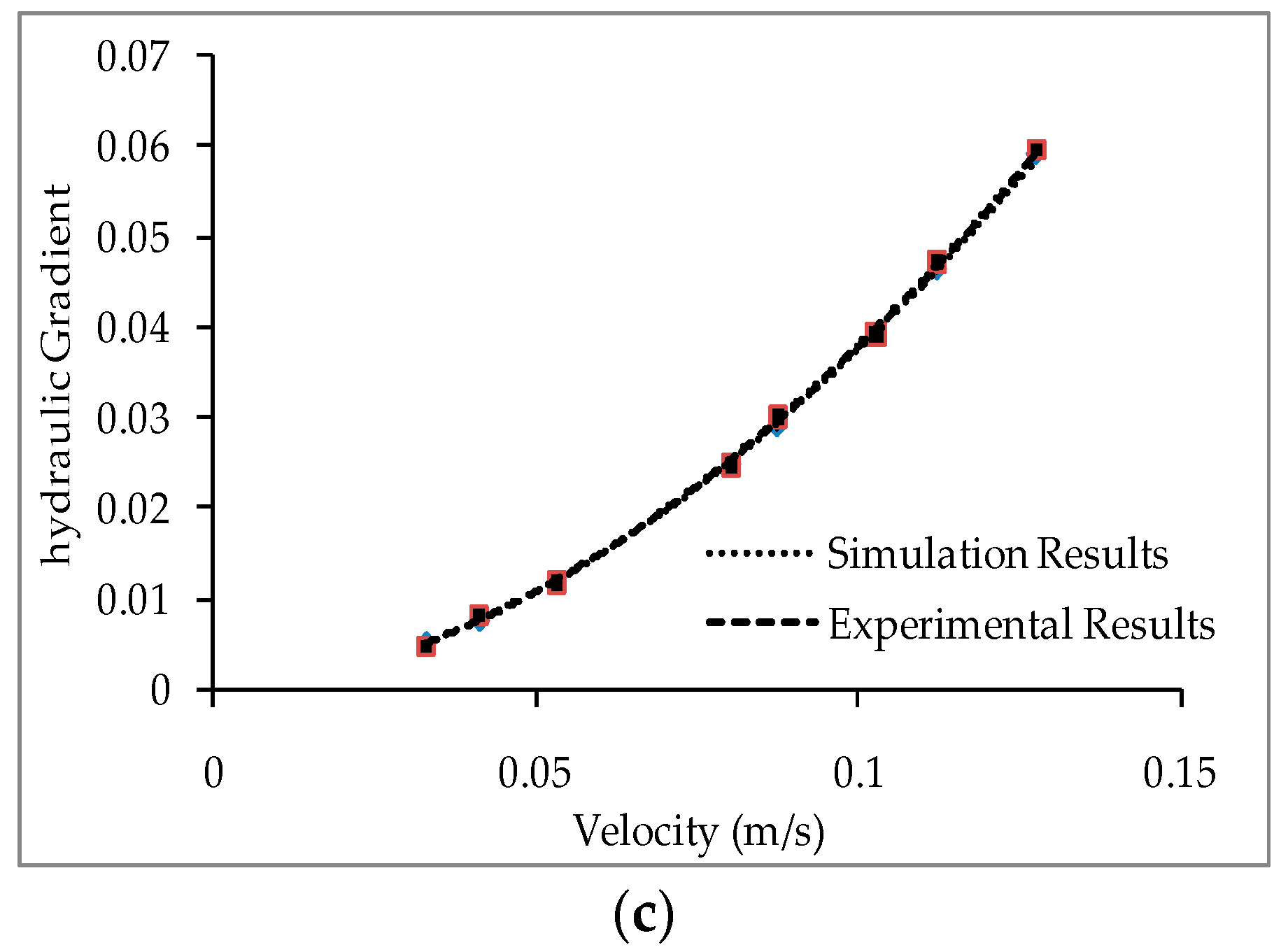
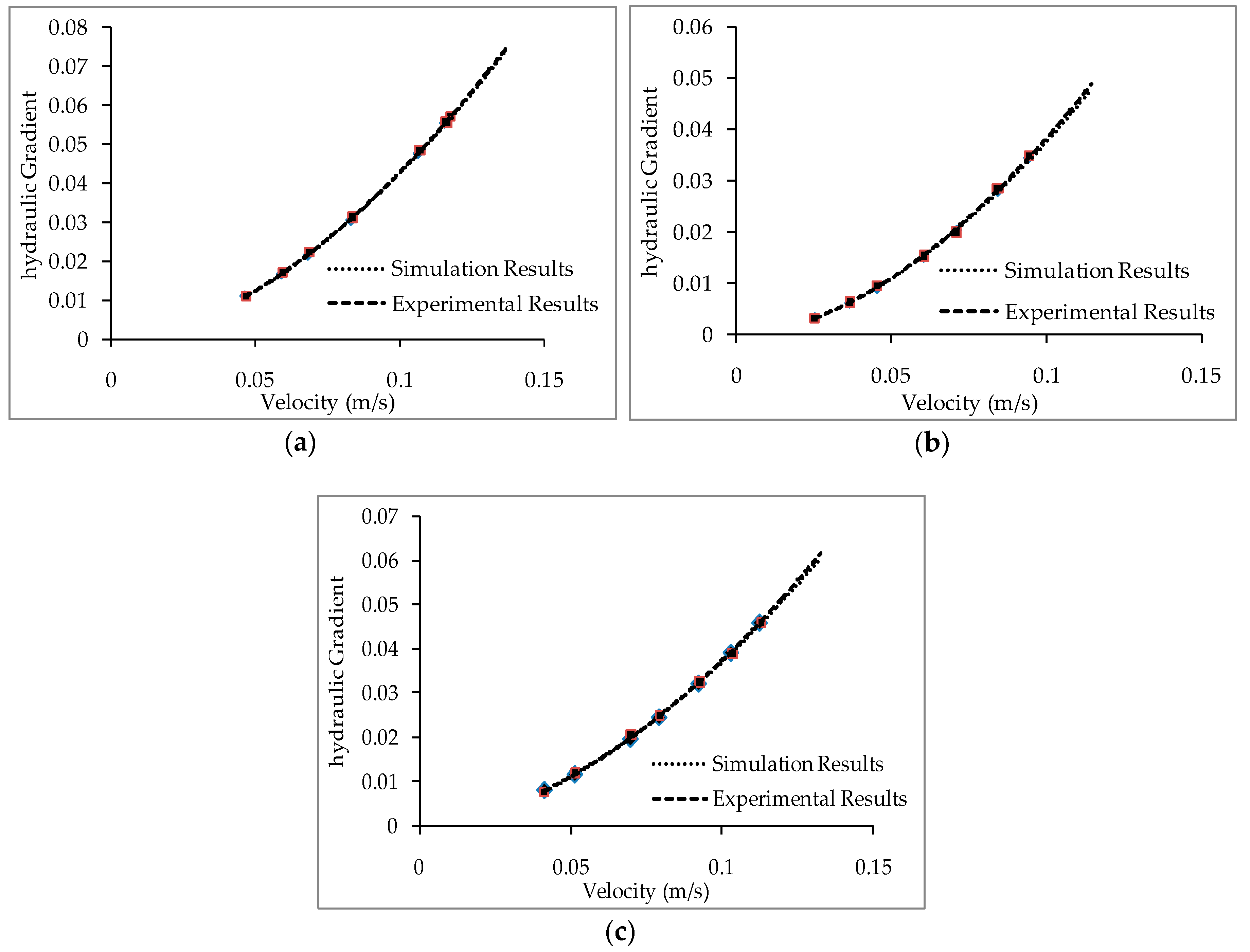
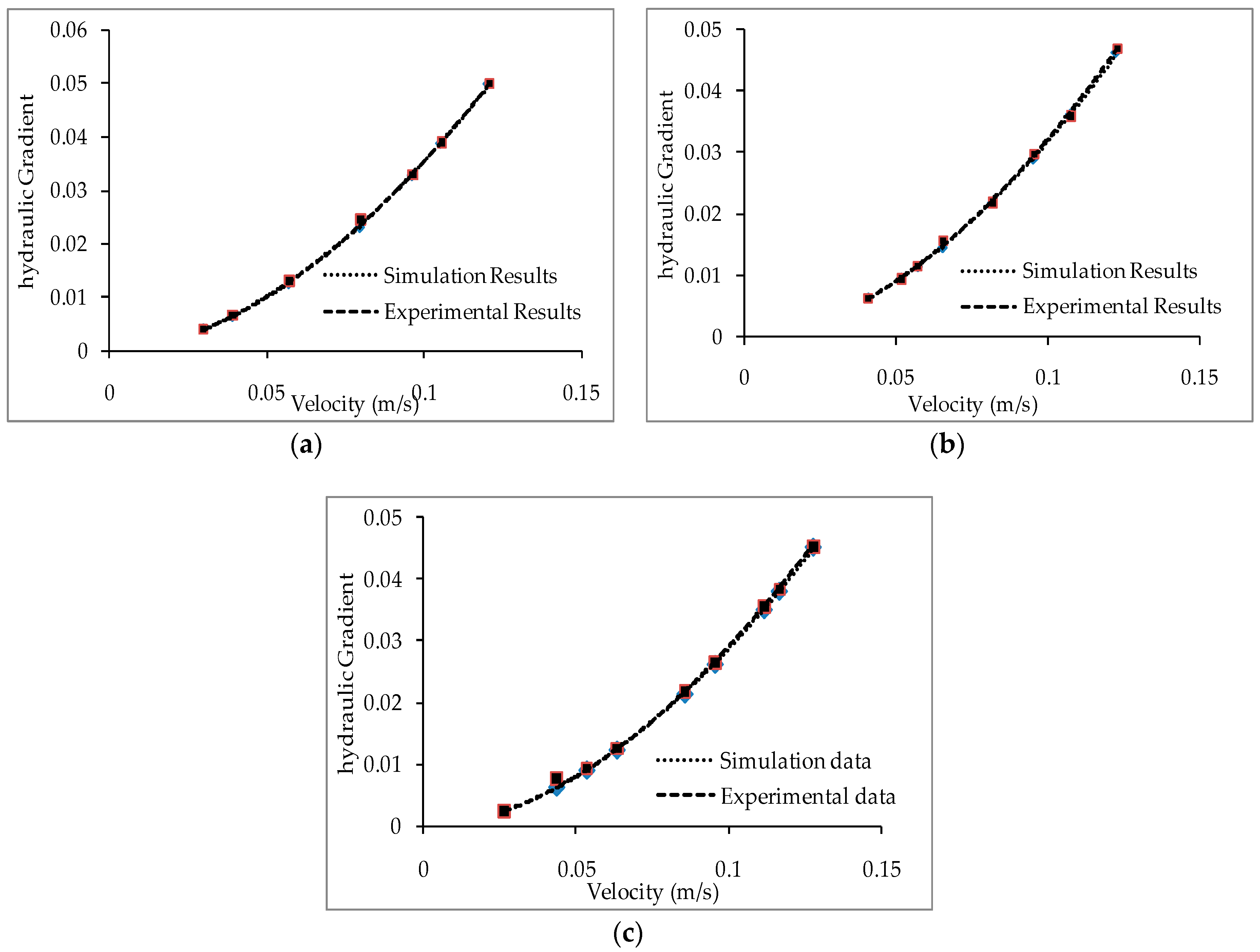
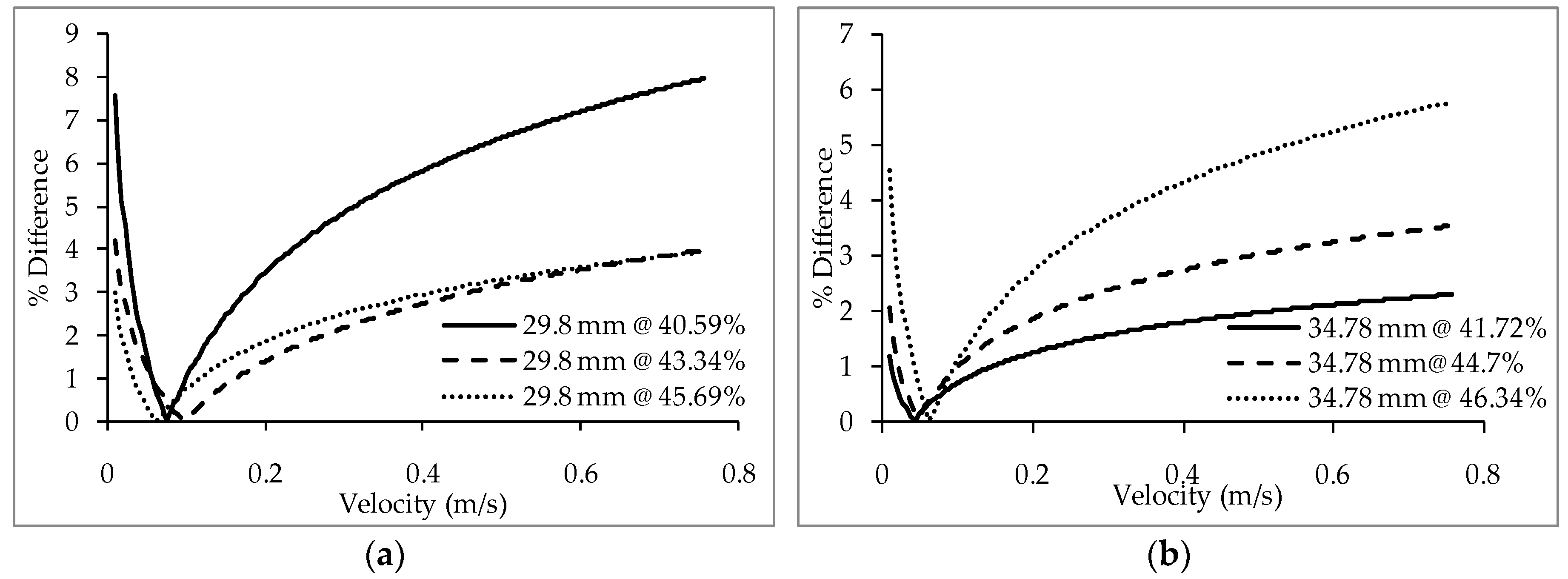
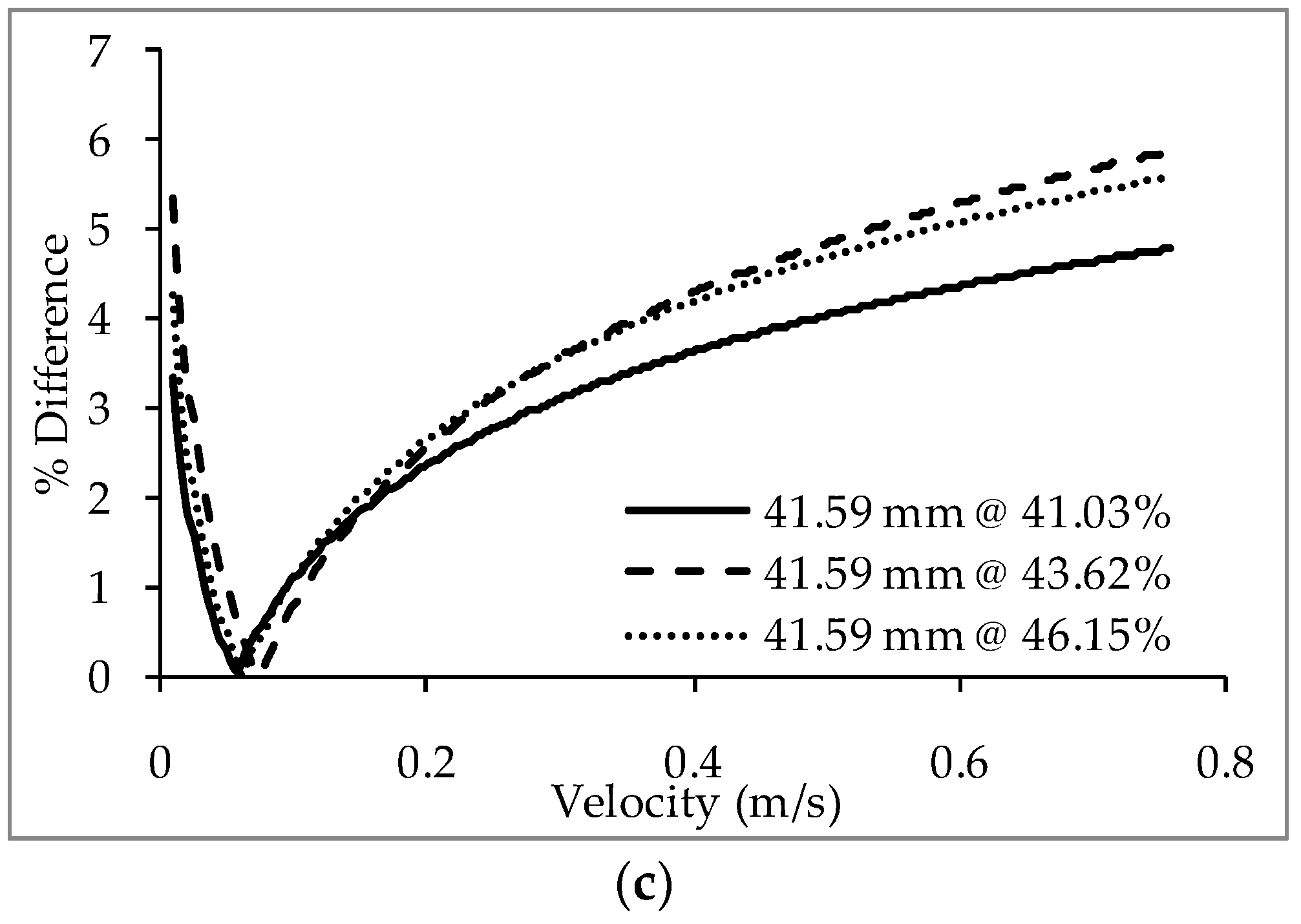
7.1. Comparison between the Experimental and Simulation Data and Statistical Validation of the Simulation
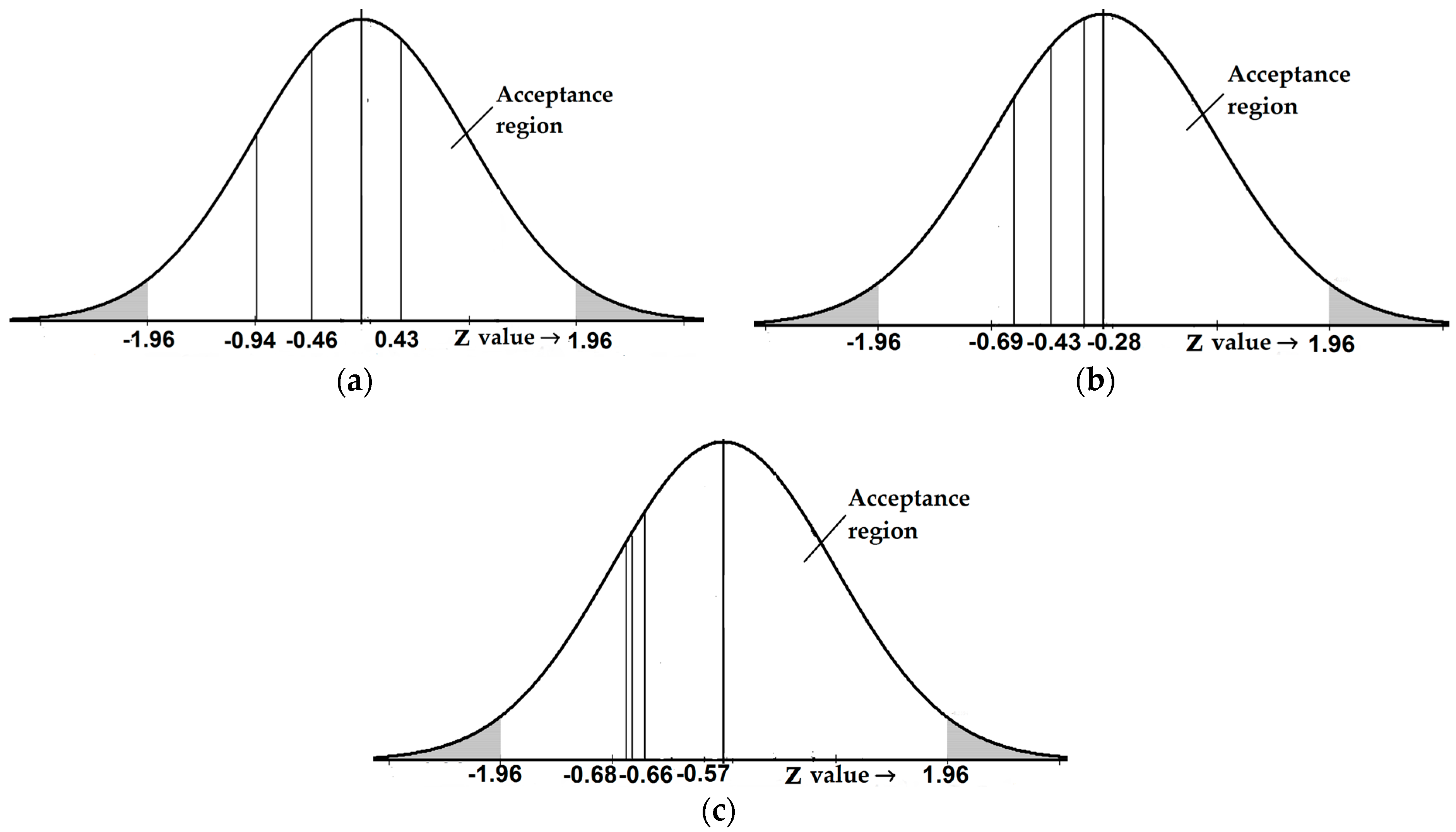
7.2. Validation of the Simulated Data Using the Z-Test
8. Conclusions
- The Wilkins equation can be satisfactorily used to represent post-laminar flow through porous media.
- The Wilkins coefficients are found to have a non-deviating nature with varying hydraulic radius. The obtained results from the present study are similar to the results reported in the literature.
- When subjected to variation in media size, the coefficients of the Wilkins equation are constant, given that the porosity is constant. However, variations in the porosity result in small variations of the coefficient W.
- The flow condition inside the experimental set up is simulated with a CFD model in the ANSYS FLUENT software. Trends similar to the experimental ones are obtained from the simulation results. The percentage deviation between the simulation and experimental results are within the acceptable range.
- For further validation, the experimental results are statistically compared with the simulation results using the standard Z-test. The values of Z calculated are found to be within the acceptable region for all the experimental results.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kovacs, G. Seepage through saturated and unsaturated layers. Hydrol. Sci. J. 1971, 16, 27–40. [Google Scholar] [CrossRef]
- Kovacs, G. Seepage Hydraulics; ESPC: New York, NY, USA, 1981; ISBN 0-444-99755-5. [Google Scholar]
- Vincent, M.C.; Pearson, C.M.; Kullman, J. Non-Darcy and multiphase flow in propped fractures: Case studies illustrate the dramatic effect on well productivity. In Proceedings of the SPE Gas Technology Symposium, Calgary, AB, Canada, 30 April–2 May 2002; pp. 71–84. [Google Scholar]
- Parkins, A.K.; Trollope, D.H.; Lawson, J.D. Rockfill structures subject to water flow. J. Soil Mech. Found. Div. 1966, 92, 135–151. [Google Scholar]
- Curtis, R.P.; Lawson, J.D. Flow over and through rockfill banks. J. Hydraul. Div. 1967, 93, 1–22. [Google Scholar]
- Thiruvengadam, M.; Pradip Kumar, G.N. Validity of Forchheimer equation in radial flow through coarse granular media. J. Eng. Mech. 1997, 123, 696–704. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Nasser, M.S.S. Radial Non-Linear Flow through Porous Media. Master’s Thesis, University of Windsor, Windsor, ON, Canada, 1970. [Google Scholar]
- Niranjan, H.S. Non-Darcy Flow through Porous Media. Master’s Thesis, Indian Institute of Technology, Kanpur, India, 1973. [Google Scholar]
- Venkataraman, P.; Rao, P.R.M. Darcian, transitional, and turbulent flow through porous media. J. Hydraul. Eng. 1998, 124, 840–846. [Google Scholar] [CrossRef]
- Venkataraman, P.; Rao, P.R.M. Validation of Forchheimer’s law for flow through porous media with converging boundaries. J. Hydraul. Eng. 2000, 126, 63–71. [Google Scholar] [CrossRef]
- Kumar, G.N.P.; Thiruvengadam, M.; Murali, T. A further study on Forchheimer coefficients as applied in seepage flow. ISH J. Hydraul. Eng. 2004, 10, 1–13. [Google Scholar] [CrossRef]
- Reddy, N.B.P.; Rao, P.R.M. Convergence effect on the flow resistance in porous media. Inst. Eng. (I) J. 2004, 85, 36–43. [Google Scholar]
- Sadeghian, J.; Kholghi, M.K.; Horfar, A.; Bazargan, J. Comparison of Binomial and Power Equations in Radial Non-Darcy Flows in Coarse Porous Media. J. Water Sci. Res. 2013, 5, 65–75. [Google Scholar]
- Bu, S.; Yang, J.; Dong, Q.; Wang, Q. Experimental study of flow transitions in structured packed beds of spheres with electrochemical technique. Exp. Therm. Fluid Sci. 2015, 60, 106–114. [Google Scholar] [CrossRef]
- Muljadi, B.P.; Blunt, M.J.; Raeini, A.Q.; Bijeljic, B. The impact of porous media heterogeneity on non-Darcy flow behaviour from pore-scale simulation. Adv. Water Resour. 2016, 95, 329–340. [Google Scholar] [CrossRef]
- Li, Z.; Wan, J.; Huang, K.; Chang, W.; He, Y. Effects of particle diameter on flow characteristics in sand columns. Int. J. Heat Mass Transf. 2017, 104, 533–536. [Google Scholar] [CrossRef]
- Dukhan, N.; Bağcı, Ö.; Özdemir, M. Experimental flow in various porous media and reconciliation of Forchheimer and Ergun relations. Exp. Therm. Fluid Sci. 2014, 57, 425–433. [Google Scholar] [CrossRef]
- Hellström, G.; Lundström, S. Flow through porous media at moderate Reynolds number. In Proceedings of the International Scientific Colloquium Modelling for Material Processing, Riga, Latvia, 8–9 June 2006; pp. 129–134. [Google Scholar]
- Kumar, G.N.P.; Venkataraman, P. Non-Darcy converging flow through coarse granular media. J. Inst. Eng. (India) Civ. Eng. Div. 1995, 76, 6–11. [Google Scholar]
- Wilkins, J.K. Flow of water through rockfill and its application to the design of dams. N. Zeal. Eng. 1955, 10, 382–387. [Google Scholar]
- Garga, V.K.; Hansen, D.; Townsend, R.D. Considerations on the design of flow through rockfill drains. In Proceedings of the 14th Annual British Columbia Mine Reclamation Symposium, Cranbrook, BC, Canada, 14–15 May1990. [Google Scholar]
- Banerjee, A.; Pasupuleti, S.; Singh, M.K.; Kumar, G.N.P. A study on the Wilkins and Forchheimer equations used in coarse granular media flow. Acta Geophys. 2017, 1–11. [Google Scholar] [CrossRef]
- Scheidegger, A.E. The Physics of Flow through Porous Media; University of Toronto Press: Toronto, ON, Canada; London, UK, 1958. [Google Scholar]
- Yu, B.M.; Li, J.H. A geometry model for tortuosity of flow path in porous media. Chin. Phys. Lett. 2004, 21, 1569–1571. [Google Scholar] [CrossRef]
- Rose, H.E.; Rizk, A.M.A. Further researches in fluid flow through beds of granular material. Proc. Inst. Mech. Eng. 1949, 160, 493–511. [Google Scholar] [CrossRef]
- Sedghi-Asl, M.; Rahimi, H.; Salehi, R. Non-Darcy Flow of Water Through a Packed Column Test. Transp. Porous Media 2014, 101, 215–227. [Google Scholar] [CrossRef]
- Kumar, G.N.P. Radial Non-Darcy Flow through Coarse Granular Media. Ph.D. Thesis, Sri Venkateswara University, Tirupati, India, 1994, unpublished. [Google Scholar]
- ANSYS Inc. Ansys Fluent 15.0: Users Guide; ANSYS Inc.: Canonsburg, PA, USA, November 2013. [Google Scholar]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k–e eddy viscosity model for high Reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Kim, S.E.; Choudhury, D.; Patel, B. Computations of Complex Turbulent Flows Using the Commercial Code Fluent; ICASE/LaRC Interdisciplinary Series in Science and Engineering; Springer: Dordrecht, The Netherlands, 1997; Volume 7, ISBN 978-94-011-4724-8. [Google Scholar]
- Jones, W.P.; Launder, B. The prediction of laminarization with a two-equation model of turbulence. Int. J. Heat Mass Transf. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- Chien, K.Y. Predictions of channel and boundary-layer flows with a low-Reynolds-number turbulence model. AIAA J. 1982, 20, 33–38. [Google Scholar] [CrossRef]
- Myong, H.K.; Kasagi, N. A new approach to the improvement of k-ε turbulence model for wall-bounded shear flows. JSME Int. J. Ser. 2 Fluids Eng. Heat Transf. Power Combust. Thermophys. Prop. 1990, 33, 63–72. [Google Scholar] [CrossRef]
- Crowe, C.T. On models for turbulence modulation in fluid-particle flows. Int. J. Multiph. Flow 2000, 26, 719–727. [Google Scholar] [CrossRef]
- Banerjee, A.; Pasupuleti, S.; Kumar, G.N.P.; Dutta, S.C. A Three-Dimensional CFD Simulation for the Nonlinear Parallel Flow Phenomena through Coarse Granular Porous Media. In Lecture Notes in Mechanical Engineering; Springer: Berlin/Heidelberg, Germany, 2018; pp. 469–480. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. 2008, 130, 0780011–0780014. [Google Scholar] [CrossRef]
- Safer, N.; Woloszyn, M.; Roux, J.J. Three-dimensional simulation with a CFD tool of the airflow phenomena in single floor double-skin facade equipped with a venetian blind. Sol. Energy 2005, 79, 193–203. [Google Scholar] [CrossRef]
- Camblor, P.M. On correlated z-values distribution in hypothesis testing. Comput. Stat. Data Anal. 2014, 79, 30–43. [Google Scholar] [CrossRef]
- Chen, Z.; Nadarajah, S. On the optimally weighted z-test for combining probabilities from independent studies. Comput. Stat. Data Anal. 2014, 70, 387–394. [Google Scholar] [CrossRef]
- Mann, P.S.; Lacke, C.J. Introductory Statistics; John Wiley and Sons Inc.: Delhi, India, 2010; ISBN 10:812652734X. [Google Scholar]



| Passing and Retaining Sieve Sizes (cm) | Volume (cm3) | Volume Diameter (cm) | Avg. Surface Area (cm2) | Specific Surface (/cm) |
|---|---|---|---|---|
| 2.50–3.15 | 14.46 | 2.98 | 44.68 | 2.88 |
| 3.15–3.75 | 23.10 | 3.48 | 58.44 | 2.53 |
| 3.75–5.00 | 38.55 | 4.16 | 82.11 | 2.13 |
| Media Size (mm) | Porosity (%) | W (m-s) | β | γ |
|---|---|---|---|---|
| 29.80 | 40.59 | 6.15 | 0.39 | 0.54 |
| 43.34 | ||||
| 45.69 | ||||
| 34.78 | 41.72 | 5.52 | 0.38 | 0.56 |
| 44.70 | ||||
| 46.34 | ||||
| 41.59 | 41.03 | 5.55 | 0.38 | 0.55 |
| 43.62 | ||||
| 46.15 |
| Proposed by | Media | Volume Diameter (mm) | Porosity (%) | W (m/s) | β | γ |
|---|---|---|---|---|---|---|
| Wilkins (1956) [21] | Crushed stone | 51.00 | 40.00 | 5.24 | 0.50 | 0.54 |
| Garga et al. (1990) [22] | Crushed stone | 24.60 | 47.00 | 5.39 | 0.50 | 0.53 |
| Pradeep Kumar (1994) [27] | Crushed stone | 13.10 | 47.00 | 4.94 | 0.51 | 0.52 |
| 20.10 | 45.88 | |||||
| 28.90 | 48.73 | |||||
| 39.50 | 48.26 |
| Parameter | Hydraulic Gradient | Velocity (m/s) at 0.285 m | Velocity (m/s) at 1.11 m |
|---|---|---|---|
| h1 | 0.005216 | 0.005216 | 0.005216 |
| h2 | 0.006937 | 0.006937 | 0.006937 |
| h3 | 0.009226 | 0.009226 | 0.009226 |
| r21 | 1.33 | 1.33 | 1.33 |
| r32 | 1.33 | 1.33 | 1.33 |
| 0.01992 | 0.01083 | 0.01156 | |
| 0.01984 | 0.01080 | 0.01159 | |
| 0.01973 | 0.01077 | 0.01096 | |
| P | 1.32772 | 1.30788 | 10.5924 |
| 0.02010 | 0.01088 | 0.01156 | |
| 0.02010 | 0.01088 | 0.01163 | |
| 0.40% | 0.20% | 0.27% | |
| 0.59% | 0.29% | 5.45% | |
| 0.86% | 0.45% | 0.01% | |
| 1.26% | 0.65% | 0.28% | |
| 1.09% | 0.56% | 0.02% |
| Media Size (mm) | Porosity (%) | Range of Velocity (m/s) | Z Value | |||||
|---|---|---|---|---|---|---|---|---|
| 29.80 | 40.59 | 0.01–0.757 | 0.643 | 0.599 | 0.540 | 0.359 | 250 | −0.940 |
| 43.34 | 0.01–0.757 | 0.586 | 0.606 | 0.497 | 0.517 | 250 | 0.429 | |
| 45.69 | 0.01–0.757 | 0.554 | 0.535 | 0.464 | 0.446 | 250 | −0.459 | |
| 34.78 | 41.72 | 0.01–0.757 | 0.565 | 0.554 | 0.463 | 0.452 | 250 | −0.276 |
| 44.70 | 0.01–0.757 | 0.527 | 0.510 | 0.435 | 0.420 | 250 | −0.425 | |
| 46.34 | 0.01–0.757 | 0.496 | 0.471 | 0.407 | 0.383 | 250 | −0.694 | |
| 41.59 | 41.03 | 0.01–0.757 | 0.511 | 0.489 | 0.422 | 0.406 | 250 | −0.574 |
| 43.62 | 0.01–0.757 | 0.464 | 0.440 | 0.391 | 0.368 | 250 | −0.684 | |
| 46.15 | 0.01–0.757 | 0.439 | 0.418 | 0.369 | 0.349 | 250 | −0.661 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banerjee, A.; Pasupuleti, S.; Singh, M.K.; Kumar, G.N.P. An Investigation of Parallel Post-Laminar Flow through Coarse Granular Porous Media with the Wilkins Equation. Energies 2018, 11, 320. https://doi.org/10.3390/en11020320
Banerjee A, Pasupuleti S, Singh MK, Kumar GNP. An Investigation of Parallel Post-Laminar Flow through Coarse Granular Porous Media with the Wilkins Equation. Energies. 2018; 11(2):320. https://doi.org/10.3390/en11020320
Chicago/Turabian StyleBanerjee, Ashes, Srinivas Pasupuleti, Mritunjay Kumar Singh, and G.N. Pradeep Kumar. 2018. "An Investigation of Parallel Post-Laminar Flow through Coarse Granular Porous Media with the Wilkins Equation" Energies 11, no. 2: 320. https://doi.org/10.3390/en11020320
APA StyleBanerjee, A., Pasupuleti, S., Singh, M. K., & Kumar, G. N. P. (2018). An Investigation of Parallel Post-Laminar Flow through Coarse Granular Porous Media with the Wilkins Equation. Energies, 11(2), 320. https://doi.org/10.3390/en11020320





