Two-Stage Stochastic Optimization for the Strategic Bidding of a Generation Company Considering Wind Power Uncertainty
Abstract
1. Introduction
1.1. Background and Motivations
1.2. Aims and Contributions
- Based on the two-stage stochastic optimization theory, the decision-making of power generation enterprises is divided into a day-ahead bidding decision and a real-time scheduling decision according to the different decision-making stages. A two-stage stochastic optimization model is constructed.
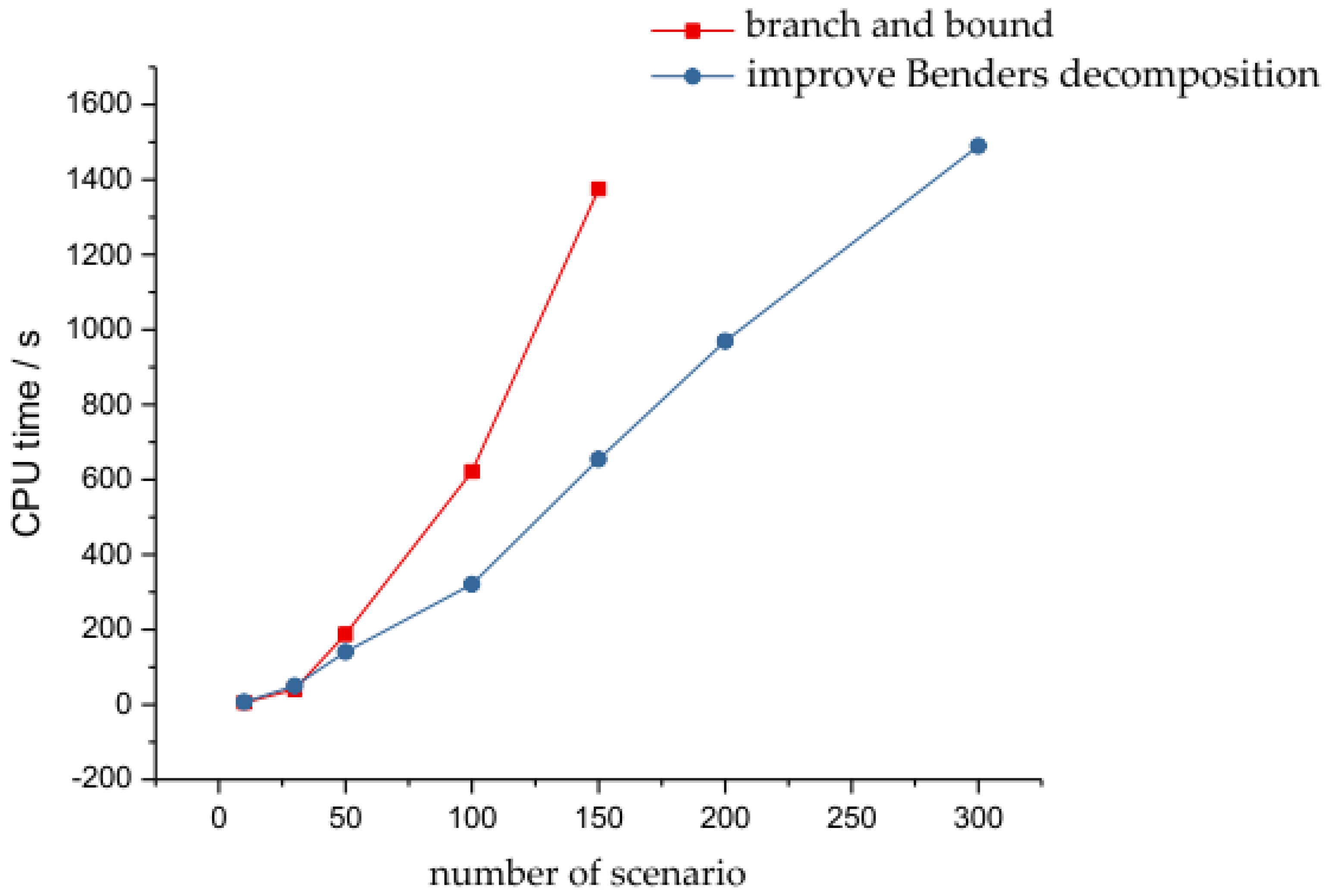
- An improved Benders decomposition algorithm is used to solve the problem. This algorithm decomposes the original problem into a master problem that only involves first-stage variables, and a set of sub-problems that only involves second-stage variable. These problems are much easier to solve compared with the original problem. This modified Benders decomposition algorithm does not requires the sub-problem to be a convex optimization problem like the traditional Benders decomposition algorithm. Note that the sub-problems in this paper are mixed integer programming since the startup and shutdown decisions of thermal power units are involved. We use a convex hull approximation method to convexify the feasible region of the sub-problem, so that the dual information of the sub-problem can be utilized.
- The actual cases from the Latin American electricity market are selected to verify the rationality and effectiveness of the constructed models and algorithms.
1.3. Paper Organization
2. Literature Review
2.1. Strategic Bidding of Generation Company
2.2. Probabilistic Scheduling of Wind Generators
3. Generation Company Return Function
3.1. Problem Description
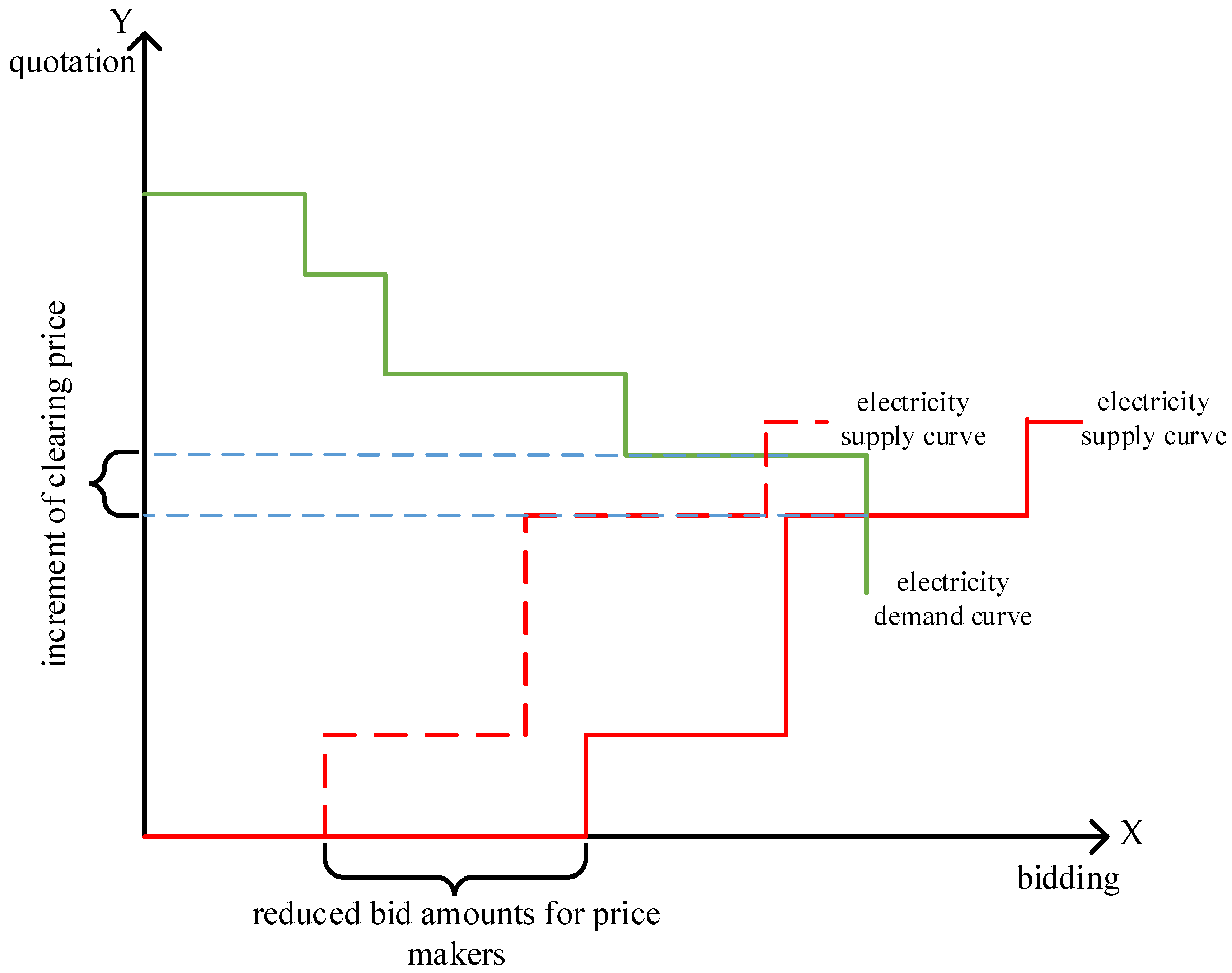
3.2. Electricity Wholesale Supply and Demand Relationship
- (1)
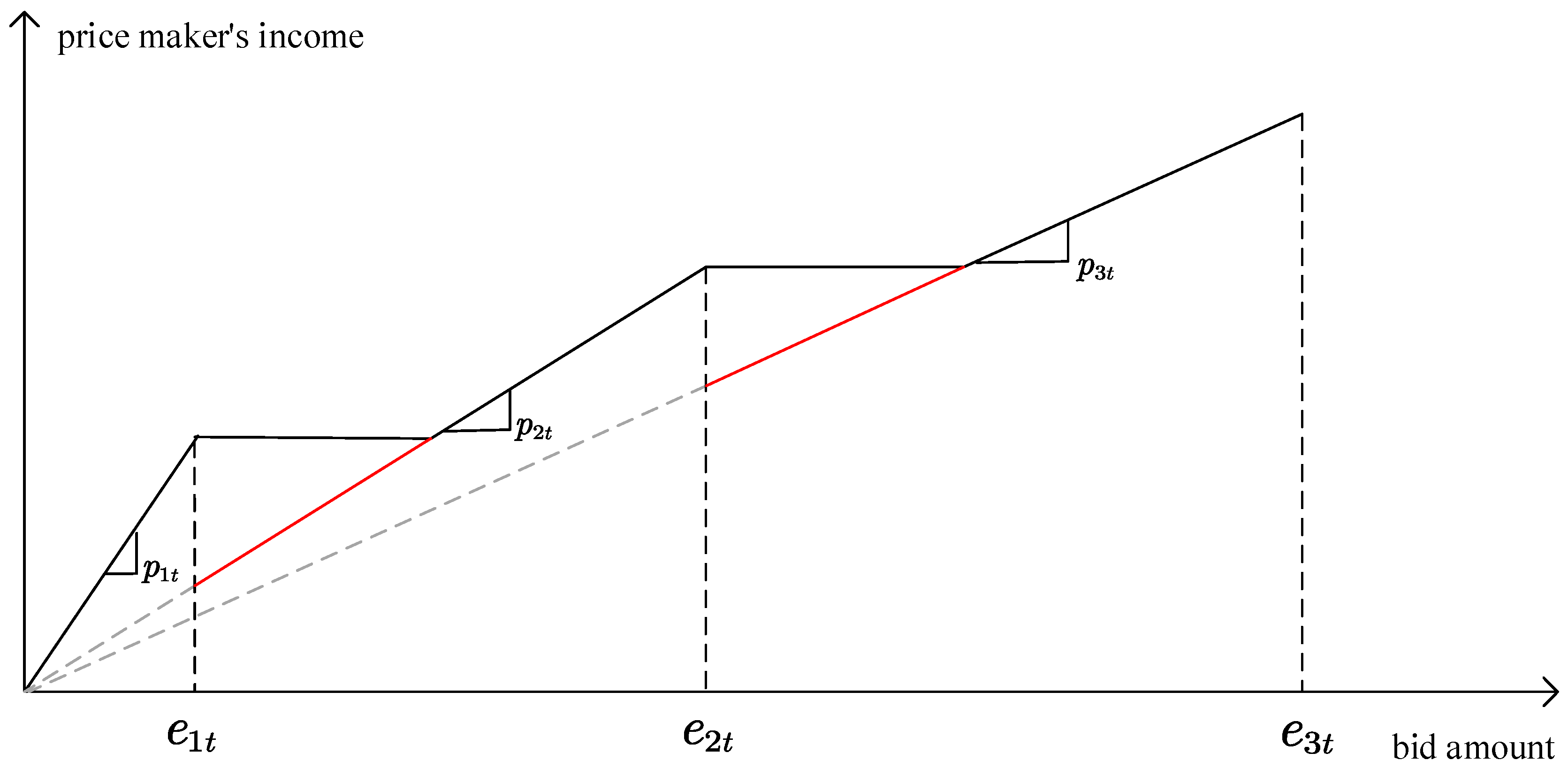
- The relevant information in the wholesale electricity market is completely transparent to the price maker. In other words, the uncertainty of the market information is not considered.
- (2)
- The bidding prices of the price maker are assumed to be 0 during the entire planning horizon. This ensures that all bidding quantities of the price maker will be sold in the market. This is because the market clearing price in each time period must be greater than 0.
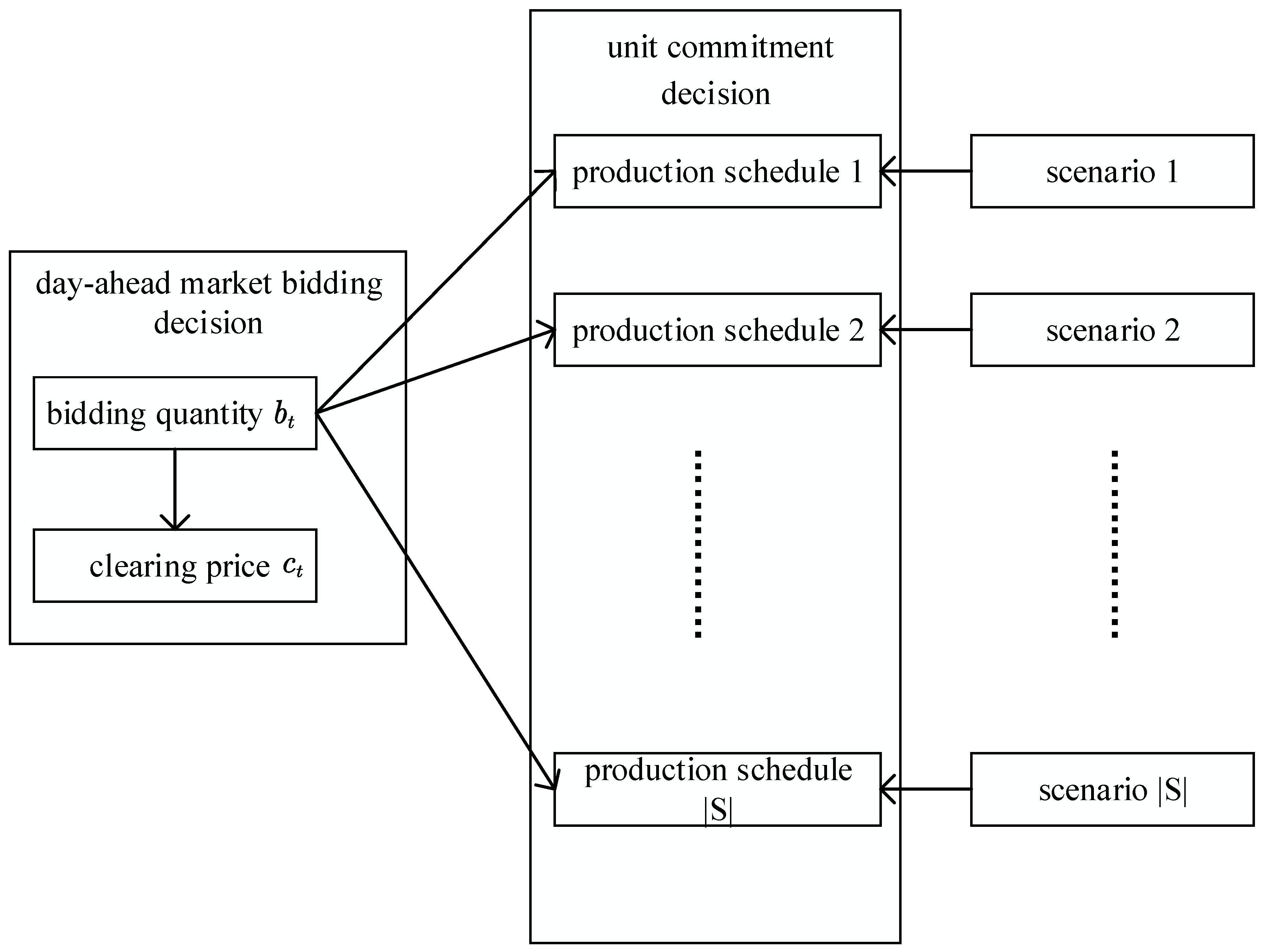
4. Two-Stage Stochastic Bidding Model for Generation Company
4.1. Method Introduction
4.2. Objective Function
4.3. Restrictions
5. Solution Methodology
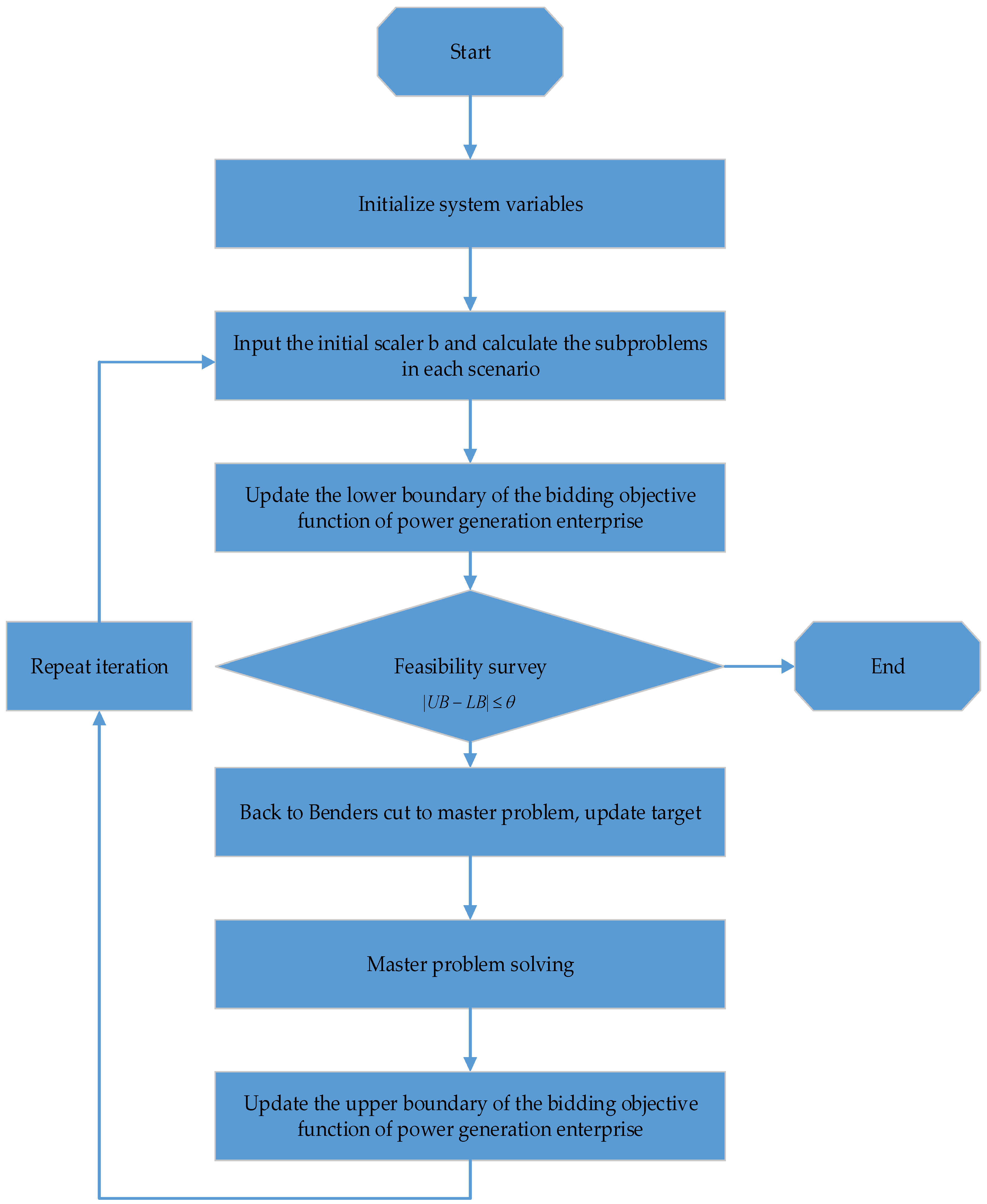
5.1. Improved Benders Decomposition
5.2. Improve the Calculation Process of the Benders Decomposition Algorithm
- Step 1:
- Initialize the upper bound and the lower bound , and set the maximum tolerance of the difference between the upper and lower bounds .
- Step 2:
- Enter a set of initial bid amount and calculate Sub-Questions (17) in each scenario, obtain the optimal value , and update the lower bound of the original problem.
- Step 3:
- Substitute the optimal value in the second step into Equation (18) for solving, and construct Constraint (19).
- Step 4:
- Substitute Constraint (19) into model (18) and relax the constraint which restricts the type of variable . Then we can obtain model (20), which is a linear program. Solve model (20) and construct the benders cut based on the optimal values of its dual variables. The benders cut is then substituted into the master problem (16) so that the master problem is updated. Solve the new master problem and update the upper bound .
- Step 5:
- Observe if is satisfied. If it is satisfied, the quality of the solution satisfies the decision-maker’s requirement, that is, the difference between the obtained optimal objective function value and the true optimal objective function value does not exceed . The calculation is stopped, and the current result is output as the optimal solution. Otherwise, substitute the obtained one into the sub-problem and return to Step 2.
6. Case Analysis
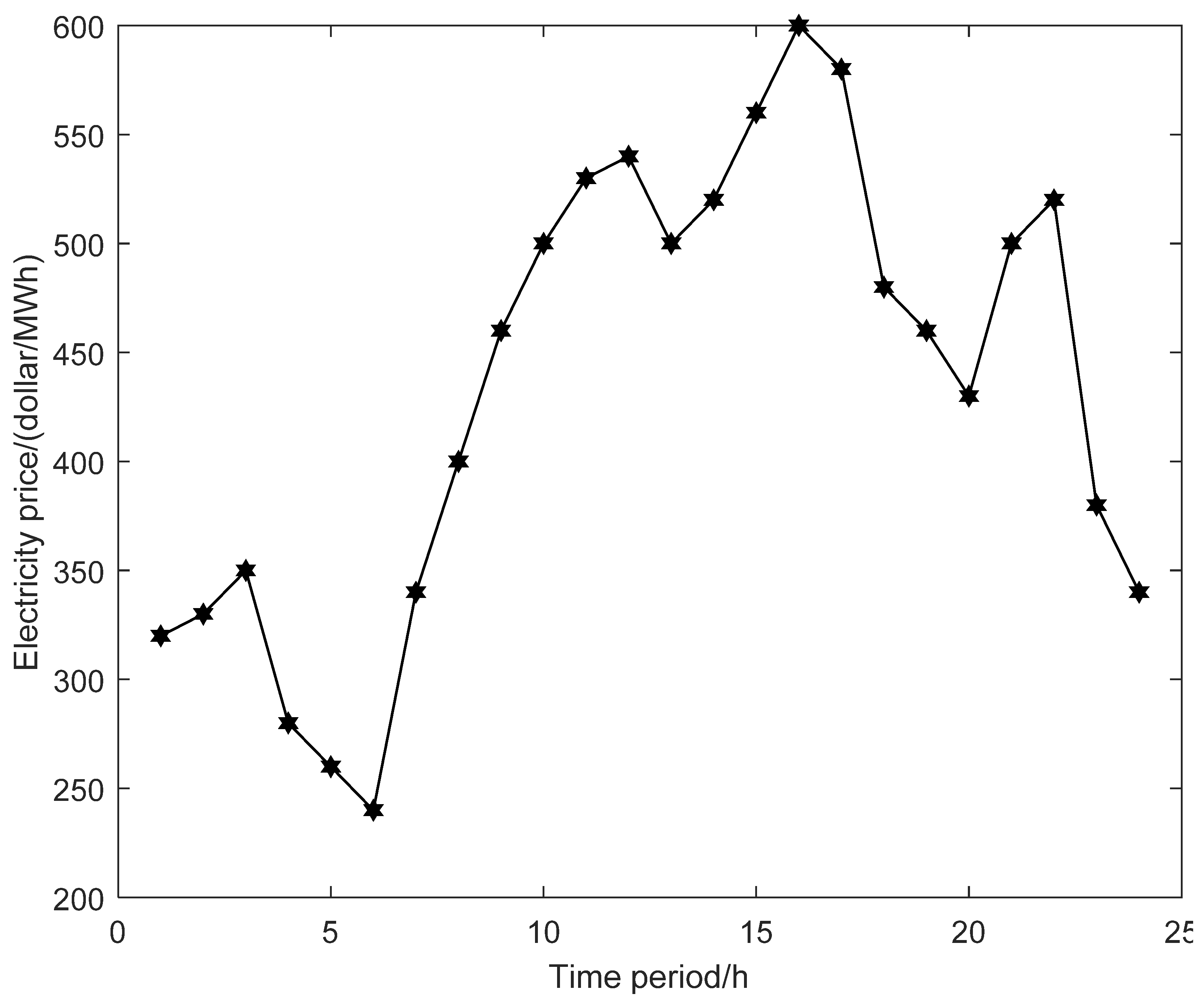
6.1. Basic Date
- (1)
- Use the nuclear density estimation method to analyze the historical data of wind power and obtain its approximate probability distribution function.
- (2)
- Use the Latin hypercube sampling method to discretize the probability distribution function and generate a wind power scene tree.
- (3)
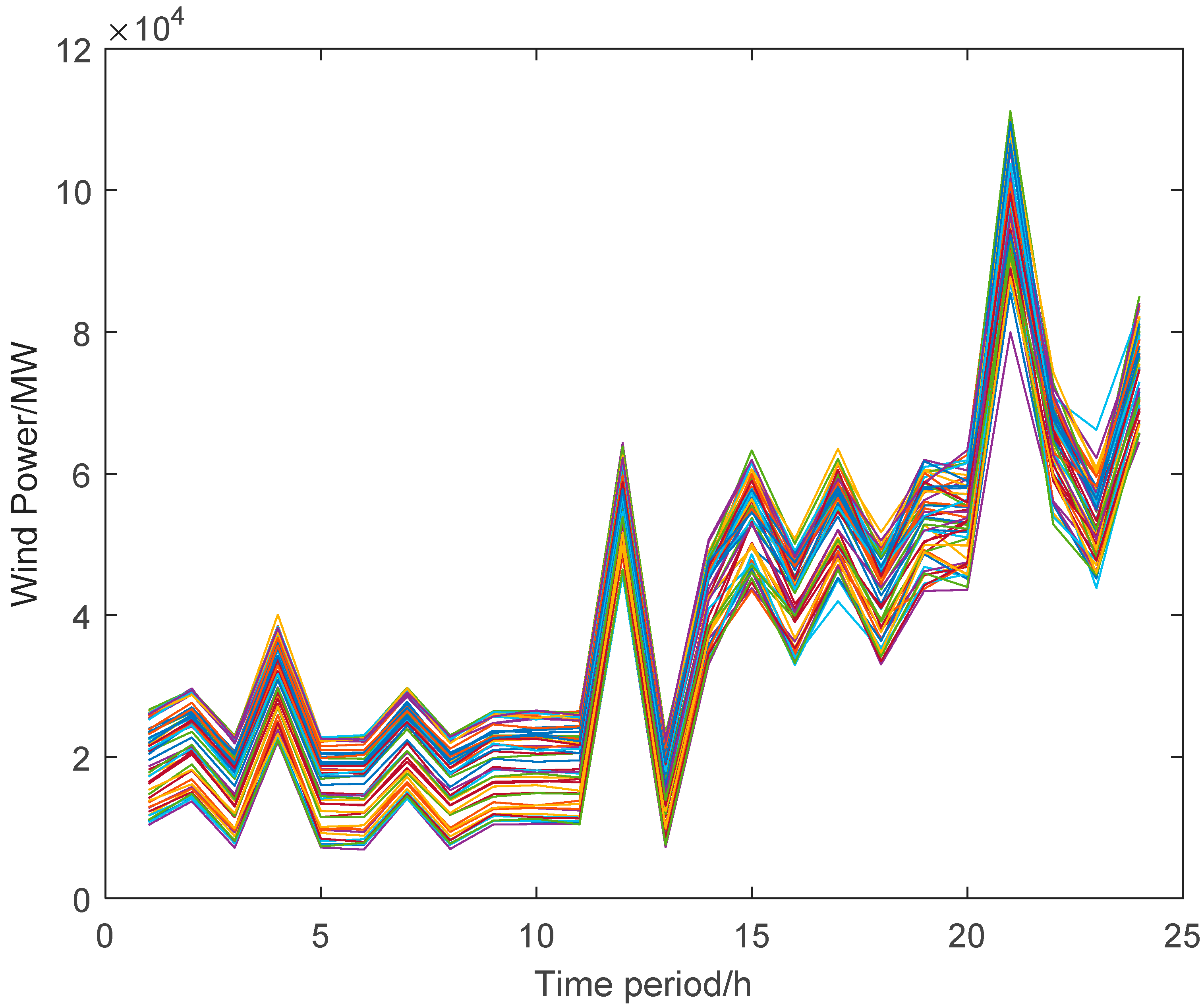
- In order to avoid too many scenes, the back-generation reduction method is used to pre-process the scene, merge similar scenes, and finally obtain 50 wind power scenes, as shown in Figure 5 below.
6.2. Results and Discussion
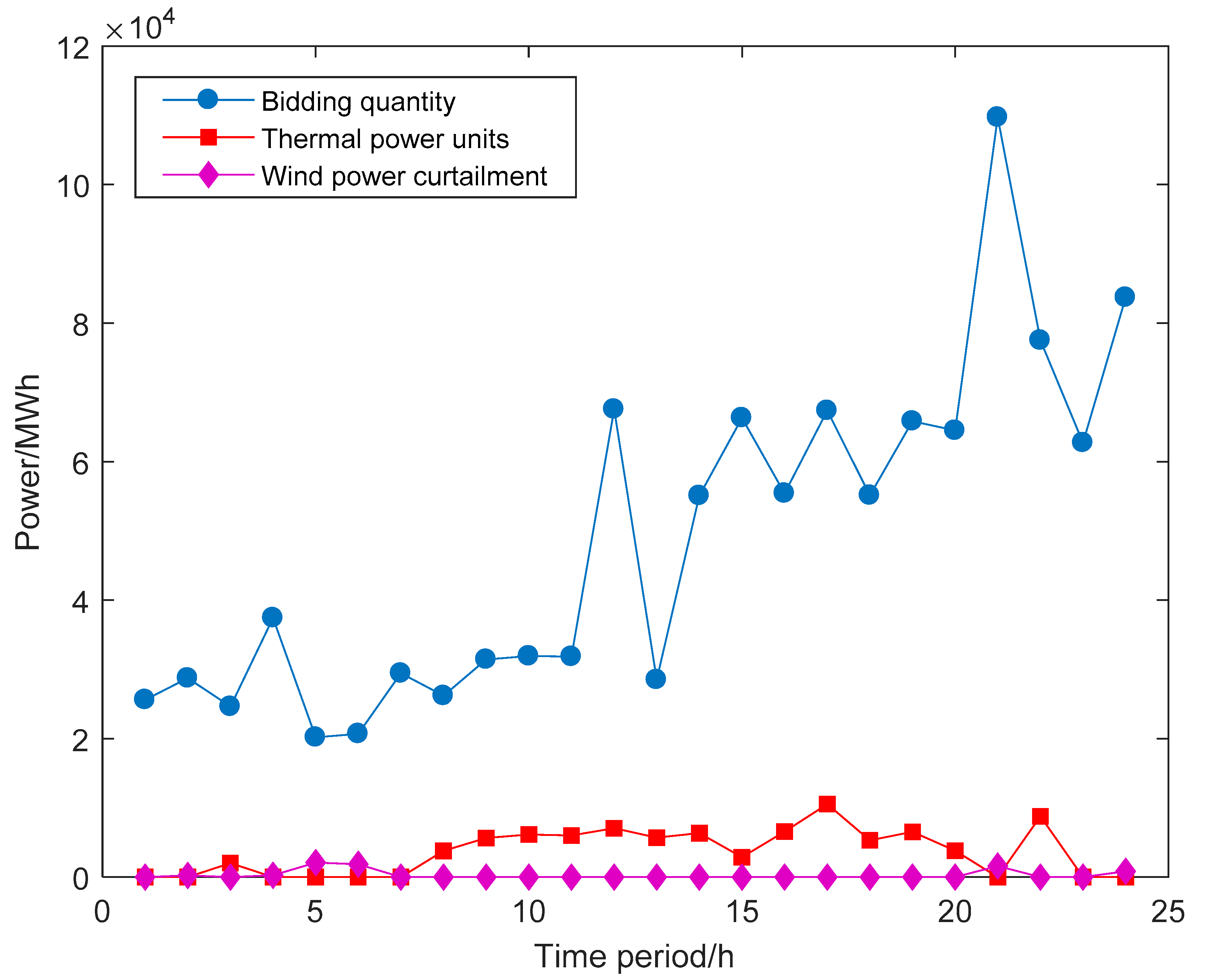
6.2.1. Additional Power Purchase Cost vs. Wind Curtailment Cost
- (1)
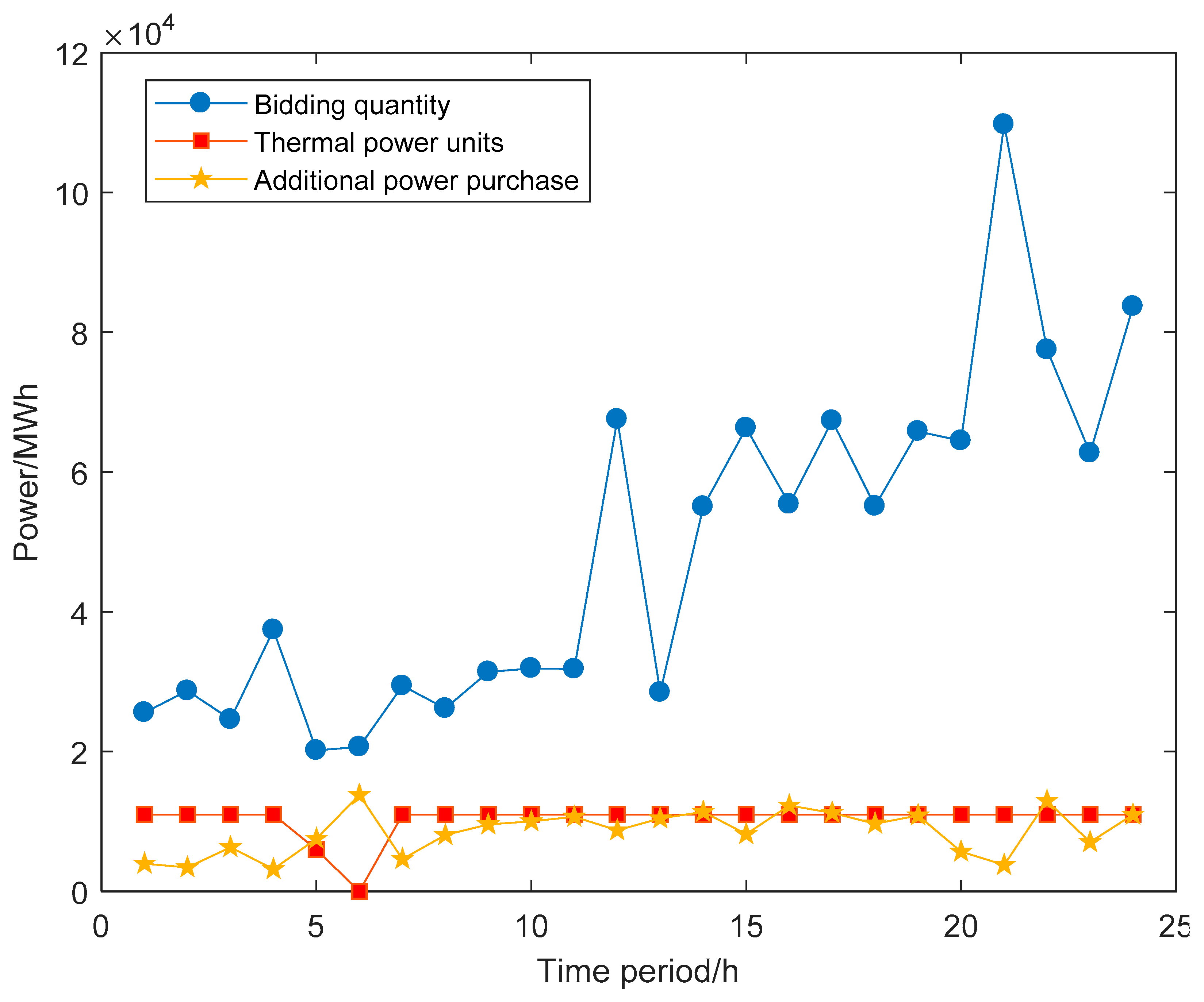
- Thermal power units play a significant role in coping with wind power uncertainty. In the most optimistic scenario where the wind power is high, the generation company reduces the generation quantities of thermal power units. Since the unit generation cost of wind power is much cheaper than the thermal power, most electricity demands are satisfied through wind power in order to save the generation cost. On the contrary, in the most pessimistic case, where the wind power is low, the generation company increases the generation quantities of thermal power units in the case of an additional power purchase cost.
- (2)
- Aggressive bidding quantities, compared with conservative bidding quantities, are preferred by the generation company. Note that, even in the most optimistic case, the wind power curtailment is still very low. However, in the most pessimistic case, the additional power purchase is relatively high. If a generation company offers low bidding quantities in the day-ahead electricity market, it will not only suffer the wind curtailment cost in some scenarios when wind power is high but also lose the opportunity of earning more revenue. Therefore, a generation company would rather offer high bidding quantities since the loss of revenue and wind curtailment cost is much higher than the additional power purchase cost.
6.2.2. The Effect of Additional Power Purchase on Decision-Makings
6.2.3. The Effect of Wind Power Volatility on Decision-Makings
7. Conclusions
- (1)
- The key to strategic bidding is the tradeoff between high bidding quantities and low bidding quantities. Too much or too little bidding can result in loss for a generation company. Various factors discussed in the examples will have an impact on the bidding quantities of power generation companies. In addition, unless the cost of additional electricity purchases is high enough, power generation companies will be more inclined to make aggressive decisions to avoid the loss of opportunity costs due to excessive power abandonment.
- (2)
- The goal of power generation companies is to maximize their expected benefits. However, even if we do not change the expected value of wind power but only increase their volatility, it will still cause the expected profit of power producers to decrease.
- (3)
- Properly retaining a certain proportion of thermal power units is important for promoting wind power consumption and improving the profitability of power generation companies.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Xu, T. 2017 Global Wind Power Installed Capacity Statistics. Wind. Energy Ind. 2018, 3, 51–57. [Google Scholar]
- Yucekayaa, A.D.; Valenzuelaa, J.; Dozierb, G. Strategic bidding in electricity markets using particle swarm optimization. Electr. Power Syst. Res. 2009, 79, 335–345. [Google Scholar] [CrossRef]
- Bompard, E.; Ma, Y.; Napoli, R.; Abrate, G. The Demand Elasticity Impacts on the Strategic Bidding Behavior of the Electricity Producers. IEEE Trans. Power Syst. 2007, 22, 188–197. [Google Scholar] [CrossRef]
- Barroso, L.A.; Carneiro, R.D.; Granville, S.; Pereira, M.V.; Famp, M.H.C. Nash Equilibrium in Strategic Bidding: A Binary Expansion Approach. IEEE Trans. Power Syst. 2006, 21, 629–638. [Google Scholar] [CrossRef]
- Li, T.; Shahidehpour, M. Strategic Bidding of Transmission-Constrained GENCOs with Incomplete Information. IEEE Trans. Power Syst. 2005, 20, 437–447. [Google Scholar] [CrossRef]
- Lamont, J.W.; Rajan, S. Strategic bidding in an energy brokeragy. IEEE Trans. Power Syst. 1997, 12, 1729–1733. [Google Scholar] [CrossRef]
- Pereira, M.V.; Granville, S.; Fampa, M.H.C.; Dix, R.; Barroso, L.A. Strategic Bidding under Uncertainty: A Binary Expansion Approach. IEEE Trans. Power Syst. 2005, 20, 180–188. [Google Scholar] [CrossRef]
- Kazemi, M.; Mohammadi-Ivatloo, B.; Ehsan, M. Risk-based bidding of large electric utilities using Information Gap Decision Theory considering demand response. Electr. Power Syst. Res. 2014, 114, 86–92. [Google Scholar] [CrossRef]
- Ren, Y.L.; Zou, X.Y.; Zhang, X.H. Bidding game model of power generation company based on first-price sealed auction. J. Syst. Eng. 2003, 18, 248–254. [Google Scholar]
- Bushnell, J. A mixed complementarity model of hydrothermal electricity competition in the western United States. Oper. Res. 2003, 51, 80–93. [Google Scholar] [CrossRef]
- Ding, H.J.; Pinson, P.; Hu, Z.C. Integrated bidding and operating strategies for wind-storage systems. IEEE Trans. Sustain. Energy 2016, 7, 163–172. [Google Scholar] [CrossRef]
- De la Nieta, A.A.S.; Contreras, J.; Muñoz, J.I. Optimal coordinated wind-hydro bidding strategies in day-ahead markets. IEEE Trans. Power Syst. 2013, 28, 798–809. [Google Scholar] [CrossRef]
- Yan, J.; Liu, Y.Q.; Han, S.; Wang, Y.M.; Feng, S.L. Reviews on Uncertainty Analysis of wind Power Forecasting. Renew. Sustain. Energy Rev. 2015, 52, 1322–1330. [Google Scholar] [CrossRef]
- Li, H.; Zhang, R.C.; Wang, X.S.; Dong, Y. Multi-Time Scale Rolling Economic Dispatch for Wind/Storage Power System based on forecast Error Feature Extraction. Energies 2018, 11, 2124. [Google Scholar]
- Zhang, X.H.; Yan, K.L.; Lu, Z.G.; Zhong, J.Q. Scenario Probability Basted Multi-Objective Optimized Low-Carton Economic Dispatching for Power Grid Integrated with Wind Farms. Power Syst. Technol. 2014, 38, 1835–1841. [Google Scholar]
- Bin, J.; Yuan, X.H.; Chen, Z.H.; Tian, H. Improved gravitational search algorithm for unit commitment considering uncertainty of wind power. Energy 2014, 67, 52–62. [Google Scholar]
- Jiang, R.; Wang, J.H.; Guan, Y.P. Robust unit commitment with wind power and pumped storage hydro. IEEE Trans. Power Syst. 2012, 27, 800–810. [Google Scholar] [CrossRef]
- Fu, Y.; Chen, T.; Li, Z.K.; Wei, S.R.; Ji, L. Robust Security Economic Dispatch Considering Wind Power Curtailment. Proc. CSEE 2017, 37, 47–54. [Google Scholar]
- Lorca, Á.; Sun, X.A. Adaptive Robust Optimization With Dynamic Uncertainty Sets for Multi-Period Economic Dispatch Under Significant Wind. IEEE Trans. Power Syst. 2015, 30, 1702–1713. [Google Scholar] [CrossRef]
- Sun, Y. Ultra-Short Term Dispatching Strategies for the System with Large-Scale Wind Power Integration; Northeast Electric Power University: Jilin, China, 2018. [Google Scholar]
- Tan, Z.F.; Li, H.H.; Ju, L.W.; Song, Y.H. An Optimization Model for Large-Scale Wind Power Grid Connection Considering Demand Response and Energy Storage Systems. Energies 2014, 7, 7282–7304. [Google Scholar] [CrossRef]
- Zhao, C.Y.; Wang, Q.F.; Wang, J.H. Expected Value and Chance Constrained Stochastic Unit Commitment Ensuring Wind Power Utilization. IEEE Trans. Power Syst. 2014, 29, 2696–2705. [Google Scholar] [CrossRef]
- Liu, B.; Liu, F.; Wang, C.; Mei, S.; Wei, W. Uncertainty Set Modeling and Evaluation of Wind Farm Power Output for Robust Dispatch. Autom. Electr. Power Syst. 2015, 39, 8–14. [Google Scholar]
- Guan, Y.P.; Wang, J.H. Uncertainty Sets for Robust Unit Commitment. IEEE Power Energy Soc. 2014, 29, 1439–1440. [Google Scholar] [CrossRef]
- Hu, B.Q.; Wu, L.; Marwali, M. On the Robust Solution to SCUC with Load and Wind Uncertainty Correlations. IEEE Trans. Power Syst. 2014, 29, 2952–2964. [Google Scholar] [CrossRef]
- Damodaran, S.K.; Kumar, T.K.S. Hydro-Thermal-Wind Generation Scheduling Considering Economic and Environmental Factors Using Heuristic Algorithms. Energies 2018, 11, 353. [Google Scholar] [CrossRef]
- Carrion, M.; Arroyo, J.M. A computationally efficient mixed-integer linear formulation for the thermal unit commitment problem. IEEE Trans. Power Syst. 2006, 21, 1371–1378. [Google Scholar] [CrossRef]
- Löfberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the 2004 IEEE International Symposium on Computer Aided Control Systems Design, New Orleans, LA, USA, 2–4 September 2004; pp. 284–289. [Google Scholar]
| Nominal Capacity (MW) | Number of Thermal Power Units (units) | Minimum Output (MW) | Climbing Speed (MW/h) | Downhill Speed (MW/h) |
|---|---|---|---|---|
| 1200 | 10 | 400 | 600 | 600 |
| 1000 | 10 | 300 | 500 | 500 |
| A (Dollar/MW2h) | B (Dollar/MWh) | C (Dollar/h) | Start-up cost (Dollar/per) | Shut-down cost (Dollar/per) |
| 0.00148 | 1.2136 | 82 | 1600 | 1000 |
| 0.00289 | 1.2643 | 49 | 1400 | 800 |
| Y/N | Expected Profit (Dollar) | Total Bidding Quantity (MWh) | Expected Additional Power Purchase (MWh) | Wind Power Curtailment (MWh) |
|---|---|---|---|---|
| Y | 4.38 × 108 | 1.17 × 106 | 5.82 × 104 | 269.99 |
| N | 4.00 × 108 | 9.54 × 105 | 0 | 2.97 × 104 |
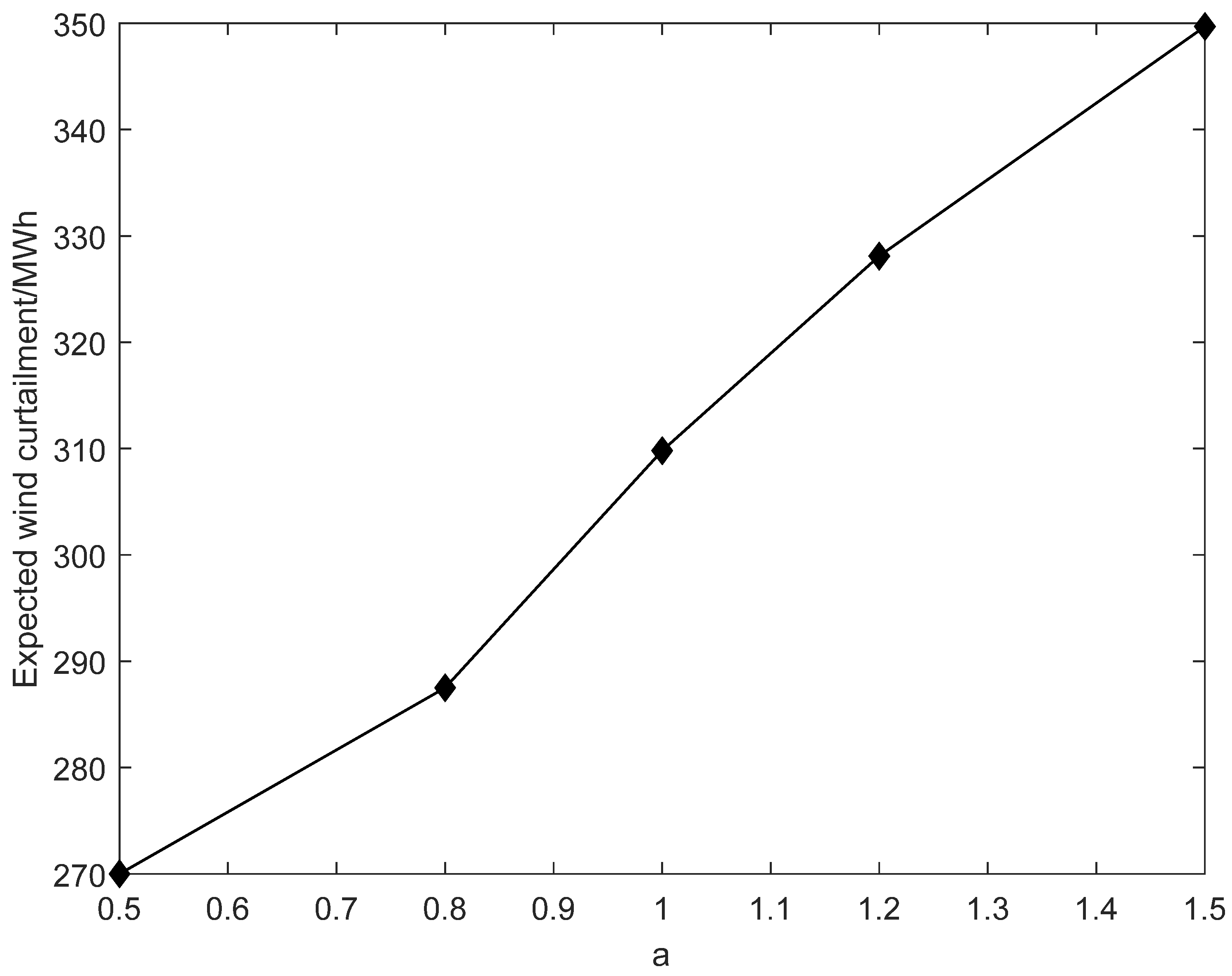
| a | Expected Profit (Dollar) | Total Bidding Quantity (MWh) | Expected Additional Power Purchase (MWh) | Expected Discarding Electricity (MWh) |
|---|---|---|---|---|
| 0.5 | 4.38 × 108 | 1.17 × 106 | 5.82 × 104 | 269.99 |
| 0.8 | 4.27 × 108 | 1.14 × 106 | 5.87 × 104 | 287.45 |
| 1.0 | 4.15 × 108 | 1.10 × 106 | 5.93 × 104 | 309.78 |
| 1.2 | 4.00 × 108 | 1.06 × 106 | 5.98 × 104 | 328.14 |
| 1.5 | 3.80 × 108 | 1.00 × 106 | 6.04 × 104 | 349.61 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De, G.; Tan, Z.; Li, M.; Huang, L.; Song, X. Two-Stage Stochastic Optimization for the Strategic Bidding of a Generation Company Considering Wind Power Uncertainty. Energies 2018, 11, 3527. https://doi.org/10.3390/en11123527
De G, Tan Z, Li M, Huang L, Song X. Two-Stage Stochastic Optimization for the Strategic Bidding of a Generation Company Considering Wind Power Uncertainty. Energies. 2018; 11(12):3527. https://doi.org/10.3390/en11123527
Chicago/Turabian StyleDe, Gejirifu, Zhongfu Tan, Menglu Li, Liling Huang, and Xueying Song. 2018. "Two-Stage Stochastic Optimization for the Strategic Bidding of a Generation Company Considering Wind Power Uncertainty" Energies 11, no. 12: 3527. https://doi.org/10.3390/en11123527
APA StyleDe, G., Tan, Z., Li, M., Huang, L., & Song, X. (2018). Two-Stage Stochastic Optimization for the Strategic Bidding of a Generation Company Considering Wind Power Uncertainty. Energies, 11(12), 3527. https://doi.org/10.3390/en11123527




