Optimization of Wave Energy Converter Arrays by an Improved Differential Evolution Algorithm
Abstract
:1. Introduction
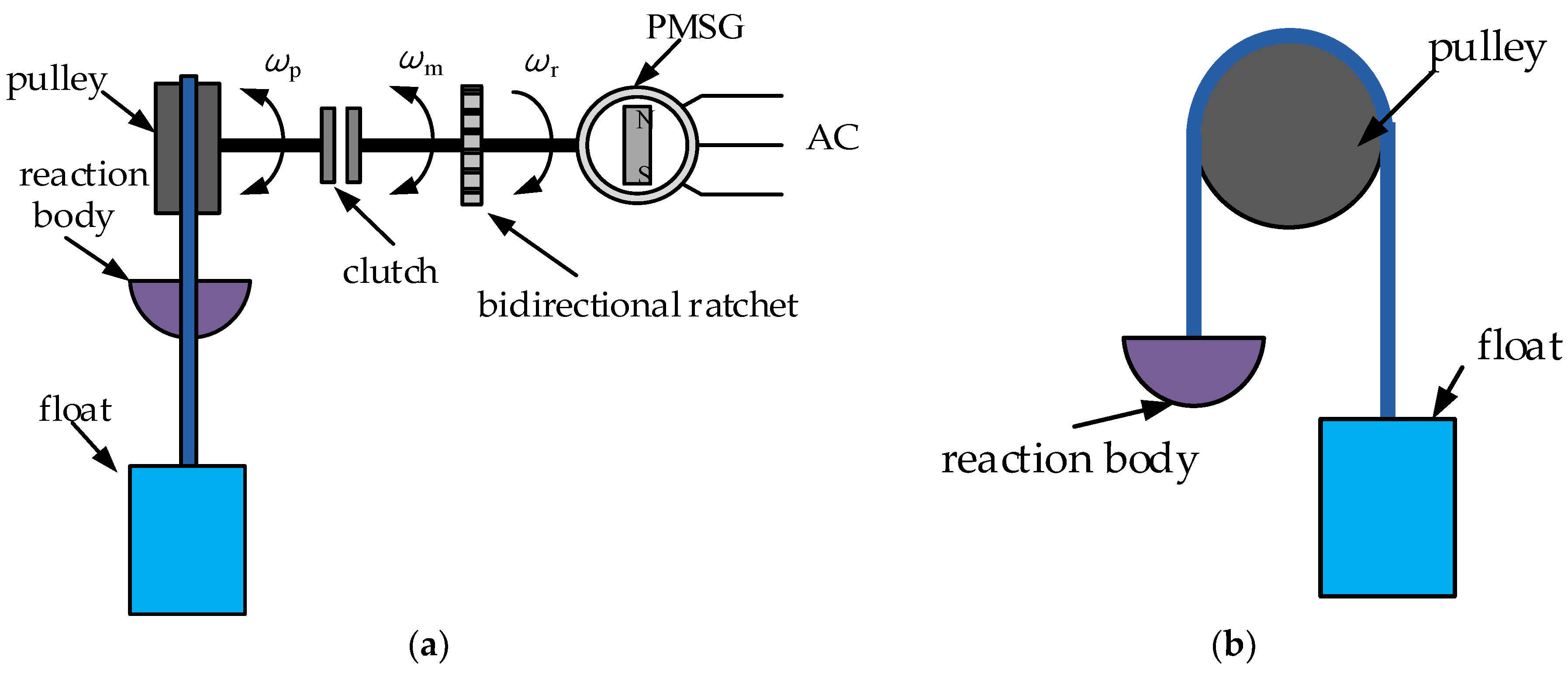
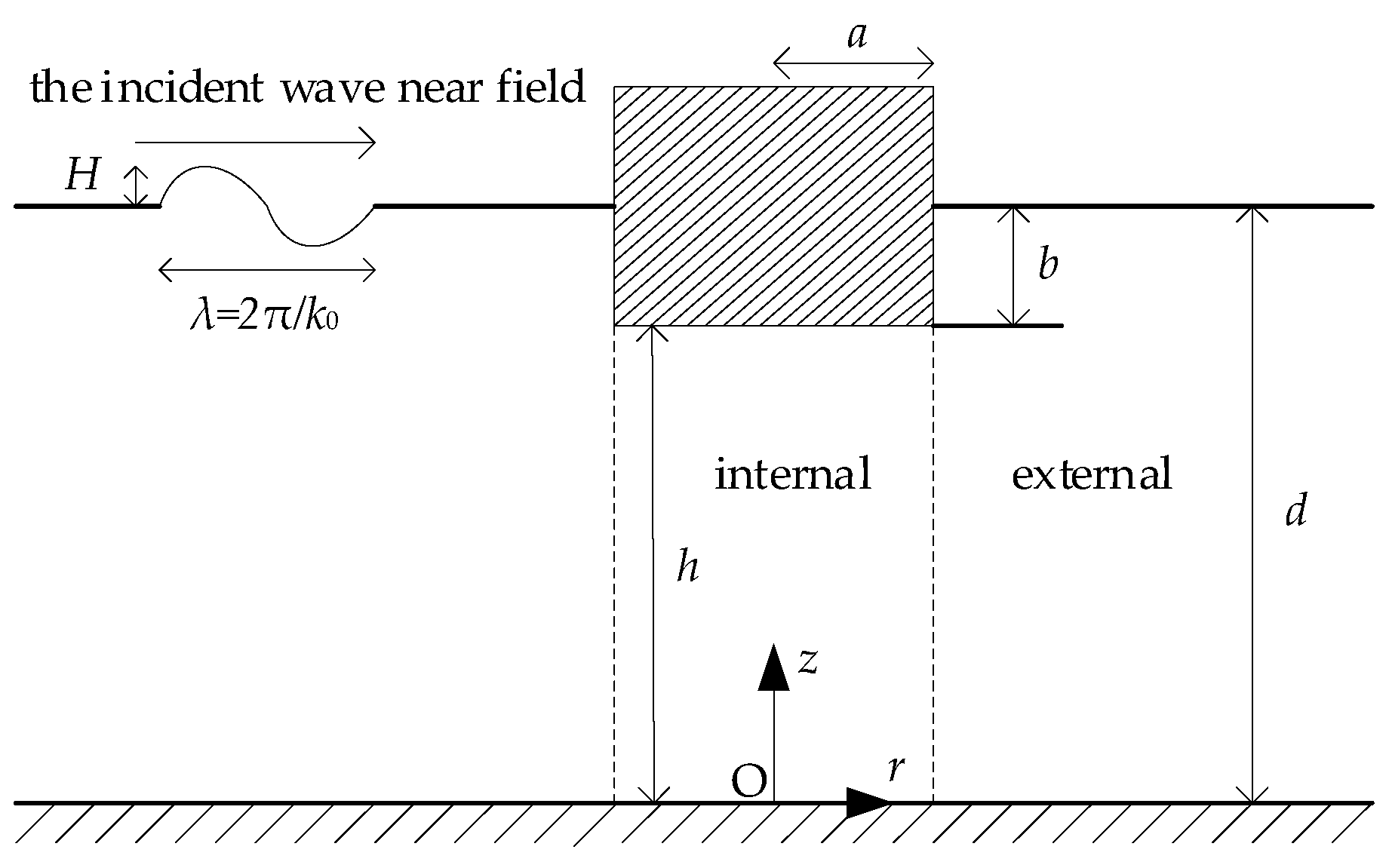
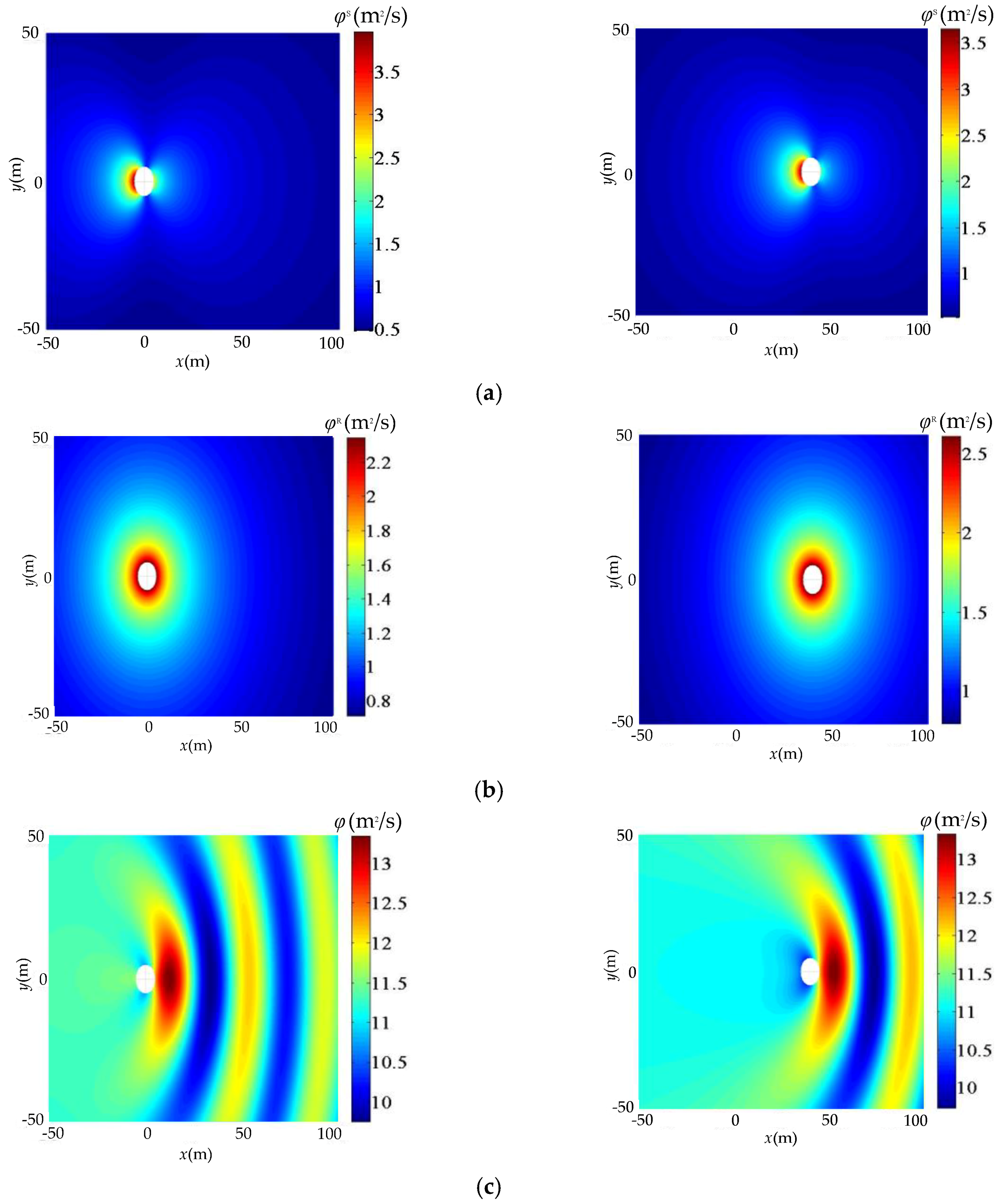
2. The Hydrodynamic Model of an Array System
3. The Differential Evolution Algorithm
- (1)
- Initialization. Randomly generate the 0-th generation population X(0) = {X1(0), X2(0), …, XNp(0)}, where Xi(0) = (x1i(0), x2i(0), …, xDi(0)). The initial population is chosen randomly under the given boundary constraints. It is generally assumed that all initialized populations satisfy the probability of uniform distribution. Set the bounds of the parameter variable as xj(L) < xj < xj(U). Thenwhere the value i is the integer between one and Np, j is the integer between one and D, and rand [0, 1] represents a series of random numbers between [0, 1].
- (2)
- Individual evaluation. Calculate every fitness value f(Xi(G)) in the population.
- (3)
- Mutation operation. Randomly generate three values r1, r2, r3 (r1, r2, r3 ∈ 1, 2, 3, …, Np), where these three different values are integers between one and Np, and they are not the same as i. The following mutation operations are performed for each Xi(G) to generate a mutation vector Vi(G + 1), where Vi(G + 1) = (v1i(G + 1), v2i(G + 1), …, vDi(G + 1)).
- (4)
- Crossover operation. Test vectors Ui(G + 1) = (u1i(G + 1), u2i(G + 1), …, uDi(G + 1)) are obtained by the following crossover operation.where randb(j) refers to the j-th estimation value of the stochastic number generator between [0, 1]. rnbr(i), a stochastically selected sequence, is an integer between one and D. The function of rnbr(i) is to ensure that a value of Vi(G + 1) can at least be obtained in Ui(G + 1), like Xi(G).
- (5)
- Selection operation. Calculate the fitness value f(Ui(G + 1)) of each test vector and compare them with f(Xi(G)). Take the minimum, for example. There existsIt is worth noting that each test vector competes only with the corresponding Xi(G) rather than with each vector in the population.
- (6)
- Calculate the maximum and minimum for corresponding fitness value f(X(G + 1)) of the new population X(G + 1). Determine whether the difference between these two values is smaller than the threshold set in advance. If the calculation result of the difference is over the threshold and the number of iterations below its maximum (i.e., G < Gm), then repeat the above operation from Steps (2) to (6).
4. Improvement in the Differential Evolution Algorithm
5. Parameters and Interaction Coefficient Analysis for WEC Arrays
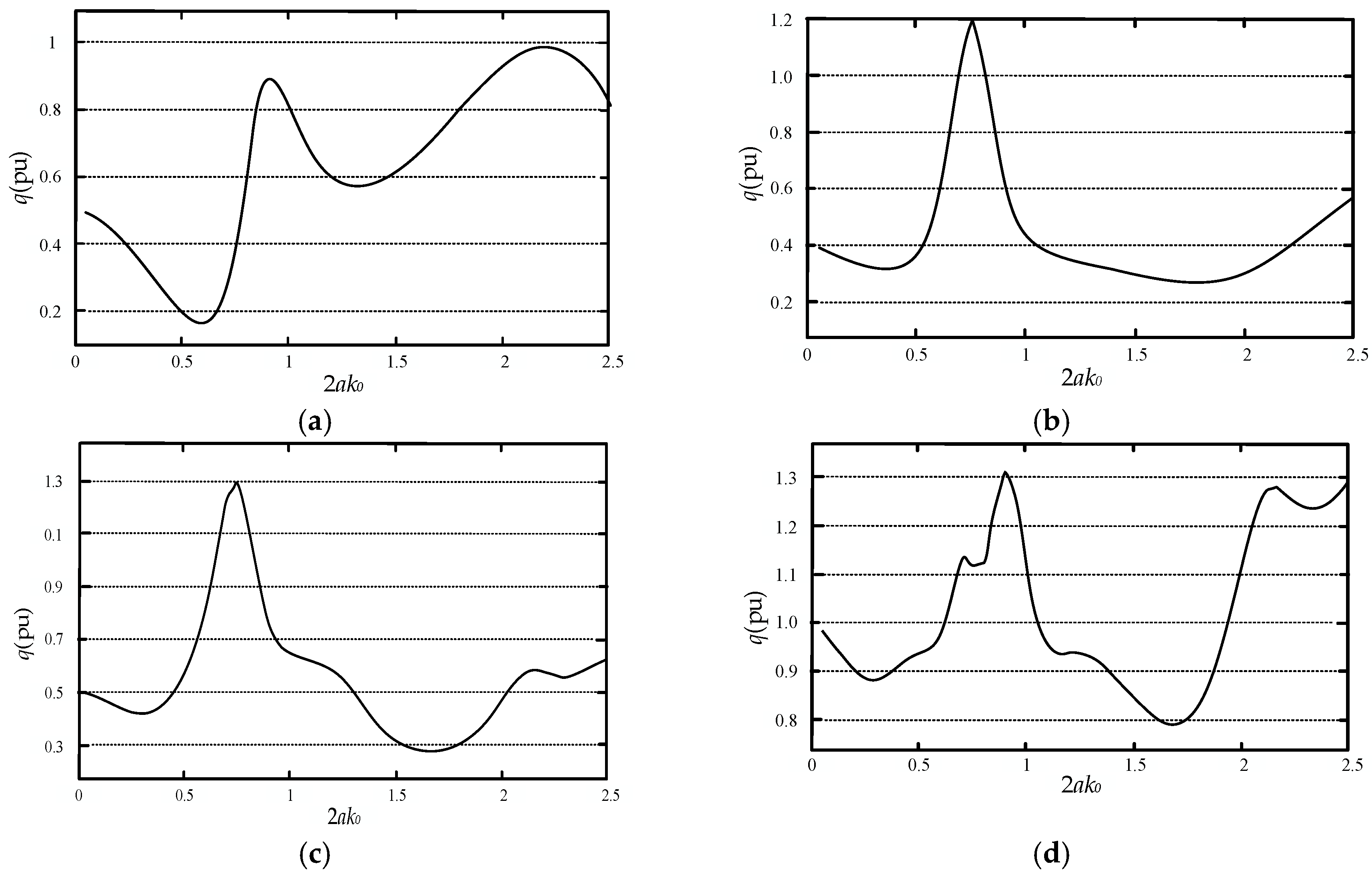
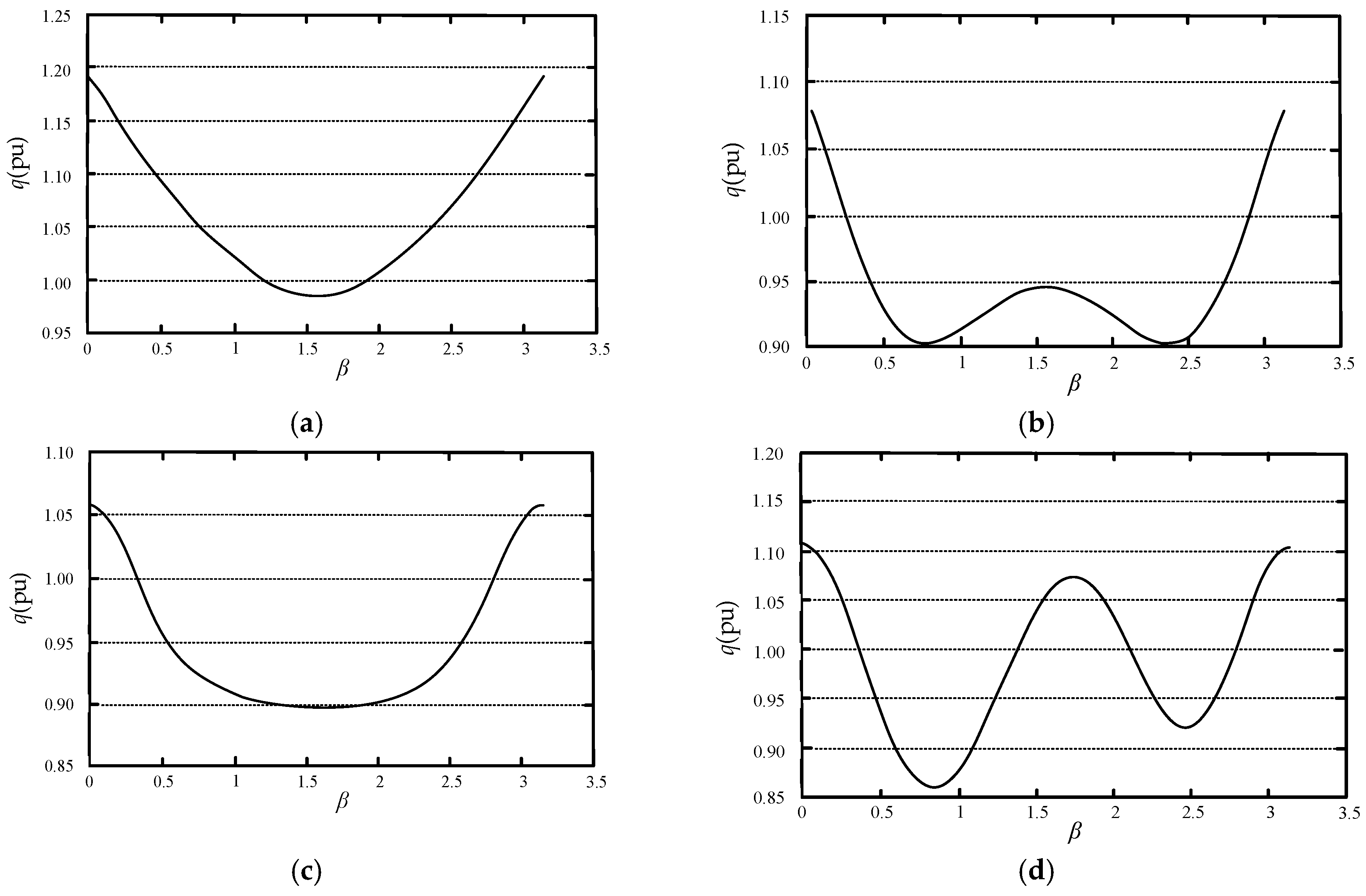
5.1. The Relationship between q and k0
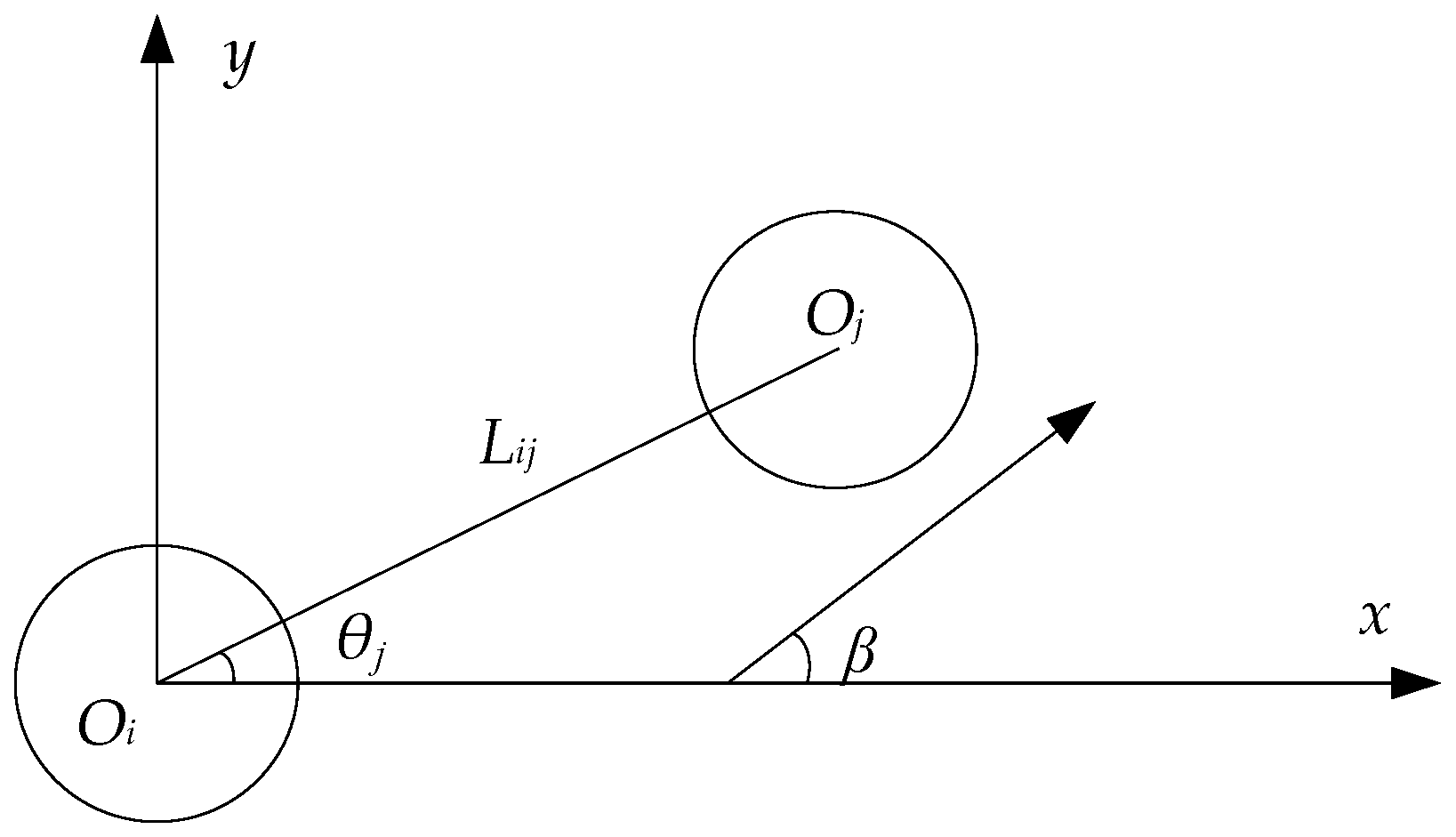
5.2. The Relationship between q and β
6. Simulation and Analysis of WEC Arrays
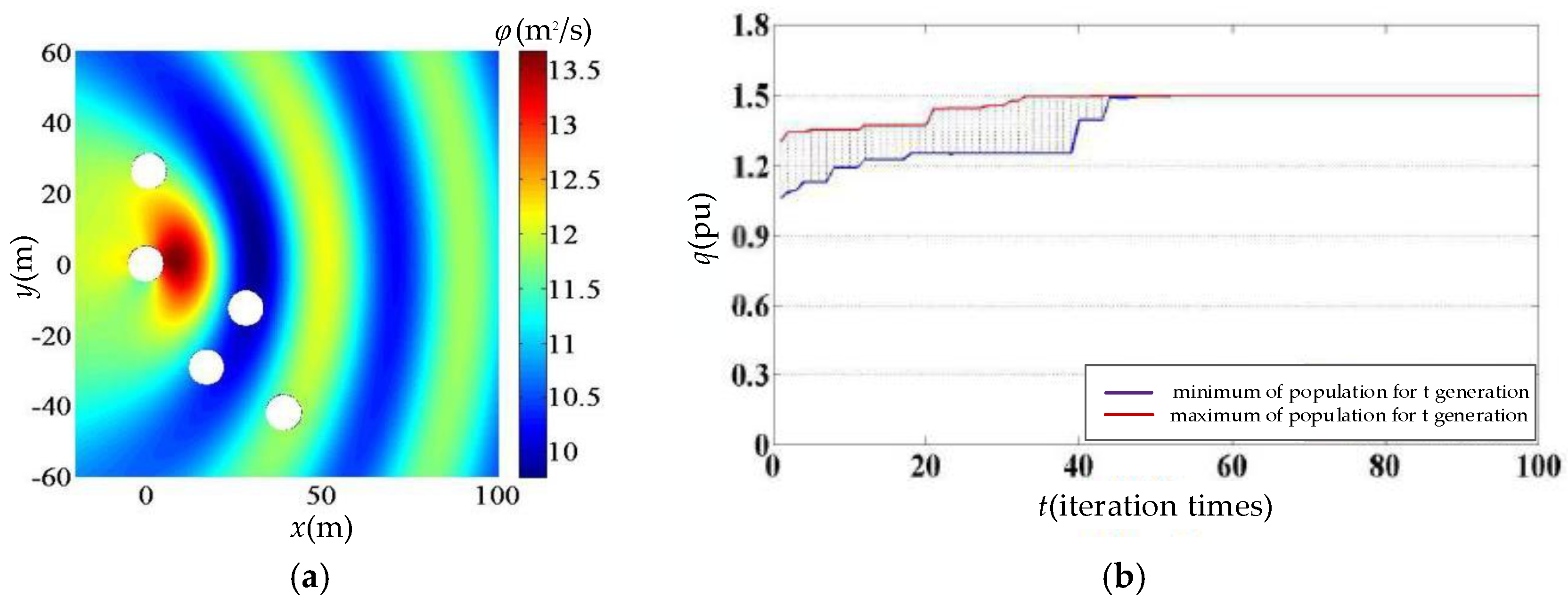
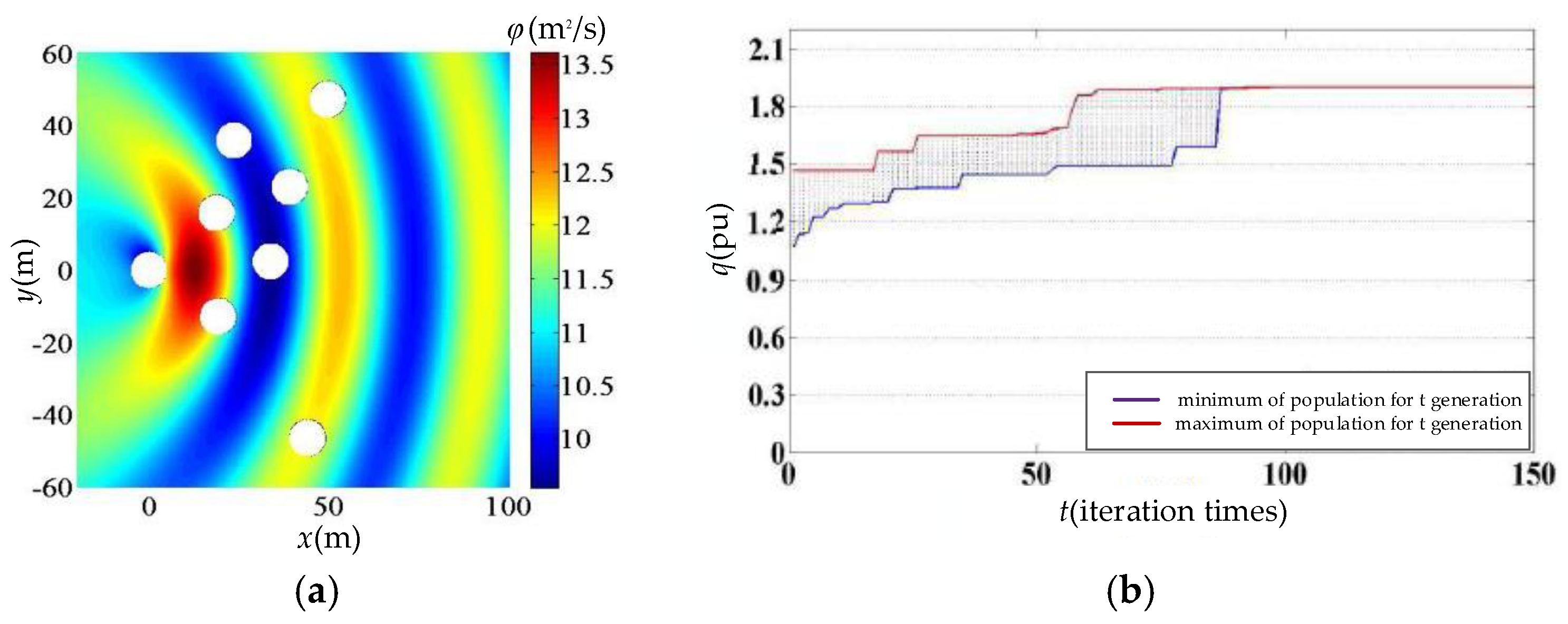
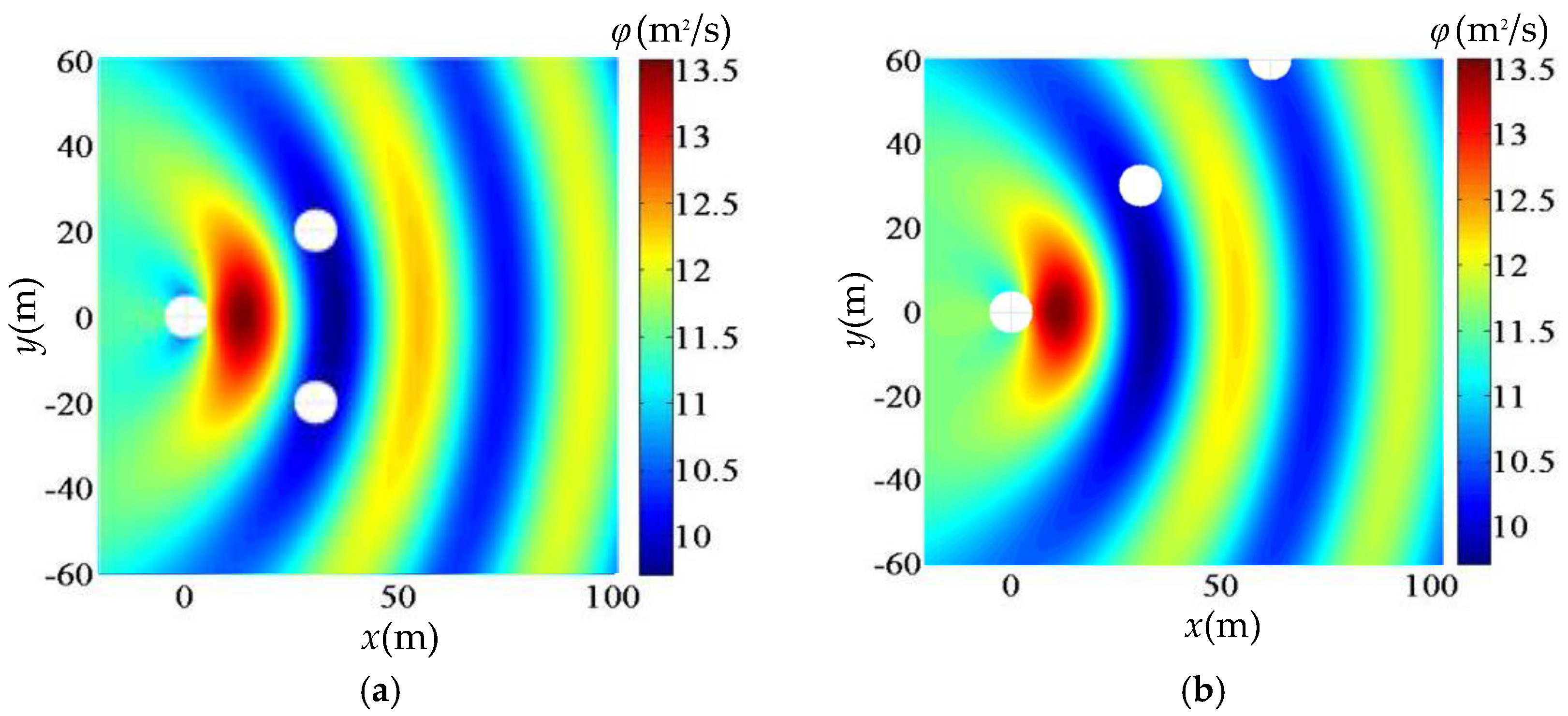
6.1. Simulation of Three-Float, Five-Float, and Eight-Float Arrays
6.2. Comparison with the Traditional DE Algorithm
6.3. Comparison with the Homogeneous Distribution of the Three-Float Array
7. Discussion
- (1)
- When the array is larger, the influence between floats is larger, and more radiation and scattered wave energy can be extracted.
- (2)
- The total wave energy extracted by WEC arrays is greatly improved compared to that of the single float running mode.
- (3)
- The optimization of an array under the improved DE algorithm greatly impacts the output of WEC arrays, simultaneously satisfying both convergence precision and speed.
- (4)
- The optimal layout of the array system is not usually homogeneously distributed. The energy obtained via an inhomogeneous array distribution is greater than that of a homogeneous distribution.
- (5)
- With the introduction of an adaptive mutation operator, the layout optimization of WEC arrays is superior to that of a constant mutation operator.
Author Contributions
Funding
Conflicts of Interest
References
- Yan, Y.B. Principle and Device of the Ocean Wave Energy Conversion Generation, 1st ed.; Shanghai Scientific & Technical Publishers: Shanghai, China, 2013; ISBN 978-7-5478-1527-4. [Google Scholar]
- Twidell, J.; Weir, A.D. Renewable Energy Resources, 2nd ed.; Taylor and Francis: London, UK, 2006; ISBN 978-0-4192-5320-4. [Google Scholar]
- Chu, H.M. Control of Wave Power Generation Arrays with Modular Multilevel Converter. Master’s Thesis, Tianjin University, Tianjin, China, 2014. [Google Scholar]
- Cheng, Y.L.; Dang, Y.; Wu, Y.J. Status and Trends of the Power Generation from Wave. Appl. Energy Technol. 2009, 12, 26–30. [Google Scholar]
- Dalton, G.J.; Alcorn, R.; Lewis, T. Case study feasibility analysis of the pelamis wave energy convertor in Ireland, Portugal and North America. Renew. Energy 2013, 35, 443–455. [Google Scholar] [CrossRef]
- He, G.Y.; Yang, S.H.; He, H.Z.; Wang, F.Y. Hydrodynamic analysis of array-type device of wave energy generation. J. Hydroelectr. Eng. 2015, 34, 118–124. [Google Scholar]
- Zhang, Y.; Lin, Z. Advances in ocean wave energy converters using piezoelectric materials. J. Hydroelectr. Eng. 2011, 30, 146–148. [Google Scholar]
- Han, B.F.; Chu, J.K.; Xiong, Y.S.; Yao, F. Progress of research on ocean energy power generation. Power Syst. Clean Energy 2012, 28, 61–65. [Google Scholar]
- Budal, K. Theory for absorption of wave power by a system of interacting bodies. J. Ship Res. 1977, 21, 248–253. [Google Scholar]
- Mavrakos, S.A.; Kalofonos, A. Power absorption by arrays of interacting vertical axisymmetric wave-energy devices. J. Offshore Mech. Arct. Eng. 1997, 119, 244–250. [Google Scholar] [CrossRef]
- Yilmaz, O. Hydrodynamic interactions of waves with group of truncated vertical cylinders. J. Waterw. Port Coast. Ocean Eng. 1998, 124, 272–279. [Google Scholar] [CrossRef]
- Yilmaz, O.; Incecik, A. Analytical solutions of the diffraction problem of a group of truncated vertical cylinders. Ocean Eng. 1998, 25, 385–394. [Google Scholar] [CrossRef]
- Garrett, C.J.R. Wave forces on a circular dock. J. Fluid Mech. 1971, 46, 129–139. [Google Scholar] [CrossRef]
- Kagemoto, H.; Yue, D.K.P. Interactions among multiple three-dimensional bodies in water waves: An exact algebraic method. J. Fluid Mech. 1986, 166, 189–209. [Google Scholar] [CrossRef]
- Child, B.F.M.; Venugopal, V. Optimal configurations of wave energy device arrays. Ocean Eng. 2010, 37, 1402–1417. [Google Scholar] [CrossRef]
- Blanco, M.; Moreno, T.; Lafoz, M.; Ramírez, D. Design Parameter Analysis of Point Absorber WEC via an Evolutionary-Algorithm-Based Dimensioning Tool. Energies 2015, 8, 1203–11233. [Google Scholar] [CrossRef]
- Bozzi, S.; Bizzozero, F.; Gruosso, G.; Passoni, G.; Giassi, M. Analysis of interaction of point absorbers’ arrays for seawave electrical energy generation in italian seas. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Anacapri, Italy, 22–24 June 2016; pp. 1369–1374. [Google Scholar]
- Mercadé Ruiz, P. Hydrodynamic Modelling and Layout Optimisation of Wave Energy Converter Arrays. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 2017. [Google Scholar]
- Ferri, F. Computationally efficient optimisation algorithms for WECs arrays. In Proceedings of the 12th EWTEC-Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017; pp. 1–7. [Google Scholar]
- Verbrugghe, T.; Stratigaki, V.; Troch, P.; Rabussier, R.; Kortenhaus, A. A Comparison Study of a Generic Coupling Methodology for Modeling Wake Effects of Wave Energy Converter Arrays. Energies 2017, 10, 1697. [Google Scholar] [CrossRef]
- Mercadé Ruiz, P.; Nava, V.; Mathew, B.R.T.; Ruiz Minguela, P.; Ferri, F.; Peter Kofoed, J. Layout Optimisation of Wave Energy Converter Arrays. Energies 2017, 10, 1262. [Google Scholar] [CrossRef]
- Thomas, S.; Eriksson, M.; Göteman, M.; Hann, M.; Isberg, J.; Engström, J. Experimental and Numerical Collaborative Latching Control of Wave Energy Converter Arrays. Energies 2018, 11, 3036. [Google Scholar] [CrossRef]
- Balitsky, P.; Verao, F.G.; Stratigaki, V.; Troch, P.; Troch, P. Assessment of the Power Output of a Two-Array Clustered WEC Farm Using a BEM Solver Coupling and a Wave-Propagation Model. Energies 2018, 11, 2907. [Google Scholar] [CrossRef]
- OceanEd. Available online: https://github.com/D-Forehand/OceanEd/ (accessed on 1 December 2018).
- Forehand, D.I.M.; Kiprakis, A.E.; Nambiar, A.J.; Wallace, A.R. A fully coupled wave-to-wire model of an array of wave energy converters. IEEE Trans. Sustain. Energy 2016, 7, 118–128. [Google Scholar] [CrossRef]
- Wang, D. Study of the Combined Oscillating Buoys’ Layout. Master’s Thesis, Ocean University of China, Qingdao, China, 2015. [Google Scholar]
- Fang, H.W.; Chen, Y.; Hu, X.L. Wave Power Generation and its Control. J. Shenyang Univ. 2015, 27, 376–384. [Google Scholar]
- Bangmin, Z. Computational Hydrodynamics, 1st ed.; Wuhan University Press: Wuhan, China, 2001; ISBN 7-307-03296-1. [Google Scholar]
- Fang, H.W.; Cheng, J.J.; Ren, Y.Q. Force analysis of float-type wave energy converter. J. Tianjin Univ. 2014, 47, 446–451. [Google Scholar]
- Mercadé Ruiz, P.; Ferri, F.; Kofoed, J.P. Experimental validation of a wave energy converter array hydrodynamics tool. Sustainability 2017, 9, 115. [Google Scholar] [CrossRef]
- Child, B.F.M. On the Configuration of Arrays of Floating Wave Energy Converters. Ph.D. Thesis, Edinburgh University, Edinburgh, UK, 2011. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions, 1st ed.; Government Printing Office: Washington, DC, USA, 1964. [Google Scholar]
- Kagemoto, H.; Yue, D.K.P. Hydrodynamic interaction analyses of very large floating structures. Mar. Struct. 1993, 6, 295–322. [Google Scholar] [CrossRef]
- Evans, D.V. Some Analytic Results for Two and Three Dimensional Wave- Energy Absorbers. Power from Sea Waves; Academic Press, Inc.: London, UK, 1980; pp. 213–249. [Google Scholar]
- Zhou, Y.P.; Gu, X.S. Development of Differential Evolution Algorithm. Control. Instruments Chem. Ind. 2007, 34, 1–5. [Google Scholar]
- Wu, L.H. The Research and Applications of Differential Evolution Algorithm; Hunan University: Hunan, China, 2007. [Google Scholar]
- Liu, B.; Wang, L.; Jin, Y.H. Advances in differential evolution. Control Decis. 2007, 22, 721–729. [Google Scholar]
- Gao, Y.L.; Liu, J.M. Parameter study of differential evolution algorithm. J. Nat. Sci. Heilongjiang Univ. 2009, 26, 81–85. [Google Scholar]
- Yang, Z.Y.; Tang, K. An overview of parameter control and adaptation strategies in differential evolution algorithm. CAAI Trans. Intell. Syst. 2011, 6, 415–423. [Google Scholar]


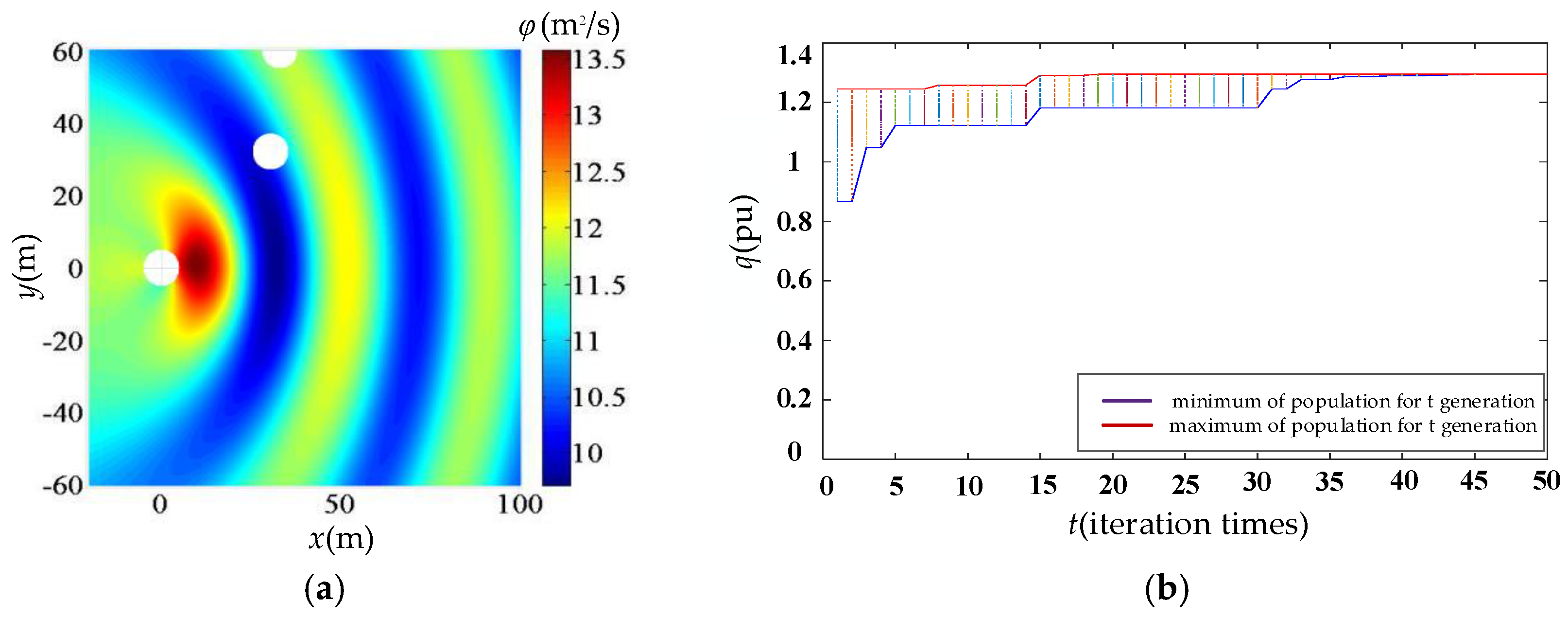
| Parameters | Value |
|---|---|
| radius of float (m) | 5 |
| depth of immersion(m) | 5 |
| depth of water (m) | 40 |
| the height of the waves (m) | 1 |
| gravitational acceleration (m/s2) | 9.8 |
| density of sea water (kg/m3) | 1025 |
| wave number | 0.08 |
| incidence angle(rad) | 0 |
| population size | 15 |
| basic value of mutation operator | 0.5 |
| mutation operator | 0.5–1 |
| crossover probability factor | 0.9 |
| The Float Number j | Abscissa x (m) | Ordinate y (m) | Interaction Coefficient qj (pu) | Interaction Coefficient q (pu) |
|---|---|---|---|---|
| 1 | 0 | 0 | 1.295 | 1.358 |
| 2 | 27.895 | 49.928 | 1.554 | |
| 3 | 29.175 | 29.323 | 1.226 |
| The Float Number j | Abscissa x (m) | Ordinatey (m) | Interaction Coefficient qj (pu) | Interaction Coefficient q (pu) |
|---|---|---|---|---|
| 1 | 0 | 0 | 1.408 | 1.500 |
| 2 | 0.808 | 26.149 | 1.673 | |
| 3 | 17.149 | −29.055 | 1.459 | |
| 4 | 28.355 | −12.462 | 1.438 | |
| 5 | 39.021 | −41.860 | 1.524 |
| The Float Number j | Abscissax (m) | Ordinatey (m) | Interaction Coefficient qj (pu) | Interaction Coefficient q (pu) |
|---|---|---|---|---|
| 1 | 0 | 0 | 1.636 | 1.898 |
| 2 | 18.661 | 15.639 | 2.969 | |
| 3 | 19.117 | −12.829 | 2.010 | |
| 4 | 23.598 | 35.684 | 1.817 | |
| 5 | 33.668 | 2.395 | 3.076 | |
| 6 | 38.959 | 22.869 | 1.771 | |
| 7 | 43.899 | −46.321 | 1.203 | |
| 8 | 49.457 | 46.982 | 0.706 |
| The Float Number j | Abscissax (m) | Ordinate y (m) | Interaction Coefficient qj (pu) | Interaction Coefficient q (pu) |
|---|---|---|---|---|
| 1 | 0 | 0 | 1.220 | 1.295 |
| 2 | 33.001 | 60.000 | 1.505 | |
| 3 | 30.401 | 32.040 | 1.163 |
| Array Layout | The Float Number j | Abscissa x (m) | Ordinate y (m) | Interaction Coefficient qj (pu) | Interaction Coefficient q (pu) |
|---|---|---|---|---|---|
| Equicrural triangle | 1 | 0 | 0 | 0.894 | 0.873 |
| 2 | 30 | 20 | 0.862 | ||
| 3 | 30 | −20 | 0.862 | ||
| Straight line | 1 | 0 | 0 | 1.216 | 0.983 |
| 2 | 30 | 30 | 1.044 | ||
| 3 | 60 | 60 | 0.691 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, H.-W.; Feng, Y.-Z.; Li, G.-P. Optimization of Wave Energy Converter Arrays by an Improved Differential Evolution Algorithm. Energies 2018, 11, 3522. https://doi.org/10.3390/en11123522
Fang H-W, Feng Y-Z, Li G-P. Optimization of Wave Energy Converter Arrays by an Improved Differential Evolution Algorithm. Energies. 2018; 11(12):3522. https://doi.org/10.3390/en11123522
Chicago/Turabian StyleFang, Hong-Wei, Yu-Zhu Feng, and Guo-Ping Li. 2018. "Optimization of Wave Energy Converter Arrays by an Improved Differential Evolution Algorithm" Energies 11, no. 12: 3522. https://doi.org/10.3390/en11123522
APA StyleFang, H.-W., Feng, Y.-Z., & Li, G.-P. (2018). Optimization of Wave Energy Converter Arrays by an Improved Differential Evolution Algorithm. Energies, 11(12), 3522. https://doi.org/10.3390/en11123522






