1. Introduction
New challenges for the efficient management of the power distribution system are posed by the ongoing deregulation of power distribution in many countries, the growing distributed power generation from renewable sources, the introduction of distributed energy storage systems and the increasing diffusion of electric vehicles. Smart grids offer a viable solution through unprecedented flexibility in energy generation and distribution [
1].
Over the last decade, a growing number of smart meters have been installed worldwide. These, together with the communication and data management network, constitute the advanced metering infrastructure (AMI) that will play a fundamental role in electrical distribution systems, by recording user load profiles, enabling two-way communication between the user and the distributor and allowing smarter systems for the management of energy resources [
2].
How to use the volume of data from smart meters to promote and improve efficiency and sustainability of demand has become a major research topic worldwide [
3]. Control decisions for the smart grid should be made continuously at both the aggregate and granular levels. To achieve this and ensure network reliability, the ability to predict future demand is of paramount importance.
Load forecasts have been widely used by the electrical sector. Power distribution companies rely on forecasts with different time horizons to support both system operability and planning. Retail electricity suppliers are making pricing, procurement and hedging decisions based largely on the expected load of their customers.
In recent years, moreover, there has been a steady trend towards the electrification of energy consumption, linked to the need for greater use of renewable energy sources, which results in a load profile increasingly characterized by the presence of peaks in consumption due to human behavior, that can lead to problems for electricity providers [
4]. The presence of peaks in consumption and generation linked to human behaviour and renewable sources leads to the research of mitigation techniques, for example using a variable pricing system that pushes users to plan as much as possible the use of energy resources, in addition to the use of distributed storage systems, as tested in the project H2020 NETfficient, in which the techniques described in this work have found application [
5].
The value that smart meters bring to load forecasting and more generally to the energy distribution system is manifold. First, smart meters enable distribution companies and electricity retailers to better understand and predict the load on a single house or building. Secondly, the high granularity of the load data provided by smart meters offers great potential for improving aggregate forecast accuracy [
3]. In addition, the forecast of energy consumption over time allows property and building managers to plan energy consumption over time, shifting energy use to off-peak periods, improving energy purchase plans, and allowing them to assess their consumption habits, identifying possible margins.
Since the household loads are more volatile than the aggregate load, the higher the load level, the more uniform the profile is and the less uncertain the forecast is. The energy forecast at the smart meter level is not a trivial problem, as it depends on the complexity of the energetic behavior of the building, in turn related to climatic conditions and to the operation of lighting systems and HVAC (heating, venting and air conditioning), but especially for the difficulty in predicting the behavior of the occupants, influenced by multiple social factors [
6,
7].
To address the problem of load forecasting at the level of smart meters, the research community has attempted different approaches, from adapting techniques already widely used for aggregate load forecasting, to developing new techniques or using a combination of the same [
3]. Methods such as the semi parametric additive model [
8], exponential smoothing [
9], and classical seasonal time series methods have been applied to load forecast at the building level [
10], as well as methods based on artificial neural networks (ANN) and support vector machines (SVM) [
11]. A 2012 [
12] study compared several existing techniques, including linear regression (LR) as well as different types of ANNs and SVMs on two datasets: one for two commercial buildings and the other for three residential homes. The results showed that the techniques used could provide reliable forecasts in the first case but not in the second, because of the greater variability of the load. In [
13] the load forecast is studied both at the building level and at the state and provincial level through a self-recurrent wavelet neural network.
The recent trend is to use deep learning techniques, with recursive or convolutional or hybrid neural networks. The conditional restricted Boltzmann machine (CRBM) and factored conditional restricted Boltzmann machine (FCRBM) have been evaluated in [
6] to estimate the energy consumption of a household. The FCRBM achieves the highest accuracy in load forecasting compared to ANN, RNN (Recurrent Neural Network), SVM and CRBM. Different resolutions ranging from one minute to one week have been tested. The same dataset has been analyzed in two successive works in which the effectiveness of recursive networks of the type long short term memory (LSTM) has been investigated both in the standard form and in the form sequence to sequence (S2S) [
14] and in which the accuracy of convolutional neural networks (CNNs) [
15] has been evaluated, obtaining comparable or superior results to those obtained with the FCRBM algorithm.
Due to the high variability of smart meter measurements, it may be necessary to perform probabilistic forecasting in operational practice. The interested reader can find in [
16] a review of the different methods proposed in this area for aggregate load forecasting. Probabilistic load forecasting has also been carried out on individual load profiles; in [
17] a method combining gradient boosting (GB) and quantile regression has been proposed to quantify uncertainty and generate probabilistic forecasts, while in [
18] the conditional kernel density (CKD) method have been tested. Recently, a point and probabilistic forecast of the load for 100 low voltage (LV) feeders has been conducted in [
19] comparing several methods such as Holt-Winters-Taylor seasonal exponential smoothing, kernel density estimation, seasonal linear regression and two autoregressive (AR) methods.
The aim of this work is to implement a forecasting procedure for household consumption using only smart-meter load data, with different time horizons and producing both deterministic and probabilistic forecasts. The most recent research sees an increased use of deep learning techniques for load forecasting, their real effectiveness for forecasting time series with seasonality is however at least partially questioned on the basis of the results actually obtained with these methods when compared with classical statistical methods. S. Makridakis in a recent article [
20] analyses the performance of the methods proposed for M3 competition, highlighting how statistical methods allow obtaining, on average, more accurate forecasts and with a lower computational cost. It also provides suggestions on how to exploit the undoubted potential of machine learning (ML) techniques also in the context of time series forecasting. In particular, it highlights, among other things, the need for data pre-treatment, applying transformations and procedures of de-trending and de-seasonalization that allow obtaining a stationary signal, and the accurate assessment of the risk of over-fitting for ML procedures.
In our case, these indications translate into a separation between the long-term components of the signal, associated with the trend and seasonality, and the short-term components linked to stochastic variations in the average trend of consumption of a consumer, which we will treat as two distinct problems in a hybrid methodology. The method we propose in fact provides for an estimate of the average long-term behavior of users, to which a short-term auto-regressive forecast is superimposed, linked to the deviation of the previous estimate from the most recent consumption measures. A similar hybrid approach, in which the effects of long and short term are separated, has been recently used by S. Smyl in the winning procedure of the recent M4 competition [
21].
The proposed methodology is implemented using ML techniques with limited computational requirements in order to allow an implementation also in low cost devices installed directly at the user’s household. In particular, we will use the random forest (RF) technique for long-term forecasting and a simple linear regression for short-term forecasting. We will also realize a probabilistic forecast through a simple persistence of the distribution of forecast errors measured in the training dataset.
This work will highlight:
The convenience of a hybrid approach, which separates long-term and short-term effects for load forecasting when using machine learning techniques;
The effectiveness of the proposed procedure for predicting smart meter loads;
The relative contribution of these two components to the accuracy of forecasting;
The importance and added value of a probabilistic forecast for household load prediction.
The application of the proposed procedure to a public dataset already studied in the literature allows direct comparison with the results obtained with other methodologies. The results obtained show a much higher accuracy than all the methods applied so far for all time resolutions and forecast horizons.
The paper is structured as follows: The proposed methodology is described in the
Section 2; the dataset is analysed and the metrics used are described in the
Section 3; the results are presented and discussed in the
Section 4 and
Section 5, finally the
Section 6 presents our conclusions and expected developments for this activity.
2. Proposed Method
The electricity consumed by a family can be decomposed into a long-term and a short-term component. The first component includes the effect of any upward or downward trends in consumption and, above all, the effect of the periodicity of average demand. In the case of electricity consumption, a number of daily, weekly and annual frequencies are distinguished. This component describes the habits of the family. However, seasonal behaviour can only describe average behaviour and not short-term fluctuations linked to deviations from the standard routine. This second component is clearly difficult to predict, it can be linked to exceptional events, to short-term changes linked for example to the ignition of a energy-intensive appliance and, more generally, to deviations from the routine. It is assumed that these short-term variations can be described by means of an auto-regressive function, i.e. linking consumption in the immediate future, with respect to the instant of emission of the forecast, to the load measured in the immediately preceding times.
The total load can therefore be described by means of an additive model:
where
is the load at the time
t,
and
are the long term and short term components, and
is the forecast error.
In this paper, the long-term component of the forecast is estimated using a random forest (RF) regression model. The RF methodology has been used for short-term load forecasting in the literature, for example in [
22] the authors use this technique to predict the hourly electrical load data of the Polish electrical system, in [
23] this technology is applied to load forecasting at a university campus in Cartagena (Spain), in [
24] the accuracy of consumption forecasts of residential customers one day in advance is analyzed as a function of time, granularity, and size of residential customers.
The random forest method, introduced by Breiman et al. [
25] is an ensemble learning methodology that can be used for both classification and regression. It is based on the construction of a forest of unrelated decision trees, which corrects the trend towards over-fitting on the training set of decision trees.
In the training phase the technique of bootstrap aggregating (bagging) is applied to tree learning, through which a random subset with replacement from the training set is selected B times, the subset of samples from the training set X is identified with and the corresponding label . For each of these subset a tree is fitted. In the decision trees training process an additional randomization, called feature bagging, is used, which consists in considering for each candidate split a random subset of features.
After training, the prediction for a
x sample is obtained by averaging the predictions of all the generated regression trees:
Our procedure uses a forest of 100 trees, whose optimal depth is established through a cross-validation procedure. The features used are only of temporal type and uniquely identify each measurement: the year, the day of the year, the day of the week, and the time of the day, expressed as a real number including fractions of an hour.
Many of the recently proposed algorithms for predicting household consumption use a purely auto-regressive approach using non-linear methods based on neural networks. For the short term component of the forecast we will use an approach based on a simple and fast step-wise multiple linear regression (MLR). It is given by:
with
The short-term forecast for each time , with , is a linear combination of the residual r of the long-term forecast relative to the actual value of power consumption for the most recent steps. denote the regression parameters. The forecast is obtained simultaneously for future steps.
Given the great variance of domestic consumption, it is important to provide an estimate of the forecast error for each forecast time. This can be obtained in a simple way by analyzing the distribution of the error that the model has made in the training set and applying the same distribution of the error also in the forecasting phase. The distribution of the error is described by 19 quantiles (), and is parameterized according to the time of forecast j and for each hour of the day h, thus creating a look-up table to be applied even in the forecast phase.
The procedures described were implemented using only public domain tools. The code is written entirely in python, using the pandas libraries [
26] and scikit-learn [
27] for machine learning tools. All libraries have been used in the latest revision available at the time of writing. The procedure has minimal requirements for its execution, the time required for training and forecasting are listed in Table 3, a PC with 16 GB of RAM and a quad core Intel i5 processor at 3.2 GHz has been used for the analysis.
3. Evaluation Setup
The presented method was evaluated on a reference dataset of electricity consumption for a single residential customer, called “Individual household electric power consumption Data Set” [
28]. This archive contains 2,075,259 measurements gathered in a house located in Sceaux (7 km of Paris, France) between December 2006 and November 2010 (47 months). The dataset contains the household global minute-averaged active power measurement, as well as measurements of reactive power, current, voltage and energy consumed in three sub-meters intended respectively for the kitchen, a laundry-room with the electric water-heater, and an air conditioner circuit. In this paper we will only deal with the global active power.
Table 1 shows a description of the time series, varying with the aggregation time being used. The original series has a sampling rate of one minute, in the following, we will analyze forecast scenarios in which we average the measurement of consumption over periods of a quarter of an hour, of an hour or of a week. The time series is not complete with 1.25% of missing data. The missing measurements are replaced with the value measured a week earlier at the same time.
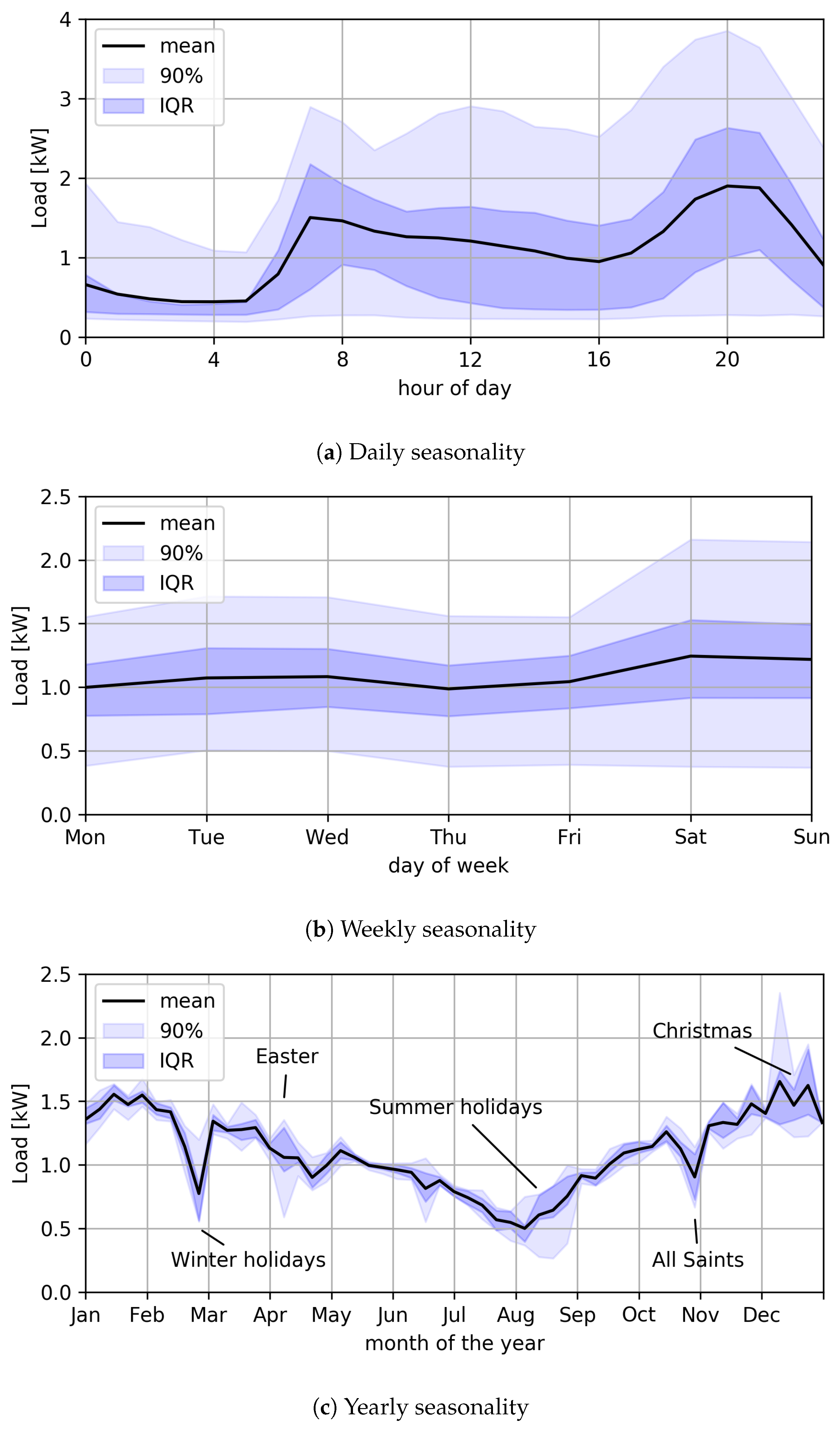
The daily, weekly and annual periodicity of the time series is illustrated in
Figure 1. In
Figure 1a the measurements are averaged over the hour, and the average value of the consumption of the whole series is shown as a function of the time of day, as well as the variation of the measurements around the average value, expressed by the inter quartile range (IQR) and by the interval between 5% and 95%. The weekly seasonality, with average daily consumption values, is shown in
Figure 1b, while
Figure 1c shows the annual seasonality with average consumption values on the week.
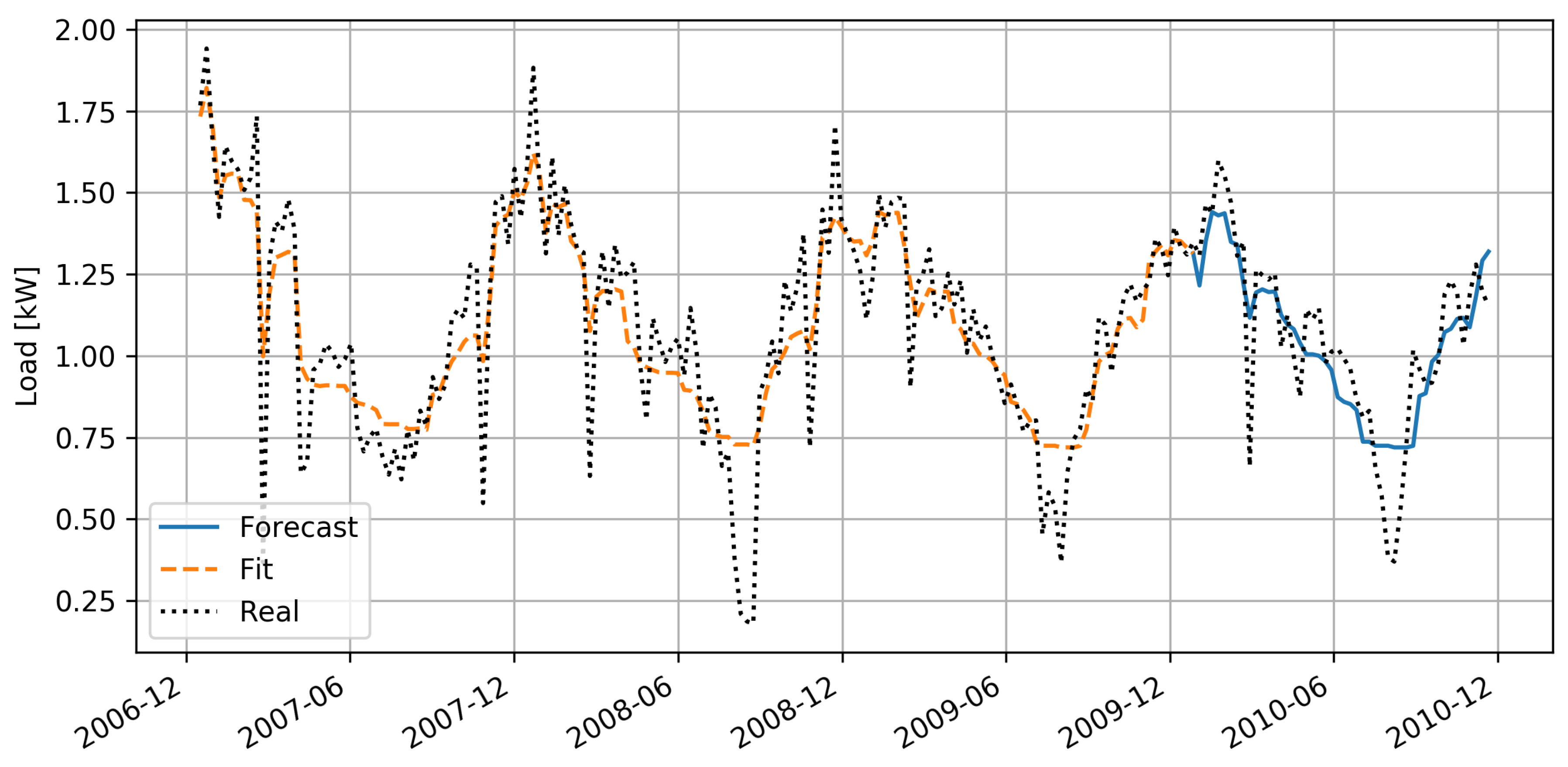
With almost four years of data available, it was decided to use the first three years of measurements for model training and to use the last year for verification, just like in [
6,
14,
15]. The choice of the parameters of the RF model was made through a validation procedure, aimed at determining the optimal depth of the tree. Validation is carried out using the third year of measurements as a validation set and training on the first two years of data. The optimal depth value is the one that determines the smallest fitting error in the validation set. The remaining parameters of the RF algorithm have been fixed, in particular, feature bagging is performed on half of the features and the number of trees in the forest is fixed at 100, having verified that a larger value does not bring any benefit in terms of accuracy for this dataset.
Some well-known accuracy metrics will be used in the following to assess the quality of the deterministic forecast. Specifically, the mean absolute error (MAE) and the root mean square error (RMSE):
where
N is the total number of power measures,
L is the number of time steps
predicted in the future with respect to time
,
is the actual power at time
,
is the power forecast
l time steps in the future, predicted at time
.
Skill scores are widely used in assessing the performance of weather forecasting methods. They are defined as a measure of the relative improvement of a forecasting method over a reference. A commonly-used reference is the persistence forecast, that predicts that the power load on a given time will be the same measured at the same time one day before for lead time up to one day, one week before for one week lead time and one year before for one year lead times. Using the RMSE as a measure of accuracy, the skill score (SS) is defined as [
29]:
where
and
are the root mean square error of the forecast method and of the persistence, respectively. The higher the skill score, the better.
To evaluate the accuracy of the probabilistic forecast we will use the continuous ranked probability score (CRPS) [
30]:
where
is the cumulative distribution function (CDF) of the probabilistic forecast for the
i-th value, while
is the CDF of the observations. Note that the CPRS coincides with the MAE for a deterministic forecast [
31]. Small values of CRPS indicate good performances.
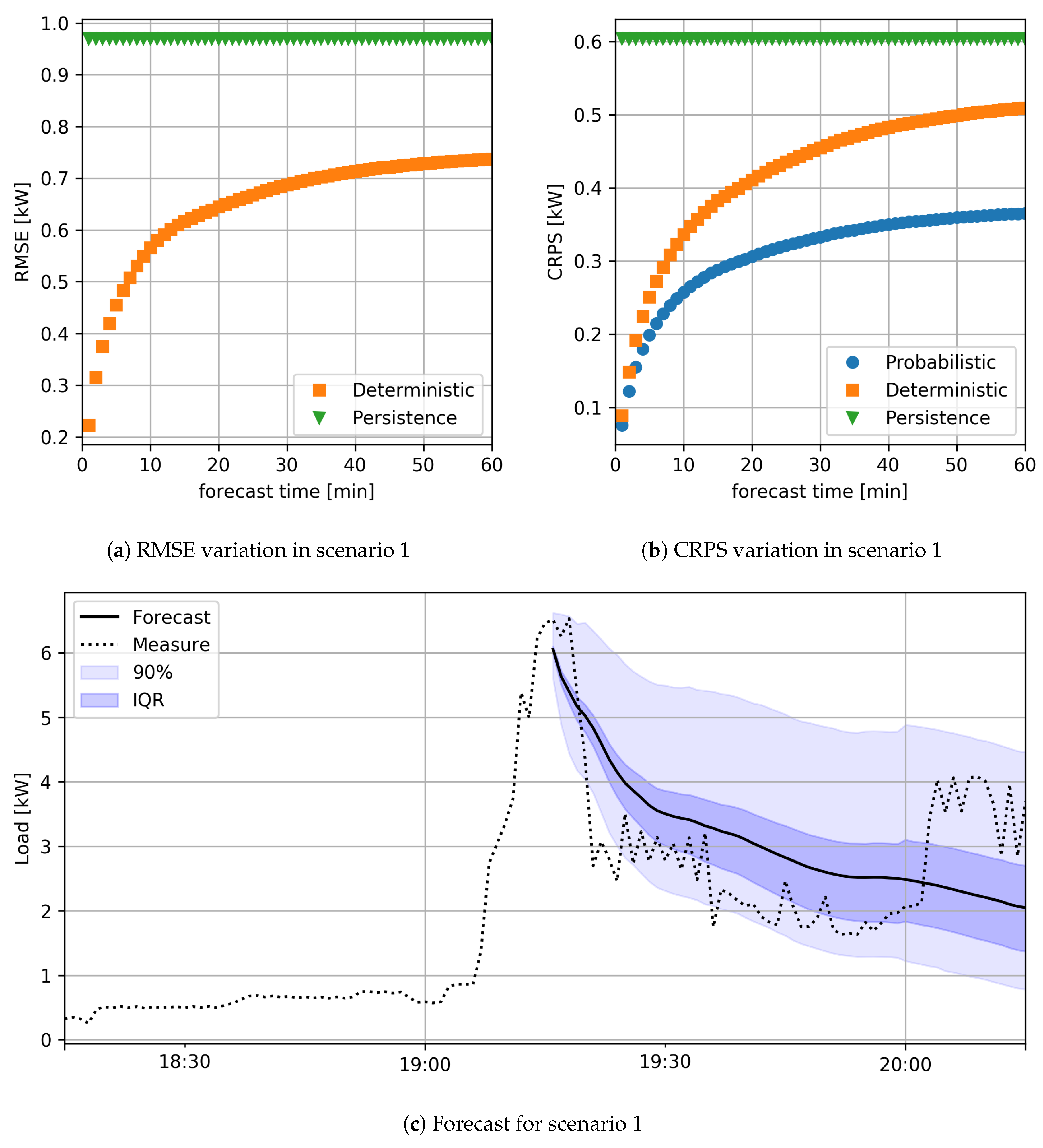
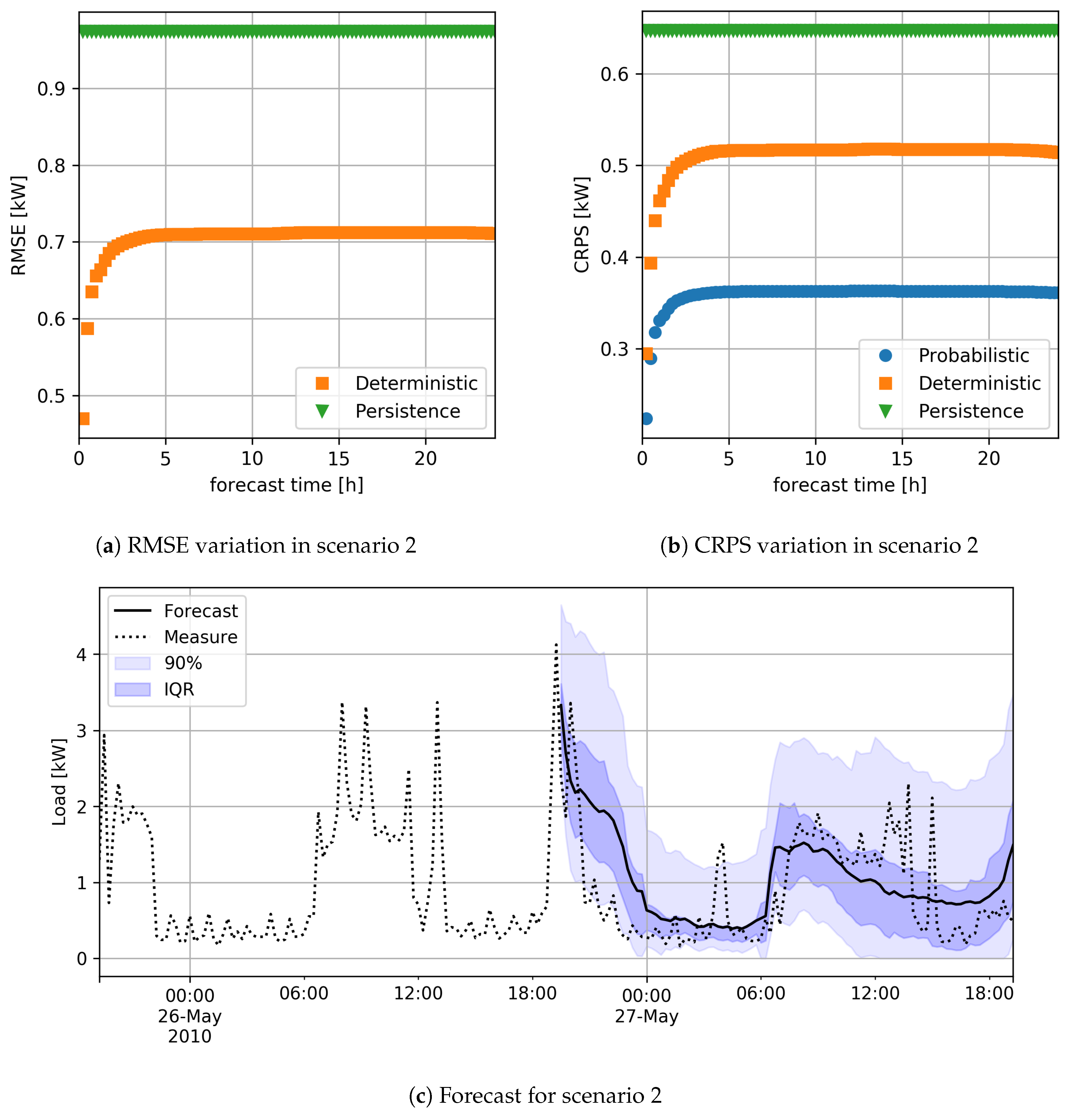
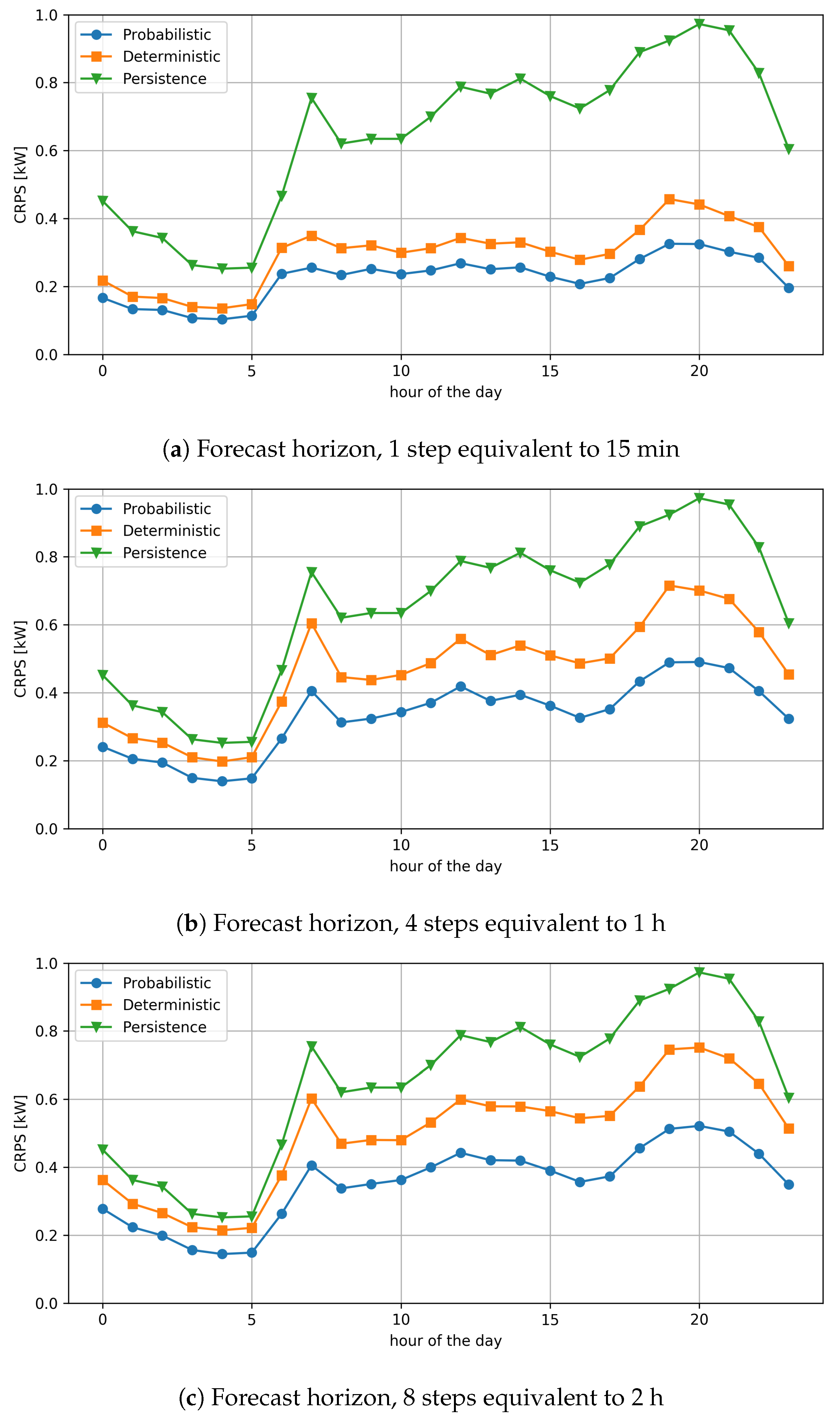
The analysis of the results will also show the variation of RMSE and CRPS according to the time of day and the forecast step in the future. Error measurements are obtained by grouping the data and applying the (
6) and (
8) on the sub-sets thus obtained; for example, the value of the RMSE at the time
h of the day is obtained by applying the (
6) only to load estimates made for times when the time of day is
h.
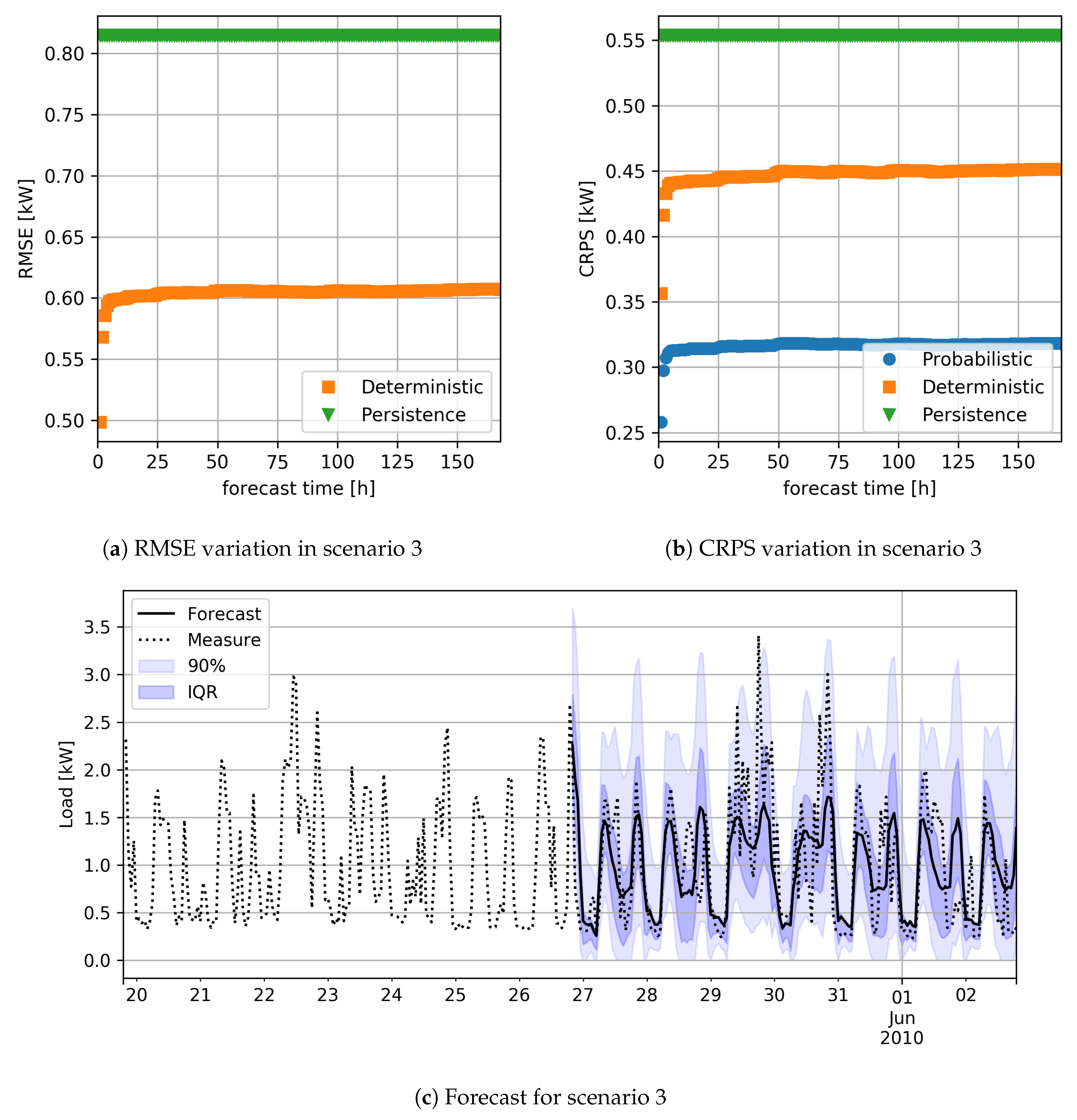
5. Discussion
The public availability of the examined dataset allows an indirect comparison of the performances obtained with the proposed methodology with previous works that have analysed the same dataset. The selection of the scenarios was partially linked to the possibility of making such a comparison.
Table 4 shows the values obtained in literature using machine learning methodologies and deep learning techniques with recursive and convolutional neural networks already cited in the introduction. The considerably better result obtained with the proposed methodology is certainly linked to the choice of a hybrid approach in which the forecasting of phenomena in the long term, characterized by more seasonality (daily, weekly and annual) were clearly separated from the forecasting of the load in the short term, which was instead estimated with a simple auto-regressive methodology. The better performances can be only partially attributed to the chosen regression algorithm, it would probably be possible to obtain similar performances using neural networks suitably trained both for the long term component and for the short term component of our model, at the price of a more complicated feature pre-processing and of longer calculation times for the training. The use of a hybrid methodology, as shown in [
32], allows instead to effectively isolate the average behavior from the alterations of the same and to train a regression model more quickly and effectively.
The proposed methodology can naturally be improved both for the long term and the short term part. For the long term, we are planning to introduce predictors based on the weather conditions and holidays scheduled in the calendar. For the short term it may be interesting to evaluate the use of a non-linear regressor, which could be based on RF as well. For both components additional features can be represented by the sub-meter readings provided as additional information in the dataset. We expect that a possible improvement can also come from the adoption of pattern recognition techniques for the identification of the appliances activation, which can allow a higher precision in identifying consumption habits by the user [
33]. These techniques typically require a much richer information content in the dataset, including the identification of the power-on periods of individual appliances, which are difficult to obtain and are not included in the dataset analyzed in this paper. In any case, given the great variability of the data to be predicted, we think of developing the forecasts from a probabilistic point of view, with a better estimate of the accuracy of the forecast, thus including the effects of the weekly and annual seasonality in the forecast interval clearly visible in
Figure 1b,c. For example, the effects of alteration and high load variability during Easter, All Saints’ Day and Christmas, winter and summer holidays are clearly detectable (see annotations in
Figure 1c). These are typical peak load periods for European countries [
4,
34].
6. Conclusions
This work presents a hybrid machine learning methodology based on random forest and linear regression for the deterministic and probabilistic prediction of household consumption at different time horizons and resolutions. The approach is based on the combined forecasting of long and short periods, using in the first case temporal features for the identification of trends and various seasonalities of the time series, and, in the second case, an auto-regressive approach using the most recent load measurements available at the time of emission of the forecast. Finally, through the analysis of the forecast error of the model, a probabilistic load forecast is realized.
The analysis highlights the relationship between the accuracy of the forecast and the lead time of the forecast and the time of the forecast, and compares the result obtained both with a reference based on persistence and with the results of the analysis of the same dataset with machine learning and deep learning methodologies published in the literature.
The method proves to be very effective in terms of absolute precision and calculation times required for model training and forecasting. The method also offers opportunities for development for both the long term and short term components, using additional predictors, experimenting with non-linear methods for short-term forecasting and refining the probabilistic forecasting methodology.