An Experimental Study of Combustion of a Methane Hydrate Layer Using Thermal Imaging and Particle Tracking Velocimetry Methods
Abstract
1. Introduction
1.1. The Key Parameters Controlling the Dissociation of Gas Hydrates
1.2. Combustion of Gas Hydrates
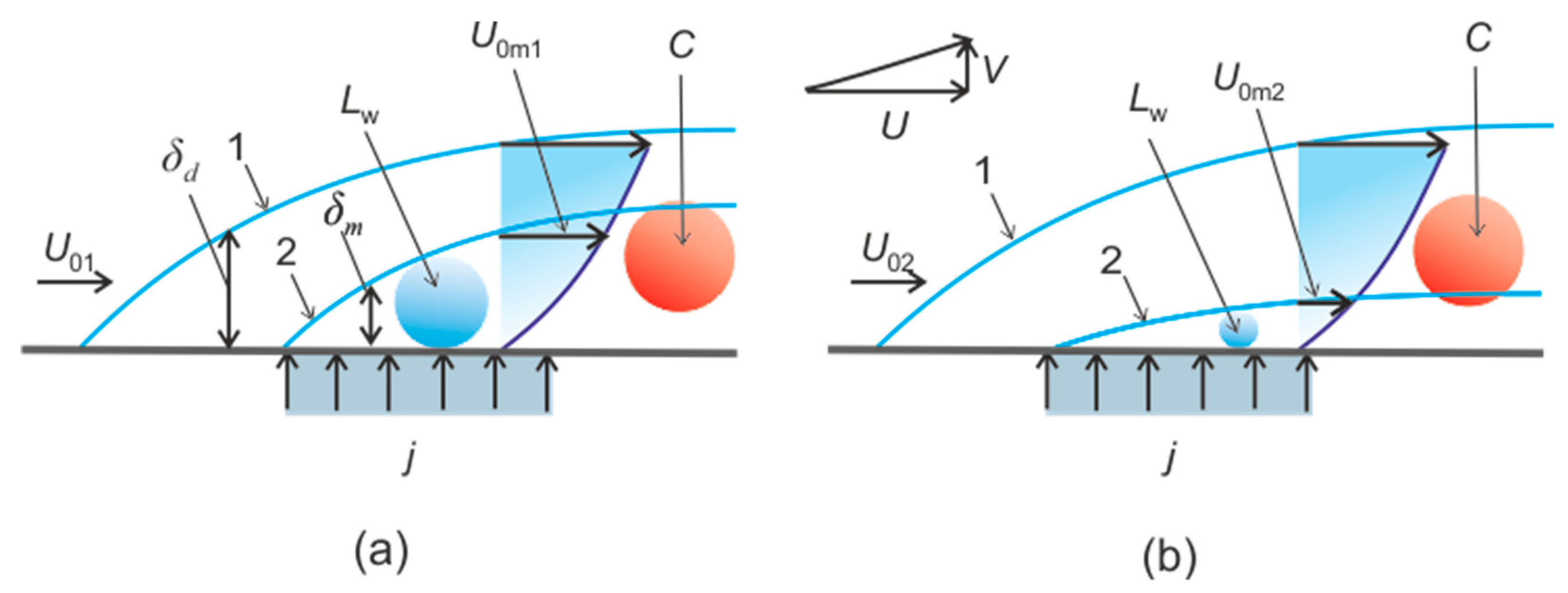
2. The Connection of Dissociation Rate and Heat Transfer
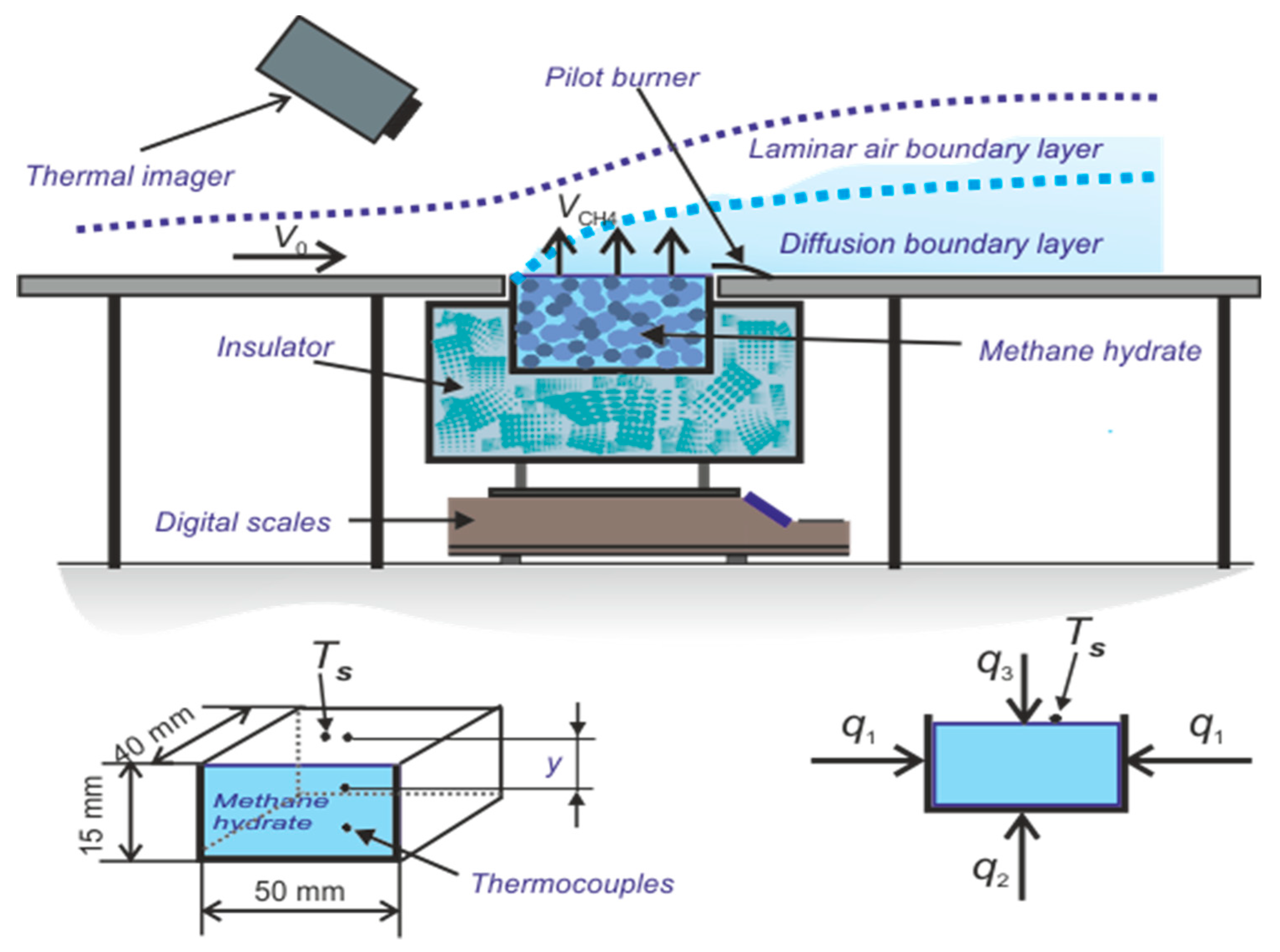
3. Experimental Apparatus and Procedure
3.1. Test Section for Organizing Methane Hydrate and Combustion
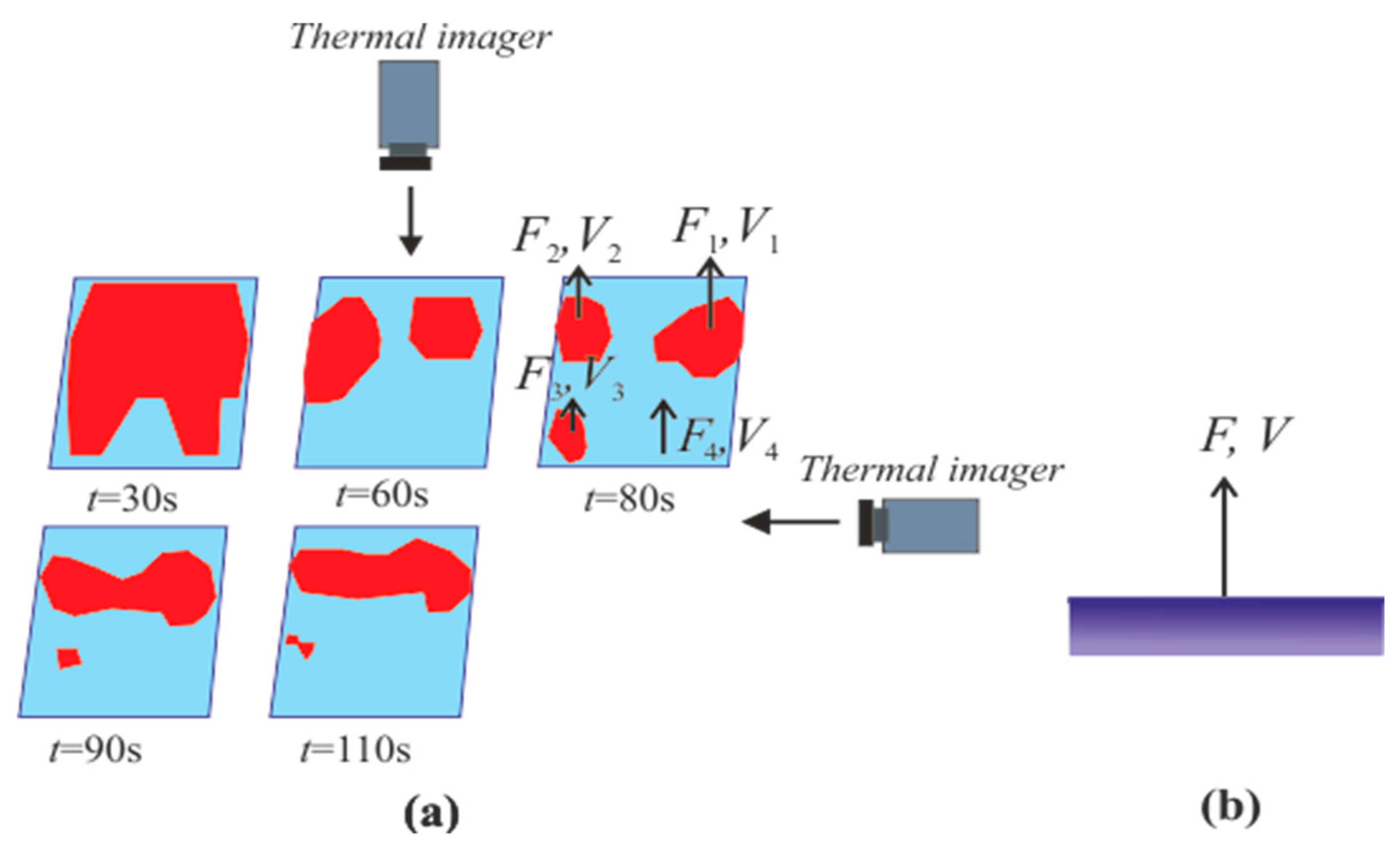
3.2. Measurement Using Particle Tracking Velocimetry (PTV) Method
4. Measurement
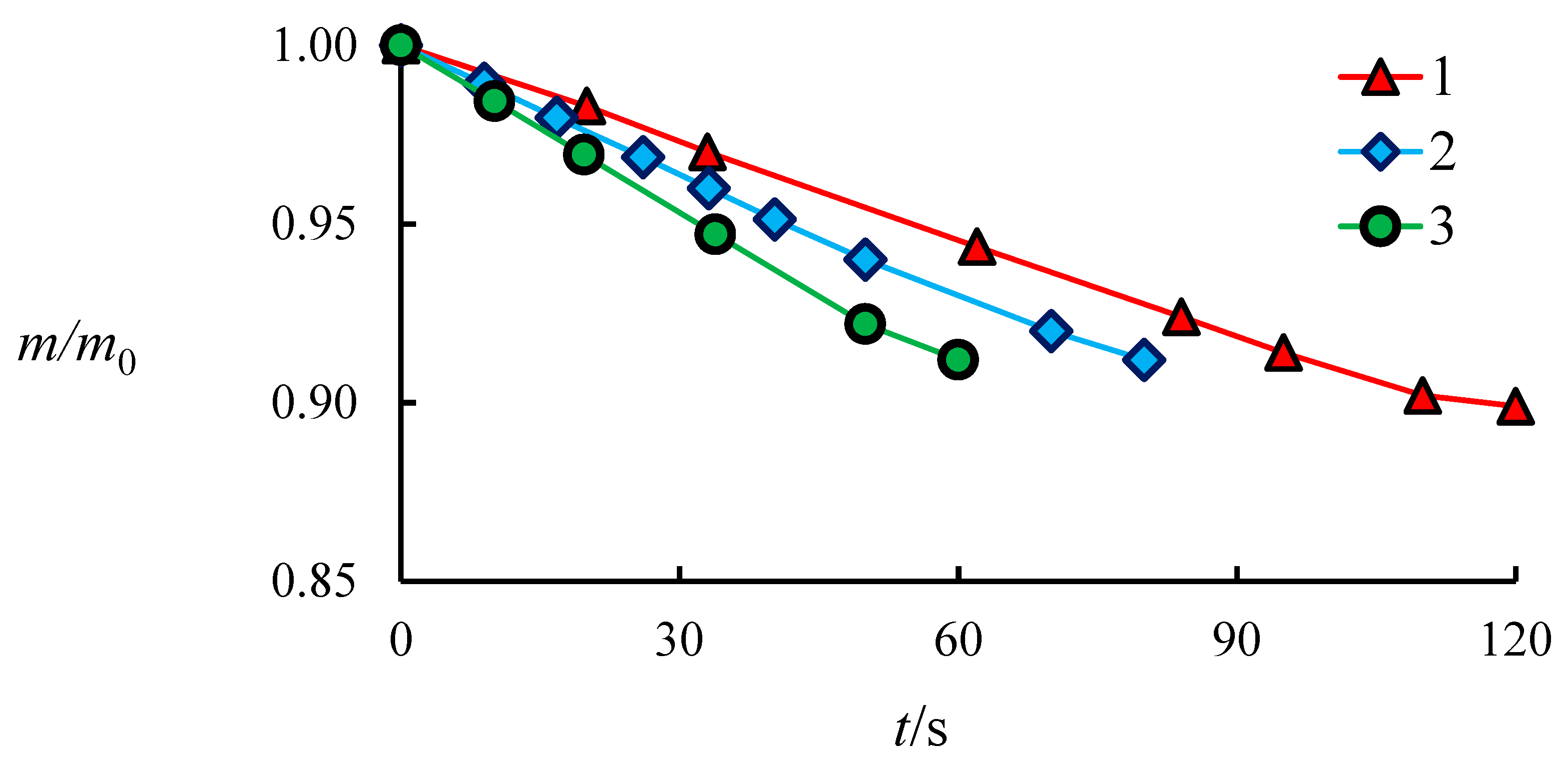
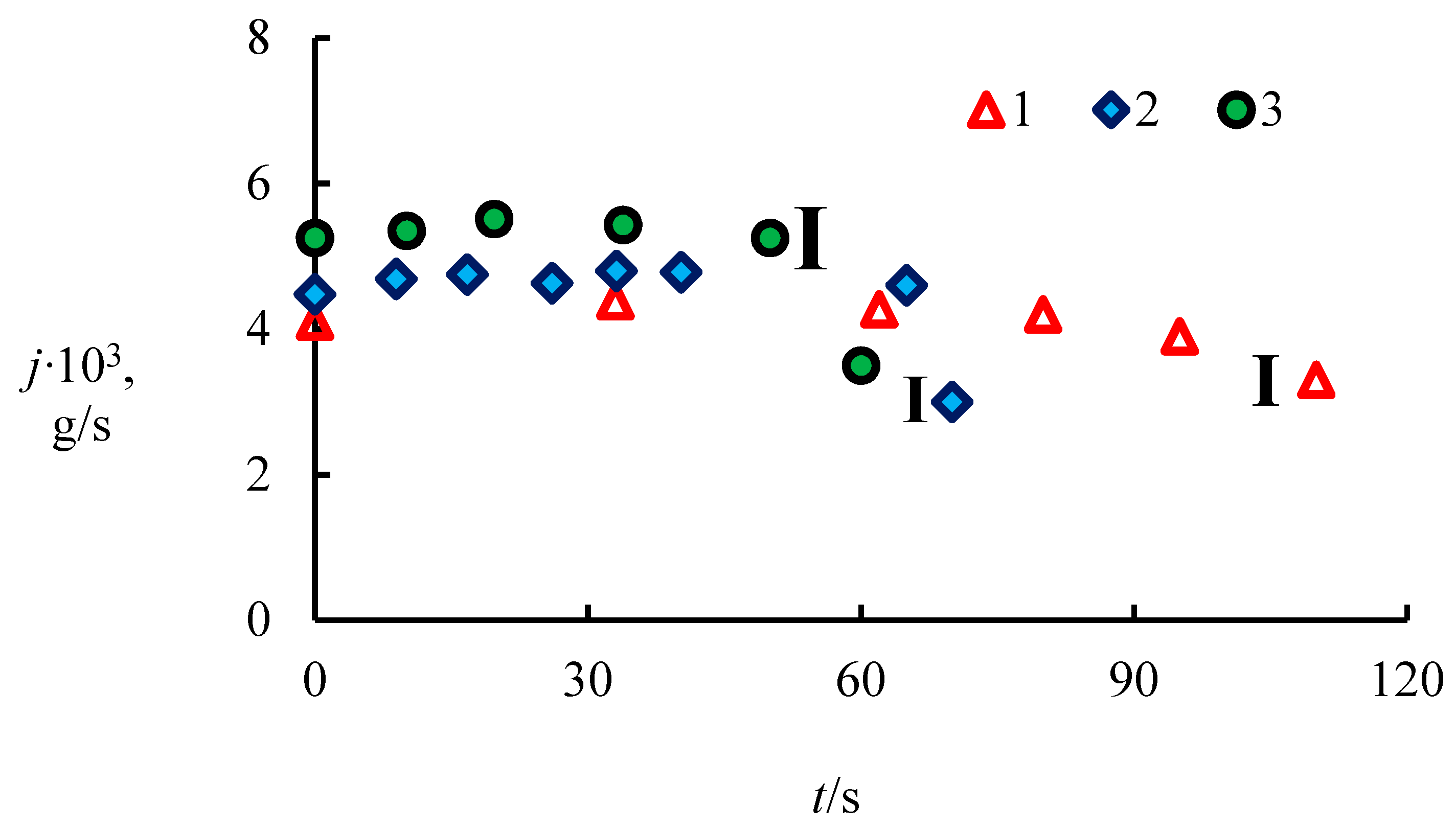
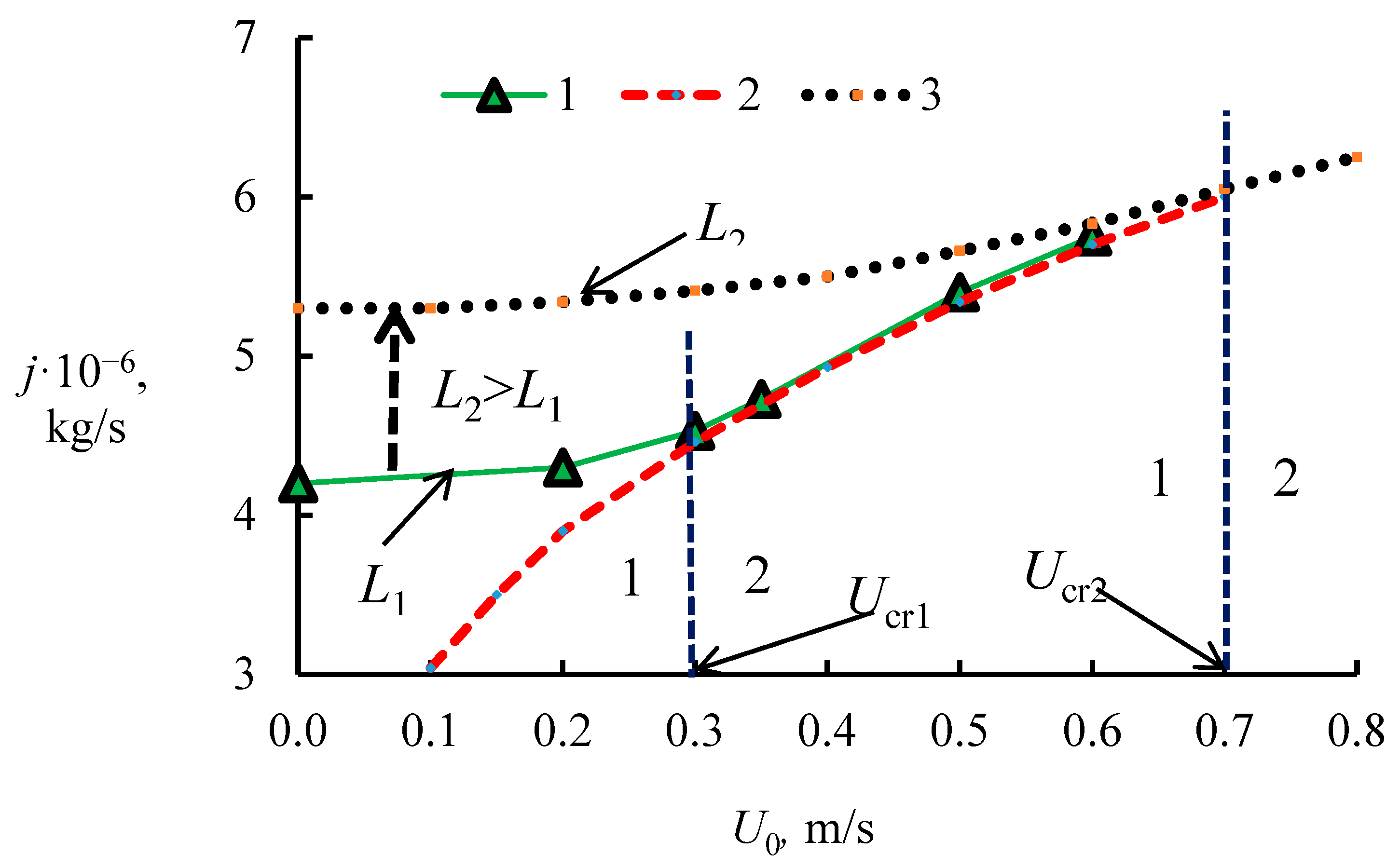
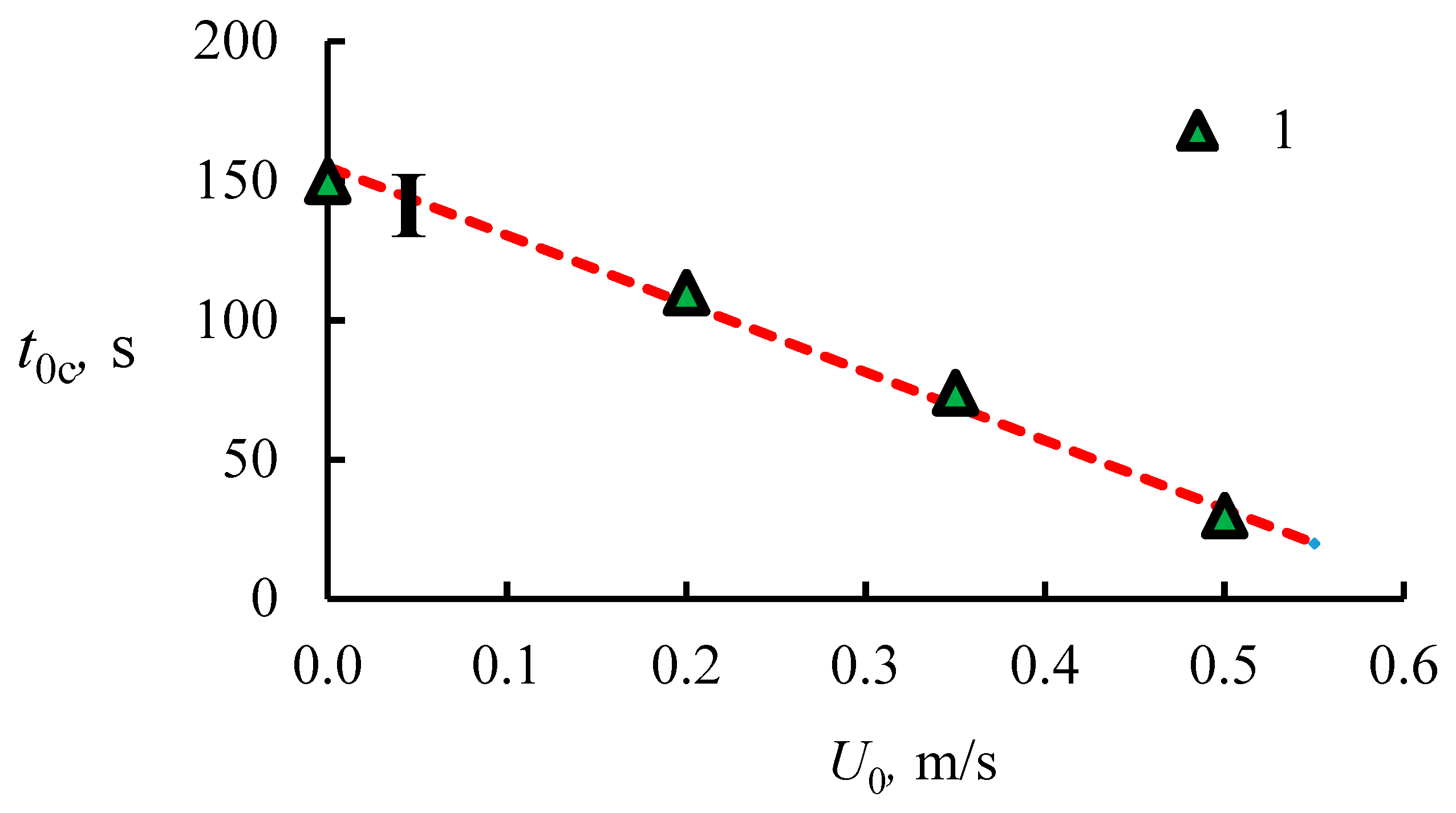
4.1. The Dissociation Rate in the Combustion of Methane Hydrate
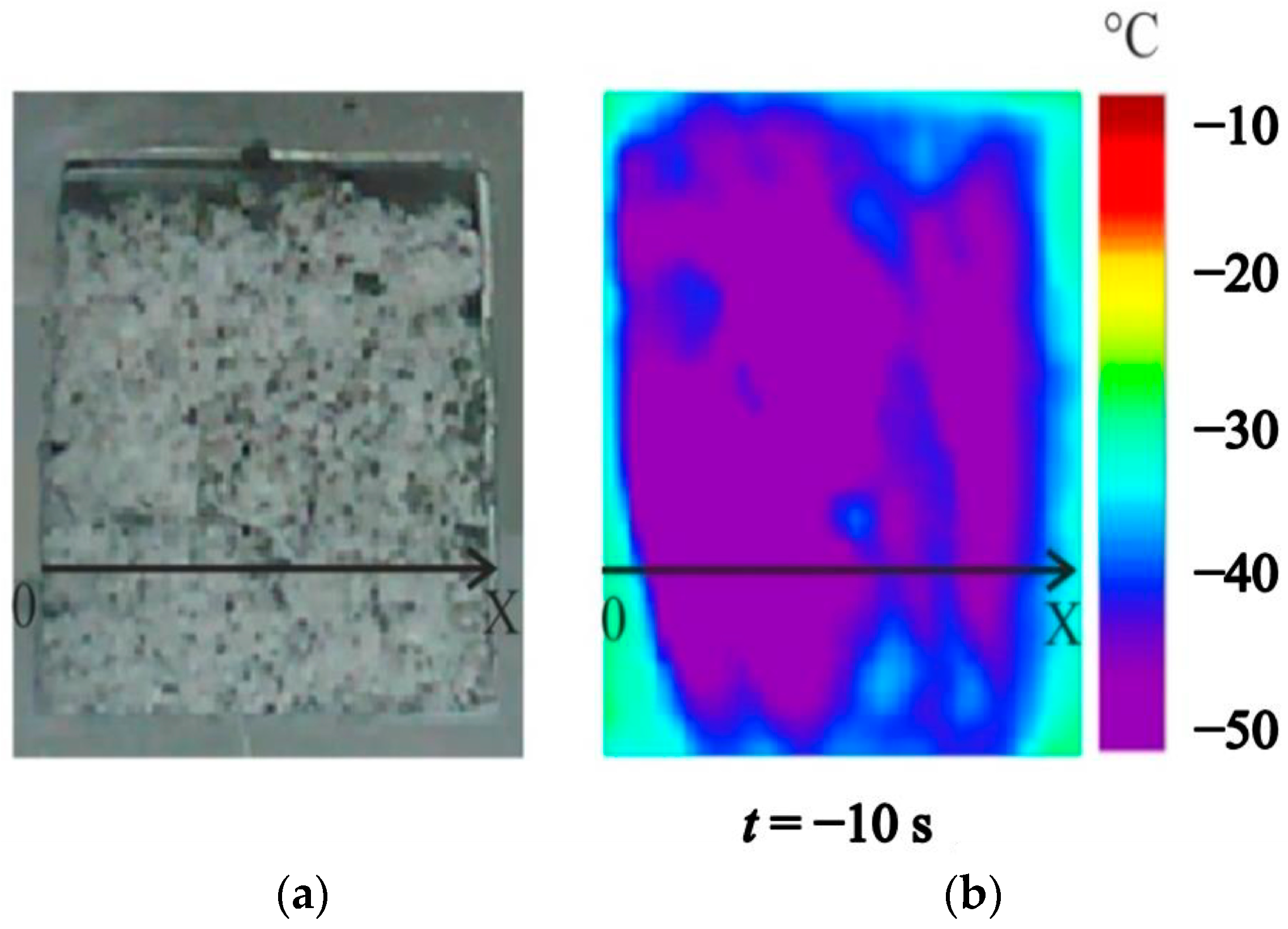
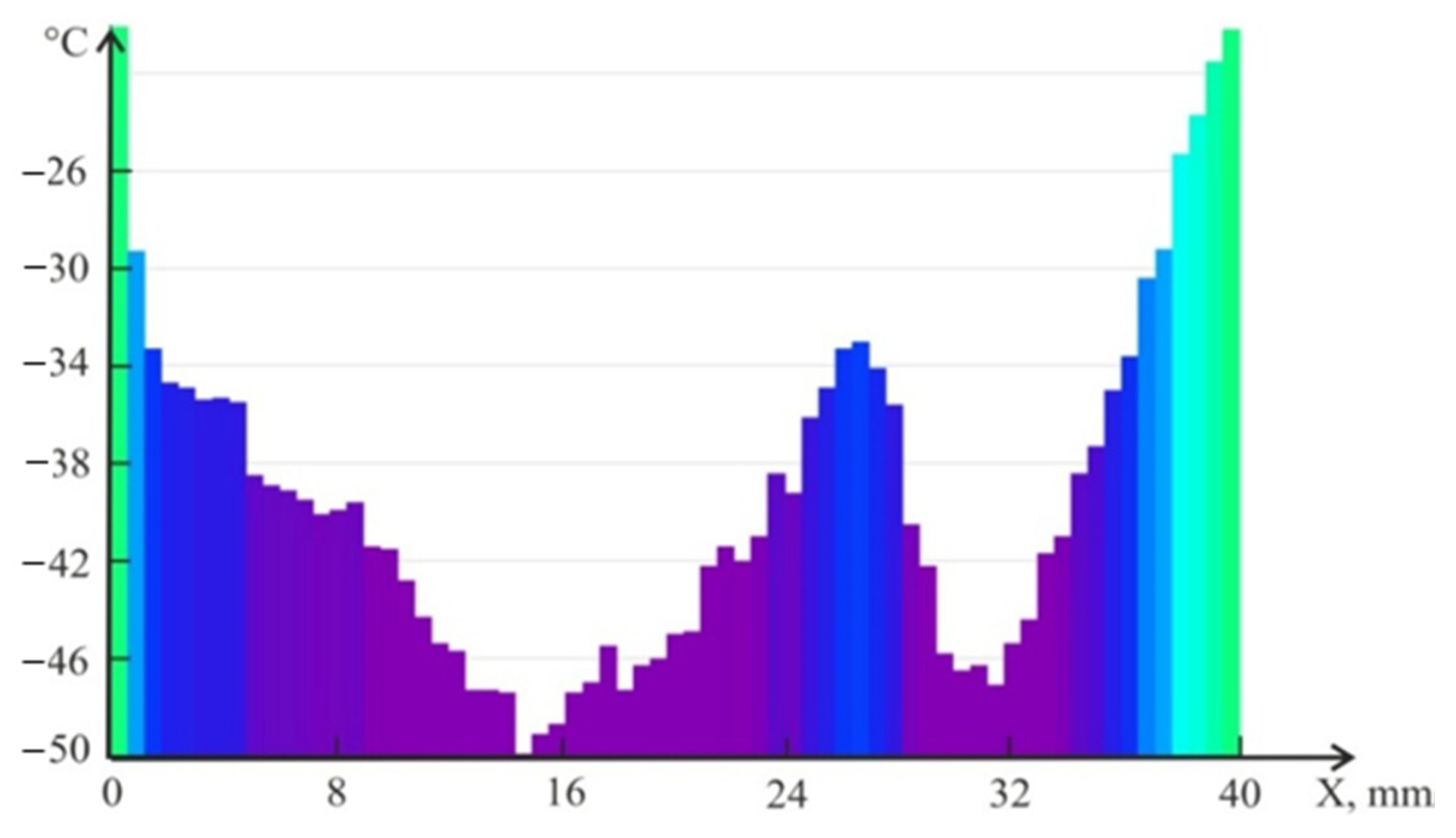
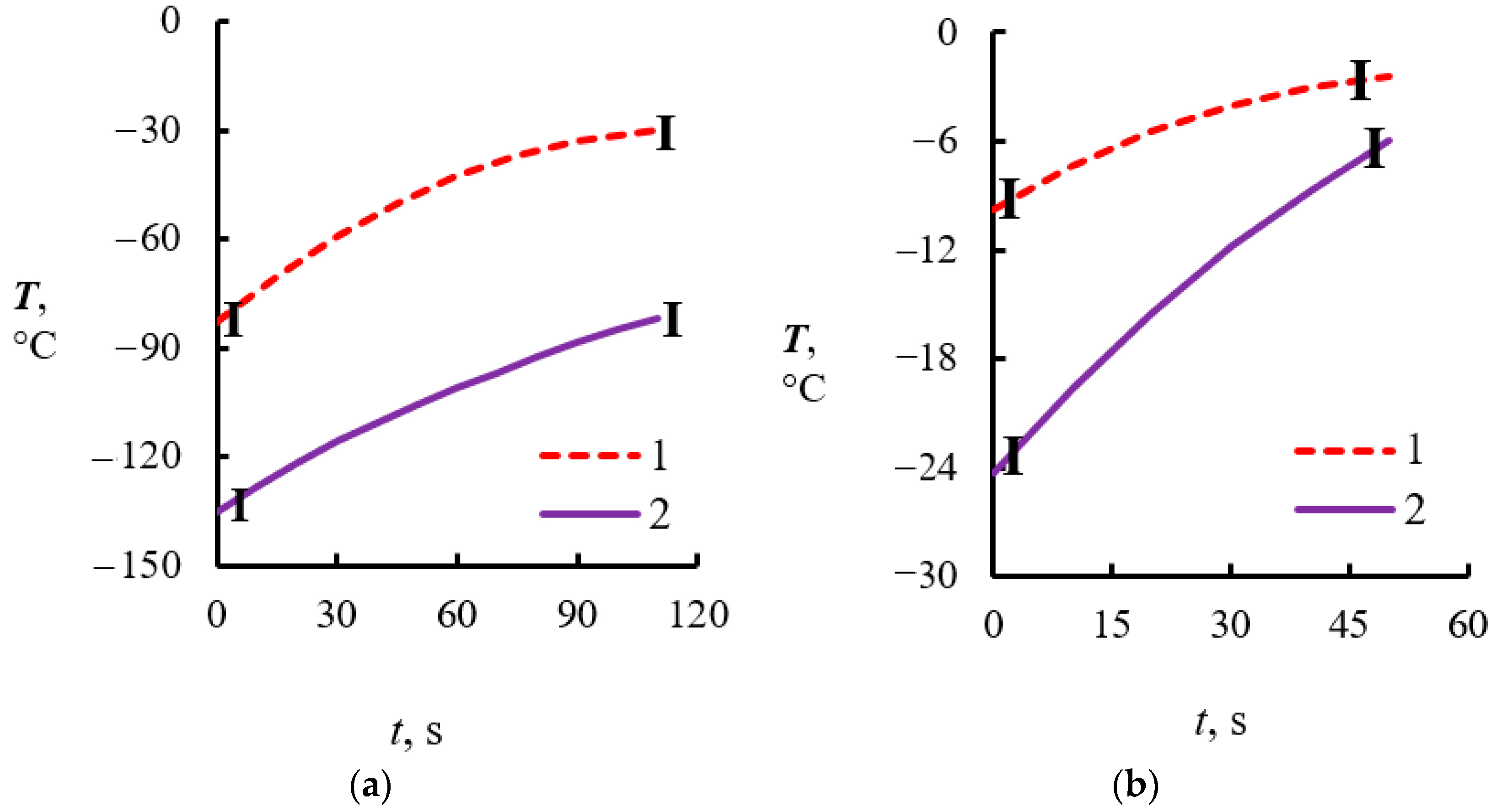
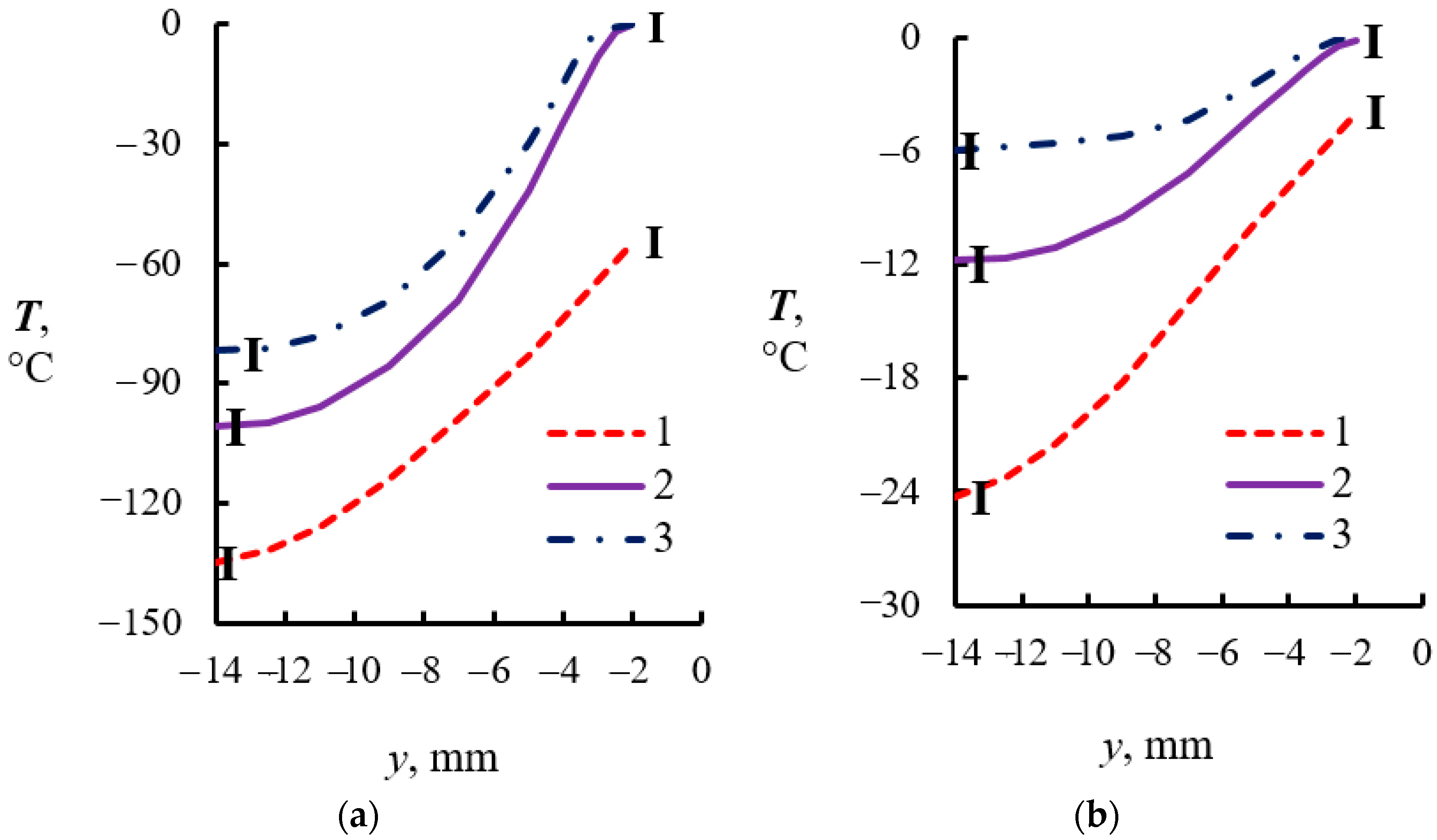
4.2. Temperature Measurements in the Powder Layer at Methane Hydrate Dissociation
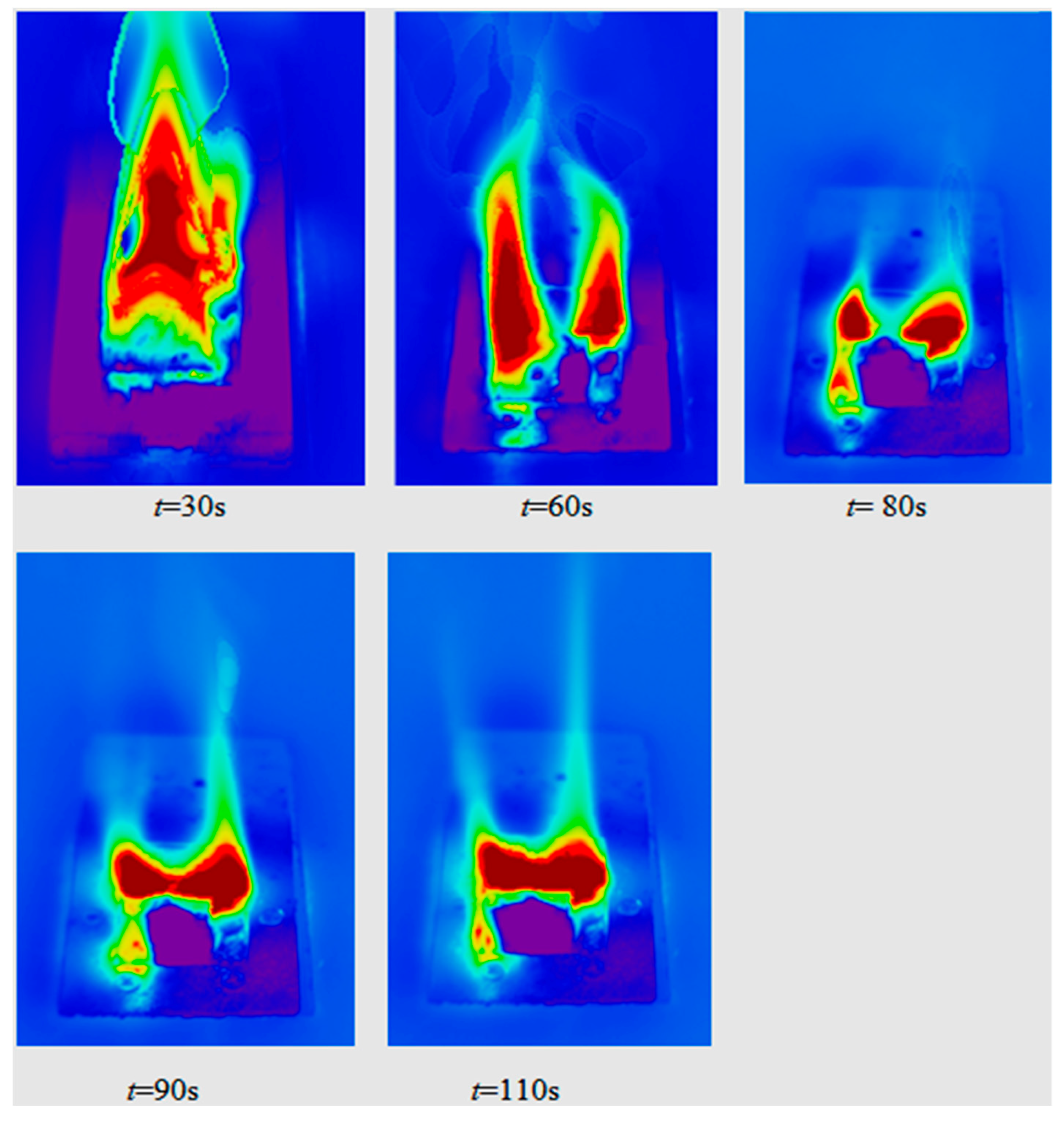
4.3. Heterogeneous Character of Methane Hydrate Combustion, Velocity Field at Combustion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rehder, G.; Eckl, R.; Elfgen, M.; Falenty, A.; Hamann, R.; Kahler, N.; Kuhs, W.F.; Osterkamp, H.; Windmeier, C. Methane hydrate pellet transport using the self-preservation effect: A Techno-Economic Analysis. Energies 2012, 5, 2499–2523. [Google Scholar] [CrossRef]
- Cui, Y.; Lu, C.; Wu, M.; Peng, Y.; Yao, Y.; Luo, W. Review of exploration and production technology of natural gas hydrate. Adv. Geo-Energy Res. 2018, 2, 53–62. [Google Scholar] [CrossRef]
- Takahashi, M.; Moriya, H.; Katoh, Y.; Iwasaki, T. Development of natural gas hydrate (NGH) pellet production system by bench scale unit for transportation and storage of NGH pellet. In Proceedings of the 6th International Conference on Gas Hydrates, Vancouver, BC, Canada, 6–10 July 2008. [Google Scholar]
- Istomin, V.A.; Yakushev, V.S. Gas Hydrates in Nature; Nedra Publisers: Moscow, Russia, 1992. [Google Scholar]
- Sum, A.K.; Koh, C.A.; Sloan, E.D. Clathrate hydrates: From laboratory science to engineering practice. Ind. Eng. Chem. Res. 2009, 48, 7457–7465. [Google Scholar] [CrossRef]
- Kuhs, W.F.; Genov, G.; Staykova, D.K.; Hansen, T. Ice perfection and onset of anomalous preservation of gas hydrates. Phys. Chem. Chem. Phys. 2004, 6, 4917–4920. [Google Scholar] [CrossRef]
- Takeya, S.; Yoneyama, A.; Ueda, K.; Mimachi, H.; Takahashi, M.; Sano, K.; Hyodo, K.; Takeda, T.; Gotoh, Y. Anomalously preserved clathrate hydrate of natural gas in pellet form at 253 K. J. Phys. Chem. 2012, 116, 13842–13848. [Google Scholar] [CrossRef]
- Yakushev, V.S.; Istomin, V.A. Gas-hydrates self-preservation effect. In Physics and Chemistry of Ice; Maeno, N., Hondoh, T., Eds.; Hokkaido Univ. Press: Sapporo, Japan, 1992; pp. 136–139. [Google Scholar]
- Sato, H.; Sakamoto, H.; Ogino, S.; Mimachi, H.; Kinoshita, T.; Iwasaki, T.; Sano, K.; Ohgaki, K. Self-preservation of methane hydrate revealed immediately below the eutectic temperature of the mother electrolyte solution. Chem. Eng. Sci. 2013, 91, 86–89. [Google Scholar] [CrossRef]
- Zhang, G.; Rogers, R.E. Ultra-stability of gas hydrates at 1 atm and 268.2 K. Chem. Eng. Sci. 2008, 63, 2066–2074. [Google Scholar] [CrossRef]
- Takeya, S.; Ripmeester, J.A. Anomalous preservation of CH4 hydrate and its dependence on the morphology of ice. ChemPhysChem 2010, 11, 70–73. [Google Scholar] [CrossRef]
- Takeya, S.; Yoneyama, A.; Ueda, K.; Hyodo, K.; Takeda, T.; Mimachi, H.; Takahashi, M.; Iwasaki, T.; Sano, K.; Yamawaki, H.; et al. Nondestructive imaging of anomalously preserved methane clathrate hydrate by phase contrast X-ray imaging. J. Phys. Chem. 2011, 115, 16193–16199. [Google Scholar] [CrossRef]
- Stern, L.A.; Circone, S.; Kirby, S.H.; Durham, W.B. Anomalous preservation of pure methane hydrate at 1 atm. J. Phys. Chem. 2011, 105, 1756–1762. [Google Scholar] [CrossRef]
- Stern, L.A.; Cirone, S.; Kirby, S.H.; Durham, W.B. Temperature, pressure and compositional effects on anomalous or “self” preservation of gas hydrates. Can. J. Phys. 2003, 81, 271–283. [Google Scholar] [CrossRef]
- Falenty, A.; Kuhs, W.F. Self-preservation of CO2 gas hydrates-surface microstructure and ice perfection. J. Phys. Chem. 2009, 113, 15975–15988. [Google Scholar] [CrossRef] [PubMed]
- Shimada, W.; Takeya, S.; Kamata, Y.; Uchida, T.; Nagao, J.; Ebinuma, T.; Narita, H. Texture change of ice on anomalously preserved methane clathrate hydrate. J. Phys. Chem. 2005, 109, 5802–5807. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, A.H.; Koc, M.A.; Shepherd, T.D.; Molinero, V. Structure of the ice-clathrate interface. J. Phys. Chem. 2015, 119, 4104–4117. [Google Scholar] [CrossRef]
- Lv, Y.; Jia, M.; Chen, J.; Sun, C.; Gong, J.; Chen, G.; Liu, B.; Ren, N.; Guo, S.; Li, Q. Self-Preservation effect for hydrate dissociation in water + diesel oil dispersion systems. Energy Fuels 2015, 29, 5563–5572. [Google Scholar] [CrossRef]
- Prasad, P.S.R.; Chari, V.D. Preservation of methane gas in the form of hydrates: Use of mixed hydrates. J. Nat. Gas Sci. Eng. 2015, 25, 10–14. [Google Scholar] [CrossRef]
- Misyura, S.Y.; Donskoy, I.G. Dissociation of natural and artificial gas hydrate. Chem. Eng. Sci. 2016, 148, 65–77. [Google Scholar] [CrossRef]
- Misyura, S.Y. Effect of heat transfer on the kinetics of methane hydrate dissociation. Chem. Phys. Lett. 2013, 583, 34–37. [Google Scholar] [CrossRef]
- Semenov, M.E.; Manakov, A.Y.; Shitz, E.Y.; Stoporev, A.S.; Altunina, L.K.; Strelets, L.A.; Misyura, S.Y.; Nakoryakov, V.E. DSC and thermal imaging studies of methane hydrate formation and dissociation in water emulsions in crude oils. J. Therm. Anal. Calorim. 2015, 119, 757–767. [Google Scholar] [CrossRef]
- Aerov, M.E.; Todes, O.M.; Narinsky, D.A. Apparatuses with the Steady Grain Layer: Hydraulic and Thermal Fundamentals of Operation; Khimiya: Leningrad, Russia, 1992. [Google Scholar]
- Chen, X.R.; Li, X.S.; Chen, Z.Y.; Zhang, Y.; Yan, K.F.; Lv, Q.-N. Experimental investigation into the combustion characteristics of propane hydrates in porous media. Energies 2015, 8, 1242–1255. [Google Scholar] [CrossRef]
- Nakoryakov, V.E.; Misyura, S.Y. Nonstationary combustion of methane with gas hydrate dissociation. Energy Fuels 2013, 27, 7089–7097. [Google Scholar] [CrossRef]
- Nakoryakov, V.E.; Misyura, S.Y.; Elistratov, S.L.; Manakov, A.Y.; Shubnikov, A.E. Combustion of methane hydrates. J. Eng. Thermophys. 2013, 22, 87–92. [Google Scholar] [CrossRef]
- Nakoryakov, V.E.; Misyura, S.Y.; Elistratov, S.L.; Manakov, A.Y.; Sizikov, A.A. Methane combustion in hydrate systems: Water-methane and water-methane-isopropanol. J. Eng. Thermophys. 2013, 22, 169–173. [Google Scholar] [CrossRef]
- Maruyama, Y.; Yokomori, T.; Ohmura, R.; Ueda, T. Flame spreading over combustible hydrate in a laminar boundary layer. In Proceedings of the 7th International Conference on Gas Hydrate, Edinburgh, UK, 17–21 July 2011. [Google Scholar]
- Nakamura, Y.; Katsuki, R.; Yokomori, T.; Ohmura, R.; Takahashi, M.; Iwasaki, T.; Uchida, K.; Ueda, T. Combustion characteristics of methane hydrate in a laminar boundary layer. Energy Fuels 2009, 23, 1445–1449. [Google Scholar] [CrossRef]
- Kitamura, K.; Nakajo, K.; Ueda, T. Numerical calculation of a diffusion flame formed in the laminar boundary layer over methane-hydrate. In Proceedings of the Fourth International Conference on Gas Hydrates, Yokohama, Japan, 19–23 May 2002; pp. 1055–1058. [Google Scholar]
- Maruyama, Y.; Fuse, M.J.; Yokomori, T.; Ohmura, R.; Watanabe, S.; Iwasaki, T.; Iwabuchi, W.; Ueda, T. Experimental investigation of flame spreading over pure methane hydrate in a laminar boundary layer. Proc. Combust. Inst. 2013, 34, 2131–2138. [Google Scholar] [CrossRef]
- Wu, F.H.; Padilla, R.E.; Dunn-Rankin, D.; Chen, G.B.; Chao, Y.C. Thermal structure of methane hydrate fueled flames. Proc. Combust. Inst. 2017, 36, 4391–4398. [Google Scholar] [CrossRef]
- Yoshioka, T.; Yamamoto, Y.; Yokomori, T.; Ohmura, R.; Ueda, T. Experimental study on combustion of methane hydrate sphere. Exp. Fluids 2015, 56, 192. [Google Scholar] [CrossRef]
- Bar-Kohany, T.; Sirignano, W.A. Transient combustion of methane-hydrate sphere. Combust. Flame 2016, 163, 284–300. [Google Scholar] [CrossRef]
- Misyura, S.Y. Efficiency of methane hydrate combustion for different types of oxidizer flow. Energy 2016, 103, 430–439. [Google Scholar] [CrossRef]
- Cuenot, B.; Poinsot, T. Effect of curvature and unsteadiness in diffusion flames implications for turbulent diffusion combustion. Proc. Combust. Inst. 1994, 25, 1383–1390. [Google Scholar] [CrossRef]
- Dehaech, S.; Van Parys, H.; Hubin, A.; Van Beeck, J.P.A.J. Laser marked shadowgraphy: A novel optical planar technique for the study of microbubbles and droplets. Exp. Fluids 2009, 47, 333–341. [Google Scholar] [CrossRef]
- Kuznetsov, G.V.; Piskunov, M.V.; Volkov, R.S.; Strizhak, P.A. Unsteady temperature fields of evaporating water droplets exposed to conductive, convective and radiative heating. Appl. Therm. Eng. 2018, 131, 340–355. [Google Scholar] [CrossRef]
- Hagiwara, Y.; Sakamoto, S.; Tanaka, M.; Yoshimura, K. PTV measurement on interaction between two immiscible droplets and turbulent uniform shear flow of carrier fluid. Exp. Therm. Fluid Sci. 2002, 26, 245–252. [Google Scholar] [CrossRef]
- Westerweel, J. Fundamentals of digital particle image velocimetry. Meas. Sci. Technol. 1997, 8, 1379–1392. [Google Scholar] [CrossRef]
- Kutateladze, S.S. Fundamentals of Heat Transfer; Arnold, E., Ed.; Wiley: London, UK, 1963. [Google Scholar]
- Volchkov, E.P.; Makarov, M.S.; Makarova, S.N. Heat and mass diffusion fluxes on a permeable wall with foreign-gasblowing. Int. J. Heat Mass Transf. 2012, 55, 1881–1887. [Google Scholar] [CrossRef]
- Kutateladze, S.S.; Leont’ev, A.I. Heat Transfer, Mass Transfer, and Friction in Turbulent Boundary Layers; Hemisphere Publishing Corporation: New York, NY, USA, 1989. [Google Scholar]
- Volchkov, E.P. Concerning the heat and mass transfer features on permeable surfaces. Int. J. Heat Mass Transf. 2006, 49, 755–762. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Y., M.S.; S., V.I.; S., M.V.; Y., M.A.; S., Y.O.; V., I.A. An Experimental Study of Combustion of a Methane Hydrate Layer Using Thermal Imaging and Particle Tracking Velocimetry Methods. Energies 2018, 11, 3518. https://doi.org/10.3390/en11123518
Y. MS, S. VI, S. MV, Y. MA, S. YO, V. IA. An Experimental Study of Combustion of a Methane Hydrate Layer Using Thermal Imaging and Particle Tracking Velocimetry Methods. Energies. 2018; 11(12):3518. https://doi.org/10.3390/en11123518
Chicago/Turabian StyleY., Misyura S., Voytkov I. S., Morozov V. S., Manakov A. Y., Yashutina O. S., and Ildyakov A. V. 2018. "An Experimental Study of Combustion of a Methane Hydrate Layer Using Thermal Imaging and Particle Tracking Velocimetry Methods" Energies 11, no. 12: 3518. https://doi.org/10.3390/en11123518
APA StyleY., M. S., S., V. I., S., M. V., Y., M. A., S., Y. O., & V., I. A. (2018). An Experimental Study of Combustion of a Methane Hydrate Layer Using Thermal Imaging and Particle Tracking Velocimetry Methods. Energies, 11(12), 3518. https://doi.org/10.3390/en11123518





