1. Introduction
The increasing demands for sustainable, clean, and environmentally friendly energy call for distributed renewable energy resources to frequently be used to support electricity demand. In an electric system, the critical safety-related loads require extremely reliable and high-quality power to function efficiently. Uninterruptible Power Supplies (UPSs) play a key role to provide a continuous power supply and protection against interruptions. When a power outage takes place, a UPS must deliver an emergency backup power to a load and prevent damages. Typically, an ideal UPS provides unity power factor, low Total Harmonic Distortion (THD) sinusoidal, high efficiency, low cost, high reliability, electric isolation, and low transients response time during the transition from grid mode to backup mode and vice versa. Besides, the most important task of UPS is to maintain the pure sinusoidal output voltage with low THD under linear and distorted load conditions. According to the standards of Institute of Electrical and Electronics Engineers (IEEE) 519–1992, the maximum THD of the output voltage in the UPS system should be less than 5% in common applications such as households’ appliances and offices. Similarly, for sensitive applications like safety devices, and airport apparatus, the THD should be less than 3%. The configuration of the UPS system is mainly categorized as off-line or line-preferred, on-line or inverter-preferred and line-interactive UPS system [
1,
2].
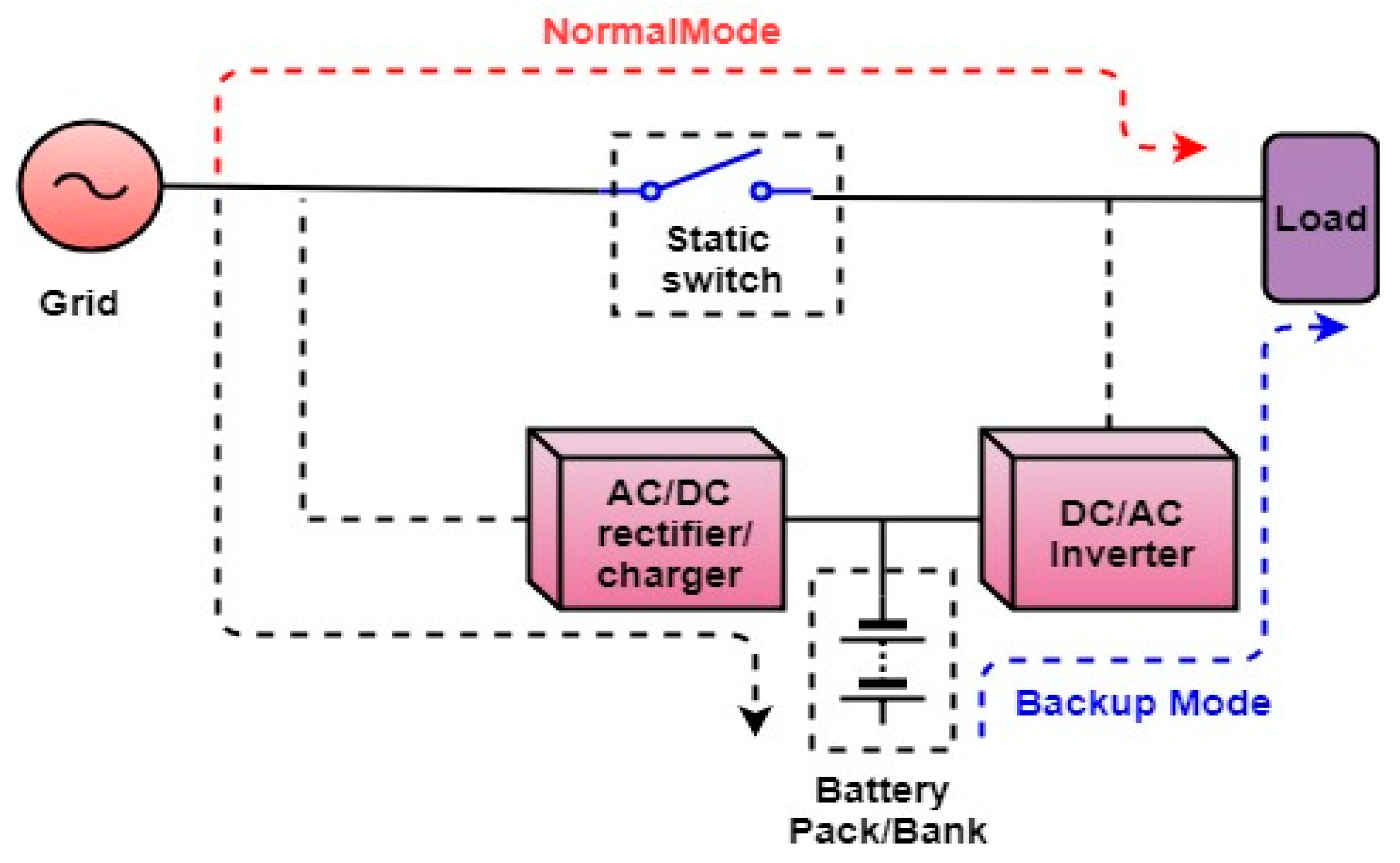
The configuration of a typical off-line UPS system is shown in
Figure 1. It usually consists of a static transfer switch, AC/DC rectifier/charger, DC/AC inverter, DC link interface, and a battery pack. The static switch connects the load to the AC grid and the battery pack charges through AC/DC rectifier/charger under normal power condition. When the grid fails, an abnormal power condition occurs, the static switch disconnects the load from the grid and the DC/AC inverter regulates power from the battery pack to the load for the period till the utility grid is back again. This topology offers some advantages such as high efficiency, simple design, passive line conditioning, cheaper, and small size. However, the major disadvantages associated with this configuration are slow transition response from the AC grid to the backup mode, lack of isolation between the load and AC line, and no output voltage regulation.
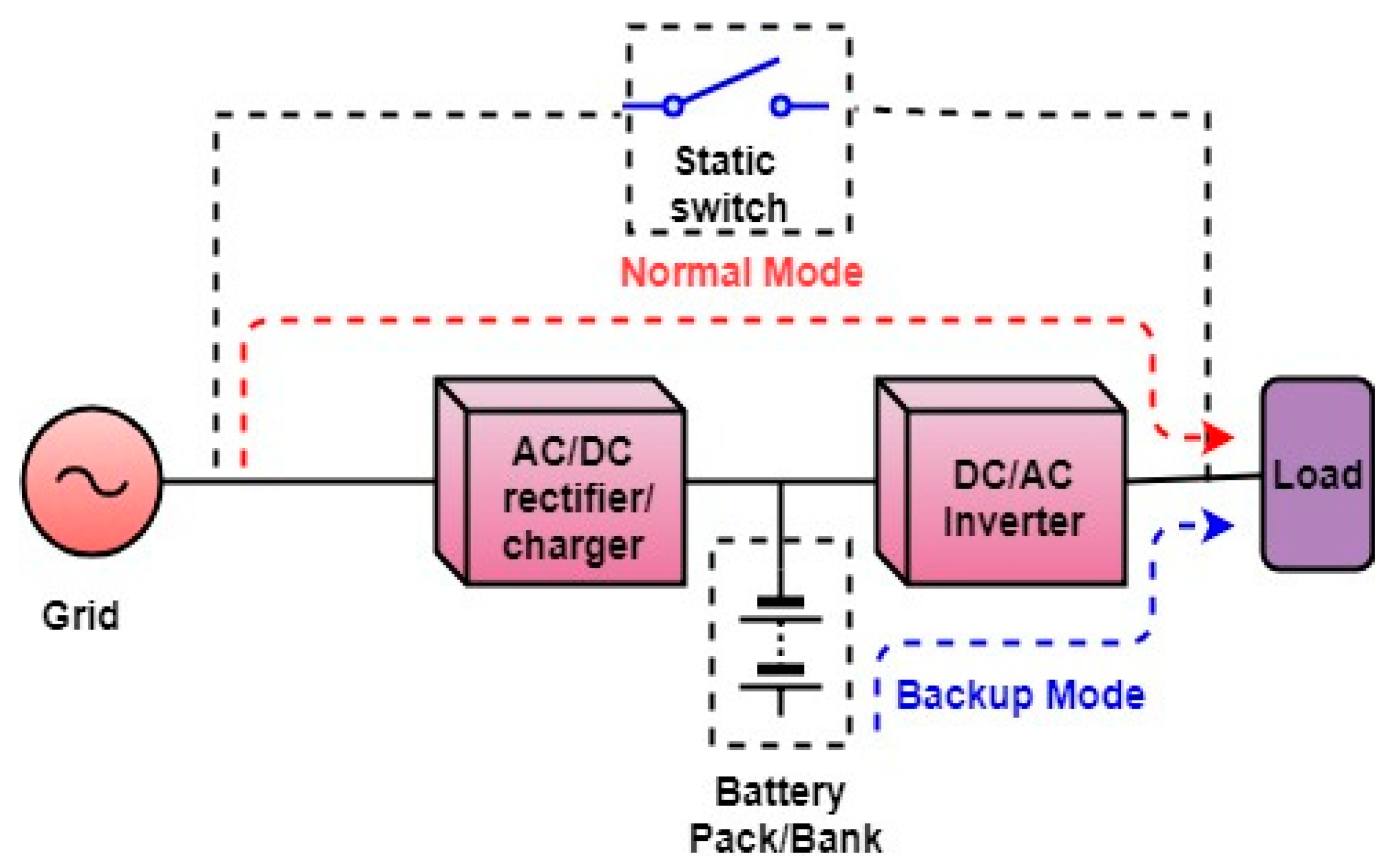
Likewise, the off-line UPS system, the on-line UPS system is the popular and most used configuration. It consists of an AC/DC rectifier charger, static transfer switch (bypass), a battery pack and a DC/AC inverter. The block diagram of the classical on-line UPS system is shown in
Figure 2. In this configuration, the power continuously provides to the load through the rectifier charger and inverter under both normal and abnormal AC grid power conditions. During normal operation the battery pack charges while in case of AC grid power outage, the battery pack discharges and supply full power to the load without utilizing the static switch. The inverter is connected in series with the load. Hence, during the transition from normal mode to the backup mode, the transfer time is zero. In this configuration, the inverter is the main powering path for the load instead of the AC grid. This topology provides advantages such as good powering conditioning, load protection, high power rating, and accurate power regulation for the load. The main drawbacks associated with this topology include low power factor, high cost, low efficiency because of the double stages of power conversion, and large size.
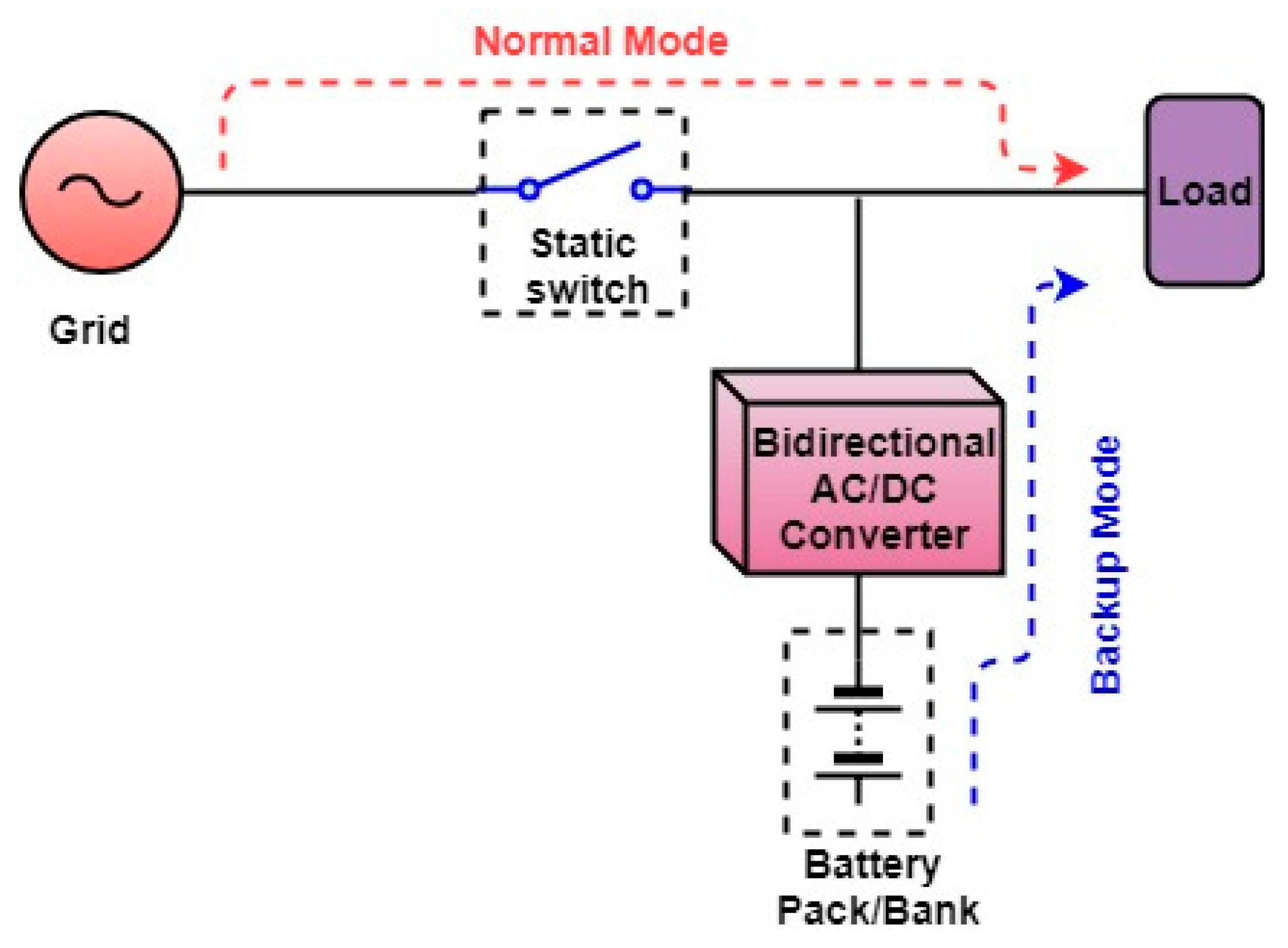
The next topology is the line-interactive UPS system. The components include the static transfer switch, a bidirectional converter, a series inductor, and a battery pack. Technically, this UPS system can work in either mode as standby UPS and as an on-line UPS (series configuration). The series inductor is not necessary for standby line-interactive UPS system. However, in order to enhance both the voltage regulation and power factor of the load, most of the line-interactive UPS system operate on-line.
The classical configuration is shown in
Figure 3. While under a normal mode of operation, the bidirectional converter charges the battery pack and the AC grid provides power to the load. In the case of AC grid failure, the static transfer switch isolates the load from the AC grid and the power to the load provides through the bidirectional converter. The main benefits of this configuration are a simple design, more reliable, high efficiency, small size, good harmonics suppression for the input current, and cheaper. The major drawback is that it does not offer any voltage regulation of the load during normal condition.
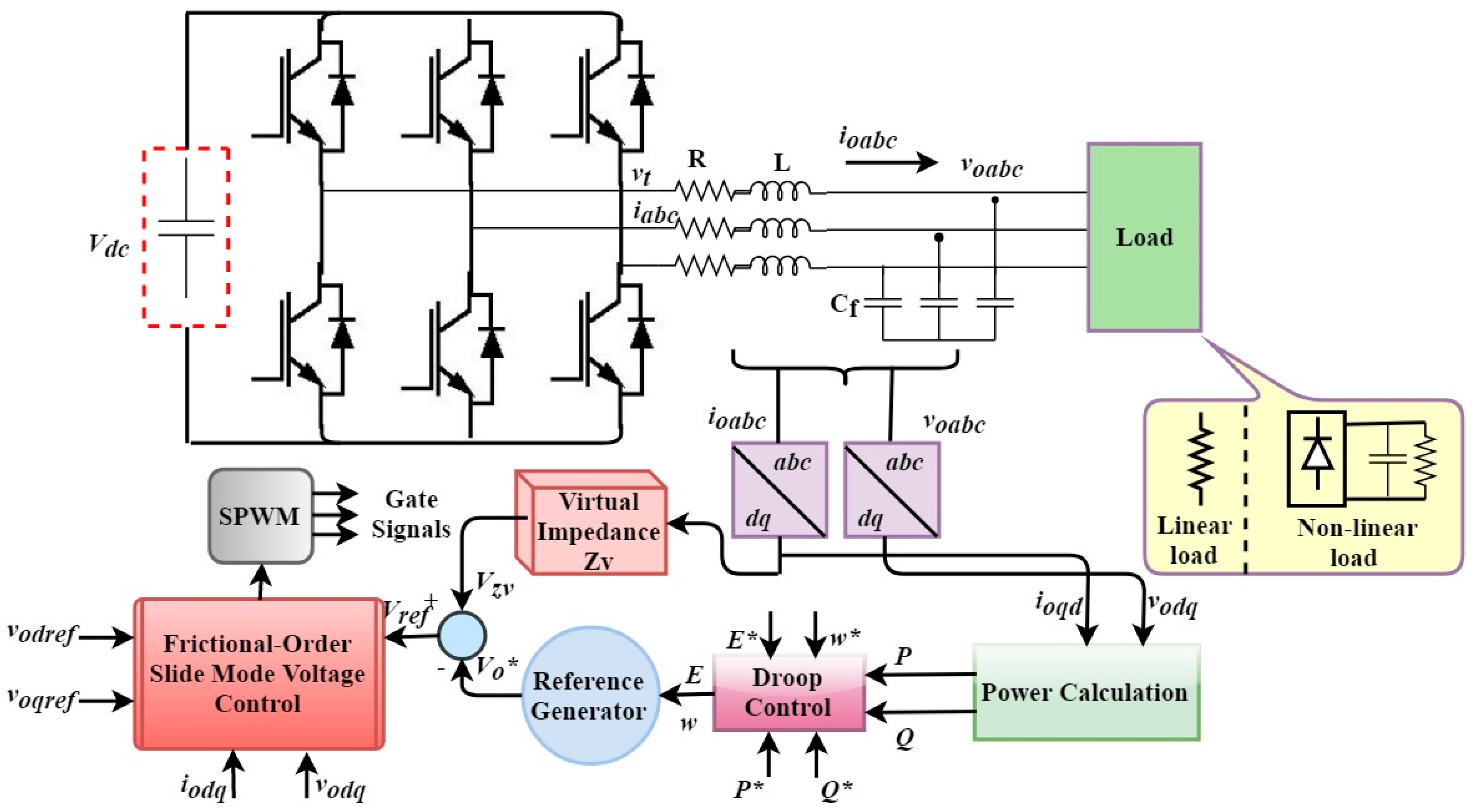
The UPS system is mainly composed of a voltage-source inverter (VSI) and an output
LC filter. Generally, the UPS system performance is influenced by the output filters of the three-phase inverter which are tuned to remove fixed harmonic frequency components. Moreover, the majority of loads supply by UPS systems are unbalanced and/or nonlinear loads. Nonlinear currents drawn by unbalanced and nonlinear loads distort the output voltage of UPS system which leads to high current flow, excessive losses, heating, and malfunctioning of the critical loads. Therefore, the designing of a high-quality three-phase inverter for UPS applications are necessary in order to achieve a pure sinusoidal voltage with low THD and fast transient response during load step variations. Considering the aforementioned issues, many advanced control strategies for UPS systems are proposed in the literature to address the voltage quality enhancement. In [
3,
4], conventional multi-feedback loop hybrid proportional-integral-derivative (PID) control strategies have been proposed. Both the schemes provide a very good dynamic performance and simple implementation. However, as neither the inductor current nor the load current is considered, if any abnormality occurs on the load side, these schemes cannot guarantee the safe and stable operation of the system. Regarding the three-phase UPS system, the Proportional Resonant (PR) controller in the stationary reference frame has been used to supply nonlinear and unbalanced loads in [
5]. This controller reduces THD of the output voltage, eliminate steady-state error, and fast dynamic response. However, in order to attenuate the lower order harmonics, the output filter inductance (
L,
LC,
LCL etc.) values are very large which increases the size and cost of the system.
Nowadays, nonlinear control techniques have gained considerable attention from researchers because these techniques offer some advantages like robustness, less sensitive to external disturbances, and fast dynamic performance. In [
6], deadbeat control has been proposed in order to enhance the closed-loop performance of the pulse width modulation (PWM) inverter. Deadbeat control technique provides some advantages such as fast dynamic response, and good performance under a linear load. However, this controller is highly sensitive to parameters changes, model uncertainties, measurement noise, and sometimes to switching frequency. In order to overcome the aforementioned issues, Observer-based deadbeat controllers have been proposed in [
7,
8]. Though, there is a trade-off between the controller stability margin and the closed-loop performance. In [
9,
10], the Repetitive controller (RC) for UPS inverters are investigated so as to compensate the unbalance and harmonic distortion. This controller provides a good regulation for distorted loads, eliminate a periodical tracking error and excellent harmonics (both odd and even components) rejection capability. However, the dynamic response is quite slow, thus RC is usually escorted by robust controllers for enhanced dynamics response time of the controller. Additionally, high memory usage which imposes a high computational burden is an extra drawback in the RC controller. Iterative Learning Control (ILC) for UPS inverters is suggested in [
11]. This technique is capable of achieving high performance. However, the design is complex and also the switching frequency is very high, which result in huge switching losses. The Model Predictive Control (MPC) techniques are proposed in [
12,
13,
14,
15,
16] which provide a simple structure and good dynamic performance. A cost function is obtained to predict the next switching state. Also, MPC has the ability to manipulate different constraints like switching frequency minimization. However, the predictive control requires accurate system parameters to reach the desired performance. Further, it is difficult to implement the MPC technique as the cost function calculation compel high computational burden. In [
17], a robust control technique for VSC is suggested to compensate the harmonics in the islanded mode of operation. The controller eliminates the system uncertainties and maintains pure sinusoidal three-phase voltage under unbalanced/nonlinear load current conditions. A robust
voltage control strategy for islanded microgrid is addressed in [
18]. The droop control and power management system provide the nominal values of voltage and frequency. Additionally, the nonlinear robust
technique provide the ride-through capability, guarantee power-sharing, eliminate small and large signal disturbances, and enhance the performance under nonlinear loads.
Sliding mode control (SMC) is a nonlinear and variable structure control technique has gained a huge interest from the researchers due to its inherent characteristics of simple implementation, strong robustness, good tracking of current reference, excellent dynamic response, high accuracy, and insensitivity to external disturbances and parameter uncertainties. Considering the abovementioned qualities, SMC is extremely suitable for the voltage-source converter (VSC) and can deal effectively with the nonlinear behavior of the power converter. The main problem of SMC is the chattering phenomena because of very high switching frequency result in excessive power losses, electro-magnetic noises, low control accuracy, and problems in the output filter design.
For single and three-phase inverters, SMC is addressed in [
2,
19,
20,
21] and [
22,
23]. The chattering phenomena are attenuated in [
19,
21] and [
23] by smoothing the feedback control law in a narrow boundary layer and the switching function. Also, accomplishing a fixed switching frequency variable hysteresis band comparator. However, the robustness and the reference tracking error of these schemes is nearly degraded. In [
24], Particle Swarm Optimization (PSO) for tuning control gains of terminal SMC with a fuzzy estimator of UPS inverter is proposed. This technique provides good dynamic response and improves the performance of the UPS inverter under the transient loading conditions. But, the THD level at the output voltage is high and also this technique cannot eliminate circulating currents. An Adaptive SMC technique with an auto-tuning idea of the sliding switching gain for a three-phase UPS system is recommended in [
25]. This technique eliminates chattering phenomena to a great extent and also minimize sliding switching gain without considering the system uncertainties and external perturbations. Nevertheless, the response time is relatively slow, hence, this may encounter a serious stability issue. Nowadays, the decentralized SMC strategies [
26,
27] have been addressed to enhance the system stability and provide the robustness under unknown load condition. Two separate SMC controllers are designed for hybrid microgrid such as for fundamental positive sequence, direct power SMC scheme is used and for the negative sequence, an SMC current scheme is adopted. The controller ensures the power-sharing, regulate active and reactive powers, and mitigate the current harmonics under unbalanced and nonlinear load current conditions in grid-tied mode and also regulate voltage and frequency in islanded mode.
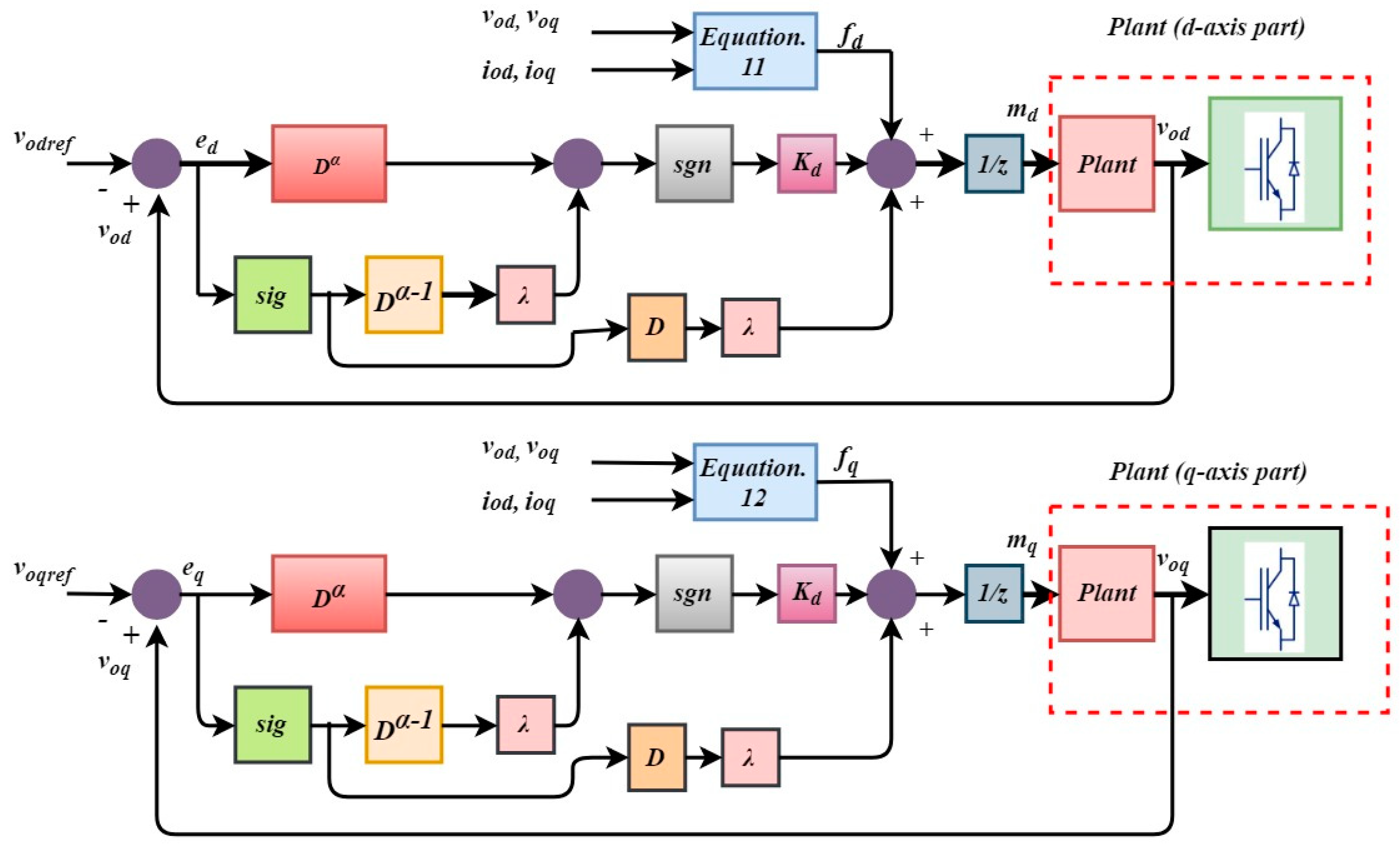
In the feedback control theory, fractional calculus is the newly emerging concept which deals with the fractional-order derivatives and integrals. In fact, the primary difference between fractional-order derivative and integer-order derivative mainly comprises of two aspects. Firstly, integer-order derivative depicts certain attributes like variation, uncertainties etc. of a physical or mechanical process at a particular instant of time, whereas, in the fractional-order derivative, the entire time domain is considered. Secondly, integer order derivative evaluates a physical process at a certain position within its local domain while on the other hand, fractional order considers the whole space for evaluation. Traditional SMC does not guarantee the convergence of the system. Moreover, chattering phenomena also exist which is not desired. In contrast to classical SMC, the fractional-order sliding mode control (FOSMC) control is an effective method to alleviate chattering phenomena and provides a more flexible degree of freedom [
28]. The Riemann-Liouville (RL) fractional derivative is used in designing the sliding surface, and the upgraded exponential law is exploited so as to alleviate the chattering phenomena and to bring and keep the state variable onto the sliding surface. Moreover, to the best of the authors’ knowledge, the behavior of FOSMC for parallel-connected UPS system has not been examined so far, hence to accomplish this research gap, this paper presents nonlinear voltage control strategy based on FOSMC for parallel operating UPS system.
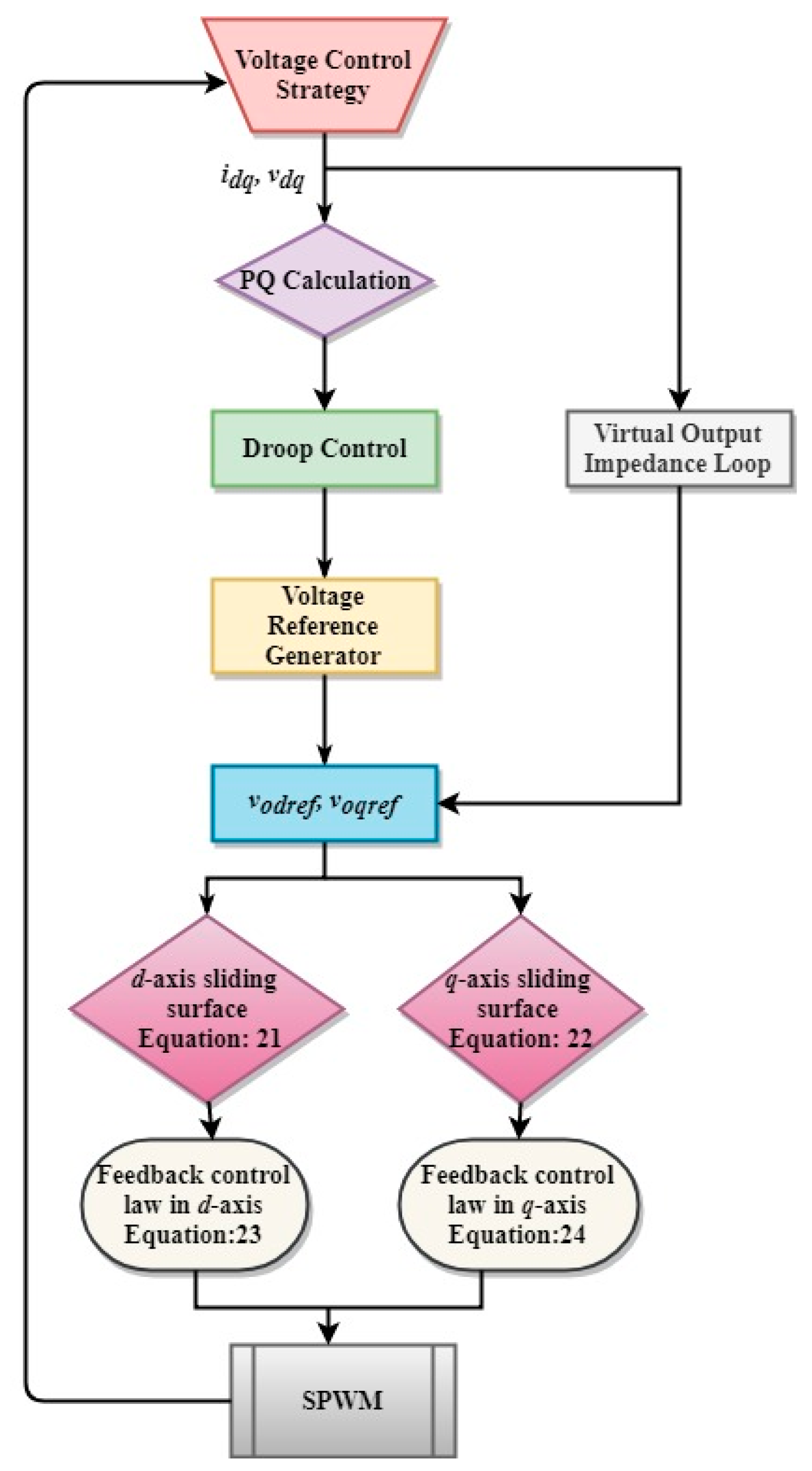
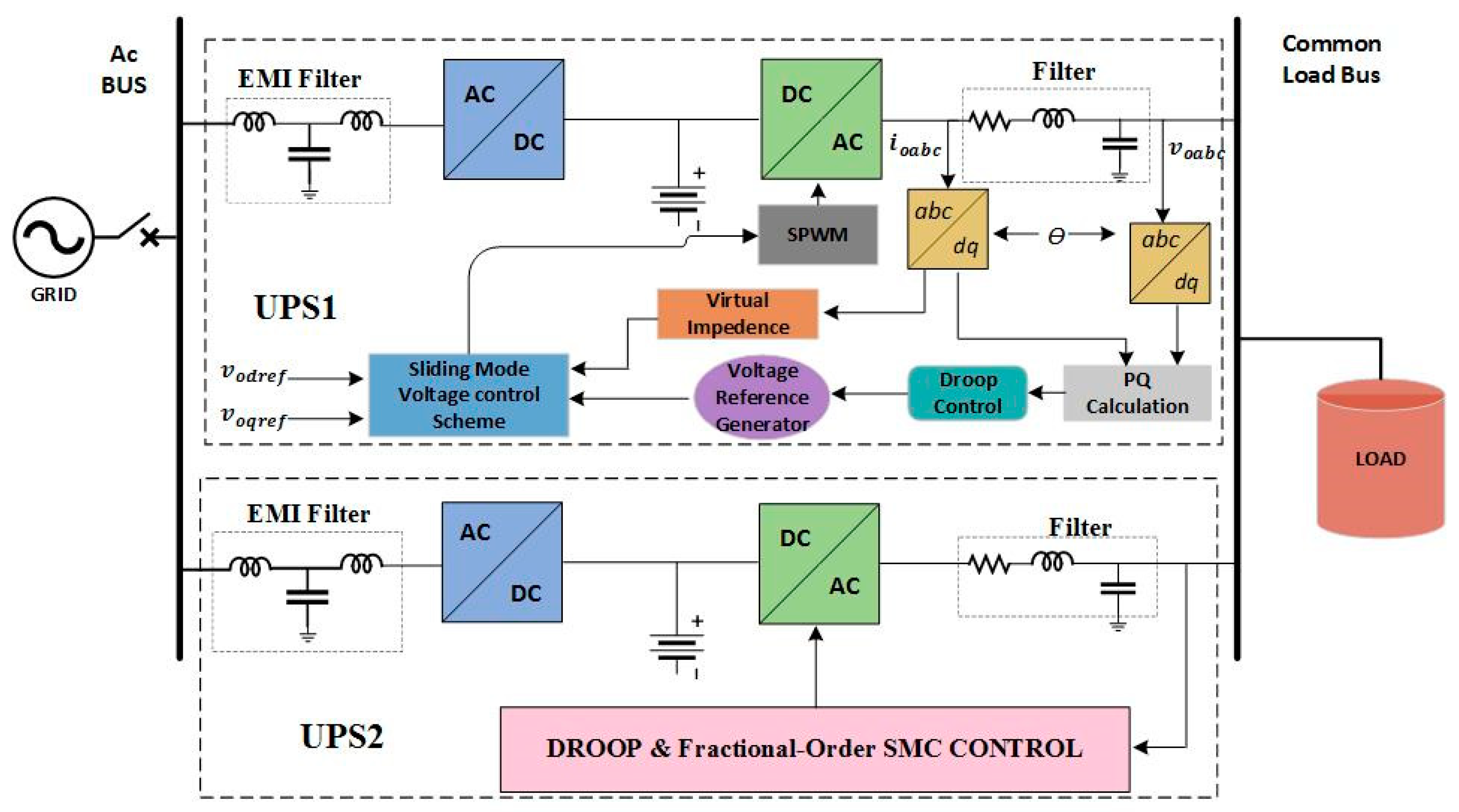
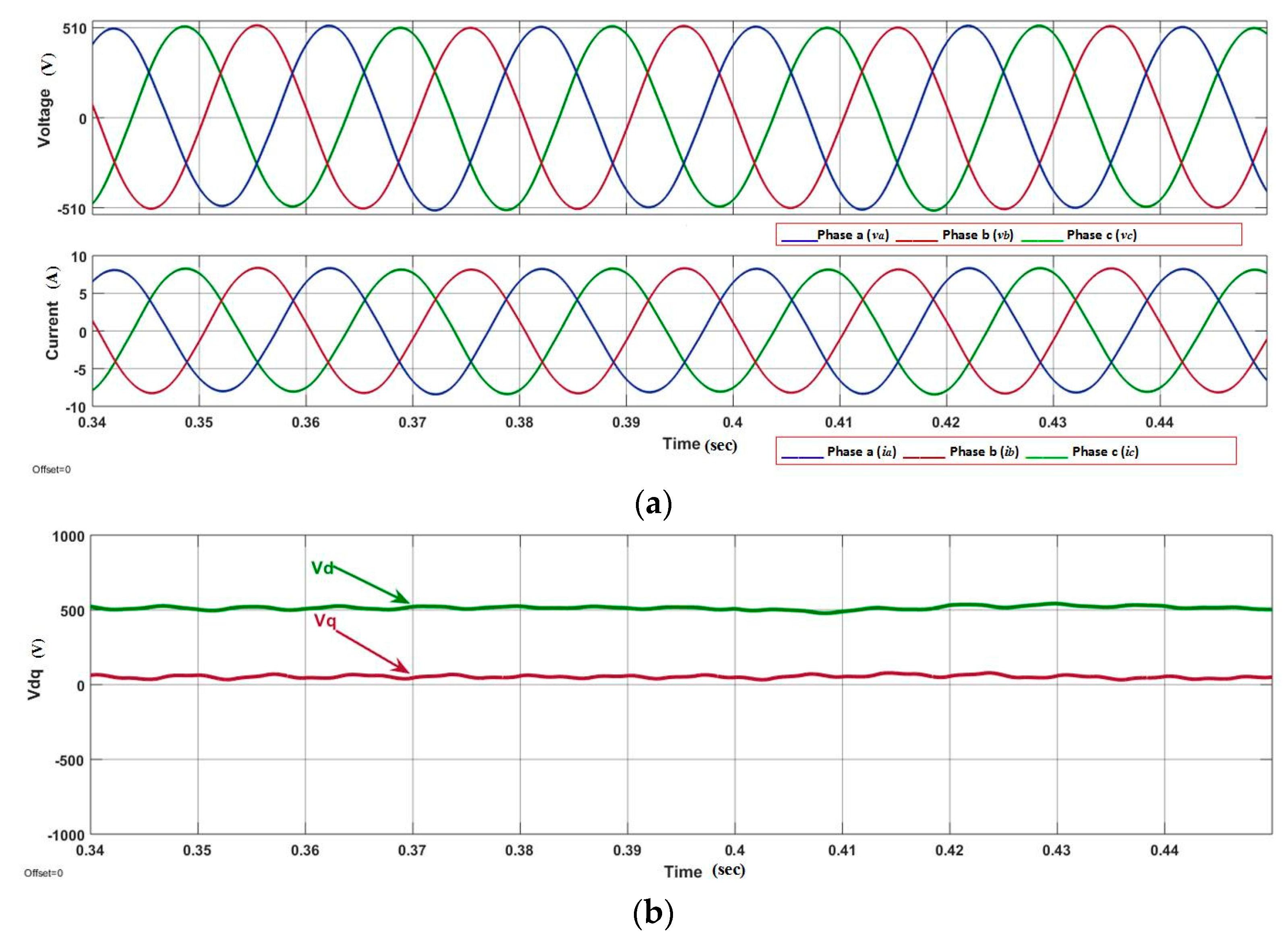
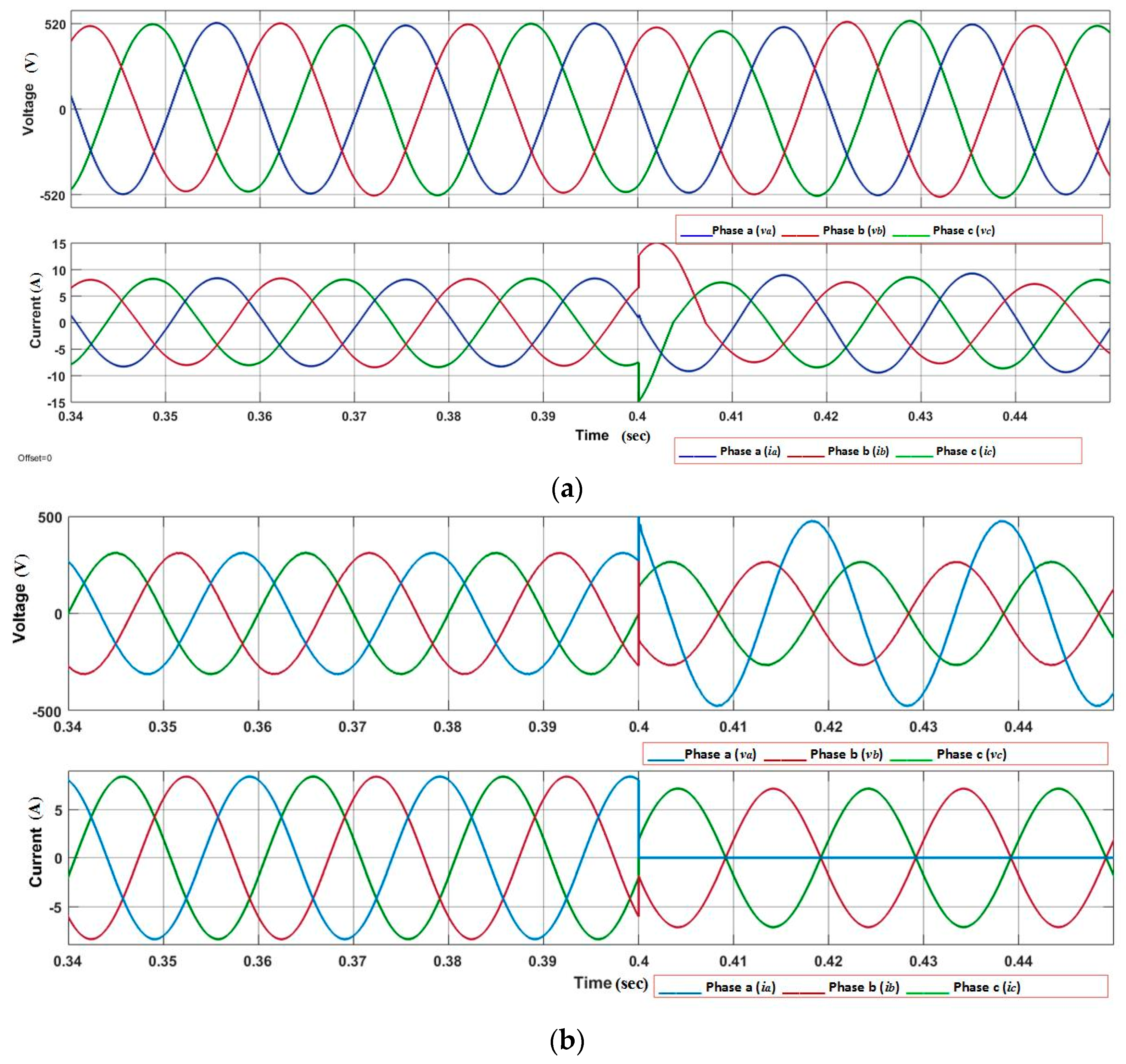
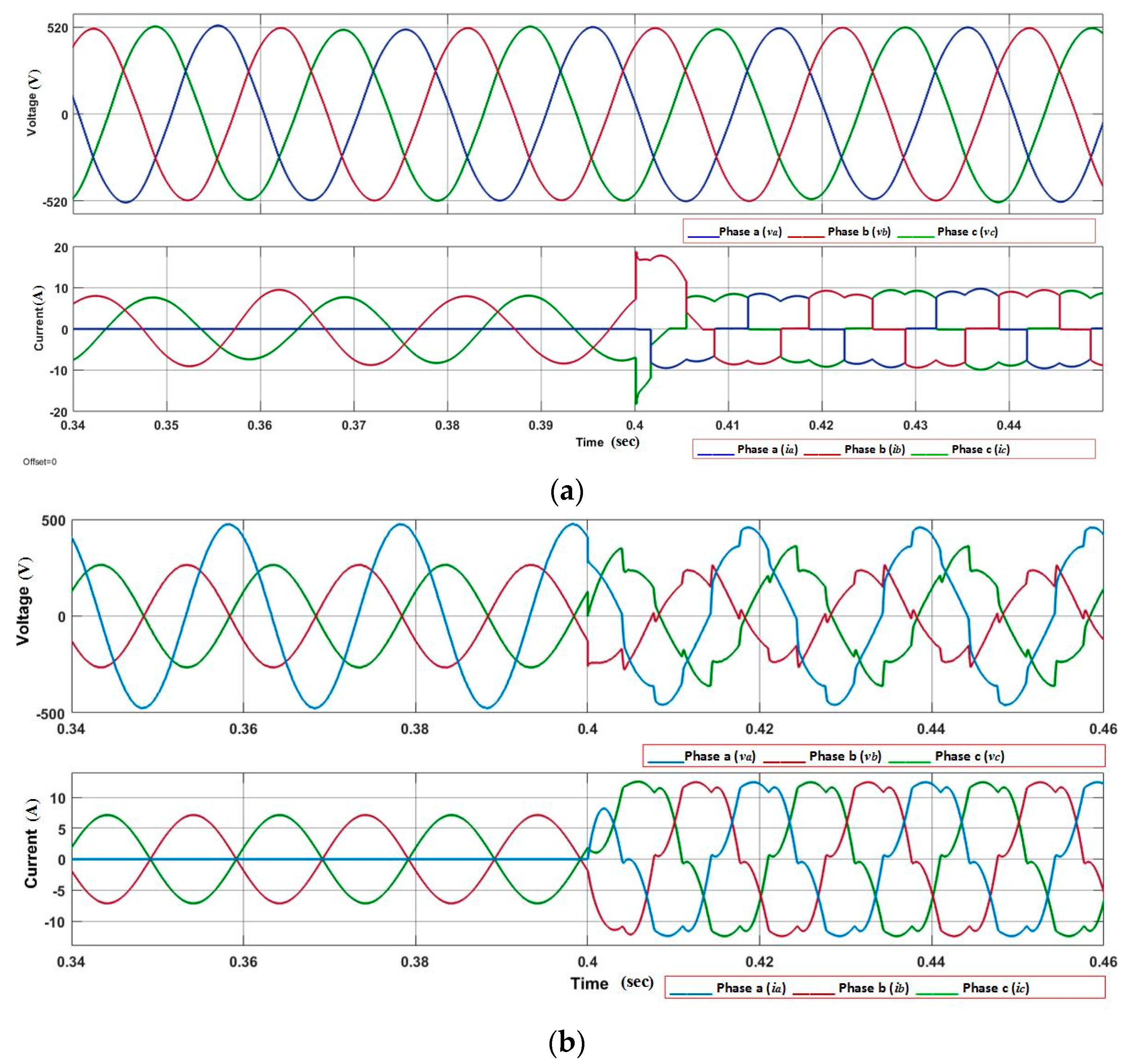
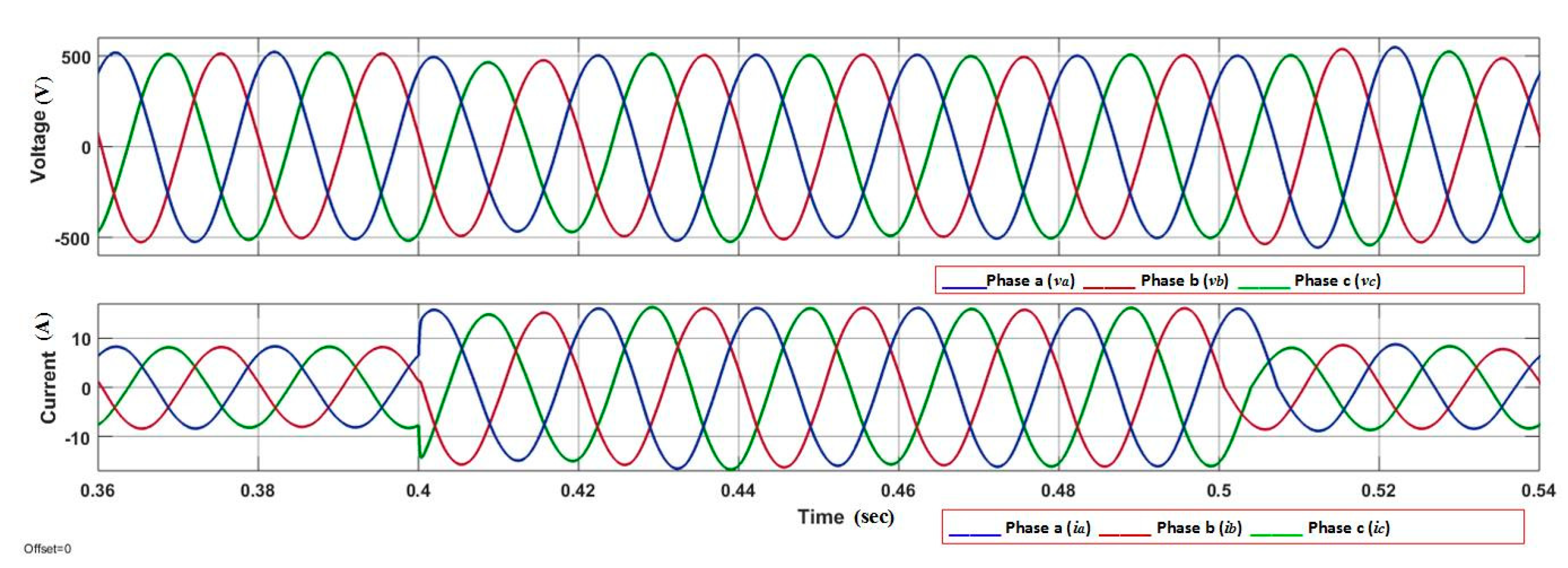
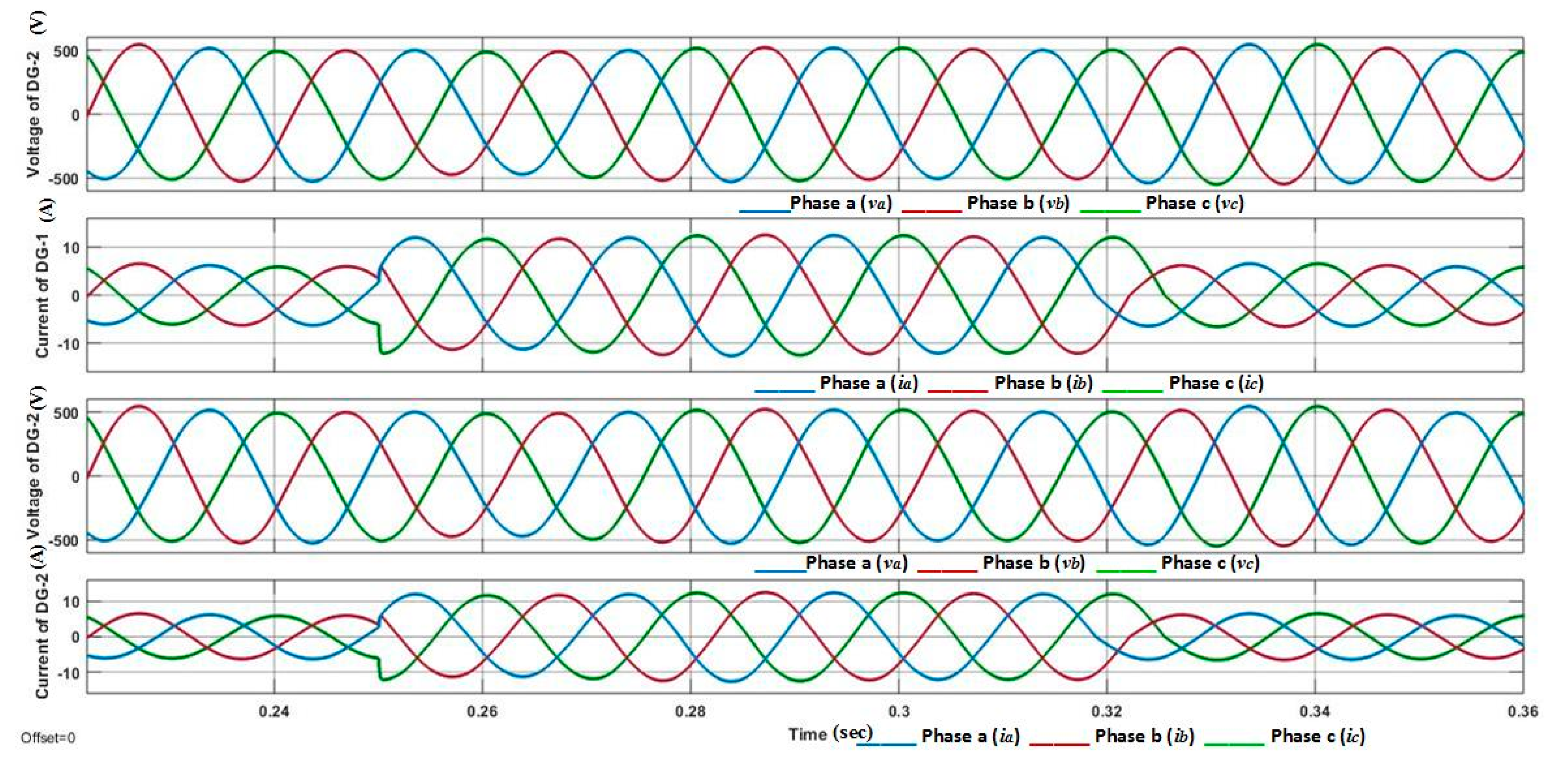
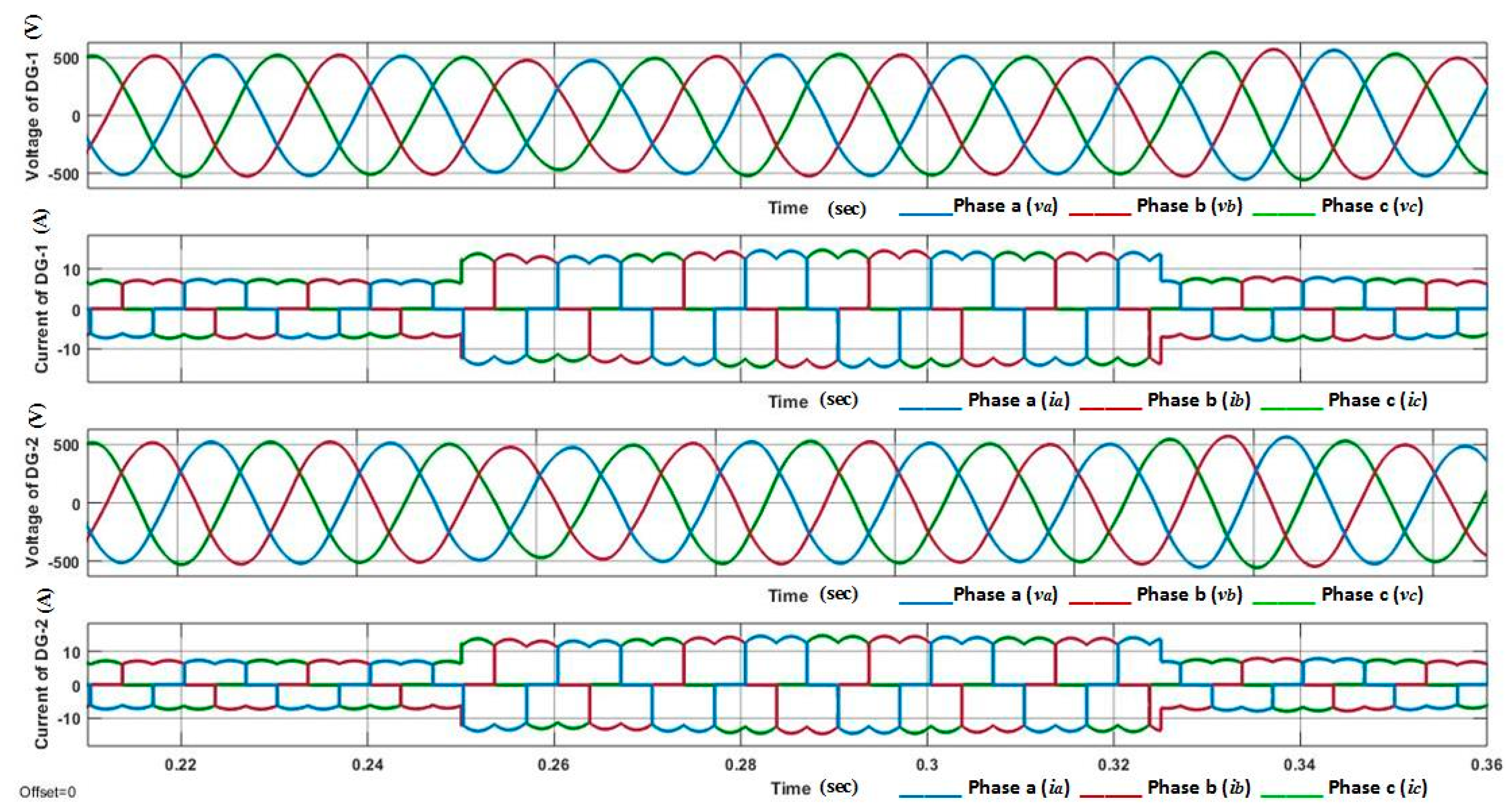
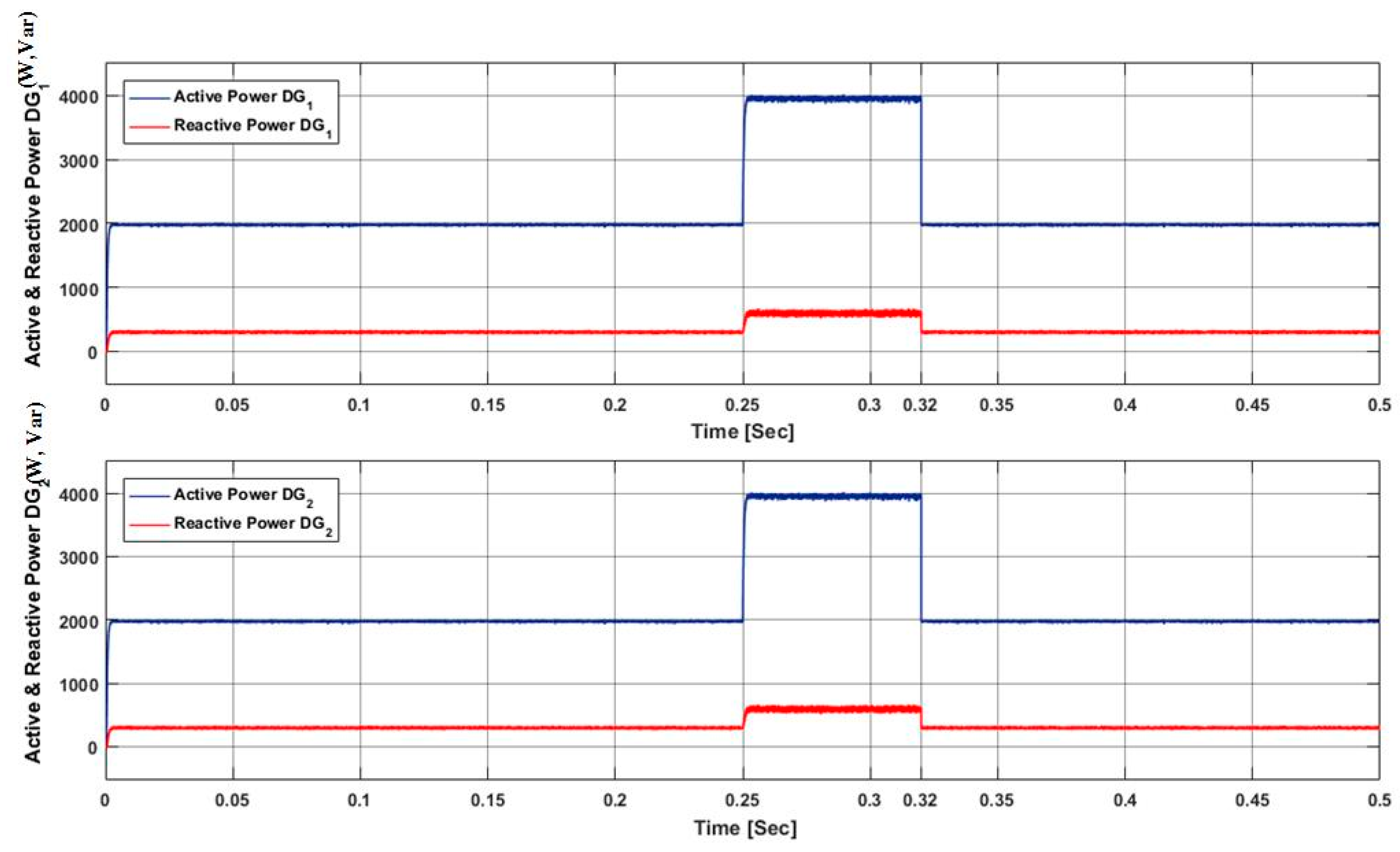
This paper presents a nonlinear control strategy for the voltage control of the parallel-connected UPS system. FOSMC scheme maintains the quality of the output voltage under multiple balanced/unbalanced dynamic load and also under distorted load current condition. Moreover, the proposed control strategy utilized fewer voltage sensors compared to model predictive control and classical SMC methods. A Lyapunov stability theorem is used to prove the stability of the proposed controller. Droop control is designed for the parallel-connected UPS systems to ensure proper power-sharing. Real-time simulation is performed in MATLAB/Simulink to show robustness and precise performance of the controller to maintain system power quality despite linear and/or distorted load current conditions. Additionally, the virtual output impedance loop is designed for the accurate reactive power-sharing with the load. The performance of the proposed FOSMC is compared with conventional proportional integral (PI) controller, and the simulation results show the THD of the output voltage of 0.40% and 1.03% for FOSMC, and 1.82% and 6.84% for PI controller under linear and nonlinear load, respectively.
The paper is organized as follows:
Section 2 describes the system description, dynamic model of the inverter, and the mathematical model of the FOSMC such as the design of the sliding surface and feedback control law.
Section 3 represents the Lyapunov stability theorem.
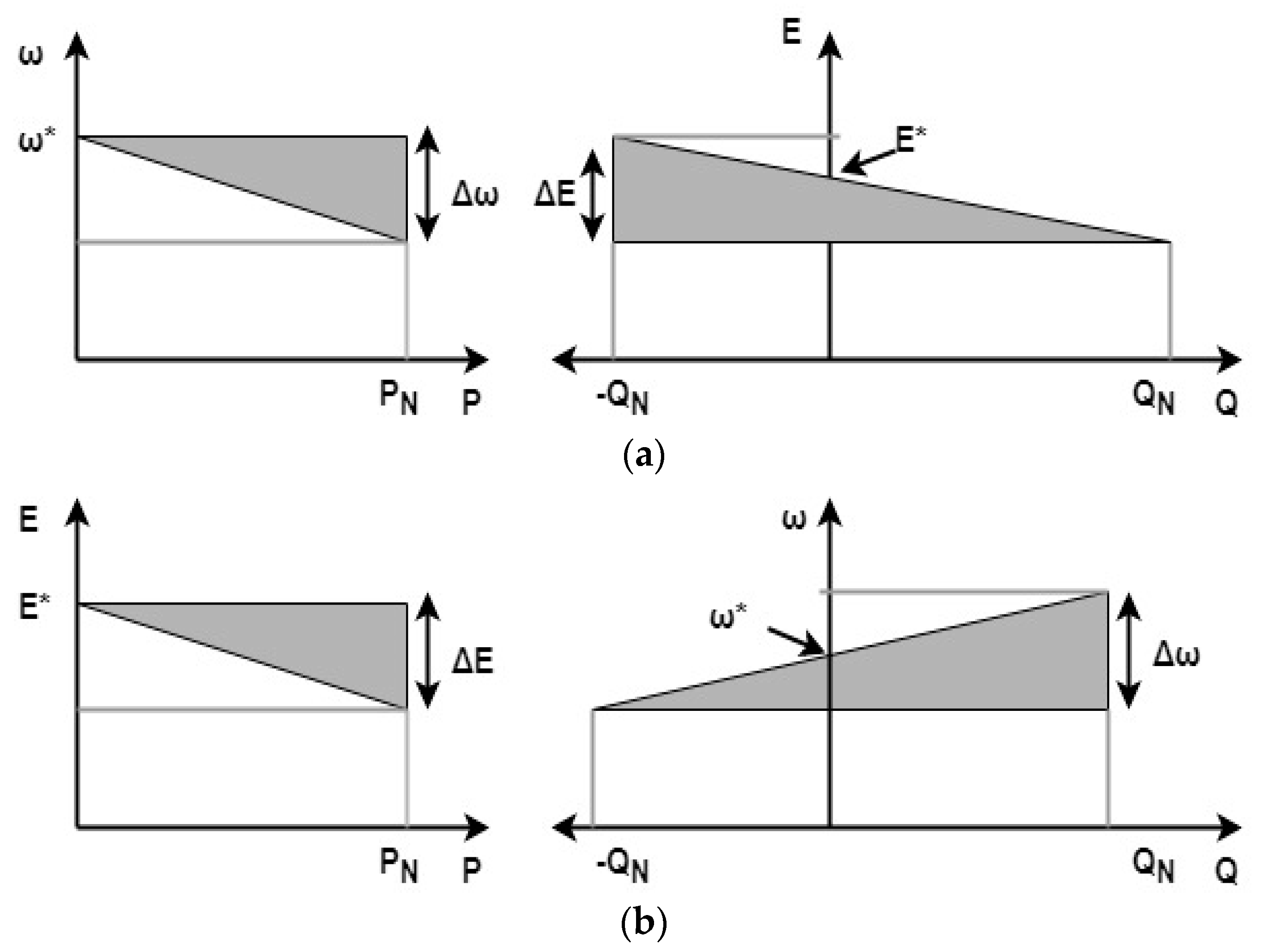
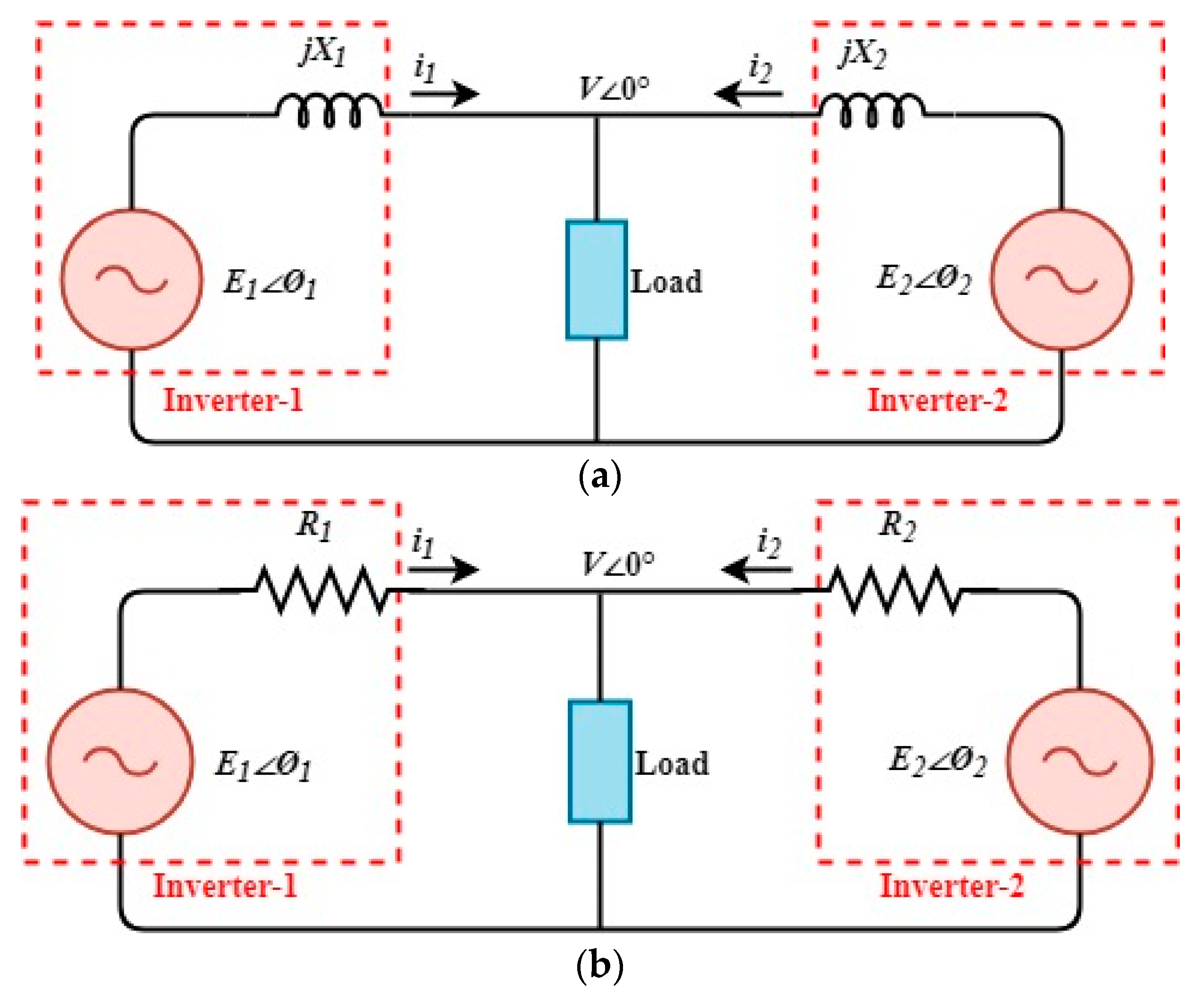
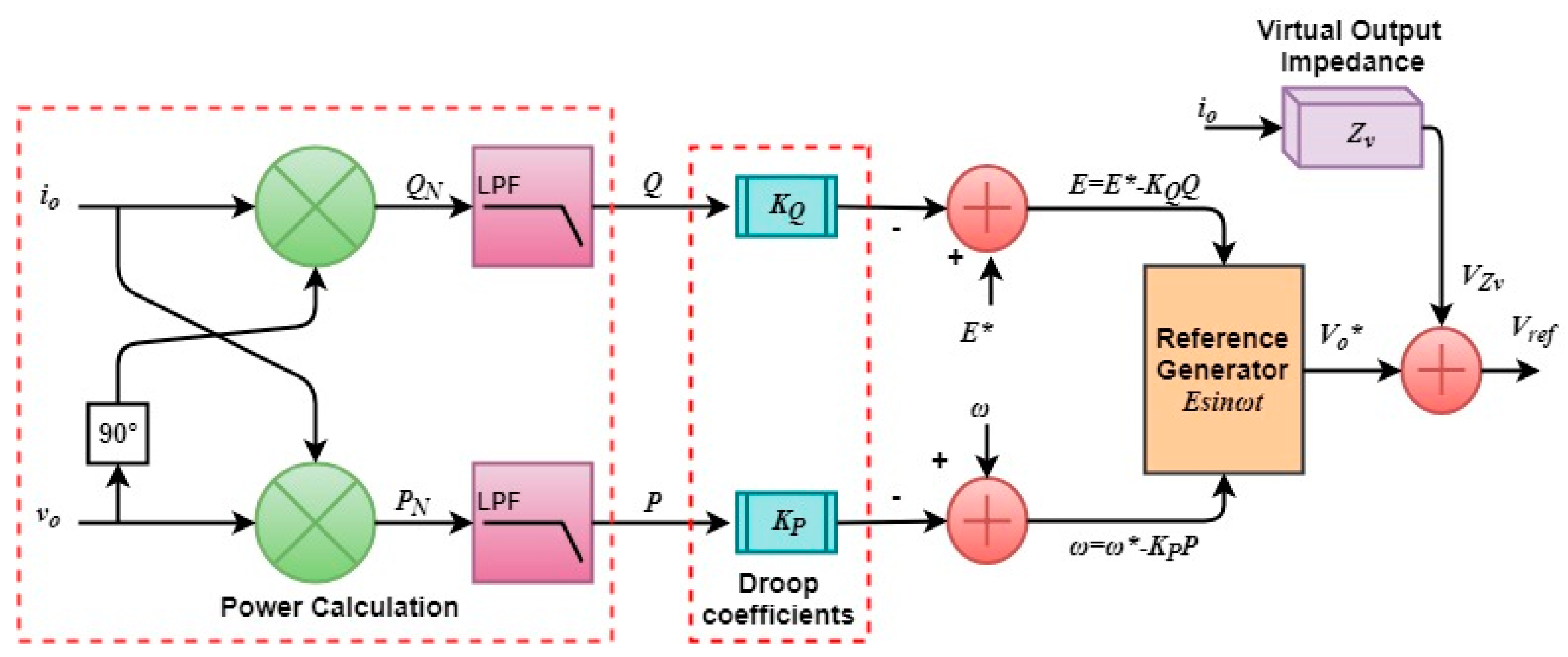
Section 4 presents the parallel UPS system and droop control explanation.
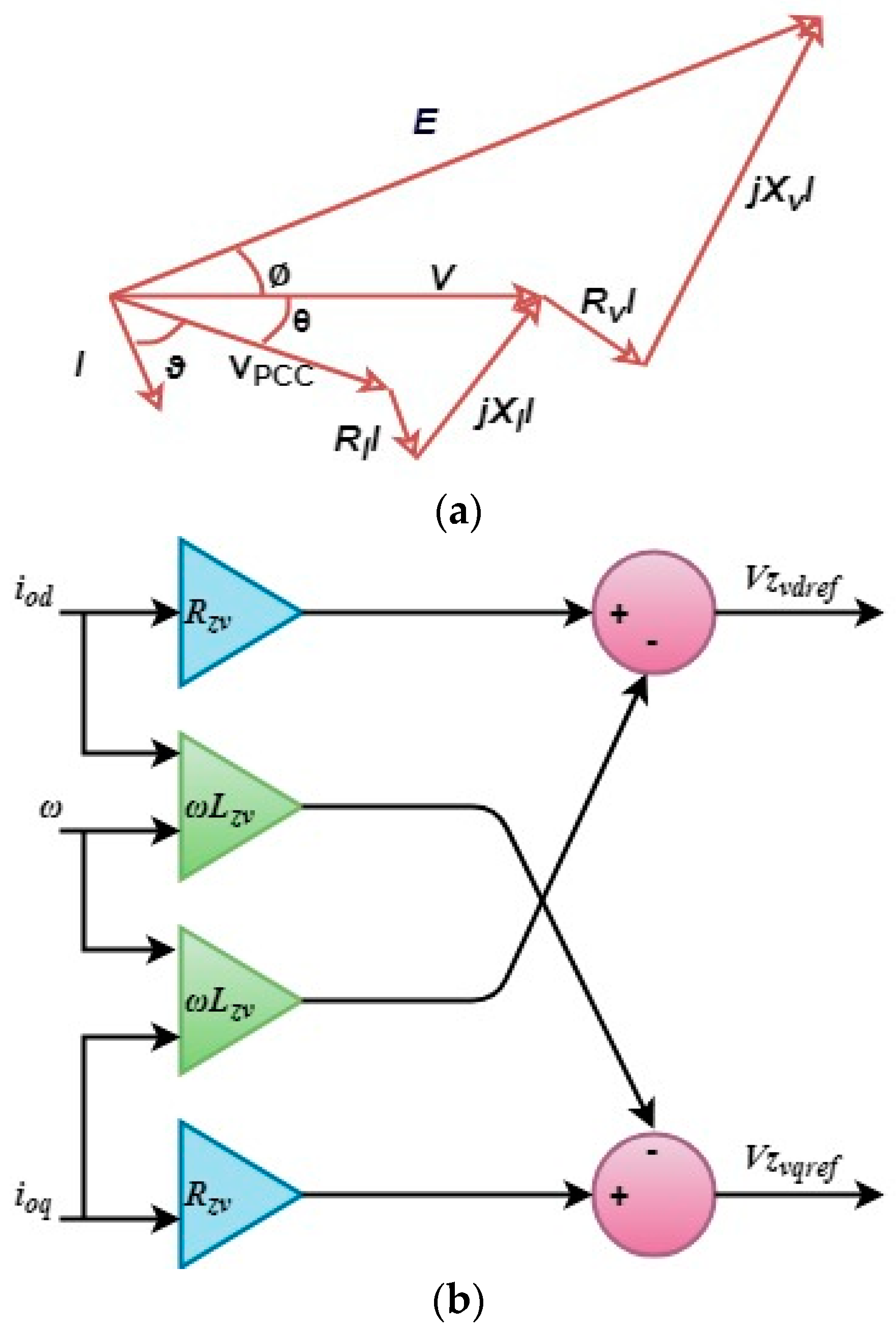
Section 5 explains the virtual output impedance (VOI). Then,
Section 6 demonstrates the simulation results and detail comparison between FOSM and the conventional PI controller. Finally, discussions and conclusion are stated in
Section 7 and
Section 8, respectively.