Fast Control-Oriented Dynamic Linear Model of Wind Farm Flow and Operation
Abstract
1. Introduction
2. Methods
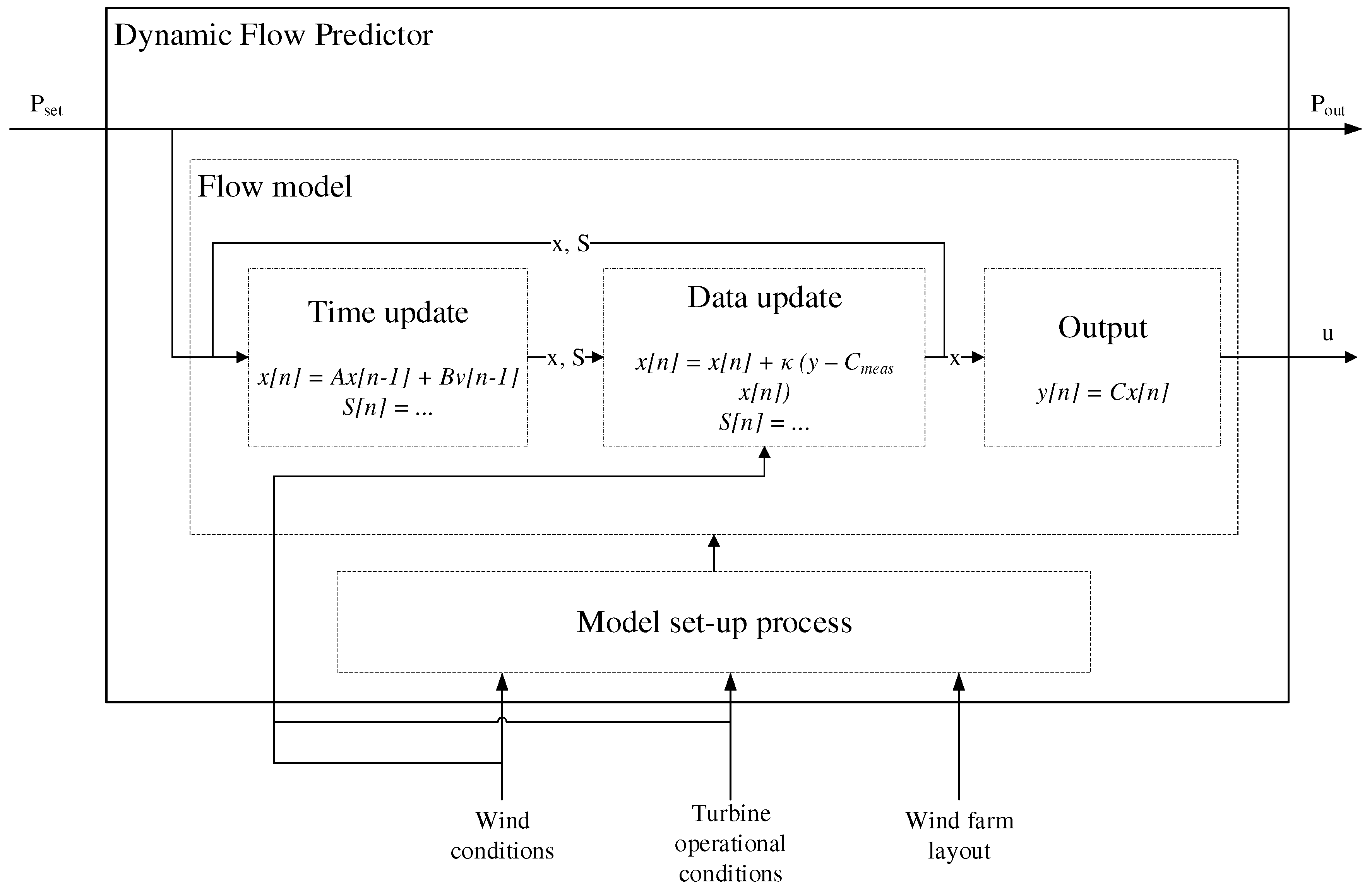
2.1. Dynamic Flow Predictor
2.1.1. Turbine Operation Model
2.1.2. Flow Model
2.1.3. Kalman Filter and System Update
Time Update
Data Update
Matrix Update
2.2. Simulation Environment: SimWindFarm
2.2.1. Modeling Approach
2.2.2. Validity as Test Environment
2.2.3. Simulation Conditions
3. Results and Discussion
3.1. Two-Turbine Case Study
3.1.1. Simulation Set-Up
Wind Farm Layout
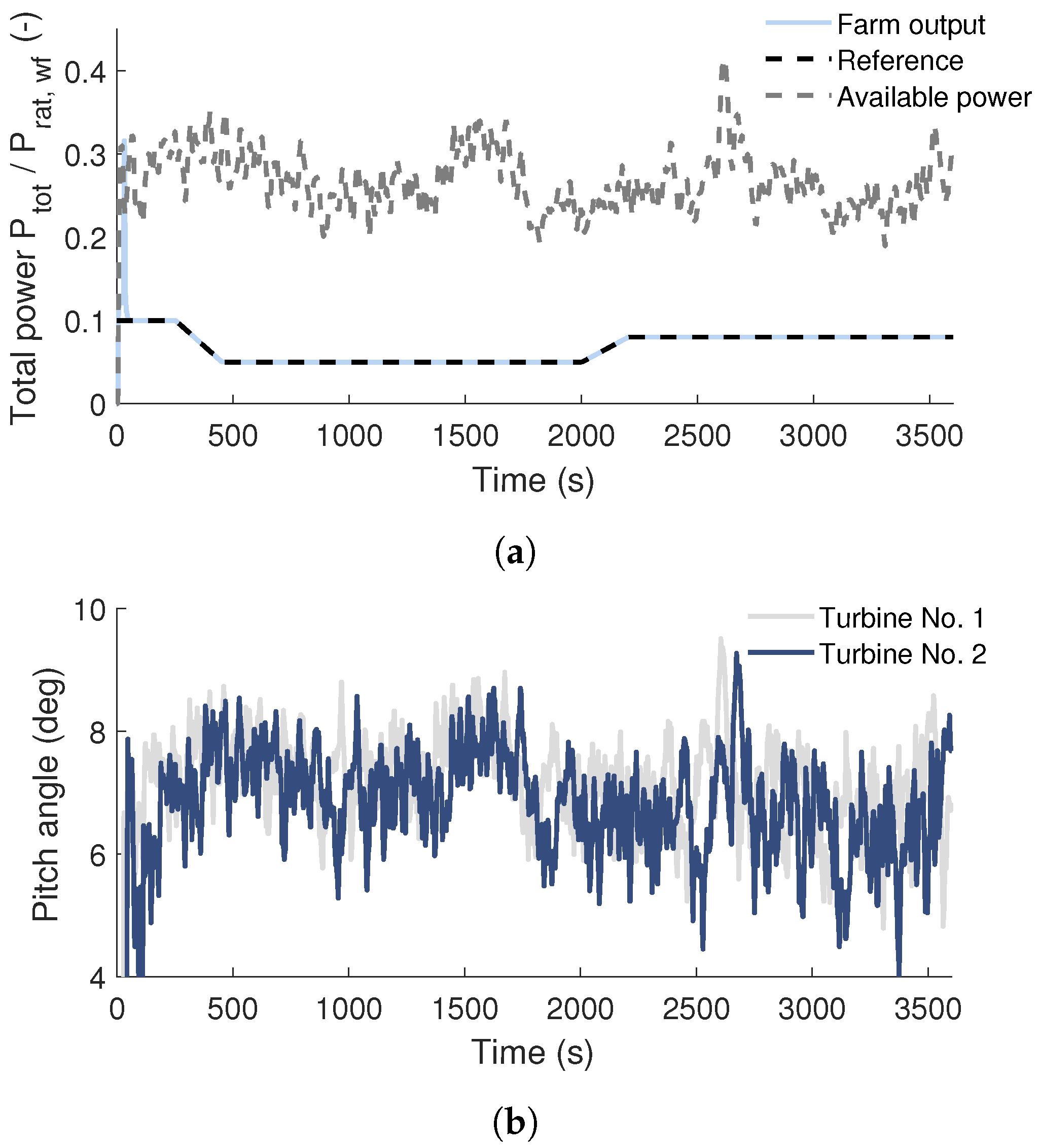
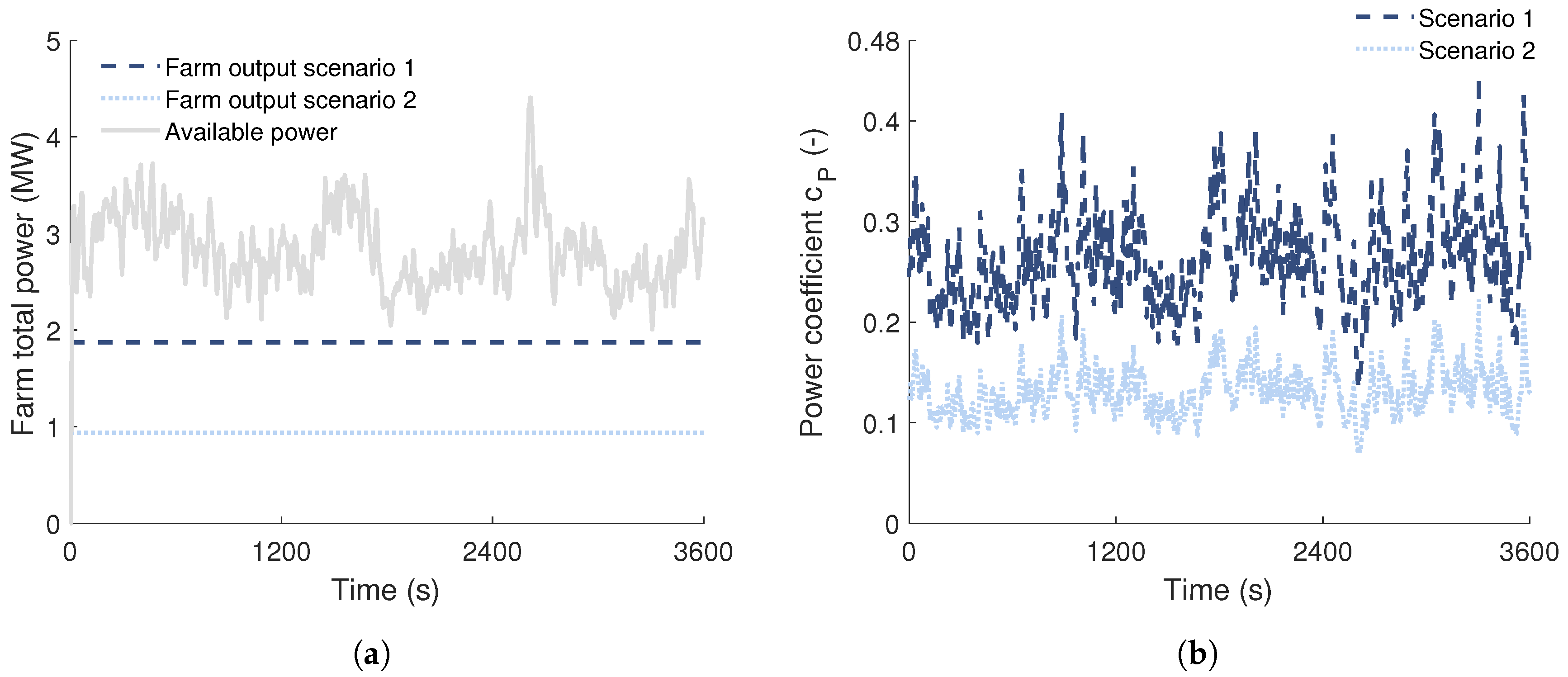
Wind Farm Operation
3.1.2. Results
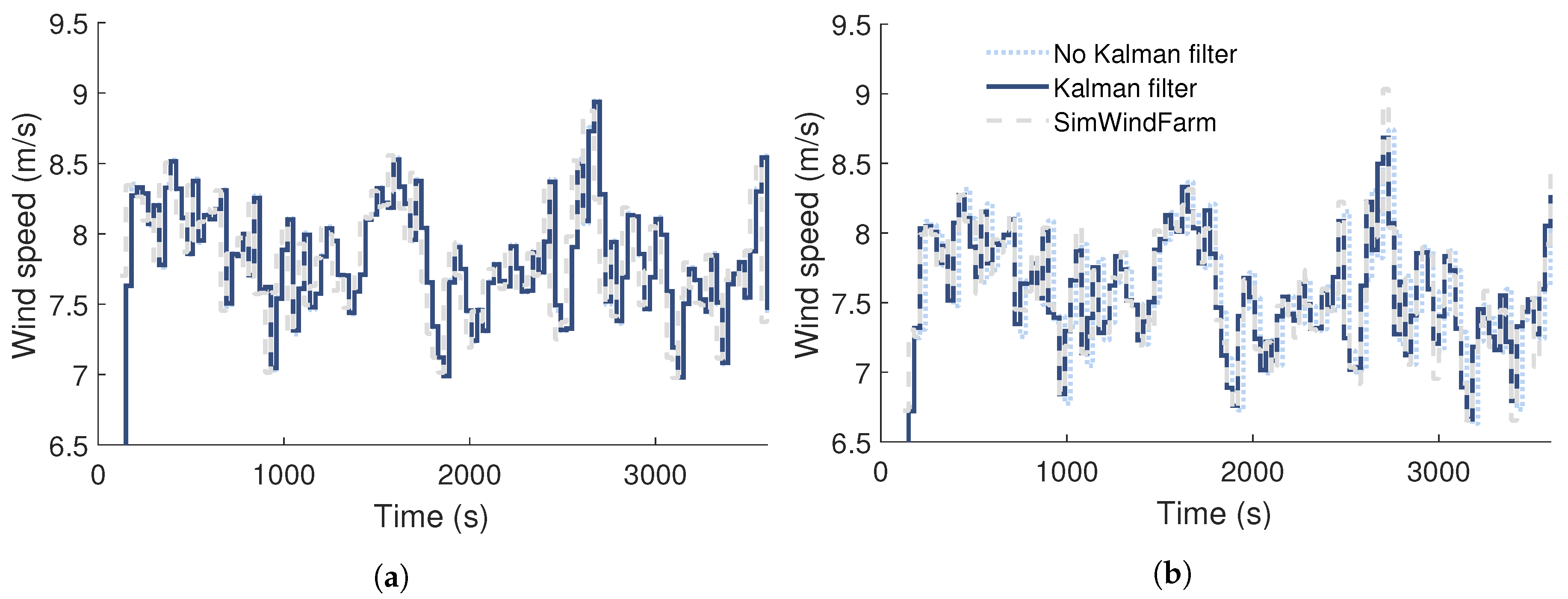
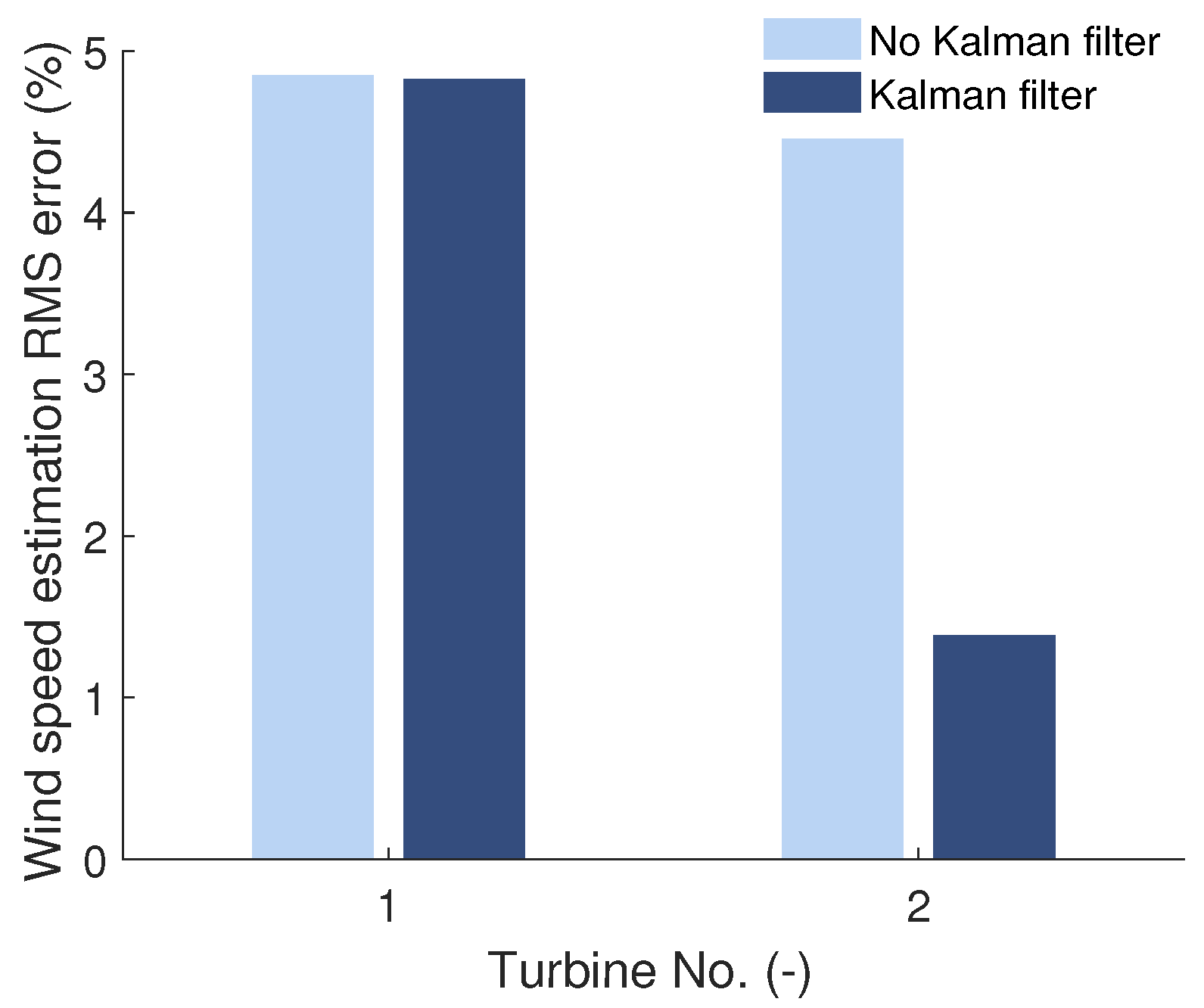
Benefits of Kalman Filtering
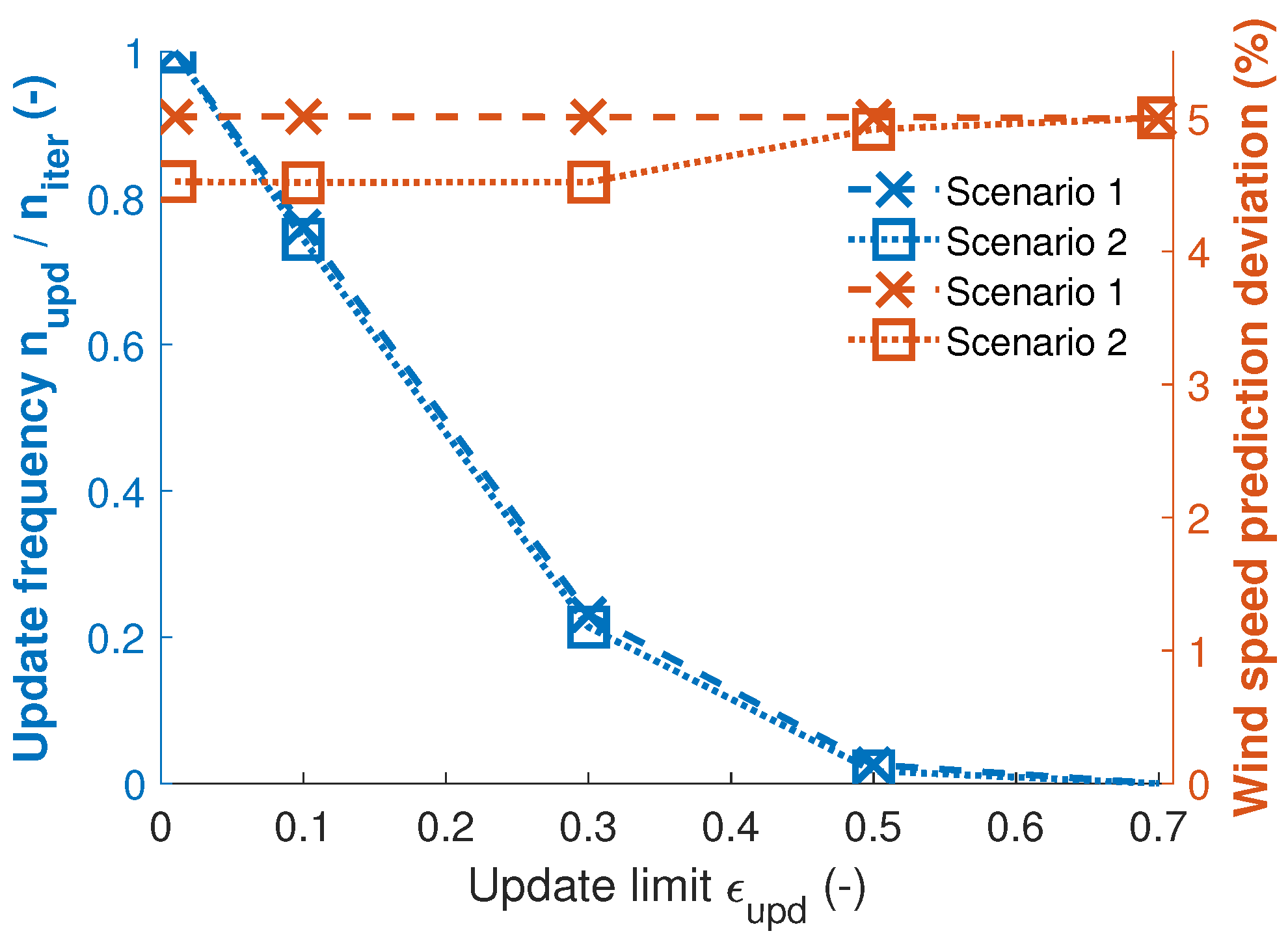
Computational Efficiency
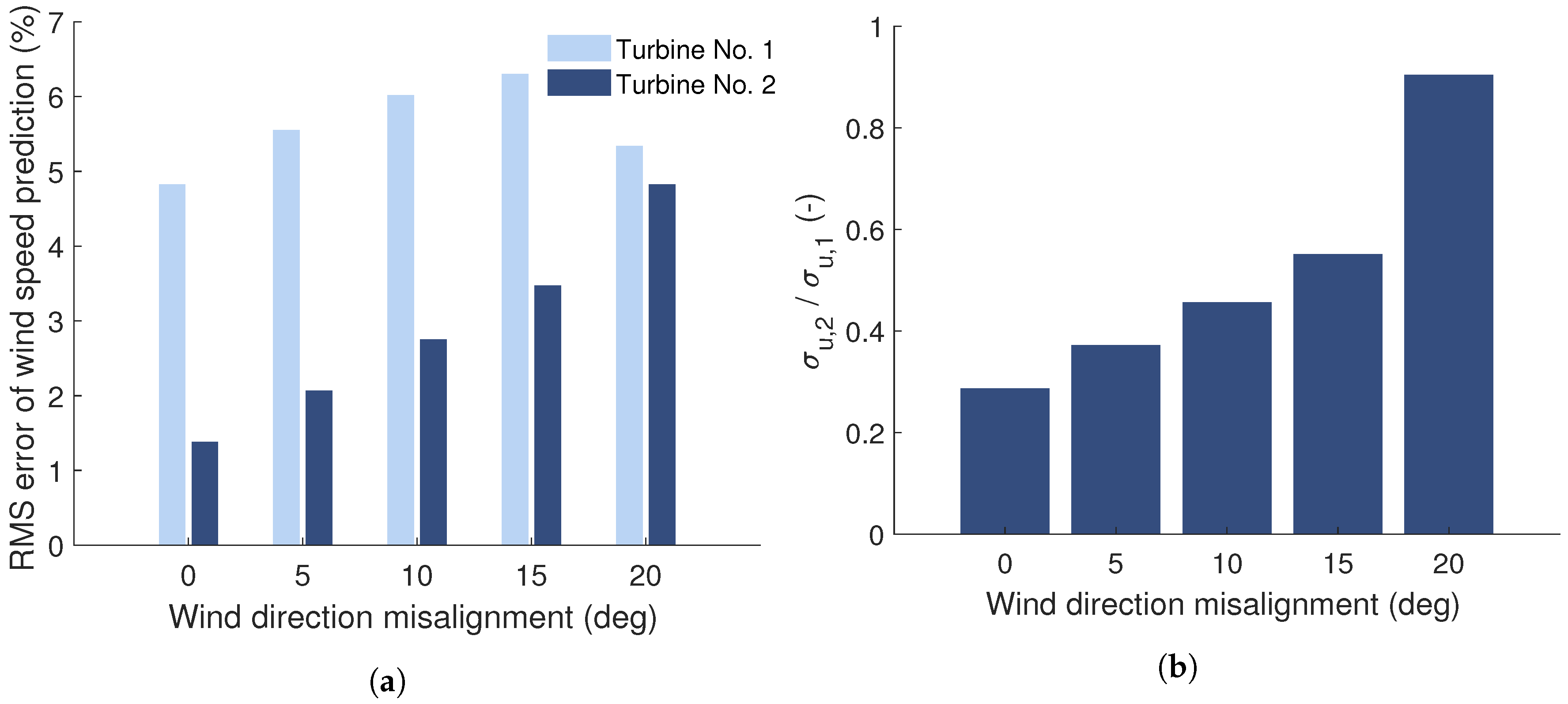
Effect of Wind Direction
3.2. Large-Scale Wind Farm Case Study
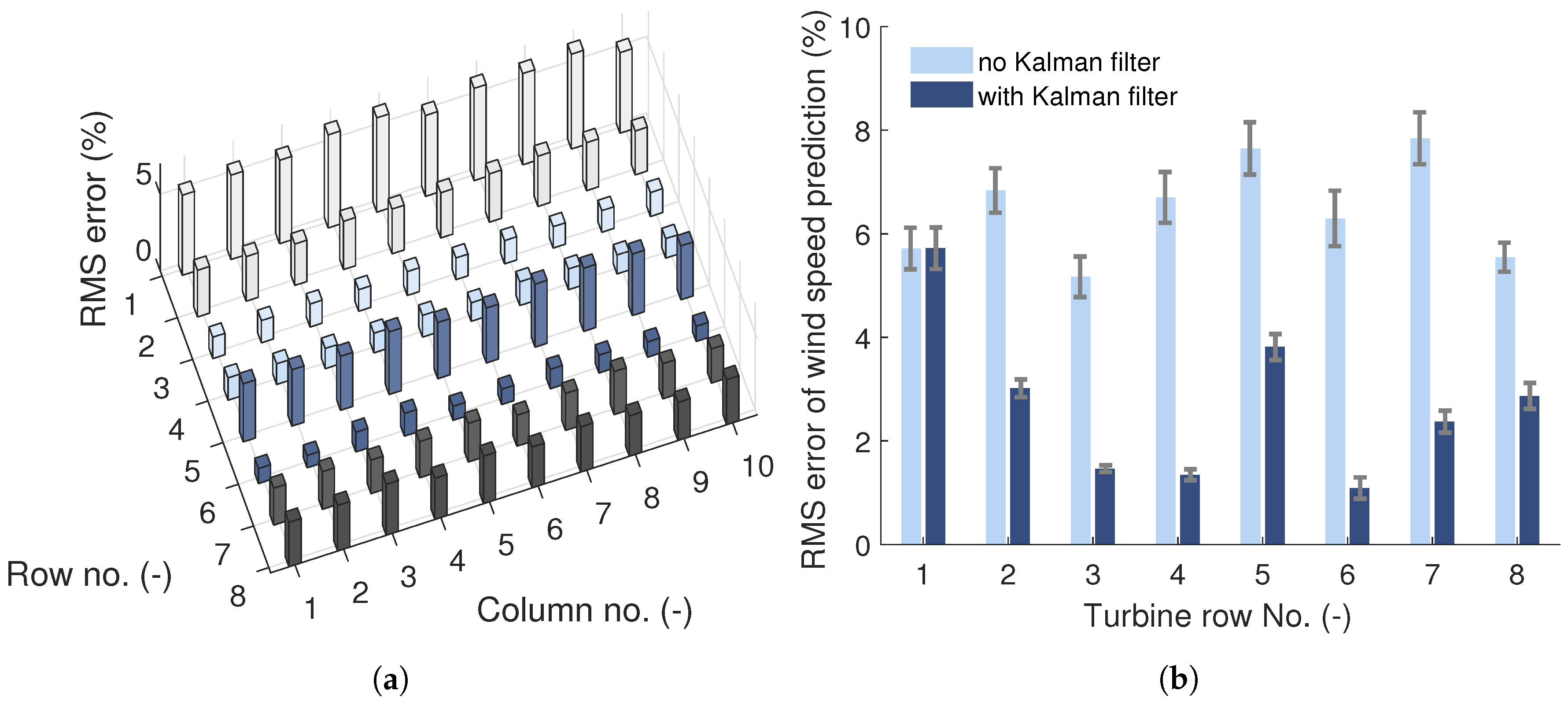
3.2.1. Benefit of Kalman Filter
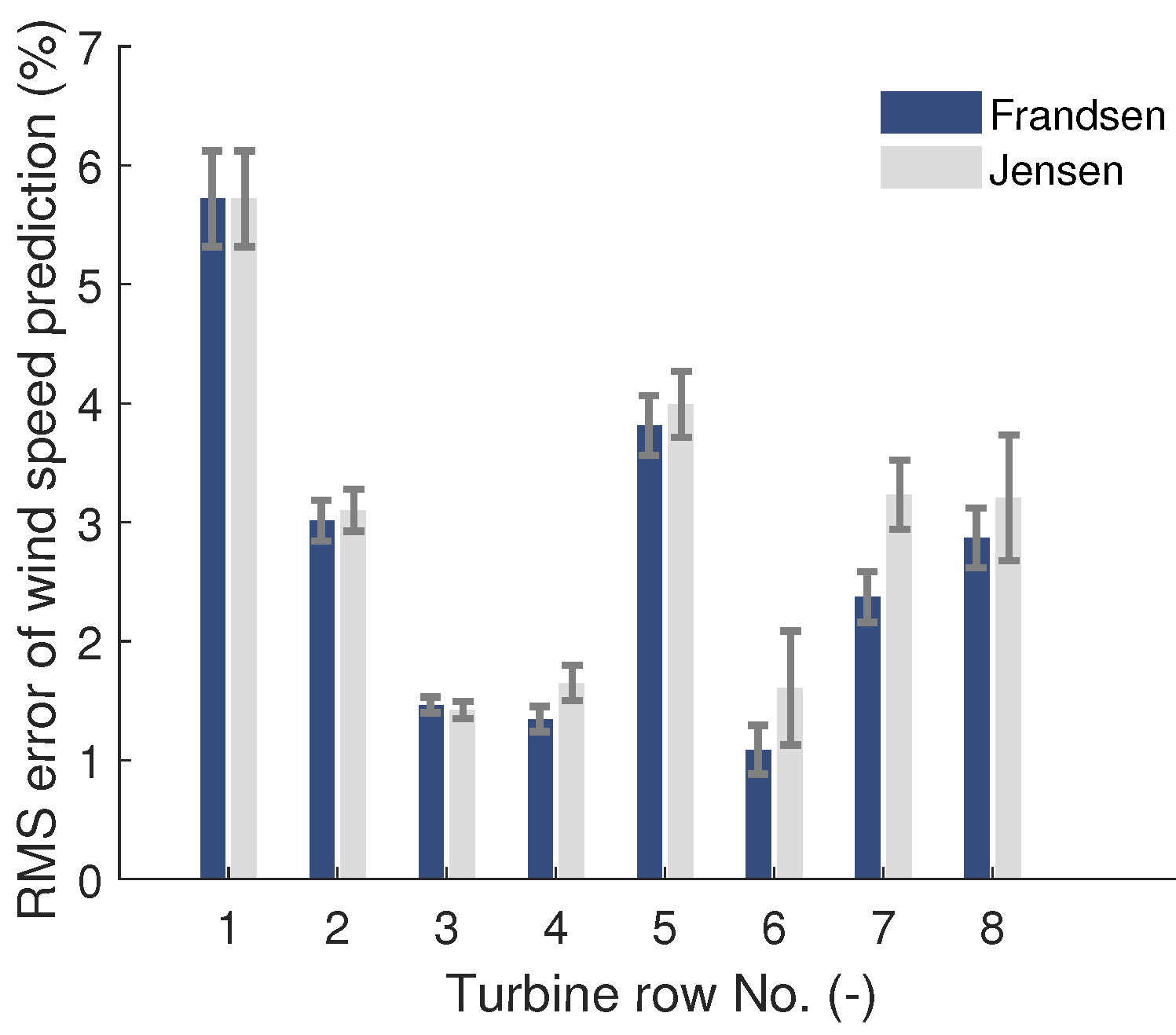
3.2.2. Sensitivity of Wake Model
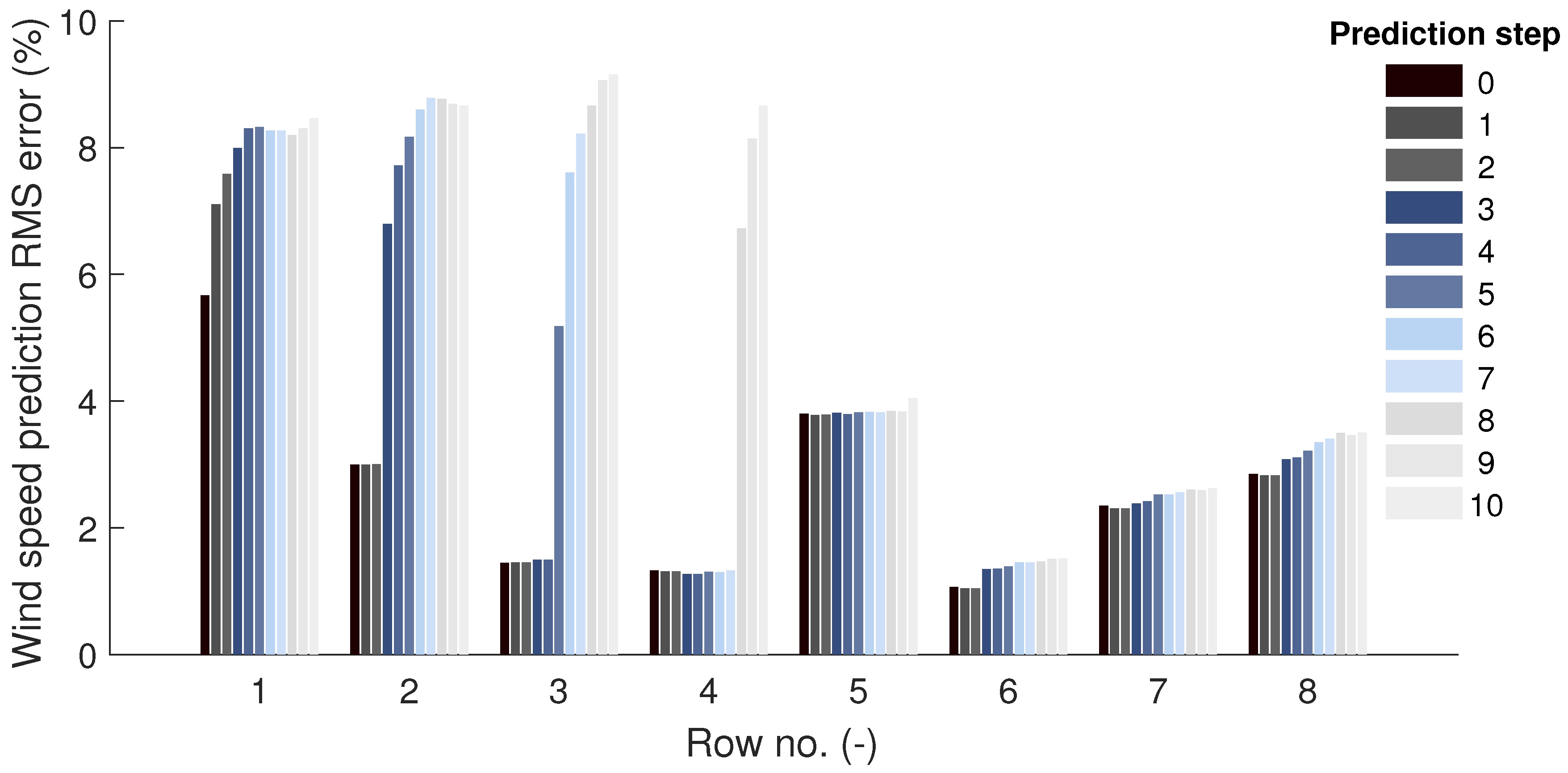
3.2.3. Wind Speed Prediction
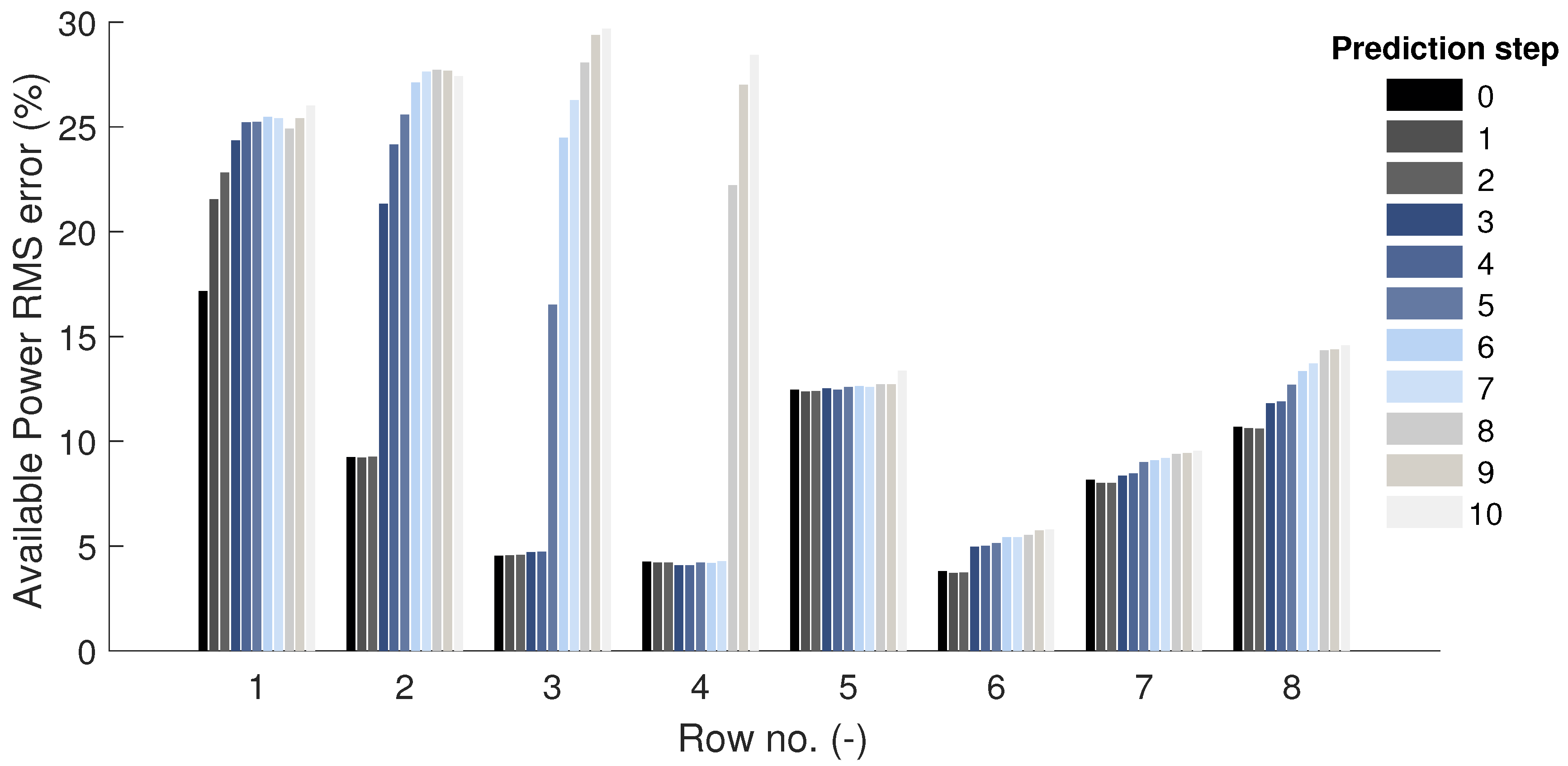
3.2.4. Available Power Prediction
3.2.5. Computation Time
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational fluid dynamics |
| DFP | Dynamic Flow Predictor |
| DTU | Technical University of Denmark |
| RMS | Root-mean-square |
| SWF | SimWindFarm |
References
- Global Wind Energy Council (GWEC). Global Wind Report 2017. Available online: http://gwec.net/ (accessed on 19 November 2018).
- Fernandez-Gamiz, U.; Zulueta, E.; Boyano, A.; Ansoategui, I.; Uriarte, I. Five megawatt wind turbine power output improvements by passive flow control devices. Energies 2017, 10, 742. [Google Scholar] [CrossRef]
- Hansen, M.O.; Sørensen, J.N.; Voutsinas, S.; Sørensen, N.; Madsen, H.A. State of the art in wind turbine aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 2006, 42, 285–330. [Google Scholar] [CrossRef]
- Pao, L.Y.; Johnson, K.E. A tutorial on the dynamics and control of wind turbines and wind farms. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 2076–2089. [Google Scholar] [CrossRef]
- Kazda, J.; Zendehbad, M.; Jafari, S.; Chokani, N.; Abhari, R.S. Mitigating adverse wake effects in a wind farm using non-optimum operational conditions. J. Wind Eng. Ind. Aerodyn. 2016, 154, 76–83. [Google Scholar] [CrossRef]
- Annoni, J.; Gebraad, P.M.; Scholbrock, A.K.; Fleming, P.A.; Wingerden, J.W.V. Analysis of axial-induction-based wind plant control using an engineering and a high-order wind plant model. Wind Energy 2016, 19, 1135–1150. [Google Scholar] [CrossRef]
- Hansen, A.D.; Sørensen, P.; Iov, F.; Blaabjerg, F. Centralised power control of wind farm with doubly fed induction generators. Renew. Energy 2006, 31, 935–951. [Google Scholar] [CrossRef]
- Van Wingerden, J.W.; Pao, L.; Aho, J.; Fleming, P. Active power control of waked wind farms. IFAC-PapersOnLine 2017, 50, 4484–4491. [Google Scholar] [CrossRef]
- Kazda, J.; Merz, K.; Tande, J.O.; Cutululis, N.A. Mitigating turbine mechanical loads using engineering model predictive wind farm controller. J. Phys. Conf. Ser. 2018, 1104, 012036. [Google Scholar] [CrossRef]
- Soleimanzadeh, M.; Wisniewski, R.; Kanev, S. An optimization framework for load and power distribution in wind farms. J. Wind Eng. Ind. Aerodyn. 2012, 107–108, 256–262. [Google Scholar] [CrossRef]
- Horvat, T.; Spudic, V.; Baotic, M. Quasi-stationary optimal control for wind farm with closely spaced turbines. In Proceedings of the 35th International Convention MIPRO, Opatija, Croatia, 21–25 May 2012; pp. 829–834. [Google Scholar]
- Gebraad, P.M.O.; Teeuwisse, F.W.; van Wingerden, J.W.; Fleming, P.A.; Ruben, S.D.; Marden, J.R.; Pao, L.Y. Wind plant power optimization through yaw control using a parametric model for wake effects—A CFD simulation study. Wind Energy 2016, 19, 95–114. [Google Scholar] [CrossRef]
- Kazda, J.; Göçmen, T.; Giebel, G.; Cutululis, N. Possible improvements for present wind farm models used in optimal wind farm controllers. In Proceedings of the 15th International Workshop on Large-Scale Integration of Wind Power into Power Systems as well as on Transmission Networks for Offshore Wind Power Plants, Vienna, Austria, 15–17 November 2016. [Google Scholar]
- Crespo, A.; Hernández, J. Turbulence characteristics in wind-turbine wakes. J. Wind Eng. Ind. Aerodyn. 1996, 61, 71–85. [Google Scholar] [CrossRef]
- Riverso, S.; Mancini, S.; Sarzo, F.; Ferrari-Trecate, G. Model predictive controllers for reduction of mechanical fatigue in wind farms. IEEE Trans. Control Syst. Technol. 2017, 25, 535–549. [Google Scholar] [CrossRef]
- Mikkelsen, T.; Angelou, N.; Hansen, K.; Sjoholm, M.; Harris, M.; Slinger, C.; Hadley, P.; Scullion, R.; Ellis, G.; Vives, G. A Spinner-integrated wind lidar for enhanced wind turbine control. Wind Energy 2013, 16, 625–643. [Google Scholar] [CrossRef]
- Schlipf, D.; Schlipf, D.J.; Kühn, M. Nonlinear model predictive control of wind turbines using LIDAR. Wind Energy 2013, 16, 1107–1129. [Google Scholar] [CrossRef]
- Boersma, S.; Gebraad, P.; Vali, M.; Doekemeijer, B.; van Wingerden, J. A control-oriented dynamic wind farm flow model: “WFSim”. J. Phys. Conf. Ser. 2016, 753, 032005. [Google Scholar] [CrossRef]
- Soleimanzadeh, M.; Wisniewski, R.; Brand, A. State-space representation of the wind flow model in wind farms. Wind Energy 2014, 17, 627–639. [Google Scholar] [CrossRef]
- Knudsen, T.; Bak, T.; Soltani, M. Prediction models for wind speed at turbine locations in a wind farm. Wind Energy 2011, 14, 877–894. [Google Scholar] [CrossRef]
- Wang, J.; Hu, J. A robust combination approach for short-term wind speed forecasting and analysis—Combination of the ARIMA (Autoregressive Integrated Moving Average), ELM (Extreme Learning Machine), SVM (Support Vector Machine) and LSSVM (Least Square SVM) Forecasts Using a GPR (Gaussian Process Regression) Model. Energy 2015, 93, 41–56. [Google Scholar] [CrossRef]
- Jung, J.; Broadwater, R.P. Current status and future advances for wind speed and power forecasting. Renew. Sustain. Energy Rev. 2014, 31, 762–777. [Google Scholar] [CrossRef]
- Shapiro, C.R.; Meyers, J.; Meneveau, C.; Gayme, D.F. Wind farms providing secondary frequency regulation: evaluating the performance of model-based receding horizon control. Wind Energy Sci. 2018, 3, 11–24. [Google Scholar] [CrossRef]
- Gebraad, P.M.O.; van Wingerden, J.W. A Control-oriented dynamic model for wakes in wind plants. J. Phys. Conf. Ser. 2014, 524, 012186. [Google Scholar] [CrossRef]
- Gogmen, T.; Giebel, G.; Poulsen, N.K.; Sørensen, P.E. Possible power of down-regulated offshore wind power plants: The PossPOW algorithm. Wind Energy 2018. [Google Scholar] [CrossRef]
- Boersma, S.; Doekemeijer, B.; Vali, M.; Meyers, J.; Wingerden, J.w.V. A Control-oriented dynamic wind farm model: WFSim. Wind Energy Sci. 2018, 3, 75. [Google Scholar] [CrossRef]
- Gebraad, P.M.O.; Fleming, P.A.; Van Wingerden, J.W. Wind turbine wake estimation and control using FLORIDyn, a control-oriented dynamic wind plant model. In Proceedings of the American Control Conference, Chicago, IL, USA, 1–3 July 2015; pp. 1702–1708. [Google Scholar] [CrossRef]
- Bay, C.J.; Annoni, J.; Taylor, T.; Pao, L.; Johnson, K. Active power control for wind farms using distributed model predictive control and nearest neighbor communication. In Proceedings of the Annual American Control Conference, Milwaukee, WI, USA, 27–29 June 2018; pp. 682–687. [Google Scholar] [CrossRef]
- Göçmen, T.; Giebel, G.; Sørensen, P.E.; Poulsen, N.K. Possible Power Estimation of Down-Regulated Offshore Wind Power Plants. Ph.D. Thesis, Technical University of Denmark (DTU), Kongens Lyngby, Denmark, 2016. [Google Scholar]
- Øye, S. Tjæreborg Wind Turbine (Esbjerg): First Dynamic Inflow Measurement; Technical Report; DTU Wind Energy: Roskilde, Denmark, 1991. [Google Scholar]
- Machefaux, E.; Larsen, G.C.; Troldborg, N.; Gaunaa, M.; Rettenmeier, A. Empirical modeling of single-wake advection and expansion using full-scale pulsed lidar-based measurements. Wind Energy 2015, 18, 2085–2103. [Google Scholar] [CrossRef]
- Frandsen, S.; Barthelmie, R.; Pryor, S.; Rathmann, O.; Larsen, S.; Hojstrup, J. Analytical modelling of wind speed deficit in large offshore wind farms. Wind Energy 2006, 9, 39–53. [Google Scholar] [CrossRef]
- Kalman, R.E.; Bucy, R.S. New results in linear filtering and prediction theory. J. Basic Eng. 1961, 83, 95. [Google Scholar] [CrossRef]
- Grunnet, J.; Soltani, M.; Knudsen, T. Aeolus toolbox for dynamics wind farm model, simulation and control. In Proceedings of the European Wind Energy Conference & Exhibition (EWEC 2010), Warszawa, Poland, 20–23 April 2010; pp. 3119–3129. [Google Scholar]
- Grunnet, J.; Soltani, M.; Knudsen, T. SimWindFarm Official Website. 2016. Available online: http://www.ict-aeolus.eu/SimWindFarm/ (accessed on 19 November 2018).
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical Report No. NREL/TP-500-38060; National Renewable Energy Laboratory: Golden, CO, USA, 2009. [Google Scholar]
- Kazda, J.; Göçmen, T.; Giebel, G.; Courtney, M.; Cutululis, N. Framework of multi-objective wind farm controller applicable to real wind farms. In Proceedings of the WindEurope Summit 2016, Hamburg, Germany, 27–29 September 2016. [Google Scholar]
- Energinet.dk. Technical Regulation for Wind Power Plants with a Power Output Above 11 kW. Available online: http://osp.energinet.dk/ (accessed on 19 November 2018).
- Jensen, N.O. A Note on Wind Generator Interaction; Risø National Laboratory: Roskilde, Denmark, 1983. [Google Scholar]
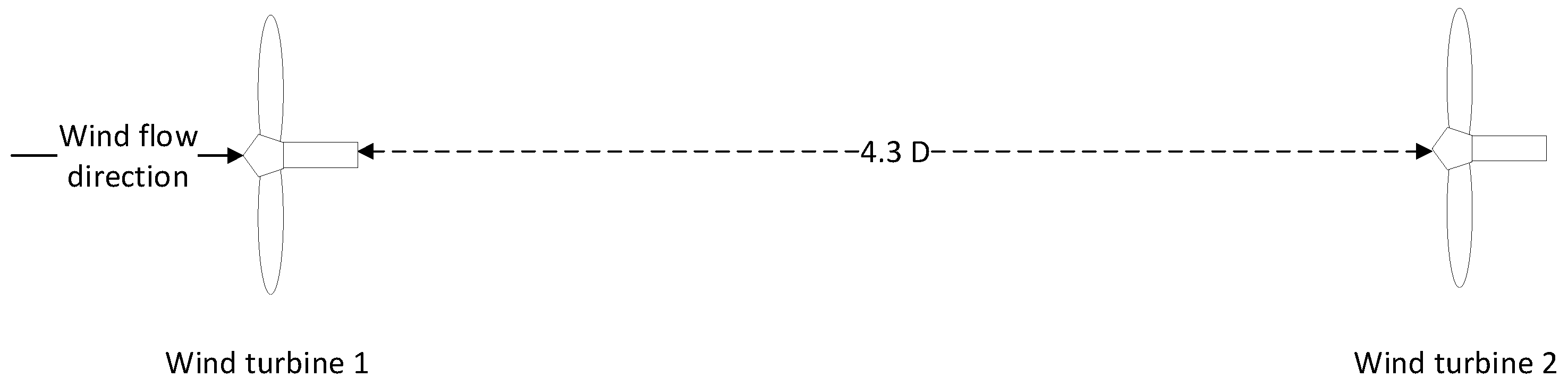

| Rated Power | Cut-In/Rated/Cut-Out Wind Speed | Rotor Diameter |
|---|---|---|
| 5 MW | 3 m/s/11.4 m/s/25 m/s | 126 m |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazda, J.; Cutululis, N.A. Fast Control-Oriented Dynamic Linear Model of Wind Farm Flow and Operation. Energies 2018, 11, 3346. https://doi.org/10.3390/en11123346
Kazda J, Cutululis NA. Fast Control-Oriented Dynamic Linear Model of Wind Farm Flow and Operation. Energies. 2018; 11(12):3346. https://doi.org/10.3390/en11123346
Chicago/Turabian StyleKazda, Jonas, and Nicolaos Antonio Cutululis. 2018. "Fast Control-Oriented Dynamic Linear Model of Wind Farm Flow and Operation" Energies 11, no. 12: 3346. https://doi.org/10.3390/en11123346
APA StyleKazda, J., & Cutululis, N. A. (2018). Fast Control-Oriented Dynamic Linear Model of Wind Farm Flow and Operation. Energies, 11(12), 3346. https://doi.org/10.3390/en11123346






