Advanced Methodology for the Optimal Sizing of the Energy Storage System in a Hybrid Electric Refuse Collector Vehicle Using Real Routes
Abstract
1. Introduction
2. Hybrid Electric Refuse Collector Vehicle
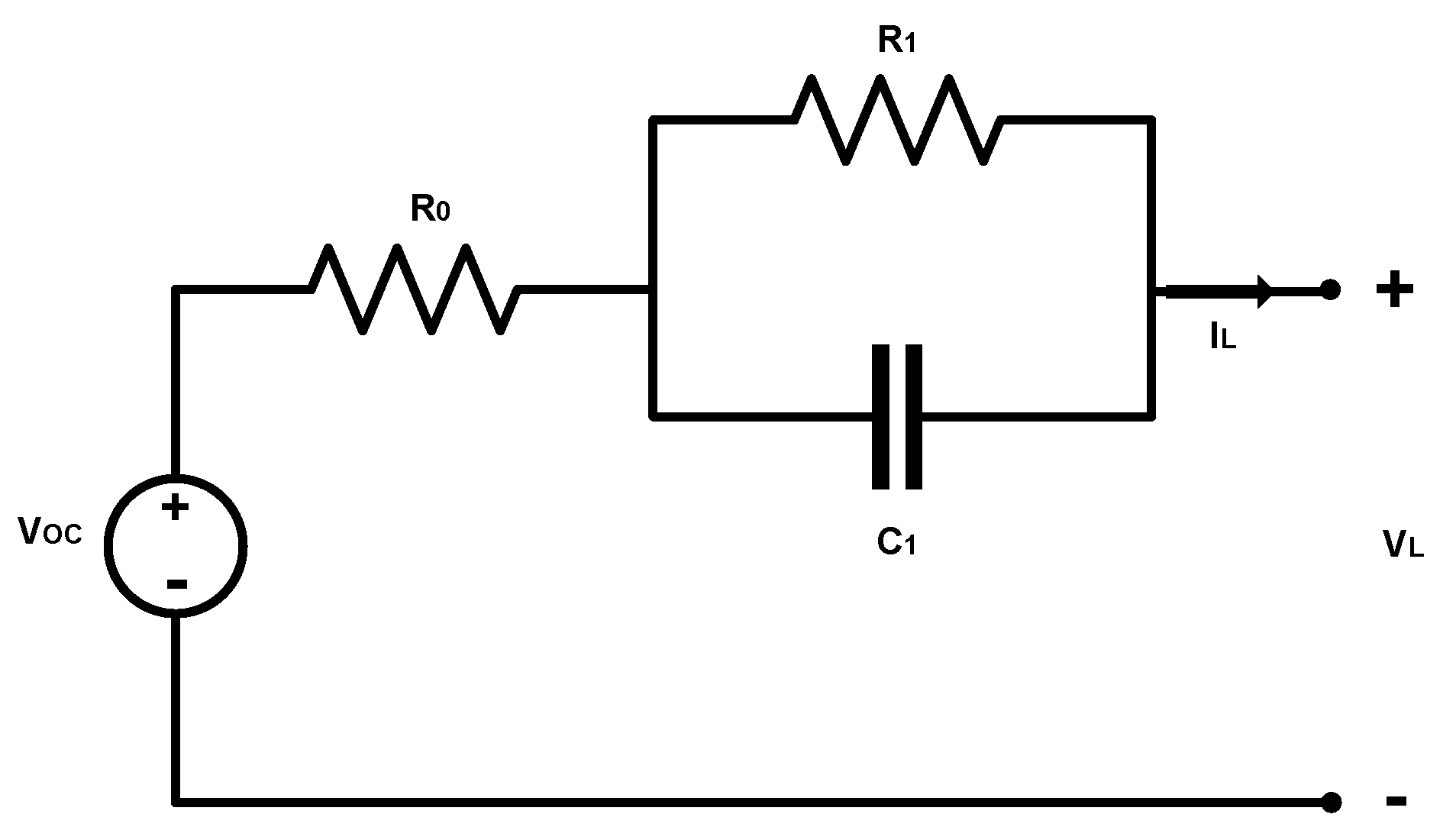
3. Energy Storage System
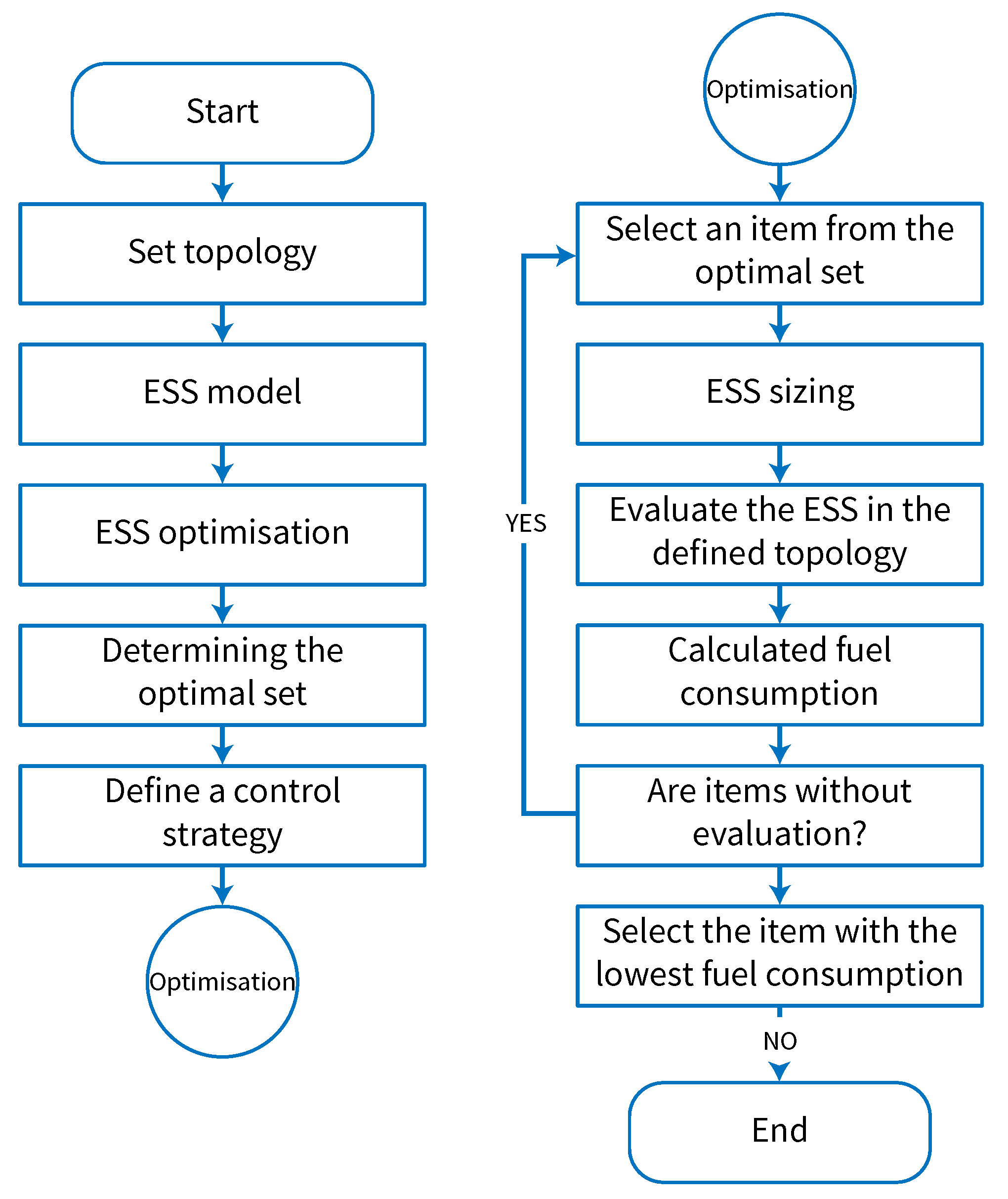
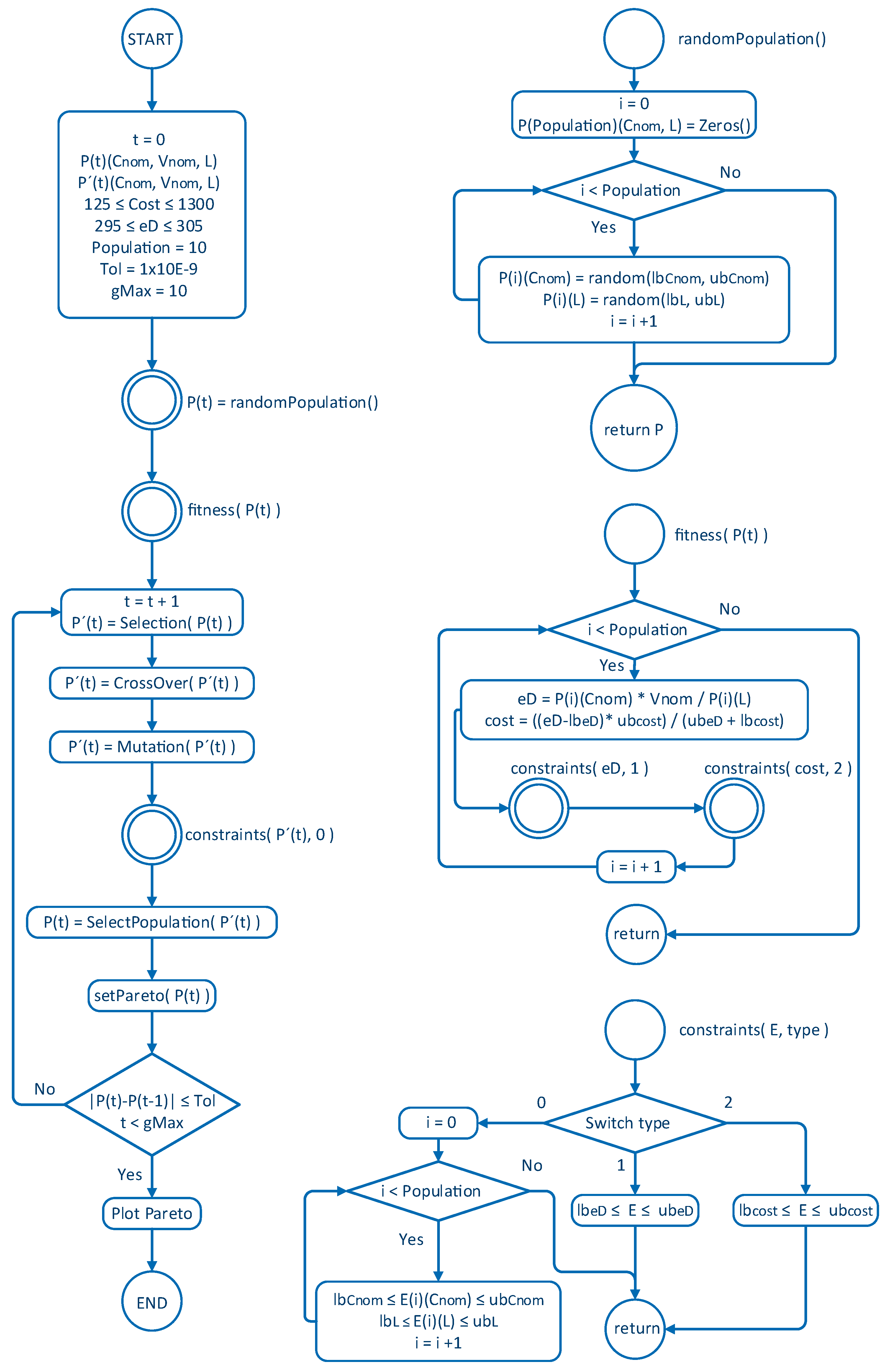
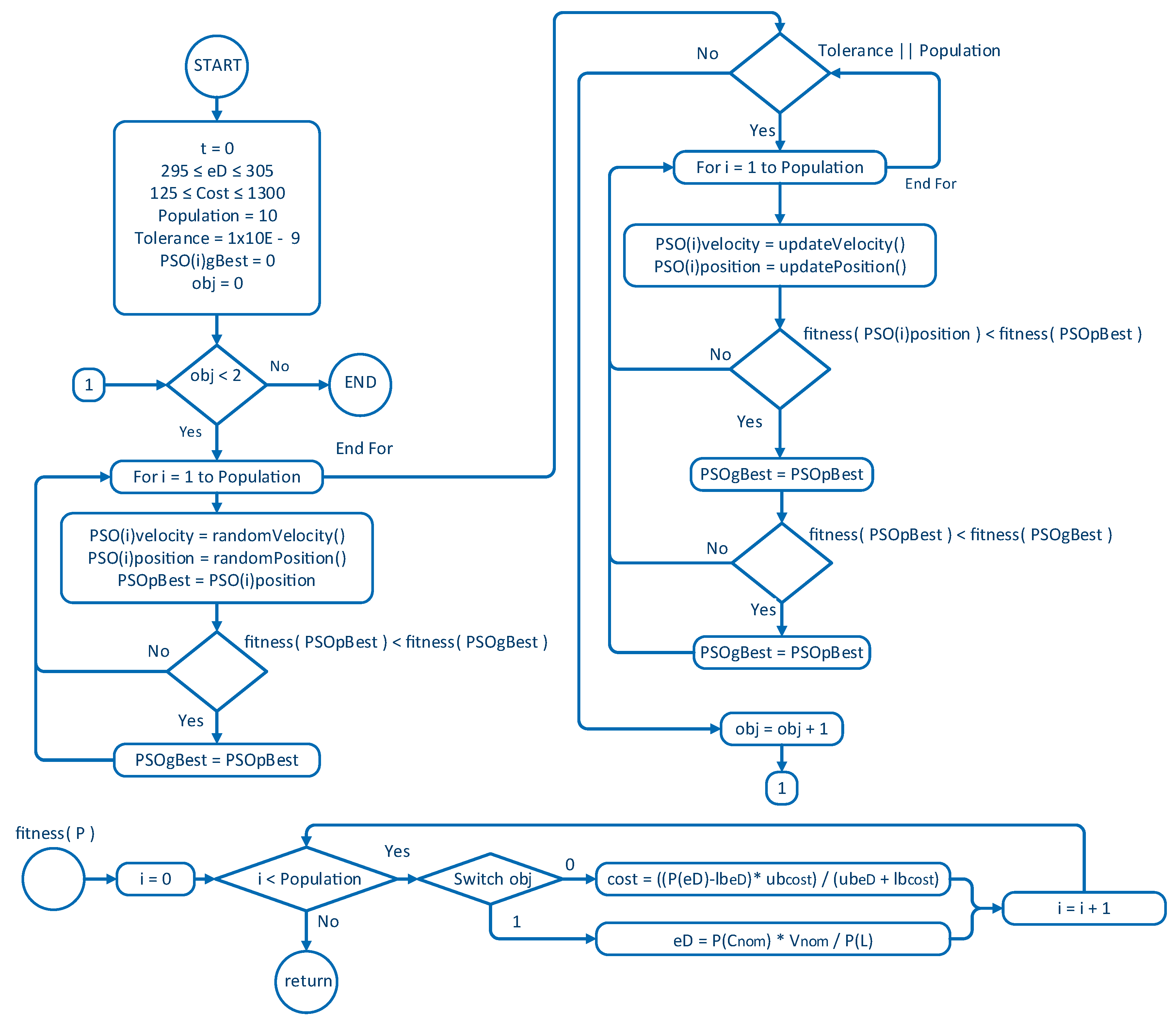
4. Optimal Sizing of the ESS
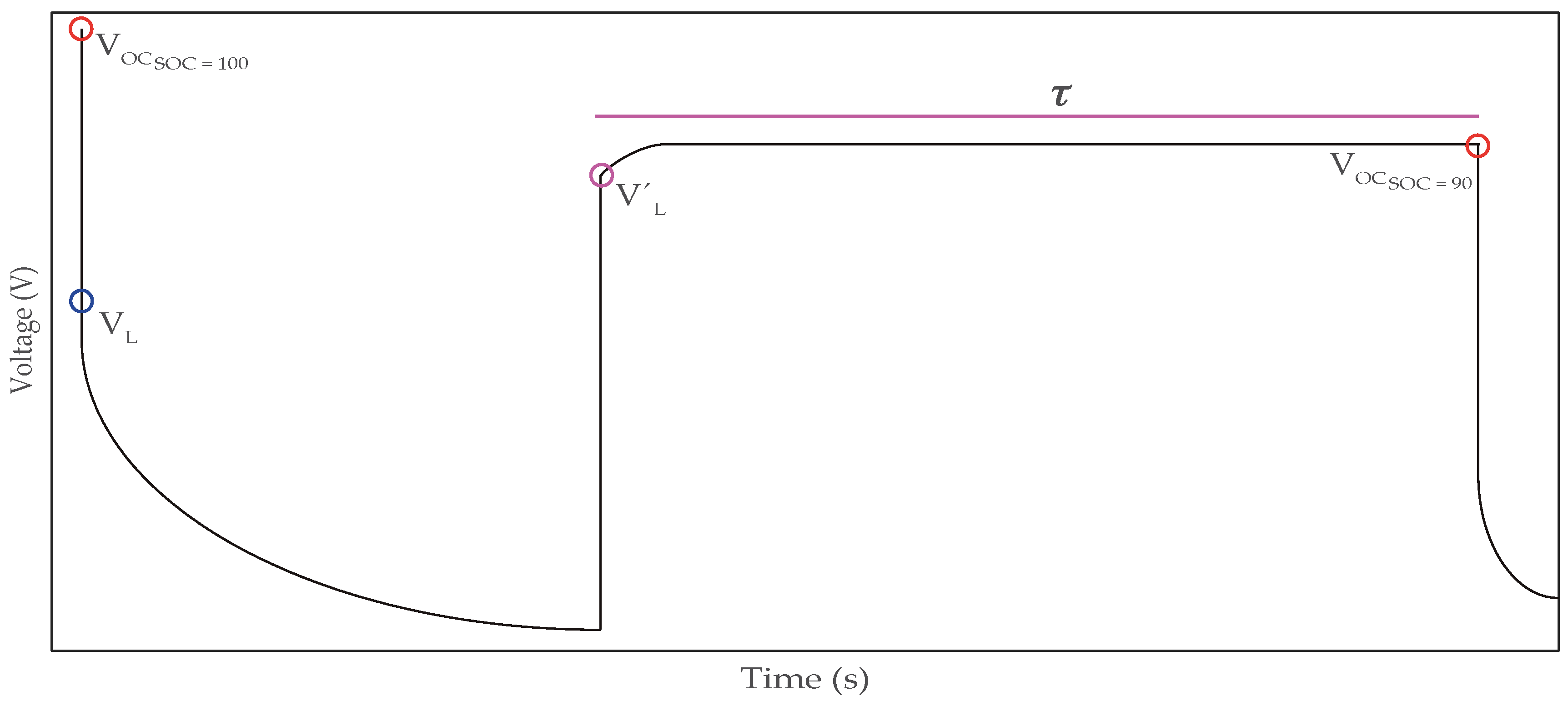
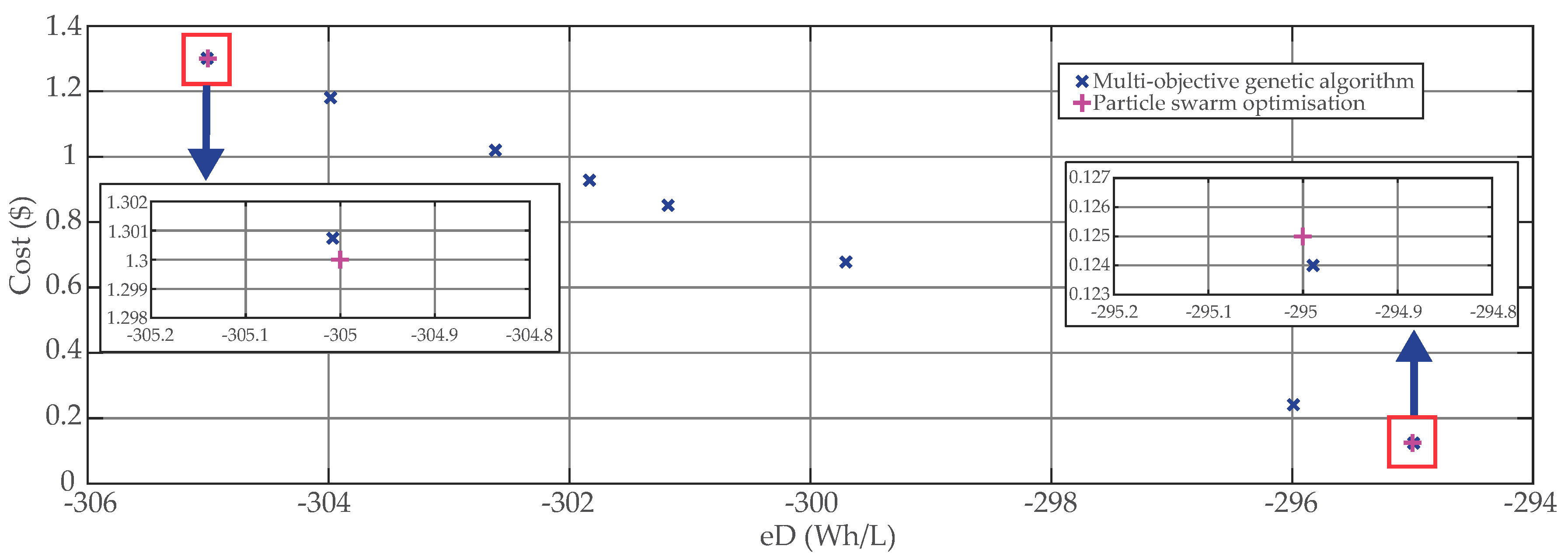
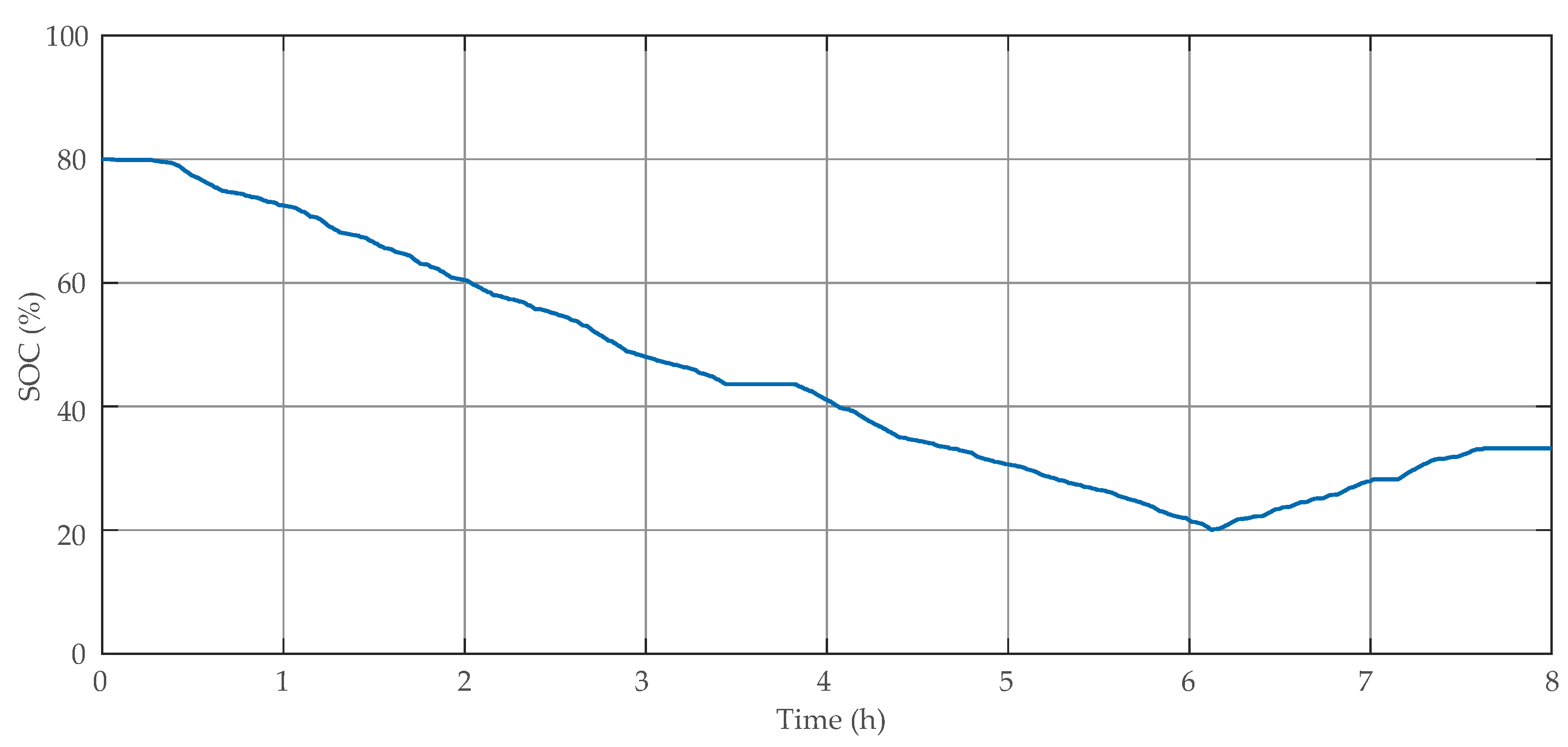
5. Validation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Refuse collector vehicle | |
| Hybrid electric vehicle | |
| – | Hybrid electric refuse collector vehicle |
| Electric machine | |
| Internal combustion engine | |
| Energy storage system | |
| Engine control module | |
| Traction force | |
| Aerodynamic resistance | |
| Rolling resistance | |
| Force caused by gravity | |
| RCV mass | |
| Vehicle mass | |
| Dynamic vehicle mass | |
| EM mass | |
| ESS mass | |
| Body power | |
| ESS power | |
| In power | |
| Out power | |
| – | Lithium polymer battery |
| Nominal capacity | |
| ESS capacity | |
| Open-circuit voltage | |
| State of charge | |
| Energy density | |
| Lower bound | |
| Upper bound |
References
- Karagulian, F.; Belis, C.A.; Dora, C.F.C.; Pruss-Ustun, A.M.; Bonjour, S.; Adair-Rohani, H.; Amann, M. Contributions to cities’ ambient particulate matter (PM): A systematic review of local source contributions at global level. Atmos. Environ. 2015, 120, 475–483. [Google Scholar] [CrossRef]
- Tan, Z. Air Pollution and Greenhouse Gases: From Basic Concepts to Engineering Applications for Air Emission Control; Springer: Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Moghbeli, H.; Niasar, A.H.; Fallahi, N. Fuzzy energy control strategy of through-to-road hybrid electric vehicle. In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istambul, Turkey, 1–4 June 2014; pp. 1660–1665. [Google Scholar] [CrossRef]
- Negarestani, S.; Fotuhi-Firuzabad, M.; Rastegar, M.; Rajabi-Ghahnavieh, A. Optimal Sizing of Storage System in a Fast Charging Station for Plug-in Hybrid Electric Vehicles. IEEE Trans. Transp. Electrif. 2016, 2, 443–453. [Google Scholar] [CrossRef]
- Soriano, F.; Moreno-Eguilaz, M.; Alvarez-Florez, J. Drive Cycle Identification and Energy Demand Estimation for Refuse-Collecting Vehicles. IEEE Trans. Veh. Technol. 2015, 64, 4965–4973. [Google Scholar] [CrossRef]
- Rupp, M.; Schulze, S.; Kuperjans, I. Comparative Life Cycle Analysis of Conventional and Hybrid Heavy-Duty Trucks. World Electr. Veh. J. 2018, 9, 33. [Google Scholar] [CrossRef]
- Zeng, Y.; Cai, Y.; Chu, C.; Kou, G.; Gao, W. Integrated Energy and Catalyst Thermal Management for Plug-In Hybrid Electric Vehicles. Energies 2018, 11, 1761. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, K.W.E.; Fong, Y.C. Non-Equal Voltage Cell Balancing for Battery and Super-Capacitor Source Package Management System Using Tapped Inductor Techniques. Energies 2018, 11, 1037. [Google Scholar] [CrossRef]
- Garcia, J.; Garcia, P.; Giulii Capponi, F.; De Donato, G. Analysis, Modeling, and Control of Half-Bridge Current-Source Converter for Energy Management of Supercapacitor Modules in Traction Applications. Energies 2018, 11, 2239. [Google Scholar] [CrossRef]
- Repp, S.; Harputlu, E.; Gurgen, S.; Castellano, M.; Kremer, N.; Pompe, N.; Wörner, J.; Hoffmann, A.; Thomann, R.; Emen, F.M.; et al. Synergetic effects of Fe3+ doped spinel Li4Ti5O12 nanoparticles on reduced graphene oxide for high surface electrode hybrid supercapacitors. Nanoscale 2018, 10, 1877–1884. [Google Scholar] [CrossRef] [PubMed]
- Genc, R.; Alas, M.O.; Harputlu, E.; Repp, S.; Kremer, N.; Castellano, M.; Colak, S.G.; Ocakoglu, K.; Erdem, E. High-Capacitance Hybrid Supercapacitor Based on Multi-Colored Fluorescent Carbon-Dots. Sci. Rep. 2017, 7, 11222. [Google Scholar] [CrossRef] [PubMed]
- Silvaş, E.; Hofman, T.; Steinbuch, M. Review of Optimal Design Strategies for Hybrid Electric Vehicles. IFAC Proc. Vol. 2012, 45, 57–64. [Google Scholar] [CrossRef]
- Lukic, S.M.; Emadi, A. Effects of drivetrain hybridization on fuel economy and dynamic performance of parallel hybrid electric vehicles. IEEE Trans. Veh. Technol. 2004, 53, 385–389. [Google Scholar] [CrossRef]
- Trigui, R.; Vinot, E.; Boujelben, M. Offline optimization for components sizing and analysis of a plug-in hybrid urban microbus. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–11 September 2009; pp. 382–387. [Google Scholar] [CrossRef]
- Silvas, E.; Hofman, T.; Murgovski, N.; Etman, L.F.P.; Steinbuch, M. Review of Optimization Strategies for System-Level Design in Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2017, 66, 57–70. [Google Scholar] [CrossRef]
- Souffran, G.; Miegeville, L.; Guerin, P. Simulation of Real-World Vehicle Missions Using a Stochastic Markov Model for Optimal Powertrain Sizing. IEEE Trans. Veh. Technol. 2012, 61, 3454–3465. [Google Scholar] [CrossRef]
- Ravey, A.; Roche, R.; Blunier, B.; Miraoui, A. Combined optimal sizing and energy management of hybrid electric vehicles. In Proceedings of the 2012 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 18–20 June 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Pourabdollah, M.; Murgovski, N.; Grauers, A.; Egardt, B. Optimal Sizing of a Parallel PHEV Powertrain. IEEE Trans. Veh. Technol. 2013, 62, 2469–2480. [Google Scholar] [CrossRef]
- Knoke, T.; Bocker, J. Optimal Power Train Design of a Hybrid Refuse Collector Vehicle. In Proceedings of the 2007 IEEE Vehicle Power and Propulsion Conference, Arlington, TX, USA, 9–12 September 2007; pp. 815–820. [Google Scholar] [CrossRef]
- Elbert, P.; Nüesch, T.; Ritter, A.; Murgovski, N.; Guzzella, L. Engine On/Off Control for the Energy Management of a Serial Hybrid Electric Bus via Convex Optimization. IEEE Trans. Veh. Technol. 2014, 63, 3549–3559. [Google Scholar] [CrossRef]
- Gao, W.; Porandla, S.K. Design optimization of a parallel hybrid electric powertrain. In Proceedings of the 2005 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 7–9 September 2005; p. 6. [Google Scholar] [CrossRef]
- Vinot, E.; Reinbold, V.; Trigui, R. Global Optimized Design of an Electric Variable Transmission for HEVs. IEEE Trans. Veh. Technol. 2016, 65, 6794–6798. [Google Scholar] [CrossRef]
- Vincent, R.; Emmanuel, V.; Lauric, G.; Laurent, G. Optimal sizing of an electrical machine using a magnetic circuit model: application to a hybrid electrical vehicle. IET Electr. Syst. Transp. 2016, 6, 27–33. [Google Scholar] [CrossRef]
- Moulik, B.; Karbaschian, M.A.; Soffker, D. Size and Parameter Adjustment of a Hybrid Hydraulic Powertrain Using a Global Multi-Objective Optimization Algorithm. In Proceedings of the 2013 IEEE Vehicle Power and Propulsion Conference (VPPC), Beijing, China, 15–18 October 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Desai, C.; Williamson, S.S. Optimal design of a parallel Hybrid Electric Vehicle using multi-objective genetic algorithms. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–11 September 2009; pp. 871–876. [Google Scholar] [CrossRef]
- Jain, M.; Desai, C.; Kharma, N.; Williamson, S.S. Optimal powertrain component sizing of a fuel cell plug-in hybrid electric vehicle using multi-objective genetic algorithm. In Proceedings of the 2009 35th Annual Conference of IEEE Industrial Electronics, Porto, Portugal, 3–5 November 2009; pp. 3741–3746. [Google Scholar] [CrossRef]
- Serrao, L.; Rizzoni, G. Optimal control of power split for a hybrid electric refuse vehicle. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 4498–4503. [Google Scholar] [CrossRef]
- Ravey, A.; Watrin, N.; Blunier, B.; Miraoui, A. Energy sources sizing for hybrid fuel cell vehicles based on statistical description of driving cycles. In Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Soriano, F.; Alvarez-Florez, J.; Moreno-Eguilaz, M. Experimentally Compared Fuel Consumption Modelling of Refuse Collecting Vehicles for Energy Optimization Purposes. SAE Int. J. Commer. Veh. 2014, 7, 324–336. [Google Scholar] [CrossRef]
- Zhao, D.; Stobart, R.; Dong, G.; Winward, E. Real-Time Energy Management for Diesel Heavy Duty Hybrid Electric Vehicles. IEEE Trans. Control Syst. Technol. 2015, 23, 829–841. [Google Scholar] [CrossRef]
- Zou, Y.; Sun, F.; Hu, X.; Guzzella, L.; Peng, H. Combined Optimal Sizing and Control for a Hybrid Tracked Vehicle. Energies 2012, 5, 4697–4710. [Google Scholar] [CrossRef]
- Silvas, E.; Bergshoeff, E.; Hofman, T.; Steinbuch, M. Comparison of Bi-Level Optimization Frameworks for Sizing and Control of a Hybrid Electric Vehicle. In Proceedings of the 2014 IEEE Vehicle Power and Propulsion Conference (VPPC), Coimbra, Portuga, 27–30 October 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Guzzella, L.; Amstutz, A. CAE tools for quasi-static modeling and optimization of hybrid powertrains. IEEE Trans. Veh. Technol. 1999, 48, 1762–1769. [Google Scholar] [CrossRef]
- Carkhuff, B.G.; Demirev, P.A.; Srinivasan, R. Impedance-Based Battery Management System for Safety Monitoring of Lithium-Ion Batteries. IEEE Trans. Ind. Electr. 2018, 65, 6497–6504. [Google Scholar] [CrossRef]
- Armstrong, T.; Nork, S. Maximize the Run Time in Automotive Battery Stacks Even as Cells Ag; Technical report; Analog Devices: Norwood, MA, USA, 2017. [Google Scholar]
- Li, Q.; Chen, W.; Li, Y.; Liu, S.; Huang, J. Energy management strategy for fuel cell/battery/ultracapacitor hybrid vehicle based on fuzzy logic. Int. J. Electr. Power Energy Syst. 2012, 43, 514–525. [Google Scholar] [CrossRef]
- Ostadi, A.; Kazerani, M.; Chen, S.K. Hybrid Energy Storage System (HESS) in vehicular applications: A review on interfacing battery and ultra-capacitor units. In Proceedings of the 2013 IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 16–19 June 2013; pp. 1–7. [Google Scholar] [CrossRef]
- Chemali, E.; Preindl, M.; Malysz, P.; Emadi, A. Electrochemical and Electrostatic Energy Storage and Management Systems for Electric Drive Vehicles: State-of-the-Art Review and Future Trends. IEEE J. Emerg. Sel. Top. Power Electr. 2016, 4, 1117–1134. [Google Scholar] [CrossRef]
- Passalacqua, M.; Lanzarotto, D.; Repetto, M.; Marchesoni, M. Advantages of Using Supercapacitors and Silicon Carbide on Hybrid Vehicle Series Architecture. Energies 2017, 10. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Z.; Li, F. Optimization of Energy Management Strategy and Sizing in Hybrid Storage System for Tram. Energies 2018, 11. [Google Scholar] [CrossRef]
- Aschilean, I.; Varlam, M.; Culcer, M.; Iliescu, M.; Raceanu, M.; Enache, A.; Raboaca, M.S.; Rasoi, G.; Filote, C. Hybrid Electric Powertrain with Fuel Cells for a Series Vehicle. Energies 2018, 11. [Google Scholar] [CrossRef]
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S.; Wild, M. A review on electric vehicle battery modelling: From Lithium-ion toward Lithium–Sulphur. Renew. Sustain. Energy Rev. 2016, 56, 1008–1021. [Google Scholar] [CrossRef]
- Zhuang, W.; Wang, L.; Yin, Z.; Ye, J.; Wu, H. Optimal energy management strategy design for a diesel parallel hybrid electric vehicle. In Proceedings of the 11th IEEE International Conference on Control & Automation (ICCA), Taichung, Taiwan, 18–20 June 2014; pp. 1050–1055. [Google Scholar] [CrossRef]
- Ostadi, A.; Kazerani, M. A Comparative Analysis of Optimal Sizing of Battery-Only, Ultracapacitor-Only, and Battery; Ultracapacitor Hybrid Energy Storage Systems for a City Bus. IEEE Trans. Veh. Technol. 2015, 64, 4449–4460. [Google Scholar] [CrossRef]
- Barcellona, S.; Grillo, S.; Piegari, L. A simple battery model for EV range prediction: Theory and experimental validation. In Proceedings of the 2016 International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Toulouse, France, 2–4 November 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Ceylan, M.; Sarıkurt, T.; Balıkçı, A. A novel Lithium-Ion-Polymer battery model for hybrid/electric vehicles. In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istambul, Turkey, 1–4 June 2014; pp. 366–369. [Google Scholar] [CrossRef]

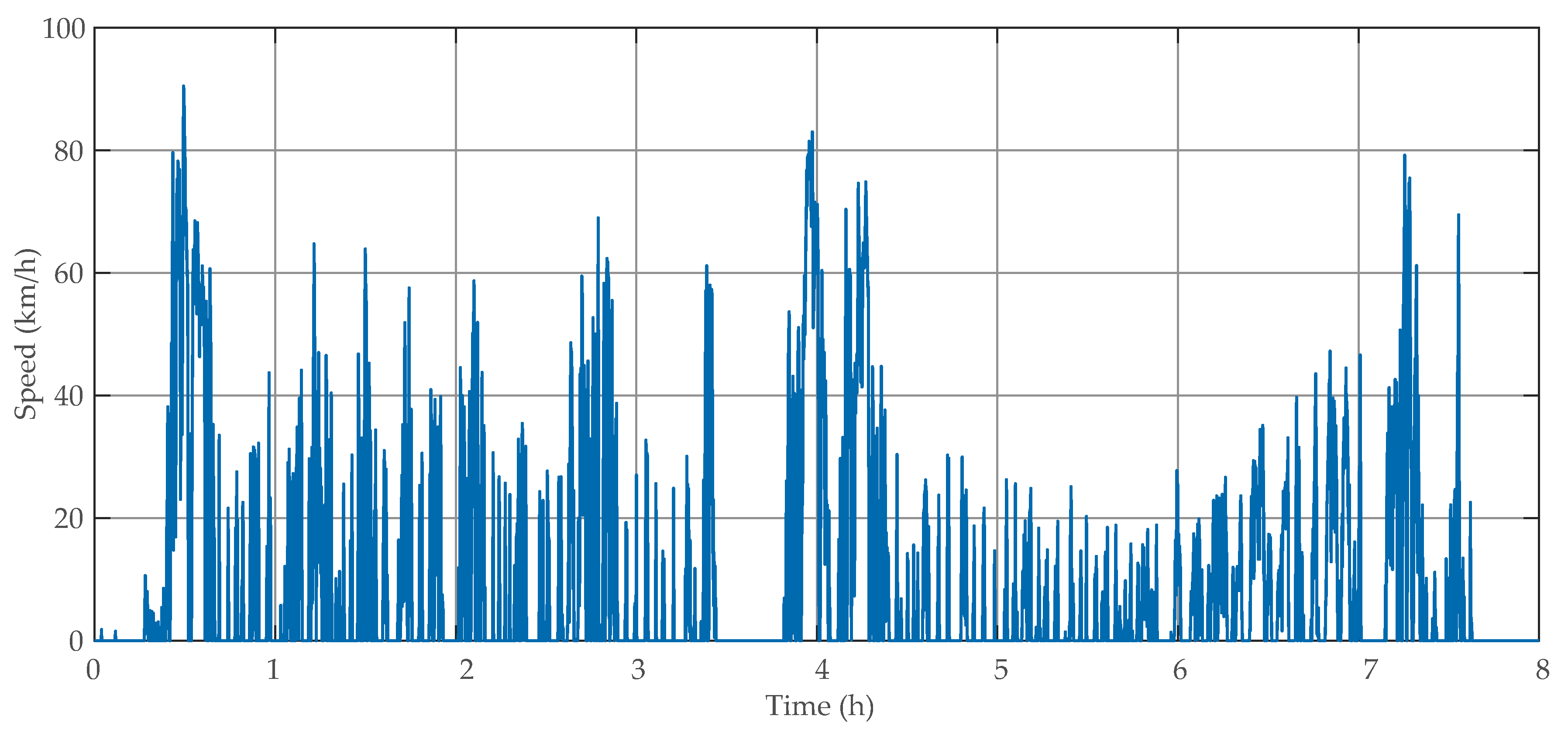
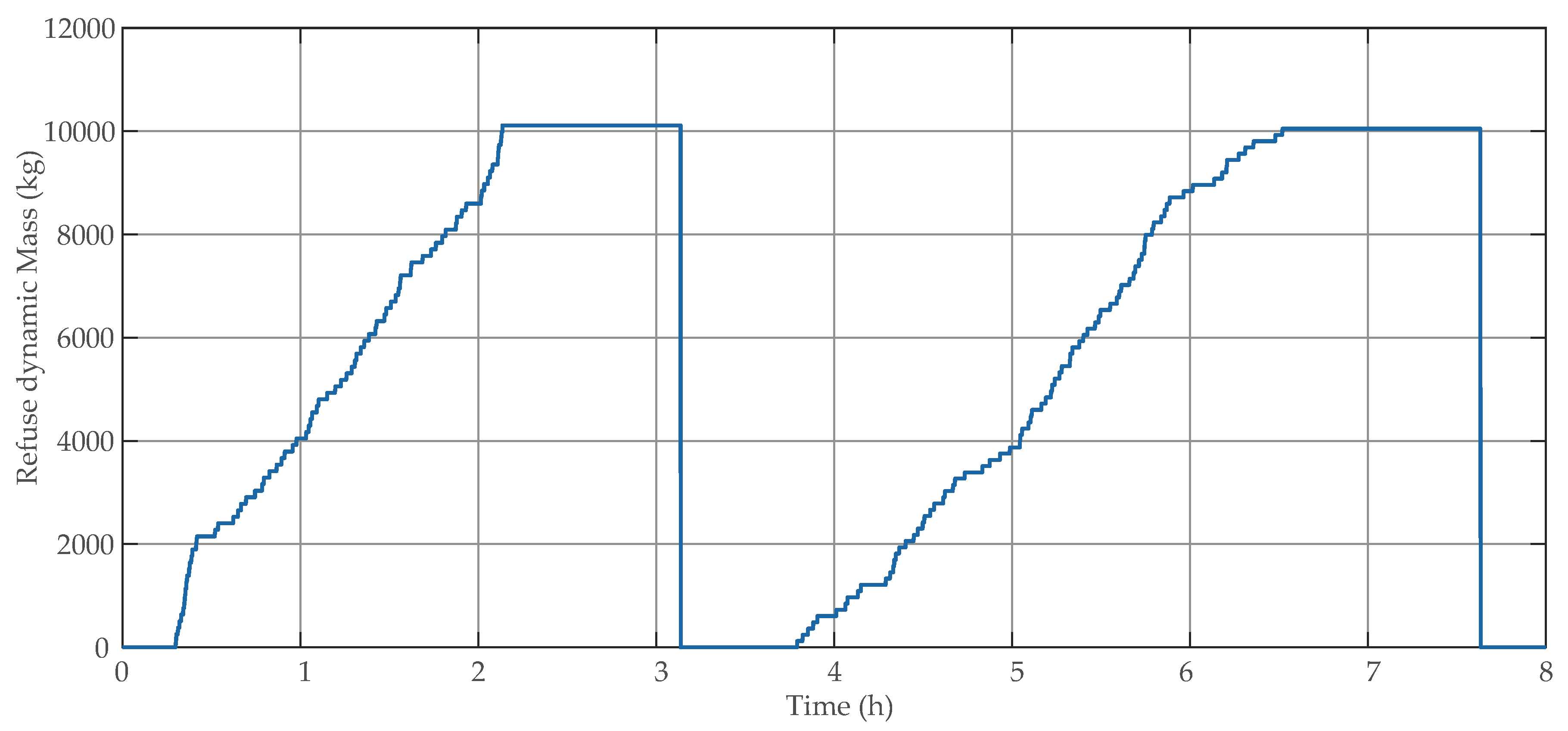
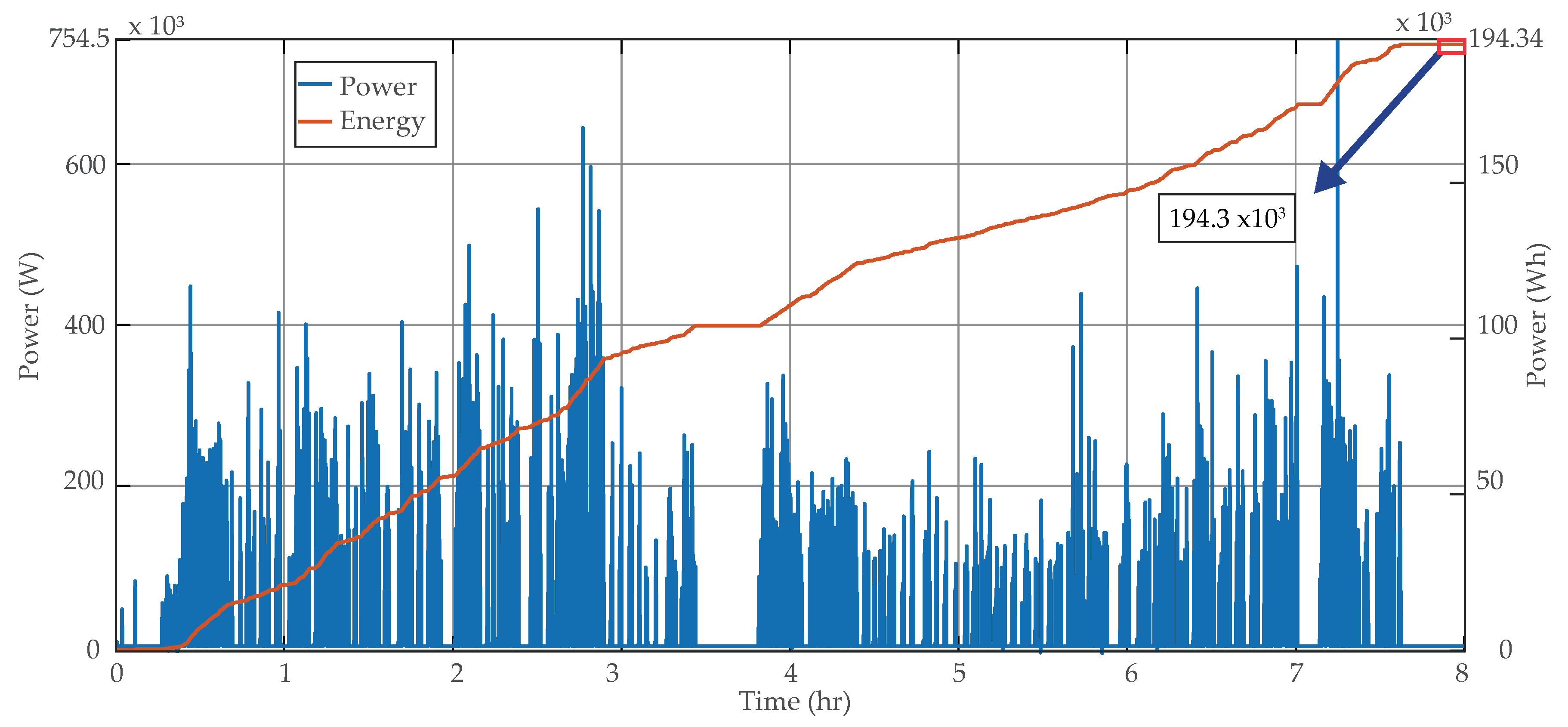
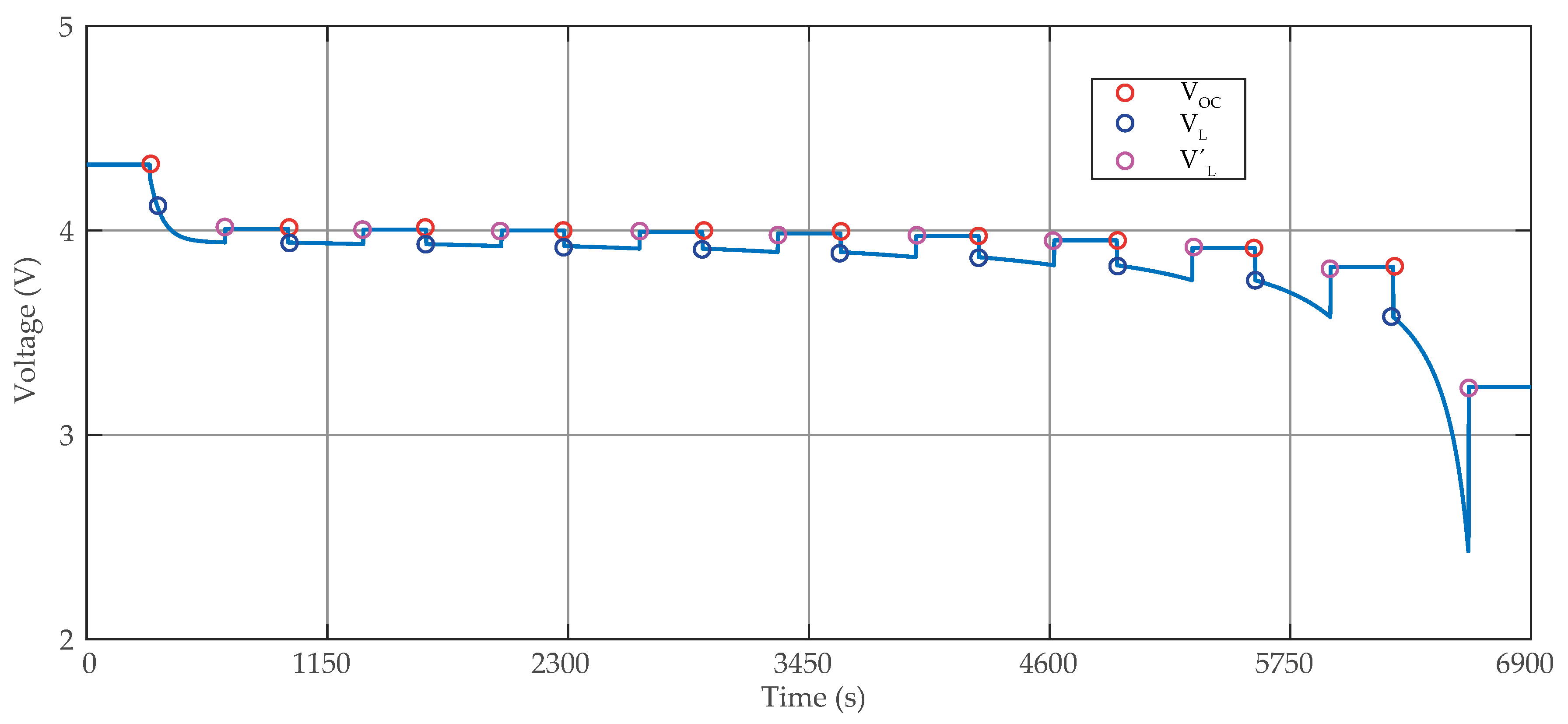
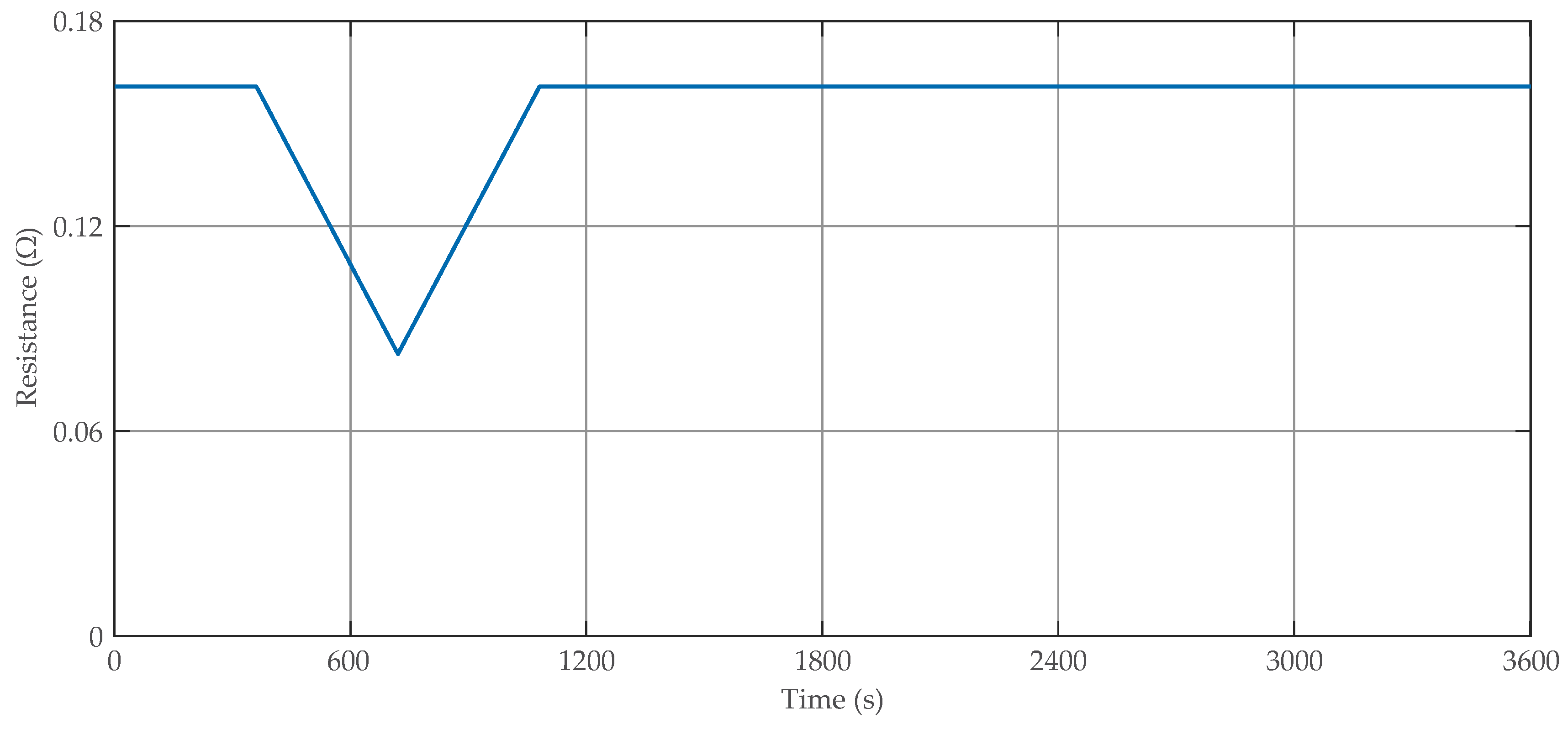
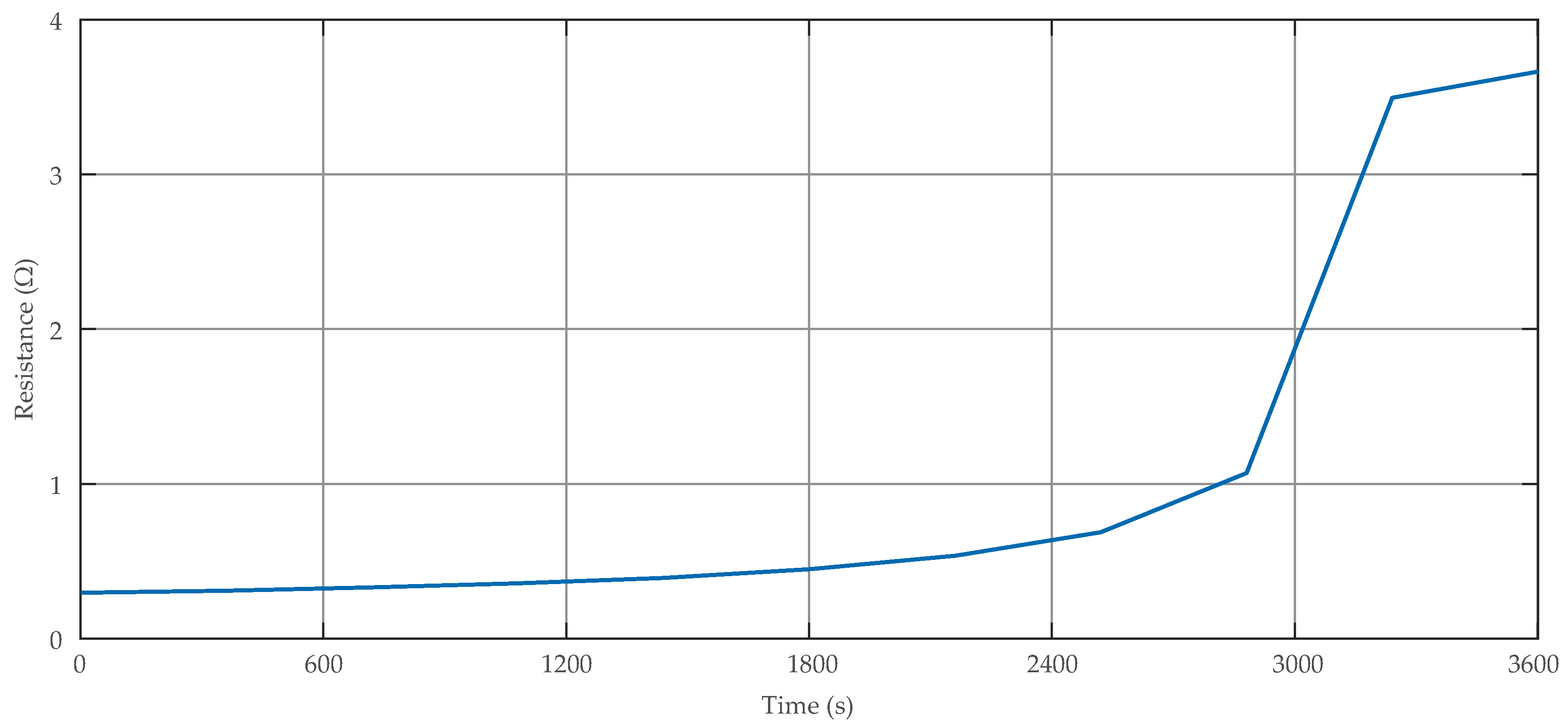
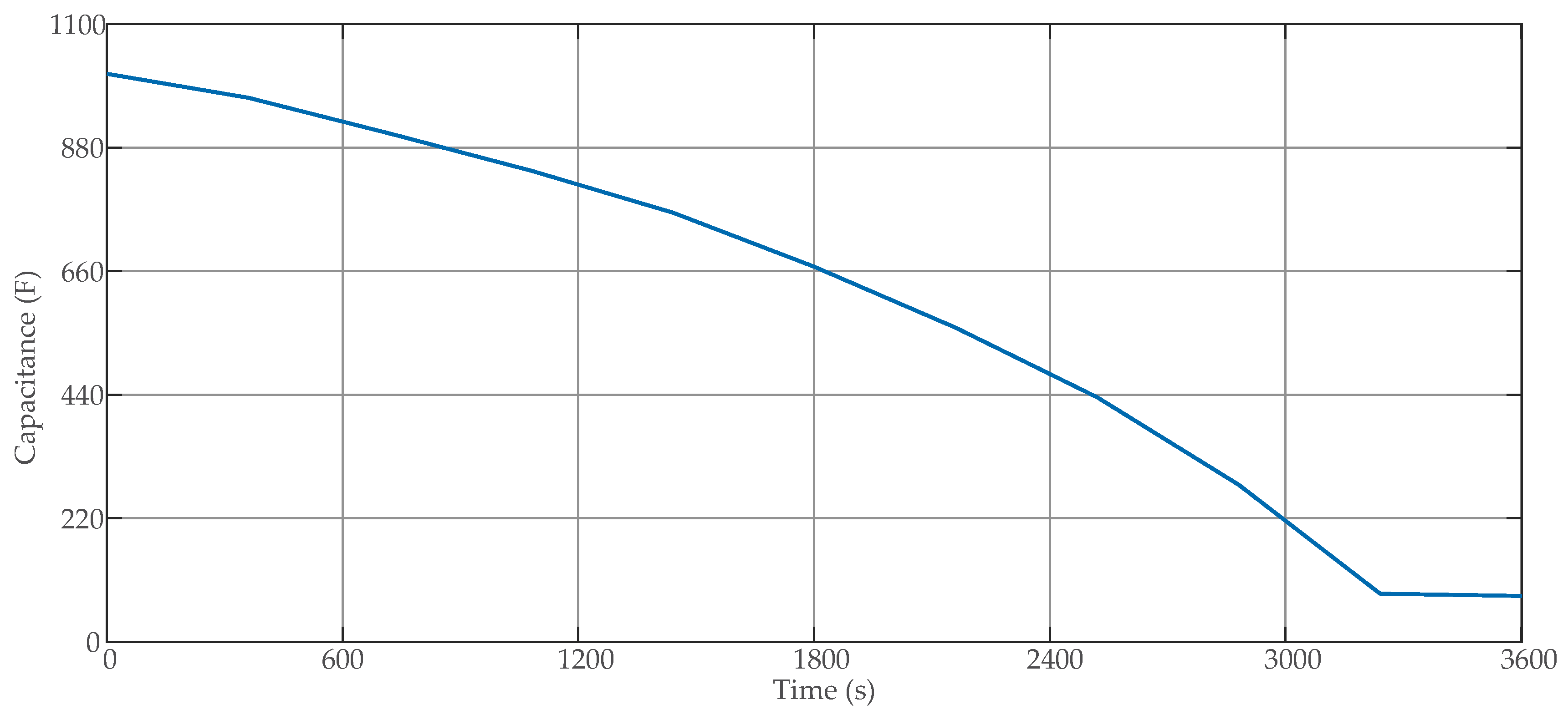
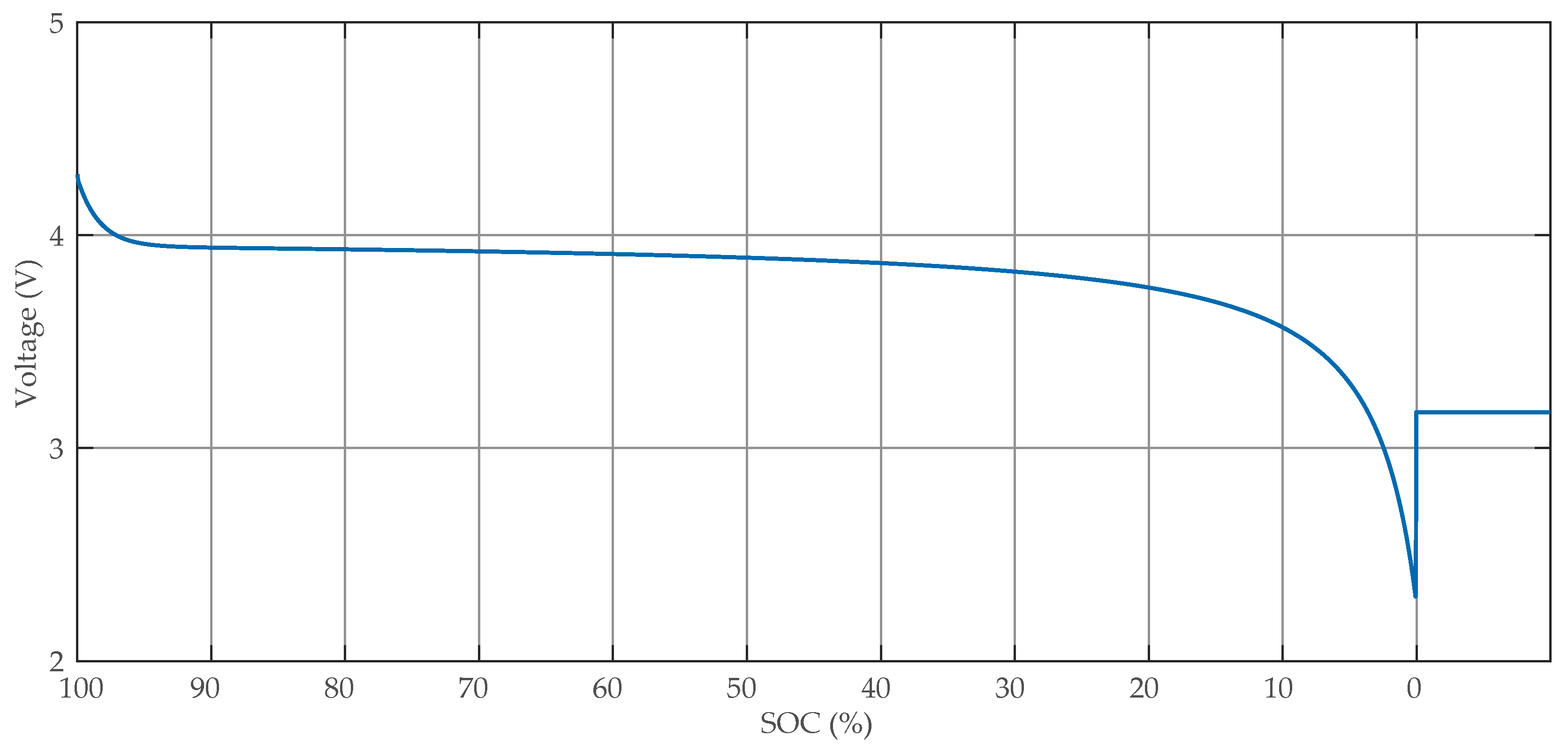
| Parameters | Value |
|---|---|
| Manufacturing cost | 125–1300 US/kWh |
| Energy density (eD) | 295–305 Wh/L |
| Objectives | 2 () |
| Variables | 3 (, , L) |
| Population | 10 |
| Crossover | 0.8 |
| Tolerance | 1 × 10 |
| Combustion engine | 200 kW |
| Gears | 6 |
| Gear ratios () | 1 (4.59), 2 (2.25), 3 (1.54) |
| 4 (1.000), 5 (0.75), 6 (0.65) | |
| Weight () | |
| (Empty/Full loaded) | 15,000/25,000 kg |
| Frontal area () | 7.5 m |
| Drag coefficient () | 0.6210 |
| Rolling resistance () | 0.009 |
| Tire (Radius) | 315/80/R22.5 (0.5455 m) |
| # | (Wh/L) | L (L) | (Ah) | ||
|---|---|---|---|---|---|
| 1 | 1.300812 | −305.006906 | 0.144788 | 11.93545 | 440 |
| 2 | 0.123982 | −294.991340 | 0.115369 | 9.198045 | 571 |
| 3 | 0.927891 | −301.833114 | 0.142080 | 11.59035 | 453 |
| 4 | 1.300812 | −305.006906 | 0.144788 | 11.93545 | 440 |
| 5 | 0.241222 | −295.989126 | 0.115397 | 9.231446 | 569 |
| 6 | 0.677771 | −299.704430 | 0.127566 | 10.33298 | 508 |
| 7 | 1.180479 | −303.982803 | 0.137194 | 11.27155 | 466 |
| 8 | 1.019624 | −302.613820 | 0.142736 | 11.67404 | 450 |
| 9 | 0.851227 | −301.180651 | 0.131935 | 10.73951 | 489 |
| 10 | 0.123982 | −294.991340 | 0.115369 | 9.198045 | 571 |
| # | (Ah) | Array Capacity (Wh) | Consumption (kg) | |
|---|---|---|---|---|
| 1 | 11.93545 | 440 | 19,430.92 | 19.64 |
| 2 | 9.198045 | 571 | 19,432.71 | 19.61 |
| 3 | 11.59035 | 453 | 19,426.60 | 19.61 |
| 4 | 11.93545 | 440 | 19,430.92 | 19.64 |
| 5 | 9.231446 | 569 | 19,434.96 | 19.03 |
| 6 | 10.33298 | 508 | 19,421.88 | 19.06 |
| 7 | 11.27155 | 466 | 19,434.42 | 20.00 |
| 8 | 11.67404 | 450 | 19,437.28 | 20.00 |
| 9 | 10.73951 | 489 | 19,431.00 | 19.47 |
| 10 | 9.198045 | 571 | 19,432.71 | 19.61 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cortez, E.; Moreno-Eguilaz, M.; Soriano, F. Advanced Methodology for the Optimal Sizing of the Energy Storage System in a Hybrid Electric Refuse Collector Vehicle Using Real Routes. Energies 2018, 11, 3279. https://doi.org/10.3390/en11123279
Cortez E, Moreno-Eguilaz M, Soriano F. Advanced Methodology for the Optimal Sizing of the Energy Storage System in a Hybrid Electric Refuse Collector Vehicle Using Real Routes. Energies. 2018; 11(12):3279. https://doi.org/10.3390/en11123279
Chicago/Turabian StyleCortez, Ernest, Manuel Moreno-Eguilaz, and Francisco Soriano. 2018. "Advanced Methodology for the Optimal Sizing of the Energy Storage System in a Hybrid Electric Refuse Collector Vehicle Using Real Routes" Energies 11, no. 12: 3279. https://doi.org/10.3390/en11123279
APA StyleCortez, E., Moreno-Eguilaz, M., & Soriano, F. (2018). Advanced Methodology for the Optimal Sizing of the Energy Storage System in a Hybrid Electric Refuse Collector Vehicle Using Real Routes. Energies, 11(12), 3279. https://doi.org/10.3390/en11123279






