A Stability Analysis of Solutions in Boundary Layer Flow and Heat Transfer of Carbon Nanotubes over a Moving Plate with Slip Effect

Abstract

The flow and heat transfer characteristics of both single-wall and multi-wall carbon nanotubes (CNTs) with water and kerosene as base fluid on a moving plate with slip effect are studied numerically. By employing similarity transformation, governing equations are transformed into a set of nonlinear ordinary equations. These equations are solved numerically using the bvp4c solver in Matlab which is a very efficient finite difference method. The influence of numerous parameters such as nanoparticle volume fraction, velocity ratio parameter and first order slip parameter on velocity, temperature, skin friction and heat transfer rate are further explored and discussed in the form of graphical and tabular forms. The results reveal that dual solutions exist when the plate and free stream move in the opposite direction and slip parameter was found to widen the range of the possible solutions. However, skin friction coefficients decrease, whereas the heat transfer increases in the presence of slip parameter. Single-wall carbon nanotubes (SWCNTs) give higher skin friction and heat transfer compared to multi-wall carbon nanotubes (MWCNTs) due to the fact that they have higher density and thermal conductivity. A stability analysis is carried out to determine the stability of the solutions obtained.

1. Introduction

In the past few decades, the thermal conductivity of nanofluids has been investigated by many researchers. Most of the studies on nanofluids are about understanding their behaviors so that they can optimize the enhancement of heat transfer in many industrial applications; i.e., nuclear reactors, power generation, transportation, the cooling and drying of paper, electronics, biomedicine and food. A good list of applications is available in Das et al. [1]. It may be noted that nanometer-sized metallic particles are an important physical parameter that can improve the heat transfer of fluids. Choi and Estman [2] were the first to introduce the word nanofluids; they defined a nanofluid as a liquid containing dispersed submicronic solid particles (nanoparticles). While plenty of materials can be used to form nanoparticles, carbon shows promising results because of its high thermal, electrical and mechanical properties [3]. Thus, Choi et al. [4] studied the thermal conductivity of oil-based carbon nanotubes. They reported that dispersion of a very small amount of nanotubes (1 vol %) produced an outstanding increase in the thermal conductivity of the base fluid. Carbon nanotubes (CNTs) are cylindrical shaped carbon atom structures with diameters ranging between 1 and 50 nm. Carbon nanotubes can consist of single-wall (SWCNTs) and multi-wall (MWCNTs) carbon nanotubes. Carbon nanotube suspensions offer higher thermal properties compared to those other nanoparticles with the same volume fraction [5,6]. Therefore, CNTs are able to enhance convective heat transfer performance and thermal conductivity of base fluids. Garg et al. [7] explored the influence of dispersing energy on viscous and heat transfer characteristic of MWCNTs dispersed in water whereby he noticed a 20% enhancement in the thermal conductivity. After that, many researchers have discovered the benefit of CNTs in their respective fields of study [8,9,10].

Blasius in 1908 [11] was most likely the first researcher to investigate the problem of boundary layer flow in a viscous fluid over a stationary flat plate. Wang [12] employed a new algorithm which known as a domian decomposition method to solve the classical Blasius equations. Later, Cortell [13] numerically investigated the classical Blasius flat-plate problem using the Runge-Kutta algorithm. Different from Blasius flow, Sakiadis [14] investigated the boundary layer flow over a continuous solid surface moving with constant velocity. Since then, many researchers [15,16,17] have considered the flow on a moving or fixed flat plate and reported that a duality exists for the case when the plate opposes the directions of the free stream.

In all previous studies, researchers only analyzed the flow field that only obeys the no-slip boundary condition. However, it is essential to substitute no-slip assumptions with partial slip boundary conditions as the former is not consistent with some practical flow situations. Bhattacharyya et al. [18,19] investigated the boundary layer slip flow over a flat plate with uniform magnetic field and considered the plate immersed into the porous medium. Later, Bhattacharyya et al. [20] studied the flow on moving flat plate in a parallel free stream with slip effect. Bachok et al. [21] generalized this idea and extended the problem to a moving plate in a copper-water nanofluid. Nevertheless, the above problems have not dealt with carbon nanotubes. Khan et al. [22] was the first to consider the flow and heat transfer of carbon nanotubes along a flat plate by employing a homogeneous flow model subjected to Navier slip and uniform heat flux boundary conditions. Various boundary layer flow problem of carbon nanotubes has also been also investigated by many authors [23,24,25,26].

The main focus here is to extend the research done by Bachok et al. [21]. This research is different from the previous related work in the sense that here we utilize the concept of carbon nanotubes consisting of water and kerosene-based nanofluid SWCNTs and MWCNTs introduced by Khan et al. [22] and the carbon nanotube model used for this research is taken from Xue [8]. Additionally, the flow considered in [22] is for a stationary plate, whereas this research considers the problem over a moving plate. We also implemented the stability analyses reported by Merkin [27], Weidman et al. [28], Merrill et al. [29] and Harris et al. [30]. We believe that this case has not been reported in any of the previous literature.

2. Problem Formulation

Consider a two-dimensional, steady and incompressible flow past a moving plate in a water and kerosene base fluid containing single-wall and multi-wall carbon nanotubes (CNTs) as a nanoparticle. A Cartesian coordinate system is used with the $x-$ axis along the plate and the $y-$ axis perpendicular to the plate. Further, we assume that the plate is maintained at uniform temperature $T_w$ and $T_{\infty }$ corresponds to the ambient fluid temperature. It is assumed that the plate moves with a constant velocity $U_w$ and $U_{\infty }$ corresponds to the free stream velocity far from the surface of the plate. The physical model is depicted in Figure 1. The boundary layer equations can be written as [21]:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(1)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{{\mu }_{nf}}{{\rho }_{nf}}\frac{{\partial }^{2}u}{\partial y^2}$$

(2)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}={\alpha }_{nf}\frac{{\partial }^{2}T}{\partial y^2}$$

(3)

and the boundary conditions are defined as follows:

$$\begin{array}{c}u=U_w+L_1\left(\frac{\partial u}{\partial y}\right),v=0,T=T_w \mathrm{at} y=0\\ u\to U_{\infty },T\to T_{\infty } \mathrm{as} y\to \infty \end{array}$$

(4)

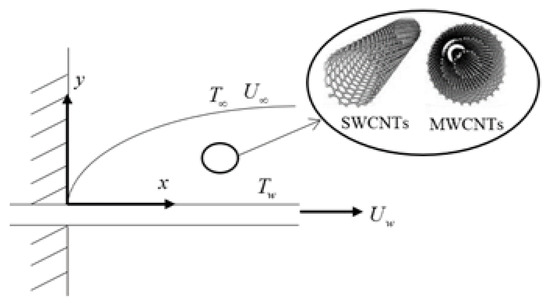
Figure 1. Schematic diagram of the problem.

The velocity components in $x$ and $y$ directions are namely $u$ and $v$, $T$ is the temperature, $L_1$ is the slip factor, $\mu ,\alpha$ and $\rho$ is the dynamic viscosity, thermal diffusivity and density where the subscripts $‘nf’,‘f’$ and $‘CNT’$ represent ‘nanofluid’, ‘fluid’ and ‘carbon nanotube’, respectively. The slip factor are defined as $L_1=L{\left({\mathrm{Re}}_w+{\mathrm{Re}}_{\infty }\right)}^{1/2}$ where $L$ is the initial length of slip factor, ${\mathrm{Re}}_w=U_{w}x/{\nu }_f$ is the Reynolds number based on the plate velocity and ${\mathrm{Re}}_{\infty }=U_{\infty }x/{\nu }_f$ is the Reynolds numbers based on the free stream velocity, respectively. The effective properties of nanofluids are given by [31]:

$$\begin{array}{c}{\alpha }_{nf}=\frac{k_{nf}}{{\left(\rho C_p\right)}_{nf}},{\mu }_{nf}=\frac{{\mu }_f}{{\left(1-\phi \right)}^{2.5}},{\rho }_{nf}=\left(1-\phi \right){\rho }_f+\phi {\rho }_{CNT},\\ {\left(\rho C_p\right)}_{nf}=\left(1-\phi \right){\left(\rho C_p\right)}_f+\phi {\left(\rho C_p\right)}_{CNT},\\ \frac{k_{nf}}{k_f}=\frac{1-\phi +2\phi \frac{k_{CNT}}{k_{CNT}-k_f}\ln \frac{k_{CNT}+k_f}{2k_f}}{1-\phi +2\phi \frac{k_f}{k_{CNT}-k_f}\ln \frac{k_{CNT}+k_f}{2k_f}}\end{array}$$

(5)

where $\left(\rho C_p\right)$ is the heat capacity, $\phi$ is the nanoparticle volume fraction and $k$ is the thermal conductivity, respectively. The use of the term for $k_{nf}/k_f$ were taken from Xue [8] where the model based on Maxwell theory considering the effect of space distribution of CNTs on thermal conductivity. Thermophysical properties for different base fluids are listed in Table 1.

Table 1. Thermophysical properties of CNTs (Khan et al. [22]).

Physical Properties	Base Fluids		Nanoparticle
	Water (Pr = 6.2)	Kerosene (Pr = 21)	SWCNT	MWCNT
$\rho \left(kg/m^3\right)$	997	783	2600	1600
$c_p\left(J/kg K\right)$	4179	2090	425	796
$k\left(W/m K\right)$	0.613	0.145	6600	3000

Similarity solutions of Equations (1)–(4) are presented in the following form:

$$\eta ={\left(\frac{U}{v_{f}x}\right)}^{\frac{1}{2}}y,\psi ={\left(v_{f}xU\right)}^{\frac{1}{2}}f\left(\eta \right),\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }}$$

(6)

where the composite velocity, $U$ is defined as $U=U_w+U_{\infty }$. Afzal et al. [32] was the first who introduced this definition of $U$. $\psi$ represents the stream function and defined as $u=\partial \psi /\partial y$ and $v=-\partial \psi /\partial x$ which identically satisfy Equation (1). By substituting Equation (6) into Equations (2) and (3), then we have:

$$\frac{1}{{\left(1-\phi \right)}^{2.5}\left(1-\phi +\phi {\rho }_{CNT}/{\rho }_f\right)}{f}^{‴}+\frac{1}{2}f{f}^{″}=0$$

(7)

$$\frac{1}{\mathrm{Pr}}\frac{k_{nf}/k_f}{\left[1-\phi +\phi {\left(\rho C_p\right)}_{CNT}/{\left(\rho C_p\right)}_f\right]}{\theta }^{″}+\frac{1}{2}f{\theta }^{\prime }=0$$

(8)

The original boundary condition (4) now takes the following form:

$$\begin{array}{c}f(0)=0,f^{\prime }(0)=\lambda +\sigma f^{″}(0),\theta (0)=1\\ f^{\prime }\left(\eta \right)\to 1-\lambda ,\theta \left(\eta \right)\to 0 \mathrm{as} \eta \to \infty \end{array}$$

(9)

Here, primes denote the differentiation with respect to $\eta$. $\mathrm{Pr}$ is the Prandtl number, $\lambda$ is the velocity parameter and $\sigma$ is the slip parameter, which are defined as:

$$\mathrm{Pr}=\frac{{\nu }_f}{{\alpha }_f}, \lambda =\frac{U_w}{U},\sigma =L\frac{U}{{\nu }_f}$$

(10)

where, ${\nu }_f$ is the kinematic viscosity. Note that, $\lambda >0$ represents the plate move in assisting flow, while $\lambda <0$ represents the plate move in opposing flow [17]. It is worth mentioning that in the absence of CNTs $\left(\phi =0\right)$ and slip parameter $\left(\sigma =0\right)$, the present problem reduces to those considered by Blasius [11] when $\lambda =0$, and Sakiadis [14] when $\lambda =1$.

The skin friction coefficient $C_f$ and the local Nusselt number $N{u}_x$, defined as:

$$C_f=\frac{{\tau }_w}{{\rho }_f{U}^2},N{u}_x=\frac{x{q}_w}{k_f\left(T_w-T_{\infty }\right)}$$

(11)

where ${\tau }_w$ and $q_w$ is the surface shear stress and heat flux which are given by:

$${\tau }_w={\mu }_{nf}{\left(\frac{\partial u}{\partial y}\right)}_{y=0},q_w=-k_{nf}{\left(\frac{\partial T}{\partial y}\right)}_{y=0}$$

(12)

using Equation (6) in (11) and (12), we obtain:

$$C_f{\mathrm{Re}}_x^{1/2}=\frac{1}{{\left(1-\phi \right)}^{2.5}}{f}^{″}(0),N{u}_x{\mathrm{Re}}_x^{-1/2}=-\frac{k_{nf}}{k_f}{\theta }^{\prime }(0)$$

(13)

where ${\mathrm{Re}}_x=Ux/{\nu }_f$ is the local Reynolds number.

3. Flow Stability

It is important to determine the physical reliability of dual solutions obtain because there is more than one solution. A further question that will arise later is which solutions are physically acceptable solutions and have physical meanings. Hence, we now investigate the stability of the solutions obtained using Equations (7) and (8) subject to the boundary conditions (9) to determine which solution is stable and physically realizable and which is not stable. These features are tested by first considering the time-dependent problem (see Merkin [27]) due to the fact that there exists a small perturbation to the solutions. Equation (1) holds, while Equations (2) and (3) are replaced by:

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{{\mu }_{nf}}{{\rho }_{nf}}\frac{{\partial }^{2}u}{\partial y^2}$$

(14)

$$\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}={\alpha }_{nf}\frac{{\partial }^{2}T}{\partial y^2}$$

(15)

where $t$ represent the time. Using the variables $\tau$ and (6), the new similarity solutions are:

$$\eta ={\left(\frac{U}{v_{f}x}\right)}^{\frac{1}{2}}y,\psi ={\left(v_{f}xU\right)}^{\frac{1}{2}}f\left(\eta ,\tau \right),\theta \left(\eta ,\tau \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }}, \tau =\frac{U}{x}\mathrm{t}$$

(16)

Equations (14) and (15) can be written as:

$$\frac{1}{{\left(1-\phi \right)}^{2.5}\left(1-\phi +\phi {\rho }_{CNT}/{\rho }_f\right)}\frac{{\partial }^{3}f}{\partial {\eta }^3}+\frac{1}{2}f\frac{{\partial }^{2}f}{\partial {\eta }^2}+\tau \left(\frac{\partial f}{\partial \eta }\frac{{\partial }^{2}f}{\partial \eta \partial \tau }-\frac{\partial f}{\partial \tau }\frac{{\partial }^{2}f}{\partial {\eta }^2}\right)-\frac{{\partial }^{2}f}{\partial \eta \partial \tau }=0$$

(17)

$$\frac{1}{\mathrm{Pr}}\frac{k_{nf}/k_f}{\left[1-\phi +\phi {\left(\rho C_p\right)}_{CNT}/{\left(\rho C_p\right)}_f\right]}\frac{{\partial }^2\theta }{\partial {\eta }^2}+\frac{1}{2}f\frac{\partial \theta }{\partial \eta }+\tau \left(\frac{\partial f}{\partial \eta }\frac{\partial \theta }{\partial \tau }-\frac{\partial f}{\partial \tau }\frac{\partial \theta }{\partial \eta }\right)-\frac{\partial \theta }{\partial \tau }=0$$

(18)

the new constrictions are now replaced by:

$$\begin{array}{c}f\left(0,\tau \right)=0,\frac{\partial f}{\partial \eta }\left(0,\tau \right)=\lambda +\sigma \frac{{\partial }^{2}f}{\partial {\eta }^2}\left(0,\tau \right),\theta \left(0,\tau \right)=1\\ \frac{\partial f}{\partial \eta }\left(\eta ,\tau \right)\to 1-\lambda ,\theta \left(\eta ,\tau \right)\to 0 \mathrm{as} \eta \to \infty \end{array}$$

(19)

To identify the stability solution $f\left(\eta \right)=f_0\left(\eta \right)$ and $\theta \left(\eta \right)={\theta }_0\left(\eta \right)$ fulfilling the boundary-value problem as in Equations (7)–(9), we introduced the following term (see [28]):

$$f\left(\eta ,\tau \right)=f_0\left(\eta \right)+e^{-\gamma \tau }F\left(\eta ,\tau \right),\theta \left(\eta ,\tau \right)={\theta }_0\left(\eta \right)+e^{-\gamma \tau }G\left(\eta ,\tau \right)$$

(20)

where $F\left(\eta ,\tau \right)$ and $G\left(\eta ,\tau \right)$ are small relative to $f_0\left(\eta \right)$ and ${\theta }_0\left(\eta \right)$ and $\gamma$ is an unknown eigenvalue. Substitute Equations (20) into Equations (17)–(19), we get the following linearized problem:

$$\frac{1}{{\left(1-\phi \right)}^{2.5}\left(1-\phi +\phi {\rho }_{CNT}/{\rho }_f\right)}\frac{{\partial }^{3}F}{\partial {\eta }^3}+\frac{1}{2}\left(f_0\frac{{\partial }^{2}F}{\partial {\eta }^2}+\frac{{\partial }^2{f}_0}{\partial {\eta }^2}F\right)+\gamma \frac{\partial F}{\partial \eta }-\frac{{\partial }^{2}F}{\partial \eta \partial \tau }=0$$

(21)

$$\frac{1}{\mathrm{Pr}}\frac{k_{nf}/k_f}{\left[1-\phi +\phi {\left(\rho C_p\right)}_{CNT}/{\left(\rho C_p\right)}_f\right]}\frac{{\partial }^{2}G}{\partial {\eta }^2}+\frac{1}{2}\left(f_0\frac{\partial G}{\partial \eta }+\frac{\partial {\theta }_0}{\partial \eta }F\right)+\gamma G-\frac{\partial G}{\partial \tau }=0$$

(22)

subject to the boundary conditions:

$$\begin{array}{c}F\left(0,\tau \right)=-2\tau \left(\gamma F\left(0,\tau \right)-\frac{\partial F}{\partial \tau }\left(0,\tau \right)\right)=0,\frac{\partial F}{\partial \eta }\left(0,\tau \right)=\sigma \frac{{\partial }^{2}F}{\partial {\eta }^2}\left(0,\tau \right), \mathrm{G}\left(0,\tau \right)=0\\ \frac{\partial F}{\partial \eta }\left(\eta ,\tau \right)\to 0, \mathrm{G}\left(\eta ,\tau \right)\to 0 \mathrm{as} \eta \to \infty \end{array}$$

(23)

To find the initial growth or decay of the solutions (21) and (20) which were proposed by Weidman et al. [28], the stability of steady flow $f_0\left(\eta \right)$ and ${\theta }_0\left(\eta \right)$ are investigated by setting $\tau =0$. Hence, $F\left(\eta \right)=F_0\left(\eta \right)$ and $G\left(\eta \right)=G_0\left(\eta \right)$. In this respect, by substituting Equation (20) into (21)–(23), we get the final equations in the following form:

$$\frac{1}{{\left(1-\phi \right)}^{2.5}\left(1-\phi +\phi {\rho }_{CNT}/{\rho }_f\right)}{F}_0{}^{‴}+\frac{1}{2}\left(f_0{F}_0{}^{″}+f_0{}^{″}{F}_0\right)+\gamma F_0{}^{\prime }=0$$

(24)

$$\frac{1}{\mathrm{Pr}}\frac{k_{nf}/k_f}{\left[1-\phi +\phi {\left(\rho C_p\right)}_{CNT}/{\left(\rho C_p\right)}_f\right]}{G}_0{}^{″}+\frac{1}{2}\left(f_0{G}_0{}^{\prime }+F_0{\theta }_0{}^{\prime }\right)+\gamma G_0=0$$

(25)

the boundary conditions in Equation (23) now reduced to:

$$\begin{array}{c}{F}_0\left(0\right)=0, {\mathrm{F}}_0{}^{\prime }\left(0\right)=\sigma F_0{}^{″}\left(0\right), {\mathrm{G}}_0\left(0\right)=0\\ F_0{}^{\prime }\left(\eta \right)\to 0, {\mathrm{G}}_0\left(\eta \right)\to 0 \mathrm{as} \eta \to \infty \end{array}$$

(26)

The stability of the dual solution obtained is determined by the smallest eigenvalue γ. The flow of a solution is said to be stable if the smallest eigenvalue γ is positive (γ ≥ 0) i.e., there is an initial decay of perturbation. However, when γ is negative (γ < 0), there is an initial growth of perturbation and thus we can conclude that the flow is in an unstable mode. Following Harris et al. [30], the smallest eigenvalues can be identified by relaxing a boundary condition on F₀(η). Therefore, for the current work, we relax the boundary condition $F_0^{\prime }\to 0$ as $\eta \to \infty$ and replace it with updated boundary condition $F_0^{″}\left(0\right)=1$.

4. Results and Discussion

The system of Equations (7) and (8) together with conditions in (9) are solved numerically using the bvp4c package in Matlab. Kierzenka and Shampine [33] introduced this function as a way to solve a two-point boundary value problems for ordinary differential equations. The numerical result was validated by comparing the present results with the results in the existing literature [11,14,17] for the case of a boundary layer with the absence of CNTs and slip $\left(\phi =\sigma =0\right)$.

As can be seen from Table 2, the comparison shows close agreement between the present results and those available in the literature [11,14,17] and thus we are assured that the present numerical method is accurate. For future references, the values of reduced skin friction $f^{″}\left(0\right)$ for $\phi \ne 0$ are also included in Table 2. The effects of dimensionless governing parameter such as slip parameter, velocity parameter and nanoparticle volume fraction on velocity, temperature, skin friction coefficient and Nusselt number are investigated and illustrated graphically. The range of nanoparticle volume fraction $\phi$ is considered from 0 to 0.2 $\left(0<\phi <0.2\right)$, where $\phi =0$ is corresponding to the regular fluid.

Table 2. Values of $f^{″}\left(0\right)$ for selected value of $\phi$ and $\lambda$ for water-SWCNT and $\sigma =0$.

$\mathit{\phi }$	$\mathit{\lambda }$	Blasius [11]	Sakiadis [14]	Bachok et al. [17] Solution		Present Result Solution
				First	Second	First	Second
0	−0.5			0.3979	0.1710	0.3978	0.1710
	−0.4			0.4357	0.0834	0.4356	0.0834
	−0.3			0.4339	0.0367	0.4339	0.0367
	−0.2			0.4124	0.0114	0.4124	0.0114
	−0.1			0.3774	0.0010	0.3774	0.0011
	0	0.332		0.3321		0.3321
	0.5			0		0
	1		−0.44375	−0.4438		−0.4438
0.1	−0.5					0.3757	0.1615
	−0.4					0.4114	0.0787
	−0.3					0.4098	0.0345
	−0.2					0.3895	0.0107
	−0.1					0.3564	0.0010
	0					0.3136
	0.5					0
	1					−0.4191
0.2	−0.5					0.3460	0.1488
	−0.4					0.3789	0.0725
	−0.3					0.3774	0.0307
	−0.2					0.3587	0.0099
	−0.1					0.3282	0.0000
	0					0.2888
	0.5					0
	1					−0.3861

Figure 2 and Figure 3 illustrate the behaviors of nanoparticle volume fraction $\phi$ on the variation of reduced skin friction $f^{″}\left(0\right)$ and reduced heat transfer $-{\theta }^{\prime }\left(0\right)$ for water-SWCNTs. From these figures, it can be seen that there exist dual solutions when ${\lambda }_c<\lambda <0$, i.e., opposing flow, while a unique solution exists when $\lambda \ge 0$. However, no solutions are found to exist when $\lambda <{\lambda }_c$, which means that there is a boundary layer separation and boundary layer approximations are not physically realizable. The variation of ${\lambda }_c$ has been shown in Table 3, where the results are in good agreement with Bachok et al. [21] when $\phi =0$. From the figures, we can conclude that an increase of nanoparticles volume fraction $\phi$ causes the skin friction to decrease whereas the heat transfer rate at the surface increases. This is because nanofluids become more viscous by adding CNTs and this also enhances their thermal conductivity.

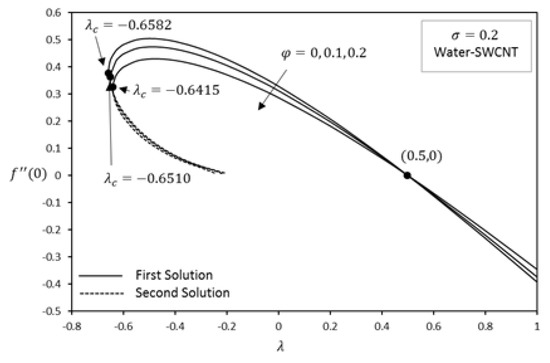
Figure 2. Effect of $\phi$ on reduced skin friction $f^{″}\left(0\right)$.

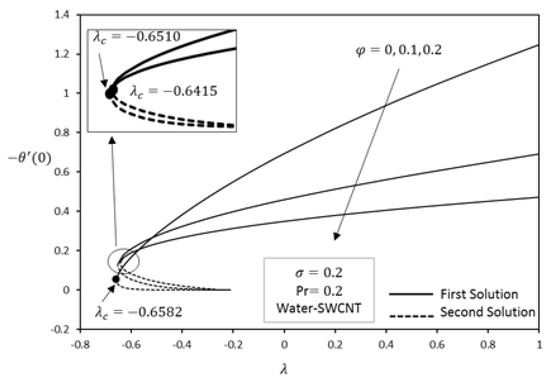
Figure 3. Effect of $\phi$ on reduced heat transfer $-{\theta }^{\prime }\left(0\right)$.

Table 3. Variation of ${\lambda }_c$ with $\sigma =0.2$ and water-SWCNT for different value of $\phi$.

$\mathit{\phi }$	Bachok et al. [21]	Present Result
0	−0.6582	−0.6582
0.1		−0.6510
0.2		−0.6415

Figure 4 and Figure 5 show the effect of slip parameter on reduced skin friction $f^{″}\left(0\right)$ and reduced heat transfer $-{\theta }^{\prime }\left(0\right)$. It is observed that for no-slip boundary conditions, i.e., $\sigma =0$, the similarity solution exists only when $\lambda \ge {\lambda }_c=-0.5482$. When the slip at the boundary increases, i.e., $\sigma =0.1$ the range of $\lambda$ values where solutions exist becomes larger $(\lambda \ge {\lambda }_c=-0.6480)$. For further increment in the slip parameter, $\sigma =0.2$ the range of $\lambda \ge {\lambda }_c=-0.7910$, respectively, so the analysis implies that with the increase in slip parameter $\sigma$, the reduced skin friction and heat loss from the surface increases. It is further observed that when the slip takes place in the boundary layer, there will be more resistance between the fluid and plate that cause the solution existence range to increase, hence postponing the boundary layer separation and this increment happens in the range where dual solutions exist. Moreover, it is noticed that for a fixed velocity ratio parameter, the value of the reduced skin friction and reduced heat transfer increases with an increase of slip parameter in the first solution and decreases in the second solution.

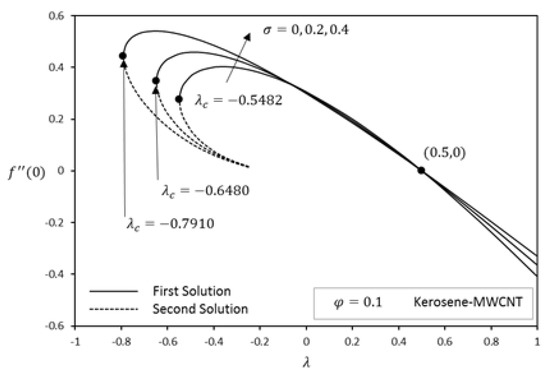
Figure 4. Effect of $\sigma$ on reduced skin friction $f^{″}\left(0\right)$.

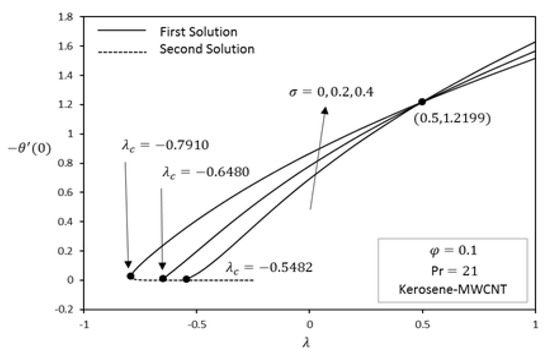
Figure 5. Effect of $\sigma$ on reduced heat transfer $-{\theta }^{\prime }\left(0\right)$.

The effect of skin friction and Nusselt numbers are investigated and shown in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17. It can be clearly seen that the value of these quantities increases almost linearly with nanoparticle volume fraction. Figure 6, Figure 7 and Figure 8 shows the variation of slip parameter on the skin friction coefficient for different base fluids (water and kerosene) and considering both SWCNTs and MWCNTs. When the plate moves in the same direction as the free stream, the skin friction coefficient decreases with an increase in slip parameter. Figure 9, Figure 10 and Figure 11 depict the numerical values of the skin friction with volume fraction of CNTs when the plate moves in an assisting flow for both SWCNTs and MWCNTs. It is observed that the skin friction decreases with an increase in the plate velocity. However, the skin friction of SWCNTs is found to be higher compared to MWCNTs. The density of SWCNTs is found to be higher than that of MWCNTs (Table 1). Further, skin friction is higher in kerosene oil compared to water.

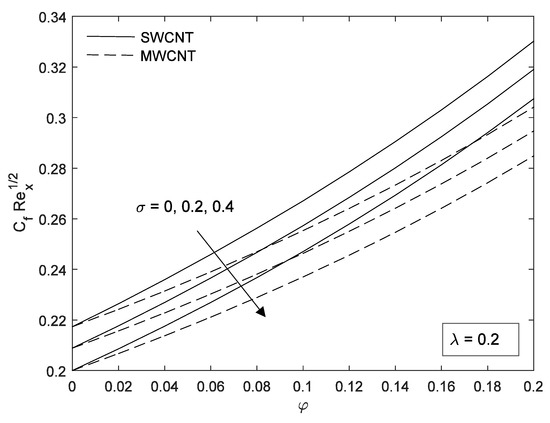
Figure 6. Effect of $\sigma$ on skin friction for water-based fluid.

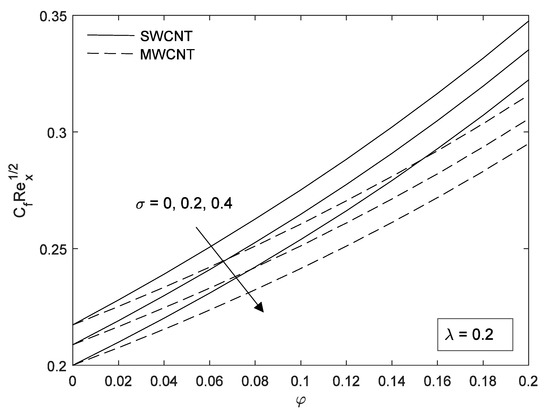
Figure 7. Effect of $\sigma$ on skin friction for kerosene-based fluid.

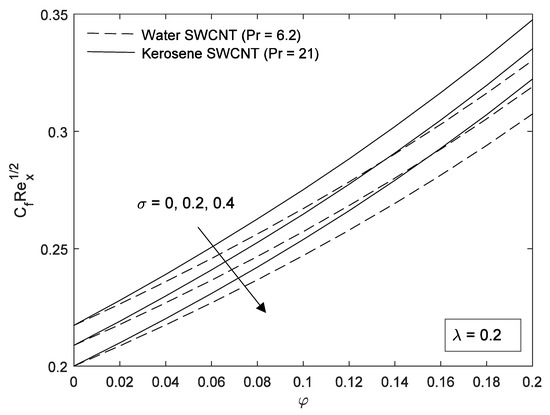
Figure 8. Effect of $\sigma$ on skin friction for water-kerosene based fluid.

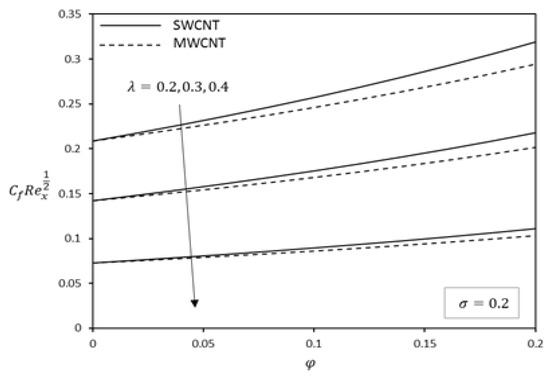
Figure 9. Effect of $\lambda$ on skin friction for water-based fluid.

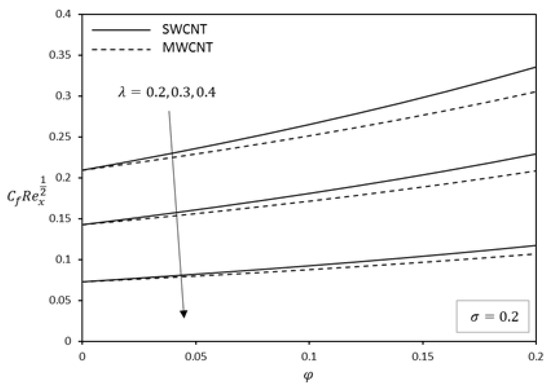
Figure 10. Effect of $\lambda$ on skin friction for kerosene-based fluid.

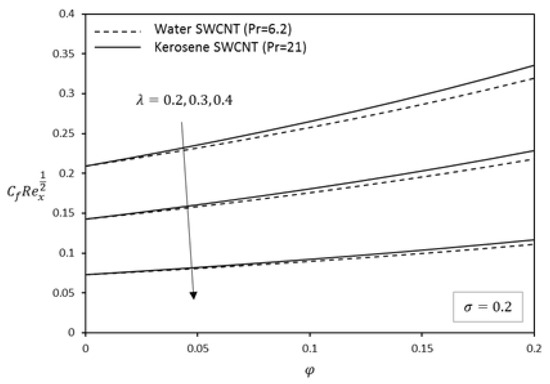
Figure 11. Effect of $\lambda$ on skin friction for water-kerosene based fluid.

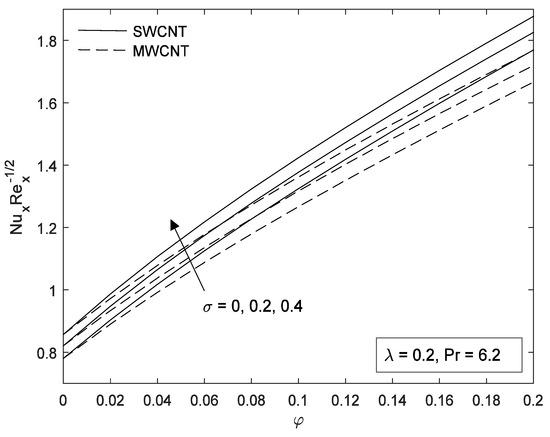
Figure 12. Effect of $\sigma$ on Nusselt number for water-based fluid.

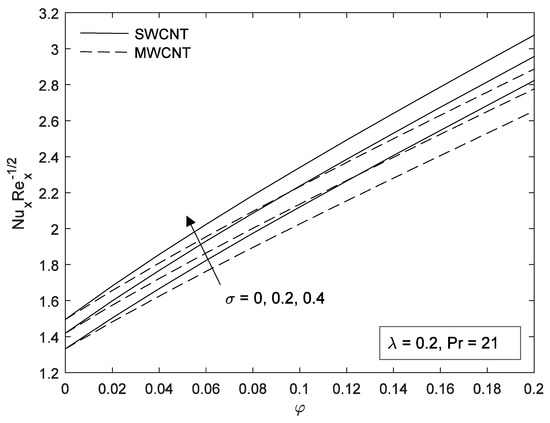
Figure 13. Effect of $\sigma$ on Nusselt number for kerosene-based fluid.

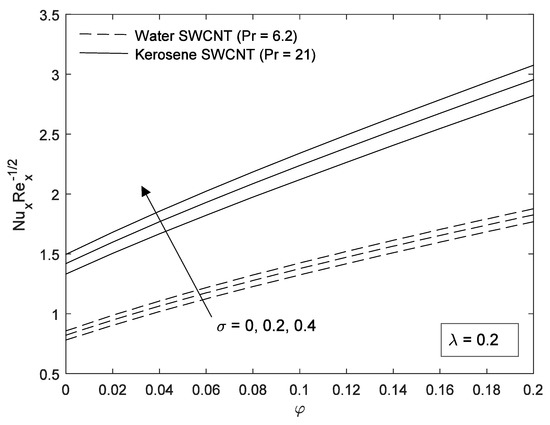
Figure 14. Effect of $\sigma$ on Nusselt number for water-kerosene based fluid.

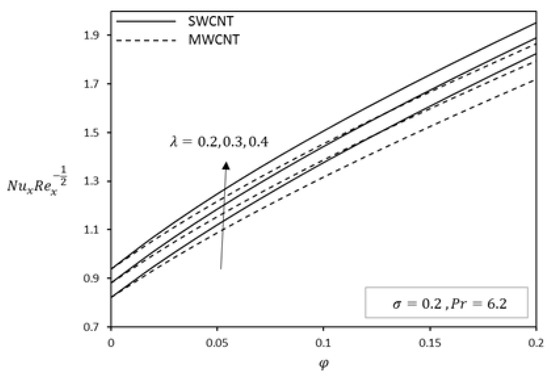
Figure 15. Effect of $\lambda$ on Nusselt number for water-based fluid.

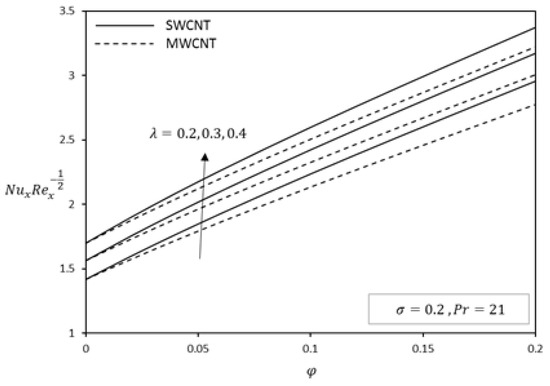
Figure 16. Effect of $\lambda$ on Nusselt number for kerosene-based fluid.

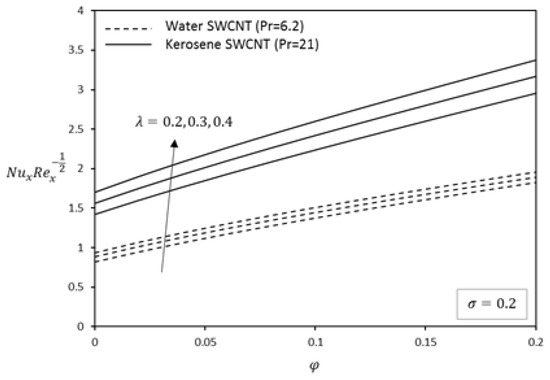
Figure 17. Effect of $\lambda$ on Nusselt number for water-kerosene based fluid.

The effect of the slip parameter on the variation of Nusselt numbers with volume fraction of CNTs is reported in Figure 12, Figure 13 and Figure 14 for different base fluids (water and kerosene) and considering both SWCNTs and MWCNTs. It is revealed that the Nusselt number increases with an increase in slip parameter. The present of slip also improves the convective heat transfer at the surface. Figure 15, Figure 16 and Figure 17 shows the influence of plate velocity on Nusselt number for both SWCNTs and MWCNTs. When the plate moves in the direction of the free stream, the Nusselt number increases with an increase in the plate velocity of both CNTs. Due to their higher thermal conductivity, SWCNTs possess higher Nusselt numbers in each case. Again, we found that kerosene oil has a higher Nusselt number compared to water. The nanofluids having a higher concentration of CNTs causes higher viscosity. In addition, carbon nanotubes have a great contribution in the flow motion of nanofluid and in the heat transfer application.

These numerical solutions and dual solution obtained were graphically supported and validated by the velocity and temperature profile plotted in Figure 18, Figure 19, Figure 20, Figure 21, Figure 22 and Figure 23. These profiles satisfy the boundary conditions (9) and converge asymptotically. The dual solutions can be clearly seen from the figures. It is also clearly observed that the first solution has a thinner boundary layer thickness compared to second solution. Variations of velocity $f^{\prime }\left(\eta \right)$ and temperature $\theta \left(\eta \right)$ profiles for different volume fractions of CNTs are presented in Figure 18 and Figure 19, respectively, for water-based SWCNTs. It is found that the velocity of fluid is decrease in both solution when the CNT volume fraction increases. We can also observe that temperature profile increases with an increase of CNT volume fraction. The addition of sufficient nanoparticles can enhance the temperature of the fluid quite significantly due to the very high thermal conductivity of carbon nanotubes compared to other nanoparticles.

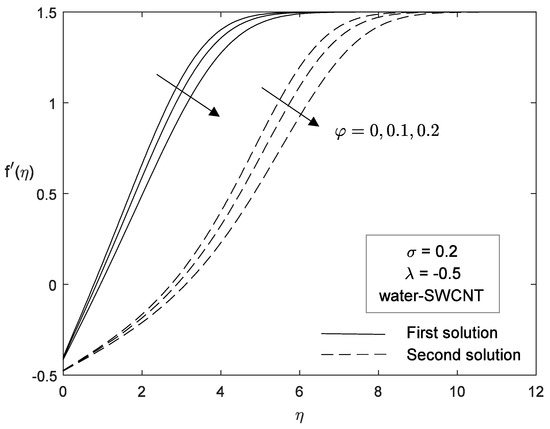
Figure 18. Effect of various $\phi$ on velocity profile.

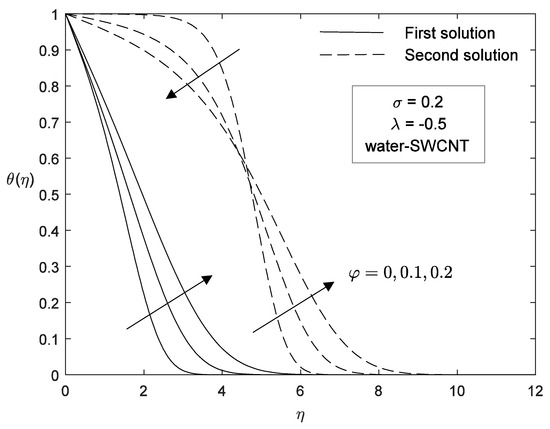
Figure 19. Effect of various $\phi$ on temperature profile.

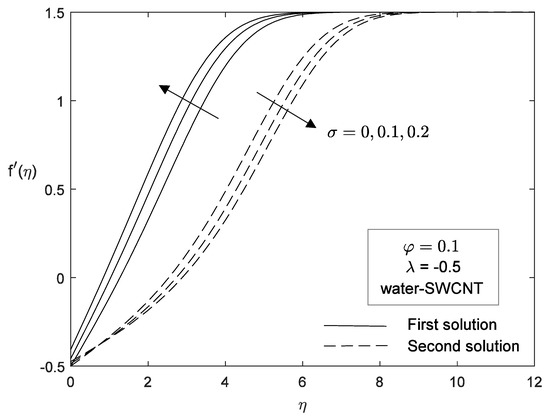
Figure 20. Effect of various $\sigma$ on velocity profile.

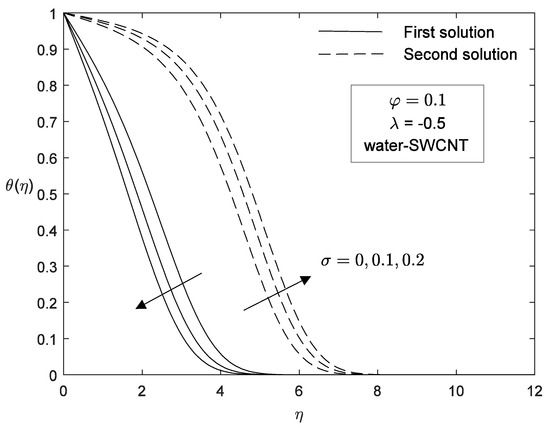
Figure 21. Effect of various $\sigma$ on temperature profile.

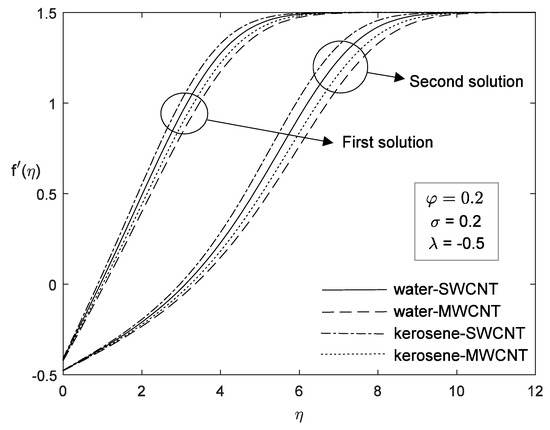
Figure 22. Effect of various nanoparticles on velocity profile.

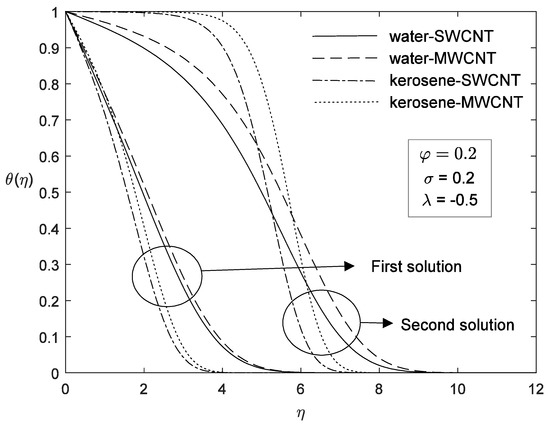
Figure 23. Effect of various nanoparticles on temperature profile.

Meanwhile in Figure 20 and Figure 21, the dual velocity and temperature profiles show that with an increases of slip parameter, the velocity profile increases in the first solution and decreases in the second solution. Meanwhile, the temperature profile is found to be decrease with an increase of slip parameter. It is noticed that kerosene-SWCNT has higher velocity and temperature compared to others in Figure 22 and Figure 23.

A stability analysis is conducted numerically in MATLAB software by using a bvp4c function to determine the stability of solutions obtained in this recent work. The set of ordinary differential Equations (24) and (25) subjected to the new boundary condition (26) is used to find the smallest eigenvalue $\gamma$. The smallest eigenvalue $\gamma$ for some values of $\phi$ and $\lambda$ when $\sigma =0.2$ are presented in Table 4. It is observed that the first solution shows a positive smallest eigenvalues, while the second solution shows a negative smallest eigenvalues. The smallest eigenvalue is drawn closer to zero $\left(\gamma \to 0\right)$ as $\lambda$ is approaching the critical point ${\lambda }_c$ either from positive or negative sign. We can finally conclude that the first solution was linearly stable and physically realizable while the second solution was an unstable solution.

Table 4. Smallest eigenvalues $\gamma$ at selected values of $\phi$ and $\lambda$ for different nanoparticle when $\sigma =0.2$.

Nanoparticles	$\mathit{\phi }$	$\mathit{\lambda }$	First Solution	Second Solution
Water-SWCNT	0	−0.658	0.0069	−0.0067
		−0.65	0.0383	−0.0340
		−0.6	0.1092	−0.0784
	0.1	−0.6509	0.0051	−0.0050
		−0.65	0.0133	−0.0127
		−0.6	0.1020	−0.0746
	0.2	−0.641	0.0098	−0.0095
		−0.64	0.0163	−0.0155
		−0.6	0.0917	−0.0689
Water-MWCNT	0	−0.635	0.0663	−0.0540
		−0.63	0.0736	−0.0587
		−0.6	0.1092	−0.0784
	0.1	−0.645	0.0110	−0.0106
		−0.64	0.0318	−0.0287
		−0.6	0.0963	−0.0715
	0.2	−0.633	0.0037	−0.0037
		−0.63	0.0232	−0.0215
		−0.6	0.0813	−0.0629

5. Conclusions

We have studied the flow and heat transfer characteristics of carbon nanotubes (single–wall and multi–wall carbon nanotube) in different base fluids for a moving flat plate. It is concluded that:

• The skin friction decreases with an increase of carbon nanotubes volume fraction, whereas the heat transfer rate increases.
• Single-wall CNTs are more efficient than multi-wall CNTs in skin friction and heat transfer rate.
• Kerosene-based CNTs have higher skin friction and heat transfer rates than water-based CNTs.
• The range of solutions widely expanded with an increment of slip parameter.
• For the opposing flow, slip parameter increases the skin friction coefficient and heat transfer.
• The existence of unique solutions occurs when the plate moves in the same direction $\left(\lambda >0\right)$ whereas dual solutions occur when the plate move in the opposite direction $\left({\lambda }_c<\lambda <0\right)$.
• The first solution was a stable solution and physically relevant, while the second solution was an unstable solution.