Assessment of Resource and Forecast Modeling of Wind Speed through An Evolutionary Programming Approach for the North of Tehuantepec Isthmus (Cuauhtemotzin, Mexico)
Abstract
:1. Introduction
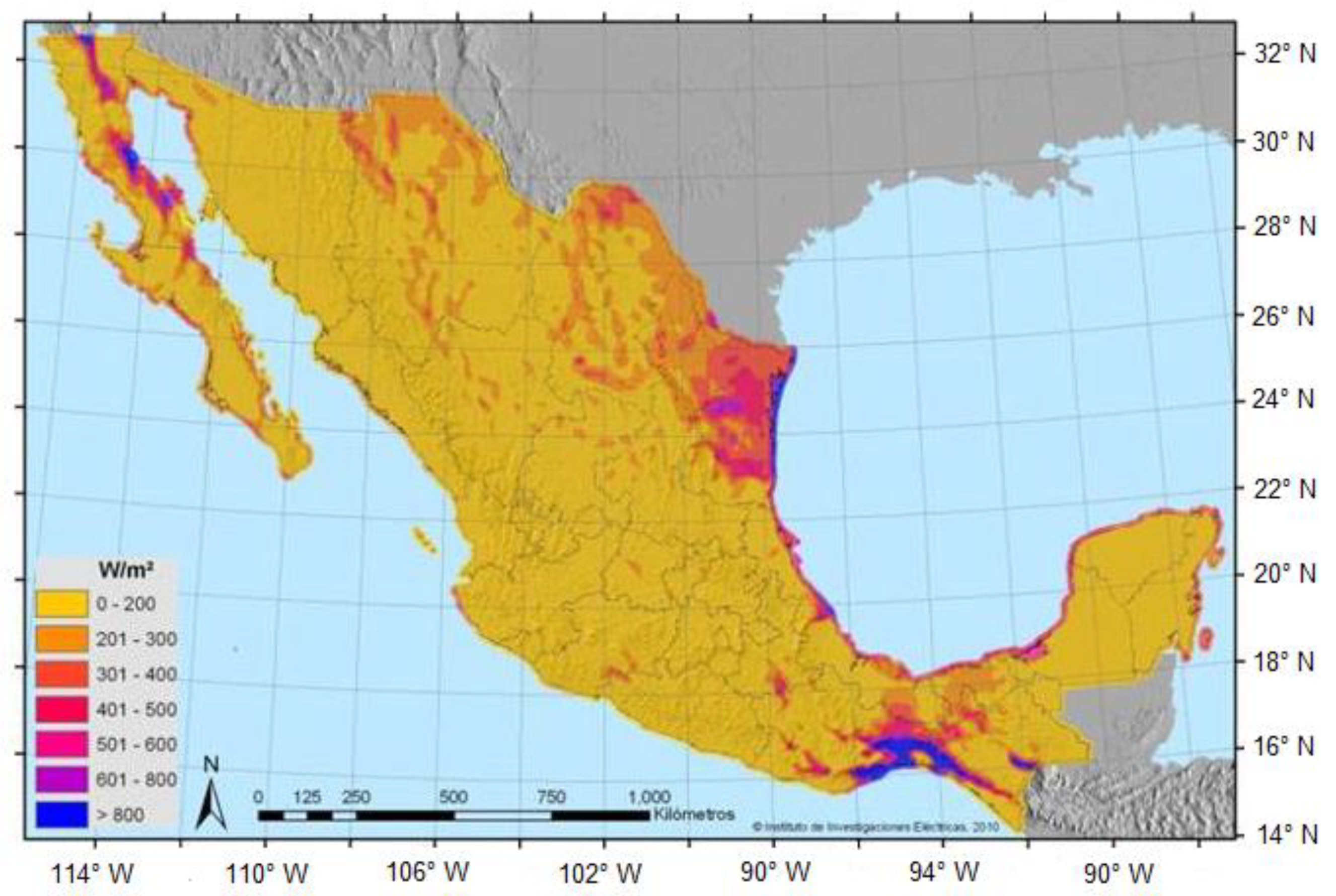
2. Study Location and Measured Data
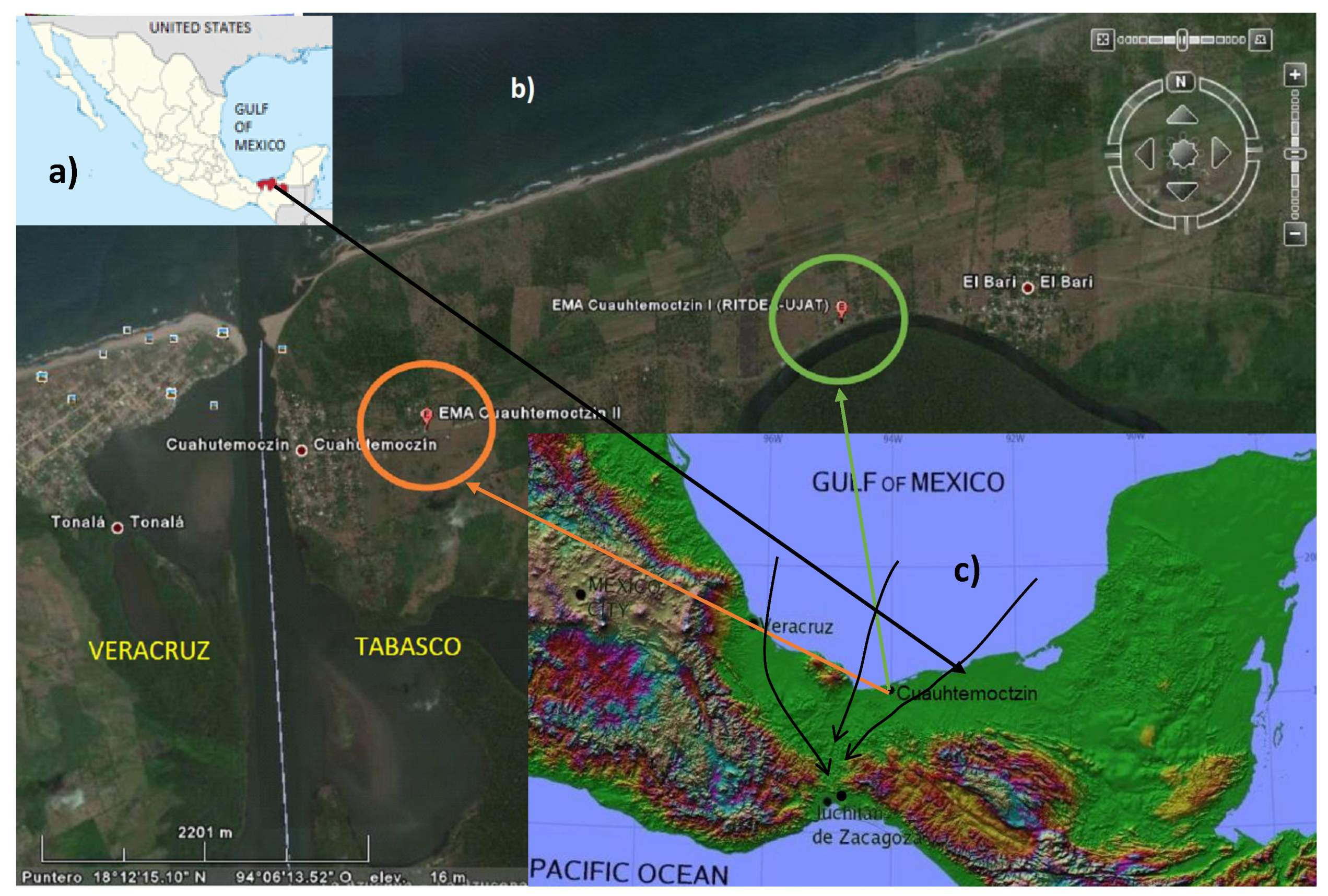
2.1. Specific Site Location
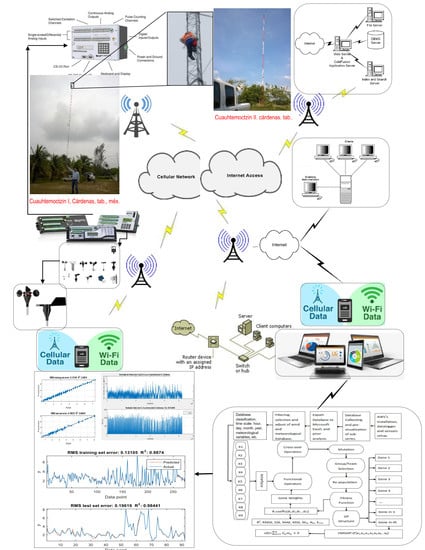
2.2. Experimental System and Instrumentation
3. Wind Assessment
3.1. Hellman Power Law
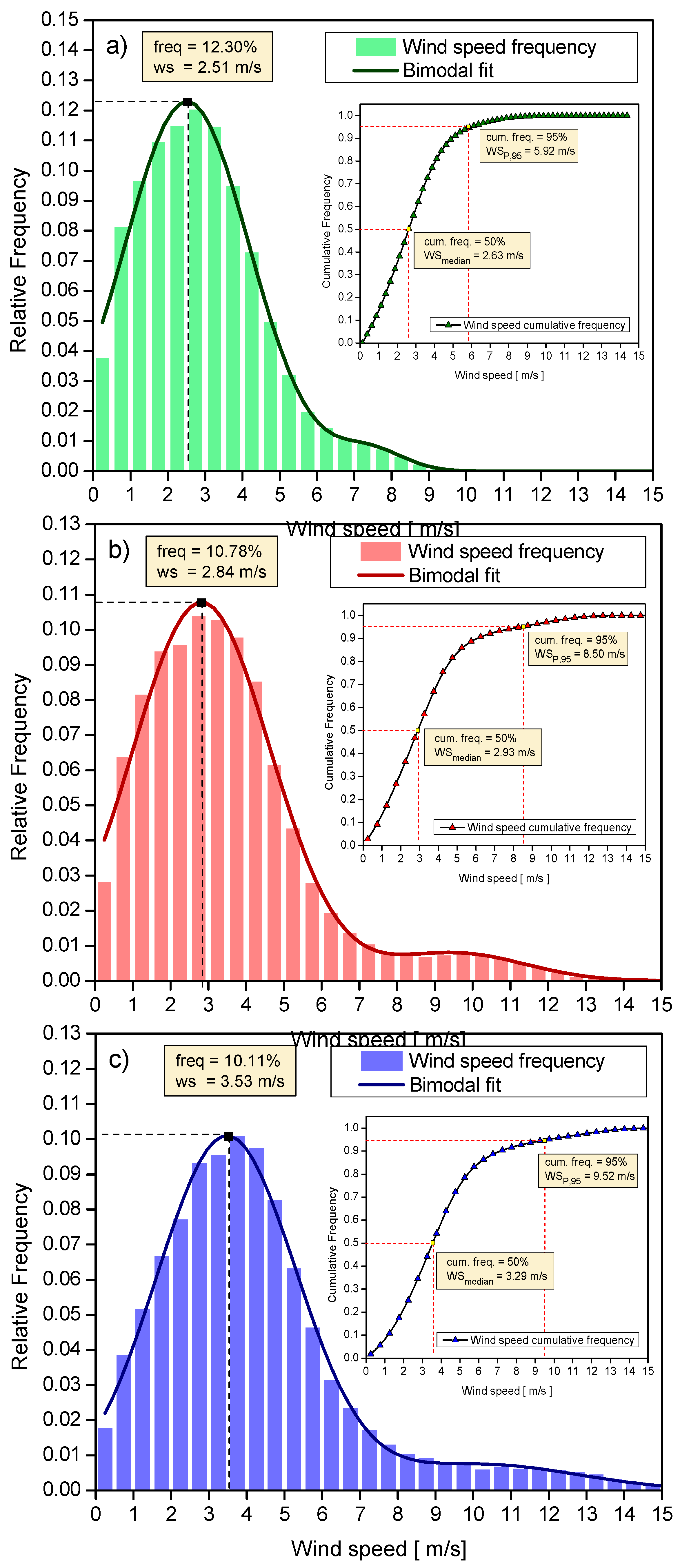
3.2. Wind Distribution Function
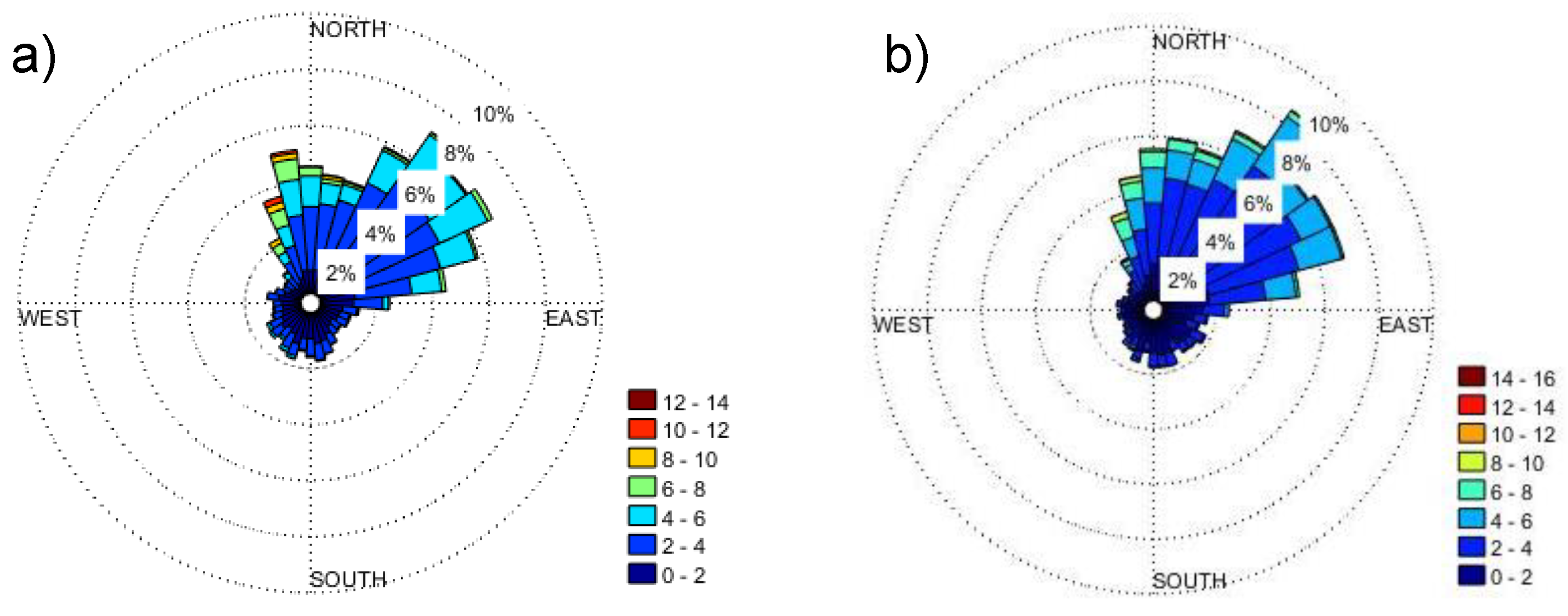
3.3. Assessment Results
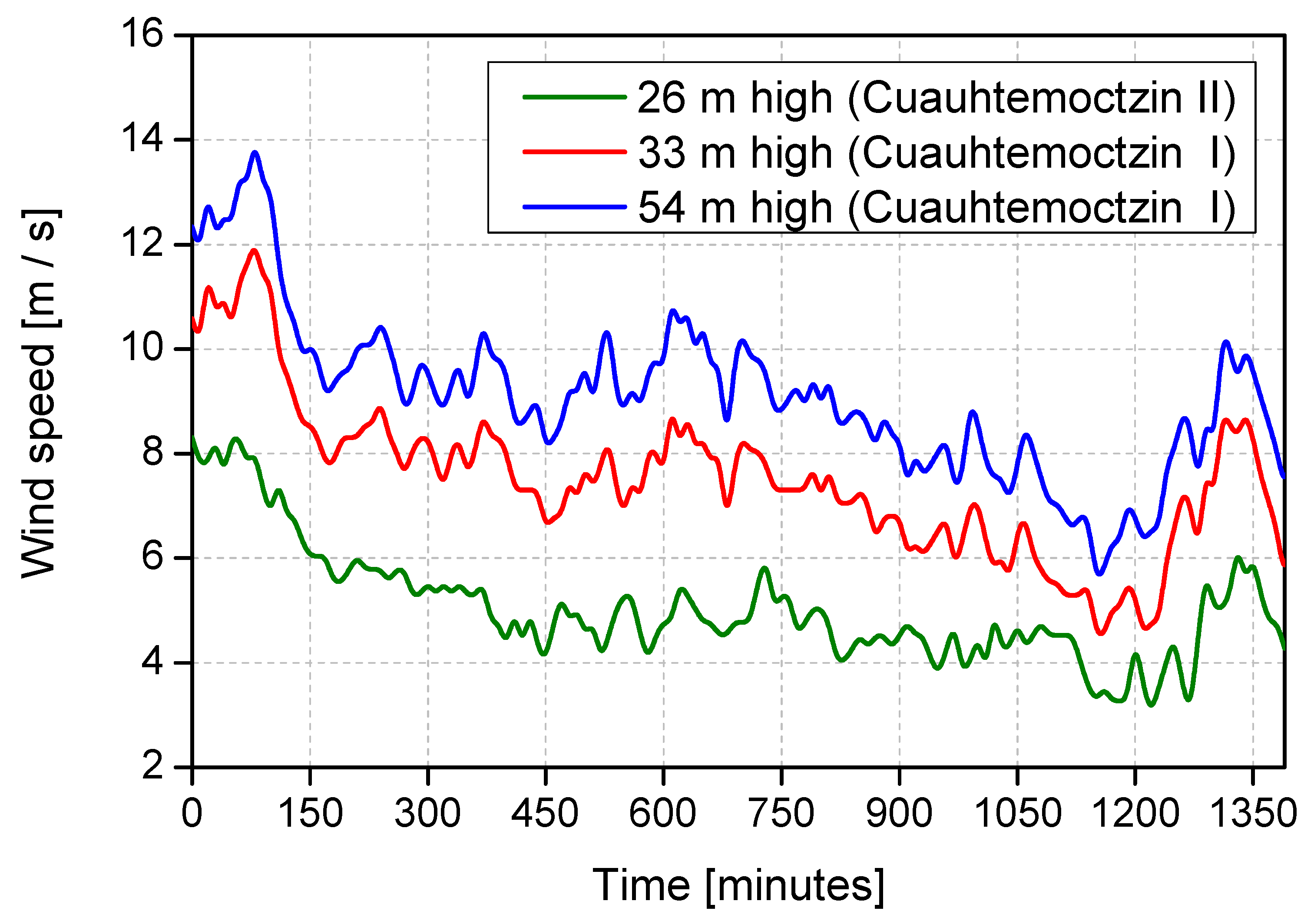
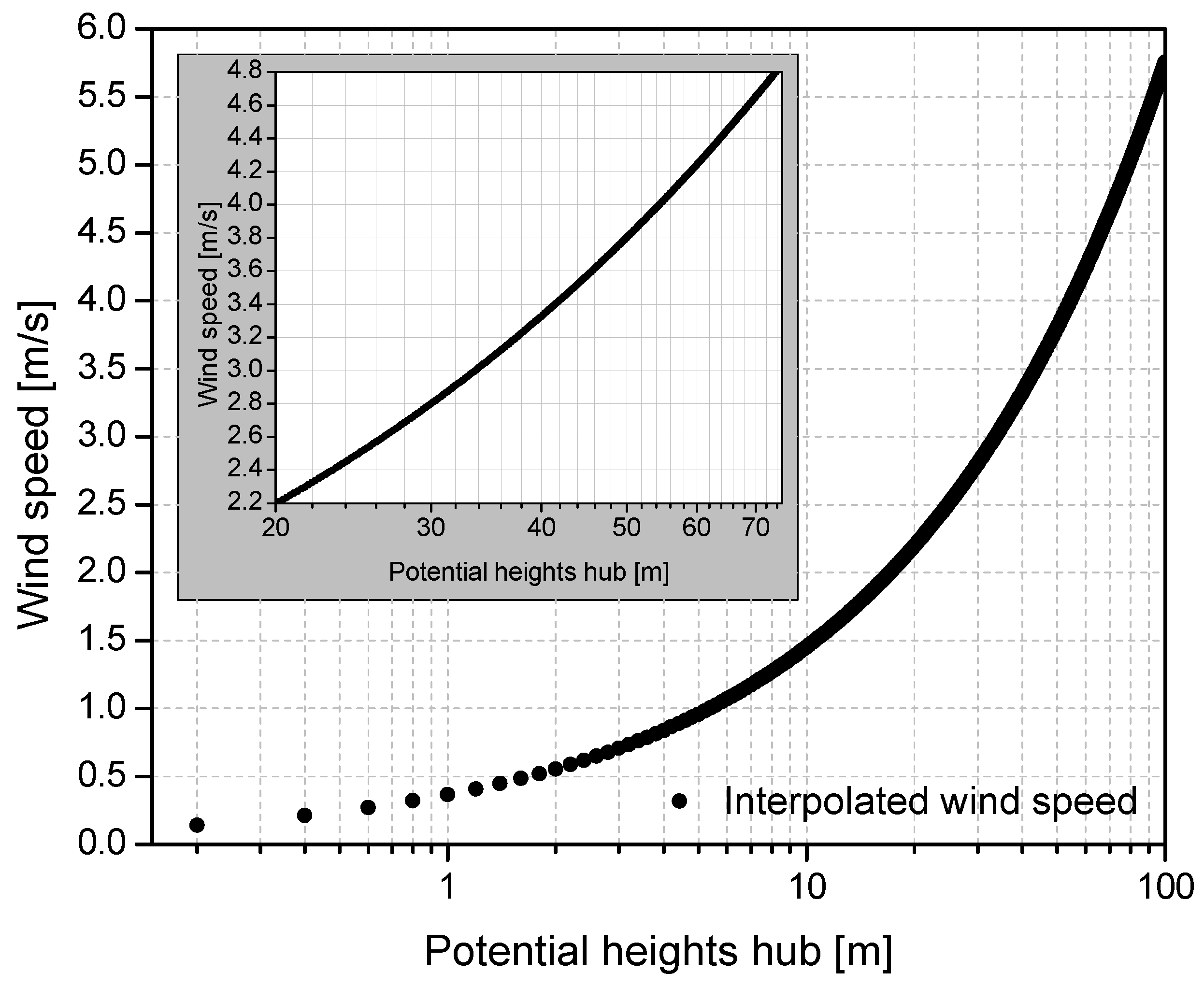
3.3.1. Wind Profile
3.3.2. Data Analysis
4. Artificial Intelligence Forecasting Modeling
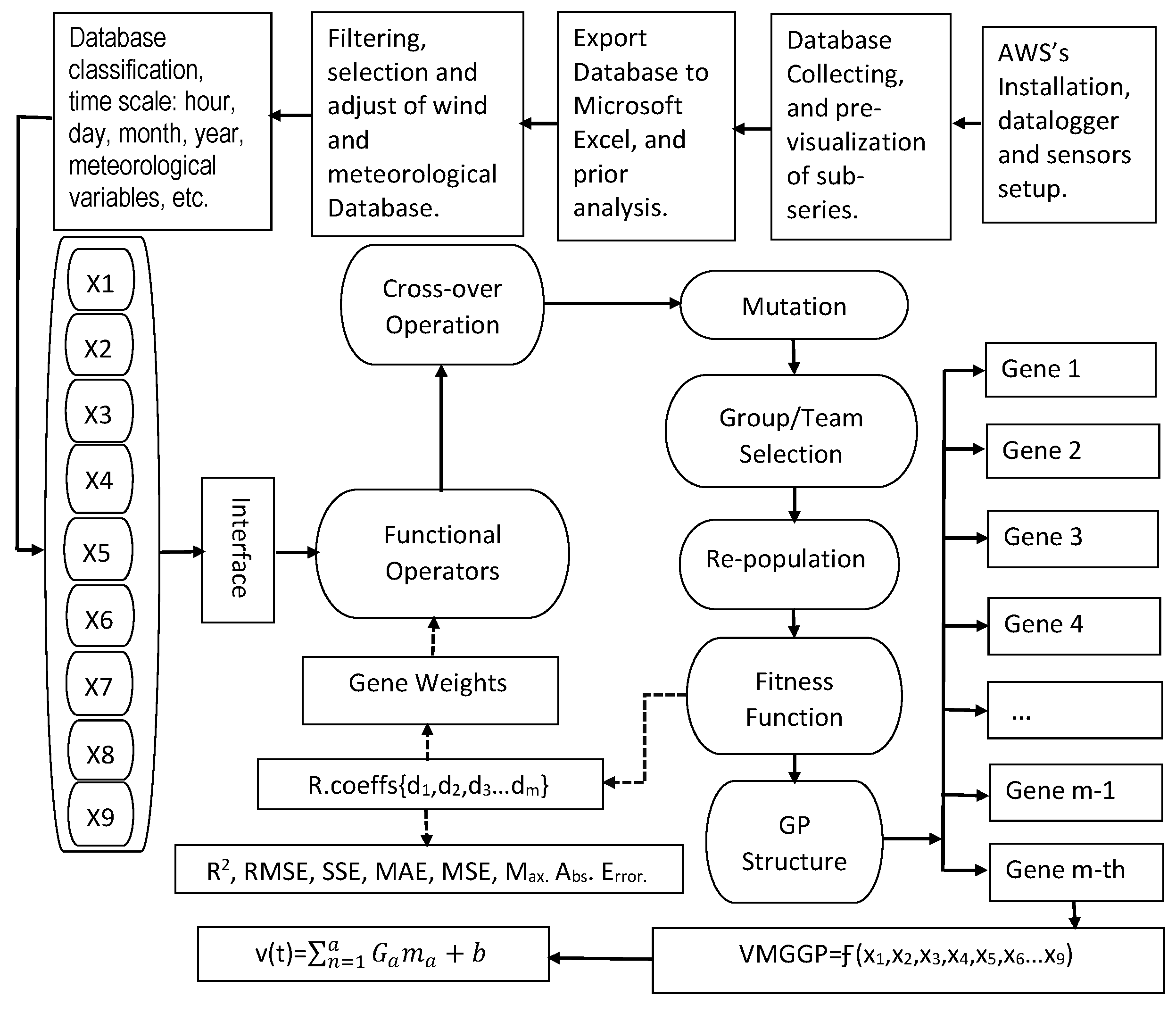
4.1. Multi-Gene Genetic Programming Approach
4.2. Computational Methodology
4.3. Sensitivity Analysis
4.4. Forecast Model Results
4.4.1. Multi-Gene Genetic Programming Model
4.4.2. Sensitivity Analysis Evaluation
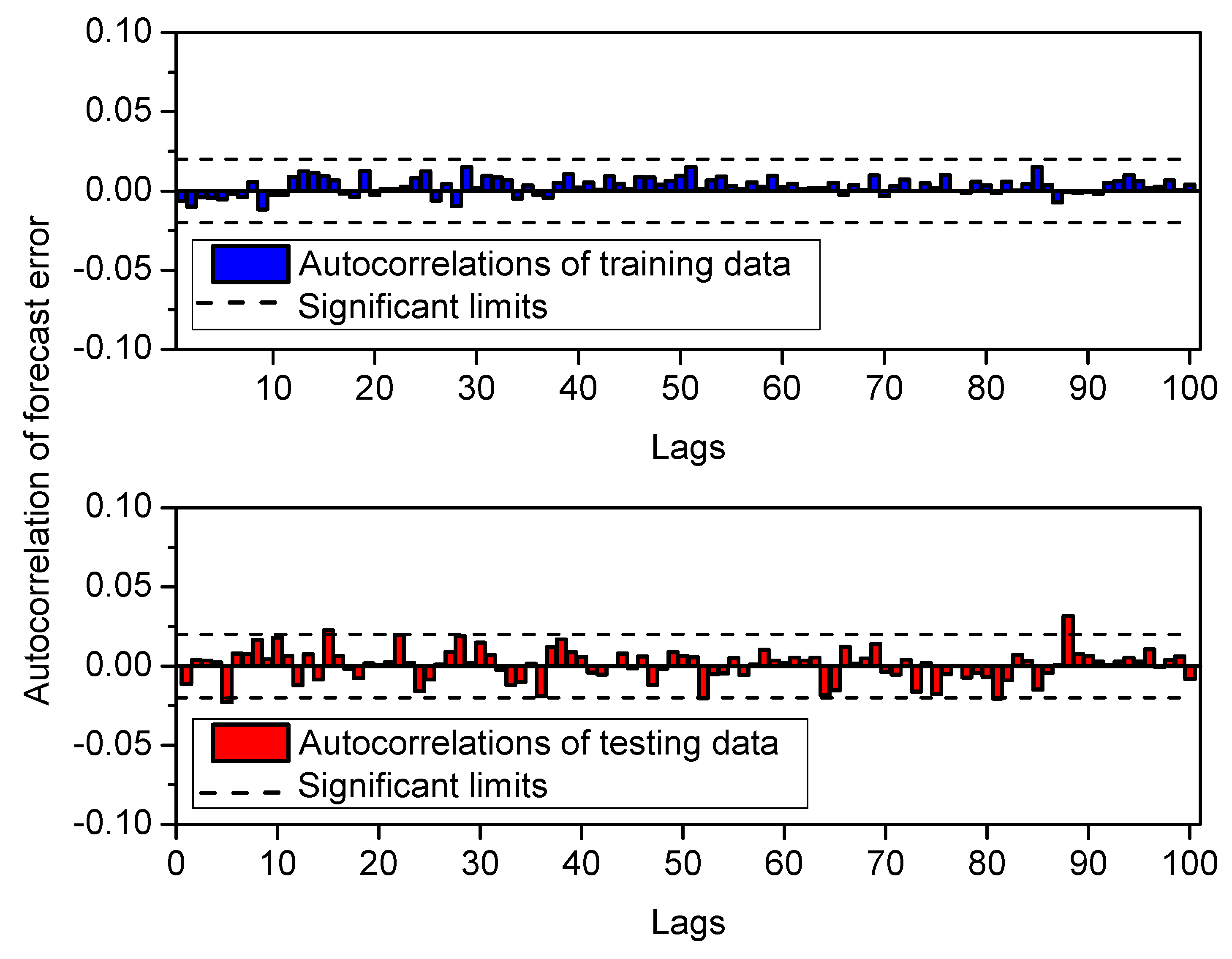
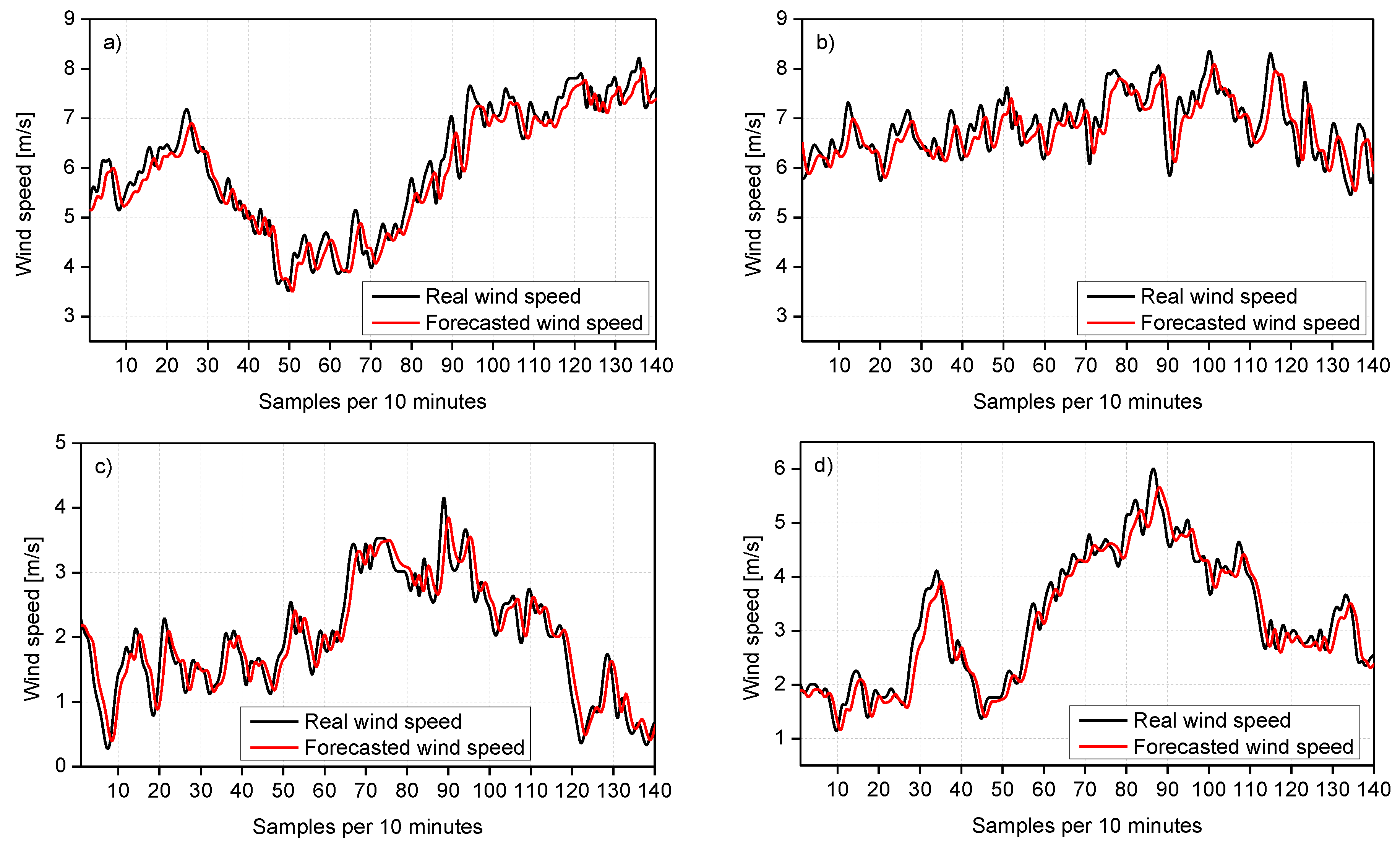
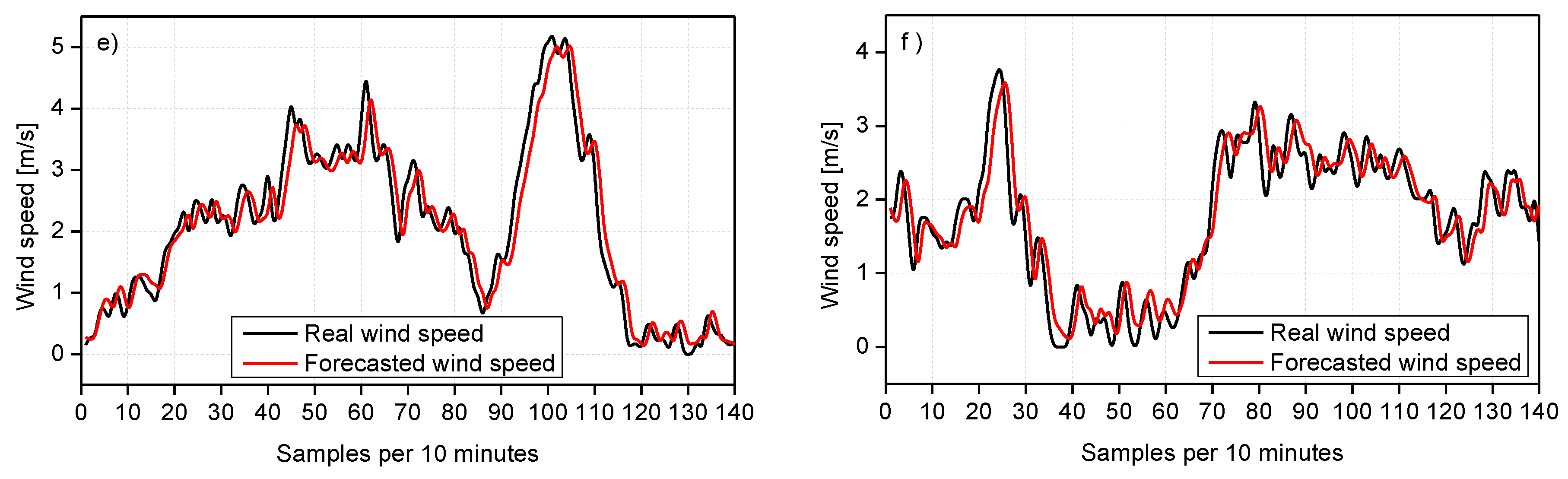
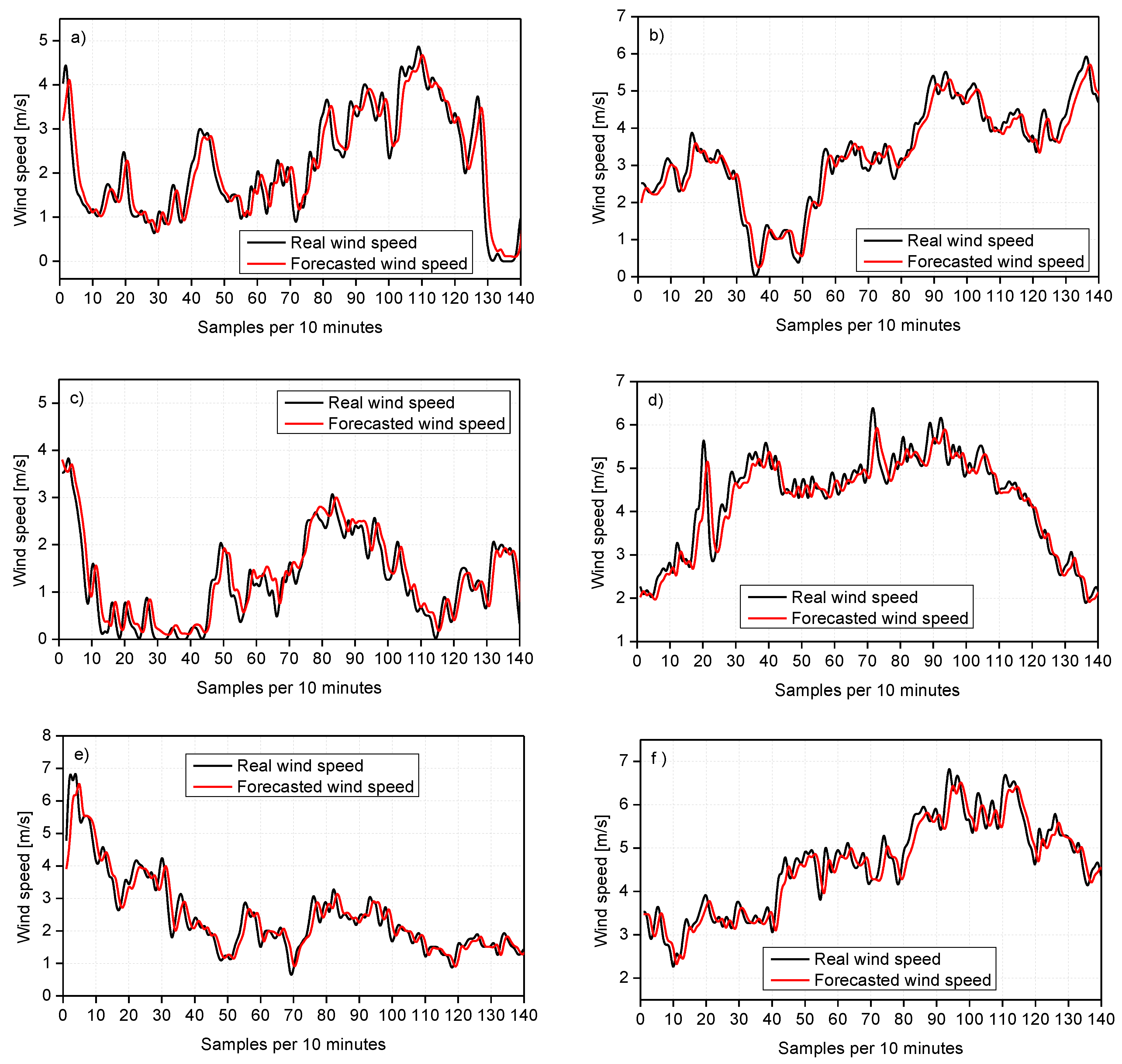
4.4.3. MGGP Forecast Model Validation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- REN21. Renewables 2017: Global Status Report; Technical Report; Renewable Energy Policy Network for the 21st Century: Paris, France, 2017. [Google Scholar]
- IEA. Renewables Information: Overview; Technical Report; International Energy Agency: Paris, France, 2018. [Google Scholar]
- Pérez-Denicia, E.; Fernández-Luqueño, F.; Vilariño-Ayala, D.; Manuel Montaño-Zetina, L.; Alfonso Maldonado-López, L. Renewable energy sources for electricity generation in Mexico: A review. Renew. Sustain. Energy Rev. 2017, 78, 597–613. [Google Scholar] [CrossRef]
- Hernández-Escobedo, Q.; Perea-Moreno, A.J.; Manzano-Agugliaro, F. Wind energy research in Mexico. Renew. Energy 2018, 123, 719–729. [Google Scholar] [CrossRef]
- Guerrero, A.L. CEMIE-EOLICO, Alianza Para la Ciencia y Tecnología del Viento; Technical Report; CEMIE Eólico, Instituto Nacional de Electricidad y Energías Limpias: Cuernava, Mexico, 2016.
- Alemán-Nava, G.S.; Casiano-Flores, V.H.; Cárdenas-Chávez, D.L.; Díaz-Chavez, R.; Scarlat, N.; Mahlknecht, J.; Dallemand, J.F.; Parra, R. Renewable energy research progress in Mexico: A review. Renew. Sustain. Energy Rev. 2014, 32, 140–153. [Google Scholar] [CrossRef]
- Hau, E. Wind Turbines; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Zhou, J.; Erdem, E.; Li, G.; Shi, J. Comprehensive evaluation of wind speed distribution models: A case study for North Dakota sites. Energy Convers. Manag. 2010. [Google Scholar] [CrossRef]
- Gräbner, J.; Jahn, J. Optimization of the distribution of wind speeds using convexly combined Weibull densities. Renew. Wind. Water Sol. 2017, 4, 7. [Google Scholar] [CrossRef]
- Jaramillo, O.A.; Borja, M.A. Wind speed analysis in La Ventosa, Mexico: A bimodal probability distribution case. Renew. Energy 2004. [Google Scholar] [CrossRef]
- Erdem, E.; Shi, J. ARMA based approaches for forecasting the tuple of wind speed and direction. Appl. Energy 2011. [Google Scholar] [CrossRef]
- Wang, J.; Song, Y.; Liu, F.; Hou, R. Analysis and application of forecasting models in wind power integration: A review of multi-step-ahead wind speed forecasting models. Renew. Sustain. Energy Rev. 2016, 60, 960–981. [Google Scholar] [CrossRef]
- Okumus, I.; Dinler, A. Current status of wind energy forecasting and a hybrid method for hourly predictions. Energy Convers. Manag. 2016, 123, 362–371. [Google Scholar] [CrossRef]
- Nowotarski, J.; Weron, R. Recent advances in electricity price forecasting: A review of probabilistic forecasting. Renew. Sustain. Energy Rev. 2018, 81, 1548–1568. [Google Scholar] [CrossRef]
- Archer, C.L.; Vasel-Be-Hagh, A.; Yan, C.; Wu, S.; Pan, Y.; Brodie, J.F.; Maguire, A.E. Review and evaluation of wake loss models for wind energy applications. Appl. Energy 2018, 226, 1187–1207. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J. A distributed approach for wind power probabilistic forecasting considering spatiooral correlation without direct access to off-site information. IEEE Trans. Power Syst. 2018. [Google Scholar] [CrossRef]
- Nielsen, H.A.; Madsen, H.; Nielsen, T.S. Using quanti le regression to extend an existing wind power forecasting system With probabilistic forecasts. Wind Energy 2006. [Google Scholar] [CrossRef]
- Pinson, P.; Kariniotakis, G. Conditional Prediction Intervals of Wind Power Generation. IEEE Trans. Power Syst. 2010. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Shi, J.; Erdem, E. An integrated wind power forecasting methodology: Interval estimation of wind speed, operation probability of wind turbine, and conditional expected wind power output of a wind farm. Int. J. Green Energy 2013. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J. K-nearest neighbors and a kernel density estimator for GEFCom2014 probabilistic wind power forecasting. Int. J. Forecast. 2016. [Google Scholar] [CrossRef]
- Palit, A.K.; Popovic, D. Computational Intelligence in Time Series Forecasting; Springer: Berlin, Germany, 2005. [Google Scholar]
- Cruz May, E.; Ricalde, L.J.; Atoche, E.J.R.; Bassam, A.; Sanchez, E.N. Forecast and Energy Management of a Microgrid with Renewable Energy Sources Using Artificial Intelligence. In Intelligent Computing Systems. ISICS 2018. Communications in Computer and Information Science; Brito-Loeza, C., Espinosa-Romero, A., Eds.; Springer International Publishing: Berlin, Germany, 2018; pp. 81–96. [Google Scholar]
- Zendehboudi, A.; Baseer, M.; Saidur, R. Application of support vector machine models for forecasting solar and wind energy resources: A review. J. Clean. Prod. 2018, 199, 272–285. [Google Scholar] [CrossRef]
- Zhang, F.; Dong, Y.; Zhang, K. A Novel Combined Model Based on an Artificial Intelligence Algorithm—A Case Study on Wind Speed Forecasting in Penglai , China. Sustainability 2016, 8, 555. [Google Scholar] [CrossRef]
- Li, G.; Shi, J.; Zhou, J. Bayesian adaptive combination of short-term wind speed forecasts from neural network models. Renew. Energy 2011. [Google Scholar] [CrossRef]
- Hocaoglu, F.O.; Gerek, Ö.N.; Kurban, M. A novel wind speed modeling approach using atmospheric pressure observations and hidden Markov models. J. Wind Eng. Ind. Aerodyn. 2010. [Google Scholar] [CrossRef]
- Cortés Pérez, E.; Nuñez Rodríguez, A.; Moreno De La Torre, R.E.; Lastres Danguillecourt, O.; Dorrego Portela, J.R. Forecasting of Wind Spedd with a Backpropagation Artificial Neural Network in the Isthmus of Tehuantepec Region in the State of Oaxaca, Mexico. Acta Univ. 2012, 22, 62–68. [Google Scholar]
- Cadenas, E.; Rivera, W.; Campos-Amezcua, R.; Cadenas, R. Wind speed forecasting using the NARX model, case: La Mata, Oaxaca, México. Neural Comput. Appl. 2016, 27, 2417–2428. [Google Scholar] [CrossRef]
- ABS. Guide for Building and Classing Floating Offshore Wind Turbine Installations; Technical Report; American Bureau of Shipping: Houston, TX, USA, 2015. [Google Scholar]
- Van der Tempel, J.; Diepeveen, N.F.B.; Cerda Salzmann, D.J.; de Vries, W.E. Design of Support Structures for Offshore Wind Turbines. In Wind Power Generation and Wind Turbine Design; WIT Press: Southampton, UK, 2006. [Google Scholar]
- Liu, Y.; Chen, D.; Yi, Q.; Li, S. Wind profiles and wave spectra for potential wind farms in South China Sea. Part I: Wind speed profile model. Energies 2017, 10, 125. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, J.; Jiang, H.; Shi, X. Intelligent optimized wind resource assessment and wind turbines selection in Huitengxile of Inner Mongolia, China. Appl. Energy 2013. [Google Scholar] [CrossRef]
- Jaramillo, O.; Borja, M. Bimodal versus Weibull Wind Speed Distributions: An Analysis of Wind Energy Potential in La Venta, Mexico. Wind Eng. 2004. [Google Scholar] [CrossRef]
- Li, M.; Li, X. MEP-type distribution function: A better alternative to Weibull function for wind speed distributions. Renew. Energy 2005. [Google Scholar] [CrossRef]
- Kantar, Y.M.; Usta, I. Analysis of wind speed distributions: Wind distribution function derived from minimum cross entropy principles as better alternative to Weibull function. Energy Convers. Manag. 2008. [Google Scholar] [CrossRef]
- Albani, A.; Ibrahim, M.Z. Wind Energy Potential and Power Law Indexes Assessment for Selected Near-Coastal Sites in Malaysia. Energies 2017, 10, 307. [Google Scholar] [CrossRef]
- Chowdhury, S.; Mehmani, A.; Zhang, J.; Messac, A. Market suitability and performance tradeoffs offered by commercialwind turbines across differingwind regimes. Energies 2016, 9, 352. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Wang, X. Review on probabilistic forecasting of wind power generation. Renew. Sustain. Energy Rev. 2014, 32, 255–270. [Google Scholar] [CrossRef]
- Handbook of Genetic Programming Aplications; Number 2015945115; Springer International Publishing Switzerland: Cham, Switzerland, 2015.
- Do Nascimento Camelo, H.; Lucio, P.; Junior, J.; de Carvalho, P. A hybrid model based on time series models and neural network for forecasting wind speed in the Brazilian northeast region. Sustain. Energy Technol. Assess. 2018, 28, 65–72. [Google Scholar] [CrossRef]
- May Tzuc, O.; Bassam, A.; Mendez-Monroy, P.E.; Sanchez Dominguez, I. Estimation of the operating temperature of photovoltaic modules using artificial intelligence techniques and global sensitivity analysis: A comparative approach. J. Renew. Sustain. Energy 2018, 10, 033503. [Google Scholar] [CrossRef] [Green Version]
- Morris, M. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 9, 161–164. [Google Scholar] [CrossRef]
- Lee, L.; Srivastava, P.K.; Petropoulos, G.P. Overview of Sensitivity Analysis Methods in Earth Observation Modeling; Elsevier Inc.: Amsterdam, The Netherlands, 2017; pp. 3–24. [Google Scholar]
- Sarrazin, F.; Pianosi, F.; Wagener, T. Global Sensitivity Analysis of environmental models: Convergence and validation. Environ. Model. Softw. 2016, 79, 135–152. [Google Scholar] [CrossRef]
- Handbook of Genetic Programming Applications; Chapter GPTIPS 2: An Open-Source Software Platform for Symbolic Data Mining; Springer Publishing International: Berlin, Germany, 2015.
- Pianosi, F.; Sarrazin, F.; Wagener, T. A Matlab toolbox for Global Sensitivity Analysis. Environ. Model. Softw. 2015, 70, 80–85. [Google Scholar] [CrossRef]

| Landscape | |
|---|---|
| Flat land with ice or grass | 0.08–0.12 |
| Sea and coasts | 0.14 |
| Little hilly areas | 0.13–0.16 |
| Rural zones | 0.20 |
| Rugged terrains and forests | 0.20–0.26 |
| Very rugged terrains and cities | 0.25–0.40 |
| Parameters | Measured | ||||||
|---|---|---|---|---|---|---|---|
| WS [m/s] | 4.12 | 2.8458 | 2.8520 | 2.9734 | 3.1067 | 3.4414 | 3.9796 |
| Error [-] | - | 0.3093 | 0.3078 | 0.2783 | 0.2460 | 0.1647 | 0.0341 |
| WTM | h [m] | [m/s] | [m/s] | [m/s] | |||
| Gamesa G58-850 | 54 | 3.0 | 12.0 | 3.9796 | |||
| Unison U54-750 | 60 | 3.0 | 12.0 | 4.2387 | |||
| Dewind D4/48-600 | 70 | 3.0 | 12.0 | 4.6486 | |||
| Variable | Units | min. | max. | mean | Std Dev | WS Cross Corr % | |
|---|---|---|---|---|---|---|---|
| Air temperature | () | [C] | 12.896 | 39.420 | 26.158 | 2.9626 | 11.13% |
| Atmospheric Pressure | () | [mbar] | 998.45 | 1027.55 | 1011.35 | 4.05087 | 21.91% |
| Relative Humidity | () | [%] | 37.8 | 100 | 86.3940 | 8.8614 | 30.53% |
| Wind Direction | () | [Deg] | 0 | 355.2 | 125.0309 | 112.5971 | 5.6566% |
| Air Density | () | [kgm] | 1.12274 | 1.24206 | 1.17845 | 0.01488 | 1.6011% |
| Solar Radiation | () | [Wm] | 0.6 | 1276.90 | 198.3771 | 295.9758 | 18.9817% |
| Rain | () | [mm] | 0 | 22.61 | 0.044 | 0.46154 | 8.641% |
| Weibull PDF | ||||||||||
| h [m] | c | k | R2 | KS | WS [m/s] | WPD [W/m] | ||||
| 26 | 6.1606 | 1.1935 | 0.4107 | 0.9564 | 2.83 | 53.26 | ||||
| 33 | 6.9670 | 1.2075 | 0.3426 | 0.9521 | 3.43 | 94.83 | ||||
| 54 | 7.5346 | 1.3035 | 0.2247 | 0.9242 | 4.12 | 144.17 | ||||
| Bimodal PDF | ||||||||||
| h [m] | A | A | R | KS | WS [m/s] | WPD [W/m] | ||||
| 26 | 0.0167 | 0.5176 | 0.9201 | 1.6791 | 7.3874 | 2.5156 | 0.9443 | 0.0115 | 2.83 | 51.64 |
| 33 | 0.0365 | 0.4949 | 1.8319 | 1.8302 | 9.5346 | 2.8232 | 0.9918 | 0.0117 | 3.43 | 114.71 |
| 54 | 0.4829 | 0.4661 | 2.5970 | 1.8458 | 10.1692 | 3.4685 | 0.9963 | 0.0045 | 4.12 | 181.73 |
| Directions [] | Average Wind Velocity [ms] | Maximum Wind Velocity [ms] | Frequency [Times] | Mean Differences [ms] |
|---|---|---|---|---|
| N | 3.3588 | 11.84 | 6588 | 0.78989 |
| NNE | 3.1223 | 11.08 | 7470 | 0.5533 |
| NE | 2.9911 | 10.07 | 8462 | 0.42205 |
| ENE | 2.8269 | 8.56 | 8091 | 0.25788 |
| E | 1.9709 | 8.81 | 3272 | −0.5981 |
| ESE | 1.4297 | 8.81 | 1830 | −1.1393 |
| SE | 1.1499 | 8.81 | 1884 | −1.4191 |
| SSE | 1.2714 | 8.31 | 1894 | −1.2976 |
| S | 1.3896 | 14.35 | 1916 | −1.1794 |
| SSW | 1.6059 | 11.84 | 1678 | −1.9631 |
| SW | 1.3656 | 11.58 | 1353 | −1.2034 |
| WSW | 1.0818 | 7.05 | 1023 | −1.4872 |
| W | 1.0568 | 6.8 | 1116 | −1.4074 |
| WNW | 1.1616 | 6.3 | 1000 | −1.4074 |
| NW | 2.0518 | 10.07 | 1140 | −0.5172 |
| NNW | 3.9586 | 11.33 | 3518 | 1.3895 |
| Parameter | Minimum | Maximum | Units |
|---|---|---|---|
| Input variables: | |||
| Temperature () | 12.896 | 39.420 | [C] |
| Relative Humidity () | 37.8 | 100 | [%] |
| Atmospheric Pressure () | 998.45 | 1027.55 | [mbar] |
| Global Solar Radiation (G) | 0.6 | 1276.90 | [Wm] |
| 1st Past WS () | 0 | 14.35 | [ms] |
| 2nd Past WS () | 0 | 14.35 | [ms] |
| 3rd Past WS () | 0 | 14.35 | [ms] |
| 4th Past WS () | 0 | 14.35 | [ms] |
| Output variables: | |||
| Wind Speed () | 0 | 14.35 | [ms] |
| Parameter | Value |
|---|---|
| Tournament Size | 10 |
| Function Set | |
| Population Size | 100 |
| Mutation Probabilities | |
| Maximum Tree Depth | 13 |
| Maximum Total Nodes | ∞ |
| Maximum Genes | 30 |
| Maximum Generations | 30 |
| Input Variables | 8 |
| Elite Fractions | |
| ERC Probability | |
| Crossover Probability |
| Statistic Parameter | ARIMA | MGGP | |
|---|---|---|---|
| Train | Test | ||
| RMSE | 0.5922 | 0.51799 | 0.52877 |
| MAE | 0.4348 | 0.38342 | 0.38831 |
| MPE | −8.4893 | −8.5578 | −13.5836 |
| R | 0.9498 | 0.95855 | 0.95668 |
| Input Variables | Units | |
|---|---|---|
| Environmental Temperature | ||
| Relative Humidity | ||
| Atmospheric Pressure | ||
| Global Solar Radiation | G | |
| 1st Past WS | ||
| 2nd Past WS | ||
| 3rd Past WS | ||
| 4th Past WS |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Manrique, L.M.; Macias-Melo, E.V.; May Tzuc, O.; Bassam, A.; Aguilar-Castro, K.M.; Hernández-Pérez, I. Assessment of Resource and Forecast Modeling of Wind Speed through An Evolutionary Programming Approach for the North of Tehuantepec Isthmus (Cuauhtemotzin, Mexico). Energies 2018, 11, 3197. https://doi.org/10.3390/en11113197
López-Manrique LM, Macias-Melo EV, May Tzuc O, Bassam A, Aguilar-Castro KM, Hernández-Pérez I. Assessment of Resource and Forecast Modeling of Wind Speed through An Evolutionary Programming Approach for the North of Tehuantepec Isthmus (Cuauhtemotzin, Mexico). Energies. 2018; 11(11):3197. https://doi.org/10.3390/en11113197
Chicago/Turabian StyleLópez-Manrique, Luis M., E. V. Macias-Melo, O. May Tzuc, A. Bassam, K. M. Aguilar-Castro, and I. Hernández-Pérez. 2018. "Assessment of Resource and Forecast Modeling of Wind Speed through An Evolutionary Programming Approach for the North of Tehuantepec Isthmus (Cuauhtemotzin, Mexico)" Energies 11, no. 11: 3197. https://doi.org/10.3390/en11113197
APA StyleLópez-Manrique, L. M., Macias-Melo, E. V., May Tzuc, O., Bassam, A., Aguilar-Castro, K. M., & Hernández-Pérez, I. (2018). Assessment of Resource and Forecast Modeling of Wind Speed through An Evolutionary Programming Approach for the North of Tehuantepec Isthmus (Cuauhtemotzin, Mexico). Energies, 11(11), 3197. https://doi.org/10.3390/en11113197