Comparison of NARX and Dual Polarization Models for Estimation of the VRLA Battery Charging/Discharging Dynamics in Pulse Cycle

Abstract

The following work presents the model-assisted research on Valve-Regulated Lead-Acid (VRLA) Absorbent Glass Mat (AGM) battery in pulse operation cycle. The experimental research was conducted for a constant value of State of Charge (SOC) of the battery, for values ranging from 0.2 to 0.8. Based on the conducted test stand research, the parameters of the battery were identified, which were later used to model the battery using the equivalent circuit based on dual polarization (DP) model with double Resistive-Capacitive (RC) loop. Simulations were performed for the identified parameters of the battery which are described by the general form of the polynomial. The second part contains the research on utilization of Nonlinear AutoRegressive eXogenous (NARX) recurrent neural network to predict SOC and a terminal voltage of the battery. Obtained validation results with the use of the identified parameters of the double RC loop and NARX model were discussed in the following work. The article also features the advantages and disadvantages of NARX model and DP model utilization for the use of in Battery Managements Systems (BMS) and micro-installations based on renewable energy sources. Furthermore, the advantages of the addition of more RC loops to describe the dynamic states of batteries in pulse states were discussed in the article.

1. Introduction

Currently more and more attention is given to distributed energy generation systems [1,2,3,4,5,6,7,8,9] and alternative routes of development for conventional, hybrid and electric vehicles [10,11,12,13,14,15,16,17,18]. The balanced development of distributed technologies and polygeneration systems with energy storages are directly related to the climate change and the energy policy [19,20,21,22], especially for members of the European Union. From the user’s perspective, the most important criteria of choice for the given type of energy storage is the price per kWh. Currently, on the Polish market, the price for 1 kWh for electrochemical batteries is within 60–150 euro/kWh [23,24,25,26] (e.g., lead-acid batteries or Valve-Regulated Lead-Acid (VRLA) Absorbent Glass Mat (AGM) batteries) and more than 300 euro/kWh (Li-ion battery) [26]. Due to this, VRLA AGM batteries have found a wide range of applications in the industry [27,28,29,30,31,32,33,34,35,36], e.g., in forklifts where VRLA batteries are used as ballast, in start-up of gas engines [27], Start and Stop systems in vehicles with conventional drivetrains [15] and cogeneration systems where the gas engines have been employed [9], as well as other distributed energy generation systems and emergency power supply systems connected with auxiliary electricity generators (e.g., in hospitals).

Battery management system (BMS) is a system that manages energy storage [37], e.g., battery, ultracapacitor or hybrid system [38,39,40,41,42,43], by monitoring its state, calculating and reporting secondary data, controlling its environment, authenticating it and balancing it. All of this is performed to protect the battery from operating outside its Safe Operating Area (SOA) defined as the voltage and current conditions over which the device can be expected to operate without self-damage. BMS ensures the optimal usage of the internal energy of the battery, achieved by monitoring and controlling the battery’s charging and discharging process [44]. To improve algorithms for prediction and control in Battery Management Systems (BMS) for distributed systems, it is crucial to know the operating characteristics of typical electrochemical batteries, which can be supported by mathematical models [45].

This approach plays an essential role in hybrid systems [46,47,48,49,50]. The research of a dynamic operation of an electrochemical battery in a specific random, pseudo-random, pulse and Hybrid Pulse Power Characterization (HPPC) cycle [51,52,53], supported by a mathematical model, e.g., physical model [43,54,55,56,57], neural network model [45], AutoRegressive–Moving-Average (ARMA) model, fuzzy model [58,59], an adaptation model based on the Kalman filter [60,61,62,63,64,65,66,67,68] can give answers to different questions regarding the operation of batteries [69,70,71,72,73] in technical facilities. It should be also emphasized that the energy storage modeling has recently had increasing interest connected with new developments in the field of hybrid, electric vehicles [74] and heavy-duty vehicles or polygeneration systems [75].

The charging and discharging processes in batteries are nonlinear as a result of activation polarization and concentration polarization [63]. In order to replicate the mentioned polarization phenomena, a correct replacement model for the battery has to be adopted. The science literature provides a number of models, such as: The Resistive-Capacitive (RC) model [63,76,77], Thevenin model [78,79], a Partnership for a New Generation of Vehicle (PNGV) model [80,81,82], dual polarization (DP) model [63,83,84,85,86,87,88,89] and many more [89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109]. From the mentioned models, the best results of battery parameters and SOC estimation are achieved with the DP model [63].

In the following article, authors utilized an identified DP model to simulate the battery terminal voltage in pulse for various battery SOC values, ranging from 0.2 to 0.8.

In the second part of the work, a Nonlinear AutoRegressive eXogenous model (NARX) in the form of the recurrent artificial neural network (R–ANN) was used to the estimation of the voltage on the VRLA battery terminals. Mostly, ANN models simplify the identification procedure with high accuracy [30,69]. They have distinct advantages over linear identification methods, i.e., the approximation of multivariable nonlinear functions, the simple gradient-based adaptation of model parameters and a rapid calculation of ANN equations. In contrast to energy-balance analytical models [44], the design procedure of the ANN does not demand an exact knowledge of model physical equations, and physical parameters that describe the model, but only values of model variables in the form of the cause-effect relationships.

In energy storage systems usefulness of standard ANNs for identification were proposed in the form of feed-forward models [66], recurrent models [110,111] and recently Long-Short-Term-Memory (LSTM) recurrent models [112]. In particular, interesting for our research are Recurrent Artificial Neural Networks (R–ANN) where connections between units form a directed cycle. Previous research [30] shows, that with properly chosen and pre-processed data, system parameters, and operating conditions, recurrent ANN model can be used for prediction, to some extent, for energy storage performance under a wide variety of operating conditions. Considered in this work, NARX model based on R–ANN plays a significant role because it can be used as a predictor, nonlinear filter and as a nonlinear model of the dynamical system which can be later used in model-based control algorithms [113,114] in the BMS systems. R–ANNs exhibit dynamic temporal behavior, a property that can be utilized for the prediction of the energy storage system performance parameters in subsequent recharging cycles [111].

Different research works study usability of NARX models for the State-of-Charge (SOC), terminals voltage and State-of-Health (SOH) estimation. The comparison of feed-forward ANN and recurrent ANN to model SOC of a lithium-ion (Li-ion) battery is given in Reference [115]. In Reference [116] NARX model is used to estimate of the lithium-iron-phosphate (LiFePO₄) battery voltage using SOC and current load signal, for the electric vehicle. In Reference [45] there is reported SOC and SOH estimation based on dynamically driven NARX recurrent networks designed for both state of charge (SOC) and State of Health (SOH) estimation for LiFePO₄ and lithium titanate (LTO) batteries. Authors of Reference [114] describe the research on SOC/SOH monitoring of Li-ion batteries with the hybrid method, combining Electrochemical Impedance Spectroscopy (EIS) models and R–ANNs. Another hybrid method is presented in Reference [117] where wavelet-neural-network-based NARX battery model combined with particle filter estimator is used for the State-Of-Energy (SOE) estimation of the LiFePO₄ battery. An interesting approach is discussed in Reference [118] where dual neural network fusion model is used to estimate the relation between Open Circuit Voltage (OCV) and SOC.

The structure of this work is the following. In Section 2 the test stand of VRLA AGM battery has been presented, in Section 3 parameter estimation methods based on NARX model and DP physical model have been discussed. Section 4 presents the main simulation results from DP model (for identified parameters) and NARX model which are subsequently validated and compared against experimental results. Finally, in Section 5, the main conclusions are given.

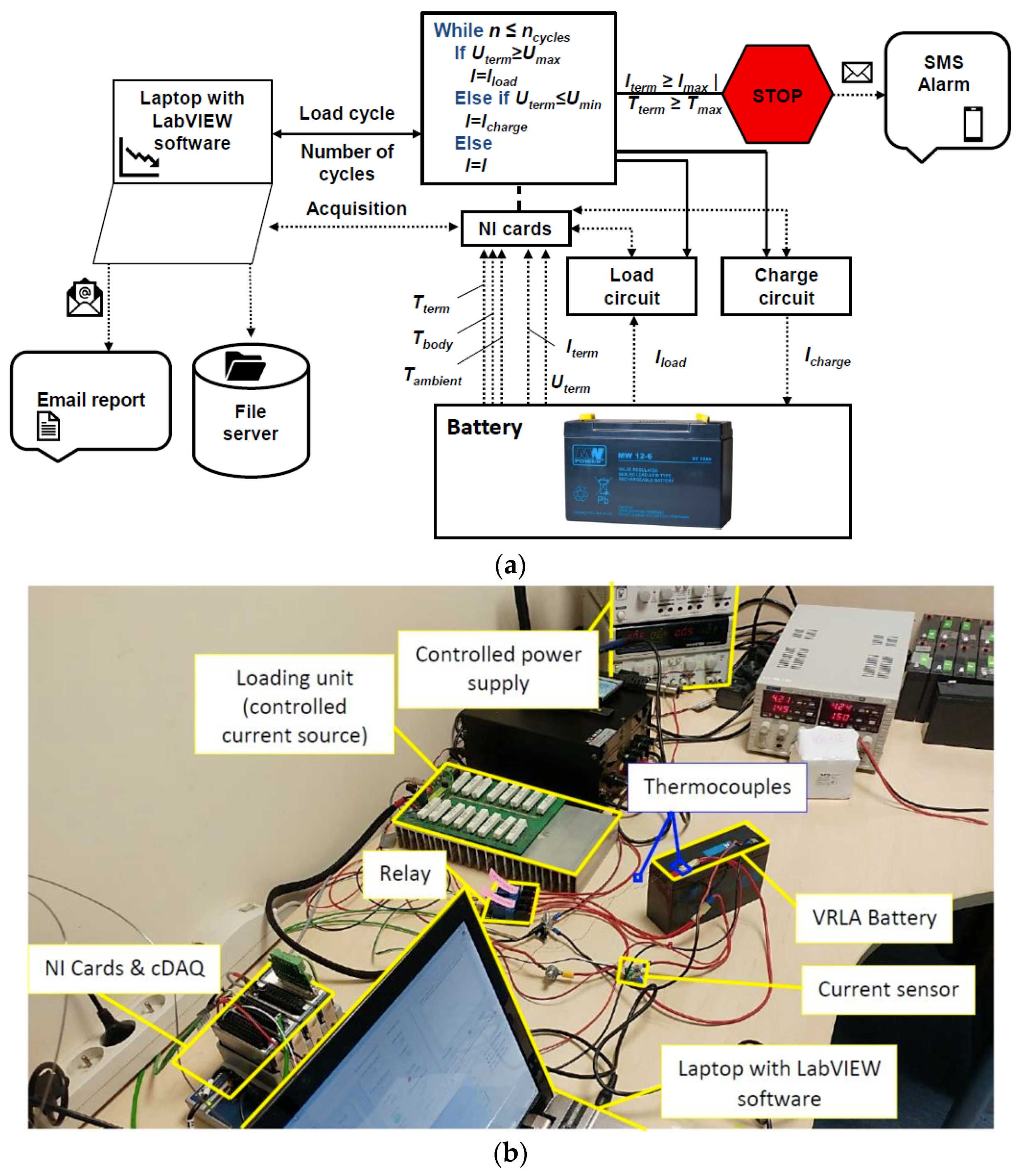
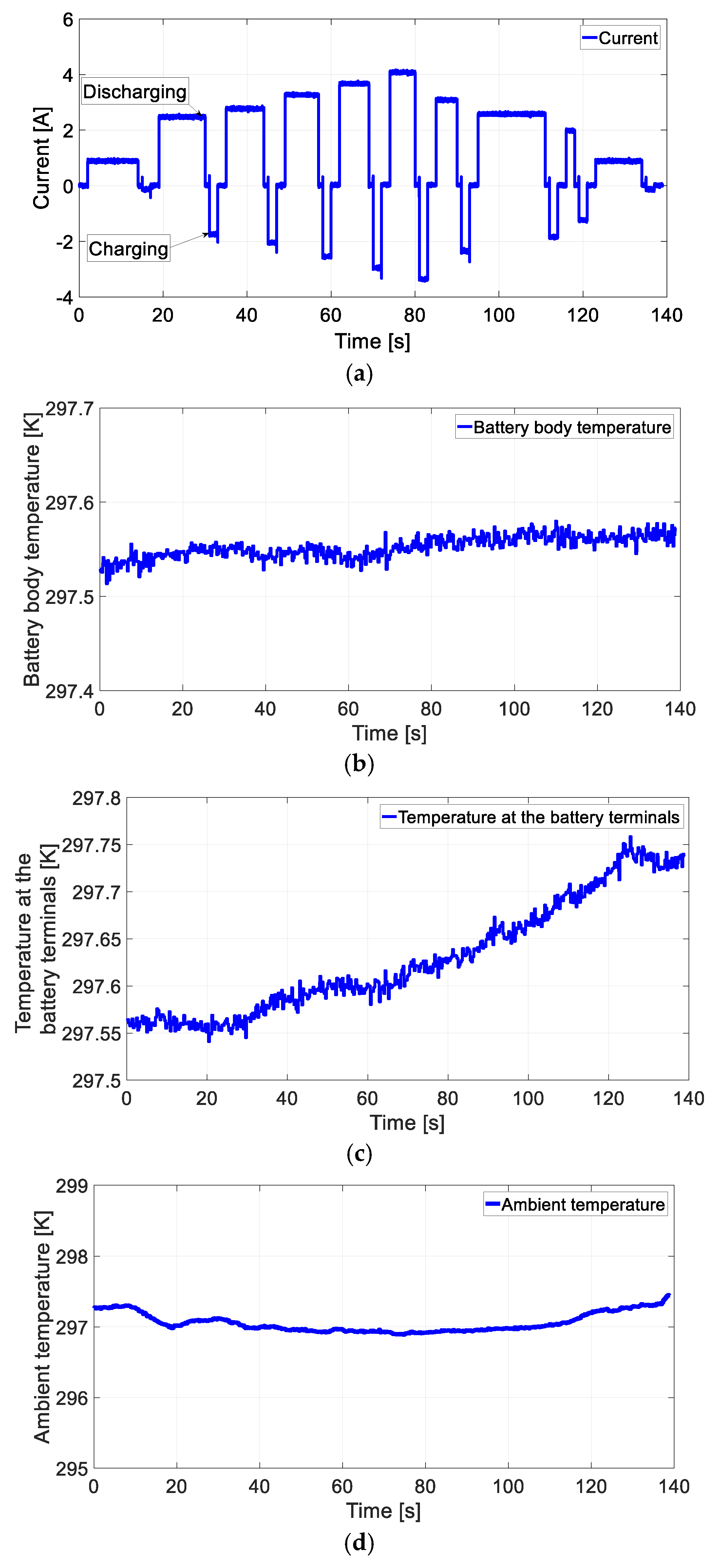
2. Test Stand Description

The following section contains the description of the test stand used to perform research on VRLA AGM battery. The technical specification of VRLA battery cell for experimental work is as follows: Nominal voltage: 6 V; nominal capacity: 7.2 Ah (1 C current was equal to 7.2 A); electrolyte trapped in a separator made of glass mat: Absorbent Glass Mat (AGM); positive electrode material: PbO₂; negative electrode material: Pb.

The test stand consisted of the following elements: PC class computer with LabVIEW application for acquiring selected research data with use of National Instruments measurement modules including: NI 9206 for voltage measurement on battery posts, NI 9213 for temperature measurements of the environment, battery terminals, and battery case. Three thermocouples of type K were used to measure the temperatures (T_term—the temperature at the terminals, T_body—body temperature, T_ambient—ambient temperature, see Figure 1a,b). The test stand also featured a NI 9263 analog output module for control over current load generating unit, which allowed for the generation of pulse load profile. Finally, a NI 9401 digital TTL input/output module was used for relay switching between charge and load circuits. Total electric power of a single load circuit reached around 1 kWe. Use of two custom load generation units allowed for the increase of total electric power to about 2 kWe. Currently, use of up to six load generation units is possible, which can operate together or independently creating independent measurement tracks. The presented test stand is currently being expanded to six independent, parallel measurement tracks for electrochemical batteries and ultracapacitors, which can be tested independently or in one of two hybrid configurations: Parallel without universal bidirectional DC-DC converter such as described in Reference [119] (without ability to control the load distribution between battery and ultracapacitor) and with two-way, universal bidirectional DC/DC converters (possible control overload distribution).

The developed test stand features several safety precautions against temperature, current and voltage exceedance—the stand automatically disconnects the power sources if any of the monitored values exceeds the set limits, which prevents the test stand from damage, which is crucial during long term operational research [29]. The measurement stand allows for email reporting over TCP/IP connection in case of warning or alarm value states, as well as SMS notifications with use of internet SMS gates.

The test stand was designed for long-term operational research measurements of electrochemical batteries, ultracapacitors, and hybrid energy storage systems containing a battery and an ultracapacitor, subjected to pulse work cycles and industrial work cycles, such as HPPC. The stand allows for conduction of wide variety of operational tests, including complete operational wear of the tested battery or ultracapacitor (operational capacity during tests is close to 0 or about several percent of the nominal capacity).

Figure 1a presents the diagram of the tests stand with parameters acquired during measurements of the battery in a pulse work cycle for SOC ranging from 0.8 to 0.2. Figure 1b presents a photograph of the test and control stand for a single controllable current load source.

The measurement cycle was set up so before each measurement, the batter was fully charged, then discharged with one-hour current value to the set SOC value. After reaching the set SOC and SOC ≈ const, the battery was subjected to pulse current values (Figure 2a). In the next stage, the battery was discharged by 10% SOC and the load cycle was repeated. The described cycle was repeated for SOC values ranging from SOC = 0.8 to SOC = 0.2. Figure 2a presents the current characteristic in the pulse cycle. Figure 2b–d show plots for: Battery body temperature (Figure 2b), the temperature at the battery terminals (Figure 2c) in pulse cycle and an ambient temperature (Figure 2d).

3. Battery Parameters Estimation Based on NARX Model and DP Physical Model

The following section contains the description of adopted models: NARX and DP used to estimate voltage values in pulse cycles.

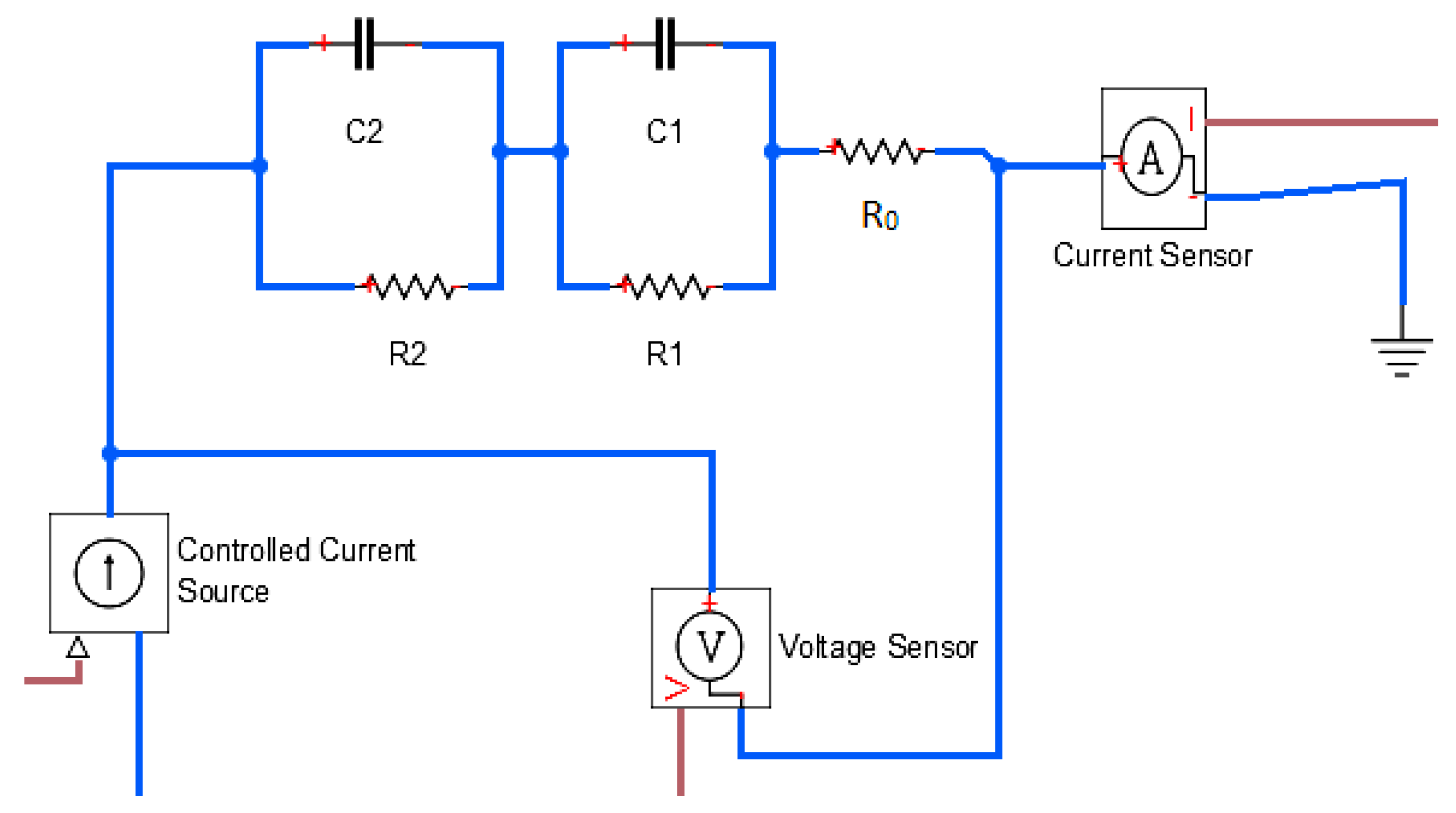
3.1. Dual Polarization (DP) Model Description and Parameters Identification

The following subsection presents the adopted equivalent circuit of VRLA AGM battery model with the internal resistance of the battery included and a model accounting for changes in the activation and concentration polarizations in pulse work cycle, featuring a double RC loop. Figure 3 presents the equivalent circuit of the battery of the adopted double polarization (DP) model with two RC loops.

The diagram presented in Figure 3 contains the following components: Open circuit voltage U_OCV(SOC) (U_OCV, measured in the work cycle during relaxation stage for the given SOC value when no charging/discharging occurs or is determined during identification); R₀(SOC)—internal resistance (ohmic resistance); activation polarization resistance R₁(SOC); R₂(SOC)—density polarization resistance. The diagram also features capacitances C₁(SOC) and C₂(SOC), which describe the transitional states during supplying power to the battery or from the battery as well as the activation and density polarizations. Currents I_b1 and I_b2 are the electric currents flowing through C₁ and C₂. U₁ and U₂ are the voltage drops occurring in the first and second loop.

Based on analysis of Figure 3, an equation describing the behavior of the DP model can be written:

$$\{\begin{array}{l}{\dot{U}}_1=-{\left(R_1{C}_1\right)}^{-1}{U}_1+C_1^{-1}{I}_b\hfill \\ {\dot{U}}_2=-{\left(R_2{C}_2\right)}^{-1}{U}_2+C_2^{-1}{I}_b\hfill \\ 0=-R_0^{-1}{U}_0+I_b\hfill \\ U_t=U_{OCV}-U_1-U_2-U_0\hfill \end{array}$$

(1)

The battery’s SOC is the ratio of its effective capacity Q_bat to nominal capacity Q_n described as:

$$SOC(t)=SO{C}_0\pm Q_{bat}{Q}_n^{-1}=SO{C}_0\pm Q_n^{-1}{\displaystyle \underset{0}{\overset{t}{\int }}{\eta }_c(I_b)\cdot I_b(t)dt}$$

(2)

where SOC₀ is the initial state of charge for time t = t₀, η_c is the columbic efficiency, I_b is the battery charging (–)/discharging (+) current at time t.

The open circuit voltage can be expressed as follows:

$$U_{OCV}=EMF\left(SOC\right)=EM{F}_{\min }+\mathsf{\Delta }{U}_{t}SOC=EM{F}_{\min }+(EM{F}_{\max }-EM{F}_{\min })SOC$$

(3)

The EMF_min and EMF_max values in Equation (3) can be determined on the basis of experiments from the following equation:

$$U_0=EMF\pm I_b{R}_0\Rightarrow EMF=U_0\mp I_b{R}_0$$

(4)

where R₀ is the internal resistance of the battery.

Based on the experimental research for I = I_ch = I_dch = 1 C the value of R₀ can be calculated as follows:

$$R_0=\left(\left|U_{ch}\right|-\left|U_{dch}\right|\right)/2I_b$$

(5)

where U_ch is the charging voltage and U_dch is the discharging voltage.

Dependencies Equations (3)–(5) present simple, technical, rough methods for estimating battery parameters. Their advantage is simplicity and rapid calculation but the drawback is low accuracy.

For VRLA batteries, the linear EMF(SOC) relationship can be roughly assumed, in the case of lithium batteries, these characteristics will be non-linear [60,63]. In further analyses, only EMF(SOC) characteristics derived from the experimental research were considered.

An alternative to the simple estimation of the dependencies (3)–(5) are other methods, e.g., an identification by using the DP and NARX models presented in Section 3.1.1 and Section 3.2, respectively.

3.1.1. Parameters Identification of DP Model

In the set of differential equations representing the model structure consisting of two RC loops and resistance R₀ connected in series and electromotive force source, a total of six parameters are present (R₁, R₂, C₁, C₂, R₀, U_OCV) that require identification. In the DP model project, the differential equations are generated automatically by Matlab Simscape software (a fragment of the project is presented in Figure 4) or they can be designated using traditional methods.

Current values acquired during measurements is used as input for the double RC loop model (DP). The voltage values at battery terminals are the result of the differential equations. Based on the assumed values of the six model parameters (R₁, R₂, C₁, C₂, R₀, U_OCV) the calculated voltage will differ from the voltage acquired during measurements.

The goal of identification is to find the set of the six parameters (R₁, R₂, C₁, C₂, R₀, U_OCV) so that the calculated voltage values differ as little as possible. The measure of identification error is the value of integral of squared error e² = (y* − y(Θ, x, u))² between the value of calculated function y(Θ, x, u) and obtained from measurements y*. The identification process is conducted with use of “nonlinear data-fitting” procedure, which minimizes the value of integral J, presented in dependency (6), of the squared error e² by iterative adaptation of ΔΘ value of parameters (R₁, R₂, C₁, C₂, R₀, U_OCV), ΔΘ = [ΔR₁, ΔR₂, ΔC₁, ΔC₂, ΔR₀, ΔU_OCV] with use of $\nabla J$ gradient and hessian H.

$$J={\displaystyle \underset{t_0}{\overset{t_{end}}{\int }}{e}^{2}dt}={\displaystyle \underset{t_0}{\overset{t_{end}}{\int }}{\left(y*-y(\theta ,x,u)\right)}^{2}dt}$$

(6)

Knowing that:

$$\frac{\partial J}{\partial \theta }=-{\displaystyle \underset{t_0}{\overset{t_{end}}{\int }}2e\frac{\partial y(\theta ,x,u)}{\partial \theta }dt}$$

(7)

Function J reaches minimum when the following condition fulfilled:

$$J=\min \iff \frac{J(\theta +\Delta \theta )-J(\theta )}{\Delta \theta }=\frac{\partial J}{\partial \theta }\Delta \theta +\frac{1}{2}\frac{{\partial }^{2}J}{\partial {\theta }^2}\Delta {\theta }^2=0\Rightarrow \Delta \theta =-2\frac{\frac{\partial J}{\partial \theta }}{\frac{{\partial }^{2}J}{\partial {\theta }^2}}=-2\frac{\nabla J}{H}$$

(8)

To modify the values of parameters Θ = [R₁, R₂, C₁, C₂, R₀, U_OCV] the Levenberg–Marquardt error back propagation method was used, which uses properly weighted approximations of gradient of the minimized function $\nabla J$ and its hessian H with use of Jacobian calculated at end of each iteration based on the obtained change of error Δe, related to vector of change of parameters ΔΘ.

Adaptation of parameter values ΔΘ is conducted iteratively until the stationarity of the integral value J of root mean squared error e² is obtained, meaning a minimum was reached. Stationarity is reached when the change of the relative value |ΔJ/J| < ε. In the research the value assumed was ε = 1 × 10⁹.

The identification procedure also requires a correct assumption of initial parameters Θ₀ = [R₁₀, R₂₀, C₁₀, C₂₀, R₀, U_OCV0], as in gradient methods a risk of founding a suboptimal local solution instead of the optimal solution exists. In the conducted research the assumed values were equal to order of magnitude of typical values for the given battery type Θ₀ = [R₁₀ = 1 × 10¹, R₂₀ = 1 × 10⁻², C₁₀ = 1 × 10¹, C₂₀ = 1.0, R₀ = 1 × 10⁻², U_OCV0 = 6.0].

Furthermore, the identification procedure has a condition imposed, that all values of parameter vectors have to be positive.

The identified parameters of the DP model for SOC values ranging from 0.2 to 0.8 was described by a polynomial function in the following form:

$$\begin{array}{l}{R}_O(SOC)=A_{R0}SO{C}^6+B_{R0}SO{C}^5+C_{R0}SO{C}^4+D_{R0}SO{C}^3+E_{R0}SO{C}^2+F_{R0}SO{C}^1+G_{R0}\\ R_1(SOC)=A_{R1}SO{C}^1+B_{R1}\\ R_2(SOC)=A_{R2}SO{C}^6+B_{R2}SO{C}^5+C_{R2}SO{C}^4+D_{R2}SO{C}^3+E_{R2}SO{C}^2+F_{R2}SO{C}^1+G_{R2}\\ C_1(SOC)=A_{C1}SO{C}^6+B_{C1}SO{C}^5+C_{C1}SO{C}^4+D_{C1}SO{C}^3+E_{C1}SO{C}^2+F_{C1}SO{C}^1+G_{C1}\\ C_2(SOC)=A_{C2}SO{C}^5+B_{C2}SO{C}^4+C_{C2}SO{C}^3+D_{C2}SO{C}^2+E_{C2}SO{C}^1+F_{C2}\\ U_{OCV}(SOC)=A_{U_{OCV}}SO{C}^4+B_{U_{OCV}}SO{C}^3+C_{U_{OCV}}SO{C}^2+D_{U_{OCV}}SOC+E_{U_{OCV}}\end{array}$$

(9)

A similar description of the dependency (9) of the general form of parameter polynomial in substitute diagram of the battery with the use of iteration-approximation method was presented in Reference [56]. The work [85] contains the description of DP model parameters identified with the general form of the polynomial equation.

Table 1. Values of polynomial coefficients from dependency (9) for DP model.

Coefficient Name	R0	R1	R2	C1	C2	UOCV
A	−42	−3.9 × 10−5	110	6 × 108	−8.9 × 104	14
B	140	3.1 × 105	−320	−1.4 × 109	2.3 × 105	−27
C	−200	–	390	1 × 109	−2.2 × 105	17
D	140	–	−250	3.6 × 108	1.1 × 105	−3.3
E	−57	–	92	1.8 × 108	−2.3 × 104	5.8
F	11	–	−18	–3.8 × 107	2 × 103	–
G	−0.85	–	1.4	3.5 × 106	–	–

contains the coefficient values of the polynomial of the identified parameters: R₁(SOC), R₂(SOC), C₁(SOC), C₂(SOC), R₀(SOC) and U_OCV(SOC) presented in dependency (9).

Figure 5 presents graphs of the identified parameters, as follows: U_OCV = f(SOC) (Figure 5a), R₀ = f(SOC) (Figure 5b), R₁ = f(SOC) (Figure 5c), R₂ = f(SOC) (Figure 5d), C₁ = f(SOC) (Figure 5e) and C₂ = f(SOC) (Figure 5f).

3.2. NARX Model Description

NARX model is the nonlinear extension of the linear AutoRegressive with eXogenous input (ARX) model, which is commonly used in time-series modeling [120]. The NARX model is an input-output recursive model where the current output is described with a nonlinear functional expansion of lagged input and output signals, plus additive noise. Several classes of models have been used for NARX identification, e.g., radial basis functions [121], multilayer perceptrons (MLP) [122], or polynomial models [123].

In the case considered in this paper, there is given an electrochemical energy storage system in the form of a VRLA AGM battery, that can be recharged in pulse cycles at the laboratory stand. Measured are: The voltage at the terminals U_term(t), current load I_load(t), ambient temperature T_ambient(t), the battery body temperature T_body(t) and the temperature at battery terminals T_term(t).

The voltage signal can be predicted using the delayed voltage signal, current load signal, and measured temperature signals. As it was described in References [116,117], the addition of measurements of the temperature of the battery terminals, and battery body to the identified model can improve its prediction properties. Therefore, the defining equation of the nonlinear part of the NARX model of the considered VRLA battery can be written as follows:

$$\begin{array}{l}\begin{array}{cc}{U}_{termNN}(k)& =f(U_{termNN}(k-1),\dots ,U_{termNN}(k-n_U),I_{laod}(k),\dots .,I_{laod}(k-n_I)\end{array}\\ \begin{array}{cc}& T_{ambient}(k),\dots ,\end{array}{T}_{ambient}(k-n_a),T_{body}(k),\dots ,T_{body}(k-n_b),\\ \begin{array}{cc}& T_{term}(k),\dots ,\end{array}{T}_{term}(k-n_t))\end{array}$$

(10)

where: U_termNN(k) is the NARX estimated output (voltage) signal at step k, n_u is the number of delayed steps of output (poles) signal, n_I, n_a, n_b, n_t are the number of delayed steps of input signals (current load, ambient temperature, battery body temperature, temperature at battery terminals, respectively).

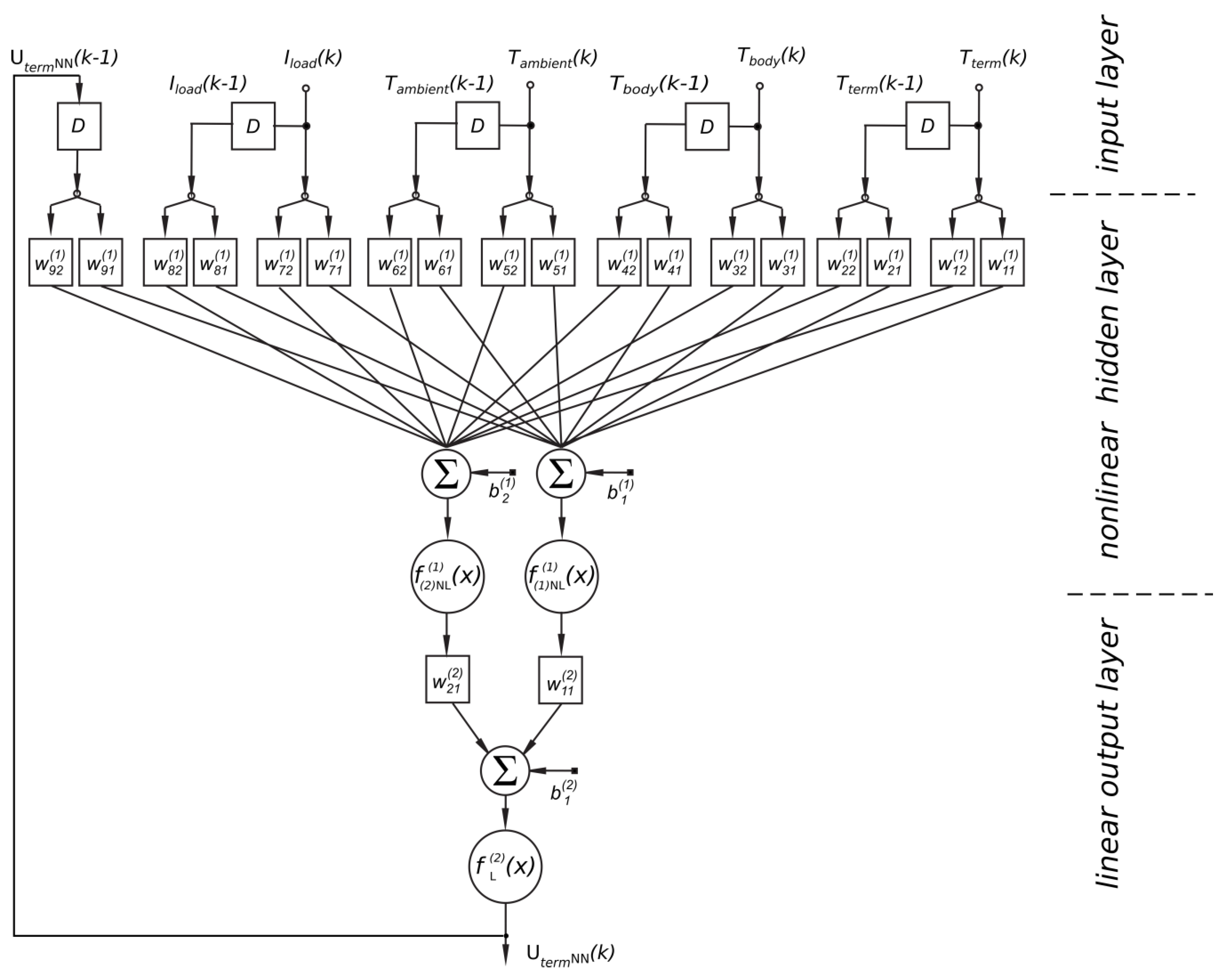
3.2.1. NARX-ANN Architecture

In the considered case, the voltage signal estimation of a VRLA AGM battery can be defined as follows: Under given assumptions, the problem is to predict changes of the voltage at the terminals in pulse cycles with NARX model using the recurrent artificial neural network, based on performed measurements.

In the research there were used Recurrent Artificial Neural Networks (R–ANN) where connections between units form a directed cycle. Due to the internal feedback loops, such networks exhibit dynamic temporal behavior, a property that can be utilized for the prediction of the voltage signal of the energy storage system in pulse cycles. With properly chosen battery data, system parameters and operating conditions, R–ANN model can be used in prediction to some extent a battery performance under a variety of operating conditions.

Therefore, taking into consideration the NARX model Equation (10), the recurrent neural network inputs were chosen as follows:

• U_termNN(k − 1), ..., U_termNN(k − n_u): Previous values of outputs on which the actual output depends. These inputs are generated in the recurrent loop with tapped delay lines.
• I_load(k), ..., I_load(k − n_I): Previous and delayed values of the current load signal.
• T_ambient(k), ..., T_ambient(k − n_a): Previous, delayed values of the ambient temperature.
• T_body(k), ..., T_body(k − n_b): Previous, delayed values of the battery body temperature.
• T_term(k), ..., T_term(k − n_t): Previous, delayed temperature at battery terminals.

Figure 6 presents a recurrent architecture of the considered NARX artificial neural network (NARX-ANN), with parameters of Equation (10) chosen as n_u = 1, n_I = 1, n_a = 1, n_b = 1, n_t = 1.

Presented NARX-ANN has one nonlinear hidden layer (Figure 6) with nonlinear neurons described by a sigmoidal activation function:

$$y^{(1)}{}_{(j)NL}(k)=f^{(1)}{}_{(j)NL}(x^{(1)}{}_{(j)NL},k)=\tan sig(x^{(1)}{}_{(j)NL},k),f^{(1)}{{}_{(j)}}_{NL}\in [-1,1]$$

(11)

where $y^{(1)}{}_{(j)NL}(k)$ is the output signal of the j-th neuron in the 1st layer, and $x^{(1)}{}_{(j)NL}(k)$ is the input signal to the j-th neuron in 1st layer, defined as

$$x^{(1)}{}_{(n)NL}(k)=b^{(1)}{}_{(n)}+w^{(1)}{}_{p+1,n}{y}^{(2)}{}_L(k-1)+{\displaystyle \sum _{i=1}^p{w}^{(1)}{}_{i,n}{x}_i}(k)$$

(12)

and n is the number of neurons in nonlinear layer, p is the number of neuron inputs in nonlinear hidden layer, $w^{(1)}{}_{i,j}$ is the weight of the i-th input to j-th neuron in the 1st layer, x_i is the i-th input to the network (with delayed inputs), $b^{(1)}{}_{(n)}$ is the threshold offset of the n-th neuron in the 1st layer. The second term of Equation (12) describes the recurrent feedback loop with tapped delay line from output to input, in case when n_u = 1.

The output of the network is $y^{(2)}{}_L(k)$ and it is also the output signal from 2nd layer, which is a linear output layer (Figure 6), with one neuron described by a linear activation function as follows

$$y^{(2)}{}_L(k)=f^{(2)}{}_L(x^{(2)}{}_L,k)=x^{(2)}{}_L(k),f^{(2)}{}_L\in R$$

(13)

where $x^{(2)}{}_L(k)$ is the input signal to the neuron in 2nd layer, defined as

$$x^{(2)}{}_L(k)=b^{(2)}+{\displaystyle \sum _{i=1}^n{w}^{(2)}{}_{i,1}{y}^{(1)}{}_{(i)NL}}(k)$$

(14)

and, $w^{(2)}{}_{i,1}$ is the weight of the i-th input to neuron in 2nd layer, $b^{(2)}$ is the threshold offset of the neuron in 2nd layer.

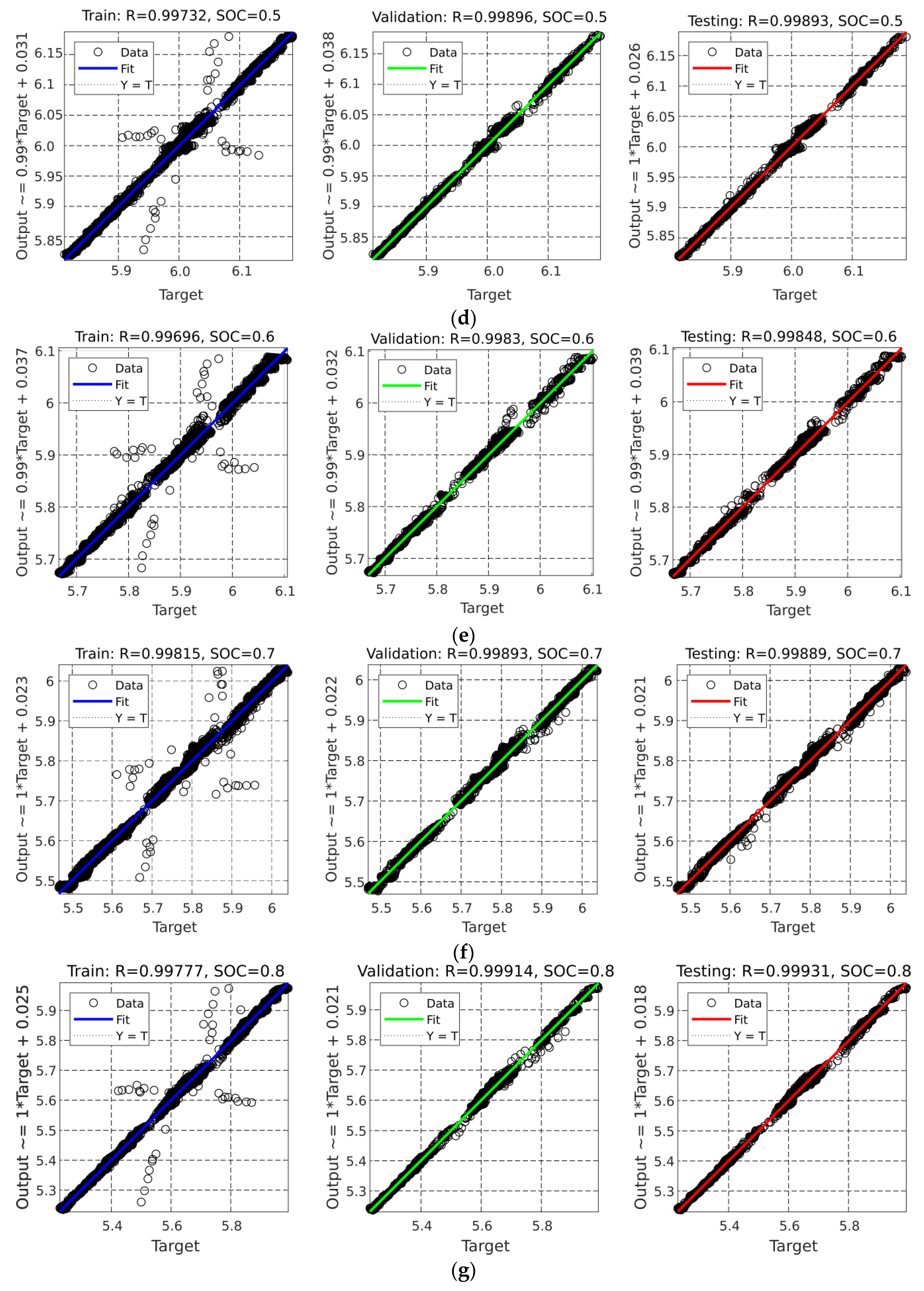
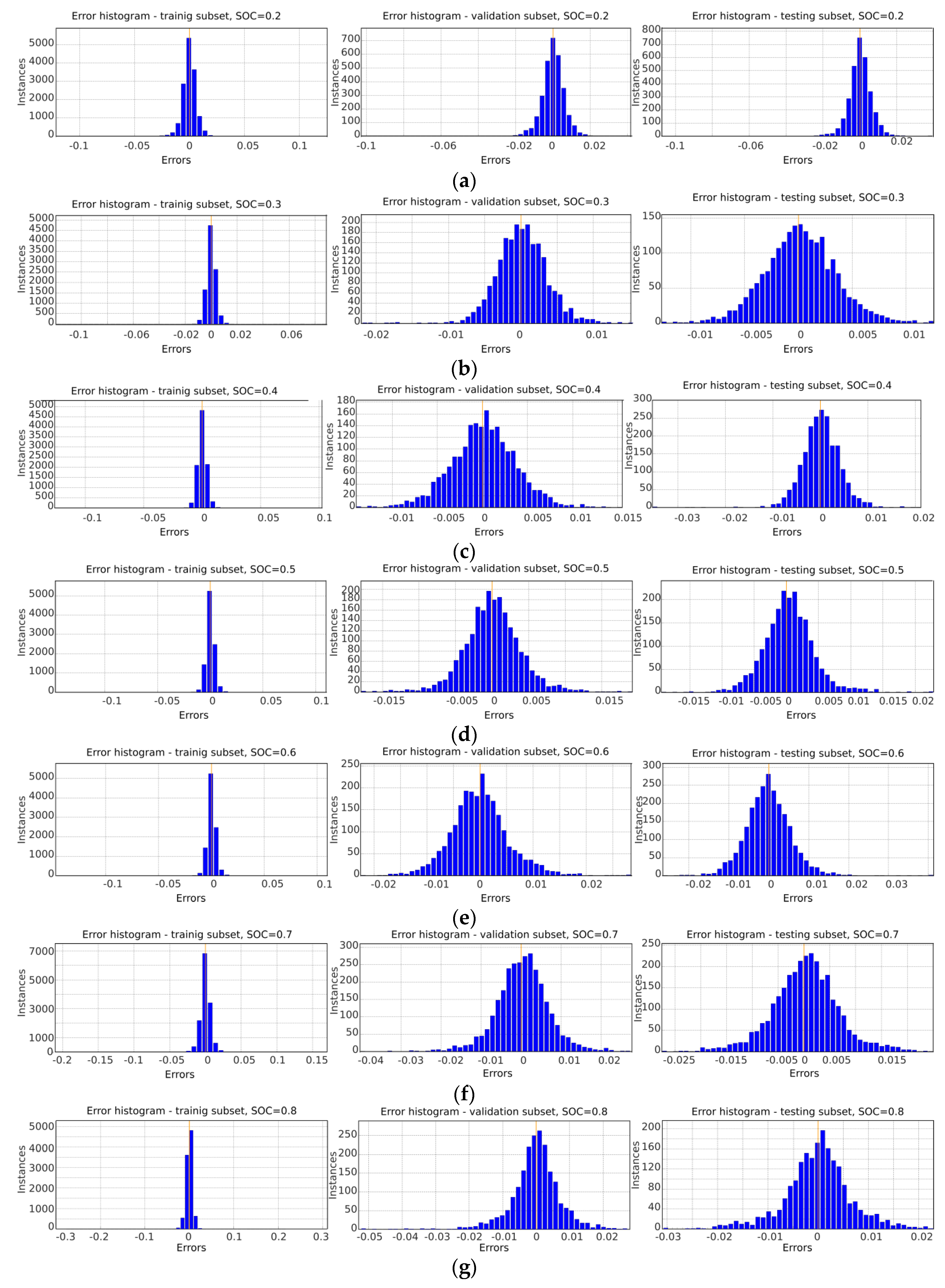
3.2.2. NARX-ANN Training

For the purpose of training and evaluating of NARX-ANN models, the error of VRLA battery voltage estimation was calculated as follows

$$e(k)=y_{NN}(k)-y(k)$$

(15)

where: y(k) = U_term(k), y_NN(k) = U_termNN(k), k is the sample number.

During training, the performance function of NARX-ANN model was chosen as a Mean Squared Error (MSE), calculated as:

$$E_{NN}=MSE=\frac{1}{N}{\displaystyle \sum _{k=1}^N{[e(k)]}^2}$$

(16)

where: N is the number of data samples.

During the evaluation, there was investigated the efficiency of the NARX-ANN models trained using the Levenberg–Marquardt algorithm [124,125], that is based on the first three terms of Taylor’s series approximation of the performance function. In the Levenberg–Marquardt method, the direction of improvement and the step coefficient are not determined, as in the case of the steepest descent or conjugate gradients algorithms. The Levenberg–Marquardt method is a special case of the variable metrics method [125] where changes in weights in the i-th training iteration are determined according to the equation

$$W_{(i+1)}=W_{(i)}-H{(W_{(i)})}^{-1}\nabla E_{NN}(W_{(i)})$$

(17)

where the weight vector is in the form of following vector $W={[w_1,\dots ,w_{nW}]}^T$, and $nW$ is the number of neural network weights.

The Levenberg–Marquardt algorithm, used for the selection of weights in the NARX-ANN during training, required knowledge of the gradient values of the objective function relative to each of the network weights. To determine it in a multi-layer network, the backpropagation algorithm [126] was used, where the values of the elements of the gradient vector $\nabla E_{NN}(W_{(i)})$ in (17) are calculated in the direction from the output layer to the input layer of the NARX-ANN model.

As a result of using the backpropagation algorithm, the vector of the first derivatives of the performance function with respect to weight changes is determined as follows:

$$\nabla E_{NN}(W_{(i)})={\left[\begin{array}{ccc}\frac{\partial E_{NN}(W_{(i)})}{\partial w_1}& \dots & \frac{\partial E_{NN}(W_{(i)})}{\partial w_{nW}}\end{array}\right]}^T$$

(18)

Moreover, the Levenberg–Marquardt algorithm requires the knowledge of Hessian matrix $H(W_{(i)})$ calculated as

$$H(W_{(i)})=\frac{{\partial }^{2}E(W)}{\partial W^2}=\left[\begin{array}{ccc}\frac{{\partial }^{2}E(W)}{\partial w_1\partial w_1}& \cdots & \frac{{\partial }^{2}E(W)}{\partial w_1\partial w_{nW}}\\ ⋮& & ⋮\\ \frac{{\partial }^{2}E(W)}{\partial w_{nW}\partial w_1}& \cdots & \frac{{\partial }^{2}E(W)}{\partial w_{nW}\partial w_{nW}}\end{array}\right]$$

(19)

In the Levenberg–Marquardt method, a positive definite Hessian matrix (19) is approximated numerically [124,125].

The NARX-ANN models were trained iteratively in the batch mode, in which in every training iteration, weights and biases were updated after all the network inputs and outputs from chosen dataset were presented [124]. For each NARX-ANN, all weights and biases were initialized using the Nguyen–Widrow initialization procedure [127]. The network architecture was based on the previous research [30,110] for energy storage systems and preliminary tests, showing that 10 neurons in the hidden layer, with input delays chosen as n_u = 1, n_I = n_a = n_b = n_t = 2 shall give satisfactory estimation results. In each NARX-ANN model there was one nonlinear hidden layer, and one linear output layer (see Figure 6).

As the number of training iterations can be very large, the conditions of stopping the training were determined. Usually, the basic values taken into account are the assumed minimum value of the NARX-ANN performance function and the assumed maximum number of training iterations. The following training stop conditions were chosen: Epochs = 1500, or $E$ ≤ 10⁻⁶.

Furthermore, the early stopping methodology was used, to train the NARX-ANN model in a supervised way. The dataset for each SOC was divided into three subsets:

• Training dataset: Subset used updating the NARX-ANN weights and biases during network training.
• Validation dataset: Subset used to validate the NARX-ANN in every iteration during training. The performance function value on the validation set was monitored during the training. The rise of the error on the validation subset was an indication that the network begins to overfit the data. When the performance function for validation error increased for a specified number of iterations, the training stopped, and the weights and biases at the minimum of the validation error were chosen for the network.
• Testing dataset: Subset not used in the training, used to compare different models during evaluation.

There were between 12,000–14,000 data samples in each dataset (depending on SOC). The datasets used for training were divided into three parts using interleaved indices [124], namely: Training dataset (70% of the full dataset), testing dataset (15% of the full dataset), and validation dataset (15% of the full dataset).

The performance of the NARX-ANN model training, for all data subsets, and for different SOC is given in Figure 7a–g. During training, the performance function decreased for each dataset, while early stopping methodology allowed to create the model with best generalization properties. The average time of the training did not exceed 10 min.

In Figure 8a–g there are given linear regression plots for trained NARX-ANN models. Values of relationship coefficient (R) are close to 1, that indicates that there is an exact linear relationship between real values of voltage and estimated values with each NARX-ANN model. However, there were few samples in training data that visibly diverge from the linear approximation in the regression plot. This indicates the possible outliers during voltage estimation, that are further described in Section 4.

For every trained model, and dataset there were calculated errors, presented in Figure 9a–g in the form of histograms (with 50-bin grouping) for each subset. Every error distribution was tested using the Pearson’s chi-squared test [128], which returns a test decision for the null hypothesis that the data in the error vector comes from a normal distribution with a mean and a variance estimated from error vector. The test proved, that the null hypothesis at the 5% significance level for all datasets and subsets used for training, validation, and testing. All trained NARX models had a mean value close to zero, with a very small variance that proves their good approximation and generalization properties.

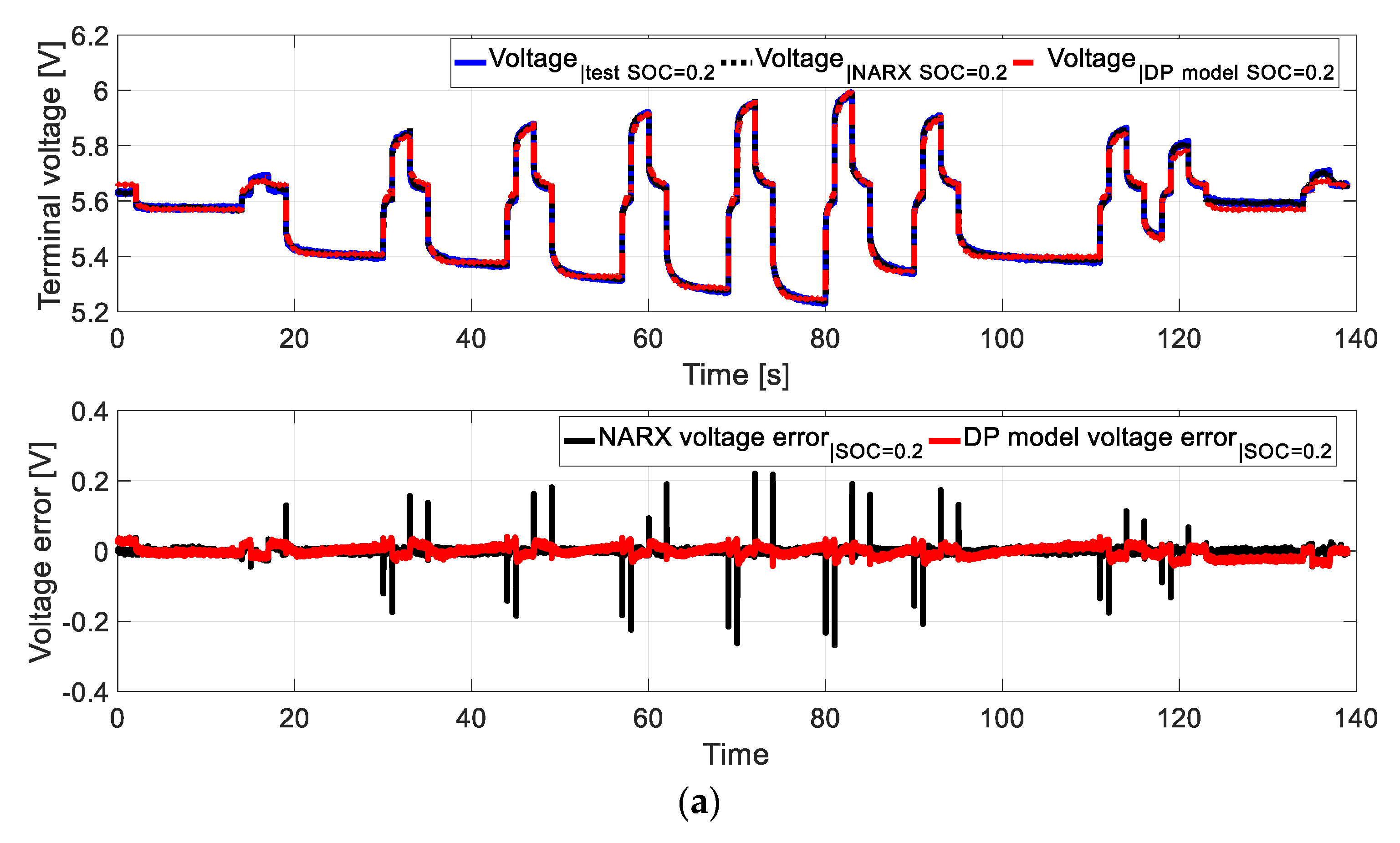
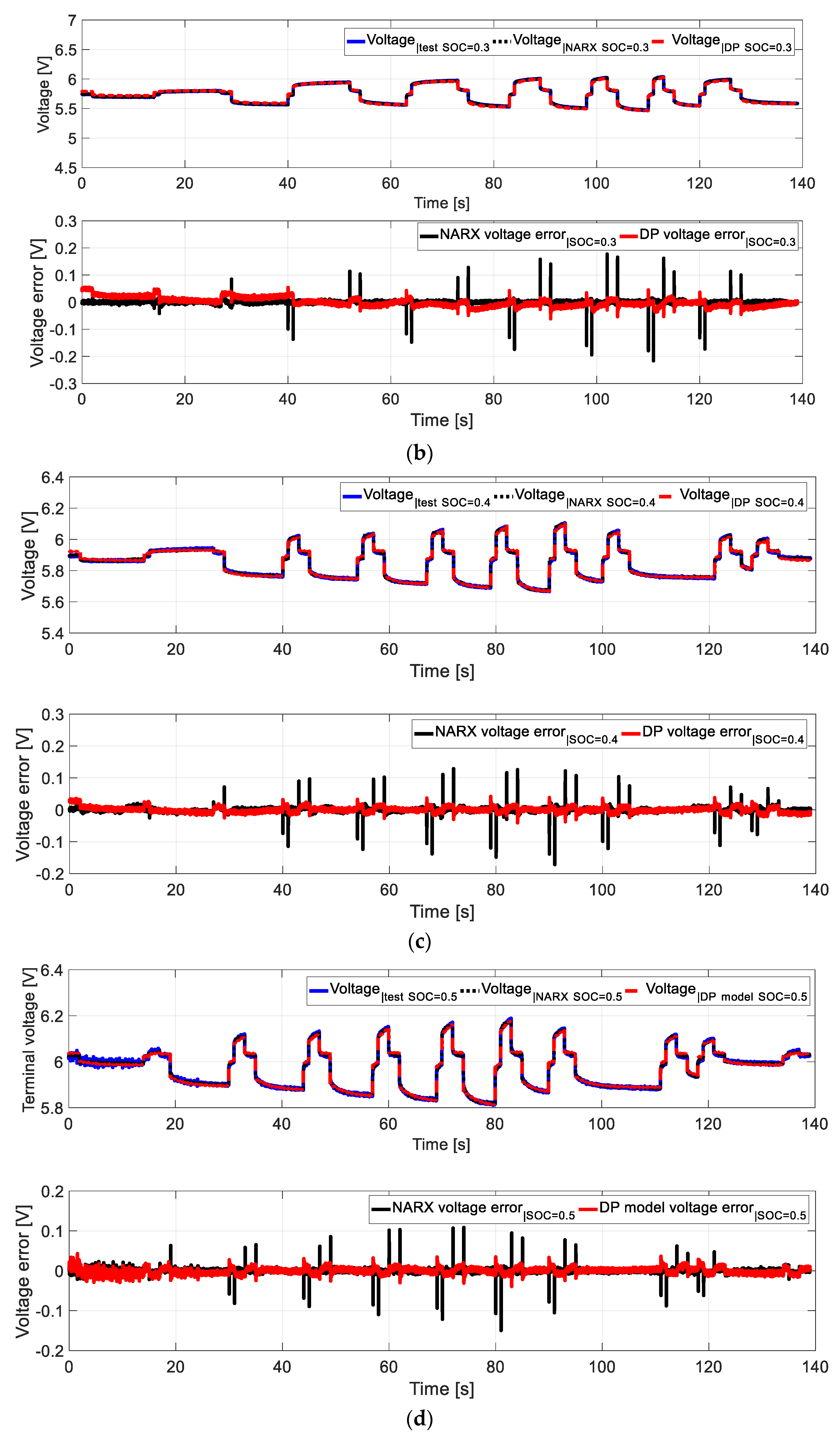
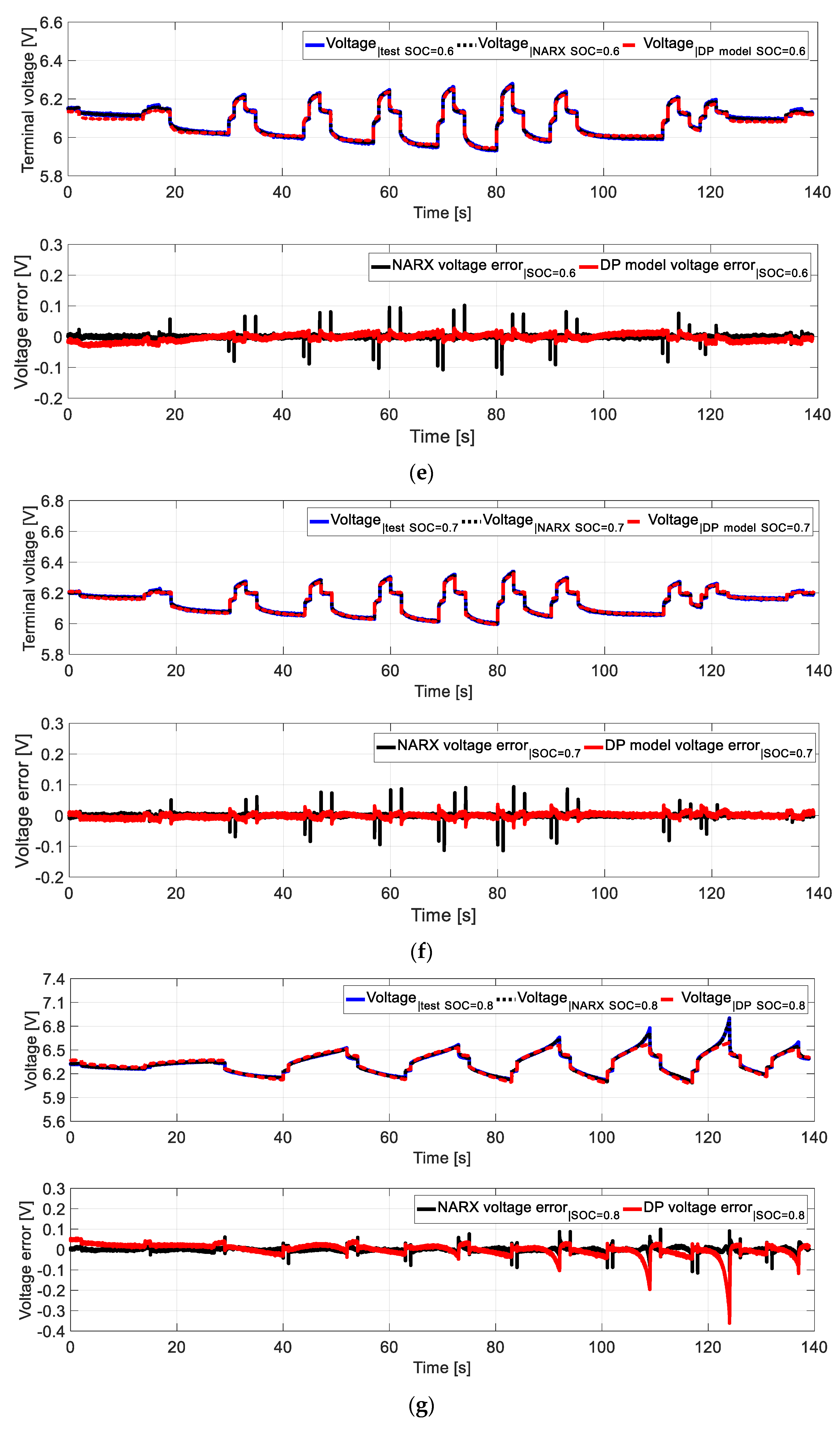
4. Validation of Results Acquired from Measurements, DP and NARX Models

The following section contains the validation results for voltage values obtained during measurements and from NARX and DP models, for SOC ranging from 0.2 to 0.8, respectively: Figure 10a for SOC = 0.2, Figure 10b for SOC = 0.3, Figure 10c for SOC = 0.4, Figure 10d for SOC = 0.5, Figure 10e for SOC = 0.6, Figure 10f for SOC = 0.7 and Figure 10g for SOC = 0.8. For SOC from 0.2 to 0.7 the voltage error obtained from NARX network was higher than for DP model. However, it did not exceed 0.27 V (Figure 10a for SOC = 0.2) while for DP model the error did not exceed 0.045 V (for SOC = 0.7). In the case of SOC = 0.8 (Figure 10g) the NARX model was more precise, the error did not exceed 0.1 V. For the DP model the maximum error was 0.36 V. The DP model presents worse results when the battery is charged to at least SOC = 0.8. During charging, nonlinear phenomena occurred related to activation and concentration polarization of reagents on the electrodes. In order to model the electrochemical processes in the range above SOC = 0.8 more precisely, additional RC loops can be added [72], which would increase the description accuracy of nonlinear processes during charging/discharging of the battery, especially in the pulse cycle. In Reference [89] it was concluded that with the increase of RC loop the accuracy of the model increases, but the time needed to identify the model parameters increases as well.

It can be seen (Figure 10) that the NARX-ANN model has good voltage generalization properties throughout the considered SOC range. However, there are some higher errors visible in the moments of sudden changes in the current load. This behavior can be connected with the small number of samples covering the vicinity of this points, comparing to the amount of data in the periods where the transitions were smooth. We can infer, that the NARX-ANN model generalizes better the periods with a higher amount of data. This indicates the sensitivity of the NARX-ANN model to such sudden changes resulting in large error range, that can be connected with the generalization properties of the neural networks [129]. In comparison, the presented DP model is more robust sudden changes of the current load.

The quality of the single NARX-ANN and DP model of the VRLA battery was evaluated using Mean Square Error (MSE) performance function (16) and the goodness of fit between estimated data and reference data calculated as Normalized Root Mean Square Error (NRMSE) [130]:

$$NRMSE(k)=1-\frac{\Vert e(k)\Vert }{\Vert y(k)-\overline{y}\Vert }$$

(20)

where: $\overline{y}{}_{–}$mean value of the modeled signal. The value of NRSME varies between −∞ (bad fit) to 1 (perfect fit).

Table 2. Quality indices for NARX and DP models of the Valve-Regulated Lead-Acid (VRLA) battery.

State of Charge (SOC) Data Set Value	NARX Model		DP Model
	MSENARX	NRMSENARX	MSEDP	NRMSEDP
0.2	9.6263 × 10−5	0.9453	0.2009 × 10−3	0.9210
0.3	4.9337 × 10−5	0.9546	0.2673 × 10−3	0.8986
0.4	3.3201 × 10−5	0.9427	0.0695 × 10−5	0.9192
0.5	2.9521 × 10−5	0.9371	0.0542 × 10−3	0.9147
0.6	2.4470 × 10−5	0.9376	0.1323 × 10−3	0.8549
0.7	2.1085 × 10−5	0.9407	0.0528 × 10−3	0.9062
0.8	4.2477 × 10−5	0.9489	0.9224 × 10−3	0.7737

presents the values of MSE and NRMSE for SOC values ranging from 0.2 to 0.8. MSE values are low and do not exceed 0.93 × 10⁻³ (DP model for SOC = 0.8) and 1 × 10⁻⁴ (NARX model for SOC = 0.2). The NRSME value for NARX model in SOC range from 0.2 to 0.8 is above 0.93 (the lowest for SOC = 0.5, NRSE_NARX = 0.9371), which indicates a well-identified model.

In the case of the DP model, the value of NRMSE_DP is above 0.77 (with the lowest value NRMSE_DP = 0.7737 for SOC = 0.8), the model was identified correctly. The lowest value of NRMSE_DP for SOC = 0.8 is mainly a result of the battery temporarily exceeding the maximum voltage of 6.8 V (the hyperbolic character of voltage increase at battery terminals).

5. Conclusions

The work presents model-aided research of VRLA AGM batteries in pulse work cycle. Two model approaches were presented, based on two RC loop model (known as DP model) and type NARX neural network model. Using the identified parameters, simulations were conducted and validated against results of experimental measurement results.

In this paper, it was shown that the DP model gives good results of voltage estimation for the considered SOC range. An advantage of the presented DP model is the possibility to estimate unidentified parameter values for a given SOC interval (e.g., SOC = 0.65).

Considering the NARX-ANN model, it has good estimation abilities for the voltage prediction. Results presented in Table 2 show that it has good repeatability, with small dispersion with changing SOC. For different datasets, it had slightly better, stable performance comparing with the DP model. However, there are a few drawbacks of such solution. First, it is a black-box model, with the structure that does not reflect the physical properties of the VRLA battery, so its usability is limited to prediction, rather than control. Secondly, it is sensitive to sudden changes in the current load, while the DP model is more robust. The possible solution can be a proper design of the current load signal [131], and research on the NARX-ANN generalization and sensitivity interconnection [129].

A well identified DP model can be used to simulate the operation of the battery during any work cycle, particularly in conjunction with a BMS system, e.g., for estimating SOC, remaining travel range, and SOH status [132]. The DP model presented in this work will be expanded in the future with the following points considered:

• Self-discharge over time, which for batteries ranges from 5 to 30% per month [133] depending on type of battery and storage conditions (it is planned to add R component to the equivalent battery circuit (Figure 3) in parallel with U_OCV).
• Changes in State of Health of the battery and its prediction with aid of operational research [29,134]. The authors of Reference [29] are currently working on expanding the functionality of the DP model.
• Increase in the accuracy of identified parameters with the use of models with additional RC loops (three and four RC loop pairs), which will greatly increase accuracy particularly for SOC >0.8 and SOC <0.2. Another approach, instead of increasing the number of RC loop pairs and also a compromise between the number of estimated parameters and the accuracy, is to use constant phase elements (CPE) [135,136,137,138].
• Kalman filter [57,58,59,60], which in quasi-only mode will allow to identify parameters that cannot be measured directly, such as: U_OCV, R₀ etc.
• Fusion of presented DP and NARX-ANN models using tailored Extendend Kamlan Filtering [139]. Such solution shall allow combining the structural and robustness properties of the DP model with the NARX-ANN model accuracy [140], and repeatability for different working conditions.