Dynamic Analyses of the Hydro-Turbine Generator Shafting System Considering the Hydraulic Instability
Abstract
1. Introduction
2. Mathematical Modeling
2.1. Modeling of the Hydraulic Unbalance Forces
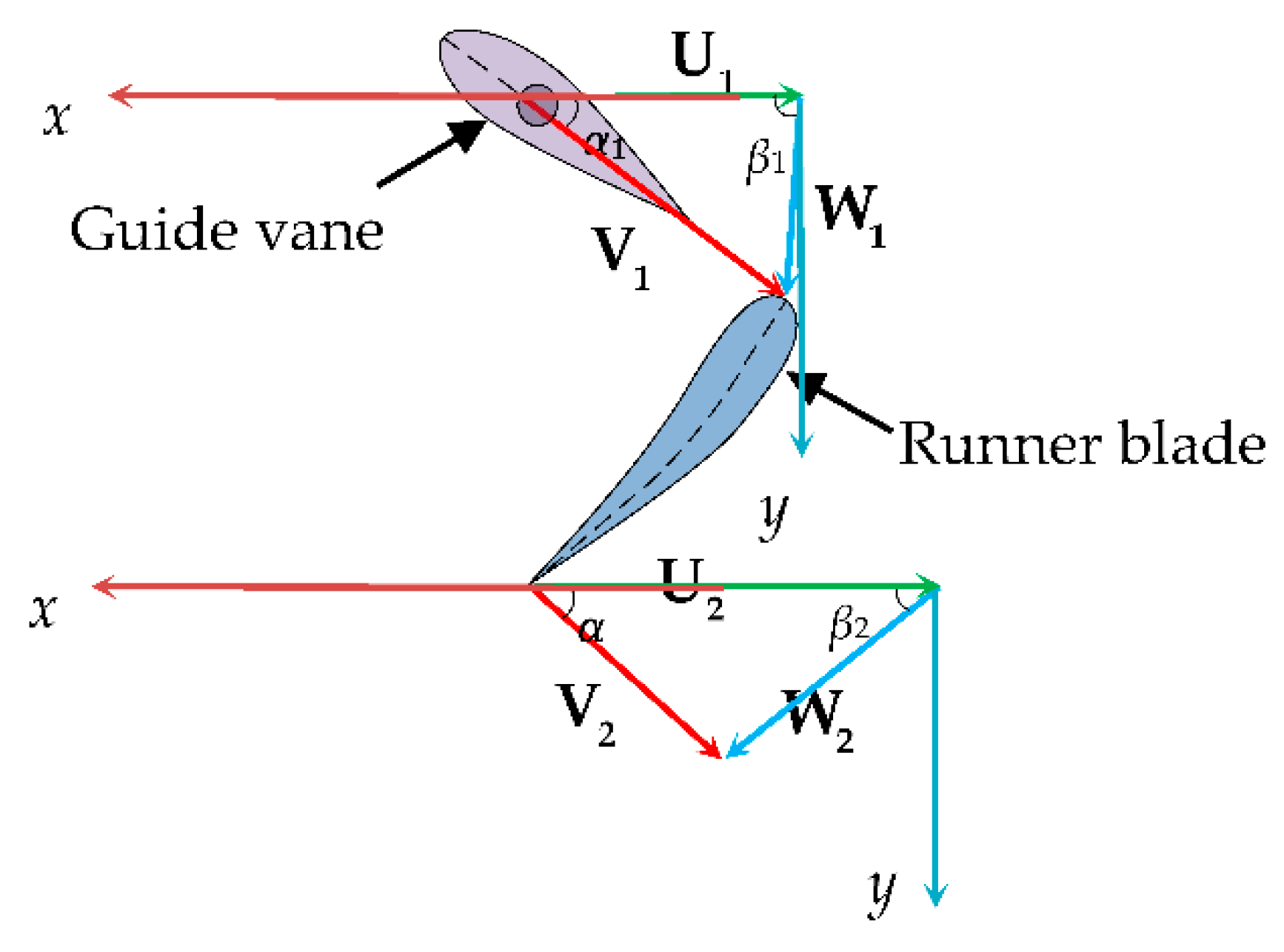
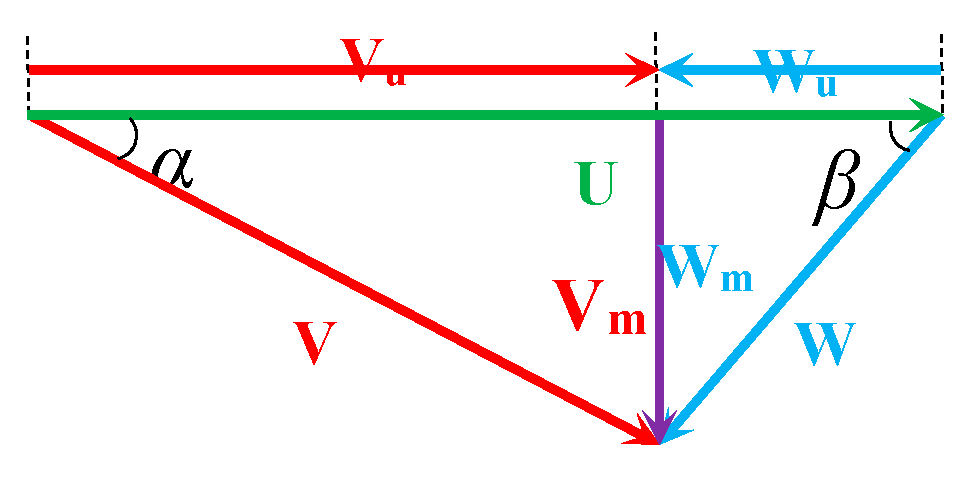
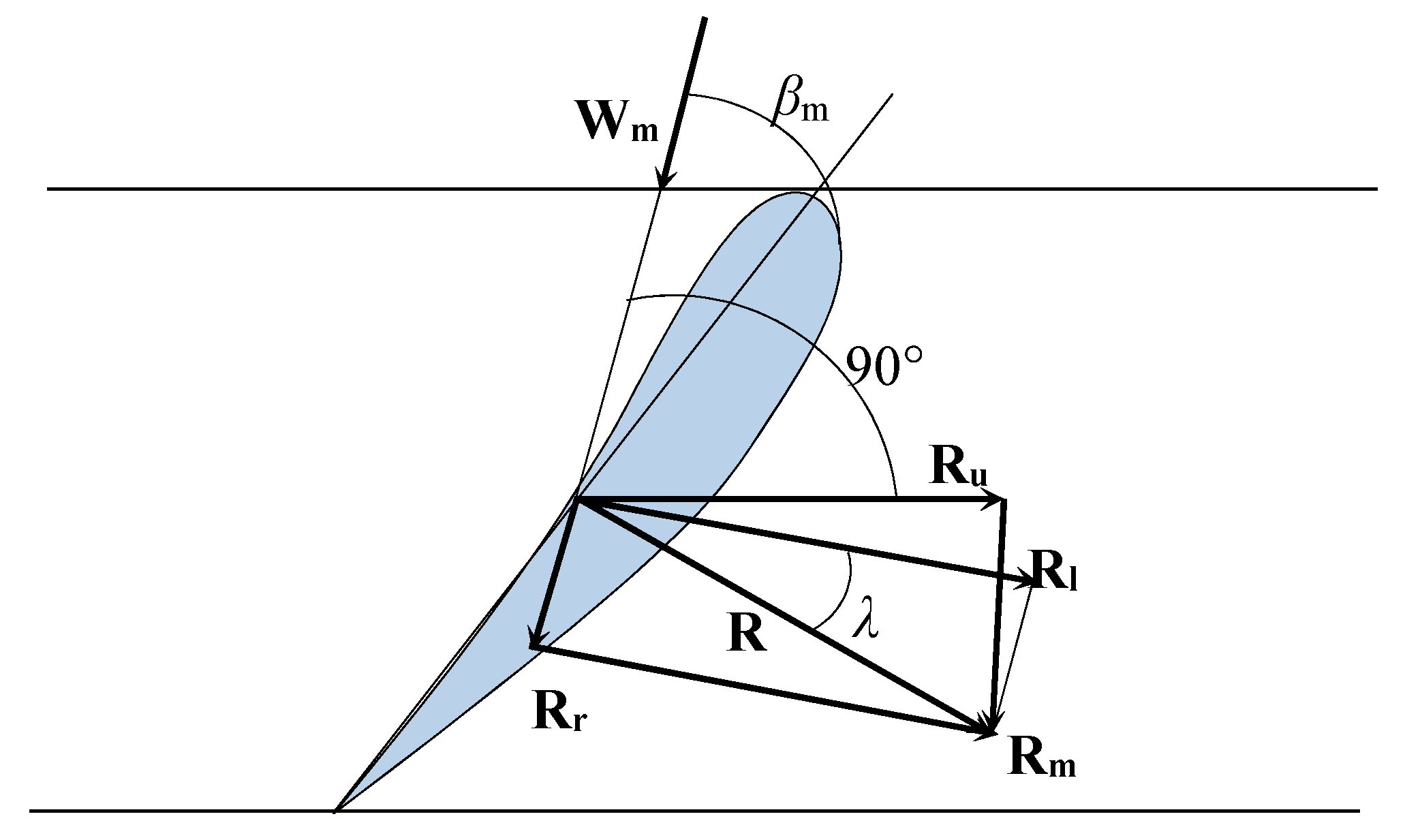
2.1.1. Hydraulic Forces on a Single Blade
2.1.2. Hydraulic Forces on a Single Blade
2.2. Modeling of the Mechanical and Electrical Unbalance Forces
2.2.1. Damping Force Model
2.2.2. Oil Film Force Model
2.2.3. Rub-Impact Force Model
2.2.4. Unbalanced Magnetic Pull Model
2.3. Modeling of the HGSS
3. Dynamic Simulation and Analyses
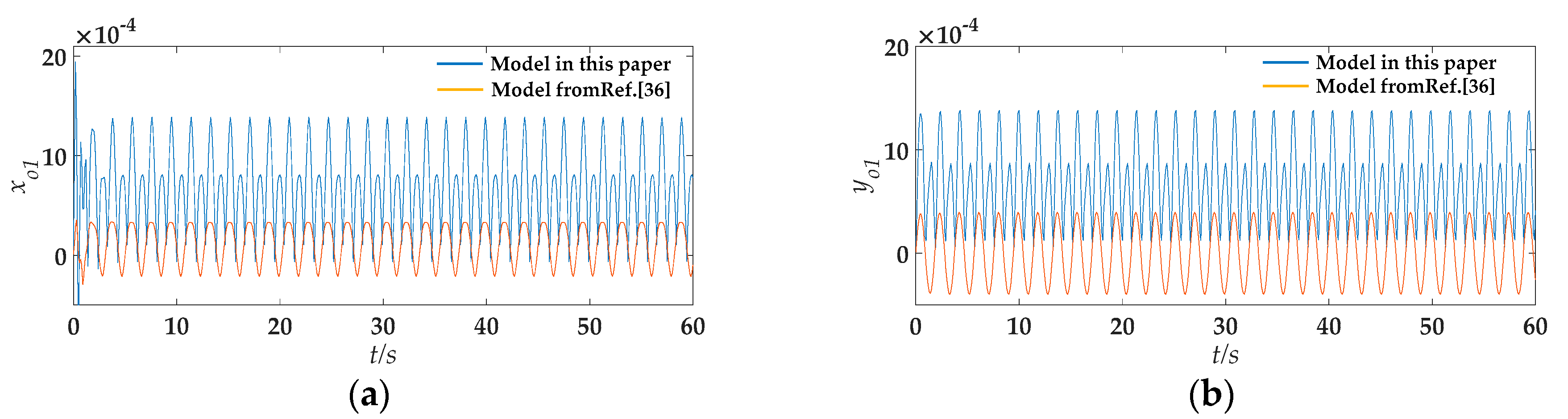
3.1. Model Verification
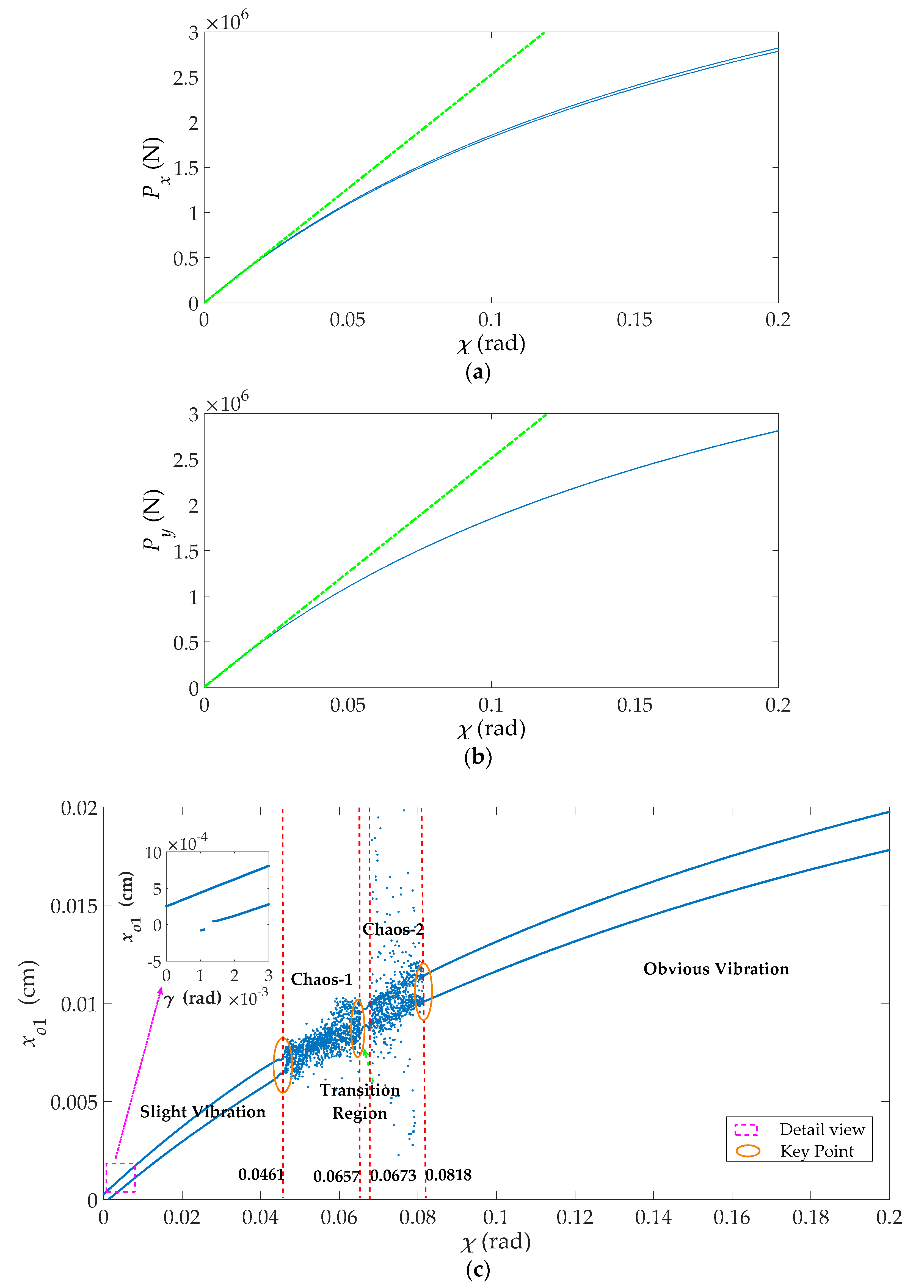
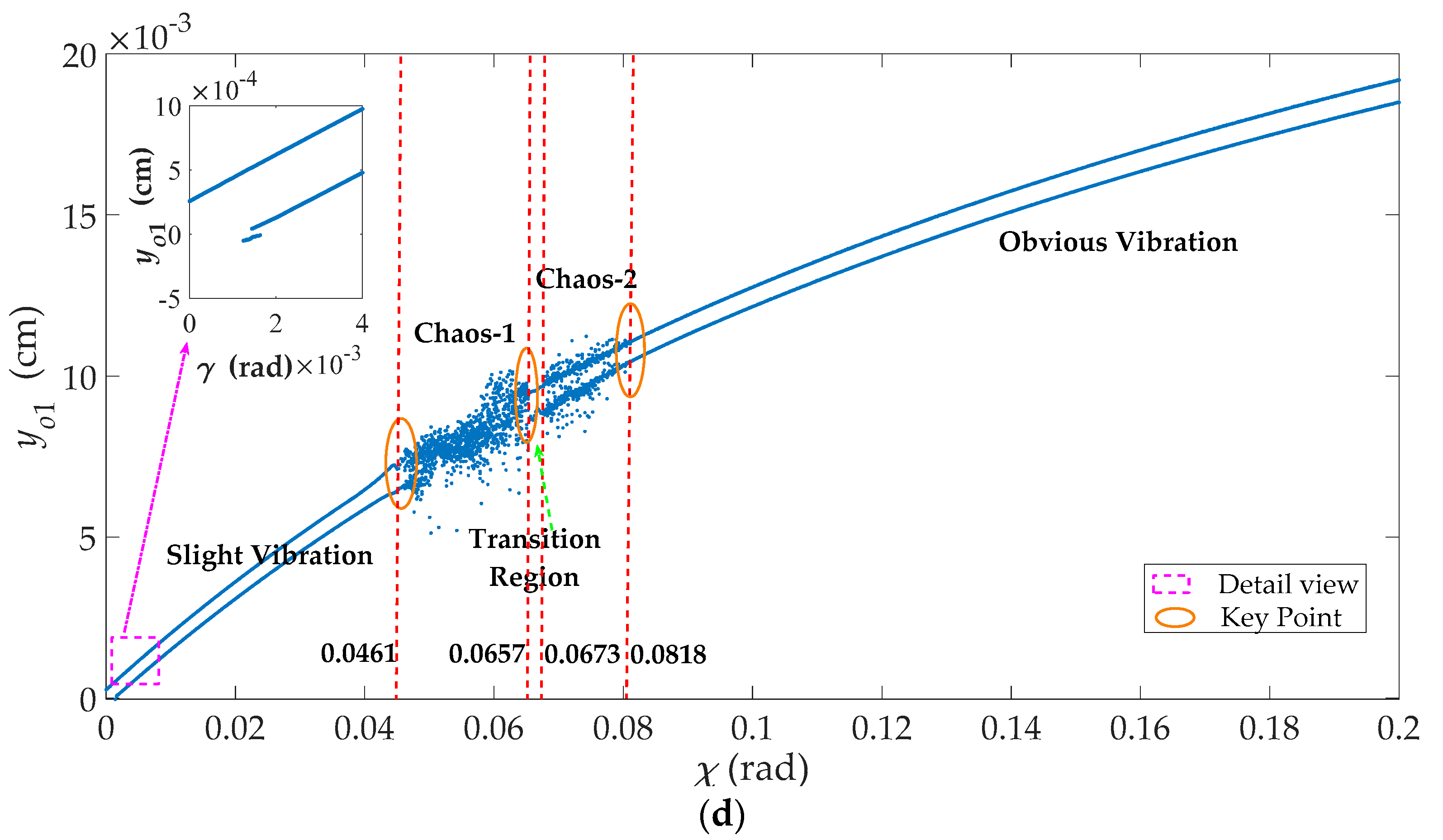
3.2. Effects of the Deviation of the Blade Exit Flow Angle (χ)
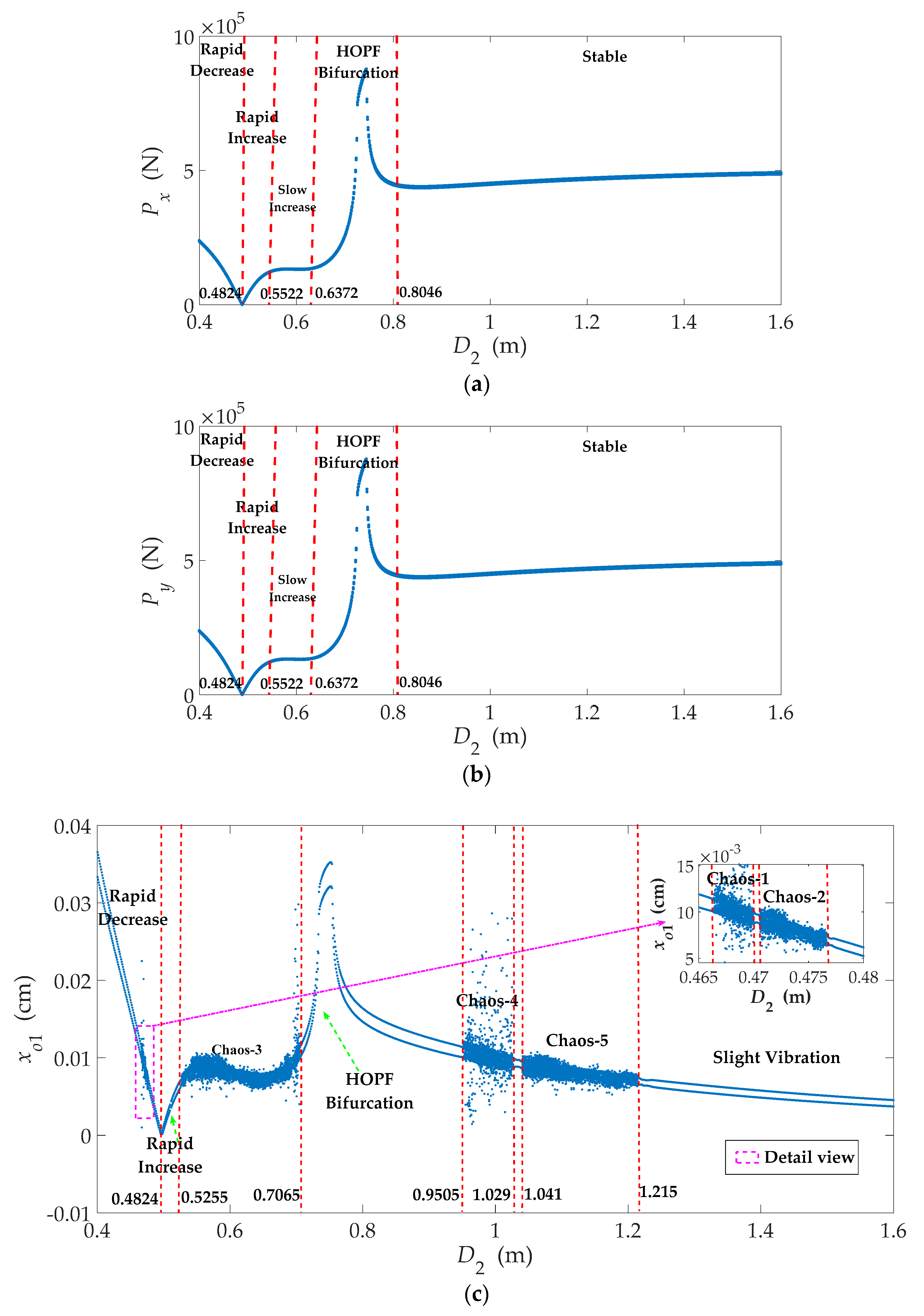
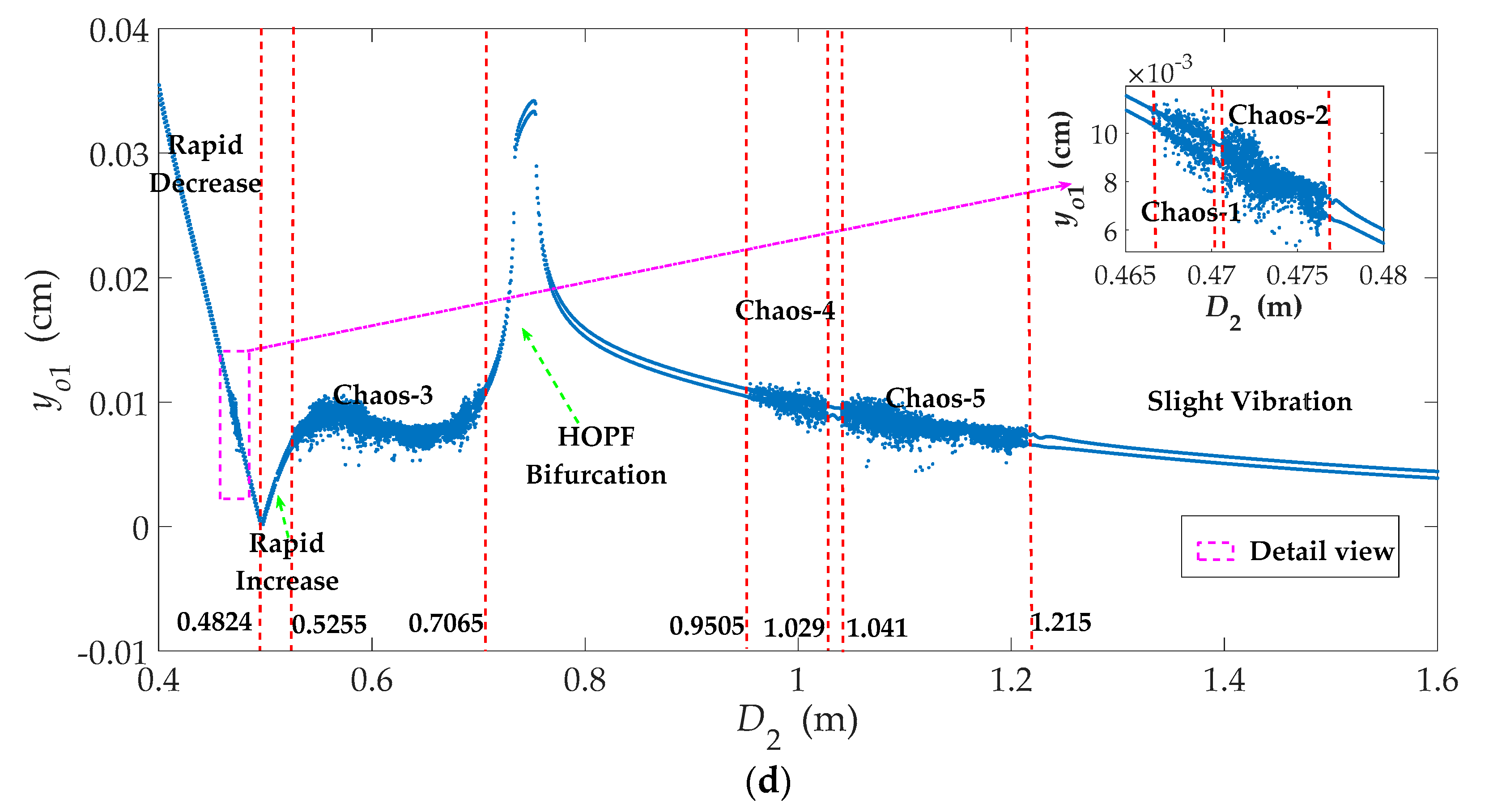
3.3. Effects of the Blade Exit Diameter (D2)
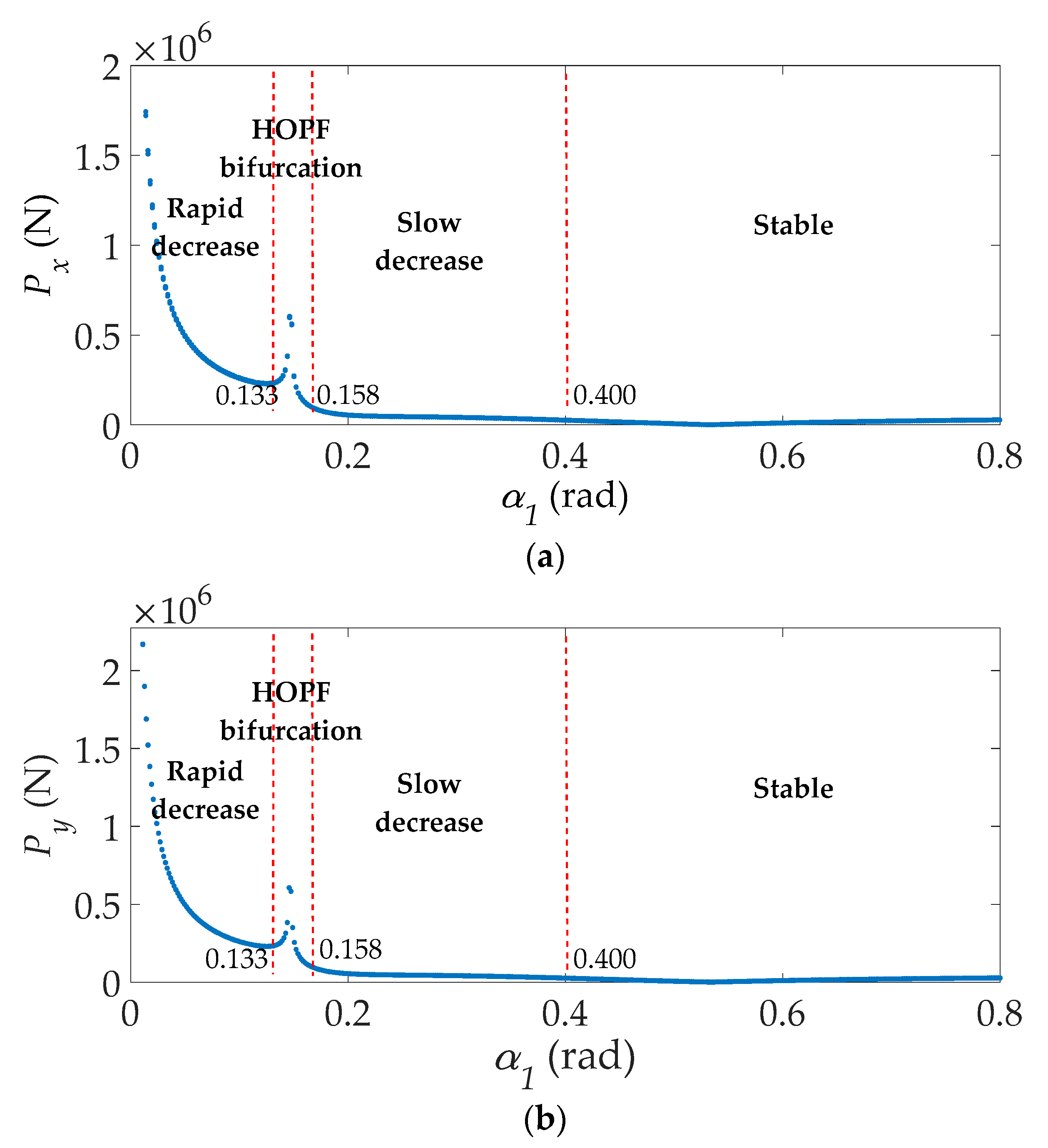
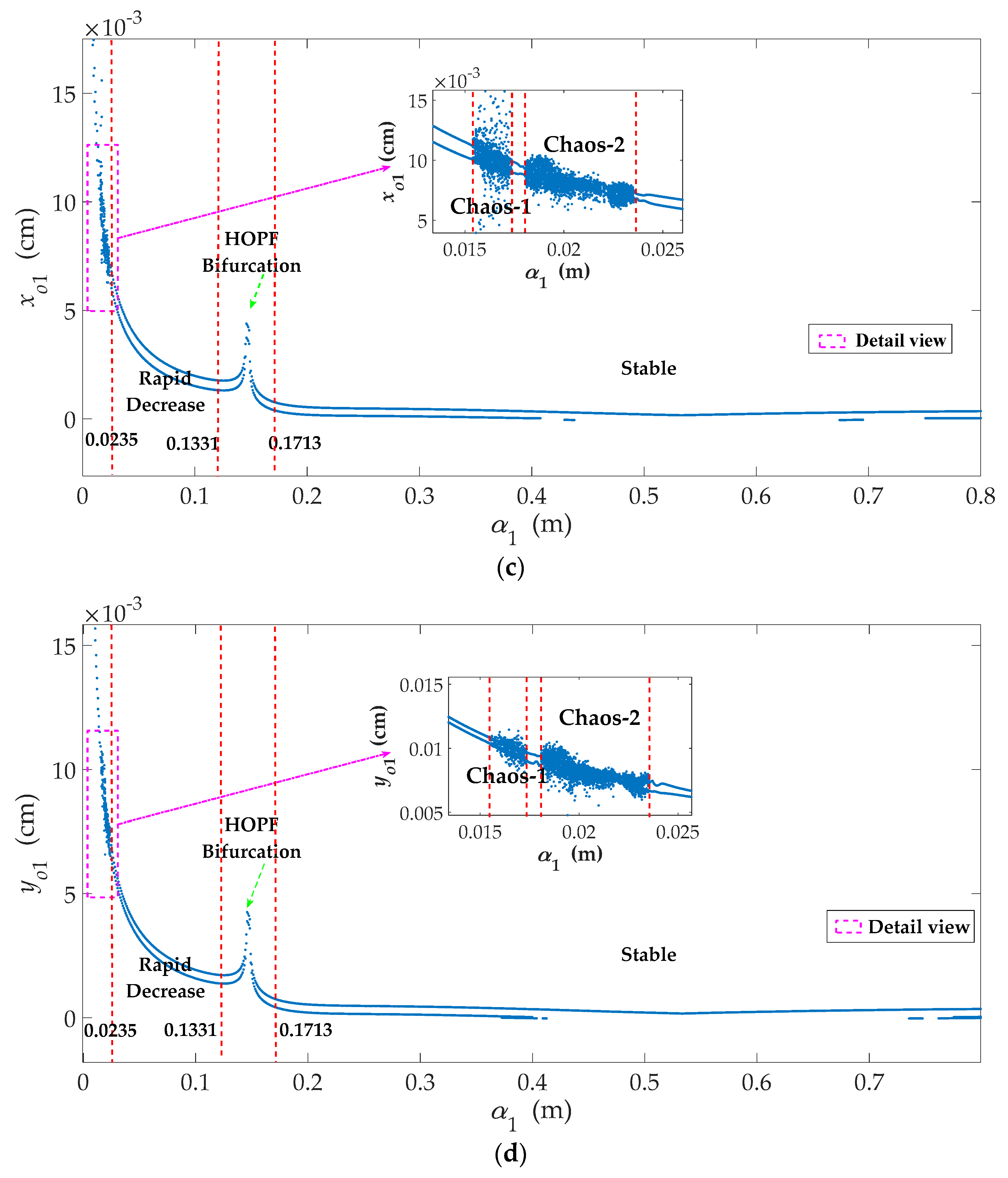
3.4. Effects of the Guide Vane Opening Angle (α1)
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Paish, O. Micro-hydropower: Status and prospects. Proc. Inst. Mech. Eng. Part A J. Power Energy 2005, 216, 31–40. [Google Scholar] [CrossRef]
- Spänhoff, B. Current status and future prospects of hydropower in Saxony (Germany) compared to trends in Germany, the European Union and the World. Renew. Sustain. Energy Rev. 2014, 30, 518–525. [Google Scholar] [CrossRef]
- Modesto, P.S.; Francisco, J.S.; Helena, M.R.; Amparo, L.J. Energy Recovery in Existing Water Networks: Towards Greater Sustainability. Water 2017, 2, 97. [Google Scholar] [CrossRef]
- Xu, B.B.; Chen, D.Y.; Behrens, P.; Ye, W.; Guo, P.C.; Luo, X.Q. Modeling oscillation modal interaction in a hydroelectric generating system. Energy Convers. Manag. 2018, 174, 208–217. [Google Scholar] [CrossRef]
- Chu, S.; Majumdar, A. Opportunities, and challenges for a sustainable energy future. Nature 2012, 488, 294–303. [Google Scholar] [CrossRef] [PubMed]
- Giosio, D.R.; Henderson, A.D.; Walker, J.M.; Brandner, P.A. Rapid Reserve Generation from a Francis Turbine for System Frequency Control. Energies 2017, 10, 496. [Google Scholar] [CrossRef]
- Zhang, L.K.; Ma, Z.Y.; Wu, Q.Q.; Wang, X.N. Vibration analysis of coupled bending-torsional rotor-bearing system for hydraulic generating set with rub-impact under electromagnetic excitation. Arch. Appl. Mech. 2016, 86, 1665–1679. [Google Scholar] [CrossRef]
- Martinez-Lucas, G.; Sarasua, J.I.; Sanchez-Fernandez, J.A.; Wilhelmi, J.R. Frequency control support of a wind-solar isolated system by a hydropower plant with long tail-race tunnel. Renew. Energy 2016, 90, 362–376. [Google Scholar] [CrossRef]
- Xu, B.B.; Chen, D.Y.; Tolo, S.; Patelli, E.; Jiang, Y.L. Model validation and stochastic stability of a hydro-turbine governing system under hydraulic excitations. Int. J. Electr. Power 2018, 95, 156–165. [Google Scholar] [CrossRef]
- Williamson, S.J.; Stark, B.H.; Booker, J.D. Performance of a low-head pico-hydro Turgo turbine. Appl. Energy 2013, 102, 1114–1126. [Google Scholar] [CrossRef]
- Trivedi, C.; Cervantes, M.J.; Gandhi, B.K. Investigation of a High Head Francis Turbine at Runaway Operating Conditions. Energies 2016, 9, 149. [Google Scholar] [CrossRef]
- Amirante, R.; Cassone, E.; Distaso, E.; Tamburrano, P. Overview on recent developments in energy storage: Mechanical, electrochemical and hydrogen technologies. Energy Convers. Manag. 2017, 132, 372–388. [Google Scholar] [CrossRef]
- Li, H.H.; Chen, D.Y.; Zhang, H.; Wang, F.F.; Ba, D.D. Nonlinear modeling and dynamic analysis of a hydro-turbine governing system in the process of sudden load increase transient. Mech. Syst. Signal Process. 2016, 80, 414–428. [Google Scholar] [CrossRef]
- Yang, W.J.; Yang, J.D.; Guo, W.C.; Zeng, W.; Wang, C.; Saarinen, L.; Norrlund, P. A Mathematical Model and Its Application for Hydro Power Units under Different Operating Conditions. Energies 2015, 8, 10260–10275. [Google Scholar] [CrossRef]
- Trivedi, C.; Cervantes, M.J.; Gandhi, B.K.; Dahlhaug, O.G. Transient pressure measurements on a high head model Francis turbine during emergency shutdown, total Load rejection, and runaway. J. Fluids Eng. 2014, 136, 121107. [Google Scholar] [CrossRef]
- Williamson, S.J.; Stark, B.H.; Booker, J.D. Low head pico hydro turbine selection using a multi-criteria analysis. Renew. Energy 2014, 61, 43–50. [Google Scholar] [CrossRef]
- Tong, W.M. Analysis of the Main Shaft Swing caused by the hydraulic unbalance of the water turbine wheel. Sichuan Water Power 1986, 1, 42–46. (In Chinese) [Google Scholar]
- Qin, W.Y.; Chen, G.R.; Meng, G. Nonlinear responses of a rub-impact overhung rotor. Chaos Soliton. Fract. 2004, 19, 1161–1172. [Google Scholar] [CrossRef]
- Yan, D.L.; Wang, W.Y.; Chen, Q.J. Nonlinear Modeling and Dynamic Analyses of the Hydro-Turbine Governing System in the Load Shedding Transient Regime. Energies 2018, 11, 1244. [Google Scholar] [CrossRef]
- Huang, Z.W.; Zhou, J.Z.; Yang, M.Q.; Zhang, Y.C. Vibration characteristics of a hydraulic generator unit rotor system with parallel misalignment and rub-impact. Arch. Appl. Mech. 2011, 81, 829–838. [Google Scholar] [CrossRef]
- Chang-Jian, C.W.; Chen, C.K. Chaos and bifurcation of a flexible rub-impact rotor supported by oil film bearings with nonlinear suspension. Mech. Mach. Theory 2007, 42, 312–333. [Google Scholar] [CrossRef]
- Ma, H.; Wang, X.L.; Niu, H.Q.; Wen, B.C. Oil-film instability simulation in an overhung rotor system with flexible coupling misalignment. Arch. Appl. Mech. 2015, 85, 893–907. [Google Scholar] [CrossRef]
- Dal, A.; Karaçay, T. Effects of angular misalignment on the performance of rotor-bearing systems supported by externally pressurized air bearing. Tribol. Int. 2017, 111, 276–288. [Google Scholar] [CrossRef]
- Yan, D.L.; Wang, W.Y.; Chen, Q.J. Fractional-order modeling and dynamic analyses of a bending-torsional coupling generator rotor shaft system with multiple faults. Chaos Soliton. Fract. 2018, 110, 1–15. [Google Scholar] [CrossRef]
- Dorji, U.; Ghomashchi, R. Hydro turbine failure mechanisms: An overview. Eng. Fail. Anal. 2014, 44, 136–147. [Google Scholar] [CrossRef]
- Feng, Z.P.; Chu, F.L. Nonstationary Vibration Signal Analysis of a Hydroturbine Based on Adaptive Chirplet Decomposition. Struct. Health Monit. 2007, 6, 265–279. [Google Scholar] [CrossRef]
- Perers, R.; Lundin, U.; Leijon, M. Saturation Effects on Unbalanced Magnetic Pull in a Hydroelectric Generator with an Eccentric Rotor. IEEE Trans. Magn. 2007, 43, 3884–3890. [Google Scholar] [CrossRef]
- Keller, S.; Xuan, M.T.; Simond, J.J.; Schwery, A. Large low-speed hydro-generators–unbalanced magnetic pulls and additional damper losses in eccentricity conditions. IET Electr. Power Appl. 2007, 1, 657–664. [Google Scholar] [CrossRef]
- Zarko, D.; Ban, D.; Vazdar, I.; Jarica, V. Calculation of Unbalanced Magnetic Pull in a Salient-Pole Synchronous Generator Using Finite-Element Method and Measured Shaft Orbit. IEEE Trans. Ind. Electron. 2012, 59, 2536–2549. [Google Scholar] [CrossRef]
- Xiang, C.L.; Liu, F.; Liu, H.; Han, L.J.; Zhang, X. Nonlinear dynamic behaviors of permanent magnet synchronous motors in electric vehicles caused by unbalanced magnetic pull. J. Sound Vib. 2016, 371, 277–294. [Google Scholar] [CrossRef]
- Kim, J.W.; Kwak, W.I.; Choe, B.S.; Kim, H.H.; Suh, S.H.; Lee, Y.B. The rotordynamic analysis of the vibration considering the hydro-electric force supported by rolling elements in 500 kW Francis turbine. J. Mech. Sci. Technol. 2017, 31, 5153–5159. [Google Scholar] [CrossRef]
- Zhang, T.X.; Liu, X.H. Reliability design for impact vibration of hydraulic pressure pipeline systems. Chin. J. Mech. Eng. 2013, 26, 1050–1055. [Google Scholar] [CrossRef]
- Zhou, J.X.; Chen, Y. Discussion on stochastic analysis of hydraulic vibration in pressurized water diversion and hydropower systems. Water 2018, 10, 353. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, X.D. Hydraulic Turbine; China Water Resources and Electric Power Press: Beijing, China, 2011. (In Chinese) [Google Scholar]
- Jiang, H.B.; Li, Y.R.; Cheng, Z.Q. Relations of Lift and Drag Coefficients of Flow around Flat Plate. Appl. Mech. Mater. 2014, 518, 161–164. [Google Scholar] [CrossRef]
- Xu, B.B.; Chen, D.Y.; Zhang, H.; Zhou, R. Dynamic analysis and modeling of a novel fractional-order hydro-turbine-generator unit. Nonlinear Dyn. 2015, 81, 1263–1274. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, L.X.; Guo, Y.K.; Qian, J.; Zhang, C.L. The generalized Hamiltonian model for the shafting transient analysis of the hydro turbine generating sets. Nonlinear Dyn. 2014, 76, 1921–1933. [Google Scholar] [CrossRef]
- Xu, B.B.; Yan, D.L.; Chen, D.Y.; Gao, X.; Wu, C.Z. Sensitivity analysis of a Pelton hydropower station based on a novel approach of turbine torque. Energy Convers. Manag. 2017, 148, 785–801. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, K.; Gao, C.; Li, Z.; Yan, D.; Fu, X. Dynamic Analyses of the Hydro-Turbine Generator Shafting System Considering the Hydraulic Instability. Energies 2018, 11, 2862. https://doi.org/10.3390/en11102862
Zhuang K, Gao C, Li Z, Yan D, Fu X. Dynamic Analyses of the Hydro-Turbine Generator Shafting System Considering the Hydraulic Instability. Energies. 2018; 11(10):2862. https://doi.org/10.3390/en11102862
Chicago/Turabian StyleZhuang, Keyun, Chaodan Gao, Ze Li, Donglin Yan, and Xiangqian Fu. 2018. "Dynamic Analyses of the Hydro-Turbine Generator Shafting System Considering the Hydraulic Instability" Energies 11, no. 10: 2862. https://doi.org/10.3390/en11102862
APA StyleZhuang, K., Gao, C., Li, Z., Yan, D., & Fu, X. (2018). Dynamic Analyses of the Hydro-Turbine Generator Shafting System Considering the Hydraulic Instability. Energies, 11(10), 2862. https://doi.org/10.3390/en11102862




