Adaptive Robust Optimization-Based Optimal Operation of Microgrids Considering Uncertainties in Arrival and Departure Times of Electric Vehicles
Abstract
:1. Introduction
2. Microgrid Operation and Uncertainty in EVs
2.1. Uncertainty Handling Methods in Microgrids
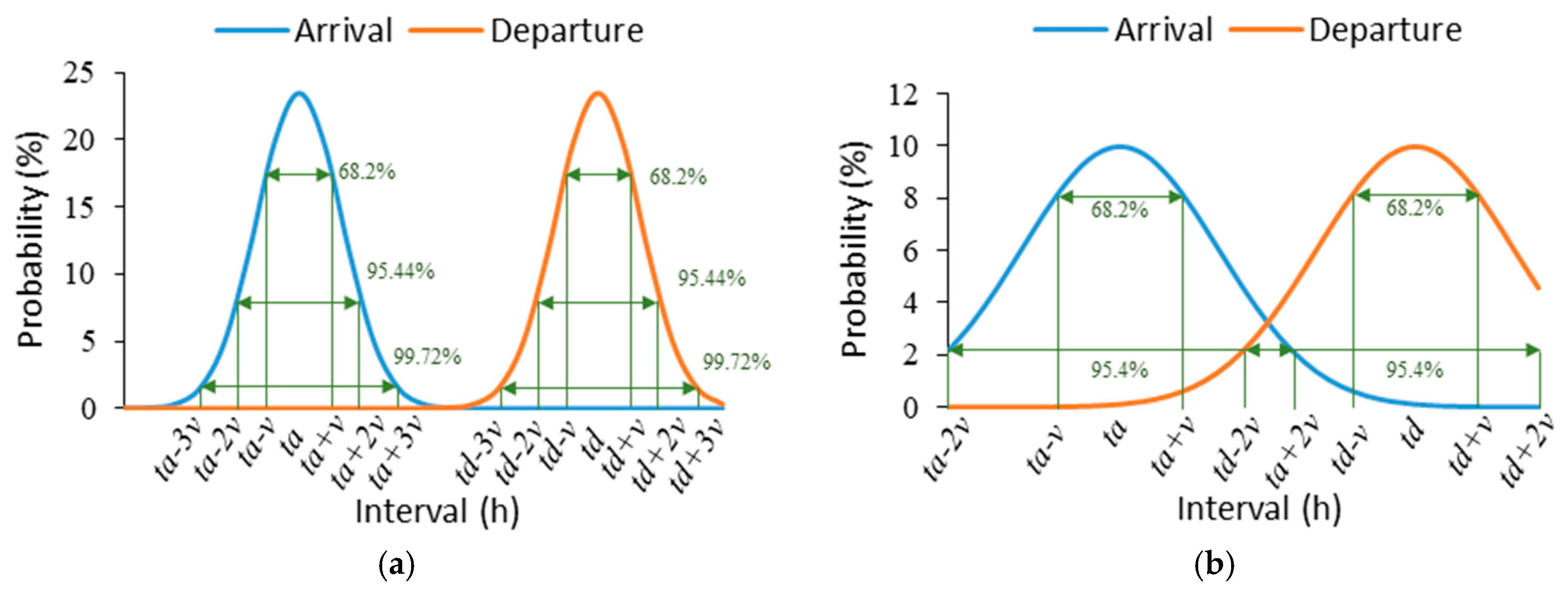
2.2. Realization of Uncertainty in EVs
2.3. Uncertainty Bounds Calculation
3. Problem Formulation
3.1. Deterministic Model
3.1.1. Objective Function
3.1.2. Load-Balancing Equation and Constraints for Controllable Generators
3.1.3. Electric Vehicle Constraints
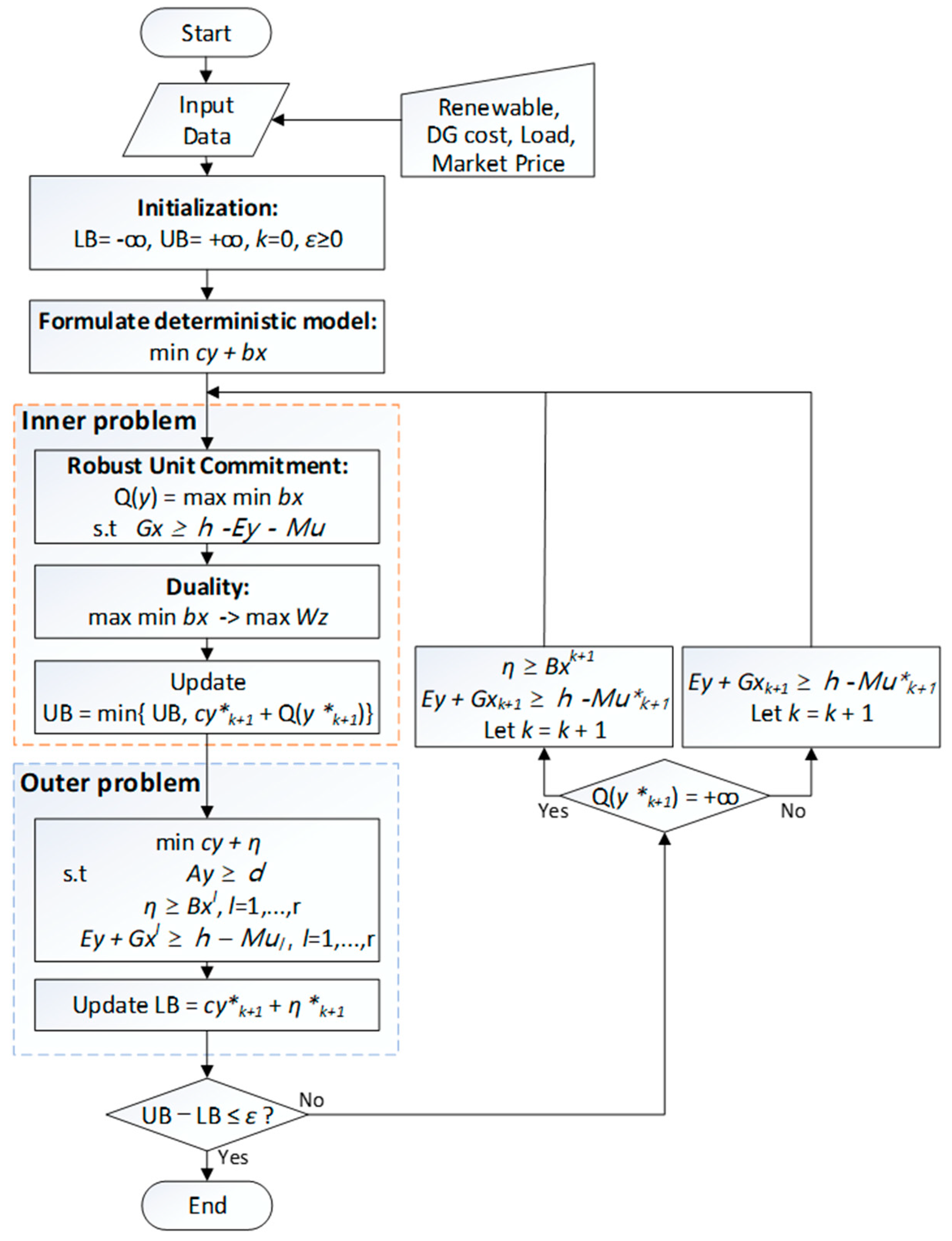
3.2. Adaptive Robust Optimization
3.2.1. Inner Problem
3.2.2. Outer Problem
3.2.3. Solution Method
4. Numerical Simulations
4.1. Input Data
4.2. Uncertainty in Arrival and Departure Times of EVs
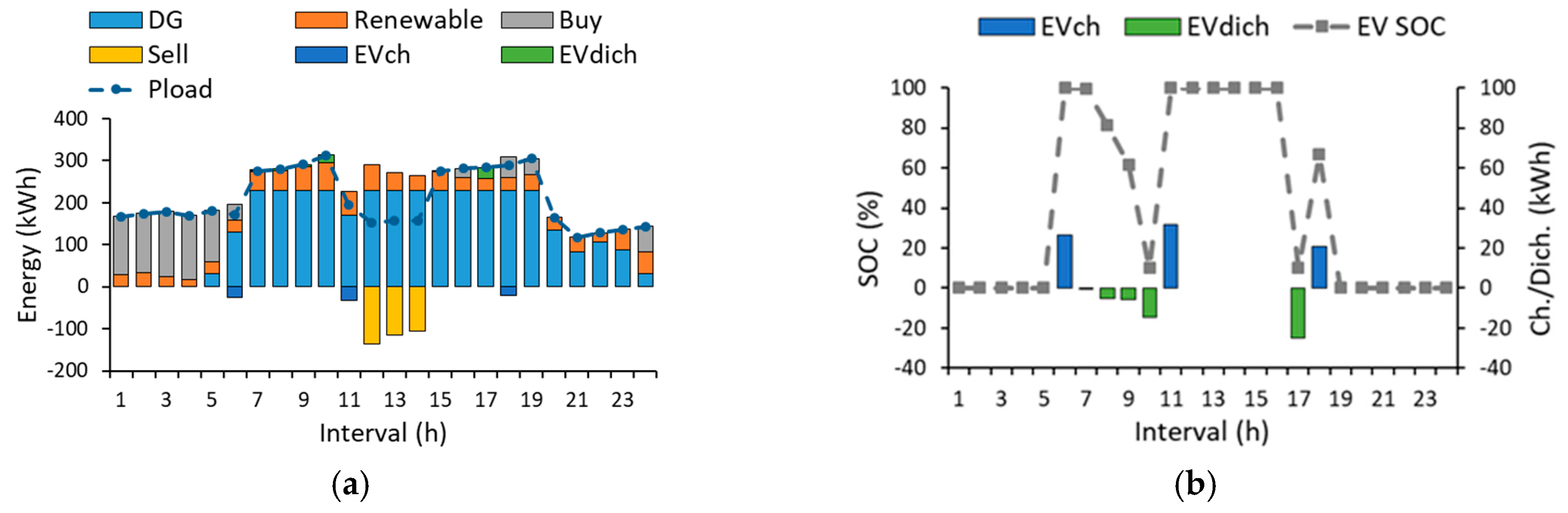
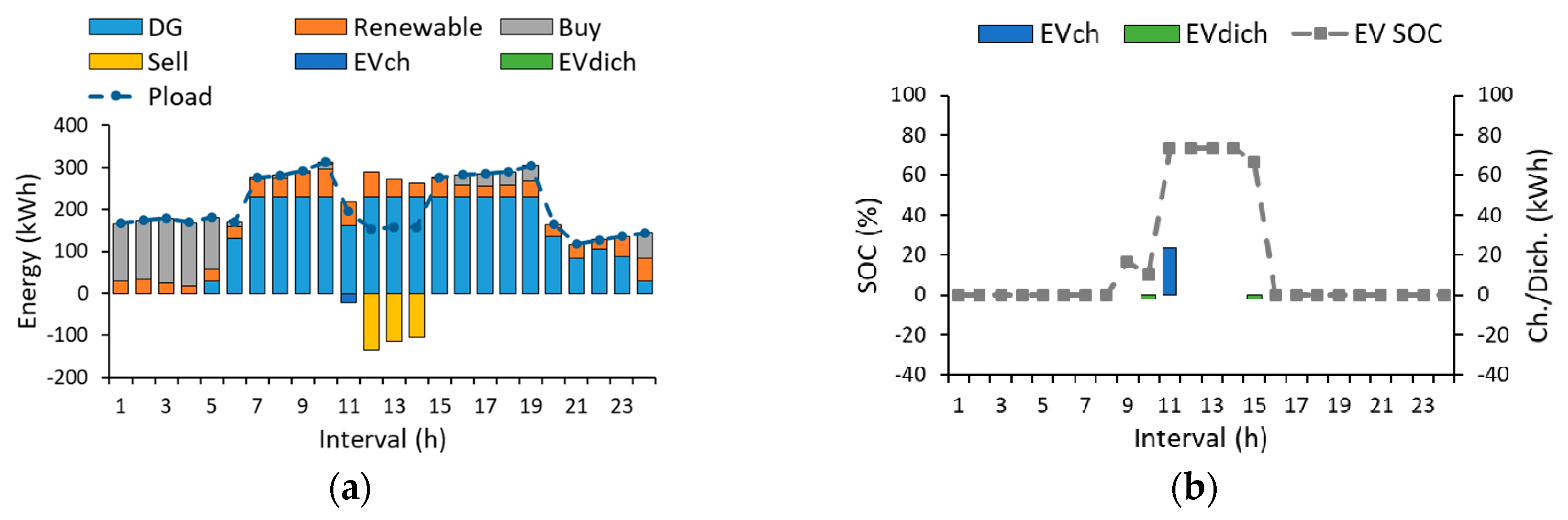
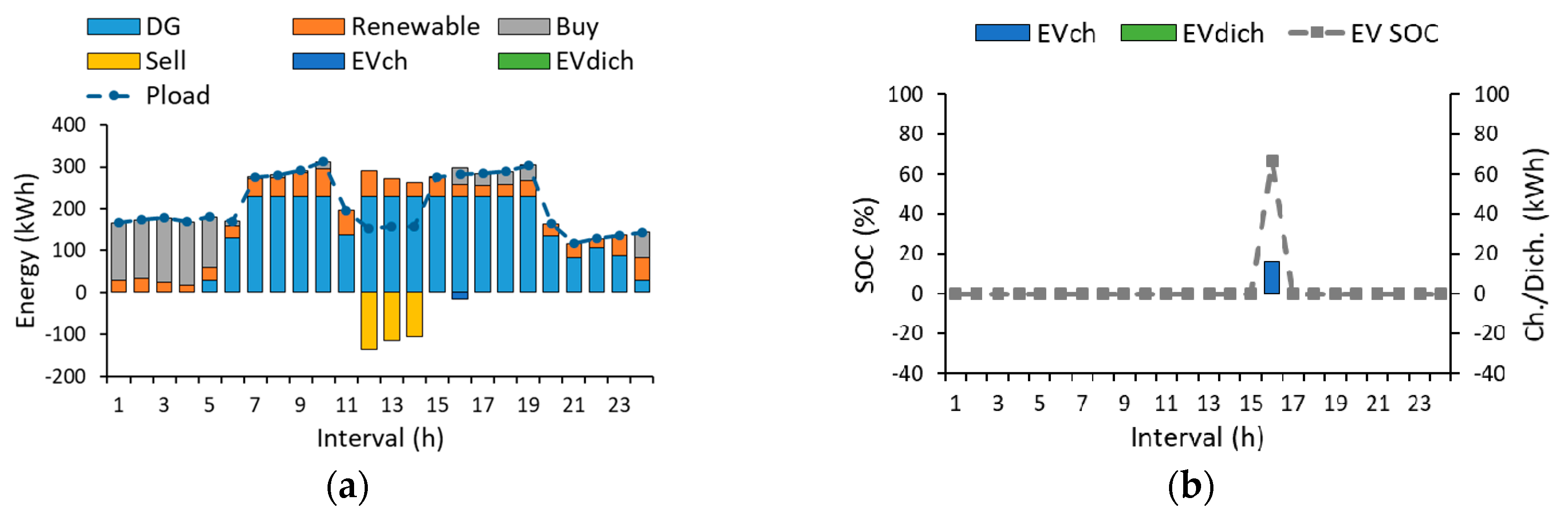
4.3. Discussion and Analysis
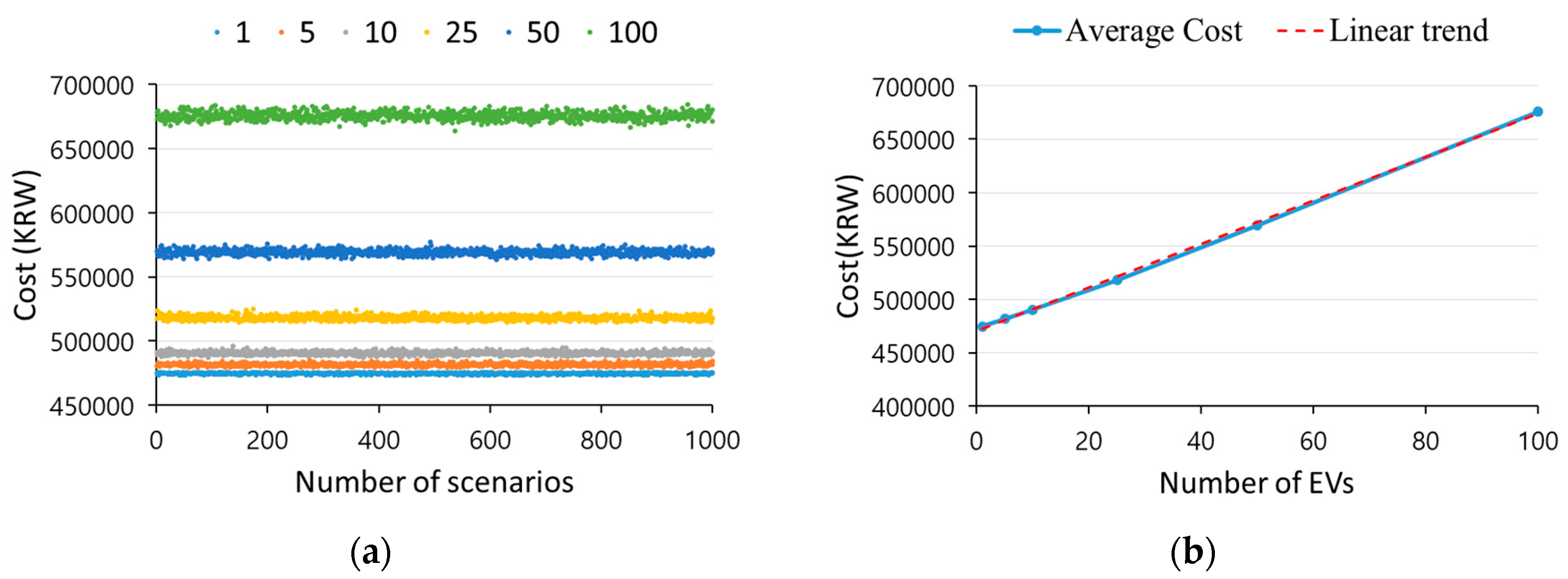
4.3.1. Budget of Uncertainty and Operation Cost
4.3.2. Number of EVs and Operation Cost
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| t | Index of time, running from 1 to T |
| d | Index of dispatchable generators, running from 1 to D |
| e | Index of electric vehicles, running from 1 to E |
| k | Index of iteration times, running from 1 to K |
| ta, td | Arrival and departure times of EV |
| Ua, Ud | Uncertain arrival and departure times of EV |
| Identifier for running status of DG d at t | |
| Identifier for start-up status of DG d at t |
| Running cost of dispatchable unit d | |
| Start-up cost of dispatchable unit d | |
| Generation cost of dispatchable unit d | |
| Price for buying and selling power from the utility grid at t | |
| Amount of power generated by dispatchable unit d at t | |
| Forecasted prices of buying and selling at t | |
| Forecasted electrical load at t | |
| Forecasted power of renewable energy resource at t | |
| Amount of electrical energy charged/discharged to/from EV unit e at t | |
| Limits of charging amount of EV unit e | |
| Limits of discharging amount of EV unit e | |
| Minimum, maximum, and departure SOC of EV unit e | |
| Capacity and initial electrical energy amount of EV unit e | |
| Charging/discharging efficiencies of EV unit e | |
| Ramp-up/down limits of dispatchable unit d | |
| Upper and lower bounds of dispatchable unit d at t | |
| Upper and lower bounds of renewable at t | |
| Upper and lower bounds of load at t | |
| Upper and lower bounds of buying price at t | |
| Upper and lower bounds of selling price at t | |
| Weights of renewable, load, buying price, and selling price prediction at t | |
| Upper and lower bounds of arrival time of EV | |
| Upper and lower bounds of departure time of EV | |
| Bounded arrival and departure times of uncertainty bounds at t | |
| Variables for uncertain buying and selling prices at t | |
| Variables for uncertain load and renewable at t | |
| Dual variables for dispatchable generator unit d at t | |
| Dual variable for load and renewable at t | |
| Dual variables for ramp-up and ramp-down limits unit d at t | |
| Dual variables for EV unit e at t |
References
- Hatziargyriou, N.; Asano, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Beer, S.; Gómez, T.; Dallinger, D.; Momber, I.; Marnay, C.; Stadler, M.; Lai, J. An economic analysis of used electric vehicle batteries integrated into commercial building microgrids. IEEE Trans. Smart Grid 2012, 3, 517–525. [Google Scholar] [CrossRef]
- Parashar, S.; Swarnkar, A.; Niazi, K.R.; Gupta, N. Optimal integration of electric vehicles and energy management of grid connected microgrid. In Proceedings of the IEEE Transportation Electrification Conference, Pune, India, 13–15 December 2017. [Google Scholar]
- IRENA. Electricity Storage and Renewables: Costs and Markets to 2030; International Renewable Energy Agency: Abu Dhabi, UAE, 2017. [Google Scholar]
- Khodaei, A.; Bahramirad, S.; Shahidehpour, M. Microgrid planning under uncertainty. IEEE Trans. Power Syst. 2015, 30, 2417–2425. [Google Scholar] [CrossRef]
- Zhao, L.; Zeng, B. Robust unit commitment problem with demand response and wind energy. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Liu, J.; Chen, H.; Zhang, W.; Yurkovich, B.; Rizzoni, G. Energy management problems under uncertainties for grid-connected microgrids: A chance constrained programming approach. IEEE Trans. Smart Grid 2017, 8, 2585–2596. [Google Scholar] [CrossRef]
- Sáez, D.; Ávila, F.; Olivares, D.; Cañizares, C.; Marín, L. Fuzzy prediction interval models for forecasting renewable resources and loads in microgrids. IEEE Trans. Smart Grid 2015, 6, 548–556. [Google Scholar] [CrossRef]
- Papaioannou, D.I.; Papadimitriou, C.N.; Dimeas, A.L.; Zountouridou, E.I.; Kiokes, G.C.; Hatziargyriou, N.D. Optimization & Sensitivity Analysis of Microgrids using HOMER Software—A Case Study. In Proceedings of the IEEE Mediterranean Conference on Power Generation, Transmission, Distribution and Energy Conversion, Athens, Greece, 2–5 November 2014. [Google Scholar]
- Chren, S.; Buhnova, B. Local load optimization in smart grids with Bayesian networks. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Budapest, Hungary, 9–12 October 2016. [Google Scholar]
- Liang, R.H.; Liao, J.H. A fuzzy-optimization approach for generation scheduling with wind and solar energy systems. IEEE Trans. Power Syst. 2007, 22, 1665–1674. [Google Scholar] [CrossRef]
- Su, W.; Wang, J.; Roh, J. Stochastic energy scheduling in microgrids with intermittent renewable energy resources. IEEE Trans. Smart Grid 2014, 5, 1876–1883. [Google Scholar] [CrossRef]
- Lazaroiu, G.C.; Dumbrava, V.; Balaban, G.; Longo, M.; Zaninelli, D. Stochastic optimization of microgrids with renewable and storage energy systems. In Proceedings of the IEEE Environment and Electrical, Westin, Pune, India, 13–15 December 2017. [Google Scholar]
- Shahidehpour, M. Security-Constrained Unit Commitment with Stochastic Constraints. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007. [Google Scholar]
- Bouffard, F.; Galiana, F.D. Stochastic Security for Operations Planning With Significant Wind Power Generation. IEEE Trans. Power Syst. 2008, 23, 306–316. [Google Scholar] [CrossRef]
- Hussain, A.; Bui, V.H.; Kim, H.M. Robust optimization-based scheduling of multi-microgrids considering uncertainties. Energies 2016, 9, 278. [Google Scholar] [CrossRef]
- Hussain, A.; Bui, V.H.; Kim, H.M.; Im, Y.H.; Lee, J.Y. Optimal operation of tri-generation microgrids considering demand uncertainties. Int. J. Smart Home 2016, 10, 131–144. [Google Scholar] [CrossRef]
- Craparo, E.; Karatas, M.; Singham, D.I. A robust optimization approach to hybrid microgrid operation using ensemble weather forecasts. Appl. Energy 2017, 201, 135–147. [Google Scholar] [CrossRef]
- Zhao, L.; Zeng, B. An Exact Algorithm for Two-Stage Robust Optimization with Mixed Integer Recourse Problems. University of South Florida, 2012. Available online: http://www.optimization-online.org/DB_FILE/2012/01/3310.pdf (accessed on 2 October 2018).
- Zeng, B.; Zhao, L. Solving two-stage robust optimization problems using a column-and-constraint generation method. Oper. Res. Lett. 2011, 41, 457–461. [Google Scholar] [CrossRef]
- Atamtürk, A.; Zhang, M. Two-stage robust network flow and design under demand uncertainty. Oper. Res. 2007, 55, 662–673. [Google Scholar] [CrossRef]
- Gupta, R.A.; Nand, K.G. A robust optimization based approach for microgrid operation in deregulated environment. Energy Convers. Manag. 2015, 93, 121–131. [Google Scholar] [CrossRef]
- Bertsimas, D.; Litvinov, E.; Sun, X.A.; Zhao, J.; Zheng, T. Adaptive robust optimization for the security constrained unit commitment problem. IEEE Trans. Power Syst. 2013, 28, 52–63. [Google Scholar] [CrossRef]
- Lorca, A.; Sun, X.A. Adaptive robust optimization with dynamic uncertainty sets for multi-period economic dispatch under significant wind. IEEE Trans. Power Syst. 2015, 30, 1702–1713. [Google Scholar] [CrossRef]
- Vagropoulos, S.I.; Bakirtzis, A.G. Optimal bidding strategy for electric vehicle aggregators in electricity markets. IEEE Trans. Power Syst. 2013, 28, 4031–4041. [Google Scholar] [CrossRef]
- Sachan, S.; Adnan, N. Stochastic charging of electric vehicles in smart power distribution grids. Sustain. Cities Soc. 2012, 40, 91–100. [Google Scholar] [CrossRef]
- Lotfi, H.; Khodaei, A. An efficient preprocessing approach for uncertainty consideration in microgrids. In Proceedings of the IEEE Transmission and Distribution Conference and Exposition (T&D), Dallas, TX, USA, 2–5 May 2016. [Google Scholar]
- Bui, V.H.; Hussain, A.; Kim, H.M. A multiagent-based hierarchical energy management strategy for multi-microgrids considering adjustable power and demand response. IEEE Trans. Smart Grid 2016, 9, 1323–1333. [Google Scholar] [CrossRef]
- Morais, H.; Kádár, P.; Faria, P.; Vale, Z.A.; Khodr, H.M. Optimal scheduling of a renewable micro-grid in an isolated load area using mixed-integer linear programming. Renew. Energy 2010, 35, 151–156. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, S.; Mozafari, B.; Solimani, S.; Niknam, T. An Adaptive Modified Firefly Optimisation Algorithm based on Hong’s Point Estimate Method to optimal operation management in a microgrid with consideration of uncertainties. Energy 2013, 51, 339–348. [Google Scholar] [CrossRef]
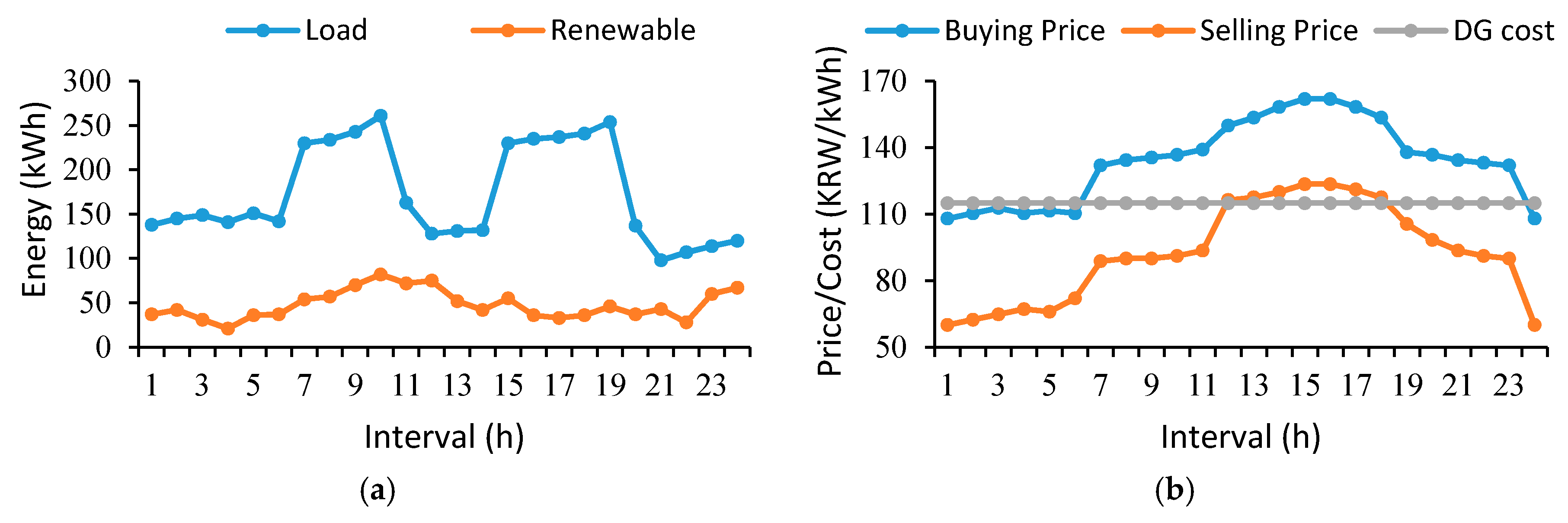
| Components | Min. (kWh) | Max. (kWh) | Departure SOC (%) | ||
|---|---|---|---|---|---|
| DG | 30 | 200 | – | – | – |
| EVs | 3 | 30 | 70 | 95 | 95 |
| Budget of Uncertainty | Cost (KRW) | Increasing Rate (%) |
|---|---|---|
| 0 | 473,399 | 0 |
| 1 | 474,004 | 0.12 |
| 2 | 474,222 | 0.17 |
| 3 | 474,482 | 0.22 |
| 4 | 474,551 | 0.24 |
| 5 | 474,591 | 0.25 |
| 6 | 474,591 | 0.25 |
| 7 | 474,623 | 0.26 |
| 8 | 474,623 | 0.26 |
| 9 | 475,333 | 0.41 |
| 10 | 475,333 | 0.41 |
| EV Number | 1 | 5 | 10 | 25 | 50 | 100 |
|---|---|---|---|---|---|---|
| Max. (KRW) | 475,333 | 484,855 | 495,791 | 524,877 | 577,323 | 684,352 |
| Min. (KRW) | 473,339 | 479,242 | 487,336 | 514,553 | 563,576 | 664,140 |
| Average (KRW) | 474,536 | 481,609 | 490,554 | 518,142 | 569,138 | 675,694 |
| Max. deviation (KRW) | 1138 | 3243 | 5238 | 6740 | 8181 | 11,555 |
| Min. deviation (KRW) | 14.4 | 5.5 | 2.5 | 1.2 | 1.0 | 0.9 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, S.-H.; Hussain, A.; Kim, H.-M. Adaptive Robust Optimization-Based Optimal Operation of Microgrids Considering Uncertainties in Arrival and Departure Times of Electric Vehicles. Energies 2018, 11, 2646. https://doi.org/10.3390/en11102646
Choi S-H, Hussain A, Kim H-M. Adaptive Robust Optimization-Based Optimal Operation of Microgrids Considering Uncertainties in Arrival and Departure Times of Electric Vehicles. Energies. 2018; 11(10):2646. https://doi.org/10.3390/en11102646
Chicago/Turabian StyleChoi, Se-Hyeok, Akhtar Hussain, and Hak-Man Kim. 2018. "Adaptive Robust Optimization-Based Optimal Operation of Microgrids Considering Uncertainties in Arrival and Departure Times of Electric Vehicles" Energies 11, no. 10: 2646. https://doi.org/10.3390/en11102646
APA StyleChoi, S.-H., Hussain, A., & Kim, H.-M. (2018). Adaptive Robust Optimization-Based Optimal Operation of Microgrids Considering Uncertainties in Arrival and Departure Times of Electric Vehicles. Energies, 11(10), 2646. https://doi.org/10.3390/en11102646






