Abstract
Using a pseudo-random sequence to encode the transmitted waveform can significantly improve the working efficiency and depth of detection of electromagnetic exploration. The selection of parameters of pseudo-random sequence plays an important role in correlation identification and noise suppression. A discrete cycle correlation identification method for extracting the earth impulse response is proposed. It can suppress the distortion in the early stage of the excitation field and the glitches of the cross correlation function by traditional method. This effectively improves the accuracy of correlation identification. The influence of the order and the cycles of m-series pseudo-random coding on its autocorrelation properties is studied. The numerical results show that, with the increase of the order of m-sequence, the maximum out-of-phase periodic autocorrelation function decreases rapidly. Therefore, it is very beneficial to achieve synchronization. The limited-cycle m-sequences have good autocorrelation properties. As the period of the m-sequence increases and the width of the symbol decreases, the overall autocorrelation becomes closer to the impact function. The discussion of the influence of symbol width and period of m-sequence on its frequency bandwidth and power spectral density shows that the narrower the symbol width, the wider its occupied band. The longer the period, the smaller the power spectral line spacing. The abilities of m-sequence to suppress DC (Direct-current) interference, Schumann frequency noise, and sine-wave noise are analyzed. Numerical results show that the m-sequence has excellent ability to suppress DC interference and Schumann frequency noise. However, for high-order harmonic noise, the correlation identification error appears severe oscillation in the middle and late stages of the impulse response. It indicates that the ability of m-sequence to suppress high-frequency sinusoidal noise is deteriorated. In practical applications, the parameters of the transmitted waveform should be reasonably selected in combination with factors including transmitter performance, hardware noise, and ambient noise level to achieve the best identification effect.
1. Introduction
The electromagnetic method is an important branch of geophysical exploration. With the features of high resolution, large depth of detection, and low cost, it has become an indispensable method in the field of resource detection. Based on the differences in conductivity, permeability, and dielectric properties of underground media, this method uses electromagnetic induction principles to observe and study the distribution of magnetotelluric responses. It establishes an underground electrical structure model to achieve underground target recognition [1,2,3]. However, there are some deficiencies in traditional artificial source exploration. For example, the controllable source audio magnetotelluric method (CSAMT) overcomes the shortcomings of magnetotelluric (MT) field source randomization and weak signal, but it still calculates the apparent resistivity according to the Kanyana formula. That is, it is necessary to measure a pair of orthogonal electrical and magnetic field components in the far area, thereby limiting its scope of application [4,5]. The odd harmonic scheme can obtain information of multiple frequencies at one time. However, the higher the harmonic order, the weaker the signal, resulting in difficulty in observation and greater errors [6,7]. Transient electromagnetic method (TEM) can be measured in the near area. However, due to the weak secondary field signal and low anti-interference ability, it is difficult to increase the detection depth [8,9,10].
On the other hand, with the development of social economy, electromagnetic interference has become stronger and stronger, which has brought a greater impact on electrical exploration. Interference noise in electromagnetic detection systems mainly includes natural electromagnetic field noise and human noise, such as noise from power line networks, mines or industrial electricity, cable broadcast networks and radio stations, and so on. Traditional electrical surveying usually uses methods such as increasing power supply, digital filters, and multiple stacking to suppress interference. However, for strong interference signals, it is difficult to obtain high signal-to-noise ratio electromagnetic signals using the above methods or instruments [11,12,13,14].
To further increase work efficiency and signal-to-noise ratio, geophysicists introduced pseudo-random sequences (PRBS) into the field of electrical surveying. This method records the emission current while observing the response, and uses the correlation operations of the two to extract the earth impulse response [15]. The m-sequence (maximal length sequence) in the PRBS is a positive–negative bipolar two-level signal that can be generated by a shift register with feedback. For an n-stage feedback linear shift register, the maximum binary sequence length generated by the appropriate tap feedback and modulo-2 adder is N = 2n − 1. In 1980, Duncan and Edwards of the University of Toronto in Canada applied m-sequences to electrical prospecting. By selecting an appropriate frequency bandwidth and transmitting-receiving distance, the detection of subsurface objects in the shallow (500 m) and deep (40 km) layers was completed [16]. In 1979, Cunningham applied pseudo-random sequence to the vibroseis control technology of seismic exploration, using its autocorrelation properties to effectively weaken the side lobes of seismic response and improve vertical resolution [17]. In 1982, He Jishan proposed pseudo-random electrical method based on the dual-frequency induced polarization method [18,19]. In about 2000, Ziolkowski, Hobbs, and Wright et al. of the University of Edinburgh established a multi-channel transient electromagnetic method (MTEM) based on correlation detection. It uses the extracted impulse response peak time or the late response of the multi-transmission step response to estimate the resistivity distribution of the earth and has achieved good results. Zhang W. et al. conducted a single-line MTEM survey in Baertaolegai-Fuxingmen silver-lead-zinc polymetallic ore investigation zone [20]. Xue G.Q. et al. summarized the research progress of MTEM and gave the field examples the MTEM method in the environment of land and sea [21,22]. Xie X. et al. confirm that time-lapse LOWTEM (long offset & window transient electromagnetic) will have bright prospects in remaining oil monitoring [23]. The results of Zhao G.Z. et al. show wavelet analysis is capable of detecting possible correlation between EM (electromagnetic) anomalies and seismic events [24]. He Jishan, Tang Jingtian, and Luo Weibin et al. have done a lot of research on theoretical analysis of pseudo-random sequence signals of controllable source electromagnetic methods and data interpretation of multi-channel electromagnetic pulses [25]. The success of the development of a pseudo-random electrical apparatus has greatly improved the research of the method.
Hyichev and Bobrovsky (2015) studied the anti-noise capability of m-sequence pseudo-random signals. The results show that the anti-noise performance of pseudo-random coding is about 100 times better than that of traditional methods [26]. In 2015, Wu Xin et al. proposed a mathematical method for extracting the earth impulse response with high accuracy through the receiver–transmitter cross correlation, and analyzed the parameters of the m-sequence launch waveform [27]. In 2016, Wang Xianxiang and his colleagues studied how to improve the anti-noise ability of pseudo-random sequences by analyzing two commonly used methods for extracting the earth impulse response [28]. Aiming at the problem that the traditional method uses linear correlation identification to extract the earth impulse response and produce large errors in the middle and late stages of the impulse response, this paper proposes a discrete cycle correlation identification method to extract the earth impulse response, which can effectively improve the identification accuracy. The anti-noise performances of this method to sine-wave noise, Schumann frequency noise, and DC interference are also analyzed, which provide a theoretical basis for the selection of the parameters of pseudo-random sequence electrical survey emission waveforms.
2. Earth Impulse Response Correlation Identification
2.1. Pseudo-Random Sequence Electromagnetic Detection Working Equipment
Compared with the conventional transient electromagnetic step source, the frequency spectrum of pseudo-random-coded signal source is relatively flat and has a wider frequency range. The observation device for pseudo-random sequence electromagnetic detection is shown in Figure 1. This method uses an electromagnetic signal encoded by a binary pseudo-random sequence as an excitation source, and the multi-component receiver is arranged in a line or parallel array with a transmitting dipole according to a certain transmission and reception distance. The profile measurement is completed by multiple superpositions by simultaneously recording the emission current signal and the electromagnetic field response of each transceiving distance. Where, the transceiving distance r and the target body depth d should generally satisfy: . The application of pseudo-random sequence signal sources and simultaneous measurement of multiple offsets enable high-density data acquisition, which helps to improve the resolution of electromagnetic detection. Through the deconvolution operation, we can separate the earth impulse response from the observed data and obtain geoelectrical section information. The related detection not only has strong anti-interference ability, but also can realize fine detection of small volume and large depth, and can work in marine, land, and other areas.
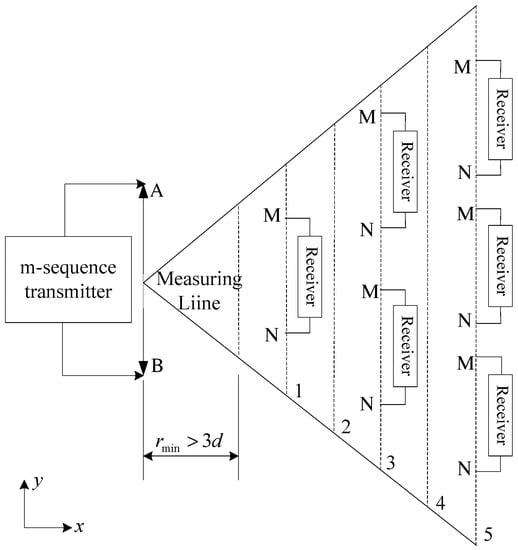
Figure 1.
Observation system of pseudo-random sequence electromagnetic detection.
Based on the Wiener–Hopf equation, the derivation process for extracting the ground impulse response from the m-sequence pseudo-random response (Ziolkowski in 2013) is detailed in Appendix A. In order to better simulate real observations, the observation sequence is generated by convolution of the ideal earth step response and derivative of actual emission current . The field excited by pseudo-random sequence can be obtained by:
where is the earth impulse response and is the ideal earth step response. In a uniform half space, the fields excited by the pulse wave and the upper step wave are [29]:
where . I represents the current intensity, dl is the length of the electrical source, is the resistivity, r is the transceiver distance, and erf is the error function.
2.2. Comparison of Identification Methods
In order to compare the effects of different methods for extracting the impulse response of earth, we use m-sequence to encode the electrical source emission waveform. The earth impulse response of a uniform half-space detection model is extracted by discrete linear correlation identification and discrete cyclic correlation identification methods, and compared with the theoretical calculation results. In the calculation, we take the uniform half-space resistivity , the length of emitted electric dipole , transceiver distance , the emission current amplitude , the symbol width , the order of the m-series , the number of cycles , and the number of sampling points after the end of emission is 100. The pseudo random emission current is shown in Figure 2a. The upper step response of the uniform half space obtained by Equation (11) is shown in Figure 2b.
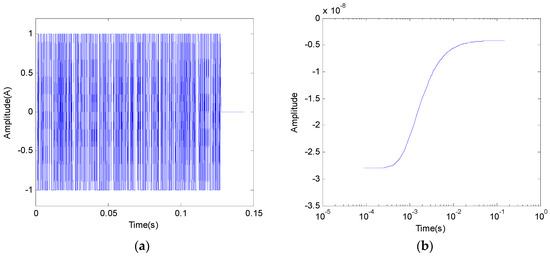
Figure 2.
Numerical calculation model. (a) Emission waveform; (b) uniform half-space step response.
It is worth noting that in the use of Equation (1) to calculate the field excited by pseudo-random sequence, we need to complete the discrete convolution calculation. Similarly, when the Equation (A8) is used to identify the earth impulse response, it is necessary to complete the discrete correlation calculation. Firstly, the impulse response of the earth is extracted by discrete linear convolution and discrete linear correlation. The identification results are shown in Figure 3. Figure 3a shows the field excited by a pseudo-random sequence calculated using discrete linear convolution, and Figure 3b is the cross-correlation function of the transmitted signal and the response signal. It can be seen that the excitation field calculated by the linear convolution has distortion at the early stage, which affects the further calculation of the cross-correlation function of the transmitted signal and its excitation field. Figure 3c shows the uniform earth impulse response extracted by the linear correlation identification method, which is compared with the ideal earth impulse response. Figure 3d represents the identification error of the discrete linear correlation identification. Here, we define the error ratio as:
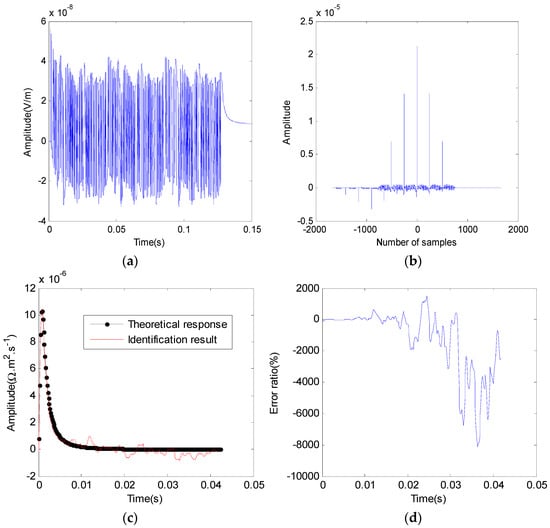
Figure 3.
Identification results of linear convolution and linear correlation. (a) The field excited by pseudo-random sequences; (b) cross correlation of emission signals and response signals; (c) the earth impulse response extraction result; (d) the identification error.
Among them, represents the earth impulse response extracted by correlation identification, and is the theoretical earth impulse response. It can be seen from Figure 3d that in the early stage of impulse response, the identification results agree well with the theoretical impulse response, and the error is small. However, with the passage of time, the identification error has increased dramatically. The identification error at peak time (t = 1 s) is −0.1918%. At about 10 times the peak response time, it has reached 127.62%, which seriously affects the identification accuracy of the earth impulse response.
In view of the influence of the above method on the identification of the ground impulse response, and considering the periodicity of m-sequence, the discrete cyclic convolution method is used to calculate the excitation field of the pseudo-random sequence. The definition of the N points cyclic convolution for and is:
In Equation (5), represents the main value interval of periodic sequences. The calculation process of discrete cyclic convolution is shown in Figure 4. In the calculation, is arranged in a counterclockwise direction on an equally divided circle, and is clockwise aligned on another circled circle concentric with it (Figure 4a). We turn counterclockwise through n points, that is, shift as a circle of n points (Figure 4b), multiply the corresponding points of x and , and then superimpose them to obtain [30].
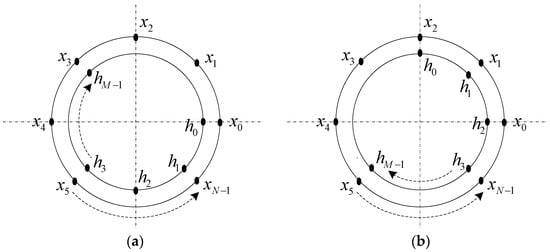
Figure 4.
Discrete cyclic convolution calculation. (a) Circular offset; (b) circular convolution.
The discrete cyclic convolution method is used to calculate the excitation field of the pseudo-random sequence, and the parameters of the transmitted signal are the same as before. The result is shown in Figure 5a. It can be seen that compared with Figure 3a, the discrete cyclic convolution method obviously eliminates the distortion phenomenon at the early stage of the excitation field. The cross correlation function between the emission signal and the excitation field is also calculated, as shown in Figure 5b. It can be seen that compared with Figure 3b, the burr phenomenon of the left half branch of the cross correlation function has been significantly suppressed. Thus, it lays a good foundation for further identifying the impulse response of the earth.
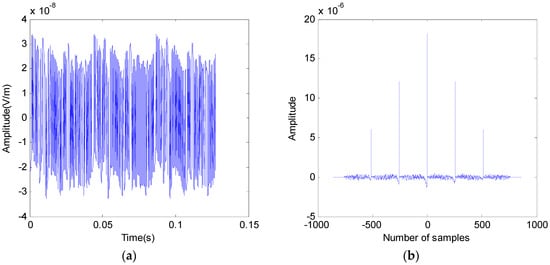
Figure 5.
Calculation result of discrete cycle correlation method. (a) The field excited by pseudo-random sequences; (b) cross correlation of emission signals and response signals.
According to Equation (A8), it is necessary to complete cross correlation calculation of m-sequence and its response signal when extracting the impulse response of the earth. Based on the calculation of the pseudo random sequence excitation field by cyclic convolution, the discrete cyclic cross correlation calculation of the transmitted signal and its excitation field is also completed. If and are all point finite sequences, then the cyclic correlation between and is defined as:
Here, cyclic correlation sequence is also point finite sequence. Usually, only the value of the principal value interval is considered. Then the Equation (6) can be simplified to:
The positive integer in Equation (7) is called cyclic correlation length, and can be selected as any integer with a maximum length of less than two sequences. In fact, the discrete cyclic correlation computation process is similar to the discrete cyclic convolution. In comparison Equations (5) and (6), it is easy to see that if the conjugate symbols in the correlation operation are removed and the relative positions of and n are changed in the , the correlation calculation becomes a convolution operation. In order to compare the effect of different convolution and correlation methods for the identification of earth impulse response, we use discrete cyclic convolution to calculate the excitation field of pseudo random sequence and identify the impulse response of the earth with discrete cyclic correlation. The results are shown in Figure 6. It can be seen that the identification results coincide well with the theoretical impulse response in the whole impulse response time. Although the identification error fluctuated in the late stage of impulse response, it did not exceed 0.3922%.
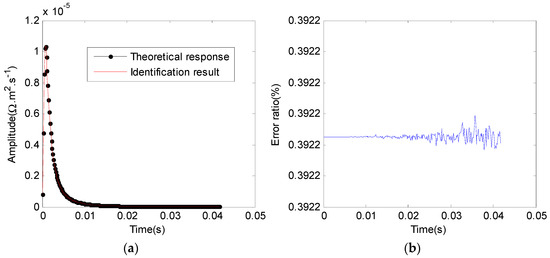
Figure 6.
Identification results of cyclic convolution and cyclic correlation. (a) The earth impulse response extraction result; (b) identification error.
Under quasi-static conditions, the propagation of electromagnetic waves in the earth satisfies the diffusion equation. The velocity of electromagnetic signals at different frequencies is very different in the medium with different conductivity. Therefore, the peak time of the earth impulse response can reflect the change of the resistivity. Ziolkowski (2007) et al. introduced the method of determining the earth resistivity by the peak time of impulse response:
In Equation (8), is the permeability of the medium, and indicates the peak time of the impulse response. For the calculation model shown in Figure 1, the uniform earth resistivity is known as 150 . The pseudorandom response of m-sequence is obtained by discrete cyclic convolution (Figure 5a), and the earth impulse response is obtained by using discrete cyclic correlation identification (Figure 6a). We calculate the peak time , and then use Equation (8) to invert the earth resistivity of 150.7964 . In this way, the correctness and effectiveness of the discrete cycle correlation and discrete cycle correlation identification methods are proved.
3. Correlation Identification Parameters Analysis
In geophysical exploration, it is important to select suitable m-sequence parameters for high-precision identification of earth impulse response. The m-sequence is a wideband signal with good randomness and cross-correlation characteristics. The autocorrelation function of m-sequence is a triangular wave similar to Dirichlet function. Its expression is as:
Here, is the period of m-sequence and is the sampling interval. Table 1 show the autocorrelation characteristics of m-sequences with different orders (different lengths). It can be seen that as the order n increases, the length of m-sequence increases obviously. The maximum heterogenous periodic autocorrelation function decreases rapidly, while the maximum periodic cross-correlation function is relatively large. It indicates that the m-sequence is very suitable for synchronization. We use m-sequence as the excitation signal for electromagnetic surveying. Simultaneously record the transmitted signal and the MT response at the receiver. By using correlation identification, accurate earth impulse response can be obtained.

Table 1.
The autocorrelation of m-sequence.
Figure 7 gives the global autocorrelation function of m-sequence with period , order , and cycle number . It can be seen that the global autocorrelation of the m-sequences of the finite number of cycles is aperiodic function, which contains several similar function peaks with different amplitudes, indicating that the pseudo-random sequence coded signal has a good autocorrelation property. The bigger the , the smaller the , the closer it is to the function.
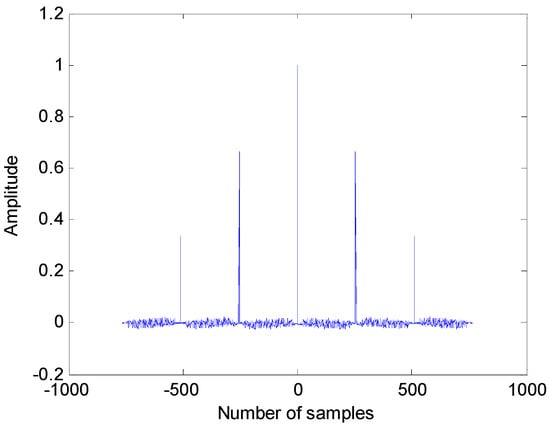
Figure 7.
Global autocorrelation function of finite order cyclic m-sequence.
We perform the Fourier transform of Equation (9) to obtain the power spectral density of the periodic m sequence:
where
It can be seen that the power spectral density of the periodic m-sequence has a linear spectrum, and the interval of each spectral line is determined by the fundamental frequency . The clock frequency affects the bandwidth occupied by this periodic signal. Figure 8 shows the influence of the period of m-sequence and the sampling interval on the power spectral density spectral line spacing and frequency bandwidth.
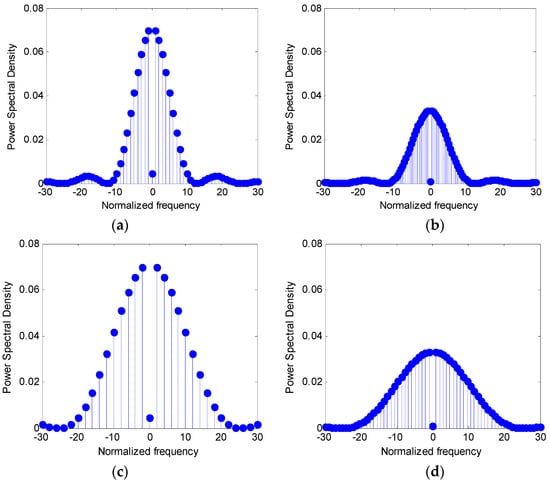
Figure 8.
Power spectral density (PSD) of periodic m-sequences with different periods and symbol widths. (a) PSD of m-sequences with N1 = 15 and ∆t1; (b) PSD of m-sequences with N2 = 31 and ∆t1; (c) PSD of m-sequences with N1 = 15 and ∆t1/2; (d) PSD of m-sequences with N2 = 31 and ∆t1/2.
To facilitate the comparison of the changes in spectral line spacing, we chose the same normalized frequency . Figure 8a,b is power spectral densities of m-sequences with periods , , and symbol width , respectively. As can be seen from the figures, when the period of the m-sequence is approximately doubled, the density of the spectral line is also doubled. Although the power is reduced to about half as the cycle is doubled, the basic shape of the power spectral density remains unchanged. Moreover, the two zero-component lines with respect to the normalized frequency are in the same place, indicating that the two sequences occupy the same bandwidth. Figure 8c,d is the power spectrum densities of m-sequence of periods and , respectively, but the sampling interval is . It can be seen that compared with Figure 8a,b, the zero component spectral lines of Figure 8c,d are at two times the frequency, indicating that their occupied bandwidth has doubled.
We use the m-sequence of period and cycle number as the transmitting signal. Under the condition of different symbol width, the earth impulse response is extracted by correlation identification. According to the peak time of the impulse response, the information of the formation resistivity obtained by inversion is shown in Table 2. It can be seen that as the symbol width decreases, the identification error tends to decrease as a whole. In the condition of , the identification error exceeds 25%, and the system has lost the ability to recognize the earth pulse response. When , the identification error reaches a minimum, only 0.531%. With the further decrease of the symbol width, the identification error is fluctuating. Therefore, in practical work, we need to combine the parameters such as period (order ) and cycle number to decide the symbol width of m-sequence.

Table 2.
Effect of m-sequence symbol width.
In summary, different symbol widths mean that the bandwidth of m-sequence is different. In order to realize the earth impulse response identification more completely, the narrower symbol width should be selected as much as possible while satisfying the transmission capability of the launcher and considering the storage capacity of the observation system. The selection of the period (or order ) of m-sequence should also take into account various factors. In theory, the longer the period , the better the signal-to-noise ratio of the system is improved by using m-sequence. However, the larger the period , the longer the observation time. Therefore, the observation process is not economical. In addition, when is too large, the ability of m-sequence to improve the signal to noise ratio also decreases.
4. Anti-Noise Performance Analysis of Correlation Identification
To study the anti-noise performance of discrete cyclic correlation identification method, we added different types of noise to the pseudo-random response. The earth impulse response is extracted in the presence of interference and compared to the theoretical impulse response. In China, the frequency of industrial electricity is 50 Hz. Interference noise is the level of 50 Hz and its harmonics. Although this interference level is greatly reduced as the receiver coil is far from the power line, it has regional characteristics. Some people have observed earth current fields with the frequency of 50 Hz and their harmonics in the Antarctic continent and the Tibet Plateau. This may be the surface circulation formed by electricity penetration into the earth. In view of this, we use the 8-order m-sequence with cycle number as the excitation signal, and add a noise signal in the pseudo-random excitation field. The amplitude of the noise signal and the amplitude of the excitation field of the pseudo-random signal are kept in the same level. The identification result is shown in Figure 9. Among them, Figure 9a is the noise signal added, Figure 9b is the cross-correlation function of m-sequence and the noise signal. Figure 9c is the earth impulse response extracted by the correlation identification method and it is overlapped with the theoretical impulse response. Figure 9d gives the identification error ratio. It can be seen that the pseudo-random signal has a strong ability to suppress sine-wave noise. The identification error of the whole impulse response is −6.99% to 3.898%.
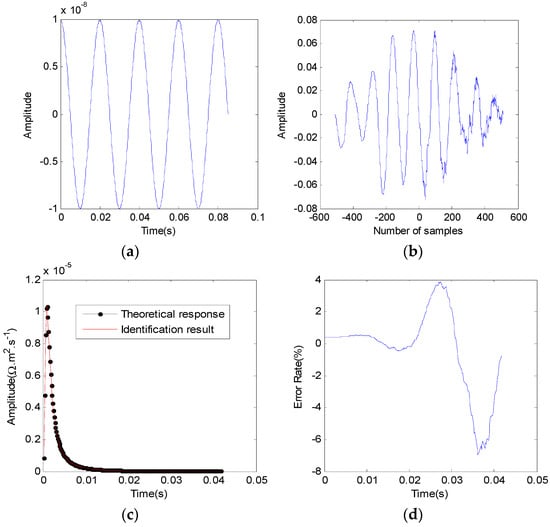
Figure 9.
The earth impulse response extracted with sine-wave noise. (a) Sinusoidal noise signal; (b) cross-correlation of m-sequence and noise signal; (c) earth impulse response extraction result; (d) identification error.
In order to study the ability of the pseudo-random transmit signal to suppress the sine wave noise, the effects of different parameters such as wave noise amplitude, initial phase, and frequency on the identification error are discussed below. Firstly, we examine the ability of m-sequence to suppress the sine-wave noise of different amplitudes. The frequency of the sine-wave noise is taken as 50 Hz and the range of amplitude variation is 10−7–10−9. Figure 10a shows the superposition of the excitation field of m-sequence and the sine-wave noise. We take the period of m-sequence , the symbol width . The amplitude of sine-wave noise is 10−7, 10−8 and 10−9, respectively. The identification errors obtained by the correlation identification method are shown in Figure 10b. It can be seen that when the sine wave noise amplitude is equal to or lower than that of the pseudo-random response, such as when the noise is or , the m-sequence has a strong suppression ability. The identification error ranges are −6.99–3.898% and −0.343–0.7427%. When the noise amplitude is amplified 10 times, that is, , the maximum value of the identification error reaches −73.12–35.45%. It is shown that when the noise signal amplitude is larger than the excitation field amplitude of the pseudo-random sequence, the m-sequence gradually weakens its noise immunity.
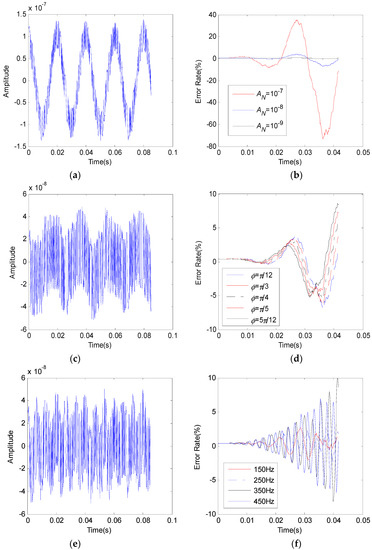
Figure 10.
Suppression of sinusoidal noise by m-sequence. (a) Superposition of excitation field and noise signal ; (b) identification error of different amplitude noise; (c) superposition of excitation field and noise signal ; (d) identification error of different phase noise; (e) superposition of excitation field and noise signal ; (f) identification error of different frequency noise.
Secondly, the ability of m-sequence to suppress the sinusoidal noise of different initial phases is analyzed. Figure 10c is the superposition of the m-sequence excitation field and the sine-wave noise . When the initial phase of sine-wave noise is and , respectively, the correlation identification errors are shown in Figure 10d. The identification results show that for the sinusoidal noise with initial phase , the identification error is −6.99% to 3.650%. For the sine wave noise whose initial phase is , the identification error range is −5.053% to 8.597%. It indicates that m-sequences have similar noise immunity to sine waves with different initial phases, and the identification error remains in the same order of magnitude.
Afterwards, we study the suppression ability of m-sequence to different harmonic components of 50 Hz sine wave noise. Figure 10e is the superposition of the m-sequence excited field and odd harmonic noise . Figure 10f gives the correlation identification errors when the noise source frequencies are 150, 250, 350, and 450 Hz, that is, the main odd harmonic components of 50 Hz frequency. The calculation results show that the recognition error of m-sequence for 150 Hz and 250 Hz harmonic noise is not much different, they are: −2.088–2.717% and −2.291–2.530%. However, with the increase of harmonic frequency, the anti-noise ability of m-sequence becomes worse. The identification errors for 350 Hz and 450 Hz harmonic noise are −8.147–9.951% and −6.820–6.921% respectively. It must be noted that with the increase of harmonic noise frequency, the identification error appeared severe oscillation in the middle and late stages of the impulse response. Obviously, the suppression ability of m-sequence to high frequency sine wave noise is worse in the middle and late stage of impulse response.
Natural electromagnetic field noise mainly comes from lightning activity, especially lightning related to thunderstorms. Due to the occurrence of thunderstorms in some parts of the earth, the electromagnetic fields generated propagate back and forth in the waveguide cavity and spread all over the world. The electromagnetic field caused by such lightning has a particularly high energy density in the frequency range of 1 to 1000 Hz. Due to the fast decay of high frequency components in the propagation process, low frequency components predominate in the field observed away from the lightning zone.
Because the waveguide cavity resonates at some frequencies, its electromagnetic field at frequencies of 8, 14, 20, 26 and 32 Hz is relatively weak, commonly referred to as the Schumann frequency. Obviously, the frequency range of the sky electric field falls within the operating frequency range of the electromagnetic system, and will exist in any area on the earth with a fairly high average value. For this reason, the ability of m-sequences to suppress Schumann frequency noise was studied. Figure 11a is the superposition of the m-sequence excitation field and the Schumann frequency noise with the frequency of 14 Hz. When the noise frequencies are taken at the frequency points of 8, 14, 20, 26 and 32 Hz, the correlation errors are shown in Figure 11b. As can be seen from the figure, the suppression ability of m-sequences for different Schumann frequency noises is not much different. The overall range of the identification error for the five frequency noises is within 7.110% to 3.495%. It indicates that m-sequence has strong anti-noise ability for Schumann frequency noise.
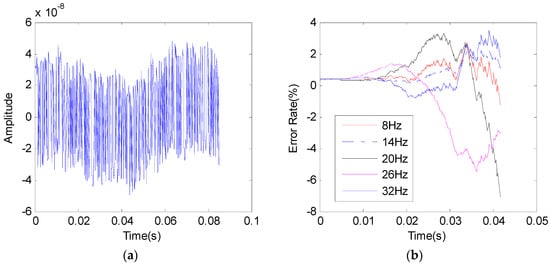
Figure 11.
Suppression of Schumann frequency noise by m-sequence. (a) Superposition of excitation field and Schumann frequency noise signal; (b) identification error of different Schuhmann frequency noise.
The following discusses the anti-noise ability of the correlation identification algorithm when there are natural potentials and constant current interference caused by electrode polarization in a pseudo-random response. Figure 12a shows the result of superimposing DC noise of amplitude 10−7 into the excitation field of the pseudo-random sequence. When the DC noise amplitude is taken as 10−7, 10−8 and 10−9, respectively, the correlation errors are shown in Figure 12b. The calculation results show that when the DC noise amplitude is higher than that of pseudo-random response by one order (noise amplitude is taken as 10−7), the maximum identification error in the entire impulse response period is −5.296%. When the DC noise amplitude is equivalent to the pseudo-random response amplitude (noise amplitude is 10−8), the maximum identification error is −0.1766%. When the DC noise amplitude is less than that of pseudo-random response by one order (noise amplitude is taken as 10−9), the maximum identification error is only 0.3353%. Therefore, when the DC noise amplitude is equal to or lower than the pseudo-random excitation field amplitude, the presence of DC interference hardly affects the identification result.
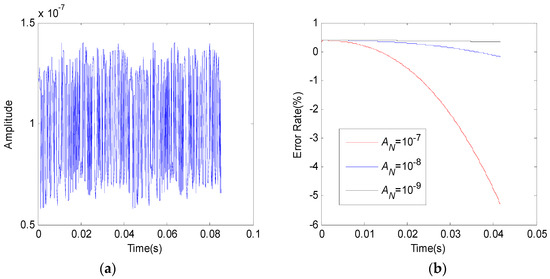
Figure 12.
Suppression of direct-current (DC) interference by m-sequence. (a) Superposition of excitation field and DC interference; (b) identification error of different DC interference.
5. Conclusions
Compared with the traditional step-wave emitters, the use of pseudo-random sequences to encode the electrical source can significantly increase the depth and resolution of electromagnetic detection. The earth impulse response extracted by the correlation identification method is rich in geoelectric information, so that the fine detection of the geoelectrical section can be realized. However, the accuracy of extracting the earth impulse response from different identification methods is not the same. Aiming at the problem that discrete linear correlation identification has a large error in the late stage of extracting impulse response, this paper proposes a method of extracting the earth impulse response by using discrete cyclic correlation identification. Using the discrete cyclic convolution to calculate the excitation field of m-sequence, the distortion of the early stage of the excitation field in the linear convolution calculation is effectively eliminated. The earth impulse response is extracted by discrete cyclic correlation identification. The numerical results show that the extraction results are in good agreement with the theoretical impulse response. The identification error is less than 0.3922% during the whole earth impulse response stage.
The autocorrelation function characteristics of different length m-sequences are analyzed. The results show that with the increase of the order n, the length of m-sequence increases obviously. The maximum out-of-phase periodic autocorrelation function decreases rapidly, but the maximum periodic cross-correlation function is relatively large. Therefore, it is very beneficial to achieve synchronization. The autocorrelation function and its power spectral density of a finite-cycle m-sequence are calculated. The influence of the order n, the period , and the symbol width of m-sequence on its spectral bandwidth and the power spectral density are also analyzed. Numerical results show that the narrower the symbol width, the greater the bandwidth of the m-sequence, and the longer the period, the denser the power spectral density of it. However, the longer observation time will affect the observation efficiency.
The anti-noise performance of the discrete cyclic correlation identification method is studied in the case of sinusoidal noise, Schumann frequency noise, and DC interference. The results show that m-sequence has a strong ability to suppress the Schumann frequency noise, and the identification error of the five frequency noises is generally within the range of −7.110% to 3.495%. When the DC noise amplitude is equal to or less than that of the pseudo-random sequence excited field, the presence of DC interference hardly affects the identification result. The effects of parameters such as amplitude, initial phase, and frequency of sine-wave noise on the identification error are also discussed. When the amplitude of sinusoidal noise is equal to or less than that of the pseudo-random response, the m-sequence has a strong ability to suppress it, and the identification error is −6.959–3.898%. For sinusoidal noise with different initial phases or different frequencies, the m-sequence has little change in its suppression ability, and the identification error remains in the same order of magnitude. However, for the high order harmonic noise, the identification error creates serious oscillation in the middle and late stages of the impulse response, which should be paid attention to in the correlation identification. Therefore, in practical work, the parameters of m-sequence should be selected and optimized according to the noise of the hardware system and the influence of the environmental noise, so as to achieve the best identification.
Author Contributions
X.S. and X.W. conceived and designed the correlation identification method; X.S. and Z.D. performed the numerical calculation; X.S., X.Z. and X.F. analyzed the anti-noise performances; All authors have contributed to the editing and proofreading of this paper.
Funding
This research was funded by National Natural Science Foundation of China under grant number41604122; and PetroChina Innovation Foundation under grant number 2017D-5007-0305.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Based on the Wiener–Hopf equation, the basic principle of extracting the earth impulse response method from the m-series pseudo-random response is shown in Figure A1. Among them, is the emission current, is the impulse response of the earth, is the response of the launcher, is the response of the receiver, is the noise, and is the observed system response.

Figure A1.
Schematic diagram of geoelectric correlation identification system.
The observed signal takes into account the effects of the instrument response of launcher, instrument response of receiver, the impulse response of the earth and noise interference. It can be expressed as:
where the actual emission current waveform is . At the signal launcher, it is common to measure the voltage with the same instrument as the receiver system, i.e.,
Based on the Wiener–Hopf equation, we correlate the measured voltage at the launcher with the signal measured at the receiver, i.e.,
In the above equation, represent the cross-correlation function of the transmitting voltage and the receiving voltage, the autocorrelation function of the transmitting voltage, and the cross-correlation function of the transmitting voltage and the noise, respectively. Since the transmit waveform uses m-series pseudo-random signals, it has a low correlation with the noise sequence. The autocorrelation function approximates the function , such that is approximately equal to . Equation (A3) is a continuous equation. For ease of calculation, it should be discretized. We take the sampling interval as , the total number of sampling points is , and the number of earth impulse response points is , then the above equation can be discretized as:
where
The above equation can be converted to a matrix, that is:
where
The impulse response of the earth can be obtained by solving Equation (A8). In fact, still represent noise. It reflects the ability of m-sequence to suppress noise, or the identification bias due to interference.
References
- Su, B.; Yu, J.; Sheng, C. Maxwell-equations based on mining transient electromagnetic method for coal mine-disaster water detection. Elektron. Elektrotech. 2017, 23, 20–23. [Google Scholar] [CrossRef]
- Chen, W.J.; Hao, Q.Q.; Chu, S.X.; Liu, J.M.; Liu, H.T.; Jiang, X. Application of very low frequency electromagnetic method to positioning of concealed metal deposits: An example of copper polymetallic ore occurrences in the southwest greater Hinggan mountains. Geol. Explor. 2017, 53, 528–532. [Google Scholar]
- Sharma, S.P.; Biswas, A.; Baranwal, V.C. Very low-frequency electromagnetic method: A shallow subsurface investigation technique for geophysical applications. In Recent Trends Modelling of Environmental Contaminants; Springer: New Delhi, India, 2014; pp. 119–141. [Google Scholar]
- Mittet, R.; Morten, J.P. The marine controlled-source electromagnetic method in shallow water. Geophysics 2013, 78, E67–E77. [Google Scholar] [CrossRef]
- Luo, Y.; Xu, Y.; Yang, B.; Liu, Y. Sensitivity study of three-dimensional marine controlled-source electromagnetic method. J. Appl. Geophys. 2017, 146, 46–53. [Google Scholar] [CrossRef]
- Zonge, K.L.; Sauck, W.A.; Sumner, J.S. Comparison of time, frequency, and phase measurements in induced polarization. Geophys. Prospect. 2010, 20, 626–648. [Google Scholar] [CrossRef]
- Hughes, L.; Zonge, L.; Van Reed, E.; Carlson, N.; Lide, C.; Urquhart, S.; Wynn, J.; Young, G.N.; Roth, J. Memorials: An appreciation of Kenneth L. Zonge (1936–2013). Lead. Edge 2014, 33, 354–356. [Google Scholar] [CrossRef]
- Huang, H.; Feng, L.I. Application of transient electromagnetic method in coal mine gob. Value Eng. 2014, 7, 321–326. [Google Scholar]
- Xi, Z.; Long, X.; Huang, L.; Zhou, S.; Song, G.; Hou, H.; Chen, X.; Wang, L.; Xiao, W.; Qi, Q. Opposing-coils transient electromagnetic method focused near-surface resolution. Geophysics 2016, 81, E279–E285. [Google Scholar] [CrossRef]
- El-Kaliouby, H.; Abdalla, O. Application of time-domain electromagnetic method in mapping saltwater intrusion of a coastal alluvial aquifer, North Oman. J. Appl. Geophys. 2015, 115, 59–64. [Google Scholar] [CrossRef]
- Azpúrua, M.A.; Pous, M.; Silva, F. A measurement system for radiated transient electromagnetic interference based on general purpose instruments. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, Dresden, Germany, 16–22 August 2015; pp. 1189–1194. [Google Scholar]
- Powell, S.R.; Tazebay, M.V. Transceiver Self-Diagnostics for Electromagnetic Interference (EMI) Degradation in Balanced Channels. U.S. Patent 9379772, 28 June 2016. [Google Scholar]
- Zhai, L.; Lin, L.; Zhang, X.; Song, C. The effect of distributed parameters on conducted EMI from DC-Fed motor drive systems in electric vehicles. Energies 2017, 10, 1. [Google Scholar] [CrossRef]
- Huangfu, Y.; Pang, S.; Nahid-Mobarakeh, B.; Rathore, A.; Gao, F.; Zhao, D. Analysis and design of an active stabilizer for a boost power converter system. Energies 2016, 9, 934. [Google Scholar] [CrossRef]
- Roinila, T.; Luhtala, R.; Salpavaara, T.; Verho, J.; Messo, T.; Vilkko, M. Rapid high-frequency measurements of electrical circuits by using frequency mixer and pseudo-random sequences. Model. Identif. Control 2016, 37, 113–119. [Google Scholar] [CrossRef]
- Duncan, P.M.; Hwang, A.; Edwards, R.N.; Bailey, R.C.; Garland, G.D. The development and applications of a wide band electromagnetic sounding system using a pseudo-noise source. Geophysics 1980, 45, 1276–1296. [Google Scholar] [CrossRef]
- Cunningham, A.B. Some alternate vibrator signals. Geophysics 2012, 44, 332. [Google Scholar] [CrossRef]
- He, J.S. Wide field electromagnetic sounding methods. J. Cent. South Univ. 2015, 41, 1065–1072. [Google Scholar]
- He, J.; Li, D.; Dai, S. Shale gas detection with wide field electromagnetic method in north-western Hunan. Oil Geophys. Prospect. 2014, 49, 1006–1012. [Google Scholar]
- Zhang, W.W.; Di, Q.Y.; Lei, D.; Ma, F.S. Multi-channel transient electromagnetic method: A new geophysical method and its application in exploring metallic ore deposits. Gold Sci. Technol. 2018, 26, 1–8. [Google Scholar]
- Xue, G.Q.; Xin, W.U.; Hai, L.I.; Di, Q.-Y. Progress of multi-transient electromagnetic method in abroad. Prog. Geophys. 2016, 31, 2187–2191. [Google Scholar]
- Zhong, H.S.; Xue, G.Q.; Xiu, L.I.; Zhi, Q.Q.; Di, Q.-Y. Pseudo wavefield extraction in the multi-channel transient electromagnetic (MTEM) method. Chin. J. Geophys. 2016, 59, 4424–4431. [Google Scholar]
- Xie, X.; Lei, Z.; Yan, L.; Hu, W. Remaining oil detection with time-lapse long offset & window transient electromagnetic sounding. Oil Geophys. Prospect. 2016, 51, 605–612. [Google Scholar]
- Zhao, G.Z.; Bi, Y.X.; Wang, L.F.; Han, B.; Wang, X.; Xiao, Q.B.; Cai, J.; Zhan, Y.; Chen, X.; Tang, J.; et al. Advances in alternating electromagnetic field data processing for earthquake monitoring in china. Sci. China Earth Sci. 2015, 58, 172–182. [Google Scholar] [CrossRef]
- He, J.S. Closed addition in a three-element set and 2n sequence pseudo-random signal coding. J. Cent. South Univ. 2010, 41, 632–637. [Google Scholar]
- Ilyichev, P.V.; Bobrovsky, V.V. Application of pseudonoise signals in systems of active geoelectric exploration (results of mathematical simulation and field experiments). Seism. Instrum. 2015, 51, 53–64. [Google Scholar] [CrossRef]
- Xin, W.U.; Xue, G.Q.; Di, Q.-Y.; Zhang, Y.M.; Fang, G.Y. Accurate identification for the electromagnetic impulse response of the earth with pseudo random coded waveforms. Chin. J. Geophys. 2015, 58, 2792–2802. [Google Scholar]
- Wang, X.X.; Di, Q.Y.; Wang, M.Y.; Deng, J.Z. A study on the noise immunity of electromagnetic methods based on m pseudo-random sequence. Chin. J. Geophys. Chin. Ed. 2016, 59, 1861–1874. [Google Scholar]
- Fang, W.Z.; Li, X.; Li, Y.G. The whole-zone definition of apparent resistivity used in the frequency domain electromagnetic methods. J. Xi’an Coll. Geol. 1992, 14, 81–86. (In Chinese) [Google Scholar]
- Antoniou, A. Digital Signal Processing; McGraw-Hill: New York, NY, USA, 2016. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).