Energy Consumption Prediction of a Greenhouse and Optimization of Daily Average Temperature

Abstract

Greenhouses are high energy-consuming and anti-seasonal production facilities. In some cases, energy consumption in greenhouses accounts for 50% of the cost of greenhouse production. The high energy consumption has become a major factor hindering the development of greenhouses. In order to improve the energy efficiency of the greenhouse, it is important to predict its energy consumption. In this study, the energy consumption mathematical model of a Venlo greenhouse is established based on the principle of energy conservation. Three optimization algorithms are used to identify the parameters which are difficult to determine in the energy consumption model. In order to examine the accuracy of the model, some verifications are made. The goal of achieving high yield, high quality and high efficiency production is a problem in the study of greenhouse environment control. Combining the prediction model of greenhouse energy consumption with the relatively accurate weather forecast data for the next week, the energy consumption of greenhouse under different weather conditions is predicted. Taking the minimum energy consumption as the objective function, the indoor daily average temperatures of 7 days are optimized to provide the theoretical reference for the decision-making of heating in the greenhouse. The results show that the optimized average daily temperatures save 9% of the energy cost during a cold wave.

1. Introduction

Greenhouses represent a trend in agricultural development that indicates the level of agricultural modernization of a region. It is necessary to regulate the greenhouse environment to obtain high yields. The energy consumption of light-supplementation, dehumidification, heating, cooling and other measures in a greenhouse, is known as the basic energy consumption. Another part of the energy consumption is for driving the actuators. The basic energy consumption could account for more than 90% of the total energy consumption in the greenhouse [1]. In order to improve the management level of the greenhouse, it is of great importance to study the prediction of greenhouse energy consumption.

Mature prediction models of greenhouse energy consumption have been established both at home and abroad. De Zwart [2] used the greenhouse climate and control model KASPRO to simulate the greenhouse microclimate and predict the greenhouse energy consumption. Gupta and Chandra [3] studied the effect of various energy conservation measures to arrive at a set of design features for an energy efficient greenhouse. Su et al. [4] used fuzzy logic systems to track the temperature and humidity in the greenhouse. Spanomitsios [5] studied the efficiency and estimation of energy consumption in thin film greenhouses under different strategies. Based on the greenhouse microclimate model, Dai et al. [6] analyzed the influence of canopy transpiration and established a greenhouse energy consumption prediction model. Xu et al. [7] took glass-type greenhouses as the research object, analyzed the greenhouse radiation, convection, heat and mass exchange caused by crop transpiration, to establish a greenhouse temperature and humidity model. Combing with weather forecast information for the outdoor temperature, Ren et al. [8] used CFD methods, taking wet curtain-fan, solar radiation and other factors of greenhouse into consideration, and established a temperature prediction model of a large multi-span plastic greenhouse located in southern Jiangsu (China). However, there is great uncertainty about the selection of model parameters in the traditional greenhouse modeling process, and the model is not universal once it is established. It should be noted that the most commonly used method of black-box modeling for a nonlinear system was based on neural network, which was applied to establish the greenhouse model by Patil et al. [9], Ferreira et al. [10], Nabavi-Pelesaraei et al. [11], Kavga and Kappatos [12], Fourati [13] and Frausto and Pieters [14]. Trejoperea et al. [15] estimated greenhouse energy consumption by using neural networks, and proved that the model gave a better estimation of energy consumption, with an accuracy of 95%. However, neural networks are easily over-trained when the training data is inadequate. Since plant-related parameters in the energy model of greenhouse can be considered as constants only within a few days, it is almost impossible to collect all possible data to develop an accurate energy model.

Consequently, the large number of unknown parameters involved are an important problem appearing in any mathematical model, which require complex instrumentation and experimentation to find the right values. In order to find these appropriate values and avoid experimental issues, some proposals exist to handle this situation. In [16,17,18,19] the authors presented different methodologies based on heuristic methods for the parameter search of a greenhouse mathematical model. Similarly, based on new algorithms, Chen et al. [20,21] illustrated that the predicted heat power consumption performs a better accuracy in an experimental greenhouse. In [22] the authors presented the application and comparison of a collection of methods based on Particle Swarm Optimization (PSO) and Differential Evolution (DE), using them as the tools to identify the parameters that completed a proposed mathematical model for a greenhouse. However, these greenhouse energy consumption studies mainly focus on proposing new algorithm to improve the accuracy of the model, ignoring the analysis of using the model under actual conditions. Typically, the validation of these models is based on known data from the past rather than that in the future.

Due to the large number of parameters in the greenhouse mathematical model, some parameters are difficult to determine. In order to increase the accuracy of greenhouse physical models, three optimization algorithms are applied to adjust uncertain parameters of energy model. In this paper, taking better performance of computation speed and accuracy as the goal, an optimized model prediction methodology is presented. According to the best result of our optimized model, the energy consumption of the greenhouse under different weather conditions is predicted and this provides a theoretical reference for decision-making about heating in a greenhouse. Furthermore, this study provides a detailed description of how to use this model in practical situations and validates the energy efficiency in the field. Compared with the abovementioned references, the main contribution of this work is the comparison of three algorithms to estimate the parameters of a mathematical greenhouse model, and the application of the resulting prediction model to optimize the daily average temperature for one week to improve the energy efficiency in a greehouse.

2. Methodology

The temperature change in greenhouses is influenced by various heat and mass transfer processes. Therefore, to establish a relatively accurate greenhouse environmental system model, it is significant to study in details the mechanism of these heat and mass transfer processes. In winter greenhouse heating is affected by various factors such as the weather, crop growth and climate control devices. The dynamic process is mainly the energy exchange occurring inside and outside of the greenhouse. Therefore, the modeling of the greenhouse environment system consists in establishing the mathematical equations of these dynamic processes based on the thermodynamic theory. According to the principle of energy balance, we can establish the energy model of each dynamic processes.

2.1. Experimental Materials

The study object of this work is the Chongming greenhouse, located at 31°57′ N, 121°7′ E, whose length, breadth and height were 38 m, 24 m, 7.5 m, and which uses natural ventilation windows (divided into north and south top windows), an indoor heater and ground source heat pump (Figure 1).

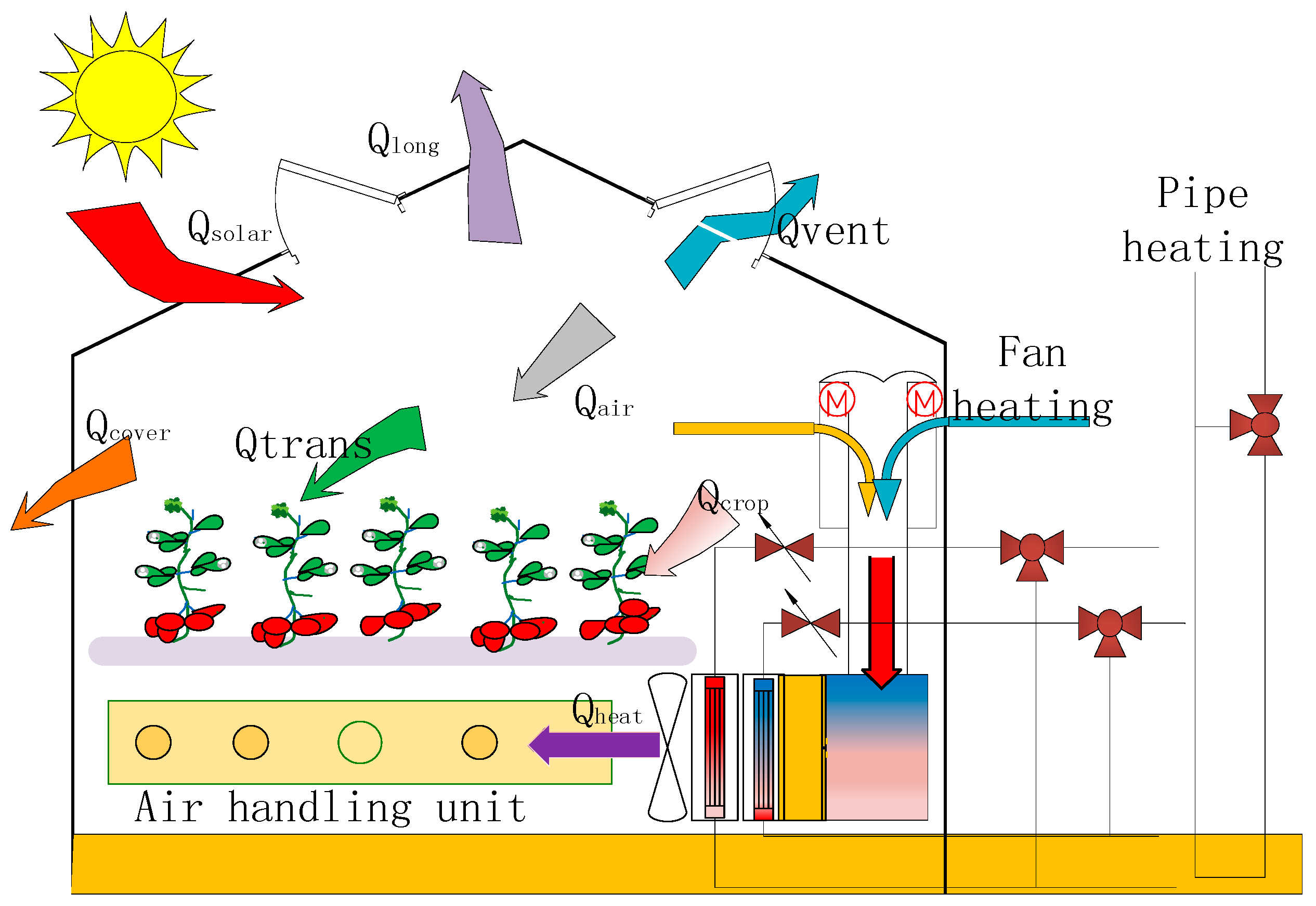
2.2. Greenhouse Mathematical Model

Energy exchange between the greenhouse and the outside environment involves many factors (Figure 1), including indoor heating pipes, fan heating, ventilation, indoor and outdoor long-wave radiation [23]. Based on the principle of conservation of energy, the rate of change of air temperature inside the greenhouse is expressed as the result of heat exchange between the inside and outside of the greenhouse. Taking the greenhouse as a whole, the energy required for heating the greenhouse can be expressed as the energy absorbed by the greenhouse minus the solar radiation. The energy transferred to the greenhouse by heating is $Q_{heat}(\mathrm{W})$, and is expressed by the following formula:

$$Q_{heat}=Q_{long}+Q_{vent}+Q_{cover}+Q_{trans}+Q_{air}+Q_{crop}-Q_{solar}$$

(1)

Heat transfer from heat pump to the inside greenhouse air depending on the difference between supply water and return water can be calculated as:

$$Q_{heat}={\rho }_{water}·c_{water}·v_{water}·(T_{in}(t)-T_{opt}(t))$$

(2)

where ${\rho }_{water}$ is water density $(\mathrm{kg}·{\mathrm{m}}^{-3})$, $c_{water}$ is the specific heat capacity of water $(\mathrm{J}·{\mathrm{kg}}^{-1}·°{\mathrm{C}}^{-1})$, $v_{water}$ is the flow rate of water in the pipeline $(\mathrm{m}·{\mathrm{s}}^{-1})$, $T_{in}(t)$, $T_{opt}(t)$ are the temperature of supply water and return water respectively (°C).

The thermal radiation transferring from the greenhouse inside to outside is significant for the greenhouse microclimate and can be expressed by the following formula:

$$Q_{long}=\epsilon ·S_g·K·[{(T_{air}(t)+273.15)}^4-{(T_{out}(t)+273.15)}^4]·X_{cover}$$

(3)

where $\epsilon$ is the mutual emission coefficient between the cover and the sky, $S_g$ is greenhouse cover surface area $({\mathrm{m}}^2)$, K is the Stefan-Boltzmann constant $(\mathrm{W}·{\mathrm{m}}^2·{\mathrm{k}}^{-4})$, $T_{air}(t)$ is the air temperature inside the greenhouse (°C), $T_{out}(t)$ is the air temperature outside the greenhouse (°C), and $X_{cover}$ is influence coefficient of external glass.

The energy loss due to ventilation depends on the inside temperature, windows opening and the outside temperature, which is expressed by the following formula [24]:

$$Q_{vent}=S_{gw}·C_d{\left[2g\frac{\Delta T_{air}}{T_{out}}\left(\frac{A_{roof}^2·A_{side}^2}{A_{roof}^2+A_{side}^2}\right)+{\left(\frac{A_{roof}+A_{side}}{2}\right)}^2{C}_w{V}_{wind}^2\right]}^{0.5}[T_{air}(t)-T_{out}(t)]{\rho }_{air}·c_{air}$$

(4)

where $S_{gw}$ is greenhouse ground surface area (${\mathrm{m}}^2)$, $C_d$ is the vent discharge coefficient, $C_w$ is the wind pressure coefficient, g is gravity acceleration coefficient $(\mathrm{m}·{\mathrm{s}}^{-2})$, $T_{air}$ is the air temperature inside the greenhouse (°C), $T_{out}$ is the air temperature outside the greenhouse $(°\mathrm{C}$), $A_{roof}$ is area ratio of top windows to the ground, $A_{side}$ is area ratio of side windows to ground, $V_{wind}$ is outdoor wind speed $(\mathrm{m}·{\mathrm{s}}^{-1})$, ${\rho }_{air}$ is air density $(\mathrm{kg}·{\mathrm{m}}^{-3})$, $C_{air}$ is specific heat capacity of air $(\mathrm{J}·{\mathrm{kg}}^{-1}·{\mathrm{K}}^{-1})$;

$$A_{side}=U_{vent}·A_{N,side}$$

(5)

$$A_{roof}=U_{vent}·A_{N,roof}$$

(6)

$U_{vent}$ is open percentage of top windows, $A_{N,side}$ is the maximum area of side windows, and $A_{N,roof}$ is the maximum area of top windows.

The energy exchange from the cover to the outside air is associated with conduction and convection, which depends on the difference between the air temperature outside and inside. Hence, the heat losses through the cover can be calculated as:

$$Q_{cover}=S_g·X_{screen}·X_{glass}·(T_{air}(t)-T_{out}(t))$$

(7)

$X_{screen}$ is coefficient of internal $\mathrm{thermal}$ curtain infiltration, $X_{glass}$ is influence coefficient of external glass $(\mathrm{W}·{\mathrm{m}}^{-2}·{\mathrm{K}}^{-1})$.

The energy exchange between the inside air with plants is related to plant transpiration and respiration of plant canopy, which depends on the inside air, carbon dioxide concentration, and the relative humidity. The energy exchange between plants with the inside air can be calculated as [25]:

$$Q_{trans}=\frac{2{\rho }_{air}·c_{air}·\mathrm{LAI}}{\Delta H·\gamma ·(r_b+r_s)}(V{P}_{can}-V{P}_{air})S_{gw}·L_{water}$$

(8)

where LAI is leaf area index, $\Delta H$ is water evaporation latent heat constant $(\mathrm{J}·{\mathrm{kg}}^{-1}$), $\mathsf{\gamma }$ is the psychometric constant, $r_s$ and $r_b$ are the somatic resistances and aerodynamic of the leaves respectively $(\mathrm{s}·{\mathrm{m}}^{-1})$, $L_{water}$ is the latent heat of evaporation for the leaf surface $(\mathrm{J}·{\mathrm{kg}}^{-1})$. $r_b$ and $r_s$ are affected by variations in canopy temperature, air temperature, concentration, and solar radiation above the canopy, which can be calculated using the following formula:

$$r_s=r_{smin}\frac{R_{can}+4.3}{R_{can}+0.6}(1+X_{co2}{({\rho }_{co2}-200)}^2)·(1+X_p{(V{P}_{can}-V{P}_{air})}^2)$$

(9)

$r_{smin}$ is the minimum somatic resistances of the leaves $(\mathrm{s}·{\mathrm{m}}^{-1})$, $X_{co2}$ is influence coefficient of carbon dioxide on the stomatal opening degree, $X_p$ is influence coefficient of saturated vapor pressure, ${\rho }_{co2}$ is the carbon dioxide concentration (ppm):

$$R_{can}=0.9·{\tau }_{cov}[1-(1-{\tau }_{scr})U_{scr}]·I_{glob}$$

(10)

is the solar radiation of the canopy $(\mathrm{W}·{\mathrm{m}}^{-2})$. And ${\tau }_{cov}$ is the transition coefficient of covering material, ${\tau }_{scr}$ is influence coefficient of shading net, $U_{scr}$ is open percentage of shading net, $I_{glob}$ is outdoor solar radiation flux $(\mathrm{W}·{\mathrm{m}}^{-2})$, $V{P}_{can}$ is the crop canopy saturated vapor pressure and can be expressed as:

$$V{P}_{can}=2.229\times {10}^{11}·e^{\frac{5385}{T_{can}+273.15}}$$

(11)

where $T_{can}$ is the temperature of crop canopy, $V{P}_{air}$ can be expressed as:

$$V{P}_{air}=\frac{H_{air}·R·(T_{air}+273.15)}{M_{H_{2}O}}\times {10}^{-3}$$

(12)

where R is the molar gas constant $(\mathrm{J}·{\mathrm{kmol}}^{-1}·{\mathrm{K}}^{-1})$, $H_{air}$ is the relative humidity, and $M_{H_{2}O}$ is the molar mass of water $(\mathrm{kg}·{\mathrm{kmol}}^{-1})$.

Heat flux of air is expressed by the temperature difference between inside air in time of t and time of t − 1, which can be expressed as:

$$Q_{air}={\rho }_{air}·v_g·c_{air}·\frac{T_{air}(t)-T_{air}(t-1)}{\Delta t}.$$

(13)

where v_g is greenhouse volume $({\mathrm{m}}^3)$, $T_{air}(t)$ is the temperature at time t ($°\mathrm{C}$), and $\Delta t$ is the difference in time between t and t − 1, with a value of 300 (s).

Heat transfer from plant to greenhouse air depending on the difference between inside air and plant canopy can be calculated as:

$$Q_{crop}=2S_{gw}·\mathrm{LAI}·\frac{{\rho }_{air}·c_{air}[T_{air}(t)-T_{leaf}(t)]}{r_b}$$

(14)

The solar radiation that penetrates the greenhouse cover is added into the greenhouse, and the energy absorbed by the greenhouse can be expressed as:

$$Q_{solar}=S_g·0.9·{\tau }_{cov}[1-(1-{\tau }_{scr})U_{scr}]·I_{glob}$$

(15)

where $I_{glob}$ is the outdoor radiation $(\mathrm{W}·{\mathrm{m}}^{-2})$.

The parameters in the mathematical model are analyzed according to the measured environmental parameters and energy consumption values inside and outside the greenhouse. Then, the parameters in the model are divided into constant and uncertain parameters. The constant parameters in the model are shown in

Table 1. Constant physical parameters in a greenhouse model.

Parameters	Physical Meaning	Value	Unit
LAI	Leaf area index	2	m2·m−2
Sg	Greenhouse cover surface area	1842	m2
K	Stefan–Boltzmann constant	$5.67\times {10}^{-8}$	W·m−2·K−4
g	Gravity acceleration	9.8	m·s−2
AN,side	Maximum area of side windows	0.10	m2·m−2
AN,roof	Maximum area of top windows	0.18	m2·m−2
ρair	Air density	1.2	kg·m−3
cair	Specific heat capacity of air	1008	J·kg−1·K−1
ΔH	Water evaporation latent heat constant	$2.45\times {10}^6$	J·kg−1
γ	Psychometric constant	65.8	Pa·K
Sgw	Greenhouse ground surface area	912	m2
rsmin	Minimum somatic resistances of the leaves	82	s·m−1
Lwater	Latent heat of evaporation for the leaf surface	$2.45\times {10}^6$	J·kg−1
$M_{H_{2}O}$	Molar mass of water	18	kg·kmol−1
R	Molar gas constant	8314	J·kmol−1·K−1
νg	Greenhouse volume	6840	m−3
rb	Aerodynamic resistances of the leaves	275	s·m−1
ρwater	Water density	1000	kg·m−3
cwater	Specific heat capacity of water	4200	J·kg−1·°C−1

.

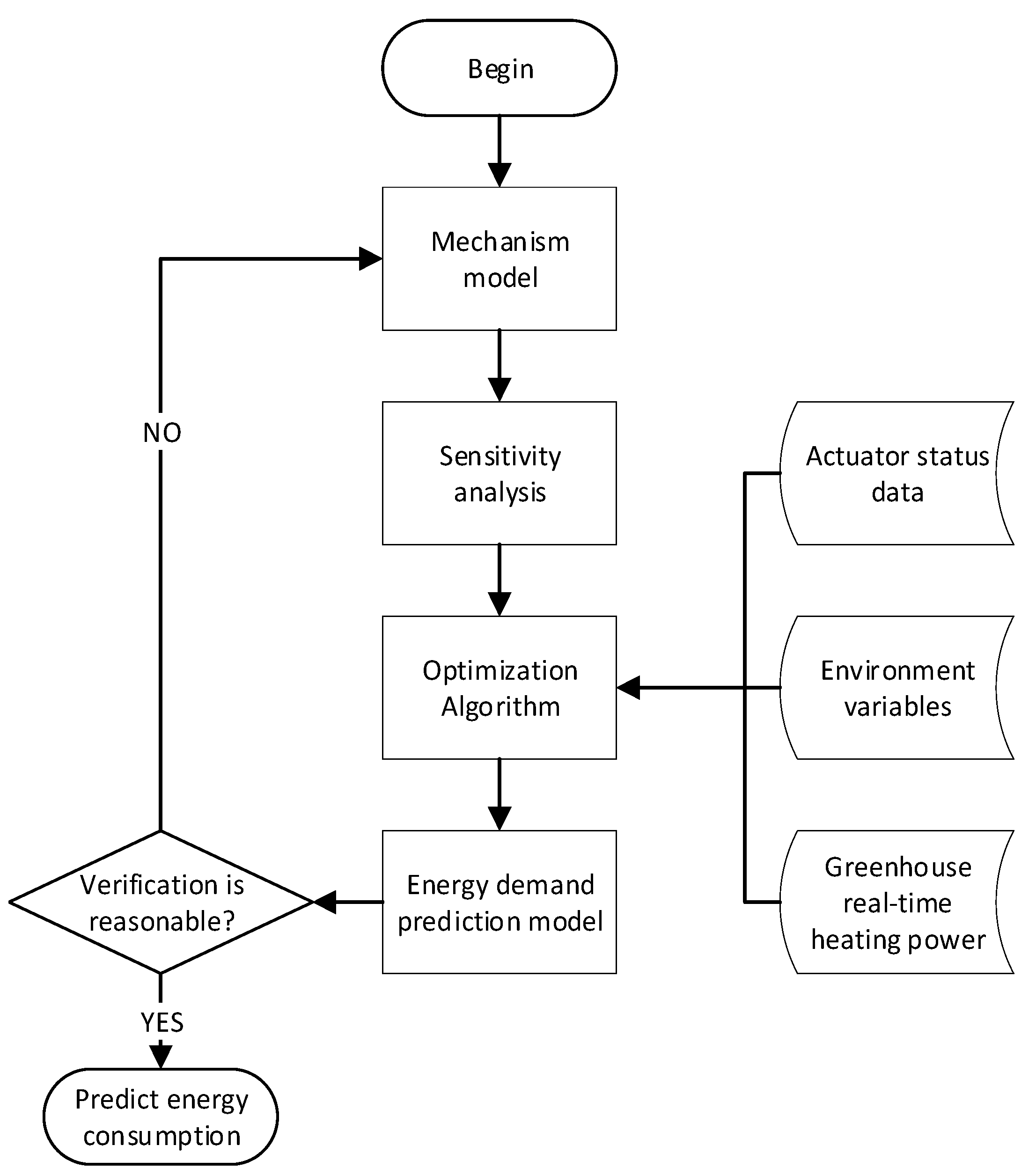
2.3. Method of Optimizing Parameters

According to the principle of conservation of energy, physical sub-models of various energy flow processes are established. As shown in Figure 2, based on each sub-model, a greenhouse energy consumption prediction model is established. The physical parameters of the greenhouse were inspected in the field. In addition, the measured data of the sensors inside and outside the greenhouse were collected and regulated. The environmental parameters such as temperature, humidity, light and wind speed inside and outside greenhouse were input into the model. In order to increase the accuracy, three optimization algorithms were used to identify the uncertain parameters. The output of the model was compared with the measured energy consumption. Consequently, the eight uncertain parameters were validated by using the data inside and outside of the greenhouse on different days.

2.4. Optimization Algorithms

Particle Swarm Optimization (PSO) is a parallel algorithm [26]. On the basis of observing the behavior of animal clusters, PSO uses the information sharing among individuals to make the entire crowd in the space of solution from disorder to orderly evolution, so as to obtain the optimal solution. In this algorithm, each particle has two characteristics of velocity and position, and the updating formula of the velocity and position of each particle in the optimization process is expressed as:

$$v_i^{k+1}=\omega ·v_i^k+c_1·r_1·(P_i^k-x_i^k)+c_2·r_2·(g^{best}-x_i^k)$$

(16)

$$x_i^{k+1}=x_i^k+v_i^{k+1}$$

(17)

$v_i^{k+1}$ in the above formula represents the speed of i-th particle in the k-th population evolution, and $\omega$ is inertia weight. $c_1$ and $c_2$ are the learning factor and the social factor respectively. $r_1$ and $r_2$ are the random number between (0, 1). $P_i^k$ is the local optimal solution of the i-th particle after the k-th evolution. $x_i^k$ is the i-th particle’s position in the k-th evolution, and $g^{best}$ is the global optimal solution. PSO presents a series of characteristics that makes it the first choice in the algorithm selection for this research:

• PSO has a real valued representation that allows avoiding the conversion to binary field and backwards, which is common in many heuristic algorithms.
• PSO presents a swarm behavior, which is a sufficient approach in search spaces of considerable extension, due to the capability of exploration in steps of different lengths and the communication between particles, which share the information of the best results.
• PSO is well known, therefore, there exists many publications about it, and numerous variations have already been proposed, in order to tackle problems of considerable complexity. In addition, there are already a lot of references about PSO calibration and stability.

Differential evolution algorithm (DE) [27], like PSO, as described in [28], is a computational algorithm based on the manipulation of a population of candidate solutions, applicable for complex search problems. It presents a series of interactions between the candidate solutions to produce new individuals, and such new members are tested and catalogued by a cost function, seeking for the survival of only the ones with the best performance. The characteristics that makes it a suitable option are enlisted below:

• DE is recognized as a greedy search algorithm. This marks the difference between the PSO and the DE, and allows to check whether the group behavior is better than the greedy search in the questions raised in this study.
• DE requires only two calibration factors, and the definition of these factors is quite small. This defines DE as a simple calibration algorithm.

Genetic algorithm (GA) [29], in the reference [30], is used to simulate natural selection and natural genetic process of reproduction, mating and mutation, one by one to produce the preferred individuals, and finally get the best individual. Genetic algorithm is also an adaptive search algorithm, its selection, crossover, mutation and other operations are carried out in the form of probability, there is a good global optimization and solving skills. The characteristics that makes it a suitable option are listed below:

• Genetic algorithms are often used to generate high-quality solutions to optimize and search for problems, relying on bio-inspired operators such as crossover, mutation and selection.
• Genetic algorithm simultaneously treats multiple individuals in a group, that is, evaluates multiple solutions in the search space, reduces the risk of falling into the local optimal solution, and simultaneously the algorithm itself is easy to realize parallelization.

According to the output of the energy consumption prediction model $Q_{heat}$ and the actual energy consumption $Q_{water}$, the objective function is formulated as follows.

$$f_i=\sqrt{\frac{1}{n}{{\displaystyle \sum }}_{t=1}^n{[Q_{heat}(t)-Q_{water}(t)]}^2}$$

(18)

Actually, the objective function means root-mean-square error (RMSE) in mathematics. Each individual is represented by a vector $X=[\epsilon ,X_{cover},C_d,C_w,X_{screen},X_{glass},{\tau }_{cov},{\tau }_{scr}]$, where $\mathsf{\epsilon },X_{cover},C_d,C_w,X_{screen},X_{glass},{\tau }_{cov}\mathrm{and}{\tau }_{scr}$ have been mentioned before. The ranges of these parameters are given in

Table 2. The optimized parameters results with three algorithms.

Parameters	Range	GA	DE	PSO
ε	[0.5, 0.8]	0.55	0.61	0.65
Xcover	[0.1, 0.9]	0.43	0.27	0.33
Cd	[0.6, 0.8]	0.71	0.74	0.77
Cw	[0.05, 0.2]	0.15	0.11	0.12
Xscreen	[0.3, 0.9]	0.49	0.52	0.55
Xglass	[1, 10]	5.79	6.23	5.19
τcov	[0.6, 1]	0.63	0.77	0.83
τscr	[0.3, 0.9]	0.72	0.87	0.71

. Here, we use PSO as a representative to describe the whole procedures of our proposed algorithms, as shown by Algorithm 1. Afterwards, the steps of three algorithms can be summarized as follows.

Algorithm 1: Outline. Steps of three algorithms in optimization.

Input: The environmental data: $T_{air},T_{out},A_{roof},V_{wind},{\rho }_{co2},U_{scr},I_{glob},T_{in},T_{opt},U_{vent},H_{air}$

Output: The best vector (solution): $\epsilon ,X_{cover},C_d,C_w,X_{screen},X_{glass},{\tau }_{cov},{\tau }_{scr}$ Step 1: Initialize the parameters of PSO such as $\omega ,c_1,c_2,$ population size N, and the total generations Gen. Randomly initialize the velocity and position of the population, generating M vectors as N1, N2, ……, XN. Set the initial iteration number gen = 0. Step 2: Calculate the objective functions of the initial population according to Equation (18), where the values of $Q_{heat}\mathrm{and}{Q}_{water}$ are computed from the input environment data as described in Section 2.2. Step 3: Execute the PSO algorithm to perform the optimization procedure. Each individual is updated according to Equations (16) and (17), and then compute the objective function. Afterwards, the global optimal solution Gbest for the population and the current optimal solution Pbest for each individual is updated. Step 4: Update gen = gen + 1, if gen < Gen, go to step3, else stop.

The common parameters of the above three algorithms are given as the same values such as population size and the total generations, while the calibration factors and updating mechanism are set up respectively. If DE and GA are utilized to perform the optimization process, only Step 1 and Step 3 of Algorithm 1 need to be adjusted. For Step 1, some parameters with respect to these two algorithms should be set instead of those for PSO. While for Step 3, PSO is replaced by DE or GA, accordingly, the population is evolved to a better condition in the objective space and a global optimal solution Gbest is generated in each generation.

3. Results and Discussion

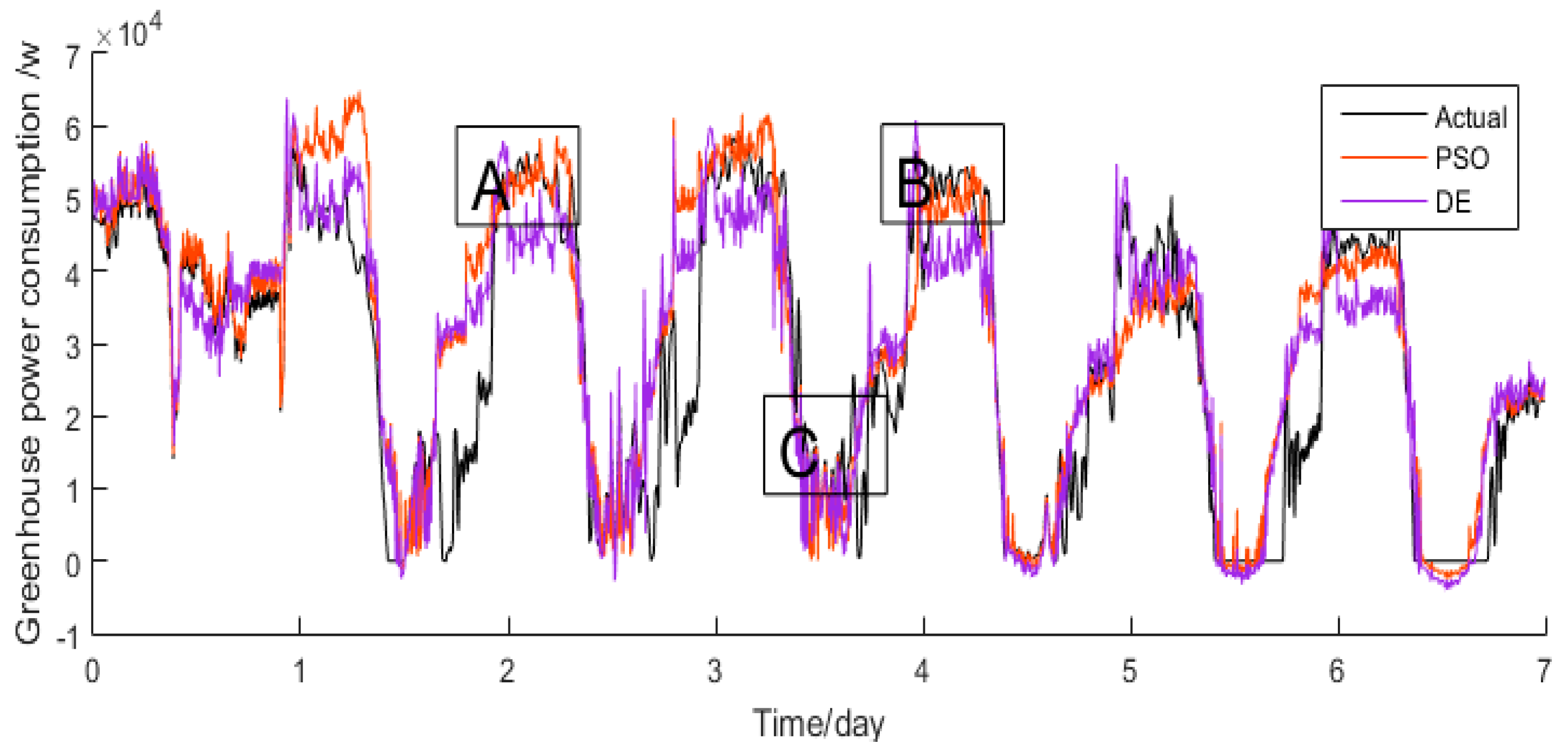
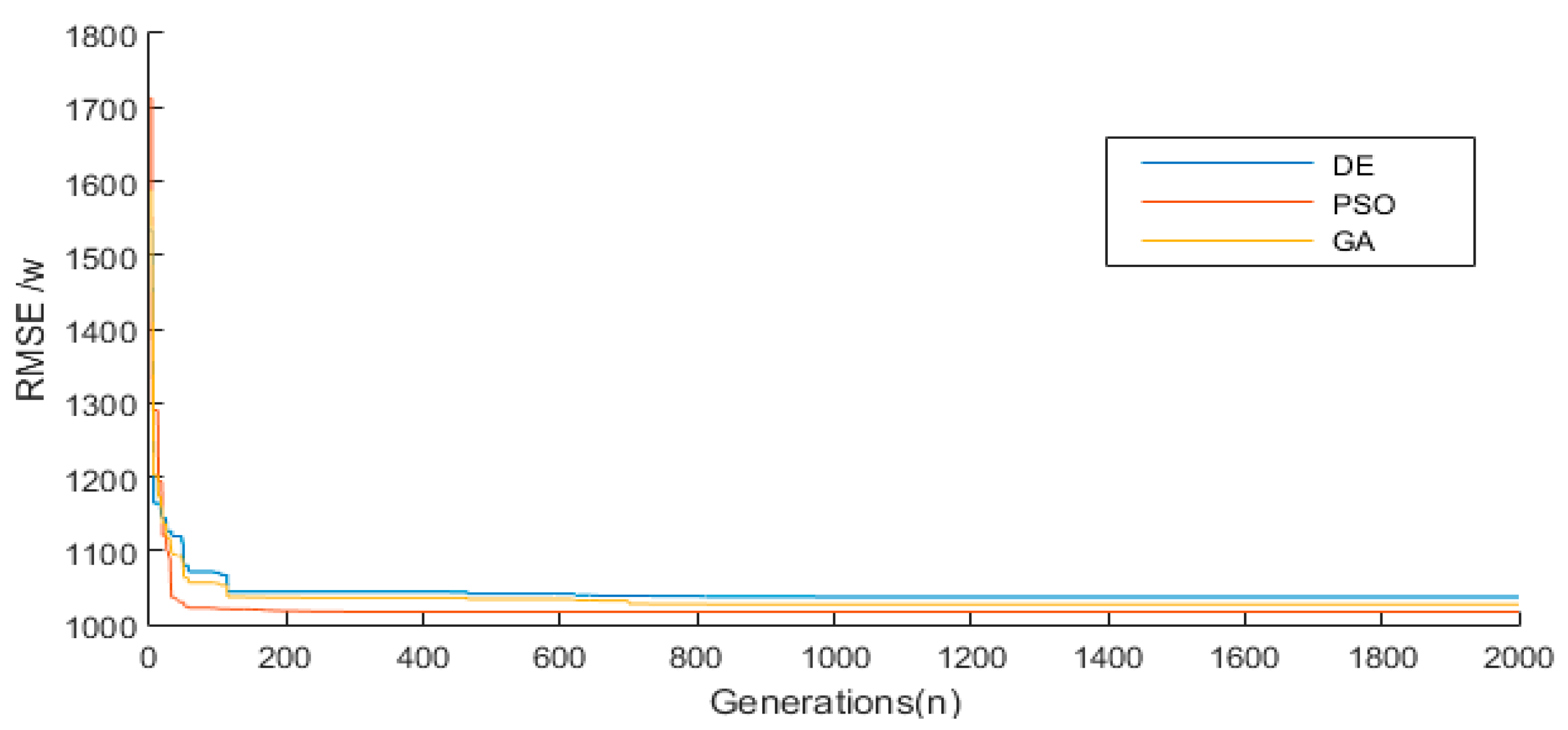
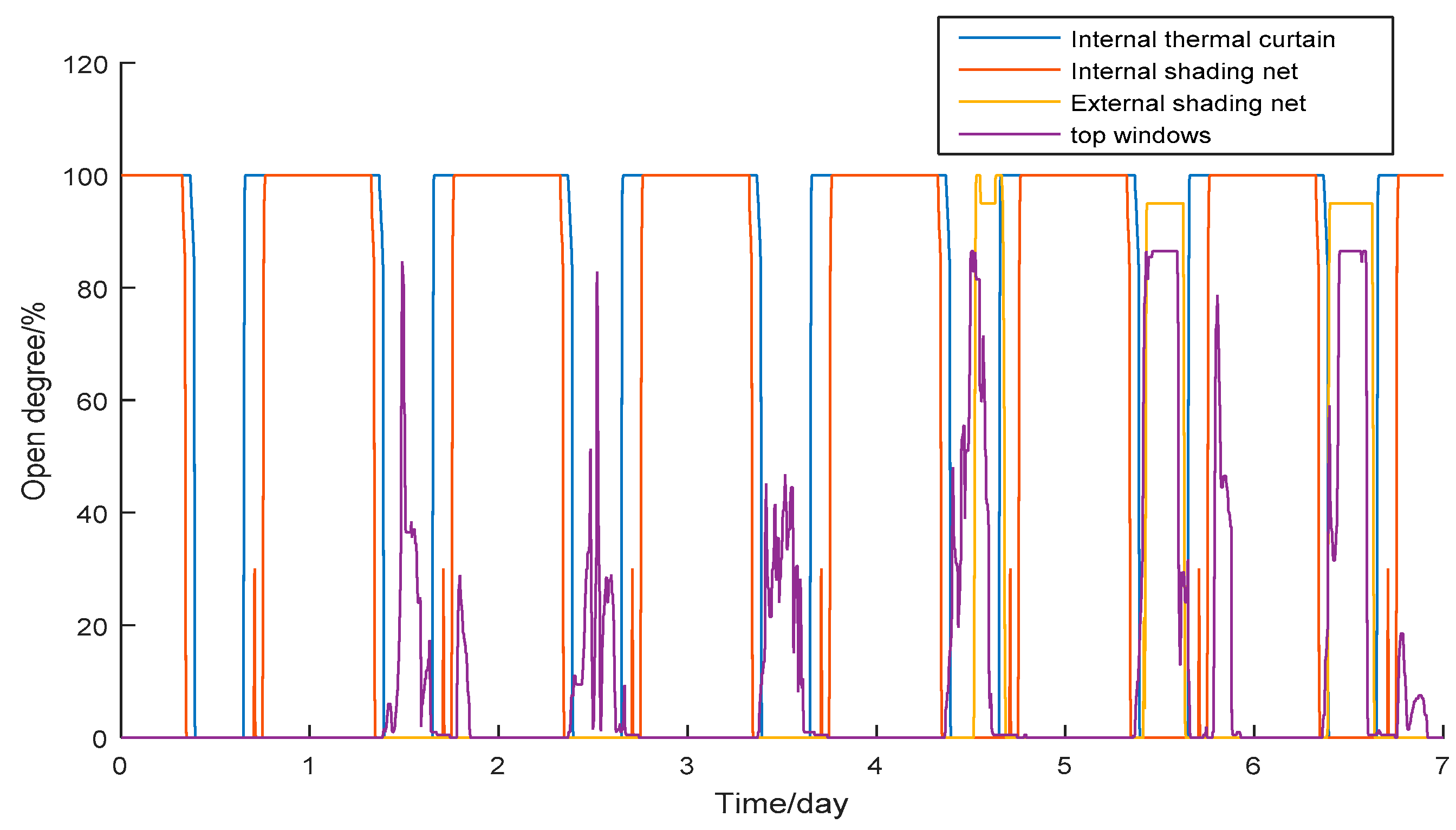
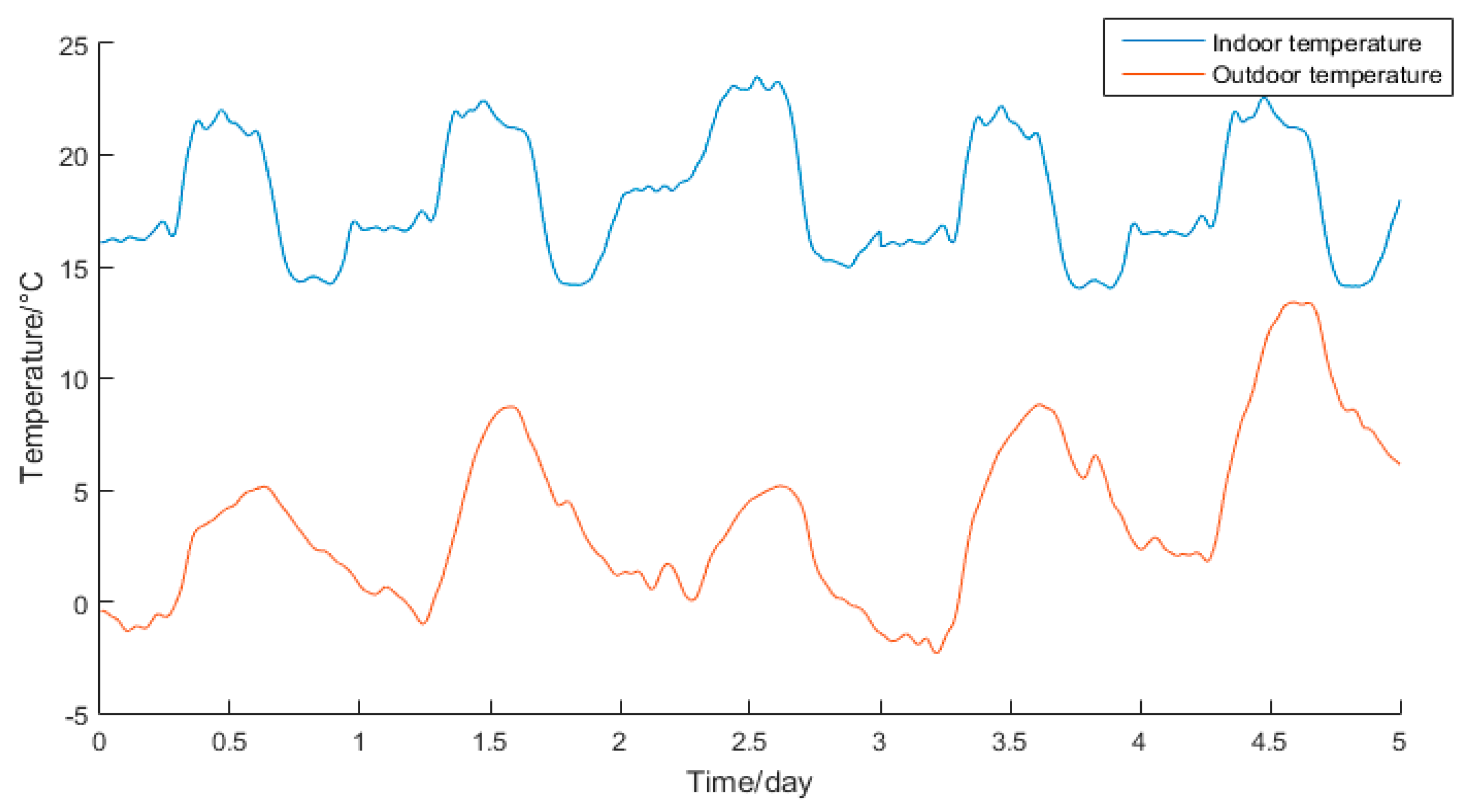
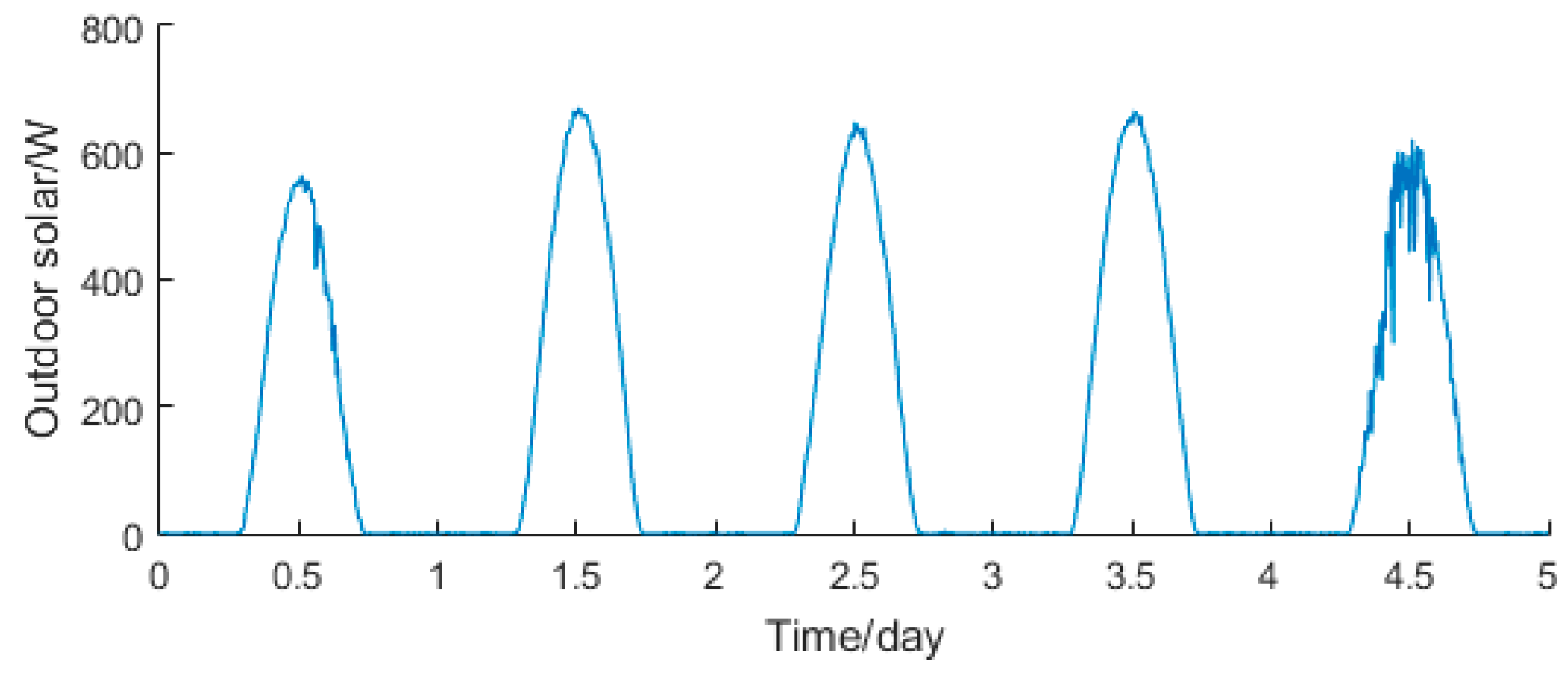
3.1. Optimization and Validation

For the computational implementation, the deployed equipment is an Intel^® Core^TM i7-2630QM, with a 2.00 GHZ processor and 8.00 GB in RAM, DDR3 1333 MHz type; the OS of the computer is Windows^TM 10 Professional Edition, and the machine is also equipped with the MATLAB^TM R2015a version software.

For the three algorithms, population size N, and the total generations Gen are respectively set as 50 and 2000. The parameters of PSO such as $\omega$, $c_1$, and $c_2$ are respectively set as 0.9, 0.12 and 1.2. For the DE algorithm, the scaling factor F and the crossover probability Cr are respectively set as 0.5 and 0.9. For the GA algorithm, the crossover and mutation probabilities are 0.8 and 0.1 respectively. Moreover, the simulated binary crossover (SBX) and polynomial mutation operators are used to generate offspring solutions, where the distribution factors in are both 20.

According to the prediction model of the energy consumption and three optimization algorithms, we write the program of Matlab and identify the uncertain parameters in the parametric model. The obtained results of parameters by each algorithm are shown in Table 2. It should be noted that calibration parameters, like in the other algorithms, were selected experimentally, based on the best results obtained after several tests.

According to the parameters obtained in Table 2, Figure 3 and Figure 4 illustrate the actual power consumption and predicted power consumption by using PSO, DE and GA in optimization process respectively from 21 to 27 January. Further, Figure 5 illustrates that the RMSE of three algorithm changes in 2000 generation.

As is illustrated in Figure 3 and Figure 4, it is important to point out that PSO, DE and GA present good behavior, that is, the actual power and predicted power are changing almost synchronously in seven days. However, when the power changes rapidly in some partial levels, PSO has better tracking results than GA and DE, such as A, B, C. In real greenhouses, tracking of short-term power changes is very important because of the rapidly changing weather. Figure 5 shows RMSE changes with the generation in three optimization algorithms and it illustrates that when PSO runs to 87 generations, it completely converges, while GA and DE converge locally at 120 generations, then jump to local convergence at 600 generations and 700 generations respectively, which shows the global search ability of GA and DE. However, the PSO converges faster, and RSME is less than GA and DE.

According to the parameters obtained by the PSO optimization algorithm, the energy consumption prediction model is obtained. In order to check the model, the actual data of the five days from February 1 to 5 February 2016 is used for verification.

As shown in Figure 6, the predicted power consumption meets the actual power well in general. There is also some difference between predicted and actual power consumption, especially during the noon when heating system fluctuates more than usual. Finally, the daily energy consumption error was 7.42% and the model shows good robustness.

Table 3. The relative errors between actual consumption and predicted consumption.

Date (yy-mm-dd)	Outdoor Average Light ($\mathbf{W}\mathbf{·}{\mathbf{m}}^{-2}$)	Outdoor Average Temperature (°C)	Average Power (kW)	Relative Error (%)
2016-02-06	167.1354	3.30	31.32	9.12
2016-02-07	210.3487	3.73	33.45	8.34
2016-02-08	223.9821	3.90	32.83	7.71
2016-02-09	218.6615	3.88	33.21	6.21
2016-02-10	228.4269	4.03	31.58	5.19
2016-02-11	245.5491	4.56	27.48	10.13
2016-02-12	230.4658	4.13	30.44	9.33
2016-02-13	248.5611	4.63	26.55	10.42
2016-02-14	270.4660	5.01	21.12	10.57
2016-02-15	297.4558	5.95	17.43	10.85

describes the relative errors between the predicted and the actual power consumption which are measured from 6 to 15 February. When the greenhouse average daily solar radiation is between 160 $(\mathrm{W}·{\mathrm{m}}^{-2})$ and 270 $(\mathrm{W}·{\mathrm{m}}^{-2})$, and the outdoor average temperature is between 3–5 (°C), the error of predicted power consumption is less than 11%. Consequently, when the daily average light and the outdoor average temperature change are small, the model shows a good performance for prediction of short-term greenhouse energy consumption.

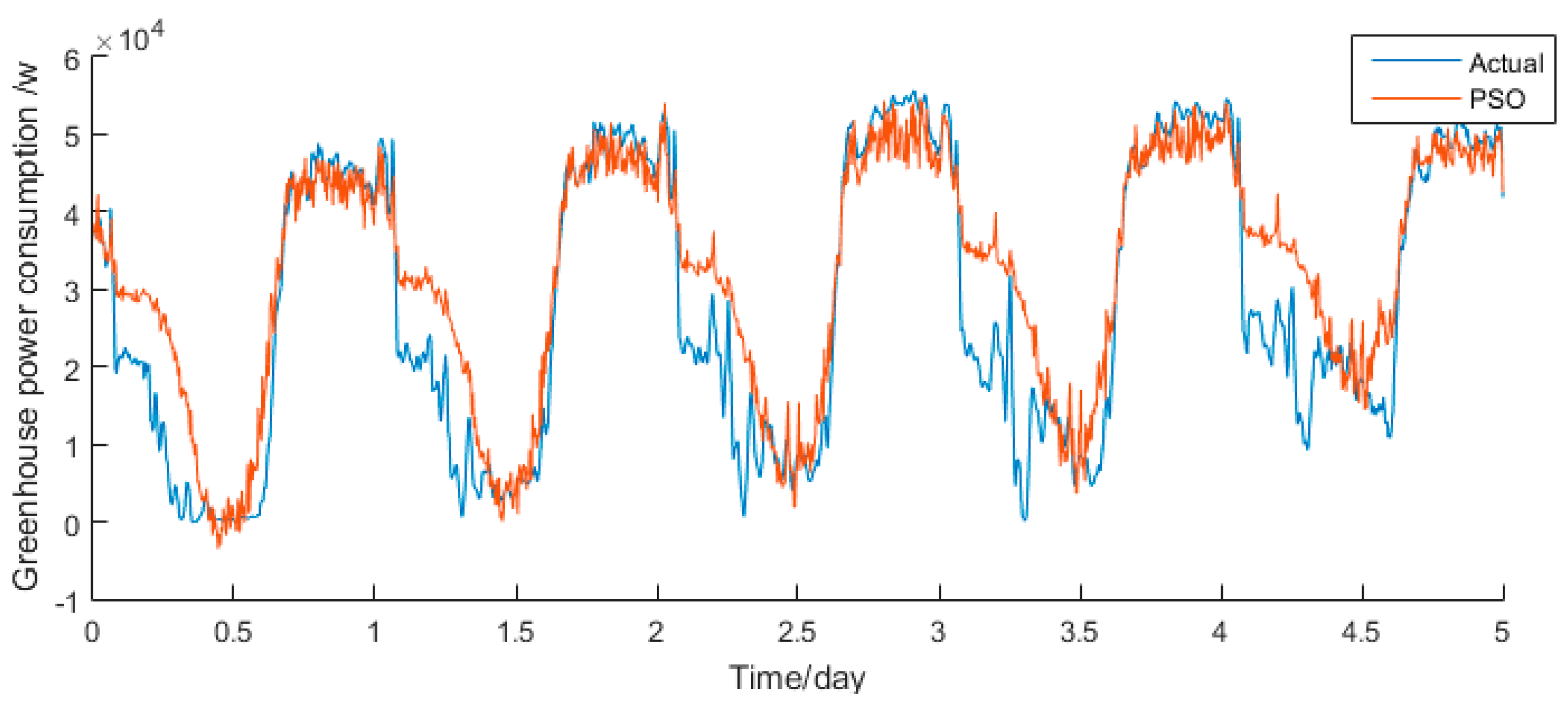
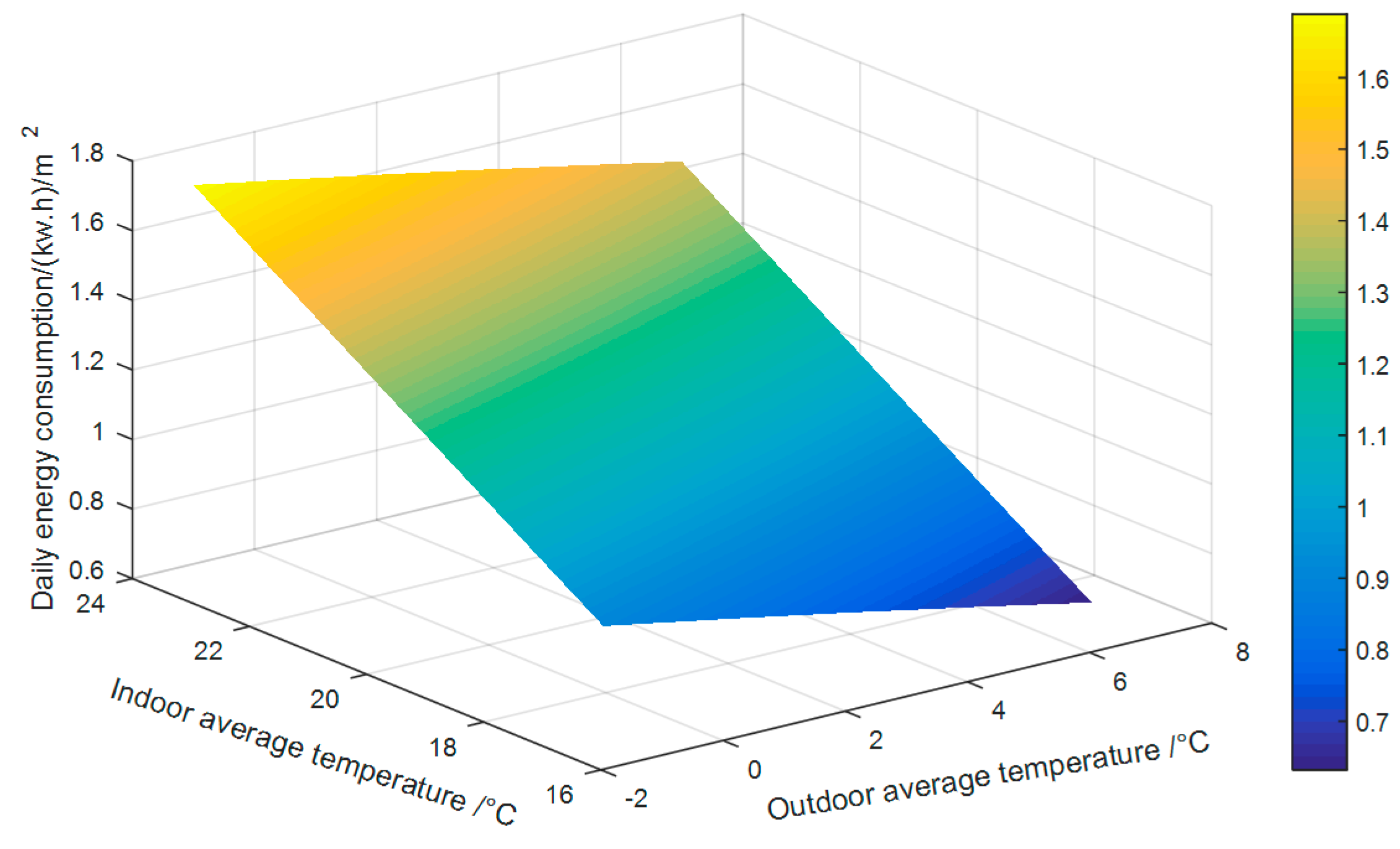
3.2. Predict Energy Consumption Based on Model

In winter, normal greenhouse production requires efficient management of energy consumption. According to statistics, heating costs in winter greenhouse can reach more than 50% of greenhouse production costs [31]. As the accuracy of weather forecasting model increases, the prediction of the outdoor environment change is more reliable. Therefore, the accuracy of the temperature, light and wind speed has been guaranteed. At present, the outdoor weather data in one week can already be used to manage the greenhouse of heating production.

Taking the Chongming greenhouse as an example in this study, energy-related devices include top windows, external shading net, internal $\mathrm{thermal}$ curtain and internal shading net. From January to March, it is the coldest season of one year. In this period of time, these devices have some rules to follow, which are shown in Figure 7.

For example, at about 1 o’clock p.m., the top windows usually open for about two hours. At this time, the temperature is in the highest stage in the day, and the temperature in the room rises sharply. Thus, opening the top windows and the shading net helps to discharge excess heat in the greenhouse. As a result, heat transfer from heat pump to the greenhouse will be close to zero.

It can be seen that the greenhouse will not be heated when the shade net and the top windows are opened. When the greenhouse absorbs redundant energy, the power output resulting from the prediction model is negative and excess energy is released through the opening of top windows and the shade net. Therefore, to ensure the decrease of inside temperature, the output power of heat pump is kept as zero. In the night (7:00 p.m. to 8:00 a.m.) in order to resist the outdoor cold, the internal insulation is open, while the shade net is also open because the shading net could decrease the heat loss from the greenhouse to outside.

As shown in Figure 8 and Figure 9, from January 23 to January 27, the actual indoor and outdoor temperature, and light in the Chongming greenhouse change slowly. Furthermore, they follow the trend of first rising and then falling during a day.

Therefore, in daily management of greenhouses, based on the day’s outdoor temperature and indoor temperature trends from 23 to 27 January, the given average outdoor temperature and solar radiation can be converted into the same time series. According to the prediction model of energy consumption in greenhouse, the indoor daily average temperature is fixed at 22 °C, and the daily total energy consumption of greenhouse is predicted with different outdoor average temperature and light, as shown in Figure 10.

When we fix the average daily outdoor solar radiation at 200 $\mathrm{W}/{\mathrm{m}}^2$, the daily total energy consumption of greenhouse is predicted according to different outdoor average temperature and indoor average temperature, as shown in Figure 11.

When the outdoor average temperature is constant, the total daily energy consumption decreases with the increase of the total solar radiation. Similarly, based on the given constant solar radiation, the total daily energy consumption also decreases with the increase of the outdoor average temperature. If the outdoor temperature and light are the same, the daily total energy consumption increases with rising of the indoor temperature. These reasonable results can provide guidance for management of the greenhouse.

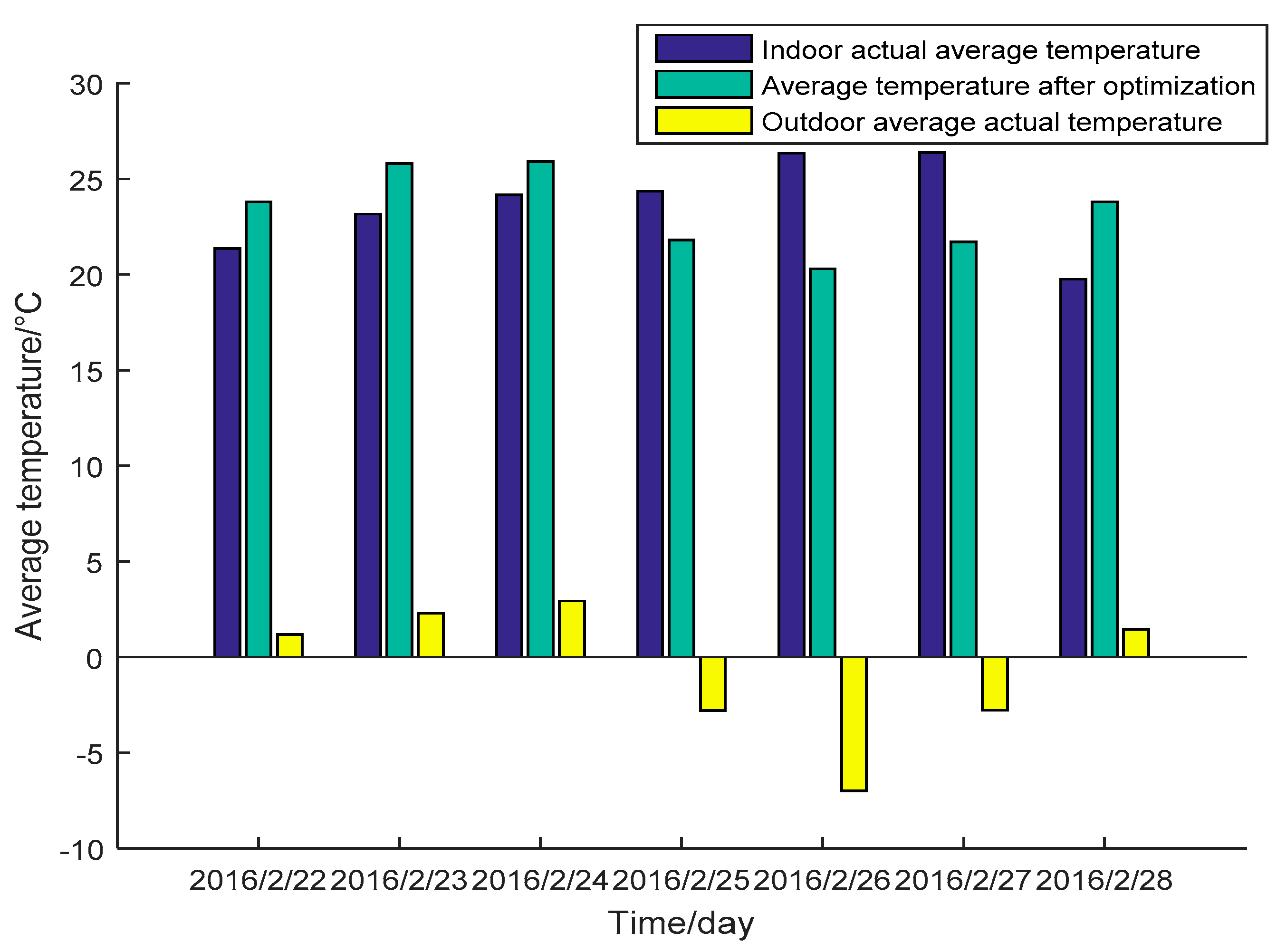
3.3. Optimization of Daily Average Temperature

At different growth stages, crops’ requirements from the environment are an average amount. For example, the temperature requirement is in the form of accumulated temperature as long as instantaneous value is not too high or too low to damage the crop. Normally, the same accumulated temperature can resulted in the same yield for many crops [32,33,34]. In order to manage the greenhouse and realize the maximum profit, the energy consumption must be planned and optimized to deal with the changeable weather. Since crop growth stage is still a long time, crops’ one week average temperature requirement can be considered as constant through the planting cycle. In the greenhouse, when the average temperature of a week is given as constant, the daily average temperature still needs to be optimized according to the outdoor weather. The reason is that weather changes are complicated and extreme weather conditions such as cold waves may occur in a week. Compared with normal climatic conditions, achieving the same temperature setting consumes more energy in a cold wave period. Therefore, it is significant to optimize daily temperature under the given condition of weekly average temperature.

3.3.1. Energy Optimization Algorithm Objective Function

In this study, the heating system of the Chongming greenhouse uses hot water pipes for heating, which accounts for more than 90% of the production costs in winter. According to the energy consumption prediction model analyzed in the previous chapter, the objective function of energy consumption for optimizing the daily average temperature is as follows:

Min:

$$J(x)={\displaystyle \sum }_{i=7}^7(Q_{heat}(T_{Di}))x=[T_{D1},T_{D2},T_{D3},T_{D4},T_{D5},T_{D6},T_{D7}]$$

(19)

subject to:

$$\frac{{{\displaystyle \sum }}_{i=7}^7{T}_{Di}}{7}=T_{week}{T}_{min}<T_{Di}<T_{max}(i=1,2,\dots ,7)$$

(20)

Among them, the objective function J(x) represents the total energy consumption of one week with different daily average temperatures. $Q_{heat}(T_{Di})$ represents the energy consumption prediction model obtained in the previous section, and $x=[T_{D1},T_{D2},T_{D3},T_{D4},T_{D5},T_{D6},T_{D7}]$ represents seven daily average temperatures. The equation constraint $T_{week}$ is according to historical planting experience and crops growth characteristics. $T_{min}$ and $T_{max}$ represent the appropriate crop temperature range.

3.3.2. Optimization Process of Daily Average Temperature

Based on the accumulated temperature theory which has been mentioned before, the single-objective particle swarm optimization is used to optimize the daily average temperature, where one-week energy consumption is used as performance index, the average temperature of one week and each day are used as constraints to optimize the daily average temperatures. Corresponding to the lowest cost, the daily average temperatures are selected as the target setting values on the basis of meeting the above constraints.

In this paper, we use the average temperature under the control of the Chongming Priva system as the given average weekly temperature. As the Priva system is a mature control system, it has good effect on a global scale. It can be considered that the control result is able to meet the requirements of crops for temperature accumulation. From 22 to 28 February, this stage is the tomato growing period in the Chongming greenhouse, requiring a higher temperature during the day to 23–26 °C [23,24,25]. Where the actual average temperature is 23.6 °C in one week, the best daily average temperature range in greenhouse is 20–25 °C, and the allowable deviation range is 1 °C. Furthermore, 19 °C and 26 °C are the lower and upper boundary of optimization variables.

As shown in Figure 12, the actual average daily temperature of the Chongming greenhouse meets the crop temperature requirements in a week. The daily average temperatures without optimization remain stable in this week, however, as shown in Figure 12, from 25 to 27 February, the greenhouse experiences a short-term cold wave, and the outdoor extreme temperature reaches below −9 (°C). When compared with 24 February, heating the greenhouse to the same temperature will lose more energy due to the lower outdoor temperature.

Based on the optimization algorithm and weather forecast for one week, the daily average temperatures of 7 days are optimized. Consequently, in order to maintain the average temperatures of 7 days meeting with the weekly average temperature constraints, the daily average temperatures are appropriately increased before and decreased after the arrival of cold wave respectively. It will help to avoid the loss of energy cost caused by the constant temperature heating during the coldest period while ensuring the normal crop growth. The optimized seven-day average temperatures are verified by the energy consumption model in this paper.

3.4. Discussion

Taking again the Chongming greenhouse as an example in this study, we compare three classic algorithms to predict energy consumption. According to the parameters obtained by the best result, the greenhouse energy consumption prediction model is established. In order to verify the accuracy of the developed model, energy consumption from 6 to 15 February is predicted according to the greenhouse environmental data. The predicted energy consumption is almost in the same trend to the actual energy consumption, and the RMSE is less than 11%. Afterwards, the model shows a good performance for prediction of short-term greenhouse energy consumption.

Generally, the average temperature over a period of time is given according to the growth demand of crops. According to the outdoor weather forecast, the energy consumption at a given average temperature needs to be predicted to adjust the heating. However, the current studies on greenhouse energy consumption focus on proposing new algorithms to improve the accuracy of the model, ignoring the application of the model in practical situations. Uniquely, in this study, the energy consumption model is exploited for the real prediction of greenhouse energy consumption in actual production. Based on the law of energy-related devices and the outdoor weather forecasting, the daily average temperatures of 7 days are optimized during a cold wave. In terms of energy conservation, the optimized average temperatures save 9% of the energy cost, and provide considerable economic benefits in a greenhouse with a heating area of 1000 square meters. Compared with the previous research, this paper studies the use of energy consumption model in practical situations, and proposes the concept of daily average temperature optimization for the first time.

4. Conclusions

Based on the analysis of energy exchange between the greenhouse and the outside world, the mechanism model of a greenhouse is established. Combining the existing measured data with the optimized algorithm, the parameters are identified by optimization algorithms. The energy consumption prediction model of greenhouse is established, which provides reference for greenhouse energy consumption optimization and management. The conclusions are as follows:

(1)

The essence of temperature change is the result of various heat and mass transfer processes in greenhouse. Therefore, based on the dynamic equations of these processes and thermodynamic theory, greenhouse energy consumption model is established.

(2)

According to the analysis of the various parameters involved in the energy consumption model, we determine the parameters to be identified and the energy consumption model of the parameters to be calibrated. The measured data of greenhouse environment and the states information of devices are input into the model. Also, three optimization algorithms are used to identify the uncertain parameters in the prediction model. Finally, five days after of the greenhouse environmental data is used to verify the effectiveness of energy consumption prediction model.

(3)

At present, the accuracy of the weather forecast in one week has been guaranteed. Based on crops’ requirements on accumulated temperature theory, the energy consumption prediction model, the optimized economy is obtained under the constraints of weekly average temperature and daily average temperature. Optimizing the daily average temperature for one week can reasonably guide the greenhouse heating production under the extreme weather conditions. As a result, the energy consumption is reduced, and the normal crop growth is ensured. At the same time, the economic benefits of the greenhouse are improved.

This paper presents a greenhouse energy consumption prediction model for winter heating optimization. Combining with accumulated temperature theory, when the accuracy of the weather forecast is guaranteed, the daily temperature averages will be optimized in the current week. Finally, good results have been obtained. However, the process of energy exchange in the greenhouse is complicated and the outdoor weather varies. The energy consumption prediction model is also difficult to be apply to the energy prediction in different seasons within about 365 days of the year. The energy consumption prediction model for cooling in summer still needs to be further studied. Similarly, subject to the accuracy of the weather forecast, the current greenhouse can be used to optimize the daily average temperature with a given average temperature for one week. The further optimization of the weekly average temperature remains to be studied.