Magnetic Field and Torque Output of Packaged Hydraulic Torque Motor
Abstract
:1. Introduction
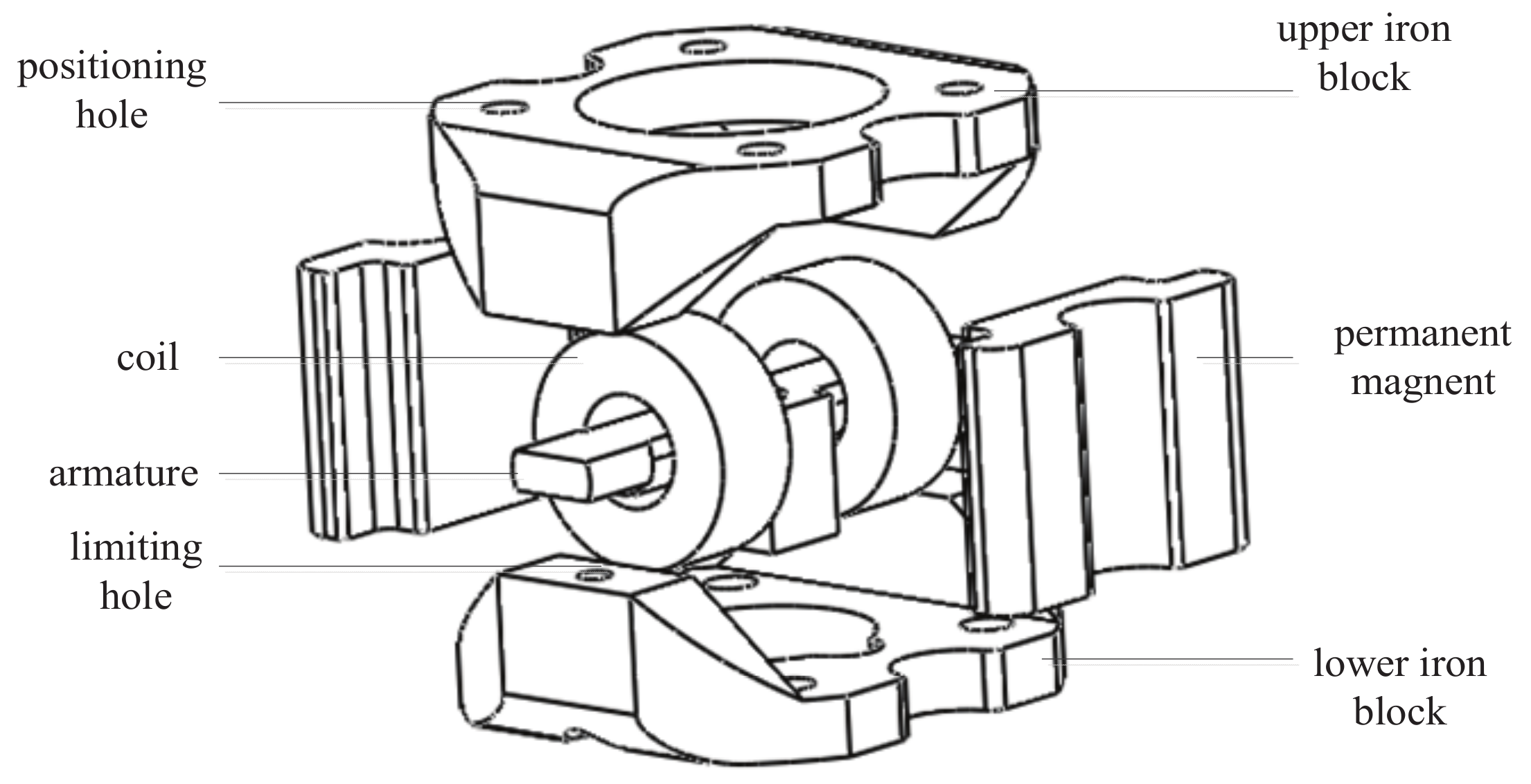
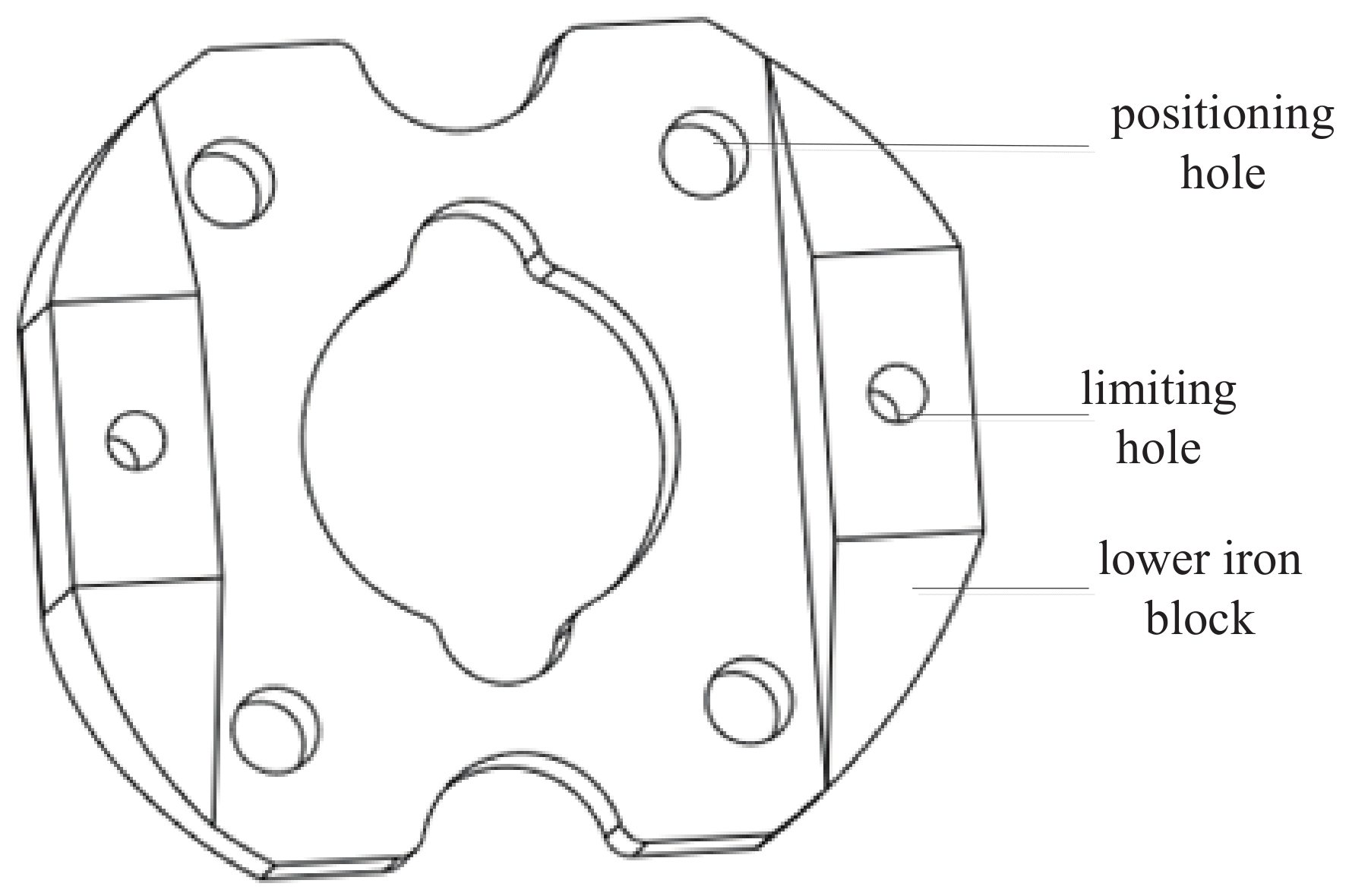
2. Schematic Structure and Operating Principle
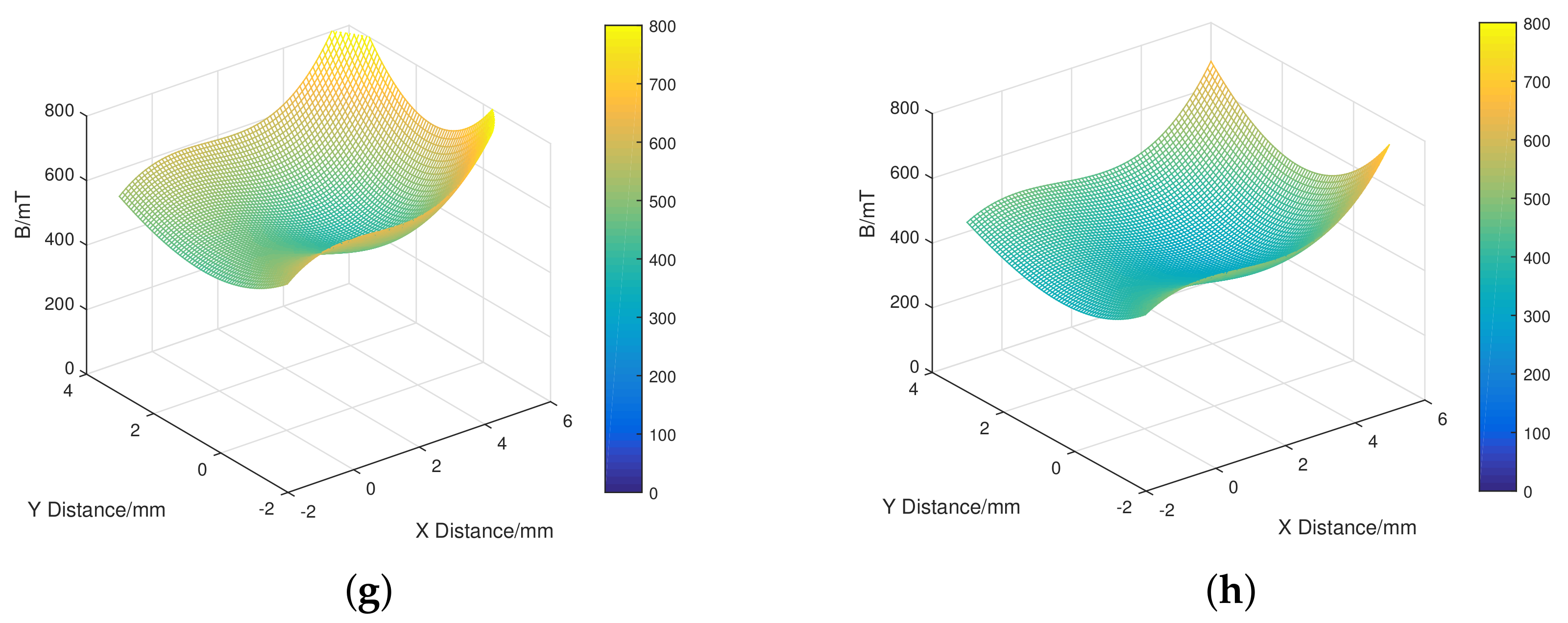
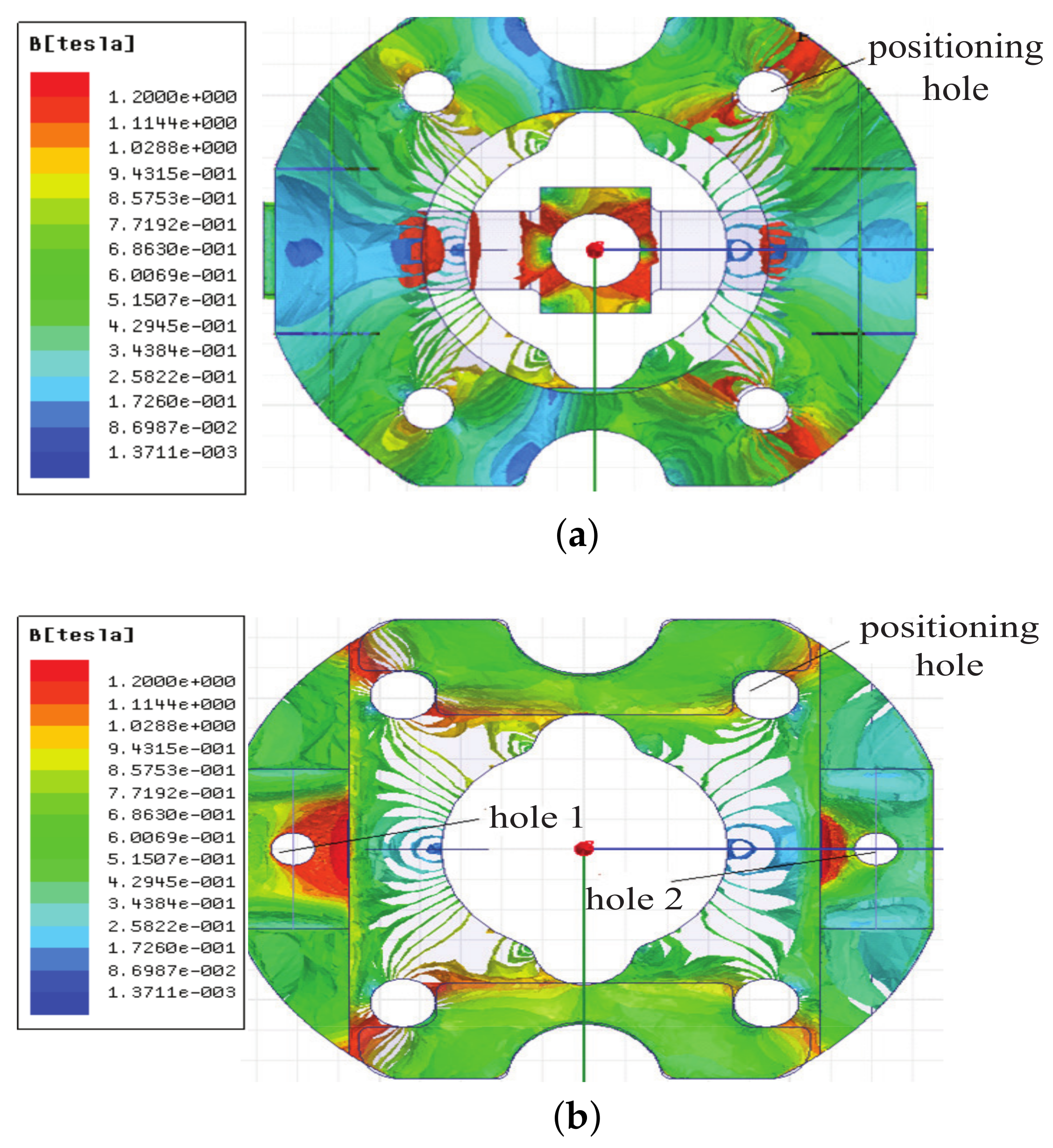
3. Analysis of Magnetic Field Distribution
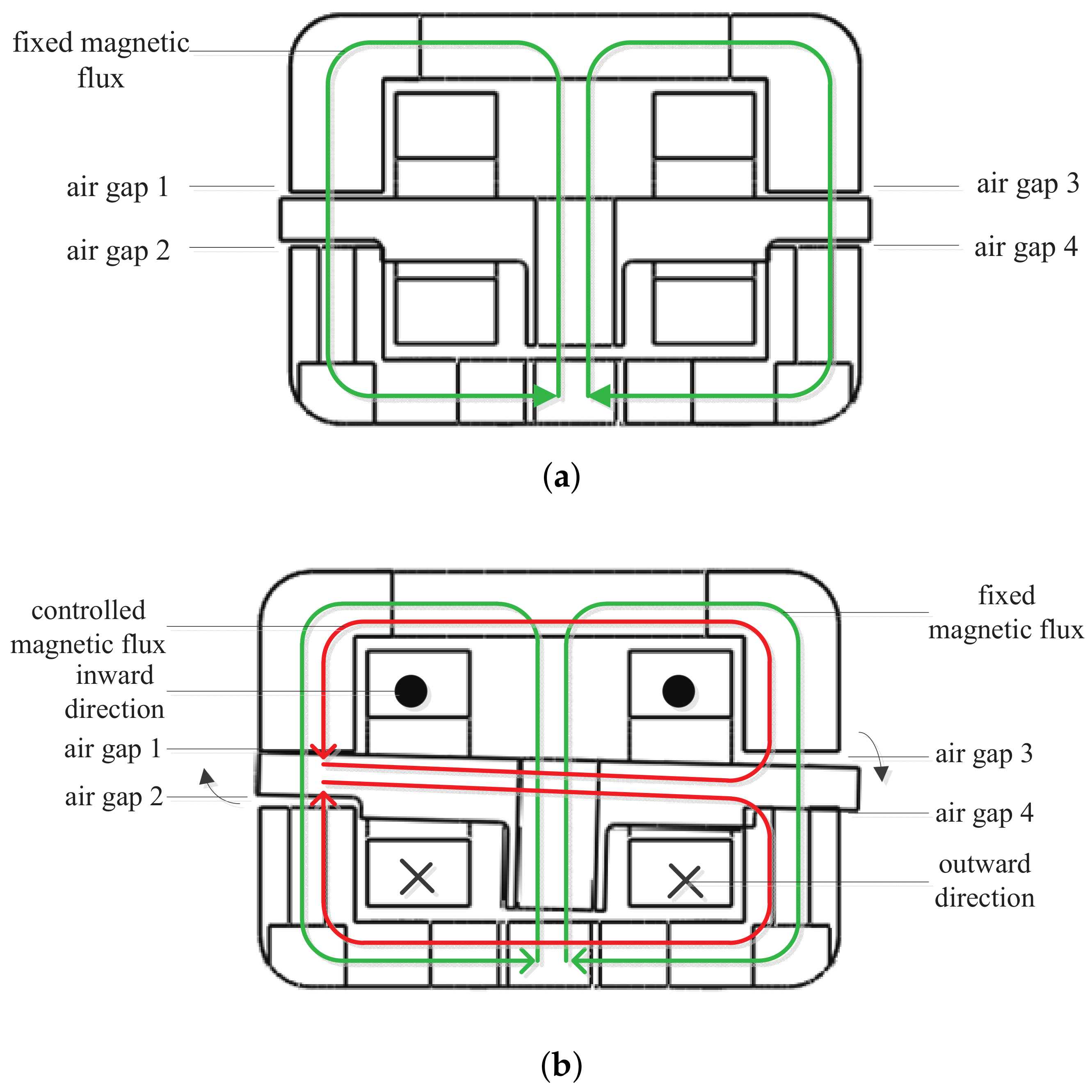
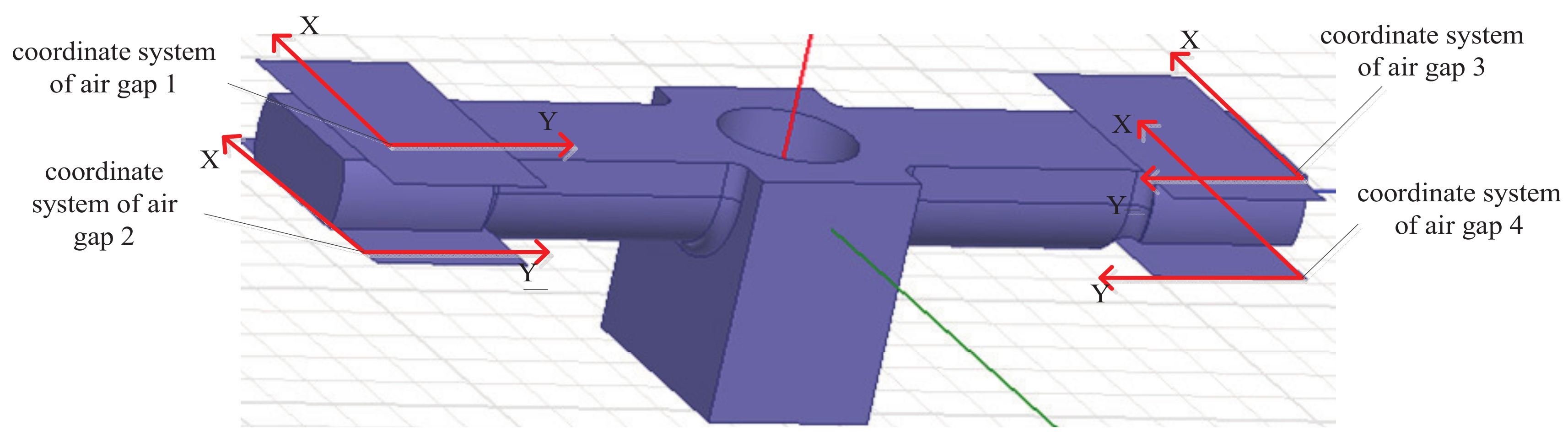
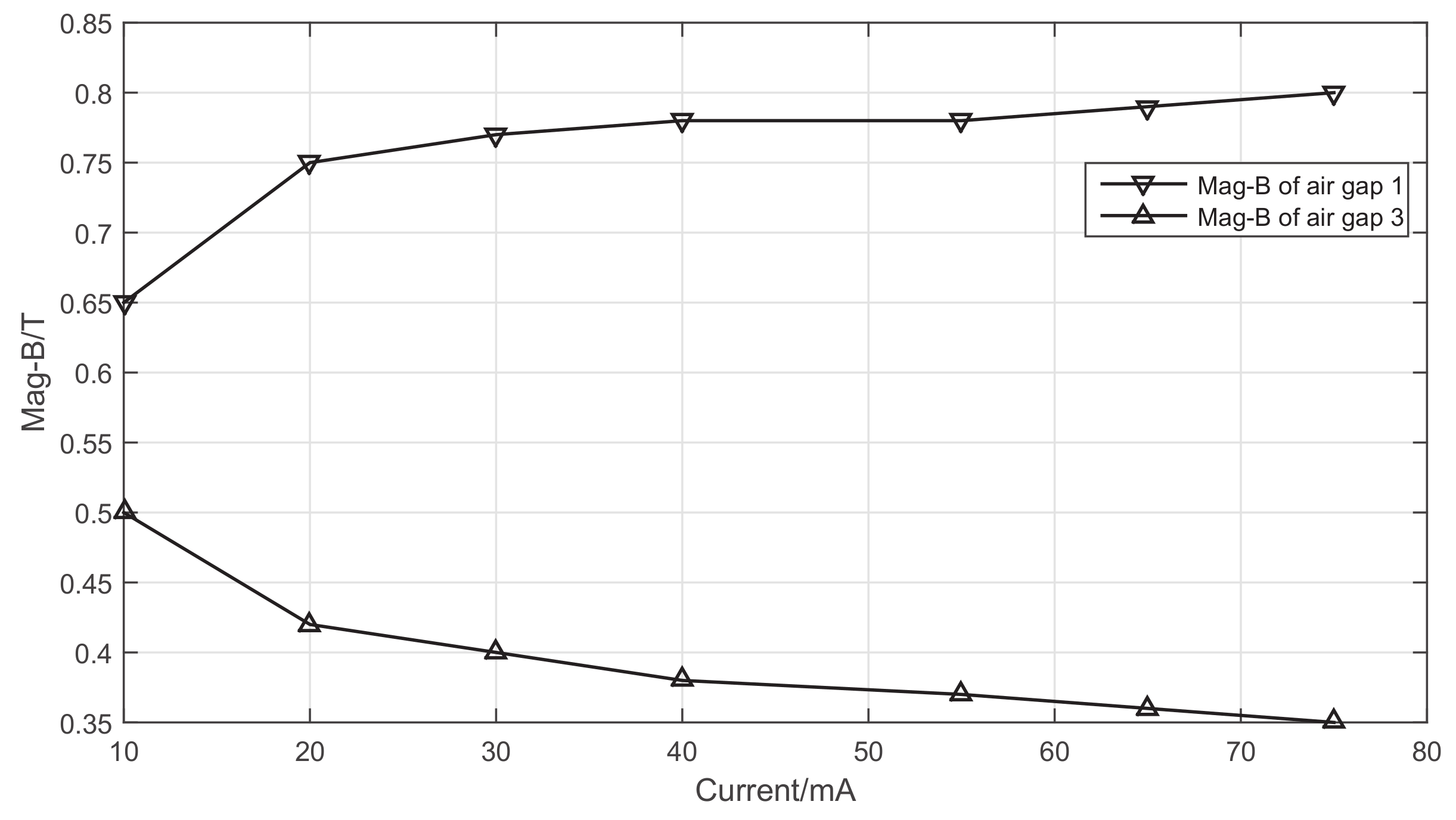
3.1. Magnetic Field Distribution in Air Gaps
- They may cause an unequal magnetic flux density at air gaps 1, 3, 2 and 4, and thus the force components at these air gaps have opposite directions but different values. The total force is not vanished, which leads to additional payload and thus friction torque on the bearings.
- They may complicate the formulation of the magnetic field and torque output and thus compromise the high-performance real-time motion control of the armature.
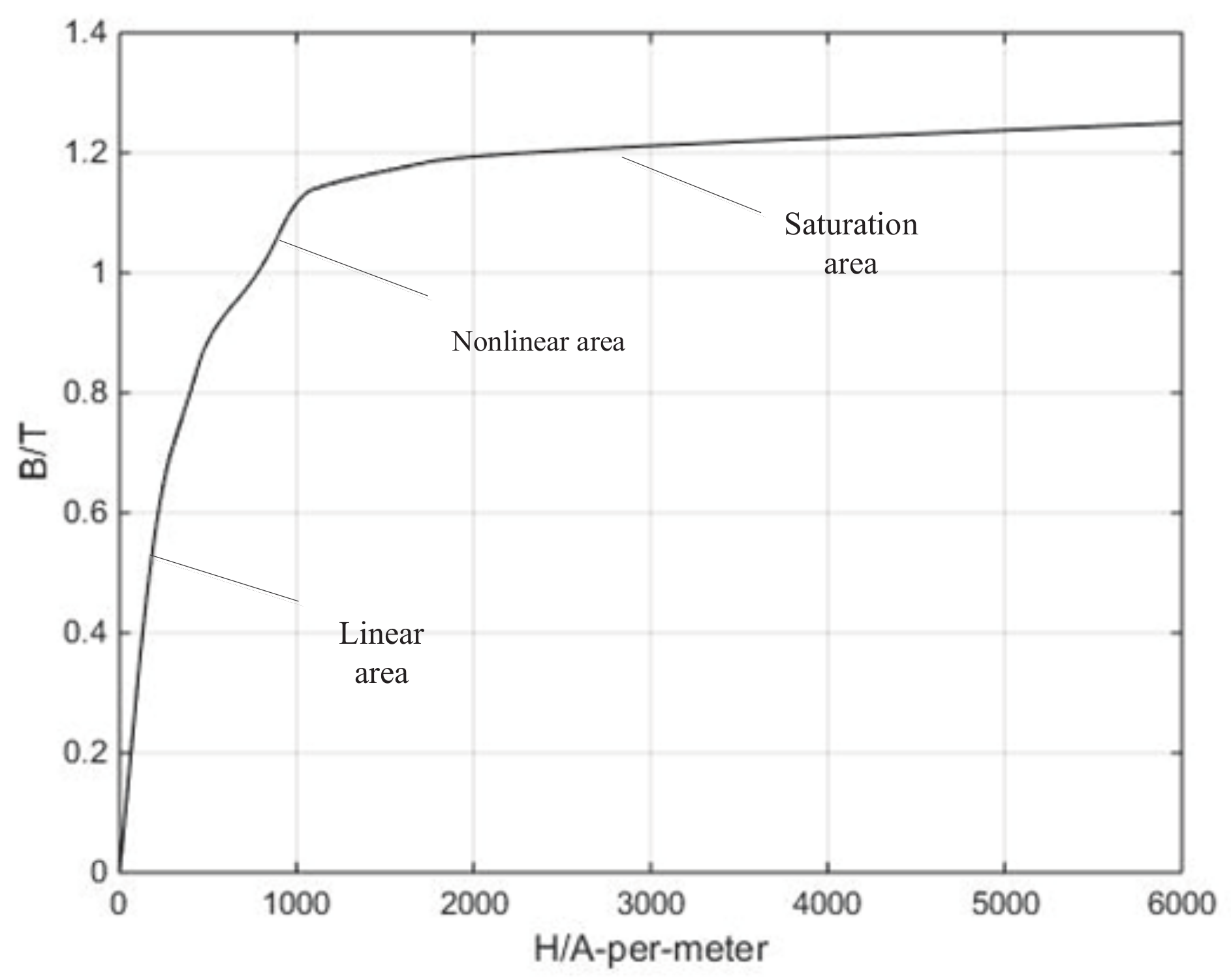
3.2. Magnetic Saturation in Iron Blocks
4. Analysis of Torque Generation
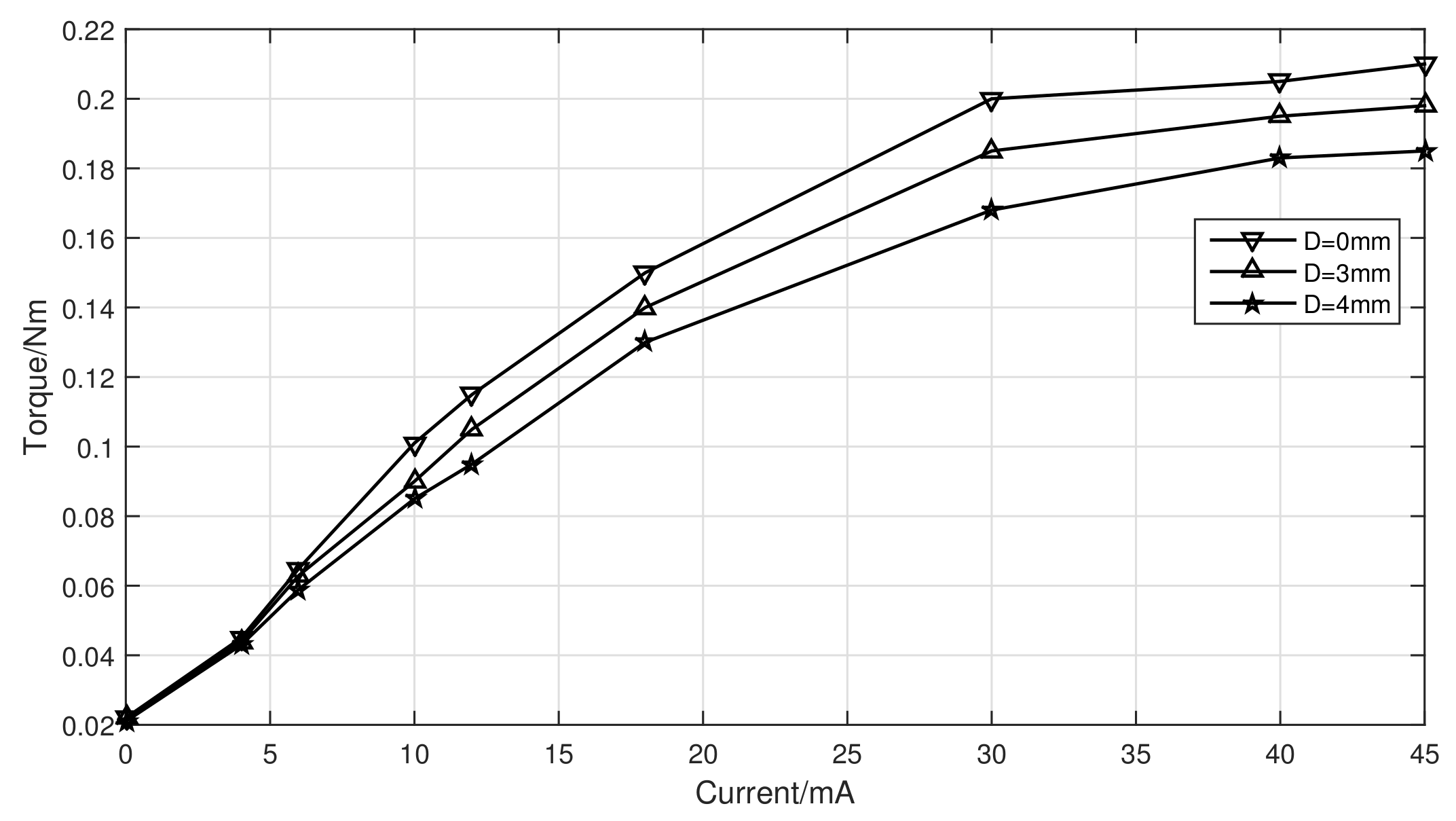
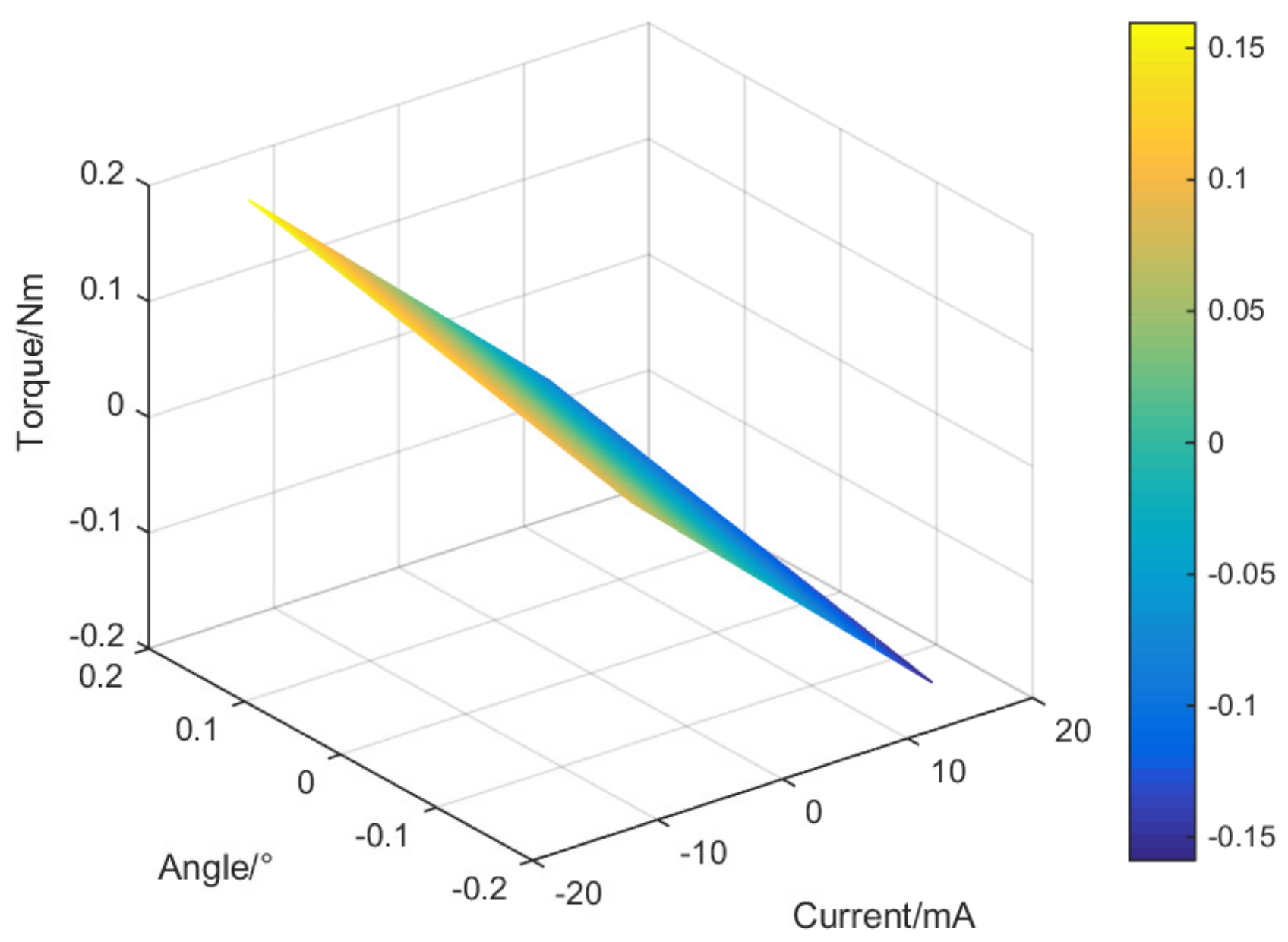
4.1. Relationship between Current Input and Torque Output
4.2. Influence of Assembly Errors on Torque Output
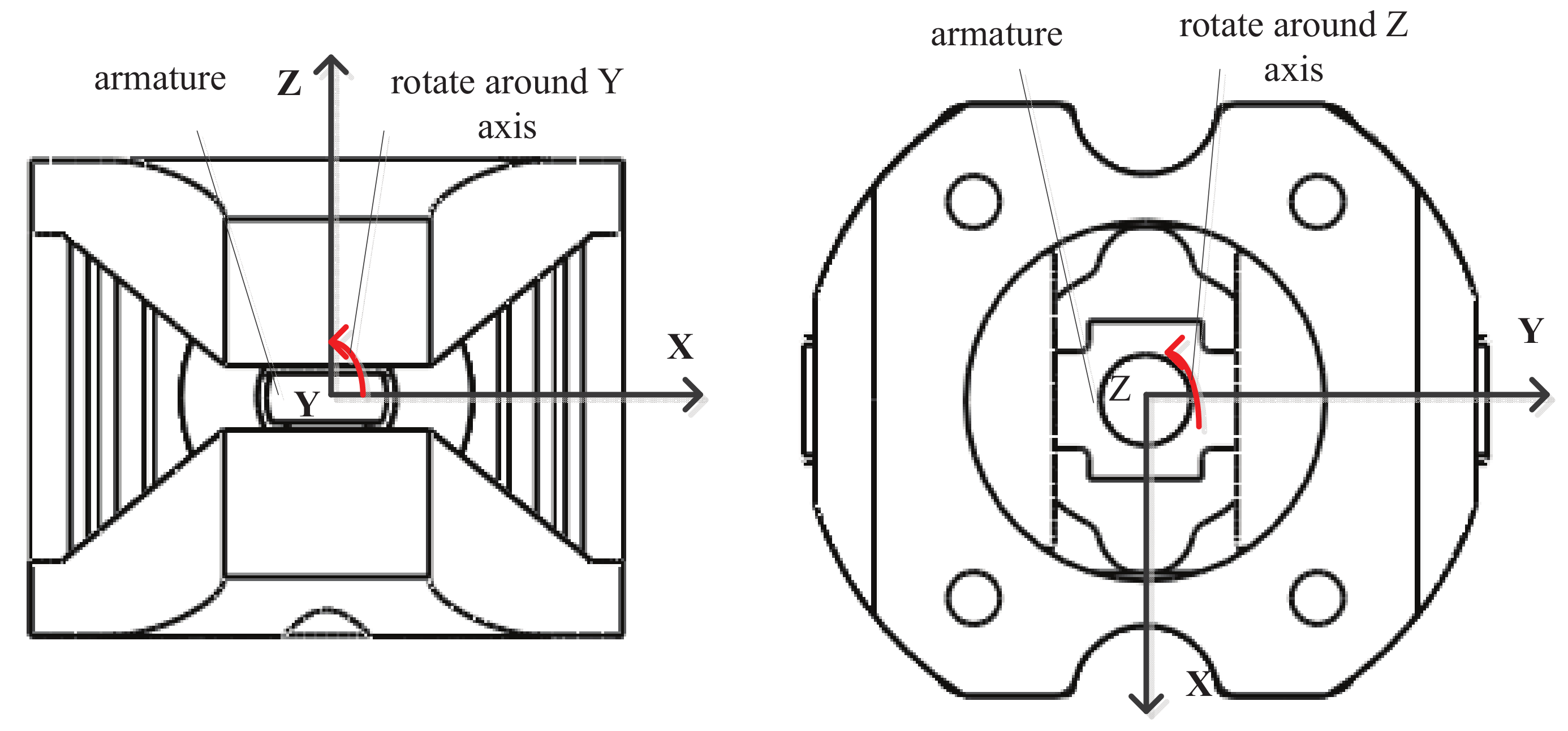
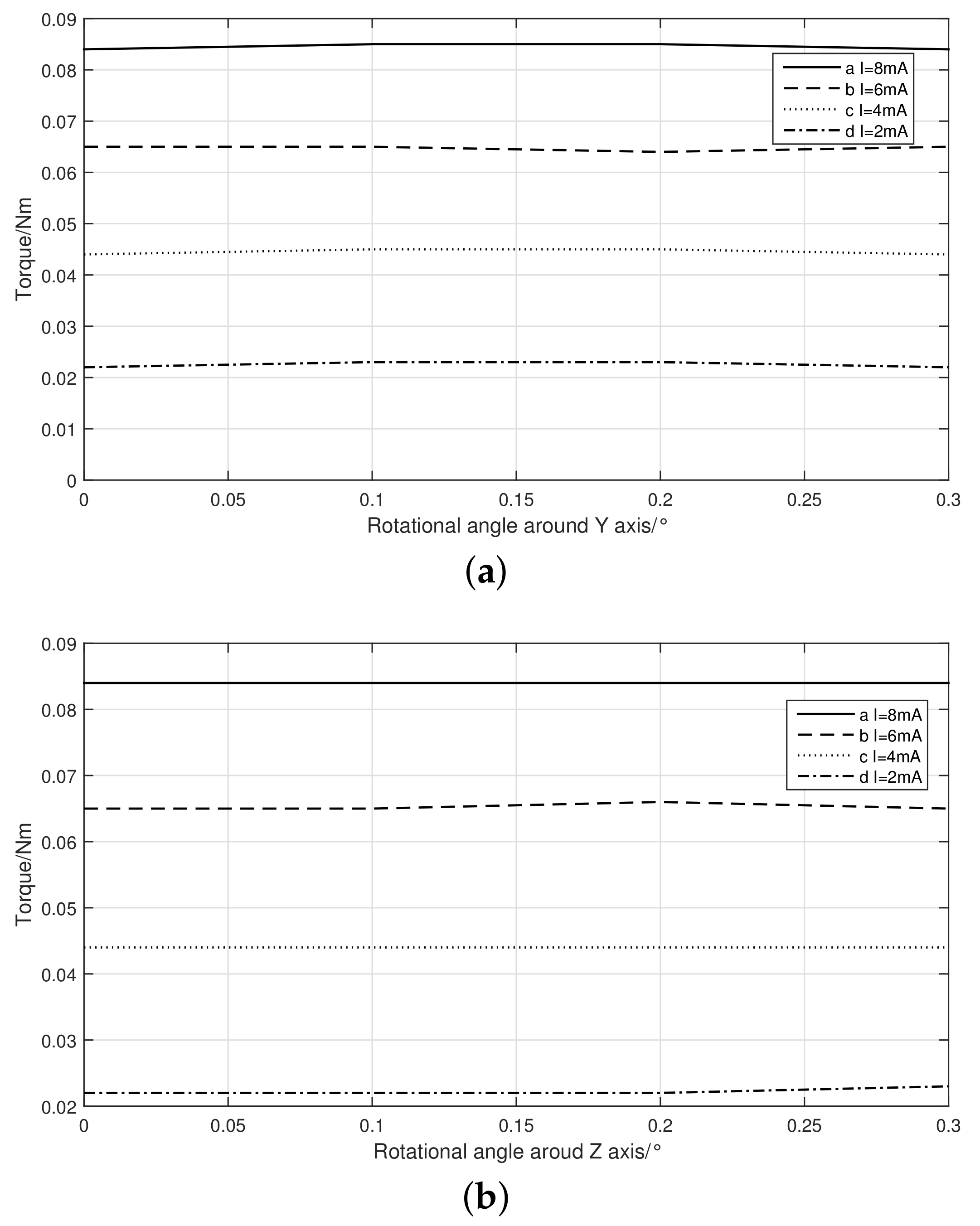
4.2.1. Rotational Assembly Error
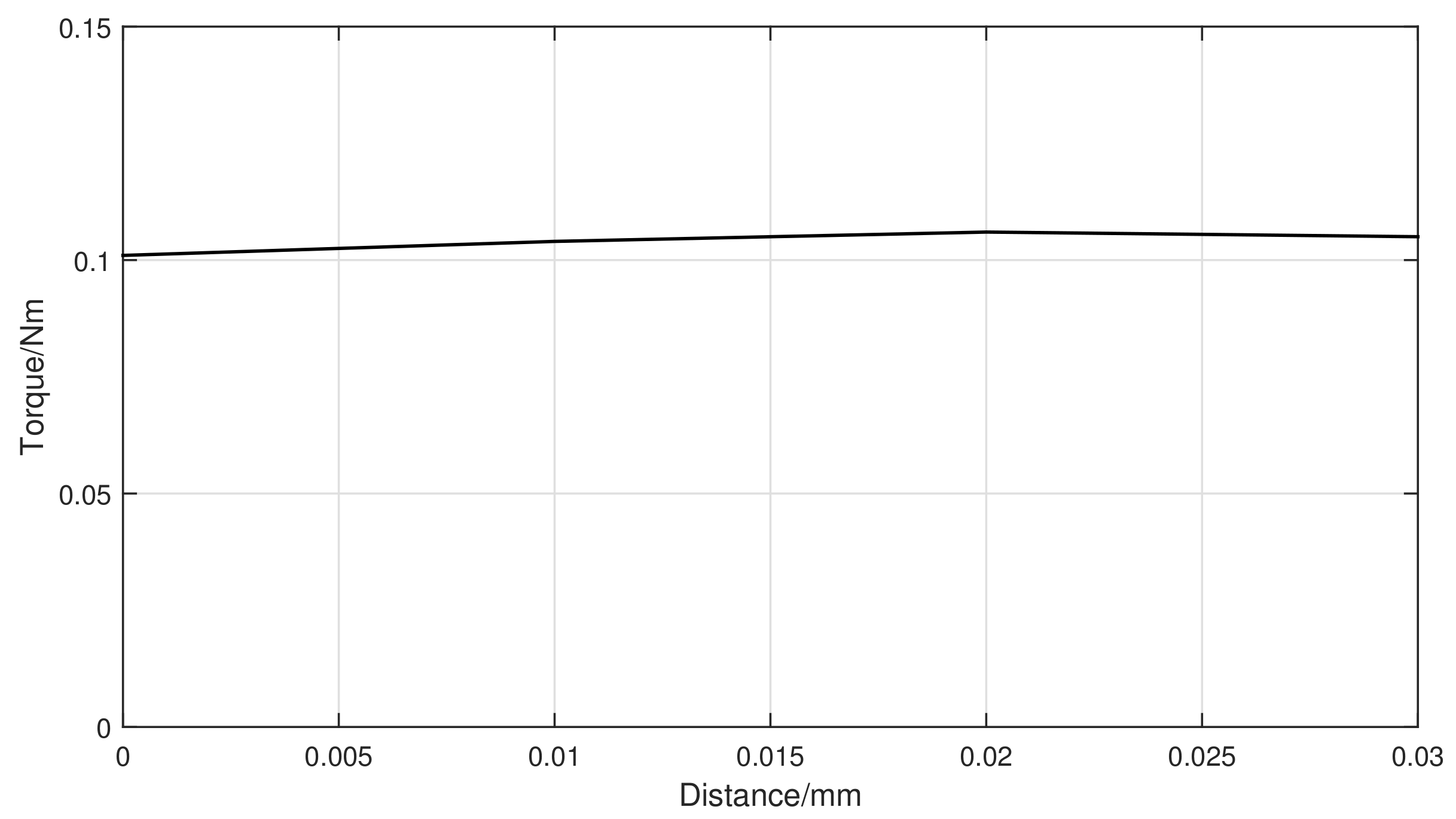
4.2.2. Displacement Assembly Error
5. Mathematical Formulation of Torque Output
5.1. Assumptions
- The thicknesses of the four air gaps are equal at the balanced position or when there is no excitation current applied to the coils.
- The ferromagnetic material or iron block works at the linear region of the curve.
- The magnetic hysteresis of the ferromagnetic material is small and negligible.
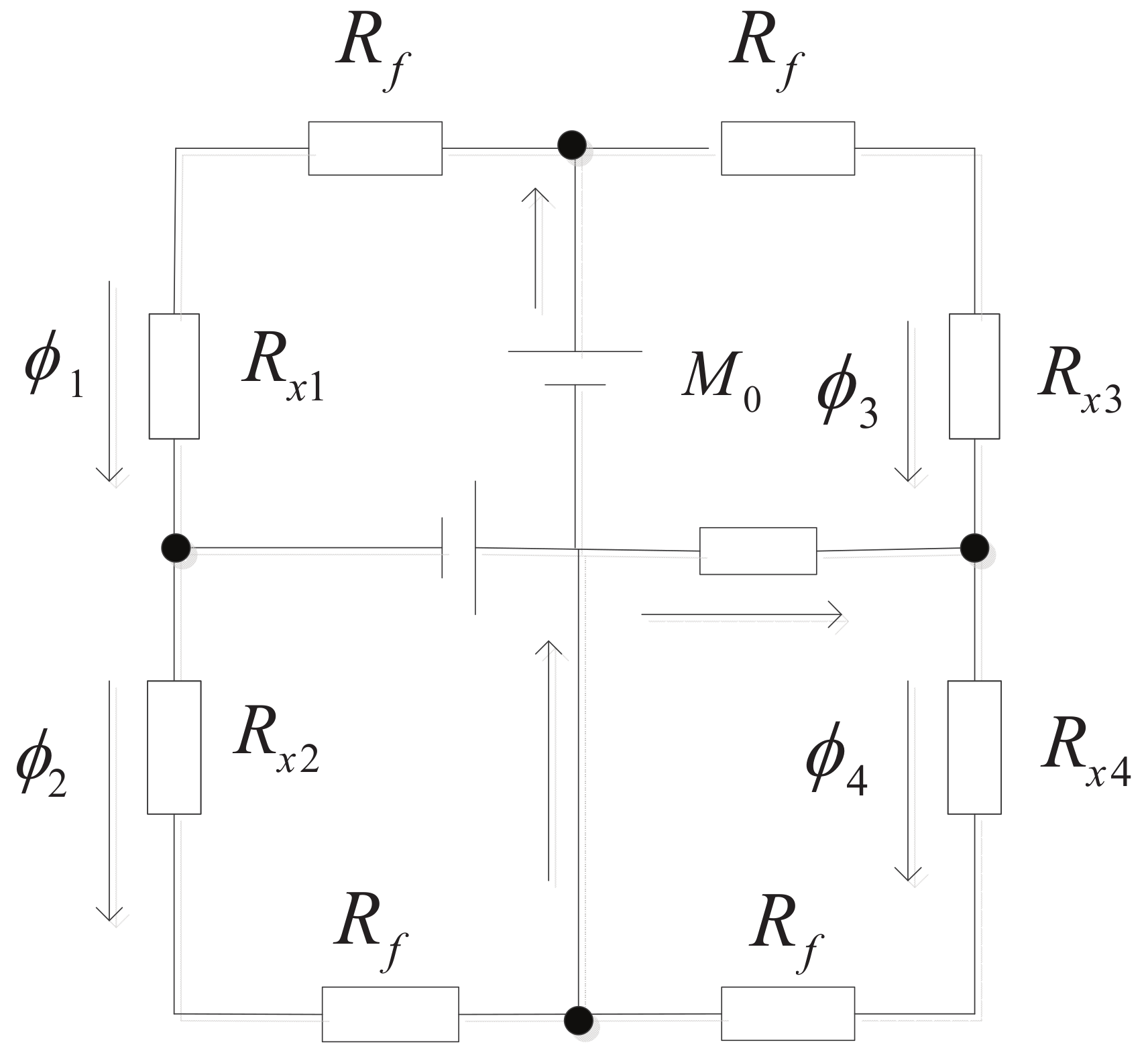
5.2. Magnetic Reluctance in the Flux Loop
5.2.1. Magnetic Circuit Equations
5.2.2. Derivation of Magnetic Force Generation
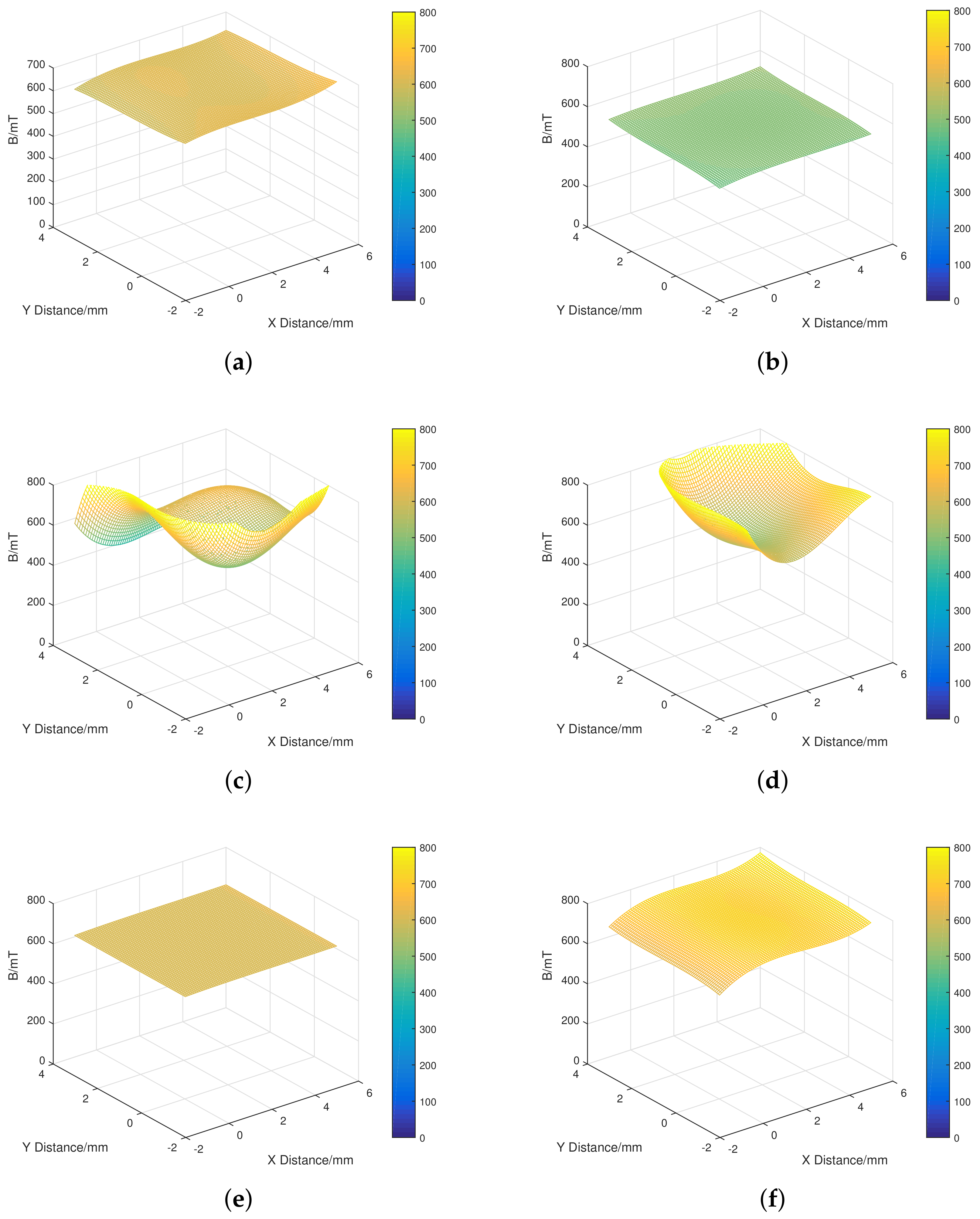
5.3. Numerical Simulation of Torque Output
5.4. Modification of Analytical Torque Model
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, C.; Jing, H. Influence of Magnetic Reluctances of Magnetic Elements on Servo Valve Torque Motors. Chin. J. Mech. Eng. 2016, 29, 136–143. [Google Scholar] [CrossRef]
- Liu, C. A Seventh-order Model for Dynamic Response of an Electro-hydraulic Servo Valve. Chin. J. Aeronaut. 2014, 27, 1605–1611. [Google Scholar] [CrossRef]
- Wang, H.; Gong, G. Steady Flow Torques in a Servo Motor Operated Rotary Directional Control Valve. Energy Convers. Manag. 2016, 112, 1–10. [Google Scholar] [CrossRef]
- Urata, E. On the Torque Generated in a Servo Valve Torque Motor Using Permanent Magnets. J. Mech. Eng. Sci. 2007, 221, 519–525. [Google Scholar] [CrossRef]
- Liu, X. The Characteristic and Control Technology Research on 3-Level Electro-Hydraulic Servo Valve; Harbin Institute of Technology: Harbin, China, 2010; pp. 1–2. [Google Scholar]
- Li, H.; Li, S. Study of Self-Excited Noise and Pressure Oscillations in a Hydraulic Jet-Pipe Servo-Valve with Magnetic Fluids; Harbin Institute of Technology: Harbin, China, 2010. [Google Scholar]
- Li, S. Influence of Magnetic Fluids on the Dynamic Characteristics of a Hydraulic Servo-valve Torque Motor. Mech. Syst. Signal Process. 2008, 22, 1008–1015. [Google Scholar] [CrossRef]
- Aung, N.; Li, S. A Numerical Study of Cavitation Phenomenon in a Flapper-nozzle Pilot Stage of an Electrohydraulic Servo-valve with an Innovative Flapper Shape. Energy Convers. Manag. 2014, 77, 31–39. [Google Scholar] [CrossRef]
- Somashekhar, S.; Singaperumal, M. Mathematical Modelling and Simulation of a Jet Pipe Electrohydraulic Flow Control Servo Valve. Syst. Control Eng. 2007, 221, 365–382. [Google Scholar] [CrossRef]
- Pham, X.H.S.; Yin, Y.B.; Zhang, X. Optimal Design for Torque Motor of Jet Pipe Electro-hydraulic Servo-valve Based on Dynamic Stiffness. In Proceedings of the 2012 4th International Conference on Intelligent Human-Machine Systems and Cybernetics, Nanchang, Jiangxi, China, 26–27 August 2012. [Google Scholar]
- Chu, Y. Research on Dynamic Reliability of a Jet Pipe Servo Valve Based on Generalized Stochastic Petri Nets. Int. J. Aerosp. Eng. 2015, 2015, 171642. [Google Scholar] [CrossRef]
- Urata, E. Influence of Unequal Air-gap Thickness in Servo Valve Torque Motors. J. Mech. Eng. Sci. 2007, 221, 1287–1297. [Google Scholar] [CrossRef]
- Wang, Z. Fault Modeling and Simulation of the Torque Motor Used in Electrohydraulic Servoo Valve. Hydraul. Pnenmatics Seals 2010, 10, 30–32. [Google Scholar]
- Liu, C.; Shao, D.; Wang, G. Development and Experimental Study of Magnetic Property for Servo Valve Torque Motor. Key Eng. Mater. 2014, 621, 233–238. [Google Scholar] [CrossRef]
- Wu, H. Non-linear Math Model of Torgue Motor Based on MATLAB. Mech. Magnet Dev. 2010, 25, 40–45. [Google Scholar]
- Liu, L.; Wang, H. Methods of Electromagnetic Force Calculation for Engineering Application. Missile Space Vehcile 2007, 1, 40–45. [Google Scholar]
- Tao, G.; Chen, H.Y.; He, Z.B. Optimal Design of the Magnetic Field of Ahigh-speed Response Solenoid Valve. J. Mater. Process. Technol. 2002, 129, 555–558. [Google Scholar] [CrossRef]
- Kar, N.; E1-Serafi, A. Measurement of the Saturation Characteristics in the Quadrature Axis of Synchronous Machines. IEEE Trans. Energy Convers. 2006, 21, 690–698. [Google Scholar] [CrossRef]
- Levi, E.; Levi, V. Impact of Dynamic Cross-saturation on Accuracy of Saturated Synchronous Machine Models. IEEE Trans. Energy Convers. 2000, 15, 224–230. [Google Scholar] [CrossRef]
- Karunanidhi, S.; Singaperumal, M. Design, Analysis and Simulation of Magnetostrictive Actuator and its Application to High Dynamic Servo Valve. J. Sens. Actuators 2009, 157, 185–197. [Google Scholar] [CrossRef]
- Merritt, H. Hydraulic Control Systems; John Wiley & Sons: New York, NY, USA, 1967; pp. 174–217. [Google Scholar]
- Heng, G.; Shang, Q. A Study of a New Type Torque Motor Modeling. J. Mech. Electr. Eng. 2010, 27, 21–25. [Google Scholar]


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| N | 4500 | ||
| g | |||
| Parameter | Value |
|---|---|
| Magnetic reluctance of iron blocks, | |
| Magnetic reluctance of armature, | |
| Magnetic reluctance of air gap when armature is at the initial position, |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, L.; Duan, Z.; Zhang, Q.; Niu, S.; Dong, Y.; Gerada, C. Magnetic Field and Torque Output of Packaged Hydraulic Torque Motor. Energies 2018, 11, 134. https://doi.org/10.3390/en11010134
Yan L, Duan Z, Zhang Q, Niu S, Dong Y, Gerada C. Magnetic Field and Torque Output of Packaged Hydraulic Torque Motor. Energies. 2018; 11(1):134. https://doi.org/10.3390/en11010134
Chicago/Turabian StyleYan, Liang, Zihao Duan, Qiongfang Zhang, Shiyong Niu, Yifeng Dong, and Christopher Gerada. 2018. "Magnetic Field and Torque Output of Packaged Hydraulic Torque Motor" Energies 11, no. 1: 134. https://doi.org/10.3390/en11010134
APA StyleYan, L., Duan, Z., Zhang, Q., Niu, S., Dong, Y., & Gerada, C. (2018). Magnetic Field and Torque Output of Packaged Hydraulic Torque Motor. Energies, 11(1), 134. https://doi.org/10.3390/en11010134





