Application of Dynamic Non-Linear Programming Technique to Non-Convex Short-Term Hydrothermal Scheduling Problem
Abstract
:1. Introduction
2. Problem Formulation
2.1. Objective Function
2.2. Power Balance Constraint
2.3. Limitations of Power Production
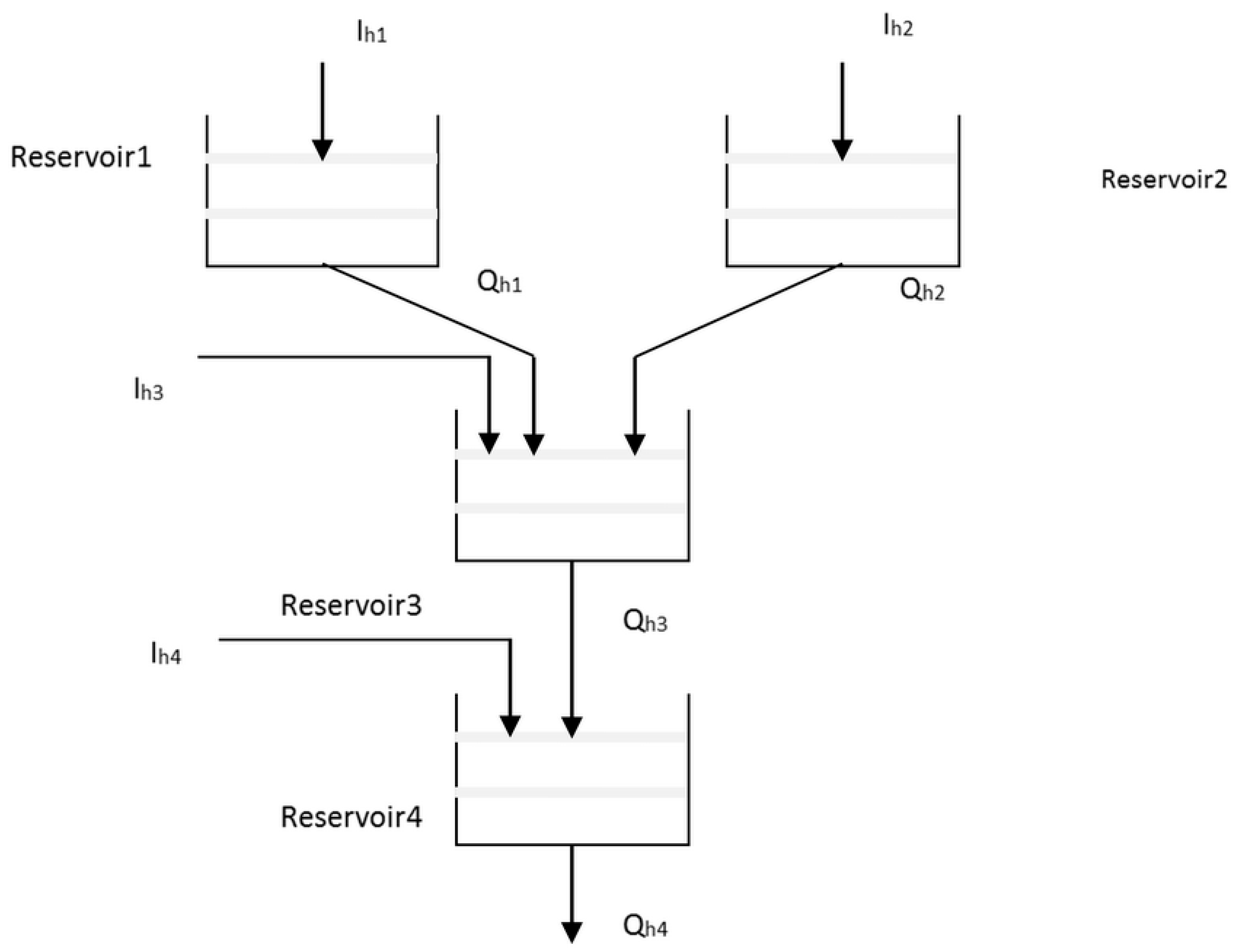
2.4. Hydraulic Network Constraints
2.4.1. Water Dynamic Balance
2.4.2. Reservoir Storage Volume Limits
2.4.3. Water Release Limits
2.4.4. Initial and Final Reservoir Storage Volume
3. Solution Methodology
4. Case Studies and Simulation Results
4.1. Test System 1
4.1.1. Test System 1 Case 1: Quadratic Cost without Valve-Point Loading Effect
4.1.2. Test System 1 Case 2: Quadratic Cost Function with Valve-Point Loading
4.2. Test System 2
4.2.1. Test System 2, Case 1: Quadratic Cost without Valve-Point Loading Effect
4.2.2. Test System 2 Case 2: Quadratic Cost Function with Valve-Point Loading
5. Conclusions
Author Contributions
Conflicts of Interest
Nomenclature
| Indexes | |
| t | Time interval of planning |
| Ns | The number of thermal plants |
| Nh | The number of hydro units |
| Constants | |
| , and | Cost coefficients of ith thermal plant |
| and | Valve-point coefficients of cost function of thermal unit i |
| Minimum power generation of thermal unit i | |
| Maximum power generation of thermal unit i | |
| Lower of operating volume of reservoir of ith hydro unit | |
| Upper bounds of operating volume of reservoir of ith hydro unit | |
| Minimum release of water reservoir of the ith hydro plant | |
| Maximum release of water reservoir of the ith hydro plant | |
| Elementary volume of reservoir | |
| Final volume of reservoir | |
| Load demand at time t | |
| , , , , , and | Hydro power generation coefficients |
| Set of instant upstream hydro plants of jth | |
| Variables | |
| Power generated by the ith thermal plant at time t | |
| Generation of hydro units | |
| Total transmission loss at time t | |
| The storage volume of reservoir | |
| The water discharge amount | |
| The inflow rate of the reservoir | |
| Acronyms | |
| STHTS | Short-term hydro-thermal scheduling |
| DNLP | Dynamic non-linear programming |
| MGS | Micro-grids |
| DGS | Distributed generations |
| DSM | Direct search method |
| ED | Economic dispatch |
| MABC | Modified artificial bee colony |
| DE | Differential evolution |
| MDNLPSO | Modified dynamic neighborhood learning based particle swarm optimization |
| QADEVT | Quadratic approximation based on differential evolution with valuable trade-off |
| PPO | Predator prey optimization |
| PSO | Particle swarm optimization |
| RCGA | Real coded genetic algorithm |
| LR | Lagrangian relaxation |
| MIP | Mixed integer programming |
| IMO | Improved merit order |
| ALHN | Augmented Lagrangian hopfield network |
| UC | Unit commitment |
| BFPSO | Bacterial foraging oriented by particle swarm optimization |
| DNLP | Dynamic non-linear programming |
| GAMS | General algebraic modeling system |
| LP | Linear programming |
| NLP | Nonlinear programming |
| MILP | Mixed-integer linear programming |
| MINLP | Mixed-integer nonlinear programming |
| DNLP | Dynamic nonlinear programming |
| QEA | Quantum-inspired evolutionary algorithm |
| WDA | Whole distribution algorithm |
| SPSO | Small population-based particle swarm optimization |
| RQEA | Real-coded quantum-inspired evolutionary algorithm |
| MDE | Modified differential evolution |
| DRQEA | Differential real-coded quantum-inspired evolutionary algorithm |
| DNLPSO | Dynamic neighborhood learning based particle swarm optimization |
| HCRO | Hybrid chemical reaction optimization |
| MAPSO | Modified adaptive particle swarm optimization |
| RCGA-AFSA | Real coded genetic algorithm and artificial fish swarm algorithm |
| TLBO | Teaching learning-based optimization |
| SOHPSO_TVAC | Self-organizing hierarchical particle swarm optimization technique with time-varying acceleration coefficients |
| IDE | Improved differential evolution |
| FAPSO | Fuzzy adaptive particle swarm optimization |
| ACDE | Adaptive chaotic differential evolution |
| CABC | Adaptive chaotic artificial bee colony |
| CSA | Clonal selection algorithm |
| IQPSO | Improved quantum-behaved particle swarm optimization |
| GSO | Group search optimization |
| ACDE | Adaptive chaotic differential evolution algorithm |
References
- Huang, W.-T.; Yao, K.-C.; Wu, C.-C. Using the direct search method for optimal dispatch of distributed generation in a medium-voltage microgrid. Energies 2014, 7, 8355–8373. [Google Scholar] [CrossRef]
- Ou, T.-C.; Lu, K.-H.; Huang, C.-J. Improvement of transient stability in a hybrid power multi-system using a designed NIDC (Novel Intelligent Damping Controller). Energies 2017, 10, 488. [Google Scholar] [CrossRef]
- Ou, T.-C.; Hong, C.-M. Dynamic operation and control of microgrid hybrid power systems. Energy 2014, 66, 314–323. [Google Scholar] [CrossRef]
- Ou, T.-C.; Su, W.-F.; Liu, X.-Z.; Huang, S.-J.; Tai, T.-Y. A modified bird-mating optimization with hill-climbing for connection decisions of transformers. Energies 2016, 9, 671. [Google Scholar] [CrossRef]
- Ou, T.-C. Ground fault current analysis with a direct building algorithm for microgrid distribution. Int. J. Electr. Power Energy Syst. 2013, 53, 867–875. [Google Scholar] [CrossRef]
- Ou, T.-C. A novel unsymmetrical faults analysis for microgrid distribution systems. Int. J. Electr. Power Energy Syst. 2012, 43, 1017–1024. [Google Scholar] [CrossRef]
- Hardiansyah, H. Solving economic dispatch problem with valve-point effect using a modified ABC algorithm. Int. J. Electr. Comput. Eng. 2013, 3, 377. [Google Scholar] [CrossRef]
- Huang, W.-T.; Yao, K.-C.; Wu, C.-C.; Chang, Y.-R.; Lee, Y.-D.; Ho, Y.-H. A Three-Stage Optimal Approach for Power System Economic Dispatch Considering Microgrids. Energies 2016, 9, 976. [Google Scholar] [CrossRef]
- Elsaiah, S.; Cai, N.; Benidris, M.; Mitra, J. Fast economic power dispatch method for power system planning studies. IET Gener. Transm. Distrib. 2015, 9, 417–426. [Google Scholar] [CrossRef]
- Benidris, M.; Elsaiah, S.; Mitra, J. An emission-constrained approach to power system expansion planning. Int. J. Electr. Power Energy Syst. 2016, 81, 78–86. [Google Scholar] [CrossRef]
- Nadakuditi, G.; Sharma, V.; Naresh, R. Application of non-dominated sorting gravitational search algorithm with disruption operator for stochastic multiobjective short term hydrothermal scheduling. IET Gener. Transm. Distrib. 2016, 10, 862–872. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Gharehpetian, G. A comprehensive review of heuristic optimization algorithms for optimal combined heat and power dispatch from economic and environmental perspectives. Renew. Sustain. Energy Rev. 2017. [Google Scholar] [CrossRef]
- Yuan, X.; Tian, H.; Yuan, Y.; Zhang, X. Multi-objective Artificial Physical Optimization Algorithm for Daily Economic Environmental Dispatch of Hydrothermal Systems. Electr. Power Compon. Syst. 2016, 44, 533–543. [Google Scholar] [CrossRef]
- Dubey, H.M.; Pandit, M.; Panigrahi, B. Hydro-thermal-wind scheduling employing novel ant lion optimization technique with composite ranking index. Renew. Energy 2016, 99, 18–34. [Google Scholar] [CrossRef]
- Rasoulzadeh-akhijahani, A.; Mohammadi-ivatloo, B. Short-term hydrothermal generation scheduling by a modified dynamic neighborhood learning based particle swarm optimization. Int. J. Electr. Power Energy Syst. 2015, 67, 350–367. [Google Scholar] [CrossRef]
- Lu, S.; Sun, C. Quadratic approximation based differential evolution with valuable trade off approach for bi-objective short-term hydrothermal scheduling. Exp. Syst. Appl. 2011, 38, 13950–13960. [Google Scholar] [CrossRef]
- Narang, N.; Dhillon, J.; Kothari, D. Scheduling short-term hydrothermal generation using predator prey optimization technique. Appl. Soft Comput. 2014, 21, 298–308. [Google Scholar] [CrossRef]
- Qin, H.; Zhou, J.; Lu, Y.; Wang, Y.; Zhang, Y. Multi-objective differential evolution with adaptive Cauchy mutation for short-term multi-objective optimal hydro-thermal scheduling. Energy Convers. Manag. 2010, 51, 788–794. [Google Scholar] [CrossRef]
- Yuan, X.; Wang, L.; Yuan, Y. Application of enhanced PSO approach to optimal scheduling of hydro system. Energy Convers. Manag. 2008, 49, 2966–2972. [Google Scholar] [CrossRef]
- Takigawa, F.Y.; da Silva, E.L.; Finardi, E.C.; Rodrigues, R.N. Solving the hydrothermal scheduling problem considering network constraints. Electr. Power Syst. Res. 2012, 88, 89–97. [Google Scholar] [CrossRef]
- Ahmadi, A.; Aghaei, J.; Shayanfar, H.A.; Rabiee, A. Mixed integer programming of multiobjective hydro-thermal self scheduling. Appl. Soft Comput. 2012, 12, 2137–2146. [Google Scholar] [CrossRef]
- Dieu, V.N.; Ongsakul, W. Improved merit order and augmented Lagrange Hopfield network for short term hydrothermal scheduling. Energy Convers. Manag. 2009, 50, 3015–3023. [Google Scholar] [CrossRef]
- Parastegari, M.; Hooshmand, R.-A.; Khodabakhshian, A.; Vatanpour, M. AC constrained hydro-thermal generation scheduling problem: Application of Benders decomposition method improved by BFPSO. Int. J. Electr. Power Energy Syst. 2013, 49, 199–212. [Google Scholar] [CrossRef]
- Arena, P.; Fazzino, S.; Fortuna, L.; Maniscalco, P. Game theory and non-linear dynamics: The Parrondo paradox case study. Chaos Solitons Fractals 2003, 17, 545–555. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, J.; Mo, L.; Zhang, R.; Zhang, Y. Short-term hydrothermal generation scheduling using differential real-coded quantum-inspired evolutionary algorithm. Energy 2012, 44, 657–671. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Haghrah, A. Optimal short-term generation scheduling of hydrothermal systems by implementation of real-coded genetic algorithm based on improved Mühlenbein mutation. Energy 2017, 128, 77–85. [Google Scholar] [CrossRef]
- Mohammadi-Ivatloo, B.; Rabiee, A.; Soroudi, A. Nonconvex dynamic economic power dispatch problems solution using hybrid immune-genetic algorithm. IEEE Syst. J. 2013, 7, 777–785. [Google Scholar] [CrossRef]
- Abdelaziz, A.; Kamh, M.; Mekhamer, S.; Badr, M. A hybrid HNN-QP approach for dynamic economic dispatch problem. Electr. Power Syst. Res. 2008, 78, 1784–1788. [Google Scholar] [CrossRef]
- Rosenthal, R.E. GAMS User’s Guide And Examples; GAMS Development Corporation: Washington DC, USA, 2012; Available online: http://www.gams.com/dd/docs/solvers/conopt.pdf (accessed on 21 August 2017).
- Brooke, A.; Kendrick, D.; Meeraus, A. Gams User’s Guide; GAMS Development Corporation: Washington, DC, USA, 1990; Available online: http://www.gams.com/docs/gams/GAMSUsers (accessed on 21 August 2017).
- Laguna, M.; Marti, R. Scatter Search: Methodology and Implementations in C; Springer Science & Business Media: New York, NY, USA, 2012; Volume 24. [Google Scholar]
- Yu, B.; Du, Z. A study on short-term hydro-thermal scheduling based on whole distribution algorithm. In Proceedings of the World Automation Congress 2012, Puerto Vallarta, Mexico, 24–28 June 2012. [Google Scholar]
- Zhang, J.; Wang, J.; Yue, C. Small population-based particle swarm optimization for short-term hydrothermal scheduling. IEEE Trans. Power Syst. 2012, 27, 142–152. [Google Scholar] [CrossRef]
- Fang, N.; Zhou, J.; Zhang, R.; Liu, Y.; Zhang, Y. A hybrid of real coded genetic algorithm and artificial fish swarm algorithm for short-term optimal hydrothermal scheduling. Int. J. Electr. Power Energy Syst. 2014, 62, 617–629. [Google Scholar] [CrossRef]
- Roy, P.K. Hybrid Chemical Reaction Optimization Approach for Combined Economic Emission Short-term Hydrothermal Scheduling. Electr. Power Compon. Syst. 2014, 42, 1647–1660. [Google Scholar] [CrossRef]
- Amjady, N.; Soleymanpour, H.R. Daily hydrothermal generation scheduling by a new modified adaptive particle swarm optimization technique. Electr. Power Syst. Res. 2010, 80, 723–732. [Google Scholar] [CrossRef]
- Roy, P.K. Teaching learning based optimization for short-term hydrothermal scheduling problem considering valve point effect and prohibited discharge constraint. Int. J. Electr. Power Energy Syst. 2013, 53, 10–19. [Google Scholar] [CrossRef]
- Mandal, K.K.; Chakraborty, N. Optimal scheduling of cascaded hydrothermal systems using a new improved particle swarm optimization technique. Smart Grid Renew. Energy 2011, 2, 282. [Google Scholar] [CrossRef]
- Wenping, C. Optimal Scheduling of Hydrothermal System Based on Improved Particle Swarm Optimization. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference (APPEEC), Chengdu, China, 28–31 March 2010. [Google Scholar]
- Basu, M. Improved differential evolution for short-term hydrothermal scheduling. Int. J. Electr. Power Energy Syst. 2014, 58, 91–100. [Google Scholar] [CrossRef]
- Bhattacharjee, K.; Bhattacharya, A.; nee Dey, S.H. Oppositional real coded chemical reaction based optimization to solve short-term hydrothermal scheduling problems. Int. J. Electr. Power Energy Syst. 2014, 63, 145–157. [Google Scholar] [CrossRef]
- Lu, Y.; Zhou, J.; Qin, H.; Wang, Y.; Zhang, Y. An adaptive chaotic differential evolution for the short-term hydrothermal generation scheduling problem. Energy Convers. Manag. 2010, 51, 1481–1490. [Google Scholar] [CrossRef]
- Liao, X.; Zhou, J.; Ouyang, S.; Zhang, R.; Zhang, Y. An adaptive chaotic artificial bee colony algorithm for short-term hydrothermal generation scheduling. Int. J. Elect. Power Energy Syst. 2013, 53, 34–42. [Google Scholar] [CrossRef]
- Roy, P.K.; Paul, C.; Sultana, S. Oppositional teaching learning based optimization approach for combined heat and power dispatch. Int. J. Electr. Power Energy Syst. 2014, 57, 392–403. [Google Scholar] [CrossRef]
- Mandal, K.K.; Chakraborty, N. Short-term combined economic emission scheduling of hydrothermal systems with cascaded reservoirs using particle swarm optimization technique. Appl. Soft Comput. 2011, 11, 1295–1302. [Google Scholar] [CrossRef]
- Swain, R.; Barisal, A.; Hota, P.; Chakrabarti, R. Short-term hydrothermal scheduling using clonal selection algorithm. Int. J. Electr. Power Energy Syst. 2011, 33, 647–656. [Google Scholar] [CrossRef]
- Roy, P.K.; Sur, A.; Pradhan, D.K. Optimal short-term hydro-thermal scheduling using quasi-oppositional teaching learning based optimization. Eng. Appl. Artif. Intell. 2013, 26, 2516–2524. [Google Scholar]
- Sun, C.; Lu, S. Short-term combined economic emission hydrothermal scheduling using improved quantum-behaved particle swarm optimization. Exp. Syst. Appl. 2010, 37, 4232–4241. [Google Scholar] [CrossRef]
- Basu, M. Quasi-oppositional group search optimization for hydrothermal power system. Int. J. Electr. Power Energy Syst. 2016, 81, 324–335. [Google Scholar] [CrossRef]
- Mandal, K.K.; Tudu, B.; Chakraborty, N. A new improved particle swarm optimization technique for daily economic generation scheduling of cascaded hydrothermal systems. In Proceedings of the International Conference on Swarm, Evolutionary and Memetic Computing, Chennai, India, 16–18 December 2010; pp. 680–688. [Google Scholar]
- Mandal, K.K.; Chakraborty, N. Daily combined economic emission scheduling of hydrothermal systems with cascaded reservoirs using self organizing hierarchical particle swarm optimization technique. Exp. Syst. Appl. 2012, 39, 3438–3445. [Google Scholar] [CrossRef]
- Gouthamkumar, N.; Sharma, V.; Naresh, R. Disruption based gravitational search algorithm for short term hydrothermal scheduling. Exp. Syst. Appl. 2015, 42, 7000–7011. [Google Scholar] [CrossRef]
- Zhang, R.; Zhou, J.; Wang, Y. Multi-objective optimization of hydrothermal energy system considering economic and environmental aspects. Int. J. Electr. Power Energy Syst. 2012, 42, 384–395. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, J.; Mo, L.; Ouyang, S.; Zhang, Y. A clonal real-coded quantum-inspired evolutionary algorithm with Cauchy mutation for short-term hydrothermal generation scheduling. Int. J. Electr. Power Energy Syst. 2012, 43, 1228–1240. [Google Scholar] [CrossRef]

| Hour | Hydro Plant Discharges (104 m3) | Hydro Power Output (megawatts (MW)) | Thermal Generation (MW) | Total Generation (MW) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Plant 1 | Plant 2 | Plant 3 | Plant 4 | Plant 1 | Plant 2 | Plant3 | Plant 4 | |||
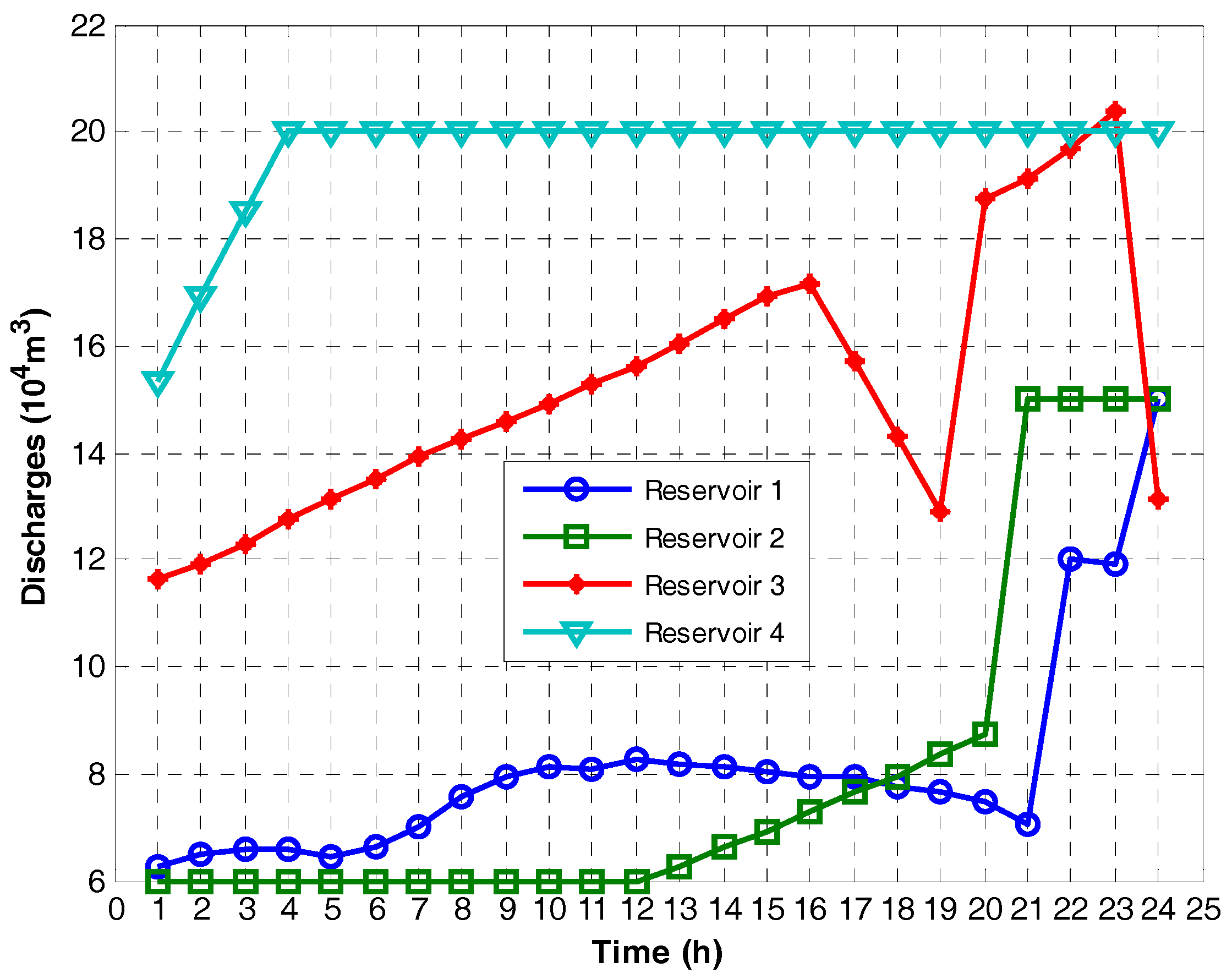
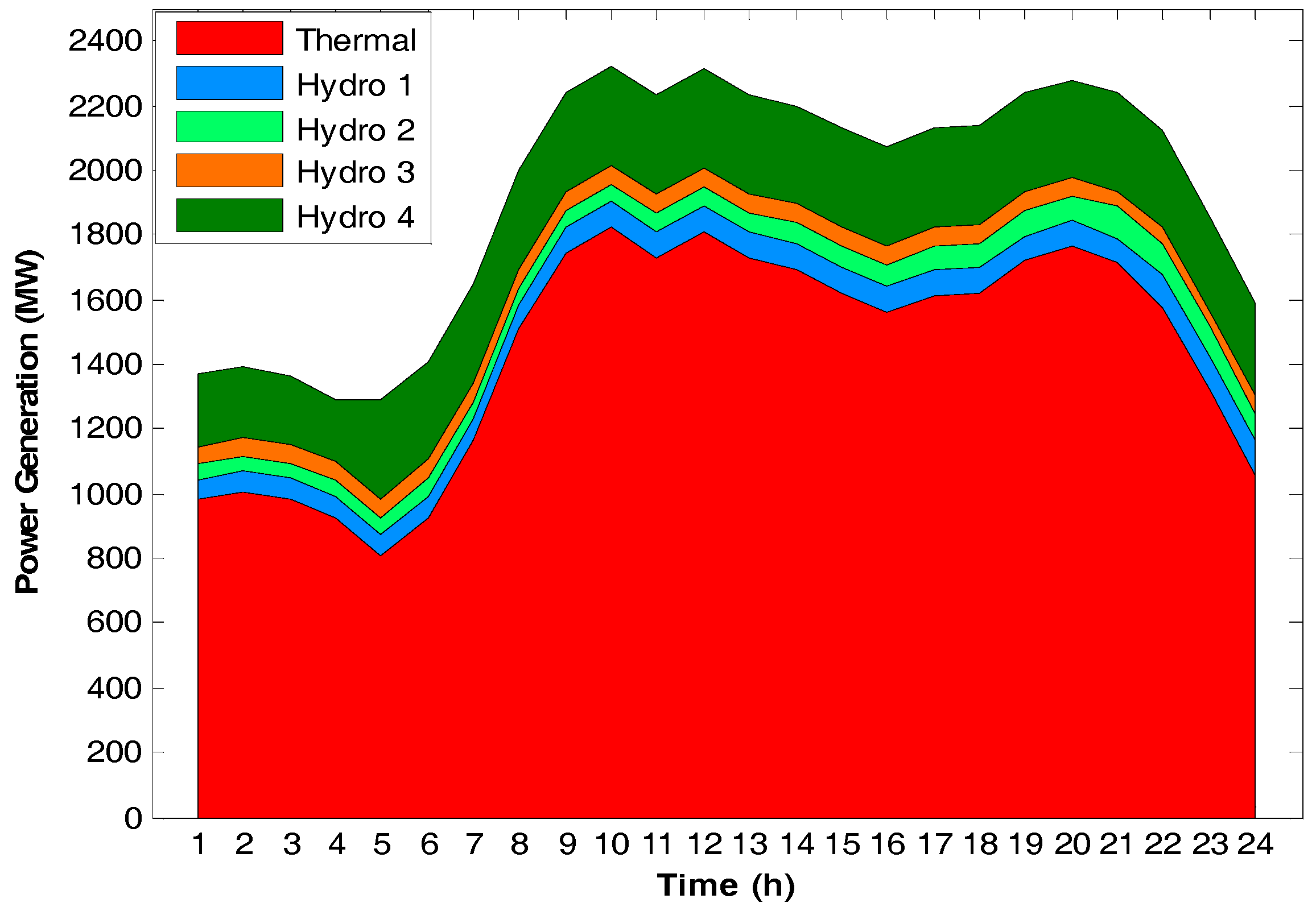
| 1 | 6.254 | 6.000 | 11.632 | 15.344 | 61.528 | 45.316 | 56.480 | 224.231 | 982.445 | 1370 |
| 2 | 6.488 | 6.000 | 11.914 | 16.919 | 64.339 | 46.576 | 55.928 | 219.694 | 1003.464 | 1390 |
| 3 | 6.594 | 6.000 | 12.303 | 18.537 | 65.777 | 47.804 | 56.376 | 209.020 | 981.024 | 1360 |
| 4 | 6.592 | 6.000 | 12.741 | 20.000 | 66.102 | 49.586 | 57.320 | 189.900 | 927.092 | 1290 |
| 5 | 6.431 | 6.000 | 13.129 | 20.000 | 64.972 | 51.296 | 57.694 | 306.000 | 810.039 | 1290 |
| 6 | 6.617 | 6.000 | 13.531 | 20.000 | 66.284 | 52.396 | 58.133 | 306.000 | 927.187 | 1410 |
| 7 | 7.005 | 6.000 | 13.923 | 20.000 | 69.238 | 52.934 | 58.611 | 306.000 | 1163.217 | 1650 |
| 8 | 7.545 | 6.000 | 14.254 | 20.000 | 73.259 | 52.934 | 58.728 | 306.000 | 1509.079 | 2000 |
| 9 | 7.927 | 6.000 | 14.568 | 20.000 | 76.166 | 53.464 | 58.565 | 306.000 | 1745.805 | 2240 |
| 10 | 8.109 | 6.000 | 14.894 | 20.000 | 77.851 | 54.500 | 58.136 | 306.000 | 1823.512 | 2320 |
| 11 | 8.087 | 6.000 | 15.277 | 20.000 | 78.367 | 55.994 | 57.612 | 306.000 | 1732.027 | 2230 |
| 12 | 8.272 | 6.000 | 15.621 | 20.000 | 80.353 | 57.416 | 57.056 | 306.000 | 1809.175 | 2310 |
| 13 | 8.165 | 6.254 | 16.047 | 20.000 | 79.963 | 60.180 | 56.475 | 306.000 | 1727.382 | 2230 |
| 14 | 8.124 | 6.613 | 16.494 | 20.000 | 80.131 | 63.512 | 56.112 | 306.000 | 1694.245 | 2200 |
| 15 | 8.043 | 6.927 | 16.939 | 20.000 | 80.074 | 66.727 | 55.351 | 306.000 | 1621.848 | 2130 |
| 16 | 7.930 | 7.272 | 17.137 | 20.000 | 79.565 | 69.947 | 54.948 | 306.000 | 1559.540 | 2070 |
| 17 | 7.950 | 7.670 | 15.694 | 20.000 | 79.858 | 72.868 | 57.561 | 306.000 | 1613.712 | 2130 |
| 18 | 7.768 | 7.950 | 14.281 | 20.000 | 78.597 | 74.372 | 59.277 | 306.000 | 1621.754 | 2140 |
| 19 | 7.662 | 8.374 | 12.888 | 20.000 | 77.830 | 76.131 | 60.031 | 306.000 | 1720.008 | 2240 |
| 20 | 7.452 | 8.751 | 18.733 | 20.000 | 76.216 | 77.728 | 51.940 | 306.000 | 1768.116 | 2280 |
| 21 | 7.063 | 15.000 | 19.145 | 20.000 | 73.145 | 101.607 | 49.988 | 303.055 | 1712.205 | 2240 |
| 22 | 11.991 | 15.000 | 19.676 | 20.000 | 101.750 | 98.082 | 47.637 | 298.534 | 1573.998 | 2120 |
| 23 | 11.931 | 15.000 | 20.368 | 20.000 | 100.691 | 94.269 | 44.320 | 292.356 | 1318.364 | 1850 |
| 24 | 15.000 | 15.000 | 13.133 | 20.000 | 107.020 | 80.950 | 59.005 | 284.400 | 1058.625 | 1590 |
| Optimization Method | Min. Cost ($) | Max. Cost ($) | Ave. Cost ($) |
|---|---|---|---|
| QEA [25] | 926,538.29 | 930,484.13 | 928,426.95 |
| WDA [32] | 925,618.5 | - | 928,219.8 |
| SPSO [33] | 925,308.86 | 923,083.48 | 926,185.32 |
| RCGA [34] | 923,966.285 | 924,108.731 | 924,232.072 |
| RQEA [25] | 923,634.53 | 926,957.39 | 924,992.46 |
| DE [25] | 923,234.56 | 928,395.84 | 925,157.28 |
| MDE [33] | 922,556.38 | 923,201.13 | 923,813.99 |
| DRQEA [25] | 922,526.73 | 925,871.51 | 923,419.37 |
| DNLPSO [15] | 922,498 | 923,580 | 922,837 |
| HCRO [35] | 922,444.79 | 922,513.62 | 922,936.17 |
| MAPSO [36] | 922,421.66 | 923,508 | 922,544 |
| RCGA-AFSA [34] | 922,339.625 | 922,346.323 | 922,362.532 |
| TLBO [37] | 922,373.39 | 922,873.81 | 922,462.24 |
| SPPSO [33] | 922,336.31 | 922,362.532 | 923,083.48 |
| SOHPSO_TVAC [38] | 922,018.24 | - | - |
| PSO [39] | 921,920 | - | - |
| IDE [40] | 917,237.7 | 917,277.8 | 917,250.1 |
| FAPSO [39] | 914,660 | - | - |
| Proposed method | 884,733.965 | - | - |
| Hour | Hydro Plant Discharges (104 m3) | Hydro Power Output (MW) | Thermal Generation (MW) | Total Generation (MW) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Plant 1 | Plant 2 | Plant 3 | Plant 4 | Plant 1 | Plant 2 | Plant 3 | Plant 4 | |||
| 1 | 5.212 | 6.000 | 10.730 | 13.080 | 53.156 | 45.316 | 55.550 | 198.539 | 1017.439 | 1370 |
| 2 | 5.555 | 6.487 | 10.976 | 16.211 | 57.199 | 49.935 | 55.337 | 210.090 | 1017.439 | 1390 |
| 3 | 5.148 | 6.000 | 10.252 | 15.327 | 54.329 | 47.508 | 54.789 | 185.936 | 943.519 | 1360 |
| 4 | 5.023 | 6.000 | 10.000 | 19.571 | 53.613 | 49.302 | 55.220 | 188.347 | 832.639 | 1290 |
| 5 | 5.052 | 6.000 | 17.571 | 20.000 | 54.126 | 51.024 | 52.771 | 299.440 | 943.519 | 1290 |
| 6 | 5.150 | 6.000 | 10.000 | 19.615 | 55.150 | 52.133 | 55.526 | 303.672 | 1168.561 | 1410 |
| 7 | 5.605 | 6.574 | 12.835 | 20.000 | 59.407 | 56.704 | 59.328 | 306.000 | 1586.197 | 1650 |
| 8 | 5.257 | 6.196 | 12.065 | 12.500 | 56.689 | 53.757 | 59.195 | 244.162 | 1756.637 | 2000 |
| 9 | 5.613 | 6.661 | 12.694 | 20.000 | 60.242 | 57.427 | 59.693 | 306.000 | 1762.699 | 2240 |
| 10 | 13.476 | 13.306 | 13.137 | 19.485 | 104.423 | 90.251 | 59.762 | 302.866 | 1719.677 | 2320 |
| 11 | 11.589 | 6.021 | 10.104 | 19.739 | 98.015 | 51.320 | 56.792 | 304.196 | 1793.597 | 2230 |
| 12 | 11.752 | 6.122 | 11.916 | 19.739 | 98.732 | 53.678 | 59.620 | 304.373 | 1740.260 | 2310 |
| 13 | 9.254 | 6.170 | 21.626 | 20.000 | 86.633 | 55.018 | 42.089 | 306.000 | 1756.637 | 2230 |
| 14 | 8.274 | 6.137 | 27.943 | 19.921 | 80.932 | 55.725 | 1.827 | 304.880 | 1675.480 | 2200 |
| 15 | 5.000 | 6.000 | 21.954 | 19.476 | 55.068 | 56.152 | 40.489 | 302.810 | 1608.797 | 2130 |
| 16 | 5.320 | 6.544 | 21.608 | 20.000 | 58.135 | 61.472 | 41.271 | 300.325 | 1645.757 | 2070 |
| 17 | 5.234 | 8.595 | 14.157 | 19.978 | 57.184 | 75.322 | 60.241 | 291.496 | 1645.757 | 2130 |
| 18 | 7.821 | 6.640 | 14.810 | 20.000 | 79.151 | 62.077 | 59.593 | 293.422 | 1719.677 | 2140 |
| 19 | 8.424 | 9.199 | 10.298 | 19.987 | 83.520 | 77.592 | 57.383 | 301.828 | 1793.597 | 2240 |
| 20 | 10.474 | 11.904 | 27.516 | 19.607 | 96.000 | 88.807 | 6.038145 | 301.595 | 1674.858 | 2280 |
| 21 | 14.459 | 14.871 | 10.000 | 19.888 | 109.205 | 94.848 | 55.758 | 305.331 | 1645.757 | 2240 |
| 22 | 8.381 | 14.998 | 27.296 | 19.993 | 82.343 | 91.135 | 0.747 | 300.017 | 1387.038 | 2120 |
| 23 | 8.425 | 14.996 | 26.778 | 19.399 | 82.203 | 86.813 | 2.930 | 291.016 | 1096.580 | 1850 |
| 24 | 15.000 | 6.721 | 13.133 | 19.190 | 107.020 | 47.557 | 59.005 | 279.837 | 1058.625 | 1590 |
| Optimization Method | Min. Cost ($) |
|---|---|
| QEA [25] | 930,647.96 |
| DE [25] | 928,662.84 |
| RCGA-AFSA [34] | 927,899.872 |
| RQEA [25] | 926,068.33 |
| DRQEA [25] | 925,485.21 |
| CRQEA [25] | 925,403.1 |
| RCCRO [41] | 925,214.20 |
| ACDE [42] | 924,661.53 |
| MAPSO [36] | 924,636 |
| TLBO [37] | 924,550.78 |
| RCGA [34] | 923,966.285 |
| RQEA [25] | 923,634.53 |
| DE [25] | 923,234.56 |
| MDE [33] | 922,556.38 |
| DRQEA [25] | 922,526.73 |
| HCRO-DE [35] | 922,444.79 |
| MAPSO [36] | 922,421.66 |
| MDNLPSO [15] | 923,961 |
| IDE [40] | 923,016.29 |
| TLBO [37] | 922,373.39 |
| RCGA-AFSA [34] | 922,339.625 |
| SPPSO [33] | 922,336.31 |
| SOHPSO_TVAC [38] | 922,018.24 |
| PSO [39] | 921,920 |
| Improved DE [40] | 917,250.1 |
| IDE [40] | 917,237.7 |
| FAPSO [39] | 914,660.00 |
| Proposed method | 901,191.9735 |
| Hour | Hydro Plant Discharges (104 m3) | Hydro Power Output (MW) | Thermal Power Output (MW) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Plant 1 | Plant 2 | Plant 3 | Plant 4 | Plant 1 | Plant 2 | Plant 3 | Plant 4 | Plant 1 | Plant 2 | Plant 3 | |
| 1 | 5.940 | 6.000 | 11.919 | 15.335 | 59.103 | 45.317 | 54.084 | 224.158 | 102.673 | 124.908 | 139.758 |
| 2 | 6.699 | 7.766 | 14.024 | 20.000 | 65.989 | 58.072 | 52.592 | 236.005 | 102.673 | 124.908 | 139.760 |
| 3 | 6.864 | 6.002 | 16.358 | 13.099 | 67.796 | 46.733 | 48.618 | 169.512 | 102.673 | 124.908 | 139.760 |
| 4 | 5.000 | 6.000 | 20.251 | 12.102 | 53.000 | 48.545 | 34.952 | 146.162 | 102.673 | 124.908 | 139.760 |
| 5 | 5.000 | 6.000 | 19.354 | 7.486 | 53.361 | 50.298 | 36.816 | 162.185 | 102.673 | 124.908 | 139.760 |
| 6 | 5.562 | 6.000 | 18.081 | 20.000 | 58.435 | 51.426 | 41.026 | 281.773 | 102.673 | 124.908 | 139.760 |
| 7 | 8.717 | 7.235 | 10.050 | 9.521 | 81.434 | 60.381 | 48.532 | 189.953 | 175.000 | 165.181 | 229.519 |
| 8 | 6.793 | 6.000 | 10.000 | 12.002 | 68.402 | 51.295 | 49.484 | 226.483 | 175.000 | 209.816 | 229.520 |
| 9 | 8.278 | 6.984 | 10.000 | 17.853 | 79.131 | 58.617 | 50.361 | 287.556 | 175.000 | 209.816 | 229.520 |
| 10 | 9.721 | 6.901 | 10.000 | 15.166 | 87.819 | 58.640 | 51.683 | 267.523 | 175.000 | 209.816 | 229.520 |
| 11 | 9.980 | 7.651 | 10.000 | 16.174 | 89.468 | 64.626 | 52.759 | 278.812 | 175.000 | 209.816 | 229.519 |
| 12 | 11.526 | 9.682 | 12.521 | 19.991 | 96.739 | 76.822 | 56.159 | 305.945 | 175.000 | 209.816 | 229.519 |
| 13 | 8.830 | 8.827 | 18.363 | 19.431 | 83.318 | 71.352 | 48.797 | 292.197 | 175.000 | 209.816 | 229.519 |
| 14 | 8.337 | 6.894 | 17.750 | 12.235 | 80.723 | 59.110 | 51.359 | 224.472 | 175.000 | 209.816 | 229.519 |
| 15 | 7.791 | 6.297 | 19.374 | 13.639 | 77.682 | 56.137 | 47.225 | 236.017 | 175.000 | 209.812 | 208.126 |
| 16 | 5.474 | 7.836 | 10.000 | 17.345 | 59.431 | 67.731 | 56.316 | 262.186 | 175.000 | 209.816 | 229.519 |
| 17 | 8.555 | 7.625 | 10.000 | 12.243 | 83.821 | 66.503 | 57.468 | 227.928 | 174.999 | 209.816 | 229.465 |
| 18 | 9.628 | 9.144 | 10.000 | 17.593 | 90.452 | 75.044 | 58.138 | 282.031 | 175.000 | 209.816 | 229.519 |
| 19 | 8.801 | 8.764 | 10.000 | 12.800 | 85.273 | 71.213 | 58.453 | 240.726 | 175.000 | 209.816 | 229.520 |
| 20 | 5.000 | 8.951 | 21.305 | 14.379 | 55.099 | 71.229 | 46.410 | 262.927 | 175.000 | 209.816 | 229.520 |
| 21 | 7.167 | 12.825 | 25.403 | 8.680 | 73.741 | 87.127 | 22.093 | 197.616 | 175.000 | 124.903 | 229.520 |
| 22 | 10.381 | 13.611 | 26.991 | 19.652 | 94.074 | 86.783 | 8.525 | 303.277 | 102.673 | 124.908 | 139.760 |
| 23 | 9.956 | 15.000 | 26.187 | 19.731 | 91.469 | 86.389 | 11.133 | 293.668 | 102.673 | 124.908 | 139.760 |
| 24 | 7.979 | 7.656 | 13.143 | 14.001 | 79.296 | 53.388 | 59.005 | 240.969 | 102.673 | 124.908 | 139.760 |
| Optimization Method | Min. Cost | Mean. Cost | Max. Cost |
|---|---|---|---|
| SA [44] | 45,466 | - | - |
| DE [32] | 44,526.11 | - | - |
| CABC [43] | 43,362.68 | - | - |
| ADE [43] | 43,222.41 | - | - |
| RCGA [34] | 42,886.352 | 43,261.912 | 43,032.334 |
| DE [25] | 42 801.04 | - | - |
| SPPSO [33] | 42,740.23 | 43,622.14 | 44,346.97 |
| RQEA [25] | 42 715.69 | - | - |
| PSO [45] | 42,474.00 | - | - |
| CDE [42] | 42,452.99 | - | - |
| CSA [46] | 42,440.574 | - | - |
| TLBO [47] | 42,386.13 | 42,407.23 | 42,441.36 |
| TLBO [33] | 42,385.88 | 42,407.23 | 42,441.36 |
| IQPSO [48] | 42,359.00 | - | - |
| GSO [49] | 42,316.39 | 42,339.35 | 42,379.18 |
| QTLBO [47] | 42,187.49 | 42,193.46 | 42,202.75 |
| QOGSO [49] | 42,120.02 | 42,130.15 | 42,145.37 |
| IDE [40] | 41,856.5 | - | - |
| ACDE [42] | 41,593.48 | - | - |
| RCCRO [41] | 41,497.85 | 41,498.21 | 41,502.36 |
| DRQEA [25] | 41,435.76 | - | - |
| ACABC [43] | 41,274.42 | - | - |
| Proposed method | 41,101.738 | - | - |
| Hour | Hydro Plant Discharge, 104 m3 | Hydro Plant Generation (MW) | Thermal Plant Generation (MW) | Loss MW | Total Generation, MW | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Plant 1 | Plant 2 | Plant 3 | Plant 4 | Plant 1 | Plant 2 | Plant 3 | Plant 4 | Plant 1 | Plant 2 | Plant 3 | |||
| 1 | 6.224 | 7.064 | 12.991 | 6.797 | 61.232 | 52.277 | 56.939 | 130.234 | 102.511 | 124.322 | 229.518 | 7.033 | 757.033 |
| 2 | 7.280 | 8.237 | 13.107 | 19.956 | 69.961 | 59.942 | 55.806 | 237.968 | 102.673 | 124.908 | 139.759 | 11.017 | 791.017 |
| 3 | 5.092 | 6.000 | 12.818 | 5.327 | 53.354 | 45.533 | 55.918 | 188.300 | 102.674 | 122.365 | 139.760 | 7.903 | 707.903 |
| 4 | 5.000 | 6.000 | 14.572 | 18.111 | 53.119 | 47.349 | 55.882 | 184.839 | 95.539 | 80.854 | 139.759 | 7.341 | 657.341 |
| 5 | 5.000 | 6.000 | 11.545 | 6.000 | 53.470 | 49.149 | 56.573 | 149.761 | 102.657 | 124.908 | 139.760 | 6.278 | 676.278 |
| 6 | 5.000 | 6.000 | 15.314 | 16.648 | 53.632 | 50.309 | 56.596 | 280.372 | 102.674 | 124.908 | 145.345 | 13.836 | 813.836 |
| 7 | 5.393 | 6.000 | 16.445 | 17.907 | 57.420 | 50.877 | 54.608 | 291.657 | 157.940 | 124.907 | 229.519 | 16.928 | 966.928 |
| 8 | 5.981 | 6.000 | 10.000 | 18.064 | 62.814 | 50.877 | 54.961 | 292.422 | 175.000 | 162.192 | 229.520 | 17.786 | 1027.786 |
| 9 | 8.635 | 6.213 | 16.133 | 19.707 | 82.533 | 52.949 | 55.354 | 304.242 | 175.000 | 209.815 | 229.520 | 19.413 | 1109.413 |
| 10 | 8.277 | 6.156 | 17.258 | 18.833 | 80.533 | 53.535 | 51.892 | 298.668 | 175.000 | 209.816 | 229.519 | 18.963 | 1098.963 |
| 11 | 9.990 | 7.668 | 10.111 | 18.233 | 91.041 | 65.154 | 54.262 | 294.077 | 175.000 | 209.816 | 229.519 | 18.870 | 1118.870 |
| 12 | 14.072 | 11.849 | 13.399 | 20.000 | 105.690 | 86.772 | 57.662 | 306.000 | 175.000 | 209.815 | 229.520 | 20.458 | 1170.458 |
| 13 | 9.023 | 6.013 | 20.356 | 13.234 | 85.283 | 52.690 | 42.348 | 246.964 | 175.000 | 294.724 | 229.520 | 16.529 | 1126.529 |
| 14 | 7.224 | 7.208 | 18.028 | 18.421 | 73.582 | 61.938 | 50.867 | 295.082 | 175.000 | 162.205 | 229.519 | 18.193 | 1048.193 |
| 15 | 8.031 | 7.651 | 16.110 | 18.682 | 79.963 | 65.732 | 57.051 | 295.698 | 175.000 | 124.908 | 229.519 | 17.872 | 1027.872 |
| 16 | 8.314 | 8.539 | 19.347 | 20.000 | 82.214 | 71.786 | 50.242 | 294.907 | 175.000 | 209.816 | 194.414 | 18.379 | 1078.379 |
| 17 | 9.238 | 9.661 | 25.080 | 16.986 | 88.314 | 77.558 | 18.529 | 268.360 | 175.000 | 209.815 | 229.520 | 17.097 | 1067.097 |
| 18 | 10.245 | 11.054 | 10.689 | 20.000 | 93.953 | 82.465 | 57.043 | 291.376 | 175.000 | 209.816 | 229.519 | 19.172 | 1139.172 |
| 19 | 8.849 | 9.962 | 10.000 | 15.111 | 85.629 | 74.482 | 56.903 | 254.959 | 175.000 | 209.815 | 229.519 | 16.308 | 1086.308 |
| 20 | 8.546 | 9.668 | 21.651 | 15.281 | 83.461 | 71.185 | 41.508 | 257.413 | 175.000 | 208.174 | 229.519 | 16.260 | 1066.260 |
| 21 | 7.029 | 9.978 | 23.588 | 20.000 | 72.399 | 71.584 | 30.674 | 294.843 | 102.674 | 124.908 | 229.520 | 16.601 | 926.601 |
| 22 | 6.077 | 11.227 | 26.324 | 15.162 | 64.681 | 76.310 | 11.250 | 265.100 | 102.673 | 124.907 | 229.520 | 14.442 | 874.442 |
| 23 | 11.224 | 13.406 | 24.422 | 20.000 | 97.745 | 81.821 | 23.040 | 295.500 | 102.673 | 124.908 | 139.760 | 15.448 | 865.448 |
| 24 | 15.000 | 15.000 | 13.133 | 9.594 | 107.020 | 80.950 | 59.005 | 194.843 | 102.674 | 124.907 | 139.757 | 9.157 | 809.157 |
| Optimization Method | Min. Cost |
|---|---|
| QEA [25] | 44,686.31 |
| ABC [43] | 43,362.00 |
| QOGSO [49] | 43,560.35 |
| DE [32] | 42,801.04 |
| SPPSO [50] | 42,740.23 |
| RQEA [25] | 42,715.69 |
| DNLPSO [15] | 42,645 |
| PSO [51] | 42,474.00 |
| CSA [44] | 42,440.574 |
| TLBO [33] | 42,386.13 |
| SA-MOCDE [37] | 42,038.00 |
| GSA [52] | 42,032.35 |
| QOTLBO [33] | 42,187.49 |
| MOCA-PSO [53] | 42,001.00 |
| SHPSO-TAC [51] | 41,983.00 |
| IDE [40] | 41,856.5 |
| RCGA-AFSA [34] | 41,818.42 |
| QABDEVT [16] | 41,762.00 |
| ACDE [54] | 41,593.48 |
| Proposed method | 41,350.5574 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoseynpour, O.; Mohammadi-ivatloo, B.; Nazari-Heris, M.; Asadi, S. Application of Dynamic Non-Linear Programming Technique to Non-Convex Short-Term Hydrothermal Scheduling Problem. Energies 2017, 10, 1440. https://doi.org/10.3390/en10091440
Hoseynpour O, Mohammadi-ivatloo B, Nazari-Heris M, Asadi S. Application of Dynamic Non-Linear Programming Technique to Non-Convex Short-Term Hydrothermal Scheduling Problem. Energies. 2017; 10(9):1440. https://doi.org/10.3390/en10091440
Chicago/Turabian StyleHoseynpour, Omid, Behnam Mohammadi-ivatloo, Morteza Nazari-Heris, and Somayeh Asadi. 2017. "Application of Dynamic Non-Linear Programming Technique to Non-Convex Short-Term Hydrothermal Scheduling Problem" Energies 10, no. 9: 1440. https://doi.org/10.3390/en10091440
APA StyleHoseynpour, O., Mohammadi-ivatloo, B., Nazari-Heris, M., & Asadi, S. (2017). Application of Dynamic Non-Linear Programming Technique to Non-Convex Short-Term Hydrothermal Scheduling Problem. Energies, 10(9), 1440. https://doi.org/10.3390/en10091440







