Acceleration of Gas Flow Simulations in Dual-Continuum Porous Media Based on the Mass-Conservation POD Method
Abstract
:1. Introduction
2. Problems Arising from the Typical POD Modeling Approach
2.1. Model Derivation via the Typical Approach
- ,
- ,
- ,
- ,
- , .
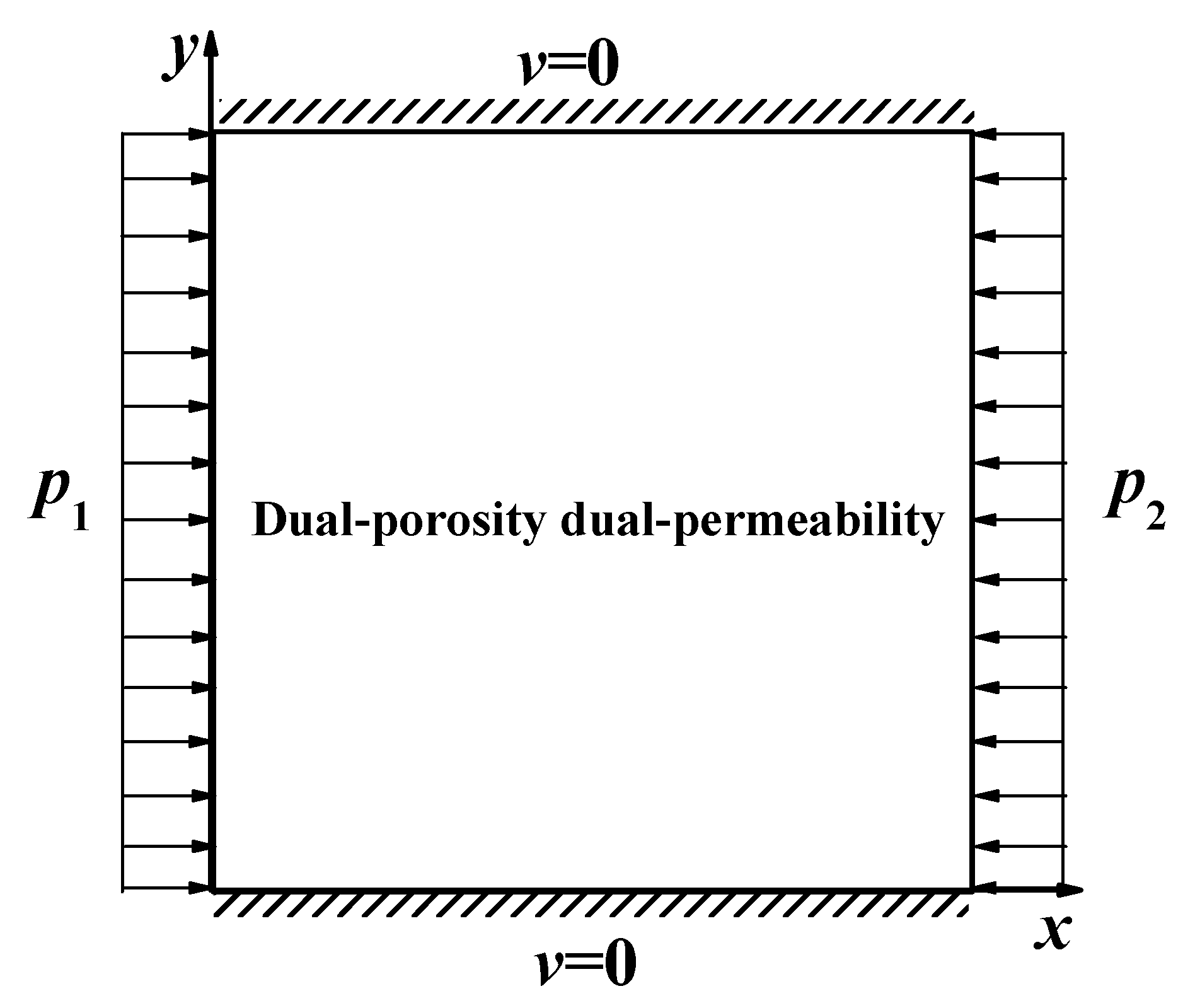
2.2. Numerical Methods and Parameters
- (1)
- Through the numerical computation of Equations (3) and (4), a sample matrix of pressure can be collected at different moments as:where Ns is the number of samples. To ensure stability and accuracy at a large time step, we used the semi-implicit finite difference method (FDM) to compute Equations (3) and (4). With the samples, a kernel for the eigenvalue decomposition can be calculated as follows:
- (2)
- Take the eigenvalue decomposition for the kernel to obtain eigenvalues and eigenvectors:where are the eigenvalues; and is the corresponding eigenvector matrix.
- (3)
- Calculate the POD modes using the eigenvectors and samples:where “” means L2 norm.
2.3. Problem Analyses
3. A New POD Modeling Approach Based on System Mass Conservation
3.1. Establishment of the New POD Model
- ,
- ,
- ,
- ,
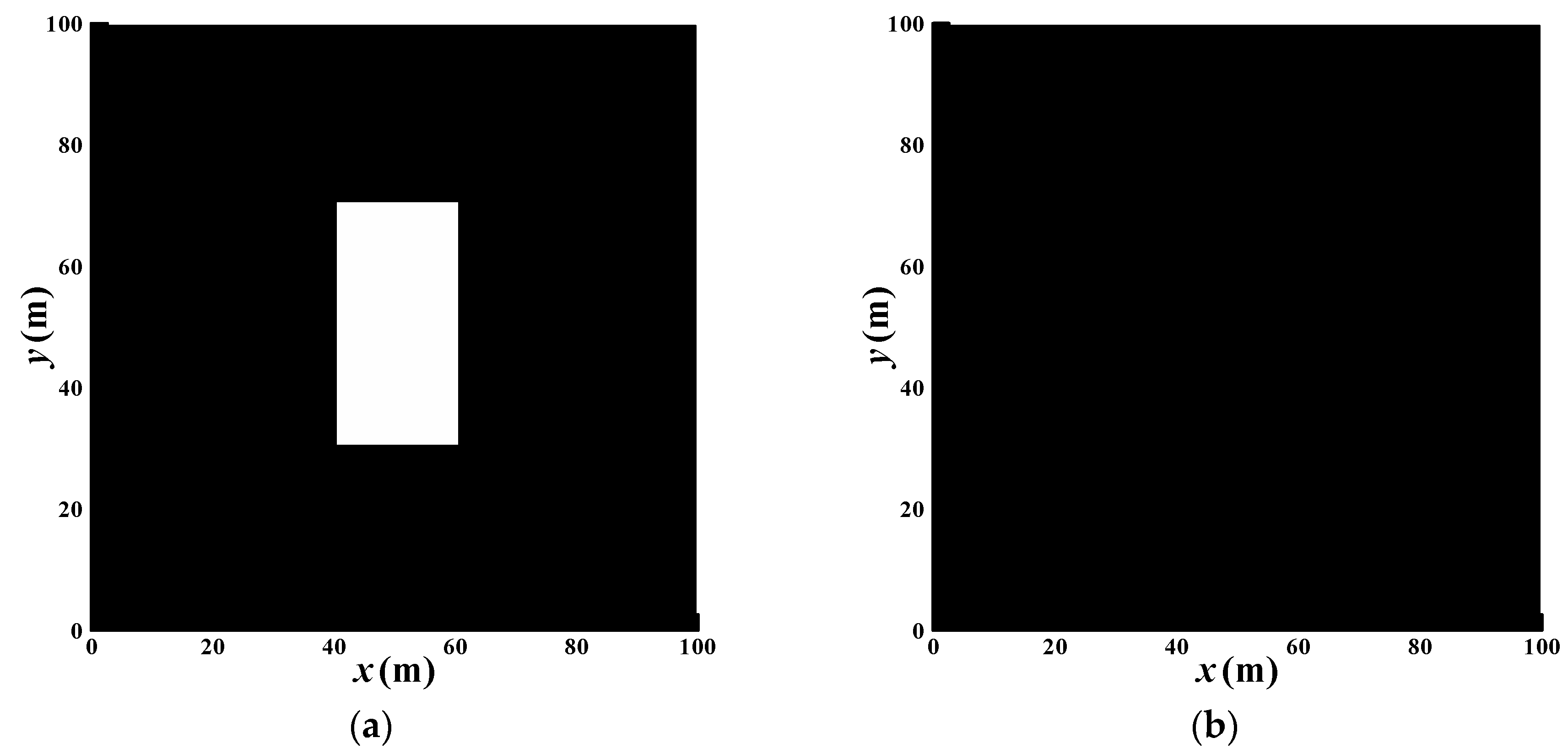
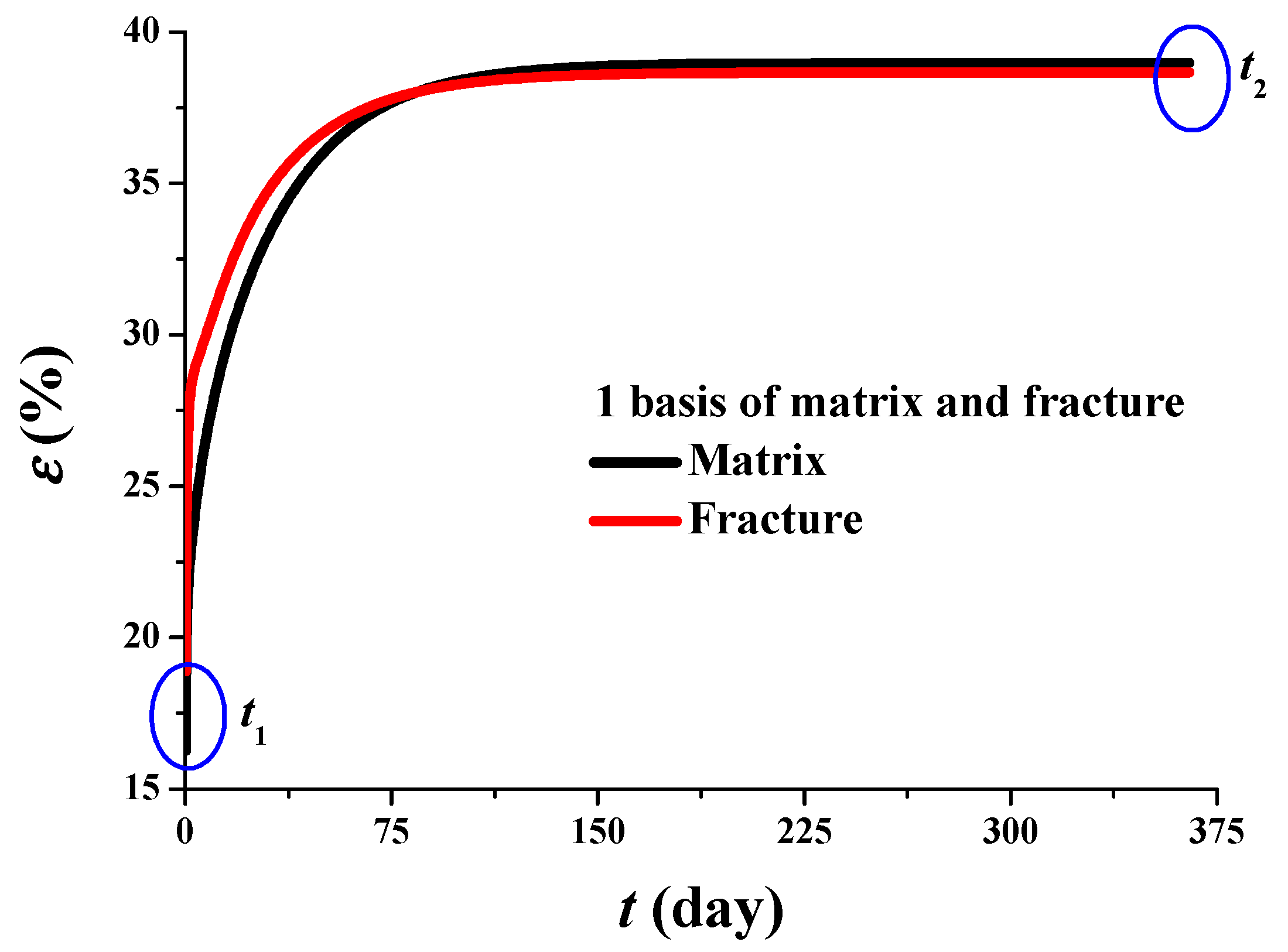
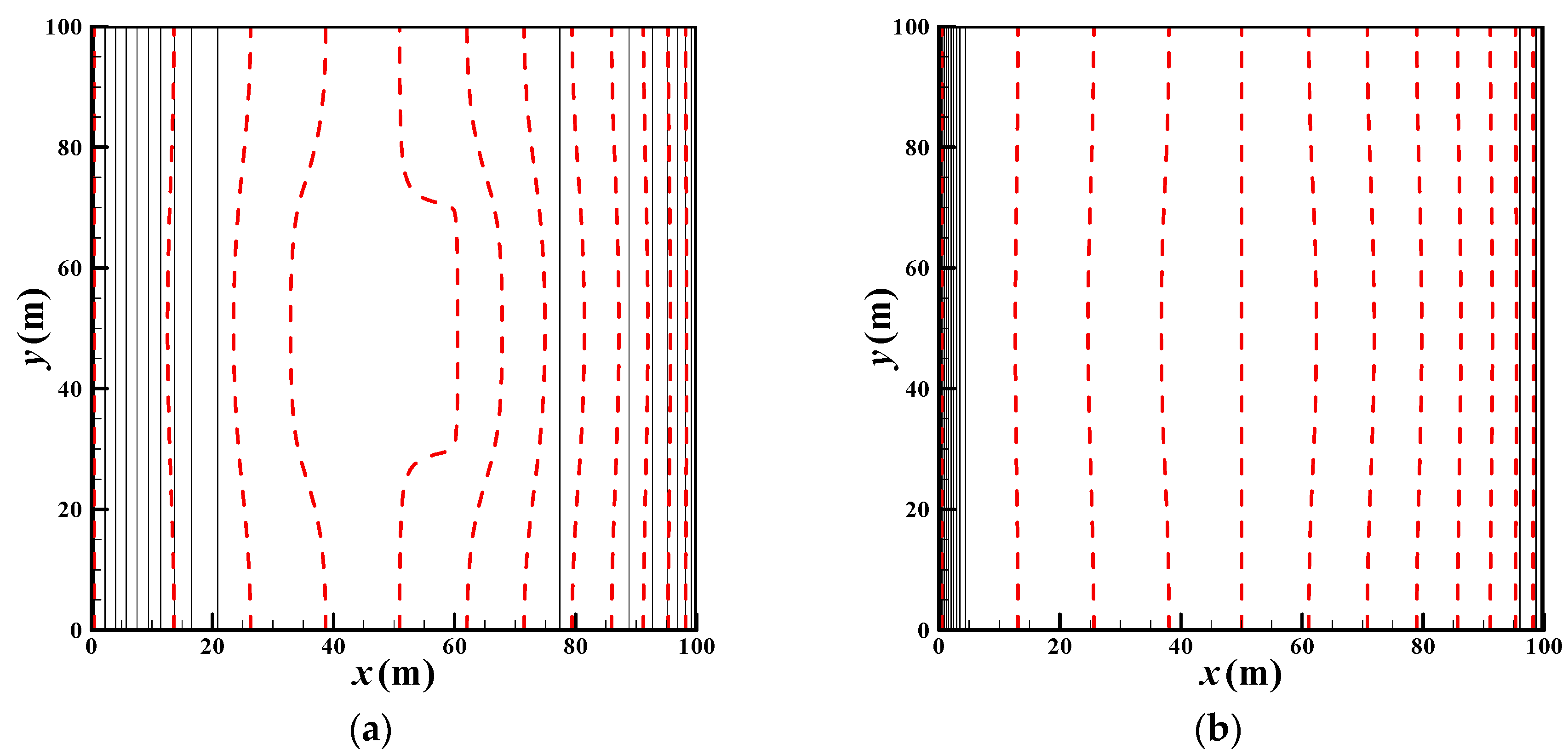
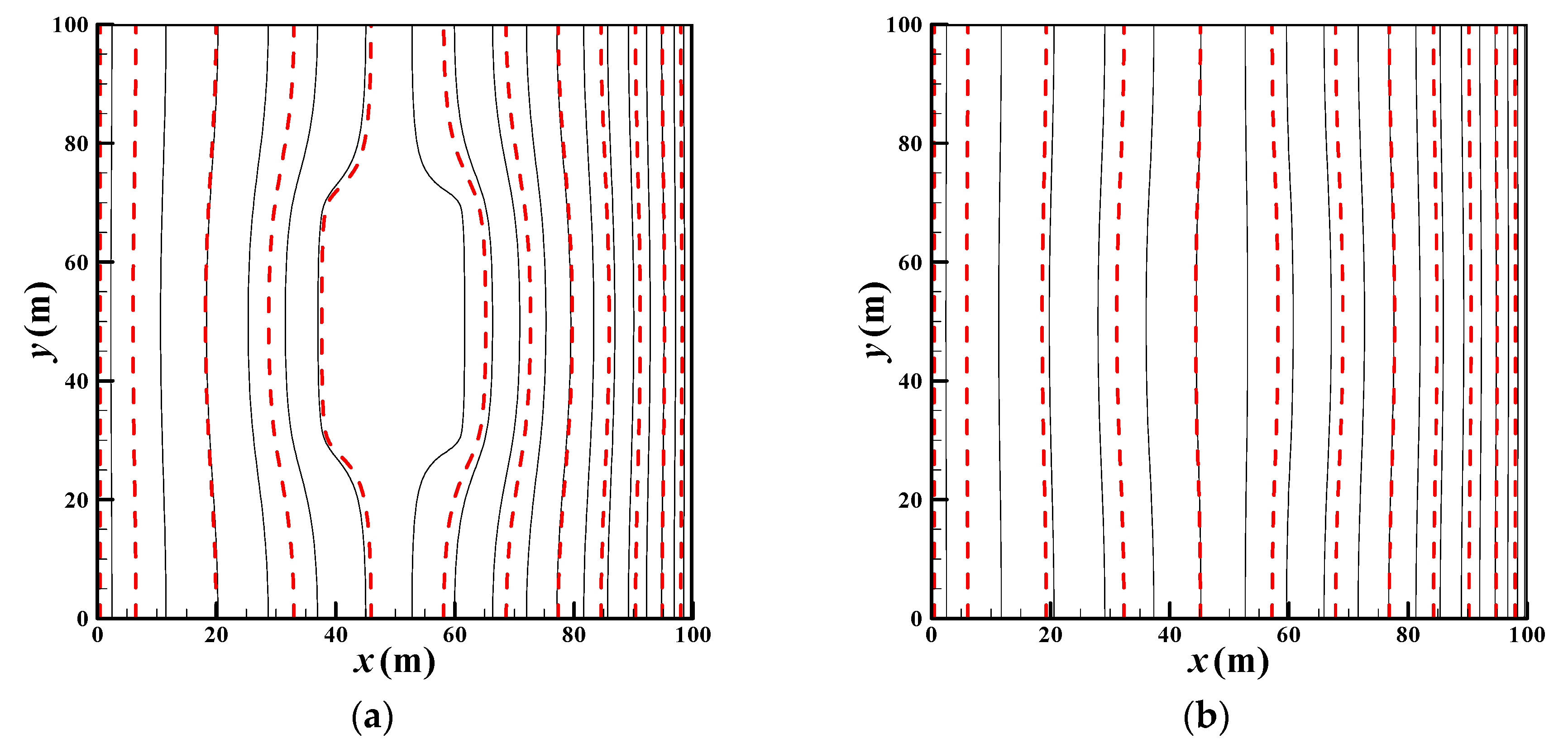
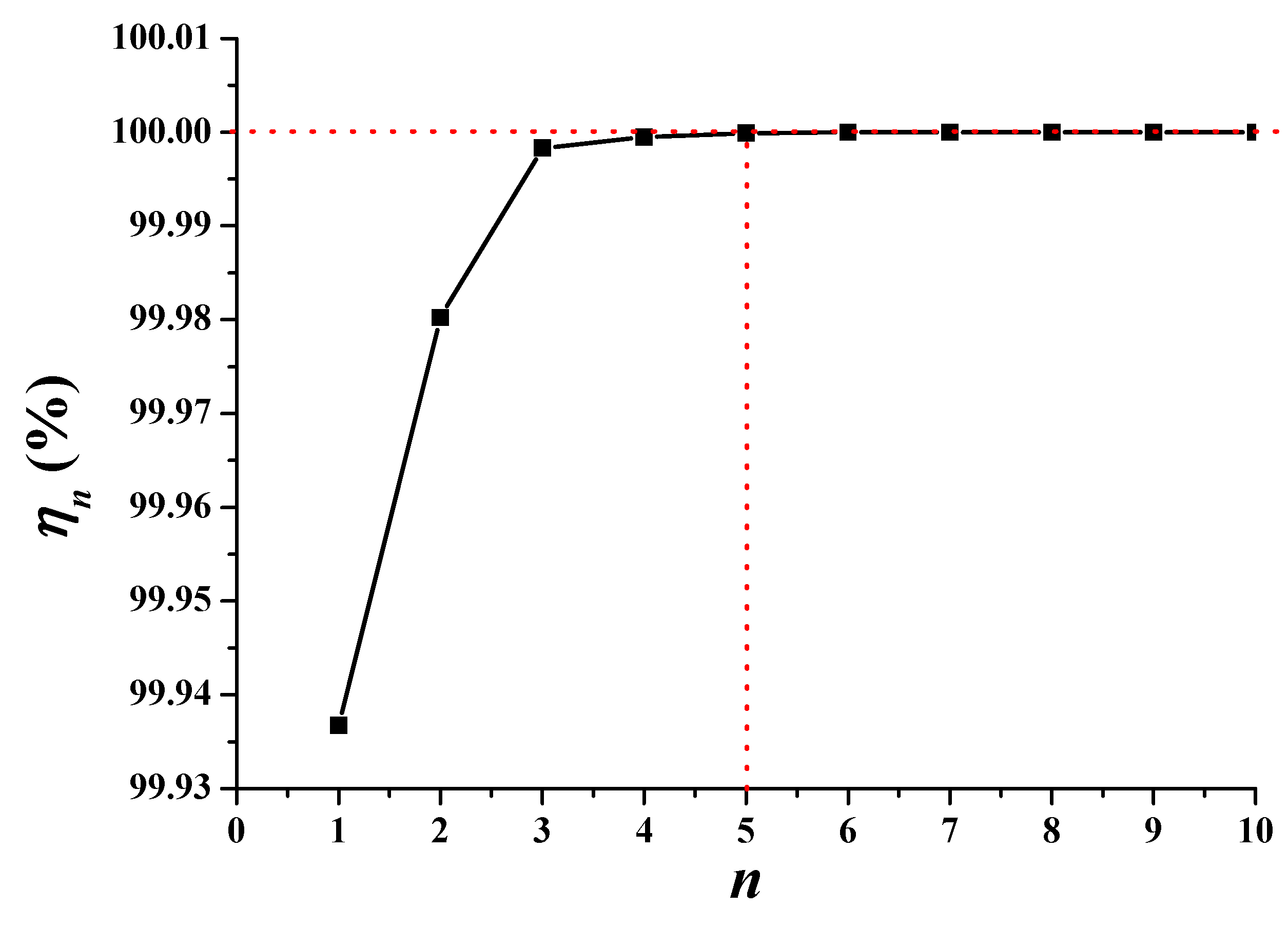
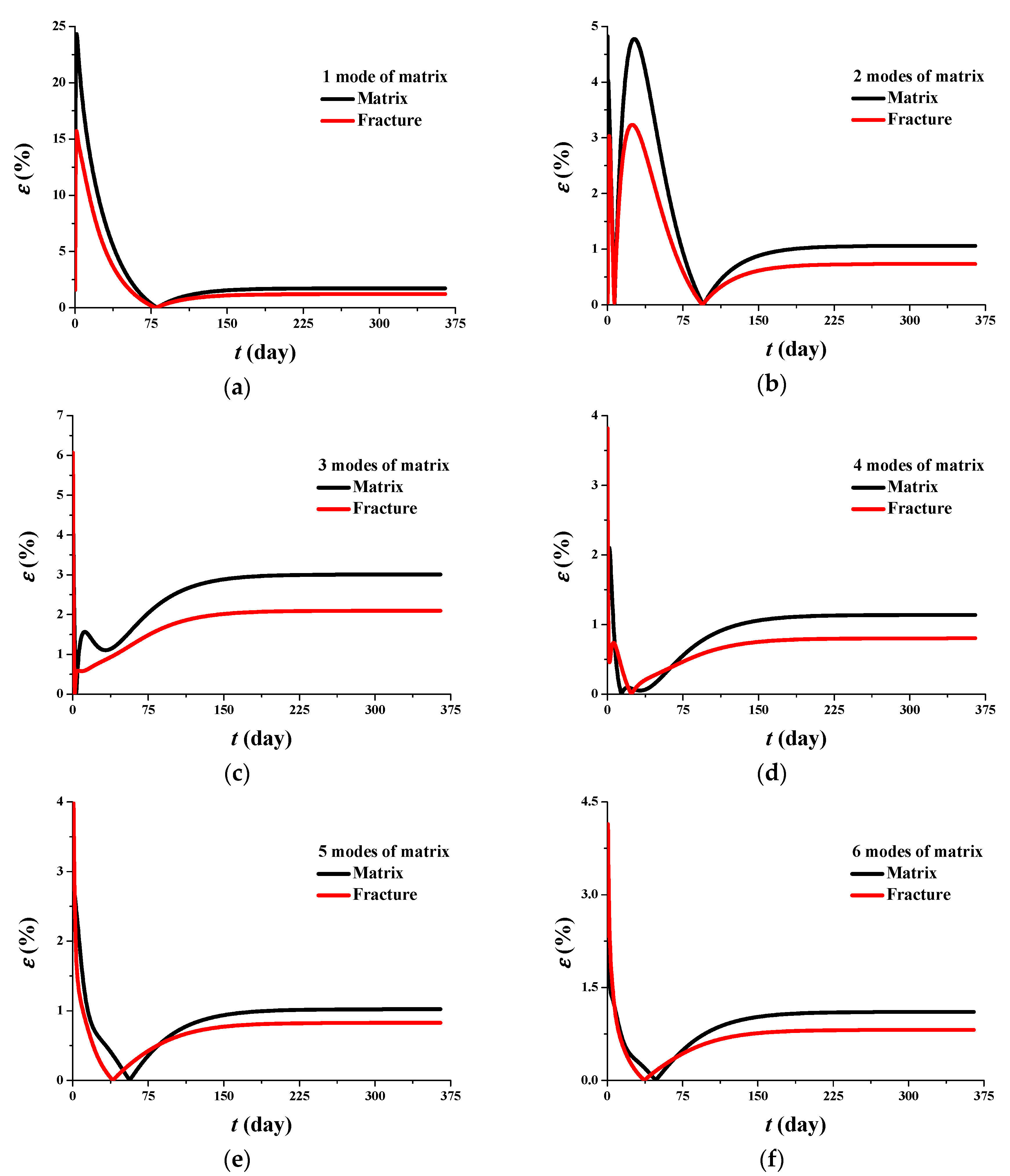
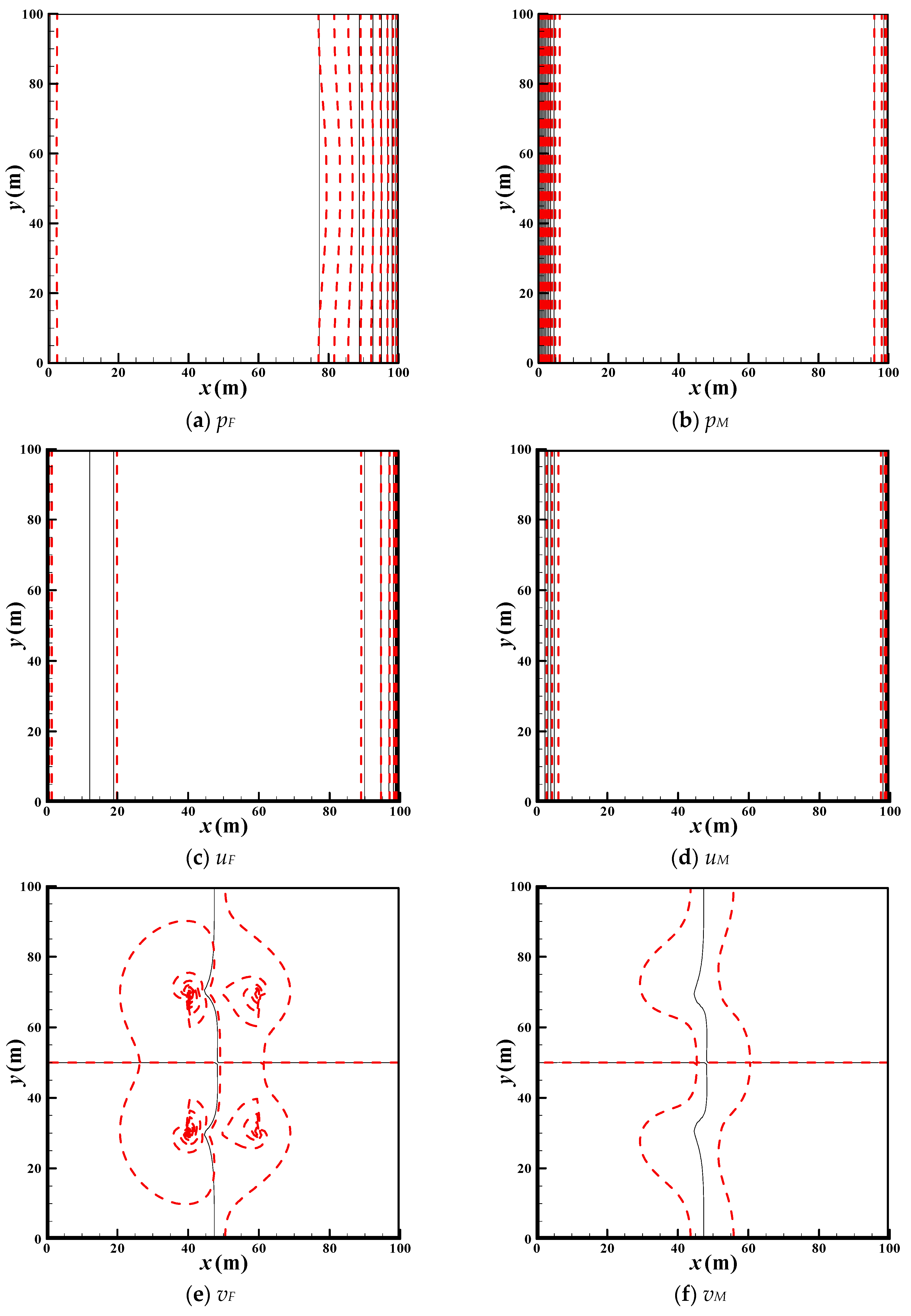
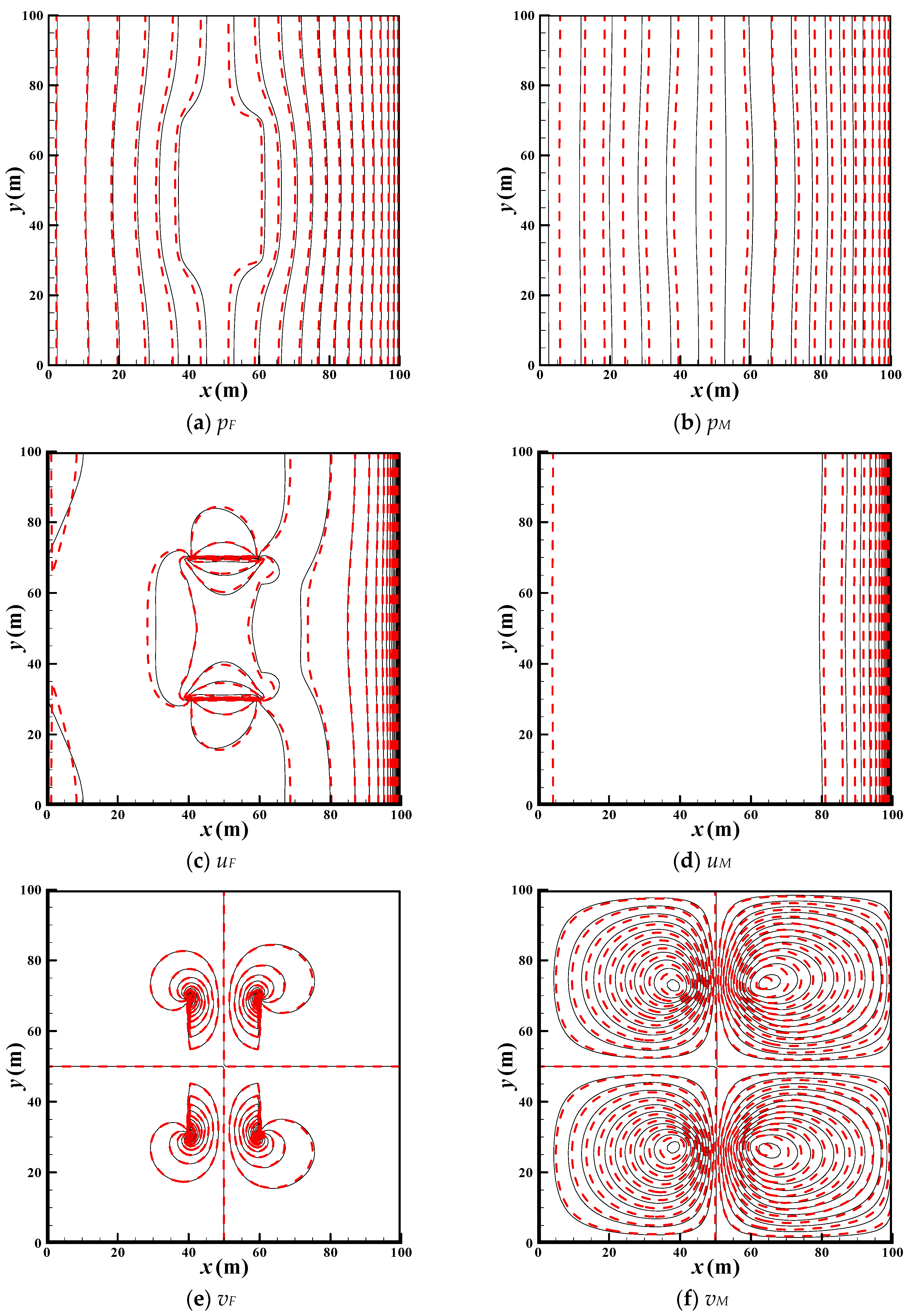
3.2. Model Verification
4. Conclusions
- (1)
- For dual-porosity, dual-permeability porous media, the typical method should be avoided to project the matrix equation and fracture equation separately. Otherwise, an artificial mass transfer term, which is 103~102 times larger than the diffusion term, will be generated to cause the failure of the POD modeling, because it violates the mass conservation of the whole system.
- (2)
- A mass conservation POD modeling method is proposed to ensure that no artificial mass transfer is generated by the POD projection process. Original governing equations should be projected onto the POD modes of matrix pressure to maintain a robust POD model.
- (3)
- The new POD model obeying the mass-conservation nature of the whole system can promote computational speed as much as 720 times under high precision: , ; , ; , .
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wu, Y.S.; Haukwa, C.; Bodvarsson, G.S. A physically based approach for modeling multiphase fracture-matrix interaction in fractured porous media. Adv. Water Resour. 2004, 27, 875–887. [Google Scholar] [CrossRef]
- Wu, Y.S.; Lu, G.; Zhang, K.; Pan, L.; Bodvarsson, G.S. Analyzing unsaturated flow patterns in fractured rock using an integrated modeling approach. Hydrogeol. J. 2007, 15, 553–572. [Google Scholar] [CrossRef]
- Wu, Y.S.; Di, Y.; Kang, Z.; Fakcharoenphol, P. A multiple-continuum model for simulating single-phase and multiphase flow in naturally fractured vuggy reservoirs. J. Petrol. Sci. Eng. 2011, 78, 13–22. [Google Scholar] [CrossRef]
- Lin, D.; Wang, J.J.; Yuan, B.; Shen, Y.H. Review on gas flow and recovery in unconventional porous rocks. Adv. Geo-Energy Res. 2017, 1, 39–53. [Google Scholar]
- Wu, Y.S.; Qin, G. A generalized numerical approach for modeling multiphase flow and transport in fractured porous media. Commun. Comput. Phys. 2009, 6, 85–108. [Google Scholar] [CrossRef]
- Presho, M.; Wo, S.; Ginting, V. Calibrated dual porosity dual permeability modeling of fractured reservoirs. J. Petrol. Sci. Eng. 2011, 77, 326–337. [Google Scholar] [CrossRef]
- De Swaan, O.A. Analytical solutions for determining naturally fractured reservoir properties by well testing. SPE J. 1976, 16, 117–122. [Google Scholar] [CrossRef]
- Chen, Z.X. Transient flow of slightly compressible fluids through double-porosity double-permeability systems—A state-of-the-art review. Trans. Porous Med. 1989, 4, 147–184. [Google Scholar] [CrossRef]
- Huang, C.S.; Chen, Y.L.; Yeh, H.D. A general analytical solution for flow to a single horizontal well by fourier and laplace transforms. Adv. Water Resour. 2011, 34, 640–648. [Google Scholar] [CrossRef]
- Nie, R.S.; Meng, Y.F.; Jia, Y.L.; Zhang, F.X.; Yang, X.T.; Niu, X.N. Dual porosity and dual permeability modeling of horizontal well in naturally fractured reservoir. Transp. Porous Med. 2012, 92, 213–235. [Google Scholar] [CrossRef]
- Cai, J.; Hu, X.; Standnes, D.C.; You, L. An analytical model for spontaneous imbibition in fractal porous media including gravity. Colloids Surf. A 2012, 414, 228–233. [Google Scholar] [CrossRef]
- Chen, J.; Chen, Z. Three-dimensional superconvergent gradient recovery on tetrahedral meshes. Int. J. Numer. Methods Eng. 2016, 108, 819–838. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, B.; Wu, X.; Wang, P. POD and wavelet analyses on the flow structures of a polymer drag-reducing flow based on DNS data. Int. J. Heat Mass Transf. 2012, 55, 4849–4861. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, B.; Cao, Z.; Zou, W.; Yu, G. A comparative study of POD interpolation and POD projection methods for fast and accurate prediction of heat transfer problems. Int. J. Heat Mass Transf. 2012, 55, 4827–4836. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, B.; Sun, S. Fast prediction method for steady-state heat convection. Chem. Eng. Technol. 2012, 35, 668–678. [Google Scholar] [CrossRef]
- Ghommem, M.; Calo, V.M.; Efendiev, Y. Mode decomposition methods for flows in high-contrast porous media: A global approach. J. Comput. Phys. 2014, 257, 400–413. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, B.; Sun, S. POD-Galerkin model for incompressible single-phase flow in porous media. Open Phys. 2016, 14, 588–601. [Google Scholar] [CrossRef]
- Kazemi, H.; Merrill, L.S.; Porterfield, K.L.; Zeman, P.R. Numerical simulation of water-oil flow in naturally fractured reservoirs. SPE J. 1976, 16, 317–326. [Google Scholar] [CrossRef]
| Parameter | Value | Unit |
|---|---|---|
| 0.5 | / | |
| 0.02 | / | |
| 1,013,250 | Pa | |
| 1,013,250 | Pa | |
| 2,026,500 | Pa | |
| 101,325 | Pa | |
| 0 | Kg/(m3·s) | |
| 0 | Kg/(m3·s) | |
| 8.9177127 × 10−11 | m2/(Pa·s) | |
| W | 16 × 10−3 | Kg/mol |
| R | 8.3147295 | J/(mol·K) |
| T | 298 | K |
| 11.067 × 10−6 | Pa·s | |
| nx | 100 | / |
| ny | 100 | / |
| Ns | 2433 | / |
| lx | 100 | m |
| ly | 100 | m |
| Lx | 0.2 | m |
| Ly | 0.2 | m |
| 1 | m | |
| 1 | m | |
| 1296 | s | |
| Simulation time scope | 365 | days |
| N | 1 | 2 | 3 |
|---|---|---|---|
| −3.62 × 102 | −1.98 × 103 | 4.85 × 103 |
| (%) | N = 1 | N = 2 | N = 3 | N = 4 | N = 5 | N = 6 |
|---|---|---|---|---|---|---|
| Project onto | 2.7527 | 1.3319 | 2.5884 | 0.9123 | 0.8826 | 0.9110 |
| Project onto | 2.7469 | 1.8863 | 1.9840 | 1.1248 | N/A | N/A |
| (%) | N = 1 | N = 2 | N = 3 | N = 4 | N = 5 | N = 6 |
|---|---|---|---|---|---|---|
| Project onto | 1.9049 | 0.9131 | 1.8079 | 0.6702 | 0.7182 | 0.7062 |
| Project onto | 1.8990 | 1.3435 | 1.3795 | 0.7912 | N/A | N/A |
| FDM | New POD Model | |
|---|---|---|
| CPU time | 3600 s | 5 s |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Sun, S.; Yu, B. Acceleration of Gas Flow Simulations in Dual-Continuum Porous Media Based on the Mass-Conservation POD Method. Energies 2017, 10, 1380. https://doi.org/10.3390/en10091380
Wang Y, Sun S, Yu B. Acceleration of Gas Flow Simulations in Dual-Continuum Porous Media Based on the Mass-Conservation POD Method. Energies. 2017; 10(9):1380. https://doi.org/10.3390/en10091380
Chicago/Turabian StyleWang, Yi, Shuyu Sun, and Bo Yu. 2017. "Acceleration of Gas Flow Simulations in Dual-Continuum Porous Media Based on the Mass-Conservation POD Method" Energies 10, no. 9: 1380. https://doi.org/10.3390/en10091380
APA StyleWang, Y., Sun, S., & Yu, B. (2017). Acceleration of Gas Flow Simulations in Dual-Continuum Porous Media Based on the Mass-Conservation POD Method. Energies, 10(9), 1380. https://doi.org/10.3390/en10091380





