Electrochemical-Thermal Modelling and Optimisation of Lithium-Ion Battery Design Parameters Using Analysis of Variance
Abstract
:1. Introduction
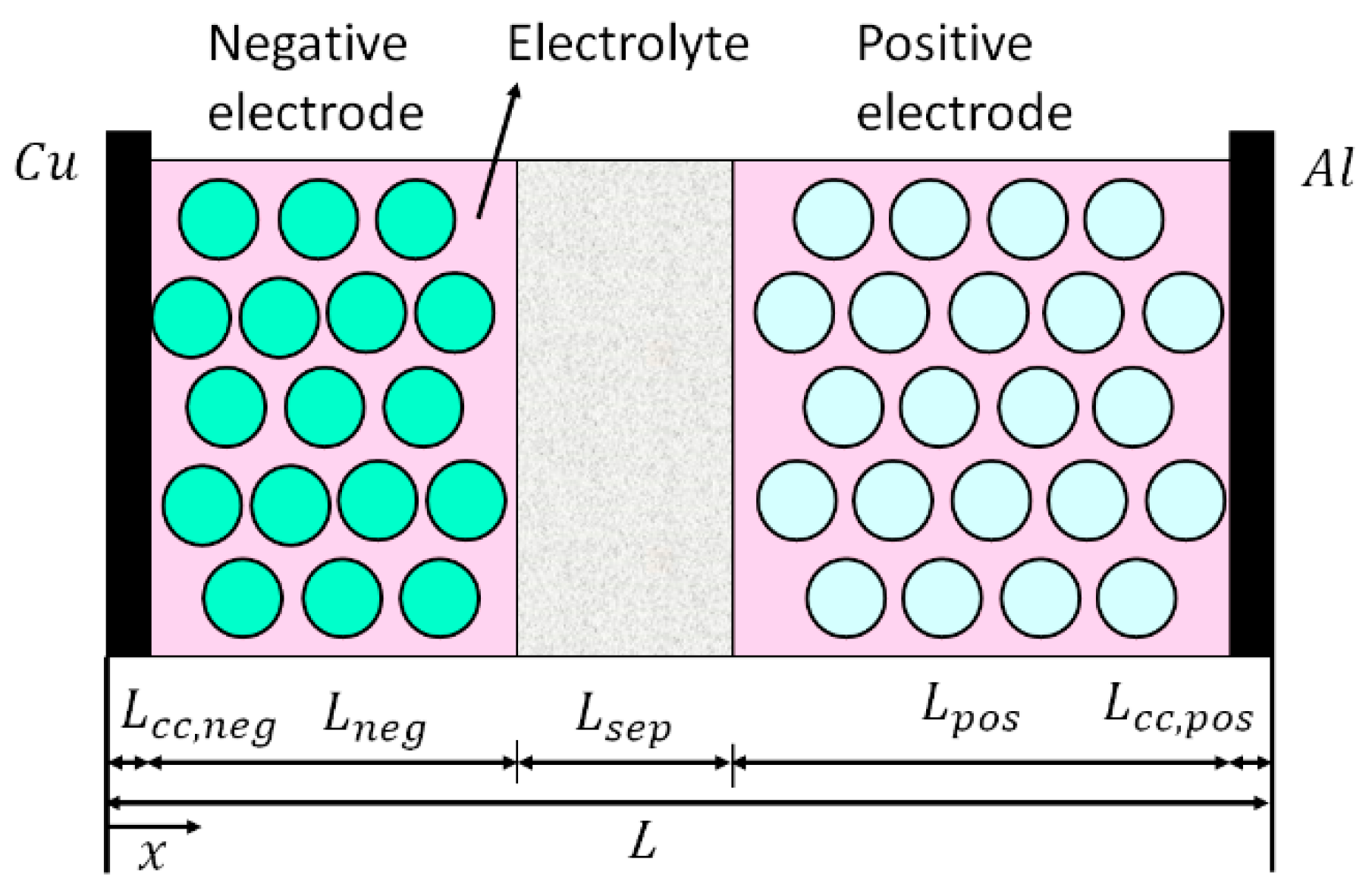
2. Mathematical Modelling
2.1. Electrochemical-Thermal Model
2.1.1. Mass Balance
Lithium in the Solid Phase
Lithium in the Electrolyte Phase
2.1.2. Electronic Charge Balance
Potential in the Solid Phase
Potential in the Electrolyte Phase
2.1.3. Electrochemical Kinetics—Reaction Current Density
2.2. Statistical Analysis of Design Variables
2.2.1. Full Factorial Design
2.2.2. Analysis of Variance
3. Results and Discussion
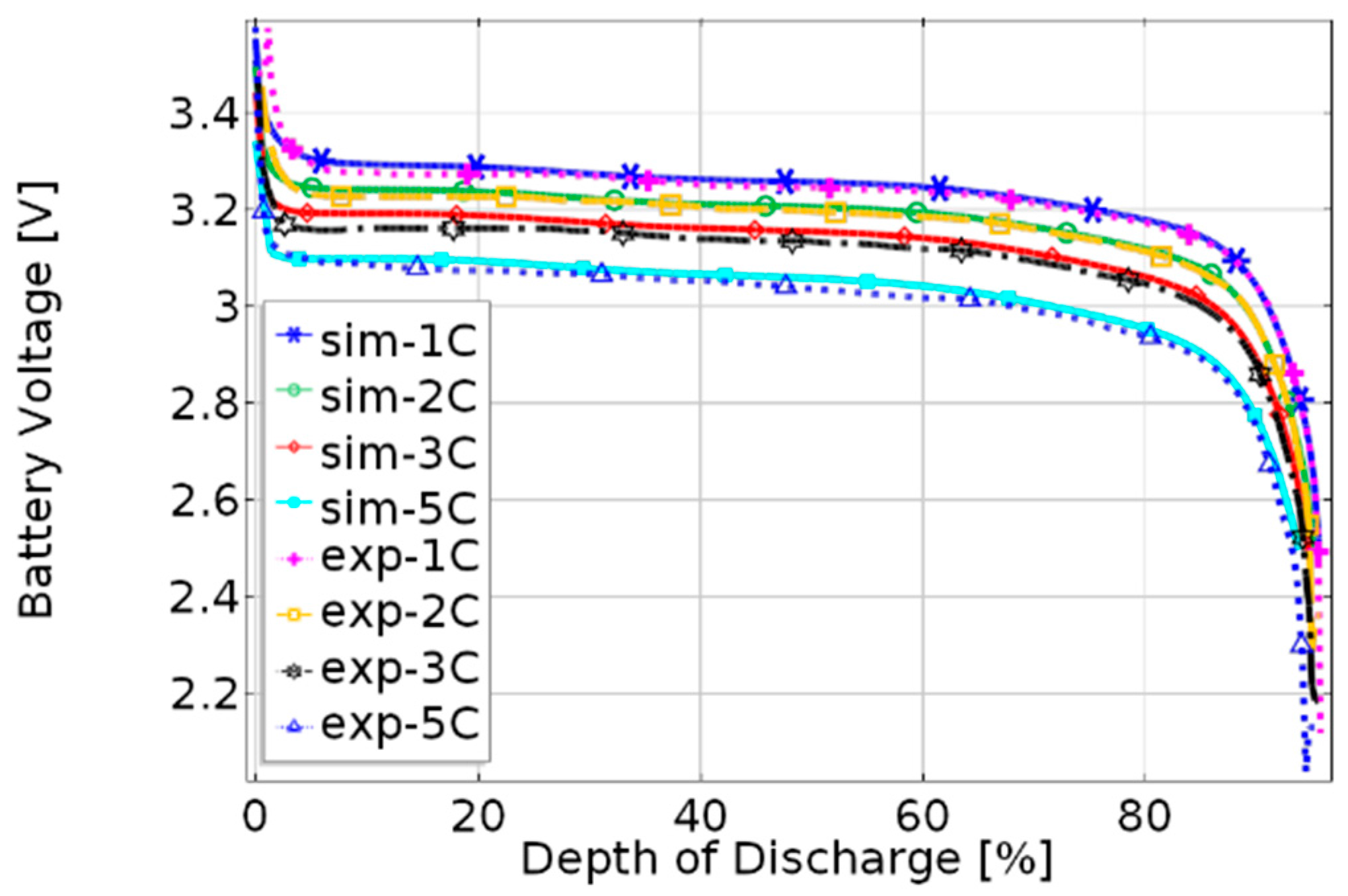
3.1. Validation of the Coupled Electrochemical—Thermal Model
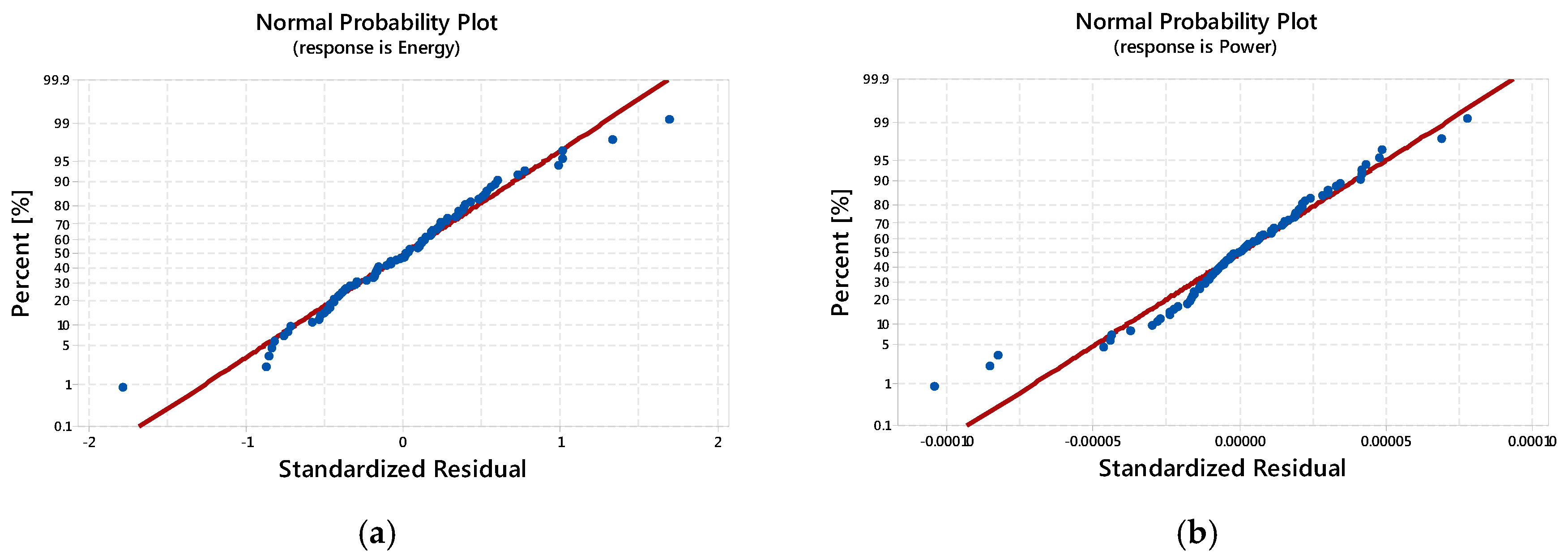
3.2. Results of ANOVA
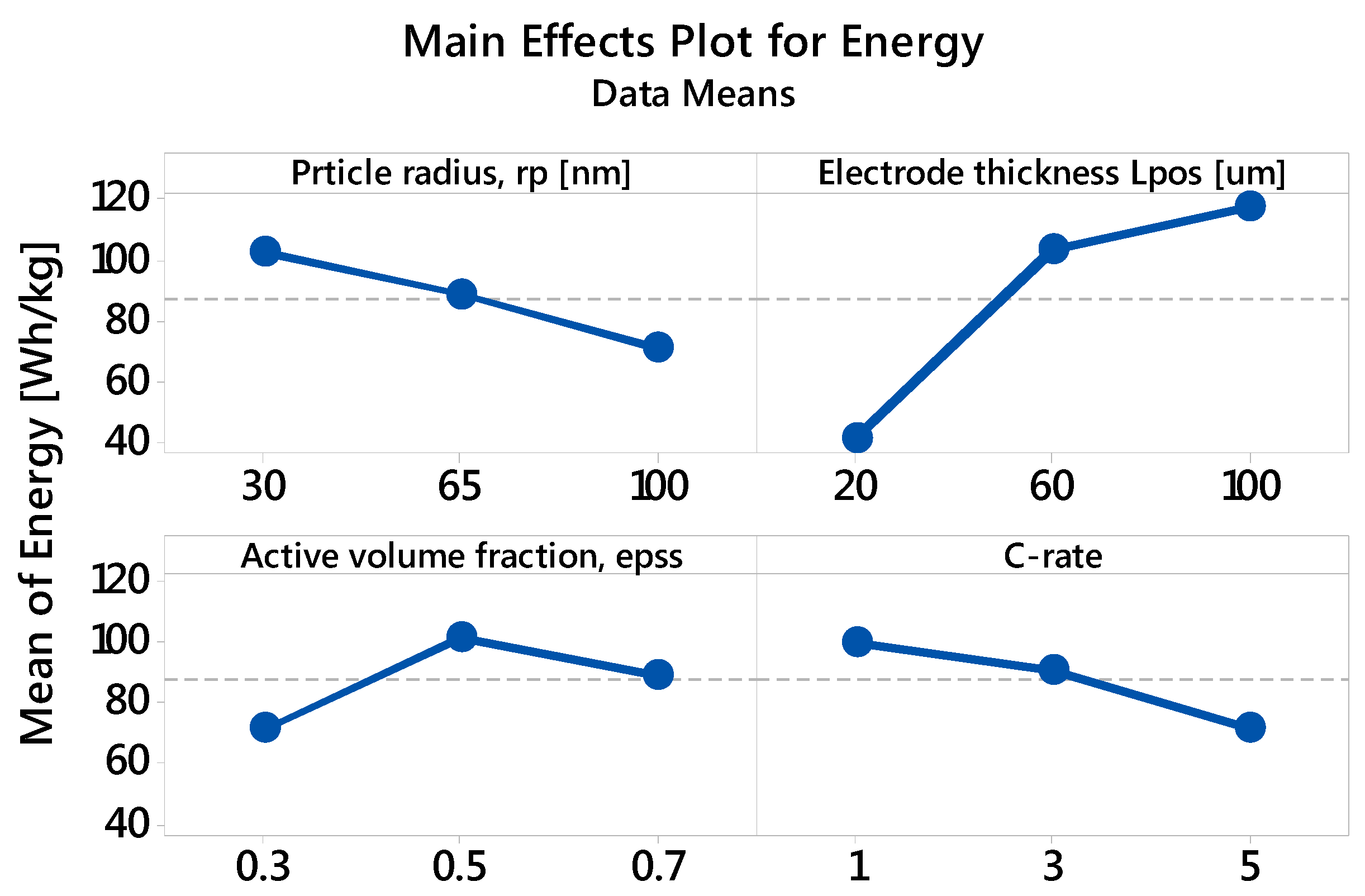
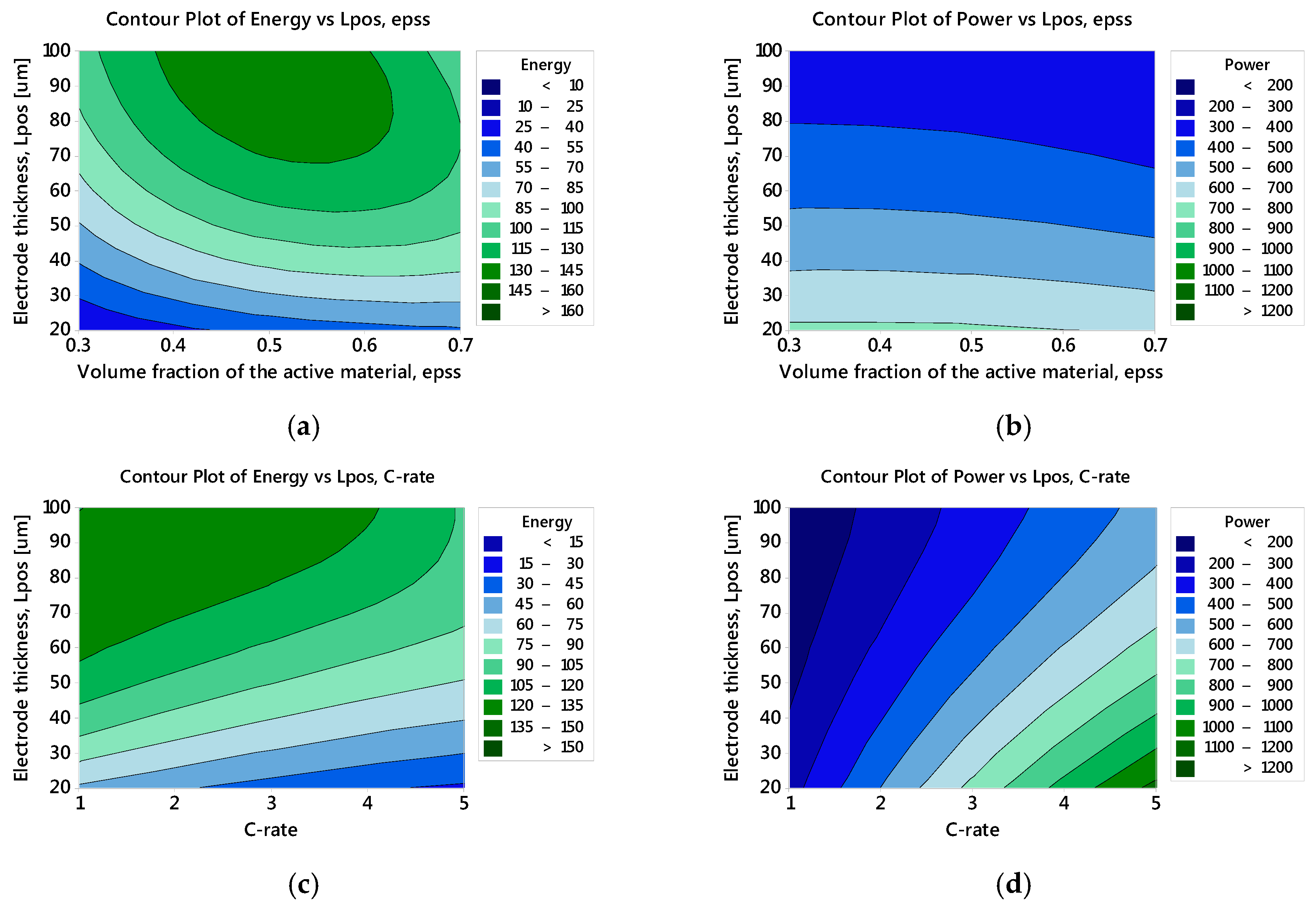
3.2.1. Specific Energy: The Main and Interaction Effects of Factors
3.2.2. Specific Power: The Main and Interaction Effects of Factors
3.2.3. Optimised Battery Response
4. Further Work
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| List of Symbols | |
| reaction surface area | |
| concentration ( | |
| D | diffusion coefficient () |
| specific energy ( | |
| Faraday’s constant () | |
| current load ( | |
| current of a single-pair electrode ( | |
| exchange current density () | |
| reaction current density () | |
| reaction rate | |
| thickness of the electrode | |
| total weight of the cell () | |
| number of electrode-pairs | |
| specific power () | |
| heat generation | |
| universal gas constant | |
| radial coordinate in spherical particle () | |
| particle radius | |
| temperature °C | |
| time (s) | |
| discharge time () | |
| transference number | |
| Open Circuit Voltage | |
| terminal voltage | |
| Greek Letters | |
| symmetry factor | |
| capacity of a cell ) | |
| volume fraction | |
| Overpotential () | |
| diffusional conductivity | |
| electronic conductivity | |
| ionic conductivity | |
| Potential () | |
| Subscripts/Superscripts | |
| cc | Current collector |
| e | electrolyte |
| f | filler |
| eff | effective |
| neg | negative |
| pos | positive |
| s | solid |
| sep | separator |
| surf | surface |
| Terms and Abbreviation | |
| ANOVA | analysis of variance |
| exp | experimental |
| OCV | open circuit voltage |
| sim | simulation |
| SOC | state of charge |
Appendix A
| Parameter | Negative Electrode | Separator | Positive Electrode |
|---|---|---|---|
| Thickness, ( | 34 | 25 | 70 |
| Particle size, ( | 3.5 | - | 0.0365 |
| Volume fraction of the active material, | 0.55 | - | 0.43 |
| Volume fraction of the electrolyte, | 0.33 | 0.54 | 0.332 |
| aximum lithium concentration in the solid phase, ( | 31,370 | - | 22,806 |
| Electrolyte lithium concentration, ( | - | 1200 | - |
| Bruggeman porosity exponent, | 1.5 | 1.5 | 1.5 |
| Dynamic Parameters | |||
| Lithium diffusion coefficient in the negative electrode, () | |||
| Lithium diffusion coefficient in the positive electrode, () | |||
| Lithium diffusion coefficient in the electrolyte, () | |||
| Reaction rate in the negative electrode, () | |||
| Reaction rate in the positive electrode, () | |||
| Open circuit potential of the negative electrode | |||
| Open circuit potential of the positive electrode | |||
| Entropy change of the negative electrode | |||
| Entropy change of the positive electrode | |||
| Local state of charge of the negative electrode | |||
| Local state of charge of the positive electrode | |||
Appendix B
| Case Study | Particle Size () | Electrode Thickness () | C-Rate | |
|---|---|---|---|---|
| 1 | 30 | 20 | 0.3 | 1 |
| 2 | 30 | 20 | 0.3 | 3 |
| 3 | 30 | 20 | 0.3 | 5 |
| 4 | 30 | 20 | 0.5 | 1 |
| 5 | 30 | 20 | 0.5 | 3 |
| 6 | 30 | 20 | 0.5 | 5 |
| 7 | 30 | 20 | 0.7 | 1 |
| 8 | 30 | 20 | 0.7 | 3 |
| 9 | 30 | 20 | 0.7 | 5 |
| 10 | 30 | 70 | 0.3 | 1 |
| 11 | 30 | 70 | 0.3 | 3 |
| 12 | 30 | 70 | 0.3 | 5 |
| 13 | 30 | 70 | 0.5 | 1 |
| 14 | 30 | 70 | 0.5 | 3 |
| 15 | 30 | 70 | 0.5 | 5 |
| 16 | 30 | 70 | 0.7 | 1 |
| 17 | 30 | 70 | 0.7 | 3 |
| 18 | 30 | 70 | 0.7 | 5 |
| 19 | 30 | 100 | 0.3 | 1 |
| 20 | 30 | 100 | 0.3 | 3 |
| 21 | 30 | 100 | 0.3 | 5 |
| 22 | 30 | 100 | 0.5 | 1 |
| 23 | 30 | 100 | 0.5 | 3 |
| 24 | 30 | 100 | 0.5 | 5 |
| 25 | 30 | 100 | 0.7 | 1 |
| 26 | 30 | 100 | 0.7 | 3 |
| 27 | 30 | 100 | 0.7 | 5 |
| 28 | 35 | 20 | 0.3 | 1 |
| 29 | 35 | 20 | 0.3 | 3 |
| 30 | 35 | 20 | 0.3 | 5 |
| 31 | 35 | 20 | 0.5 | 1 |
| 32 | 35 | 20 | 0.5 | 3 |
| 33 | 35 | 20 | 0.5 | 5 |
| 34 | 35 | 20 | 0.7 | 1 |
| 35 | 35 | 20 | 0.7 | 3 |
| 36 | 35 | 20 | 0.7 | 5 |
| 37 | 35 | 70 | 0.3 | 1 |
| 38 | 35 | 70 | 0.3 | 3 |
| 39 | 35 | 70 | 0.3 | 5 |
| 40 | 35 | 70 | 0.5 | 1 |
| 41 | 35 | 70 | 0.5 | 3 |
| 42 | 35 | 70 | 0.5 | 5 |
| 43 | 35 | 70 | 0.7 | 1 |
| 44 | 35 | 70 | 0.7 | 3 |
| 45 | 35 | 70 | 0.7 | 5 |
| 46 | 35 | 100 | 0.3 | 1 |
| 47 | 35 | 100 | 0.3 | 3 |
| 48 | 35 | 100 | 0.3 | 5 |
| 49 | 35 | 100 | 0.5 | 1 |
| 50 | 35 | 100 | 0.5 | 3 |
| 51 | 35 | 100 | 0.5 | 5 |
| 52 | 35 | 100 | 0.7 | 1 |
| 53 | 35 | 100 | 0.7 | 3 |
| 54 | 35 | 100 | 0.7 | 5 |
| 55 | 100 | 20 | 0.3 | 1 |
| 56 | 100 | 20 | 0.3 | 3 |
| 57 | 100 | 20 | 0.3 | 5 |
| 58 | 100 | 20 | 0.5 | 1 |
| 59 | 100 | 20 | 0.5 | 3 |
| 60 | 100 | 20 | 0.5 | 5 |
| 61 | 100 | 20 | 0.7 | 1 |
| 62 | 100 | 20 | 0.7 | 3 |
| 63 | 100 | 20 | 0.7 | 5 |
| 64 | 100 | 70 | 0.3 | 1 |
| 65 | 100 | 70 | 0.3 | 3 |
| 66 | 100 | 70 | 0.3 | 5 |
| 67 | 100 | 70 | 0.5 | 1 |
| 68 | 100 | 70 | 0.5 | 3 |
| 69 | 100 | 70 | 0.5 | 5 |
| 70 | 100 | 70 | 0.7 | 1 |
| 71 | 100 | 70 | 0.7 | 3 |
| 72 | 100 | 70 | 0.7 | 5 |
| 73 | 100 | 100 | 0.3 | 1 |
| 74 | 100 | 100 | 0.3 | 3 |
| 75 | 100 | 100 | 0.3 | 5 |
| 76 | 100 | 100 | 0.5 | 1 |
| 77 | 100 | 100 | 0.5 | 3 |
| 78 | 100 | 100 | 0.5 | 5 |
| 79 | 100 | 100 | 0.7 | 1 |
| 80 | 100 | 100 | 0.7 | 3 |
| 81 | 100 | 100 | 0.7 | 5 |
References
- Ramadesigan, V.; Northrop, P.W.C.; De, S.; Santhanagopalan, S.; Braatz, R.D.; Subramanian, V.R. Modeling and Simulation of Lithium-Ion Batteries from a Systems Engineering Perspective. J. Electrochem. Soc. 2012, 159, R31–R45. [Google Scholar] [CrossRef]
- Franco, A. A Multiscale modelling and numerical simulation of rechargeable lithium ion batteries: Concepts, methods and challenges. RSC Adv. 2013, 3, 13027–13058. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; Guo, Q.; Ramadass, P.; White, R.E. Review of models for predicting the cycling performance of lithium ion batteries. J. Power Sources 2006, 156, 620–628. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; Guo, Q.; White, R.E. Parameter Estimation and Model Discrimination for a Lithium-Ion Cell. J. Electrochem. Soc. 2007, 154, A198. [Google Scholar] [CrossRef]
- Tanim, T.R.; Rahn, C.D.; Wang, C.-Y. A Temperature Dependent, Single Particle, Lithium Ion Cell Model Including Electrolyte Diffusion. J. Dyn. Syst. Meas. Control 2014, 137, 11005. [Google Scholar] [CrossRef]
- Ramadesigan, V.; Methekar, R.N.; Latinwo, F.; Braatz, R.D.; Subramanian, V.R. Optimal Porosity Distribution for Minimized Ohmic Drop across a Porous Electrode. J. Electrochem. Soc. 2010, 157, A1328–A1334. [Google Scholar] [CrossRef]
- Doyle, M.; Newman, J. Modeling the performance of rechargeable lithium-based cells: Design correlations for limiting cases. J. Power Sources 1995, 54, 46–51. [Google Scholar] [CrossRef]
- Bizeray, A.M.; Zhao, S.; Duncan, S.R.; Howey, D.A. Lithium-ion battery thermal-electrochemical model-based state estimation using orthogonal collocation and a modified extended Kalman filter. J. Power Sources 2015, 296, 400–412. [Google Scholar] [CrossRef]
- Lawder, M.T.; Northrop, P.W.C.; Subramanian, V.R. Model-Based SEI Layer Growth and Capacity Fade Analysis for EV and PHEV Batteries and Drive Cycles. J. Electrochem. Soc. 2014, 161, A2099–A2108. [Google Scholar] [CrossRef]
- Lee, T.; Leok, M.; McClamroch, N.H. Geometric numerical integration for complex dynamics of tethered spacecraft. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 1885–1891. [Google Scholar]
- Srinivasan, V.; Newman, J. Design and Optimization of a Natural Graphite/Iron Phosphate Lithium-Ion Cell. J. Electrochem. Soc. 2004, 151, A1530. [Google Scholar] [CrossRef]
- Christensen, J.; Srinivasan, V.; Newman, J. Optimization of Lithium Titanate Electrodes for High-Power Cells. J. Electrochem. Soc. 2006, 153, A560. [Google Scholar] [CrossRef]
- Singh, M.; Kaiser, J.; Hahn, H. Thick Electrodes for High Energy Lithium Ion Batteries. J. Electrochem. Soc. 2015, 162, A1196–A1201. [Google Scholar] [CrossRef]
- Wu, W.; Xiao, X.; Huang, X. The effect of battery design parameters on heat generation and utilization in a Li-ion cell. Electrochim. Acta 2012, 83, 227–240. [Google Scholar] [CrossRef]
- Golmon, S.; Maute, K.; Dunn, M.L. A design optimization methodology for Li+ batteries. J. Power Sources 2014, 253, 239–250. [Google Scholar] [CrossRef]
- Darling, R.; Newman, J. Modeling a Porous Intercalation Electrode with Two Characteristic Particle Sizes. J. Electrochem. Soc. 1997, 144, 4201–4208. [Google Scholar] [CrossRef]
- Newman, J. Optimization of Porosity and Thickness of a Battery Electrode by Means of a Reaction-Zone Model. J. Electrochem. Soc. 1995, 142, 97. [Google Scholar] [CrossRef]
- Chen, Y.H.; Wang, C.W.; Zhang, X.; Sastry, A.M. Porous cathode optimization for lithium cells: Ionic and electronic conductivity, capacity, and selection of materials. J. Power Sources 2010, 195, 2851–2862. [Google Scholar] [CrossRef]
- Doyle, C.M. Design and Simulation of Lithium Recharable Batteries. Ph.D. Thesis, University of California, Berkeley, CA, USA, August 1995. [Google Scholar]
- Zimmerman, R.W.; Chen, D.-W.; Cook, N.G.W. Lawrence Berkeley Laboratory. J. Hydrol. 1992, 139, 79–96. [Google Scholar] [CrossRef]
- Zhang, L.; Lyu, C.; Wang, L.; Luo, W.; Ma, K. Thermal-electrochemical modeling and parameter sensitivity analysis of lithium-ion battery. Chem. Eng. Trans. 2013, 33, 943–948. [Google Scholar] [CrossRef]
- Edouard, C.; Petit, M.; Forgez, C.; Bernard, J.; Revel, R. Parameter sensitivity analysis of a simplified electrochemical and thermal model for Li-ion batteries aging. J. Power Sources 2016, 325, 482–494. [Google Scholar] [CrossRef]
- Zhang, L.; Lyu, C.; Hinds, G.; Wang, L.; Luo, W.; Zheng, J.; Ma, K. Parameter Sensitivity Analysis of Cylindrical LiFePO4 Battery Performance Using Multi-Physics Modeling. J. Electrochem. Soc. 2014, 161, A762–A776. [Google Scholar] [CrossRef]
- Du, W.; Gupta, A.; Zhang, X.; Sastry, A.M.; Shyy, W. Effect of cycling rate, particle size and transport properties on lithium-ion cathode performance. Int. J. Heat Mass Transf. 2010, 53, 3552–3561. [Google Scholar] [CrossRef]
- Ghaznavi, M.; Chen, P. Sensitivity analysis of a mathematical model of lithium e sulfur cells part I: Applied discharge current and cathode conductivity. J. Power Sources 2013, 257, 4–11. [Google Scholar] [CrossRef]
- Wu, B.; Yufit, V.; Marinescu, M.; Offer, G.J.; Martinez-Botas, R.F.; Brandon, N.P. Coupled thermal-electrochemical modelling of uneven heat generation in lithium-ion battery packs. J. Power Sources 2013, 243, 544–554. [Google Scholar] [CrossRef]
- Yazdanpour, M. Electro-thermal Modeling of Lithium-ion Batteries. Ph.D. Thesis, Simon Fraser University, Burnaby, BC, Canada, 2015. [Google Scholar]
- Li, J.; Cheng, Y.; Ai, L.; Jia, M.; Du, S.; Yin, B.; Woo, S.; Zhang, H. 3D simulation on the internal distributed properties of lithium-ion battery with planar tabbed configuration. J. Power Sources 2015, 293, 993–1005. [Google Scholar] [CrossRef]
- Li, J.; Cheng, Y.; Jia, M.; Tang, Y.; Lin, Y.; Zhang, Z.; Liu, Y. An electrochemical-thermal model based on dynamic responses for lithium iron phosphate battery. J. Power Sources 2014, 255, 130–143. [Google Scholar] [CrossRef]
- Samba, A.; Omar, N.; Gualous, H.; Capron, O.; Van Den Bossche, P.; Van Mierlo, J. Impact of tab location on large format lithium-ion pouch cell based on fully coupled tree-dimensional electrochemical-thermal modeling. Electrochim. Acta 2014, 147, 319–329. [Google Scholar] [CrossRef]
- Gerver, R.E. 3D Thermal-Electrochemical Lithium-Ion Battery Computational Modeling. Master’s Thesis, University of Texas, Austin, TX, USA, August 2009. [Google Scholar]
- Xiao, M.; Choe, S.-Y. Dynamic modeling and analysis of a pouch type LiMn2O4/Carbon high power Li-polymer battery based on electrochemical-thermal principles. J. Power Sources 2012, 218, 357–367. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, Z.; Wang, X.; Jia, L.; Yang, L. Two-dimensional electrochemical-thermal coupled modeling of cylindrical LiFePO4 batteries. J. Power Sources 2014, 256, 233–243. [Google Scholar] [CrossRef]
- Smith, K.; Wang, C.-Y. Power and thermal characterization of a lithium-ion battery pack for hybrid-electric vehicles. J. Power Sources 2006, 160, 662–673. [Google Scholar] [CrossRef]
- Nasirabadi, P.S.; Conseil, H.; Mohanty, S.; Jabbari, M.; Ambat, R.; Hattel, J.H. Semi-Empirical Prediction of Moisture Build-up in an Electronic Enclosure Using Analysis of Variance (ANOVA). In Proceedings of the IEEE 18th Electronics Packaging Technology Conference, Singapore, 30 November–3 December 2016. [Google Scholar]
- Su, L.; Zhang, J.; Wang, C.; Zhang, Y.; Li, Z.; Song, Y.; Jin, T.; Ma, Z. Identifying main factors of capacity fading in lithium ion cells using orthogonal design of experiments. Appl. Energy 2016, 163, 201–210. [Google Scholar] [CrossRef]
- Guo, J.; Li, Z.; Pecht, M. A Bayesian approach for Li-Ion battery capacity fade modeling and cycles to failure prognostics. J. Power Sources 2015, 281, 173–184. [Google Scholar] [CrossRef]
- Zaccaria, M.; Gualandi, C.; Fabiani, D.; Focarete, M.L.; Croce, F. Effect of oxide nanoparticles on thermal and mechanical properties of electrospun separators for lithium-ion batteries. J. Nanomater. 2012, 2012, 119. [Google Scholar] [CrossRef]
- Zhang, Y.G.; Ma, L.L.; Li, J.L.; Yu, Y. In situ Fenton reagent generated from TiO2/Cu2O composite film: A new way to utilize TiO2 under visible light irradiation. Environ. Sci. Technol. 2007, 41, 6264–6269. [Google Scholar] [CrossRef] [PubMed]
- Cheng, S.J.; Miao, J.M.; Wu, S.J. Investigating the effects of operational factors on PEMFC performance based on CFD simulations using a three-level full-factorial design. Renew. Energy 2012, 39, 250–260. [Google Scholar] [CrossRef]
- Calì, M.; Santarelli, M.G.L.; Leone, P. Computer experimental analysis of the CHP performance of a 100 kWe SOFC Field Unit by a factorial design. J. Power Sources 2006, 156, 400–413. [Google Scholar] [CrossRef]
- Wong, N.H.; Heryanto, S. The study of active stack effect to enhance natural ventilation using wind tunnel and computational fluid dynamics (CFD) simulations. Energy Build. 2004, 36, 668–678. [Google Scholar] [CrossRef]
- Yang, Y.-T.; Wang, Y.-H.; Tseng, P.-K. Numerical optimization of heat transfer enhancement in a wavy channel using nanofluids. Int. Commun. Heat Mass Transf. 2014, 51, 9–17. [Google Scholar] [CrossRef]
- Cervantes, M.J.; Engström, T.F. Factorial Design Applied to CFD. J. Fluids Eng. 2004, 126, 791. [Google Scholar] [CrossRef]
- Jabbari, M.; Shojaee Nasirabadi, P.; Jambhekar, V.A.; Hattel, J.H.; Helmig, R. Drying of a tape-cast layer: Numerical investigation of influencing parameters. Int. J. Heat Mass Transf. 2017, 108, 2229–2238. [Google Scholar] [CrossRef]
- Mstali, M.; Farkhondeh, M.; Farhad, S.; Fraser, R.; Fowler, M. Electrochemical Modeling of Commercial LiFePO4 and Graphite Electrodes: Kinetic and Transport Properties and Their Temperature Dependence. J. Electrochem. Soc. 2016, 163, 2803–2816. [Google Scholar] [CrossRef]
- Amiribavandpour, P.; Shen, W.; Mu, D.; Kapoor, A. An improved theoretical electrochemical-thermal modelling of lithium-ion battery packs in electric vehicles. J. Power Sources 2015, 284, 328–338. [Google Scholar] [CrossRef]
- Stewart, S.B.D.; Albertus, P.D.; Srinivasan, V.D.D.; Plitz, I.; Pereira, N.D.D.; Amatucci, G.D.D.; Newman, J.D.B.D. Optimizing the performance of lithium titanate spinel paired with activated carbon or iron phosphate. J. Electrochem. Soc. 2008, 155, A253–A261. [Google Scholar] [CrossRef]
- Jiang, F.; Peng, P.; Sun, Y. Thermal analyses of LiFePO4/graphite battery discharge processes. J. Power Sources 2013, 243, 181–194. [Google Scholar] [CrossRef]
- Yang, K.; Tan, F.; Wang, F.; Long, Y.; Wen, Y. Response Surface Optimization for Process Parameters of LiFePO4/C Preparation by Carbothermal Reduction Technology. Chin. J. Chem. Eng. 2012, 20, 793–802. [Google Scholar] [CrossRef]
- Suthar, B.; Northrop, P.W.C.; Rife, D.; Subramanian, V.R. Effect of Porosity, Thickness and Tortuosity on Capacity Fade of Anode. J. Electrochem. Soc. 2015, 162, A1708–A1717. [Google Scholar] [CrossRef]
- Heidarzadeh, A.; Saeid, T.; Khodaverdizadeh, H.; Mahmoudi, A.; Nazari, E. Establishing a mathematical model to predict the tensile strength of friction stir welded pure copper joints. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2013, 44, 175–183. [Google Scholar] [CrossRef]
- Thorat, I.V.; Joshi, T.; Zaghib, K.; Harb, J.N.; Wheeler, D.R. Understanding Rate-Limiting Mechanisms in LiFePO4 Cathodes for Li-Ion Batteries. J. Electrochem. Soc. 2011, 158, A1185–A1193. [Google Scholar] [CrossRef]
- Braun, P.V.; Cho, J.; Pikul, J.H.; King, W.P.; Zhang, H. High power rechargeable batteries. Curr. Opin. Solid State Mater. Sci. 2012, 16, 186–198. [Google Scholar] [CrossRef]
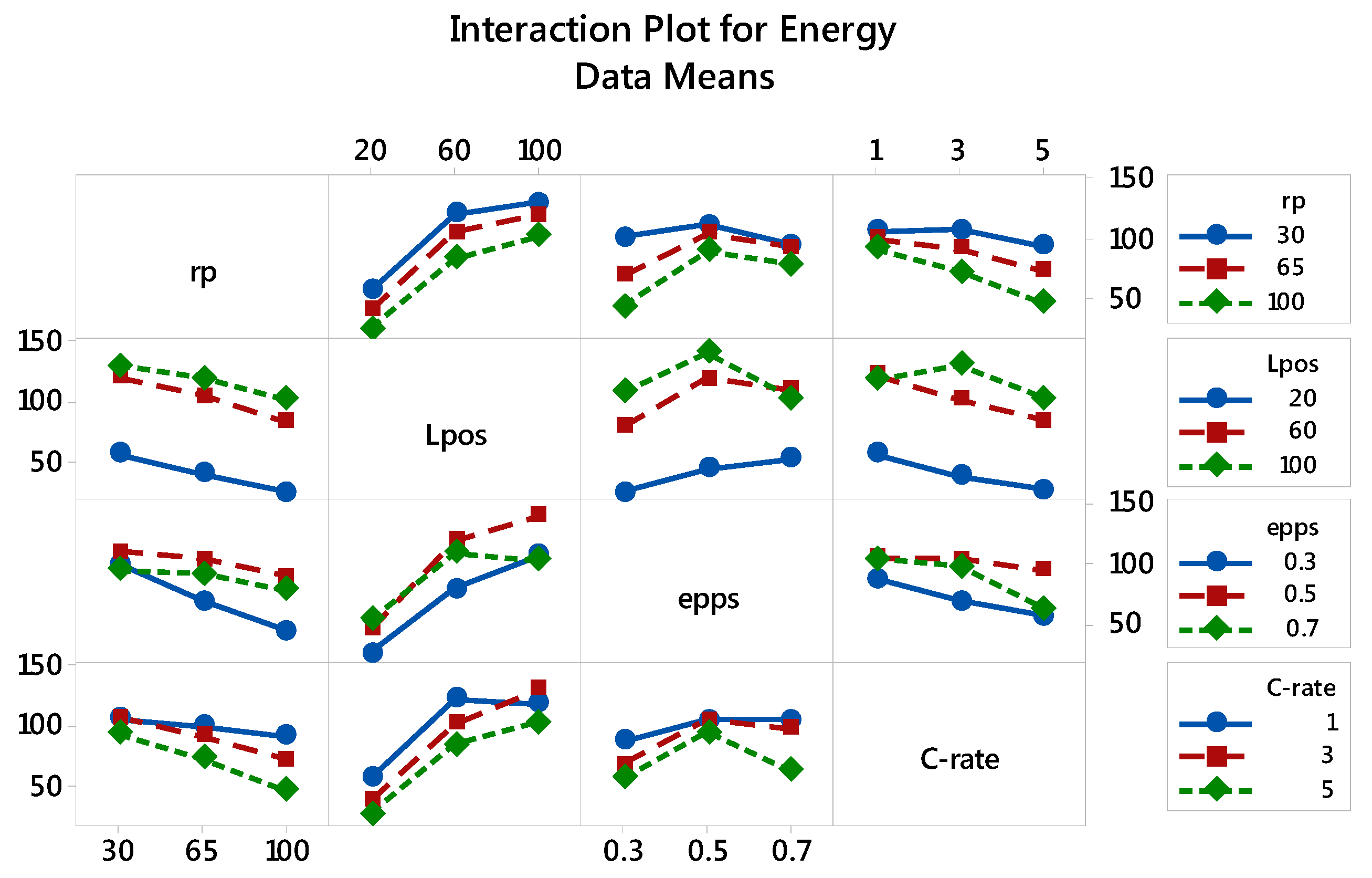
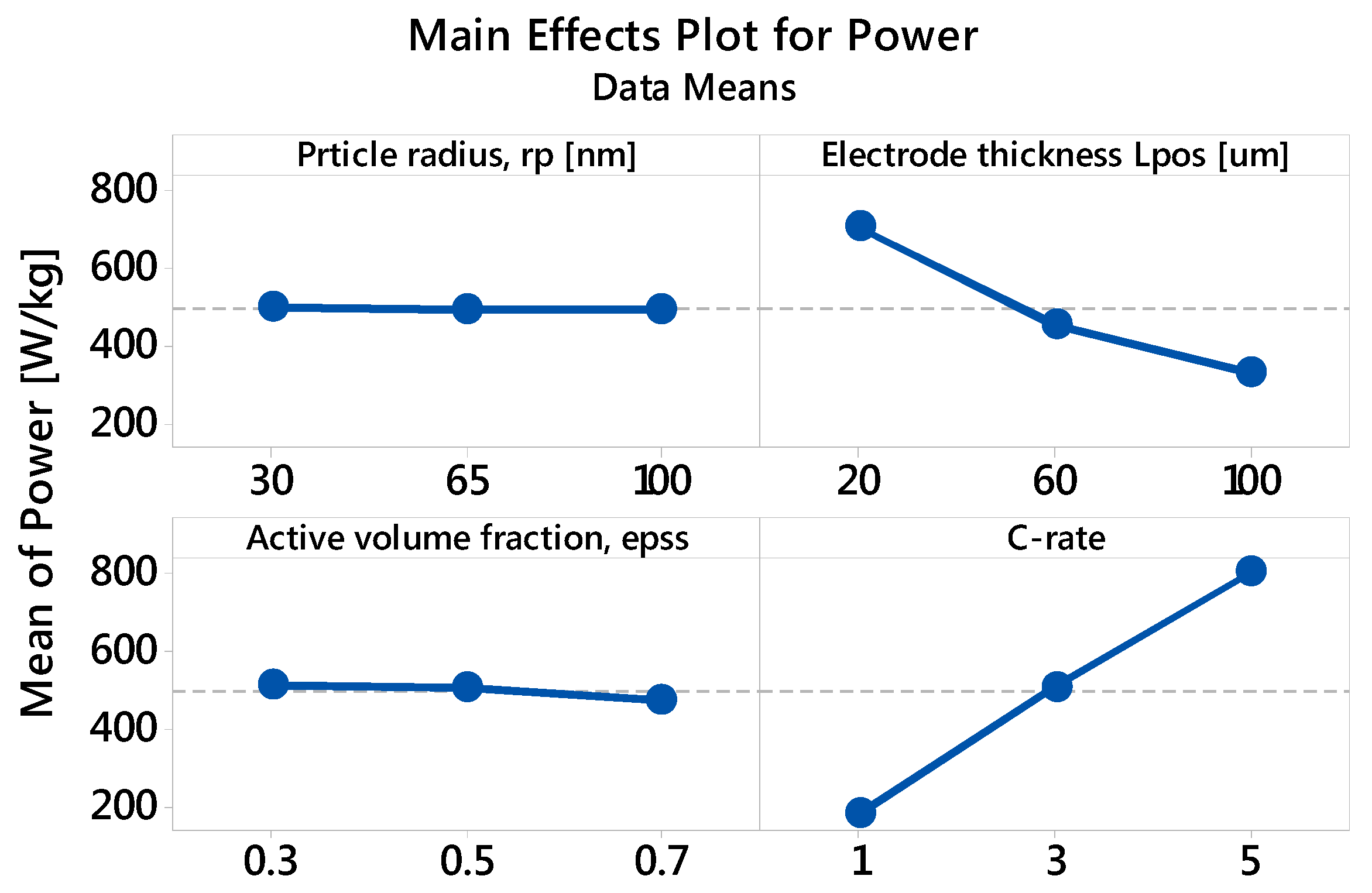
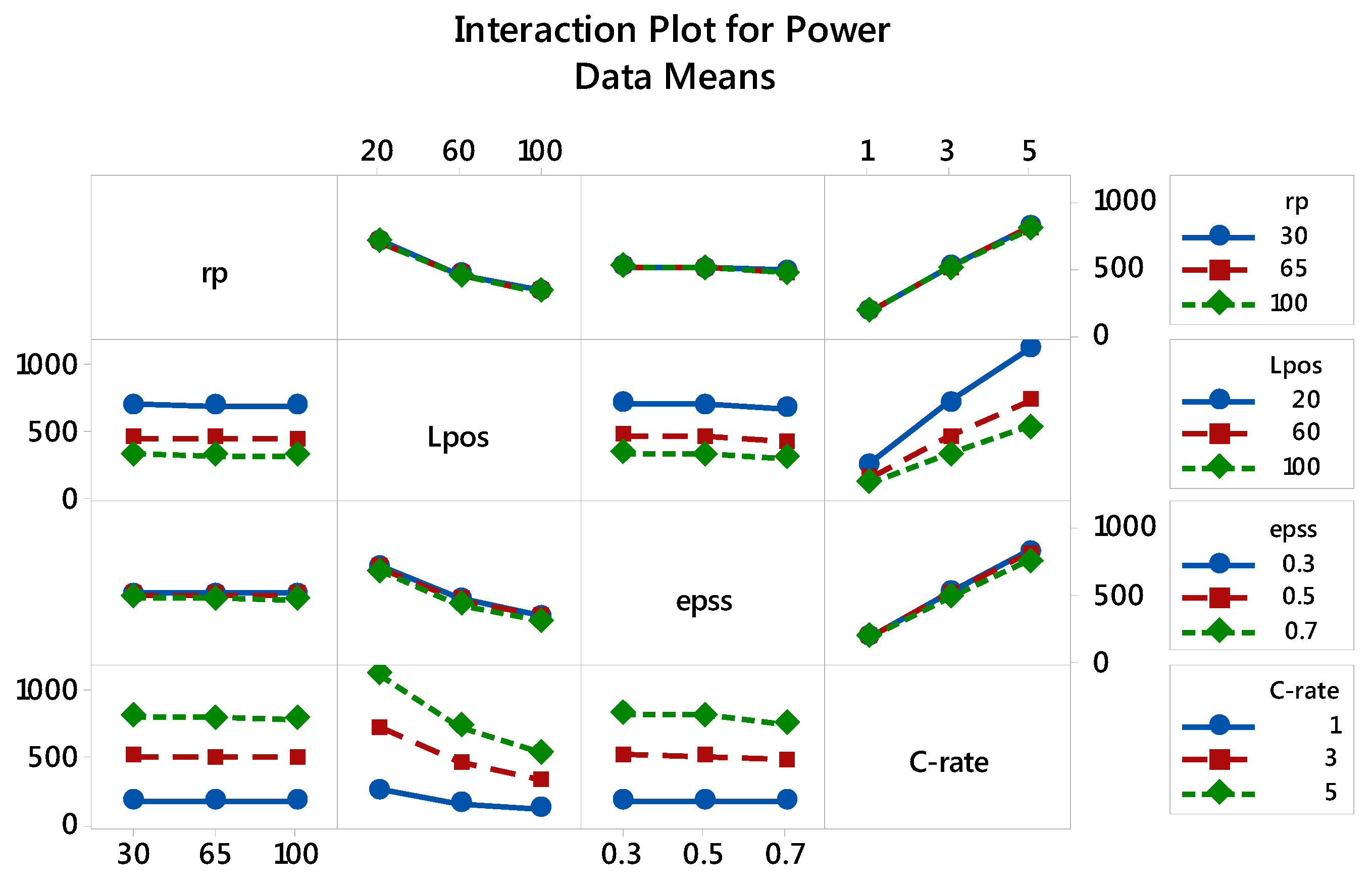
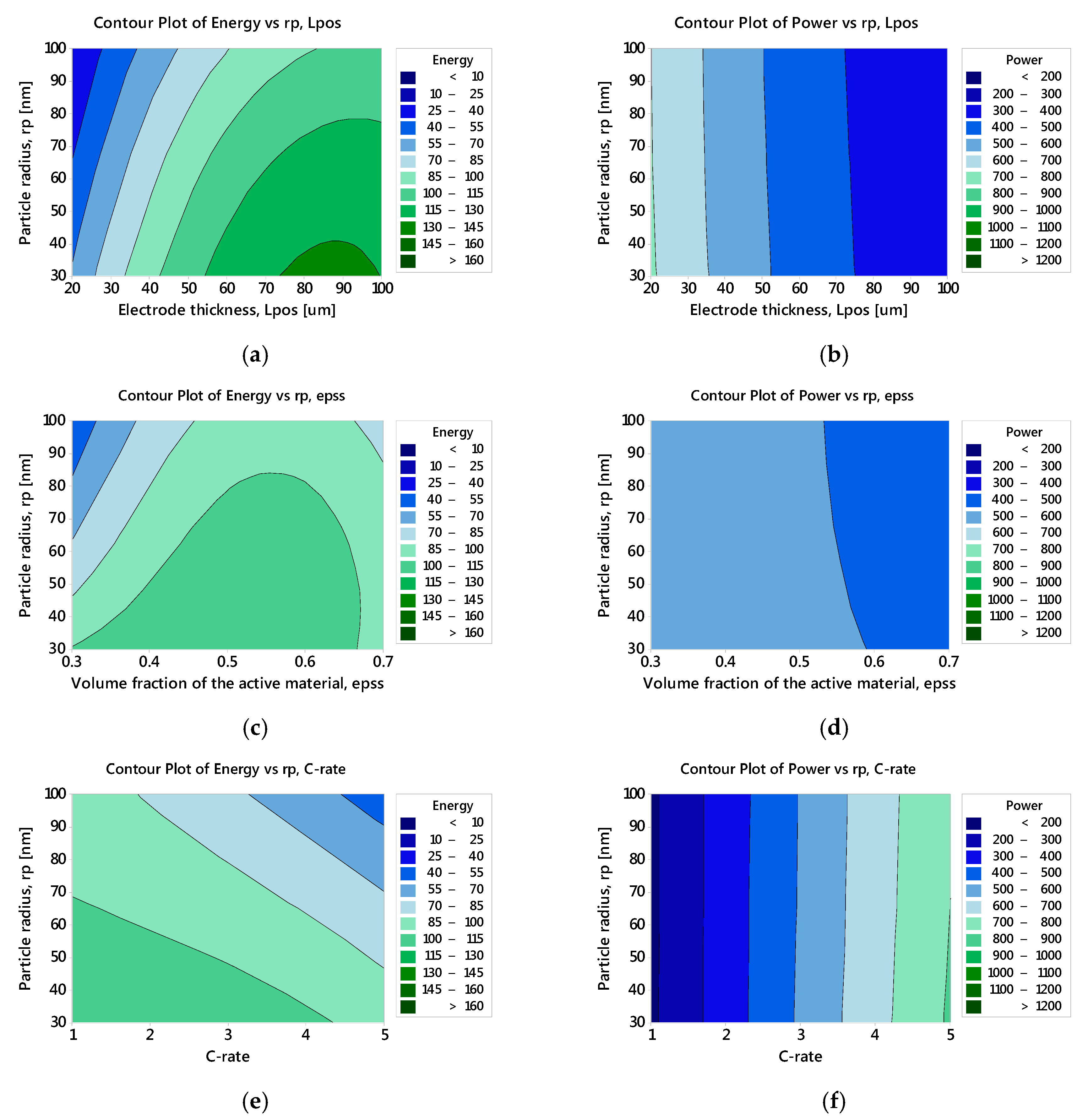
| Factor | Level 1 | Level 2 | Level 3 |
|---|---|---|---|
| Particle radius, , () | 30 | 65 | 100 |
| Electrode thickness , () | 20 | 60 | 100 |
| Volume fraction of the electrode | 0.3 | 0.5 | 0.7 |
| C-rate | 1 | 3 | 5 |
| Parameter | Negative Electrode | Positive Electrode |
|---|---|---|
| Particle radius, () | 3.5 | 0.0365 |
| Thickness, () | 34 | 70 |
| Active material volume fraction | 0.55 | 0.43 |
| Electrolyte volume fraction/Porosity ( | 0.33 | 0.332 |
| R1 | R2 | |||
|---|---|---|---|---|
| Factors | F-Value | p-Value | F-Value | p-Value |
| 62.41 | 0.000 | 39.18 | 0.000 | |
| 339.36 | 0.000 | 132,788.79 | 0.000 | |
| 50.68 | 0.000 | 1113.13 | 0.000 | |
| C | 49.53 | 0.000 | 604,485.14 | 0.000 |
| × | 2.39 | 0.064 | 2.84 | 0.034 |
| × | 9.62 | 0.000 | 9.83 | 0.000 |
| × C | 6.49 | 0.000 | 0.47 | 0.756 |
| × | 11.30 | 0.000 | 154.15 | 0.000 |
| × C | 5.06 | 0.002 | 19,700 | 0.000 |
| × C | 4.86 | 0.002 | 4.28 | 0.005 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosseinzadeh, E.; Marco, J.; Jennings, P. Electrochemical-Thermal Modelling and Optimisation of Lithium-Ion Battery Design Parameters Using Analysis of Variance. Energies 2017, 10, 1278. https://doi.org/10.3390/en10091278
Hosseinzadeh E, Marco J, Jennings P. Electrochemical-Thermal Modelling and Optimisation of Lithium-Ion Battery Design Parameters Using Analysis of Variance. Energies. 2017; 10(9):1278. https://doi.org/10.3390/en10091278
Chicago/Turabian StyleHosseinzadeh, Elham, James Marco, and Paul Jennings. 2017. "Electrochemical-Thermal Modelling and Optimisation of Lithium-Ion Battery Design Parameters Using Analysis of Variance" Energies 10, no. 9: 1278. https://doi.org/10.3390/en10091278
APA StyleHosseinzadeh, E., Marco, J., & Jennings, P. (2017). Electrochemical-Thermal Modelling and Optimisation of Lithium-Ion Battery Design Parameters Using Analysis of Variance. Energies, 10(9), 1278. https://doi.org/10.3390/en10091278






