Impact of Firms’ Observation Network on the Carbon Market
Abstract
1. Introduction
2. Model
2.1. Model Structure
2.2. Low-Carbon Technology and Marginal Abatement Cost Curve
2.3. Agents
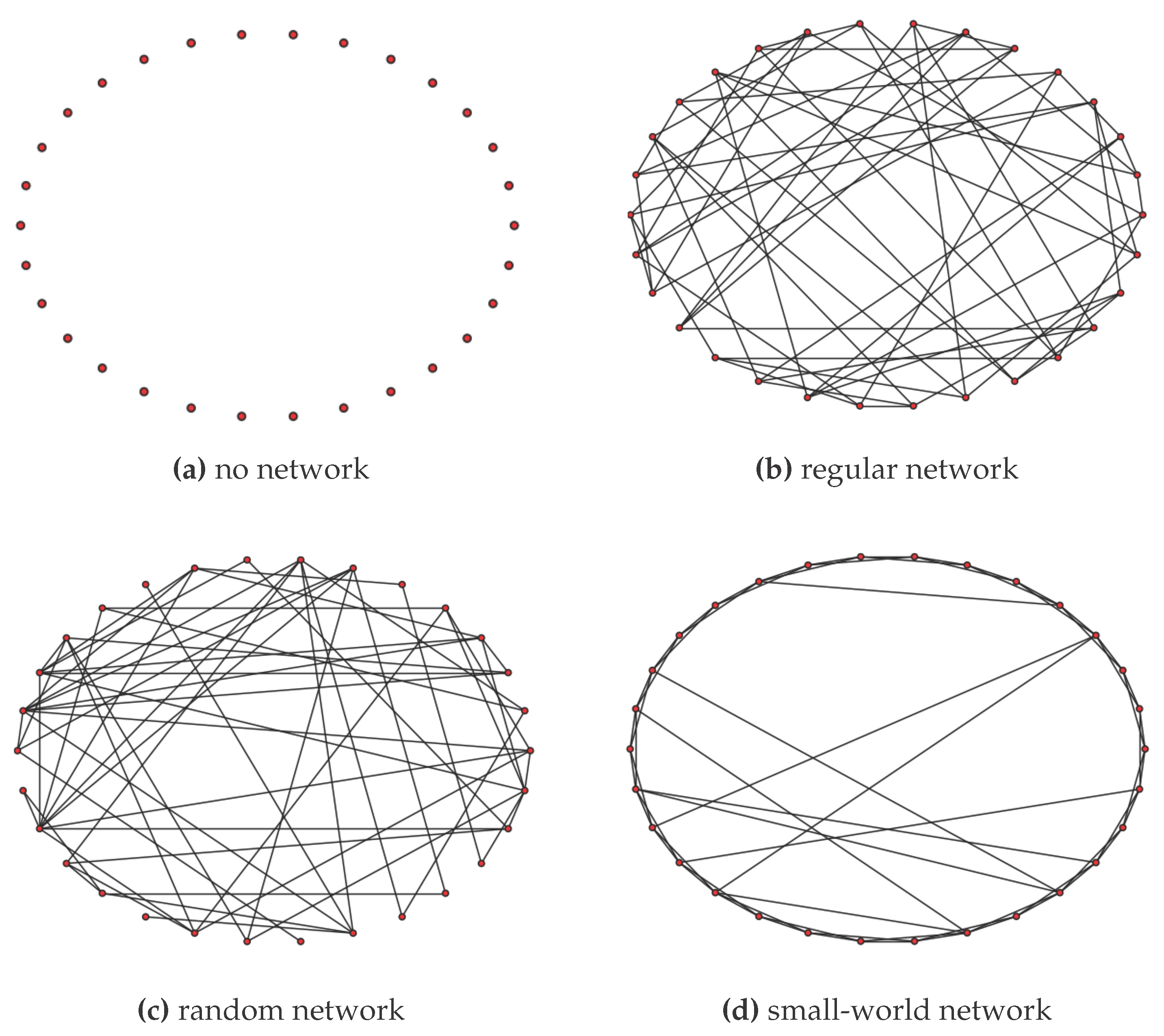
2.3.1. Observation Network and Forecast
2.3.2. Abatement-Oriented Decisions
- 1.
- Production Adjustment DecisionIn each period, agent i has a probability of of adjusting its daily production. We introduce a probability to characterize agent i’s propensity to adjust its production coefficient (Agent i’s daily production is , and is set to 1, indicating that agent i’s initial daily production was equal to its average daily production in the last year. Then, during the abatement phase, when agent i wants to reduce its production, we let . In turn, when agent i decides to increase its production, we let . Here, is an exogenous parameter.). When agent i’s profit of unit emission from the output market (Here the emission allowance is treated as a production factor. Suppose that the product price is per ton, and the production cost is per ton. The energy intensity of agent i is . The emission factor of the energy is . Then, profit of unit emission for agent i is calculated as .) is higher than a benchmark price (Here, is a benchmark price for agent i to make production decision, and it is calculated as . are agent i’s three behavioural parameters related to its production decision. A detailed explanation of the behavioural parameters can be found in the Appendix of [10].), it might increase its production, and the probability is calculated as . When agent i’s profit of unit emission from the output market is lower than a benchmark price , it might decrease its production and the probability is calculated as .
- 2.
- Low-Carbon Technology Adoption DecisionFor simplicity, we assume that in each period t, agent i only considers the adoption of the available low-carbon technology with the lowest average abatement cost. A probability is used to characterize its propensity to adopt this technology. Reasonably, we assume that is related to four factors: (1) , which is the average abatement cost of the technology being considered, and we assume ; (2) , which is the potential emission abatement of the technology in the remaining periods of the whole abatement phase, and we assume ; (3) , which is agent i’s expected net allowance, which is its holdings of allowance minus the expected total emission in the whole abatement phase, and we assume ; and (4) (like , is a benchmark price for agent i to make production decision, and it is calculated as ), which is the benchmark price for agent i to compare with when making adoption decisions, and we assume .On the other hand, as a probability, the value domain of is . Thus, based on the four factors listed above and their relationship with , we introduce a modified sigmoid function for the calculation of as follows (here are agent i’s seven behavioural parameters related to its adoption decision; among them, , , and are larger than 1).
- 3.
- Allowance Trading DecisionIn this model, there are ticks in each period, each of which is denoted by s. On each tick, an agent is randomly selected to trade with other agents in the carbon market. The trading process is organized based on the continuous double-auction mechanism.Once selected, an agent first considers whether to trade as a buyer or a seller. Then, it will submit a bid or ask order to the order book. The order is a combination of a limit price and a limit volume , meaning that agent i would like to sell (or buy) units of allowance at a price no lower (or higher) than . Following the work by Raberto and Cincotti [23], we let agent i decides its limit price and volume randomly according to the current allowance price and its allowance gap (a detailed introduction can be found in our previous work [10]).Additionally, concerning agent i’s decision of trading direction, we introduce a probability to characterize its propensity to trade as a buyer or seller, and it is calculated as follows. When the current price of allowance is higher than the benchmark price (The calculation of is different from and for containing the influence of agent i’s net allowance , the difference between holdings of allowance and expected total emission in the whole abatement phase. Here we reasonably assume that the higher (or lower) is, the lower (or higher) agent i’s is, and the higher propensity for agent i to trade as a seller. Because given other factors equal, when agent i’s is high, it faces a lower probability of being fined by the end of the abatement phase, and a higher probability of losing the value of excess allowance in hands. In order to characterize this impact of on , we also introduce a modified sigmoid function as follows: .), agents might trade as a seller, and the probability is calculated as . When the current price of allowance is lower than the benchmark price , agents might trade as a buyer, and the probability is calculated as (here, are agent i’s four behavioural parameters related to its allowance trading decision). This probabilistic framework also follows the idea of Raberto and Cincotti [23], but the introduction of reflects the abatement motivation of agents’ allowance trading behaviours.
3. Simulation Settings
4. Results and Discussion
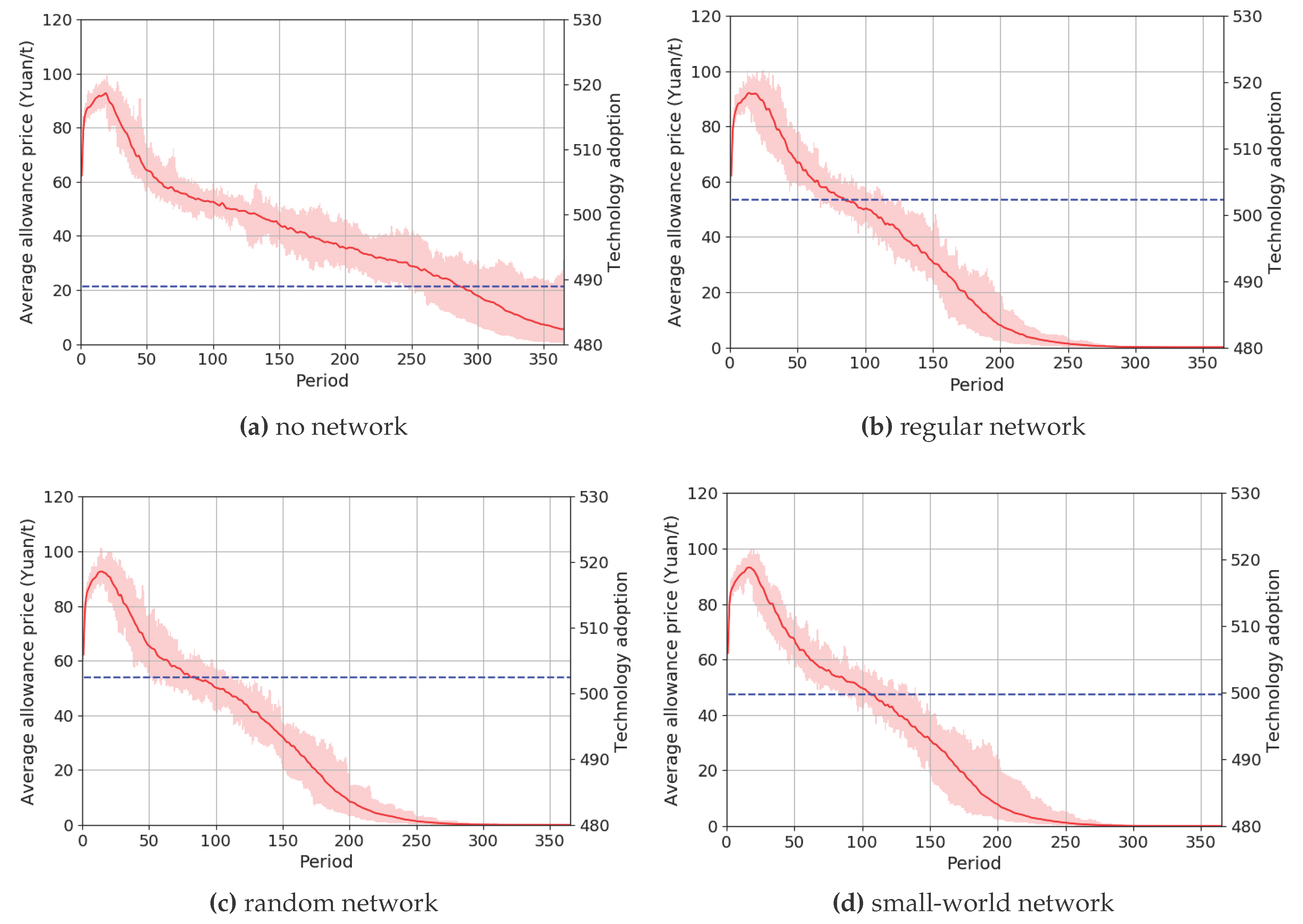
4.1. Allowance Price and Low-Carbon Technology Adoption
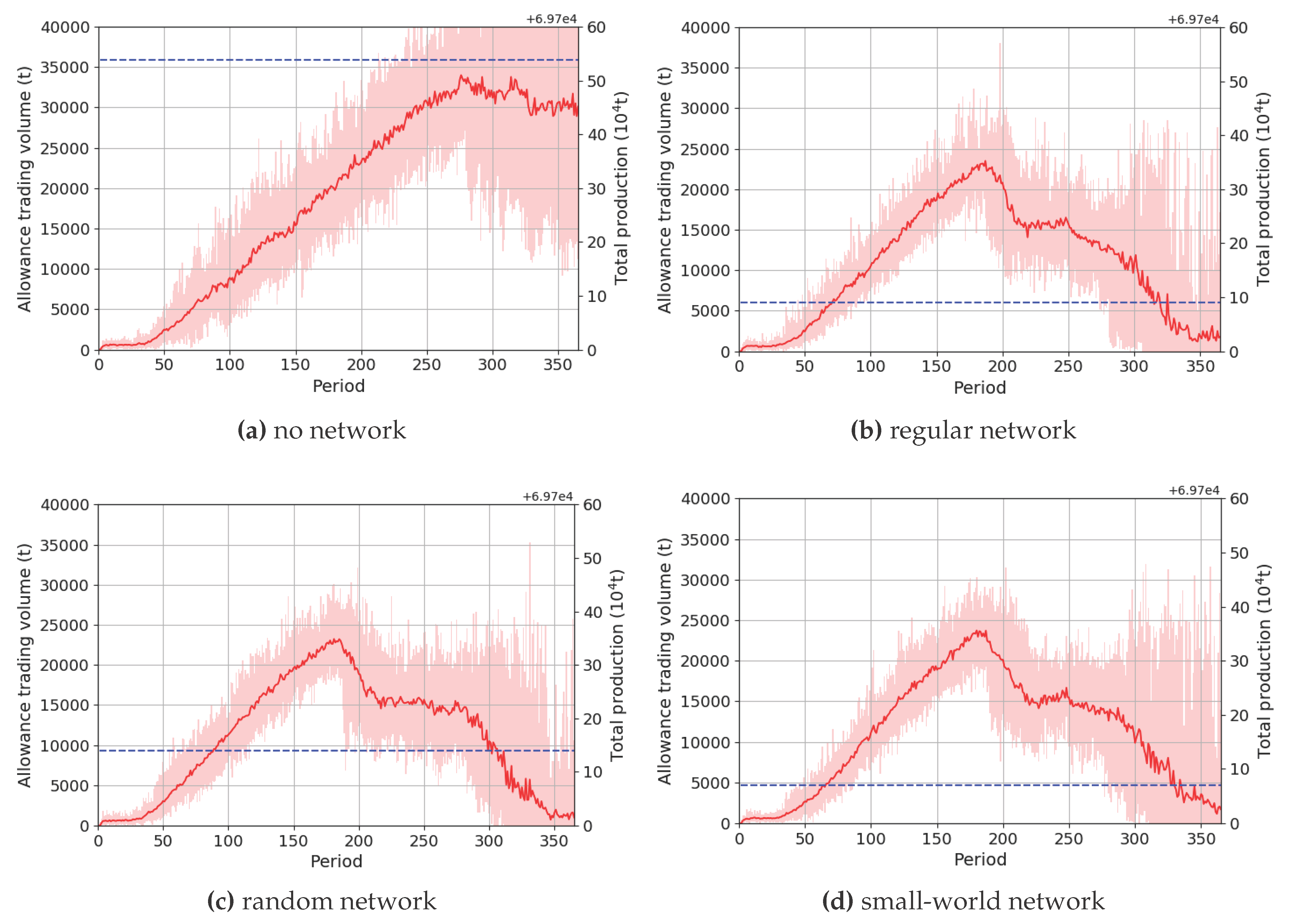
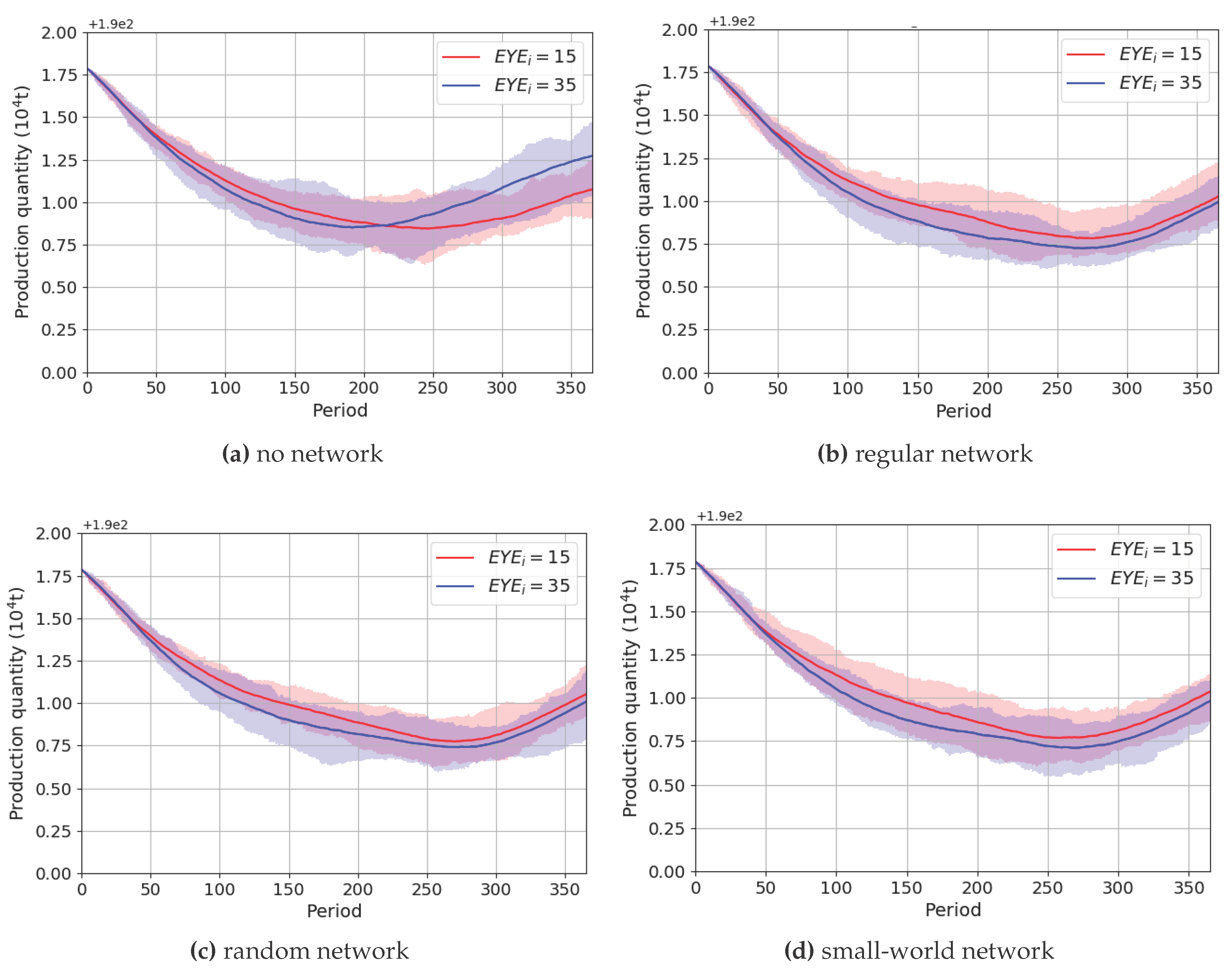
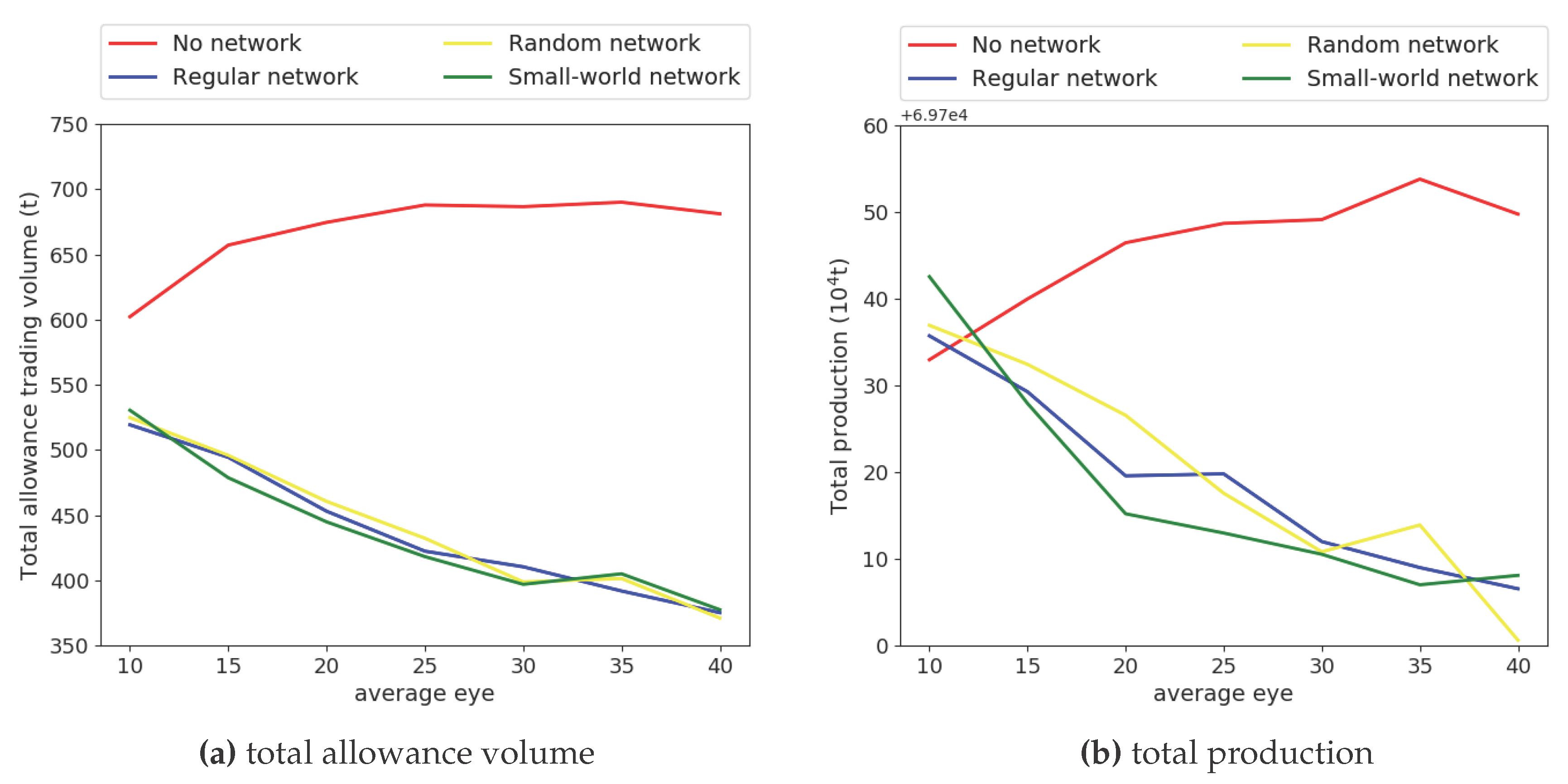
4.2. Allowance Trading Volume and Total Production
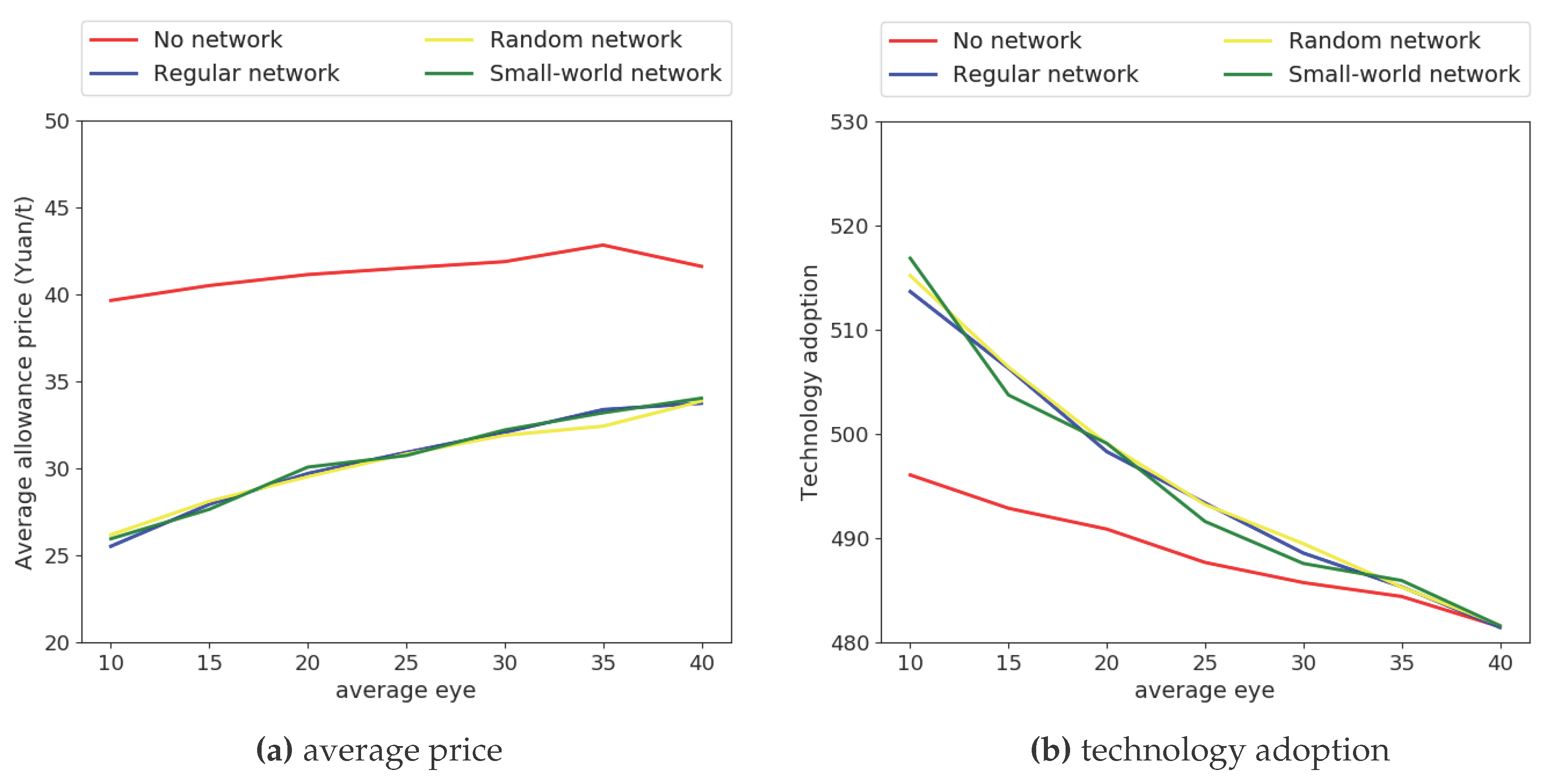
4.3. Efficiency of Carbon Emission Trading Mechanism
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sumner, J.; Bird, L.; Dobos, H. Carbon taxes: A review of experience and policy design considerations. Clim. Policy 2011, 11, 922–943. [Google Scholar] [CrossRef]
- Bakam, I.; Matthews, R.B. Emission trading in agriculture: A study of design options using an agent-based approach. Mitig. Adapt. Strateg. Glob. Chang. 2009, 14, 755–776. [Google Scholar] [CrossRef]
- Wu, J.; Fan, Y.; Xia, Y. The Economic Effects of Initial Quota Allocations on Carbon Emissions Trading in China. Energy J. 2016, 37, 129–151. [Google Scholar] [CrossRef]
- Goulder, L.H.; Hafstead, M.A.; Dworsky, M. Impacts of alternative emissions allowance allocation methods under a federal cap-and-trade program. J. Environ. Econ. Manag. 2010, 60, 161–181. [Google Scholar] [CrossRef]
- Cui, L.B.; Fan, Y.; Zhu, L.; Bi, Q.H. How will the emissions trading scheme save cost for achieving China’s 2020 carbon intensity reduction target? Appl. Energy 2014, 136, 1043–1052. [Google Scholar] [CrossRef]
- Damien, D.; Philippe, Q. European Emission Trading Scheme and competitiveness: A case study on the iron and steel industry. Energy Econ. 2008, 30, 2009–2027. [Google Scholar]
- Martin, R.; Muûls, M.; Wagner, U.J. The impact of the European Union Emissions Trading Scheme on regulated firms: What is the evidence after ten years? Rev. Environ. Econ. Policy 2015, 10, 129–148. [Google Scholar] [CrossRef]
- Oestreich, A.M.; Tsiakas, I. Carbon emissions and stock returns: Evidence from the EU Emissions Trading Scheme. J. Bank. Financ. 2015, 58, 294–308. [Google Scholar] [CrossRef]
- Mo, J.L.; Zhu, L.; Fan, Y. The impact of the EU ETS on the corporate value of European electricity corporations. Energy 2012, 45, 3–11. [Google Scholar] [CrossRef]
- Yu, S.; Fan, Y.; Zhu, L. How Do Heterogeneity and Incomplete Information Influence the Carbon Market? An Agent-Based Approach. 2017. Working Paper. Available online: https://www.researchgate.net/project/Agent-based-simulation-for-emission-trading-scheme (accessed on 24 May 2017).
- Zhang, J.; McBurney, P.; Musial, K. Convergence of trading strategies in continuous double auction markets with boundedly-rational networked traders. Rev. Quant. Financ. Account. 2017, 1–52. [Google Scholar] [CrossRef]
- Alfarano, S.; Milaković, M.; Raddant, M. A note on institutional hierarchy and volatility in financial markets. Eur. J. Financ. 2013, 19, 449–465. [Google Scholar] [CrossRef]
- Chapman, M.; Tyson, G.; Atkinson, K.; Luck, M.; McBurney, P. Social networking and information diffusion in automated markets. In Agent-Mediated Electronic Commerce. Designing Trading Strategies and Mechanisms for Electronic Markets; Springer: Berlin, Germany, 2013; pp. 1–15. [Google Scholar]
- Delre, S.A.; Jager, W.; Janssen, M.A. Diffusion dynamics in small-world networks with heterogeneous consumers. Comput. Math. Organ. Theory 2007, 13, 185–202. [Google Scholar] [CrossRef]
- Kocsis, G.; Kun, F. The effect of network topologies on the spreading of technological developments. J. Stat. Mech. Theory Exp. 2008, 2008. [Google Scholar] [CrossRef]
- Janssen, M.A.; Jager, W. Simulating market dynamics: Interactions between consumer psychology and social networks. Artif. Life 2003, 9, 343–356. [Google Scholar] [CrossRef] [PubMed]
- Baker, E.; Clarke, L.; Shittu, E. Technical change and the marginal cost of abatement. Energy Econ. 2008, 30, 2799–2816. [Google Scholar] [CrossRef]
- Bauman, Y.; Lee, M.; Seeley, K. Does technological innovation really reduce marginal abatement costs? Some theory, algebraic evidence, and policy implications. Environ. Resour. Econ. 2008, 40, 507–527. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, L. Cost of energy saving and CO2 emissions reduction in China’s iron and steel sector. Appl. Energy 2014, 130, 603–616. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Gigerenzer, G. Fast and frugal heuristics: The tools of bounded rationality. In Blackwell Handbook of Judgment and Decision Making; Wiley-Blackwell: Hoboken, NJ, USA, 2004. [Google Scholar]
- Raberto, M.; Cincotti, S.; Focardi, S.M.; Marchesi, M. Agent-based simulation of a financial market. Phys. A Stat. Mech. Appl. 2001, 299, 319–327. [Google Scholar] [CrossRef]
- Fischer, C.; Fox, A.K. Output-based allocation of emissions permits for mitigating tax and trade interactions. Land Econ. 2007, 83, 575–599. [Google Scholar] [CrossRef]



© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.-m.; Zhu, L. Impact of Firms’ Observation Network on the Carbon Market. Energies 2017, 10, 1164. https://doi.org/10.3390/en10081164
Yu S-m, Zhu L. Impact of Firms’ Observation Network on the Carbon Market. Energies. 2017; 10(8):1164. https://doi.org/10.3390/en10081164
Chicago/Turabian StyleYu, Song-min, and Lei Zhu. 2017. "Impact of Firms’ Observation Network on the Carbon Market" Energies 10, no. 8: 1164. https://doi.org/10.3390/en10081164
APA StyleYu, S.-m., & Zhu, L. (2017). Impact of Firms’ Observation Network on the Carbon Market. Energies, 10(8), 1164. https://doi.org/10.3390/en10081164




