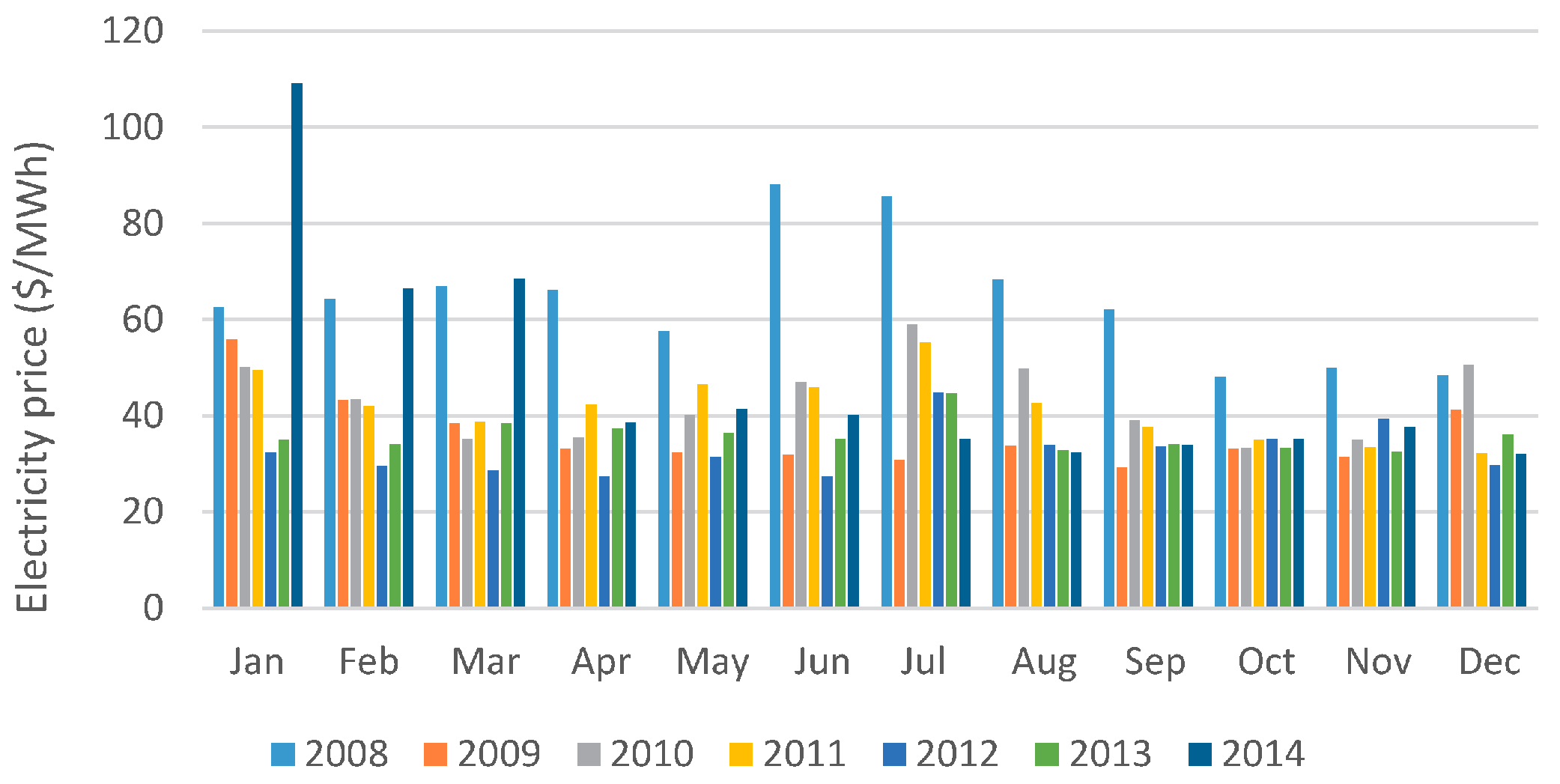Potential Arbitrage Revenue of Energy Storage Systems in PJM

Abstract

The volatility of electricity prices is attracting interest in the opportunity of providing net revenue by energy arbitrage. We analyzed the potential revenue of a generic Energy Storage System (ESS) in 7395 different locations within the electricity markets of Pennsylvania-New Jersey-Maryland interconnection (PJM), the largest U.S. regional transmission organization, using hourly locational marginal prices over the seven-year period 2008–2014. Assuming a price-taking ESS with perfect foresight in the real-time market, we optimized the charge-discharge profile to determine the maximum potential revenue for a 1 MW system as a function of energy/power ratio, or rated discharge duration, from 1 to 14 h, including a limited analysis of sensitivity to round-trip efficiency. We determined minimum potential revenue with a similar analysis of the day-ahead market. We presented the distribution over the set of nodes and years of price, price volatility, and maximum potential arbitrage revenue. From these results, we determined the breakeven overnight installed cost of an ESS below which arbitrage would be profitable, its dependence on rated discharge duration, its distribution over grid nodes, and its variation over the years. We showed that dispatch into real-time markets based on day-ahead market settlement prices is a simple, feasible method that raises the lower bound on the achievable arbitrage revenue.

1. Introduction

Energy storage systems (ESS) offer benefits to grid operations from distributed generation-to-utility scale installations. The costs of ESS have been decreasing, and new technologies are still in development. They can be physically connected at generation, transmission, and distribution, or at the customer side. In general, the benefits provided by an ESS are related to energy time shift, ancillary services, upgrade deferral, power quality, reliability, and variable generation smoothing [1,2]. The United States (including all territories) has already installed 52 units (411 MW) of electrochemical ESS over 1 MW of rated power (i.e., power capacity); 12 units (74.5 MW) are under construction and 26 units (330 MW) are already contracted or announced [3]. Among 90 installations (totaling 815 MW), the primary services provided are concentrated on four types [3]:

• Frequency Regulation (217 MW);
• Reserve Capacity (116 MW);
• Energy Time Shift (131 MW);
• Billing Management (95 MW).

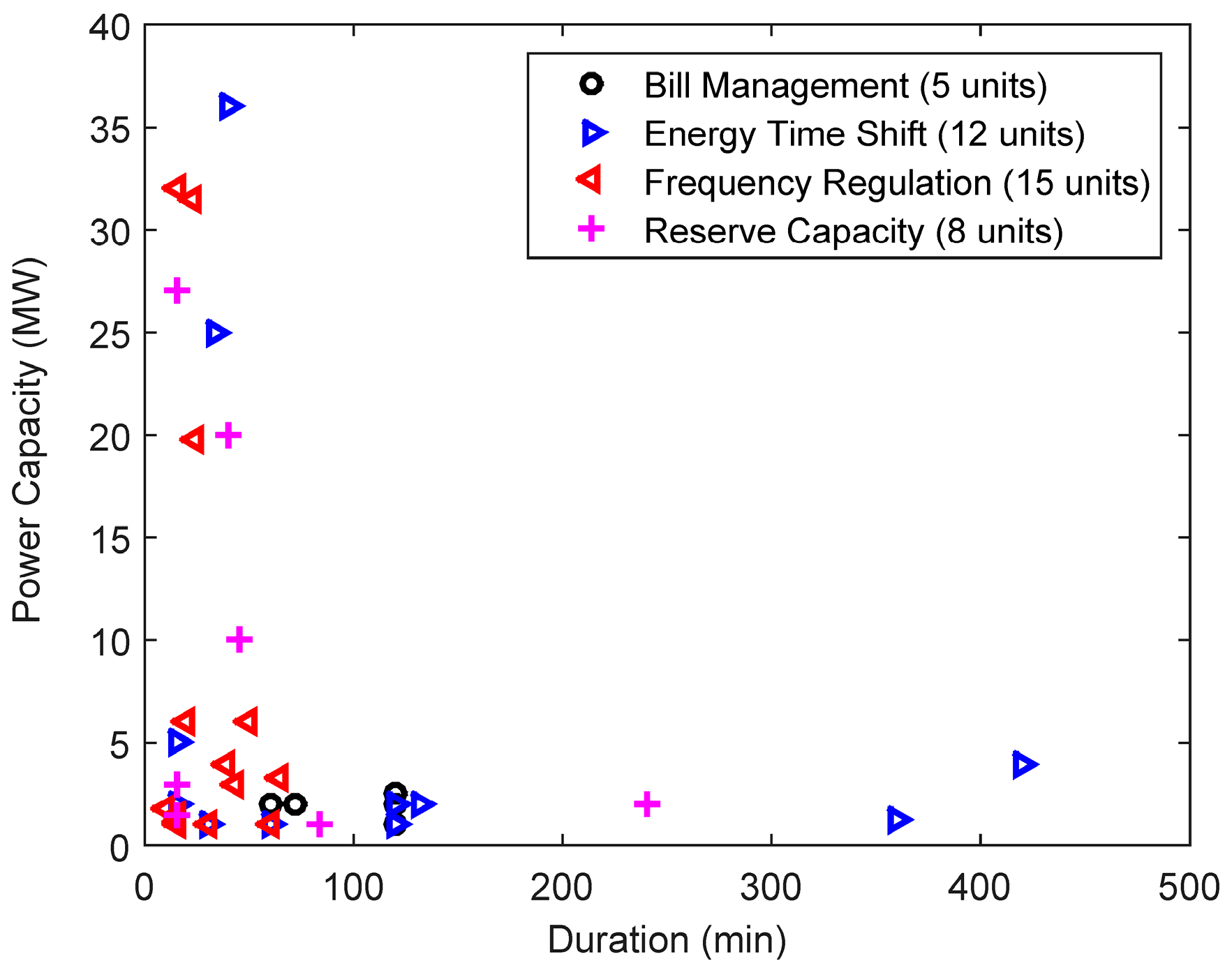
Whereas electrochemical ESS can operate to provide more than one service at the same time, such as voltage support and frequency regulation, some services are mutually exclusive. Currently, the focus is on ancillary services, which include frequency regulation and reserve capacity. Ancillary services represent more than 40% of the power capacity of those 90 installations. The characteristics of frequency regulation and reserve capacity do not require great energy capacity from the storage system, as shown in Figure 1. For ease of comparison, we present the discharge duration at rated power, i.e., the energy/power ratio, instead of the energy capacity for the abscissa. Most of the units for energy time shift have more than one hour of discharge duration at the rated power capacity.

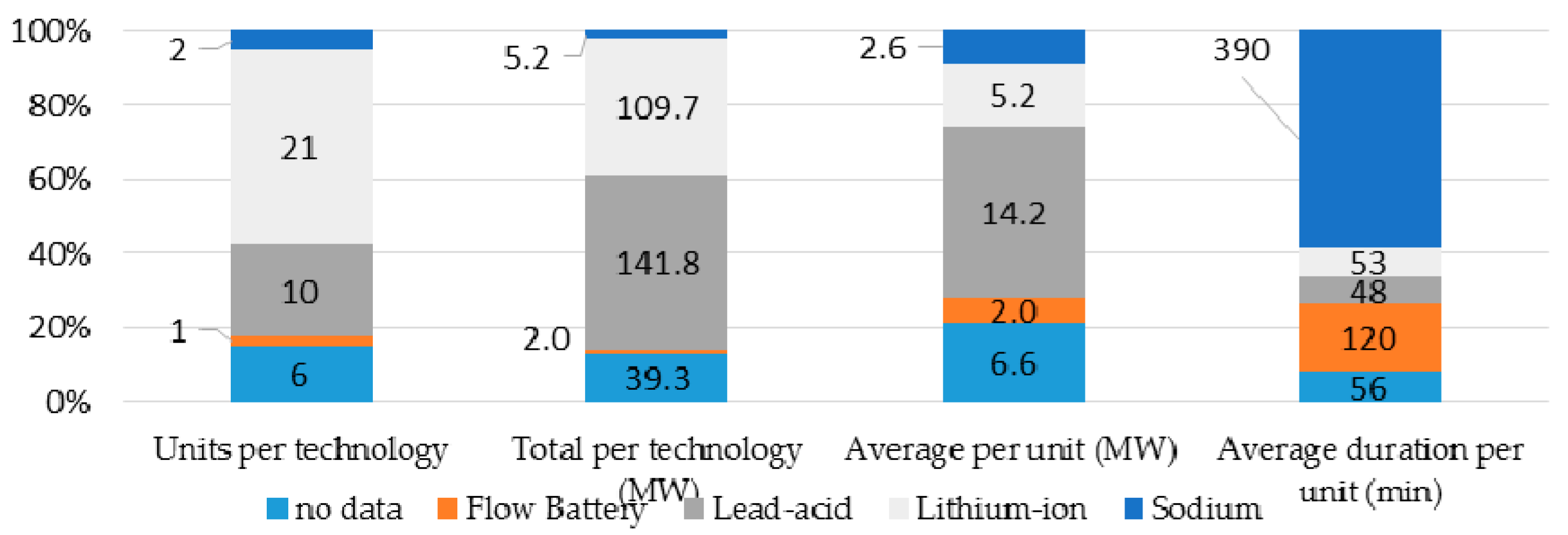
The lithium-ion battery has the highest percentage in number of units, as shown in Figure 2, but the total power capacity is dominated by lead-acid batteries. Figure 2 shows that the most commonly used technologies for longer duration are the flow and the sodium-sulfur batteries, which are also used for energy time shift (Figure 1). Both technologies are considered to be promising options for energy time shift and peak shaving [2,4]. Because flow batteries, in principle, can be designed with arbitrarily large energy/power ratios, they become more interesting for long discharge duration applications. This paper investigates the requirements for economic viability at discharge durations up to 14 h, in anticipation of growth in photovoltaic and wind supply leading to increased need for energy time-shift services. The analyses, however, are pertinent to all ESS technologies.

The round trip efficiency of EES technologies is continuously improving. This manuscript considers instead a foreseeable future in which costs should be lower and efficiencies higher. Flywheels, at 95% [4], excluding power electronics losses, inspired an aspirational target of 95%. Values around 95% are realistic for some ESS technologies (for example some Li-ion batteries, flywheels, and supercapacitors). However, the process of choosing a suitable ESS may not be only a question of investment, efficiency, maturity, and reliability, but it is also a question of the environmental impact of the chemical materials. This paper does not concentrate on a specific ESS type of technology, but rather on a generic model.

The wholesale electricity markets in the United States have been affected by increases in average electricity prices and in their volatility, before 2007 [5]. In 2008, the prices started to decline because of the exploitation of shale gas. A significant increase occurred in 2014 due to the extremely cold weather in the beginning of the year [6], but the average price subsequently returned to the values of 2013.

The use of ESS for energy time shift has a great potential for creating revenue in these scenarios, buying energy when the prices are low and selling back to the grid when prices are high. The estimation of this potential arbitrage revenue is presented in [5] for a period from 2002 to 2007 for a few nodes in the PJM day-ahead market (DAM). This work reported a method of short-term forecasting of hourly prices to maximize revenue, using a one day back-casting dispatch. The theoretical value capture from that approach was close to that obtainable with perfect foresight.

A similar approach was presented in [7] highlighting that energy arbitrage and operating reserves revenues could make conventional compressed air energy storage (CAES) devices profitable in several day-ahead electricity markets. An economic evaluation of 14 ESS technologies was performed in [8], considering real-time energy prices in 2008 (the highest of the past decade) from seven different markets. The studies performed in the current work extend the analysis presented in [5,6,7,8] and evaluate the potential arbitrage revenue of a generic ESS using real-time prices from 2008 to 2014, including more than 7,300 different locations in PJM.

The organization of the paper is as follows. Section 2 gives an overview and statistical description of the energy prices in the PJM wholesale markets. In Section 3, the potential arbitrage revenue of an ESS in the market over the period from 2008 to 2014 is determined for a price-taking ESS with perfect forecast of hourly locational marginal prices, providing an upper limit to arbitrage revenue. Section 4 evaluates the impact of forecast on potential arbitrage revenue, providing a lower limit on revenue from the day-ahead market and raising the lower limit with a novel approach to dispatch. In Section 5 we determine the breakeven overnight installed cost that an ESS must fall below for profitability, its dependence on rated discharge duration, its variation over grid nodes, and its variation over the years. Finally, the main conclusions are presented in Section 6.

2. PJM Electricity Markets

The PJM Interconnection is a regional transmission organization (RTO) in the United States coordinating the wholesale electricity market in 13 states and in the District of Columbia. In 2014, the electricity generation in PJM was 780 TWh for an installed power capacity of 183 GW. The total billings were $50.03 billion in 2014 and $35.89 billion in 2013 [9]. The high demand and high prices in the beginning of 2014 (consequences of extremely cold weather) caused the 40% increase [9]. This section is dedicated to discussing the wholesale electricity prices from 2008 to 2014.

2.1. Locational Marginal Price

Locational marginal price (LMP) can be defined as the price of supplying an additional MW of load at a specific location, or node (likely a bus) in the power system. The total LMP value is based on three pricing components: system energy price, transmission congestion cost and cost of marginal losses. The values are determined by an economic dispatch algorithm following operation security constraints. In PJM, there are two energy markets with separate settlements: the day-ahead market (DAM) and the real-time market (RTM).

The DAM produces bid-based schedules with hourly-based prices and the RTM is a physical market with a five minute interval price. Both market settlements are performed on hourly-based LMPs, but the RTM is based on actual system condition deviations from the day-ahead schedule [10,11,12].

2.2. Electricity Prices in the PJM Real-Time Market

PJM has a special tool called Data Miner to download the historical electricity price data for RTM and DAM. We selected all of the nodes that have a complete data set from 2008 through 2014. The PJM downloaded data must be treated carefully to identify changes in the node identifications (node IDs can be changed for various reasons) and to find missing data within the period analyzed. We analyzed 906 million price observations, including both RTM and DAM.

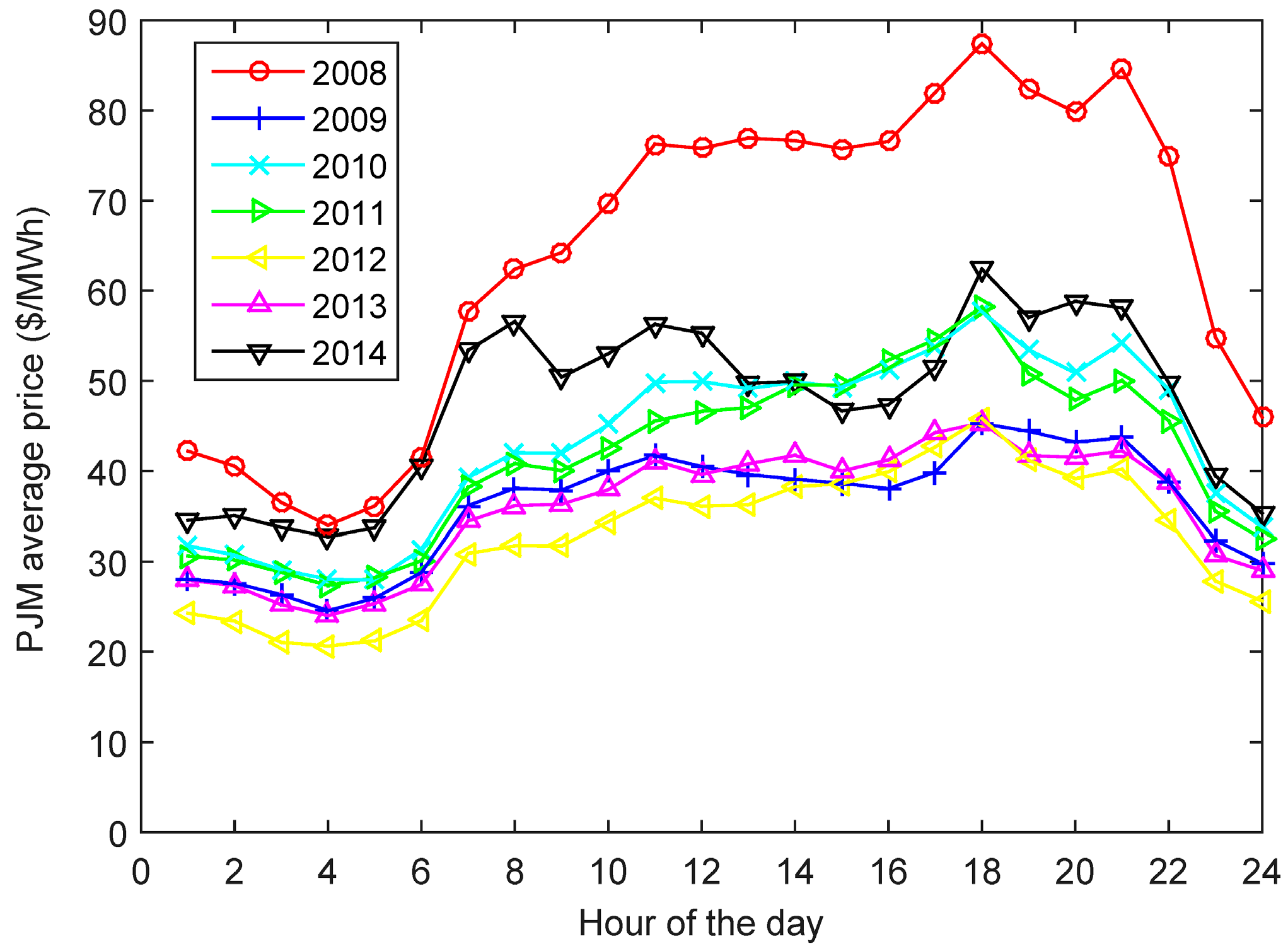
The price deviations between DAM and RTM should be small if no significant events happen in the system. The annual average electricity price of all the PJM nodes analyzed over a seven-year period is presented in Figure 3. The prices in 2008 were the highest observed. Figure 3 suggests a possible simplified model considering two periods of charging (22:00 to 6:00 and 12:00 to 16:00) and two periods of discharging (to 12:00 and 16:00 to 22:00) per day. However, the simulations showed that this simple model leads to very poor performance, and an optimization analysis using a linear program was required.

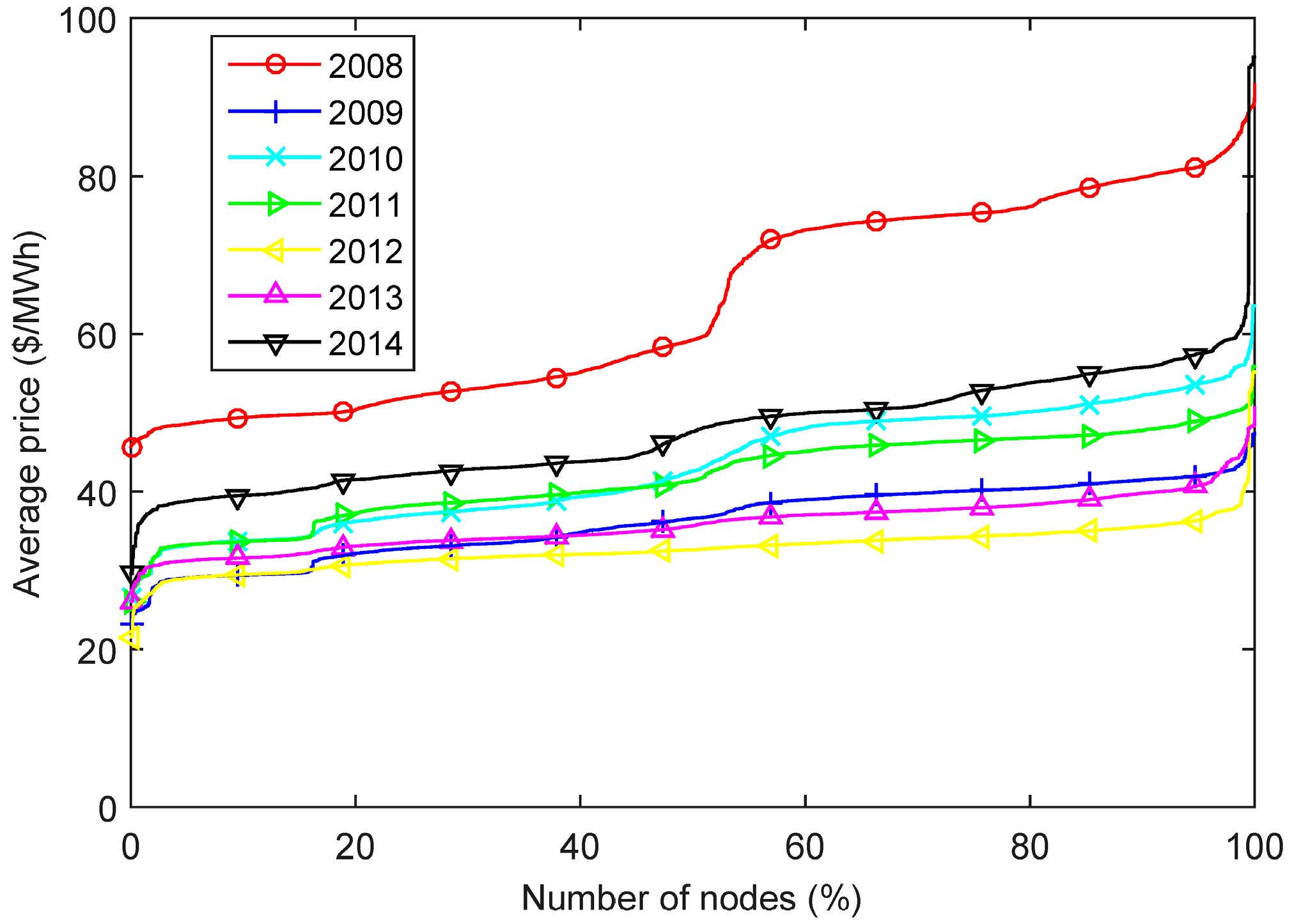
Another way to study price distribution is using the average of RTM prices per year per PJM node. The average price is a variable that influences the potential arbitrage revenue. Figure 4 shows the number of nodes for which the average electricity price fell below a given value for a given year. It demonstrates that the average LMP values vary significantly with location. The nodes can be divided into three groups, considering price: (a) 50% with low prices; (b) 45% with medium prices and (c) 5% with high prices.

2.3. Volatility of Electricity Prices in PJM

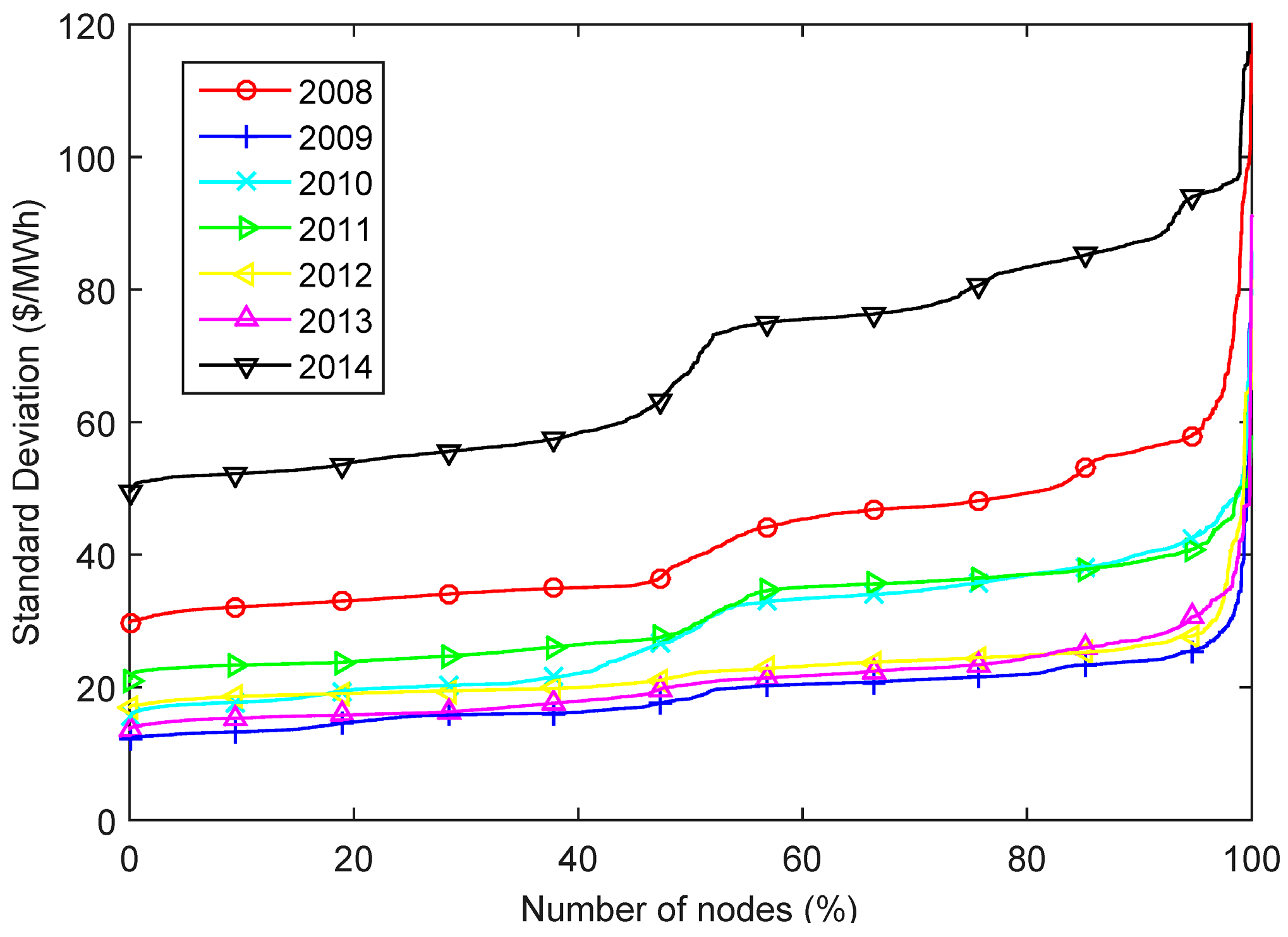
In Figure 5, the historical volatility of all the 7395 PJM nodes was measured by annual standard deviation [13]. The values in 2014 were the highest in all nodes, followed by the values of 2008.

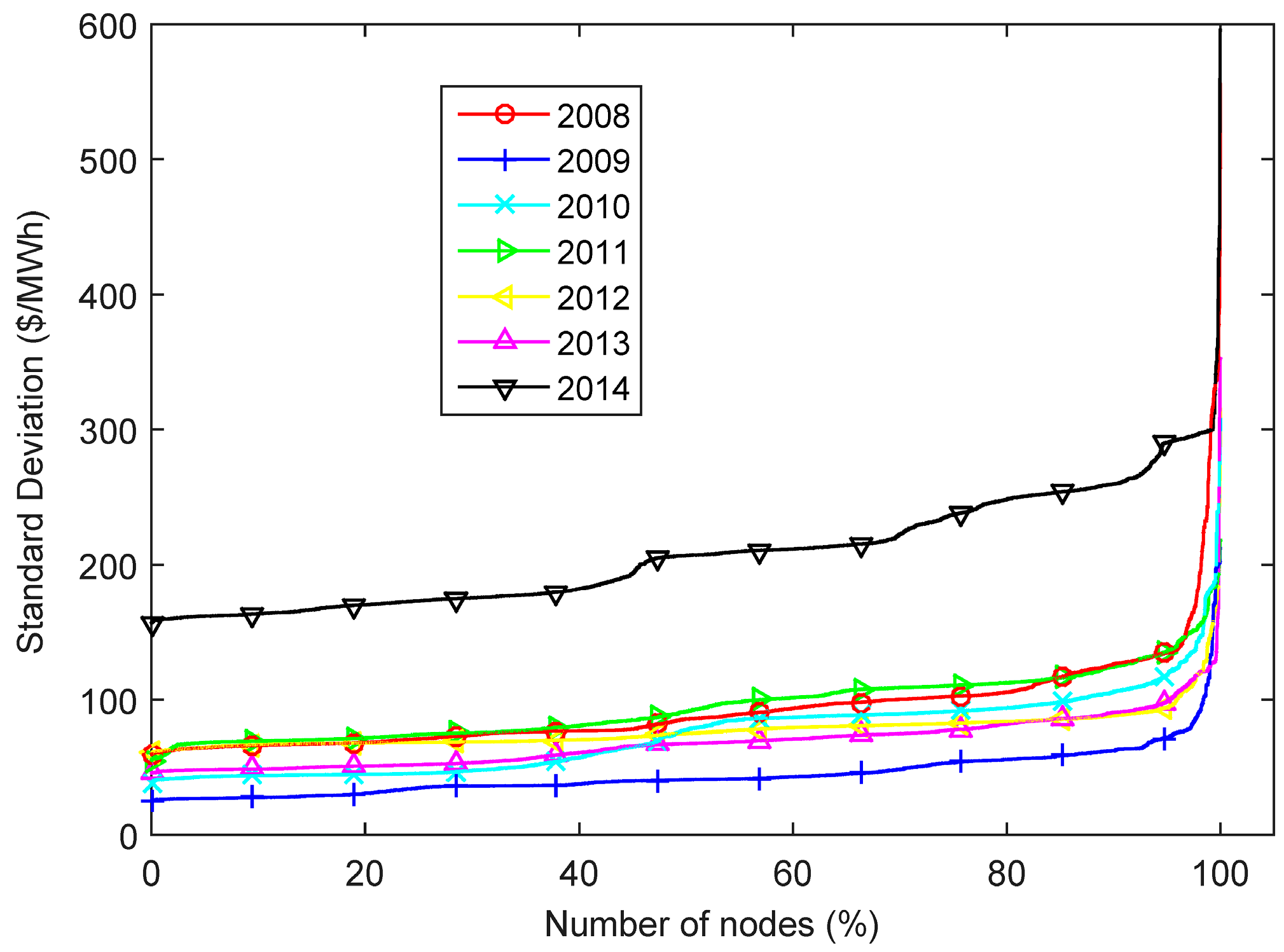
The volatility of the electricity prices can also influence the potential arbitrage revenue of ESS. However, an annual calculation might not have information on the effects resulting from severe contingences or congestions to consider the potential revenue in specific days.

Figure 6 sheds light on the distribution of the standard deviation. The standard deviation was calculated for every day within the period of analysis and for all the nodes. The average of the 10 highest values in each node is shown in Figure 6. The values in 2014 were even higher than the year values.

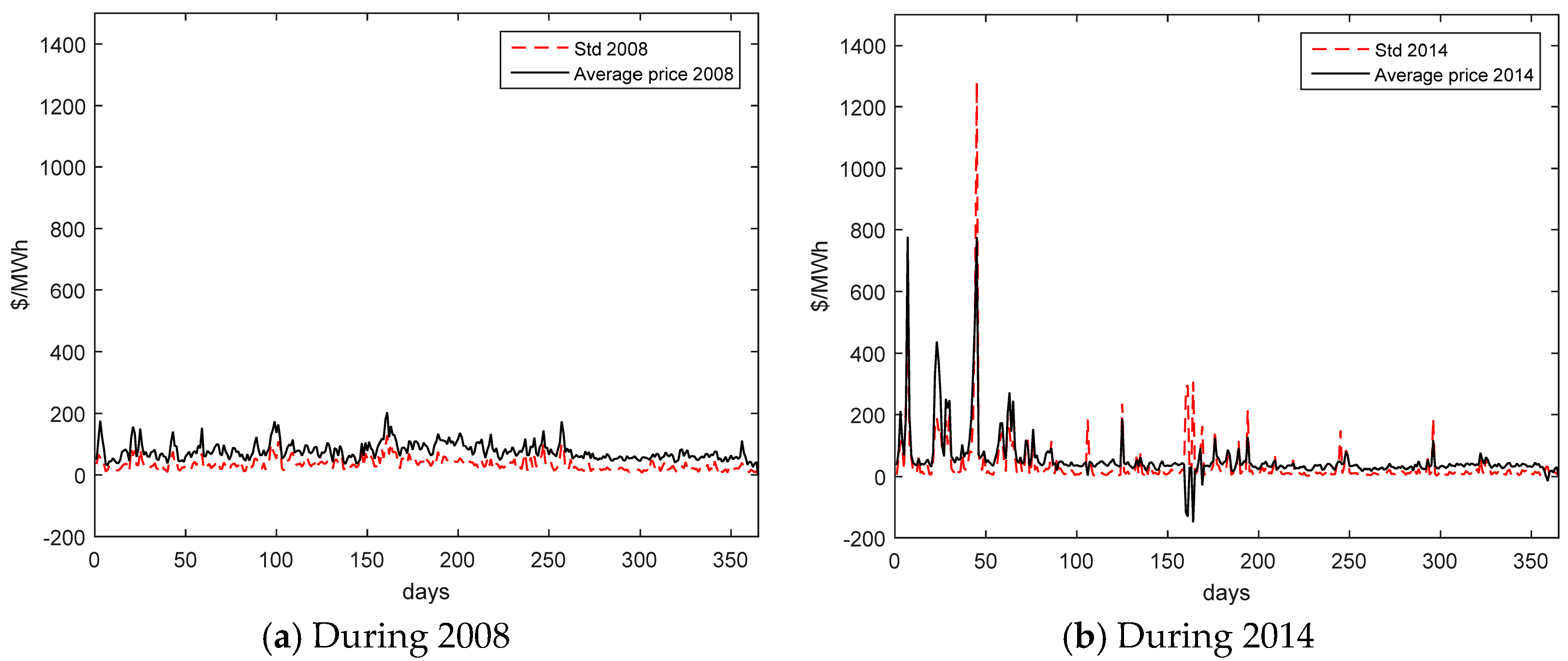
The highest standard deviation value in 2014 (from Figure 5) happened in a load bus in Delaware, price node number 49984 and node name NEWMERED69 KV N-MERD. The standard deviation and the average price per day for the two years with the highest yearly-based values (2008 and 2014) are presented in Figure 7. The same node had very different profiles for daily-based investigation and only small spikes appeared in 2008.

2.4. Seasonality of Electricity Prices for PJM

Electricity prices can increase because of different reasons; however, the impact of the extreme weather at the beginning of 2014 is shown in Figure 8. In almost all years, the prices in January and July are verified to be higher than in other months, presumably because of a higher demand.

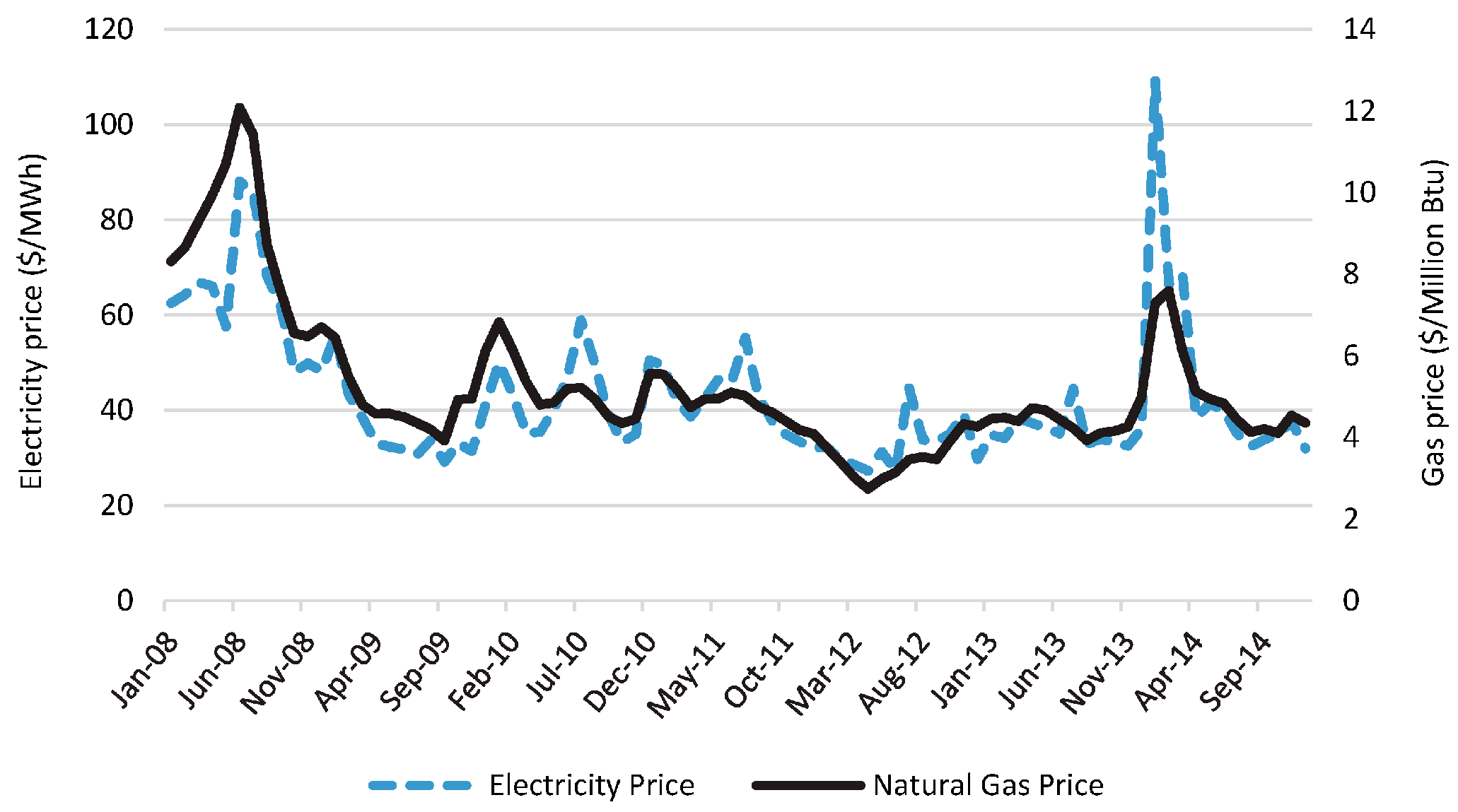
Figure 8 also shows that the price of electricity in 2008 was the highest in the period analyzed. The reason could be the high prices of natural gas for electricity generation, as shown in Figure 9. From the same figure, a very strong relation between natural gas and electricity prices can be verified. The price of coal is not volatile [14].

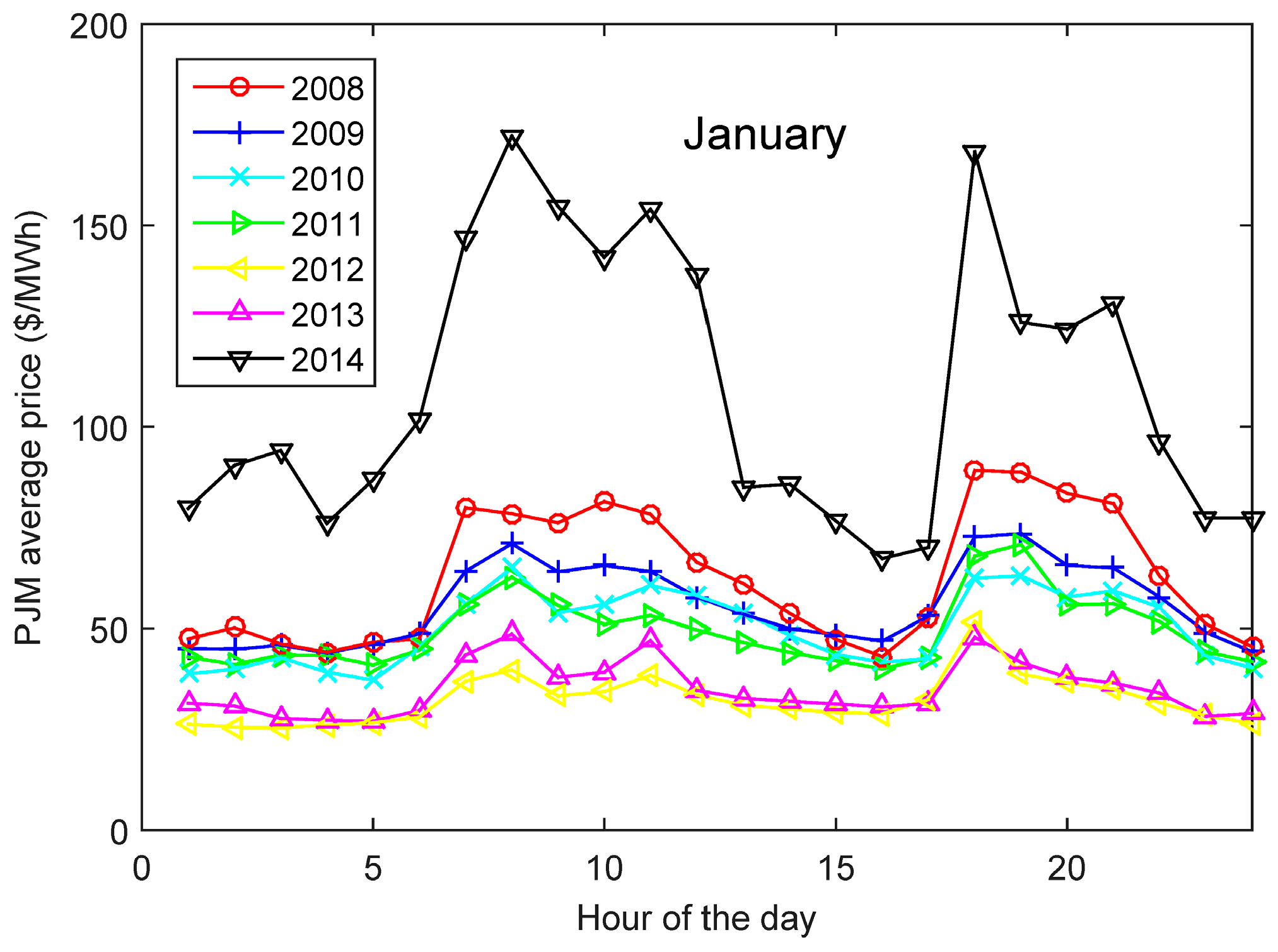
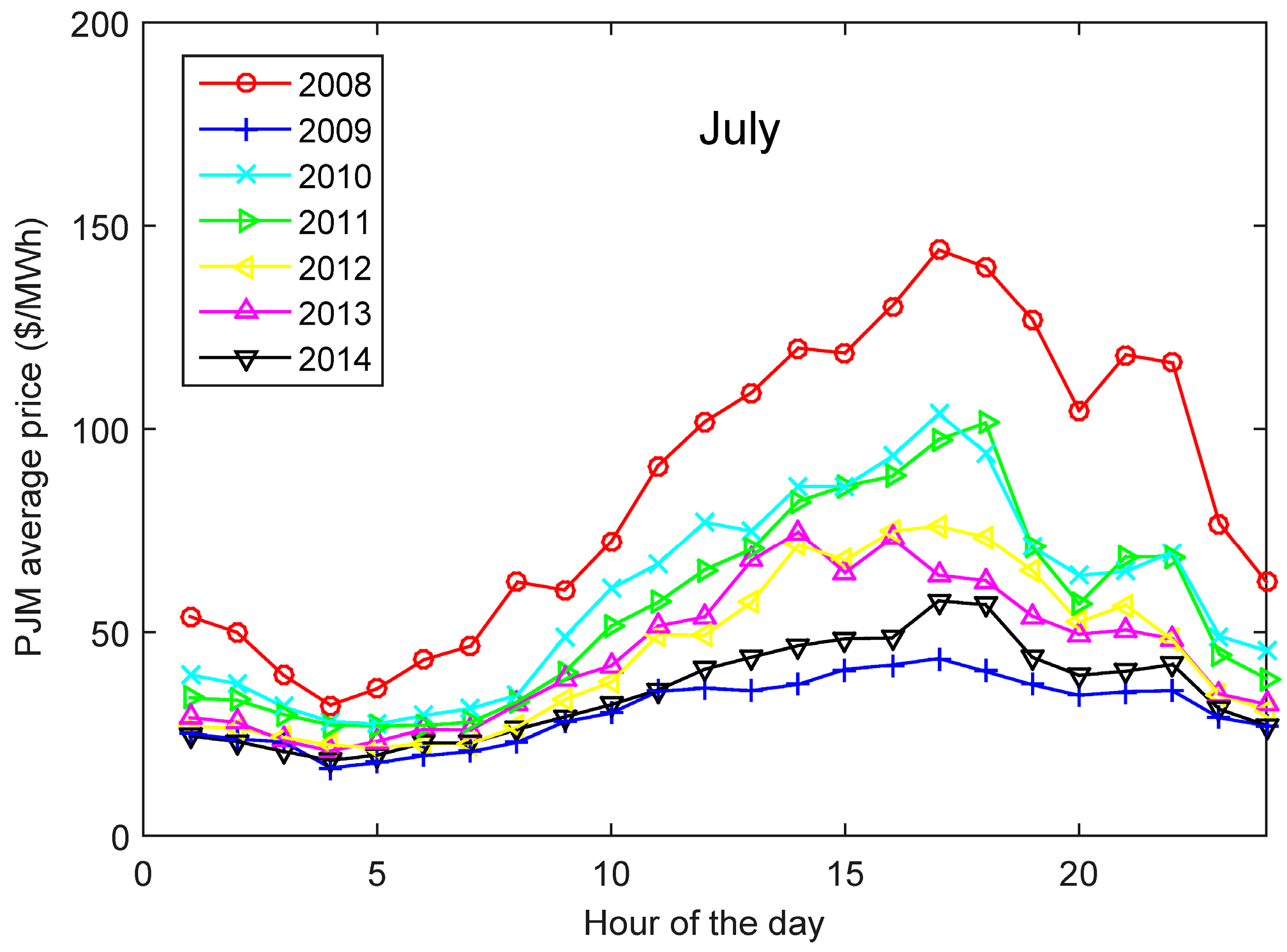
The seasonality shown in Figure 8 was also observed in the daily profile of electricity prices in different months of the year. Figure 10 shows the average price of electricity in January for the 7395 nodes in RTM. There were two peaks per day in January and only one in July (Figure 11). The revenue was probably affected not only because of the high prices, but also because of the difference between off- and on-peak price. The January profile would have had more potential revenue if the average price were the same, and they would lead to different values for the optimum energy capacity of the ESS. The optimum energy capacity with only one peak per day would be much higher than for two peaks per day.

2.5. Electricity Prices in PJM Zones

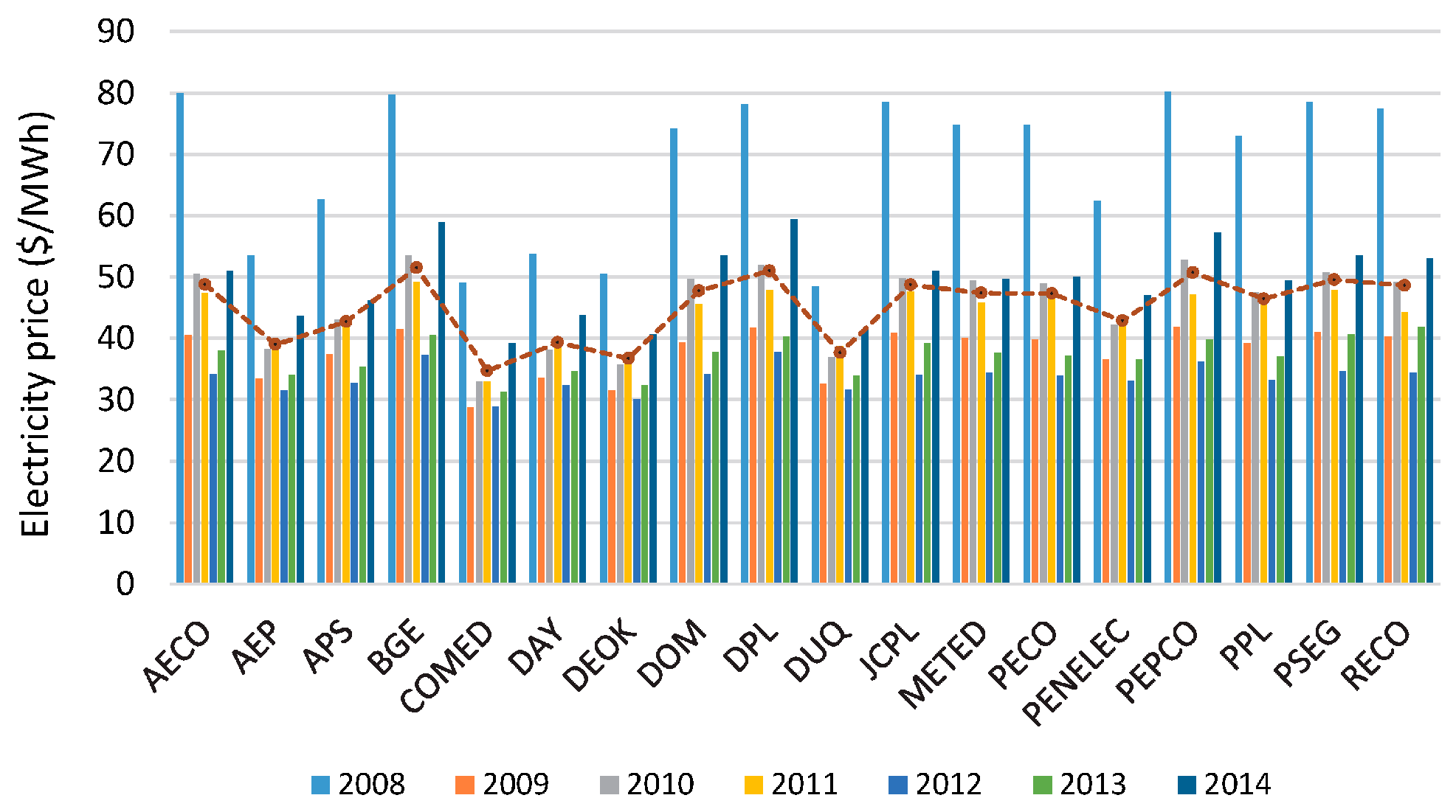
The nodal prices varied in time and location in wholesale markets based on LMP. Observation of the PJM price profile across time and location was important for understanding when and where the potential revenue could be captured. Figure 12 shows the average price of electricity in 18 PJM zones (zones ATSI and Duke joined PJM in 2011 and are not analyzed in this paper). The dotted line represents the average per zone in the period.

The COMED and BGE zones were observed to have the lowest (34.74 $/MWh) and the highest (51.53 $/MWh) prices, respectively. The high prices of natural gas in 2008 (Figure 9) had moderate impact in the COMED, DEOK, DUQ zones. Another interesting point was that the impact of extreme weather in the early 2014 was stronger in the BGE and DPL zones.

3. Potential Arbitrage Revenue in RTM

PJM is one the most engaged RTOs in the United States in stimulating the use of ESS at utility scale [15]. Considering electrochemical ESS, there are already 123 MW of power capacity (14 units over 1 MW) in operation in PJM and 28 MW in CAISO (California Independent System Operator) [3]. The installed ESSs in CAISO have more hours of discharge duration at rated power capacity than in PJM, but no electrochemical ESS is used exclusively for energy arbitrage to provide revenue.

In CAISO, there is one multiple-purpose project (the Tehachapi Wind Energy Storage Project), which also aims to verify the energy arbitrage potential [3]. However, no report of a real energy arbitrage operation has been found, except for a report regarding a simulation for Tehachapi [16]. The battery technology of the Tehachapi project is provided by the A123 Systems (Lithium-ion, 8 MW, 32 MWh, 4 h, 80% round trip efficiency) [3,16]. They have found that for the DAM, the potential revenue with perfect forecast (i.e., maximum theoretical values) for 2010 and 2011 are $198,330 and $331,992, respectively [16].

3.1. Generic ESS Model

A generic linear optimization model of price-taking ESS was adopted, considering a perfect forecast of a year of hourly-based price data to maximize arbitrage revenue, as presented in [5]. The energy arbitrage model in [5] describes a perfect foresight analysis of optimal storage policy. The price-taking model assumes that the individual storage facility has no impact on the equilibrium price outcomes. Equation (1), presented below, represents the implemented model:

$$\begin{array}{l}\underset{c,d,s}{Max}{\displaystyle \sum _{t=1}^T{p}_t\left(d_t-c_t\right)}\\ s_t=s_{t-1}+\eta c_t-d_t\\ d_t,c_t\in \left[0,\kappa \right]\\ s_t\in \left[0,h\kappa \right]\end{array},$$

(1)

where T: number of hours in dispatch horizon, p_t: energy price in hour t, κ: power capacity of storage device, h: number of hours of discharge at rated power, d_t: discharge power in hour t of storage device, c_t: charge power in hour t of storage device, $s_t$: state of charge in hour t of storage device, η: round trip efficiency of storage device.

Application of this model provided preliminary estimates of the net revenues that would be accrued through price arbitrage. The optimal solution always had charging and discharging at either zero or the maximum power rate.

The choice of a round trip efficiency of 95% was taken to represent a forward-looking upper limit of revenue for highly efficient ESS technologies; sensitivity to efficiency is presented in Section 4.1. Direct current/alternating current (DC/AC) conversion efficiencies are improving, and new storage technologies (for example some Li-ion batteries, flywheels and supercapacitors) can have such high efficiency [4]. Without loss of generality, the maximum power capacity of charge and discharge was selected to be 1 MW for all analyses. The energy capacity of the ESS for the base case was 10 MWh, and we varied it from 1 to up to, in some analyses, 14 MWh.

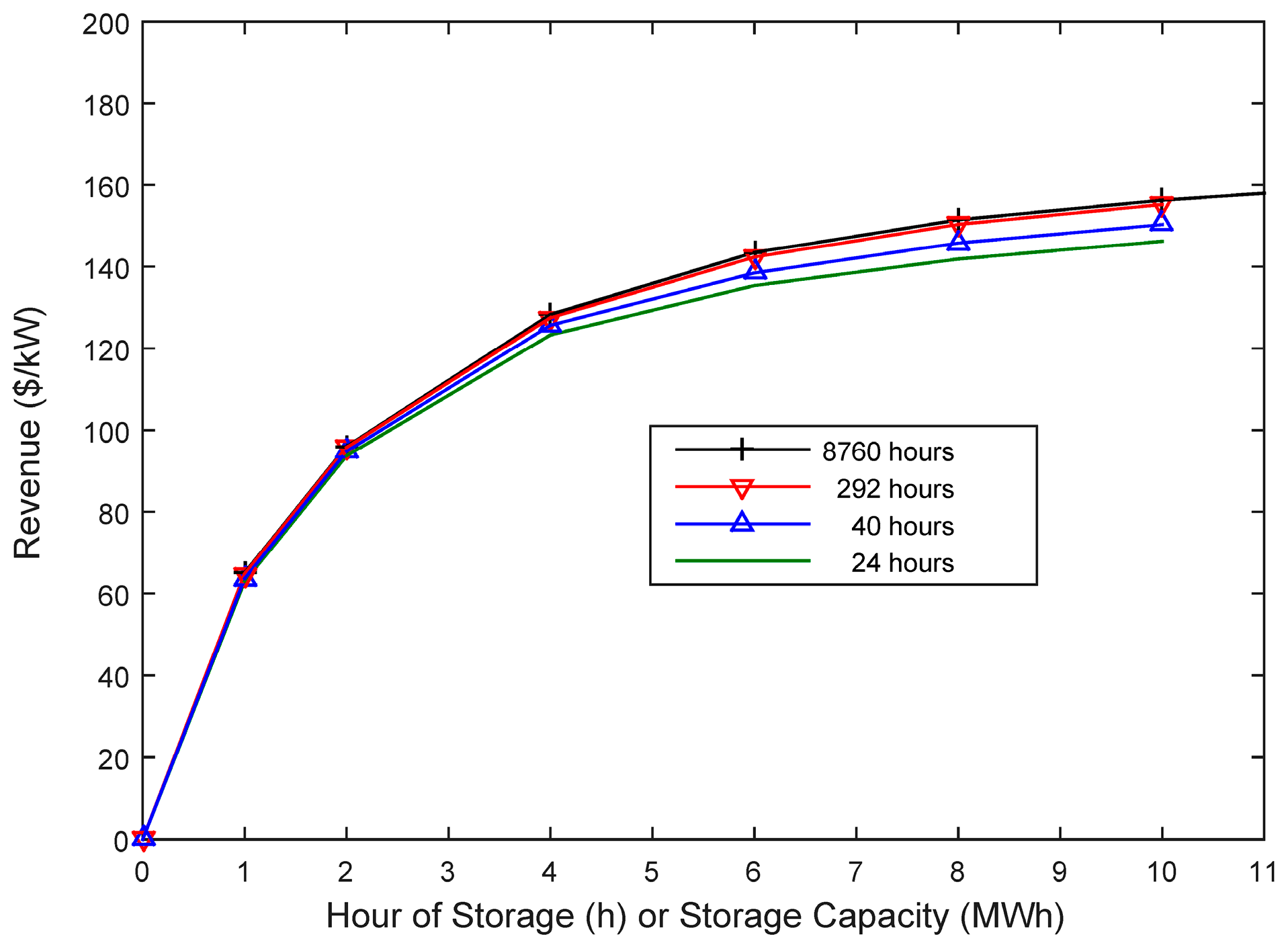
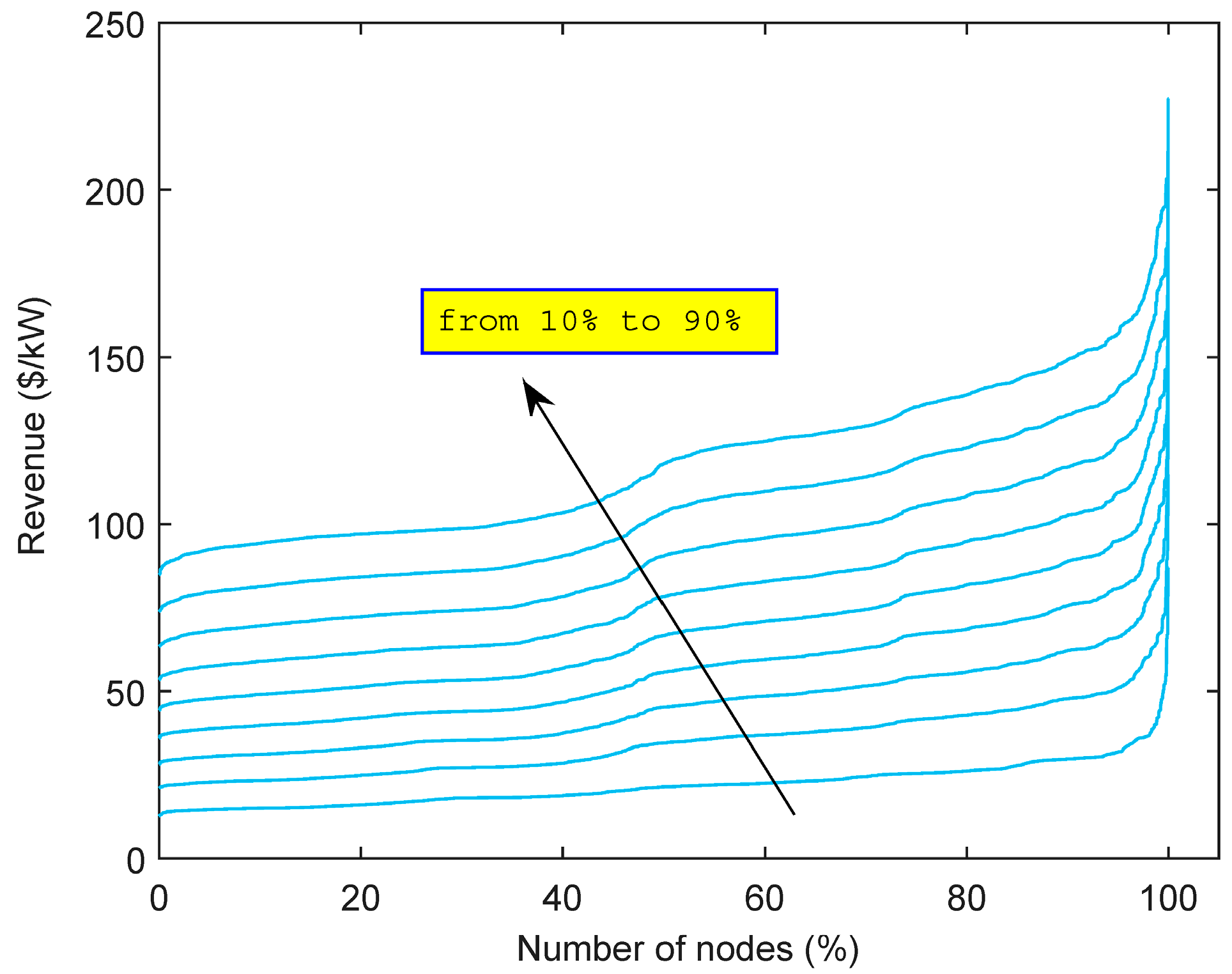
Figure 13 shows the dependence of annual arbitrage revenue per kW of power capacity on energy/power ratio for a selected node with high price standard deviation. It also shows the lack of sensitivity of the result, for this particular node, to the period of perfect forecasting.

The perfect forecast considering the simulation period of 24 h (365 simulations/year) for 10 MWh captured only 6.4% less than for the period of 8760 h (one simulation/year), and for 4 MWh captured only 3.2% less than for one simulation/year. Figure 13 also shows the diminishing returns of increasing the energy/power ratio.

3.2. The Energy Arbitrage Revenue in PJM

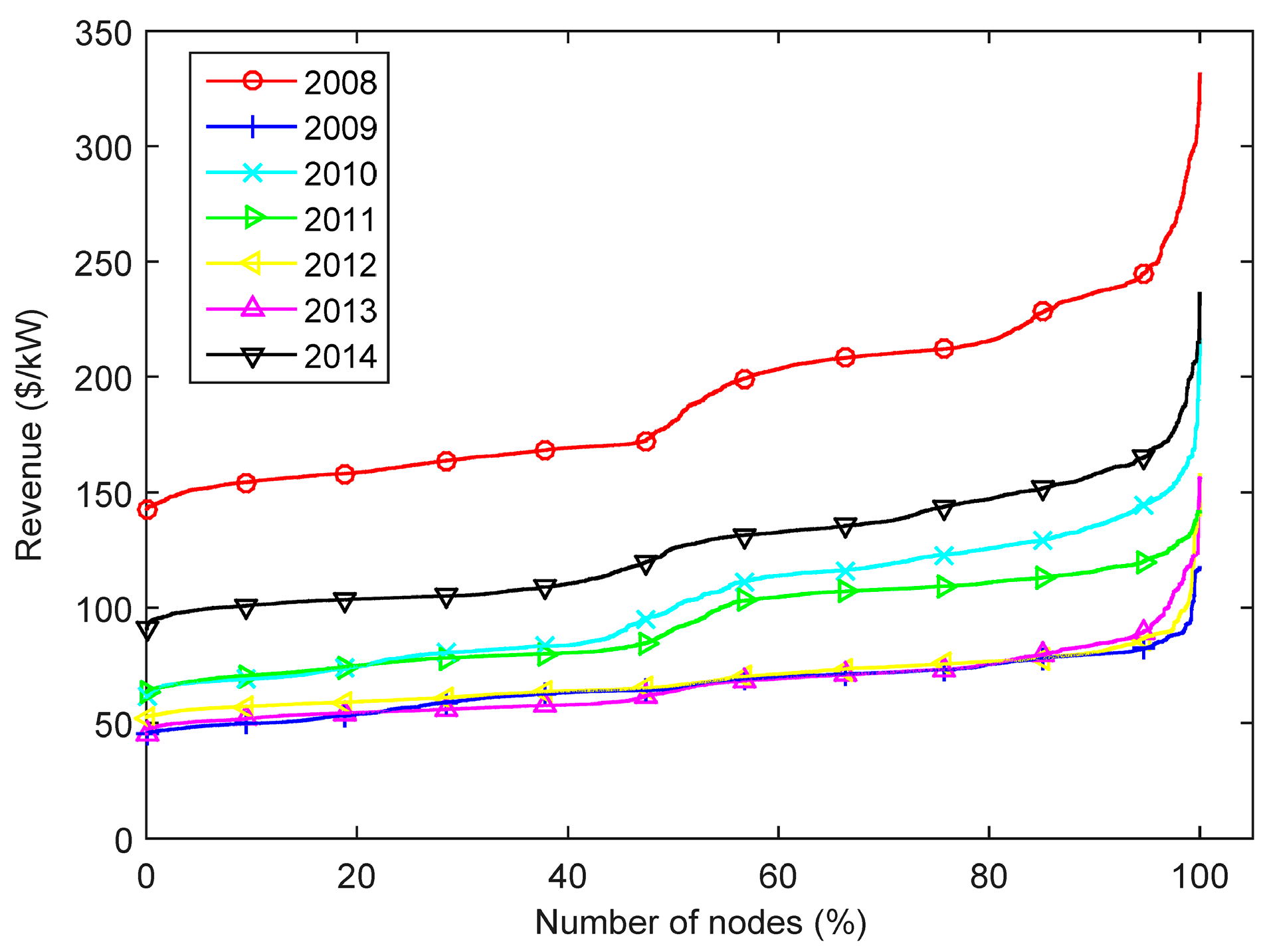
The potential arbitrage revenue of an ESS using a yearly-based perfect forecast in the PJM RTM for the period of 2008 to 2014 is presented in Figure 14. It shows that the highest potential revenue occurred in 2008, followed by 2014. Considering the presented yearly-based standard deviation and average price curves, the potential revenue has a strong correlation with high average electricity prices (as shown for 2008 and recently found in [17]) and a weaker correlation with high standard deviation (as shown for 2014 in Figure 5).

The potential arbitrage revenue for different energy/power ratios in 2008 is shown in Figure 15. The potential revenue presents very small increments for energy/power ratio above 10 h. This pattern is similar to 2014, as presented in [18], with small differences in the higher potential revenue nodes.

3.3. Seasonality of Revenue in PJM

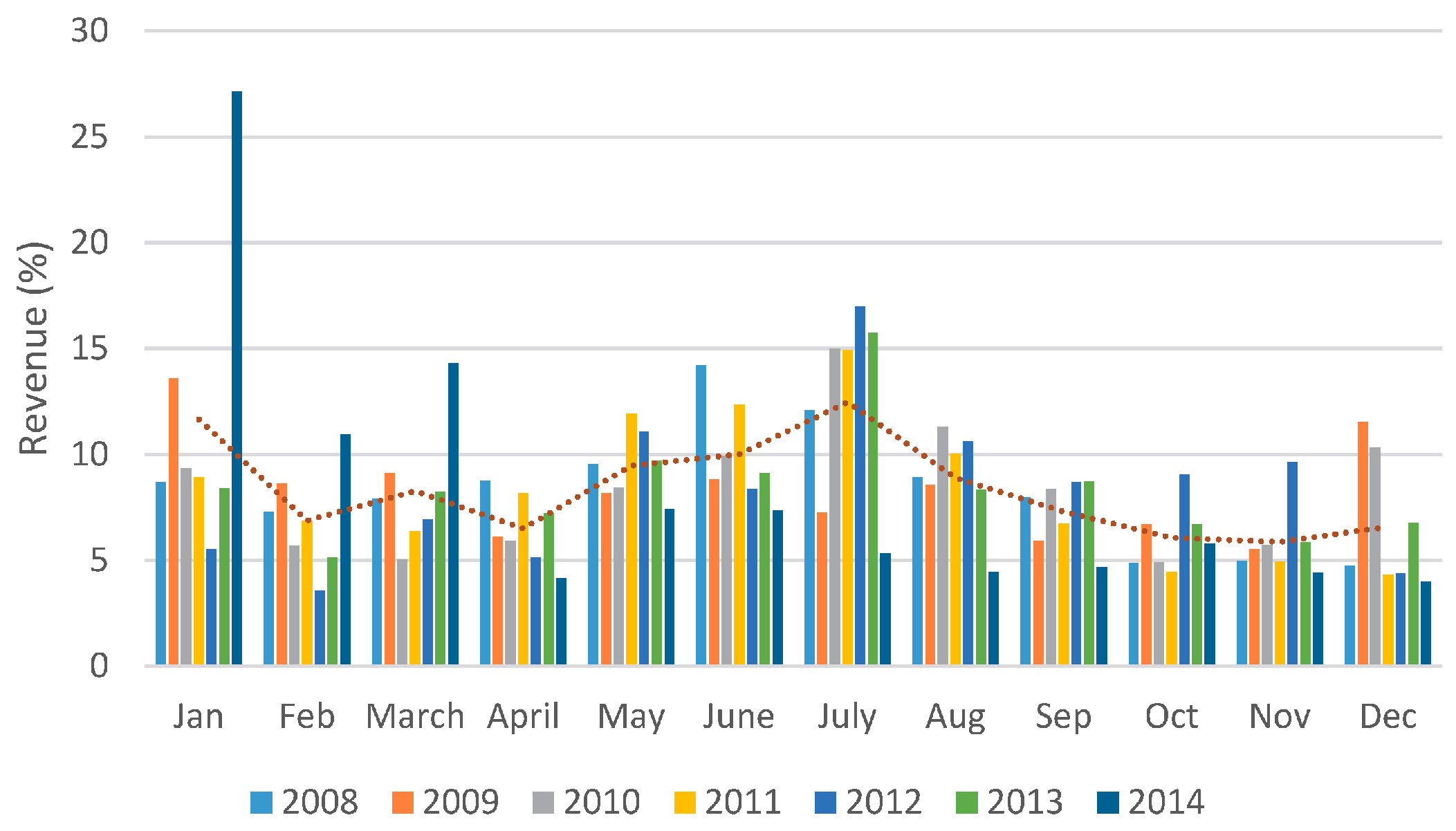
The average revenue was evaluated to investigate the monthly distribution for a 1 MW/5 MWh ESS. Figure 16 shows the percentage normalized per year. June and July are very important months for revenue capture. In 2014, the potential revenue was higher still for the first two months of the year. The cold weather in the beginning of 2014 (between 1 January and 28 February) was probably responsible for 38% of the year’s total revenue. Recently, a similar finding has also been reported by McConnell et al. [19]. The ESS would provide an analogous service to peak generators and would also depend on extreme price events for a significant amount of its revenue. In 2008, the highest revenue occurred in June and July; during this two-month period the ESS would have captured 26% of the year’s total.

Figure 14 and Figure 16 shows two different profiles for the best two years of potential arbitrage revenue: concentrated in few months (2014) or distributed along the year (2008). The dotted line for the monthly average over the years in Figure 16 showed that the three best months to explore the potential of arbitrage revenue are January, June and July.

3.4. Spatial Distribution of Revenue Across Locations

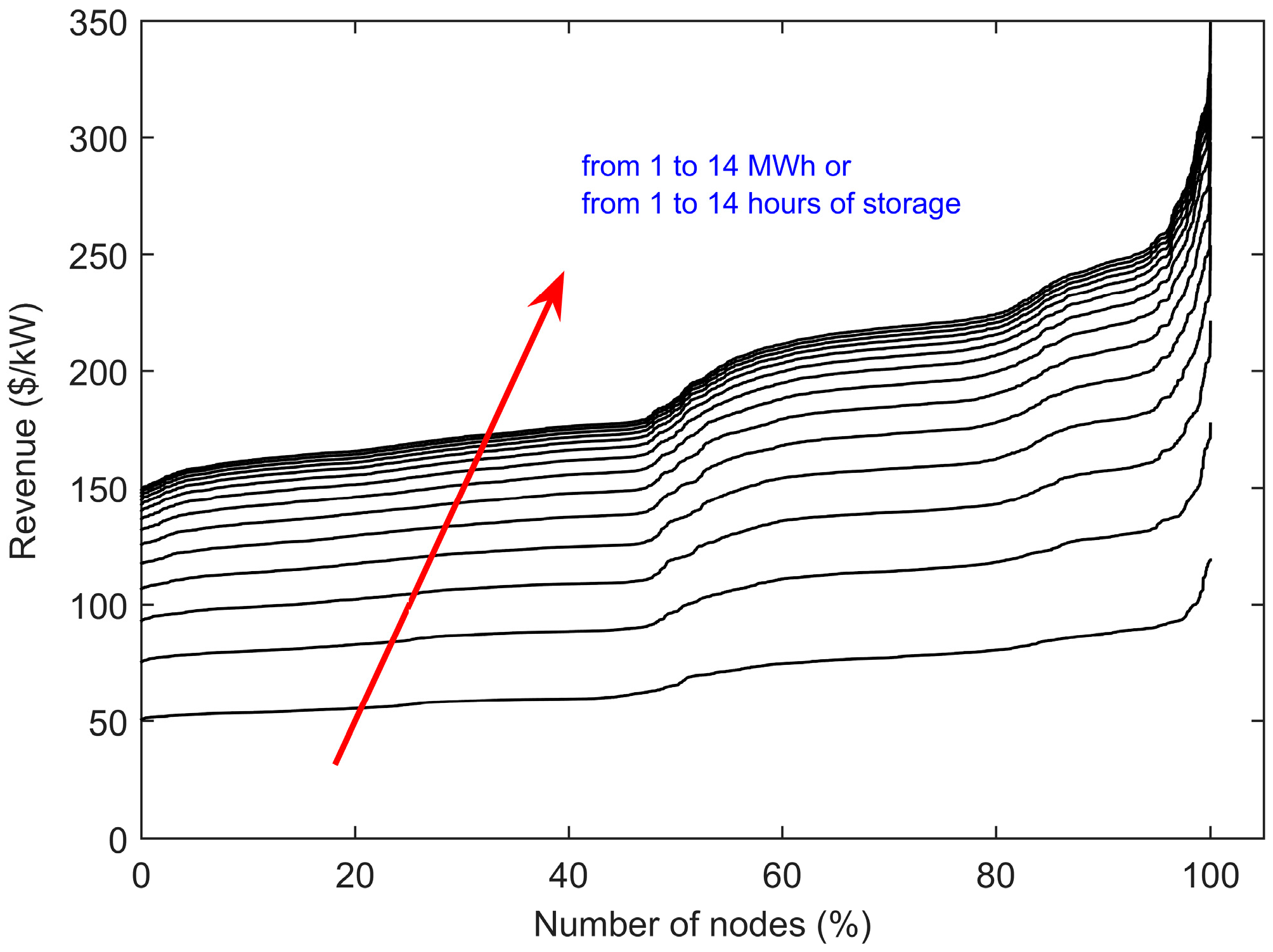
The potential revenue presented in Figure 14 is reorganized to include location information, using node zip codes obtained from the PJM website. Figure 17 and Figure 18 show, respectively, revenue for 2008 and 2014 across locations. The color scale is normalized to the maximum revenue of each year.

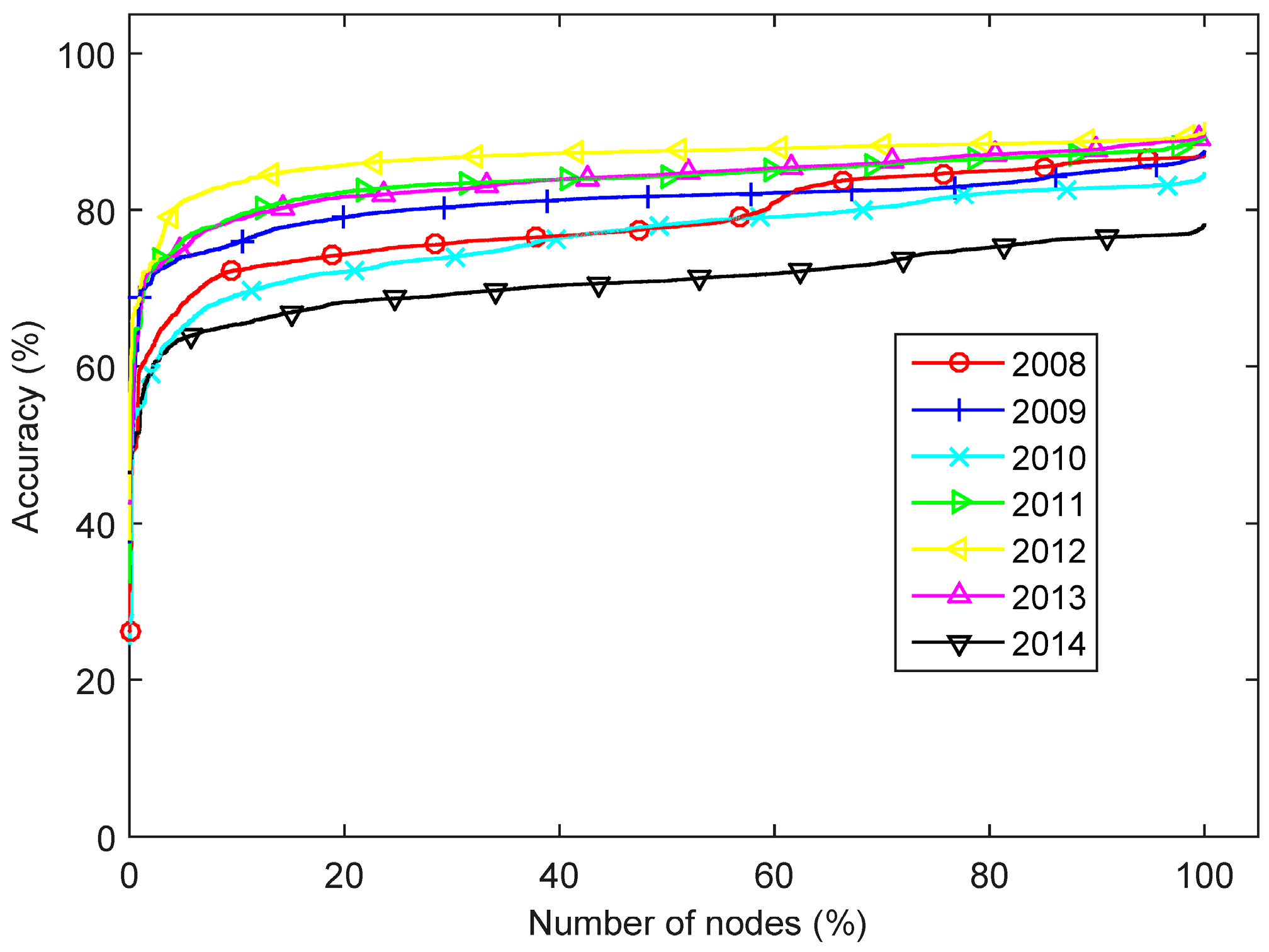
From these figures, it was apparent that the best arbitrage opportunities were not always at the same nodes. We selected the best (highest) potential revenue nodes in 2008 and categorized them in percentage groups of the best 5%, 10% and 20%. We followed them across the seven years and we found that only 19 nodes stayed in the same group of 5%, 185 nodes stayed in the best 10% and 577 nodes stayed in the best 20%.

4. Arbitrage Revenue in RTM and DAM

The price volatility in the RTM was higher than in the DAM. This fact reflected generator or transmission line outages, generator bid strategies, changes in energy demand, and transmission line congestion; however, daily average prices in RTM and DAM did not vary as much. The price volatility is the reason why the potential arbitrage revenue was higher in the RTM than in the DAM, as reported for PJM in [18].

4.1. Sensitivity to Round Trip Efficiency for Dispatching in RTM

The round trip efficiency of 95% meant that in each 10 h of charge, one may have 9.5 h of discharge, both at rated power. We analyzed the sensitivity to round trip efficiency in order to quantify the decrease in potential revenue when efficiency decreases, using the data from 2014 in RTM for a 10 MWh energy capacity device (Figure 19). At the upper end of the efficiency range, the potential revenue was nearly proportional to efficiency at most of the nodes. Reference [8] previously found a proportionality relationship between revenue and efficiency using different data.

4.2. Additional Arbitrage Revenue in RTM

The additional arbitrage revenue in RTM compared to DAM, both assuming perfect foresight, depended on the energy/power ratio as shown in Figure 20. The price profile during the year also influenced the potential revenue.

Figure 20 shows that the percentage of extra revenue gained in RTM compared to DAM decreased as discharge duration increases. Figure 20 shows that for 2008 (solid line) the additional revenue was higher for the best 55% of the nodes (abscissa from 45% to 100%) for 1, 2 and 3 MWh of energy capacity. Significantly higher additional revenue can be captured more likely in the best 5% of the nodes (abscissa from 95% to 100%) in RTM for 2008 and 2014 compared to the other 95% of the nodes (abscissa from 0% to 95%). This reflects that short-duration fluctuations are more frequent than long-duration fluctuations in the RTM.

As a general rule, an increment on the energy capacity of the ESS decreases the percentage of additional revenue that could be captured in the RTM relative to the DAM; however, the absolute revenue is higher for greater energy capacity. The starting points of the curves in Figure 20 showed that there was at least 20% additional potential revenue in RTM for a 10 MWh ESS (the magenta line) and around 50% more for a 3 MWh ESS (blue line).

4.3. Price Forecast Impact on Arbitrage in RTM

The use of historical price data has been often used in ESS optimal dispatch analysis as an upper bound [7,8,16,17,18,19,20,21,22]. This kind of analysis gives an indication of the theoretical value of storage. Simple forecasting methods have been proposed to represent the imperfections of guessing the price in advance for the DAM. McConnell et al. [19] achieved 85% of perfect-foresight revenue using pre-dispatch prices from the AEMO (Australian Energy Market Operator) available a day ahead of time for six hours of storage. Sioshansi et al. [5] evaluates the use of the PJM historic prices (from 2002 to 2007) of the previous two weeks for 12 h of storage, achieving values from 84% to almost 90% of perfect-foresight-in-DAM values (depending on the year). Analogous results have been also reported recently in [17,20,21].

Our approach was similar to the above; however, we applied a method that can capture the equivalent of more than 100% of the potential revenue opportunities in the DAM. It would be an easy matter to exactly capture the DAM price arbitrage schedule, such as by dispatching in real-time optimally for the known DAM prices, which would be feasible under the PJM market definition. By contrast, capturing the deviations embodied in the real-time market prices presents a high payoff but a greater challenge in optimizing the storage profile. Bidding in the RTM presents more risk and this market has higher volatility compared to the DAM. The locational marginal prices on a day-ahead basis could be easily taken after the DAM settlement. The dispatch resulting from the linear optimization analysis for the DAM for the next day could be applied directly to dispatching in the RTM in real time. This approach can capture a portion of the additional revenue appearing in Figure 20. Figure 21 shows the evaluated accuracy of the dispatch using the proposed method, expressed as a percentage of the revenue from a perfect forecast of the prices in the RTM itself. The best performance of the proposed forecast was achieved for 2012; however, a similar accuracy was achieved for 2009, 2011 and 2013. The worst performance of the forecasting method was reached for 2014. The accuracy for 2008 was among the highest for 40% of the nodes.

Figure 22 shows another way to look at the same results presented in Figure 20. The curves presented in Figure 22 show the potential revenue in the RTM using DAM settlement prices as forecast for optimizing dispatch, divided by the potential revenue in the DAM with perfect forecast. Most of the nodes reached more than 100% of the theoretical arbitrage opportunity in the DAM. The exception is 2014, during which the method slightly underperforms participation in the DAM.

This feasible forecast method allowed the ESS owner to capture more revenue opportunities than are provided in the DAM. However, a more sophisticated forecast method may be necessary to deal with scarcity and high price spikes during extreme weather conditions (as in 2014).

5. Breakeven Overnight Installed Cost

We analyzed the breakeven overnight installed cost [23] of an ESS using the PJM net revenue analysis described above for the various years and locations. The adopted approach is to derive the net installed costs (after taxes and depreciation) to obtain an annualized capital recovery factor (CRF) that would return the present value of the investment over the life of the project. This capital recovery factor can be compared with the net revenues based on the project storage profile [24].

The PJM revenue data applied to the price arbitrage model of storage economics is based on several input assumptions. Although the approach is independent of the particular ESS technology deployed, parameter values will differ from one technology to another. We choose parameter values anticipated to characterize a future-state mature flow battery technology, rather than any current technology, because the latter are too costly for immediate implementation. The total life of a new ESS is uncertain. The analysis in [25] assumes 20-year life for flow batteries. A range of battery technologies analyzed in [8] have lifetimes of 5–15 years. Here we considered a 20-year project life. The basic application assumed no long-term policy support such as through special subsidies. The Net Operating Revenue Before Corporate Taxes (NR) was equal to the PJM net revenue analysis for the various years and locations. Hence, the energy purchase costs, round trip losses, and pricing assumptions followed the various sensitivity cases for the net revenues.

Typically, the annual Fixed Operating and Maintenance Cost (OM) (ν) is assumed to be very small for large scale flow based batteries. For example, reference [25] adopts a range from 0.9% to 3% of the initial capital costs. The present calculations use 2%. The assumptions for tax rates and related financial parameters come from the analysis of the Energy Information Administration for the Annual Energy Outlook [26]. All quantities are in real terms except where specified:

i = Nominal corporate borrowing rate = 7.1%

τ = Corporate tax rate = 38%

d = Share of investment financed by debt = 45%

E = Risk adjusted real return on equity = 9.3%

π = Expected inflation rate = 2.0%

The Real Corporate Discount Rate ($\tilde{r}$) can be calculated as in Equation (2):

$$\tilde{r}=d\left(i\left(1-\tau \right)-\pi \right)+\left(1-d\right)E$$

(2)

Tax Depreciation (D) requires separate treatment for each year. The IRS (Internal Revenue Service) applies different rules for deprecation of capital expenditures, accessed in Table 4-1 for Modified Accelerated Cost Recovery System (MACRS) in [27]. The depreciation rate applies to the nominal capital values. Hence, the real capital depreciation must be discounted by the anticipated inflation rate. We assume in our analysis 7-year depreciation, as suggested in [25]. The base case assumption for storage is no investment tax credit (ITC), i.e., ${\rho }_{ITC}=0\%$.

Here, with no ITC, the full investment is subject to depreciation deductions. With these elements of the model, for given net revenue (NR), assumed constant in real terms over the life of the facility (N) in years, the resulting breakeven overnight installed cost (CC) satisfies Equation (3):

$$CC={\rho }_{ITC}CC+{\displaystyle \sum _{t=1}^N\frac{\left(NR-\nu CC\right)\left(1-\tau \right)+\frac{{\delta }_t^{MACRS}}{{\left(1+\pi \right)}^t}CC\tau }{{\left(1+\tilde{r}\right)}^t}}$$

(3)

The implied tax Adjusted Capital Recovery Factor (ACRF) is presented in Equation (4):

$$\begin{array}{l}ACRF=\frac{NR}{CC}=\frac{1-{\rho }_{ITC}+\nu \left(1-\tau \right){\displaystyle \sum _{t=1}^N\frac{1}{{\left(1+\tilde{r}\right)}^t}-\tau {\displaystyle \sum _{t=1}^N\frac{{\delta }_t^{MACRS}}{{\left(1+\tilde{r}\right)}^t{\left(1+\pi \right)}^t}}}}{{\displaystyle \sum _{t=1}^N\frac{1}{{\left(1+\tilde{r}\right)}^t}}}\\ =\frac{\tilde{r}{\left(1+\tilde{r}\right)}^N}{{\left(1+\tilde{r}\right)}^N-1}\left[1-{\rho }_{ITC}-\tau {\displaystyle \sum _{t=1}^N\frac{{\delta }_t^{MACRS}}{{\left(1+\tilde{r}\right)}^t{\left(1+\pi \right)}^t}}\right]+\nu \left(1-\tau \right)\end{array}$$

(4)

Under the base case assumptions of 0% ITC, a 20-year project life and a 15-year tax depreciation life, the Adjusted Capital Recovery Factor is equal to 8.66%. Applying this capital recovery rate to data in the PJM net revenue analysis produces the implied breakeven installed cost. For a flow battery, the cost is a linear combination of the marginal cost per unit power capacity and the marginal cost per unit energy capacity. To simplify the comparison with other storage systems, the total requirement is converted to (total system cost)/(total energy capacity) in $/kWh.

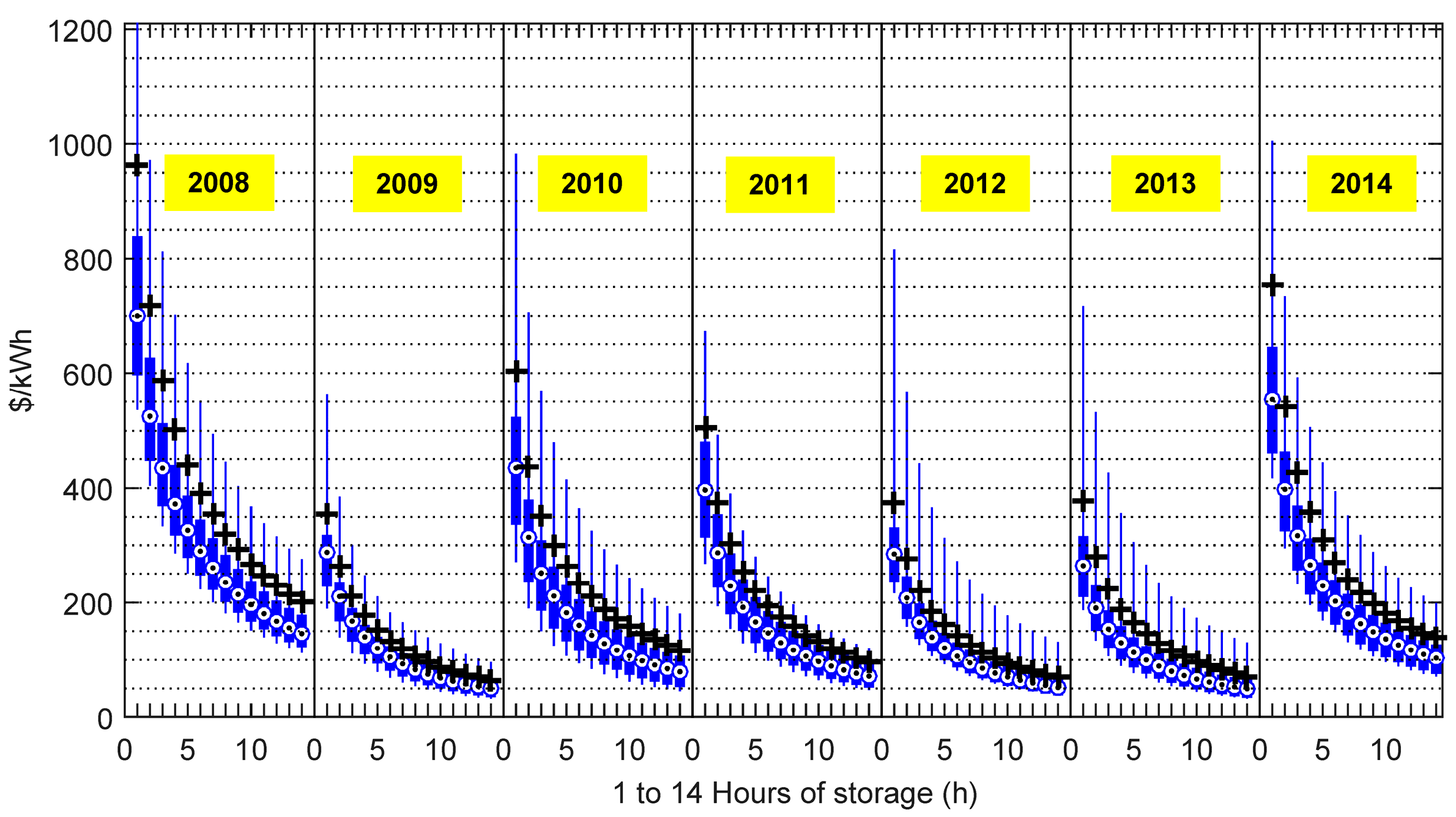
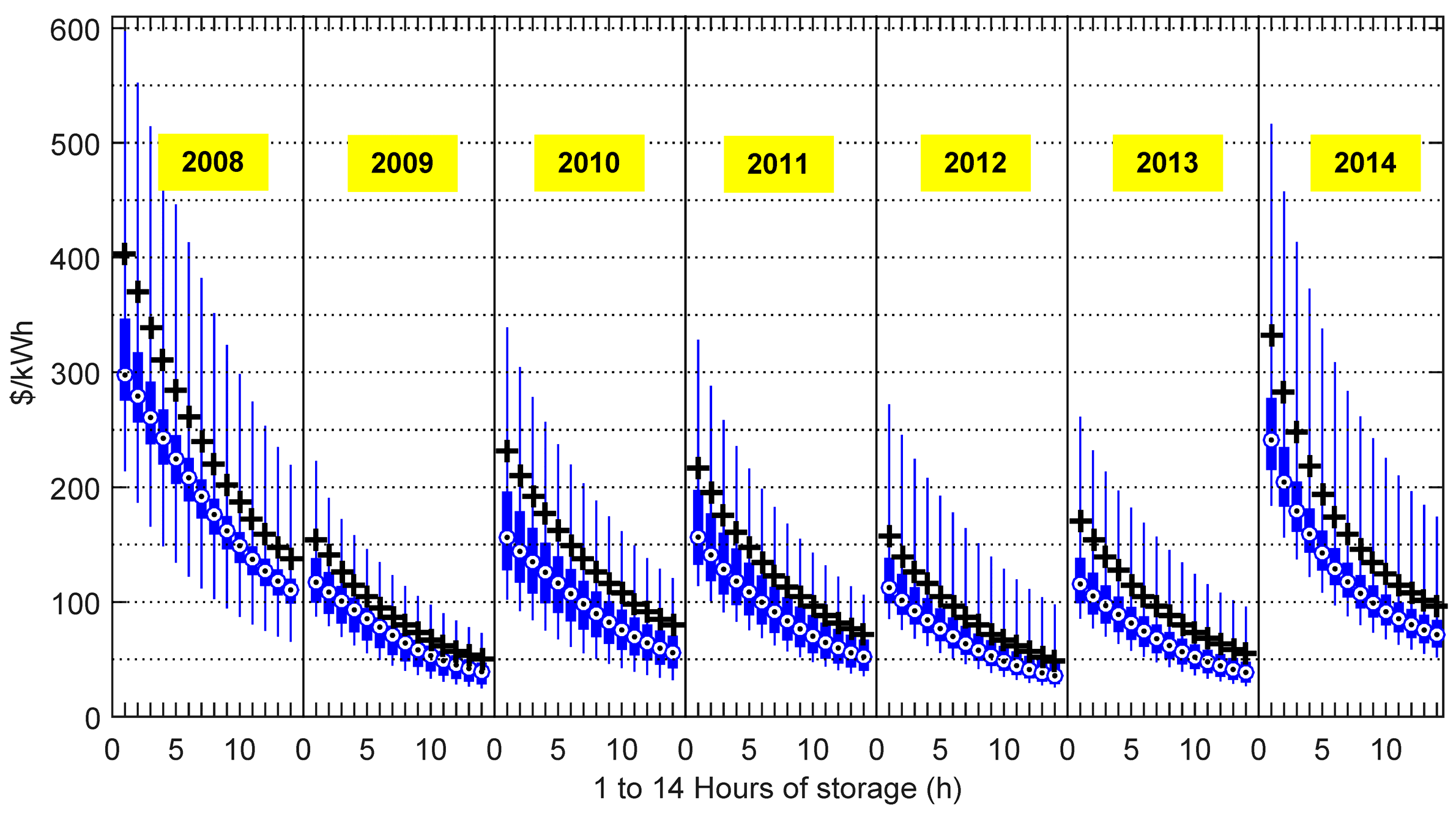
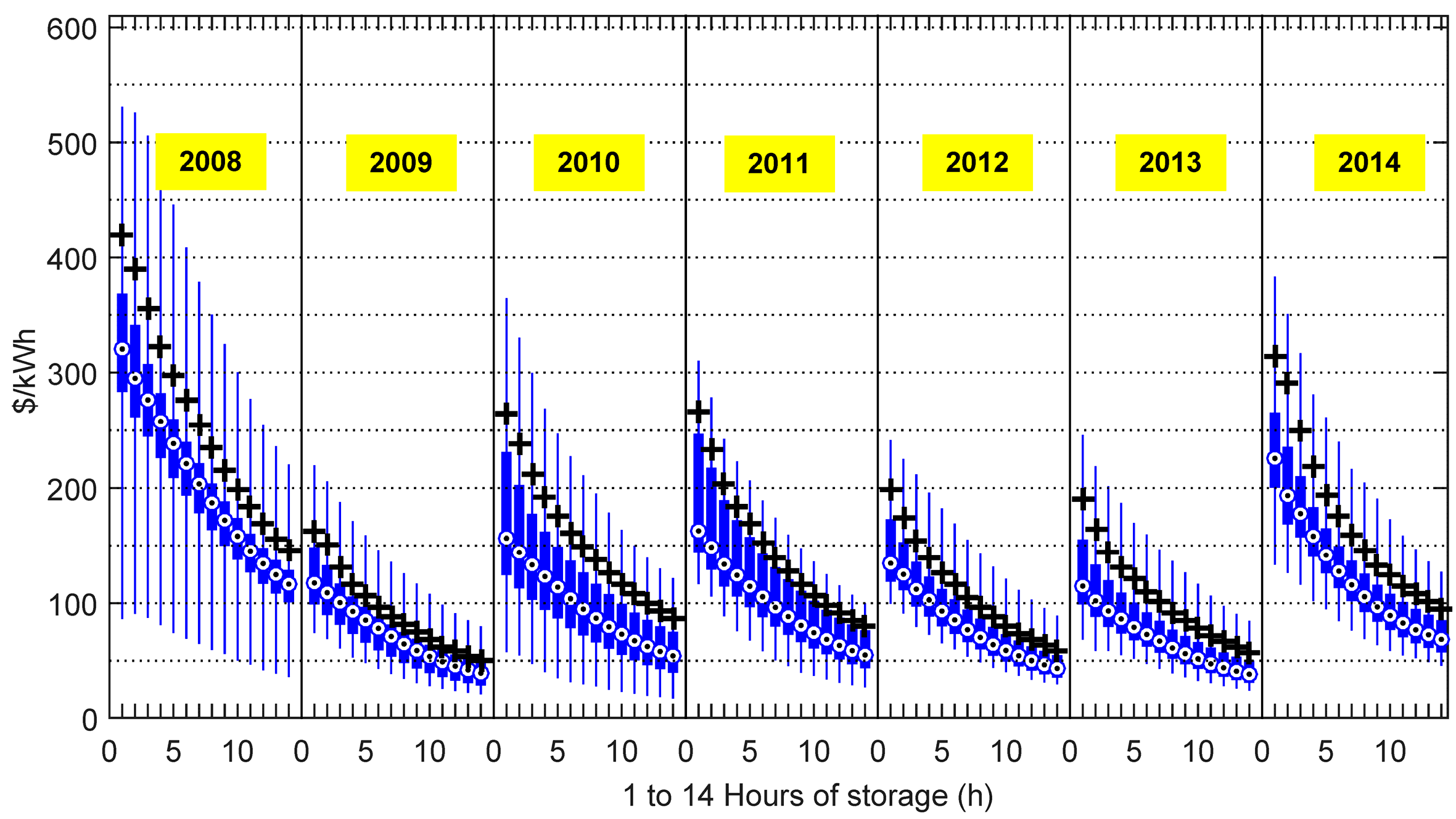
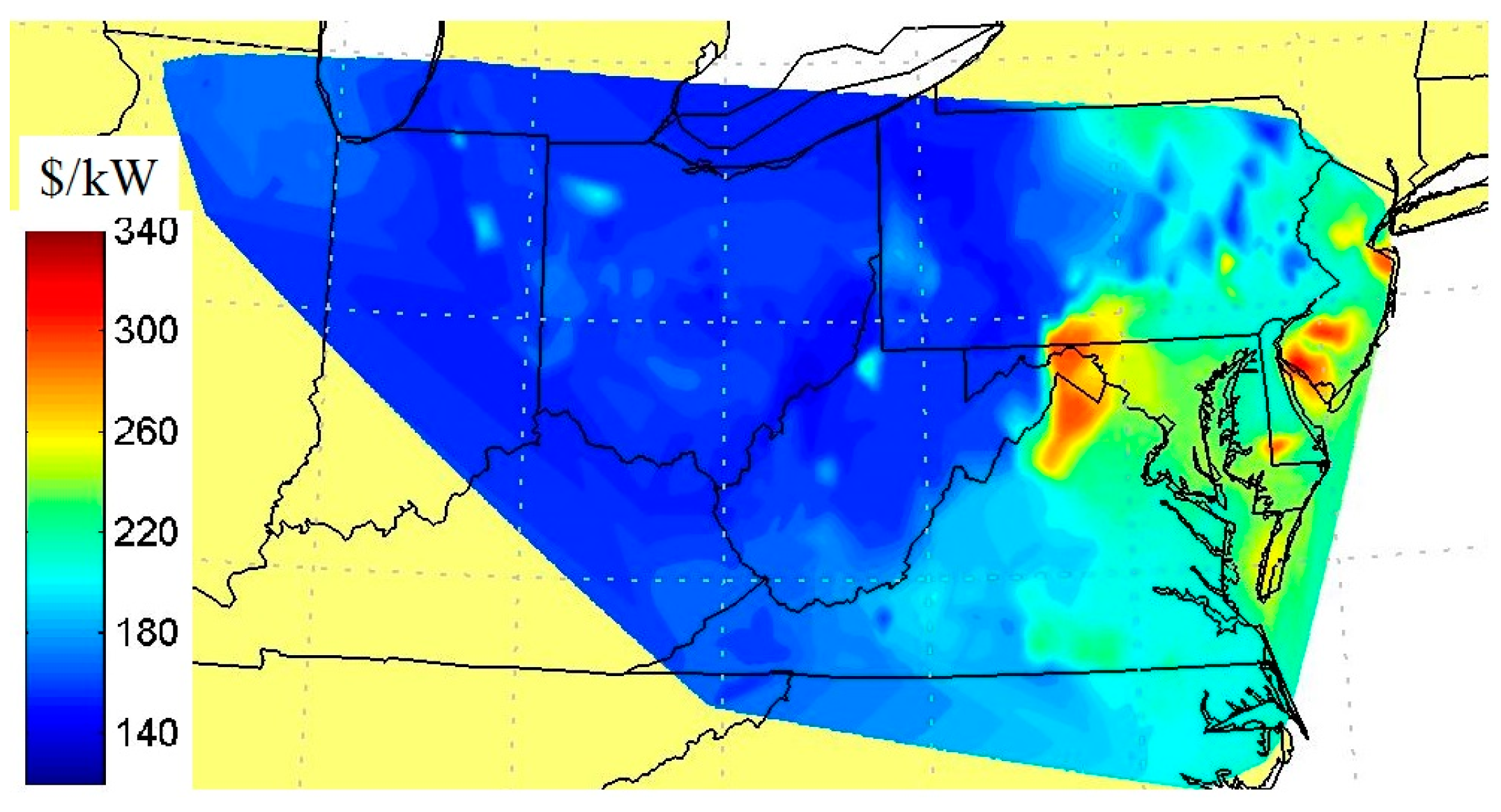
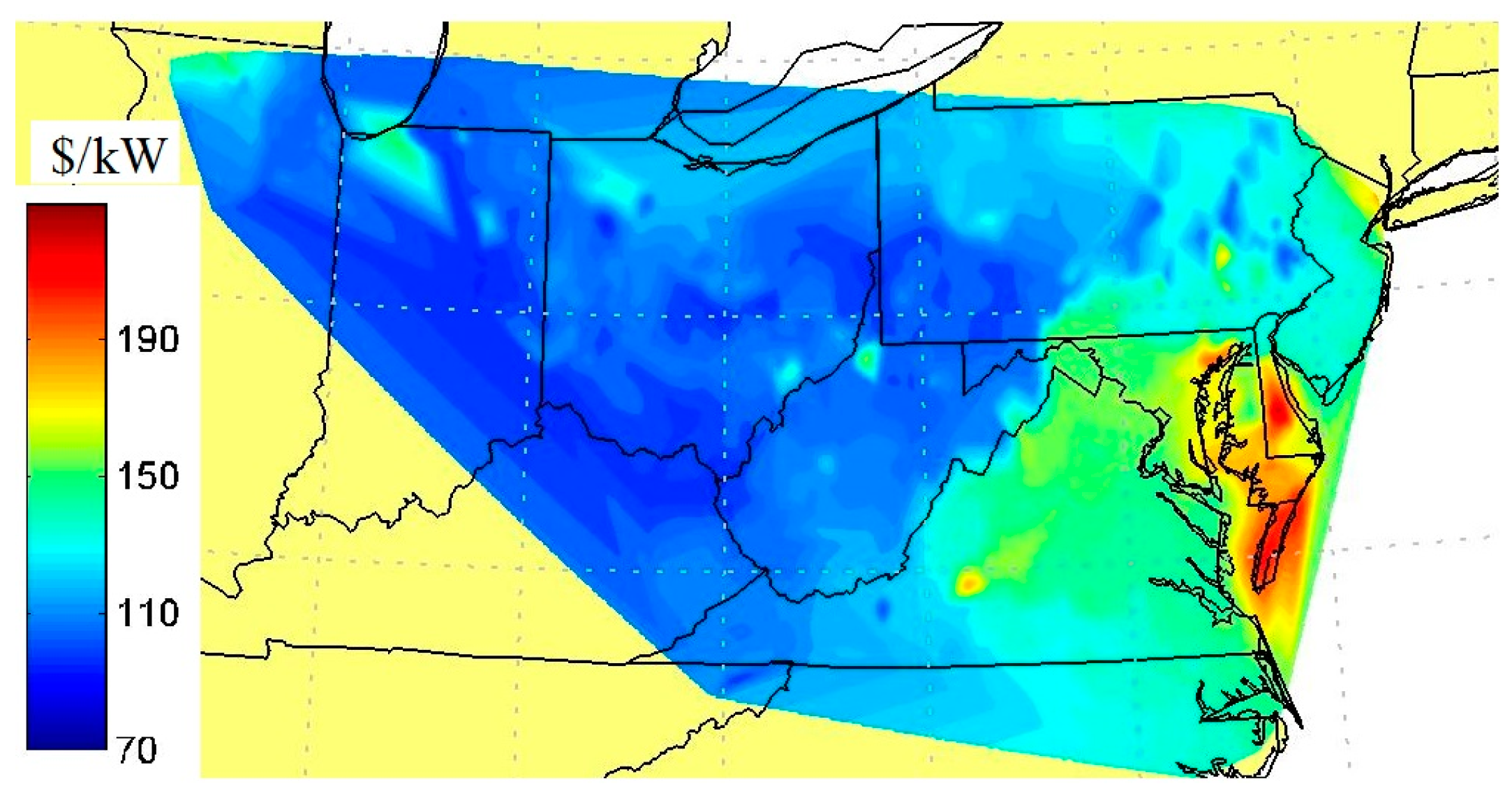
We performed the analysis for an ESS with perfect forecast, 90% round trip efficiency, and 20-year project life for Real-time (Figure 23) and Day-ahead (Figure 24) Markets. The distribution of breakeven costs, spanned by the thin vertical bars, was dependent on discharge duration and year. The 95th percentile of the nodes, by revenue, are marked by the black crosses, which indicate the installed cost below which ESS penetration into the grid would first become very significant. The 50th percentile of the nodes are marked by the circles, which indicated the installed cost below which ESS penetration might be entirely transformative. This latter statement is only qualitative because by the time this level of penetration is reached, the price-taking assumption would certainly have broken down. The assumption of perfect forecast in the RT-market implied an upper limit on the breakeven cost, and the assumption of perfect forecast in the DA-market implied a lower limit on the breakeven cost.

An additional analysis, performed using DA prices as a forecast for dispatch into the RT-Market, is presented in Figure 25. These breakeven overnight installed costs are somewhat higher than those in the DA-Market.

All ESS installed costs are currently higher than the breakeven costs indicated by Figure 25 for the vast majority of nodes, and thus the current opportunities for profitability are extremely limited. However, ESS costs are falling and are anticipated to fall significantly farther, bringing an increasing percentage of nodes into profitability over time.

All of Figure 23, Figure 24 and Figure 25 indicate rapidly declining ESS breakeven cost/kWh with increasing energy/power ratio. This trend reflects the diminishing returns in revenue/kWh with increasing discharge duration, as fewer occasions arise requiring full discharge without the opportunity for interspersed periods of recharging. Nevertheless, the actual cost of flow batteries drops markedly with increasing discharge duration. Thus, further study is required to determine the discharge durations at which the cost of a flow battery installation might first penetrate into the range of breakeven costs such as those shown in these figures.

Future works on this topic should consider detailed ESS dispatch models, including bids for each five minute period in RTM [28], to determine the extent to which increased temporal granularity can achieve higher values of revenue. An optimal bidding strategy across both DAM and RTM could also be attractive when both choices are available to the same optimization process [29,30]. Finally, the participation in the frequency regulation market as an addition to the energy arbitrage market should also increase the revenues [31].

6. Conclusions

This paper has analyzed the potential arbitrage revenue of energy storage systems in PJM day-ahead and real-time markets from 2008 to 2014 for all 7395 locations for which complete hourly LMP data are available. The opportunity for energy arbitrage through storage arises from the scale of the energy market and the volatility of prices. The potential revenue generated by a 1-MW system with various energy/power ratios was determined as the solution of an optimization problem assuming perfect foresight. Perfect foresight represents an upper limit to arbitrage revenue in the RTM and represents essentially a lower limit to revenue in the DAM.

The main characteristics of the best nodes to install an ESS were verified through the presented analysis. They were: high average prices, periods of high price volatility, and high forecast accuracy to exploit spikes in the RTM. Increasing the discharge duration at rated power increases the potential revenue per kW of power capacity, but returns diminish rapidly after 4–6 h of discharge duration at rated power. Net revenue is approximately proportional to round-trip energy efficiency for the upper portion of the range of energy efficiencies, as shown in Figure 19.

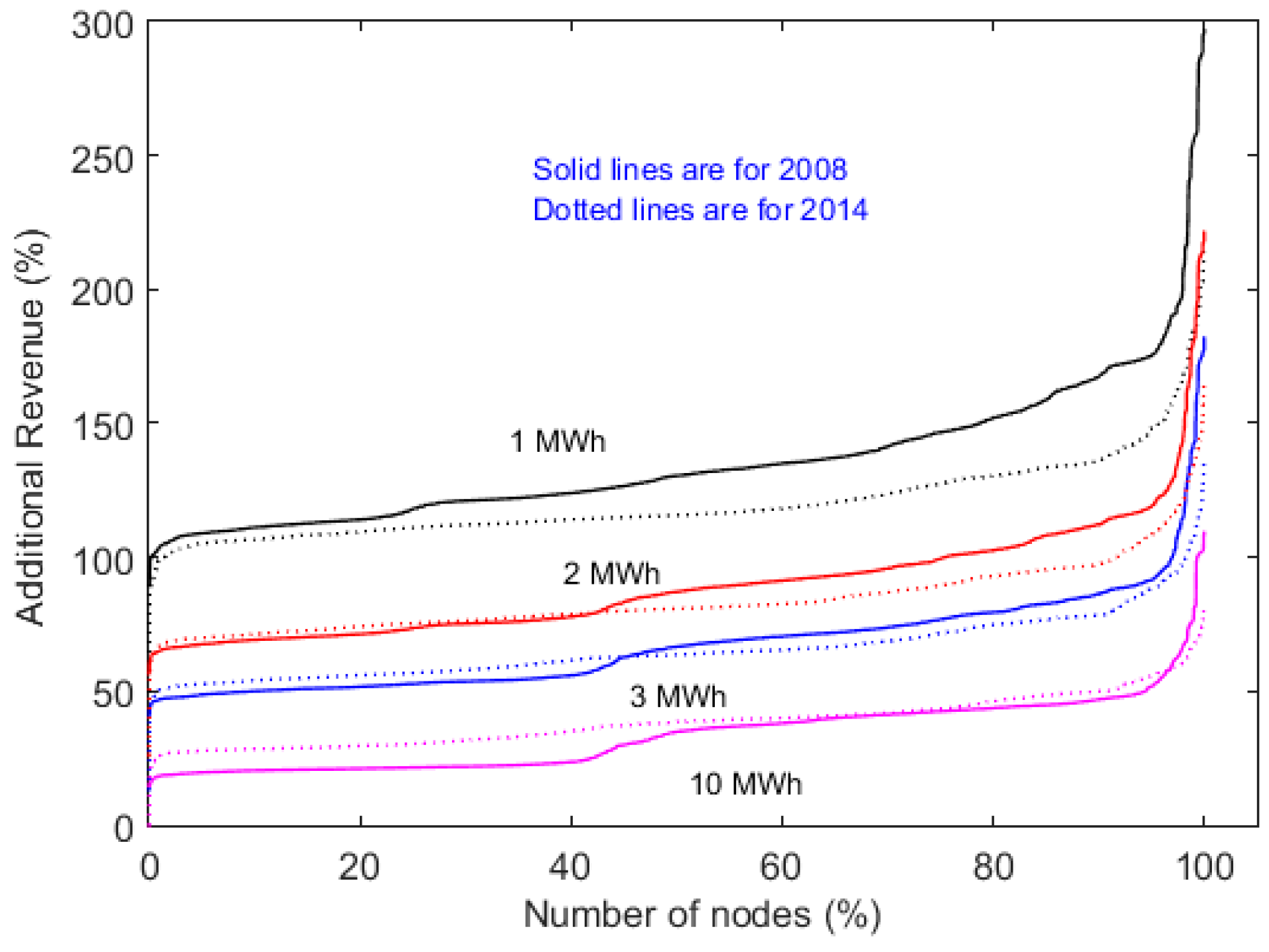
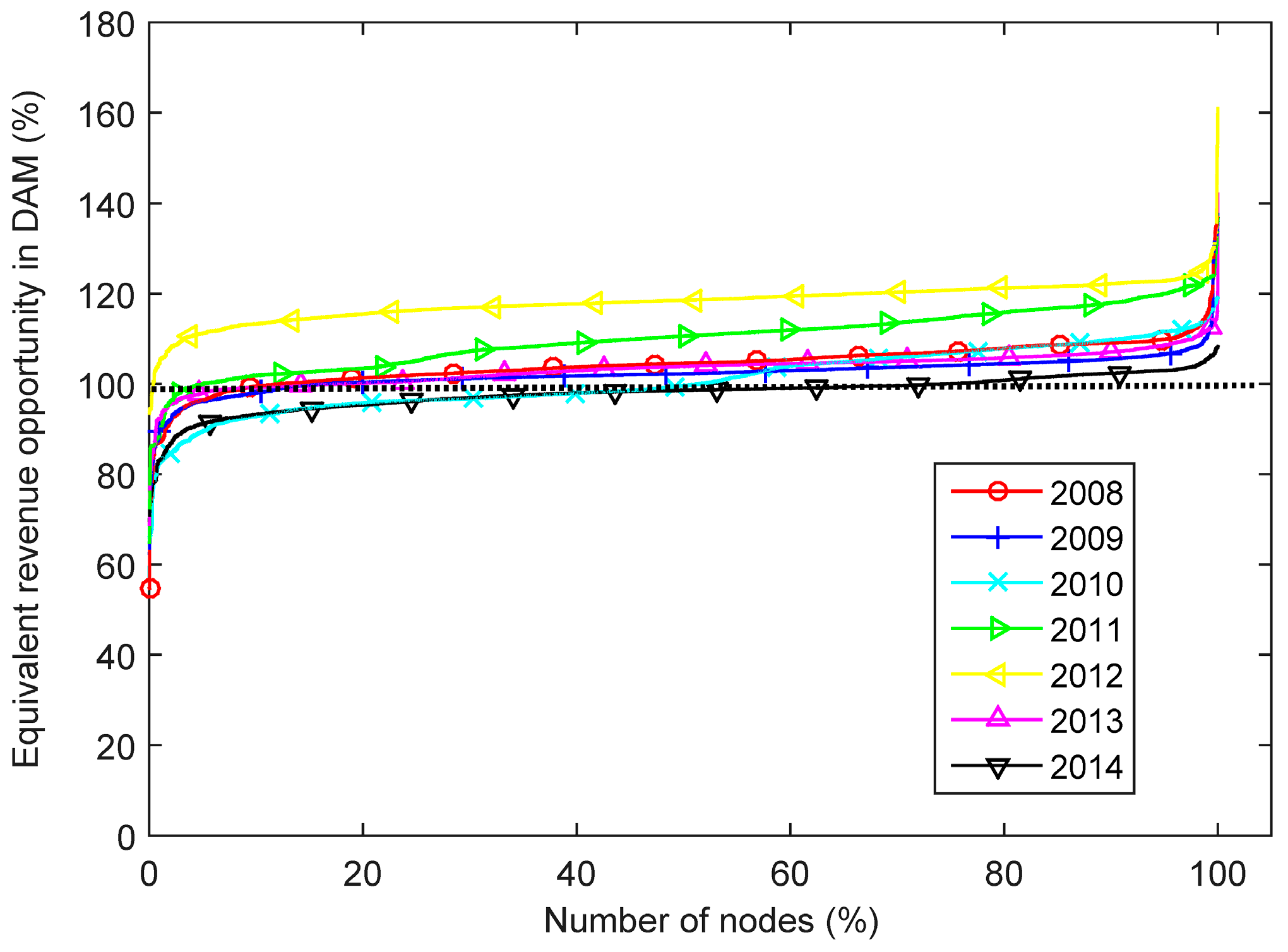
A simple, implementable forecast method was proposed in order to capture a portion of the additional revenue opportunity in the RTM compared to that available in the DAM using the day-ahead price settlement as a forecast for optimizing dispatch into the RTM. This approach increases the revenue over that available in the DAM for the vast majority of nodes, as shown in Figure 22, and thus can be considered a new lower bound on the potential revenues.

From the revenue forecasts we have evaluated the distribution, over all 7395 nodes, of breakeven overnight installed cost for an ESS vs. its discharge duration when arbitrage is the only source of revenue. The results are presented in Figure 23, Figure 24 and Figure 25. Although breakeven costs per kWh of energy capacity drop markedly with discharge duration, the actual cost of flow batteries per kWh drops markedly with discharge duration as well.

Current ESS costs are not low enough for profitability at the vast majority of nodes, but recent ESS cost reductions are expected to continue, bringing an increasing percentage of nodes into profitability over time.