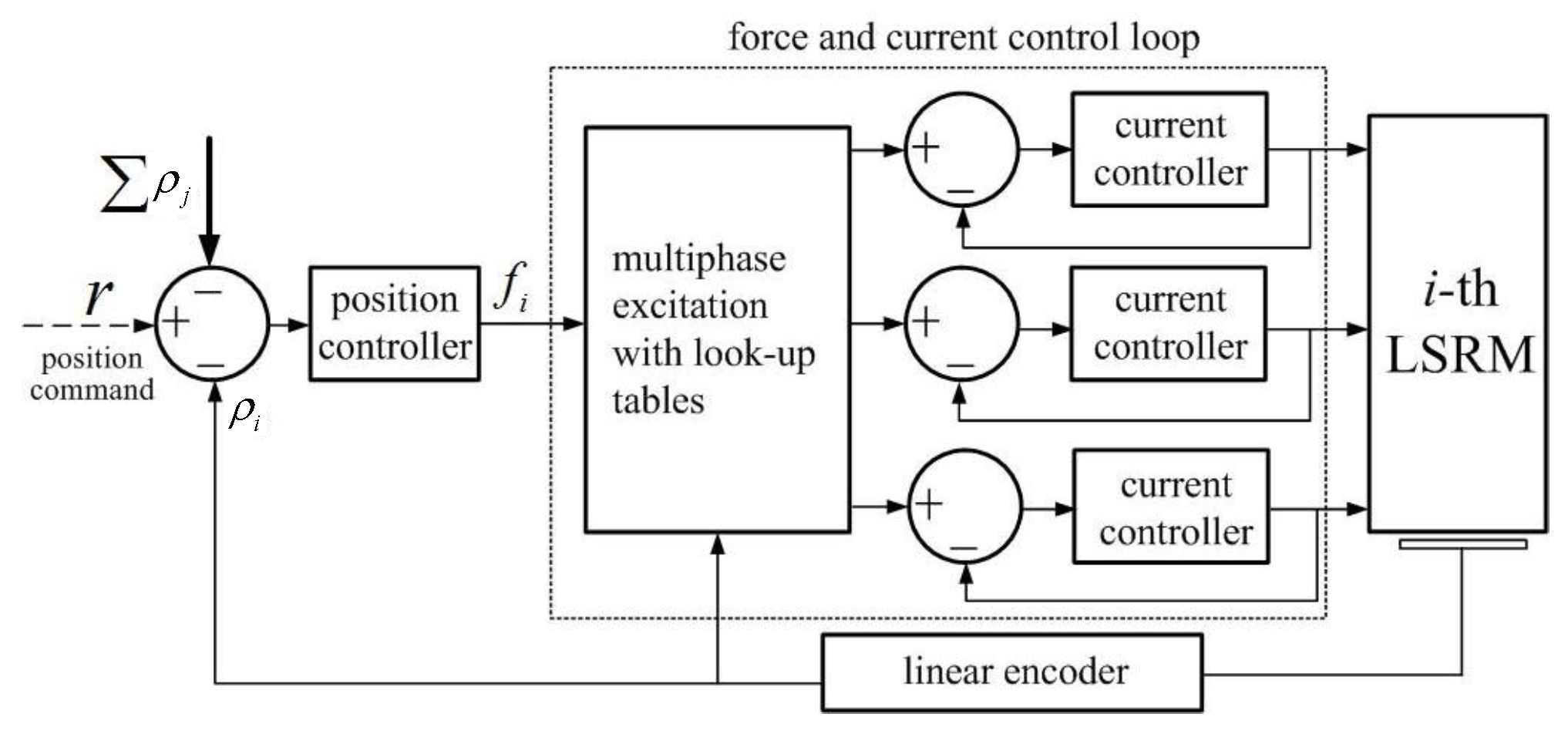
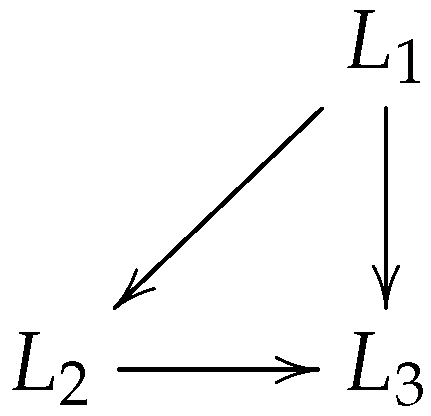1. Introduction
Linear tracking control systems based on direct drive linear machines are vastly used in the manufacturing industry, such as parts assembly, printed circuit boarding (PCB) drilling and chip processing, etc. In addition, there are many tasks that require a cooperation of many linear machines to work harmonically. For example, in a multi-station PCB drilling machine, each linear machine acts as one working unit. The board being processed requires the linear machines to track the command position precisely and coordinates with each other to finish the whole drilling work. Therefore, each linear machine often demands the state information from other machines, so as to work cooperatively and synchronously. The overall motion control performance can be improved such as faster operation time, more efficiency and the annihilation of accumulated errors, etc., compared to a traditional sequenced working manner [
1]. Furthermore, if multiple linear machines can be organized as a coordinated and distributed motion tracking network and each machine has the position controller, sensor and driver of its own, the ultimate global tracking control goal can be emerged by local communications among the independent linear machine nodes with local controllers, without the necessity of any global supervision or decision [
2].
Among different types of linear machines, a linear switched reluctance motor (LSRM) has the advantages of a simple and robust mechanical structure, low cost, high reliability and free of frequent maintenance or adjustments [
3]. Current motion tracking research on LSRMs mainly focuses on the control performance improvement for single machine based position control systems [
4,
5,
6,
7]. In [
4], an adaptive position controller is inspected to compensate uncertain behaviors of a double-sided LSRM. A nonlinear proportional differential (PD) tracking controller based on the tracking differentiator is proposed for a real-time LSRM suspension system, to achieve a better dynamic position response [
5]. A sliding mode position control technique is investigated in [
6] and a passivity-based control algorithm is proposed for the LSRM position tracking system to overcome the inherent nonlinear characteristics and ameliorate system robustness against uncertainties and bounded disturbances [
7]. From the latest development on the tracking control performance of LSRMs, the ratio of an absolute dynamic tracking error to full range of 5% can be achieved in single LSRM position control applications.
As mentioned above, by employing a multi-agent network formed by distributed control on the same product line, all LSRMs can be coordinated to work together harmonically. Up until now, the experiment and technique studies on the tracking control network based on LSRMs have gained much attention, and related research is increasing [
8,
9]. Current analysis of motion coordinated control of multi-agent networks mainly focuses on distributed control methods with multi-agent networks [
10,
11,
12,
13,
14,
15,
16], which provides a guidance to the LSRMs network. Reference [
10] primarily investigated the consensus for coordinated control of multi-agent networks, and established the connections between structural properties and the performance of networks. Cao et al. [
11] elaborated the main results and the progress about coordinated control algorithms for multi-agent networks and summarized the future directions of the distributed coordination of multi-agent. At present, multi-agent network study has been classified into several major aspects, which include constrained or imperfect communication [
12], delay or switching information linkage [
13,
14], agents with nonlinear dynamics [
15], influence of noise [
16], etc., Furthermore, the multi-agent networks bound by distributed control algorithms have been exploited in the regime of spacecraft cluster [
17], robot coordination [
18], and unmanned aerial vehicle formation [
19].
It can be concluded from the above analysis that current theoretical work mainly concentrates on distributed control methods to achieve the network synchronization under some network topology constraint condition. The ultimate goal is to form a stable synchronized motion among the multiple agents within the network employing distributed and networked control algorithms. However, in most industry processes, multiple LSRMs composing a multi-agent network are not only required for motion synchronization but also to track some specific desired trajectory [
20]. In practice, directly controlling every agent in a multi-agent network with a number of agents might be impossible or unnecessary. Therefore, pinning control is regarded as a desirable method [
21]. Accordingly, the multi-agent network formed by the pinning control is defined as the leader-following network [
2]. In a leader-following network, a reference can be accessed directly by minority agents named as leaders only, and then the rest of the agents named as followers are steered to implement the synchronized motion to the common reference by the effect of the distributed control. Wang et al. [
22] elaborately reviewed advances in pinning control approaches, including the feasibility, stability and effectiveness of pinning control and pinning-based consensus and flocking control of mobile multi-agent networked systems. One of the challenges with a leader-following network is that the reference possesses different dynamic characteristics from all agents. Cao et al. [
23] proposed a distributed consensus tracking algorithm for second-order dynamics guarantees global exponential tracking without acceleration measurements, and the dynamic reference was modeled as the virtual leader with time-varying velocity. Especially, in industrial processes, for implementing much of repetitive work, some periodic motion modes such as sinusoid always were as the desired motion. Wang et al. [
24] proposed an internal model controller compensating the reference dynamics for output synchronization of more general heterogeneous multi-agents systems. Wieland et al. [
25] proved that an internal model principle is necessary and sufficient for exponential synchronizability of the group to some common, non-trivial output trajectory, bounded by a polynomial function in time, and also note that the internal model components may give rise to the instability of the multi-agent network under the influence of parametric uncertainties.
In this paper, the mathematical model of each LSRM is derived by the online system identification, which is essentially modeled as a general second-order linear system. Second, inspired by coupled harmonic oscillators [
26,
27], a distributed control is designed to track a sinusoidal reference with zero phase-difference among each LSRM and the reference as virtual node, so as to improve the tracking performance of the LSRMs network. Last, simulation and experimental verification is provided to prove the effectiveness of the network controller design scheme.
The main contributions of this paper are threefold. First, for the convenience of the coordinated motion control, the reference signal is modeled as a virtual LSRM node that has the same dynamic characteristics as three motor nodes based on the proposed distributed tracking control strategy. Second, three motor nodes and the virtual node can be realized by the synchronization control by adopting the coupled harmonic oscillators method, so as to achieve for tracking the sinusoidal reference signal with zero phase-difference. Finally, the distributed tracking control performance for the LSRMs network is investigated by a simulation and experimental platform testing.
3. Synchronization Tracking Control Design
Since each LSRM is a mechatronic device fulfilling double-acting periodic line motion, some sinusoidal signals or its combinatorial patterns are often applied as the predefined trajectory planning some desired reciprocating motion for the LSRMs network. For this purpose, inspired by coupled harmonic oscillators synchronization proposed in [
26,
27], the distributed control law can be formulated as:
where
is a parameter associated with the angular frequency
of the reference sinusoidal signal. Substituting Equation (
12) into Equation (
11) , the LSRM node
can be depicted as:
Let
,
,
, the model of LSRMs network can be derived as:
According to Equation (
14), the LSRMs network can be reformulated as:
where
.
To prove the LSRMs network, Equation (
15) has the ability to track a sinusoidal reference signal
without phase disparity, and the following lemma is provided.
Lemma 1. Let be the left and right eigenvectors of Laplacian matrix associated to the i-th eigenvalue , respectively. The eigenvalues of in Equation (15) can thus be represented as:and its left and right eigenvectors can be denoted as the following: Proof of Lemma 1. We divide
in two parts, denoted as
and
, respectively. For convenience, we omit the subscript index
i or
. For
, we have:
Similarly, for
, we have:
From Equation (
14), Equation (
16) can be derived as:
Likewise, we can obtain the equation as:
Substituting Equation (18a) into Equation (18b), we obtain:
In addition, substituting Equation (19a) into Equation (19b), we have:
According to Equation (21b), we notice
,
are the eigenvalue and left eigenvector of Laplacian matrix
, respectively. Therefore, we have:
Equation (22) can thus be solved as:
In addition, from Equations (18a) and (19a), we know , . Lemma 1 is proved. ☐
Theorem 1. If graph describing the coordinated network includes a directed spanning tree, and the root node can access to the reference position as sinusoidal signal such as shown in Figure 3a, the LSRMs network in Equation (15) can track asymptotically the reference with zero phase-difference.
Proof of Theorem 1. According to [
29], for a directed graph
with a spanning tree in the network topology, its Laplacian matrix
has the left eigenvector
and the right eigenvector
. They correspond to a simple zero eigenvalue
of
, and all rest of eigenvalues
satisfy
, where
is the real part of a complex number. Furthermore,
satisfies:
According to
Lemma 1, the first two eigenvalues of
in Equation (
15) are
,
j is the imaginary unit. Accordingly, the left eigenvector and right eigenvector are
,
respectively. We have:
where
Here, is the Jordan block matrix associated to .
Since
,
, it follows that:
where
is a block matrix of
associated to
and the simple zero eigenvalue of
.
Let
, the solution of LSRMs network in Equation (
14) can be obtained as:
Moreover, according to Equation (26) :
According to Equation (24), it can be seen that
can be set as
in Equation (28). Therefore, Equation (28) is derived as:
where
is the initial value of the LSRM node
as the root of a directed spanning tree in the coordinated network topology
, as shown in
Figure 1. In addition, the states of LSRM nodes
converge to the steady state as:
Obviously, the steady state values are determined by the initial values
of root node
. Therefore, the states of other
LSRM nodes
converge to the state of root without phase disparity. The fact verifies, under the effect of the coordinated control Equation (
12), that the states of LSRMs network can track the state of root node
represented as:
Letting
, Equation (31) is rewritten as:
Accordingly, if the reference sinusoidal position signal
in
Figure 3a and its derivative is regarded as the state
of a virtual root node
, as shown in
Figure 3b, the sinusoidal reference signal can be tracked asymptotically by the LSRMs network Equation (
15) in a coupled harmonic oscillators synchronization manner .
Theorem 2 is proved. ☐
Remark 1. By selecting appropriate initial values of virtual root node , the LSRMs network Equation (15) can converge to the specified sinusoidal reference, which has phase and angular frequency .
4. Illustrative Examples
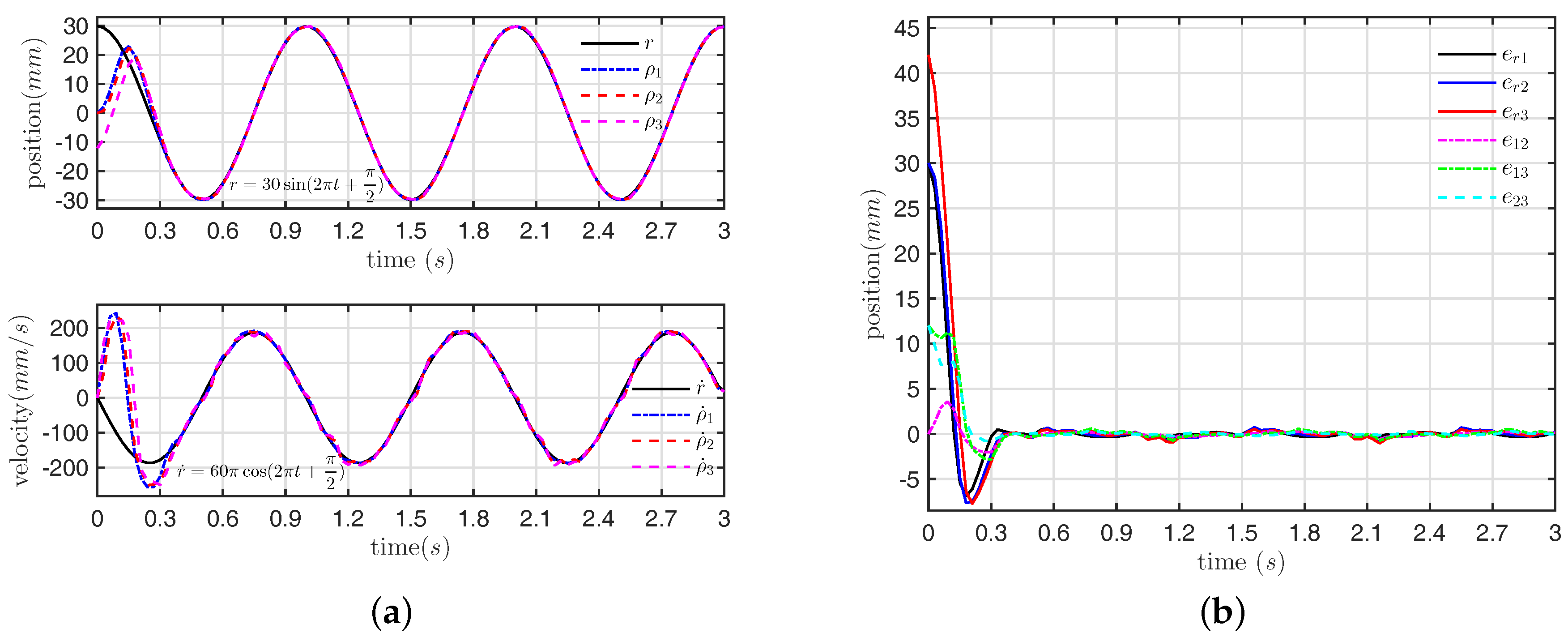
Example 1. The sinusoidal reference r is modeled as a virtual LSRM node , and its initial phase and amplitude are , respectively. In addition, the angular frequency of is set as to investigate the system control feature tracking a higher frequency sine signal.
Each LSRM can be characterized by the second-order dynamics Equation (
11). According to the method proposed in [
8], system matrices
and
(
) can be obtained by the online least squares identification [
4] with a sampling time of T = 0.001 s, and they can be derived as:
The initial positions of three LSRM nodes are set as
, respectively, and all velocities of three LSRM nodes are 0. The control gain
is set as 0.25 empirically (according to some parameter tuning experience). The topology of the LSRMs network is depicted as
Figure 3.
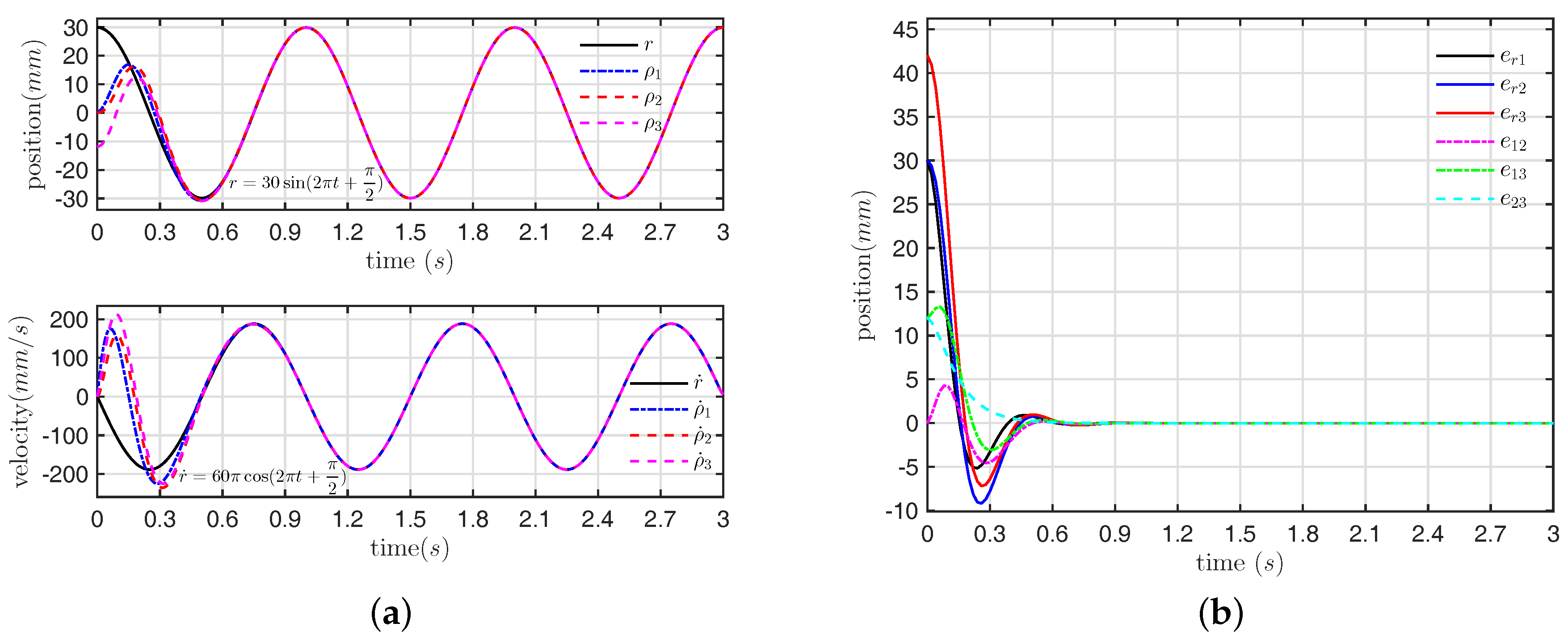
The results of the state and position error responses are depicted in
Figure 4a,b, respectively.
Figure 4a illustrates that the LSRMs network Equation (
14) tracks the reference
in a zero phase-difference and asymptotic manner by applying the proposed control law Equation (
12). The position errors among all nodes including
are illustrated in
Figure 4b. The disparity of position errors are eliminated for all LSRM nodes after about
s.
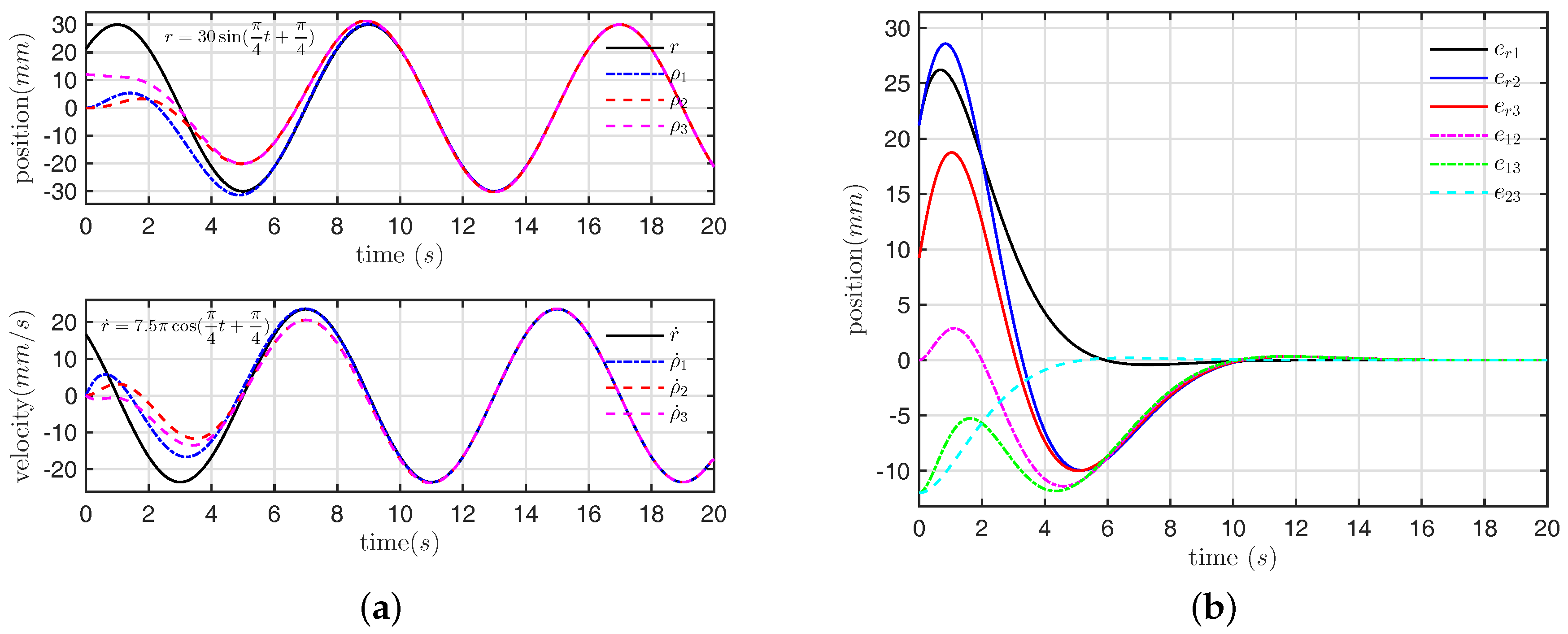
Example 2. To further verify the effectiveness of the proposed control strategy, a comparative study with Example 1 is addressed. We locate the initial positions of three LSRM nodes at , respectively, and three LSRM nodes start work from static state. We set the reference r initial phase as , and the angular frequency are selected as to test the track feature to a lower frequency sine wave. The other systems parameters, such as the control gain, etc., are given the identical values as in Example 1.
The simulation results are shown in
Figure 5a,b, respectively. The control performance from the proposed control method shows that a slower dynamic response can be achieved with a lower frequency sinusoidal reference, and compared to Example 1 for the same system without considering uncertain parameters and external disturbances. The results also demonstrate that the LSRMs network has successfully achieved the stable state without phase-difference after 10s. Therefore, the proposed tracking control scheme has certain superior stability.
Remark 2. From two example comparative results, it is noted that the response effectiveness of Example 2 is counterintuitive, since the state consensus process of Example 2 takes a longer time rather than Example 1, as expected. The main cause is that the angular frequency of the reference sinusoidal signal strongly affects the response rate of each LSRM node through Equation (12).