Experimental Investigation on Propagation Characteristics of PD Radiated UHF Signal in Actual 252 kV GIS
Abstract
:1. Introduction
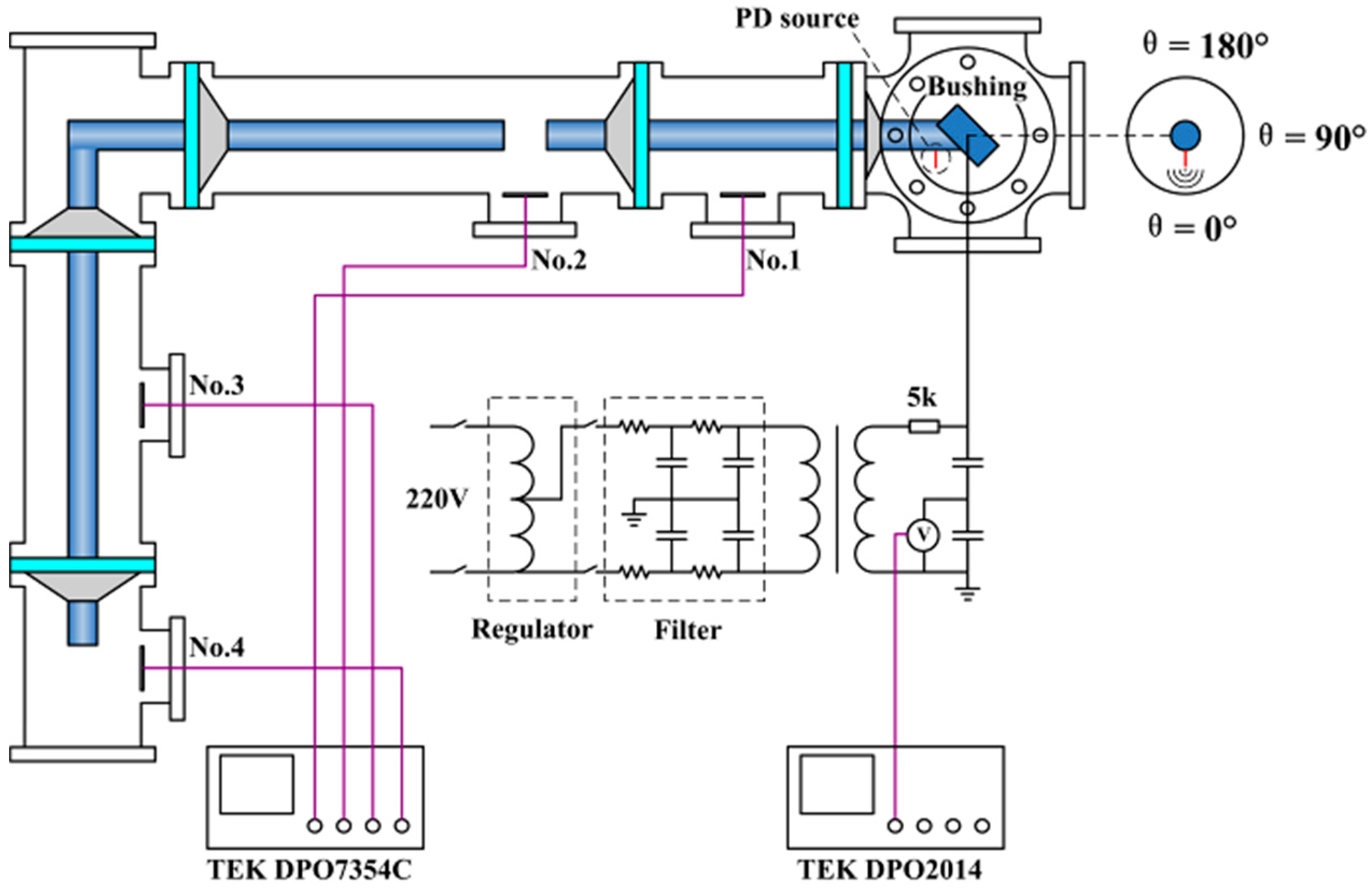
2. Experimental Platform and Setup
2.1. Experimental Platform
2.2. Signal Sampling
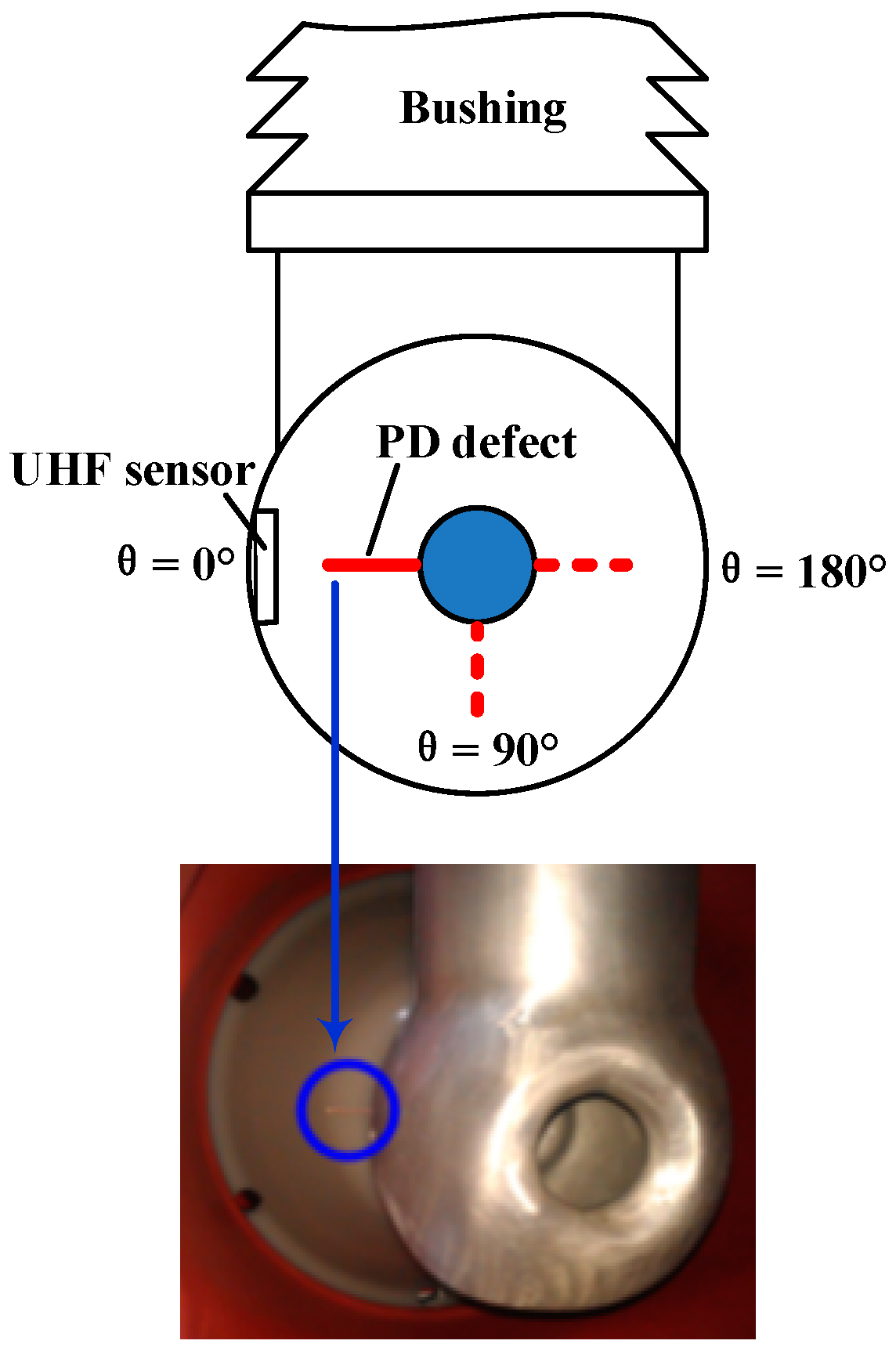
2.3. PD Defect
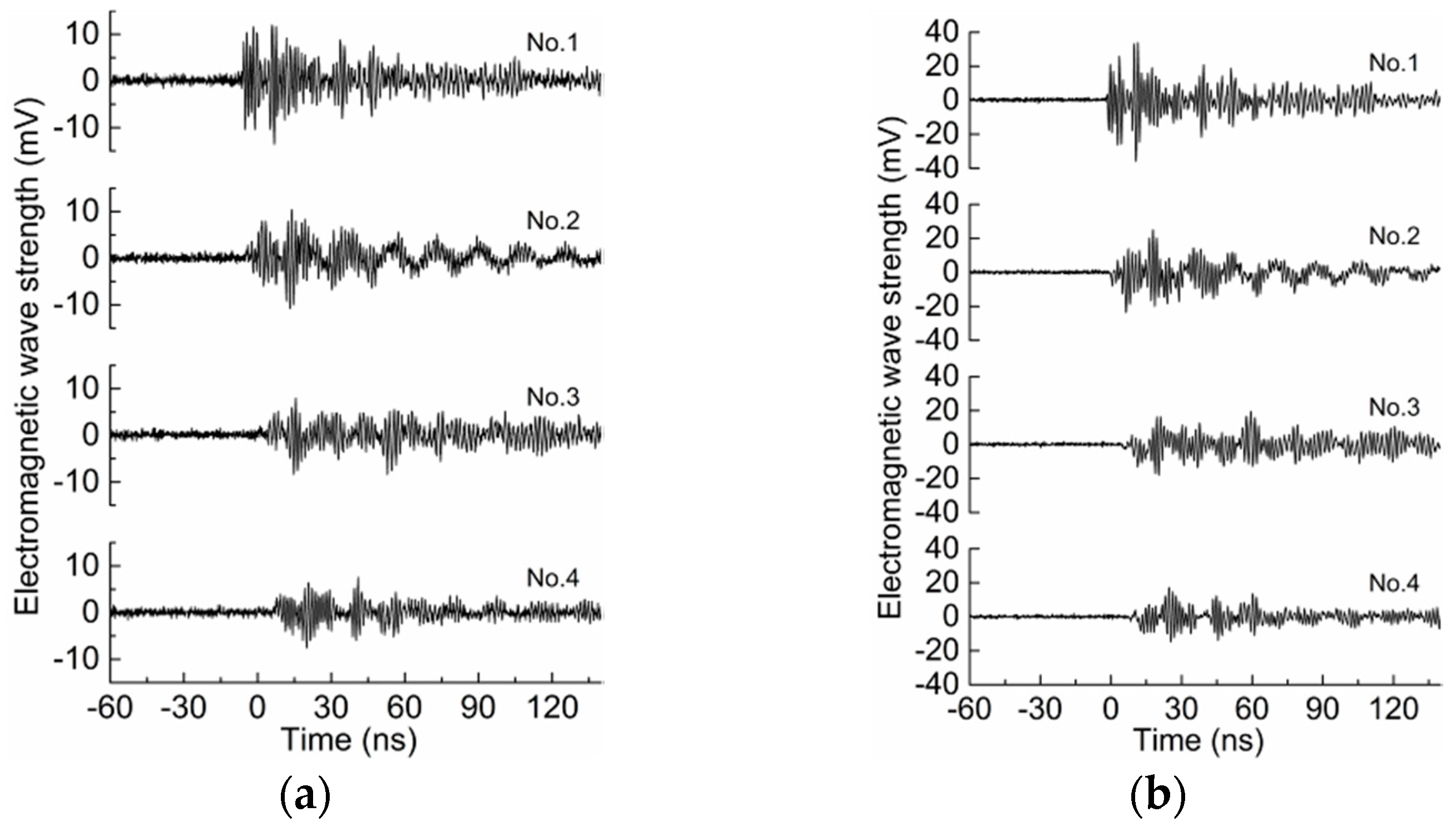
3. Experimental Results of the Defect at θ = 0°
3.1. Statistical Analysis
3.2. Frequency Domain Analysis
4. The Optimal Circumferential Angle Position of UHF Sensor
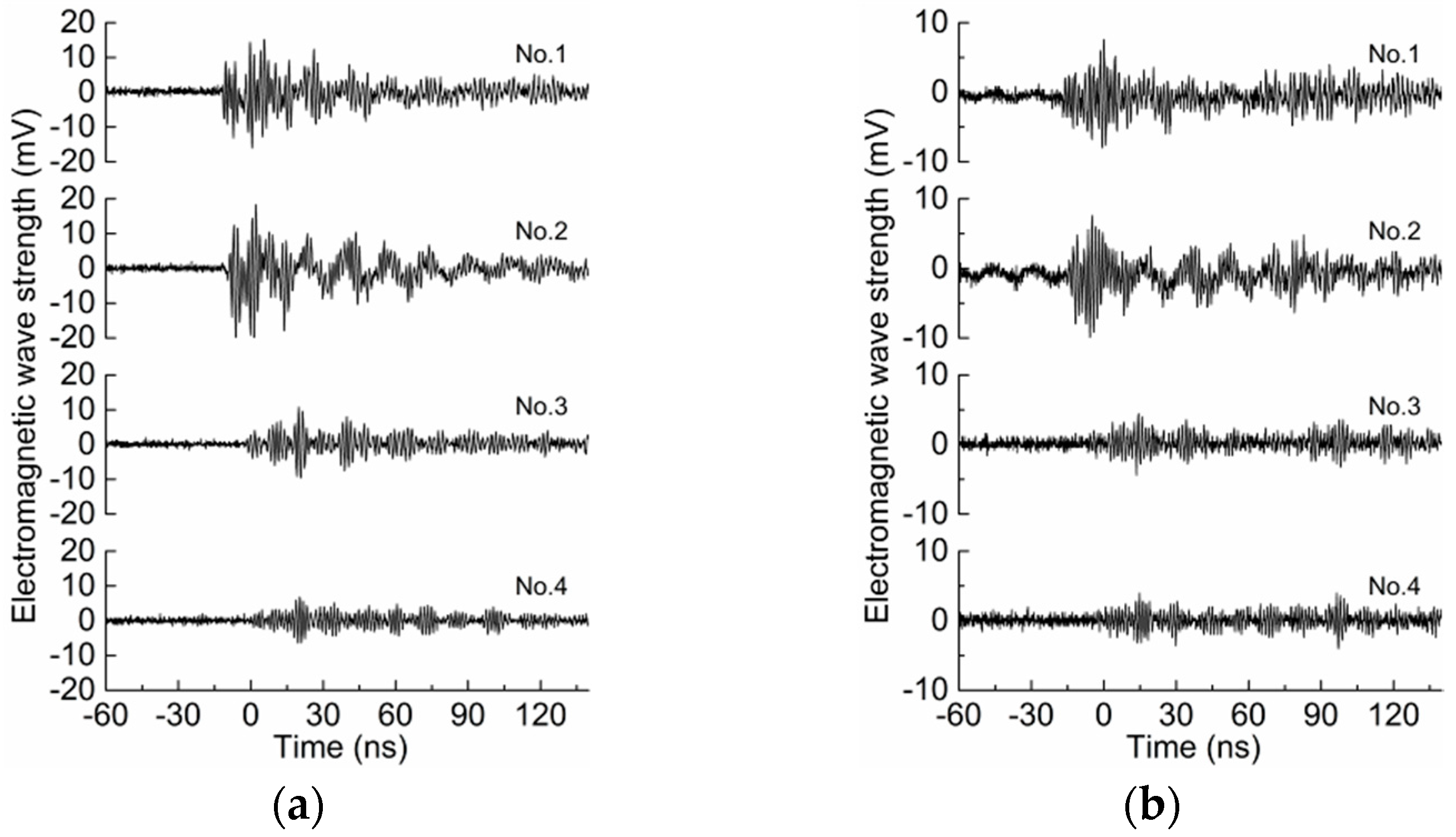
4.1. Experimental Results of the Defect at θ = 90°
4.2. Experimental Results of the Defect at θ = 180°
4.3. Discussion of UHF Sensor’s Position
5. Conclusions
- The UHF sensor, which works properly with the available installation in GIS, can effectively receive PD-radiated signal and accurately reflect its features in practical PD detection. This could be applied in on-line monitoring of PD in GIS in the future.
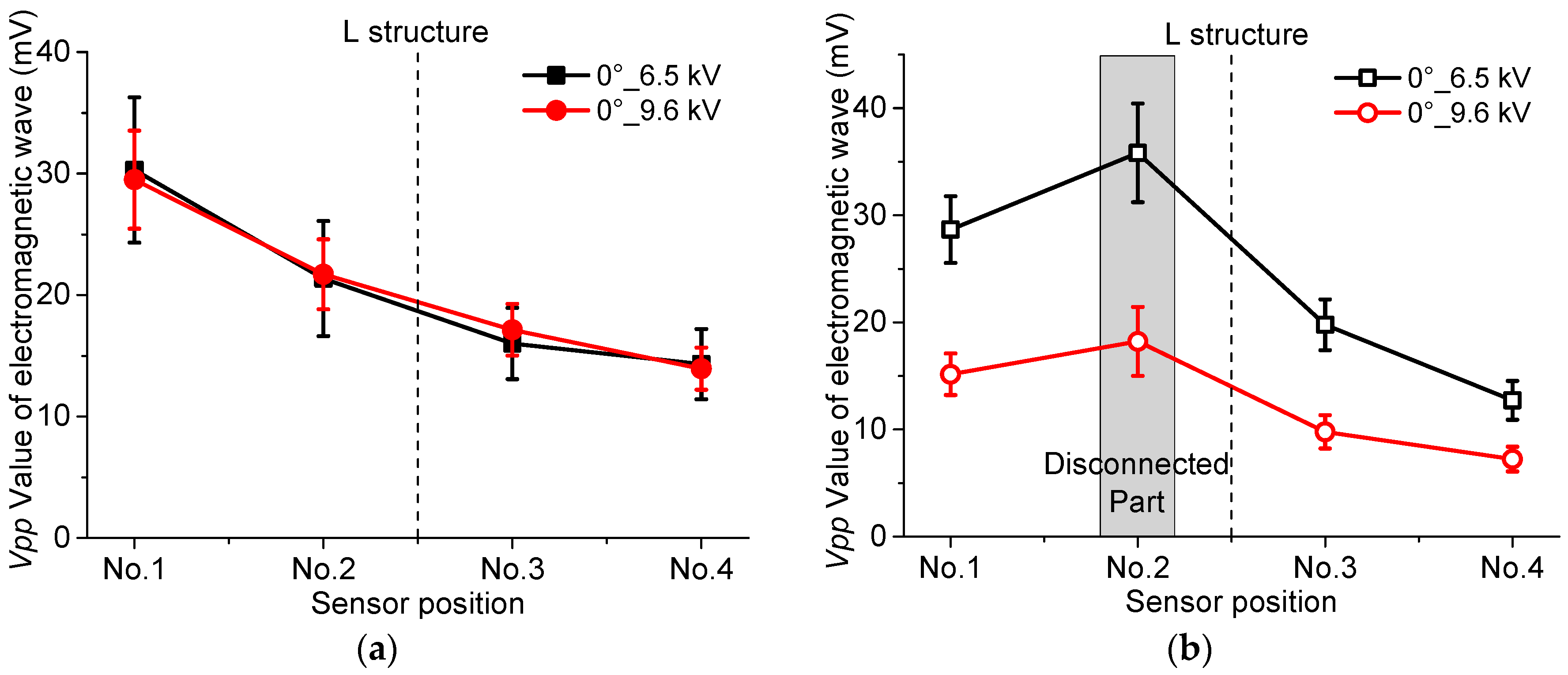
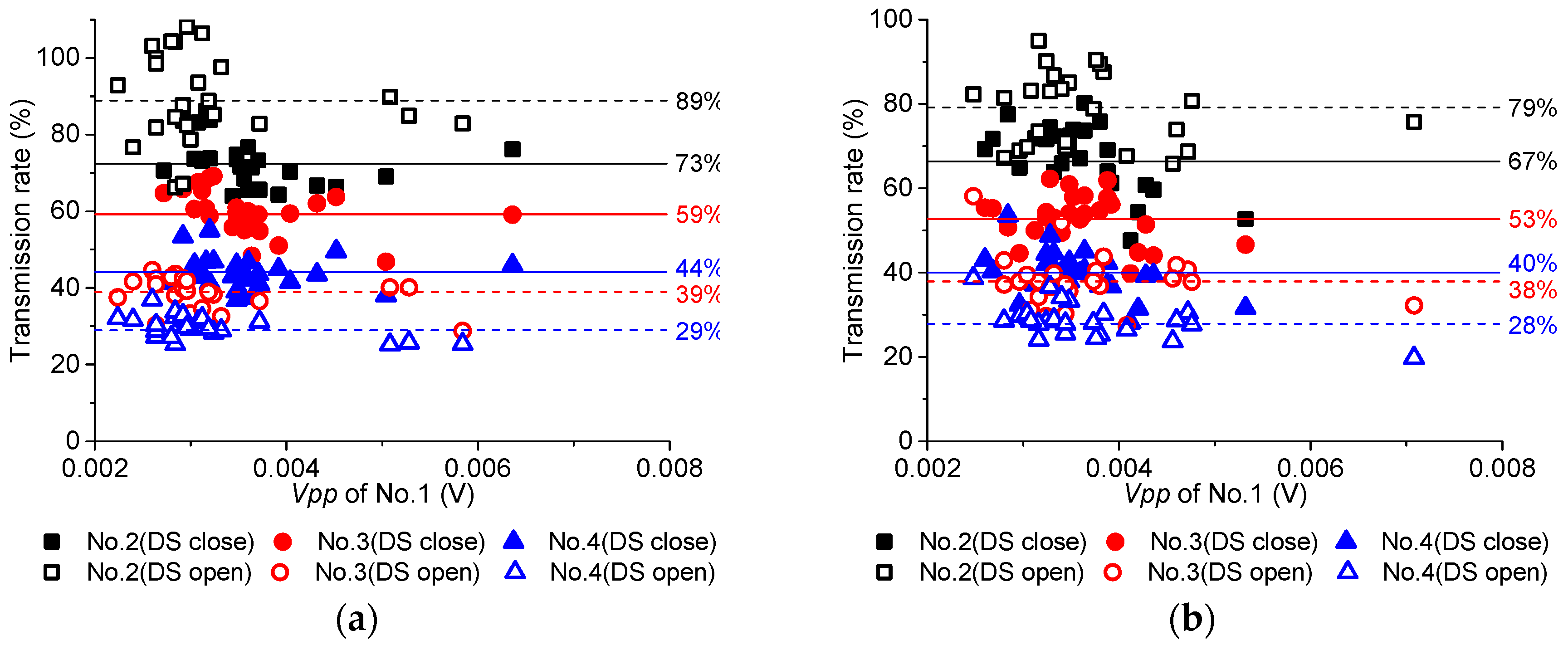
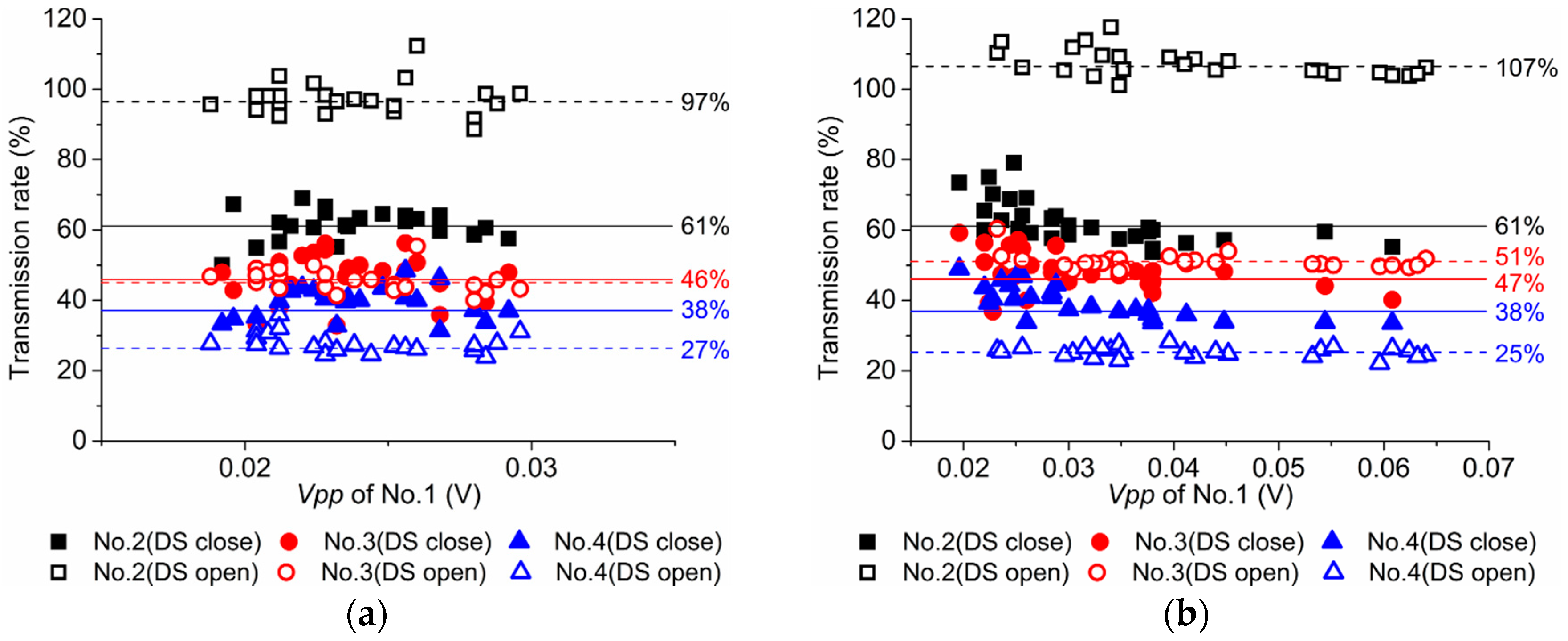
- Generally, the special structures in GIS, such as LS, have an attenuating effect on UHF signals, and will make is more difficult to identify the start of the rising edge of the waveform. However, the discontinuity conductor of the DS leads to a peak of the Vpp attenuation curve, while the signal transmission rate is also enhanced. In the actual diagnosis, choosing the simplified GIS structure to detect PD can help to accurately demonstrate the discharge characteristics of the defect and evaluate the severity better.
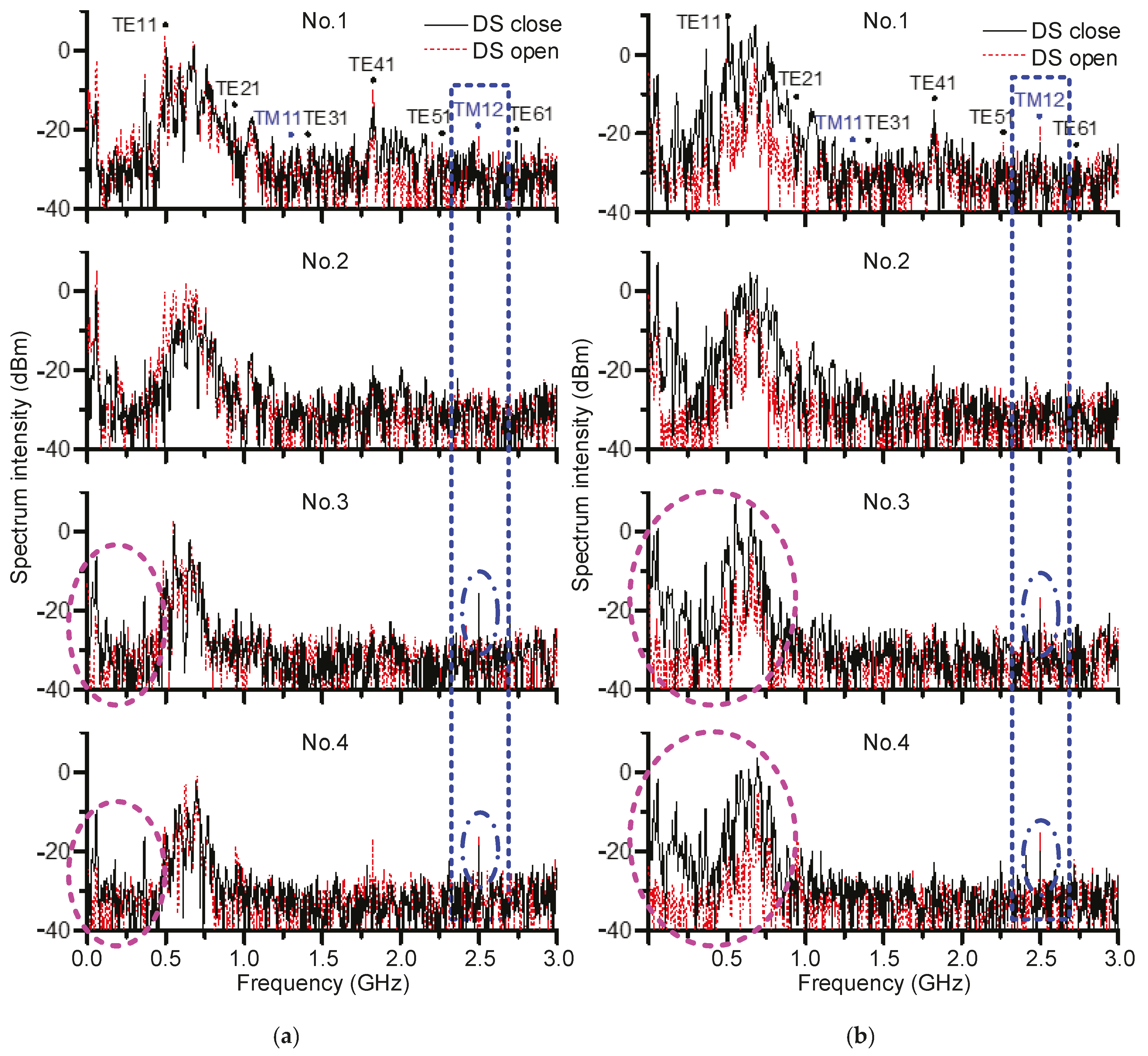
- The frequency domain analysis demonstrates that it is the variation of mode components in the PD signal affected by special structure of GIS that lead to the distinctions in amplitude and transmission rates. For instance, the prevention of the TEM mode by the discontinuity conductor, the enhancement of the TM mode and the decrease in TE mode by LS.
- The relative position of the sensor and the defect will influence the received signal, especially for the transmission rate. When the circumferential angle between the sensor and defect is 0°, the transmission rate of the UHF signal is found to be at maximum. Thus, this position is considered to be the optimal circumferential angle position of UHF Sensor to detect PD in GIS.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Okabe, S.; Ueta, G.; Hama, H.; Ito, T.; Hikita, M.; Okubo, H. New Aspects of UHF PD Diagnostics on Gas-insulated Systems. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 2245–2258. [Google Scholar] [CrossRef]
- Dai, D.D.; Wang, X.P.; Long, J.C.; Tian, M.; Zhu, G.W.; Zhang, J.M. Feature extraction of GIS partial discharge signal based on S-transform and singular value decomposition. IET Sci. Meas. Technol. 2017, 11, 186–193. [Google Scholar] [CrossRef]
- Feger, R.; Feser, K.; Knapp, M. The Application of Ultra-High-Frequency Partial Discharge Measurements to Gas-Insulated Substations. IEEE Trans. Power Deliv. 1998, 13, 777–782. [Google Scholar]
- Jiang, T.Y.; Li, J.; Zheng, Y.B.; Sun, C.X. Improved Bagging Algorithm for Pattern Recognition in UHF Signals of Partial Discharges. Energies 2011, 4, 1087–1101. [Google Scholar] [CrossRef]
- Tang, J.; Zhou, J.B.; Zhang, X.X.; Liu, F. A Transformer Partial Discharge Measurement System Based on Fluorescent Fiber. Energies 2012, 5, 1490–1502. [Google Scholar] [CrossRef]
- Hikita, M. Recent Technology Development on Partial Discharge Measurements in Diagnosis for GIS, Transformers, Cables and Inverter-fed Motors. In Proceedings of the 14th Asian Conference on Electrical Discharge, Bandung, Indonesia, 23–25 November 2008; pp. 1–8. [Google Scholar]
- Hikita, M.; Otsuka, S.; Teshima, T.; Okabe, S. Examination of Electromagnetic Mode Propagation Characteristics in Straight and L-Section GIS Model Using FD-TD Analysis. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 1477–1483. [Google Scholar] [CrossRef]
- Hikita, M.; Otsuka, S.; Okabe, S.; Ueta, G.; Hoshino, T.; Maruyama, S. Propagation Properties of PD-induced Electromagnetic Wave in GIS Model Tank with T Branch Structure. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 256–263. [Google Scholar] [CrossRef]
- Nishigouchi, K.; Kozako, M.; Hikita, M.; Hoshino, T.; Maruyama, S.; Nakajima, T. Waveform Estimation of Particle Discharge Currents in Straight 154 kV GIS Using Electromagnetic Wave Propagation Simulation. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 2239–2245. [Google Scholar] [CrossRef]
- Hikita, M.; Otsuka, S.; Okabe, S.; Wada, J.; Hoshino, T.; Maruyama, S. Influence of Disconnecting Part on Propagation Properties of PD-induced Electromagnetic Wave in Model GIS. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 1731–1737. [Google Scholar] [CrossRef]
- Yoshimura, M.; Muto, H.; Nishida, C.; Kamei, M. Propagation Properties of Electromagnetic Wave through T-branch in GIS. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 328–333. [Google Scholar] [CrossRef]
- Okabe, S.; Kaneko, S.; Yoshimura, M.; Muto, H.; Nishida, C. Partial Discharge Diagnosis Method Using Electromagnetic Wave Mode Transformation in Gas Insulated Switchgear. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 702–709. [Google Scholar] [CrossRef]
- Kaneko, S.; Okabe, S.; Yoshimura, M.; Muto, H.; Nishida, C.; Kamei, M. Partial Discharge Diagnosis Method Using Electromagnetic Wave Mode Transformation in Actual GIS Structure. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 1329–1339. [Google Scholar] [CrossRef]
- Okabe, S.; Kaneko, S. Electromagnetic Wave Propagation in a Coaxial Pipe GIS Model. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 1161–1169. [Google Scholar] [CrossRef]
- Kaneko, S.; Okabe, S.; Muto, H.; Yoshimura, M.; Nishida, C.; Kamei, M. Electromagnetic wave radiated from an insulating spacer in gas insulated switchgear with partial discharge detection. IEEE Trans. Dielectr. Electr. Insul. 2009, 16, 60–68. [Google Scholar] [CrossRef]
- Hoshino, T.; Nojima, K.; Hanai, M. Real-time PD identification in diagnosis of GIS using symmetric and asymmetric UHF sensors. IEEE Trans. Power Del. 2004, 19, 1072–1077. [Google Scholar] [CrossRef]
- Hoshino, T.; Maruyama, S.; Nojima, K.; Hanai, M. A unique sensitivity verification combined with real-time PD identification method. IEEE Trans. Power Del. 2005, 20, 1890–1896. [Google Scholar] [CrossRef]
- Hoshino, T.; Maruyama, S.; Sakakibara, T. Simulation of Propagating Electromagnetic Wave Due to Partial Discharge in GIS Using FDTD. IEEE Trans. Power Deliv. 2009, 24, 153–159. [Google Scholar] [CrossRef]
- Judd, M.D.; Farish, O.; Hampton, B.F. The Excitation of UHF Signals by Partial Discharges in GIS. IEEE Trans. Dielectr. Electr. Insul. 1996, 3, 213–228. [Google Scholar] [CrossRef]
- Judd, M.D.; Hampton, B.F.; Farish, O. Modeling partial discharge excitation of UHF signals in waveguide structures using Green's functions. IEEE Proc. Sci. Meas. Technol. 1996, 143, 63–70. [Google Scholar] [CrossRef]
- Judd, M.D. Using finite difference time domain techniques to model electrical discharge phenomena. In Proceedings of the Annual Report Conference on Electrical Insulation Dielectric Phenomena, Victoria, BC, Canada, 15–18 October 2000; Volume 2, pp. 518–521. [Google Scholar]
- Judd, M.D.; Farish, O. FDTD simulation of UHF signals in GIS. In Proceedings of the 10th International Symposium on High Voltage Engineering, Montreal, QC, Canada, 25–29 August 1997; Volume 6. [Google Scholar]
- Reid, A.J.; Judd, M.D. High Bandwidth Measurement of Partial Discharge Pulses in SF6. In Proceedings of the 14th International Symposium on High Voltage Engineering, Beijing, China, 25–29 August 2005; Volume 1, pp. 25–29. [Google Scholar]
- Reid, A.J.; Stewart, M.; Judd, M.D. FDTD Modeling of UHF Partial Discharge Sensor Response. In Proceedings of the International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009; Volume 14, pp. 2294–2297. [Google Scholar]
- Li, T.H.; Rong, M.Z.; Zheng, C.; Wang, X.H. Development simulation and experiment study on UHF Partial Discharge Sensor in GIS. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 1421–1430. [Google Scholar] [CrossRef]
- Li, T.H.; Rong, M.Z.; Wang, X.H. Experimental Investigation on UHF Partial Discharge Sensor in GIS. In Proceedings of the 2015 3rd International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), ICEPE, Busan, Korea, 25–28 October 2015; pp. 46–49. [Google Scholar]
- Li, T.H.; Wang, X.H.; Zheng, C.; Liu, D.X.; Rong, M.Z. Investigation on the Placement Effect of UHF Sensor and Propagation Characteristics of PD-induced Electromagnetic Wave in GIS Based on FDTD Method. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 1015–1025. [Google Scholar] [CrossRef]
- Wang, X.H.; Li, T.H.; Ding, D.; Rong, M.Z. The Influence of L-shaped Structure on Partial Discharge Radiated Electromagnetic Wave Propagation in GIS. IEEE Trans. Plasma Sci. 2014, 42, 2536–2537. [Google Scholar] [CrossRef]
- Rong, M.Z.; Li, T.H.; Wang, X.H.; Liu, D.X.; Zhang, A.X. Investigation on Propagation Characteristics of PD-induced Electromagnetic Wave in T-Shaped GIS Based on FDTD Method. IEICE Trans. Electron. 2014, E97-C, 880–887. [Google Scholar] [CrossRef]
- Pearson, J.S.; Hampton, B.F.; Sellers, A.G. A continuous UHF monitor for gas-insulated substation. IEEE Trans. Electr. Insul. 1991, 26, 469–478. [Google Scholar] [CrossRef]
- Meijer, S.; Smit, J.J. UHF Defect Evaluation in Gas Insulated Equipment. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 285–296. [Google Scholar] [CrossRef]
- Hikita, M.; Otsuka, S.; Wada, J.; Okabe, S.; Hoshino, T.; Maruyama, S. Study of partial discharge radiated electromagnetic wave propagation characteristics in an actual 154 kV model GIS. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 8–17. [Google Scholar] [CrossRef]
- Chen, X.X.; Qian, Y.; Sheng, G.H.; Jiang, X.C. A Time-domain Characterization Method for UHF Partial Discharge Sensors. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 110–119. [Google Scholar] [CrossRef]
- Wang, X.H.; Li, X.; Rong, M.Z.; Xie, D.L.; Ding, D.; Wang, Z.X. UHF Signal Processing and Pattern Recognition of Partial Discharge in Gas-Insulated Switchgear Using Chromatic Methodology. Sensors 2017, 17, 177. [Google Scholar] [CrossRef] [PubMed]
- Balanis, C.A. Advanced Engineering Electromagnetics, 2nd ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]



| m | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| (TE) | 0.47 | 0.93 | 1.4 | 1.86 | 2.33 | 2.79 |
| n | 1 | 2 | ||||
| (TM) | 1.3 | 2.61 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Rong, M.; Wang, X.; Pan, J. Experimental Investigation on Propagation Characteristics of PD Radiated UHF Signal in Actual 252 kV GIS. Energies 2017, 10, 942. https://doi.org/10.3390/en10070942
Li T, Rong M, Wang X, Pan J. Experimental Investigation on Propagation Characteristics of PD Radiated UHF Signal in Actual 252 kV GIS. Energies. 2017; 10(7):942. https://doi.org/10.3390/en10070942
Chicago/Turabian StyleLi, Tianhui, Mingzhe Rong, Xiaohua Wang, and Jin Pan. 2017. "Experimental Investigation on Propagation Characteristics of PD Radiated UHF Signal in Actual 252 kV GIS" Energies 10, no. 7: 942. https://doi.org/10.3390/en10070942
APA StyleLi, T., Rong, M., Wang, X., & Pan, J. (2017). Experimental Investigation on Propagation Characteristics of PD Radiated UHF Signal in Actual 252 kV GIS. Energies, 10(7), 942. https://doi.org/10.3390/en10070942





