A Novel Modular-Stator Outer-Rotor Flux-Switching Permanent-Magnet Motor
Abstract
:1. Introduction
2. Structure and Operation Principle of the MSOR-FSPM Motor
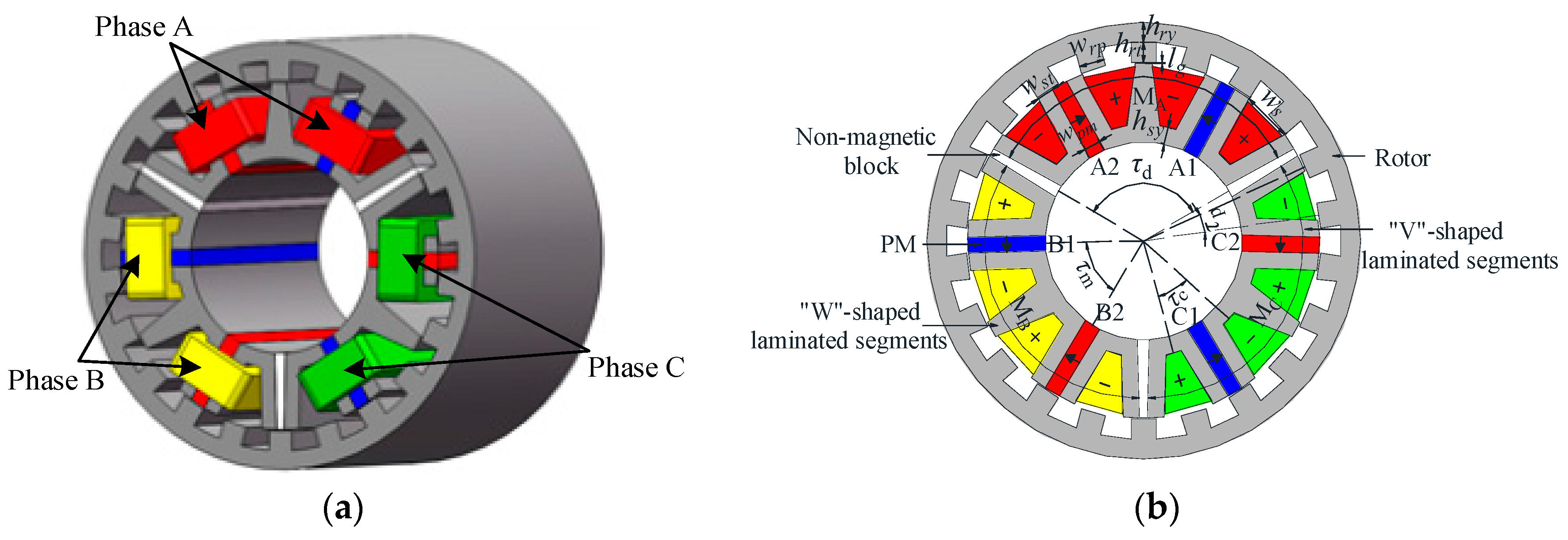
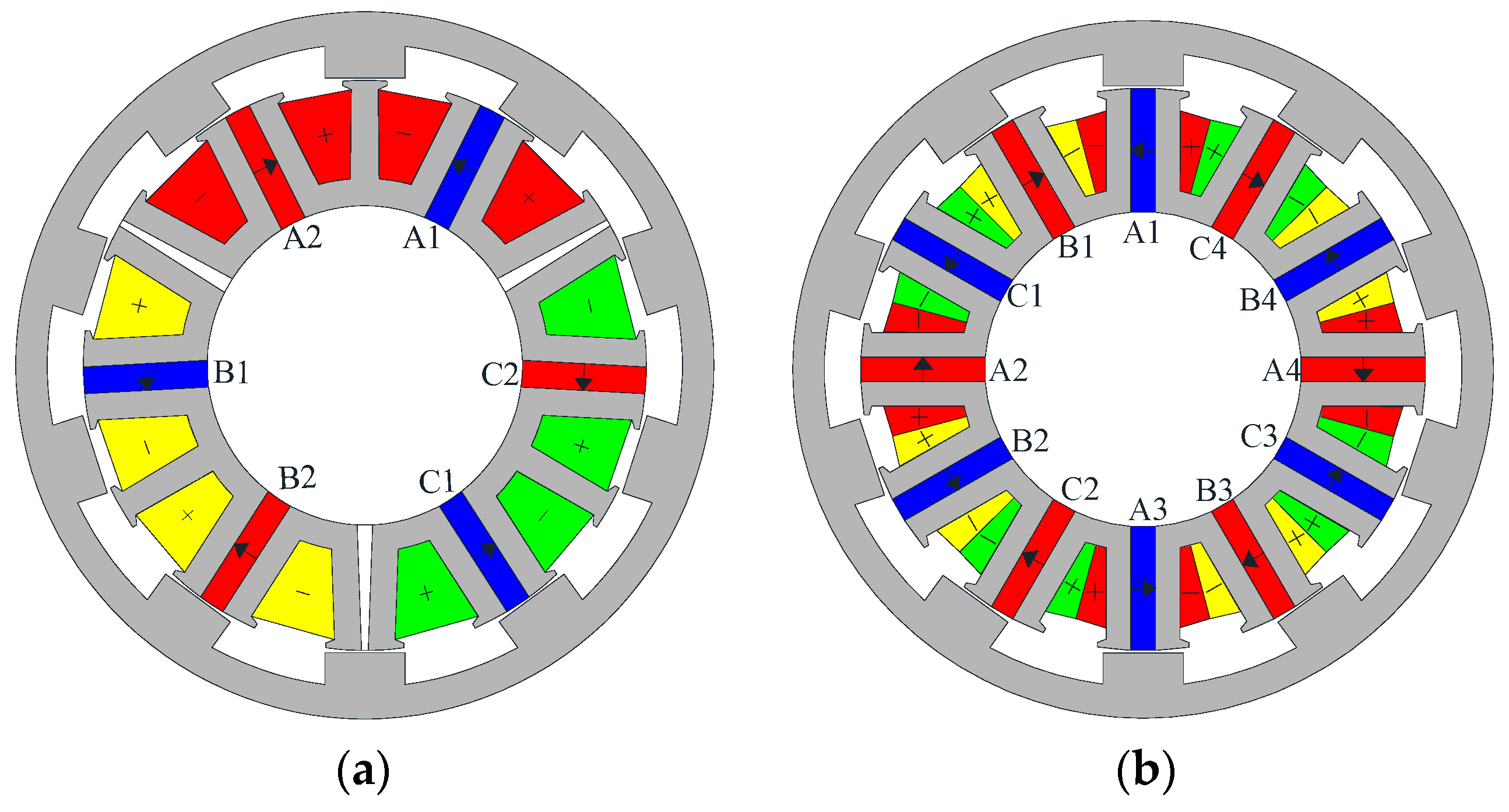
2.1. Structure of the MSOR-FSPM Motor
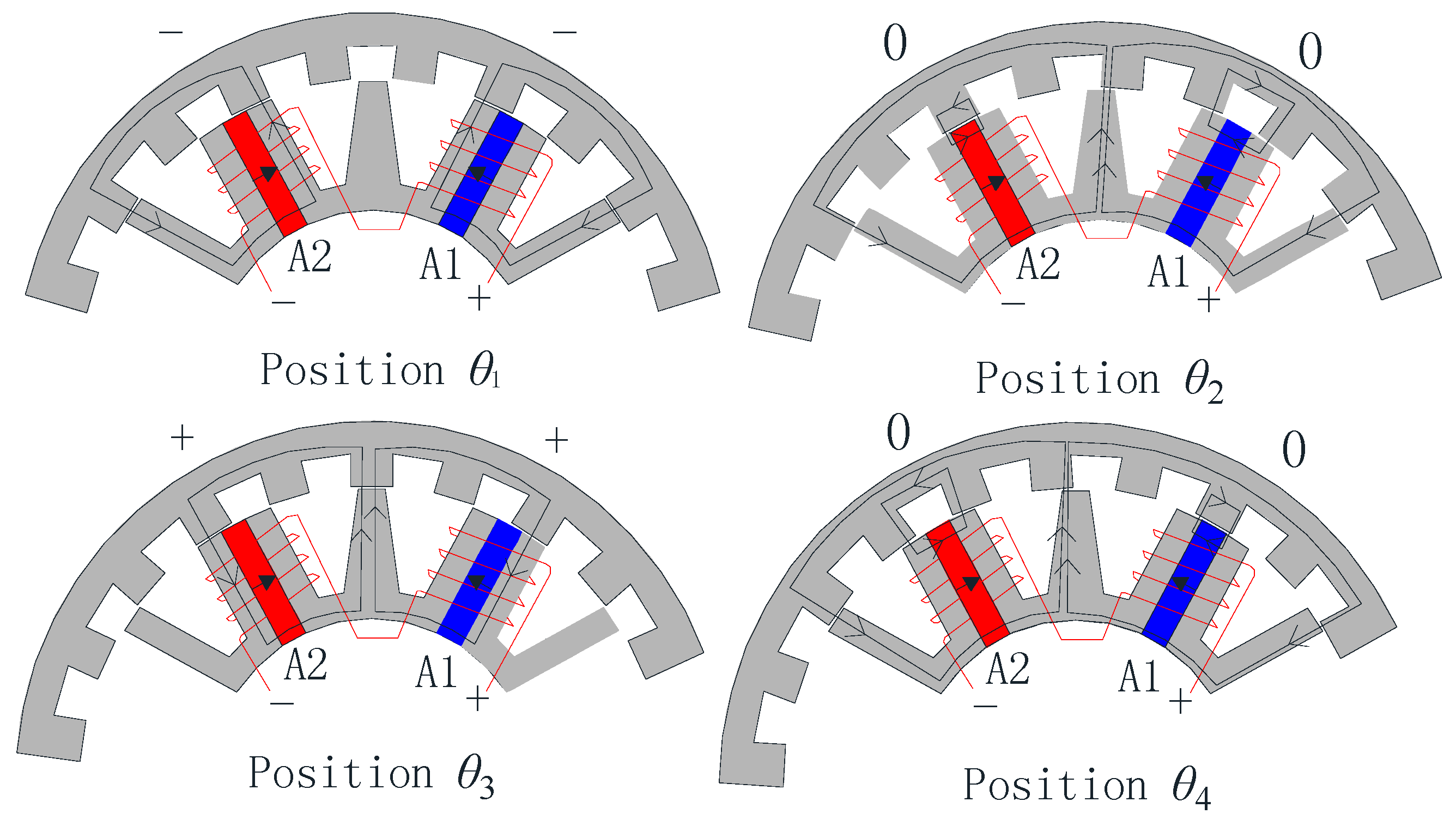
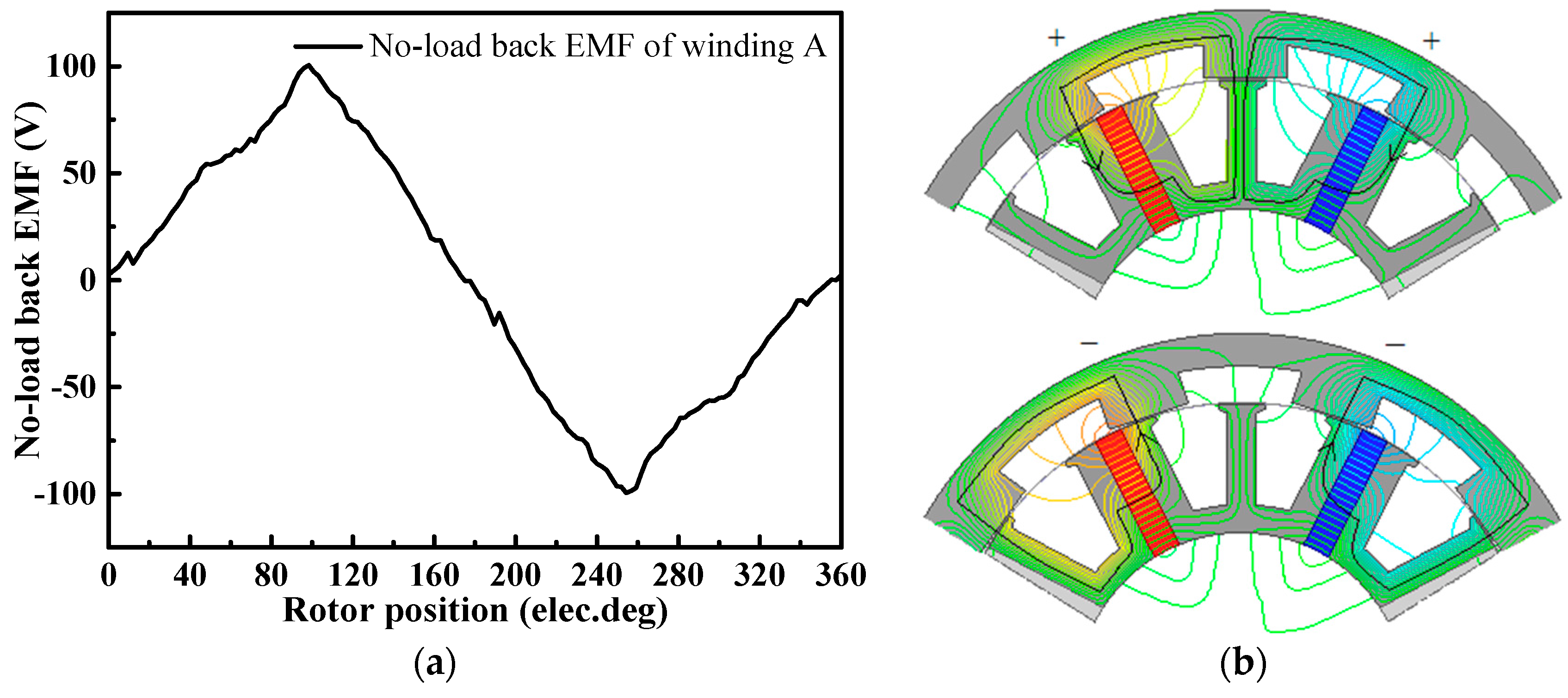
2.2. Operation Principle of the MSOR-FSPM Motor
2.3. Basic Design Principles of the MSOR-FSPM Motor
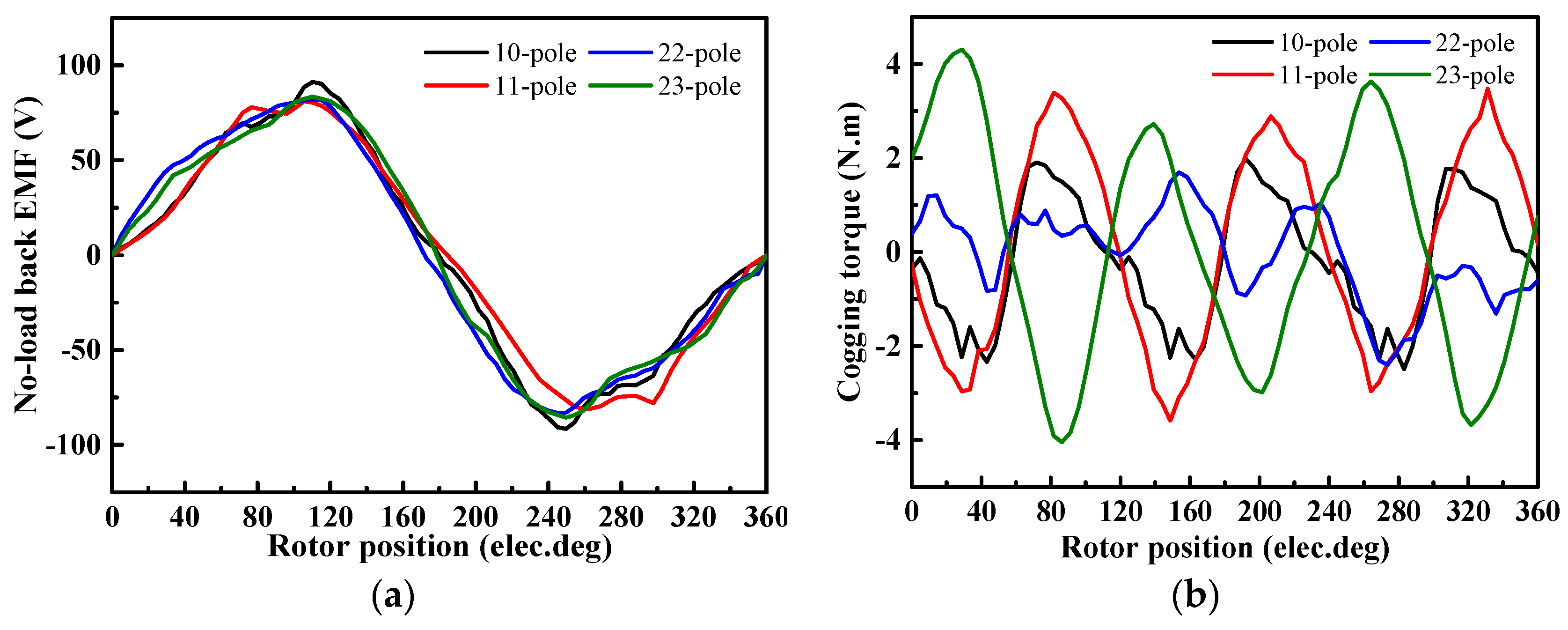
3. Influences of Rotor Pole Number
- The number of rotor poles cannot be too large to ensure appropriate mechanical strength of rotor poles.
- The number of rotor poles cannot be a multiple of 3 to obtain three-phase back-EMF.
- The outside diameter, air gap length, stack length, PM width, and stator tooth width of different topologies keep constant.
- Equations (6)–(8) must be satisfied.
- The stator tooth cannot be supersaturated.
- The stator slot area is utilized as fully as possible.
4. Optimization of the Main Parameters in the 12-Slot/10-Pole MSOR-FSPM Motor
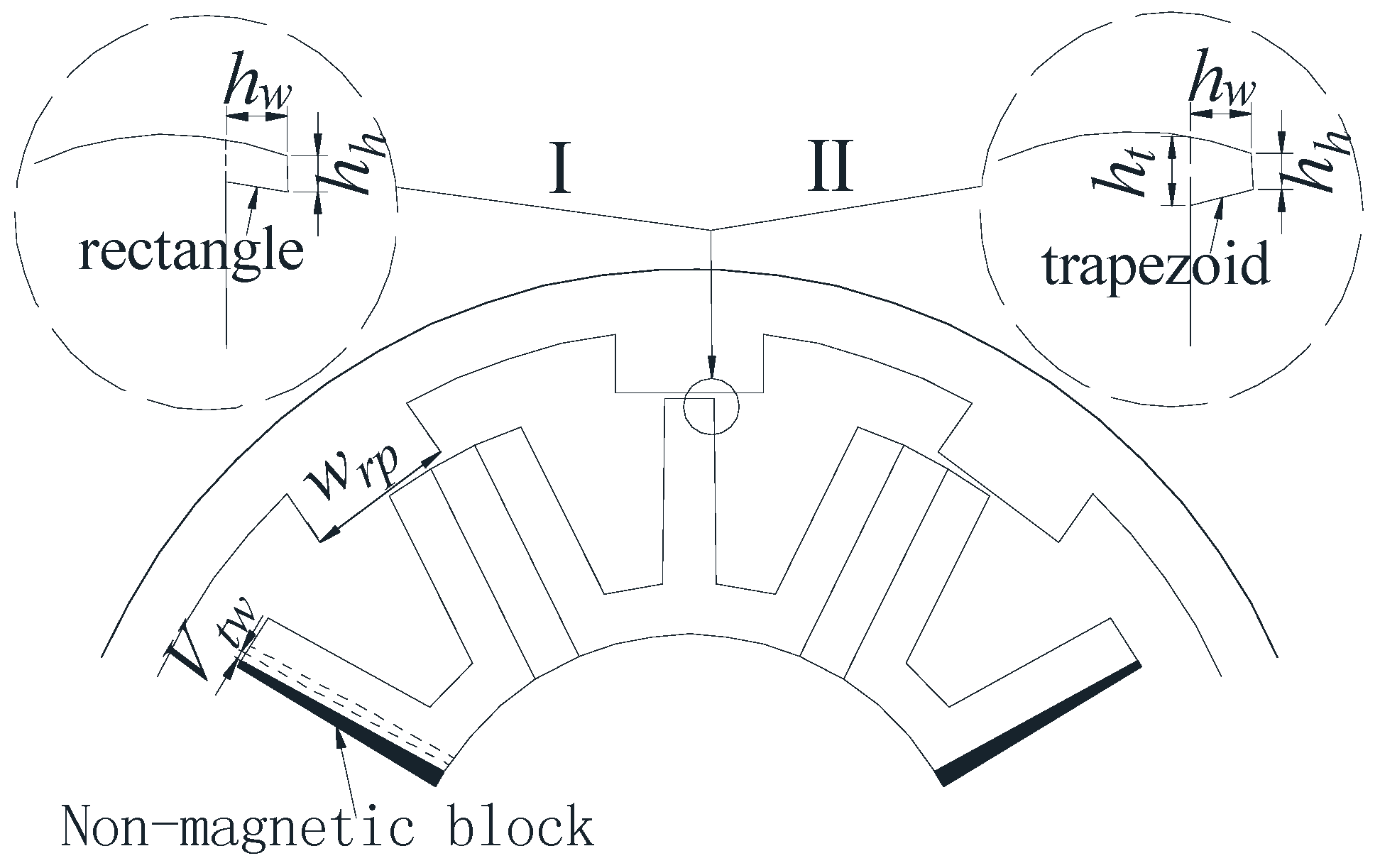
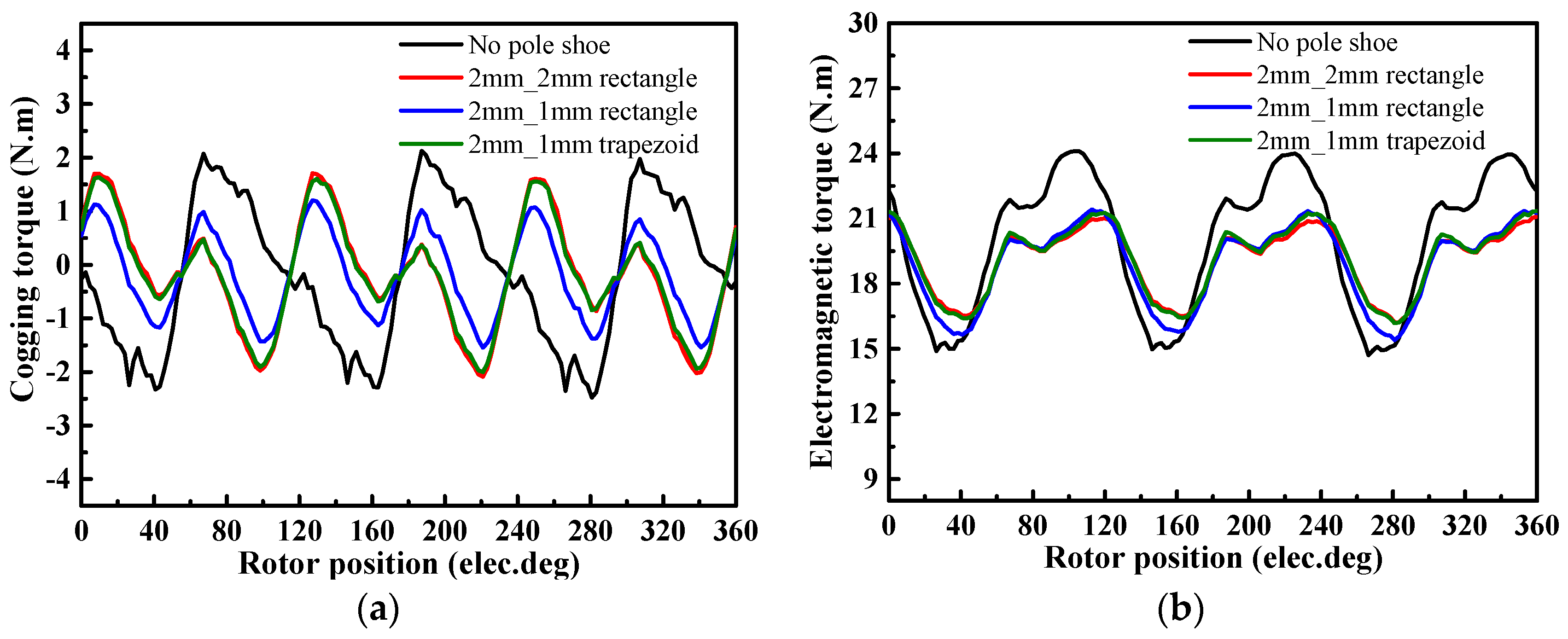
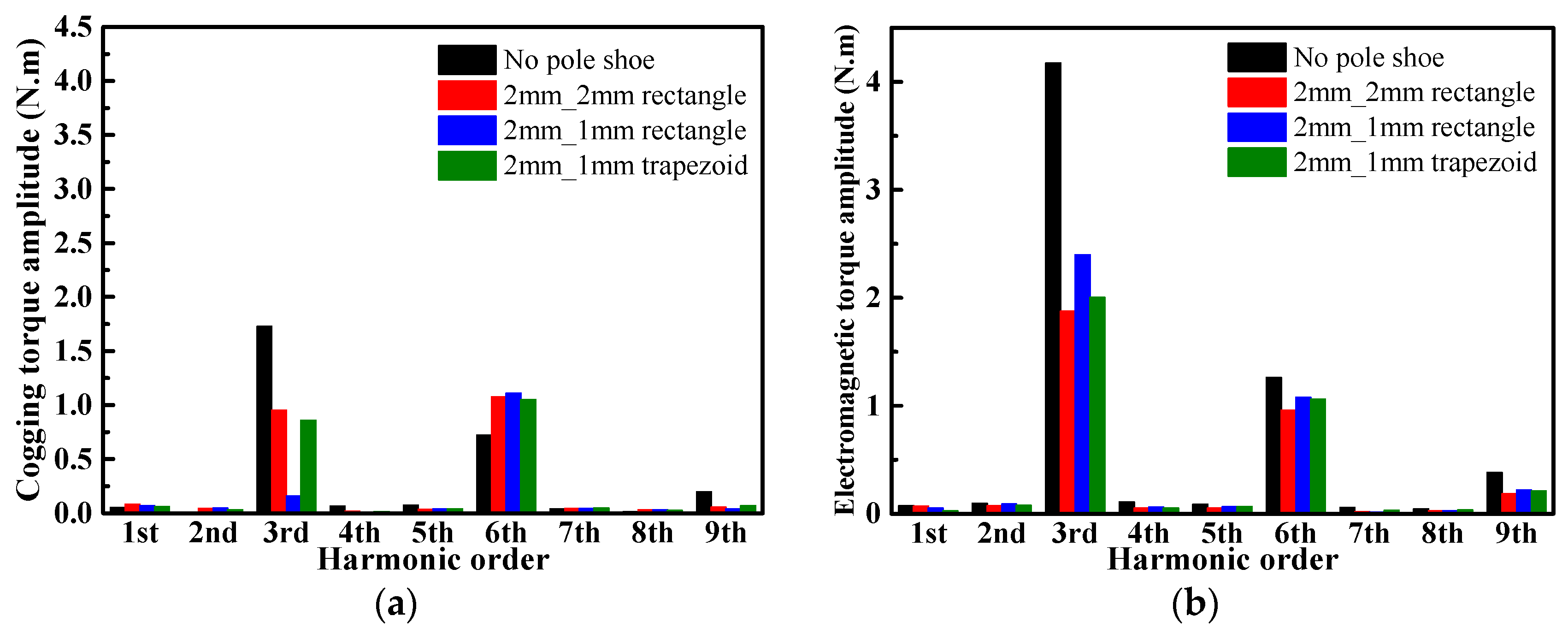
4.1. Stator Pole Shoe
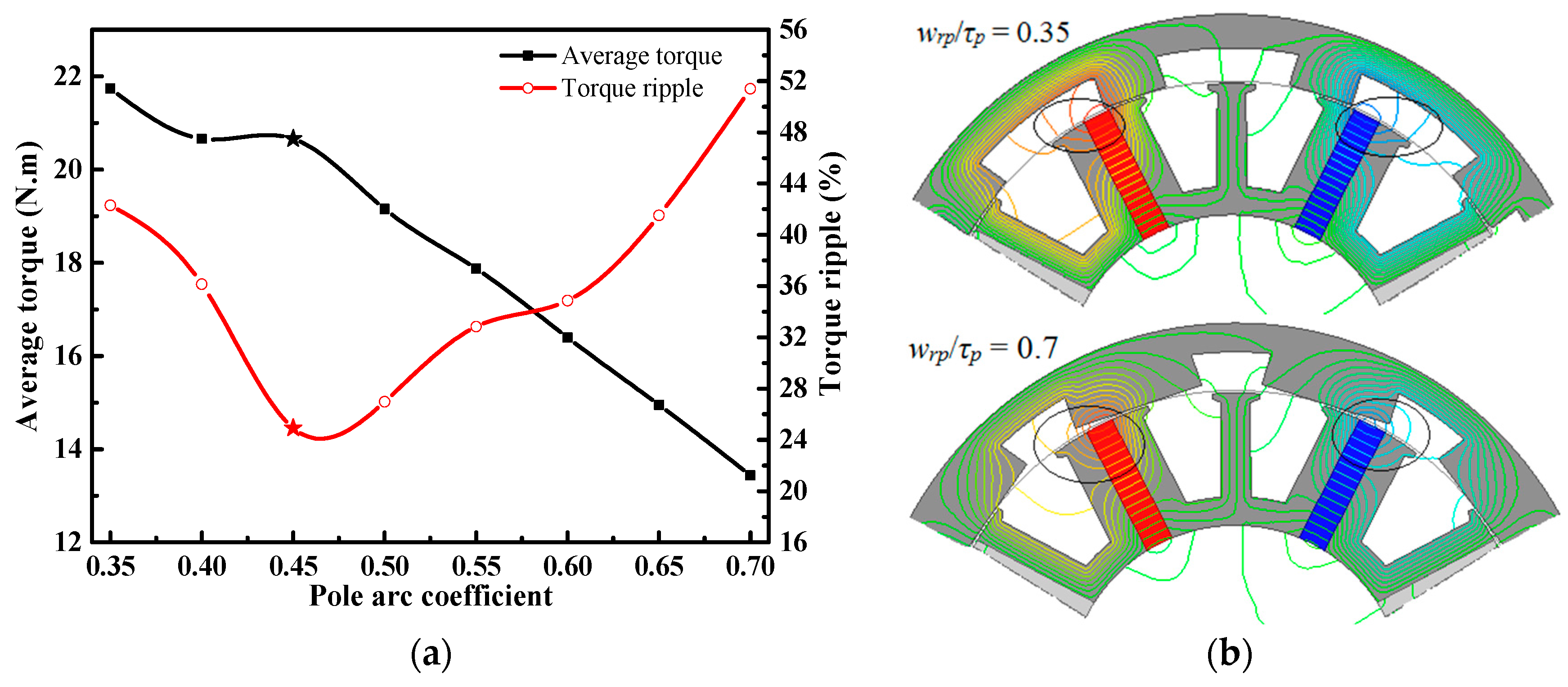
4.2. Rotor Pole Arc Coefficient
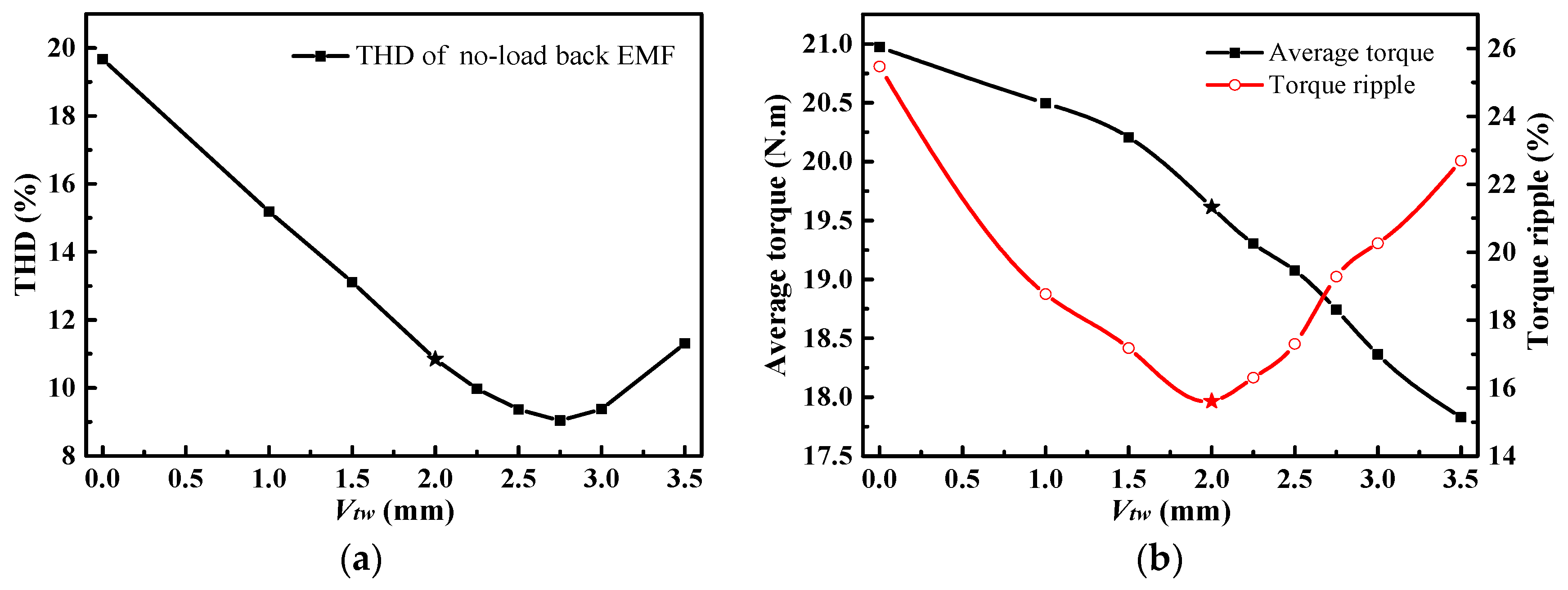
4.3. “V”-Shaped Laminated Segment Tooth Width
4.4. Analysis and Discussion
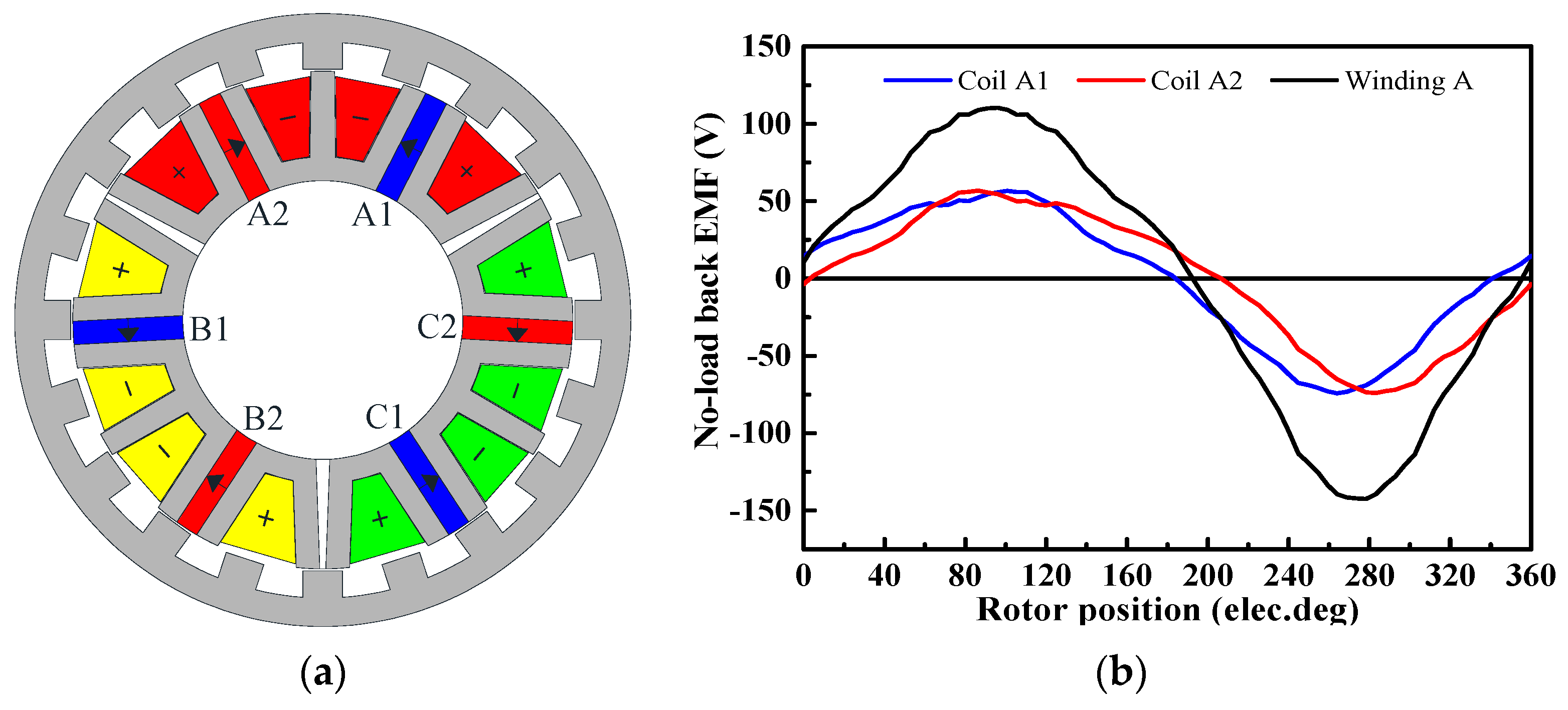
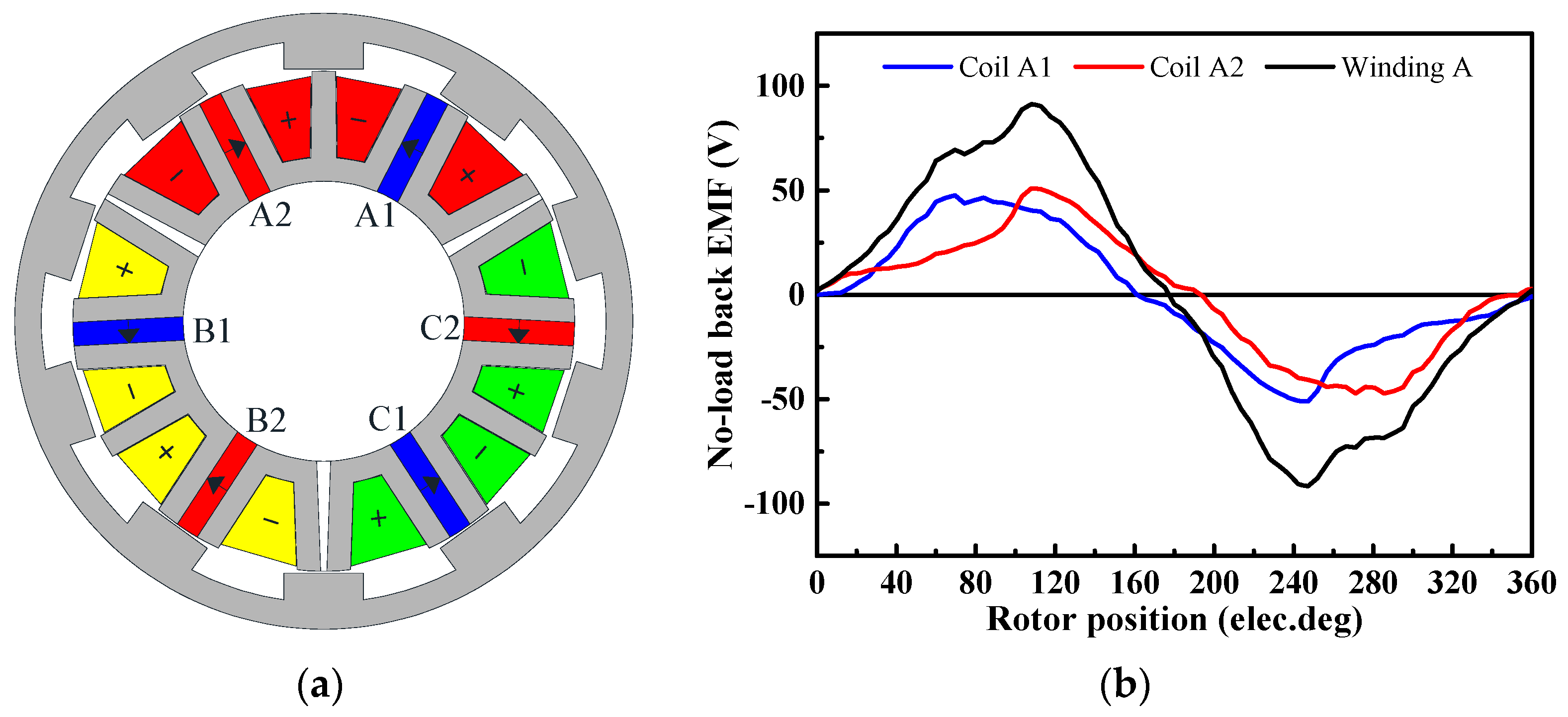
5. Comparison of the MSOR-FSPM Motor and COR-FSPM Motor
5.1. Parameters of the MSOR-FSPM Motor and COR-FSPM Motor
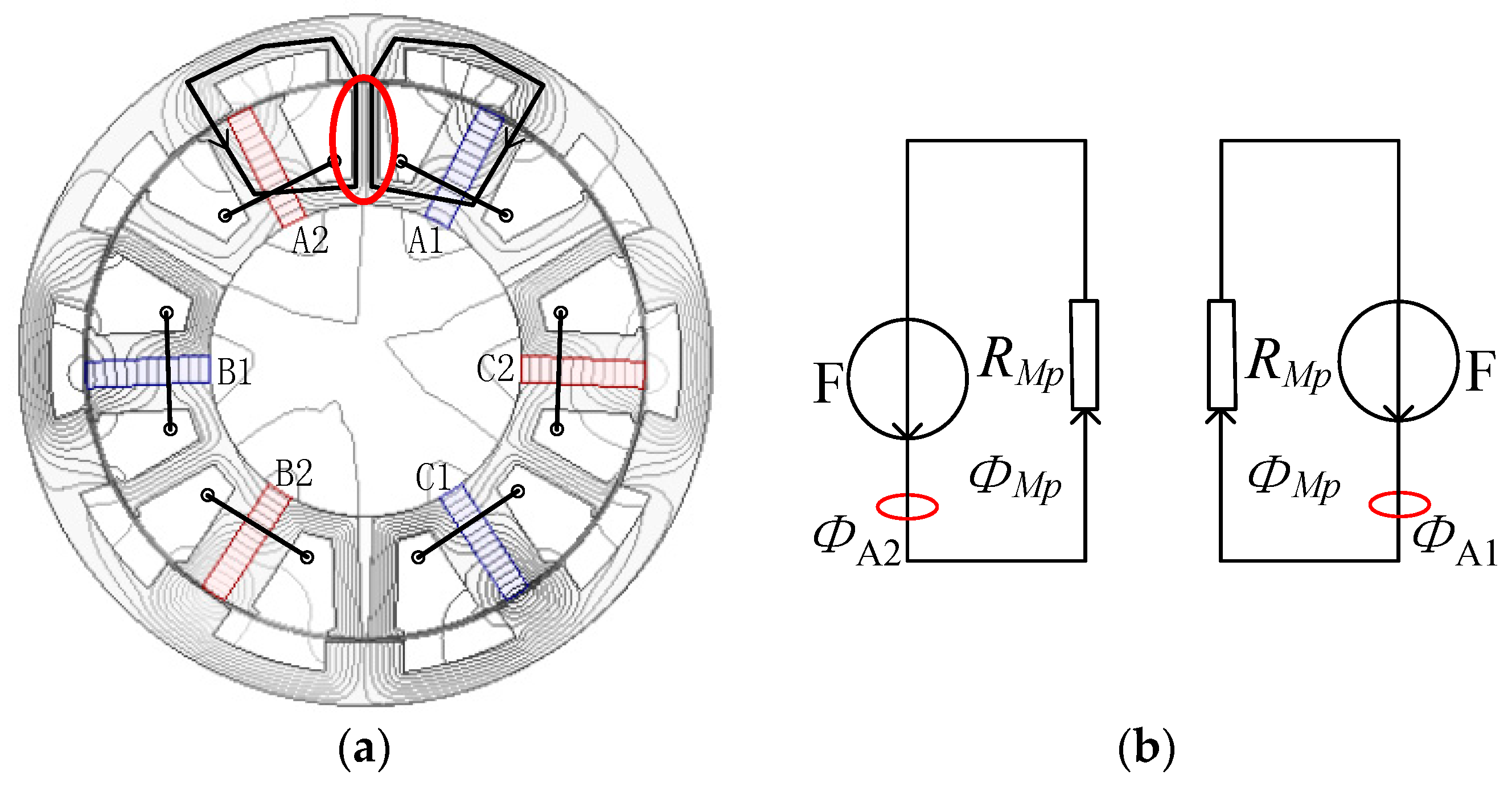
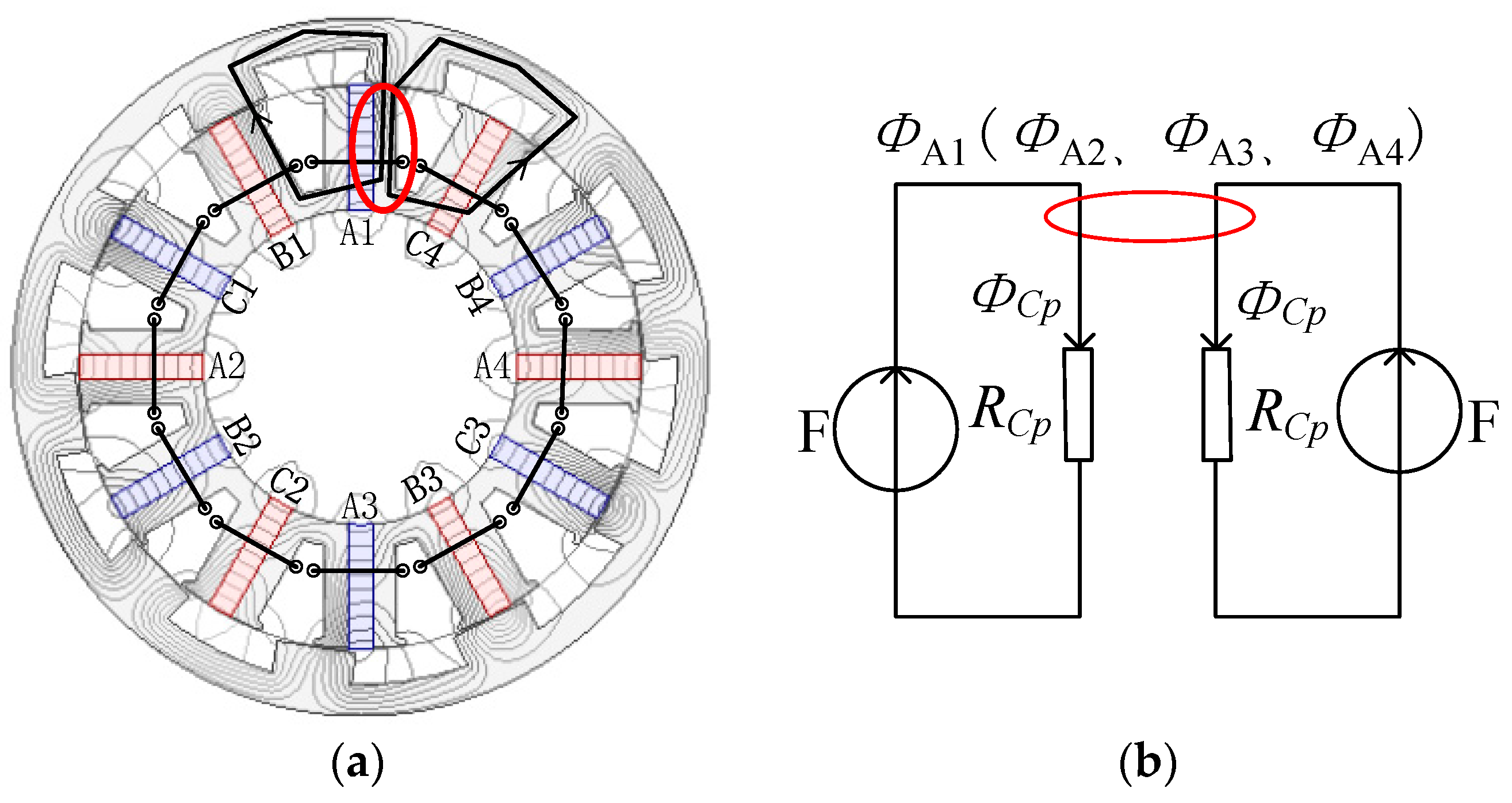
5.2. Analysis of Theory and Magnetic Circuit
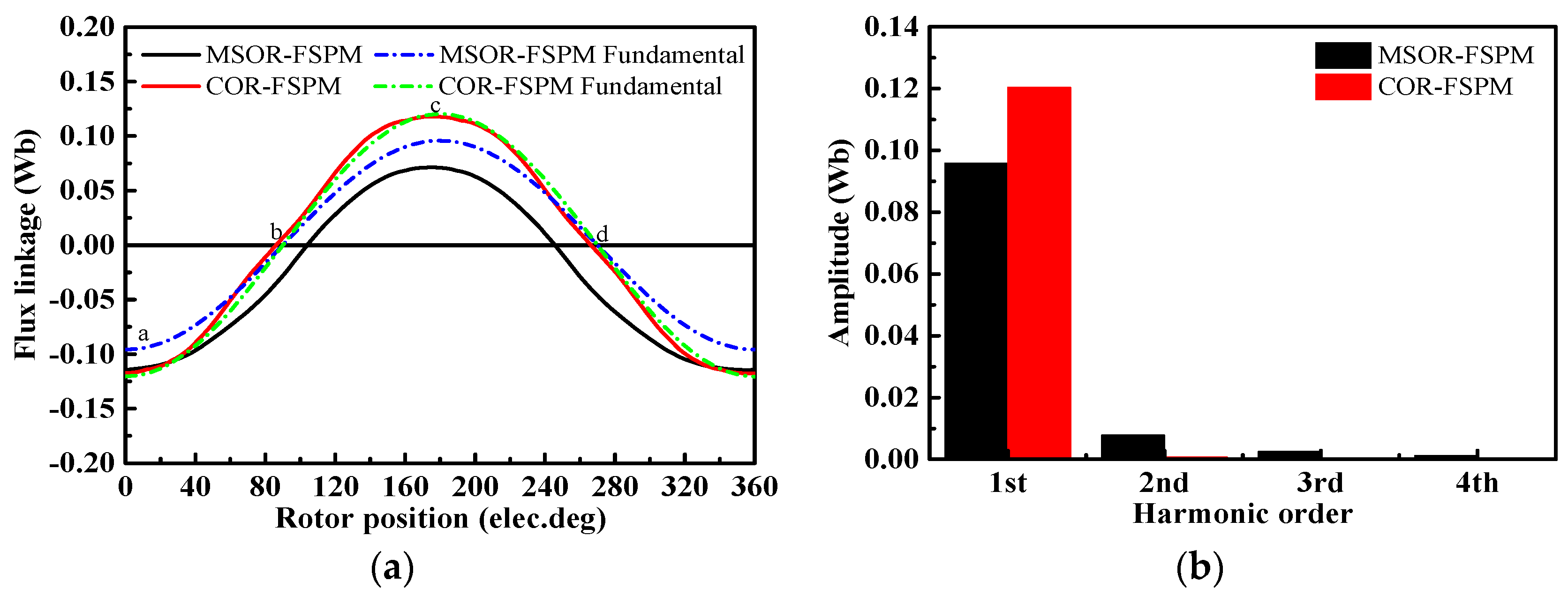
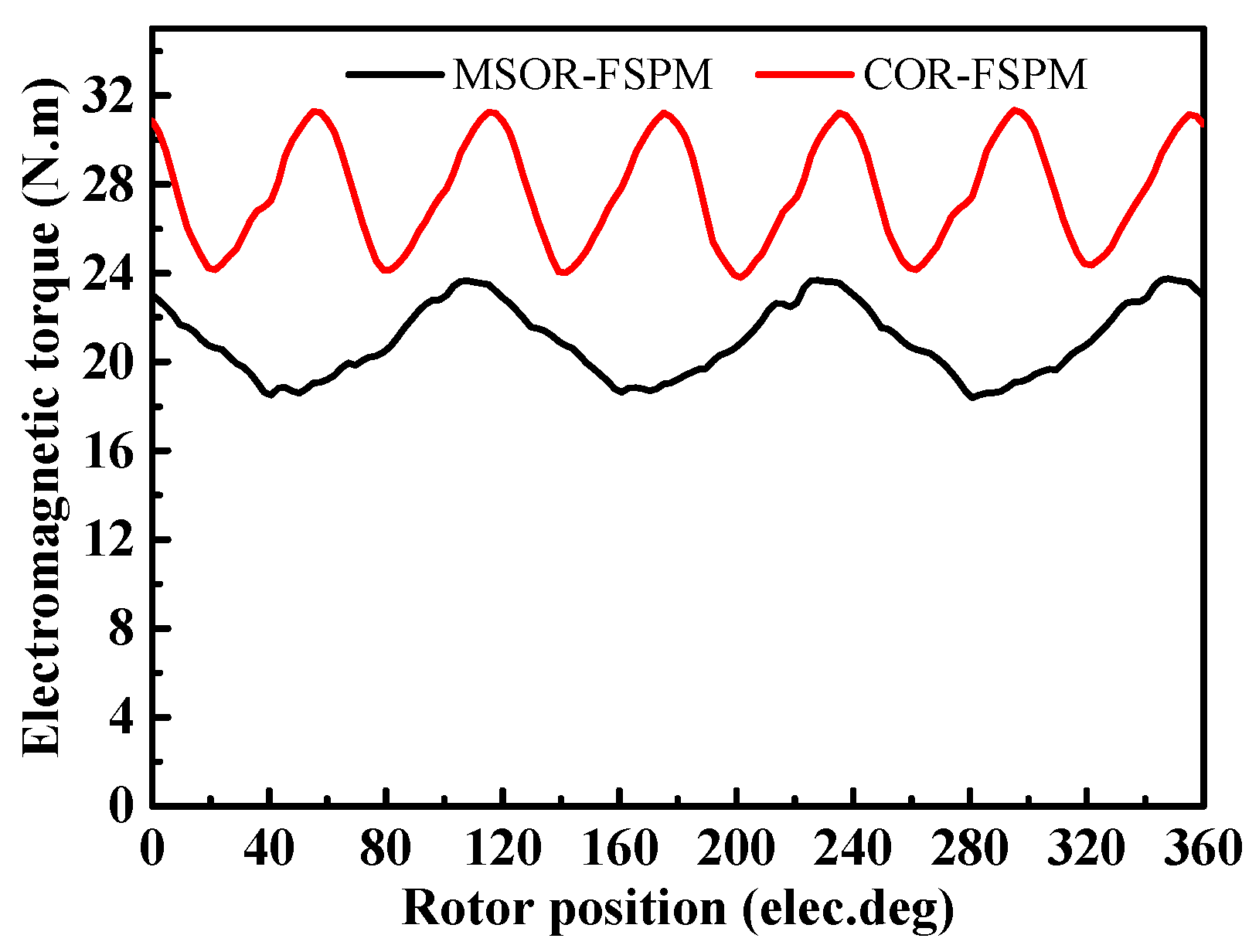
5.3. Validation by FEM
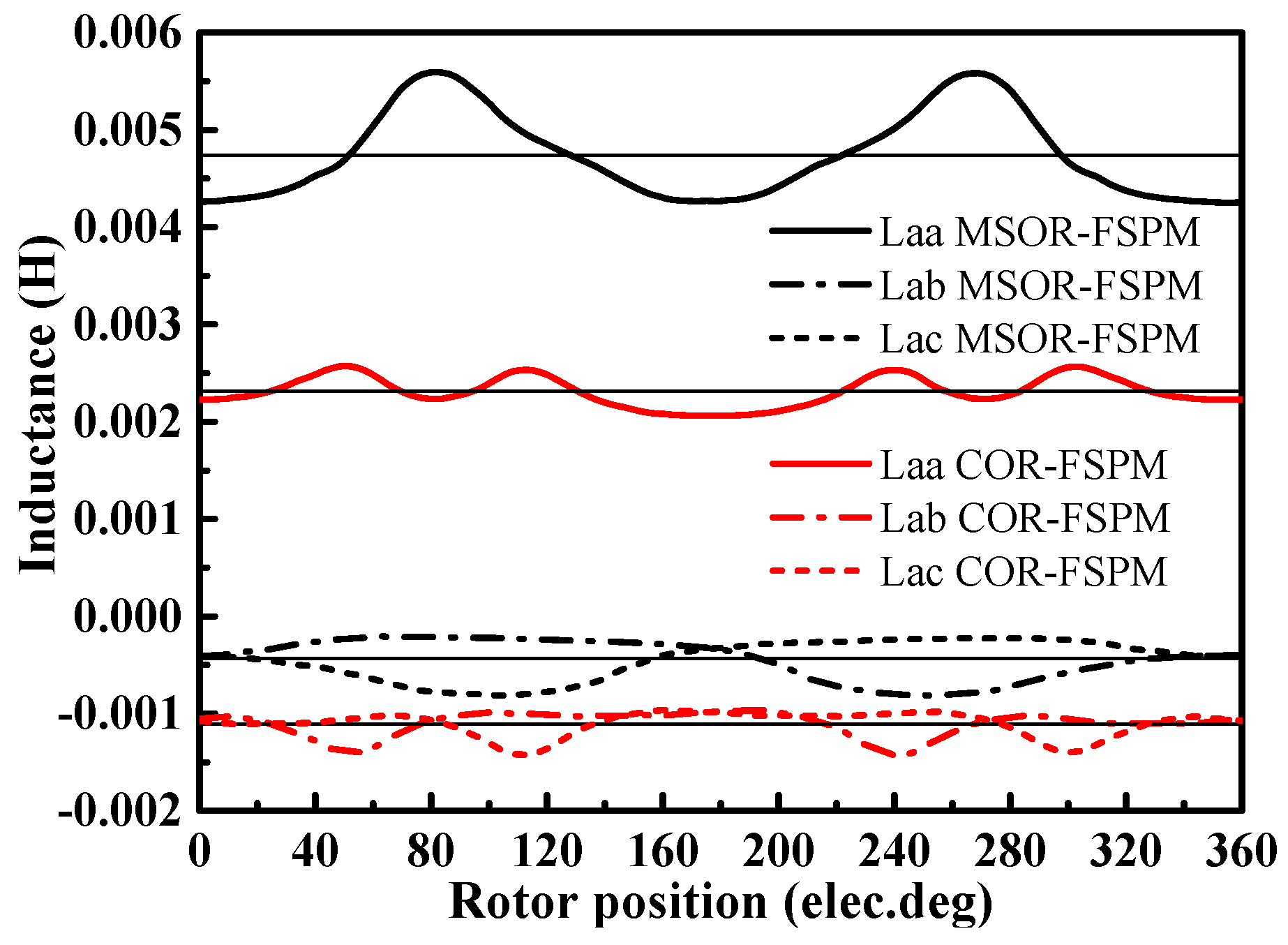
5.4. Inductance of the MSOR-FSPM Motor and COR-FSPM Motor
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chau, K.T.; Chan, C.C.; Liu, C. Overview of permanent-magnet brushless drives for electric and hybrid electric vehicles. IEEE Trans. Ind. Electron. 2008, 55, 2246–2257. [Google Scholar] [CrossRef]
- Zhu, X.Y.; Chen, L.; Li, Q.; Sun, Y.B.; Hua, W.; Wang, Z. A New Magnetic-Planetary-Geared Permanent Magnet Brushless Machine for Hybrid Electric Vehicle. IEEE Trans. Magn. 2012, 48, 4642–4645. [Google Scholar] [CrossRef]
- Ghariani, M.; Hachicha, M.R.; Ltifi, A.; Bensalah, I.; Ayadi, M.; Neji, R. Sliding mode control and neuro-fuzzy network observer for induction motor in EVs applications. Int. J. Electr. Hybrid Veh. 2011, 3, 20–46. [Google Scholar] [CrossRef]
- Arkkiol, A.; Jokinen, T.; Lantto, E. Design, simulation and construction of two synchronized DC motors’ driver for EVs. IEEE Trans. Electr. Mach. Syst. 2005, 2, 871–876. [Google Scholar]
- Pellegrino, G.; Vagati, A.; Boazzo, B.; Guglielmi, P. Comparison of induction and PM synchronous motor drives for EV application including design examples. IEEE Trans. Ind. Appl. 2012, 48, 2322–2332. [Google Scholar] [CrossRef]
- Zhu, X.Y.; Cheng, M.; Zhao, W.X.; Liu, C.H.; Chau, K.T. A transient cosimulation approach to performance analysis of hybrid excited doubly salient machine considering indirect field-circuit coupling. IEEE Trans. Magn. 2007, 43, 2558–2560. [Google Scholar] [CrossRef]
- Deodhar, R.P.; Andersson, S.; Boldea, I.; Miller, T.J.E. The flux-reversal machine: A new brushless doubly-salient permanent-magnet machine. IEEE Trans. Ind. Appl. 1997, 33, 925–934. [Google Scholar] [CrossRef]
- Li, D.W.; Qu, R.H.; Li, J.; Xu, W.; Wu, L.L. Synthesis of Flux Switching Permanent Magnet Machines. IEEE Trans. Energy Convers. 2016, 31, 1447–1453. [Google Scholar] [CrossRef]
- Abdollahi, S.E.; Vaez-Zadeh, S. Back-EMF analysis of a novel linear flux switching motor with segmented secondary. IEEE Trans. Magn. 2014, 50, 1–9. [Google Scholar] [CrossRef]
- Hua, W.; Zhu, Z.Q.; Cheng, M.; Pang, Y.; Howe, D. Comparison of Flux-Switching and Doubly-Salient Permanent Magnet Brushless Machines. In Proceedings of the Eighth International Conference on Electrical Machines and Systems (ICEMS 2005), Nanjing, China, 27–29 September 2005; pp. 165–170. [Google Scholar]
- Sulaiman, E.; Kosaka, T.; Matsui, N. Parameter optimization study and performance analysis of 6S-8P permanent magnet flux switching machine with field excitation for high speed hybrid electric vehicles. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications (EPE 2011), Birmingham, UK, 30 August–1 September 2011; pp. 1–9. [Google Scholar]
- Rauch, S.E.; Johnson, L.J. Design principles of flux-switching alternators. Trans. Ame. Inst. Electr. Eng. Part III Power Appar. Syst. 1995, 74, 1261–1268. [Google Scholar]
- Zhu, Z.Q.; Chen, J.T.; Pang, Y.; Howe, D.; Iwasaki, S.; Deodhar, R. Analysis of a Novel Multi-Tooth Flux-Switching PM Brushless AC Machine for High Torque Direct-Drive Applications. IEEE Trans. Magn. 2008, 44, 4313–4316. [Google Scholar] [CrossRef]
- Fei, W.Z.; Luk, P.C.K.; Shen, J.X. Torque Analysis of Permanent-Magnet Flux Switching Machines with Rotor Step Skewing. IEEE Trans. Magn. 2012, 48, 2664–2673. [Google Scholar] [CrossRef]
- Zulu, A.; Mecrow, B.C.; Armstrong, M. A Wound-Field Three-Phase Flux-Switching Synchronous Motor with All Excitation Sources on the Stator. IEEE Trans. Ind. Appl. 2010, 46, 2363–2371. [Google Scholar] [CrossRef]
- Hua, W.; Zhang, G.; Cheng, M. Flux-Regulation Theories and Principles of Hybrid-Excited Flux-Switching Machines. IEEE Trans. Ind. Electron. 2015, 62, 5359–5369. [Google Scholar] [CrossRef]
- Yu, F.; Cheng, M.; Chau, K.T.; Li, F. Control and Performance Evaluation of Multiphase FSPM Motor in Low-Speed Region for Hybrid Electric Vehicles. Energies 2015, 8, 10335–10353. [Google Scholar] [CrossRef]
- Aboelhassan, M.O.E.; Raminosoa, T.; Goodman, A.; Lillo, L.D.; Gerada, C. Performance Evaluation of a Vector-Control Fault-Tolerant Flux-Switching Motor Drive. IEEE Trans. Ind. Electron. 2013, 60, 2997–3006. [Google Scholar] [CrossRef]
- Mao, Y.X.; Liu, G.H.; Zhao, W.X.; Ji, J.H. Vibration prediction in fault-tolerant flux-switching permanent-magnet machine under healthy and faulty conditions. IET Electr. Power Appl. 2017, 11, 19–28. [Google Scholar] [CrossRef]
- Zhao, J.; Yan, Y.S.; Li, B.; Liu, X.D.; Chen, Z. Influence of Different Rotor Teeth Shapes on the Performance of Flux Switching Permanent Magnet Machines Used for Electric Vehicles. Energies 2014, 7, 8056–8075. [Google Scholar] [CrossRef]
- Ehsani, M.; Gao, Y.; Miller, J.M. Hybrid electric vehicles: Architecture and motor drives. IEEE Proc. 2007, 95, 719–728. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, M.J.; Shen, J.X.; Fei, W.Z.; Luk, P.C.K. An Outer-Rotor Flux-Switching Permanent Magnet Motor for Traction Applications. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition (ECCE 2010), Atlanta, GA, USA, 12–16 September 2010; pp. 1723–1730. [Google Scholar]
- Fei, W.Z.; Luk, P.C.K.; Shen, J.X.; Wang, Y.; Jin, M.J. A Novel Permanent-Magnet Flux Switching Machine with an Outer-Rotor Configuration for In-Wheel Light Traction Applications. IEEE Trans. Ind. Appl. 2012, 48, 1496–1506. [Google Scholar] [CrossRef]
- Zhu, X.Y.; Xiang, Z.X.; Zhang, C.; Quan, L.; Du, Y.; Gu, W.W. Co-Reduction of Torque Ripple for Outer Rotor Flux-Switching PM Motor Using Systematic Multi-Level Design and Control Schemes. IEEE Trans. Ind. Electron. 2017, 64, 1102–1112. [Google Scholar] [CrossRef]
- Hua, W.; Zhang, H.L.; Cheng, M.; Meng, J.J.; Hou, C. An Outer-Rotor Flux-Switching Permanent-Magnet-Machine with Wedge-Shaped Magnets for In-Wheel Light Traction. IEEE Trans. Ind. Electron. 2017, 64, 69–80. [Google Scholar] [CrossRef]
- Ahmad, M.Z.; Sulaiman, E.; Haron, Z.A.; Kosaka, T. Preliminary Studies on a New Outer-Rotor Permanent Magnet Flux Switching Machine with Hybrid Excitation Flux for Direct Drive EV Applications. In Proceedings of the 2012 IEEE International Conference on Power and Energy (PEcon 2012), Kota Kinabalu, Malaysia, 2–5 December 2012; pp. 928–933. [Google Scholar]
- Zhu, X.Y.; Shu, Z.M.; Quan, L.; Xiang, Z.X.; Pan, X.Q. Multi-Objective Optimization of an Outer-Rotor V-Shaped Permanent Magnet Flux Switching Motor Based on Multi-Level Design Method. IEEE Trans. Magn. 2016, 52, 8205508. [Google Scholar] [CrossRef]
- Hua, W.; Cheng, M.; Zhu, Z.Q.; Howe, D. Design of Flux-Switching Permanent Magnet Machine Considering the Limitation of Inverter and Flux-Weakening Capability. In Proceedings of the 2006 IEEE Industry Applications Conference/Forty-First IAS Annual Meeting, Tampa, FL, USA, 8–12 October 2006; pp. 2403–2410. [Google Scholar]
- Liu, X.D.; Gu, Z.X.; Zhao, J. Torque ripple reduction of a novel modular arc-linear flux-switching permanent-magnet motor with rotor step skewing. Energies 2016, 9, 404–421. [Google Scholar] [CrossRef]
- Sikder, C.; Husain, I.; Wen, O. Cogging Torque Reduction in Flux-Switching Permanent-Magnet Machines by Rotor Pole Shaping. IEEE Trans. Ind. Appl. 2015, 51, 3609–3619. [Google Scholar] [CrossRef]



| Symbol | Machine Parameter | MSOR-FSPM | Unit |
|---|---|---|---|
| m | Phase number | 3 | |
| Ns | Number of stator poles | 12 | |
| Nr | Number of rotor poles | 10 | |
| α | Rotor pole arc coefficient | 0.5 | |
| Ncoil | Number of turns per coil | 70 | |
| PM | Magnet material | NTP40UH | |
| n | Base speed | 800 | r/min |
| Pout | Based output power | 1.5 | kW |
| Dro | Rotor outer diameter | 155 | mm |
| Dsi | Stator inner diameter | 70 | mm |
| Dso | Stator outer diameter | 125 | mm |
| wst | Stator tooth width | 5.5 | mm |
| lef | Motor active length | 100 | mm |
| hrp | Rotor pole height | 7.5 | mm |
| hry | Rotor yoke height | 7 | mm |
| wrp | Rotor pole width | 19.8 | mm |
| lg | Air gap length | 0.5 | mm |
| Br | Magnet remanence (20 °C) | 1.26 | T |
| Ismax | Rated current amplitude | 15.4 | A |
| Main Parameter | 10P | 11P | 22P | 23P |
|---|---|---|---|---|
| τc (°) | 36 | 32.73 | 32.72 | 31.30 |
| τm (°) | 54 | 49.09 | 57.27 | 54.78 |
| τd (°) | 120 | 120 | 120 | 120 |
| τp (°) | 36 | 32.73 | 16.36 | 15.65 |
| n | 1 | 1 | 2 | 2 |
| i | 1 | 1 | 3 | 3 |
| j | 3 | 3 | 7 | 7 |
| l | 0 | 1 | 0 | 1 |
| Performance | Initial Motor | hw, hh = “2 mm_1 mm Trapezoid“ | wrp/τp = 0.45 | Vtw = 2.0 mm | Optimized Motor |
|---|---|---|---|---|---|
| Cogging torque (N·m) | 4.60 | 3.64 | 5.29 | 3.66 | 3.66 |
| Average electromagnetic torque (N·m) | 19.97 | 19.15 | 20.66 | 19.61 | 19.61 |
| Torque ripple (%) | 47.08 | 26.98 | 24.92 | 15.61 | 15.61 |
| Symbol | Machine Parameter | MSOR-FSPM | COR-FSPM | Unit |
|---|---|---|---|---|
| α | Rotor pole arc coefficient | 0.45 | ||
| wrp | Rotor pole width | 17.8 | mm | |
| ht | Pole shoe thickness | 2 | mm | |
| hw | Pole shoe width | 2 | mm | |
| hh | Pole shoe height | 1 | mm | |
| Ncoil | Number of turns per coil | 70 | 35 | |
| Sslot | Area per phase | 955.44 | 785.28 | mm2 |
| Vpm | Volume of PMs | 97,185 | 179,850 | mm2 |
| Performance | MSOR-FSPM-1 | MSOR-FSPM-2 | COR-FSPM |
|---|---|---|---|
| Ratio of PM volume (%) | 54.04 | 54.04 | 100 |
| ΨPM_d (Wb) | 0.09586 | 0.11092 | 0.12039 |
| Ratio of ΨPM_d (%) | 79.62 | 92.13 | 100 |
| Average torque calculated indirectly (N·m) | 22.14 | 25.62 | 27.81 |
| Ratio of average torque calculated indirectly (%) | 79.61 | 92.12 | 100 |
| Average torque calculated directly (N·m) | 20.97 | 23.98 | 27.61 |
| Ratio of average torque calculated directly (%) | 75.95 | 86.53 | 100 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Zheng, Y.; Zhu, C.; Liu, X.; Li, B. A Novel Modular-Stator Outer-Rotor Flux-Switching Permanent-Magnet Motor. Energies 2017, 10, 937. https://doi.org/10.3390/en10070937
Zhao J, Zheng Y, Zhu C, Liu X, Li B. A Novel Modular-Stator Outer-Rotor Flux-Switching Permanent-Magnet Motor. Energies. 2017; 10(7):937. https://doi.org/10.3390/en10070937
Chicago/Turabian StyleZhao, Jing, Yun Zheng, Congcong Zhu, Xiangdong Liu, and Bin Li. 2017. "A Novel Modular-Stator Outer-Rotor Flux-Switching Permanent-Magnet Motor" Energies 10, no. 7: 937. https://doi.org/10.3390/en10070937
APA StyleZhao, J., Zheng, Y., Zhu, C., Liu, X., & Li, B. (2017). A Novel Modular-Stator Outer-Rotor Flux-Switching Permanent-Magnet Motor. Energies, 10(7), 937. https://doi.org/10.3390/en10070937




