Numerical Analysis of Flatback Trailing Edge Airfoil to Reduce Noise in Power Generation Cycle
Abstract
:1. Introduction
2. Methodology
2.1. Large Eddy Simulation
2.2. Acoustic Analogy
- The procedure starts with a sequence of emission times (conveniently taken as the flow times).
- The source strengths are calculated (thickness surface noise and loading surface noise) at all source elements (faces of the integration surfaces) for a given emission time.
- The contributions of the sources are interpolated in the far-field time domain to build the sound signal.
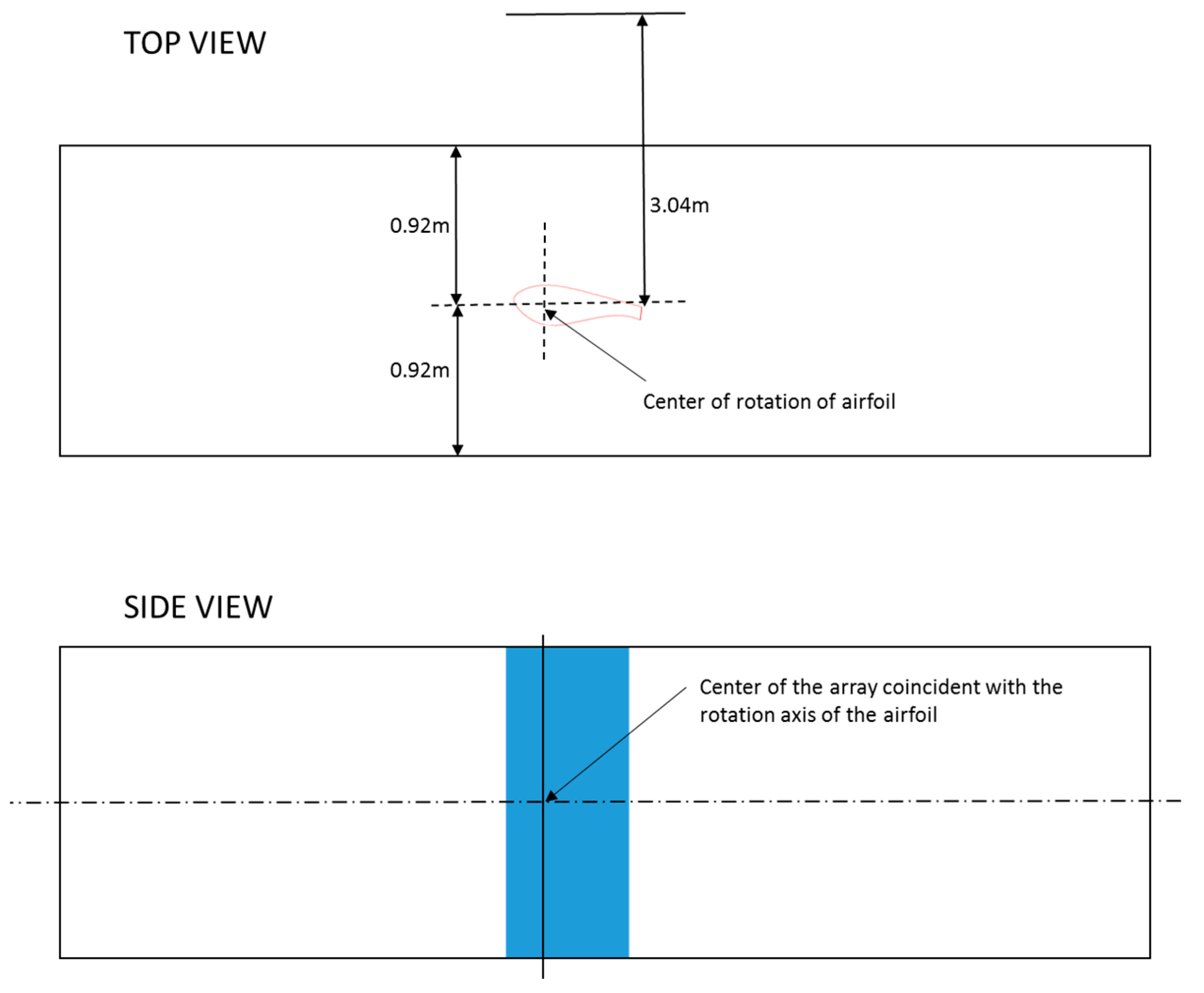
2.3. Numerical Conditions
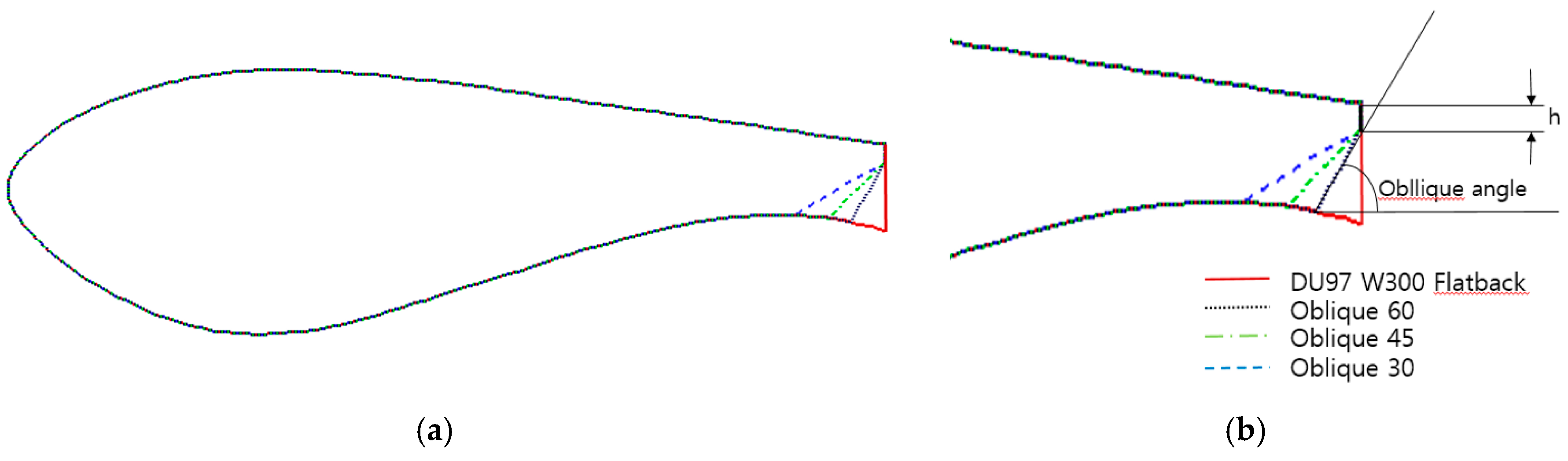
2.4. Test Cases
3. Results and Discussion
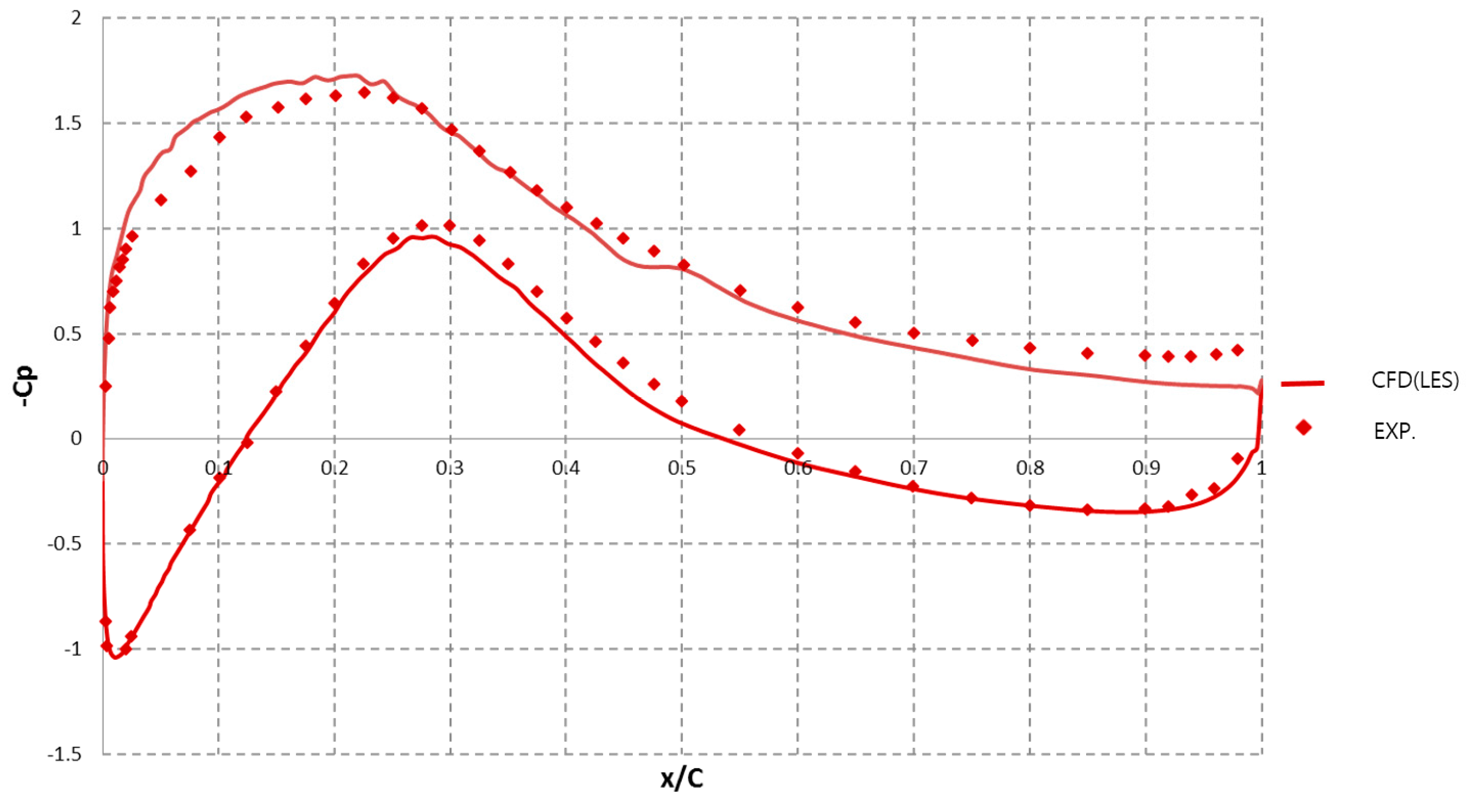
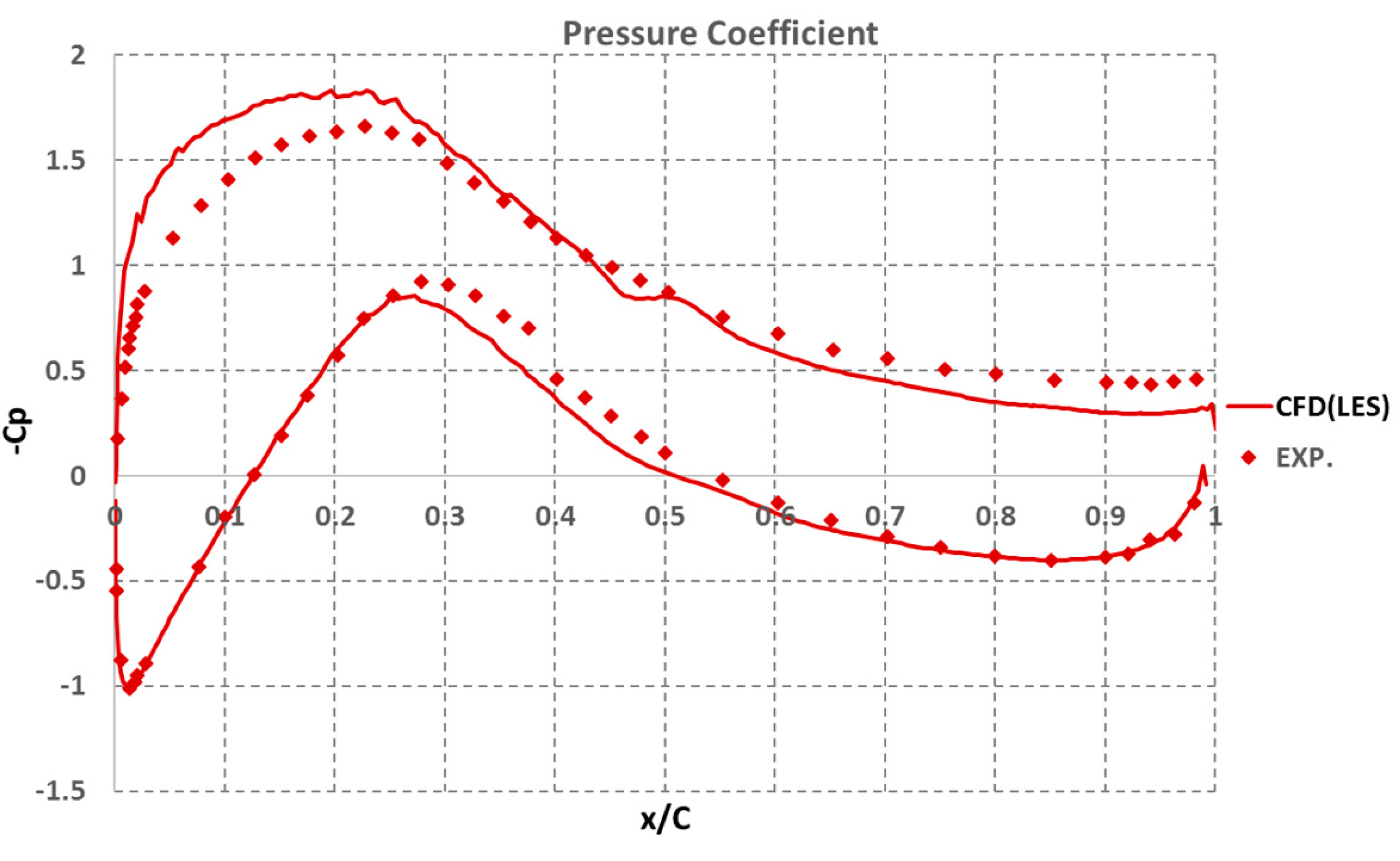
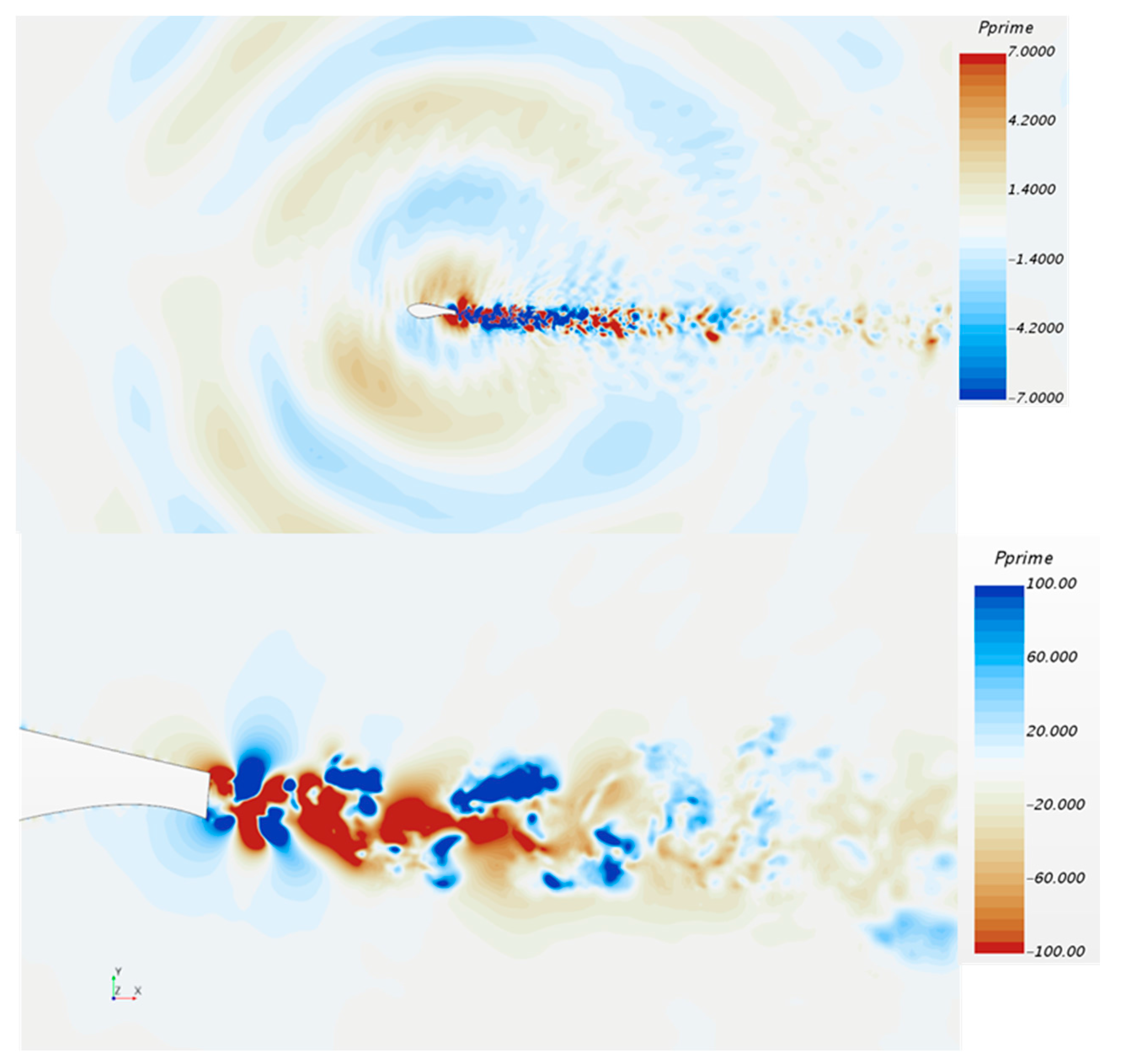
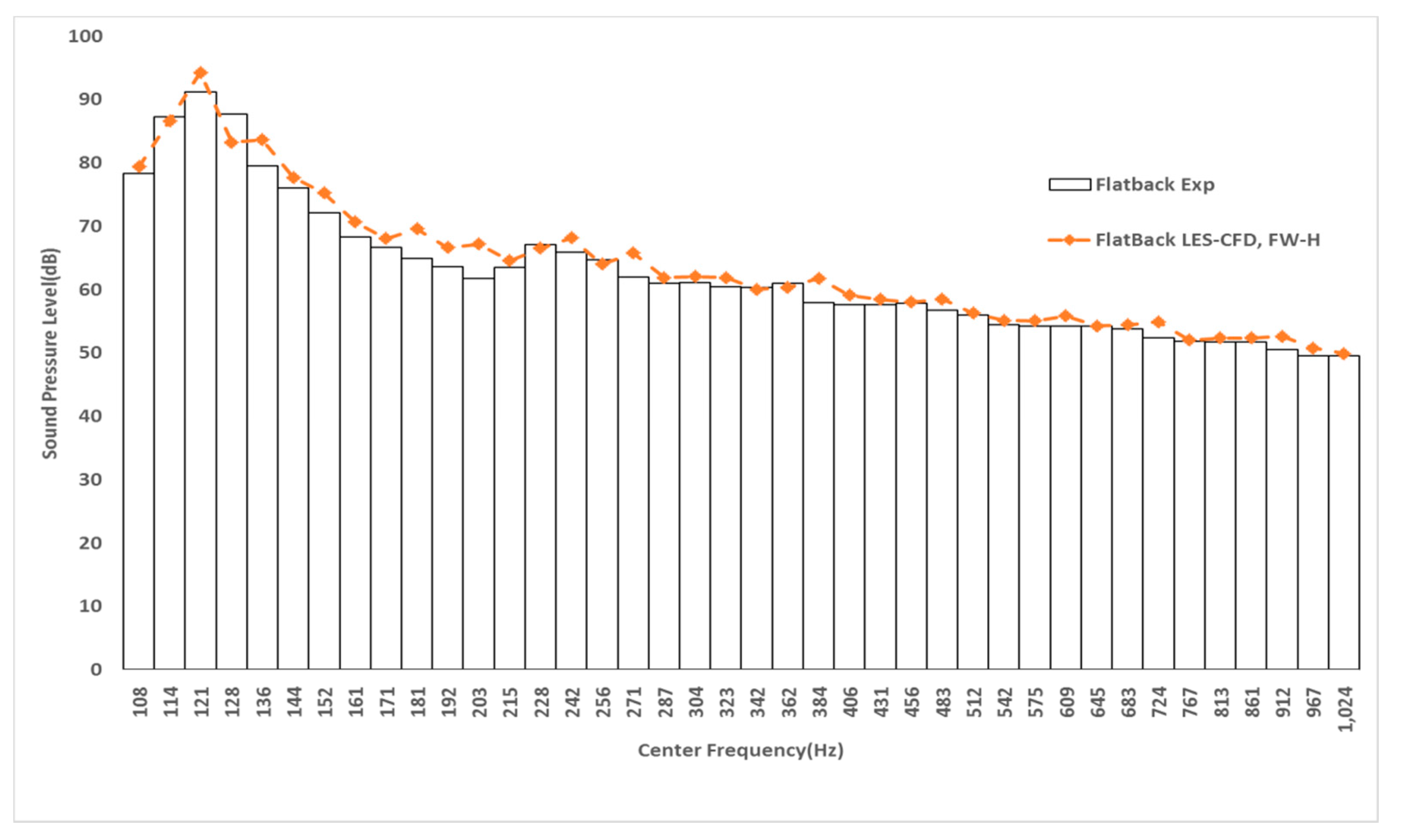
3.1. Validation of Aerodynamic and Aero-Acoustic Results
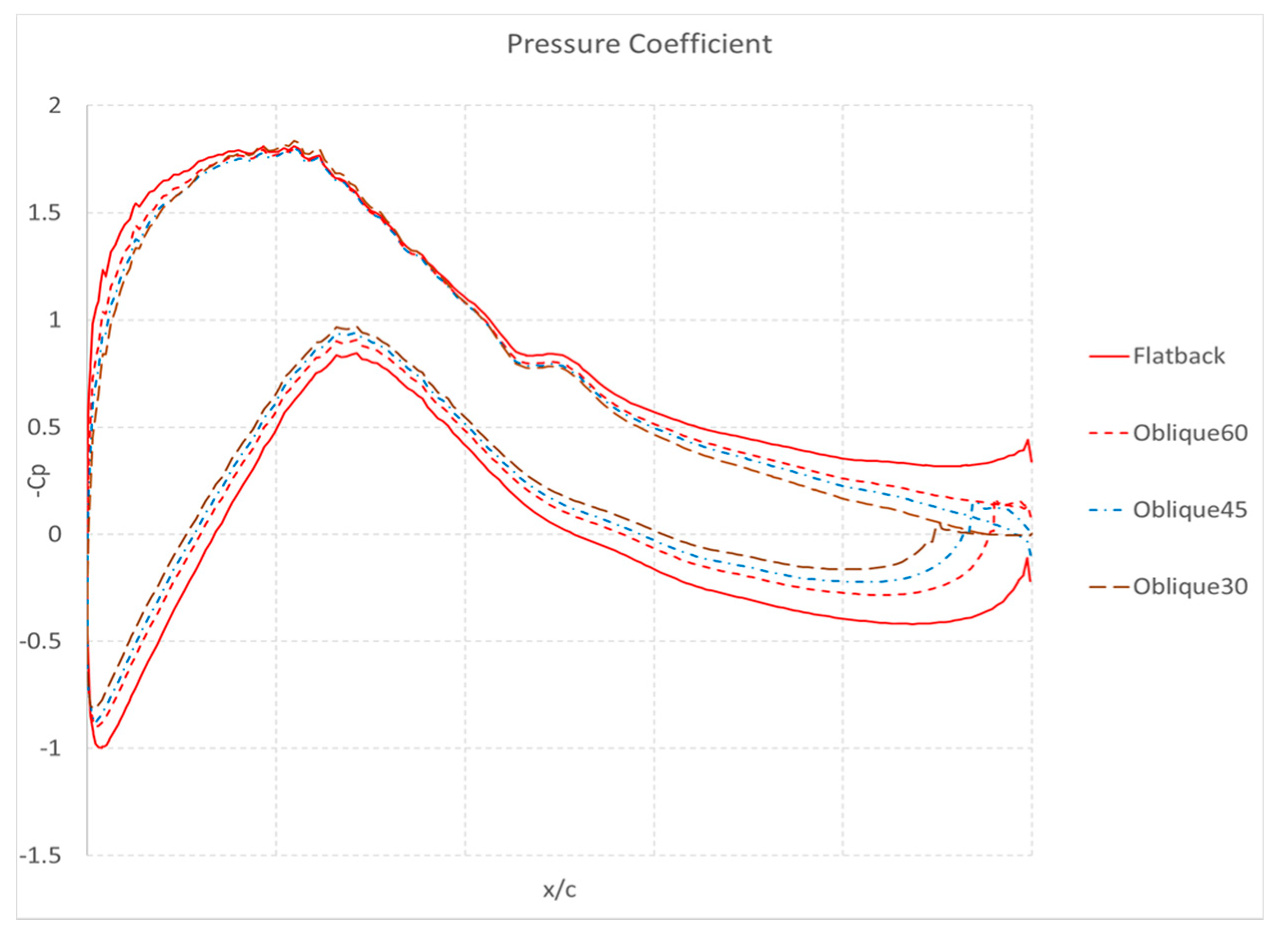
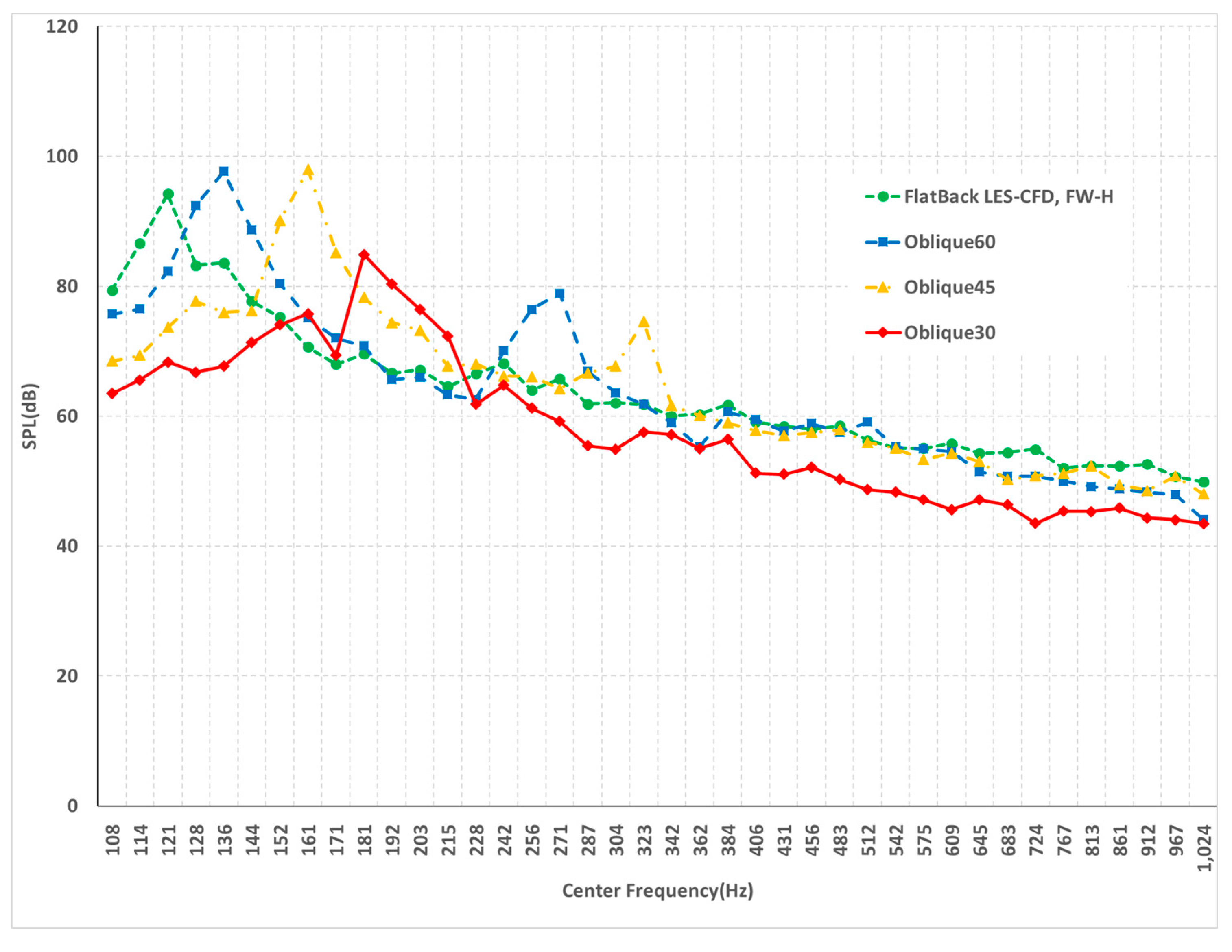
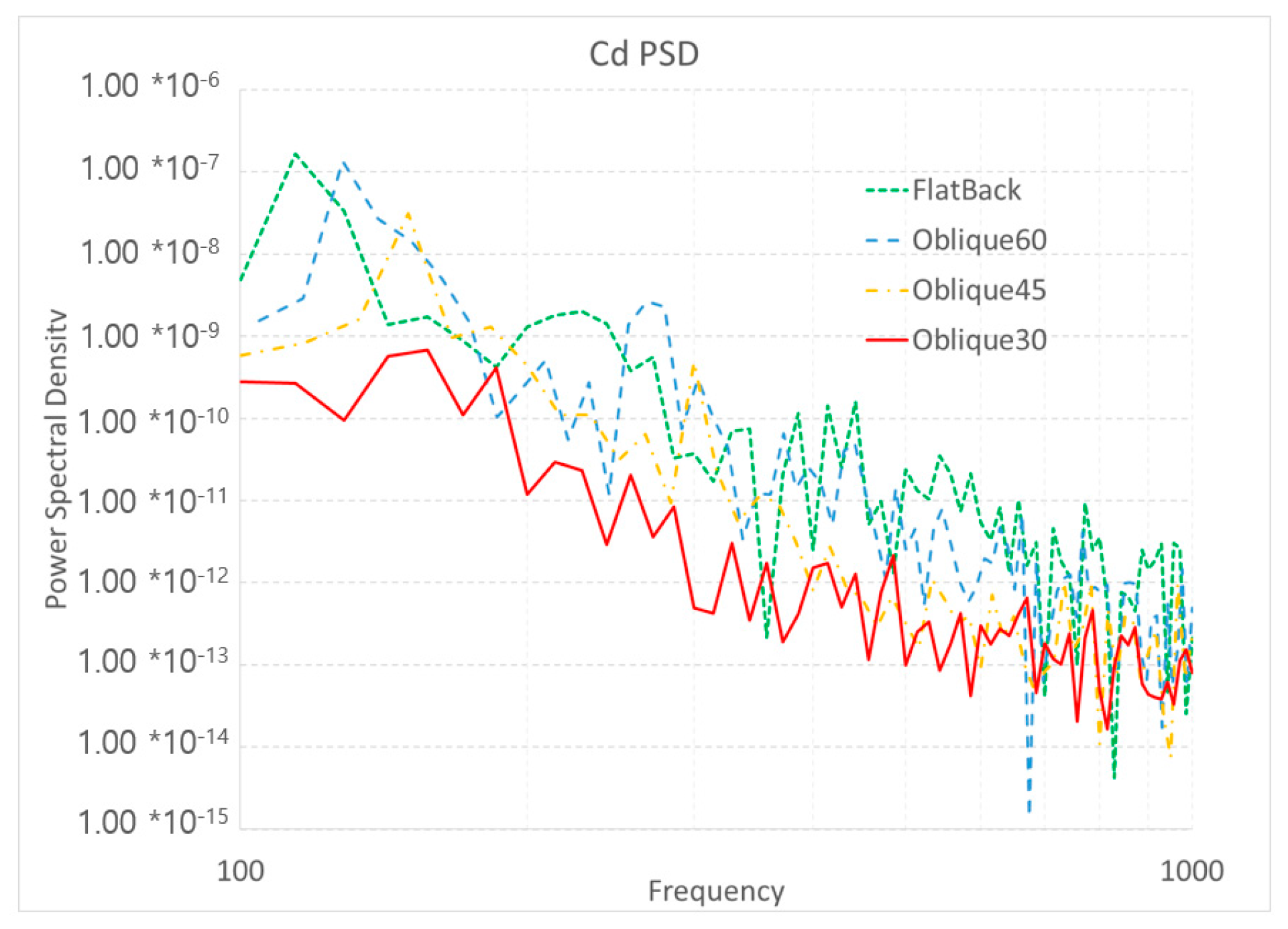
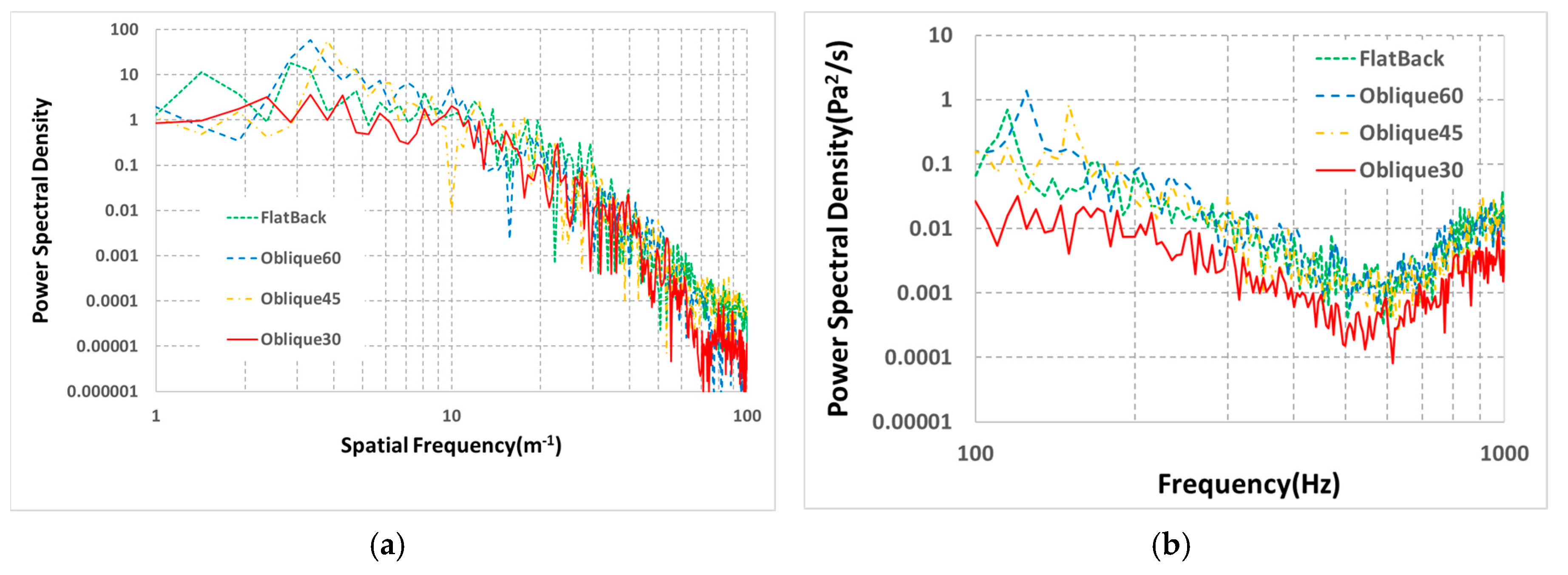
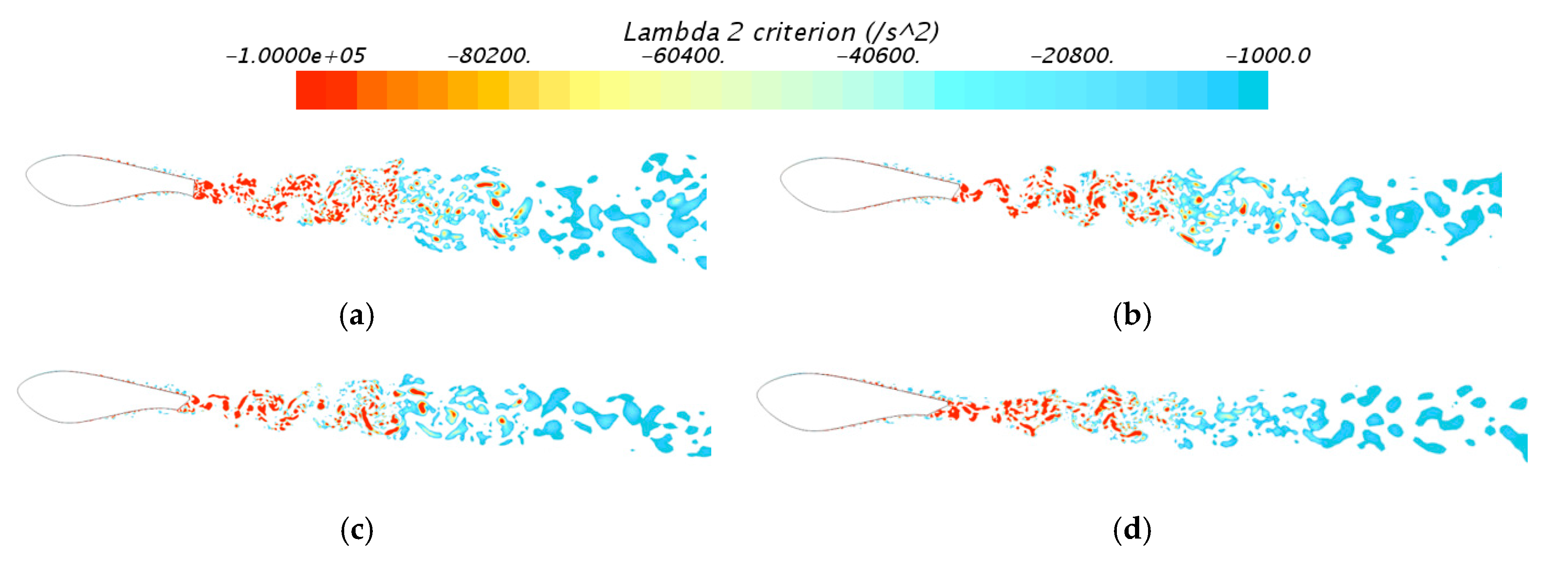
3.2. Noise Analysis of Oblique Trailing Edge Airfoils
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lowson, M.V. Reduction of compressor noise radiation. J. Acoust. Soc. Am. 1968, 43, 37–47. [Google Scholar] [CrossRef]
- Tyler, J.; Sofrin, T. Axial flow compressor noise studies. SAE Trans. 1962, 70, 309. [Google Scholar]
- Horlock, J.H. Turbomachinery noise technology. J. Fluids Eng. 1975, 97, 283–284. [Google Scholar] [CrossRef]
- Thompson, B.E.; Whitelaw, J.H. Flow-around airfoils with blunt, round, and sharp trailing edges. J. Aircr. 1988, 25, 334–342. [Google Scholar] [CrossRef]
- Sant, R.; Ayuso, L.; Meseguer, J. Influence of open trailing edge on laminar aerofoils at low Reynolds number. Proc. Inst. Mechan. Eng. Part G J. Aerosp. Eng. 2013, 227, 1456–1467. [Google Scholar] [CrossRef]
- Available online: https://en.wikipedia.org/wiki/File:Axial_geometry.jpg (accessed on 4 April 2017).
- Herrig, L.J.; Emery, J.C.; Erwin, J.R. Effect of Section Thickness and Trailing Edge Radius on the Performance of NACA 65-Series Compressor Blade in Cascade at Low Speeds. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19930086925.pdf (accessed on 24 June 2017).
- Emery, J.C.; Herrig, L.J.; Erwin, J.R.; Felix, A.R. Systematic Two-Dimensional Cascade Tests of NACA 65-Series Compressor Blades at Low Speeds. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19930084843.pdf (accessed on 24 June 2017).
- Suder, K.L.; Chima, R.V.; Strazisar, A.J.; Roberts, W.B. The effect of adding roughness and thickness to a transonic axial compressor rotor. J. Turbomach. 1995, 117, 419–505. [Google Scholar] [CrossRef]
- Roelke, R.J.; Haas, J.E. The effect of rotor blade thickness and surface finish on the performance of a small axial flow turbine. J. Eng. Power 1983, 105, 377–382. [Google Scholar] [CrossRef]
- Ghedin, F. Structural Design of a 5 MW Wind Turbine Blade Equipped with Boundary Layer Suction Technology—Analysis and Lay-Up Optimisation Applying a Promising Technology. Master’s Thesis, TU Delft, Delft, The Netherlands, 2010. [Google Scholar]
- Van Dam, C.P. Research on Thick Blunt Trailing Edge Wind Turbine Airfoils. Available online: http://windpower.sandia.gov/2008BladeWorkshop/PDFs/Tues-05-vanDam.pdf (accessed on 24 June 2017).
- Jackson, K.J.; Zuteck, M.D.; van Dam, C.P.; Berry, D. TPI composites, innovative design approaches for large wind turbine blades—Final report. Wind Energy 2005, 8, 141–171. [Google Scholar] [CrossRef]
- Van Dam, C.P.; Mayda, E.A.; Chao, D.D. Computational Design and Analysis of Flatback Airfoil Wind Tunnel Experiment. Available online: http://prod.sandia.gov/techlib/access-control.cgi/2008/081782.pdf (accessed on 24 June 2017).
- Cooperman, A.M.; McLennan, A.W.; Chow, R.; Baker, J.P.; van Dam, C.P. Aerodynamic performance of thick blunt trailing edge airfoils. In Proceedings of the 28th AIAA Applied Aerodynamics Conference, Chicago, IL, USA, 28 June 2010–1 July 2010. [Google Scholar]
- Nedić, J.; Vassilicos, J.C. Vortex shedding and aerodynamic performance of airfoil with multiscale trailing-edge modifications. AIAA J. 2015, 53, 3240–3250. [Google Scholar]
- Němec, J. Noise of axial fans and compressors: Study of its radiation and reduction. J. Sound Vib. 1967, 6, 230–236. [Google Scholar] [CrossRef]
- Hubbard, H.H.; Lansing, D.L.; Runyan, H.L. A review of rotating blade noise technology. J. Sound Vib. 1971, 19, 227–249. [Google Scholar] [CrossRef]
- Nash, E.C.; Lowson, M.V.; McAlpine, A. Boundary-layer instability noise on aerofoils. J. Fluid Mech. 1999, 382, 27–61. [Google Scholar] [CrossRef]
- Simley, E.; Moriarty, P.; Palo, S. Aeroacoustic noise measurements of a wind turbine with BSDS blades using an acoustic array. In Proceedings of the AIAA Aerospace Sciences Meeting, Orlando, FL, USA, 4–7 January 2010. [Google Scholar]
- Manela, A. Nonlinear effects of flow unsteadiness on the acoustic radiation of a heaving airfoil. J. Sound Vib. 2013, 332, 7076–7088. [Google Scholar] [CrossRef]
- Svennberg, U.; Fureby, C. Vortex-shedding induced trailing-edge acoustics. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar]
- Meher-Homji, C.B. Blading vibration and failures in gas turbines part B: Compressor and turbine airfoil distress. In Proceedings of the International Gas Turbine and Aemengine Congress and Exposition, Houston, TX, USA, 5–8 June 1995. [Google Scholar]
- Brooks, T.F.; Hodgson, T.H. Trailing edge noise prediction from measured surface pressure. J. Sound. Vib. 1981, 78, 69–117. [Google Scholar] [CrossRef]
- Williams, F.J.; Hawkings, D. Sound generated by turbulence and surface in arbitrary motion. Philos. Trans. Roy. Soc. Lond. A 1969, 264, 321–342. [Google Scholar] [CrossRef]
- Blake, W.K.; Gershfeld, J.L. The aeroacoustics of trailing edges. Front. Exp. Fluid Mech. 1989, 46, 457–532. [Google Scholar]
- Prasad, A.; Williamson, C.H.K. The instability of the shear layer separating from a bluff body. J. Fluid Mech. 1997, 333, 375–402. [Google Scholar] [CrossRef]
- Shannon, D.W.; Morris, S.C. Experimental investigation of a blunt trailing edge flow field with application to sound generation. Exp. Fluids 2006, 41, 777–788. [Google Scholar] [CrossRef]
- Huerre, P.; Monkewitz, P.A. Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 1990, 22, 473–537. [Google Scholar] [CrossRef]
- Desquesnes, G.; Terracol, M.; Sagaut, P. Numerical investigation of the tone noise mechanism over laminar airfoils. J. Fluid Mech. 2007, 591, 155–182. [Google Scholar] [CrossRef]
- Berg, D.E.; Zayas, J.R. Aerodynamic and aeroacoustic properties of flatback airfoils. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008. [Google Scholar]
- Kim, T.; Jeon, M.; Lee, S.; Shin, H. Numerical simulation of flatback airfoil aerodynamic noise. Renew. Energy 2014, 65, 192–201. [Google Scholar] [CrossRef]
- Kim, T.; Lee, S. Aeroacoustic simulations of a blunt trailing-edge wind turbine airfoil. J. Mech. Sci. Technol. 2014, 28, 1–9. [Google Scholar] [CrossRef]
- Van Dam, C.P.; Kahn, D.L. Trailing Edge Modifications for Flatback Airfoils. Available online: http://prod.sandia.gov/techlib/access-control.cgi/2008/081781.pdf (accessed on 24 June 2017).
- Barone, M.F.; Berg, D.E.; Devenport, W.J.; Burdisso, R. Aerodynamic and Aeroacoustic Tests of a Flatback Version of the DU97-W-300 Airfoil; SAND2009-4185, Sandia Report; Sandia National Laboratories: Albuquerque, NM, USA, 2009. [Google Scholar]
- Stone, C.; Barone, M.; Smith, M.; Lynch, E. A comparative study of the aerodynamics and aeroacoustics of a flatback airfoil using hybrid RANS-LES. In Proceedings of the ASME Wind Energy Symposium, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Fosas de Pando, M.; Schmid, P.J.; Sipp, D. Tonal noise generation in the flow around an aerofoil: A global stability analysis. In Proceedings of the 21ème Congrès Français de Mècanique, Bordeaux, French, 26–30 August 2013. [Google Scholar]
- Mitchell, B.E.; Lele, S.K.; Moin, P. Direct computation of the sound from a compressible co-rotating vortex pair. J. Fluid Mech. 1995, 285, 181–202. [Google Scholar] [CrossRef]
- Tomoaki, I.; Takashi, A.; Shohei, T. Direct simulations of trailing-edge noise generation from two-dimensional airfoils at low Reynolds numbers. J. Sound Vib. 2012, 331, 556–574. [Google Scholar]
- Kim, S.H.; Bang, H.J.; Shin, H.K.; Jang, M.S. Composite structural analysis of flat-back shaped blade for multi-MW class wind turbine. Appl. Compos. Mater. 2014, 21, 525–539. [Google Scholar] [CrossRef]
- Kim, S.H.; Shin, H.; Bang, H.J. Bend-twist coupling behavior of 10 MW composite wind blade. Compos. Res. 2016, 29, 369–374. [Google Scholar] [CrossRef]
- Schmitt, F.G. About Boussinesq’s turbulent viscosity hypothesis: Historical remarks and a direct evaluation of its validity. CR Méc. 2007, 335, 617–627. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Lighthill, M.J. On sound generated aerodynamically. 1: General theory. Proc. Roy. Soc. A Math. Phys. Eng. Sci. 1952, 211, 564–587. [Google Scholar] [CrossRef]
- Nitzkorski, Z.; Mahesh, K. A dynamic end cap technique for sound computation using the Ffowcs Williams and Hawkings equations. Phys. Fluids 2014, 26, 115101. [Google Scholar] [CrossRef]
- Brentner, K.S.; Farassat, F. Analytical comparison of the acoustic analogy and Kirchoff formulation for moving surfaces. AIAA J. 1998, 36, 1379–1386. [Google Scholar] [CrossRef]
- Brentner, K.S.; Farassat, F. Modeling aerodynamically generated sound of helicopter rotors. Progr. Aerosp. Sci. 2003, 39, 83–120. [Google Scholar] [CrossRef]
- CD-adapco. Star-CCM+ V11.02 User Guide; CD-adapco: Melville, NY, USA, 2017; pp. 3838–3844. [Google Scholar]
- Baggett, J.S.; Jimenez, J.; Kravchenko, A.G. Resolution requirements in large-eddy simulations of shear flows. Annu. Res. Brief. 1997, 51–66. [Google Scholar]
- Mendonca, F.G.; Kumar, S.B.; Kim, G. Transitional flow and aeroacoustic prediction of NACA0018 at Re = 1.6 × 105. In Proceedings of the 7th AIAA Theoretical Fluid Mechanics Conference (AIAA Aviation Forum (AIAA 2014–2929)), Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Kim, S.H.; Bang, H.J.; Shin, H. Design of Flatback Composite Blade for 10 MW Class Wind Turbine. Available online: http://www.dem.ist.utl.pt/iccst10/files/ICCST10_Proceedings/pdf/Abstracts_web/abstracts_ICCST_2015_ID98.pdf (accessed on 24 June 2017).
- Blake, W.K. Mechanics of Flow-Induced Sound and Vibration; Academic Press, Inc.: Orlando, FL, USA, 1986. [Google Scholar]
- Brooks, T.F.; Pope, D.S.; Marcolini, M.A. Airfoil Self-Noise and Prediction. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19890016302.pdf (accessed on 24 June 2017).
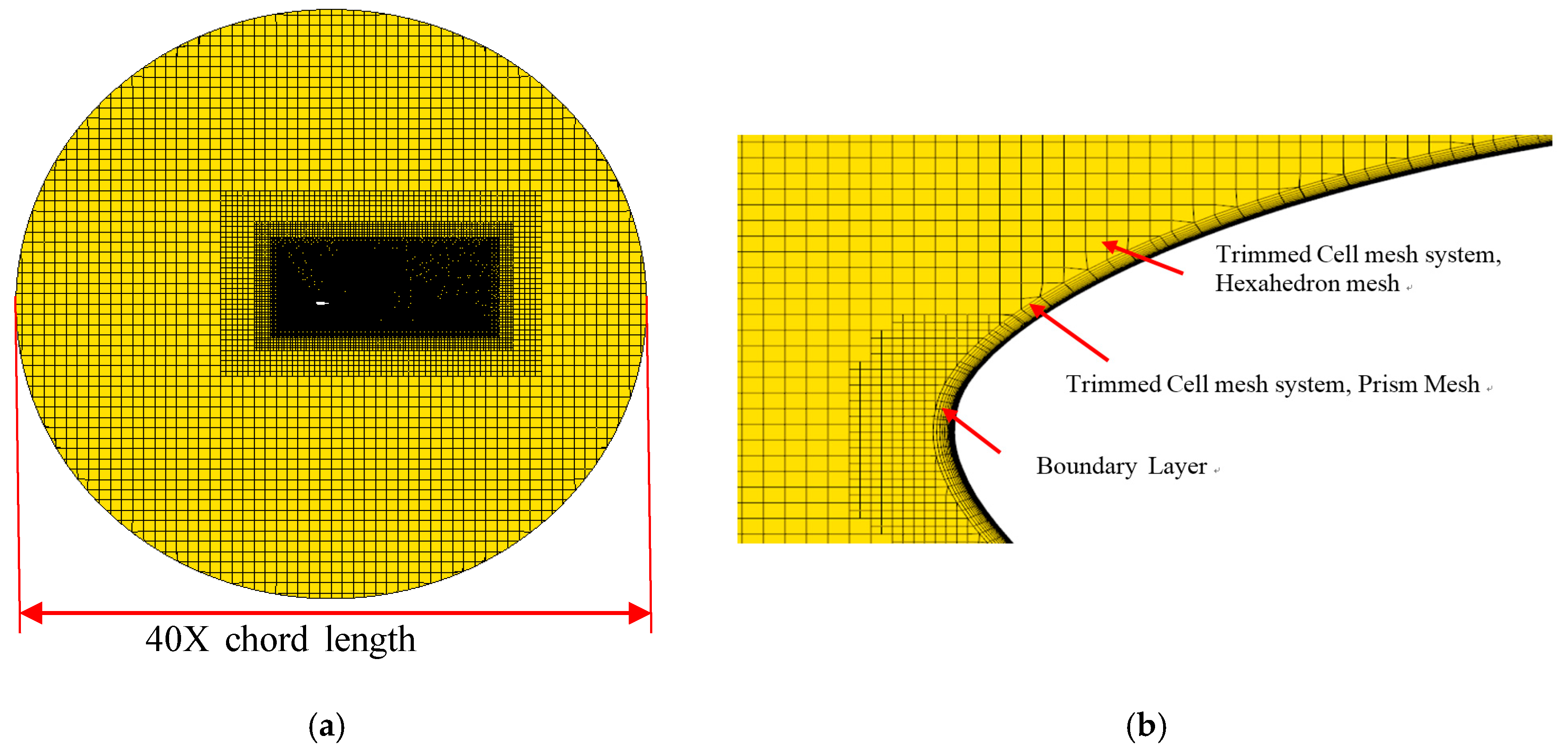
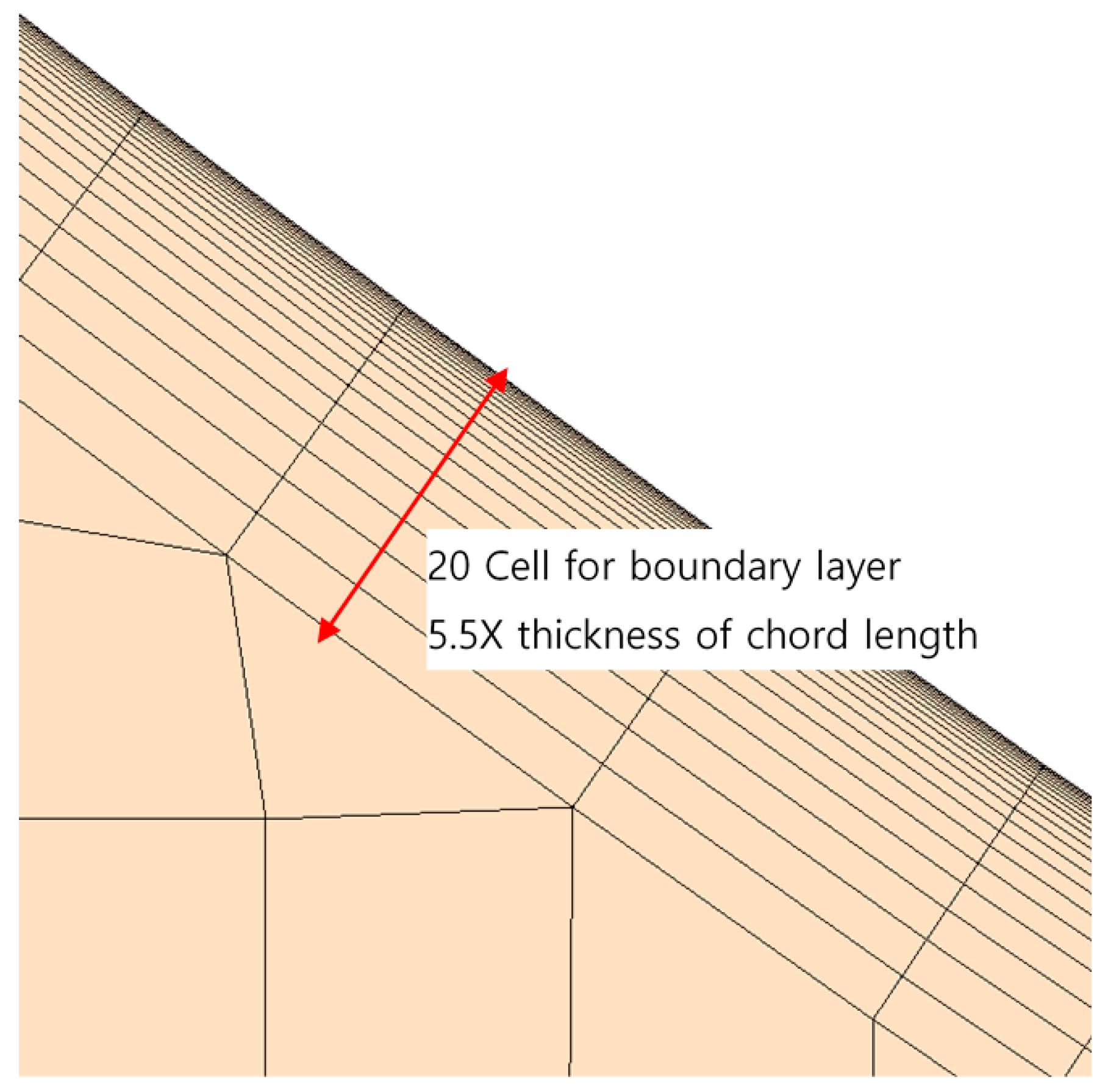

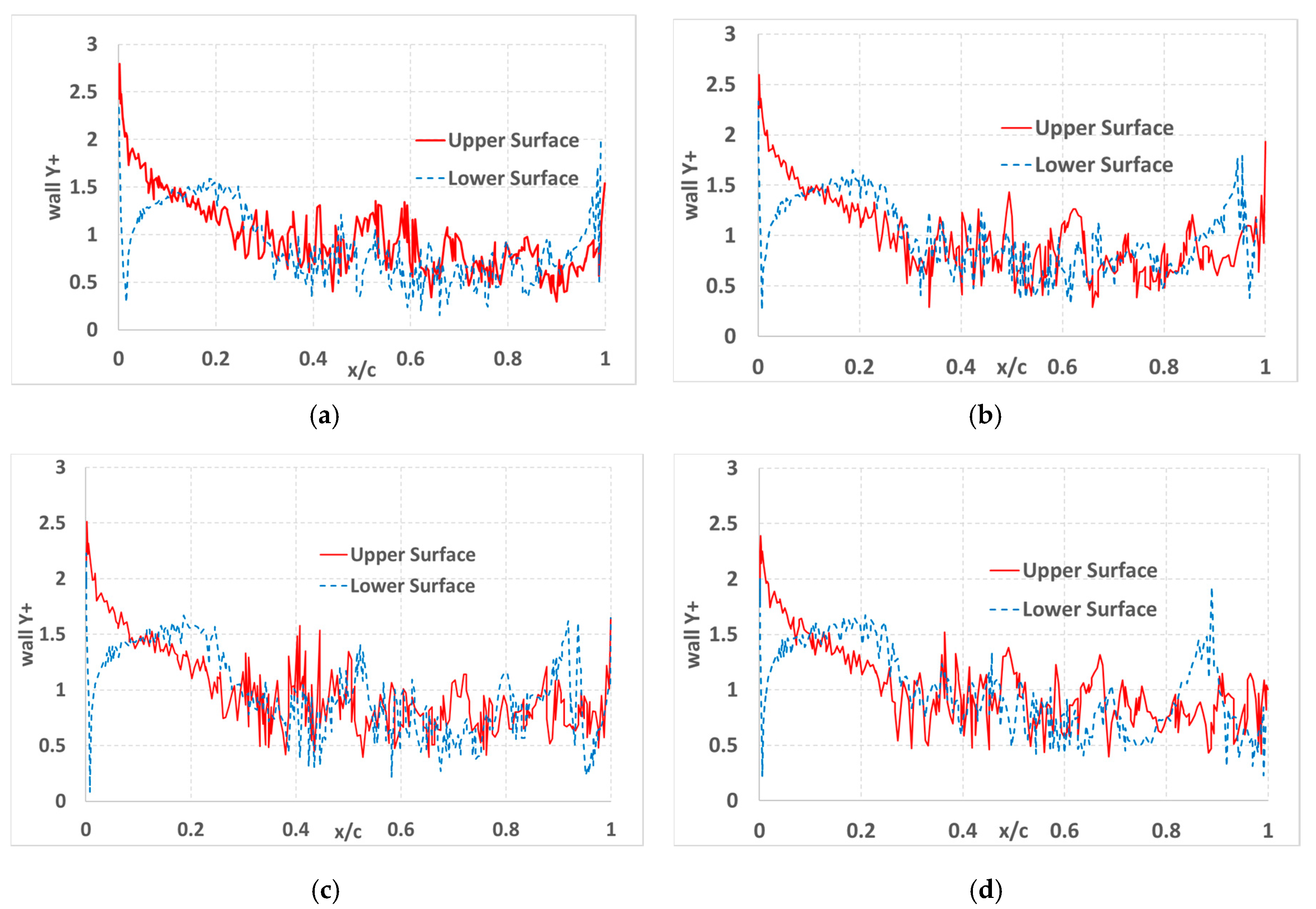





| Layer Number from the Surface Wall | Mid-Chord Region | Leading Edge Region |
|---|---|---|
| No. | dx/dy | dx/dy |
| 1 | 186.7 | 93.3 |
| 2 | 155.6 | 77.8 |
| 3 | 129.6 | 64.8 |
| 4 | 108 | 54 |
| 5 | 90 | 45 |
| 6 | 75 | 37.5 |
| 7 | 62.5 | 31.3 |
| 8 | 52.1 | 26.1 |
| 9 | 43.4 | 21.7 |
| 10 | 36.2 | 18.1 |
| 11 | 30.2 | 15.1 |
| 12 | 25.1 | 12.6 |
| 13 | 20.9 | 10.5 |
| 14 | 17.4 | 8.7 |
| 15 | 14.5 | 7.3 |
| 16 | 12.1 | 6.1 |
| 17 | 10.1 | 5 |
| 18 | 8.4 | 4.2 |
| 19 | 7 | 3.5 |
| 20 | 5.8 | 2.9 |
| Airfoil Name | Sectional Stiffness Based on Flatbak Airfoil (%) | Cl | Peak Noise Level (dB) |
|---|---|---|---|
| Flatback | 100 | 0.98 | 94.2 |
| Oblique60 | 95.8 | 0.79 | 97.7 |
| Oblique45 | 94.6 | 0.72 | 97.9 |
| Oblique30 | 93.6 | 0.66 | 84.8 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, H.; Kim, H.; Kim, T.; Kim, S.-H.; Lee, S.; Baik, Y.-J.; Lee, G. Numerical Analysis of Flatback Trailing Edge Airfoil to Reduce Noise in Power Generation Cycle. Energies 2017, 10, 872. https://doi.org/10.3390/en10070872
Shin H, Kim H, Kim T, Kim S-H, Lee S, Baik Y-J, Lee G. Numerical Analysis of Flatback Trailing Edge Airfoil to Reduce Noise in Power Generation Cycle. Energies. 2017; 10(7):872. https://doi.org/10.3390/en10070872
Chicago/Turabian StyleShin, Hyungki, Hogeon Kim, Taehyung Kim, Soo-Hyun Kim, Soogab Lee, Young-Jin Baik, and Gilbong Lee. 2017. "Numerical Analysis of Flatback Trailing Edge Airfoil to Reduce Noise in Power Generation Cycle" Energies 10, no. 7: 872. https://doi.org/10.3390/en10070872
APA StyleShin, H., Kim, H., Kim, T., Kim, S.-H., Lee, S., Baik, Y.-J., & Lee, G. (2017). Numerical Analysis of Flatback Trailing Edge Airfoil to Reduce Noise in Power Generation Cycle. Energies, 10(7), 872. https://doi.org/10.3390/en10070872






