Hybrid, Multi-Megawatt HVDC Transformer Topology Comparison for Future Offshore Wind Farms

Abstract

With the wind industry moving further offshore, High Voltage Direct Current (HVDC) transmission is becoming increasingly popular. HVDC transformer substations are not optimized for the offshore industry though, increasing costs and reducing redundancy. A suggested medium frequency, modular hybrid HVDC transformer located within each wind turbine nacelle could mitigate these problems, but the overall design must be considered carefully to minimize losses. This paper’s contribution is a detailed analysis of the hybrid transformer, using practical design considerations including component library minimization. The configurations investigated include combinations of single phase H-Bridge and Modular Multilevel Converter topologies operating under minimum switching frequency control strategies. These were modelled in the MATLAB/Simulink environment. The impact of the minimum switching control strategy and converter topology on power transfer stability and overall efficiency is then investigated. It was found that the H-Bridge converter generated the lowest overall losses, but there was a trade off with power flow sensitivity due in part to the additional harmonics generated.

1. Introduction

Over the last decade, the average distance to shore for new wind farms has increased to exploit the higher and more consistent wind conditions, resulting in more High Voltage Direct Current (HVDC) connected wind farms [1,2]. The HVDC substation designs used to date are ill-suited for the offshore environment though. Based on their onshore counterparts, they offer little redundancy and account for 12% of a wind farm’s capital costs [3,4,5], most of which is attributed to the structural and installation costs. To address this, a concept was introduced in [6] to eliminate the offshore substation by modularizing and miniaturizing the electrical equipment to fit within the turbines themselves. This hybrid HVDC transformer was investigated as part of a conference paper in [7], and is now further expanded in this article. As the hybrid HVDC transformer is located within each turbine, the turbines themselves are connected in parallel directly to a HVDC collection grid (Figure 1). The HVDC substations are therefore not required, and the system redundancy is improved. To accommodate the additional equipment within the turbine and simplify its foundation and installation, it is proposed that the hybrid HVDC transformer should operate in the Medium Frequency (MF) range (0.5–2 kHz).

While solid state DC-DC transformers have been proposed to mitigate potential magnetic transformer design complications [8], such as the increased impact of inter winding lamination and capacitances, which are particularly prevalent at high frequencies [9,10], their step ratios are limited. Therefore, a magnetic transformer is required to comply with the Hybrid HVDC Transformer design specifications.

Magnetic, medium frequency power transformers have been investigated in the literature, but have focused on H-Bridge (HB) or full bridge configurations and switching strategies [11,12,13], or the magnetic transformer design assuming a two or three level input [14,15]. Several multilevel converter topologies are available though, including the Neutral Point Clamp (NPC) and Cascade HB (CHB). These present significant advantages over the HB, including lower converter losses and lower Total Harmonic Distortion (THD). However, the NPC is known to be unstable [16], requiring additional, complex circuitry to balance capacitor voltages, and multiple voltage sources are required for the CHB, which are not available within a HVDC network. The Modular Multilevel Converter (MMC) does not suffer from such limitations, and is now the preferred topology for offshore wind HVDC converter stations. While it is widely recognized that the MMC is superior to the HB, the previous works have focused on High Voltage (HV), 3-phase converters connecting to an AC grid [17,18], or have only considered low step ratio transformers [19].

In a practical design, the component library should be minimized wherever possible to reduce both construction and maintenance costs, considerations not made in other analyses. With a high step-up ratio, the primary converter will be subject to a very high current but low voltage stress, while the secondary converter will experience high voltage but low current stresses. Additionally, as the operating frequency of the transformer increases to reduce the overall hybrid HVDC transformer’s size, converter switching losses will become appreciable.

Given these application specific operating conditions, this paper proposes and evaluates three single phase hybrid HVDC transformer configurations, controlled to minimize switching losses and overcome the practical design limitations. These configurations include a HB on both primary and secondary (HB-HB), which lends itself to the high primary side current; an MMC on either side (MMC-MMC), as it is optimized for the high voltage stress of the secondary, and a HB-MMC configuration to investigate the practicality of a hybrid configuration. To constrain the hybrid HVDC transformer’s switching losses while operating in the MF range, Pulse Width Modulation (PWM) has not been used, and a minimal switching frequency module balancing algorithm has been designed for the MMC. This takes advantage of the smaller module capacitance to reduce losses while maintaining stable operation. Operating in single phase minimizes the total switch count, particularly for the secondary side converter, where the arm current is very low compared to the switch’s current rating.

This paper’s contribution is the detailed evaluation of the HB-HB, MMC-MMC, and HB-MMC configurations using simulations in the MATLAB/Simulink environment. These simulations are used to calculate their conduction, switching, and transformer core loss at operating frequencies ranging from 0.5 to 2 kHz. The magnetic transformer design and winding losses are not considered here for brevity however, as they have been calculated in [20]. Furthermore, the ability for each configuration to maintain stable power transfer over the tested frequency range is considered. This will reveal control stability concerns relating to the HB-HB and HB-MMC configurations and inefficiencies in the MMC-MMC case, primarily due to the primary side converter. This will impact on the design considerations for MF transformer design, particularly on the tradeoff between losses and power transfer stability.

The rest of the paper is structured as follows. The MATLAB/Simulink models are described in Section 2. The converter and magnetic transformer loss calculations carried out on the waveforms generated by the computer modules are detailed in Section 3, and the results presented in Section 4. These results are discussed in detail in Section 5, and a conclusion is drawn in Section 6.

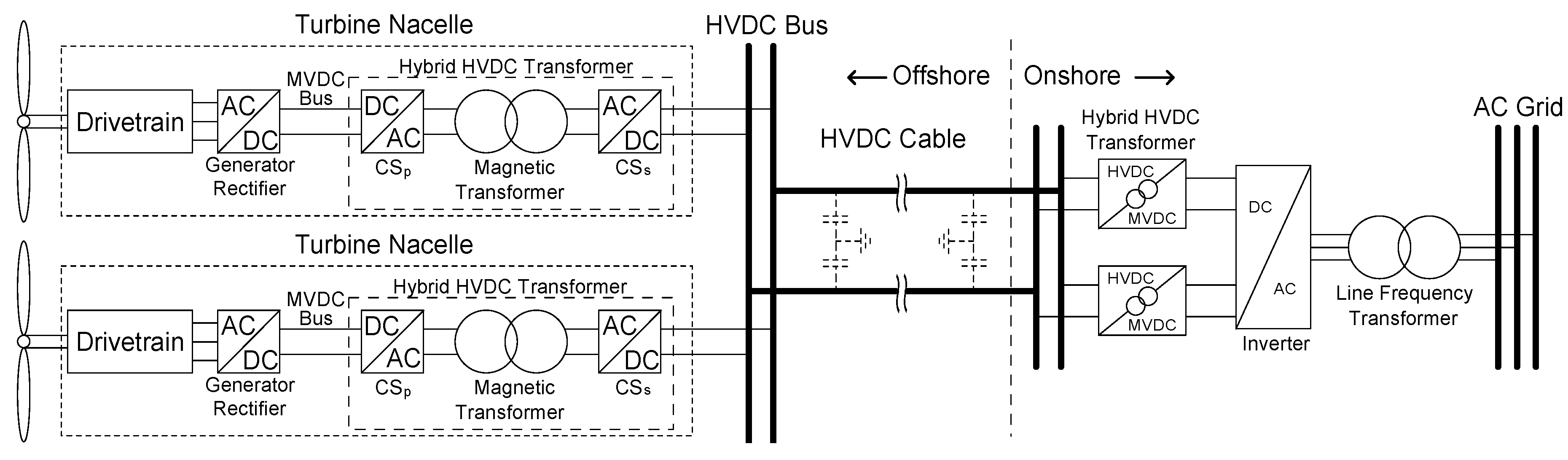
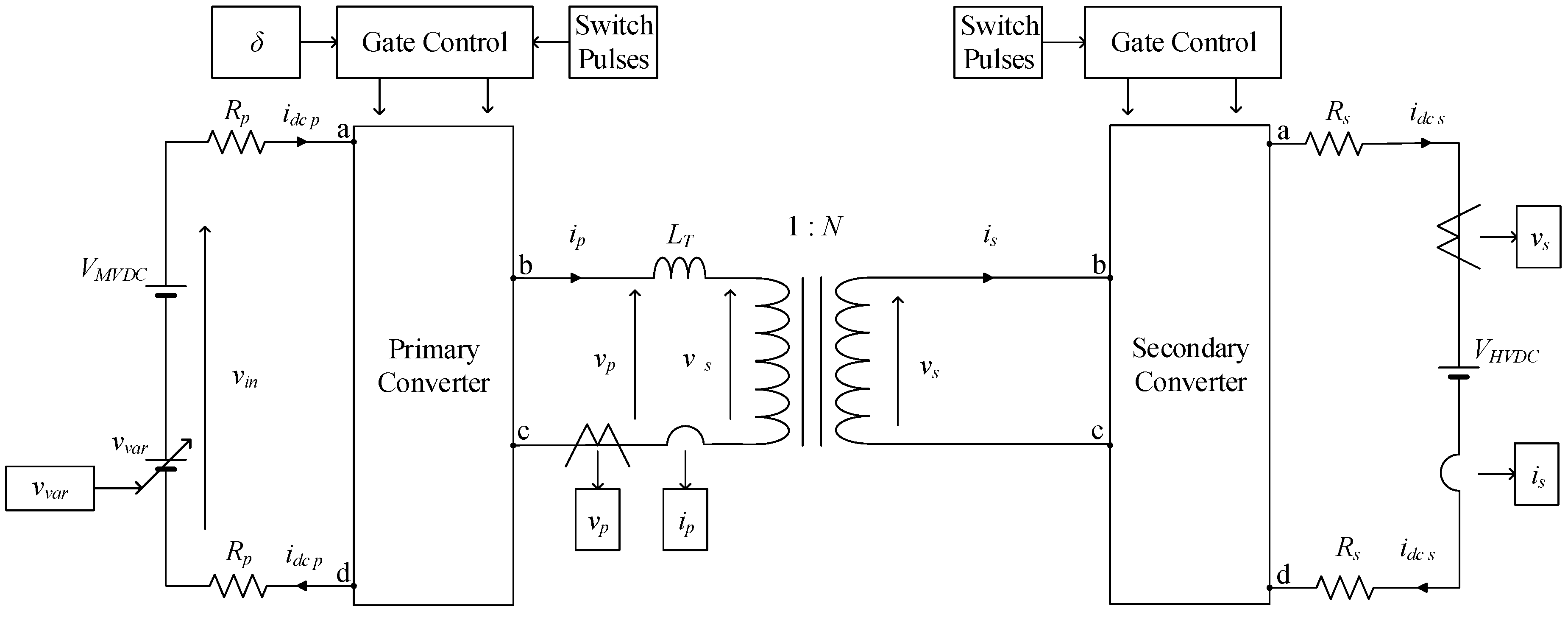
2. Computer Simulation

2.1. Simulation Models

The models were arbitrarily designed for a 6.5 MW wind turbine with a nominal 6 kV Medium Voltage Direct Current (MVDC) bus voltage (v_in) between the fully rated generator rectifier and hybrid transformer (Figure 1). Steady state operation at the rated power was assumed throughout the simulations with the generator rectifier allowing a variable speed turbine operation. The transformer output connects to a ±300 kV HVDC via a shunt connection.

The model used to evaluate the performance of each transformer configuration is shown in generic form in Figure 2, and the converter topologies are shown in Figure 3. In the model, the HVDC bus is assumed to be constant and is modelled using a DC voltage source. In modern wind turbines, the MVDC bus voltage is variable to allow the grid side converter to control reactive power flow. This is reflected in the model by a constant and variable DC voltage source in series, managed by the primary side converter control. The control of the output real power (P_out) and reactive power (Q_T) are governed by the algorithms shown in Figure 4, where voltage (v_p) and current (i_p) inputs are taken at the locations shown in Figure 2. The primary and secondary DC bus resistances are embodied by R_p and R_s respectively, and the magnetic transformer has a turns ratio of 1:100. It is known that the power transferred through the transformer (P_T) is given by (1) for a primary and referred secondary voltage (v_p and v_s′ respectively), transformer reactance (X_T), and load angle (δ).

$$P_T=\frac{v_p{v_s}^{\prime }\sin \left(\delta \right)}{X_T}$$

(1)

Since v_p and v_s′ are fixed by the turbine specifications, the δ range is determined by the transformer inductance (L_T) and should be selected to maintain stable control and allow 6.5 MW to be transferred. Moreover, L_T was designed to prevent high frequency voltage harmonics generated by switching events from showing in the arm current and magnetic flux waveforms, and hence prevent core saturation. With these considerations, L_T lumped on the primary side was chosen to be 0.1 mH.

The different transformer configurations are achieved by inserting one of two topologies (Figure 3) into the primary (CS_p) and secondary (CS_s) converter blocks in Figure 2. Connection points a and d are positive and negative DC bus points respectively, while b and c are the AC live and neutral points. In both converters, each valve is composed of n Insulated-Gate Bipolar Transistors (IGBTs) in series and parallel to withstand the voltage and current stresses. The y Sub Modules (SMs) in the MMC are composed of two valves (V_y and Vx_y) and a module capacitor C_mod.

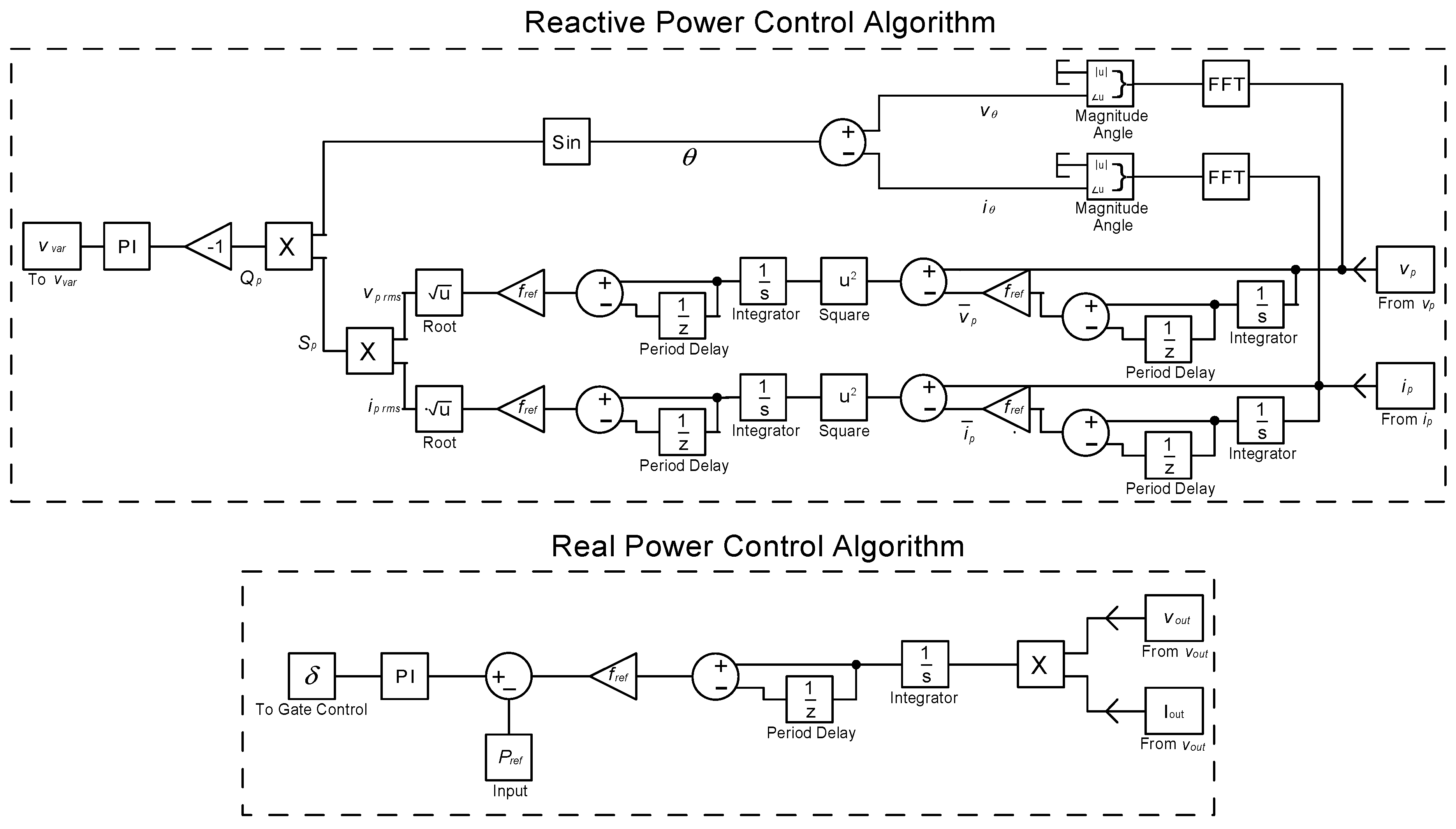
2.2. Active and Reactive Power Control Algorithms

Direct Quadrature Zero (dq0) based control systems are normally used in power converters as they provide stable DC control signals. The voltage and current readings are provided by a Phase Lock Loop (PLL) connected to the grid side, as clean (low Total Harmonic Distortion (THD)) signals are required. While the HB was operated with a 0.33 duty ratio, the induced harmonics were too high for reliable PLL or dq0 based control operation without significant filtering. This impacted both the control response and stability. A single phase control algorithm suitable for all of the converter topologies examined was therefore derived (Figure 4) to ensure consistency. The proposed algorithm contains integrals which have been known to create instabilities; this was mitigated through careful tuning. This control structure was used as it provided a simple method to compare the performance of each converter topology, and while it is included for reference, the focus of this paper is the converter’s performance and not its control.

The primary converter controller was used to govern the power transfer through the hybrid HVDC transformer by comparing the calculated output power (1) to a reference value. The difference was fed into a Proportional Integrator (PI) to calculate the required δ to correct the error in the output power.

$$P_{out}= f_{ref}{{\displaystyle \int }}^{\text{}}{v}_{out}{i}_{out}·dt$$

(2)

The hybrid HVDC transformer should be operated at a unity power factor to maximize efficiency, necessitating the control of reactive power. However, the high THD present in v_p and i_p, particularly in the HB configurations, makes this complicated, as their magnitudes are not accurately calculated by the Fast Fourier Transform (FFT) and the time domain does not directly provide their phase (θ). A combined approach was therefore taken, where θ was calculated using an FFT and time domain calculations were used to determine the apparent power (S_T).

$$S_T=\sqrt{f_{ref}{{\displaystyle \int }}^{\text{}}\left[{\left(v_p{-f}_{ref}{{\displaystyle \int }}^{\text{}}{v}_p·dt\right)}^2·{\left(i_p{-f}_{ref}{{\displaystyle \int }}^{\text{}}{i}_p·dt\right)}^2·dt\right]}$$

(3)

To eliminate any possible DC elements in the v_p and i_p measurements, their means were calculated and subtracted from the recorded values. The reactive power was then calculated from:

$$Q_T=S_T·\sin \left(\theta \right)$$

(4)

A PI was then used to calculate the revised primary DC bus voltage based on the difference between the calculated reactive power and its reference (0 MVar). In practice, the bus voltage is raised by reducing P_out with respect to the power generated, or lowered by decreasing it. However, as the bus is represented by a DC source in the model, its voltage magnitude is raised or lowered to achieve the same effect.

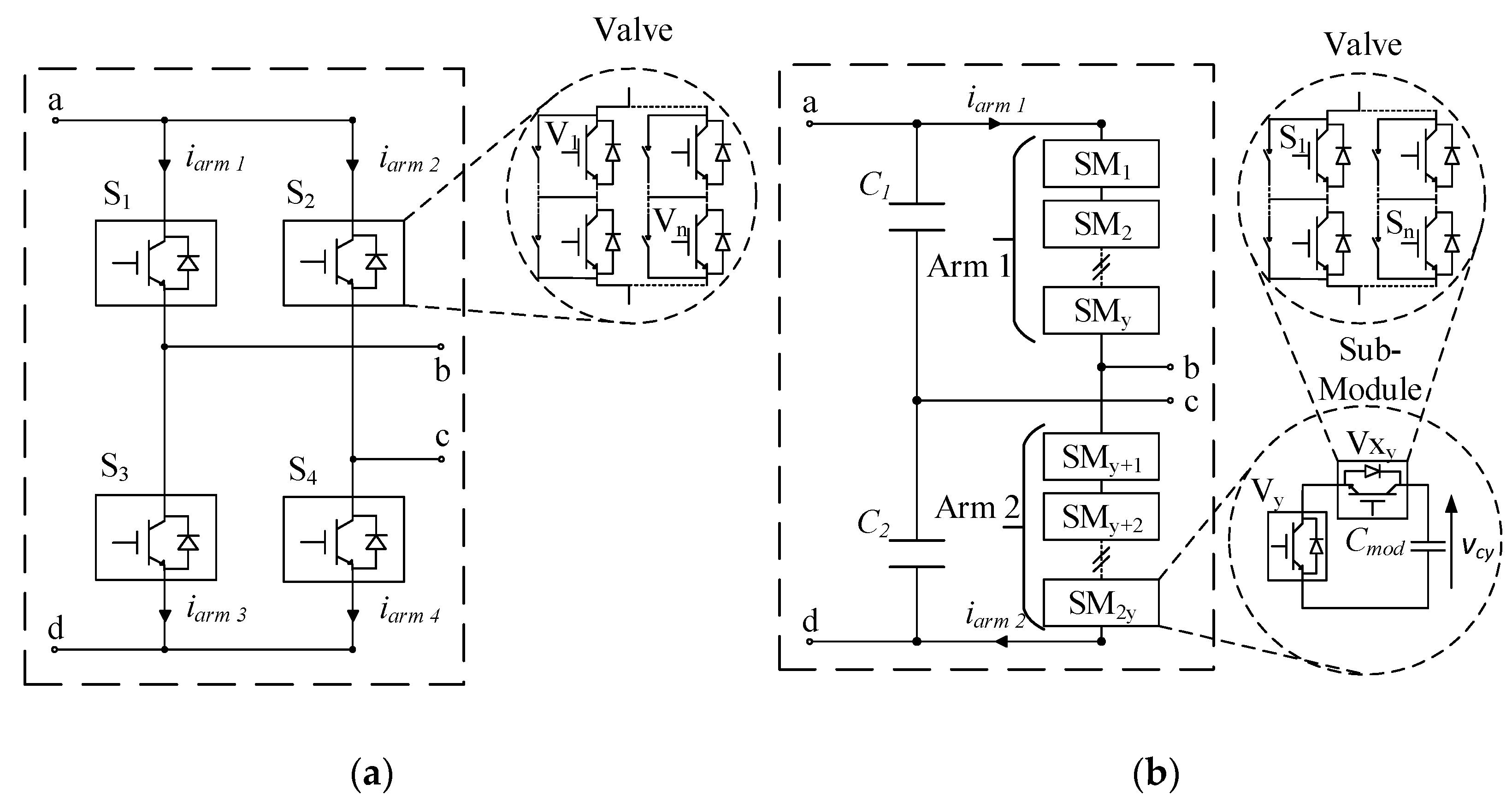
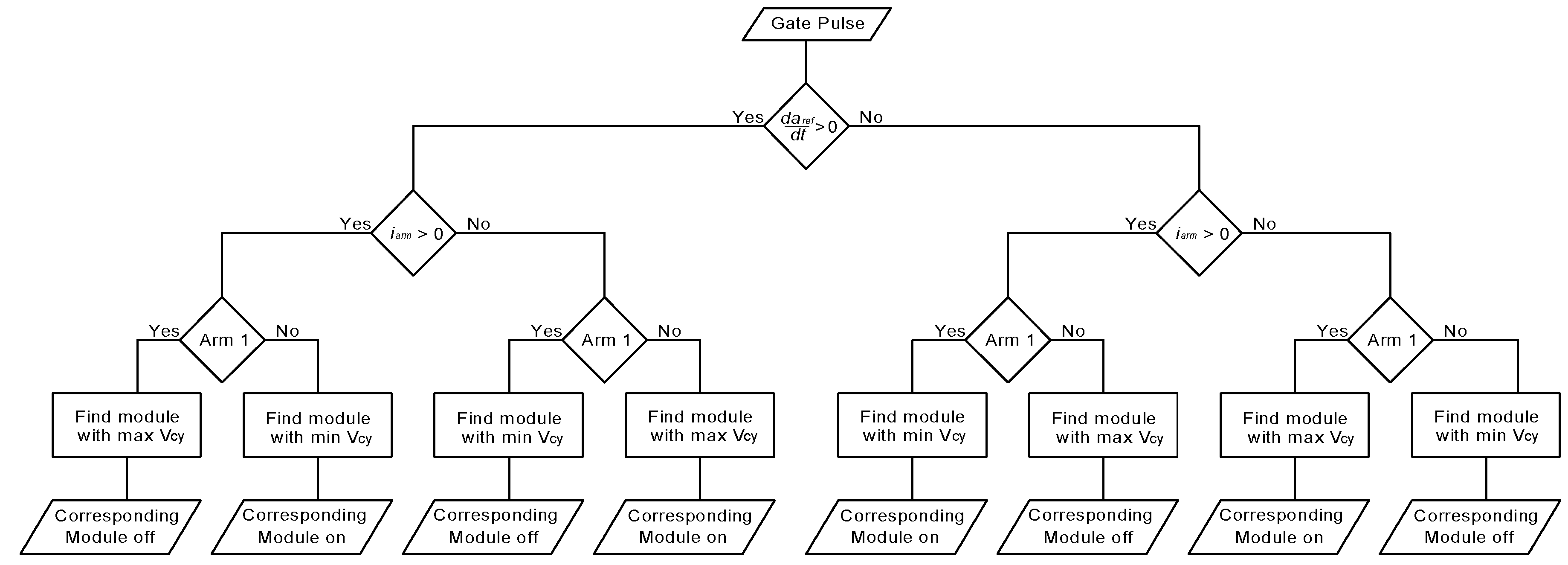
2.3. MMC Control Algorithm

While the same algorithms used for the HB are used to control P and Q, the MMC requires a more complex switching algorithm to balance the module capacitor voltages (v_c). Depending on the direction of the arm current (i_arm), the module capacitors will either charge or discharge when they are switched in or placed in the current path. Modules are switched in when Sx_y is conducting and bypassed when S_y is conducting to create the desired voltage steps. Sx_y and S_y must never both conduct though, or the module capacitor will be short-circuited. Multiple module combinations are possible for each voltage level, apart from the maximum and minimum voltage level (Figure 5).

An algorithm can therefore be devised to provide the desired output voltage waveform while balancing the module capacitor voltages, such that each remains at the average voltage. This algorithm determines the switching strategy of the converter, and hence directly influences the switching losses and quality of the AC and DC waveforms. Algorithms utilizing PWM have been suggested in the literature [21] to improve capacitor voltage balancing, as the instantaneous duty of each module is reduced. The module capacitor voltage remains closer to the average module voltage and DC ripple is minimized. However, this will increase the switching frequency of the converter and increase losses.

As the converters analyzed here are to operate in the MF range, the switching losses for PWM would be too great. That said, the higher switching frequency also reduces the effect of the DC ripple. An alternative control algorithm (Figure 6) has therefore been developed, taking advantage of the reduced DC ripple for the purposes of this study.

The proposed control algorithm reduces switching losses by minimizing the number of switching operations per cycle, while effectively balancing the module capacitor voltages. In the rising interval of the reference waveform, the algorithm searches for, and switches out, the module in Arm 1 with the greatest capacitor voltage when i_arm is positive. If the current is negative, the module with the lowest voltage is switched out. This module is then removed from the selection process until the reference voltage gradient becomes negative. At this point, all of the modules are placed once again into the decision matrix, and if the arm current is positive the module with the lowest voltage is switched in; otherwise, the highest voltage module is used. The algorithm selects the modules in Arm 2 similarly, except the inverse reference voltage gradients are used. In this way, the duty ratio of each module varies between cycles to effectively balance the capacitor voltages. However, each module only switches in and out once per cycle, minimizing switching losses.

3. Transformer Loss Calculation

3.1. Converter Losses

The core, switching, and conduction losses were calculated in MATLAB based on the results generated by the converter simulations. The converter losses were calculated based on the parameters of the chosen IGBT, the Infineon FD300R12KS4_B5 with a rated voltage and current of V_{ce rate} = 1.2 kV and I_{c rate} = 400 A, respectively. This fast switching IGBT was selected as it was found to be the most efficient in the MF range, and was used for both the CS_p and CS_s to simplify their construction and maintenance. In the loss calculation, the junction temperature was assumed to be at the rated value (125 °C), a reasonable assumption since the wind turbine was operating at rated power.

It is known that in semiconductors, the on resistance (R_on) and losses during switching vary with collector current i_c. This relationship was not adequately accounted for by Simulink, so ideal switches were used in the simulations and in the conduction and switching losses calculated later in MATLAB. The switch datasheets provided by the manufacturer were used to derive equations relating i_c to v_ce and the diode forward voltage (v_F) through the use of a curve fitting tool. Combining with the piecewise linear current waveforms from the Simulink models, the conduction loss (P_con) can be calculated as follows:

$$E{S}_{co{n}_y}=n·{\displaystyle \sum }_{i=1}{i}_{c_{y,i}}·v_{c{e}_{y,i}}·T_{step}$$

(5)

$$E{D}_{co{n}_y}=n·{\displaystyle \sum }_{i=1}{i}_F{}_{y,i}·v_{F_{y,i}}·T_{step}$$

(6)

$$P_{con}=\frac{1}{T_{cycle}}·{\displaystyle \sum }_{y=1}E{S}_{co{n}_y}+E{D}_{con}{}_y$$

(7)

where T_step is the length of each time step i, ES_con and ED_con are the conduction energy losses for the IGBT and diode for the y^th valve composed of n IGBTs and antiparallel diodes, and T_cycle is the period over which the energy calculation took place.

A similar method can be used to derive an equation relating the switching (E_IGBT) and reverse recovery (E_Diode) losses for the IGBT and antiparallel diode to I_c or I_F, respectively, to calculate the switching losses. Here, a switching operation is determined to have occurred when I_c or I_F increases or decreases from 0, respectively. The total switching loss (P_switch) can therefore be calculated from:

$$ES{s}_{total}=n·{\displaystyle \sum }_{y=1}{E}_{IGB{T}_y}$$

(8)

$$ED{s}_{total}=n·{\displaystyle \sum }_{y=1}{E}_{Diode}{}_y$$

(9)

$$P_{switch}=\frac{ED{s}_{total}+ES{s}_{total}}{T_{cycle}}$$

(10)

where the IGBT energy loss is given by ESs_total, the diode reverse recovery loss is given by EDs_total, and E_IGBT and E_Diode are the switching and reverse recovery losses for each IGBT, respectively.

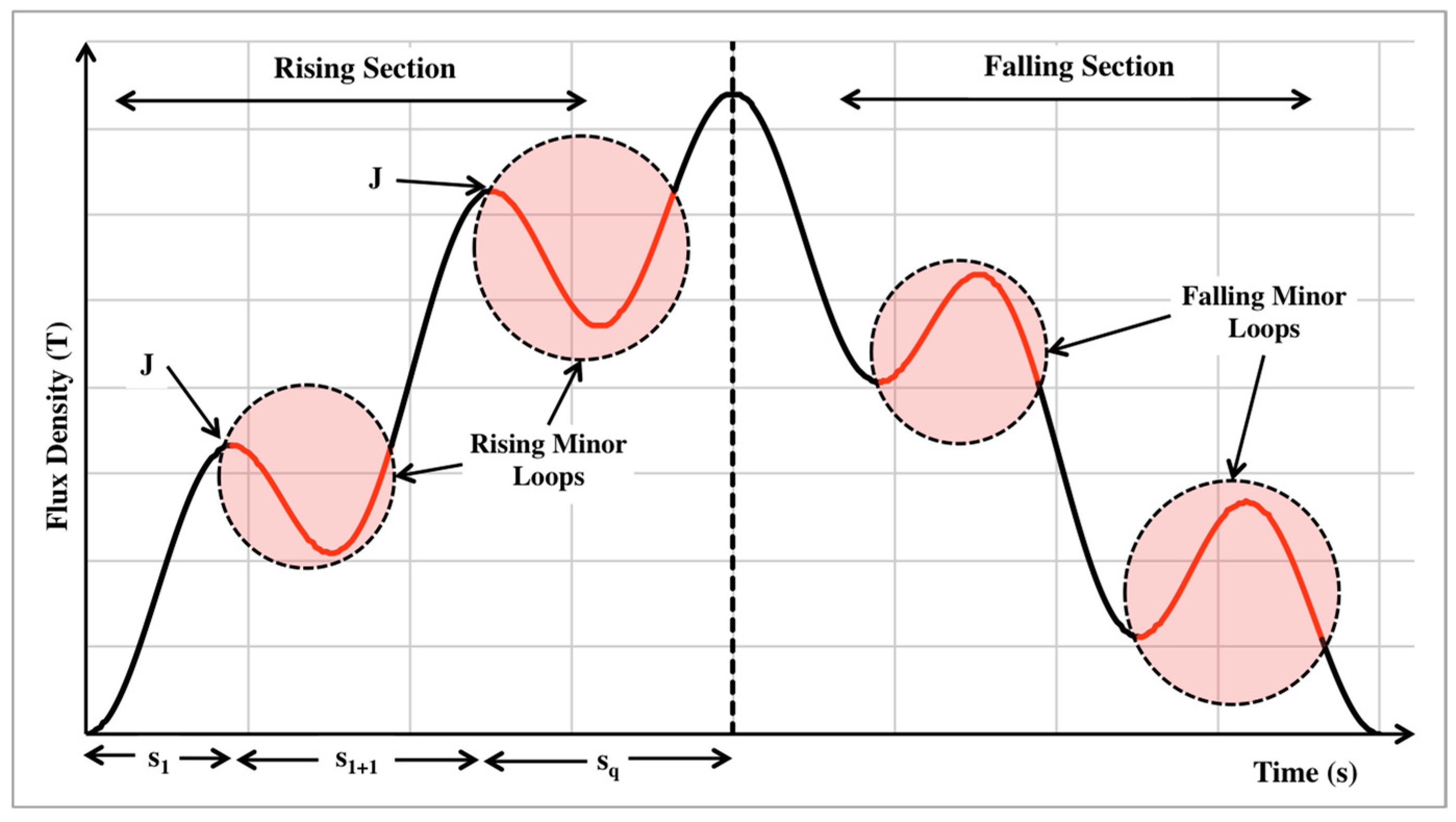
3.2. Core Losses

Magnetics’ Material F was chosen for the magnetic transformer core in the calculations, as this ferrite material has been designed to operate in the MF range. Traditionally, core loss is calculated using the Steinmetz Equation (SE) shown below in (11).

$$p_{core}=k{f}_{ref}^{\alpha }{\widehat{B}}^{\beta }$$

(11)

where p_core is the per volume power loss for the magnetic core, $\widehat{B}$ is the maximum flux density, and k, α, and β are constants collectively named the Steinmetz Parameters. The SE is only valid for sinusoidal flux density waveforms though [22], and so cannot be used in this analysis. The power electric converters on either side of the magnetic transformer create stepped, square voltage waveforms. From (12), it can be seen that flux density is the integral of voltage and so is also non-sinusoidal.

$$B=\frac{1}{N{A}_e}{{\displaystyle \int }}^{\text{}}v\left(t\right)dt$$

(12)

where B is the flux density waveform, N is the number of turns, A_e the effective core area, and v(t) the time varying voltage.

With the proliferation of power electronics applications, many equations now exist in the literature to calculate the core losses emanating from non-sinusoidal flux density waveforms. These can be broadly categorized into three groups: separation of core loss components, macroscopic energy or statistical domain wall calculations, and empirical calculations. That said, the former two groups require parameters not readily provided by core manufacturers, complicating their use [23,24,25].

As the empirical formulae in this group are based on the SE, often only the Steinmetz parameters are required in the calculation. In recent years, the accuracy of this method has greatly improved, particularly after the introduction of the improved General Steinmetz Equation (iGSE) in 2003 [26]. Even so, many in the industry continue to use the SE by taking the Fourier Transform of the waveform (FTSE). The calculated core loss of each harmonic is then summed using vector addition to find the total loss. Due to its simplicity, the FTSE was initially considered over using the iGSE, but later rejected for the reasons detailed below.

In [27], the loss predictions of three empirical formulae including the iGSE, SE, and FTSE were compared to experimentally measured core losses. The iGSE was found to perform best overall for the voltage waveforms tested: sinusoid, distorted sinusoid (10% THD), triangular, 33% duty ratio square, and 50% duty ratio square wave. The accuracy of the FTSE fell significantly for the square wave cases, performing worse than the SE in most situations. Based on this, the iGSE was chosen to calculate the core loss in this study.

A detailed description of the iGSE is given in [26], and only a brief overview of its implementation is given here. The flux density waveform is first split into n_c individual cycles, and then further into its rising and falling sections; i.e., the cycle’s global minimum to maximum and global maximum to minimum, respectively. If there are multiple global maxima or minima, either can be chosen. An example flux density waveform is shown in Figure 7. It has been split into its rising and falling sections, with the minor loops in each identified in red; the black line forms the major loop of the rising and falling sections.

An algorithm, loosely based on rain flow analysis, was used here to identify and separate each minor loop from the major loops. Taking the rising section as an example, the algorithm adds each point in turn to a first set, s₁, until a negative gradient is detected, i.e., point J in Figure 7. A new set is then created (s₁₊₁), and each point is added to this until either the next negative gradient is reached (J’), after which an additional set is created or the end of the section is reached. Each set is then examined, starting at the final set s_q. Any points greater than the set’s initial flux density, i.e., point J’ for the last set in this example or point J for the second set, are moved to the lower set, i.e., s_q−1, until the first set s₁ is reached. Now s₁ contains a monotonically increasing major loop with sets s₁₊₁ to s_q holding each minor loop. The power loss can then be calculated separately for each loop and cycle using (13) and (14).

$$k_{iGSE}=\frac{k}{{\left(2\pi \right)}^{\alpha -1}·2^{\beta -\alpha }{\int }_0^{2\pi }{\left|cos\theta \right|}^{\alpha }d\theta }$$

(13)

$$p_o=\frac{1}{T_o}{{\displaystyle \int }}_0^{T_o}{k}_{iGSE}{\left|\frac{dB}{dt}\right|}^{\alpha }{\left(\Delta B\right)}^{\beta -\alpha }dt$$

(14)

or, as a discrete function:

$$p_o=\frac{k_{iGSE}\Delta B^{\alpha -1}}{T_o}{\displaystyle \sum }_{i=1}{\left|\frac{\delta B_i}{\delta t_i}\right|}^{\alpha }\delta t_i$$

(15)

The total core loss is then determined by a weighted average of the power from each loop, as in (16), and the average loss of all of the cycles of the waveform calculated by applying (17).

$$p_{cor{e}_l}={\displaystyle \sum }_{o=1}{p}_o\frac{T_o}{T_{cycle}}$$

(16)

$$p_{core}=\frac{1}{n_c}{\displaystyle \sum }_{l=1}{p}_{core}{}_l$$

(17)

where p_o is the core loss for each major or sub loop of the l^th cycle, δB_i and δt_i are the change in flux and time between time step i and i−1, and T_cycle and T_o are the periods of the cycle of the o^th loop.

Using the core loss vs. flux density and frequency data from the core manufacturer’s data sheet, the Steinmetz parameters can be calculated from the three dimensional linear regression the logarithm of (11), shown in (18)

$$\ln (p_{core})=K+\alpha \ln \left(f_{ref}\right)+\beta \ln \left(\widehat{B}\right)$$

(18)

where K is the natural log of k. The Steinmetz parameters for the Magnetics F material core were calculated over the 500 Hz to 2000 Hz range to ensure a good fit and are shown in

Table 1. Calculated Steinmetz Parameters.

Frequency Range (Hz)	k	α	β
500–2000 Hz	230.76	1.09	2.81

.

As the magnetic transformer design is outside the scope of this paper, the flux density waveform was derived as follows. The number of primary turns was set at 10 and held constant for each simulation, allowing the flux waveform (θ) to be calculated from (12), given that:

$$\theta =B{A}_e.$$

(19)

Then, assuming the maximum permissible flux density (B_max) is 90% of the core’s saturation flux density (B_sat) and the core volume and hence area should be minimized, A_e can be found from (20).

$$A_e=\frac{\left|\widehat{\theta }\right|}{B_{max}}$$

(20)

The flux density waveform is then merely calculated by rearranging (19).

4. Results

The results from the three hybrid HVDC transformer topologies—comparing the converter and magnetic transformer core efficiencies and control stability—are presented in this section. While winding losses are not considered in the analysis, they have been shown to be small compared to the converter losses, and so have a limited effect on the transformer’s topology [20].

The MMC-MMC topology was run with three different combinations of modules on the primary and secondary converters, while only one combination was run for the HB-HB and HB-MMC topologies. The first MMC-MMC combination (7-11L MMC) consists of a 7 level (7L) CS_p with six modules, as this is the optimum number of Voltage Levels (OVL) at 500 Hz, and was paired with an 11L CS_s. The OVL is defined here as the fewest voltage levels and hence modules required to withstand peak voltage (including safety margin) with only one series connected to the IGBT in each module valve. In the second combination (11-11L MMC), an 11L CS_p was paired with an 11L CS_s to demonstrate the impact of increasing the number of CS_p levels above the minimum requirement to withstand the applied voltage stress. In the third combination (11-25L MMC), an 11L CS_p was paired with a 25L CS_s to investigate increasing the number of CS_s levels. In practice, the CS_s would consist of hundreds of modules to resist the exhibited voltage stress, resulting in the generation of many levels. A very high number of switching elements would be required to generate such a waveform, greatly increasing the computational time for such a model. By limiting the CS_s to 25L and only modelling the IGBT valves in each module (i.e., Figure 8), the model’s run time was greatly reduced while allowing the impact of increasing the number of voltage levels on transformer performance to be investigated. It should be noted that the number of switches within the valves were varied to resist the different voltage and current stresses of each configuration. 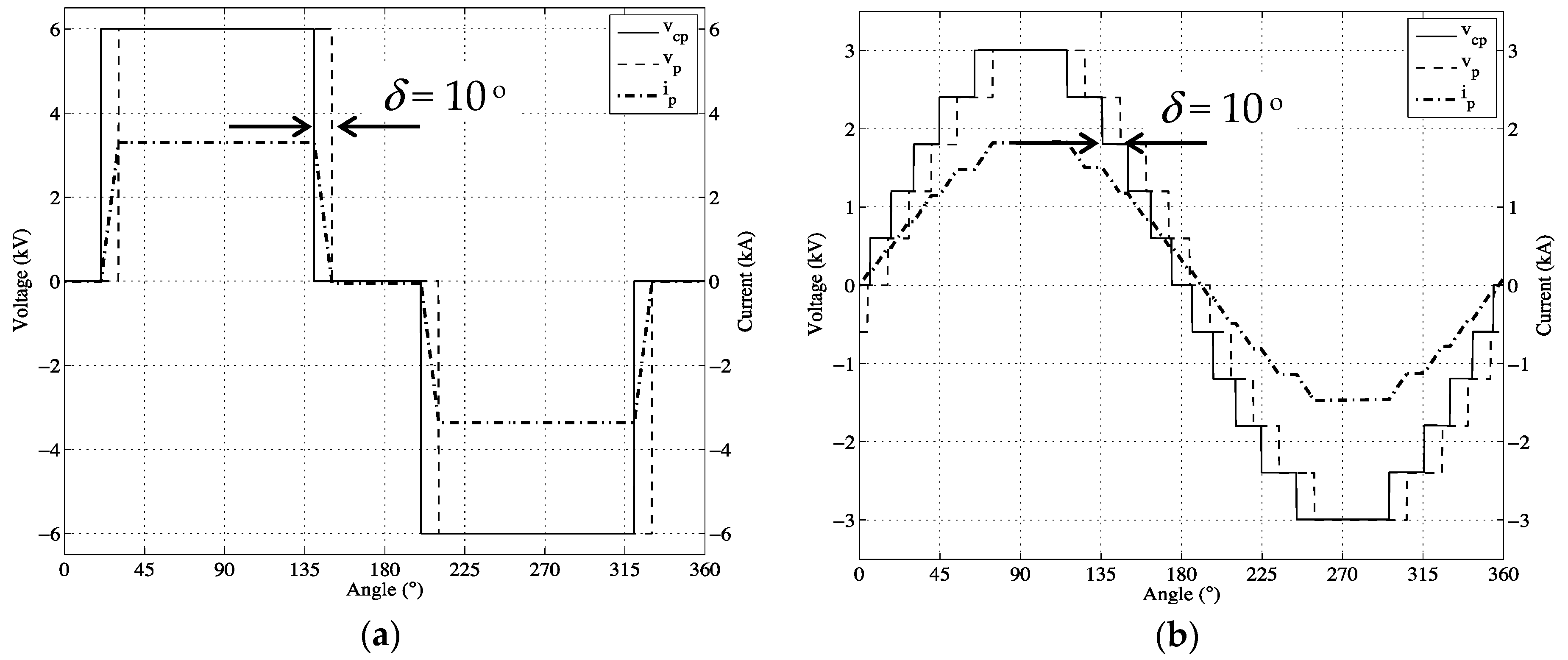This did not impact on simulation time, as only the valves were simulated as the number of switches was only taken into account for the loss calculations.

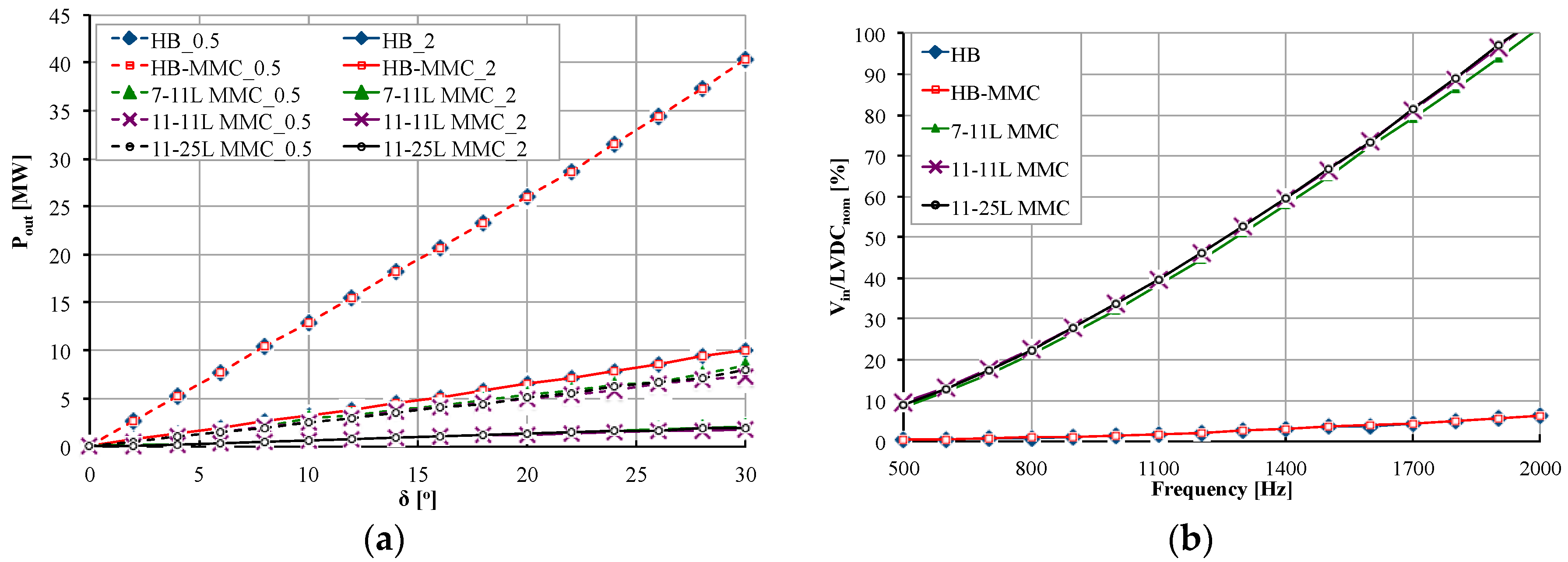
4.1. Power Control

The response of P_out with increasing frequency and δ is shown in Figure 8a for the three topologies operating at 0.5 and 2 kHz. Since the HB-HB and HB-MMC configurations have a higher gradient than the MMC-MMC configuration, it can be said that their control is more sensitive. Therefore, a small deviation in δ can translate to large response in P_out, potentially destabilizing the control, especially in the lower frequency range. While this does improve at higher frequencies, the lower gradient offered by the MMC-MMC configuration provides improved stability across the whole frequency range.

As stated previously, reactive power was controlled in the simulations by increasing or decreasing the primary side bus voltage. As a result, the amount of reactive power support needed for each configuration is indicated by the increase in the MVDC bus voltage above its nominal value. This increase has therefore been plotted in Figure 8b against frequency, and shows that the amount of compensation required increases with frequency for all cases. The MMC-MMC configuration, however, requires significantly more compensation than either the HB-HB or HB-MMC configurations. In the most extreme case, i.e., operating at 2 kHz, the MMC-MMC configuration voltage increases by 110% compared to only 10% in the HB-HB and HB-MMC cases. There is also a marginal increase in reactive power compensation in the MMC-MMC configurations as the number of modules on the CS_p increases, particularly at higher frequencies.

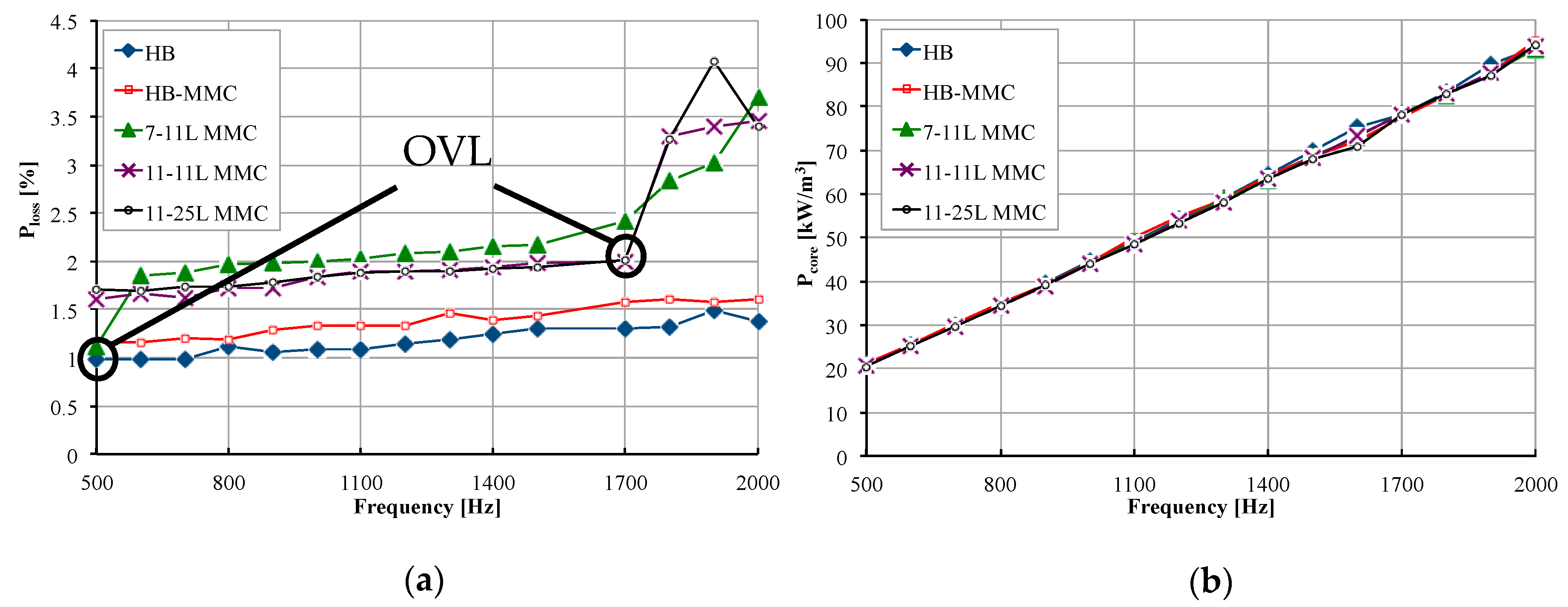
4.2. System Losses

The calculated losses for the magnetic transformer core and the converter are shown in Figure 9 for the whole MF range. The HB-HB and HB-MMC configurations have very similar converter losses, as shown in Figure 9a, and increase fairly linearly with frequency. The losses for the 7-11L MMC configuration are very similar to the HB-HB configuration at 0.5 kHz, but suddenly increase at 0.6 kHz, where they increase linearly up to 1.7 kHz before rapidly increasing again. The losses of the 11-11L and 11-25L MMC configurations also increase linearly up to 1.7 kHz before suddenly rising. This is because as the frequency increases, the MVDC bus voltage also increases (Figure 8b), as well as the voltage stress experienced by each module. Therefore, as the frequency rises, each MMC configuration will approach and fall below its OVL when the number of switches in each valve doubles, significantly increasing converter losses as they become overrated. This occurs at 0.6 kHz for the 7-11L and 1.7 kHz for the 11-11L and 11-25L MMC configurations.

The core losses of all hybrid transformer configurations increase steadily with frequency as shown in Figure 9b. However, while the converter losses differed significantly for each hybrid transformer configuration, the transformer core losses are remarkably similar, although those of the MMC-MMC topologies are marginally smaller.

5. Discussion

The results show the HB-HB and HB-MMC configurations to be less stable than their MMC-MMC counterparts, particularly at lower frequencies, due to two main drivers. Firstly, from Figure 10, a small rise in δ results in large rise of i_p and P_out in the HB-HB configuration. The MMC-MMC configurations have a much lower THD though, resulting in a smaller change in the voltage drop across L_T. The rise in P_out is therefore also smaller, thereby improving the converter’s stability. Secondly, the peak primary voltage created by the HB converter is twice that of the MMC converter. As P_out is calculated from (1) and v_p ≈ v_cp, doubling v_cp means sin δ must reduce by a factor of four to keep P_out constant. Power is therefore more sensitive to small changes in δ. While increasing the number of primary turns—and hence L_T—could mitigate this, e.g., with a turns ratio of 1:100, it would greatly affect the hybrid transformer volume. Given this, the MMC-MMC configuration may prove better at lower frequencies for the given hybrid transformer parameters.

The MMC-MMC requires a lot of reactive power compensation though, due to the large load angle required to transfer the desired real power. This is achieved though increasing the MVDC bus voltage; however, it is envisioned that this would be limited to ±15% of the nominal value, limiting the operational frequency of the MMC-MMC configuration to around 700 Hz. However, this could be improved by decreasing L_T through reducing the number of primary windings, although A_e would have to increase to compensate for the increased flux.

The core losses for all of the hybrid transformer topologies are very similar and small compared to the converter losses. If a core volume of 1 m³ at 500 Hz is assumed, then the core losses would be 0.33% compared to 1% converter loss for the HB-HB configuration. Clearly, converter losses dominate core losses, demonstrating the importance of the converter’s design. While the literature [28] suggests that the MMC configuration has lower losses, this is based on the HB using Pulse Width Modulation (PWM). Without PWM, the HB-HB configuration has fewer losses (1.21% vs. 1.31% at 500 Hz) over the whole frequency range, and hence lower total hybrid transformer losses. The higher efficiency of the HB-HB configuration is considered to outweigh the improved controllability offered by the MMC one, and so is recommended here.

The HB-MMC configuration was only modelled here with a 3L MMC, as at higher voltage levels the harmonic mismatch between the primary and secondary side lead to significant difficulties in power control, particularly at part load. However, if this could be resolved, more voltage levels could be used to increase the transformer’s power stability without increasing converter losses, as the number of levels on the secondary does not influence losses. Additionally, the transformer’s turns ratio can be halved, since ${\widehat{v}}_p=V_{MVDC}$ while ${\widehat{v}}_s=0.5·V_{HVDC}$, and hence possibly reduce the volume and winding losses of the hybrid transformer. Further work will therefore seek ways to mitigate the harmonic mismatch between the 3L primary and nL secondary waveforms.

6. Conclusions

This paper has evaluated three different topologies including the HB-HB, HB-MMC, and MMC-MMC for the hybrid HVDC transformer over the MF range. Using simulations run in the MATLAB/Simulink environment, the converter losses were calculated for each case, and the range and stability of the real and reactive power control determined. The HB-HB configuration was found to be the most efficient configuration, but P_out was very sensitive, particularly at low operating frequencies. The MMC-MMC configuration increased P_out stability, but to improve Q_T control above 700 Hz, the number of transformer windings should be reduced. The higher efficiency of the HB-HB topology is preferred overall, particularly at higher frequencies. However, the MMC-MMC configuration at the OVL may prove beneficial at lower frequencies if the hybrid transformer volume is reduced significantly.

The losses in the HB-MMC converter were calculated to be slightly larger than in the HB-HB configuration; however, the turns ratio was halved. This could reduce the volume of the magnetic transformer and reduce the winding losses. Also, since the number of IGBTs within the valves of the secondary converter are reduced, construction of the converter will be simplified. Further work will focus on improving the THD generated by the primary converter without significantly increasing its losses to mitigate the large difference in THDs between the primary and secondary converters.