Economic Optimization of Component Sizing for Residential Battery Storage Systems
Abstract
:1. Introduction and Related Work
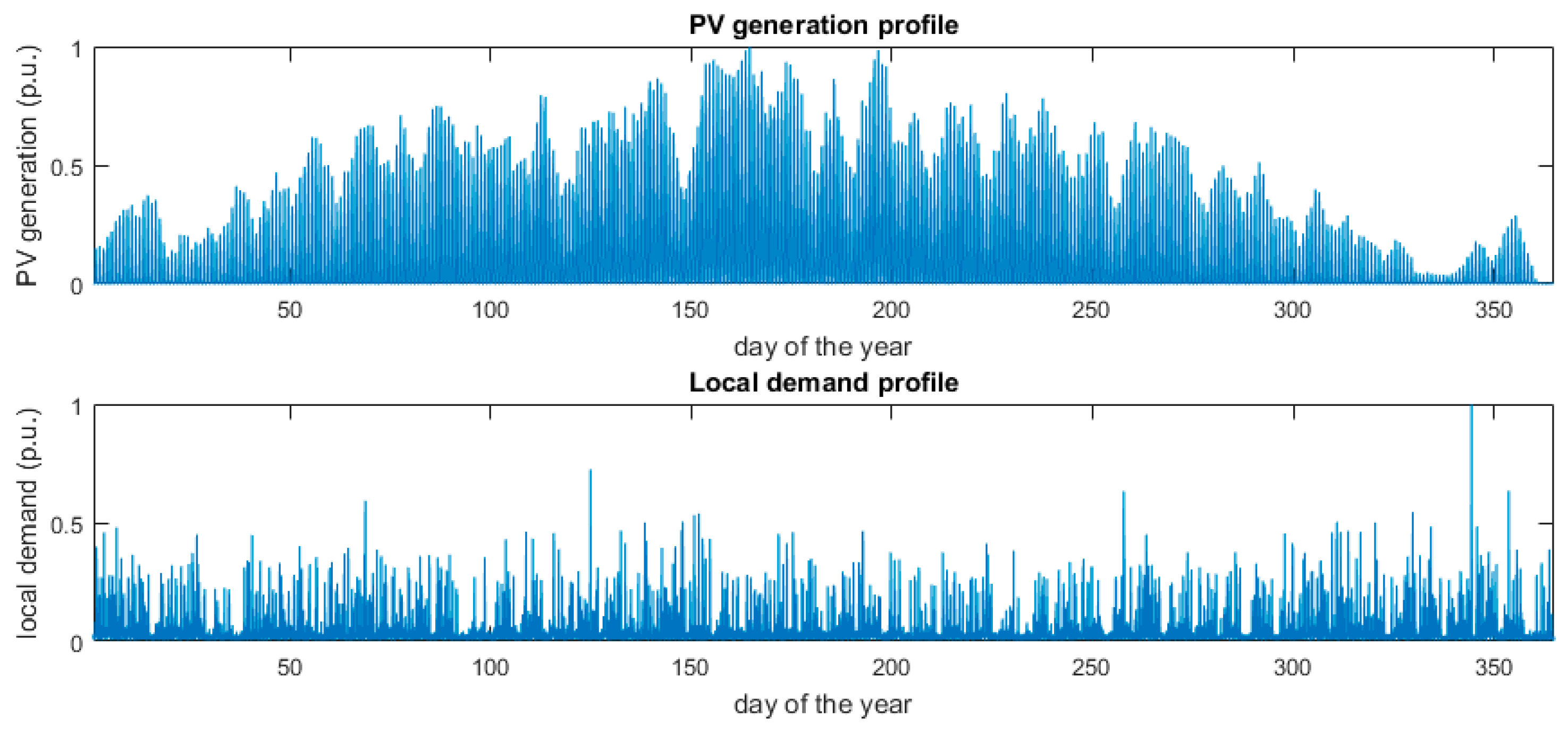
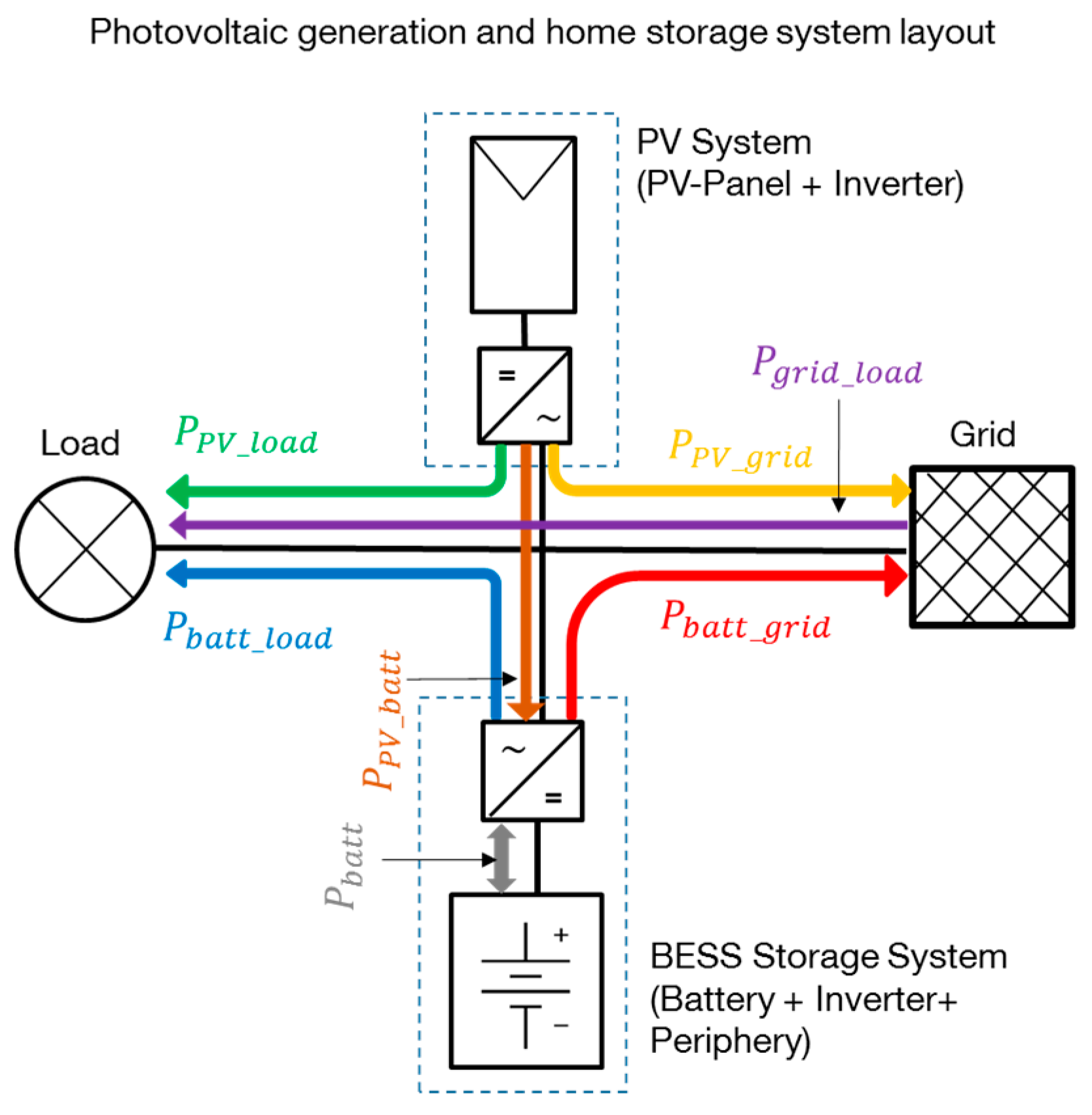
2. Photovoltaic-Battery Energy Storage Systems Layout, Storage Model and Parametrization
2.1. System Layout
2.2. Storage System Technical Parameters, Cost Assumptions and Battery Aging Model
2.3. Economic and Legal Framework for Battery Energy Storage Systems
3. Linear Optimization of Photovoltaic-Battery Energy Storage Systems
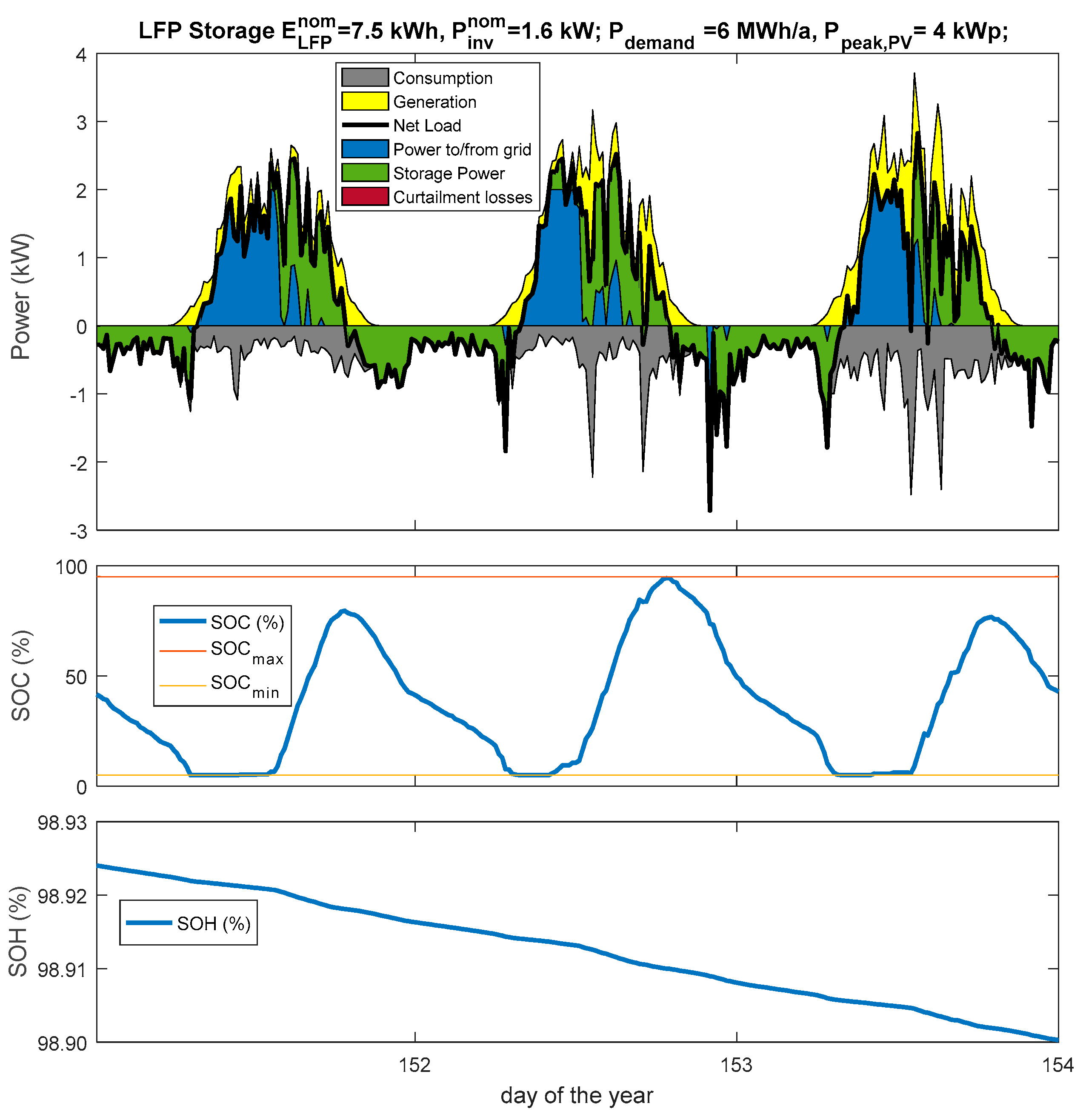
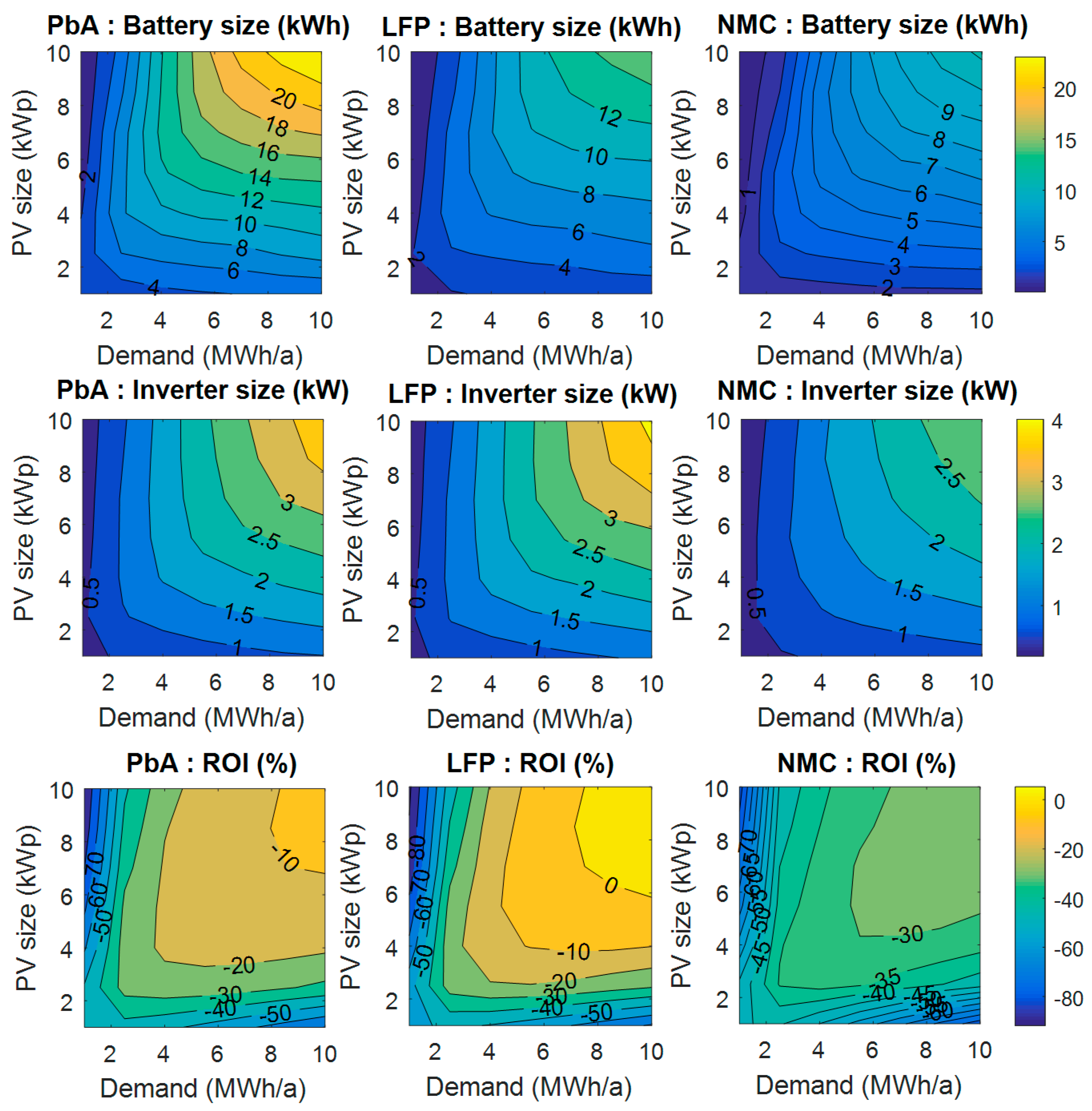
4. Results and Discussion
5. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BESS | Battery energy storage system |
| EOL | End of life |
| LFP | Lithium-ion battery with graphite anode and iron (Fe)-phosphate cathode |
| LP | Linear programming (mixed integer LP) |
| NMC | Lithium-ion battery with graphite anode and nickel-manganese-cobalt cathode |
| PbA | Lead (Pb)-(sulfuric)-acid battery |
| PV | Photovoltaic generator |
| ROI | Return on invest |
| SOH | Battery state of health |
Appendix A
| Parameter | Variable | Unit | PbA | LFP | NMC |
|---|---|---|---|---|---|
| Battery round trip efficiency | % | 85 [41,42] * (80 [43]) | 98 [41,42] * (95 [43]) | 95 [43] ** | |
| Battery self-discharge | %/day | 0.17 [41] (0.2 [1,44] 0.1 [1]) | 0.02 [41,42] * (0.33 [44] 0.1 [1,44]) | 0.02 [45] | |
| Calendric lifetime | (years) | 10 [41] (5 [1] 8 [46]) | 15 [1] (12–20+ [42]) | 13 [44,45] | |
| Cyclic lifetime | FEC | 1500 [46] *** (200–1300 [1,41]) | 10,000 [45] **** (6000 [42,47] 1000–10,000+ [1,48]) | 4500 [29] (700–1000 [49]) |
Appendix B
References
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
- Nykvist, B.; Nilsson, M. Rapidly falling costs of battery packs for electric vehicles. Nat. Clim. Chang. 2015, 5, 329–332. [Google Scholar] [CrossRef]
- Kairies, K.; Haberschusz, D.; van Ouwerkerk, J.; Strebel, J.; Wessels, O.; Magnor, D.; Badeda, J.; Sauer, D. Wissenschaftliches Mess—Und Evaluierungsprogramm Solarstromspeicher: Jahresbericht 2016; Speicher Monitoring: Aachen, Germany, 2016. [Google Scholar]
- Fitzgerald, G.; Mandel, J.; Morris, J. The Economics of Battery Energy Storage. 2015. Available online: http://www.rmi.org/ELECTRICITY_BATTERY_VALUE (accessed on 26 October 2016).
- Naumann, M.; Karl, R.C.; Truong, C.N.; Jossen, A.; Hesse, H.C. Lithium-ion Battery Cost Analysis in PV-household Application. Energy Procedia 2015, 73, 37–47. [Google Scholar] [CrossRef]
- Truong, N.C.; Naumann, M.; Karl, C.R.; Müller, M.; Jossen, A.; Hesse, C.H. Economics of Residential Photovoltaic Battery Systems in Germany: The Case of Tesla’s Powerwall. Batteries 2016, 2, 14. [Google Scholar] [CrossRef]
- Garimella, N.; Nair, N.K.C. Assessment of battery energy storage systems for small-scale renewable energy integration. In Proceedings of the TENCON 2009–2009 IEEE Region 10 Conference, Singapore, 23–26 January 2009. [Google Scholar]
- Quaschning, V. Unabhängigkeitsrechner. 2015. Available online: pvspeicher.htw-berlin.de/unabhaengigkeitsrechner/ (accessed on 9 February 2017).
- Benz, M. Online-Rechner für SENEC.IES Stormspeicher. Available online: www.speicher-rechnen.de (accessed on 4 May 2017).
- Piepenbrinck, A. E3/DC System Calculator. Available online: http://s10.e3dc.com/E3dcWeb/SystemCalculator/syscalc.php (accessed on 4 May 2017).
- Varta-storage GmbH. Varta-Storage Berechnungstool. 2017. Available online: https://www.varta-storage.com/de/produkte/heimspeichersysteme/berechnungstool.html (accessed on 4 May 2017).
- Tesla Motors. The Tesla Home Battery. Available online: https://www.tesla.com/powerwall (accessed on 4 May 2017).
- Mercedes-Benz. Mercedes-Benz Energy Storage. Available online: https://www.mercedes-benz.com/en/mercedes-benz-energy/products/ (accessed on 4 May 2017).
- Nissan. xStorage by Nissan-Clean Power Energy. 2017. Available online: https://www.nissan.co.uk/experience-nissan/electric-vehicle-leadership/xstorage-by-nissan.html (accessed on 4 May 2017).
- Fuhs, M. Marktübersicht Home-Speicher. PV-Magazine 2016, 2016, 35–39. [Google Scholar]
- Hoppmann, J.; Volland, J.; Schmidt, T.S.; Hoffmann, V.H. The economic viability of battery storage for residential solar photovoltaic systems–A review and a simulation model. Renew. Sustain. Energy Rev. 2014, 39, 1101–1118. [Google Scholar] [CrossRef]
- Magnor, D.; Sauer, D.U. Optimization of PV Battery Systems Using Genetic Algorithms. Energy Procedia 2016, 99, 332–340. [Google Scholar] [CrossRef]
- Muenzel, V.; Mareels, I.; Hoog, J.D.; Vishwanath, A.; Kalyanaraman, S.; Gort, A. PV generation and demand mismatch: Evaluating the potential of residential storage. In Proceedings of the 2015 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 18–20 February 2015. [Google Scholar]
- Weniger, J.; Tjaden, T.; Bergner, J.; Quaschning, V. Sizing of Battery Converters for Residential PV Storage Systems. Energy Procedia 2016, 99, 3–10. [Google Scholar] [CrossRef]
- Lauinger, D.; Caliandro, P.; van Herle, J.; Kuhn, D. A linear programming approach to the optimization of residential energy systems. J. Energy Storage 2016, 7, 24–37. [Google Scholar] [CrossRef]
- Merei, G.; Moshövel, J.; Magnor, D.; Sauer, D.U. Optimization of self-consumption and techno-economic analysis of PV-battery systems in commercial applications. Appl. Energy 2016, 168, 171–178. [Google Scholar] [CrossRef]
- Geth, F.; Tant, J.; Haesen, E.; Driesen, J.; Belmans, R. Integration of energy storage in distribution grids. In Proceedings of the 2010 IEEE Power and Energy Society General Meeting, Providence, RI, USA, 25–29 July 2010; pp. 1–6. [Google Scholar]
- Tant, J.; Geth, F.; Six, D.; Tant, P.; Driesen, J. Multiobjective battery storage to improve PV integration in residential distribution grids. IEEE Trans. Sustain. Energy 2013, 4, 182–191. [Google Scholar] [CrossRef]
- Merei, G.; Berger, C.; Sauer, D.U. Optimization of an off-grid hybrid PV-Wind-Diesel system with different battery technologies using genetic algorithm. Sol. Energy 2013, 97, 460–473. [Google Scholar] [CrossRef]
- Schiffer, J.; Sauer, D.; Bindner, H.; Cronin, T.; Lundsager, P.; Kaiser, R. Model prediction for ranking lead-acid batteries according to expected lifetime in renewable energy systems and autonomous power-supply systems. J. Power Sources 2007, 168, 66–78. [Google Scholar] [CrossRef]
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.-C.; Besenhard, J.O.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Sources 2005, 147, 269–281. [Google Scholar] [CrossRef]
- Fuchs, G.; Lunz, B.; Leuthold, M.; Sauer, D.U. Technology Overview on Electricity Storage, Overview on the Potential and on the Deployment Perspectives of Electricity Storage Technologies. 2012. Available online: http://www.sefep.eu/activities/projects-studies/120628_Technology_Overview_Electricity_Storage _SEFEP_ISEA.pdf (accessed on 16 June 2016).
- Schmalstieg, J.; Käbitz, S.; Ecker, M.; Sauer, D.U. A holistic aging model for Li(NiMnCo)O2 based 18650 lithium-ion batteries. J. Power Sources 2014, 257, 325–334. [Google Scholar] [CrossRef]
- Goebel, C.; Hesse, H.; Schimpe, M.; Jossen, A.; Jacobsen, H.-A. Model-based Dispatch Strategies for Lithium-Ion Battery Energy Storage applied to Pay-as-Bid Markets for Secondary Reserve. IEEE Trans. Power Syst. 2016. [Google Scholar] [CrossRef]
- Hesse, H.; Müller, M. Price and Market Trends for Battery Stationary Storage Systems. Unpublished work. 2017. [Google Scholar]
- Photovoltaik4all. Available online: http://www.photovoltaik4all.de/en/wechselrichter (accessed on 7 September 2016).
- Bundesverband der Energie-und Wasserwirtschaft e.V. BDEW Strompreisanalyse Mai. 2016. Available online: https://www.bdew.de/internet.nsf/res/886756C1635C3399C1257FC500326489/$file/160524_BDEW _Strompreisanalyse_Mai2016.pdf (accessed on 4 May 2017).
- Bundesnetzagentur. Dateneldungen und EEG-Vergütungssätze für Photovoltaikanlagen. 2017. Available online: https://www.bundesnetzagentur.de/DE/Sachgebiete/ElektrizitaetundGas/Unternehmen_ Institutionen/ErneuerbareEnergien/Photovoltaik/DatenMeldgn_EEG-VergSaetze/DatenMeldgn_EEG-VergSaetze_node.html (accessed on 4 May 2017).
- KfW Bank. Förderprogram Erneuerbare Energien-Speicher. 2016. Available online: https://www.kfw.de/Download-Center/F%C3%B6rderprogramme-(Inlandsf%C3%B6rderung)/PDF-Dokumente/6000002700_M_275_Speicher.pdf (accessed on 14 July 2016).
- Beck, T.; Kondziella, H.; Huard, G.; Bruckner, T. Assessing the influence of the temporal resolution of electrical load and PV generation profiles on self-consumption and sizing of PV-battery systems. Appl. Energy 2016, 173, 331–342. [Google Scholar] [CrossRef]
- Wenzl, H.; Baring-Gould, I.; Kaiser, R.; Liaw, B.Y.; Lundsager, P.; Manwell, J.; Ruddell, A.; Svoboda, V. Life prediction of batteries for selecting the technically most suitable and cost effective battery. In Selected Papers from the Ninth European Lead Battery Conference; Elsevier: Amsterdam, The Netherlands, 2005; Volume 144, pp. 373–384. [Google Scholar]
- Battke, B.; Schmidt, T.S.; Grosspietsch, D.; Hoffmann, V.H. A review and probabilistic model of lifecycle costs of stationary batteries in multiple applications. Renew. Sustain. Energy Rev. 2013, 25, 240–250. [Google Scholar] [CrossRef]
- Quaschning, V. Representative Electrical Load Profiles of Residential Buildings in Germany with a Temporal Resolution of One Second; HTW Berlin—University of Applied Sciences: Berlin, Germany, 2015. [Google Scholar]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer Science & Business Media: New York, NY, USA, 2006. [Google Scholar]
- Rodway, J.; Musilek, P.; Lozowski, E.; Prauzek, M.; Heckenbergerova, J. Pressure-based prediction of harvestable energy for powering environmental monitoring systems. In Proceedings of the 2015 IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 10–13 June 2015. [Google Scholar]
- Sterner, M.; Stadler, I. Energiespeicher. Bedarf, Technologien, Integration, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- European Society for Clinical Nutrition and Metabolism (ESPEN). Potentiale Elektrochemischer Speicher in Elektrischen Netzen in Konkurrenz zu Anderen Technologien und Systemlösungen (ESPEN); EFZN Project Report; ESPEN: Goslar, Germany, 2016. [Google Scholar]
- Jossen, A.; Weydanz, W. Moderne Akkumulatoren Richtig Einsetzen, 1st ed.; Reichardt: Untermeitingen, Germany, 2006. [Google Scholar]
- Reddy, T. Linden’s Handbook of Batteries, 4th ed.; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Naumann, M.; Keil, P. TUM institute for electrical storage technology internal calendric aging studies. Unpublished work.
- GNB Industrial Power. Handbuch für Verschlossene Gel-Blei-Batterien; Exide Technologies GmbH.: Büdingen, Germany, 2013. [Google Scholar]
- Sony Energy Devices Corporation. Sony Energy Devices Quality, Operations and Management. Available online: http://www.sonyenergy-devices.co.jp/en/csr/quality.php (accessed on 4 May 2017).
- Omar, N.; Monem, M.A.; Firouz, Y.; Salminen, J.; Smekens, J.; Hegazy, O.; Van Mierlo, J. Lithium iron phosphate based battery—Assessment of the aging parameters and development of cycle life model. Appl. Energy 2014, 113, 1575–1585. [Google Scholar] [CrossRef]
- Schuster, S.; Bach, T.; Fleder, E.; Müller, J.; Brand, M.; Sextl, G.; Jossen, A. Nonlinear aging characteristics of lithium-ion cells under different operational conditions. J. Energy Storage 2015, 1, 44–53. [Google Scholar] [CrossRef]
| Application | Type/Focus of Research | References |
|---|---|---|
| Vehicle | Economic analysis | [2] |
| Residential | Market analysis | [3,15] |
| Techno-economic analysis | [5,6,7,16] | |
| Online economic estimation tools | [8,9,10,11] | |
| Size optimization (genetic algorithm) | [17] | |
| Optimization of power flow (dynamic programming) | [18] | |
| Inverter size (sensitivity analysis) | [19] | |
| Co-optimization of electricity and thermal energy flow | [20] | |
| Commercial | Techno-economic analysis | [21] |
| Other/grid level | BESS for distribution grid support | [22,23] |
| BESS microgrid support | [24] | |
| Various/comparison of applications | Technical review | [1] |
| Economic value assessment | [4] |
| Parameter | Unit | Battery Technology | ||
|---|---|---|---|---|
| PbA | LFP | NMC | ||
| Battery round-trip efficiency | % | 85 | 98 | 95 |
| : Self-discharge per day | % | 0.17 | 0.02 | 0.02 |
| (): Usable SOC | % | 50–100% | 5–95% | 5–95% |
| Calendric life indicator in years | (years) | 10 | 15 | 13 |
| Cycle life indicator in FEC | (FEC) | 1500 | 10,000 | 4500 |
| : Variable battery price | €/kWh | 271 | 752 | 982 |
| Fixed price for storage (price for housing, cooling, and periphery) | € | 1182 | 1723 | 580 |
| Inverter Data | Unit | Value |
|---|---|---|
| : Average one way inverter efficiency | % | 97.5 |
| : Assumed inverter lifetime in years | (years) | 20 |
| : Cost of inverter per nominal power | €/kW | 155 |
| Economic and Legal Framework | Variable | Value |
|---|---|---|
| Retail energy price | 28.69 ct€/kWh | |
| Feed-in energy reimbursement tariff | 12.31 ct€/kWh | |
| Maximum feed-in ratio (without BESS subsidy) | 0.7 | |
| Maximum feed-in ratio (with BESS subsidy) | 0.5 | |
| Government subsidy rate for storage systems | 0.22 |
| Battery Modelling Parameter | Variable | Unit | Constraints/Comments |
|---|---|---|---|
| Load demand (historical data) | kW | ; input data | |
| PV power generated (historical data) | kW | ; input data | |
| Nominal power of the battery inverter | kW | subject to optimization | |
| Nominal battery capacity | kWh | subject to optimization | |
| Bidirectional power flow from/to the battery | kW | result of optimization | |
| PV power fed to the load | kW | ; see Equations (8) and (10) | |
| PV power stored in the battery | kW | ; see Equation (8) | |
| PV power exported to the grid | kW | ; see Equation (8) | |
| Power transferred from the battery to the load | kW | see Equation (10) | |
| Power exported from the battery to the grid | kW | ; see Equation (13) | |
| Power imported from the grid to the load | kW | ; see Equation (10) | |
| Surplus power-curtailed according to regulations | kW | ; see Equation (9) | |
| State of health | p.u. | see Equations (18) and (19) | |
| Battery energy content at time i | kWh | see Equations (14) and (15) | |
| State of charge | p.u. | [] |
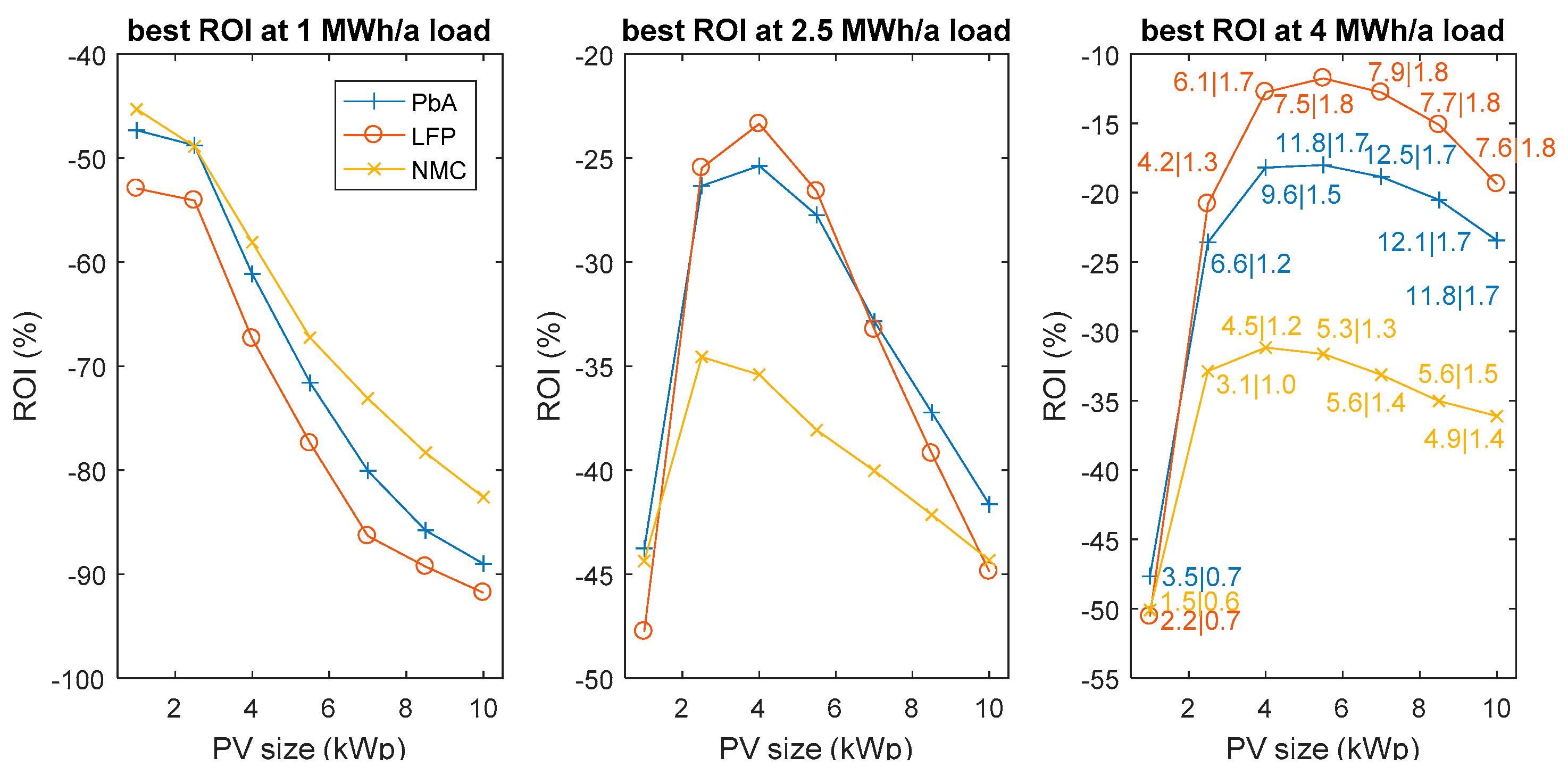
| PV Size (kWp) | 1 | 2.5 | 4 | 5.5 | 7 | 8.5 | 10 |
|---|---|---|---|---|---|---|---|
| PbA battery (kWh) | 3.51 | 6.61 | 9.57 | 11.76 | 12.46 | 12.10 | 11.82 |
| Inverter for PbA system (kW) | 0.67 | 1.18 | 1.55 | 1.69 | 1.73 | 1.72 | 1.69 |
| LFP battery (kWh) | 2.23 | 4.18 | 6.12 | 7.50 | 7.94 | 7.68 | 7.56 |
| Inverter for LFP system (kW) | 0.69 | 1.26 | 1.66 | 1.75 | 1.80 | 1.78 | 1.76 |
| NMC battery (kWh) | 1.52 | 3.10 | 4.51 | 5.27 | 5.60 | 5.63 | 4.89 |
| Inverter for NMC system (kW) | 0.56 | 0.95 | 1.19 | 1.32 | 1.38 | 1.46 | 1.41 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hesse, H.C.; Martins, R.; Musilek, P.; Naumann, M.; Truong, C.N.; Jossen, A. Economic Optimization of Component Sizing for Residential Battery Storage Systems. Energies 2017, 10, 835. https://doi.org/10.3390/en10070835
Hesse HC, Martins R, Musilek P, Naumann M, Truong CN, Jossen A. Economic Optimization of Component Sizing for Residential Battery Storage Systems. Energies. 2017; 10(7):835. https://doi.org/10.3390/en10070835
Chicago/Turabian StyleHesse, Holger C., Rodrigo Martins, Petr Musilek, Maik Naumann, Cong Nam Truong, and Andreas Jossen. 2017. "Economic Optimization of Component Sizing for Residential Battery Storage Systems" Energies 10, no. 7: 835. https://doi.org/10.3390/en10070835
APA StyleHesse, H. C., Martins, R., Musilek, P., Naumann, M., Truong, C. N., & Jossen, A. (2017). Economic Optimization of Component Sizing for Residential Battery Storage Systems. Energies, 10(7), 835. https://doi.org/10.3390/en10070835









